По теме: методические разработки, презентации и конспекты
Подготовка к ЕГЭ по математике. Учебная презентация «Наибольшее и наименьшее значение функции»
В работе приводятся примеры решения задач на исследование функции с помощью производной….
Подготовка к ЕГЭ по математике. Учебная презентация «Объем пирамиды».
Решение задач В-9, В-11…
Подготовка к ЕГЭ по математике. Учебная презентация «Объем цилиндра и призмы».
Решение задач В-9, В-11…
Подготовка к ЕГЭ по математике. Учебная презентация «Экстремумы функции»
Решение В-14…
СЕЧЕНИЕ КОНУСА И ЦИЛИНДРА
В презентации показано поэтапное построение сечений конуса и цилиндра…
Методическая разработка урока математики на тему «Тела вращения: цилиндр, конус, шар»
Методическая разработка урока математики на тему «Тела вращения: цилиндр, конкс, шар» предназначена для студентов СПО, социально-экономического профиля, 1 курс…
Контрольная работа № 2 по теме «Цилиндр. Конус. Усечённый конус. Комбинации цилиндра, конуса и усечённого конуса с многогранниками»
Контрольная работа №2по теме: «Цилиндр.Конус.Усеченный конус…
Презентация по предмету «Математика» на тему: «Решение задач ЕГЭ по теме «Конус» Открытый банк заданий ЕГЭ по математике». Скачать бесплатно и без регистрации. — Транскрипт:
1
Решение задач ЕГЭ по теме «Конус» Открытый банк заданий ЕГЭ по математике
2
Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом В ответе укажите. А О С 30 0
3
Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 3 раза? V = S o H 13 О r h 1 3 h V1V1V1V1 V2V2V2V2
4
Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен V ц =
5
Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на. А О 10 С 6
6
6 Конус получается при вращении равнобедренного прямоугольного треугольника АВС вокруг катета, равного 6. Найдите его объем, деленный на. 6 А В С
7
Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на. О А В С S D
8
Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду? О А В С S D 2 a r Rr
9
Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса V2V2V2V2 1 = V1V1V1V1 V2V2V2V2 h 2 h r2 r
1.
2.
Даны два конуса. Радиус основания и
образующая первого конуса равны
соответственно 3 и 9, а второго — 6 и 9. Во
сколько раз площадь боковой поверхности
второго конуса больше площади боковой
поверхности первого?
Решение:
Т.к. площадь боковой
поверхности конуса: S=πrl.
Значит S1= π·3·9= 27π,
S2= π·6·9= 54π, тогда S2: S1= 54π : 27π = 2
3.
Решить самостоятельно
1) Даны два конуса. Радиус основания и образующая первого конуса
равны, соответственно, 2 и 4, а второго — 6 и 8. Во сколько раз
площадь боковой поверхности второго конуса больше площади
боковой поверхности первого? Ответ: 6
4.
Объём конуса равен 160., Через середину высоты конуса проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.
Решение:
Отношение объемов конусов
равно кубу их коэффициента
подобия. Высоты конусов относятся как 1:2, поэтому их объемы относятся как 1:8.
Следовательно, объем отсекаемого конуса равен 160 : 8 = 20
5. Решить самостоятельно
1) Объём конуса равен 135. Через точку, делящую высоту конуса
в отношении 1:3, считая от вершины, проведена плоскость,
параллельная основанию. Найдите объём конуса,
отсекаемого от данного конуса проведённой плоскостью.
Ответ:5
2) Объем конуса равен 16. Через середину высоты параллельно
основанию конуса проведено сечение, которое является
основанием меньшего конуса с той же вершиной. Найдите
объем меньшего конуса. Ответ:2
3) Объем конуса равен 128. Через середину высоты параллельно
основанию конуса проведено сечение, которое является
основанием меньшего конуса с той же вершиной. Найдите
объем меньшего конуса. Ответ:16
6.
Объём конуса равен 150π а его высота равна 6 . Найдите радиус
основания конуса.
Решение: Найдём радиус основания конуса по формуле:
V=1/3·πR²h
Откуда R²=3V:πh => R²= 150π :
6π = 25. Тогда R=5
7. Решить самостоятельно
1) Объём конуса равен 9π, а его высота равна 3 . Найдите радиус
основания конуса.
Ответ:3
2) Объём конуса равен 25π, а его высота равна 3 . Найдите
радиус основания конуса.
Ответ:5
8.
Во сколько раз уменьшится объем конуса, если его высоту
уменьшить в 3 раза?
Решение: Объем конуса вычисляется по
формуле V=1/3·Socн·h .
Значит, если высоту уменьшить в 3 раза,
то и объём уменьшится в 3 раза
9. Решить самостоятельно
1) Во сколько раз уменьшится объем конуса, если его высоту
уменьшить в 18,5 раза?
2) Во сколько раз уменьшится объем конуса, если его высоту
уменьшить в 24 раза?
3) Во сколько раз уменьшится объем конуса, если его высоту
уменьшить в 10 раз?
10.
Во сколько раз увеличится объем конуса, если его радиус
основания увеличить в 1,5 раза?
Решение: Объем конуса
вычисляется по формуле
V=1/3·Soc.·h = 1/3·πR²·h.
Значит, если радиус основания
увеличить в 1,5 раза, то объём
конуса увеличится в 2,25 раза
11. Решить самостоятельно
1) Во сколько раз увеличится объем конуса, если его
радиус основания увеличить в 40 раз?
2) Во сколько раз увеличится объем конуса, если его
радиус основания увеличить в 22 раза?
3) Во сколько раз увеличится объем конуса, если его
радиус основания увеличить в 31 раз?
12.
Во сколько раз увеличится площадь боковой поверхности конуса,
если его образующую увеличить в 3 раза?
Решение: Площадь боковой
поверхности
конуса
вычисляется по формуле
S= πR·L, где L-образующая.
Значит если увеличить L в 3
раза, то площадь боковой
поверхности
конуса
тоже
увеличится в 3 раза.
13. Решить самостоятельно
1) Во сколько раз увеличится площадь боковой поверхности
конуса, если его образующую увеличить в 36 раз?
2) Во сколько раз увеличится площадь боковой поверхности
конуса, если его образующую увеличить в 11 раз?
3) Во сколько раз увеличится площадь боковой поверхности
конуса, если его образующую увеличить в 1,5 раза?
14.
Во сколько раз уменьшится площадь боковой поверхности конуса,
если радиус его основания уменьшится в 1,5 раза, а образующая
останется прежней?
Решение: Площадь боковой
поверхности конуса вычисляется
по формуле S= πR·L.
Значит, если радиус основания
уменьшится в 1,5 раза, то
площадь боковой поверхности
конуса тоже уменьшится в 1,5
раза.
15. Решить самостоятельно
1) Во сколько раз уменьшится площадь боковой поверхности
конуса, если радиус его основания уменьшится в 8 раз, а
образующая останется прежней?
2) Во сколько раз уменьшится площадь боковой поверхности
конуса, если радиус его основания уменьшится в 36 раз, а
образующая останется прежней?
3) Во сколько раз уменьшится площадь боковой поверхности
конуса, если радиус его основания уменьшится в 21 раз, а
образующая останется прежней?
16.
Высота конуса равна 4, а диаметр основания — 6. Найдите
образующую конуса.
Решение: По теореме Пифагора
Данную презентацию можно использовать при прдготовке к ЕГЭ по математике. Здесь рассматриваются задачи на нахождение образующей конуса, диаметра основания конуса, объема, высоты конуса/
Цель урока: сформировать навык решения задач на нахождение элементов конуса, площади боковой и полной поверхности конуса.
Задачи урока:
- образовательная: обеспечить усвоение знаний по теме;
- воспитательная: эстетическое воспитание (аккуратность, четкость при выполнение чертежей);
- развивающая: способствовать развитию логического мышления: способствовать развитию умения анализировать, сравнивать, делать выводы.
Оборудование: использование ИКТ, раздаточный материал с печатной основой.
Просмотр содержимого документа
«Решение задач по теме «Конус» »
Слайд 1Решение задачи ЕГЭ по темам
«Цилиндр» и «Конус».
Задания части В
Игра
«Загадочный мешочек»
Учитель математики
Максимова Вера
Спиридоновна

Слайд 2Девиз урока:
«Я думаю, что никогда до настоящего времени мы не
жили в такой геометрический период. Все вокруг-геометрия»
Ле Корбюзье.

Слайд 3 Цель: Повторить и обобщить понятия прямого цилиндра и конуса, формулы для
вычисления площади поверхностей и объемов этих тел.
Задачи:
Образовательная : углубить знания учащихся по данной теме, совершенствовать навыки решения задач и подготовиться к ЕГЭ;
Развивающая: развивать умение обобщать, сравнивать, сопоставлять и систематизировать пройденный материал;
Воспитательная: воспитание самостоятельности, последовательности и аккуратности при решении задач;

Слайд 6Задания части В
Площадь поверхности
№ 1, 2 (цилиндр)
№ 3, 4 (конус)
№ 11
(конус)
№ 12 (конус)
Объем
№ 5 (цилиндр)
№ 6 (конус)
№ 7 (цилиндр и конус)
№ 8 (цилиндр и конус)
№ 9 (конус)
№10 (цилиндр)

Слайд 7№ 1,2
Площадь боковой поверхности цилиндра равна 30π. Найдите площадь сечения цилиндра
плоскостью, проходящей через центры его оснований.
Ответ: 30
2. Длина окружности цилиндра равна 2. Площадь боковой поверхности равна 14. Найдите высоту цилиндра.
Ответ: 7

Слайд 8№3 , 4
Высота конуса равна 30, Ɩ длина образующей – 34.
Найдите диаметр основания конуса.
Решение:
Ответ: 32
Площадь полной поверхности конуса равна 90π, а радиус основания равен 5. Найдите высоту конуса.
Ответ: 12

Слайд 9№ 5
Объём первого цилиндра равен 12 м³. У второго цилиндра высота
в три раза больше, а радиус основания в два раза меньше, чем у первого. Найдите объём второго цилиндра (в м³).
Решение

Слайд 10№ 6
Объем конуса равен 6 см³. У второго конуса и высота,
и образующая в два раза больше, чем у первого. Найдите объем второго конуса.
Решение:
Ответ:48

Слайд 11№ 7
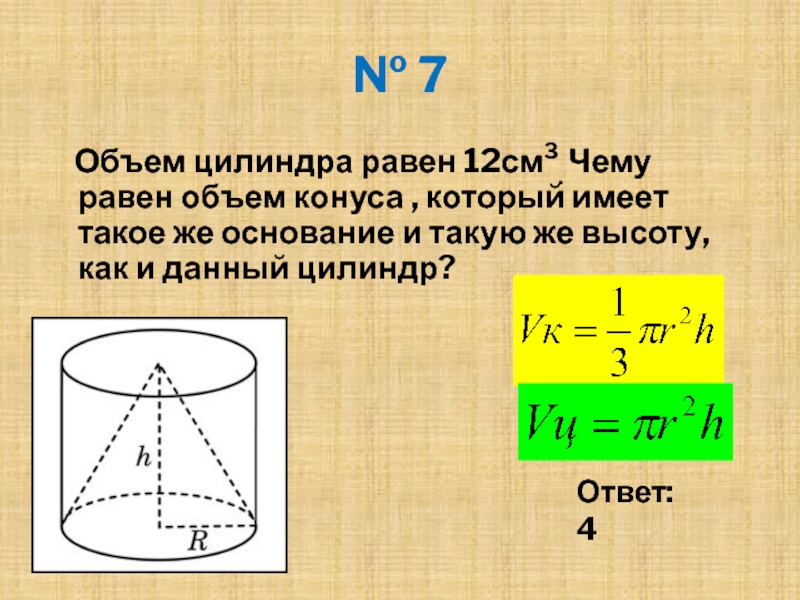
Объем цилиндра равен 12см3. Чему равен
объем конуса , который имеет такое же основание и такую же высоту, как и данный цилиндр?
Ответ: 4
Слайд 12№ 8
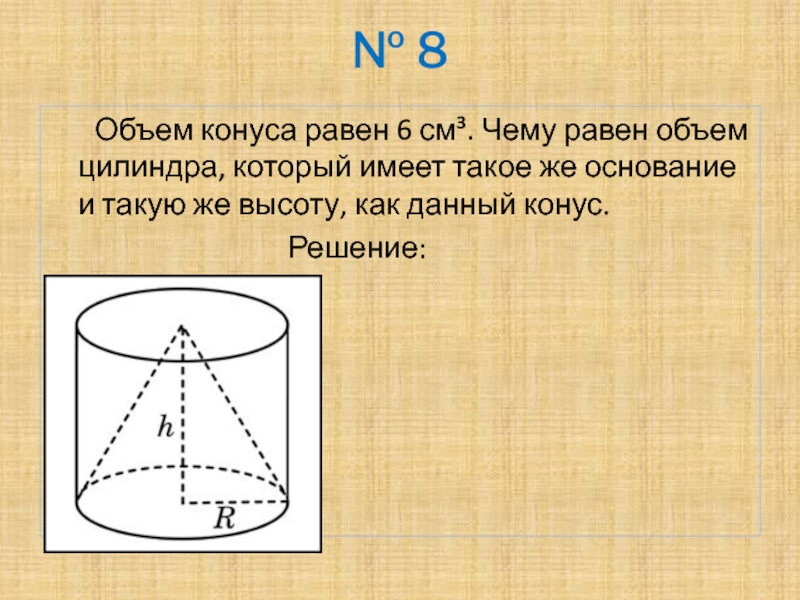
Объем конуса равен 6 см³. Чему равен объем цилиндра,
который имеет такое же основание и такую же высоту, как данный конус.
Решение:
Слайд 13№ 9
В сосуд, имеющий форму конуса, налили 25 мл жидкости до
половины высоты сосуда. Сколько миллилитров жидкости нужно долить в сосуд, чтобы заполнить его доверху?
Решение:

Слайд 14№ 10
В цилиндрический сосуд налили 5000 см³ воды. Уровень воды
при этом достигает высоты 24 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 18 см. Чему равен объем детали? Ответ выразите в см³.
Решение:
Ответ: 3750

Слайд 15№ 11
Объем конуса равен 25π, высота конуса равна 3. найдите площадь
сечения конуса плоскостью, проходящей через его вершину и центр основания.
Решение: 1)
s 2)
r=5 АВ=2∙5=10
B 3)
A Ответ: 15

Слайд 16№ 12
Длина окружности основания конуса равна 8π, высота конуса равна 5.
Найдите площадь сечения конуса плоскостью, проходящей через его вершину и центр основания.
Ответ: 20

Слайд 17Домашнее задание
За решение 3 задач «5»
2 задач «4»
1 задачи «3»

Слайд 18Рефлексия:
теперь я умею…
мне понравилось…
— я хотел бы…

Слайд 20Литература
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Геометрия. 10-11 класс. Базовый и
профильный уровень. М., «Просвещение», 2008.
Самое полное издание типовых вариантов реальных заданий ЕГЭ: 2014: Математика/ авт.- сост.И.Р.Высоцкий, Д.Д.Гущин, П.И.Захаров и др.; под ред. А.Л.Семенова, И.В.Ященко. – М.: АСТ: Астрель, 2013. – (ФИПИ)
ЕГЭ 2014.Математика: сборник заданий/ В.В.Кочагин , М.Н. Кочагина. – М.-Эксмо, 2014.
ЕГЭ 2014.Математика.Типовые тестовые задания/ под ред.А.Л.Семенова, И.В.Ященко. – М.: Издательство «Экзамен»,2014.
ЕГЭ. Математика.Практикум по выполнению типовых тестовых заданий ЕГЭ: учебно-методическое пособие/ Л.Д.Лаппо, М.А.Попов.- М.: Издательство «Экзамен»,2014.

Слайд 21№ 3
Высота конуса равна 30, Ɩ длина образующей – 34. Найдите
диаметр основания конуса.
Решение:
s sB=34 и so= 30
по теореме Пифагора находим 2 катет
oB²= sB²-so²
oB²=1156-900=256=16²
oB=16 AB=16∙2=32
A o B Ответ: 32
В меню

Слайд 22№ 5
Решение:
V₁=12 м³ 12 м³=πR²h
V₂= π∙ ∙h∙3=
∙ πR²h= ∙12=9
Ответ: V₂= 9
Объём первого цилиндра равен 12 м³. У второго цилиндра высота в три раза больше, а радиус основания в два раза меньше, чем у первого. Найдите объём второго цилиндра (в м³).
В меню

Конус. Решение задач
Виды конусов
Круговые конусы: наклонный
и прямой
Усеченный конус: наклонный и прямой
Элементы конуса
Элементы усеченного конуса
Задача 1
Какой фигурой является сечение конуса плоскостью, параллельной основанию?
Ответ: Кругом.
Задача 2
Какой фигурой является осевое сечение: а) прямого конуса; б) наклонного конуса?
Ответ: а) равнобедренным треугольником;
б) треугольником.
Задача 3
Какая фигура является осевым сечением : а) прямого усеченного конуса; б) наклонного усеченного конуса?
Ответ: а) Равнобедренная трапеция;
б) трапеция.
Развертка конуса. Основные формулы
Развертка усеченного конуса. Основные формулы
Задача 4
Радиус основания конуса равен 4 см. Осевым сечением служит прямоугольный треугольник. Найдите его площадь.
Ответ: 16 см2.
Так как в сечении прямоугольный треугольник, а образующие конуса равны, то он равнобедренный.
Радиус конуса 4 см, значит диаметр 8 см, найдем образующую по теореме Пифагора:
Откуда см.
Площадь прямоугольного треугольника равна половине произведения катетов:
см2
А
В
С
Высота конуса 1. На каком расстоянии от вершины надо провести плоскость параллельно основанию, чтобы площадь сечения была равна половине площади основания?
Ответ:
Задача 5
Плоскость, параллельная основанию конуса, делит его на два подобных конуса.
Так как площадь основания меньшего конуса равна половине площади исходного, то квадрат коэффициента подобия этих площадей равен
Тогда
Высоты этих конусов также подобны и соотносятся как коэффициент подобия:
Высота конуса равна 8 м, радиус основания — 6 м. Найдите образующую конуса. Его площадь поверхности и объем.
Ответ: 10 м, м2, м3.
Задача 6
8
6
l
Найдем образующую по теореме Пифагора:
м.
м2
м3
Осевое сечение конуса — равносторонний треугольник со стороной 10 см. Найдите радиус основания и высоту конуса.
Ответ: 5 см, см.
Задача 7
Так как в сечении равносторонний треугольник, то диаметр основания и образующие равны 10 см.
Тогда радиус конуса см.
Найдем высоту из ∆АСН по теореме Пифагора:
см.
А
В
С
Н
Высота конуса равна радиусу основания. Найдите угол при вершине осевого сечения конуса.
Ответ: 90о.
Задача 8
А
Н
В
С
Так как высота конуса равна радиусу, то ∆АСН и ∆ВСН прямоугольные и равнобедренные.
Углы при гипотенузах (АС и ВС) у обоих из них равны по 45о.
В углу при вершине конуса () сходятся два таких угла, значит он равен 45о + 45о = 90о.
Образующая конуса равна 6 м и наклонена к плоскости основания под углом 60°. Найдите площадь полной поверхности и объем конуса.
Ответ: 27 м2, м3.
Задача 9
60о
А
В
Н
6
Значит катет ВН (радиус конуса) равен половине гипотенузы 3 м.
30о
3
Рассмотрим ∆АВН, он прямоугольный, в нем , тогда .
Найдем высоту АН по теореме Пифагора:
м.
Подставляем найденные величины в формулы площади и объема:
м2
м3
Найдите геометрическое место точек конуса, равноудаленных от всех его образующих.
Ответ: Высота конуса.
Задача 10
А
В
С
D
3
6
5
Радиусы оснований усеченного конуса равны 3 см и 6 см, образующая – 5 см. Найдите площадь полной поверхности и объем.
Ответ: см2, см3.
Задача 11
Н
Рассмотрим трапецию ABCD, она прямоугольная. Проведем в ней высоту ВН.
Тогда DH = 3 см, СН = 6 – 3 = 3 см.
3
3
Из треугольника ВСН по теореме Пифагора найдем высоту ВН, которая также является высотой усеченного конуса.
м.
4
Подставляем найденные величины в формулы площади и объема:
см2
см3
В сосуд, имеющий форму конуса, налили 25 мл жидкости до половины высоты сосуда. Сколько миллилитров жидкости нужно долить в сосуд, чтобы заполнить его доверху?
Ответ. 175 мл.
Задача 12
Высота конуса, образующегося из налитой воды равна половине высоты конуса, значит коэффициент подобия этих конусов .
Отношение объемов подобных тел равно коэффициенту подобия в кубе, т. е.
Тогда осталось долить от всего объема конуса.
Нам известно, что всего объема равна 25 мл.
Значит, искомый объем жидкости равен 25 · 7 = 175 мл.
- Найдите площадь полной поверхности и объем усеченного конуса, если он образован вращением прямоугольной трапеции с основаниями 9 и 14 см вокруг меньшей боковой стороны, равной 12 см.
- Объем первого конуса равен 60 м3. У второго конуса высота в три раза меньше, а радиус основания — в два раза больше, чем у первого. Найдите объем второго конуса.
- Радиус основания конуса равен 9 см. Найдите площадь полной поверхности и объем конуса, если осевое сечение конуса равносторонний треугольник.
- Площадь основания конуса равна 64π, а образующая — 10. Найдите площадь полной поверхности и объем конуса.
- В сосуд, имеющий форму конуса, налили 186 мл жидкости до трети высоты сосуда. Сколько миллилитров жидкости нужно долить в сосуд, чтобы заполнить его доверху?
Задачи для самостоятельного решения
Тема урока: «Обобщение по теме «Объём конуса»».
Подготовила:
Балыкина Татьяна Владимировна
учитель математики и физики
МБОУ «Крупецкая СОШ»
Рыльского района
Курской области
Какова связь между этим телом и этой картиной ?
Эта картина называется«Сосновый бор»,её написал художник И.И.Шишкин. Тело, как Вы уже знаете, называется конус. Конус в переводе с греческого языка« konos » означает сосновая шишка.
Тестовые задания (конус)
1)Тело ,ограниченное конической поверхностью и кругом с границей L называется: б) конусом.
2)Установите соответствие между элементами конуса: а) S О- высота б) S А-образующая в) S -вершина г)АО-радиус.
3)Конус может быть получен вращением прямоугольного треугольника вокруг : б) катета.
4)Выбери чертёж с сечением, перпендикулярным оси конуса :б)
Тестовые задания(усечённый конус)
5)Установите соответствие(рис.4):а) ОК -радиус основания в)АР-образующая г)ОО1-высота.
6)Вращением какой трапеции вокруг её боковой стороны может быть получен усечённый конус? б) прямоугольной
Историческая справка
В далеком прошлом, важнейшей задачей египетской и вавилонской геометрии было определение объема различных пространственных тел. Эта задача отвечала необходимости строить дома, дворцы, храмы и другие сооружения. Объемы зерновых амбаров и других сооружений в виде кубов, призм и цилиндров египтяне и вавилоняне, китайцы и индийцы вычисляли путем умножения площади основания на высоту. Однако древнему Востоку были известны в основном только отдельные правила, найденные опытным путем. В более позднее время, когда геометрия сформировалась как наука, был найден общий подход к вычислению объемов многогранников и тел вращения.
Греческие ученые V-IV вв. до н.э., которые разрабатывали теорию объемов:
Архимед
Евклид
Демокрит
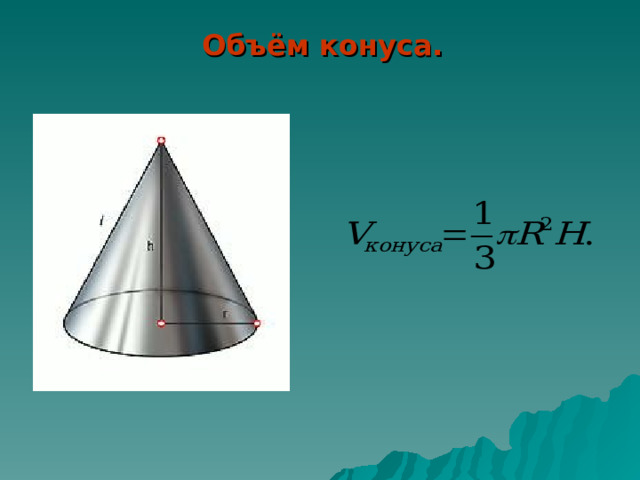
Объём конуса.
Первое доказательство:
Сечение конуса плоскостью, параллельной основанию, подобно основанию. Если плоскость проходит на расстоянии х от вершины, то коэффициент подобия равен
Поэтому площадь сечения такой плоскостью равна:
где S — площадь основания.
Значит, объем конуса К будет:
О
х
x
S сеч
М 1
H
А 1
М
А
S осн
Объём усечённого конуса.
Цели урока:
1)Применить полученные знания при решении задач на нахождение элементов конуса, показать применение формул при решении задач на нахождение объёмов , приобрести опыт решения задач по теме «Объём конуса»
из ЕГЭ;2) способствовать развитию творческой активности обучающихся; 3)формировать внимательность в вычислениях, аккуратность в записях.
Решите задачи:
- Вычислите объём конуса, если его высота 6 см, а площадь основания 42 см 2 .
- Объём конуса с радиусом основания 4 м и высотой 6 м равен:
- Вычислите объём усеченного конуса, высота которого 3 см, а площадь оснований 16 см 2 и 4 см 2 .
Вычислите объём усеченного конуса, если радиусы его оснований равны 3 см и 9 см, а высота 6 см.
Задачи для самостоятельного решения:
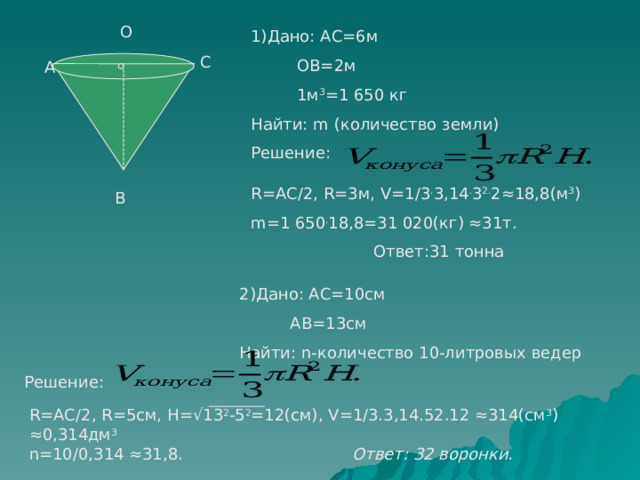
Задача 1. Авиационная бомба среднего калибра дает при взрыве воронку диаметром 6 м и глубиной 2м. Какое количество земли (по массе) выбрасывает эта бомба, если 1м 3 земли имеет массу 1650 кг?
Задача 2. Смолу для промышленных нужд собирают, подвешивая конические воронки к соснам. Сколько воронок диаметром 10см с образующей 13 см нужно собрать, чтобы заполнить десятилитровое ведро?
О
1)Дано: АС=6м
ОВ=2м
1м 3 =1 650 кг
Найти: m (количество земли)
С
А
Решение:
R =АС/2, R=3 м, V =1/3 . 3,14 . 3 2. 2≈18,8(м 3 )
m =1 650 . 18,8=31 020(кг) ≈31т.
Ответ:31 тонна
В
2)Дано: АС=10см
АВ=13см
Найти: n -количество 10-литровых ведер
Решение:
R =АС/2, R =5см, H =√13 2 -5 2 =12(см), V =1/3.3,14.52.12 ≈314(см 3 ) ≈0,314дм 3
n =10/0,314 ≈31,8. Ответ: 32 воронки.
Профилактическое упражнение для глаз «Буратино»
Закрыть глаза и представить, что нос вырос , как у Буратино. Мысленно обмакнуть его , как сказке А.Н. Толстого «Золотой ключик или приключения Буратино»,в чернила и написать как можно красивее носом в воздухе число «пи»( ϖ),но сделать мысленно или движением головы. Зафиксировать перед глазами записанное число. Запомнить.
«Знаете ли , Вы…»
«Конусами» называется род брюхоногих моллюсков отряда переднежабренных, группы стрелоязычных, семейства конусовых. Раковина коническая (2-16 см), ярко окрашенная. Конусов свыше 520 видов. Живут в теплых морях, особенно в Вест–Индии и около Америки. Некоторые съедобны, другие ценятся благодаря красоте раковины.
В геологии существует понятие «конус выноса». Это форма рельефа, образованная скоплением обломочных пород (гальки, гравия, песка), вынесенными горными реками на предгорную равнину или в более плоскую широкую долину.
В биологии есть понятие «конус нарастания». Это верхушка побега и корня растений, состоящая из клеток образовательной ткани .
Дифференцированная самостоятельная работа
Группа 1(профильный уровень)
Вариант 21 №5
1)Цилиндр и конус имеют общие основание
и высоту. Объём цилиндра равен 162см³.
Найдите объём конуса.
Группа 2(базовый уровень)
Вариант 10 №16
2)Объём конуса равен 12 ϖ ,а радиус его основания равен 3.Найдите высоту.
Объём конуса равен 12п,а радиус его
основания равен 3.Найдите высоту конуса1
Практическое применение
1)конические детали в машинах и механизмах;
2)конические шестерни в танках, автомобилях, бронетранспортёрах;
3)носовые части самолётов, ракет;
4)конические поверхности домов, замков.
Домашнее задание
И.В.Ященко Математика . Типовые экзаменационные варианты. Издательство «Национальное образование»,2022
Базовый уровень Вариант 11
Профильный уровень Вариант 22
Итоги урока . Рефлексия.
Оцени себя и сделай для себя вывод о пользе проведенного на уроке времени . На полях в конце записей поставьте оценку: 1) Я доволен уроком, мне очень понравилось , я всё понял(а);
2)Мне понравился урок , но в моих знаниях есть пробелы;
3)Я не доволен уроком , ничего не понял(а) и как решать , я не знаю.