Объем многогранника формула в11 егэ

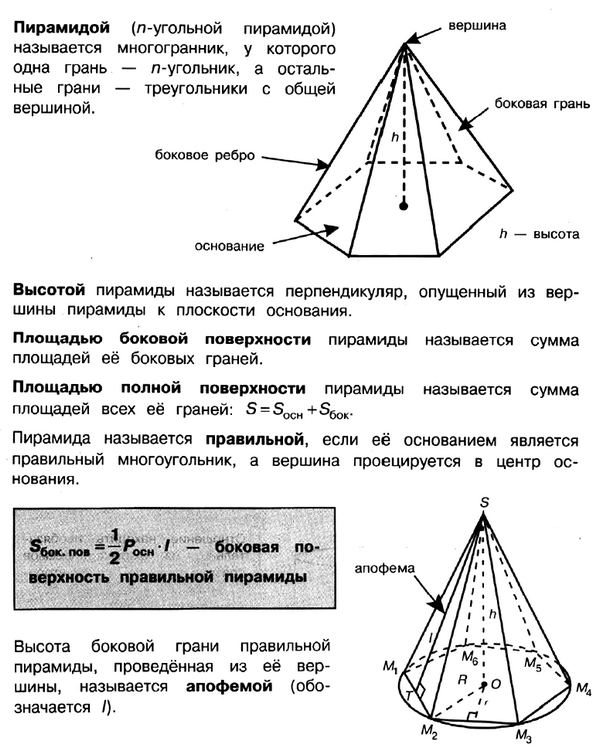
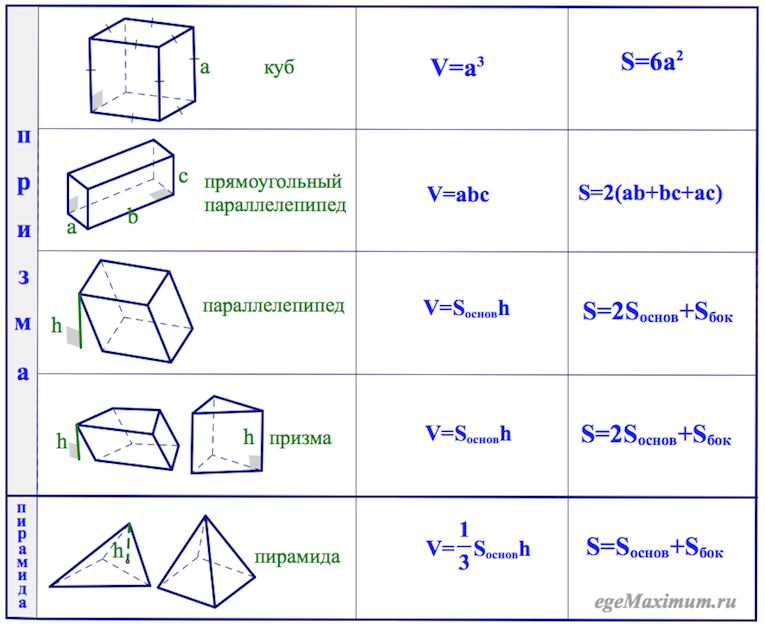
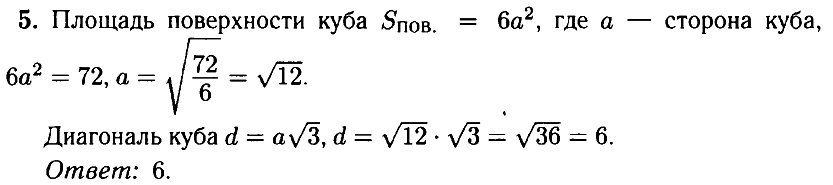Формулы объёма и площади поверхности. Многогранники.

Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:

1. Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
2. Элементарная логика.

Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.

Куб		диагональ
Параллелепипед	высота
Прямоугольный параллелепипед
Призма
Пирамида

Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».

Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.

Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.

Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.

Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.

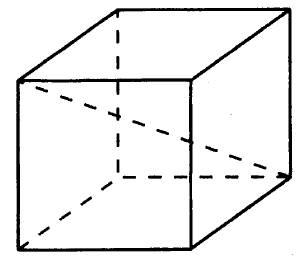
Задача 1.Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Решение:

Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб

Очевидно, их 6, поскольку у куба 6 граней.

Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше — читайте о приемах решения задач по стереометрии.

Разберем задачи, где требуется найти площадь поверхности многогранника.

Мы рассмотрим призмы и пирамиды. Начнем с призмы.

Площадь полной поверхности призмы можно найти как сумму площадей всех ее граней. А это площади верхнего и нижнего оснований плюс площадь боковой поверхности.

Площадь боковой поверхности призмы – это сумма площадей боковых граней, которые являются прямоугольниками. Она равна периметру основания, умноженному на высоту призмы.

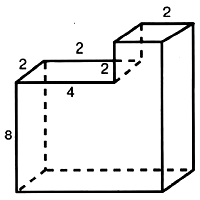
Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Многогранник на рисунке – это прямая призма с высотой 12.

Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:

(больший квадрат), (маленький прямоугольник),

Подставим все данные в формулу: и найдем площадь поверхности многогранника:

Ответ: 424.

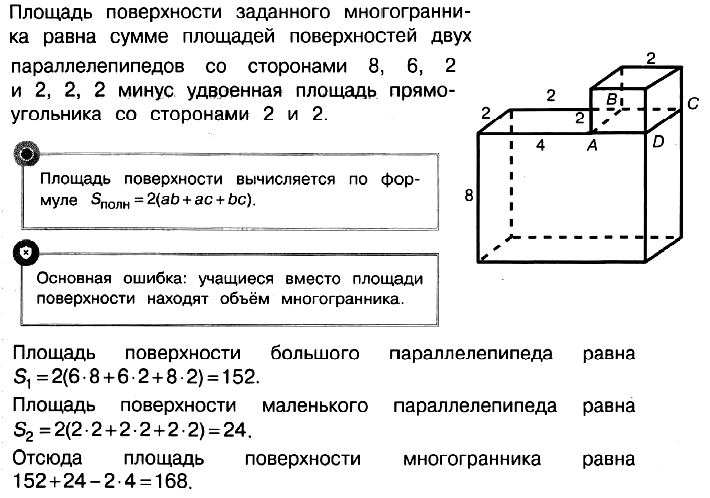
Задача 3. Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).

Решение.

Перевернем многогранник так, чтобы получилась прямая призма с высотой 1.
Площадь поверхности этой призмы находится по формуле:

Найдем площадь основания. Для этого разделим его на два прямоугольника и посчитаем площадь каждого:

(большой прямоугольник), (маленький прямоугольник).

Найдем площадь полной поверхности:

Ответ: 54

Задача 4.Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Покажем еще один способ решения задачи.

Посмотрим, как получился такой многогранник. Можно сказать, что к «кирпичику», то есть прямоугольному параллелепипеду со сторонами 4, 1 и 3, сверху приклеен «кубик», все стороны которого равны 1.

И значит, площадь поверхности данного многогранника равна сумме площадей поверхностей прямоугольного параллелепипеда со сторонами 4,1,3 и
куба со стороной 1, без удвоенной площади квадрата со стороной 1:

Почему мы вычитаем удвоенную площадь квадрата? Представьте себе, что нам надо покрасить это объемное тело. Мы красим все грани параллелепипеда, кроме квадрата на верхней его грани, где на него поставлен кубик. И у куба мы покрасим все грани, кроме этого квадрата.

Ответ: 42

Задача 5. . Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом 120° между ними. Наибольшая из площадей боковых граней равна 35 см². Найдите площадь боковой поверхности призмы.

Решение.

Пусть АВ = 5 см, ВС = 3 см, тогда

Из по теореме косинусов найдем ребро АС:

Отрезок АС – большая сторона , следовательно, большая боковая грань призмы.

Поэтому или откуда

Ответ: 75

Теперь две задачи на площадь боковой поверхности пирамиды.

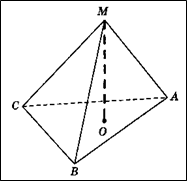
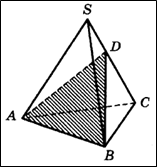
Задача 6. Основанием пирамиды DАВС является треугольник АВС, у которого АВ = АС = 13, ВС = 10; ребро АD перпендикулярно к плоскости основания и равно 9. Найдите площадь боковой поверхности пирамиды.

Решение.

Площадь боковой поверхности пирамиды – это сумма площадей всех ее боковых граней.

Проведем , тогда (по теореме о 3-х перпендикулярах), то есть DК – высота треугольника DВС.

– равнобедренный (по условию АВ = АС), то высота АК, проведенная к основанию ВС, является и медианой, то есть ВК = КС = 5.

Из прямоугольного получим:

Из прямоугольного имеем:

(по двум катетам), тогда следовательно

Ответ: 192

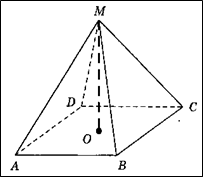
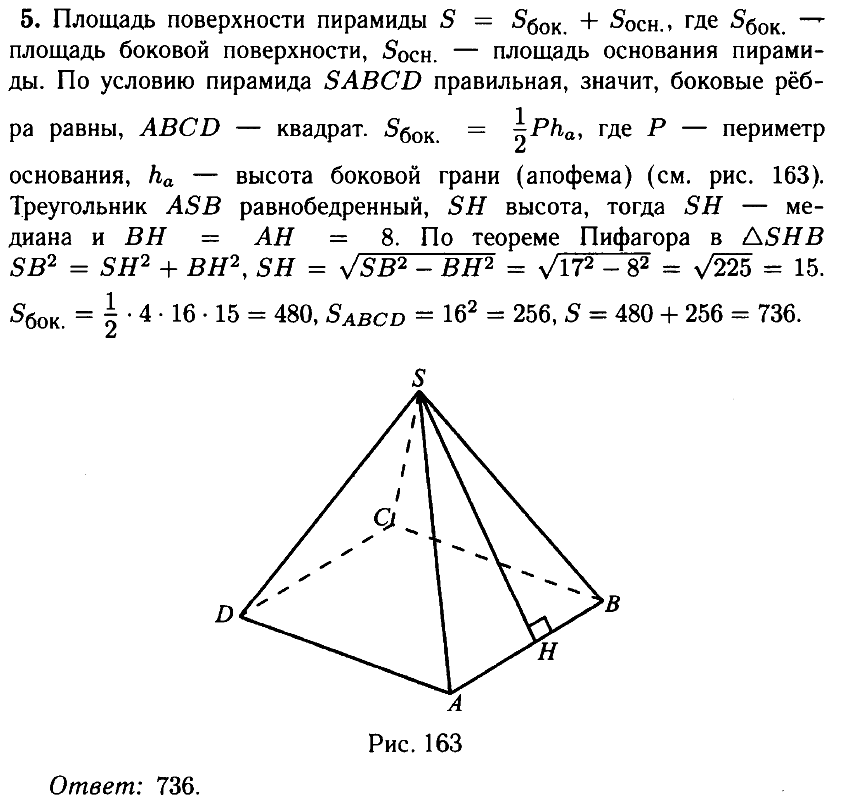
Задача 8. Стороны основания правильной четырехугольной пирамиды равны 24, боковые ребра равны 37. Найдите площадь поверхности пирамиды.

Решение:

Так как четырехугольная пирамида правильная, то в основании лежит квадрат, а все боковые грани — равные равнобедренные треугольники.

Площадь поверхности пирамиды равна

где р – полупериметр основания, h — апофема (высота боковой грани правильной пирамиды), a – сторона основания.

Значит, полупериметр основания .

Апофему найдем по теореме Пифагора:

Ответ: 2256

Как решать задачи на нахождение объема многогранника сложной формы?

Покажем два способа.

Первый способ

1.Составной многогранник достроить до полного параллелепипеда или куба.
2.Найти объем параллелепипеда.
3.Найти объем лишней части фигуры.
4.Вычесть из объема параллелепипеда объем лишней части.

Второй способ.

1.Разделить составной многогранник на несколько параллелепипедов.
2.Найти объем каждого параллелепипеда.
3.Сложить объемы.

Задача 9. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

1) Достроим составной многогранник до параллелепипеда.

2) Найдем объем параллелепипеда – для этого перемножим его длину, ширину и высоту:

3) Найдем объем лишней части, то есть маленького параллелепипеда.

Его длина равна 9 – 4 = 5, ширина 4, высота 7, тогда его объем

4) Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры:

Ответ: 220.

Задача 10. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 7, боковое ребро равно 6. Найдите объем призмы.

Объем призмы равен , а так как призма прямая, то ее боковое ребро является и высотой, то есть

Основанием призмы является прямоугольный треугольник c катетами 6 и 7, тогда площадь основания

Ответ: 126

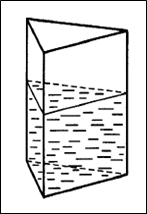
Задача 11. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 324 см. На какой высоте будет находиться уровень воды, если ее перелить в другой сосуд, у которого сторона в 9 раз больше, чем у первого? Ответ выразите в сантиметрах.

Решение.

Объем призмы равен

Воду перелили в другой такой же сосуд. Это значит, что другой сосуд также имеет форму правильной треугольной призмы, но все стороны основания второго сосуда в 9 раз больше, чем у первого.

Основанием второго сосуда также является правильный треугольник. Он подобен правильному треугольнику в основании первого сосуда. Отношение площадей подобных фигур равно квадрату коэффициента подобия.

Если все стороны треугольника увеличить в 9 раз, его площадь увеличится в раз. Мы получили, что площадь основания второго сосуда в 81 раз больше, чем у первого.

Объем воды не изменился, Так как высота воды должна быть в 81 раз меньше, чем Она равна (см).

Ответ: 4

Задача 12. Объем параллелепипеда Найдите объем треугольной пирамиды

Решение.
Опустим из вершины высоту Н на основание

Диагональ основания делит его на два равных треугольника, следовательно,

Имеем:

Ответ: 3,5

Задача 13. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 8, а высота равна

Решение.
По формуле объема пирамиды, .

В основании пирамиды лежит правильный треугольник. Его площадь равна

Объем пирамиды

Ответ: 96

Задача 14. Через середины сторон двух соседних ребер основания правильной четырехугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объем меньшей из частей, на которые эта плоскость делит призму, если объем призмы равен 32.

Решение.

По условию, призма правильная, значит, в ее основании лежит квадрат, а высота равна боковому ребру.

Пусть тогда

Так как точки М и К – середины АD и DС соответственно, то

Площадь треугольника MDK, лежащего в основании новой призмы, составляет часть площади квадрата в основании исходной призмы.
Высоты обеих призм одинаковые. Согласно формуле объема призмы: , и значит, объем маленькой призмы в 8 раз меньше объема большой призмы. Он равен

Ответ: 4

Докажем полезную теорему.

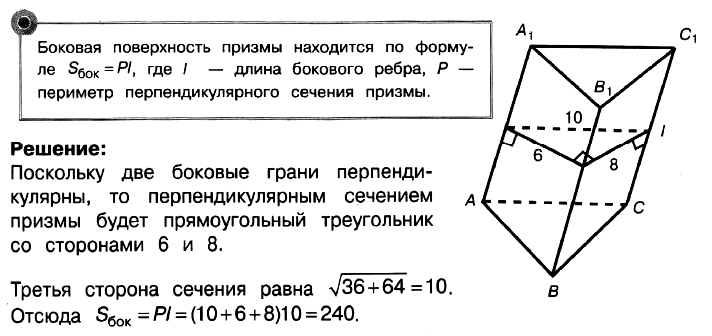
Теорема: Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.

Доказательство:

Плоскость перпендикулярного сечения призмы перпендикулярна к боковым ребрам, поэтому стороны перпендикулярного сечения призмы являются высотами параллелограммов.

Больше задач на формулы объема и площади поверхности здесь.

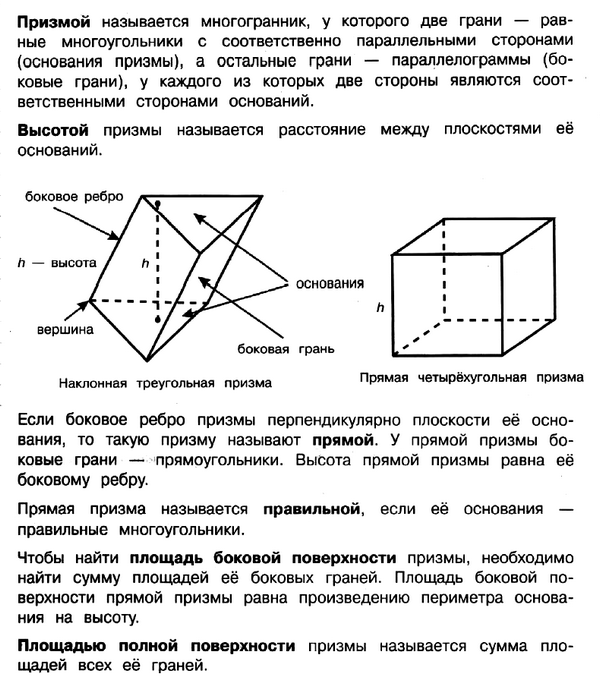
Многогранники

Многогранник – это поверхность, составленная из многоугольников, ограничивающая некоторое геометрическое тело.

В данной теме мы рассмотрим составные многогранники (многогранники, состоящие обычно из нескольких параллелепипедов).

Объемы различных многогранников:

• Призма $V=S_{осн}·h$
• Пирамида $V={1}/{3}S_{осн}·h$
• Параллелепипед $V=a·b·c$, где $a, b$ и $c$ — длина, ширина и высота.
• Куб $V=а^3$, где $а$ — сторона куба

Задачи на нахождение объема составного многогранника:

• Первый способ.

1. Составной многогранник надо достроить до полного параллелепипеда или куба.
2. Найти объем параллелепипеда.
3. Найти объем лишней части фигуры.
4. Вычесть из объема параллелепипеда объем лишней части.

• Второй способ

1. Разделить составной многогранник на несколько параллелепипедов.
2. Найти объем каждого параллелепипеда.
3. Сложить объемы.

Задачи на нахождение площади поверхности составного многогранника.

— Если можно составной многогранник представить в виде прямой призмы, то находим площадь поверхности по формуле:

$S_{полн.пов.}=P_{осн}·h+2S_{осн}$

Чтобы найти площадь основания призмы, надо разделить его на прямоугольники и найти площадь каждого.

— Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.

Задачи на нахождение расстояния между точками составного многогранника.

В данных задачах приведены составные многогранники, у которых двугранные углы прямые. Надо соединить расстояние между заданными точками и достроить его до прямоугольного треугольника. Далее остается воспользоваться теоремой Пифагора для нахождения нужной стороны.

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

$АС^2+ВС^2=АВ^2$

Задачи на нахождение угла или значения одной из тригонометрических функций обозначенного в условии угла составного многогранника.

Так как в данных задачах приведены составные многогранники, у которых все двугранные углы прямые, то достроим угол до прямоугольного треугольника и найдем его значение по тригонометрическим значениям.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$:

Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	${1}/{2}$	${√2}/{2}$	${√3}/{2}$
$cosα$	${√3}/{2}$	${√2}/{2}$	${1}/{2}$
$tgα$	${√3}/{3}$	$1$	$√3$
$ctgα$	$√3$	$1$	${√3}/{3}$

Задачи на рассмотрение подобия фигур.

При увеличении всех линейных размеров многогранника в $k$ раз, площадь его поверхности увеличится в $k^2$ раз.

При увеличении всех линейных размеров многогранника в $k$ раз, его объём увеличится в $k^3$ раз.

Данное занятие может быть проведено после изучения формул объемов многогранников на уроках геометрии в 11-м классе или в рамках элективного курса по подготовке к ЕГЭ. Материал также доступен и учащимся 10-го класса (во 2-м полугодии).

Цели занятия:

• показать примеры задач, аналогичных заданиям ЕГЭ по математике базового уровня и первой части профильного уровня;
• повторить теоретический материал, связанный с площадями фигур, со свойствами многогранников;
• отработка навыков самоконтроля;
• отработка навыков сотрудничества между учащимися.

Оборудование:

• оборудование для демонстрации презентации Microsoft PowerPoint (компьютер, проектор, экран или доска);
• раздаточный материал (тексты задач с чертежами);
• таблица квадратов натуральных чисел.

План занятия

1. Организационный момент
2. Устная работа
3. Решение задач
4. Работа в группах
5. Подведение итогов

Ход занятия

Занятие сопровождается демонстрацией презентации.

1. Организационный момент

Cообщение целей занятия, деление класса на группы по 4 человека (можно объединить учащихся, сидящих за соседними партами).

2. Устная работа

Условия задач и правильные ответы демонстрируются на слайдах. Задачи решаются устно, ответы можно спросить у нескольких учащихся, один из них коротко рассказывает путь решения.

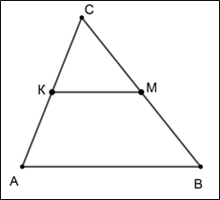
Задача 1. (Слайд №4) Площадь треугольника АВС равна 120. КМ – средняя линия, параллельная стороне АВ. Найти площадь четырехугольника АКМВ. (Ответ: 90)

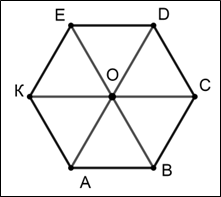
Задача 2. (Слайды №5,6) Площадь правильного шестиугольника АВСДЕК равна 60, О – центр шестиугольника. Найти площади треугольника АОВ, треугольника  АВС, треугольника АВЕ, четырехугольника ВСДЕ. (Ответ: 10; 10; 20; 30)

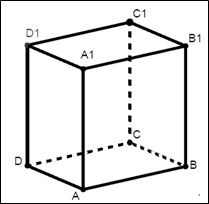
Задача 3. (Слайд №7) Площадь грани прямоугольного параллелепипеда равна 15. Ребро, перпендикулярное этой грани, равно 6. Найти объем параллелепипеда. (Ответ: 90)

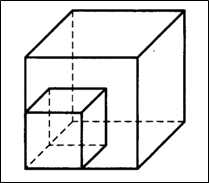
Задача 4. (Слайд №8) Во сколько раз увеличится объем куба, если его ребро увеличить в 5 раз? (Ответ:  125)

Задача 5. (Слайд №9) В правильной треугольной пирамиде МАВС О – точка пересечения медиан основания. Площадь треугольника АВС равна 5, а объем пирамиды – 35. Найти длину отрезка МО. (Ответ: 21)

Задача 6. (Слайд №10) Как изменится объем пятиугольной пирамиды, если её высоту увеличить в 4 раза? (Ответ: увеличится в 4 раза)

Задача 7. (Слайд №11) В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды составил 20 см. На какой высоте будет находиться уровень воды, если ее перелить в другой сосуд такой же формы, у которого сторона основания в 2 раза больше, чем у первого? (Ответ: 5 см)

При подведении итогов устной работы необходимо обратить внимание на формулы для вычисления объемов призмы и пирамиды.

3. Решение задач

Чертежи заранее сделаны на доске, каждый ученик получает заготовку с чертежами (Приложение 1). Учащиеся у доски записывают краткие решения, сопровождая их устными пояснениями. Также можно использовать слайды №13, 14, 15.

Задача 8. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 6 и 3. Объем параллелепипеда равен 108. Найти его диагональ.

Задача 9. В сосуд, имеющий форму правильной треугольной призмы, налили 1000 см³ воды и погрузили в воду деталь. При этом  уровень воды поднялся с отметки 25 см до отметки 27 см. Найти объем детали. Ответ выразить в см³.

Задача 10. Объем треугольной пирамиды SABC равен 15. Плоскость проходит через сторону АВ основания этой пирамиды и пересекает противоположное боковое ребро в точке D, делящей ребро SC в отношении 1 : 2, считая от вершины S. Найти объем пирамиды DABC.

4. Работа в группах

Каждая группа получает набор задач (Приложение 2), к которым надо записать краткие решения. После истечения отведенного времени проверяются ответы, представители групп могут прокомментировать ход решения задач. В это время чертежи демонстрируются на слайдах №17, 18, 19. Для быстрой проверки можно использовать слайд №20. После этого листы с решениями сдаются учителю.

5. Подведение итогов

При подведении итогов следует обратить внимание на две основные формулы объемов и их частные случаи, а также на отношение объемов подобных тел (слайд 22).

Задача. (Слайд №23) Боковые ребра правильной треугольной пирамиды взаимно перпендикулярны и равны 6. Найти объем пирамиды. (Ответ: 36)

При решении этой задачи очень важно обратить внимание на метод решения. Если тетраэдр перевернуть, то задачу можно решить устно.

Задача. (Слайды №24, 25) Объем тетраэдра равен 12. Найти объем многогранника, вершинами которого являются середины сторон данного тетраэдра. (Ответ: 6)

6. Домашнее задание (Приложение 3)

Литература

1. Ященко И. В. ЕГЭ: 4000 задач с ответами по математике. Все задания «Закрытый сегмент». Базовый и профильный уровни. – М: Издательство «Экзамен», 2020.
2. Балаян Э. Н. Геометрия: задачи на готовых чертежах для подготовки к ЕГЭ: 10-11 классы. – Ростов н/Д: Феникс, 2018.
3. Материалы сайта: https://math-ege.sdamgia.ru/

Список приложений

• Приложение 1 – задачи для работы в классе
• Приложение 2 – задачи для работы в группах
• Приложение 3 – домашнее задание
• Приложение 4 – ПРЕЗЕНТАЦИЯ

ЕГЭ Профиль №13. Объем многогранникаadmin2023-02-06T10:59:02+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №13. Объем многогранника

Объем параллелепипеда находится по формуле:   (V = S cdot H),   где S – площадь основания; H – длина высоты параллелепипеда.

Прямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом. Все диагонали прямоугольного параллелепипеда равны и ({d^2} = {a^2} + {b^2} + {c^2}), где d – длина диагонали; a, b, c – длины трех ребер, выходящих из одной вершины прямого параллелепипеда (измерения прямоугольного параллелепипеда). Объем прямоугольного параллелепипеда вычисляется по формуле:    (V = a,b,c).

Прямоугольный параллелепипед, у которого все ребра равны, называется кубом. При этом   (d = asqrt 3 ),  (V = {a^3}),  ({S_{text{пов}}} = 6,{a^2}),    где  d – диагональ куба,  a – его ребро.

Объем призмы находится по формуле:   (V = S cdot H),   где S – площадь основания; H – длина высоты призмы.

Объем пирамиды вычисляется по формуле:  (V = frac{1}{3}S,H),   где S – площадь основания; H – длина высоты пирамиды.

Если у пирамиды все боковые ребра равны между собой или наклонены под одним и тем же углом к плоскости основания, то основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды (эта же точка служит точкой пересечения серединных перпендикуляров к сторонам основания пирамиды).

Если у пирамиды боковые грани наклонены к плоскости основания под одним и тем же углом, то основание высоты пирамиды совпадает с центром окружности, вписанной в основание (эта же точка служит точкой пересечения биссектрис углов в основании пирамиды).

Объем усеченной пирамиды вычисляется по формуле:    (V = frac{1}{3}Hleft( {,{S_1} + {S_2} + sqrt {,{S_1} cdot {S_2}} ,} right)), где H – высота усеченной пирамиды; ({S_1}) и ({S_2}) – площади ее оснований.

---

1В. В треугольной пирамиде ABCD двугранные углы при ребрах AD и BC равны, AB = BD = DC = AC = 5.

а) Докажите, что AD = BC.

б) Найдите объём пирамиды, если двугранные углы равны при рёбрах AD и BC равны ({60^ circ }).

ОТВЕТ: (frac{{10sqrt {15} }}{3}.)

---

2В. В правильной треугольной пирамиде SABC сторона основания AB равна 30, а боковое ребро SA равно 28. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.

а) Докажите, что плоскость α делит медиану CE основания в отношении 5 : 1, считая от точки C.

б) Найдите объём пирамиды, вершиной которой является точка C, а основанием — сечение пирамиды SABC плоскостью α.

ОТВЕТ: (frac{{2750sqrt 3 }}{3}).

---

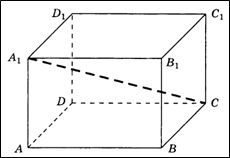
3В. В кубе ABCDA₁B₁C₁D₁ все рёбра равны 5. На его ребре BB₁ отмечена точка K так, что KB = 3. Через точки K и C₁ проведена плоскость α, параллельная прямой BD₁.

а) Докажите, что A₁P : PB₁ = 1 : 2, где P — точка пересечения плоскости α с ребром A₁B₁.

б) Найдите объём большей из двух частей куба, на которые он делится плоскостью α.

ОТВЕТ: (frac{{1075}}{9}.)

---

4В. В правильной треугольной призме ABCA₁B₁C₁ все рёбра равны 6. На рёбрах AA₁ и CC₁ отмечены точки M и N соответственно, причём AM = 2, CN = 1.

а) Докажите, что плоскость MNB₁ разбивает призму на два многогранника, объёмы которых равны.

б) Найдите объём тетраэдра MNBB₁.

---

5В. Есть правильная треугольная призма ABCA₁B₁C₁ со стороной основания 12 и высотой 3. Точка K — середина BC, точка L лежит на стороне A₁B₁ так, что В₁L = 5. Точка М — середина A₁C₁. Через точки K и L проведена плоскость таким образом, что она параллельна прямой AC.

а) Доказать, что указанная выше плоскость перпендикулярна прямой MB.

б) Найти объем пирамиды с вершиной в точке В и у которой основанием является сечение призмы плоскостью.

ОТВЕТ: (frac{{33sqrt 3 }}{2}.)

---

6В. На рёбрах AB и BC треугольной пирамиды ABCD отмечены точки M и N соответственно, причём AM : BM = CN : NB = 1 : 2. Точки P и Q — середины сторон DA и DC соответственно.

а) Докажите, что P, Q, M и N лежат в плоскости.

б)* Найти отношение объёмов многогранников, на которые плоскость PQM разбивает пирамиду.

---

7В. Ребро куба ABCDA₁B₁C₁D₁ равно 6. Точки K, L и M — центры граней ABCD, AA₁D₁D и CC₁D₁D соответственно.

а) Докажите, что B₁KLM — правильная пирамида.

б) Найдите объём B₁KLM.

---

8В. Основанием прямой треугольной призмы ABCA₁B₁C₁ является прямоугольный треугольник ABC с прямым углом C. Диагонали боковых граней AA₁B₁B и BB₁C₁C равны 15 и 9 соответственно, AB = 13.

а) Докажите, что треугольник BA₁C₁ прямоугольный.

б) Найдите объём пирамиды AA₁C₁B.

ОТВЕТ: (20sqrt {14} .)

---

9В. SABCD — правильная четырёхугольная пирамида с вершиной S. Точка M расположена на SD так, что SM : SD = 2 : 3. P — середина ребра AD, а Q середина ребра BC.

а) Доказать, что сечение пирамиды плоскостью MQP — равнобедренная трапеция.

б) Найдите отношение объёмов многогранников, на которые плоскость MQP разбивает пирамиду.

---

10В. Дана пирамида PABCD, в основании — трапеция ABCD с большим основанием AD. Известно, что сумма углов BAD и ADC равна 90 градусов, а плоскости PAB и PCD перпендикулярны основанию, прямые AB и CD пересекаются в точке K.

а) Доказать, что плоскость PAB перпендикулярна плоскости PCD.

б) Найдите объём PKBC, если AB = BC = CD = 2, а PK = 12.

---

11В. В треугольной пирамиде PABC с основанием ABC известно, что AB = 13, PB = 15, (cos angle ,PBA = frac{{48}}{{65}}). Основанием высоты этой пирамиды является точка C. Прямые PA и BC перпендикулярны.

а) Докажите, что треугольник ABC прямоугольный.

б) Найдите объем пирамиды PABC.

---

12В. Основанием прямой четырехугольной призмы ABCDA₁B₁C₁D₁ является ромб ABCD, AB = AA₁.

а) Докажите, что прямые A₁C и BD перпендикулярны.

б) Найдите объем призмы, если A₁C = BD = 2.

ОТВЕТ: (frac{{4sqrt 6 }}{5}.)

---

13В. В треугольной пирамиде SABC известны боковые рёбра: SA = SB = 13, (SC = 3sqrt {17} ). Основанием высоты этой пирамиды является середина медианы CM треугольника ABC. Эта высота равна 12.

а) Докажите, что треугольник ABC равнобедренный.

б) Найдите объём пирамиды SABC.

---

14В. Диагональ прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ равна 13, а диагонали двух соседних граней равны (4sqrt {10} ) и (3sqrt {17} ).

а) Докажите, что треугольник AC₁D₁ прямоугольный.

б) Найдите объём параллелепипеда.

---

15В. Диагональ прямоугольного параллелепипеда равна (4sqrt 2 ) и образует с боковыми гранями углы ({30^ circ }) и ({45^ circ }).

а) Докажите, что одна из этих граней — квадрат.

б) Найдите объём параллелепипеда.

---

16В. Сторона основания ABC правильной треугольной пирамиды ABCD равна 6, а площадь сечения, проходящего через ребро AB и середину бокового ребра CD, равна (6sqrt 6 ).

а) Докажите, что плоскость сечения образует с плоскостью основания угол ({45^ circ }).

б) Найдите объём пирамиды ABCD.

---

17В. Сторона основания ABCDEF правильной шестиугольной пирамиды SABCDEF равна 4, а площадь сечения, проходящего через прямую CF и середину бокового ребра SD, равна (10sqrt 3 ).

а) Докажите, что плоскость сечения образует с плоскостью основания угол ({60^ circ }).

б) Найдите объём пирамиды SABCDEF.

---

18В. Точки M и N — середины рёбер соответственно CC₁ и B₁C₁ треугольной призмы ABCA₁B₁C₁ с основаниями ABC и A₁B₁C₁.

а) Докажите, что плоскость BA₁M делит отрезок AN в отношении 4 : 3, считая от точки A.

б) В каком отношении плоскость BA₁M делит объём призмы?

---

19В. Точка P — середина медианы BK основания ABC треугольной пирамиды ABCD.

а) Докажите, что плоскость α, проходящая через точку B и середины рёбер AD и CD, делит отрезок DP в отношении 2 : 1, считая от вершины D.

б) Найдите расстояние от вершины C до плоскости ?, если объём пирамиды ABCD равен 16, а площадь её сечения плоскостью α равна 3.

---

20В. Высота SH правильной треугольной пирамиды SABC относится к высоте основания ABC как 4 : 9. Плоскость α проходит через ребро AB и делит пополам двугранный угол пирамиды при этом ребре.

а) Докажите, что плоскость α делит высоту пирамиды в отношении 3 : 5, считая от точки H.

б) Найдите объём меньшей из частей, на которые пирамида разбивается плоскостью α, если сторона основания пирамиды равна 6.

ОТВЕТ: (frac{{30}}{7}).

---

21В. Дана правильная четырёхугольная пирамида SABCD с вершиной S. Апофема пирамиды вдвое больше стороны основания. Плоскость α проходит через ребро AB и делит пополам двугранный угол пирамиды при этом ребре.

а) Докажите, что плоскость α делит высоту пирамиды в отношении 4 : 1, считая от вершины S.

б) Найдите объём большей из частей, на которые пирамида разбивается плоскостью α, если сторона основания пирамиды равна (sqrt {15} ).

ОТВЕТ: (frac{{125}}{6}).

---

22В. Дан параллелепипед ABCDA₁B₁C₁D₁. На лучах AB, AD и AA₁ отмечены точки K, L и M соответственно, причём  (AK = frac{5}{2}AB,;;AL = frac{5}{2}AD) и (AM = frac{5}{2}A{A_1}.)

а) Докажите, что плоскость KLM делит ребро B₁C₁ пополам.

б) В каком отношении плоскость KLM делит объём параллелепипеда?

---

23В. На диагонали BD₁ параллелепипеда ABCDA₁B₁C₁D₁ отмечена точка M, причём BM : MD₁ = 1 : 3. Через точку M проведена плоскость α, параллельная прямым AB₁ и CB₁.

а) Докажите, что плоскость α делит ребро AB в отношении 1 : 3, считая от вершины A.

б) В каком отношении плоскость α делит объём параллелепипеда?

---

24В. Точка M — середина ребра B₁C₁ правильной треугольной призмы ABCA₁B₁C₁ с основаниями ABC и A₁B₁C₁. Прямые BA₁ и CB₁ перпендикулярны.

а) Докажите, что треугольник BMA₁ равнобедренный.

б) Найдите объём призмы, если расстояние между прямыми BA₁ и CB₁ равно 2.

---

25В. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ грань ABCD — квадрат. Точка M лежит на ребре BC, причём CM : MB = 1 : 2. Известно, что диагональ DB₁ параллелепипеда перпендикулярна отрезку C₁M.

а) Докажите, что угол между прямой CB₁ и плоскостью A₁B₁C₁ равен (30^circ ).

б) Найдите объём параллелепипеда, если расстояние между прямыми DB₁ и C₁M равно (frac{{sqrt {21} }}{7}).

---

26В. Через середину бокового ребра правильной треугольной пирамиды проведена плоскость α, перпендикулярная этому ребру. Известно, что она пересекает остальные боковые рёбра и разбивает пирамиду на два многогранника, объёмы которых относятся как 1 к 3.

а) Докажите, что плоский угол при вершине пирамиды равен  45°.

б) Найдите площадь сечения пирамиды плоскостью α, если боковое ребро пирамиды равно 4.

ОТВЕТ: (sqrt[4]{8} cdot sqrt {4 — 2sqrt 2 } .)

---

27В. В правильной треугольной усеченной пирамиде ABCA₁B₁C₁ площадь нижнего основания ABC в девять раз больше площади меньшего основания A₁B₁C₁. Через ребро AB проведена плоскость α, которая пересекает ребро СС₁ в точке N и делит пирамиду на два многогранника равного объёма.

а) Докажите, что точка N делит ребро СС₁ в отношении 5 : 13, считая от вершины С₁.

б) Найдите площадь сечения усеченной пирамиды плоскостью α, если высота этой пирамиды равна 13, а ребро меньшего основания равно 3.

---

28В. В правильной четырехугольной пирамиде SABCD сторона основания равна 6, а боковое ребро SA равно 5. На ребрах AB и SB отмечены точки M и K соответственно, причем  АM = 2,  SK = 1.

а) Докажите, что плоскость CKM перпендикулярна плоскости ABC.

б) Найдите объём пирамиды BCKM.

ОТВЕТ: (frac{{16sqrt 7 }}{5}).

---

29В. В правильной четырёхугольной пирамиде SABCD с основанием ABCD из точки В опущен перпендикуляр BH на плоскость SAD.

а) Докажите, что ∠ AHC = 90°.

б) Найдите объём пирамиды, если (HA = sqrt 2 )  и  HC = 4.

ОТВЕТ: (frac{{9sqrt {14} }}{4}.)

ЕГЭ по математике Профиль. Задание 5: Уметь выполнять действия с геометрическими фигурами, координатами и векторами. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».

ЕГЭ Профиль. Задание № 5

АЛГОРИТМ ВЫПОЛНЕНИЯ

Задание № 5 рассчитано на умение решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объёмов), использовать при выполнении знание свойств основных пространственных тел, применять планиметрические факты и методы.

Задание состоит из текстовой задачи и рисунка. Рассматриваются простые пространственные тела: куб, прямоугольный параллелепипед, правильная пирамида, правильная призма. Ответом является конечная десятичная дробь или целое число.

План выполнения:

1. Внимательно прочитайте задачу.
2. При необходимости выполните на черновике чертёж и дополнительные построения.
3. Сделайте на черновике необходимые вычисления.
4. Запишите полученное число в поле ответа КИМ и бланк ответов № 1.

Задачи на Прямоугольный параллепипед

Для решения подобных задач необходимо повторить свойства куба и прямоугольного параллелепипеда, формулы для вычисления площади поверхности, объёма этих тел.

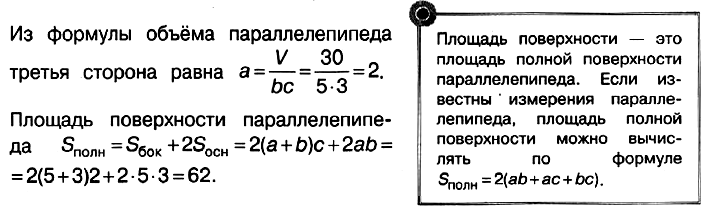
Задача № 5 (1). Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 5. Объём параллелепипеда равен 30. Найдите площадь его поверхности.

Решение:

Ответ: 62.

Задачи на Составные многогранники

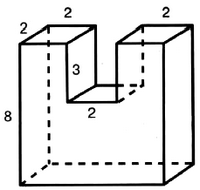
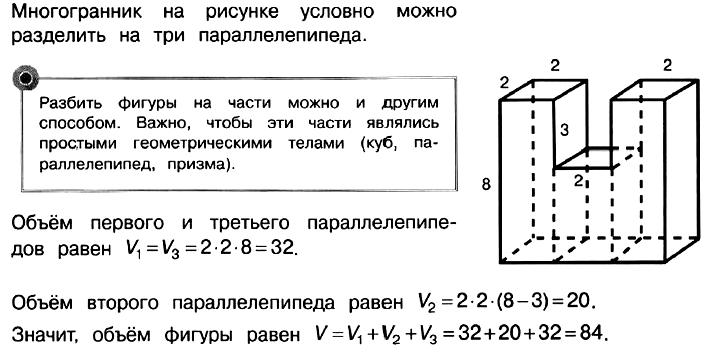
Задача № 5 (2). Найдите объём многогранника, изображённого на рисунке. Все двугранные углы многогранника прямые.

Решение:

Ответ: 84.

Задача № 5 (3). Найдите площадь поверхности многогранника, изображённого на рисунке. Все двугранные углы многогранника прямые.

Решение:

Ответ: 168.

Задачи на Призмы

Для решения задач этого типа необходимо повторить свойства призмы, формулы для вычисления площади поверхности и объёма призмы.

Задача № 5 (4). В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых рёбер на 6 и 8. Найдите площадь боковой поверхности этой призмы.

Решение:

Ответ: 240.

Задачи на Пирамиды

При подготовке нужно повторить основные свойства пирамиды, формулы для вычисления площади поверхности и объёма пирамиды.

Задача № 5 (5). Основание пирамиды — треугольник, у которого длины двух сторон равны 2 и 6, а угол между этими сторонами составляет 30°. Вычислите объём пирамиды, если её высота равна 3.

Решение:

Ответ: 3.

Задачи на Цилиндры

Для решения задач этого типа необходимо повторить формулы вычисления площади круга, длины окружности, площади поверхности цилиндра, объёма цилиндра.

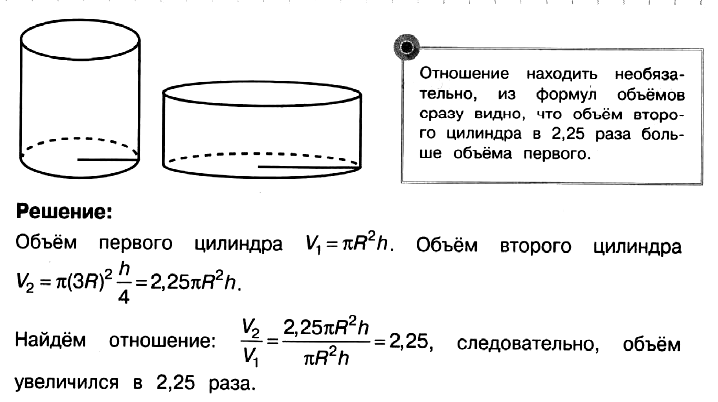
Задача № 5 (6). Радиус основания цилиндра увеличили в 3 раза, а его высоту уменьшили в 4 раза. Во сколько раз увеличится объём цилиндра?

Решение:

Ответ: 2,25.

Задачи на Конусы

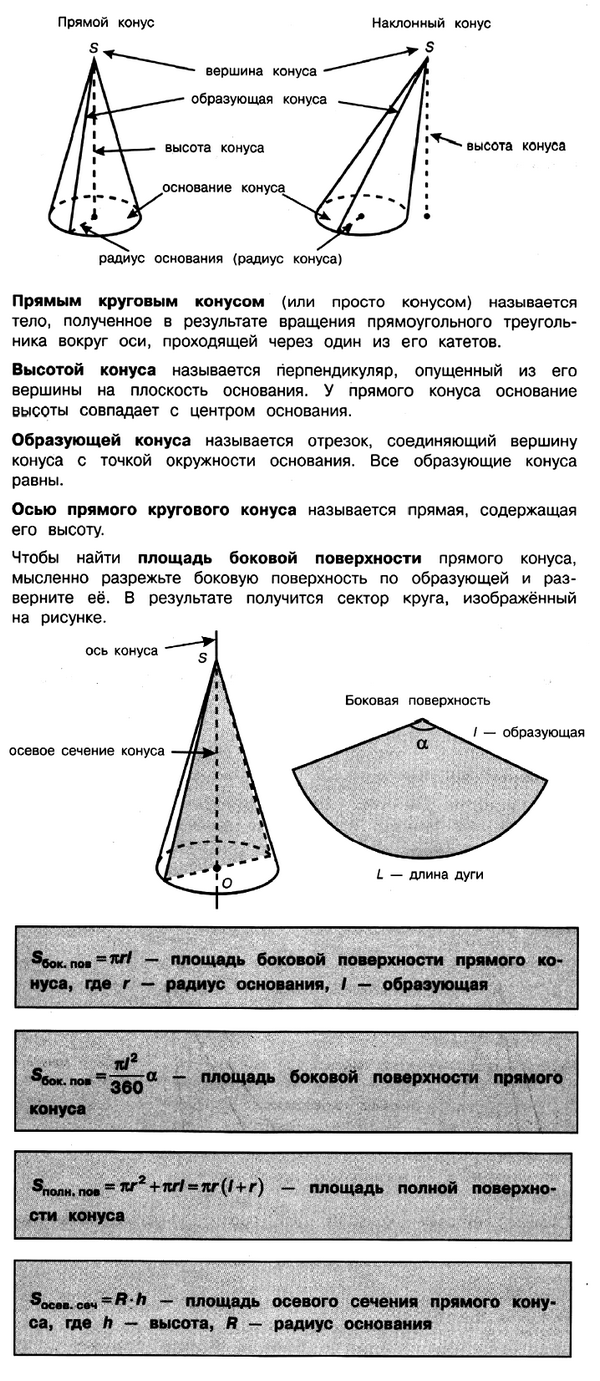
При подготовке необходимо повторить свойства конуса, формулы для вычисления площади поверхности и объёма конуса, площади круга и длины окружности.

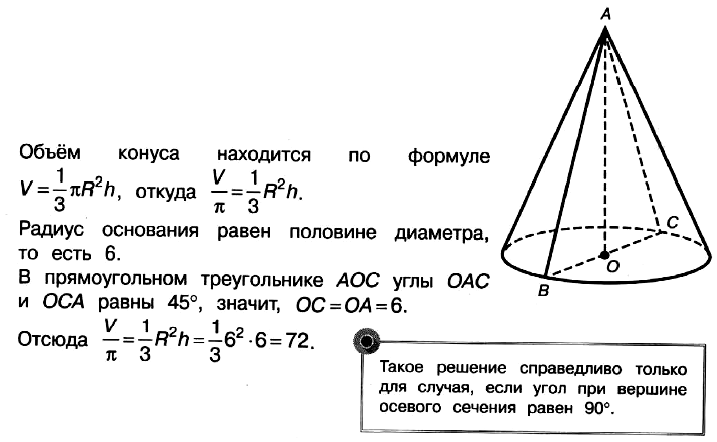
Задача № 5 (7). Диаметр основания конуса равен 12, угол при вершине осевого сечения равен 90°. Вычислите объём конуса, делённый на π.

Решение:

Ответ: 72.

Задачи на Шары

Для решения задач этого типа необходимо повторить формулы для вычисления площади круга, длины окружности, площади поверхности шара, объёма шара.

Задача № 5 (8). Площадь сечения шара плоскостью равна 36π см². Найдите радиус шара, если плоскость находится на расстоянии 8 см от центра шара.

Решение:

Ответ: 10.

Задачи на Комбинации многогранников
и тел вращения

Задача № 5 (9). В основании прямой призмы лежит прямоугольный треугольник с катетами 3 и 4. Боковые рёбра призмы равны 4/π. Найдите объём цилиндра, описанного около этой призмы.

Решение:

Ответ: 25.

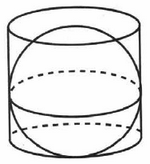
Задача № 5 (10). Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 15. Найдите площадь поверхности шара.

Решение:

Ответ: 10.

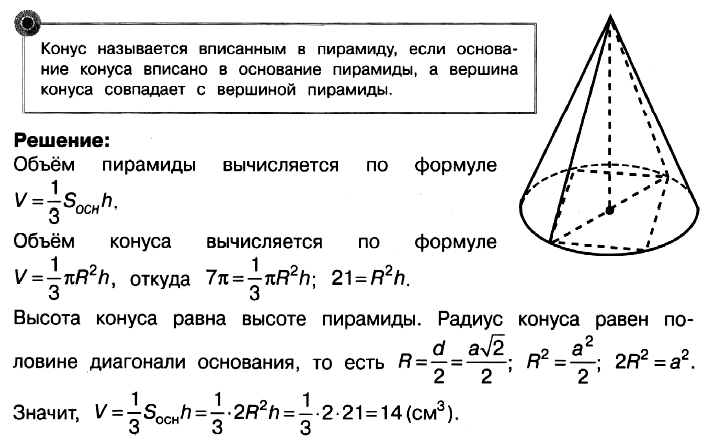
Задача № 5 (11). Объём конуса равен 7π см³. Найдите объём правильной четырёхугольной пирамиды, вписанной в конус.

Решение:

Ответ: 14.

Задача № 5 (12). Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 20. Найдите объём конуса.

Решение:

Ответ: 5.

Тренировочные задания с самопроверкой

№ 5.1. Площадь поверхности куба равна 72 (см. рис.). Найдите его диагональ.

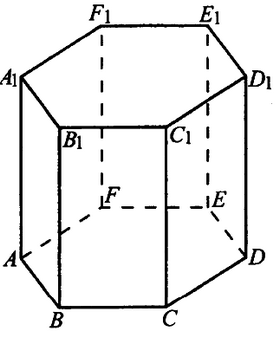
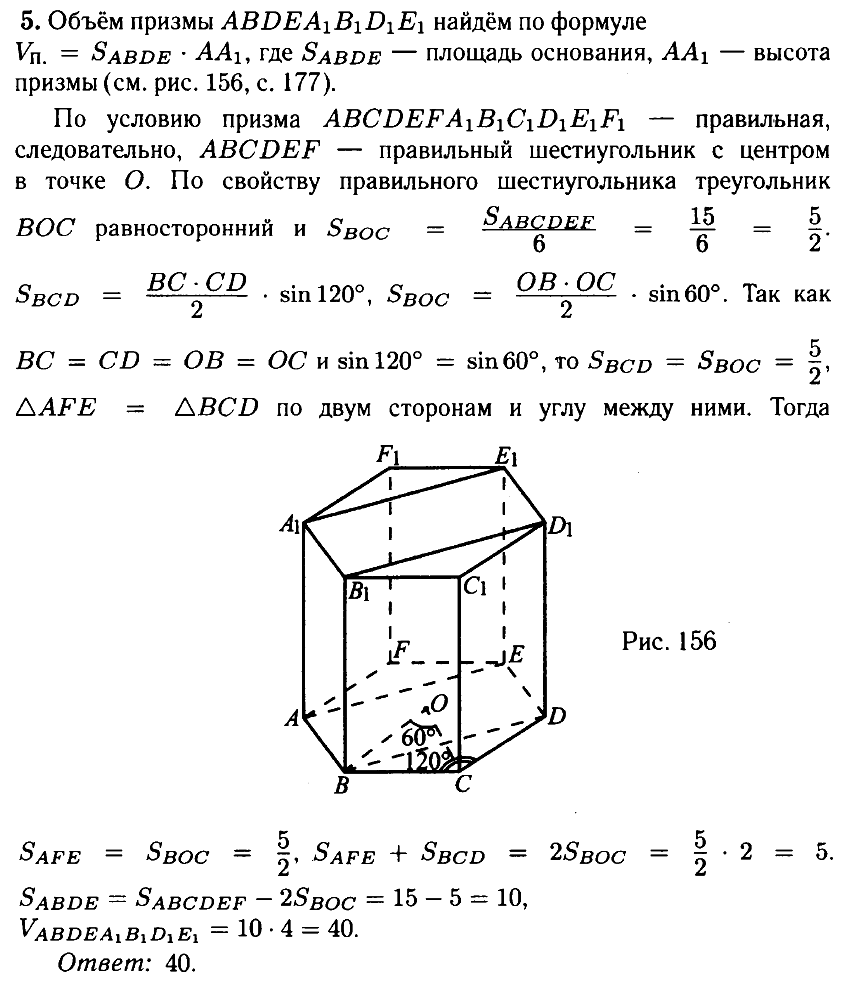
№ 5.2. Найдите объём многогранника, вершинами которого являются точки А, В, D, Е, А₁, В₁, D₁, E₁ правильной шестиугольной призмы ABCDEFA₁B₁C₁D₁E₁F₁ (см. рис.). Площадь основания призмы равна 15, а боковое ребро равно 4.

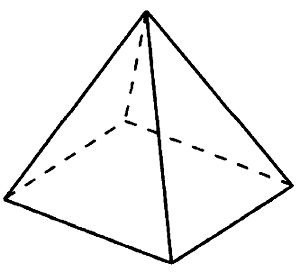
№ 5.3. Стороны основания правильной четырёхугольной пирамиды равны 16, боковые рёбра равны 17 (см. рис.). Найдите площадь поверхности этой пирамиды.

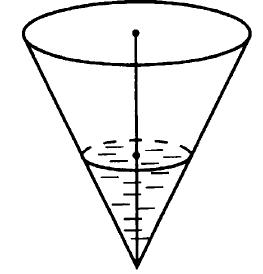
№ 5.4. В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты (см. рис.). Объём жидкости равен 60 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

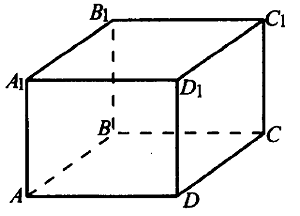
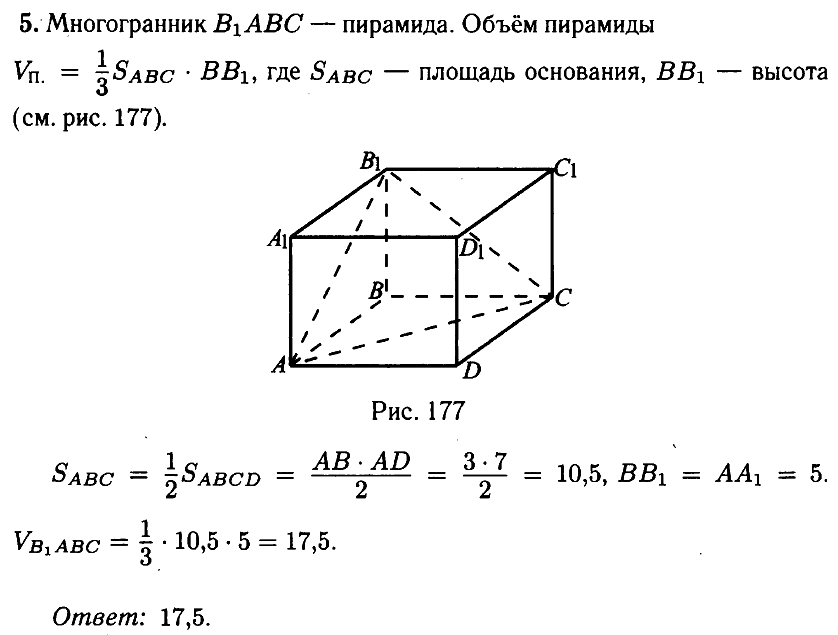
№ 5.5. Найдите объём многогранника, вершинами которого являются точки А, В, С, В прямоугольного параллелепипеда ABCDA₁B₁C₁D₁, у которого АВ = 3, AD = 7, АА₁ = 5 (см. рис.).

---

Вы смотрели: ЕГЭ по математике Профиль. Задание 5: Уметь выполнять действия с геометрическими фигурами, координатами и векторами. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».

Просмотров:
13 529

Объёмы многогранников

Куб 

V = a3 , где а — ребро куба

Прямоугольный параллелепипед 

V = a * b * c, где a, b, c — рёбра фигуры: высота, ширина и длина

Параллелепипед

V = Sоснования * h, где  h — высота параллепипеда.

Призма

V = Sоснования * h, где  h — высота призмы

Пирамида

V = 1/3 Sоснования * h, где  h — высота пирамиды

Объёмы тел вращения

Цилиндр 

V = πR2h, где R — радиус основания, h — высота

Конус

V = 13 Sоснования * h

Шар

V = 43πR3 , где R — радиус шара

• Материалы для подготовки к ЕГЭ

•    

• Рубрики
  • 01 Геометрия (13)
  • 02 Стереометрия (9)
  • 03 Теория вероятностей ч.1 (1)
  • 04 Теория вероятностей ч.2 (1)
  • 05 Простейшие уравнения (5)
  • 06 Вычисления (5)
  • 07 Производная, ПО (4)
  • 08 «Прикладные» задачи (5)
  • 09 Текстовые задачи (7)
  • 10 Графики функций (7)
  • 11 Исследование функции (2)
  • 12 (С1) Уравнения (78)
  • 13 (С2) Стереометр. задачи (94)
  • 14 (С3) Неравенства (89)
  • 15 (С4) Практич. задачи (71)
  • 16 (С5) Планиметр. задачи (86)
  • 17 (С6) Параметры* (79)
  • 18 (С7) Числа, их свойства (38)
  • A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
  • A2 Читаем графики (нет в ЕГЭ-22) (1)
  • Видеоуроки (44)
  • ГИА (11)
    • II часть (11)
  • ЕГЭ (диагностич. работы) (70)
  • Иррациональные выражения, уравнения и неравенства (15)
  • Логарифмы (39)
  • МГУ (12)
  • Метод интервалов (4)
  • Метод рационализации (18)
  • Модуль (9)
  • Параметр (40)
  • Переменка (5)
  • Планиметрия (60)
  • Показательные выражения, уравнения и неравенства (8)
  • Разложение на множители (1)
  • Рациональные выражения, уравнения и неравенства (10)
  • Справочные материалы (92)
  • Стереометрия (52)
  • Т/P A. Ларина (443)
  • Текстовые задачи (12)
  • Теория чисел (2)
  • Тесты по темам (80)
  • Тригонометрические выражения, уравнения и неравенства (43)
  • Функции и графики (10)
• Дружественные сайты

  Сайт А. Ларина
  ЕгэТренер – О. Себедаш
  Математика?Легко!
  Егэ? Ок! – И. Фельдман
  

• Свежие записи
  • Тест «Гиперболы»
  • Тест. Графики функций. Комбинированные задачи
  • 10. Графики функций. Комбинированные задачи
  • Тест. Тригонометрические функции
  • 10. Тригонометрическая функция
  • Тест. Кусочно-линейная функция
  • 10. Кусочно-линейная функция
• Архивы Архивы