Опубликовано 13.11.2012 — 11:12 — Кашина Наталья Вадимовна
Решение задач В-9, В-11
Скачать:
| Вложение | Размер |
|---|---|
| 1.18 МБ |
Предварительный просмотр:
Подписи к слайдам:
По теме: методические разработки, презентации и конспекты
Подготовка к ЕГЭ по математике. Учебная презентация «Наибольшее и наименьшее значение функции»
В работе приводятся примеры решения задач на исследование функции с помощью производной….
Подготовка к ЕГЭ по математике. Учебная презентация «Объем конуса и цилиндра».
Решение задач В-9, В-11…
Подготовка к ЕГЭ по математике. Учебная презентация «Объем цилиндра и призмы».
Решение задач В-9, В-11…
Подготовка к ЕГЭ по математике. Учебная презентация «Экстремумы функции»
Решение В-14…
АВТОРСКАЯ ПРОГРАММА по элективному учебному курсу «Подготовка к ЕГЭ по математике» 10-11 класс
Тематическое планирование курса…
План работы с учащимися «группы риска» 9 класса по подготовке к ГИА по математике в 2013-2014 учебном году
План работыс учащимися «группы риска» 9 класса по подготовке к ГИА по математике в 2019-2020 учебном году…
Сценарий урока по математике «Прямоугольный параллелепипед, пирамида»
урок на развитие пространственного мышления в 5 классе…
- Мне нравится
1. Решение задач по теме «ОБЪЕМ ПИРАМИДЫ»
(по материалам ЕГЭ)
2. Виды пирамид
3. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой
пирамиды.
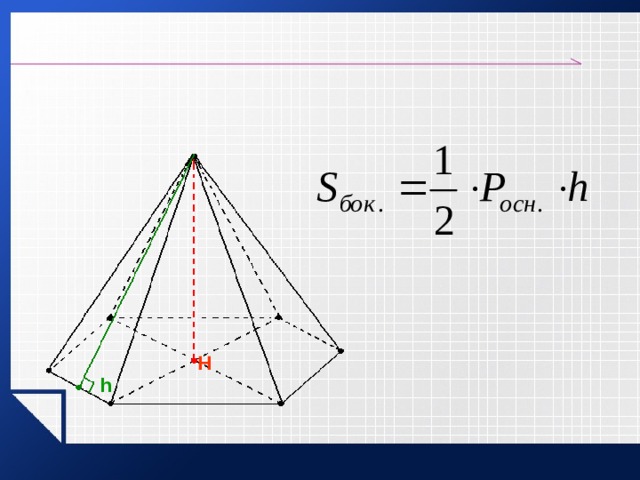
Sбок = ½ Росн.h,
(h – высота боковой грани)
Росн = 6a
=
60
2
h
169 – 25 = 144
h = 12 ; Sбок = ½∙ 60 ∙12
Sбок = 360
4. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите объем пирамиды.
V = 1/3 Sосн.H
Sосн =
3à
2
3
2
Sосн = 150 3
R = a ; H = 169 100 69
V = 150 23
V = 1/3 ∙150 3 69
5. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.
V = 1/3 Sосн.H
Боковые грани –
равные,прямоугольные
равнобедренные треугольники
a=R 3
a=3 2
V = 4,5
à2 3
Sосн =
4
Sосн =
R= 6
3 H= 3
9
2
6. Объем параллелепипеда равен 9. Найдите объем треугольной пирамиды .
Объем параллелепипеда равен 9. Найдите
объем треугольной пирамиды .
Объем пирамиды
равен
1/6 объема
параллелепипеда
V = 1,5
7.
8
Презентация по предмету «Математика» на тему: «« ОБЪЕМ ПИРАМИДЫ » (по материалам ЕГЭ) Решение задач по теме « ОБЪЕМ ПИРАМИДЫ » (по материалам ЕГЭ) Учитель математики МБОУСОШ 55 Канина И.В.». Скачать бесплатно и без регистрации. — Транскрипт:
1
« ОБЪЕМ ПИРАМИДЫ » (по материалам ЕГЭ) Решение задач по теме « ОБЪЕМ ПИРАМИДЫ » (по материалам ЕГЭ) Учитель математики МБОУСОШ 55 Канина И.В.
2
Виды пирамид
3
Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды. S бок = ½ Р осн. h, (h – высота боковой грани) h2h2 169 – 25 = 144 Р осн = 6a = 60 h = 12 ; S бок = ½ S бок = 360
4
Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите объем пирамиды. V = 1/3 S осн. H S осн = S осн = 150 R = a ; H = V = 1/3 150 V = 150
5
Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды. V = 1/3 S осн. H Боковые грани – равные,прямоугольные равнобедренные треугольники a = 3 S осн = a = R R = H = V = 4,5
6
Объем параллелепипеда равен 9. Найдите объем треугольной пирамиды. Объем пирамиды равен 1/6 объема параллелепипеда V = 1,5
7
8
Презентация на тему «Объем пирамиды»
-
Скачать презентацию (0.44 Мб)
-
280 загрузок -
4.2 оценка
Ваша оценка презентации
Оцените презентацию по шкале от 1 до 5 баллов
- 1
- 2
- 3
- 4
- 5
Комментарии
Добавить свой комментарий
Аннотация к презентации
Смотреть презентацию онлайн с анимацией на тему «Объем пирамиды» по математике. Презентация состоит из 19 слайдов. Для учеников 10-11 класса. Материал добавлен в 2017 году. Средняя оценка: 4.2 балла из 5.. Возможность скчачать презентацию powerpoint бесплатно и без регистрации. Размер файла 0.44 Мб.
-
Формат
pptx (powerpoint)
-
Количество слайдов
19
-
Аудитория
-
Слова
-
Конспект
Отсутствует
Содержание
-
Слайд 1
Открытый банк заданий по математике http://mathege.ru:8080/or/ege/Main.action
Объем
пирамиды -
Слайд 2
Найдем отношение объемов
Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?
V = SoH
1
33
х
1
0
хВ 11
8
h
a
2a
2h
a
ab
S
sin
2
1
= -
Слайд 3
Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.
3
х
1
0
хВ 11
4
Н
3
4V = SoH
1
312
16
-
Слайд 4
Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна .
3
х
1
0
хВ 11
5
0
,
2V = SoH
1
31
1a
ab
S
sin
2
1
=1
1
600
-
Слайд 5
3
х
1
0
хВ 11
3
.
Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен .2
2V = SoH
1
3?
a
ab
S
sin
2
1
=2
2
600
3
3
-
Слайд 6
3
х
1
0
хВ 11
4
Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в четыре раза?
A
F
B
C
D
E
Найдем отношение
объемовV = SoH
1
3h
4h -
Слайд 7
3
х
1
0
хВ 11
7
1
1
1600
?
.
Объем правильной шестиугольной пирамиды 6.
Сторона основания равна 1. Найдите боковое ребро.
A
F
B
C
D
E
1
1?
1
S
62
3
3О
Из АОS по теореме Пифагора
найди ребро AS.a
ab
S
sin
2
1
=1
1
600
Для правильного 6-уг. сторона равна радиусу описанной окружности.
Можно вычислить площадь правильного шестиугольника, разбив его на 6 треугольников. -
Слайд 8
3
х
1
0
хВ 11
2
0
0.
В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.Н
6
10
10V = SoH
1
3a
S
=
кв.
2 -
Слайд 9
3
х
1
0
хВ 11
4
8.
Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 600. Высота пирамиды равна 6. Найдите объем пирамиды.
.Н
S
D
C
BV = SoH
1
3?
6Из SHG:
Из SHA:
36
=
ab
S
пр.
312
G
6006
A600
-
Слайд 10
3
х
1
0
хВ 11
4
,
5Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.
A
В
С
SA
S
B
CV = SoH
1
33
3
3
3
3
3
Задача очень простая, если догадаться опрокинуть пирамиду на удобную грань, например, SCB.
Основание – прямоугольный треугольник SCB, высота AS.ab
S
2
1
=3
3
катет
катет
высота -
Слайд 11
Сторона основания правильной шестиугольной пирамиды равна 4,
а угол между боковой гранью и основанием равен 450.
Найдите объем пирамиды.3
х
1
0
хВ11
4
8.
.
A
F
B
C
D
E
4
4S
О
КV = SoH
1
3450
?
?
4
4
4600
a
ab
S
sin
2
1
=4
4
600
Можно вычислить площадь правильного шестиугольника, разбив его на 6 треугольников.
2
32
32
3
2
Найдем ОК по теореме ПифагораК
О
С -
Слайд 12
Найдем отношение объемов
Объем параллелепипеда ABCDA1B1C1D1 равен 12.
Найдите объем треугольной пирамиды B1ABC.Vпир. = SoH
1
3A
B
C
D
B1
C1
D1
A1Vприз. = SoH
h
h12
3
х
1
0
хВ 11
2
2SABC
= -
Слайд 13
Пирамида AD1CB1 получается, если мы отрежем от параллелепипеда четыре пирамиды по углам — ABCB1, D1B1CC1, AA1D1B1 и ADCD1. А объем каждой из них легко посчитать — мы делали это в предыдущей задаче. Например, найдем объем пирамиды ABCB1.
Объем параллелепипеда ABCDA1B1C1D1 равен 4,5. Найдите объем треугольной пирамиды AD1CB1.
C1
A
B
C
D
A1
B1
D1Найдем отношение объемов
Vпир. = SoH
1
3Vпар. = SoH
4,5
3
х
1
0
хВ 11
1
,
5Четыре пирамиды по углам — ABCB1, D1B1CC1, AA1D1B1 и ADCD1
Объем пирамиды АD1CB1h
2SABC
= -
Слайд 14
Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
Найдем отношение объемов
Vпир. = SoH
1
33
х
1
0
хВ 11
2
h
h
2
1A
B
C
D
A1
B1
C1
D1
12 -
Слайд 15
От треугольной призмы, объем которой равен 150, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания.
Найдите объем оставшейся части.h
Найдем отношение объемов
Vпир. = SoH
1
3Vприз. = SoH
150
3
х
1
0
хВ 11
5
0 -
Слайд 16
F
E
A
B
C
D
A
B
C
D
E
FОбъем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 8. Найдите объем шестиугольной пирамиды.
S
У треугольной и шестиугольной пирамид, о которых говорится в условии, одинаковые высоты. Убедимся в этом, изменим расположение букв…
Одинаковая высота, но площадь оснований различна.Найдем отношение объемов
Vпир. = SoH
1
38
3
х
1
0
хВ 11
4
8V1
V2
Поработаем с выносным чертежом. Видим, что площадь основания треугольной пирамиды в 6 раз меньше, чем у шестиугольной. -
Слайд 17
Объем правильной четырехугольной пирамиды SABCD равен 12. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC.
S
B
D
A
CO
h
2
1Точка E – середина ребра SB, значит, точка N – середина SO (по т. Фалеса).
Высота пирамиды EABC равна половине высоты пирамиды SABCD.
EN
Найдем отношение объемовVпир. = SoH
1
312
3
х
1
0
хВ 11
3
2SABC
= -
Слайд 18
От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через
вершину пирамиды и среднюю линию основания.
Найдите объем отсеченной треугольной пирамиды.B
S
C
AМ
NS
А
В
СМ
NУ треугольной пирамиды и отсеченной пирамиды, о которых говорится в условии, одинаковые высоты. Убедимся в этом, изменим расположение букв… Одинаковая высота, но площадь оснований различна.
Работать можно с любым из этих чертежей.
Найдем отношение объемовVпир. = SoH
1
312
3
х
1
0
хВ 11
3
a
b
V2
V1a
ab
S
sin
2
1
= -
Слайд 19
Найдем объем пирамиды NABC. Сравним его с объемом всей пирамиды SABC, составив отношение.
Основания у них одинаковые – треугольник АВС.
А высоты разные, сравним их.
По т. Фалеса FP:SP = 2:3.
Тогда, если SP=h, то FP=h, NO= h
2
32
3Объем треугольной пирамиды равен 15. Плоскость проходит
через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1 : 2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду.S
C
A
BN
1 часть
2частиP
Надо сравнить объемы пирамид NABC и NSAC. Найдем объем пирамиды NABC. Затем из VSABC(это 15) вычтем VNABC,, найдем VNSAC.
O
F
h
3
215
3
х
1
0
хВ 11
1
0
Посмотреть все слайды
Сообщить об ошибке
Похожие презентации












Спасибо, что оценили презентацию.
Мы будем благодарны если вы поможете сделать сайт лучше и оставите отзыв или предложение по улучшению.
Добавить отзыв о сайте
Подписи к слайдам:
Объем пирамиды
Определение. Формулы. Интересные сведения. Задачи.
Определение
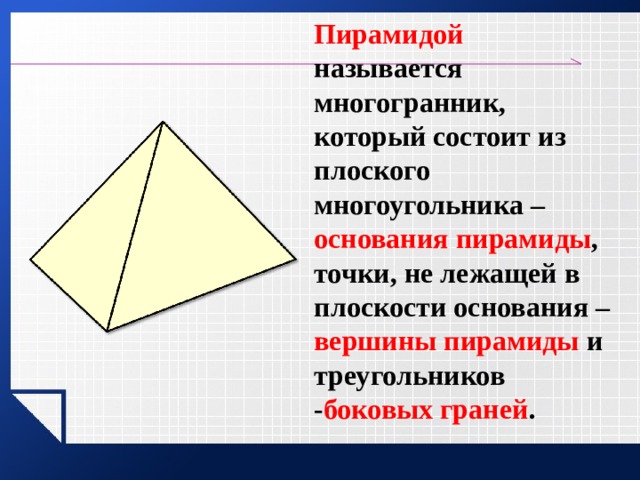
- Пирамидой называется многогранник, одна грань которого – произвольный многоугольник, а остальные грани – треугольники, имеющие общую вершину.
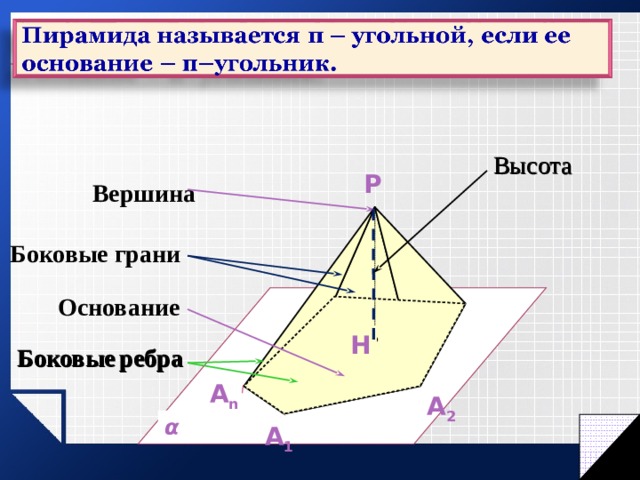
Элементы пирамиды
- МО – высота
- МН – апофема
- АМ, ВМ, СМ, ДМ – боковые ребра
- АМД, ДМС, СМВ, ВМА – боковые грани
- АВСД – основание
Формулы
- h – высота
- S – площадь основания
Интересные факты
- Однажды один великий математик решил узнать побольше об уникальных свойствах пирамиды. Он приехал в Египет и тщательно обследовал пирамиду Хеопса. На самой вершине он обнаружил маленькую незаметную кнопку и он на нее нажал. Нажмите на кнопку и Вы.
Задача 1
- ABCD – квадрат со стороной 4. Боковые ребра пирамиды равны 6.
- Найти: V
далее
Задача 2
- АВ=12, АС=ВС=10, АМ=ВМ=СМ=12
- Найти: V
далее
Задача 3
- АС=15, ВС=14, АВ=13. Все двугранные углы при ребрах основания равны 600
- Найти: V
далее
Тема урока:
Объем пирамиды.
Что мы знаем о пирамиде?
Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды , точки, не лежащей в плоскости основания – вершины пирамиды и треугольников — боковых граней .
Высота
P
Вершина
Боковые грани
Основание
H
Боковые ребра
А n
А 2
α
А 1
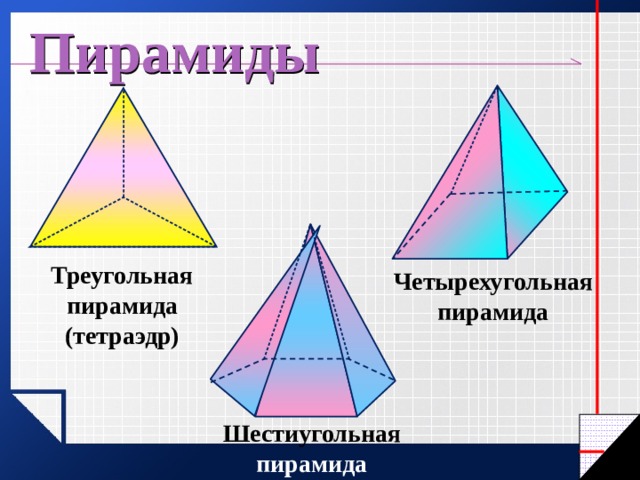
Пирамиды
Треугольная пирамида (тетраэдр)
Четырехугольная пирамида
Шестиугольная пирамида
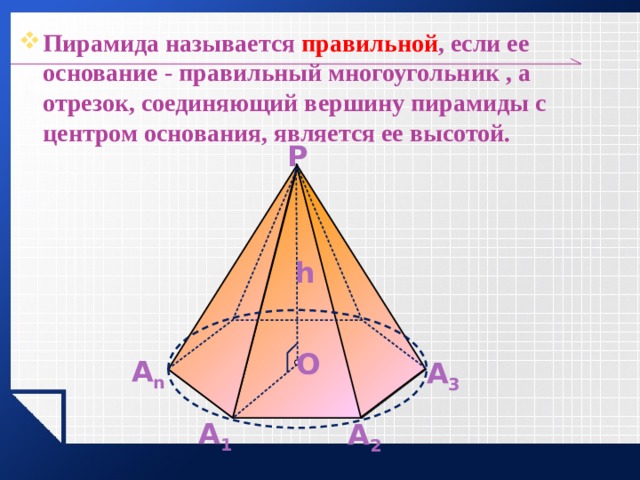
- Пирамида называется правильной , если ее основание — правильный многоугольник , а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.
P
h
O
А n
А 3
А 1
А 2
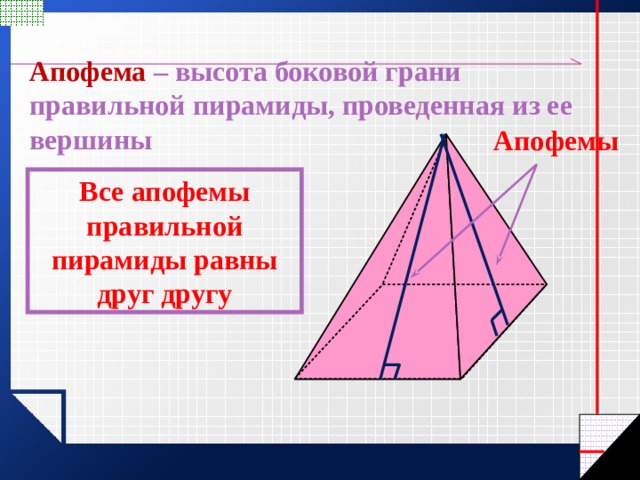
Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины
Апофемы
Все апофемы правильной пирамиды равны друг другу
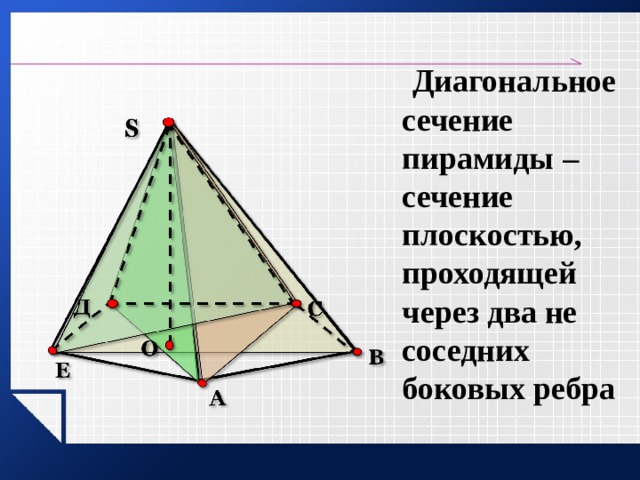
Диагональное сечение пирамиды – сечение плоскостью, проходящей через два не соседних боковых ребра
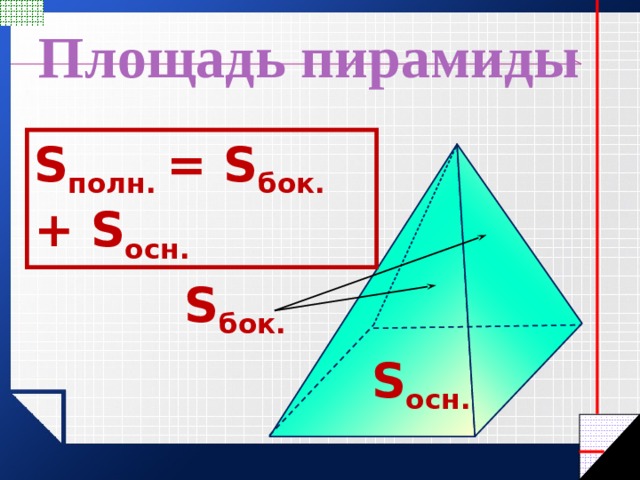
Площадь пирамиды
S полн. = S бок. + S осн.
S бок.
S осн.
H
h
Свойства пирамиды:
У правильной пирамиды:
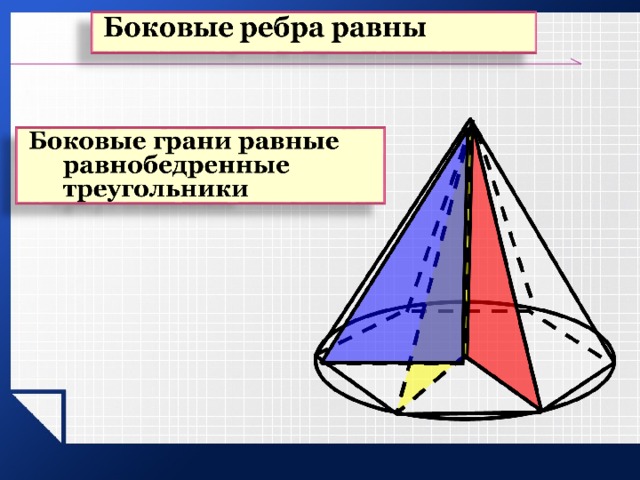
- боковые ребра равны;
- боковые грани являются равными равнобедренными треугольниками;
- апофемы равны;
- площадь боковой поверхности правильной пирамиды равна половине произведения периметра на апофему.
Свойства пирамиды:
- если боковые ребра пирамиды равны (или составляют равные углы с плоскостью основания), то вершина пирамиды проецируется в центр окружности, описанной около основания.
- если двугранные углы при основании пирамиды равны (или равны высоты боковых граней, проведенные из вершины пирамиды), то вершина пирамиды проецируется в центр окружности, вписанной в основание пирамиды.
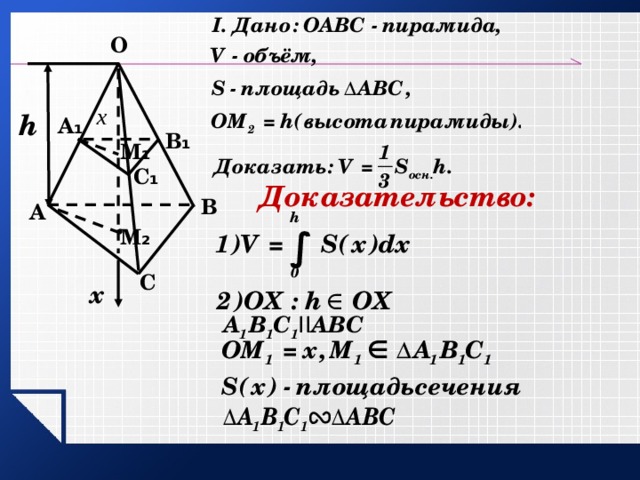
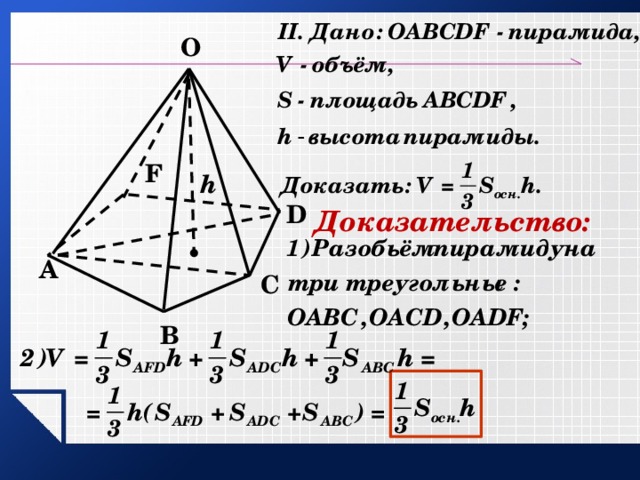
Теорема: Объём пирамиды равен одной трети произведения площади основания на высоту.
∙
O
h
А ₁
В ₁
М ₁
С ₁
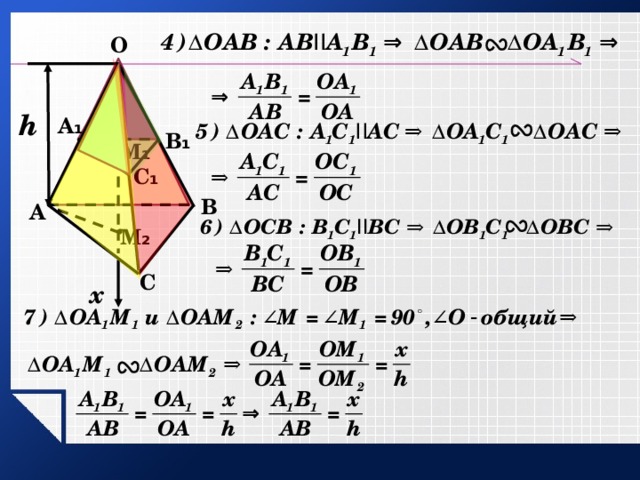
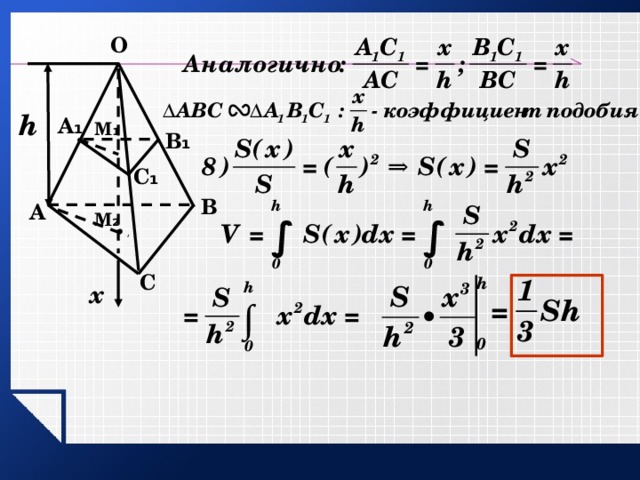
Доказательство:
В
А
М ₂
С
х
O
h
А ₁
В ₁
М ₁
С ₁
В
А
М ₂
С
х
O
h
А ₁
М ₁
В ₁
С ₁
В
А
М ₂
С
х
О
F
h
D
Доказательство:
А
С
В
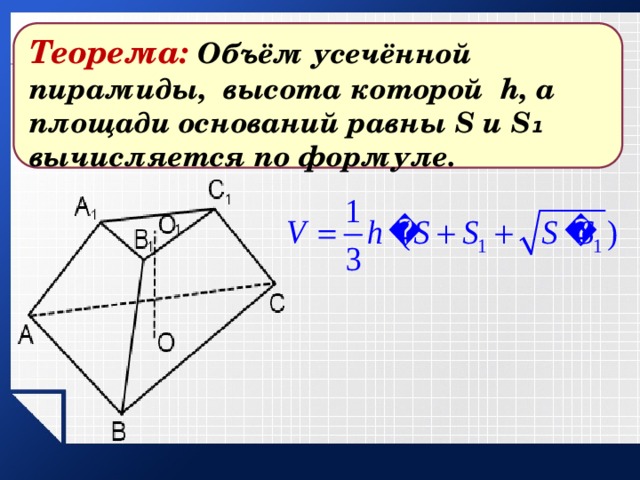
Теорема: Объём усечённой пирамиды, высота которой h, а площади оснований равны S и S₁ вычисляется по формуле.
- Объем усеченной пирамиды будем рассматривать как разность объемов полной пирамиды и той, что отсечена от нее плоскостью, параллельной основанию
Объем полной пирамиды
(1)
Подставляем в уравнение 1
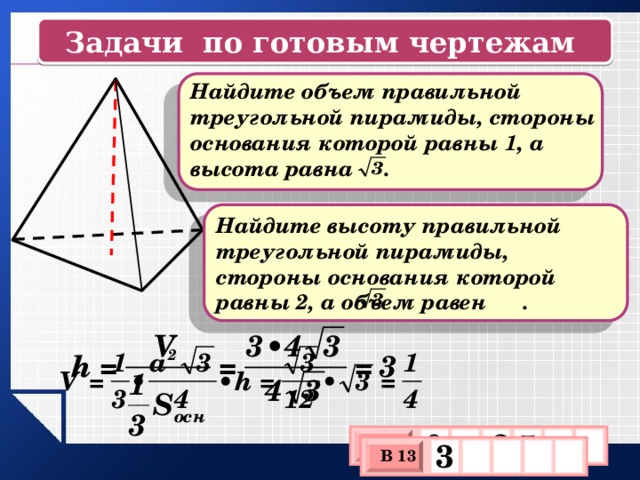
Задачи по готовым чертежам
Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна .
Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен .
0
2
,
5
В 13
3
х
3
х
1
0
В 13
х
3
х
1
0
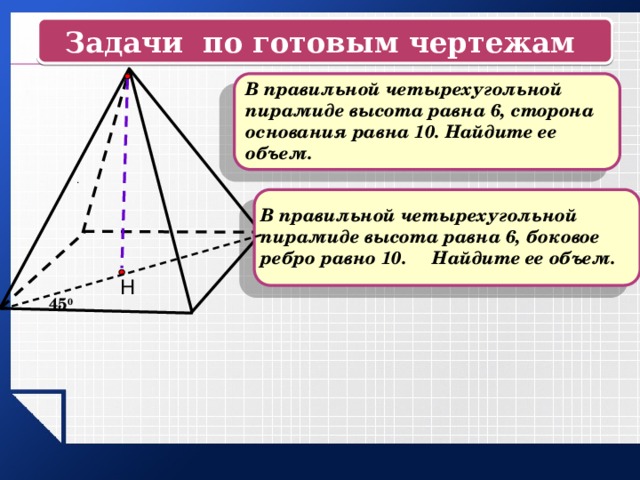
Задачи по готовым чертежам
В правильной четырехугольной пирамиде высота равна 6, сторона основания равна 10. Найдите ее объем.
.
В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
Н
45 0
Задачи (база)
Сторона основания правильной треугольной пирамиды равна 6, а боковое ребро образует с плоскостью основания угол 45 0 . Найдите объем пирамиды.
Высота правильной треугольной пирамиды равна , а боковая грань образует с плоскостью основания угол 60 0 . Найдите объем пирамиды.
Задачи (профиль)
Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 8. Найдите объем шестиугольной пирамиды.
От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания.
Найдите объем отсеченной треугольной пирамиды.
Домашнее
задание:
П. 80, № 685,
686.
Презентация на тему Объем пирамиды. Решение задач по материалам ЕГЭ
Содержание
-
1.
Объем пирамиды. Решение задач по материалам ЕГЭ -
2.
Виды пирамид -
3.
Стороны основания правильной шестиугольной -
4.
Стороны основания правильной -
5.
Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое -
6.
Объем параллелепипеда равен 9. Найдите -
7.
8 -
8.
Скачать презентацию -
9.
Похожие презентации
Виды пирамид
Слайды и текст этой презентации
Слайд 1
Решение задач
по теме
«ОБЪЕМ ПИРАМИДЫ»
(по материалам ЕГЭ)

Слайд 3
Стороны основания правильной шестиугольной пирамиды равны 10,
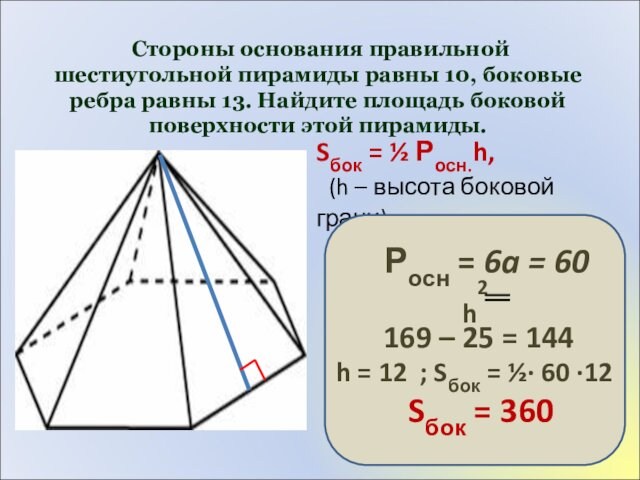
боковые ребра равны 13. Найдите площадь боковой поверхности этой
пирамиды.
Sбок = ½ Росн.h,
(h – высота боковой грани)
h2
169 – 25 = 144
Росн = 6a = 60
h = 12 ; Sбок = ½∙ 60 ∙12
Sбок = 360
Слайд 4
Стороны основания правильной шестиугольной пирамиды равны 10,
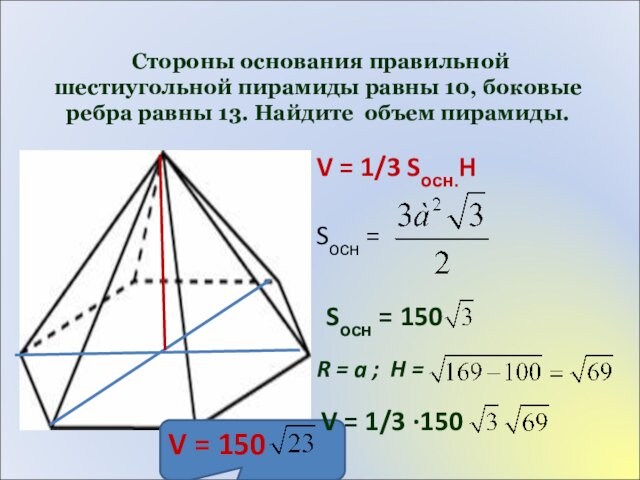
боковые ребра равны 13. Найдите объем пирамиды.
V = 1/3
Sосн.H
Sосн =
Sосн = 150
R = a ; H
=
V = 1/3 ∙150
V = 150
Слайд 5
Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из
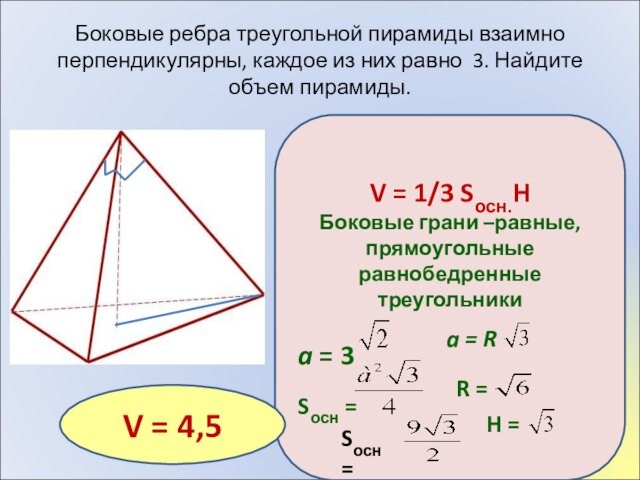
них равно 3. Найдите объем пирамиды.
V = 1/3 Sосн.H
Боковые
грани –равные,прямоугольные равнобедренные треугольники
a = 3
Sосн =
Sосн =
a
= R
R =
H =
V = 4,5
Слайд 6
Объем параллелепипеда равен 9. Найдите объем треугольной пирамиды
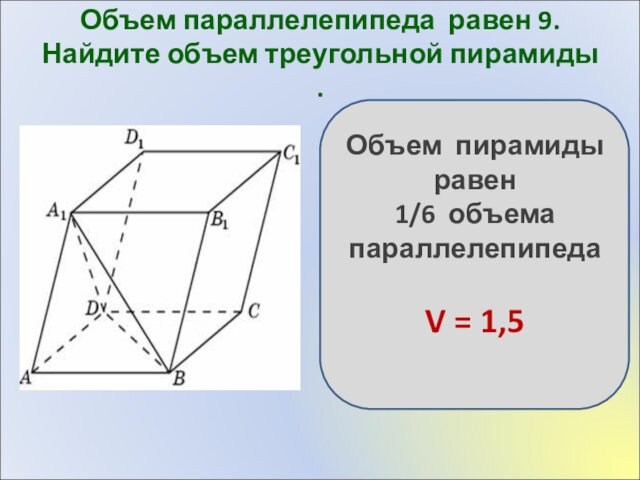
.
Объем пирамиды равен
1/6 объема параллелепипеда
V = 1,5