Объем прямоугольного параллелепипеда 11 класс презентация атанасян задачи егэ

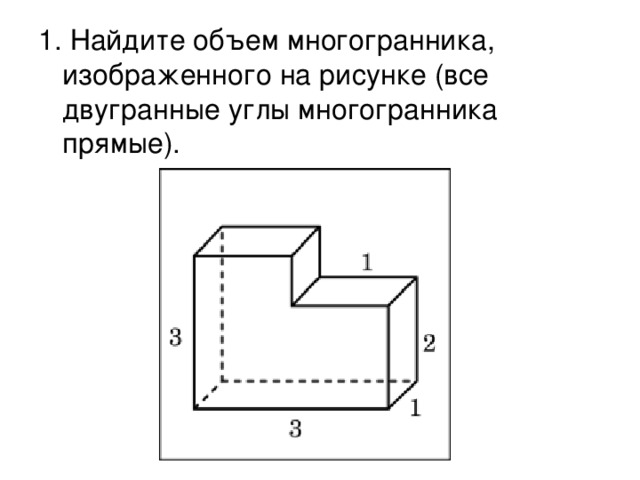
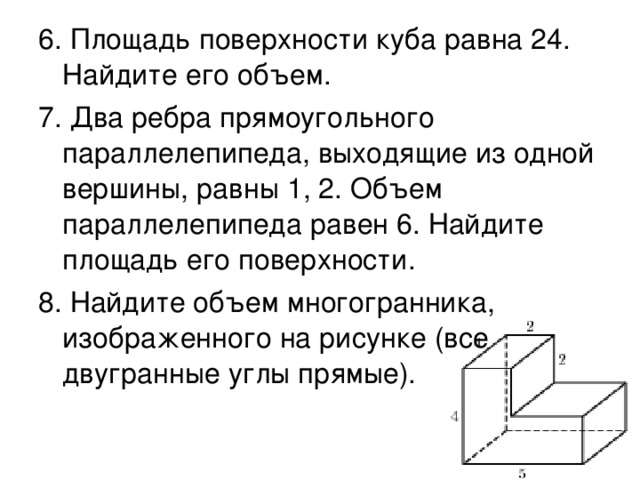
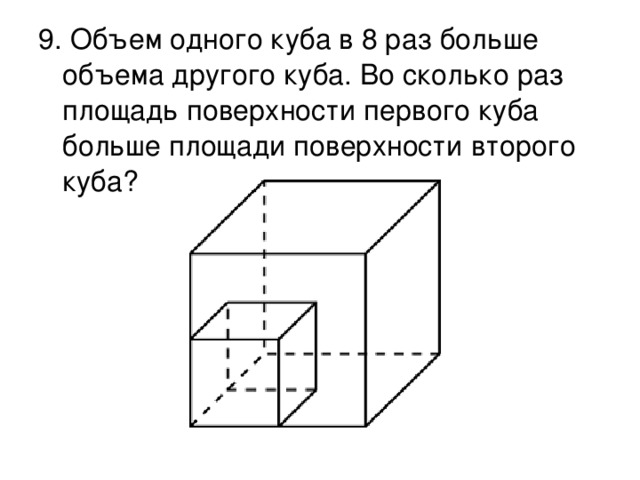
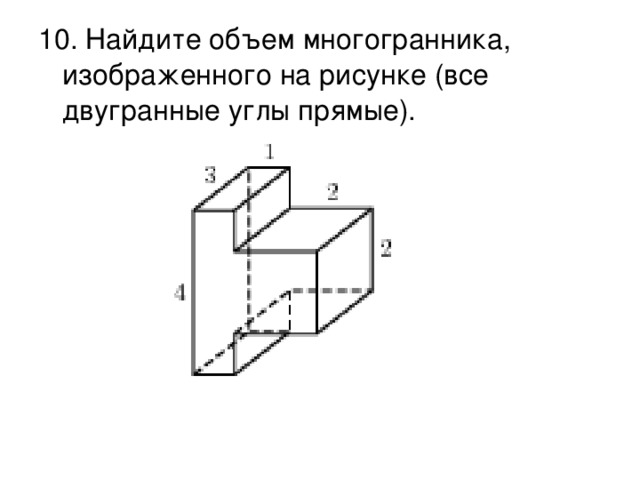
Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Прямоугольный параллелепипед
  Типовые задачи
  ЕГЭ
  Учитель математики: Бондарева Виктория Викторовна
  Экономический лицей ФГБОУ ВО РЭУ им. Г.В Плеханова

• 

  2 слайд

  b
  Формулы полной поверхности и объёма
  прямоугольного параллелепипеда
  a
  c

   d

• 

  3 слайд

  Найдите квадрат расстояния между вершинами С и А1 прямоугольного
  параллелепипеда, для которого АВ = 5, AD = 4, AA1 = 3.
  A
  B
  C
  D
  A1
  B1
  C1
  D1
  № 1

• 

  4 слайд

  Найдите квадрат расстояния между вершинами А и D1 прямоугольного
  параллелепипеда, для которого АВ = 5, AD = 4, AA1 = 3.
  A
  B
  C
  D
  A1
  B1
  C1
  D1
  № 2

• 

  5 слайд

  Найдите угол ABD1 прямоугольного параллелепипеда,
  для которого АВ = 5, AD = 4, AA1 = 3. Ответ дайте в градусах
  A
  B
  C
  D
  A1
  B1
  C1
  D1
  AA1 = 3
  № 3

• 

  6 слайд

  Найдите угол CBC1 прямоугольного параллелепипеда,
  для которого АВ = 5, AD = 4, AA1 = 4. Ответ дайте в градусах
  A
  B
  C
  D
  A1
  B1
  C1
  D1
  № 4

• 

  7 слайд

  Найдите угол DBD1 прямоугольного параллелепипеда,
  для которого АВ = 4, AD =3, AA1 = 5. Ответ дайте в градусах
  A
  B
  C
  D
  A1
  B1
  C1
  D1
  № 5

• 

  8 слайд

  В прямоугольном параллелепипеде (А…D1) известно, что
  ВD1 = 3, AD = 2, CD = 2. Найдите длину ребра АА1.
  A
  B
  C
  D
  A1
  B1
  C1
  D1
  a
  b
  h
  № 6

• 

  9 слайд

  В прямоугольном параллелепипеде (А…D1) известно, что
  DD1 = 1, AD = 2, CD = 2. Найдите длину длину диагонали СА1.
  A
  B
  C
  D
  A1
  B1
  D1
  a
  b
  h
  № 7

• 

  10 слайд

  В кубе (А…D1) точка К – середина ребра АА1, точка L – середина А1В1,
  Точка М – середина А1D1 . Найдите угол MLK. Ответ дайте в градусах
  A
  B
  C
  D
  A1
  B1
  D1
  № 8
  К
  L
  M

• 

  11 слайд

  9.Стороны основания прямоугольного параллелепипеда 3 и 4
  Диагональ параллелепипеда образует с плоскостью основания угол 450.
  Найдите полную поверхность параллелепипеда.

• 

  12 слайд

  10. Найдите площадь четырёхугольника, вершинами которого являются
  середины рёбер AD, A1D1, DC, D1C1 прямоугольного
  параллелепипеда ABCDA1B1C1D1 с рёбрами AB=4, AD=3,

• 

  13 слайд

  В кубе (А…D1) найдите угол между прямыми AD1 и B1D1.
  Ответ в градусах
  A
  B
  C
  D
  A1
  B1
  C1
  D1
  № 11

• 

  14 слайд

  В прямоугольном параллелепипеде (А…D1) известно, что
  АА1 = 21, AВ = 8, АD = 6. Найти синус угла между прямыми СD и А1С1.
  A
  B
  C
  D
  A1
  B1
  C1
  D1
  № 12
  M

• 

  15 слайд

  13. Площадь основания прямоугольного параллелепипеда
  равна 16. Ребро, перпендикулярное этой грани, рано 5.
  Найдите объём параллелепипеда.

• 

  16 слайд

  №14. Найдите квадрат расстояния между вершинами B₂ и D ₃ многогранника , изображенного на рисунке. Все двугранные углы многогранника прямые.

• 

  17 слайд

  № 15.
  Найдите угол CAD₂ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
  Ответ:60°.

  AD₂ = CD₂= CA- диагонали
  равных квадратов .

  ∆ CAD₂ — равносторонний
  треугольник.

  CAD₂=60°.
  60°

• 

  18 слайд

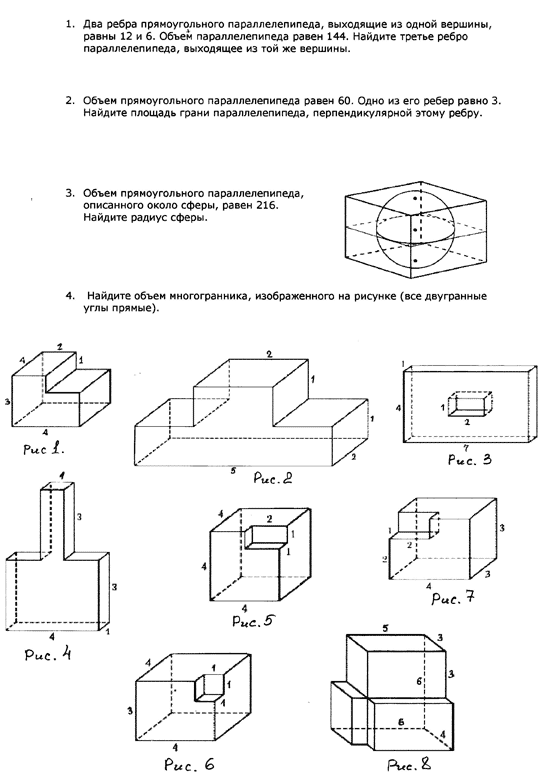
  № 16. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
  Площадь поверхности данной фигуры будет равна площади поверхности прямоугольного параллелепипеда.
  6
  4
  3
  2
  10
  8

• 

  19 слайд

  №17. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
  2
  3
  4
  6
  4
  5
  3

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 154 748 материалов в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вам будут интересны эти курсы:

• Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»

• Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»

• Курс профессиональной переподготовки «Управление персоналом и оформление трудовых отношений»

• Курс повышения квалификации «Управление финансами: как уйти от банкротства»

• Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»

• Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Использование активных методов обучения в вузе в условиях реализации ФГОС»

• Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»

• Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»

• Курс профессиональной переподготовки «Управление сервисами информационных технологий»

• Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»

• Курс профессиональной переподготовки «Деятельность по хранению музейных предметов и музейных коллекций в музеях всех видов»

• Курс профессиональной переподготовки «Теория и методика музейного дела и охраны исторических памятников»

---

Целевая аудитория: для 11 класса

Автор: Отдельнова Любовь Владимировна
Место работы: МОУ Новолядинская СОШ
Добавил: lotdelnova

© 2007 — 2023 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.

---

Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.

---

Фотографии предоставлены

Слайд 1

Решение задач практического содержания на вычисление объема прямоугольного параллелепипеда

Слайд 2

Карточка № 1. Прочитайте задачи практического содержания: Вычислить объем стены, сложенной из 1200 кирпичей. Учесть, что за счет раствора объем увеличивается на 15 %. Размер одного кирпича 25*12*6 см. Сколько строительного кирпича потребуется для постройки стены длиной 12 м, толщиной 0,5 м и высотой 2,5 м, если в 1 м 3 кирпичной площадки содержится 400 штук кирпича? Определите массу мраморной плиты, размер которой 100 * 80* 10 см. Плотность мрамора 2,7 г/см 3 .

Слайд 3

Сравните вопросы задач с теми, которые мы поставили. Что вы заметили? Где в жизни могут пригодиться задачи такого типа? Что нам нужно знать для разрешения данных вопросов?

Слайд 4

Какую форму имеет кирпич? Как найти объем кирпича, его массу? Алгоритм решения задачи: Найти объем кирпича по формуле V = Найти массу кирпича по формуле m =

Слайд 5

А если стена состоит из нескольких кирпичей? Что еще нам нужно учесть при укладке кирпича? Что такое 1%? Как вычислить процент от числа?

Слайд 6

Найти объем одного кирпича. Найти объем всех кирпичей. Найти объем раствора. Найти объем стены Как будем работать на «строительной площадке»: индивидуально, в парах или коллективно с помощью учителя? Алгоритм решения задачи:

Слайд 7

1. Кирпич имеет форму прямоугольного параллелепипеда с измерениями 25 см. 12 см и 6,5 см. Плотность кирпича равна 1,8 г/см 3 . Найдите его массу. 2. Строительный кирпич имеет размер 25*12*6 см. Найдите объем стены, выложенной из 10 000 кирпичей. Учтите, что раствор увеличивает объем на 15 %.

Слайд 8

Карточка № 2. Следует изготовить емкость кубической формы, чтобы она вмещала 2.5 м 3 шлака. Найдите высоту емкости. Из медной болванки прокатан лист, площадь которого равна 10 дм 2 . Найти толщину этого листа, если вес болванки равен 440 г (плотность меди 8,8 г/см 3 ). Из прутика стали квадратного сечения 45 мм* 45 мм нужно отковать 6 поковок для квадратных гаек размером 50 мм*50 мм*25 мм. Какой длины нужно взять прутик? Припуск на угар и обработку составляет 6% объема поковок.

Данная презентация предназначена учащимся одиннадцатого класса при подготовке к единому государственному экзамену по математике. А так же эту работу могут использовать учителя математики на своих уроках при обобщении и повторении темы «Объём прямоугольного параллелепипеда» по геометрии.

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

Цели урока:

• Образовательные:   ввести понятие
  объёма, рассмотреть свойства объёмов
  геометрических тел, рассмотреть формулу объёма
  прямоугольного параллелепипеда, рассмотреть
  решение основных типов задач (из банка заданий
  ЕГЭ) по теме,  учить решать задачи
  практического содержания
• Развивающие:   развивать
  логическое  мышление, пространственное
  воображение,  расширять представления об
  окружающем нас мире, развивать умение
  осуществлять самоконтроль
• Воспитательные:   воспитывать
  ответственное отношение к учебному труду,
  уважительное отношение к сверстникам, развивать
  умение оказывать взаимопомощь, воспитывать
  интерес к предмету.

Оборудование: набор карточек с
формулами для вычисления площадей, модели
многоугольников, презентации к уроку,
мультимедийная установка.

ХОД УРОКА

1. Организационный этап

Учитель проверяет готовность учащихся к уроку
и подготовленность классного помещения.

2. Проверка выполнения домашнего задания

Учитель: К сегодняшнему уроку вам
предлагалось вспомнить формулы для вычисления
площадей плоских фигур.

(К доске прикреплены бумажные модели известных
учащимся геометрических фигур (прямоугольник,
трапеция, прямоугольный треугольник, ромб,
квадрат, произвольный треугольник,
параллелограмм)).

Вызванный к доске ученик из имеющегося набора
карточек с формулами площадей выбирает нужные и
прикрепляет их рядом с соответствующей фигурой.

Учитель: А мы пока проверим, как вы
выполнили задание по карточкам.

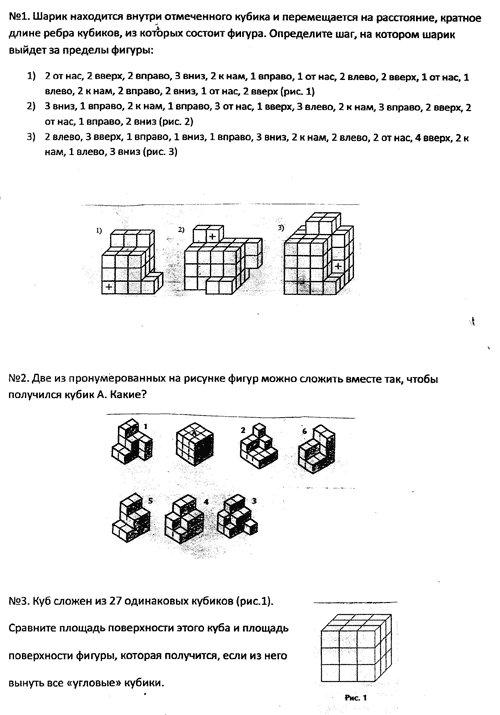
Рисунок 1

В ходе фронтальной беседы с классом обсуждаем
получившиеся результаты:

№1. Рис.1 – «3 вниз», рис. 2 – «3 от нас», рис. 3– « 2
к нам»;
№2. Фигуры  2 и  4;
№3. «останется без изменений»

3. Подготовка учащихся к работе на основном
этапе

Учитель: При решении задач на уроках
геометрии (в том числе и при решении задач ЕГЭ)
нам очень часто приходится вычислять площади
геометрических фигур.
Давайте вспомним соответствующие формулы (класс
проверяет работу вызванного к доске ученика).
А теперь предлагаю вашему вниманию  задачи 
из банка заданий ЕГЭ.

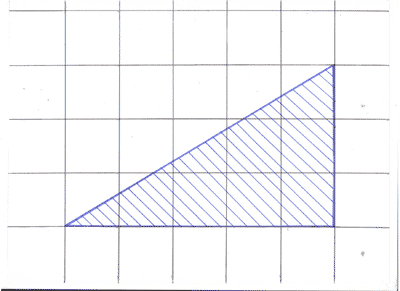
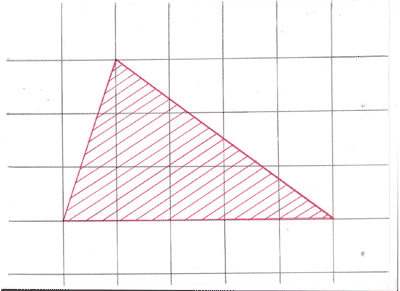
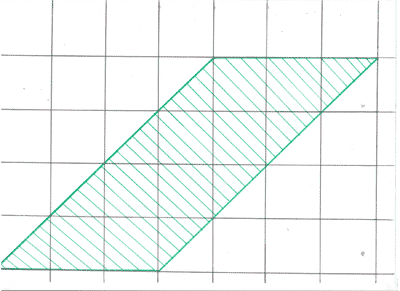
Задание 1. (Устно). Найдите площади
фигур, изображённых на рисунке (клетка 1см х 1см).

Рисунок 2

Рисунок 3

Рисунок 4

Задание 2. Найдите площадь
четырёхугольника ABCD, заданного координатами
своих вершин A(– 4; 3), B(5; 5), C(8; – 1), D(2; – 2).

Учащиеся работают в тетрадях, а один из
учеников решает задачу у доски.

4. Этап усвоения новых знаний и способов
действий

Учитель: Что отличает геометрические
тела, с которыми мы работаем на уроках
стереометрии, от рассмотренных геометрических
фигур?
Правильно, геометрические тела объёмные.
Итак, мы с вами приступаем к изучению ещё одного
очень важного понятия – объём.

Тема урока: «Понятие объёма. Объём
прямоугольного параллелепипеда»

Учащимся демонстрируются слайды №1-3
презентации (смотри Приложение
1). Сегодня мы:

• совершим небольшой экскурс в историю
• узнаем, какими свойствами обладают объёмы
• вспомним, как вычисляется объём прямоугольного
  параллелепипеда
• посмотрим, как эти сведения используются на
  практике.

Также сегодня вам предстоит поработать в
группах, а закончится урок математическим
диктантом, так что будьте внимательны!

В качестве девиза нашего занятия я выбрала
античный афоризм  «Незнающие пусть научатся, а
знающие вспомнят ещё раз».
А сейчас слово Ивановой Даше, она вкратце
ознакомит нас с историей возникновения понятия
объёма.

(Ребятам демонстрируется презентация,
выполненная этой ученицей; смотри Приложение
2).

Учитель:Объёмы, также как и длины
отрезков, и площади многоугольников, обладают
рядом свойств. Эти свойства достаточно очевидны
и аналогичны известным вам свойствам.
После этих слов учителя на экране «всплывают»
слова «Свойства длин отрезков, площадей
многоугольников, объёмов тел». Далее по щелчку
мыши на экране появляются вышеупомянутые
свойства, известные учащимся, а соответствующее
свойство объёмов тел дети формулируют
самостоятельно, после чего это свойство тоже
«всплывает» на экране.

(На этом этапе работы используется слайд №4
презентации, смотри Приложение
1).

В современной архитектуре, да и не только в
современной, используются различные формы,
представляющие из себя известные нам
геометрические тела  (демонстрируются слайды
№5-6 презентации, смотри Приложение
1). Назовите эти тела.

Изучение теории объёмов мы начнём с достаточно
часто встречающегося геометрического тела –
прямоугольного параллелепипеда.

А теперь блиц-опрос.

• Сколько граней у прямоугольного
  параллелепипеда?
• Какими фигурами являются грани прямоугольного
  параллелепипеда?
• Сколько измерений у прямоугольного
  параллелепипеда?
• Как мы их обычно называем?
• Верно ли, что куб является прямоугольным
  параллелепипедом?
• Все грани куба – это …
• Назовите предметы окружающей обстановки,
  имеющие форму прямоугольного параллелепипеда.

Теперь давайте вспомним формулу, по которой
вычисляется объём прямоугольного
параллелепипеда. Эта формула хорошо вам известна
из курса математики 5 класса.
Итак, как вычислить объём прямоугольного
параллелепипеда?

Учитель на доске, а учащиеся в тетрадях
записывают формулу V = abc

5. Этап закрепления новых знаний и способов
действий

Учитель: Пришла пора потренироваться
в решении задач на нахождение объёмов
прямоугольных параллелепипедов.

Задача 1. Кабинет, в котором проходит
наш урок, имеет форму прямоугольного
параллелепипеда с измерениями 6,5 м, 8 м и 3,6 м. По
принятым санитарным нормам на одного учащегося в
учебном кабинете должно приходиться не менее 6 м³
воздуха. Какое наибольшее количество учащихся
можно разместить в этом кабинете, не нарушая
санитарных правил?

(Дети решают эту задачу самостоятельно в
своих тетрадях, после чего обсуждаем
получившиеся результаты).

Решение. Вычислим объём классной комнаты:
6,5 ^. 8 ^. 3,6 = 187,2 м³
. Узнаем, сколько учащихся можно разместить в
этом помещении, при условии, что на одного
учащегося приходится 6 м³ воздуха: 187,2 : 6 = 31,2.
Следовательно, в кабинете может заниматься 31
ученик.

Задача 2. При подготовке к ЕГЭ вам
наверняка встречались задания на нахождение
объёмов многогранников такого вида (на экране
появляется слайд №7 презентации, смотри Приложение 1).
В процессе обсуждения способов решения задачи
вспоминаем изученное на уроке свойство объёмов,
которое позволяет нам разбивать многогранник на
части, объёмы которых мы в состоянии вычислить.

После проведённой с ребятами беседы на экране
поочерёдно появляются те самые «части
многогранника» со всплывающими измерениями
(демонстрация слайда с анимацией).

6.  Применение знаний и способов действий

На этом этапе урока учащиеся работают в группах
по 4 человека. Каждой группе предлагается
карточка с заданиями по изученному на уроке
материалу.

Рисунок 5

На работу в группе отводится 7 минут.
По окончании работы полученные результаты
обсуждаются (каждое из предложенных заданий
высвечивается на экране, слайды №8-11 презентации,
смотри Приложение 1).

7. Контроль и самоконтроль знаний и
способов действий

Учащиеся в тетрадях выполняют задания
математического диктанта:

• Заполни пропуски: «Равные тела имеют … объёмы».
• Заполни пропуски: «Если тело составлено из
  нескольких тел, то его объём равен … объёмов этих
  тел».
• Заполни пропуски: «Объём прямоугольного
  параллелепипеда равен … трёх его измерений».
• Заполни пропуски: «Объём куба равен … его
  ребра».
• Найдите объём многогранника, изображённого на
  рисунке (все двугранные углы прямые).
• Измерения прямоугольного параллелепипеда
  равны 10 см, 10 см и 5 см. Найдите ребро куба, объём
  которого в 2 раза больше объёма данного
  параллелепипеда.
• Во сколько раз нужно увеличить каждое из трёх
  измерений прямоугольного бруса, чтобы объём его
  увеличился в 8 раз?

(При выполнении заданий 1-5 соответствующая
информация демонстрируется учащимся на экране;
слайды №12-13 презентации, смотри Приложение
1).
После выполнения всех заданий диктанта ребята
осуществляют самопроверку (открываются
правильные ответы, записанные за доской).

8. Информация о домашнем задании

а) из учебника п. 74, 75 (до следствия 1)
б) подобрать, используя различные ресурсы, 2-3
задачи рассмотренных на уроке типов из банка
заданий ЕГЭ
в) выполните задание на карточке: «Когда человеку
уютно, приятно, спокойно, он говорит, что ему
комфортно. Оказывается, комфортность
определяется формой помещения, его линейными
размерами. Коэффициент комфортности можно найти
по формуле:  ,
где  – коэффициент комфортности, V – объём
жилища, S – площадь поверхности жилища,
включая пол. Чем меньше коэффициент, тем
комфортнее жилище. Используя данную формулу,
определите наиболее комфортную комнату в вашей
квартире».

9. Рефлексия

Закончите фразу «Сегодня на уроке я …».

Ребята, а кому из вас сегодняшний урок поможет
лучше подготовиться к сдаче ЕГЭ?

10. Подведение итогов занятия

Учитель даёт качественную оценку работы класса
и отдельных учащихся.
Спасибо за урок! (Демонстрация последнего слайда
№14 презентации, смотри Приложение
1).

Понятие объема.
Объем прямоугольного параллелепипеда.
задача

• Резервуар для воды следует установить на площадке, которая служит для него дном. Какая должна быть высота резервуара? Емкость резервуара , размер площадки ?

 

•  

Надо знать!
*Объем геометрического тела — положительное число, которое характеризует часть пространства, занимаемую геометрическим телом и удовлетворяющую следующим условиям:

• равные тела имеют равные объемы;
• если тело разбито на несколько частей, то его объем равен сумме объемов всех этих частей;
• объем куба, ребро которого равно единицы длины, равен единице.
• Единичнымназывают куб, ребро которого равно единице.
• Объем единичного куба принимают за единицу объема.
• Поясните, что такое .
• Вспомните, как по-другому называют .
• Измерить объем геометрического тела – это значит найти число, показывающее, сколько единичных кубов содержит данное тело.
• Равновеликими называют геометрические тела, объемы которых равны.

•  

Работа по учебнику.
П.74,75

План работы:

• п.74;
• п.75;
• теорема;
• следствие 1;
• следствие 2;
• на отдельном листе составить опорный конспект.

Обратите внимание!

V=

Решение задачи 1.

Будем рассматривать резервуар как прямоугольный параллелепипед объемом , основанием которого является прямоугольник со сторонами 2,5 м и 1, 75 м.

Тогда , где искомая высота,

.

Тогда .

Ответ: 2,29 м

Объем прямой призмы

• Объём прямой призмы равен произведению площади основания на высоту

V = S*h

Закрепление материала

• Определите верность утверждений.
• Равные тела имеют равные объемы.
• Два прямоугольных параллелепипеда имеют равные объемы, если их высоты равны.
• Два прямоугольных параллелепипеда имеют равные объемы, если равны площади их оснований .

Ответ: 1)

Закрепление материала!

Ребро
Объем

Ребро
Объем

2. Заполните таблицу, зная, что в ней говорится о кубе:

Проверь себя!

Ребро				0,5 м
Объем		27

Ребро				0,5 м
Объем

2. Заполните таблицу, зная, что в ней говорится о кубе:

Закрепление материала!

3. Найдите объем прямоугольного параллелепипеда, стороны основания которого равны 3 см и 4 см, а боковое ребро – 5 см.

Закрепление материала!

4. Основание прямой призмы – прямоугольный треугольник с катетами 3 см и 4 см, а боковое ребро – 5 см. Найдите объем призмы.

Работа в парах

• Полная поверхность куба равна . Найдите куба.
• Объем куба равен . Найдите боковой поверхности куба.
• Каждое ребро прямого параллелепипеда равно 4 см, а острый угол основания . Найдите
• Измерения прямоугольного параллелепипеда равны 8 см, 12 см,18 см. Найдите ребро куба, объем которого равен объему этого параллелепипеда.

Работа в парах

• В основании прямой призмы лежит прямоугольный треугольник с гипотенузой 13 см и одним из катетов 12 см. Высота призмы 5 см. Найдите объем призмы.
• Диагональ прямоугольного параллелепипеда равна 10 см и образует с плоскостью основания угол . Найдите объем параллелепипеда, если разность сторон основания равна 1 см.

Проверь себя!

• 64
• 96
• 32
• 12

6. 150

Домашнее задание

• Конспект, учебник: геометрия 10-11 кл.,п.74,75.,
• решить задачи №648,648, 652
• Индивидуально:

В основании прямого параллелепипеда лежит ромб, диагонали которого относятся как . Найти объем параллелепипеда, если его диагонали равны 17 см и 25 см. (Ответ: 1200)

ГОКУ АО «ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА

ПРИ УЧРЕЖДЕНИЯХ ИСПОЛНЕНИЯ НАКАЗАНИЯ»

УКП ПРИ ФКУ СИЗО-1 Г. БЛАГОВЕЩЕНСКА

ОТКРЫТЫЙ УРОК

ПО ГЕОМЕТРИИ

12 КЛАСС

ВЫПОЛНИЛА УЧИТЕЛЬ МАТЕМАТИКИ

I КВАЛИФИКАЦИОННОЙ КАТЕГОРИИ

ТЕРЕНТЬЕВА ЕЛЕНА АРКАДЬЕВНА

Незнающие пусть научатся, а знающие вспомнят ещё раз

Античный афоризм

Цели урока

• ввести понятие объёма
• рассмотреть свойства объёмов геометрических тел
• рассмотреть формулу объёма прямоугольного параллелепипеда
• рассмотреть решение основных типов задач (из банка заданий ГИА) по теме
• научиться решать задачи практического содержания

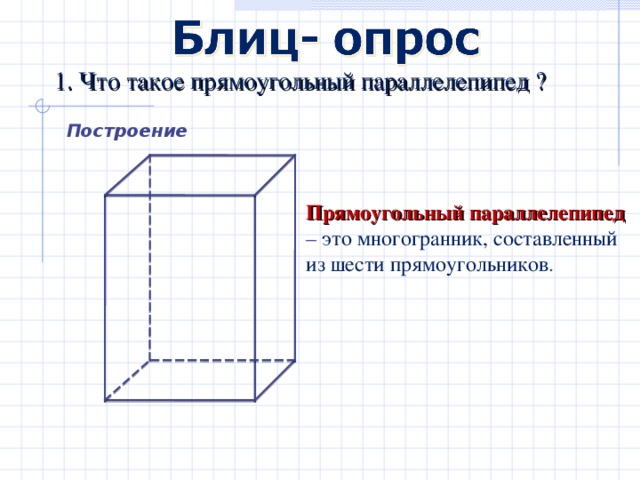
1. Что такое прямоугольный параллелепипед ?

Построение

Прямоугольный параллелепипед – это многогранник, составленный

из шести прямоугольников .

8 вершин

3.Сколько ребер у прямоугольного параллелепипеда?

Три четверки равных ребер параллелепипеда.

12 ребер

4. Какими фигурами являются грани прямоугольного

параллелепипеда?

Грани- прямоугольники

Противолежащие

грани параллельны и равны !

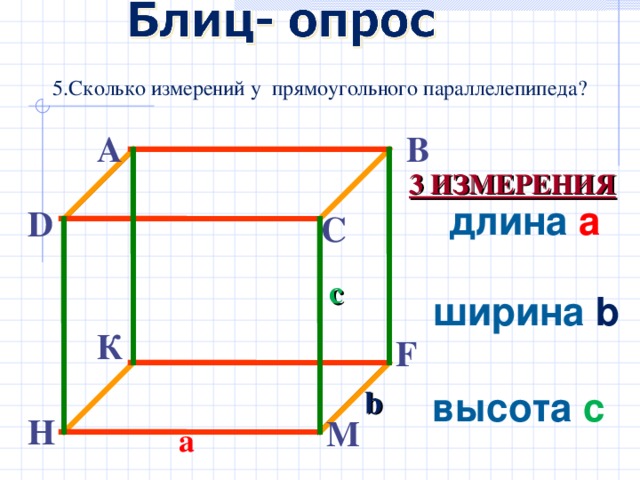
5.Сколько измерений у прямоугольного параллелепипеда?

A

B

3 ИЗМЕРЕНИЯ

длина а

D

C

c

ширина b

К

F

b

высота с

H

М

а

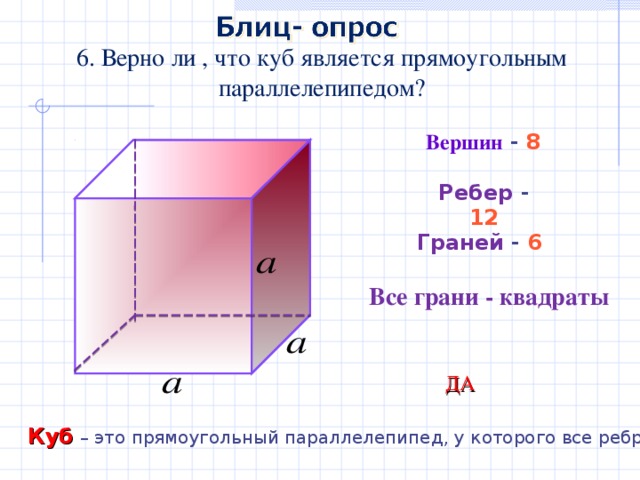
6. Верно ли , что куб является прямоугольным параллелепипедом?

Вершин — 8

Ребер — 12

Граней — 6

Все грани — квадраты

ДА

Куб – это прямоугольный параллелепипед, у которого все ребра равны.

Что такое объем?

Объём — количественная характеристика пространства, занимаемого телом или веществом.

Единица измерения объёма – куб со стороной 1

1

1

1

V = 1 ед 3

1 мм 3

1 см 3

1 дм 3 =1л

1000

1000

1 000 000 000

1000

мм 3

см 3

дм 3

м 3

км 3

:

:

:

:

1000

1000

1000

1 000 000 000

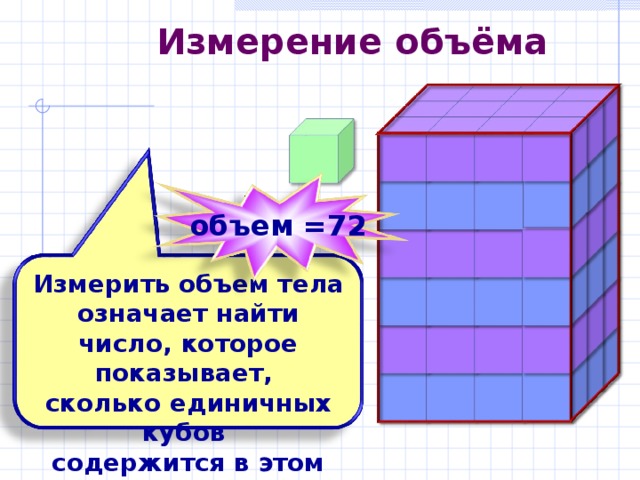
Измерение объёма

объем =72

Измерить объем тела означает найти число, которое показывает, сколько единичных кубов содержится в этом теле.

СВОЙСТВА ОБЪЕМОВ

1.Равные геометрические тела имеют равные объемы

2. Если геометрическое тело составлено из нескольких геометрических тел,

то объем данного тела равен сумме объемов тел его составляющих .

СВОЙСТВА ОБЪЕМОВ

3 . Объем куба, ребро которого равно единице длины, равен единице.

4. Два тела, объемы которых равны называются равновеликими .

1

1

1

3 л

3 л

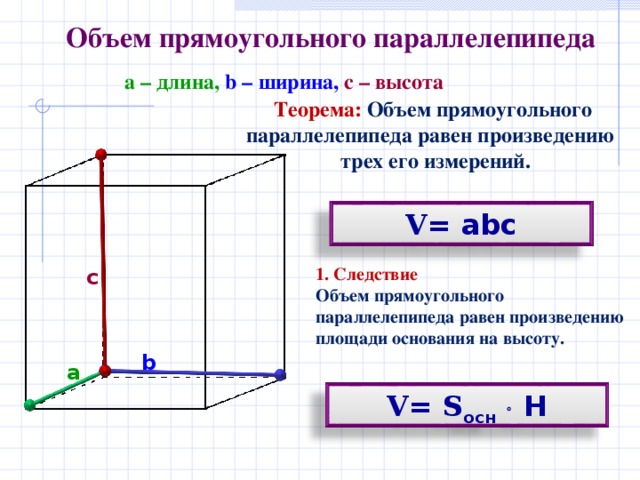
Объем прямоугольного параллелепипеда

a – длина, b – ширина, с – высота

Теорема: Объем прямоугольного

параллелепипеда равен произведению

трех его измерений.

V = abc

1. Следствие Объем прямоугольного параллелепипеда равен произведению площади основания на высоту.

c

b

а

V = S осн  Н

2. Следствие Объем прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту.

V = S осн  Н

Объем куба

V = a 3

а

а

а

4 м

4 м

6 дм

2 дм

3 см

5 cм

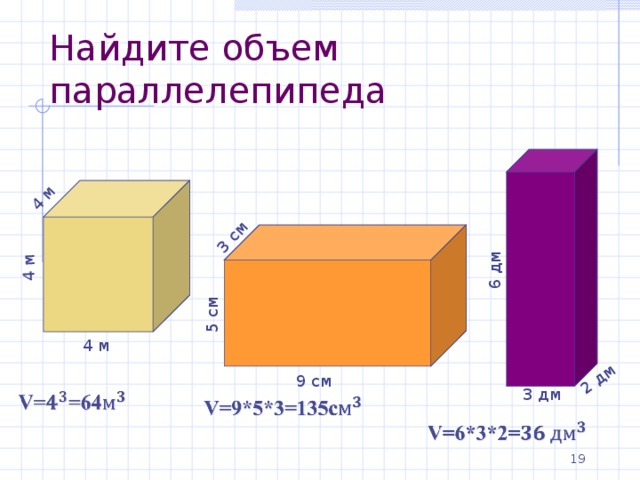
Найдите объем параллелепипеда

4 м

9 см

3 дм

18

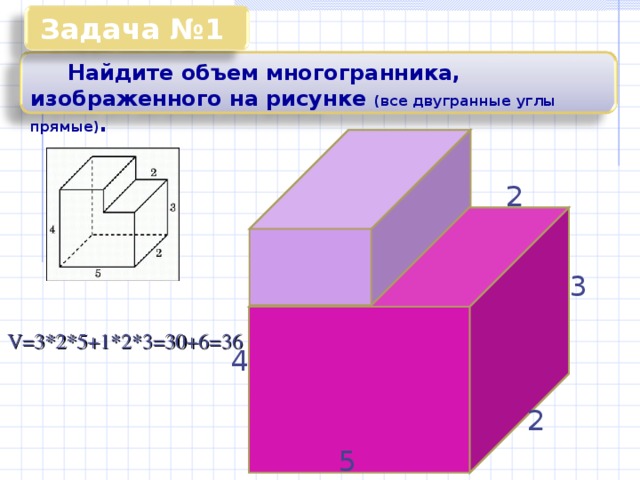
Задача №1

Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые) .

2

4

3

V=3*2*5+1*2*3=30+6=36

2

5

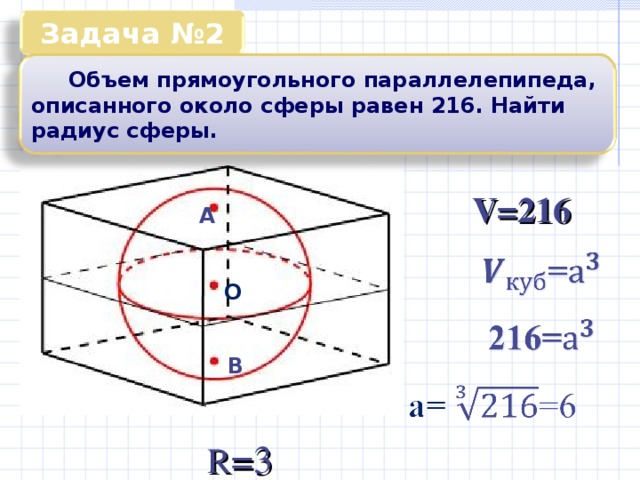
Задача №2

Объем прямоугольного параллелепипеда, описанного около сферы равен 216. Найти радиус сферы.

V=216

А

О

B

R =3

Строительство

Задача:

Сколько нужно рабочих для переноса дубовой балки размером 6,5 м х 30 см х 45 дм? Каждый рабочий может поднять в среднем 80 кг. Плотность дуба 800 кг/см 3 .

Сельское хозяйство

Задача:

Сколько сена (в тоннах) вмещает сеновал в форме прямоугольного параллелепипеда , если его длина 6м,высота 4м, ширина6 м, а тюк сена имеет размеры 0,8 × 0,4× 0,5 м и весит 20 кг?

Задача –экспертиза

Классное помещение должно быть таким, чтобы на одного человека приходилось не менее 6 м³ воздуха. Какое наибольшее количество человек можно разместить в этом кабинете, не нарушая санитарных правил, если он имеет измерения 9,3м; 6,3 м; 3,5м.?

205,065:6=34 человека

Математический диктант

• Равные тела имеют ___________ объемы

2. Если тело составлено из нескольких тел, то его объем равен ________ объемов этих тел.

3. Объем прямоугольного параллелепипеда равен _____________ трех его измерений

• Объем прямоугольного параллелепипеда равен произведению____________________на ____________

5. Объем куба равен ___________ его ребра.

6 Найти объем прямоугольного параллелепипеда с измерениями 6 см,5 см, 3 см_________

равные

сумме

произведению

площади основания

высоту

кубу

7.Во сколько раз нужно увеличить каждое из трех измерений прямоугольного бруска, чтобы объем увеличился в 8 раз. _______________

8.Найти объем куба, если длина его ребра равна 5 м __________

в два раза

Рефлексия урока:

Урок

Я на уроке

1. интересно

Итог

1. работал

2. скучно

2. отдыхал

1. понял материал

3.безразлично

2. узнал больше, чем знал

3.помогал другим

3.не понял