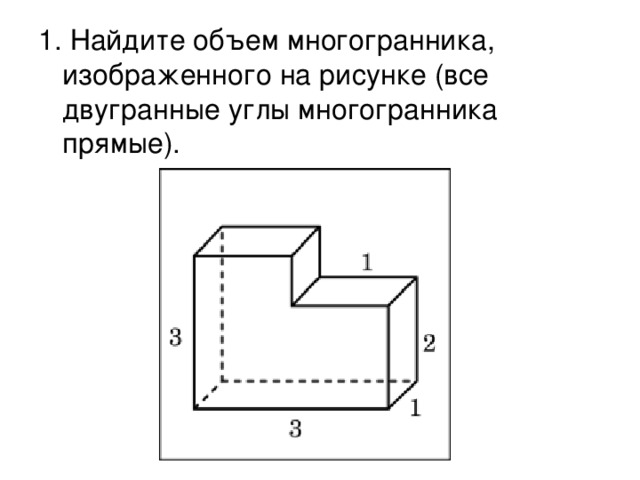
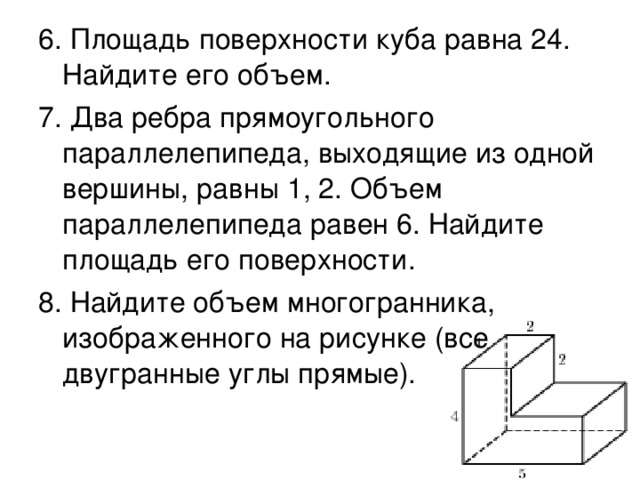
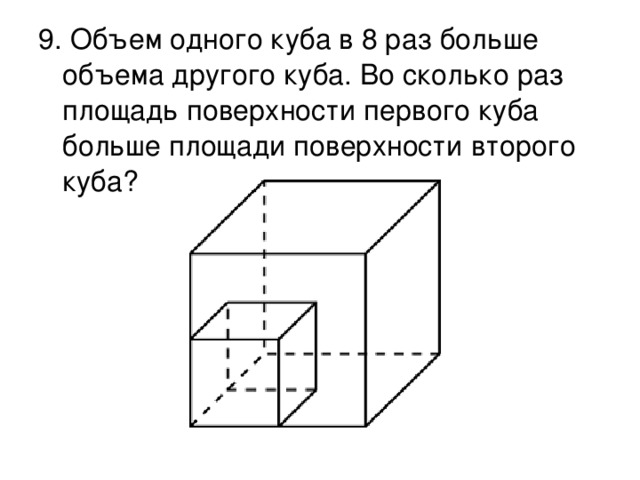
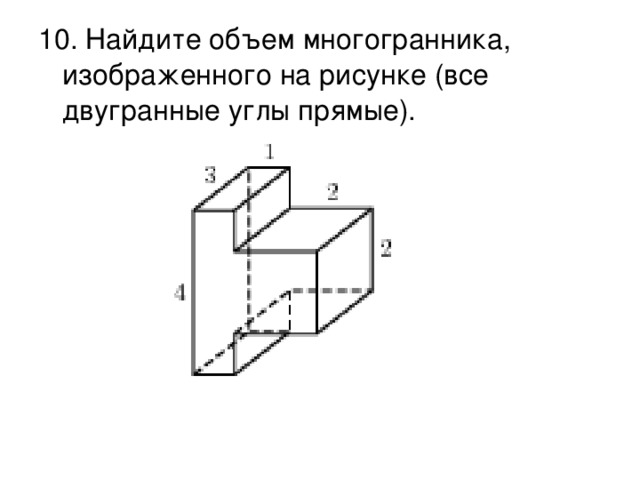
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
2
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.
3
Прямоугольный параллелепипед описан около сферы радиуса 1. Найдите его площадь поверхности.
4
Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда.
5
Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.
Пройти тестирование по этим заданиям
ЕГЭ Профиль №8. Куб, прямоугольный параллелепипед
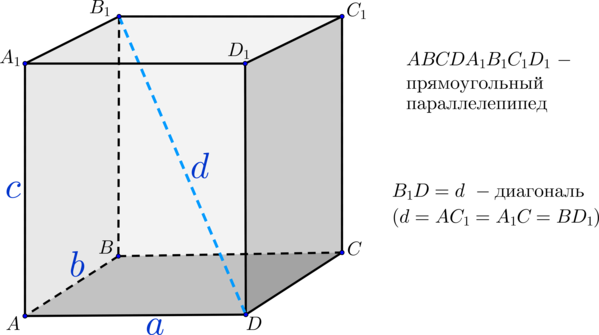
Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.
На рисунке изображен прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Его основаниями являются прямоугольники $ABCD$ и $A_1B_1C_1D_1$, а боковые ребра $AA_1, BB_1, CC_1$ и $DD_1$ перпендикулярны к основаниям.
Свойства прямоугольного параллелепипеда:
- В прямоугольном параллелепипеде $6$ граней и все они являются прямоугольниками.
- Противоположные грани попарно равны и параллельны.
- Все двугранные углы прямоугольного параллелепипеда – прямые.
- Диагонали прямоугольного параллелепипеда равны.
- Прямоугольный параллелепипед имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.
- Любая грань прямоугольного параллелепипеда может быть принята за основание.
- Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
- Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
$B_1D^2=AD^2+DC^2+C_1C^2$
Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.
Чтобы были понятны формулы, введем обозначения:
$а$ — длина;
$b$ — ширина;
$с$ — высота(она же боковое ребро);
$P_{осн}$ — периметр основания;
$S_{осн}$ — площадь основания;
$S_{бок}$ — площадь боковой поверхности;
$S_{п.п}$ — площадь полной поверхности;
$V$ — объем.
$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.
$S_{бок}=P_{осн}·c=2(a+b)·c$ – площадь боковой поверхности равна произведению периметра основания на боковое ребро.
$S_{п.п}=2(ab+bc+ac).$
Дополнительные сведения, которые пригодятся для решения задач:
Куб
$а$ — длина стороны.
$V=a^3;$
$S_{бок}=4а^2;$
$S_{п.п}=6а^2;$
$d=a√3$ – диагональ равна длине стороны, умноженной на $√3$.
Пирамида
Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) — треугольники, имеющие общую вершину.
Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.
Объем любой пирамиды равен трети произведения основания и высоты.
$V={1}/{3}S_{осн}·h$
В основании у произвольной пирамиды могут лежать различные многоугольники, рассмотрим площади некоторых из них.
В основании лежит треугольник.
Площадь треугольника.
- $S={a·h_a}/{2}$, где $h_a$ — высота, проведенная к стороне $а$.
- $S={a·b·sinα}/{2}$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
- Формула Герона $S=√{p(p-a)(p-b)(p-c)}$, где $р$ — это полупериметр $p={a+b+c}/{2}$.
- $S=p·r$, где $r$ — радиус вписанной окружности.
- $S={a·b·c}/{4R}$, где $R$ — радиус описанной окружности.
- Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ — катеты прямоугольного треугольника.
- Для равностороннего треугольника $S={a^2√3}/{4}$, где $а$ — длина стороны.
В основании лежит четырехугольник.
- Прямоугольник.
$S=a·b$, где $а$ и $b$ — смежные стороны. - Ромб.
$S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ — диагонали ромба.
$S=a^2·sinα$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами. - Трапеция.
$S={(a+b)·h}/{2}$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции. - Квадрат.
$S=a^2$, где $а$ — сторона квадрата.
Пример:
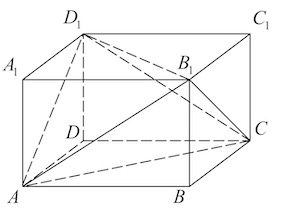
Найдите объём многогранника, вершинами которого являются точки $C, A_1, B_1, C_1, D_1$ параллелепипеда $ABCDA_1B_1C_1D_1$, у которого $AB=8, AD=12, AA_1=4$.
Решение:
Изобразим прямоугольный параллелепипед и на нем отметим вершины многогранника $C, A_1, B_1, C_1, D_1$, получим в итоге четырехугольную пирамиду. В основании пирамиды лежит прямоугольник, так основание пирамиды и прямоугольного параллелепипеда совпадают.
Объем пирамиды, в основании которой лежит прямоугольник
$V={S_{прямоугольника}·h}/{3}={a·b·h}/{3}$, где $a$ и $b$ — стороны прямоугольника.
Для нашего рисунка стороны прямоугольника – это $А_1В_1$ и $A_1D_1$.
В прямоугольном параллелепипеде противоположные ребра равны и параллельны, следовательно, $AB=А_1В_1=8; AD=A_1D_1=12$.
Высотой в пирамиде $CA_1B_1C_1D_1$ будет являться ребро $СС_1$, так как оно перпендикулярно основанию (из прямоугольного параллелепипеда).
$СС_1=АА_1=4$
$V={А_1В_1·A_1D_1·СС_1}/{3}={8·12·4}/{3}=128$
Ответ: $128$
Теорема Пифагора.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи по теме «Прямоугольный параллелепипед»
(blacktriangleright) Прямоугольный параллелепипед – это параллелепипед, все грани которого являются прямоугольниками.
Другими словами, это прямая призма, основания которой – прямоугольники.
(эти определения эквивалентны).
Тогда:
1) противоположные грани равны между собой;
2) боковые ребра перпендикулярны основаниям, то есть являются высотами;
3) как следствие, формула для объема принимает вид: ({Large{V=abc}}), где (a, b, c) – три различных боковых ребра.
(blacktriangleright) Диагональ прямоугольного параллелепипеда – это отрезок, соединяющий две противоположные (не лежащие в одной грани) вершины.
1) Все диагонали равны, пересекаются в одной точке и делятся ею пополам;
2) Диагональ (d) можно найти по формуле: ({Large{d^{,2}=a^2+b^2+c^2}}).
Задание
1
#2863
Уровень задания: Легче ЕГЭ
Дан прямоугольный параллелепипед, стороны основания которого равны (4) и (5), а боковое ребро равно (3). Найдите наибольшую площадь его грани.
Заметим, что все варианты для площадей его граней – это всевозможные попарные произведения чисел (3,4,5), то есть (3cdot
4), (4cdot 5) или (3cdot 5). Среди этих произведений наибольшим является (4cdot 5=20).
Ответ: 20
Задание
2
#2864
Уровень задания: Легче ЕГЭ
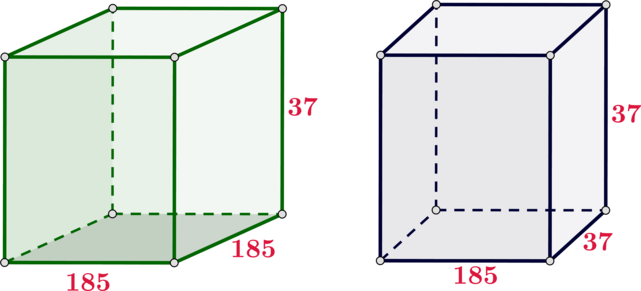
Даны два прямоугольных параллелепипеда: ребра одного равны (185), (185) и (37); а ребра другого равны (185, 37) и (37). Во сколько раз объем первого параллелепипеда больше объема второго параллелепипеда?
Отношение их объемов равно: [dfrac{V_1}{V_2}=dfrac{185cdot 185cdot 37}{185cdot 37cdot 37}=
dfrac{185}{37}=5.]
Ответ: 5
Задание
3
#2865
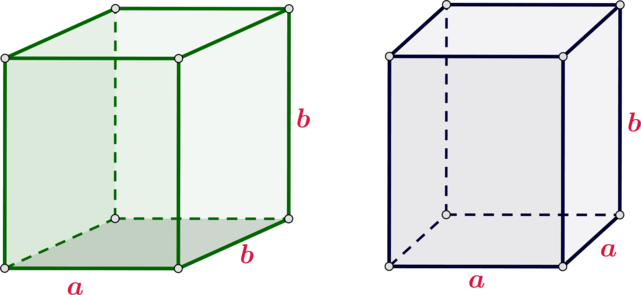
Уровень задания: Легче ЕГЭ
Даны два прямоугольных параллелепипеда: ребра одного равны (a, b) и (b), а ребра другого равны (a, a) и (b). На сколько площадь полной поверхности первого параллелепипеда больше, чем площадь поверхности второго параллелепипеда, если (a=1000, b=1001).
Площадь полной поверхности первого параллелепипеда [S_1=2(ab+b^2+ab)] Площадь полной поверхности второго параллелепипеда [S_2=2(ab+ab+a^2)] Следовательно, [S_1-S_2=2(b^2-a^2)=2(b-a)(b+a)=2(1001-1000)(1001+1000)=4002.]
Ответ: 4002
Задание
4
#3974
Уровень задания: Равен ЕГЭ
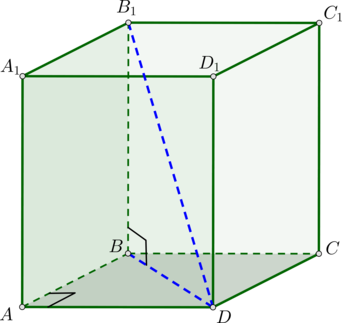
Дан прямоугольный параллелепипед (ABCDA_1B_1C_1D_1). Во сколько раз объем пирамиды (AA_1BD) меньше объема этого параллелепипеда?
Пусть (AB=x), (AD=y), (AA_1=z). Тогда объем параллелепипеда равен [V_{par}=S_{ABCD}cdot AA_1=xycdot z.] Так как (S_{ABD}=0,5S_{ABCD}) (потому что по определению прямоугольного параллелепипеда в основании лежит прямоугольник), то объем пирамиды [V_{pir}=dfrac13cdot S_{ABC}cdot AA_1=
dfrac13cdot dfrac12xycdot z=dfrac16xyz.] Следовательно, объем пирамиды в 6 раз меньше объема параллелепипеда.
Ответ:
6
Задание
5
#2867
Уровень задания: Равен ЕГЭ
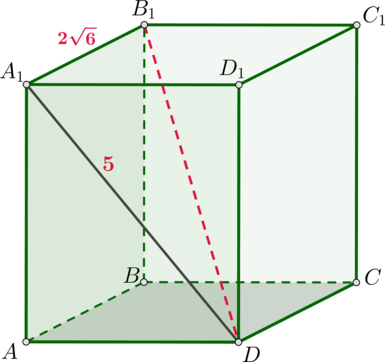
В прямоугольном параллелепипеде диагональ грани (AA_1D_1D) равна (5), а (AB=2sqrt6). Найдите диагональ параллелепипеда.
Так как параллелепипед прямоугольный, то все его грани – прямоугольники, а у прямоугольника обе диагонали равны. Следовательно, (A_1D=AD_1). Рассмотрим диагональ (A_1D) и диагональ параллелепипеда (B_1D). Треугольник (A_1B_1D) прямоугольный, так как ребро (A_1B_1) перпендикулярно грани (AA_1D_1D) (по определению прямоугольного параллелепипеда). Следовательно, гипотенуза [B_1D=sqrt{A_1B_1^2+A_1D^2}=sqrt{5^2+(2sqrt6)^2}=7.]
Ответ: 7
Задание
6
#2641
Уровень задания: Равен ЕГЭ
Дан прямоугольный параллелепипед с ребрами (2, 3) и (6). Найдите его диагональ.
Пусть (AB=2, AD=3 , AA_1=6).
По теореме Пифагора из прямоугольного треугольника (ABD) ((angle
A=90^circ)) имеем: (BD^2=AB^2+AD^2).
Из прямоугольного треугольника (BB_1D) ((angle B=90^circ)) по теореме Пифагора (B_1D^2=BD^2+BB_1^2).
Подставляя (BD^2) из первого равенства во второе, получим:
[B_1D^2=AB^2+AD^2+BB_1^2=2^2+3^2+6^2=4+9+36=49 quad Leftrightarrow quad B_1D=7.]
Ответ: 7
Задание
7
#2689
Уровень задания: Равен ЕГЭ
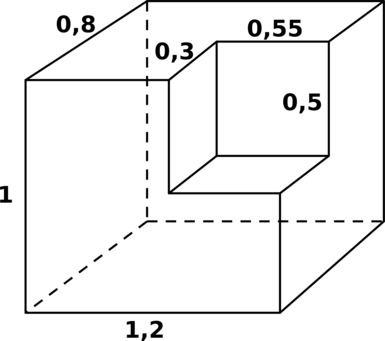
Найдите объём фигуры, получившейся после удаления маленького прямоугольного параллелепипеда из большого.
Объём оставшейся фигуры равен разности объёмов большого прямоугольного параллелепипеда (каким он был до удаления) и маленького (удалённого).
Таким образом, искомый объём равен [0,8cdot 1cdot 1,2 — 0,3cdot 0,5cdot 0,55 = 0,8775,.]
Ответ: 0,8775
Учащимся старших классов будет полезно научиться решать задачи ЕГЭ на нахождение объема и других неизвестных параметров прямоугольного параллелепипеда. Опыт предыдущих лет подтверждает тот факт, что подобные задания являются для многих выпускников достаточно сложными.
При этом понимать, как найти объем или площадь прямоугольного параллелепипеда, должны старшеклассники с любым уровнем подготовки. Только в этом случае они смогут рассчитывать на получение конкурентных баллов по итогам сдачи единого госэкзамена по математике.
Основные нюансы, которые стоит запомнить
- Параллелограммы, из которых состоит параллелепипед, являются его гранями, их стороны — ребрами. Вершины этих фигур считаются вершинами самого многогранника.
- Все диагонали прямоугольного параллелепипеда равны. Так как это прямой многогранник, то боковые грани представляют собой прямоугольники.
- Так как параллелепипед — это призма, в основании которой находится параллелограмм, эта фигура обладает всеми свойствами призмы.
- Боковые ребра прямоугольного параллелепипеда перпендикулярны основанию. Следовательно, они являются его высотами.
Готовьтесь к ЕГЭ вместе со «Школково»!
Чтобы занятия проходили легко и максимально эффективно, выбирайте наш математический портал. Здесь вы найдете весь необходимый материал, который потребуется на этапе подготовки к единому государственному экзамену.
Специалисты образовательного проекта «Школково» предлагают пойти от простого к сложному: сначала мы даем теорию, основные формулы и элементарные задачи с решением, а затем постепенно переходим к заданиям экспертного уровня. Вы можете потренироваться, например, с решением задач на тему “Призма”.
Нужную базовую информацию вы найдете в разделе «Теоретическая справка». Вы также можете сразу приступить к решению задач по теме «Прямоугольный параллелепипед» в онлайн-режиме. В разделе «Каталог» представлена большая подборка упражнений разной степени сложности. База заданий регулярно пополняется.
Проверьте, легко ли вы сможете найти объем прямоугольного параллелепипеда, прямо сейчас. Разберите любое задание. Если упражнение дается вам легко, переходите к более сложным задачам. А если возникли определенные сложности, рекомендуем вам планировать свой день таким образом, чтобы ваше расписание включало занятия с дистанционным порталом «Школково».

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Геометрия 11
класс. Задачи по теме «Прямоугольный параллелепипед». Задания №13 (базовый
уровень), №8 (профильный уровень) ЕГЭ.
|
№ |
Задания |
Ответы |
|
1 |
Рёбра |
22 |
|
2 |
Два |
3 |
|
3 |
Два |
64 |
|
4 |
Во |
4 |
|
5 |
Диагональ |
18 |
|
6 |
В |
13 |
|
7 |
В |
11 |
|
8 |
В |
1 |
|
9 |
Найдите |
54 |
|
10 |
Найдите квадрат |
89 |
|
11 |
Найдите |
1,5 |
|
12 |
Найдите |
60 |
|
13 |
Найдите |
1 |
|
14 |
Найдите |
36 |
|
15 |
Найдите |
40 |
|
16 |
Найдите |
130 |
|
17 |
Найдите |
80 |
|
18 |
Найдите |
76 |
|
19 |
Найдите |
40 |
|
20 |
Найдите |
82 |
|
21 |
Найдите площадь |
116 |
|
22 |
Найдите |
178 |
|
23 |
Найдите |
204 |
|
24 |
Найдите |
134 |
|
25 |
Диагональ |
6 |
|
26 |
В кубе |
45 |
|
27 |
Если |
7 |
|
28 |
Если |
3,5 |
Данная презентация предназначена учащимся одиннадцатого класса при подготовке к единому государственному экзамену по математике. А так же эту работу могут использовать учителя математики на своих уроках при обобщении и повторении темы «Объём прямоугольного параллелепипеда» по геометрии.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Объем прямоугольного параллелепипеда в ЕГЭ по математике »
Объем прямоугольного параллелепипеда в ЕГЭ по математике.
2. Объем куба равен 8. Найдите площадь его поверхности.
3. Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда.
4. Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.
5. Диагональ куба равна 1. Найдите площадь его поверхности.
Задача 1. В прямоугольном параллелепипеде известно, что
Найдите длину диагонали
Решение: + показать
Задача 2. Найдите угол прямоугольного параллелепипеда, для которого
. Ответ дайте в градусах.
Решение: + показать
Задача 3. В прямоугольном параллелепипеде известны длины рёбер
Найдите синус угла между прямыми
и
Решение: + показать
Задача 4. Площадь поверхности куба равна Найдите его диагональ.
Решение: + показать
Задача 5. Объем куба равен Найдите площадь его поверхности.
Решение: + показать
Задача 6. Диагональ куба равна . Найдите его объем.
Решение: + показать
Задача 6. Объем куба равна . Найдите его диагональ.
Решение: + показать
Задача 7. Во сколько раз увеличится объем куба, если его ребра увеличить в десять раз?
Решение: + показать
Задача 8. Если каждое ребро куба увеличить на , то его площадь поверхности увеличится на
Найдите ребро куба.
Решение: + показать
Задача 9. Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в раза?
Решение: + показать
Задача 10. Объем одного куба в раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
Решение: + показать
Задача 11. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны и
Площадь поверхности этого параллелепипеда равна
Найдите третье ребро, выходящее из той же вершины.
Решение: + показать
Задача 12. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны
и
Найдите ребро равновеликого ему куба.
Решение: + показать
Задача 13. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны и
Диагональ параллелепипеда равна
Найдите объем параллелепипеда.
Решение: + показать
Задача 14. Площадь грани прямоугольного параллелепипеда равна Ребро, перпендикулярное этой грани, равно
Найдите объем параллелепипеда.
Решение: + показать
Задача 15. В прямоугольном параллелепипеде известны длины рёбер:
Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки
и
Решение: + показать
Задача 16. Диагональ прямоугольного параллелепипеда равна и образует углы
,
и
с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.
Решение: + показать
Задача 17. В прямоугольном параллелепипеде ребро
, ребро
, ребро
. Точка
— середина ребра
Найдите площадь сечения, проходящего через точки
.
Решение: + показать
Задача 18. Одна из граней прямоугольного параллелепипеда — квадрат. Диагональ параллелепипеда равна и образует с плоскостью этой грани угол
°. Найдите объем параллелепипеда.
Решение: + показать
Задача 19. Найдите объем многогранника, вершинами которого являются точки прямоугольного параллелепипеда
у которого
Решение: + показать
Задача 20. Найдите объем параллелепипеда , если объем треугольной пирамиды
равен
Решение: + показать
Задача 21. Найдите объем многогранника, вершинами которого являются точки прямоугольного параллелепипеда
у которого
Решение: + показать
Задача 22. Найдите объем многогранника, вершинами которого являются точки прямоугольного параллелепипеда
у которого
Решение: + показать
Задача 23. Объем параллелепипеда равен
Найдите объем треугольной пирамиды
Решение: + показать
Задача 24. В кубе точка
— середина ребра
, точка
— середина ребра
, точка
— середина ребра
Найдите угол
. Ответ дайте в градусах.
Решение: + показать
Вы можете пройти тест