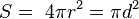Каталог заданий.
Шар
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 2 № 27059
Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
Аналоги к заданию № 27059: 5049 27185 72765 72719 72721 72723 72725 72727 72729 72731 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
2
Тип 2 № 27072
Даны два шара. Радиус первого шара в 2 раза больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Аналоги к заданию № 27072: 5075 73287 520653 520694 26551 73243 73245 73247 73249 73251 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Классификатор планиметрии: Отношение длин, площадей, объемов подобных фигур
Классификатор стереометрии: Площадь сферы
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
3
Тип 2 № 27097
Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
Аналоги к заданию № 27097: 74403 74405 74407 74409 74411 74413 74415 Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Классификатор планиметрии: Отношение длин, площадей, объемов подобных фигур, Подобие
Классификатор стереометрии: Площадь сферы
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
4
Тип 2 № 27125
Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов.
Аналоги к заданию № 27125: 75307 75309 75311 75313 Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Классификатор стереометрии: Объём цилиндра, конуса, шара
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
5
Тип 2 № 27162
Объем первого шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Аналоги к заданию № 27162: 76349 76355 505443 76351 76353 76357 76359 Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Классификатор планиметрии: Отношение длин, площадей, объемов подобных фигур, Подобие
Классификатор стереометрии: Объём цилиндра, конуса, шара, Площадь сферы
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
08
Сен 2013
Категория: 02 Стереометрия
02. Шар
2013-09-08
2022-09-11
Задача 1. Объем шара равен 12348. Найдите площадь его поверхности, деленную на
Решение: + показать
Задача 2. Площадь большого круга шара равна Найдите площадь поверхности шара.
Решение: + показать
Задача 3. Площадь поверхности шара равна Найдите площадь большого круга шара.
Решение: + показать
Задача 4. Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в раз?
Решение: + показать
Задача 5. Во сколько раз увеличится объем шара, если его радиус увеличить в пять раз?
Решение: + показать
Задача 6. Объем первого шара в раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Решение: + показать
Задача 7. Радиусы двух шаров равны и
Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
Решение: + показать
Задача 8. Радиусы трех шаров равны ,
и
Найдите радиус шара, объем которого равен сумме их объемов.
Решение: + показать
Вы можете пройти тест
Автор: egeMax |
комментариев 7
Геометрия 10-11 класс. Объём шара
Скачать файл в формате pdf.
Геометрия 10-11 класс. Объём шара
Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии от данной точки, не большем данного положительного числа. Эта точка называется центром шара, а данное расстояние радиусом шара. Шаровой поверхностью или сферой шара называется множество всех точек пространства, находящихся на равном положительном расстоянии от некоторой точки. Эта точка называется центром сферы, а данное расстояние радиусом сферы. Таким образом, точками сферы являются все точки шара, которые удалены от центра на расстояние, равное радиусу. Любой отрезок, соединяющий центр шара с точкой шаровой поверхности, также называется радиусом. Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром.
Площадь поверхности шара находится по формуле: (S = 4,pi ,{R^2}); объем шара находится по формуле: (V = frac{4}{3}pi ,{R^3}), где R – радиус шара.
Шар, так же как цилиндр и конус, является телом вращения. Он получается при вращении полукруга вокруг его диаметра как оси. Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость. Плоскость, проходящая через центр шара, называется диаметральной плоскостью. Сечение шара диаметральной плоскостью называется большим кругом, а сечение сферы – большой окружностью. Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Шаровой сегмент можно получить, вращая круговой сегмент вокруг диаметра, перпендикулярного его хорде.
Площадь сегментной поверхности находится по формуле: (S = 2,pi ,R,H); объем шарового сегмента находится по формуле: (V = pi ,{H^2},left( {,R — frac{H}{3},} right)), где H – высота сегмента; R – радиус шара.
Шаровым сектором называется тело, которое получается из шарового сегмента и конуса следующим образом. Если шаровой сегмент меньше полушара, то он дополняется конусом, у которого вершина в центре шара, а основанием является основание сегмента. Если же сегмент больше полушара, то указанный конус из него удаляется.
Объем шарового сектора находится по формуле: (V = frac{2}{3}pi ,{R^2}H); площадь полной поверхности шарового сектора складывается из площади сегментной поверхности и площади боковой поверхности конуса и находится по формуле:({S_{{text{шар}}{text{.}};{text{сект}}}} = {S_{{text{шар}}{text{.}};{text{сегм}}}} + {S_{{text{б}}{text{.}};{text{п}}{text{.}};{text{кон}}}} = 2,pi ,R,H + pi ,R,sqrt {,2,R,H — {H^2}} ), где H – высота соответствующего шарового сегмента; R – радиус шара.
Задачи для самостоятельного решения
| Задача 1. Из центра сферы провели два радиуса, угол между которыми ({90^circ }). Расстояние между концами радиусов равно (3sqrt 2 ). Найдите объём шара, деленный на π. |
| Задача 2. Диаметр сечения шара равен 8, расстояние от центра шара до его сечения равно (2sqrt 5 ). Найдите объём шара, деленный на π. |
| Задача 3. В сечение шара вписан треугольник со сторонами 6, 8 и 10. Расстояние от центра шара до плоскости треугольника равно (sqrt {11} .) Найдите объём шара, деленный на π. |
| Задача 4. В шаре проведено сечение площадью 4π. Расстояние от центра шара до плоскости сечения равно (sqrt 5 .) Найдите объём шара, деленный на π. |
| Задача 5. В куб с ребром, равным (frac{6}{{sqrt[3]{pi }}}), вписан шар. Найдите объём шара. |
| Задача 6. Около куба с ребром, равным (frac{{sqrt 3 }}{{sqrt[3]{pi }}}), описан шар. Найдите объём шара. |
| Задача 7. В правильную треугольную призму со стороной основания, равной (6sqrt 3 ), вписан шар. Найдите объём шара, деленный на π. |
Основные геометрические формулы шара (сферы).
Площадь поверхности S и объём V шара радиуса r, диаметра d можно определить по формулам:
- Площадь сферы
-
- Объём шара, ограниченного сферой
-
-
- Объём шара в 1,5 раз меньше, чем объём описанного вокруг этого шара цилиндра, а поверхность
шара в 1,5 раз меньше полной поверхности этого цилиндра:
где Sшара и Vшара – поверхность и объём шара;
Sцил и Vцил – полная поверхность и объём описанного цилиндра вокруг шара.
Шар — это тело, все точки которого находятся от заданой точки на расстоянии, не превышающем R.
Онлайн-калькулятор объема шара
Заданная точка, о которой говорится в определении шара называется центром этого шара. А упомянутое расстояние — радиусом данного шара.
У шара, по аналогии с кругом, так же есть диаметр DD, который по длине в два раза больше радиуса:
D=2⋅RD=2cdot R
Формула объема шара через его радиус
Объем шара вычисляется по следующей формуле:
V=43⋅π⋅R3V=frac{4}{3}cdotpicdot R^3
RR — радиус данного шара.
Рассмотрим несколько примеров.
Шар вписан в куб, диагональ dd которого равна 500 см.sqrt{500}text{ см.} Найти объем шара.
Решение
d=500d=sqrt{500}
Для начала необходимо определить длину стороны куба. Будем считать, что она равна aa. Следовательно, диагональ куба, равна (исходя из теоремы Пифагора):
d=a2+a2+a2d=sqrt{a^2+a^2+a^2}
d=3⋅a2d=sqrt{3cdot a^2}
d=3⋅ad=sqrt{3}cdot a
500=3⋅asqrt{500}=sqrt{3}cdot a
a=5003a=sqrt{frac{500}{3}}
a≈12.9aapprox12.9
Если в куб вписан шар, то его радиус равен половинке длины стороны этого куба. В результате имеем:
R=12⋅aR=frac{1}{2}cdot a
R=12⋅12.9≈6.4R=frac{1}{2}cdot 12.9approx6.4
Заключительный этап — нахождение объема шара по формуле:
V=43⋅π⋅R3≈43⋅π⋅(6.4)3≈1097,5 см3V=frac{4}{3}cdotpicdot R^3approxfrac{4}{3}cdotpicdot (6.4)^3approx1097,5text{ см}^3
Ответ
1097,5 см3.1097,5text{ см}^3.
Формула объема шара через его диаметр
Так же объем шара можно найти через его диаметр. Для этого используем связь между радиусом и диаметром шара:
D=2⋅RD=2cdot R
R=D2R=frac{D}{2}
Подставим это выражение в формулу для объема шара:
V=43⋅π⋅R3=43⋅π⋅(D2)3=π6⋅D3V=frac{4}{3}cdotpicdot R^3=frac{4}{3}cdotpicdotBig(frac{D}{2}Big)^3=frac{pi}{6}cdot D^3
V=π6⋅D3V=frac{pi}{6}cdot D^3
DD — диаметр данного шара.
Диаметр шара равен 15 см.15text{ см.} Найдите его объем.
Решение
D=15D=15
Сразу подставляем значение диаметра в формулу:
V=π6⋅D3=π6⋅153≈1766.25 см3V=frac{pi}{6}cdot D^3=frac{pi}{6}cdot 15^3approx1766.25text{ см}^3
Ответ
1766.25 см3.1766.25text{ см}^3.
Не знаете, где оформить выполнение контрольных работ на заказ? Профильные эксперты Студворк помогут вам с решением!