Каталог заданий.
Объем составного многогранника
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 2 № 27044
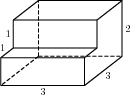
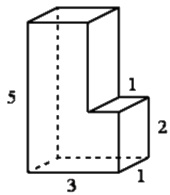
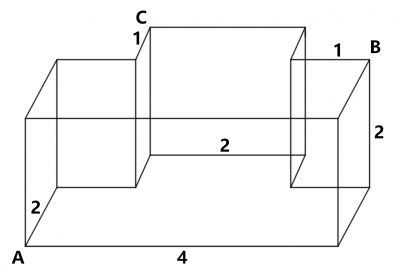
Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
Аналоги к заданию № 27044: 4893 4903 4895 4897 4899 4901 Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы
Решение
·
·
Курс Д. Д. Гущина
·
1 комментарий · Сообщить об ошибке · Помощь
2
Тип 2 № 27117
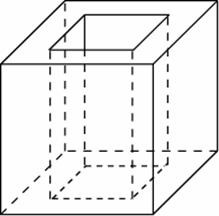
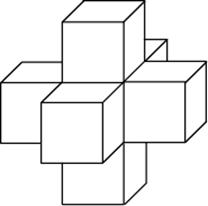
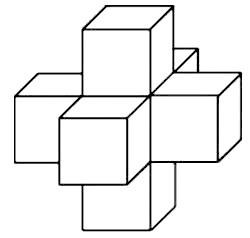
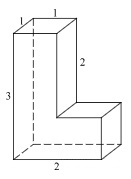
Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы
Решение
·
·
Курс Д. Д. Гущина
·
1 комментарий · Сообщить об ошибке · Помощь
3
Тип 2 № 27187
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Аналоги к заданию № 27187: 25531 25539 25533 25535 25537 Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
4
Тип 2 № 27188
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Аналоги к заданию № 27188: 25551 25559 25553 25555 25557 Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
5
Тип 2 № 27189
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Аналоги к заданию № 27189: 25571 25579 25573 25575 25577 Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
Всего: 19 1–19
Добавить в вариант
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Цифры на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
Источник: Апробация базового ЕГЭ по математике, 13—17 октября: вариант 137752.
Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Цифры на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
Номер в банке ФИПИ: 9D0CDF
Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.
Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Всего: 19 1–19
ЕГЭ Профиль №5. Площадь поверхности и объем составного многогранника
Скачать файл в формате pdf.
ЕГЭ Профиль №5. Площадь поверхности и объем составного многогранника
| Задача 1. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 18. |
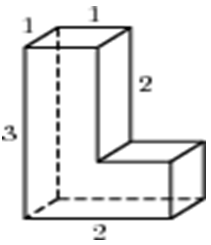 |
| Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 76. |
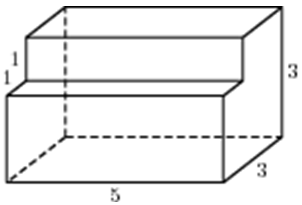 |
| Задача 3. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 92. |
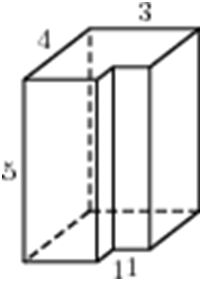 |
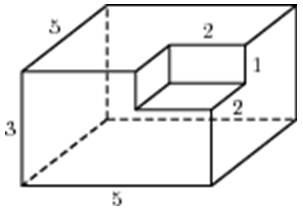
| Задача 4. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 110. |
 |
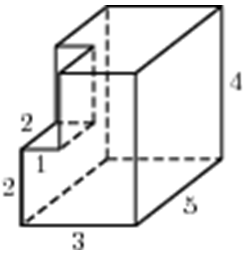
| Задача 5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 94. |
 |
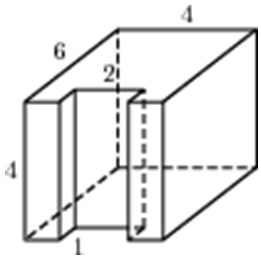
| Задача 6. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 132. |
 |
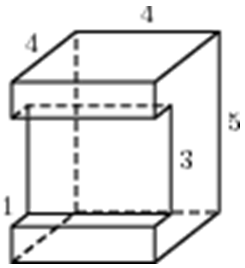
| Задача 7. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 114. |
 |
| Задача 8. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 48. |
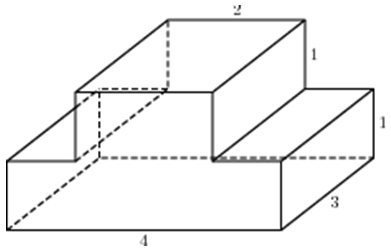 |
| Задача 9. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 84. |
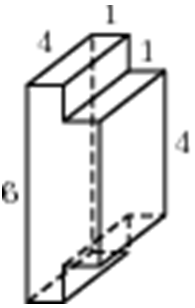 |
| Задача 10. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 96. |
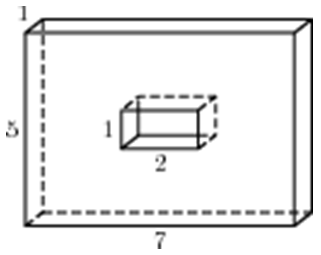 |
| Задача 11. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 124. |
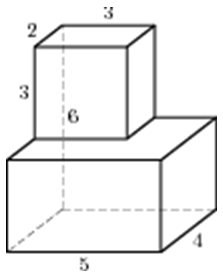 |
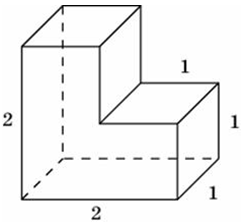
| Задача 12. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Ответ
ОТВЕТ: 14. |
 |
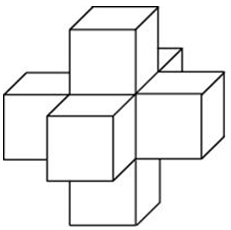
| Задача 13. Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.
Ответ
ОТВЕТ: 30. |
 |
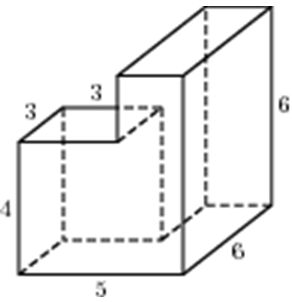
| Задача 14. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 162. |
 |
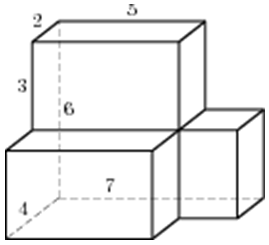
| Задача 15. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 156. |
 |
| Задача 16. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 152. |
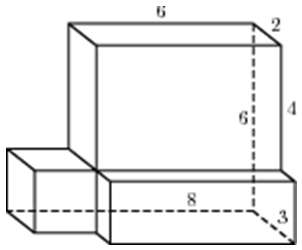 |
| Задача 17. Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
Ответ
ОТВЕТ: 8. |
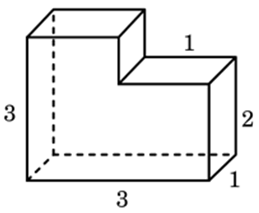 |
| Задача 18. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 56. |
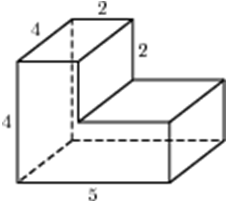 |
| Задача 19. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 7. |
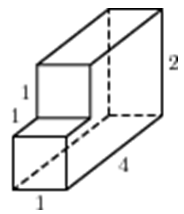 |
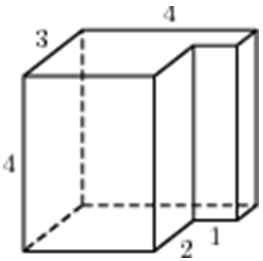
| Задача 20. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 40. |
 |
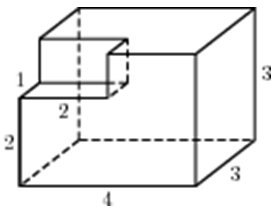
| Задача 21. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 34. |
 |
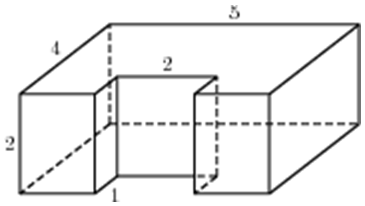
| Задача 22. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 36. |
 |
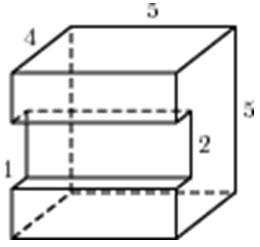
| Задача 23. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 90. |
 |
| Задача 24. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 18. |
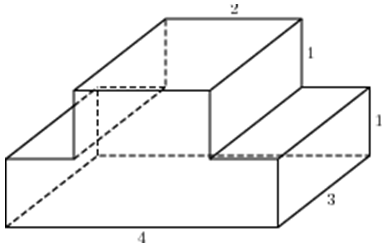 |
| Задача 25. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 24. |
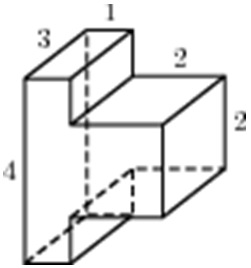 |
| Задача 26. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 45. |
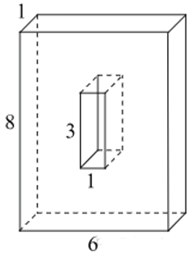 |
| Задача 27. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 78. |
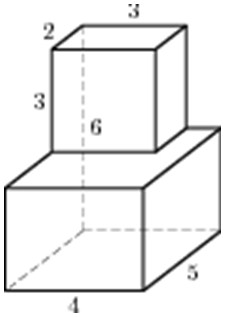 |
| Задача 28. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 104. |
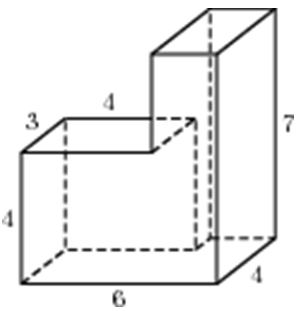 |
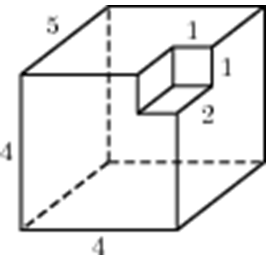
| Задача 29. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 87. |
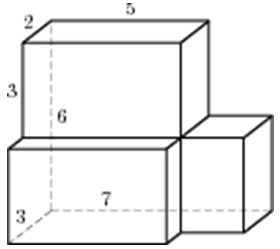 |
| Задача 30. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 114. |
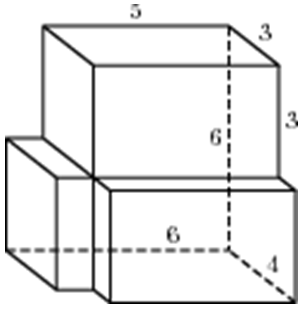 |
| Задача 31. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ
ОТВЕТ: 78. |
 |
Многогранники
Многогранник – это поверхность, составленная из многоугольников, ограничивающая некоторое геометрическое тело.
В данной теме мы рассмотрим составные многогранники (многогранники, состоящие обычно из нескольких параллелепипедов).
Объемы различных многогранников:
- Призма $V=S_{осн}·h$
- Пирамида $V={1}/{3}S_{осн}·h$
- Параллелепипед $V=a·b·c$, где $a, b$ и $c$ — длина, ширина и высота.
- Куб $V=а^3$, где $а$ — сторона куба
Задачи на нахождение объема составного многогранника:
- Первый способ.
- Составной многогранник надо достроить до полного параллелепипеда или куба.
- Найти объем параллелепипеда.
- Найти объем лишней части фигуры.
- Вычесть из объема параллелепипеда объем лишней части.
Пример:
Найдите объём многогранника, изображённого на рисунке (все двугранные углы прямые).
Решение:
1. Достроим составной многогранник до параллелепипеда.
Найдем его объем. Для этого перемножим все три измерения параллелепипеда:
$V=10·9·4=360$
2. Найдем объем лишнего маленького параллелепипеда:
Его длина равна $9-4=5$
Ширина равна $4$
Высота равна $7$
$V=7·4·5=140$
3. Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры:
$V=360-140=220$
Ответ: $220$
- Второй способ
- Разделить составной многогранник на несколько параллелепипедов.
- Найти объем каждого параллелепипеда.
- Сложить объемы.
Задачи на нахождение площади поверхности составного многогранника.
— Если можно составной многогранник представить в виде прямой призмы, то находим площадь поверхности по формуле:
$S_{полн.пов.}=P_{осн}·h+2S_{осн}$
Чтобы найти площадь основания призмы, надо разделить его на прямоугольники и найти площадь каждого.
Пример:
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
Представим данный многогранник как прямую призму с высотой равной $12$.
$S_{полн.пов.}=P_{осн}·h+2S_{осн}$
$P_{осн}=8+6+6+2+2+4=28$
Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:
$S_1=6·6=36$
$S_2=2·4=8$
$S_осн=36+8=44$
Далее подставим все данные в формулу и найдем площадь поверхности многогранника
$S_{полн.пов.}=28·12+2·44=336+88=424$
Ответ: $424$
— Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.
Задачи на нахождение расстояния между точками составного многогранника.
В данных задачах приведены составные многогранники, у которых двугранные углы прямые. Надо соединить расстояние между заданными точками и достроить его до прямоугольного треугольника. Далее остается воспользоваться теоремой Пифагора для нахождения нужной стороны.
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Задачи на нахождение угла или значения одной из тригонометрических функций обозначенного в условии угла составного многогранника.
Так как в данных задачах приведены составные многогранники, у которых все двугранные углы прямые, то достроим угол до прямоугольного треугольника и найдем его значение по тригонометрическим значениям.
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$:
Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Задачи на рассмотрение подобия фигур.
При увеличении всех линейных размеров многогранника в $k$ раз, площадь его поверхности увеличится в $k^2$ раз.
При увеличении всех линейных размеров многогранника в $k$ раз, его объём увеличится в $k^3$ раз.
07
Сен 2013
Категория: 02 Стереометрия
02. Составные многогранники. Площадь поверхности. Объем
2013-09-07
2022-09-11
Задача 1. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение: + показать
Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение: + показать
Задача 3. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение: + показать
Задача 4. Из единичного куба вырезана правильная четырехугольная призма со стороной основания и боковым ребром
Найдите площадь поверхности оставшейся части куба.
Решение: + показать
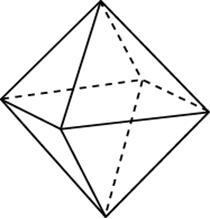
Задача 5. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в раз?
Решение: + показать
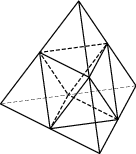
Задача 6. Площадь поверхности тетраэдра равна Найдите площадь поверхности многогранника, вершинами которого являются середины сторон данного тетраэдра Видео*
Решение: + показать
Задача 7. Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.
Решение: + показать
Задача 8. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение: + показать
Задача 9. Объем тетраэдра равен Найдите объем многогранника, вершинами которого являются середины сторон данного тетраэдра.
Решение: + показать
Задача 10. Найдите объем многогранника, вершинами которого являются точки правильной треугольной призмы
, площадь основания которой равна 3, а боковое ребро равно 7.
Решение: + показать

Автор: egeMax |
комментариев 14
Найдите объём многогранника, изображённого на рисунке (все двугранные углы прямые).
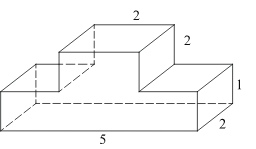
Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
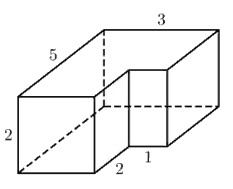
Деталь имеет форму изображённого на рисунке многогранника(все двугранные углы прямые). Числа на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Дайте объём в кубических сантиметрах.
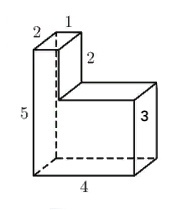
Найдите объём многогранника, изображённого на рисунке (все двугранные углы – прямые).
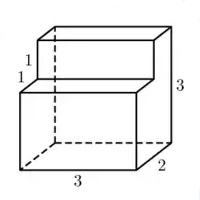
Найдите объём многогранника, изображённого на рисунке (все двугранные углы – прямые).
Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.
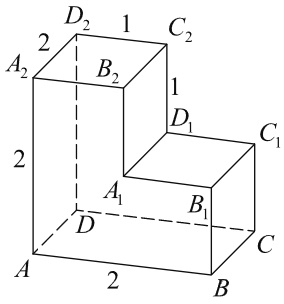
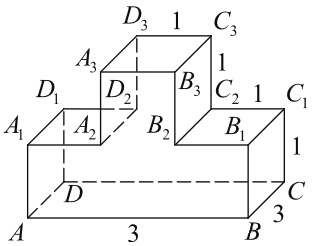
На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите тангенс угла B₂A₂C₂.
Найдите отношение квадратов длин отрезков AC и CB. Все двугранные углы многогранника прямые.
На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите квадрат расстояния между вершинами A и C₃.
Найдите площадь поверхности многогранника (все двугранные углы прямые).
Задание 3371
Радиус основания конуса равен 3, а высота 4. Центр шара совпадает с центром основания конуса и касается боковой поверхности конуса. Найдите отношение объемов шара и конуса.
Ответ: 1,536
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$OB-R$$ конуса
$$OH-R$$ шара
из $$bigtriangleup AOB$$: $$AB=sqrt{OA^{2}+OB^{2}}=sqrt{4^{2}+3^{2}}=5$$
$$OH=frac{OAcdot OB}{AB}=frac{4cdot3}{5}=2,4$$
Vконуса$$=frac{1}{3}cdot S_{osn}cdot h=frac{1}{3}cdotpicdot3^{2}cdot4=12pi$$
Vшара$$=frac{4}{3}cdotpicdot R^{3}=18,432pi$$
Vшара/Vконуса$$=frac{18,432pi}{12pi}=1,536$$
Задание 3715
Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
Ответ: 8
Задание 3716
Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.
Ответ: 7
Задание 3717
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 56
Задание 3718
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 40
Задание 3719
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 34
Задание 3720
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 90
Задание 3721
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 18
Задание 3722
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 45
Задание 3723
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 78
Задание 4908
Во сколько раз уменьшится объем октаэдра, если все его ребра уменьшить в два раза?
Ответ: 8
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Для решения данных заданий надо помнить, что периметры подобных фигур относятся как коэффициент подобия, площади — как квадрат коэффициента подобия, а объемы — как куб коэффициента подобия. То есть, если уменьшить ребро в два раза, объем изменится в 8 раз
Задание 5098
Для каждой грани куба с ребром 6 проделали сквозное квадратное отверстие со стороной квадрата 2. Найдите объем оставшейся части.
Ответ: 160
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Внутри будет пространственный крест , состоящий из 7 кубов со стороной 2. Тогда его объем : $$V_{1}=2^{3}*7=56$$ Объем изначального куба: $$V=6^{3}=216$$ Объем оставшейся части: 216-56=160
Задание 6563
Найдите объем октаэдра, ребро которого равно $$3sqrt{2}$$ .
Ответ: 36
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Рассмотрим четырехугольную пирамиду ABCDS с ребром $$3sqrt{2}$$:
1)$$S_{ABCD}=(3sqrt{2})^{2}=18$$
2) $$BD=sqrt{(3sqrt{2})^{2}+(3sqrt{2})^{2}}=6Rightarrow BH=3$$
3) $$Delta BHS$$: $$SH=sqrt{(3sqrt{2})^{2}-3^{2}}=3$$
4) $$V_{ABCDS}=frac{1}{3}*18*3=18$$
5) Тогда объем октаэдра : $$V=2*V_{ABCDS}=2*18=36$$
Задание 6966
В конус вписан цилиндр так, что плоскость его верхнего основания делит высоту конуса пополам. Найдите объем цилиндра, если объем конуса равен 12.
Ответ: 4,5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть R-радиус основания большого конуса, h-его высота, тогда $$V=frac{1}{3}pi R^{2} h=12$$ – его объем . Пусть r-радиус основания цилиндра ,тогда: $$r=frac{R}{2}$$ и m-его высота, тогда $$m=frac{h}{2}$$ Объем цилиндра: $$V_{1}= pi r^{2}m=pi *frac{R^{2}}{4}*frac{h}{2}=$$$$frac{pi R^{2}h}{8}=frac{36}{8}=4,5$$
Задание 7033
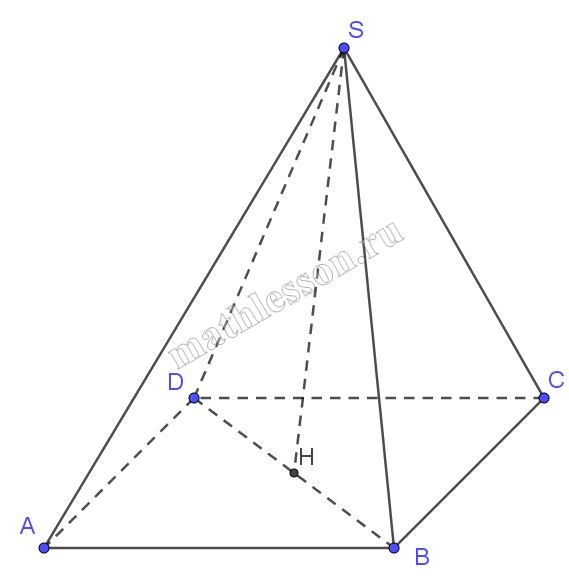
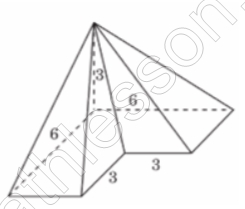
Найдите объём пирамиды, изображённой на рисунке. Её основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых рёбер перпендикулярно плоскости основания и равно 3.
Ответ: 27
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Найдем объем пирамиды без учета выреза: $$V_{1}=frac{1}{3}*6*6*3=36$$
Найдем объем вырезанной: $$V_{2}=frac{1}{3}*3*3*3=9$$
Найдем объем оставшейся: $$V=V_{1}-V_{2}=27$$