По теме: методические разработки, презентации и конспекты
Геометрия в задачах ЕГЭ. Объём фигур в пространстве. А1
Электронные дидактические материалы, выполненные в форме презентации, по геометрическим заданиям как базового, так и профильного уровня ЕГЭ по математике. Могут быть использованы учителем математики к…
Геометрия в задачах ЕГЭ. Объём фигур в пространстве. А2
Электронные дидактические материалы, выполненные в форме презентации, по геометрическим заданиям как базового, так и профильного уровня ЕГЭ по математике. Могут быть использованы учителем математики к…
Геометрия в задачах ЕГЭ. Объём фигур в пространстве. А3
Электронные дидактические материалы, выполненные в форме презентации, по геометрическим заданиям как базового, так и профильного уровня ЕГЭ по математике. Могут быть использованы учителем математики к…
Геометрия в задачах ЕГЭ. Объём фигур в пространстве. В1
Электронные дидактические материалы, выполненные в форме презентации, по геометрическим заданиям как базового, так и профильного уровня ЕГЭ по математике. Могут быть использованы учителем математики к…
Геометрия в задачах ЕГЭ. Объём фигур в пространстве. В2
Электронные дидактические материалы, выполненные в форме презентации, по геометрическим заданиям как базового, так и профильного уровня ЕГЭ по математике. Могут быть использованы учителем математики к…
Геометрия в задачах ЕГЭ. Объём фигур в пространстве. В3
Электронные дидактические материалы, выполненные в форме презентации, по геометрическим заданиям как базового, так и профильного уровня ЕГЭ по математике. Могут быть использованы учителем математики к…
Геометрия в задачах ЕГЭ. Объём фигур в пространстве. В4
Электронные дидактические материалы, выполненные в форме презентации, по геометрическим заданиям как базового, так и профильного уровня ЕГЭ по математике. Могут быть использованы учителем математики к…
Данное занятие может быть проведено после изучения формул объемов многогранников на уроках геометрии в 11-м классе или в рамках элективного курса по подготовке к ЕГЭ. Материал также доступен и учащимся 10-го класса (во 2-м полугодии).
Цели занятия:
- показать примеры задач, аналогичных заданиям ЕГЭ по математике базового уровня и первой части профильного уровня;
- повторить теоретический материал, связанный с площадями фигур, со свойствами многогранников;
- отработка навыков самоконтроля;
- отработка навыков сотрудничества между учащимися.
Оборудование:
- оборудование для демонстрации презентации Microsoft PowerPoint (компьютер, проектор, экран или доска);
- раздаточный материал (тексты задач с чертежами);
- таблица квадратов натуральных чисел.
План занятия
- Организационный момент
- Устная работа
- Решение задач
- Работа в группах
- Подведение итогов
Ход занятия
Занятие сопровождается демонстрацией презентации.
1. Организационный момент
Cообщение целей занятия, деление класса на группы по 4 человека (можно объединить учащихся, сидящих за соседними партами).
2. Устная работа
Условия задач и правильные ответы демонстрируются на слайдах. Задачи решаются устно, ответы можно спросить у нескольких учащихся, один из них коротко рассказывает путь решения.
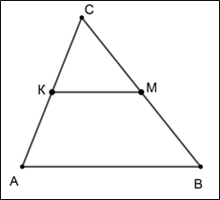
Задача 1. (Слайд №4) Площадь треугольника АВС равна 120. КМ – средняя линия, параллельная стороне АВ. Найти площадь четырехугольника АКМВ. (Ответ: 90)
Рисунок 1
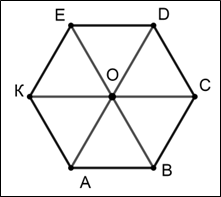
Задача 2. (Слайды №5,6) Площадь правильного шестиугольника АВСДЕК равна 60, О – центр шестиугольника. Найти площади треугольника АОВ, треугольника АВС, треугольника АВЕ, четырехугольника ВСДЕ. (Ответ: 10; 10; 20; 30)
Рисунок 2
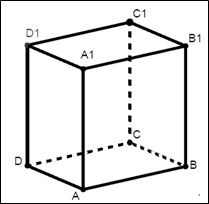
Задача 3. (Слайд №7) Площадь грани прямоугольного параллелепипеда равна 15. Ребро, перпендикулярное этой грани, равно 6. Найти объем параллелепипеда. (Ответ: 90)
Рисунок 3
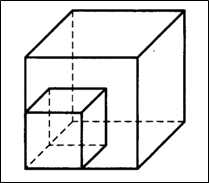
Задача 4. (Слайд №8) Во сколько раз увеличится объем куба, если его ребро увеличить в 5 раз? (Ответ: 125)
Рисунок 4
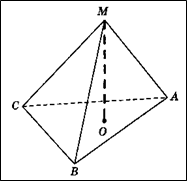
Задача 5. (Слайд №9) В правильной треугольной пирамиде МАВС О – точка пересечения медиан основания. Площадь треугольника АВС равна 5, а объем пирамиды – 35. Найти длину отрезка МО. (Ответ: 21)
Рисунок 5
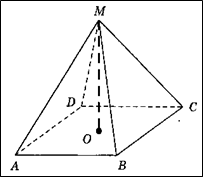
Задача 6. (Слайд №10) Как изменится объем пятиугольной пирамиды, если её высоту увеличить в 4 раза? (Ответ: увеличится в 4 раза)
Рисунок 6
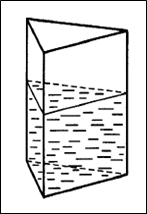
Задача 7. (Слайд №11) В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды составил 20 см. На какой высоте будет находиться уровень воды, если ее перелить в другой сосуд такой же формы, у которого сторона основания в 2 раза больше, чем у первого? (Ответ: 5 см)
Рисунок 7
При подведении итогов устной работы необходимо обратить внимание на формулы для вычисления объемов призмы и пирамиды.
3. Решение задач
Чертежи заранее сделаны на доске, каждый ученик получает заготовку с чертежами (Приложение 1). Учащиеся у доски записывают краткие решения, сопровождая их устными пояснениями. Также можно использовать слайды №13, 14, 15.
Задача 8. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 6 и 3. Объем параллелепипеда равен 108. Найти его диагональ.
Рисунок 8
Задача 9. В сосуд, имеющий форму правильной треугольной призмы, налили 1000 см3 воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 27 см. Найти объем детали. Ответ выразить в см3.
Рисунок 9
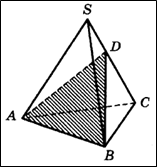
Задача 10. Объем треугольной пирамиды SABC равен 15. Плоскость проходит через сторону АВ основания этой пирамиды и пересекает противоположное боковое ребро в точке D, делящей ребро SC в отношении 1 : 2, считая от вершины S. Найти объем пирамиды DABC.
Рисунок 10
4. Работа в группах
Каждая группа получает набор задач (Приложение 2), к которым надо записать краткие решения. После истечения отведенного времени проверяются ответы, представители групп могут прокомментировать ход решения задач. В это время чертежи демонстрируются на слайдах №17, 18, 19. Для быстрой проверки можно использовать слайд №20. После этого листы с решениями сдаются учителю.
5. Подведение итогов
При подведении итогов следует обратить внимание на две основные формулы объемов и их частные случаи, а также на отношение объемов подобных тел (слайд 22).
Задача. (Слайд №23) Боковые ребра правильной треугольной пирамиды взаимно перпендикулярны и равны 6. Найти объем пирамиды. (Ответ: 36)
При решении этой задачи очень важно обратить внимание на метод решения. Если тетраэдр перевернуть, то задачу можно решить устно.
Задача. (Слайды №24, 25) Объем тетраэдра равен 12. Найти объем многогранника, вершинами которого являются середины сторон данного тетраэдра. (Ответ: 6)
6. Домашнее задание (Приложение 3)
Литература
- Ященко И. В. ЕГЭ: 4000 задач с ответами по математике. Все задания «Закрытый сегмент». Базовый и профильный уровни. – М: Издательство «Экзамен», 2020.
- Балаян Э. Н. Геометрия: задачи на готовых чертежах для подготовки к ЕГЭ: 10-11 классы. – Ростов н/Д: Феникс, 2018.
- Материалы сайта: https://math-ege.sdamgia.ru/
Список приложений
- Приложение 1 – задачи для работы в классе
- Приложение 2 – задачи для работы в группах
- Приложение 3 – домашнее задание
- Приложение 4 – ПРЕЗЕНТАЦИЯ
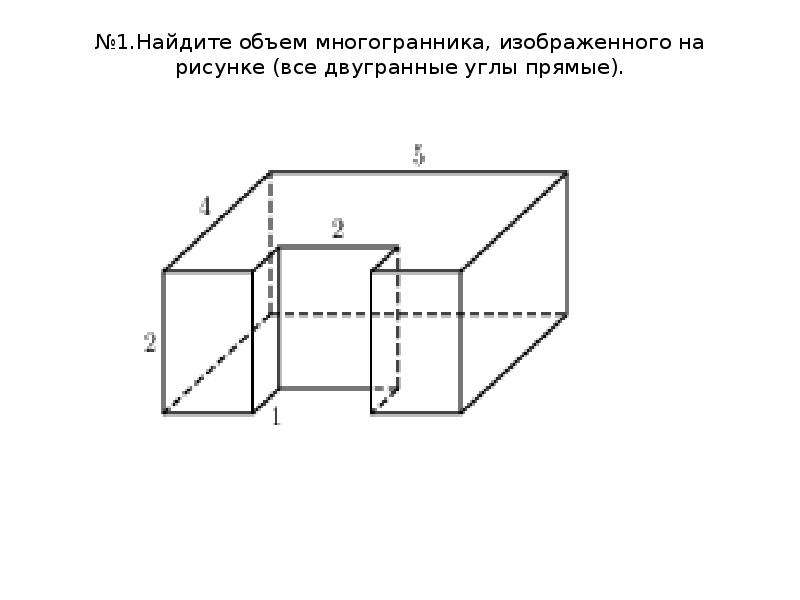
Слайд 2Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые)
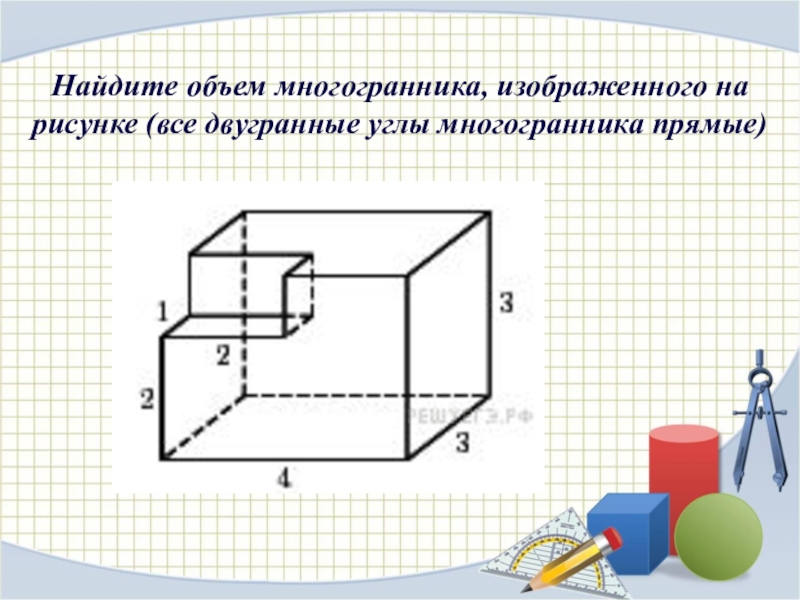
Слайд 3Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые)
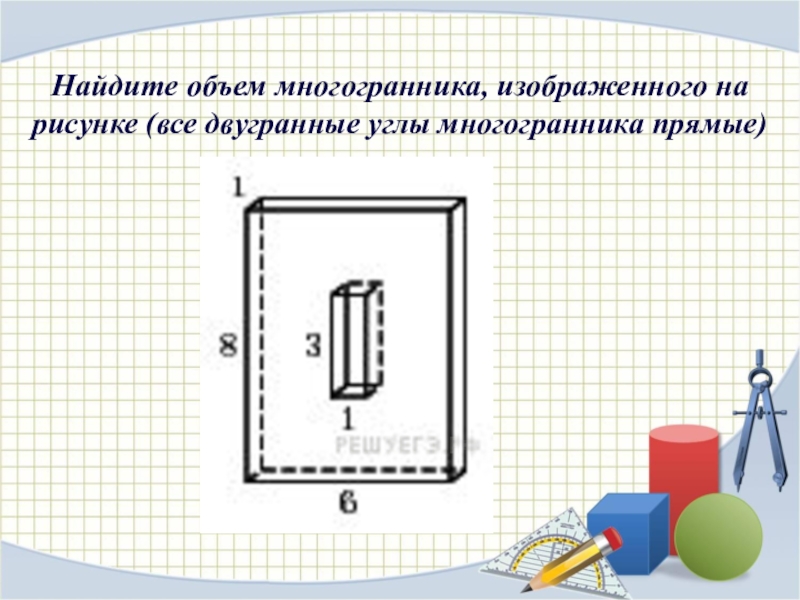
Слайд 4Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые)
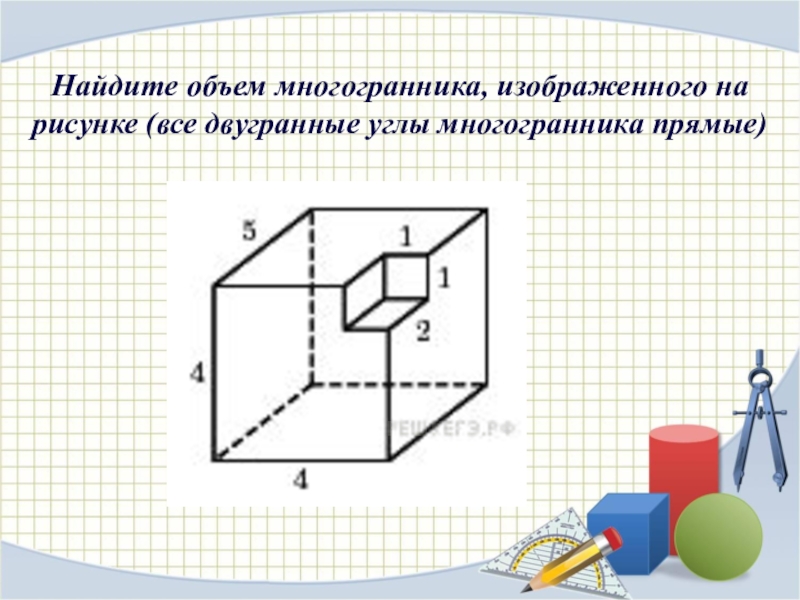
Слайд 5Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые)
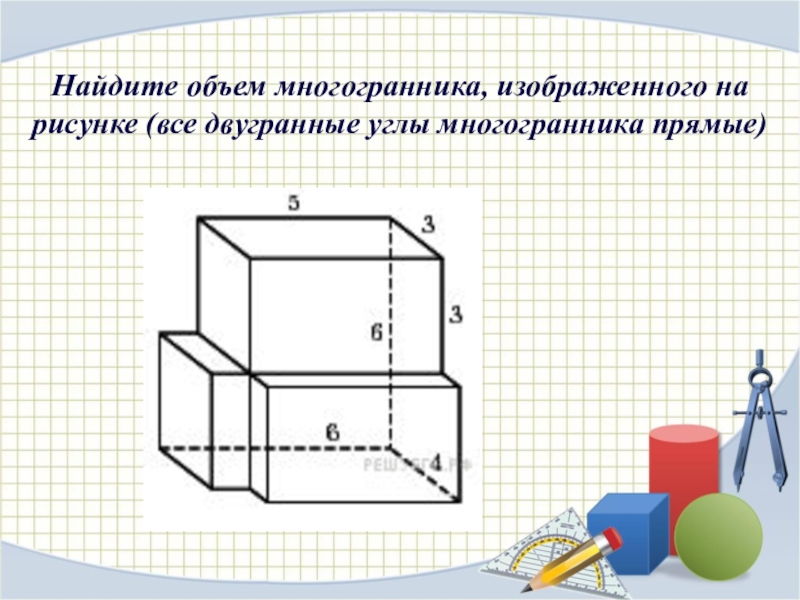
Слайд 6Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 5.
Объем
параллелепипеда равен 120.
Найдите высоту цилиндра.

Слайд 7Прямоугольный параллелепипед описан около сферы радиуса 5. Найдите его объем.
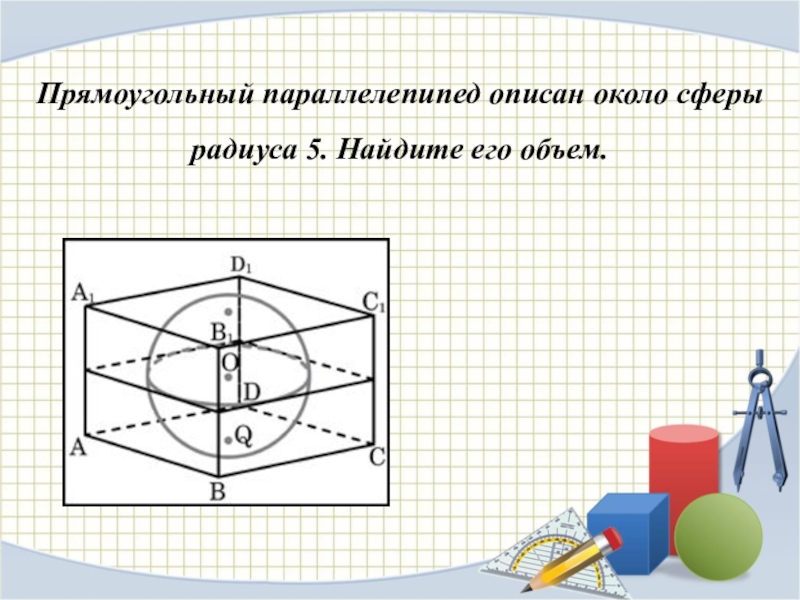
Слайд 8Объем прямоугольного параллелепипеда, описанного около сферы, равен 125.
Найдите радиус сферы.

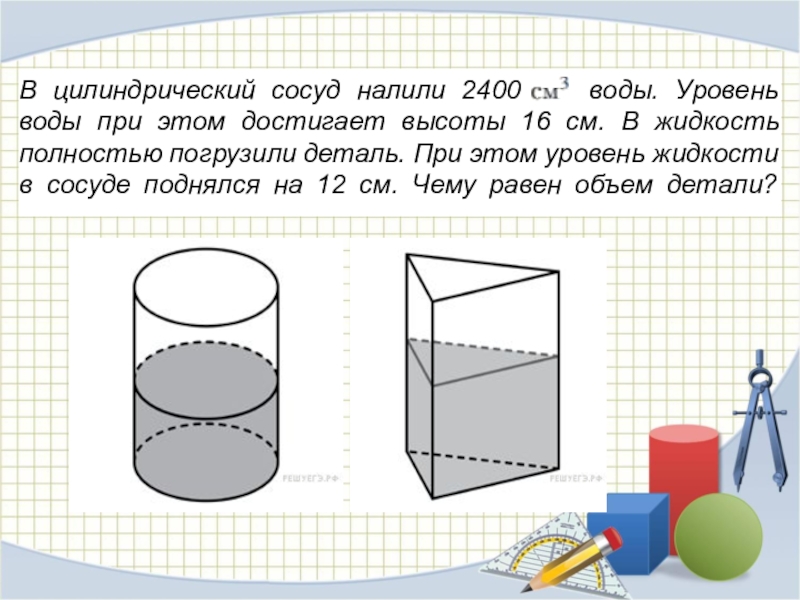
Слайд 9В цилиндрический сосуд налили 2400 воды. Уровень воды при этом достигает
высоты 16 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 12 см. Чему равен объем детали?
Слайд 10Объем первого цилиндра равен 60 м3.
У второго цилиндра высота в 3
раза больше,
а радиус основания — в 2 раза меньше,
чем у первого.
Найдите объем второго цилиндра.
Ответ дайте в кубических метрах.

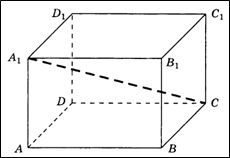
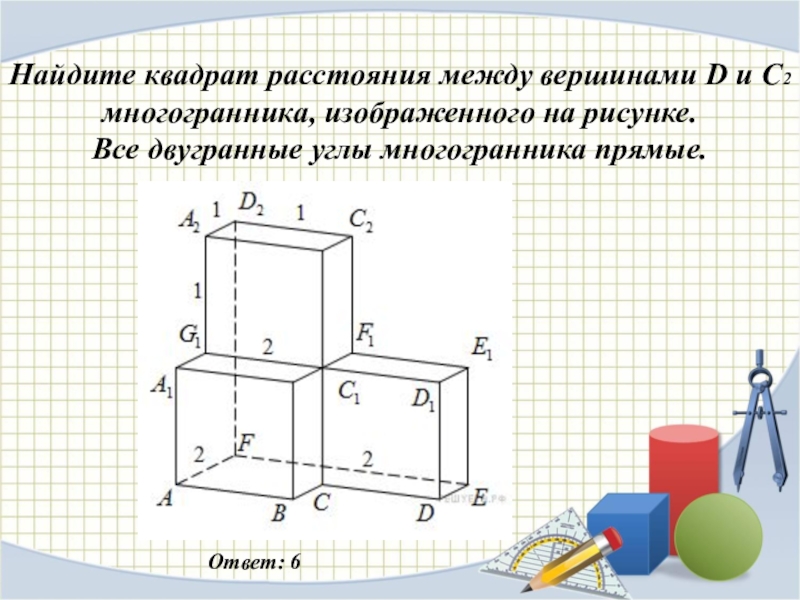
Слайд 11Найдите квадрат расстояния между вершинами D и C2 многогранника, изображенного на рисунке.
Все двугранные углы многогранника прямые.
Ответ: 6
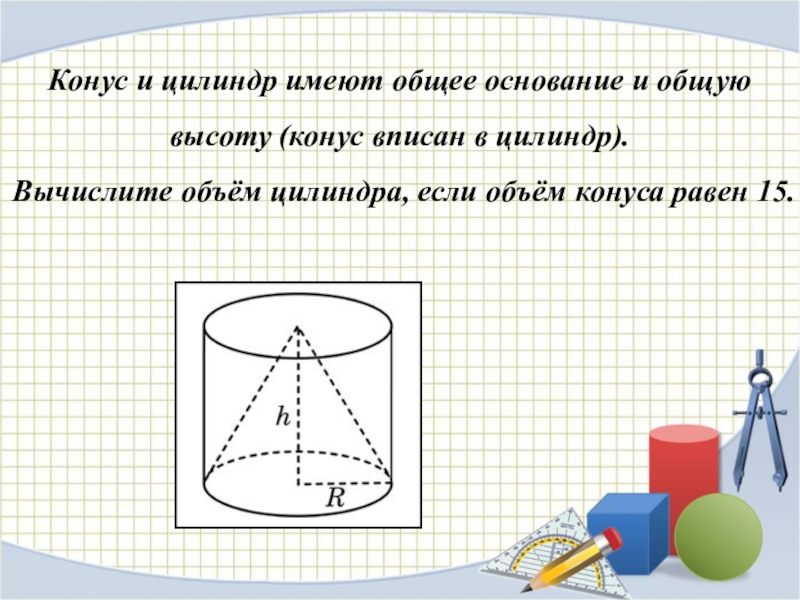
Слайд 12Конус и цилиндр имеют общее основание и общую высоту (конус вписан
в цилиндр).
Вычислите объём цилиндра, если объём конуса равен 15.
Слайд 13Цилиндр и конус имеют общие основание и высоту.
Найдите объем конуса, если
объем цилиндра равен 120.
Ответ: 40

Слайд 14Конус вписан в цилиндр. Объем конуса равен 5.
Найдите объем цилиндра.
Ответ:
15.

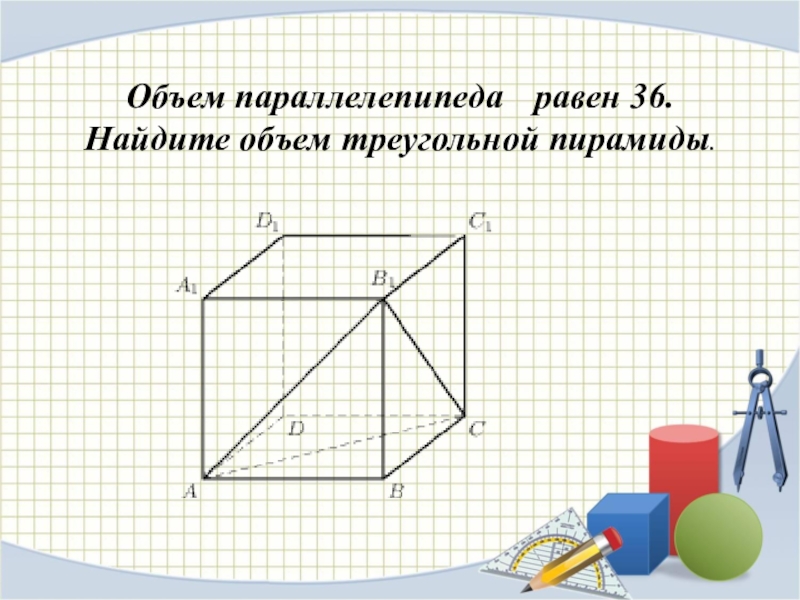
Слайд 15Объем параллелепипеда равен 36.
Найдите объем треугольной пирамиды.
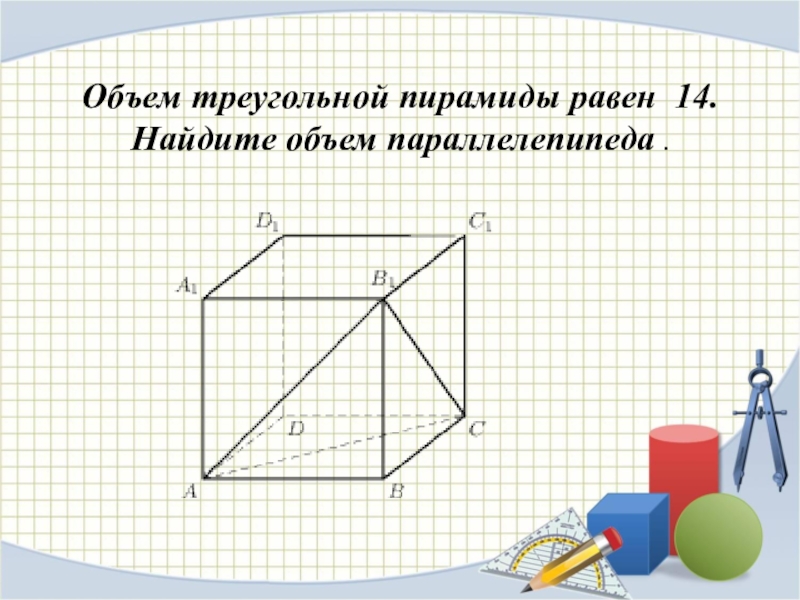
Слайд 16Объем треугольной пирамиды равен 14.
Найдите объем параллелепипеда .
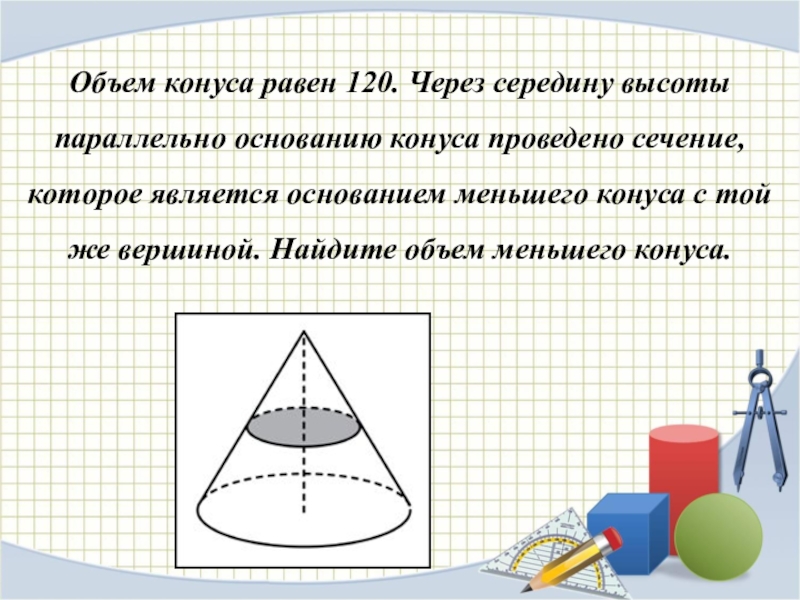
Слайд 17Объем конуса равен 120. Через середину высоты параллельно основанию конуса проведено
сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Слайд 18Объем конуса равен 144. Через середину высоты параллельно основанию конуса проведено
сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Слайд 19Во сколько раз уменьшится объем конуса, если его высоту уменьшить в

Слайд 20Во сколько раз уменьшится объем конуса, если его высоту уменьшить в

Слайд 21Во сколько раз увеличится объем конуса,
если его радиус основания увеличить
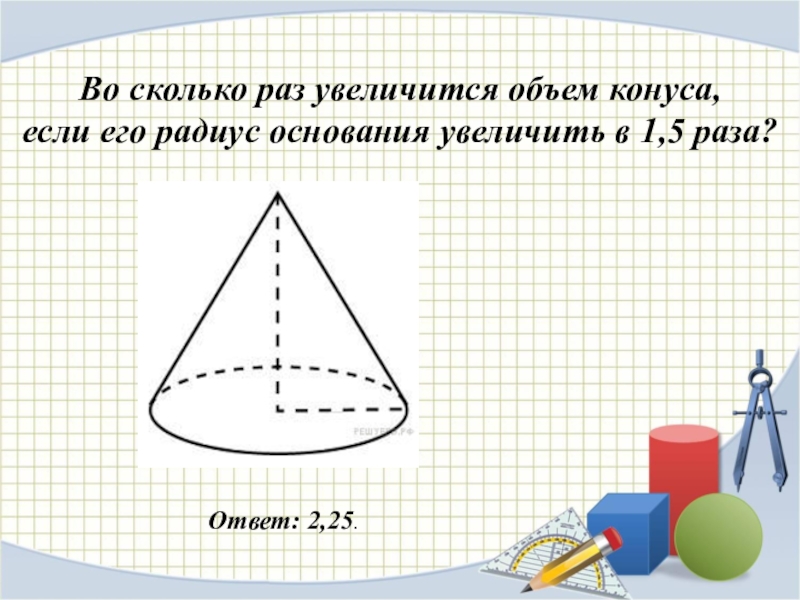
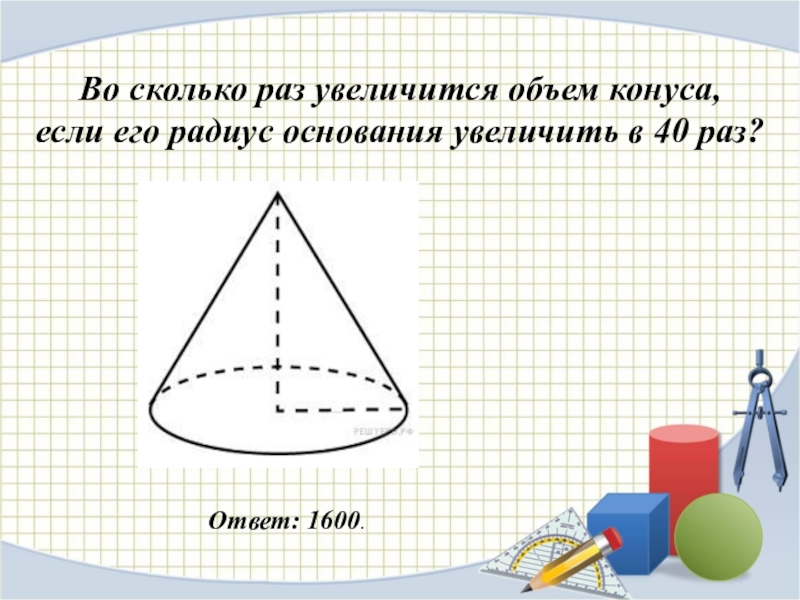
Слайд 22Во сколько раз увеличится объем конуса,
если его радиус основания увеличить
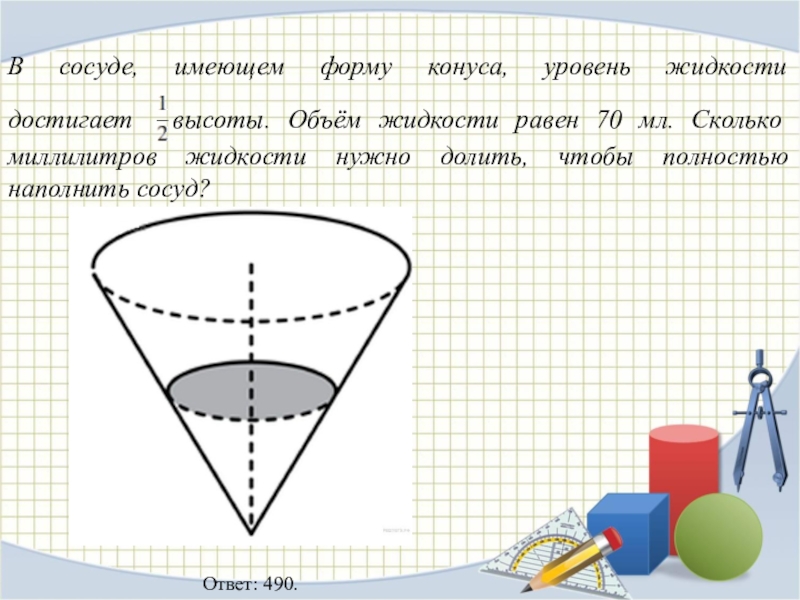
Слайд 23В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объём жидкости
равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Ответ: 490.
Слайд 24В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объём жидкости
равен 54 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
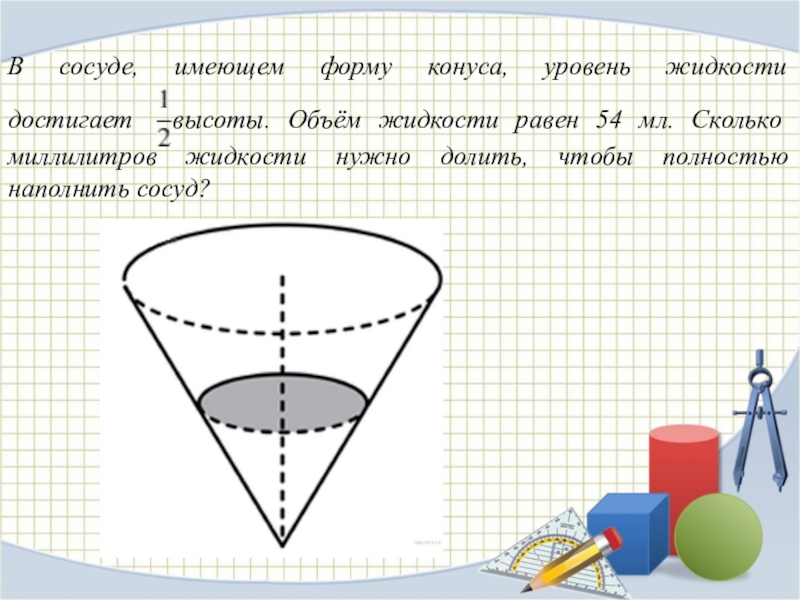
Слайд 25Во сколько раз увеличится объем правильного тетраэдра, если все его ребра
Слайд 26Во сколько раз увеличится объем правильного тетраэдра, если все его ребра
увеличить в одиннадцать раз?
Слайд 27Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в
Слайд 28Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в
сорок шесть раз?
Слайд 29Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является
грань куба,
а вершиной — центр куба.
1. Подготовка к ЕГЭ
Математический диктант
Геометрия №8 (стереометрия)
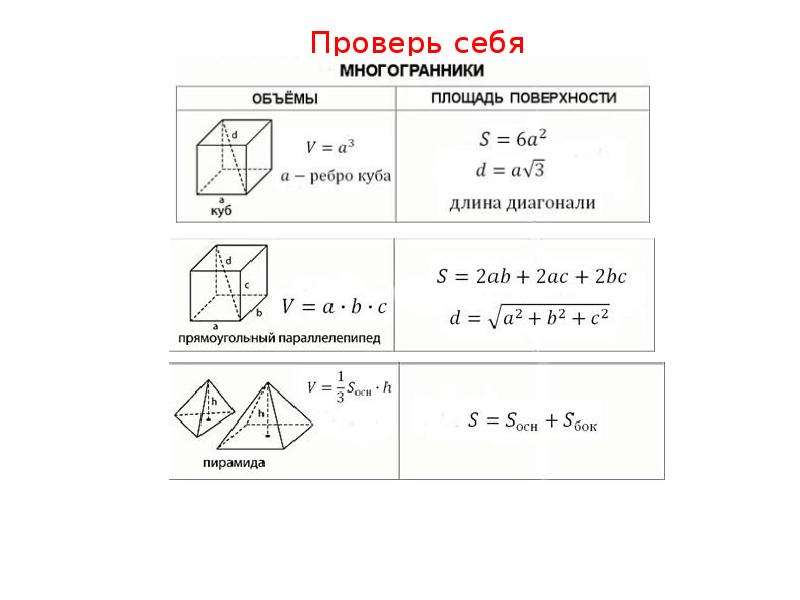
ОБЪЕМЫ
2.
3.
4. №1.Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
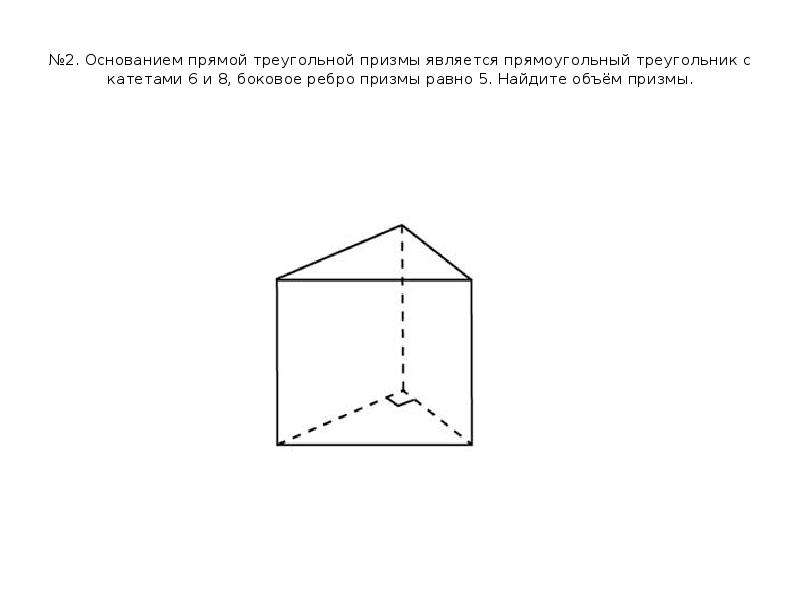
5. №2. Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 6 и 8, боковое ребро призмы равно 5.
Найдите объём призмы.
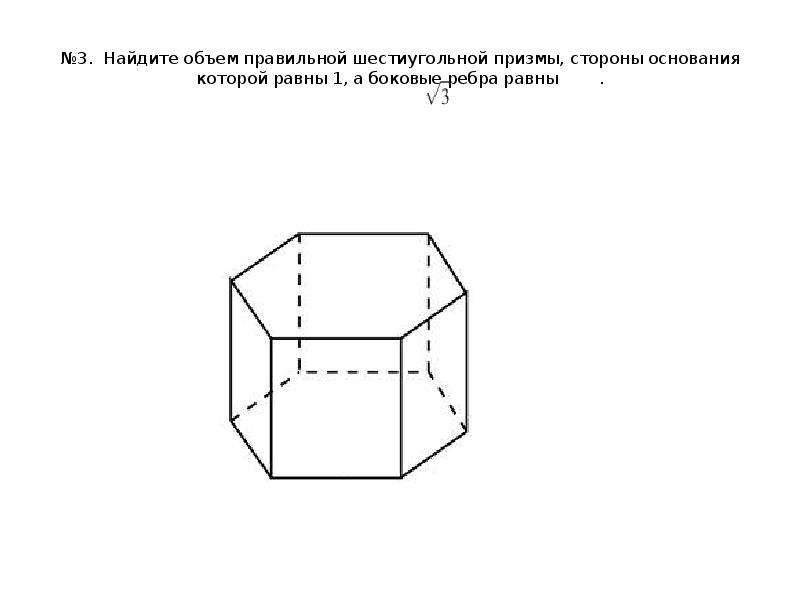
6. №3. Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны .
№3. Найдите объем правильной шестиугольной призмы,
стороны основания которой равны 1, а боковые ребра
равны
.
7. №4. Объем куба равен 8. Найдите площадь его поверхности.
№4. Объем куба равен 8.
Найдите площадь его поверхности.
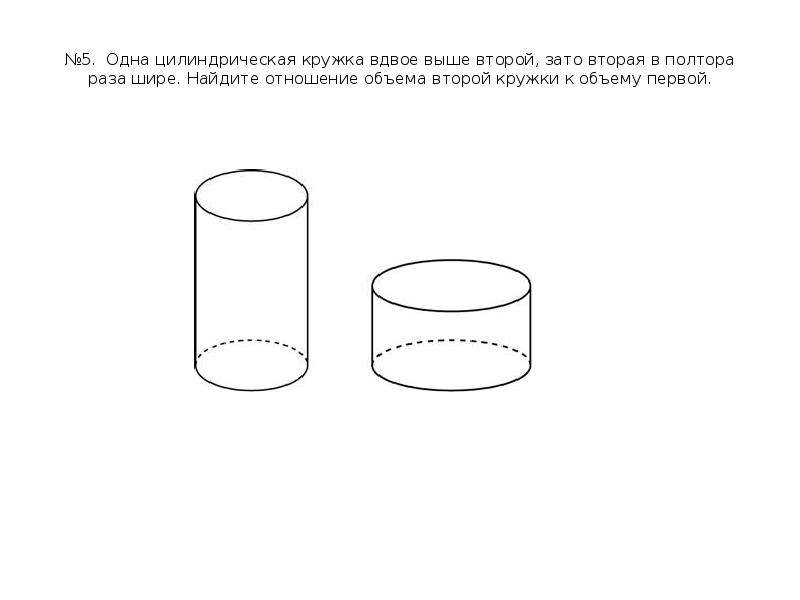
8. №5. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к
объему первой.
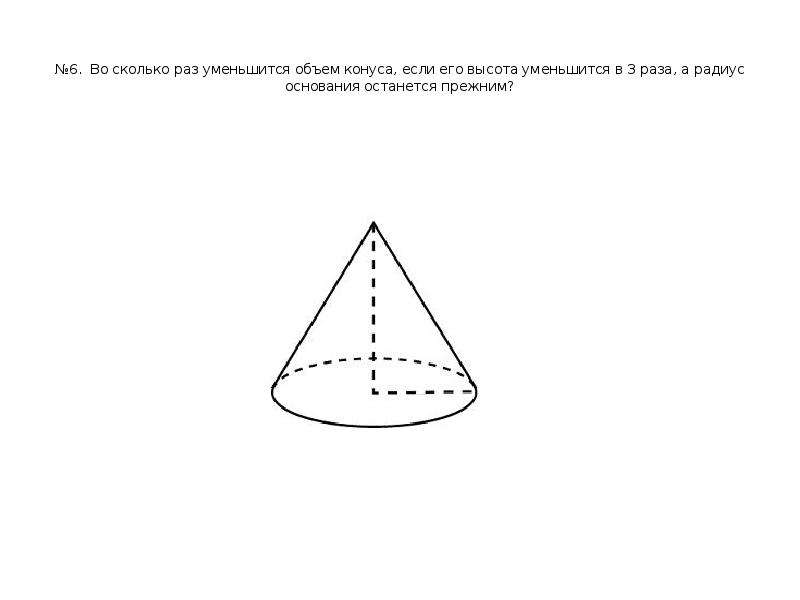
9. №6. Во сколько раз уменьшится объем конуса, если его высота уменьшится в 3 раза, а радиус основания останется прежним?
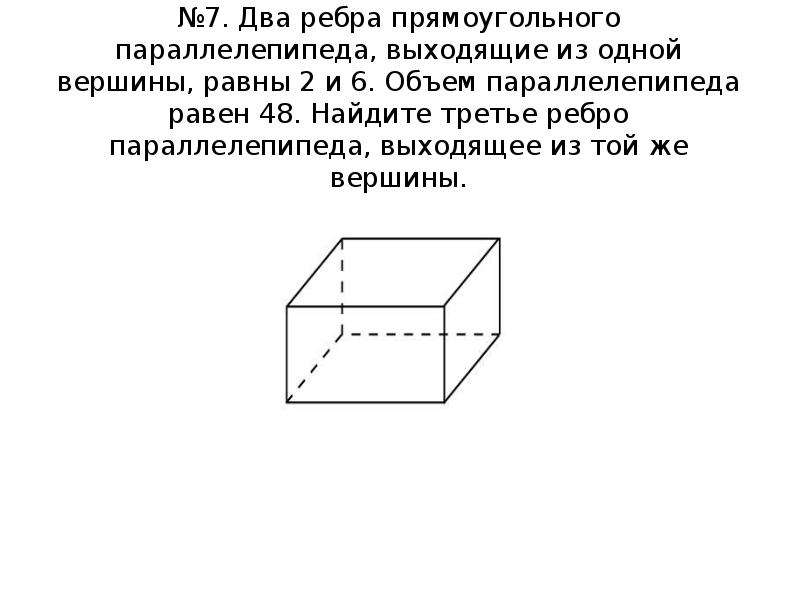
10. №7. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите
третье ребро
параллелепипеда, выходящее из той же вершины.
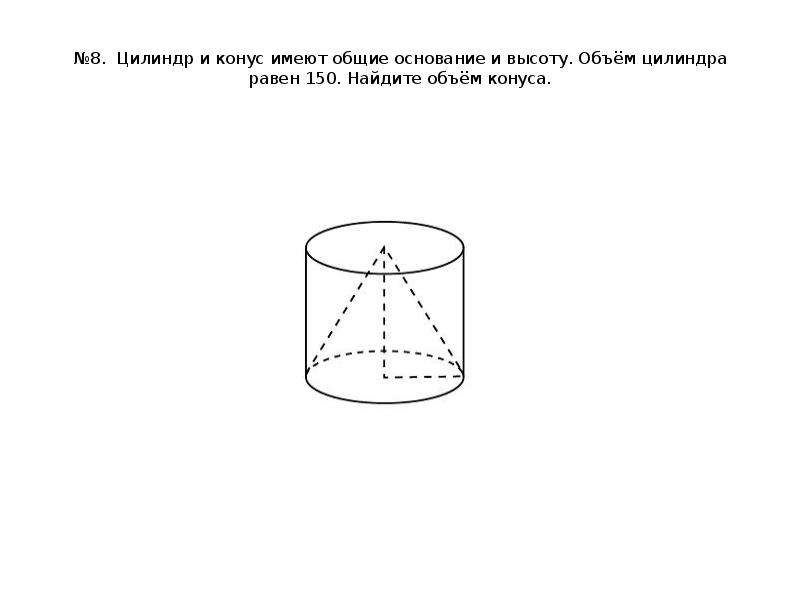
11. №8. Цилиндр и конус имеют общие основание и высоту. Объём цилиндра равен 150. Найдите объём конуса.
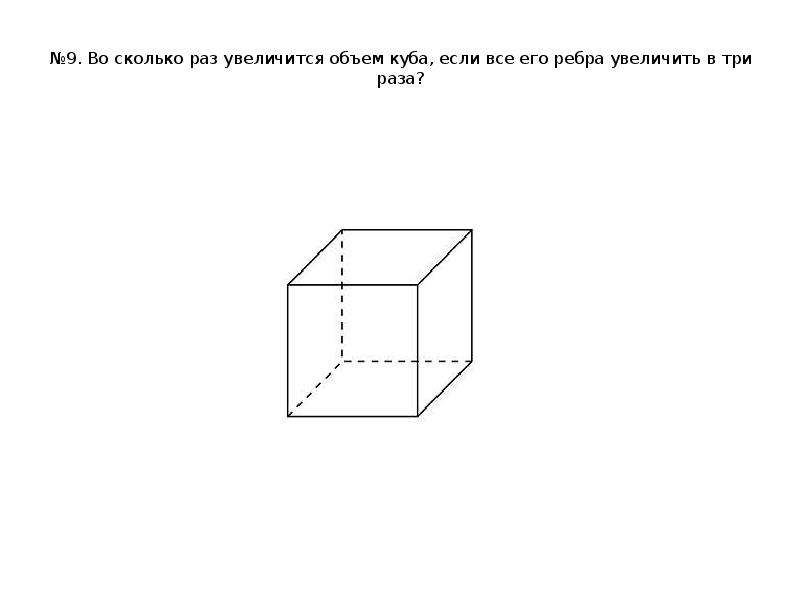
12. №9. Во сколько раз увеличится объем куба, если все его ребра увеличить в три раза?
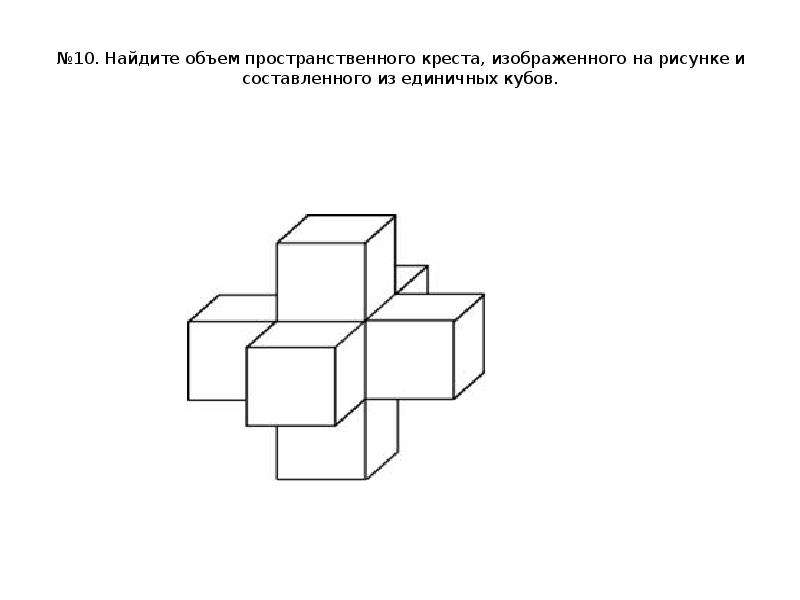
13. №10. Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.
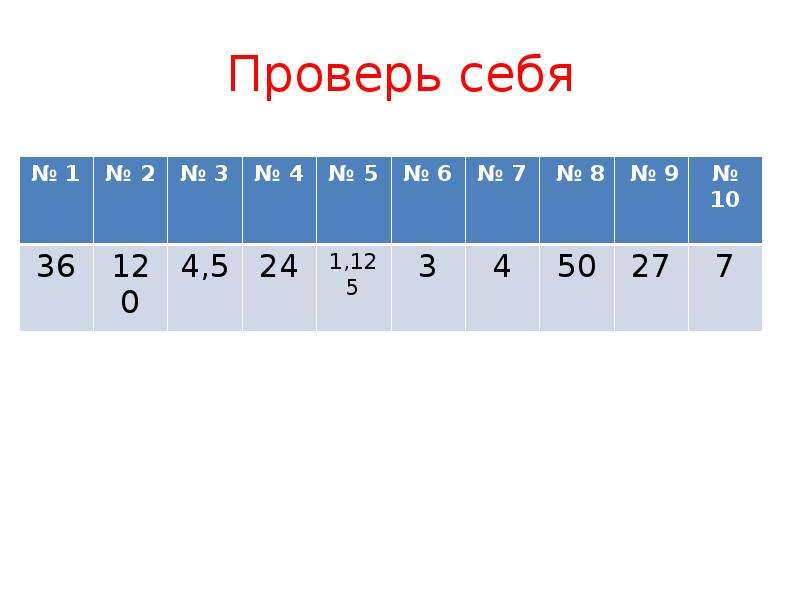
14. Проверь себя
15.
Проверь себя
16. Проверь себя
№1
№2
№3
№4
№5
№6
№7
№8
№9
№ 10
36
120
4,5
24
1,125
3
4
50
27
7
1
Объемы многогранников на ЕГЭ Открытое занятие в 11 классе Ставрополь, 2014
2
3
формулы
4
Задания первого типа Нахождение объема многогранников по формулам с известными длинами ребер
5
1. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
6
2. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
7
3. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
8
4. Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 3. Практическая работа
9
Задания второго типа Объем многогранников: формулы – формулы…
10
5. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 4. Диаго наль параллелепипеда равна 6. Найдите объем па раллелепипеда.
11
6. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 8 и 6, боко вое ребро равно 5. Найдите объем призмы.
12
7. В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
13
8. Сторона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найди те объем пирамиды.
14
9. Гранью параллелепипеда является ромб со сто роной 1 и острым углом 60. Одно из ребер парал лелепипеда составляет с этой гранью угол в 60 и равно 2. Найдите объем параллелепипеда.
15
Задания третьего типа Объем многогранников: подобие и преобразования
16
10. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в 4 раза?
17
11. Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в два раза?
18
12. В сосуд, имеющий форму правильной треуголь ной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в сантиметрах.
19
13. Через среднюю линию основания треугольной призмы, объем которой равен 52, проведена плос кость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
20
14. Объем куба равен 132. Найдите объем четырех угольной пирамиды, основанием которой является грань куба, а вершиной центр куба.
21
15. Объем правильной четырехугольной пирамиды SABCD равен 132. Точка E середина ребра SB. Найдите объем треугольной пирамиды EABC.
22
Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их. Джордж Пойа
23
Домашнее задание Вариант
24
Сторона основания правильной шестиугольной пи рамиды равна 11, а угол между боковой гранью и основанием равен 45°. Найдите объем пирамиды.
Слайды презентации
Слайд 1
Подготовка к ЕГЭ
Математический диктант
Геометрия № 8 ( стереометрия
)
ОБЪЕМЫ
Слайд 4
№ 1.Найдите объем многогранника, изображенного на рисунке (все
двугранные
углы прямые).
Слайд 5
№ 2. Основанием прямой треугольной призмы является прямоугольный треугольник
с катетами 6 и
8, боковое ребро призмы равно
5. Найдите объём призмы.
Слайд 6
№ 3. Найдите объем правильной шестиугольной призмы, стороны основания
которой равны 1, а
боковые ребра равны
.
Слайд 7
№ 4. Объем куба равен 8.
Найдите площадь
его поверхности.
Слайд 8
№ 5. Одна цилиндрическая кружка вдвое выше второй, зато
вторая в полтора раза шире. Найдите
отношение объема второй
кружки к объему первой.
Слайд 9
№ 6. Во сколько раз уменьшится объем конуса, если
его высота уменьшится в 3 раза, а радиус основания
останется
прежним?
Слайд 10
№ 7. Два ребра прямоугольного параллелепипеда,
выходящие из одной
вершины, равны 2 и 6. Объем
параллелепипеда равен 48.
Найдите третье ребро
параллелепипеда, выходящее из той же вершины.
Слайд 11
№ 8. Цилиндр и конус имеют общие основание и
высоту. Объём цилиндра равен 150. Найдите
объём конуса.
Слайд 12
№ 9. Во сколько раз увеличится объем куба, если
все его ребра увеличить в три раза?
Слайд 13
№ 10. Найдите объем пространственного креста, изображенного на рисунке
и составленного из
единичных кубов.
Слайд 16
№ 1 № 2 № 3 № 4 №
5 № 6 № 7 № 8 № 9
№ 10
36 120 4,5 24 1,125
3 4 50 27 7Проверь
себя
Чтобы скачать презентацию — поделитесь ей с друзьями с помощью
социальных кнопок.
Слайд 1
Описание слайда:
Подготовка к ЕГЭ
Математический диктант
Слайд 2
Слайд 3
Слайд 4
Описание слайда:
№1.Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Слайд 5
Описание слайда:
№2. Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 6 и 8, боковое ребро призмы равно 5. Найдите объём призмы.
Слайд 6
Описание слайда:
№3. Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны .
Слайд 7
Описание слайда:
№4. Объем куба равен 8.
Найдите площадь его поверхности.
Слайд 8
Описание слайда:
№5. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
Слайд 9
Описание слайда:
№6. Во сколько раз уменьшится объем конуса, если его высота уменьшится в 3 раза, а радиус основания останется прежним?
Слайд 10
Описание слайда:
№7. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
Слайд 11
Описание слайда:
№8. Цилиндр и конус имеют общие основание и высоту. Объём цилиндра равен 150. Найдите объём конуса.
Слайд 12
Описание слайда:
№9. Во сколько раз увеличится объем куба, если все его ребра увеличить в три раза?
Слайд 13
Описание слайда:
№10. Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.
Слайд 14
Описание слайда:
Проверь себя
Слайд 15
Слайд 16
Описание слайда:
Проверь себя