Поиск
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 11 1–11
Добавить в вариант
Тип 14 № 508457
Решите неравенство:
Аналоги к заданию № 508457: 508554 508564 508566 508569 511539 511571 511577 Все
Классификатор алгебры: Неравенства, однородные, относительно показательных функций, Неравенства рациональные относительно показательной функции
Методы алгебры: Введение замены
Кодификатор ФИПИ/Решу ЕГЭ: 2.2.3 Показательные неравенства, 2.2.9 Метод интервалов
Решение
·
·
Курс Д. Д. Гущина
·
3 комментария · Сообщить об ошибке · Помощь
Тип 14 № 508554
Решите неравенство:
Аналоги к заданию № 508457: 508554 508564 508566 508569 511539 511571 511577 Все
Классификатор алгебры: Неравенства, однородные, относительно показательных функций, Неравенства рациональные относительно показательной функции
Методы алгебры: Введение замены
Кодификатор ФИПИ/Решу ЕГЭ: 2.2.9 Метод интервалов
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Тип 14 № 508564
Решите неравенство:
Аналоги к заданию № 508457: 508554 508564 508566 508569 511539 511571 511577 Все
Классификатор алгебры: Неравенства, однородные, относительно показательных функций, Неравенства рациональные относительно показательной функции
Методы алгебры: Введение замены
Кодификатор ФИПИ/Решу ЕГЭ: 2.2.9 Метод интервалов
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Тип 14 № 508566
Решите неравенство:
Аналоги к заданию № 508457: 508554 508564 508566 508569 511539 511571 511577 Все
Классификатор алгебры: Неравенства, однородные, относительно показательных функций, Неравенства рациональные относительно показательной функции
Методы алгебры: Введение замены
Кодификатор ФИПИ/Решу ЕГЭ: 2.2.9 Метод интервалов
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
1 комментарий · Сообщить об ошибке · Помощь
Тип 14 № 508569
Решите неравенство:
Аналоги к заданию № 508457: 508554 508564 508566 508569 511539 511571 511577 Все
Классификатор алгебры: Неравенства, однородные, относительно показательных функций, Неравенства рациональные относительно показательной функции
Методы алгебры: Введение замены
Кодификатор ФИПИ/Решу ЕГЭ: 2.2.9 Метод интервалов
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Тип 14 № 624604
Решите неравенство
Источник: А. Ларин. Тренировочный вариант № 376.
Классификатор алгебры: Логарифмические неравенства, Неравенства смешанного типа, Неравенства, однородные, относительно показательных функций
Методы алгебры: Метод интервалов, Сведение к однородному
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Задания Д11 C3 № 504242
Решите систему неравенств:
Аналоги к заданию № 500113: 504242 510364 Все
Раздел: Алгебра
Классификатор алгебры: Неравенства, однородные, относительно показательных функций, Системы неравенств
Методы алгебры: Введение замены, Метод интервалов
Кодификатор ФИПИ/Решу ЕГЭ: 2.2.4 Логарифмические неравенства
Решение
·
Прототип задания
·
·
1 комментарий · Сообщить об ошибке · Помощь
Задания Д11 C3 № 510364
Решите систему неравенств:
Аналоги к заданию № 500113: 504242 510364 Все
Классификатор алгебры: Неравенства, однородные, относительно показательных функций, Системы неравенств
Методы алгебры: Введение замены, Метод интервалов
Кодификатор ФИПИ/Решу ЕГЭ: 2.2.4 Логарифмические неравенства
Решение
·
Прототип задания
·
·
Сообщить об ошибке · Помощь
Задания Д11 C3 № 500113
Решите систему неравенств
Аналоги к заданию № 500113: 504242 510364 Все
Классификатор алгебры: Неравенства, однородные, относительно показательных функций, Системы неравенств
Методы алгебры: Введение замены, Метод интервалов
Кодификатор ФИПИ/Решу ЕГЭ: 2.2.4 Логарифмические неравенства
Решение
·
·
1 комментарий · Сообщить об ошибке · Помощь
Задания Д12 C3 № 515107
Решите неравенство
Источник: А. Ларин: Тренировочный вариант № 165.
Классификатор алгебры: Иррациональные неравенства, Неравенства смешанного типа, Неравенства, однородные, относительно показательных функций
Методы алгебры: Введение замены
Кодификатор ФИПИ/Решу ЕГЭ: 2.2.9 Метод интервалов
Решение
·
·
Сообщить об ошибке · Помощь
Тип 14 № 514053
Решите неравенство
Источник: А. Ларин: Тренировочный вариант № 152.
Классификатор алгебры: Неравенства рациональные относительно показательной функции
Методы алгебры: Введение замены, Сведение к однородному
Кодификатор ФИПИ/Решу ЕГЭ: 2.2.9 Метод интервалов
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Всего: 11 1–11
Неравенство с параметром
( displaystyle {{x}^{2}}-3ax+2{{a}^{2}}le 0), при ( displaystyle ane 0).
Его мы сможем решить с помощью метода интервалов, если разложим левую часть на множители. Но как это сделать?
Заметим, что если поделить каждое слагаемое на ( displaystyle {{a}^{2}}), получим:
( displaystyle {{x}^{2}}-3ax+2{{a}^{2}}le 0text{ }left| :{{a}^{2}} right.text{ }Leftrightarrow )
( displaystyle frac{{{x}^{2}}}{{{a}^{2}}}-frac{3ax}{{{a}^{2}}}+frac{2{{a}^{2}}}{{{a}^{2}}}le 0text{ }Leftrightarrow text{ }{{left( frac{x}{a} right)}^{2}}-3frac{x}{a}+2le 0)
Сделав замену ( displaystyle t=frac{x}{a}), получим обычное квадратное неравенство относительно ( displaystyle t):
( displaystyle {{t}^{2}}-3t+2le 0text{ }Leftrightarrow text{ }left( t-2 right)left( t-1 right)le 0text{ }Leftrightarrow text{ 1}le tle 2).
Обратная замена: ( displaystyle 1le frac{x}{a}le 2text{ }Leftrightarrow text{ }left[ begin{array}{l}ale xle 2a,text{ } при a>0\2ale xle a,text{ } при a<0end{array} right.)
Такие неравенства называются однородными.
Однородным называется неравенство вида:( displaystyle {{k}_{0}}{{x}^{n}}+{{k}_{1}}{{x}^{n-1}}y+{{k}_{2}}{{x}^{n-2}}{{y}^{2}}+…+{{k}_{n-1}}x{{y}^{n-1}}+{{k}_{n}}{{y}^{n}}ge 0)(вместо знака ( displaystyle ge ) может, конечно, стоять любой знак неравенства).
То есть это неравенство с двумя неизвестными, в каждом слагаемом которого одинаковая сумма степеней этих неизвестных. Например, в примере выше эта сумма равна ( displaystyle 2). Решаются такие неравенства делением на одну из неизвестных в этой степени:
( displaystyle {{k}_{0}}{{x}^{n}}+{{k}_{1}}{{x}^{n-1}}y+{{k}_{2}}{{x}^{n-2}}{{y}^{2}}+…+{{k}_{n-1}}x{{y}^{n-1}}+{{k}_{n}}{{y}^{n}}le 0text{ }left| :{{y}^{n}}text{ } right.Leftrightarrow )
( displaystyle {{k}_{0}}{{left( frac{x}{y} right)}^{n}}+{{k}_{1}}{{left( frac{x}{y} right)}^{n-1}}+{{k}_{2}}{{left( frac{x}{y} right)}^{n-2}}+…+{{k}_{n-1}}left( frac{x}{y} right)+{{k}_{n}}le 0),
и последующей заменой переменных: ( displaystyle t=frac{x}{y}). Таким образом получаем рациональное неравенство ( displaystyle n)-ной степени с одной неизвестной ( displaystyle t):
( displaystyle {{k}_{0}}{{t}^{n}}+{{k}_{1}}{{t}^{n-1}}+{{k}_{2}}{{t}^{n-2}}+…+{{k}_{n-1}}t+{{k}_{n}}le 0).
Ты заметил ошибку в моих рассуждениях?
Ведь нельзя просто так взять и поделить неравенство на переменную! Она (переменная) может оказаться отрицательной или нулевой.
Поэтому всегда нужно специально проверять, можно ли это сделать.
Чаще всего нам будут встречаться неравенства второй степени (то есть квадратные), тогда делить придется на переменную в квадрате, а она заведомо неотрицательна:
( displaystyle a{{x}^{2}}+bxy+c{{y}^{2}}ge 0text{ }left| :{{y}^{2}}ne text{0 }Leftrightarrow text{ }a{{left( frac{x}{y} right)}^{2}}+bcdot frac{x}{y} right.+cge 0text{ }underset{t=frac{x}{y}}{mathop{Leftrightarrow }},text{ })
( displaystyle underset{t=frac{x}{y}}{mathop{Leftrightarrow }},text{ }a{{t}^{2}}+bt+cge 0 )
Отметим также, что эта переменная не может быть равна нулю. В случаях, когда это не очевидно, необходимо отдельно проверять случай когда эта переменная равна нулю. Например:
Решите неравенство ( displaystyle {{x}^{2}}-3ax+2{{a}^{2}}le 0) при всех ( displaystyle a).
Однородные уравнения – это уравнения, в которых все слагаемые имеют одинаковую суммарную степень.
Однородные неравенства – это неравенства, в которых все слагаемые имеют одинаковую суммарную степень.
Примеры:
((x-1)^4-10x^2 (x-1)^2+9x^4<0)
(sinx=sqrt{3}cosx)
(9^x-2cdot 3^xcdot 4^x+16^x≥0)
(sin^2x-4sinxcosx+3cos^2 x=0)
(3^{3x}-3^{x+1}cdot2^{2x}+18^x-3cdot8^x≥0)
Что значит «все слагаемые имеют одинаковую суммарную степень»?

Пример не однородных уравнений и неравенств:

Слагаемые, которые делают уравнения (неравенства) не однородными – подчеркнуты.
Решение однородных уравнений
Хотя однородные уравнения и выглядят «большими» и «страшными», решить их не сложнее, чем биквадратные. Надо знать лишь об одной «фишке»: если поделить однородное уравнение на одночлен (без коэффициента), то потом можно легко сделать замену переменных.
Пример. Решить уравнение (sinx=sqrt{3}cosx).
|
(sinx=sqrt{3}cosx) |
Перед нами типичное однородно-тригонометрическое уравнение. Надо разделить уравнение на cosx, но делить на число равное нулю нельзя, поэтому проверим, является ли (cosx=0) решением уравнения. Если (cosx=0), то (sinx=±1). Очевидно, что (±1≠0). |
|
|
(cosx≠0) |
Теперь с чистой совестью поделим уравнение на (cosx) |
|
|
(frac{sinx}{cosx})(=sqrt{3}) |
Заменим (frac{sinx}{cosx})(=tgx) |
|
|
(tg x= sqrt{3}) |
Решим тригонометрическое уравнение. |
|
|
(x=)(frac{π}{3})(+πk), (k∈Z) |
Запишем ответ. |
Ответ: (x=)(frac{π}{3})(+πk), (k∈Z).
Заметьте, что в этом примере перед тем, как делить на (cosx), была сделана проверка — является ли (cosx=0) решением уравнения. Нужно каждый раз проверять, является ли выражение, на которое вы хотите поделить, решением. Иначе вы рискуете потерять корни уравнения.
Пример. Решить уравнение (7cdot 9^{x^2-3x+1}+5cdot 6^{x^2-3x+1}-48cdot 4^{x^2-3x}=0).
|
(7cdot9^{x^2-3x+1}+5cdot6^{x^2-3x+1}-48cdot 4^{x^2-3x}=0) |
Показатели степеней в уравнении похожи – в каждом есть (x^2-3x). Давайте сделаем их одинаковыми. |
|
|
(7cdot 9^{x^2-3x+1}+5cdot 6^{x^2-3x+1}-12 cdot 4^1cdot 4^{x^2-3x}=0) |
«Соединим» (4^1) и (4^{x^2-3x}) по свойству степеней (a^mcdot a^n=a^{m+n}) . |
|
|
(7cdot 9^{x^2-3x+1}+5cdot 6^{x^2-3x+1}-12 cdot 4^{x^2-3x+1}=0) |
Получился классический вид однородного уравнения. |
|
|
(7cdot)((frac{9}{4})^{x^2-3x+1})(+5cdot)((frac{6}{4})^{x^2-3x+1})(-12=0) |
Сократим (6) и (4). |
|
|
(7cdot)((frac{9}{4})^{x^2-3x+1})(+5cdot)((frac{3}{2})^{x^2-3x+1})(-12=0) |
Обратите внимание: ((frac{3}{2})^2)(=)(frac{9}{4}). С учетом этого сделаем замену. |
|
|
(t=)((frac{3}{2})^{x^2-3x+1}) |
Положительное число в любой степени всегда больше нуля, поэтому (t>0). Отметим это в решении, чтобы не забыть. |
|
|
(7t^2+5t-12=0) |
Решим уравнение. |
|
|
(D=25+336=361=(19)^2) |
Сделаем обратную замену. |
|
|
((frac{3}{2})^{x^2-3x+1})(=1) |
Ответ: (frac{3pmsqrt{5}}{2}).
Пример. Решите неравенство (5cdot25^{frac{1}{x}}+3cdot10^{frac{1}{x}}≥2cdot4^{frac{1}{x}}).
|
(5cdot25^{frac{1}{x}}+3cdot10^{frac{1}{x}}≥2cdot4^{frac{1}{x}}) |
Здесь показатели степени уже в «приличном» виде. Можно поделить на (4^{frac{1}{x}}), т.к., (4^{frac{1}{x}}>0). |
|
|
(5cdot)(frac{25^{frac{1}{x}}}{4^{frac{1}{x}}})(+3cdot)(frac{10^{frac{1}{x}}}{4^{frac{1}{x}}})(≥2) |
Применим свойство степеней (frac{a^n}{b^n})(=)((frac{a}{b})^n). |
|
|
(5cdot)((frac{25}{4})^{frac{1}{x}})(+3cdot)({(frac{10}{4})}^{frac{1}{x}})(≥2) |
Сократим вторую дробь и перенесем двойку в левую часть. |
|
|
(5cdot)((frac{25}{4})^{frac{1}{x}})(+3cdot)({(frac{5}{2})}^{frac{1}{x}})(-2≥0) |
Сделаем замену (t=)({(frac{5}{2})}^{frac{1}{x}}) (отметим, что (t>0) при любом (x)). |
|
|
(5t^2+3t-2≥0) |
Решим квадратное неравенство. |
|
|
(D=9+40=49=7^2) |
||
|
|
Чтобы вернуться к исходной переменной (иксу) перейдем к совокупности неравенств, дающих такое же решение, как получилось на числовой оси. |
|
|
(left[ begin{gathered}t≤-1 \ t≥frac{2}{5} end{gathered}right.) |
Первое неравенство не имеет смысла (помните условие (t>0)?) , поэтому решаем только второе. |
|
|
(t≥)(frac{2}{5}) (⇔) ((frac{5}{2})^{frac{1}{x}})(≥)(frac{2}{5}) (⇔) (frac{1}{x})(≥-1) |
Перенесем (-1) в левую часть и приведем к общему знаменателю. |
|
|
(frac{1+x}{x})(≥0) |
Применим метод интервалов. |
|
|
|
Обратите внимание, ноль – выколот, так как при (x=0) у нас будет деление на ноль слева. А вот точка (-1) вколота, так как неравенство нестрогое. |
Ответ: ((-∞;-1]∪(0;∞)).
Смотрите также:
Решение уравнений методом разложения на множители
Рассмотрим основные типы показательных неравенств.
При решении показательных неравенств мы будем использовать следующие переходы:
и
Поясним, первый переход возникает в силу возрастания показательной функции
, второй – в силу убывания функции
.
Показательные неравенства, сводящиеся к простейшим
Задание 1.
Решить неравенство .
Решение:
Перепишем неравенство следующим образом:
А далее вот так:
Так как – возрастающая функция, то знак неравенства остается без изменения при переходе к новому неравенству:
Ответ: .
Задание 2.
Решить неравенство:
Решение:
Перепишем неравенство следующим образом:
Заметим, что .
В силу того, что основание степени () меньше 1, то есть мы имеем дело с убывающей функцией, переходим к следующему неравенству (не забывая поменять знак
на
):
Ответ:
Однородные показательные неравенства
Задание 3.
Решить неравенство:
Решение:
Вынесем за скобку
Тогда переходим к следующему неравенству (в силу того, что основание степени больше 1, знак неравенства не меняется):
Ответ:
Показательные неравенства, сводящиеся к квадратным
Задание 4.
Решить неравенство
Решение:
Разделим обе части неравенства на 3:
Мы видим квадратное неравенство относительно которое будем решать методом интервалов.
Имеем:
или
или
Ответ:
Задание 5.
Решить неравенство
Решение:
Мы видим квадратное неравенство относительно , которое будем решать методом интервалов.
Находим при помощи дискриминанта корни квадратного трехчлена . Переходим к следующему неравенству:
Получаем: или
. Заметьте, нет смысла указывать, что
, так как по определению
положительно.
Итак,
Ответ:
Задание 6.
Решить неравенство
Решение:
Разделим обе части неравенства на (можно и на
,
– как хотите…). Заметим,
.
Заметим, что . Аналогично с
.
Мы имеем квадратное неравенство относительно
которое будем решать методом интервалов.
Воспользуемся следующим способом превращения суммы в произведение:
где
– корни уравнения
(в случае неотрицательного дискриминанта квадратного трехчлена).
Заготавливаем шаблончик и находим корни при помощи дискриминанта, тогда
То есть
Ответ:
Задание 7.
Решить неравенство
Решение:
Перепишем неравенство следующим образом:
Домножим обе части неравенства на (заметим,
):
Ответ:
Показательные неравенства, сводящиеся к рациональным
Задание 8.
Решить неравенство:
Решение:
Переносим все в левую сторону неравенства и приводим к общему знаменателю:
Мы можем “отбросить” сумму в силу ее положительности:
Неравенство равносильно следующему:
Ответ:
Неравенства, решаемые графическим методом
Задание 9.
Решить неравенство:
Решение:
Рассмотрим функции и
Обе они определены на
. Первая – возрастает, вторая – убывает. Значит, уравнение
имеет не более одного решения. Несложно заметить, что
является корнем указанного уравнения.
А значит, если вернуться к неравенству и посмотреть на него с графической точки зрения, мы должны взять те значения , которые отвечают за ту часть графика
, что лежит выше графика
, то есть
.
Ответ:
Для самостоятельной работы:
Решить неравенства:
1.
Ответ: + показать
2.
Ответ: + показать
3.
Ответ: + показать
4.
Ответ: + показать
5.
Ответ: + показать
6.
Ответ: + показать
7.
Ответ: + показать
8.
Ответ: + показать
Посмотрите на еще одну таблицу. В ней представлены степени (frac{1}{3}):
$$left(frac{1}{3}right)^0=1;$$
$$left(frac{1}{3}right)^1=frac{1}{3};$$
$$left(frac{1}{3}right)^2=frac{1}{9};$$
$$left(frac{1}{3}right)^3=frac{1}{27};$$
$$left(frac{1}{3}right)^4=frac{1}{81};$$
$$left(frac{1}{3}right)^5=frac{1}{243};$$
Оказывается, чем в большую степень мы будем возводить (frac{1}{3}), тем МЕНЬШЕЕ значение будем получать. Показательная функция с основанием (frac{1}{3}) будет убывающей. Более того, если возводить в степень любую дробь меньшую единицы, с увеличением степени вы всегда будете получать всё меньшие и меньшие значения. Чтобы наглядно это продемонстрировать, нарисуем еще один график функции (y=(frac{1}{3})^x):
Из всего этого занудства следует очень важное общее правило:
Если основание у степени больше единицы (a>1), то показательная функция будет возрастающей, а если меньше единицы (0 lt a lt 1), то убывающей. Это ключевой момент при решении показательных неравенств!
Решение показательных (степенных) неравенств похоже на решение показательных уравнений с некоторыми оговорками. Начнем изучение с простейшего примера:
Пример 1
$$ 2^x>2^3; $$
Это неравенство решается интуитивно. Понятное дело, что чем в большую степень мы будем возводить двойку, тем большее значение будем получать. Основание больше единицы, а значит, показательная функция возрастающая!
Основания у нас одинаковые. Значит, если вместо (x) подставить любое число большее 3, мы получим верное неравенство. Решением нашего первого показательного неравенства будет:
$$ x>3;$$
Пример 2
$$3^{x+4}<3^{3x-10};$$
Основания одинаковые, большие единицы, а значит, у нас опять возрастающие функции — чем больше степень, тем больше значение показательной функции. Логично, что наше неравенство в таком случае сводится к сравнению степеней с сохранением знака неравенства:
$$x+4<3x-10;$$
$$-2x<-14;$$
При делении на отрицательное число не забываем поменять знак неравенства:
$$x>7;$$
Пример 3
$$ left(frac{1}{2}right)^x>left(frac{1}{2}right)^5;$$
Очень похожее неравенство, основания опять одинаковые, но они меньше единицы. Что это меняет? Знак неравенства!
Раз основание показательной функции меньше единицы, значит она убывающая — чем больше степень, тем меньше значение показательной функции. Поэтому для того, чтобы неравенство выполнялось, необходимо опять сравнить степени, но с противоположным знаком:
$$x<5;$$
Пример 4
$$left(frac{2}{3}right)^{2x-5}geleft(frac{2}{3}right)^{x+1};$$
Основания одинаковые и меньше единицы, значит избавляемся от основания (frac{2}{3}) и сравниваем степени, не забывая при этом изменить знак неравенства:
$$2x-5 le x+1;$$
$$x le 6;$$
Пример 5
$$2^{x+2} le 8^{2x-1};$$
Этот пример немного сложнее — здесь разные основания (слева 2, справа 8). Чтобы решить по аналогии с предыдущими примерами, нужно привести к одинаковым основаниям. Заметим, что восемь можно представить в виде степени двойки: (8=2^3). Подставим в исходное неравенство:
$$2^{x+2} le (2^3)^{2x-1};$$
Из свойства степеней: $$(a^n)^m=a^{n*m}.$$
$$2^{x+2} le 2^{3*(2x-1)};$$
Теперь основания одинаковые и больше единицы, избавляемся от них, оставляя знак неравенства неизменным:
$$x+2 le 3*(2x-1);$$
$$x+2 le 6x-3;$$
$$-5x le -5;$$
$$x ge 1.$$
Общий алгоритм
Сформулируем еще раз общие правила решения простых показательных неравенств:
- Необходимо привести показательные функции слева и справа к одинаковому основанию
- Избавляемся от оснований
- Если основание больше единицы, то знак неравенства сохраняется
- Если основание меньше единицы, то меняем знак неравенства на противоположный
- Решаем получившееся неравенство
Схема решения
$$a^{f(x)}>a^{g(x)};$$
где (a>0; ; aneq1) — некоторое положительное число, а (f(x)) и (g(x)) какие-то зависящие от (x) выражения.
Если (a>1): то (f(x)>g(x));
Если (0 lt a lt 1:) то (f(x) lt g(x)).
В принципе, схема решения простых показательных неравенств очень похожа на решение показательных уравнений. За исключением необходимости внимательно следить за основаниями и знаком неравенства.
Разберем еще несколько интересных и важных примеров.
Пример 6
$$2^{x+1} ge 4;$$
Справа от знака неравенства стоит не показательная функция, а просто число. Но его легко представить в виде степени двойки:
$$2^{x+1} ge 2^2;$$
Основания одинаковые, большие единицы. Избавляемся от них, знак неравенства сохраняем.
$$ x+1 ge 2;$$
$$x ge 1.$$
Как приводить степени к одному основанию
Пример 7
$$5^x le 3;$$
На первый взгляд, пример аналогичен предыдущему. Чтобы решить неравенство, нужно привести к одинаковому основанию. Так и есть, но вот как представить (3-ку) в виде степени (5-ки)?
Ничего сложного в этом нет. Оказывается, любое число (a) можно представить в виде степени с нужным нам основанием (b). Правда, без логарифмов тут не обойтись. Это можно сделать при помощи формулы:
$$ a=b^{log_{b}(a)}; qquad (*)$$
Например: (3=5^{log_{5}(3)};)
Кто забыл, что такое логарифмы, вам обязательно нужно посмотреть сюда.
Мы уже пользовались этой формулой в главе про показательные уравнения. На самом деле, для решения неравенств ее необязательно понимать, можно в лоб подставлять числа в формулу. Но я бы настоятельно рекомендовал разбираться во всем, чем вы пользуетесь. Поэтому подумайте самостоятельно, почему эта формула верна?
Посмотрим на правую часть формулы (*). В степени у нас стоит логарифм (log_{b}(a)). Логарифм — это число, в которое нужно возвести основание (b), чтобы получить (a). И в итоге, в правой части формулы (*) мы (b) возводим в степень, в которую нужно возвести (b), чтобы получить число (a). Так немного запутанно эта формула и работает. Но, если подумать, все не так сложно.
Возвращаемся к примеру 7. Теперь мы знаем, как (3-ку) представить в виде степени (5-ки):
$$3=5^{log_{5}(3)};$$
Подставляем в исходное неравенство
$$5^x le 5^{log_{5}(3)};$$
Наши основания одинаковые, избавляемся от них
$$x le log_{5}(3);$$
Ответ оставляем с некрасивым логарифмом. Мы его не сможем посчитать без калькулятора. На ЕГЭ именно так и поступаем.
Пример 8
$$left(frac{1}{81}right)^{-4x} < 27^{x+8};$$
Здесь привести к одному основанию несколько сложнее. Обратите внимание, что числа 27 и (frac{1}{81}) являются степенями (3-ки):
$$ 27=3^3; $$
$$ frac{1}{81}=3^{-4}; $$
Кто забыл, как работать со степенями, посмотрите главу про свойства степеней. Приведем к основанию (3) левую и правую части неравенства:
$$(3^{-4})^{-4x} < (3^3)^{x+8};$$
$$3^{16x} < 3^{3x+24};$$
Основания одинаковые, избавляемся от них:
$$16x<3x+24;$$
$$ 13x<24;$$
$$x<frac{24}{13};$$
Пример 9
$$ 5^x <-3;$$
Казалось бы, пример ничем не отличается от примера №7 — приводи себе ((-3)) к основанию (5) по формуле и решай.
Но здесь проблема кроется в определении показательной функции. Показательная функция ВСЕГДА больше нуля!
А значит, (5^x>0) и никак не может быть меньше ((-3)), какие бы (x) вы не подставляли.
Попробуйте подставить вместо (x) минус миллион, что вы получите? По определению отрицательной степени:
$$a^{-n}=frac{1}{a^n};$$
$$ 5^{-1000000}=frac{1}{5^{1000000}};$$
Это, несомненно, будет очень маленькое, но положительное число.
Итак, в этом примере корней нет. Запомните это!
Пример 10
$$ 7^x >-6;$$
Неравенство аналогичное примеру №9, но с другим знаком неравенства.
Что меняется? Теперь нас просят найти такие (x), при которых показательная функция (7^x) будет больше отрицательного числа ((-7)). Но так как показательная функция больше (0) при любых (x), то она уже точно будет больше ((-7)).
Что бы вы не подставили, всегда будете получать верное неравенство.
Ответом здесь будет любое число.
Теперь разберем пример посложнее.
Пример 11
$$ 25^{x^2-2x+10}-0,2^{2x^2-4x-80} le 0;$$
Постараемся привести данное неравенство к виду, аналогичному предыдущим примерам. Для этого перенесем вправо второе слагаемое (0,2^{2x^2-4x-80}):
$$ 25^{x^2-2x+10} le 0,2^{2x^2-4x-80};$$
Приведем к одному основанию. Советую десятичные дроби записывать в виде обыкновенных дробей, так вы сразу увидите, к какому основанию удобно привести:
$$0,2=frac{2}{10}=frac{1}{5};$$
$$ 25^{x^2-2x+10} le left(frac{1}{5}right)^{2x^2-4x-80};$$
Слева и справа в основаниях стоят числа, которые легко можно представить в виде степени (5-ки):
$$25=5^2;$$
$$ frac{1}{5}=5^{-1};$$
Подставим
$$ (5^2)^{x^2-2x+10} le (5^{-1})^{2x^2-4x-80};$$
$$ 5^{2*(x^2-2x+10)} le 5^{-1*(2x^2-4x-80)};$$
$$ 5^{2*x^2-4x+20} le 5^{-2x^2+4x+80};$$
Основания одинаковые, избавляемся от них:
$$ 2x^2-4x+20 le -2x^2+4x+80; $$
$$4x^2-8x-60 le 0;$$
Через дискриминант раскладываем квадратный многочлен на множители:
$$ 4(x+3)(x-5) le 0;$$
И решаем методом интервалов:
Замена в показательных неравенствах
Мы разобрали все виды простейших степенных неравенств. Опираясь на эти знания, можно перейти к более сложным неравенствам, которые решаются при помощи замены переменной. В ЕГЭ по профильной математике такие примеры попадаются довольно часто.
Если вы раньше решали любые уравнения или неравенства на замену переменной, то разобраться будет совсем не трудно. Давайте посмотрим на примерах:
Пример 12
$$ 4^x-29*2^x+168le 0. $$
Согласно обычной логике в показательных неравенствах, приведем все показательные функции к одинаковому основанию. Здесь это сделать довольно легко:
$$ (2^2)^x-29*2^x+168 le 0$$
$$ 2^{2x}-29*2^x+168 le 0$$
Готово. Теперь обратите внимание, что (2^{2x}=(2^x)^2), согласно свойству степеней. Подставим:
$$ (2^x)^2-29*2^x+168 le 0$$
В любом примере на замену переменной нужно найти одинаковые конструкции (выражения), зависящие от (x). В нашем примере есть такая конструкция — (2^x).
Обозначим за (t=2^x), и подставим в наше неравенство:
$$ t^2-29t+168 le 0 $$
В итоге получили обыкновенное квадратное неравенство, которое я обычно решаю при помощи универсального метода интервалов:
$$ D=29^2-4*168=841-672=169;$$
$$t_{1}=frac{29+13}{2}=21;$$
$$t_{2}=frac{29-13}{2}=8;$$
Зная корни, раскладываем квадратный многочлен на множители:
$$(t-8)(t-21) le 0;$$
Для метода интервалов рисуем числовую прямую, отмечаем нули функции (корни) и исследуем промежутки. Кто не помнит метод интервалов, настоятельно рекомендую его повторить, без него решать показательные неравенства бесполезно.
Получаем промежутки для переменной (t):
$$ t in [8;21];$$
И тут частая ошибка в том, что школьники заканчивают на этом решение. Но нас же не просят в условии задачи найти (t), нас просят найти (x)!
Поэтому обязательно нужно сделать обратную замену, чтобы вернуться к исходной переменной (x).
Для этого будем пользоваться простой логикой: раз (tin[8;21]), значит (t) может принимать такие значения, которые больше либо равны 8, но и не больше 21. Перепишем то же самое в виде системы (система, потому что эти условия должны выполняться одновременно):
$$ begin{cases}
t ge 8, \
t le 21.
end{cases}$$
Теперь нужно вспомнить, а что такое собственно (t). Это же переменная, за которую мы обозначили (2^x=t). Подставим вместо (t) (2^x).
Обратная замена:
$$ begin{cases}
2^x ge 8, \
2^x le 21.
end{cases}$$
Получили систему из двух простейших показательных неравенств, которые выше мы уже научились с вами решать.
$$ begin{cases}
2^x ge 2^3, \
2^x le 2^{log_{2}(21)}.
end{cases}$$
Основания везде одинаковые, можно от них избавиться:
$$ begin{cases}
x ge 3, \
x le log_{2}(21).
end{cases}$$
Запишем эту систему в виде промежутка
Ответ: (x in [3;log_{2}(21)].)
Как видите, все не так уж сложно. Разберем еще примеры на замену переменной в показательных неравенствах.
Пример 13
$$ 2^x+6*2^{-x} le 7$$
Этот пример тоже на замену. Хотя основания у показательных функций у нас одинаковые — двойка, но вот степень у них отличаются, а значит, делать замену пока нельзя. Нужно сделать так, чтобы одинаковым было абсолютно все — и степени, и основания.
Вспомним свойство степени с отрицательным показателем:
$$a^{-n}=frac{1}{a^n};$$
И применим его в нашем неравенстве:
$$ 2^x+6*frac{1}{2^x} le 7$$
Обозначим за (t=2^x) и подставим:
$$ t+6*frac{1}{t} le 7 $$
Для того, чтобы тут воспользоваться методом интервалов, нужно перекинуть все в левую часть и привести к общему знаменателю.
$$ frac{t^2-7t+6}{t} le 0 $$
Я не рекомендую избавляться в неравенствах от знаменателя, как вы привыкли это делать в уравнениях. В неравенствах в подавляющем большинстве случаев ни в коем случае этого делать нельзя, он тоже влияет на знак всей функции. Это одна из самых частых ошибок на ЕГЭ.
Поэтому я рекомендую всегда в неравенствах тащить знаменатель за собой, не убирать его. Подробнее про это можно почитать в теории обыкновенных неравенств.
Но я вынужден отметить, что именно в этом примере убрать знаменатель (t) можно, так как (t=2^x>0). Показательная функция у нас ВСЕГДА больше нуля, поэтому и (t>0), а значит он не влияет на знак неравенства. Однако делать мы это не будем, чтобы не запутаться. Знаменатель всегда будем оставляем на месте.
Раскладываем на множители числитель:
$$ frac{(t-1)(t-6)}{t} le 0 $$
Метод интервалов, с учетом того, что (t=2^x>0):
$$ t in[1;6];$$
Запишем промежуток в виде системы:
$$ begin{cases}
t ge 1, \
t le 6.
end{cases}$$
Вспоминаем, что (t=2^x) и делаем обратную замену:
$$ begin{cases}
2^x ge 1, \
2^x le 6.
end{cases}$$
$$ begin{cases}
2^x ge 2^0, \
2^x le 2^{log_{2}(6)}.
end{cases}$$
$$ begin{cases}
x ge 0, \
x le log_{2}(6).
end{cases}$$
Ответ: (x in [0;log_{2}(6)].)
Пример 14
$$16^{x+frac{1}{4}}-9*4^{x-frac{1}{2}}+1ge0$$
Пример очень похож на предыдущие, но перед тем, как делать замену, нам придется преобразовать левую часть неравенства. Выпишем отдельно показательные функции и постараемся привести их к одному виду. Иначе мы не сможем сделать замену. Для этого нам понадобятся свойства степеней:
$$a^{n+m}=a^n*a^m;$$
$$(a^n)^m=a^{n*m};$$
$$a^{n-m}=frac{a^n}{a^m};$$
$$16^{x+frac{1}{4}}=16^x*16^{frac{1}{4}}=16^x*2=2*16^x=2*(4^2)^x=2*(4^x)^2;$$
$$4^{x-frac{1}{2}}=frac{4^x}{4^{frac{1}{2}}}=frac{4^x}{2}=frac{1}{2}*4^x;$$
Подставим наши преобразования в исходное неравенство:
$$2*(4^x)^2-9*frac{1}{2}*4^x+1 ge 0;$$
Все готово к замене. Пусть (t=4^x):
$$2*t^2-frac{9}{2}*t+1 ge 0;$$
Домножим на (2), чтобы избавиться от знаменателя
$$4t^2-9t+2 ge 0;$$
Обыкновенное квадратное неравенство. Решаем, как обычно, методом интервалов. Для этого разложим на множители:
$$4(t-frac{1}{4})(t-2) ge 0;$$
$$left[
begin{gathered}
tle frac{1}{4}; \
tge 2, \
end{gathered}
right.$$
Обратите внимание на знак совокупности! Он означает, что нас устраивают оба промежутка, как показано на числовой прямой.
Очень важно уметь различать системы и совокупности.
Знак системы используется, когда нужно, чтобы значения (x) удовлетворяли всем неравенствам, входящим в систему. Другими словами, система — это знак пересечения решений всех неравенств.
Знак совокупности показывает, что значения (x) удовлетворяют хотя бы одному из неравенств в системе. Совокупность — это знак объединения решений.
Делаем обратную замену (t=4^x):
$$left[
begin{gathered}
4^xle frac{1}{4}; \
4^xge 2, \
end{gathered}
right.$$
$$left[
begin{gathered}
4^xle 4^{-1}; \
4^xge 4^{frac{1}{2}}, \
end{gathered}
right.$$
$$left[
begin{gathered}
xle -1; \
xge frac{1}{2}, \
end{gathered}
right.$$
Запишем получившуюся совокупность в виде промежутков.
Ответ:(xin(-infty;-1] cup [frac{1}{2};+infty).)
Теперь наших знаний достаточно, чтобы решать некоторые реальные примеры из ЕГЭ по профильной математике. Поехали:
Пример 15
$$ frac{5^x}{5^x-4}+frac{5^x+5}{5^x-5}+frac{22}{25^x-9*5^x+20} le 0$$
Перед вами настоящий пример из ЕГЭ 2016 года. Возможно, выглядит неприятно, но на самом деле, он решается очень легко. А самое главное, у нас уже есть все необходимые знания, чтобы его решить.
Обращаем внимание, что почти везде есть конструкция (5^x). Это и будет наша замена, осталось только представить (25^x=(5^x)^2):
$$ frac{5^x}{5^x-4}+frac{5^x+5}{5^x-5}+frac{22}{(5^x)^2-9*5^x+20} le 0$$
Пусть (t=5^x):
$$ frac{t}{t-4}+frac{t+5}{t-5}+frac{22}{t^2-9*t+20} le 0$$
В третьей дроби разложим знаменатель на множители при помощи дискриминанта
$$ frac{t}{t-4}+frac{t+5}{t-5}+frac{22}{(t-4)(t-5)} le 0$$
Приводим к общему знаменателю
$$ frac{t(t-5)+(t+5)(t-4)+22}{(t-4)(t-5)} le 0$$
Раскрываем скобки и приводим подобные слагаемые в числителе
$$ frac{2t^2-4t+2}{(t-4)(t-5)} le 0$$
$$ frac{2(t^2-2t+1)}{(t-4)(t-5)} le 0$$
В скобках стоит полный квадрат
$$ frac{2(t-1)^2}{(t-4)(t-5)} le 0$$
Теперь применяем метод интервалов
$$left[
begin{gathered}
t=1, \
4 lt t lt 5. \
end{gathered}
right.$$
Перепишем двойное неравенство в виде системы
$$left[
begin{gathered}
t=1, \
begin{cases}
t > 4, \
t < 5.
end{cases}. \
end{gathered}
right.$$
Делаем обратную замену (t=5^x):
$$left[
begin{gathered}
5^x=1, \
begin{cases}
5^x > 4, \
5^x < 5.
end{cases}. \
end{gathered}
right.$$
$$left[
begin{gathered}
5^x=5^0, \
begin{cases}
5^x > 5^{log_{5}(4)}, \
5^x < 5^1.
end{cases}. \
end{gathered}
right.$$
$$left[
begin{gathered}
x=0, \
begin{cases}
x > log_{5}(4), \
x < 1.
end{cases}. \
end{gathered}
right.$$
В ответе не забываем отдельную точку (x=0), она нас тоже устраивает! Если на ЕГЭ забудете точки, в зависимости от критериев, потеряете какое-то количество баллов. Отдельная точка всегда записывается при помощи фигурных скобок.
Ответ: (x in [0] cup (log_{5}(4);1).)
Пример 16
$$ frac{3}{(2^{2-x^2}-1)^2}-frac{4}{2^{2-x^2}-1}+1 ge 0$$
Тут сразу бросается в глаза одинаковая конструкция (2^{2-x^2}-1). Замену мы можем делать абсолютно любую. Поэтому ничто не мешает нам тут обозначить за (t=2^{2-x^2}-1).
Подставим в исходное неравенство
$$ frac{3}{t^2}-frac{4}{t}+1 ge 0$$
Приводим к общему знаменателю
$$frac{t^2-4t+3}{t^2} ge 0$$
$$frac{(t-3)(t-1)}{t^2} ge 0$$
Самое время для метода интервалов:
$$t in (-infty;0) cup (0;1] cup [3;+infty);$$
Нас устраивает сразу три промежутка для (t). Запишем эти промежутки в виде большой совокупности, ведь нас устраивают все три промежутка:
$$left[
begin{gathered}
t < 0; \
begin{cases}
t > 0, \
t le 1.
end{cases} ; \
tge 3, \
end{gathered}
right.$$
Обратите внимание на то, что в совокупности у нас есть еще знак системы. Действительно, во втором промежутке (t) должно быть с одной стороны больше 0, а с другой меньше 1, и это должно выполняться одновременно. Поэтому второй промежуток описывается при помощи знака системы.
Сделаем обратную замену:
$$left[
begin{gathered}
2^{2-x^2}-1< 0; \
begin{cases}
2^{2-x^2}-1 > 0, \
2^{2-x^2}-1 le 1.
end{cases} ; \
2^{2-x^2}-1ge 3, \
end{gathered}
right.$$
$$left[
begin{gathered}
2^{2-x^2}< 1; \
begin{cases}
2^{2-x^2}> 1, \
2^{2-x^2} le 2.
end{cases} ; \
2^{2-x^2}ge 4, \
end{gathered}
right.$$
$$left[
begin{gathered}
2^{2-x^2}< 2^0; \
begin{cases}
2^{2-x^2}> 2^0, \
2^{2-x^2} le 2^1.
end{cases} ; \
2^{2-x^2}ge 2^2, \
end{gathered}
right.$$
$$left[
begin{gathered}
2-x^2< 0; \
begin{cases}
2-x^2> 0, \
2-x^2 le 1.
end{cases} ; \
2-x^2ge 2, \
end{gathered}
right.$$
Разложим все квадратные неравенства по формуле разности квадратов:
$$left[
begin{gathered}
(sqrt{2}-x)(sqrt{2}+x)< 0; \
begin{cases}
(sqrt{2}-x)(sqrt{2}+x)> 0, \
(1-x)(1+x) le 0 .
end{cases} ; \
-x^2ge 0, \
end{gathered}
right.$$
Обратите внимание на последнее неравенство: так как квадрат всегда положителен, то это неравенство выполняется только, если (x=0).
И остальное решим методом интервалов. Я сразу напишу, что получается:
$$left[
begin{gathered}
xin (-infty;-sqrt{2}) cup (sqrt{2};+infty); \
begin{cases}
xin(-sqrt{2};sqrt{2}), \
xin(-infty;-1] cup [1;+infty).
end{cases} ; \
x=0, \
end{gathered}
right.$$
Для наглядности нарисуем числовую ось и отметим на ней все промежутки. Различными цветами показаны соответствующие промежутки из совокупности, а фиолетовой штриховкой показано итоговое решение. Там, где знак системы находим пересечение, там где совокупность – объединение.
Однородные показательные неравенства
Разберемся еще с одним типом показательных неравенств — однородными неравенствами. Такие неравенства часто встречаются, если в примере есть несколько показательных функций с разными основаниями, и свести их к одному основанию не представляется возможным.
Как обычно, давайте сразу будем разбираться на конкретном примере.
Пример 17
$$25^x-20^x-2*16^x le 0$$
Чем же это уравнение примечательно? Давайте попробуем по нашему старому алгоритму привести все к одинаковому основанию.
$$25^x=5^{2x};$$
$$20^x=(5*4)^x=5^x*4^x;$$
$$16^x=4^{2x};$$
Как видите, привести к одному основанию не получается. Мы никак не можем сделать одинаковые показательные функции, если основания 5 и 4. Будем работать с тем, что есть. Подставим получившееся разложение в исходное неравенство.
$$5^{2x}-5^x*4^x-2*4^{2x} le 0;$$
Так как делить неравенства на положительные числа можно, поделим получившееся неравенство на (5^{2x}). На всякий случай напомню: при делении неравенств на положительные числа полностью делится и левая, и правая части неравенства, только в этом случае преобразование будет равносильным, то есть его корни не изменятся. Делить неравенство на (5^{2x}) можно, потому что это показательная функция, а она по определению всегда строго больше нуля.
$$frac{5^{2x}-5^x*4^x-2*4^{2x}}{5^{2x}} le frac{0}{5^{2x}};$$
Разобьем левую часть на несколько дробей. То есть, поделим каждый одночлен числителя на знаменатель дроби. В правой части, очевидно, получается 0.
$$frac{5^{2x}}{5^{2x}}-frac{5^x*4^x}{5^{2x}}-2*frac{4^{2x}}{5^{2x}} le 0;$$
$$1-frac{4^x}{5^x}-2*frac{4^{2x}}{5^{2x}} le 0;$$
$$1-left(frac{4}{5}right)^x-2*left(frac{4}{5}right)^{2x} le 0;$$
$$1-left(frac{4}{5}right)^x-2*left(frac{4}{5}right)^{2x} le 0;$$
После некоторых преобразований в результате деления мы получили везде показательную функцию (left(frac{4}{5}right)^x), которую смело можно заменить на (t=left(frac{4}{5}right)^x).
$$1-t-2*t^2 le 0;$$
$$-2*t^2-t+1 le 0;$$
Разложим квадратный многочлен на множители при помощи дискриминанта, при этом не забываем про коэффициент (-2).
$$-2(t+1)(t-frac{1}{2}) le 0;$$
Решением этого квадратного неравенства будет:
$$ t in (-infty;-1]in[frac{1}{2};+infty);$$
Перепишем промежуток в виде совокупности:
$$left[
begin{gathered}
t le -1, \
t ge frac{1}{2}. \
end{gathered}
right.$$
И сделаем обратную замену. Напомню (t=left(frac{4}{5}right)^x):
$$left[
begin{gathered}
left(frac{4}{5}right)^x le -1, \
left(frac{4}{5}right)^x ge frac{1}{2}. \
end{gathered}
right.$$
$$left[
begin{gathered}
left(frac{4}{5}right)^x le -1, \
left(frac{4}{5}right)^x ge left(frac{4}{5}right)^{log_{left(frac{4}{5}right)}(frac{1}{2})}. \
end{gathered}
right.$$
$$left[
begin{gathered}
left(frac{4}{5}right)^x le -1, \
x ge log_{left(frac{4}{5}right)}(frac{1}{2}). \
end{gathered}
right.$$
Первое неравенство в совокупности не имеет решений, так как показательная функция всегда больше нуля, значит, тем более больше (-1).
Ответ: (xin(log_{left(frac{4}{5}right)}(frac{1}{2}); +infty)).
Когда нет возможности привести к одинаковому основанию все содержащиеся в неравенстве функции, попробуйте решить как однородное уравнение при помощи деления. Разные основания — это звоночек о том, что пример может решаться при помощи деления.
Рассмотрим еще один интересный пример с разными основаниями. Только это уже не однородное уравнение.
Пример 18
$$6^x-4*3^x-2^x+4 le 0$$
Обратите внимание, что у нас в неравенстве сразу 4 слагаемых. Четное количество слагаемых иногда намекает на метод группировки. Его проходят в 8м классе, но если вы не помните, то сейчас научитесь прямо на этом примере.
Первым делом сгруппируем слагаемые попарно — первое со вторым, а третье с четвертым. И вынесем общий множитель. У первого и второго слагаемых общий множитель (3^x), а у третьего и четвертого общий множитель пусть будет (-1).
$$3^x*(2^x-4)-1*(2^x-4) le 0;$$
Обратите внимание на скобки, они получились одинаковые! Теперь у нас вместо четырех слагаемых стало два, но больших. У них тоже есть общий множитель — это как раз скобка ((2^x-4)). Вынесем скобку за скобку!
$$(2^x-4)(3^x-1) le 0;$$
У нас получилось произведение двух множителей. Произведение меньше нуля может быть только в том случае, если множители имеют разные знаки. То есть, нас устраивает либо:
$$ begin{cases}
2^x-4 ge 0, \
3^x-1 le 0.
end{cases}$$
Либо:
$$ begin{cases}
2^x-4 le 0, \
3^x-1 ge 0.
end{cases}$$
Решим обе системы и объединим решения, так как нам подходят оба случая.
$$ begin{cases}
2^xge 4, \
3^x le 1.
end{cases}$$
$$ begin{cases}
2^xge 2^2, \
3^x le 3^0.
end{cases}$$
$$ begin{cases}
xge 2, \
x le 0.
end{cases}$$
Эти два неравенства в системе не имеют решений, подходящих одновременно обоим. Поэтому в первой системе нет решений. Решим вторую:
$$ begin{cases}
2^x le 4, \
3^x ge 1.
end{cases}$$
$$ begin{cases}
2^x le 2^2, \
3^x ge 3^0.
end{cases}$$
$$ begin{cases}
x le 2, \
x ge 0.
end{cases}$$
Ответ: (xin[0;2].)
Рассмотрим еще один не очень приятный пример, который, тем не менее, может встретиться на ЕГЭ.
Пример 19
$$frac{5^{2x+1}-75*0,2^{2x}-10}{x+2} le 0.$$
Неравенство неприятное, потому что в числителе дроби у нас (x) везде в степени показательной функции, а в знаменателе (x) стоит отдельно. Никак не получится сделать замену. Но обратите внимание, нас спрашивают, при каких (x) дробь будет отрицательная. А дробь отрицательна только тогда, когда у нее числитель и знаменатель имеют разные знаки. Опять, как в предыдущем примере, можем по отдельности рассмотреть числитель и знаменатель. Нас устраивает:
Либо:
$$ begin{cases}
5^{2x+1}-75*0,2^{2x}-10 ge 0, \
x+2 < 0.
end{cases}$$
Либо система с противоположными знаками:
$$ begin{cases}
5^{2x+1}-75*0,2^{2x}-10 le 0, \
x+2 > 0.
end{cases}$$
Вторые неравенства в системах имеют строгий знак, так как это — условия, накладываемые на знаменатель.
Разберемся сначала с первой системой. Постараемся привести показательные функции к одинаковым основаниям в первом неравенстве системы:
$$ begin{cases}
5^{2x}*5^1-75*left(frac{1}{5}right)^{2x}-10 ge 0, \
x+2 < 0.
end{cases}$$
$$ begin{cases}
5*25^x-75*left(frac{1}{25^{x}}right)-10 ge 0, \
x+2 < 0.
end{cases}$$
Выпишем отдельно первое неравенство и решим его, сделав замену (t=25^x>0).
$$ 5*25^x-75*left(frac{1}{25^{x}}right)-10 ge 0;$$
$$5*t-frac{75}{t}-10 ge 0;$$
$$frac{5*t^2-10*t-75}{t} ge 0;$$
Так как (t=25^x>0), то мы можем спокойно избавиться от знаменателя в дроби, ведь он всегда положительный и не влияет на знак всего выражения.
$$5*t^2-10*t-75 ge 0;$$
$$5*(t-5)(t+3) ge 0;$$
$$ tin(-infty;-3] cup [5;+infty);$$
Но так как (t>0):
$$tin[5;+infty);$$
Запишем в виде неравенства:
$$t ge 5;$$
Сделаем обратную замену
$$ 25^x ge 5;$$
$$5^{2x} ge 5^1;$$
$$2x ge 1;$$
$$xgefrac{1}{2};$$
Напоминаю, что мы решили только первое неравенство в первой системе
$$ begin{cases}
5^{2x+1}-75*0,2^{2x}-10 ge 0, \
x+2 < 0.
end{cases}$$
C учетом нашего решения, ее теперь можно переписать в виде
$$ begin{cases}
xgefrac{1}{2}, \
x < -2.
end{cases}$$
Такая система решений не имеет. Но не грустим и вспоминаем, что у нас еще одна система неравенств с противоположным случаем — когда числитель отрицательный, а знаменатель положительный:
$$ begin{cases}
5^{2x+1}-75*0,2^{2x}-10 le 0, \
x+2 > 0.
end{cases}$$
Так как отличие только в знаках неравенства, то все преобразования, которые мы делали выше, справедливы и тут. Не будем заново решать то же самое, просто возьмем решение из предыдущей системы и изменим знаки неравенства:
$$ begin{cases}
xlefrac{1}{2}, \
x > -2.
end{cases}$$
Эта система уже имеет решения. Можно, наконец, записать ответ.
Ответ: (xin(-2;frac{1}{2}].)
Мне лично не нравится рассматривать кучу случаев в подобных примерах. А что, если знаменатель будет сложнее чем в примере выше? А еще может быть не два множителя, а сразу пять или больше, тут всех случаев не рассмотришь.
Поэтому существует отличный и очень удобный метод рационализации. Я написал статью с полным его разбором. Кстати, в ЕГЭ часто встречаются примеры именно на метод рационализации, поэтому, если вы хотите сдать профиль на высокие баллы, то это прямо обязательно знать.
Показательные неравенства
О чем эта статья:
10 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение показательных неравенств
Показательными считаются неравенства, которые включают в себя показательную функцию. Другими словами, это неравенства с переменной в показателе степени: a f(x) > a g(x) , a f(x) g(x) .
Из них показательно-степенными неравенствами являются те, в которых есть переменные и в показателе степени, и в основании.
Для изучения этой темы стоит повторить:
И, конечно, для решения тригонометрических и логарифмических показательных неравенств также придется вспомнить формулы соответствующих разделов алгебры.
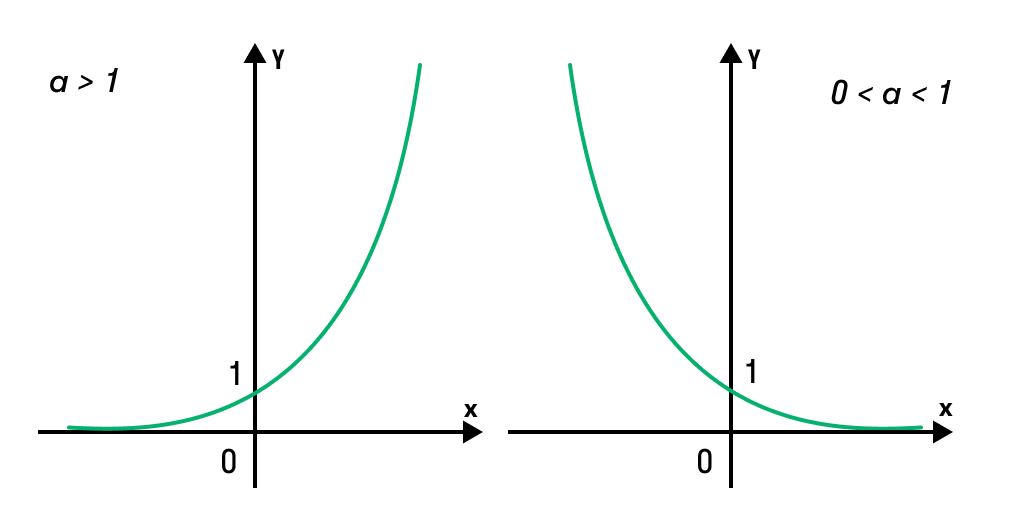
Если все это еще свежо в памяти, давайте приступим. Как и к показательным уравнениям, к неравенствам стоит подходить, помня о свойствах показательной функции. Напомним, что она выглядит так: y = a x , где a > 0 и a ≠ 1. Два графика ниже дают представление о том, на что похожа такая функция, когда основание степени а больше и меньше единицы. Наверняка вы уже догадались, каково главное свойство этой функции. Да, она монотонна.
При этом заметьте — значения а всегда больше нуля. На практике в этом несложно убедиться, если возводить какое-либо число во всевозможные степени, включая отрицательные. Например: 2 -2 = 4, 2 -4 = 1/16 и т. д. Значение функции будет уменьшаться, но никогда не достигнет нуля.
Для любых а и х верно неравенство a x > 0, т. е. показательная функция не принимает отрицательных значений.
Запишем следствие монотонности показательной функции в виде формул:
- a f(x) > a g(x) f(x) > g (x), когда функция возрастает, т. е. а > 1;
- a f(x) > a g(x) f(x)
Как решать показательные неравенства
Как мы уже говорили, для успешного освоения этой темы нужно хорошенько повторить все, что касается показательных уравнений. Способы решения показательных неравенств выглядят примерно так же — мы будем пытаться упростить выражение, получить одинаковые степени или одинаковые основания, по возможности свести все к квадратному или рациональному уравнению. Но есть и свои тонкости.
Допустим, у нас есть простейшее показательное неравенство:
Если вы помните, как решались показательные уравнения, не придется долго думать, что делать с таким неравенством — приведем его к одинаковому основанию:
Казалось бы, все логично, но всегда ли можно смело вычеркивать одинаковые основания степеней? А что, если вместо 3 у нас основание степени будет 0,5? Посмотрим:
Проверим, верно ли в таком случае х > 2.
0,5 3 = 0, 125 и т. д.
Как видите, на самом деле в этом случае х
Если а > 1, то a x > a n a > n, и при решении неравенства можно просто убрать одинаковые основания степени.
Если 0 x > a n a
Наконец, если рассмотреть случай, когда а х > 9
Логичное, на первый взгляд, предположение, что х > 2, не выдержит проверки, потому что:
Если продолжить этот ряд, знаки будут чередоваться, и наш корень будет попеременно то меньше, то больше 2. Поэтому для ясности всегда предполагается, что основание степени — положительное число.
Это были общие правила, а сейчас рассмотрим разные виды показательных неравенств и примеры с решениями.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Показательные неравенства, сводящиеся к простейшим
Решая показательные уравнения, вы наверняка первым делом исследовали их на возможность приведения к одинаковым основаниям или одинаковым степенным функциям. Так вот, с неравенствами можно делать то же самое! Помните лишь о смене знака, если основание степени меньше единицы. И да пребудет с вами сила. 😎
Попробуем на примере несложного показательного неравенства с разными основаниями.
Пример 1
Поскольку 3 больше 1, знак не меняем:
Показательные неравенства, сводящиеся к квадратным
Снова давайте вспомним, как аналогичный метод применялся к показательным уравнениям. Если все переменные имели общий множитель, его можно было обозначить новой переменной — в итоге у нас, как правило, получалось квадратное уравнение. Нужно было лишь найти дискриминант и произвести обратную замену. И снова алгоритм решения показательных неравенств будет совершенно таким же.
Пример 1
Наименьший общий множитель в данном случае будет 3 х , обозначим его новой переменной у и перенесем все слагаемые в левую сторону.
(3 х ) 2 — 12 × 3 х + 27 х = у
y 2 — 12y + 27 х 1 х 2
Поскольку 3 > 1, мы не меняем знак.
1 2 x — 5 sinx + 2 2 — 5y + 2
Показательные неравенства, сводящиеся к рациональным
Как вы, наверное, помните из предыдущего курса алгебры, рациональные показательные неравенства — это такие, в которых левая и правая часть представляют собой дробно-рациональные функции. Метод их решения таков: нужно перенести все в левую часть, чтобы в правой остался лишь ноль, и привести к общему знаменателю. Далее решаем уравнение, отмечаем все корни на оси и применяем метод интервалов (если забыли, что это такое — повторите).
Важно помнить: если в числителе и знаменателе встретятся одинаковые множители с переменной, сокращать их нельзя.
Пример 1
Преобразуем неравенство указанным выше способом:
(обратите внимание, мы избавились от минуса в числителе и поменяли знак неравенства).
Поскольку выражение 2 х + 2 в любом случае будет больше нуля, мы можем смело его исключить из неравенства.
(2 х — 2) × (2 х — 1/2) × (2 х — 3) > 0
Пример 2
Обозначим 3 х через новую переменную y:
3 х = y, при условии что 3 х > 0.
Применим метод интервалов и получим:
Вернем на место нашу старую переменную:
Однородные показательные неравенства
Однородными называются такие показательные неравенства, где в каждом слагаемом сумма степеней одинакова.
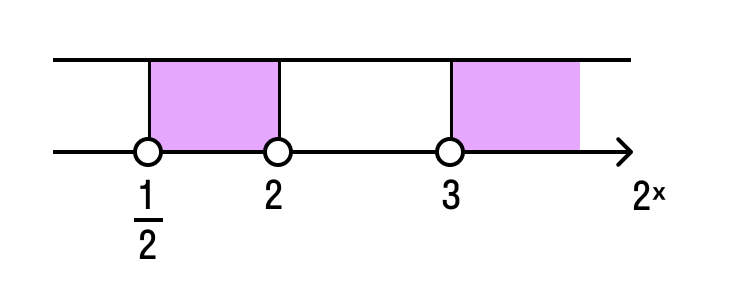
Иногда такие выражения бывают очень длинными и запутанными, но не стоит этого пугаться. Практически все неравенства с однородными показательными функциями решаются по одному принципу: стараемся упростить выражение, разделив его на одночлен, а затем при необходимости делаем замену переменных.
Пример 1
4 х — 2 × 5 2х — 2 х × 5 х > 0
2 × 2 х — 2 × 5 2х — 2 х × 5 х > 0
В левой части неравенства мы видим однородные функции относительно 2 х и 5 х . Следовательно, можно разделить обе части на 2 2х или 5 2х . Выберем 5 2х , т. е. 25 х . В итоге у нас получится:
Если обозначить (2/5) х новой переменной y, получим квадратное неравенство:
Неравенства, решаемые графическим методом
Этот метод решения показательных неравенств — самый наглядный, и для многих он может показаться самым простым. Нужно лишь построить графики функций, заданных в левой и правой части выражения, а затем посмотреть, в какой точке они пересекаются. Если бы мы имели дело с уравнением, эта точка стала бы корнем.
Но поскольку мы рассматриваем неравенства, нужно будет выделить искомую область. Для неравенства f(x) > g(x) это будет та область, где график функции f(x) находится выше.
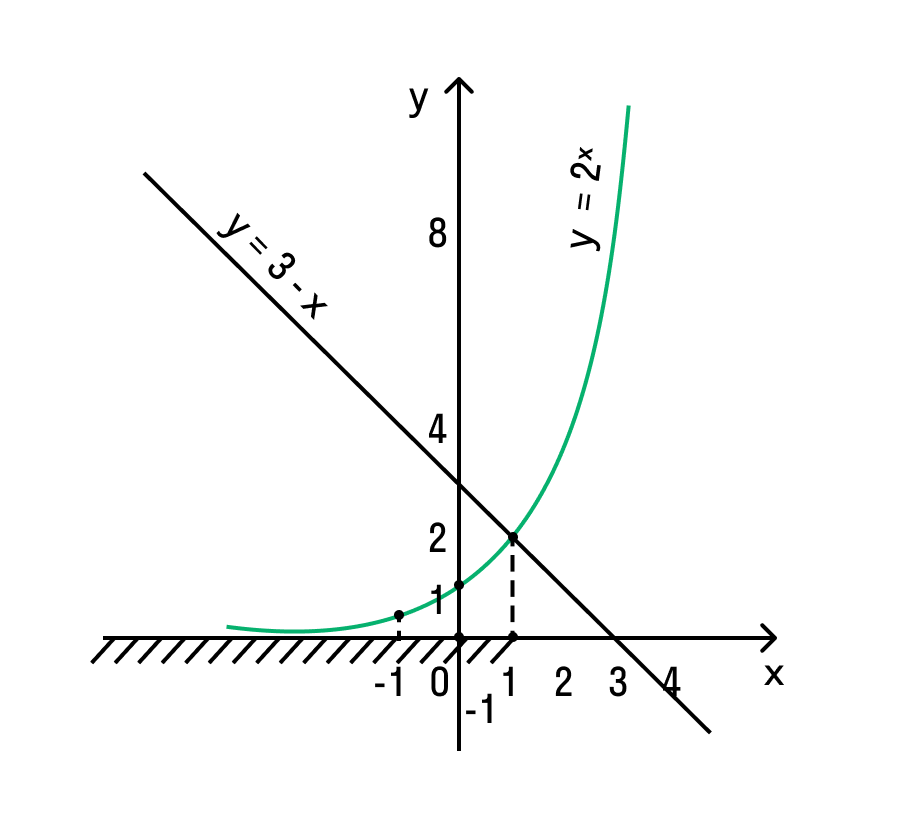
Пример 1
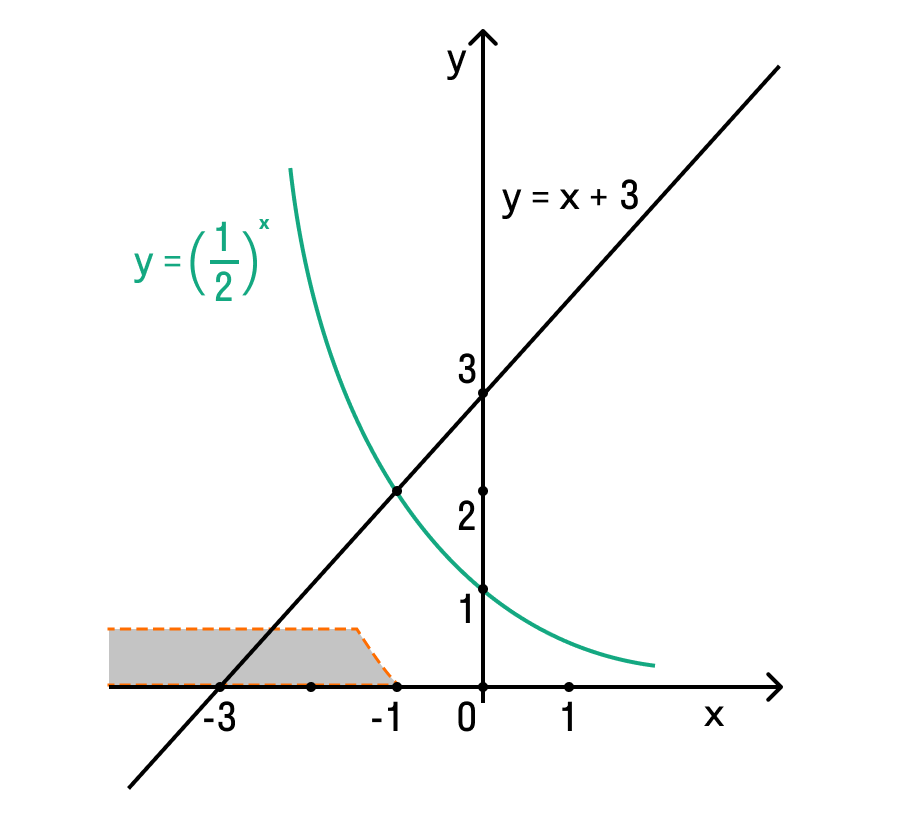
2 х х и 3 — х, а также точка их пересечения.
Очевидно, что точкой пересечения является х = 1, при этом график функции 2 х ниже в области от -∞ до 1.
Пример 2
Начертим графики этих двух функций, чтобы найти точку пересечения.
Искомой точкой будет х = -1, а областью, где функция (1/2) х находится выше — диапазон от -∞ до -1.
Однородные уравнения и неравенства
Однородные уравнения – это уравнения, в которых все слагаемые имеют одинаковую суммарную степень.
Однородные неравенства – это неравенства, в которых все слагаемые имеют одинаковую суммарную степень.
Пример. Решить уравнение (sinx=sqrt<3>cosx).
Перед нами типичное однородно-тригонометрическое уравнение. Надо разделить уравнение на cosx, но делить на число равное нулю нельзя, поэтому проверим, является ли (cosx=0) решением уравнения. Если (cosx=0), то (sinx=±1). Очевидно, что (±1≠0).
Теперь с чистой совестью поделим уравнение на (cosx)
Заметьте, что в этом примере перед тем, как делить на (cosx), была сделана проверка — является ли (cosx=0) решением уравнения. Нужно каждый раз проверять, является ли выражение, на которое вы хотите поделить, решением. Иначе вы рискуете потерять корни уравнения .
Пример. Решить уравнение (7cdot 9^+5cdot 6^-48cdot 4^=0).
Показатели степеней в уравнении похожи – в каждом есть (x^2-3x). Давайте сделаем их одинаковыми.
Представим (48cdot 4^) как (12cdot 4^1cdot 4^).
Получился классический вид однородного уравнения.
Поделим уравнение на (4^) .
Положительное число в степени никогда не будет равно нулю, поэтому проверку можно не делать.
Обратите внимание: ((frac<3><2>)^2) (=) (frac<9><4>) . С учетом этого сделаем замену.
Положительное число в любой степени всегда больше нуля, поэтому (t>0). Отметим это в решении, чтобы не забыть.
Показательные уравнения и неравенства с примерами решения
Содержание:
Рассмотрим уравнения, в которых переменная (неизвестное) находится в показателе степени. Например:
Уравнения такого вида принято называть показательными.
Решении показательных уравнений
При решении показательных уравнений нам будет полезно следствие из теоремы о свойствах показательной функции.
Пусть
Каждому значению показательной функции 
Пример:
Решение:
Согласно следствию из равенства двух степеней с одинаковым основанием 3 следует равенство их показателей. Таким образом, данное уравнение равносильно уравнению
Пример:
Решение:
а) Данное уравнение равносильно (поясните почему) уравнению
Если степени с основанием 3 равны, то равны и их показатели:
Решив это уравнение, получим
Ответ:
При решении каждого уравнения из примера 2 сначала обе части уравнения представили в виде степени с одним и тем же основанием, а затем записали равенство показателей этих степеней.
Пример:
Решение:
а) Данное уравнение равносильно уравнению
Решая его, получаем:
Так как две степени с одинаковым основанием 2 равны, то равны и их показатели, т. е. 
б) Разделив обе части уравнения на 

Ответ:
При решении примера 3 а) левую часть уравнения разложили на множители. Причем за скобку вынесли такой множитель, что в скобках осталось числовое выражение, не содержащее переменной.
Пример:
Решить уравнение
Решение:
Обозначим 
Таким образом, из данного уравнения получаем
откуда находим:
Итак, с учетом обозначения имеем:
При решении примера 4 был использован метод введения новой переменной, который позволил свести данное уравнение к квадратному относительно этой переменной.
Пример:
Решить уравнение
Решение:
Можно заметить, что 2 — корень данного уравнения. Других корней уравнение не имеет, так как функция, стоящая в левой части уравнения, возрастающая, а функция, стоящая в правой части уравнения, убывающая. Поэтому уравнение имеет не более одного корня (см. теорему из п. 1.14).
Пример:
Решить уравнение
Решение:
Пример:
При каком значении а корнем уравнения 
Решение:
Поскольку х = 2 — корень, то верно равенство
Решив это уравнение, найдем
Ответ: при
Показательные уравнения и их системы
Показательным уравнением называется уравнение, в ко тором неизвестное входит в показатель степени. При решении показательных уравнений полезно использовать следующие тождества:
Приведем методы решения некоторых типов показательных уравнений.
1 Приведение к одному основанию.
Метод основан на следующем свойстве степеней: если две степени равны и равны их основания, то равны и их показатели, т.е. уравнения надо попытаться привести к виду 
Пример №1
Решите уравнение
Решение:
Заметим, что 
Применив тождество (1), получим Зх — 7 = -7х + 3, х = 1.
Пример №2
Решить уравнение
Решение:
Переходя к основанию степени 2, получим:
Согласно тождеству (2), имеем
Последнее уравнение равносильно уравнению 4х-19 = 2,5х.
2 Введение новой переменной.
Пример №3
Решить уравнение
Решение:
Применив тождество 2, перепишем уравнение как
Введем новую переменную: 
которое имеет корни 


Пример №4
Решить уравнение
Решение:
Разделив обе части уравнения на 
последнее уравнение запишется так:
Решая уравнение, найдем
Значение 

Пример №5
Решить уравнение
Решение:
Заметим что 
Перепишем уравнение в виде
Обозначим 
Получим
Корнями данного уравнения будут
Следовательно,
III Вынесение общего множителя за скобку.
Пример №6
Решить уравнение
Решение:
После вынесения за скобку в левой части 



Системы простейших показательных уравнений
Пример №7
Решите систему уравнений:
Решение:
По свойству степеней система уравнений равносильна следующей
системе :
Очевидно, что последняя система имеет решение
Пример №8
Решите систему уравнений:
Решение:
По свойству степеней система уравнений равносильна следующей системе: 
Умножив второе уравнение этой системы на (-2) и сложив с первым, получим уравнение —9х=-4. Отсюда, найдем 
Пример №9
Решите систему уравнений:
Решение:
Сделаем замену: 
Очевидно, что эта система уравнений имеет решение
Тогда получим уравнения
Приближенное решение уравнений
Пусть многочлен f(х) на концах отрезка [a,b] принимает значения разных знаков, то есть 

Это утверждение проиллюстрировано на следующем чертеже.
Рассмотрим отрезок 
Метод последовательного деления отрезка пополам заключается в последовательном разделении отрезка [a, b] пополам до тех пор, пока длина полученного отрезка не будет меньше заданной точности
- вычисляется значение f(х) выражения
- отрезок делится пополам, то есть вычисляется значение
- вычисляется значение
выражения f(х) в точке
- проверяется условие
- если это условие выполняется, то в качестве левого конца нового отрезка выбирается середина предыдущего отрезка, то есть полагается, что
(левый конец отрезка переходит в середину);
- если это условие не выполняется, то правый конец нового отрезка переходит в середину, то есть полагается, что b=x;
- для нового отрезка проверяется условие
- если это условие выполняется , то вычисления заканчиваются. При этом в качестве приближенного решения выбирается последнее вычисленное значение х. Если это условие не выполняется, то, переходя к пункту 2 этого алгоритма, вычисления продолжаются.
Метод последовательного деления пополам проиллюстрирован на этом чертеже:
Для нахождения интервала, содержащего корень уравнения 
Оказывается, что для корня 


Пример №10
Найдите интервал, содержащий корень уравнения
Решение:
Поделив обе части уравнения на 2 , получим,
Так как, для нового уравнения
Значит, в интервале, 




Значит, уравнение имеет корень, принадлежащий интервалу (-1; 0).
Нахождение приближенного корня с заданной точностью
Исходя из вышесказанного, заключаем, что если выполнено неравенство 



корень уравнения с точностью 




Пример №11
Найдите приближенное значение корня уравнения 
Решение:
Из предыдущего примера нам известно, что корень лежит в интервале
(-1; 0). Из того, что 
Так как, |(-0,25)41,5(-0,25)2+2,5(-0,25)+0,5| = |-0,046| 1. Если
Пусть
Изображения графиков показательной функции подсказывают это свойство. На рисунке 27 видно, что при а > 1 большему значению функции соответствует большее значение аргумента. А на рисунке 30 видно, что при 0
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
источники:
http://cos-cos.ru/math/247/
http://www.evkova.org/pokazatelnyie-uravneniya-i-neravenstva
Подготовка к ЕГЭ по математике
Эксперимент
Урок 1. Повторение. Показательная функция. Показательные уравнения
Практика
Простейшие показательные неравенства
Конспект урока
Пример №1. Решить неравенство:
Правило: привести к одинаковому основанию.
Так как основание больше 1, знак неравенства не меняется
Ответ:
Пример №2. Решить неравенство:
Так как основание больше 1, знак неравенства не меняется
Ответ:
Пример №3. Решить неравенство:
Так как основание меньше 1, знак неравенства меняется
Ответ:
Пример №4. Решить неравенство:
Вспоминаем свойства показательной функции: , значит,
Данное неравенство не имеет решений.
Пример №5. Решить неравенство:
По аналогии с предыдущим неравенством: (а, значит,
) для всех
из области определения, то есть
.
Показательные неравенства, которые сводятся к простейшим
Пример №1.
Так как основание меньше 1, знак неравенства меняется
Ответ:
Пример №2. Решите неравенство
Рассмотрим решение данного неравенства двумя способами.
1 способ:
Приведем обе части неравенства к основанию 2:
Так как основание больше 1, знак неравенства не меняется
2 способ:
Приведем обе части неравенства к основанию :
Так как основание меньше 1, знак неравенства меняется
Ответ:
Пример №3. Решите неравенство
Подсказка: чтобы не ошибиться, лучше приводить обе части неравенства к основанию больше 1, так как в этом случае нет риска забыть о смене знака неравенства.
Вспомним, что:
Поэтому:
Так как основание больше 1, знак неравенства не меняется
Ответ:
Пример №4. Решите неравенство
Приведем обе части неравенства к основанию 2:
Так как основание больше 1, знак неравенства не меняется
Ответ:
Показательные неравенства, которые решаются с помощью вынесения общего множителя
С вынесением общей степени
Пример №1. Решите неравенство
Так как основание больше 1, знак неравенства не меняется
Ответ:
Показательное неравенство, которое решается с помощью замены
Сводящиеся к квадратным
Пример №1. Решите неравенство:
Замена:
Обратная замена:
Ответ:
Пример №2. Решите неравенство:
Замена:
Обратная замена:
Ответ:
Пример №3. Решите неравенство:
Замена:
Обратная замена:
Левое неравенство, как мы помним, выполняется всегда.
Ответ:
Однородные показательные неравенства
Однородные
Пример №1. Решите неравенство:
Замена:
Обратная замена:
Ответ:
Системы показательных уравнений
Системы показательных уравнений
Пример №1. Решите систему уравнений:
«Решаем» каждое из уравнений по отдельности, приводя к обычной линейной системе.
1)
2)
Получаем систему:
Ответ:
Пример №2. Решите систему уравнений:
1) Перемножим оба уравнения:
2) Поделим второе уравнение на первое:
Получаем систему:
Ответ:
Пример №3. Решите систему уравнений:
Замена:
—
Обратная замена:
Ответ:
Пример №4.
Замена:
Рассмотрим решение данной системы двумя способами:
1 способ:
Обратная замена:
2 способ:
Обратная замена:
Ответ:
Системы показательных неравенств
Пример №1.
Правило: решаем каждое из неравенств по отдельности.
1)
Замена:
Обратная замена:
2)
3)
Ответ: решений нет.












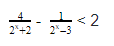
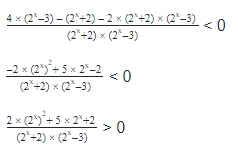
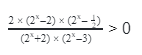
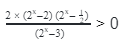
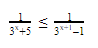
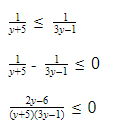
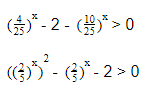










































































 выражения f(х) в точке
выражения f(х) в точке 

 (левый конец отрезка переходит в середину);
(левый конец отрезка переходит в середину);



























