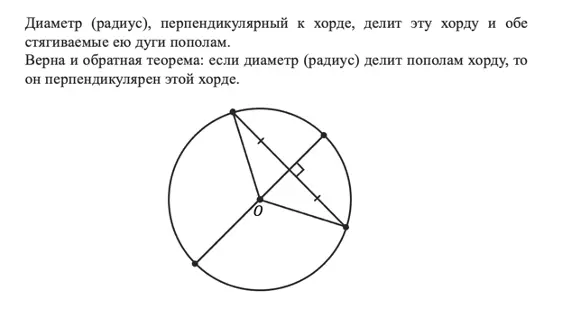
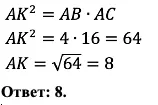Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник- описанным около этой окружности.
В любой треугольник можно вписать окружность. Центром вписанной окружности (точка $О$) является точка пересечения биссектрис внутренних углов треугольника.
$OD$ – это радиус $(r)$ вписанной окружности
$r={2S_{ABC}}/{a+b+c}$
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.
$S={P∙r}/{2}$
В равнобедренном треугольнике вписанная окружность точкой касания делит основание пополам
В равностороннем треугольнике радиус вписанной окружности равен трети высоты данного треугольника.
$r={h}/{3}$
В прямоугольном треугольнике радиус вписанной окружности равен:
$r={a+b-c}/{2}$, где $а$ и $b$ – это катеты, $с$ – гипотенуза.
Пример:
В прямоугольном треугольнике $АВС$ катет и гипотенуза соответственно равны $8$ и $10$. Найдите радиус окружности, вписанной в этот треугольник.
Решение:
В прямоугольном треугольнике радиус вписанной окружности равен:
$r={a+b-c}/{2}$, где $а$ и $b$ – это катеты, $с$ – гипотенуза.
Нам неизвестен один из катетов, найдем его по теореме Пифагора:
$a^2+b^2=c^2$
$8^2+b^2=10^2$
$64+b^2=100$
$b^2=100-64$
$b^2=36$
$b=6$
Теперь подставим все величины в формулу нахождения радиуса вписанной окружности в прямоугольном треугольнике:
$r={6+8-10}/{2}={4}/{2}=2$
Ответ: $2$
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
$АВ+CD=BC+AD$
В трапеции и ромбе центр вписанной окружности лежит в точке пересечения биссектрис внутренних углов, радиус вписанной окружности равен половине высоты.
$r={h}/{2}$
В квадрате радиус вписанной окружности равен половине стороны.
$r={a}/{2}$
Площадь любого многоугольника можно найти как произведение полупериметра на радиус вписанной окружности.
$S={P∙r}/{2}$
Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник- вписанным в эту окружность.
Около любого треугольника можно описать окружность, причем только одну. Центром описанной окружности является точка $(О)$ пересечения серединных перпендикуляров к сторонам треугольника.
$ОА$ — радиус описанной окружности $(R)$
В равностороннем треугольнике радиус описанной окружности равен две трети высоты данного треугольника.
$R={2h}/{3}$
Центр описанной окружности может находиться в различных положениях относительно треугольника:
1. В остроугольном треугольнике центр описанной окружности лежит внутри треугольника.
2. В тупоугольном треугольнике центр описанной окружности лежит снаружи треугольника.
3. В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы и радиус равен половине гипотенузы.
$R={c}/{2}$
Радиус описанной окружности можно найти как:
$R={a}/{2sinA}={b}/{2sinB}={c}/{2sinC};$
$R={a∙b∙c}/{4S}$, где $S$ — это площадь заданного треугольника.
Около четырехугольника не всегда можно описать окружность. Если сумма противоположных углов четырехугольника равна $180°$, то только тогда около него можно описать окружность.
$∠В+∠D=180°$
$∠A+∠C=180°$
В прямоугольнике и квадрате центр описанной окружности лежит в точке пересечения диагоналей, а радиус описанной окружности равен половине диагонали.
$R={d}/{2}$
Только вокруг равнобедренной трапеции можно описать окружность.
Выпуклый многоугольник называется правильным, если у него все стороны и все углы равны.
Связь между сторонами правильного n-угольника и радиусами описанной и вписанной окружностей:
$АВ=an$ — сторона правильного многоугольника
$R$ — радиус описанной окружности
$r$ — радиус вписанной окружности
$n$ — количество сторон и углов
$a_n=2∙R∙sin{180°}/{n};$
$r=R∙cos{180°}/{n};$
$a_n=2∙r∙tg{180°}/{n}.$
Углы в окружности:
1. Угол, образованный двумя радиусами, называется центральным. Центральный угол равен градусной мере дуги, на которую он опирается
$∠О=∪BmA$
2. Угол, вершина которого лежит на окружности, а стороны являются хордами, называется вписанным. Вписанный угол равен половине градусной меры дуги, на которую он опирается
$∠B={∪AmC}/{2}$
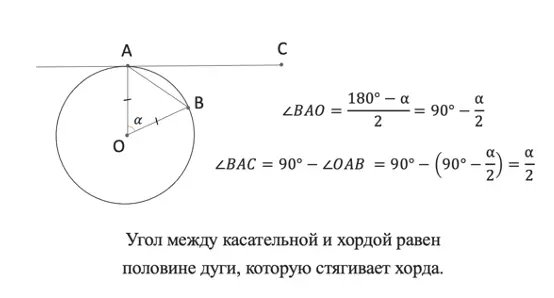
3. Угол между хордой и касательной равен половине дуги, заключенной внутри него.
$∠B={∪BmC}/{2}$
ЕГЭ Профиль №16. Окружности
Скачать ЕГЭ Профиль №16. Окружности в формате pdf.
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Точки A, B, C, расположенные на окружности, делят ее на три дуги, градусные величины которых относятся как 1 : 3 : 5. Найдите больший угол треугольника ABC. Ответ дайте в градусах.
2
Угол A четырехугольника ABCD, вписанного в окружность, равен 58°. Найдите угол C этого четырехугольника. Ответ дайте в градусах.
4
Точки A, B, C, D, расположенные на окружности, делят эту окружность на четыре дуги AB, BC, CD и AD, градусные величины которых относятся соответственно как 4 : 2 : 3 : 6. Найдите угол A четырехугольника ABCD. Ответ дайте в градусах.
5
Четырехугольник ABCD вписан в окружность. Угол ABD равен 75°, угол CAD равен 35°. Найдите угол ABC. Ответ дайте в градусах.
Пройти тестирование по этим заданиям
Задания по теме «Окружность»
Открытый банк заданий по теме окружность. Задания B6 из ЕГЭ по математике (профильный уровень)
Задание №1070
Условие
Через концы A и B дуги окружности с центром O проведены касательные AC и BC . Меньшая дуга AB равна 56^<circ>. Найдите угол ACB . Ответ дайте в градусах.
Решение
Центральный угол равен угловой величине дуги, на которую он опирается, то есть
angle BOA = 56^<circ>. Углы OBC и OAC прямые как углы между касательными и радиусами, проведёнными в точки касания. Сумма углов четырёхугольника равна 360^<circ>, можем найти угол ACB .
Ответ
Задание №1069
Условие
Точки A , B , C , расположенные на окружности, делят её на три дуги, градусные меры которых относятся как 2:3:4 . Найдите больший угол треугольника ABC . Ответ дайте в градусах.
Решение
Угловая величина всей окружности составляет 360^<circ>, дуги, на которые опираются углы треугольника, составляют 2 , 3 и 4 из 2 + 3 + 4 = 9 частей, то есть большая из них равна frac49 окружности, 360^<circ>cdotfrac49=160^<circ>. Вписанный угол равен половине дуги, на которую он опирается, то есть 160^ <circ>: 2 = 80^<circ>.
Ответ
Задание №1068
Условие
Хорда AB делит окружность на две дуги, градусные меры которых относятся как 13 : 7 . Под каким углом видна эта хорда из точки C , принадлежащей большей дуге окружности? Ответ дайте в градусах.
Решение
Угловая величина всей окружности составляет 360^<circ>, дуга, на которую опирается угол C , составляет 7 из 7+13 = 20 частей, то есть frac<7> <20>окружности, 360^<circ>cdot frac<7> <20>= 126^<circ>. Вписанный угол равен половине дуги, на которую он опирается, то есть 126^ <circ>: 2 = 63^<circ>.
Ответ
Задание №896
Условие
Найдите вписанный угол, опирающийся на дугу, длина которой равна frac13 длины окружности. Ответ дайте в градусах.
Решение
Угловая величина всей окружности составляет 360^<circ>, дуга составляет треть окружности, то есть 360^<circ>:3=120^<circ>. Вписанный угол равен половине дуги, на которую он опирается, то есть 120^<circ>:2=60^<circ>.
Ответ
Задание №51
Условие
На рисунке изображена окружность с центром O . Прямые AC и BD являются диаметрами окружности. Угол ACB равен 21^ <circ>. Найдите угол AOD . Ответ дайте в градусах.
Решение
Так как угол ACB вписан в окружность, то градусная мера дуги AB , на которую он опирается, в 2 раза больше величине этого угла, и равна:
cup AB=2cdotangle ACB=2cdot21^<circ>=42^
Так как BD — диаметр окружности, то его градусная мера равна 180^ <circ>. Найдем градусную меру угла дуги AD :
Так как угол AOD — центральный, то его величина равна градусной мере дуги окружности AD , следовательно:
angle AOD=cup AD=138^
Ответ
Задание №48
Условие
Угол ACB равен 54^ <circ>. Градусная мера дуги AB окружности, не содержащих точек D и E , равна 138^ <circ>. Найдите угол DAE . Ответ дайте в градусах.
Решение
Угол DAE мы можем найти зная два остальных угла треугольника ACD . Угол ACB нам известен и равен углу ACD . Угол ADC является разностью развернутого угла BDC и угла ADB . Угол ADB является вписанным в окружность, а значит его величина равна половине градусной меры дуги, на которую он опирается.
Из условия задачи градусная мера дуги AB известна. Найдем угол ADB :
Найдем угол ADC :
Угол DAE равен углу DAC . Зная два угла треугольника, найдем искомый угол DAE :
Ответ
Задание №47
Условие
На рисунке изображена окружность с центром O . Прямые CA и CB являются касательными к окружности. Меньшая дуга AB равна 64^ <circ>. Найдите угол ACB . Ответ дайте в градусах.
Решение
Прямые CA и CB являются касательными к окружности, значит они образуют прямой угол с радиусом окружности, то есть с прямыми OA и OB . Сумма углов четырехугольника равна 360^ <circ>. Найдем неизвестный угол ACB :
Ответ
Задание №46
Условие
На рисунке изображена окружность с центром O . Угол ACO равен 27^ <circ>. Сторона CA – касательная к окружности. Сторона CO пересекает окружность в точке B. Найдите величину меньшей дуги окружности AB . Ответ дайте в градусах.
Решение
Прямая AC является касательной к окружности, значит радиус AO образует с ней прямой угол, следовательно треугольник AOC прямоугольный. Величину меньшей дуги окружности AB вы можем найти зная градусную меру угла AOB . Учитывая, что сумма углов треугольника равна 180^ <circ>, найдем угол AOB :
Так как угол AOB – центральный, то величина меньшей дуги окружности AB равна градусной мере этого угла, а значит величина дуги равна 63^
Основные теоремы, связанные с окружностями
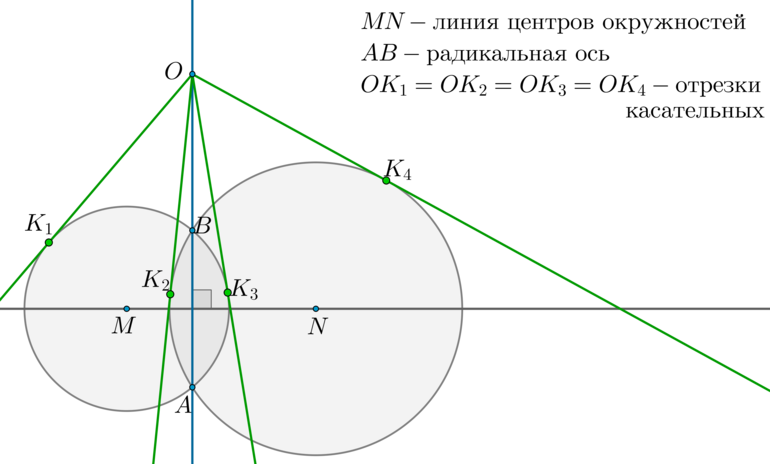
Радикальная ось — прямая, проходящая через точки пересечения двух окружностей.
Линия центров окружностей — прямая, проходящая через центры двух окружностей.
Теорема 1.
1) Радикальная ось перпендикулярна линии центров окружностей.
2) Отрезки касательных, проведенных из любой точки радикальной оси к этим окружностям, равны.
Доказательство:
1) Рассмотрим (triangle BMN) и (triangle AMN) : они равны по трем сторонам ( (BM=AM=R_1, BN=AN=R_2) — радиусы первой и второй окружностей соответственно). Таким образом, (angle BNM=angle ANM) , следовательно, (MN) — биссектриса в равнобедренном (triangle ANB) , следовательно, (MNperp AB) .
2) Отметим произвольную точку (O) на радикальной оси и проведем касательные (OK_1, OK_3) к первой окружности и (OK_2, OK_4) ко второй окружности. Т.к. квадрат отрезка касательной равен произведению секущей на ее внешнюю часть, то (OK_1^2=OK_2^2=OK_3^2=OK_4^2=OBcdot OA) .
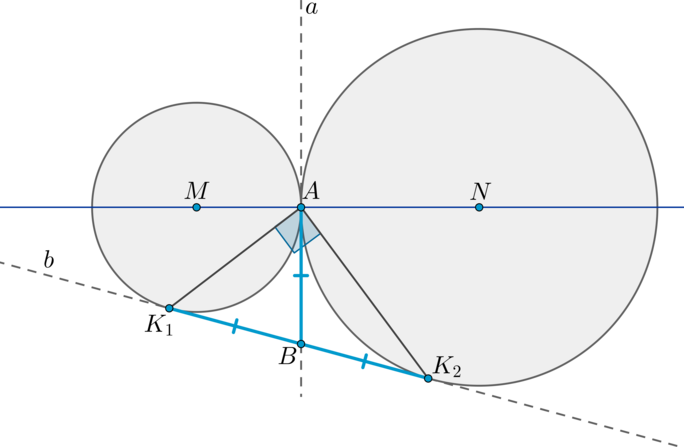
Теорема 2.
Пусть две окружности с центрами (M) и (N) касаются внешним образом в точке (A) . Две общие касательные (внутренняя и внешняя) (a) и (b) этих окружностей пересекаются в точке (B) . Точки касания — точки (A, K_1, K_2) (как показано на рисунке). Тогда [(1) <large>] [(2) <large<angle K_1AK_2=90^circ>>]
Доказательство:
1) Т.к. (BA) и (BK_1) — две касательные, проведенные к первой окружности из одной точки, то отрезки касательных равны: (BA=BK_1) . Аналогично, (BA=BK_2) . Таким образом, (BA=BK_1=BK_2) .
2) Значит, (BA) — медиана в (triangle K_1AK_2) , равная половине стороны, к которой она проведена. Значит, (angle A=90^circ) .
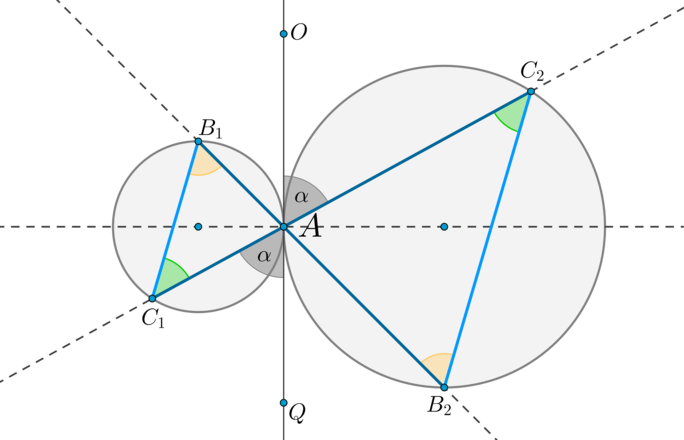
Теорема 3.
Пусть две окружности касаются внешним образом в точке (A) . Через точку (A) проведены две прямые (B_1B_2) и (C_1C_2) , пересекающие каждую окружность в двух точках, как показано на рисунке. Тогда: [(1) <large<triangle AB_1C_1 sim triangle AB_2C_2>>] [(2) <large>]
Доказательство:
1) Проведем через точку (A) общую касательную этих окружностей (OQ) . (angle OAC_2=angle QAC_1=alpha) как вертикальные. Т.к. угол между касательной и хордой, проведенной через точку касания, равен половине дуги, заключенной между ними, то (angle OAC_2=frac12buildrelsmileover) , (angle QAC_1=frac12buildrelsmileover) . Следовательно, (buildrelsmileover=buildrelsmileover=2alpha) . Таким образом, (angle AB_1C_1=angle AB_2C_2=alpha) . Значит, по двум углам (triangle AB_1C_1sim triangle AB_2C_2) .
2) Т.к. (angle AB_1C_1=angle AB_2C_2) , то прямые (B_1C_1parallel B_2C_2) по накрест лежащим углам при секущей (B_1B_2) .
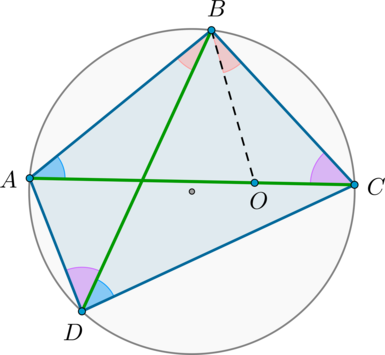
Теорема Птолемея
Во вписанном четырехугольнике произведение диагоналей равно сумме произведений противоположных сторон: [ACcdot BD=ABcdot CD+BCcdot AD]
Доказательство
Пусть для определенности (angle ABD . Проведем отрезок (BO) так, чтобы (O) лежала на (AC) и (angle ABD=angle CBO) :
Т.к. (angle ACB=angle ADB) (опираются на одну и ту же дугу), то по двум углам (triangle OBCsim triangle ABD) . Значит: [dfrac=dfrac Rightarrow ADcdot BC=OCcdot BDphantom <00000000000>(1)]
Т.к. (angle BAC=angle BDC) (опираются на одну и ту же дугу), (angle ABO=angle CBD) (состоят из равных по построению (оранжевых) углов и общего угла (angle DBO) ), то по двум углам (triangle ABOsim triangle BDC) . Значит: [dfrac=dfrac Rightarrow ABcdot CD=AOcdot BD phantom <00000000000>(2)]
Сложим равенства ((1)) и ((2)) : (ADcdot BC+ABcdot CD=OCcdot BD+AOcdot BD=ACcdot BD) , чтд.
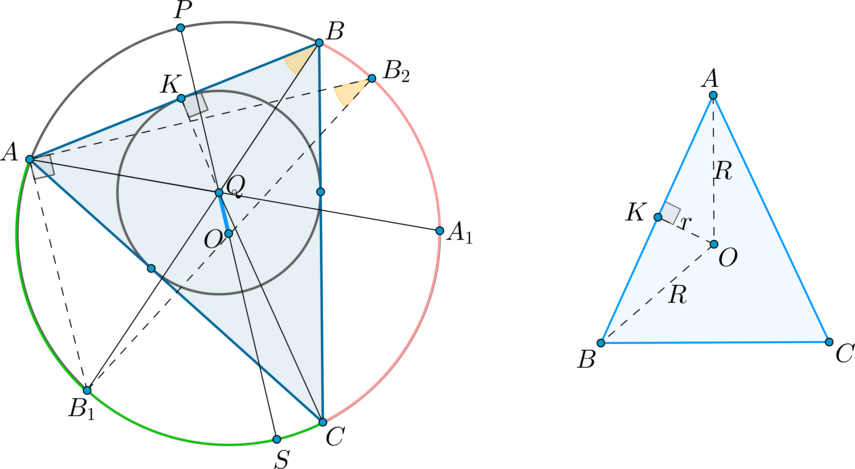
Формула Эйлера:
Пусть (R) — радиус описанной около треугольника (ABC) окружности, (r) — радиус вписанной окружности. Тогда расстояние (d) между центрами этих окружностей вычисляется по формуле: [<large>]
Доказательство:
а) Предположим, что (dne 0) . Пусть (O, Q) — центры описанной и вписанной окружности соответственно. Проведем диаметр описанной окружности (PS) через точку (Q) . Проведем также биссектрисы углов (angle A, angle B) — (AA_1, BB_1) соответственно (заметим, что они пересекутся в точке (Q) , т.к. центр вписанной окружности лежит на пересечении биссектрис). Хорды (PS) и (BB_1) пересекаются, следовательно, отрезки этих хорд равны: (PQcdot QS=BQcdot QB_1) .
Т.к. (OP=OS=R, OQ=d) , то последнее равенство можно переписать в виде ((R-d)(R+d)=BQcdot QB_1 (*)) .
Заметим, что т.к. (AA_1, BB_1) — биссектрисы, то (buildrelsmileover=buildrelsmileover=x, buildrelsmileover=buildrelsmileover=y) . Т.к. угол между хордами равен полусумме дуг, заключенных между ними, то:
(angle AQB_1=frac12(x+y)) .
С другой стороны, (angle B_1AA_1=frac12big(buildrelsmileover+buildrelsmileoverbig)=frac12(x+y))
Таким образом, (angle AQB_1=angle B_1AA_1) . Следовательно, (triangle QB_1A) — равнобедренный и (B_1Q=B_1A) . Значит, равенство ((*)) можно переписать как:
(R^2-d^2=BQcdot AB_1 (**)) .
Проведем еще один диаметр описанной окружности (B_1B_2) . Тогда (triangle B_1AB_2) — прямоугольный ( (angle A) опирается на диаметр). Пусть также вписанная окружность касается стороны (AB) в точке (K) . Тогда (triangle BKQ) — прямоугольный.
Заметим также, что (angle KBQ=angle AB_2B_1) (т.к. они опираются на одну и ту же дугу).
Значит, (triangle B_1AB_2sim triangle BKQ) по двум углам, следовательно:
(dfrac=dfrac Rightarrow dfrac=dfrac <2R>Rightarrow BQcdot AB_1=2Rr) .
Подставим это в ((**)) и получим:
(R^2-d^2=2Rr Rightarrow d^2=R^2-2Rr) .
б) Если (d=0) , т.е. центры вписанной и описанной окружностей совпадают, то (AK=BK=sqrt Rightarrow AB=2sqrt) . Аналогично (AC=BC=AB=sqrt) , т.е. треугольник равносторонний. Следовательно, (angle A=60^circ Rightarrow angle KAO=30^circ Rightarrow r=frac12R Rightarrow R=2r) или (0=R^2-2Rr) (т.е. в этом случае формула также верна).
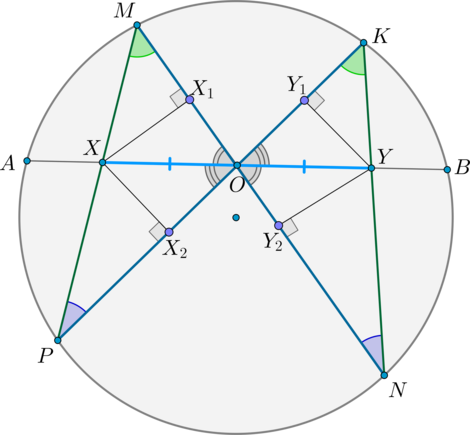
Теорема о бабочке:
Пусть через середину хорды (AB) — точку (O) , проведены две хорды (MN) и (KP) . Пусть (MPcap AB=X, KNcap AB=Y) . Тогда [<large>]
Доказательство:
Проведем перпендикуляры (XX_1, YY_2perp MN, XX_2, YY_1perp KP) .
Следующие углы равны, т.к. опираются на одну и ту же дугу: (angle PMO=angle NKO, angle MPO=angle KNO) .
Следующие углы равны, т.к. вертикальные: (angle XOX_1=angle YOY_2, angle XOX_2=angle YOY_1) .
Следующие прямоугольные треугольники подобны:
1) (triangle XX_1Osim triangle YY_2O Rightarrow dfrac=dfrac)
2) (triangle XX_2Osim triangle YY_1O Rightarrow dfrac=dfrac)
3) (triangle MXX_1sim triangle KYY_1 Rightarrow dfrac=dfrac)
4) (triangle PXX_2sim triangle NYY_2 Rightarrow dfrac=dfrac)
Из 1) и 2) следует, что
Из 3) и 4) следует, что
Совместив последние два равенства, получим:
Заметим, что для пересекающихся хорд (AB) и (MP) : (AXcdot XB=MXcdot PX) . Аналогично (AYcdot YB=KYcdot NY) . Значит:
Обозначим (OX=x, OY=y, OA=OB=t Rightarrow)
Окружность и круг
теория по математике 📈 планиметрия
Определения
Окружность – множество всех точек плоскости, равноудаленных от одной данной точки (центра окружности). Другими словами – это замкнутая линия, длину которой можно измерить.
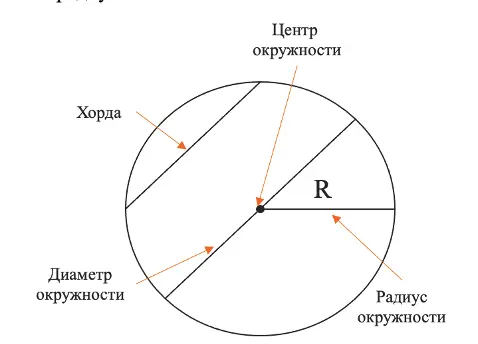
На рисунке центр окружности обозначен точкой О. 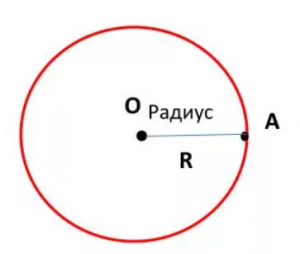
Радиус – расстояние от центра до любой точки окружности. На рисунке радиус обозначен АО. Все радиусы одной окружности равны. Радиус можно обозначать латинскими буквами R или r.
Диаметр – отрезок, который соединяет две точки окружности и проходит через её центр. На рисунке диаметр обозначен АВ. Все диаметры одной окружности равны. В одном диаметре содержится два радиуса. Диаметр обозначается буквой d.
Хорда – отрезок, соединяющий две любые точки окружности. На рисунке это отрезок CD.
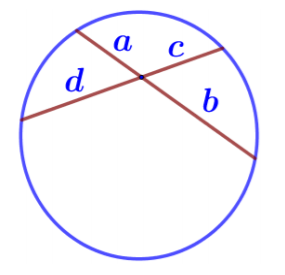
Свойство хорд
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. Так, на рисунке показаны две пересекающиеся хорды, одна состоит из отрезков a и b, вторая из отрезков d и с, следовательно, ab=dс.
Длина окружности
Длину окружности можно вычислить по формуле:
C=2πR, где π=3,14.
Дуга – часть окружности, которая соединяет две точки. На рисунке мы видим несколько дуг, например, дуги CD (малая и большая). Дуга АВ – называется полуокружностью, так как стягивает концы диаметра. Обозначается дуга значком ∪АВ.
Дуга, касательная, круг, сектор, сегмент
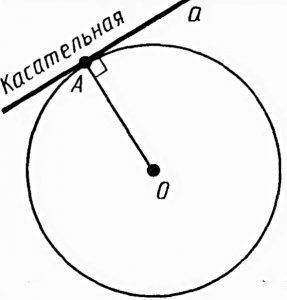
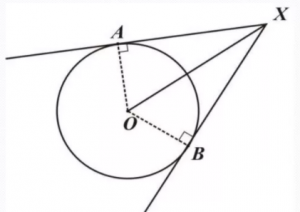
Из точки, не лежащей на окружности можно провести касательную – прямую, которая имеет с окружностью только одну общую точку (рисунок 4).
Свойства касательной
На рисунке видно, что АХ=ВХ, угол АХО равен углу ВХО.
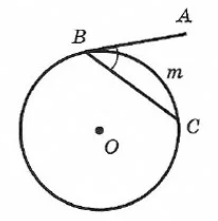
Угол АВС (образован касательной АВ и хордой ВС) равен половине дуги m.
Круг – часть плоскости, ограниченная окружностью. Другими словами, круг – это всё, что находится внутри окружности.
Площадь круга вычисляется по формуле:
S=πR 2 , где π=3,14.
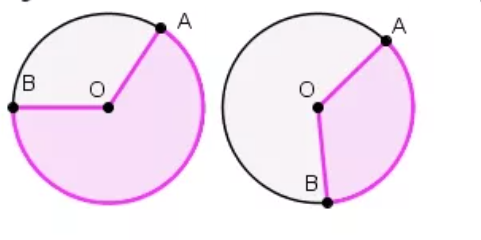
Сектор и его площадь
Сектор – область круга, ограниченная двумя радиусами. На рисунке сектор выделен сиреневым цветом, он ограничен радиусами ОА и ОВ.
Площадь кругового сектора вычисляется по формуле:
S= π R 2 360 . . × α , где α – угол между радиусами.
Сегмент – это область круга, ограниченная хордой и дугой. На рисунке сегмент выделен сиреневым цветом. Также можно сказать, что это часть круга, отсекаемая от него хордой. На рисунке видно, как хорда АВ отсекает сегмент.
источники:
http://shkolkovo.net/theory/41
http://spadilo.ru/okruzhnost-i-krug/
Окружность на ЕГЭ и ОГЭ — сложно. Все потому, что эта фигура не похожа на остальные: у неё нет углов и сторон, зато есть совсем другие элементы. В этой статье мы подробно поговорим про элементы окружности, углы, отрезки и прямые, которые с ней связаны, а также обсудим длину окружности и площадь круга. Ну и разберем основные задания ЕГЭ и ОГЭ, конечно же!
Для начала давайте разберёмся, что же такое окружность. Окружность — это замкнутая линия, состоящая из множества точек, которые равноудалены от центра окружности. Основной элемент окружности — это радиус, он соединяет центр с любой точкой на окружности.
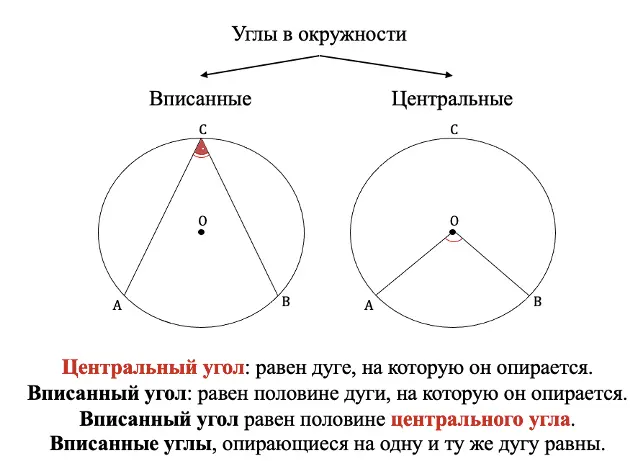
Углы у окружности на ЕГЭ и ОГЭ
У окружности есть 2 вида углов:
- вписанные (их вершина лежит на окружности);
- центральные (тут всё понятно из названия, у них вершина в центре окружности).
Расположение и свойства углов в окружности можно увидеть на схеме ниже:
Давайте отработаем это на практике:
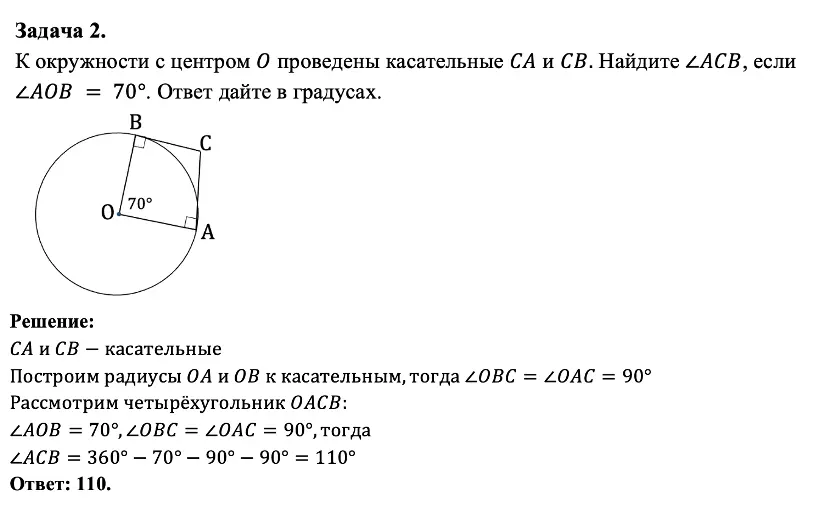
Решение
Можно заметить, что угол АСВ — вписанный и опирается на дугу АВ, соответственно, центральный угол АОD, опирающийся на ту же дугу будет в 2 раза больше, то есть 70 градусов. Теперь рассмотрим развёрнутый угол ВОD, он состоит из углов АОВ и АОD. Градусная мера развёрнутого угла 180 градусов, следовательно искомый угол АОD будет равен 180 – 70 = 110 градусов.
Отрезки и прямые в окружности на ЕГЭ и ОГЭ
Теперь рассмотрим отрезки и прямые в окружности. Приготовьтесь, их будет много!
Есть хорда — это отрезок, который соединяет 2 любые точки на окружности. Если хорда пройдёт через центр окружности, то она превратится в диаметр. Кстати, если внимательно посмотреть, то можно увидеть, что диаметр — это 2 радиуса!
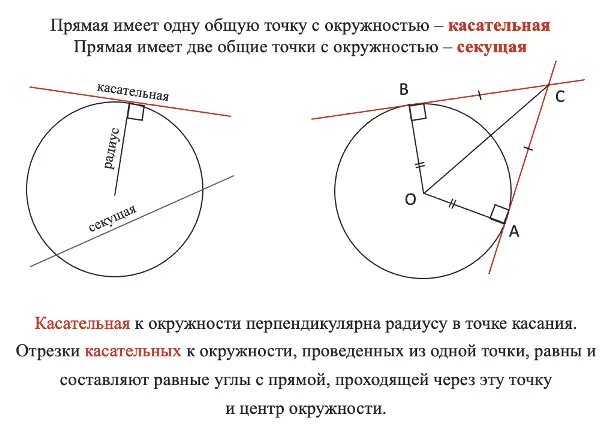
Теперь продлим хорду в обе стороны за пределы окружности, получим прямую, которая переСЕКает нашу окружность, отсюда и её название — секущая. Можно заметить, что секущая имеет 2 общих точки пересечения с окружностью. А ещё мы можем провести прямую так, чтобы она имела с окружностью только 1 точку пересечения, то есть касалась её, такая прямая будет называться касательная.
Подробнее со свойствами касательной и секущей можно ознакомиться на рисунке:
Рассмотрим на примерах заданий про окружность в ЕГЭ и ОГЭ:
4 теоремы про окружность в ЕГЭ и ОГЭ
Теперь я предлагаю ознакомиться с теоремами, которые появляются в комбинациях различных прямых и отрезков в окружности.
Теорема № 1: теория и задания из ЕГЭ и ОГЭ
Первая теорема про хорду и касательную звучит так:
Угол между касательной и хордой равен половине дуге, которую стягивает хорда.
Подробнее с выведением вы можете ознакомиться на рисунке:
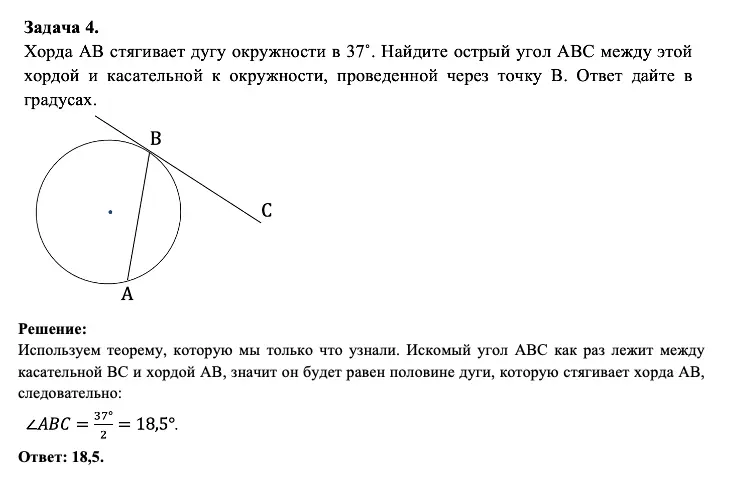
Однако хочу обратить ваше внимание, что если вы просто запомните формулировку, то многие задачи на окружность в ЕГЭ и ОГЭ покажутся вам супер-простыми и будут решаться в 1 действие. Давайте в этом убедимся:
Вот так просто и быстро в 1 действие мы справились с задачей. Правда здорово?!
Теорема № 2: теория и задания из ЕГЭ и ОГЭ
А теперь давайте посмотрим на одну из моих самых любимых теорем. А любимая она, потому что без неё некоторые задачи кажутся практически нерешаемыми, а с ней их можно решить быстро и просто! Звучит она так:
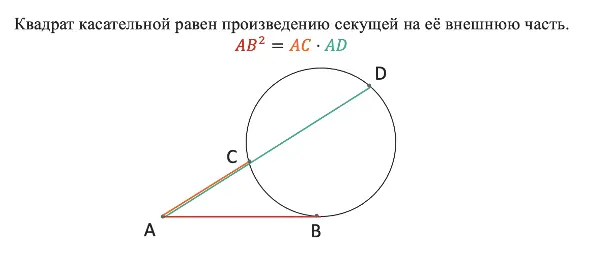
Квадрат касательной равен произведению секущей на её внешнюю часть.
Я советую запоминать именно словесную формулировку, так как чертежи и буквы на них могут быть разными, и есть риск всё перепутать.
Наглядно познакомиться с теоремой можно на рисунке ниже:
И конечно же давайте отработаем на практике!
Если бы мы не знали ту теорему, которую только что прошли, то было бы много версий, как можно решить задачу. Кто-то начал бы строить радиус к касательной и рассматривать треугольники, а кто-то просто не стал бы решать, однако у нас есть формула: давайте её используем!
Решение:
Теорема № 3: теория и задания из ЕГЭ и ОГЭ
Если вы ещё не устали от теорем, то давайте познакомимся с ещё одной, которая связывает хорду с диаметром (радиусом).
Эта теорема интересна тем, что работает в обе стороны:
Конечно же я не могу оставить вас без тренировки, поэтому посмотрим на следующую задачу:
Теорема № 4: пересекающиеся хорды
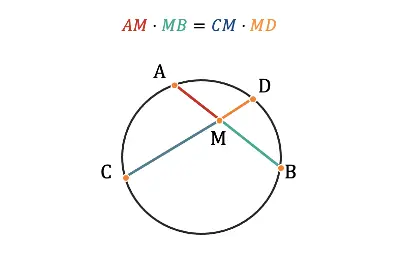
Последнее, с чем я вас познакомлю в контексте прямых и отрезков в окружности будет свойство пересекающихся хорд:
Произведения отрезков пересекающихся хорд равны.
Для наглядности отрезки выделены разными цветами, так вам будет проще запомнить свойство.
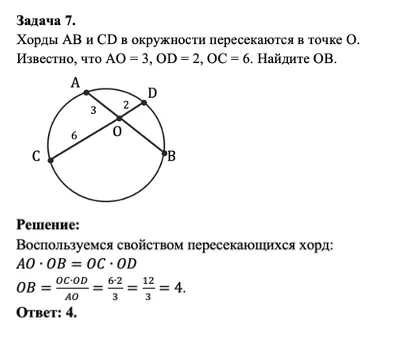
А теперь отработаем его на практике:
Длина окружности и площадь круга
Вот мы и подошли с вами к самому интересному, формулам длины окружности и площади круга, давайте их запишем:
Эти формулы очень походы, в них есть двойка, число Pi и радиус, однако можно заметить, что у формулы длины окружности двойка слева, а у площади круга справа в степени.
Так как же их не путать? Очень просто: запомните, что вторая степень (или квадрат) должна быть у площади, значит двойка слева будет у длины.
Давайте это закрепим:
Вот так просто и быстро мы закрепили сразу обе формулы.
Как находить площадь и длину дуги сектора круга: задачи
А теперь перейдём к самому интересному — нахождению площади и длины дуги сектора круга. Многие ученики думаю, что это сложно, но на самом деле это не так. Я предлагаю записать 2 коротких алгоритма, с помощью которых вы сможете легко найти площадь или длину дуги сектора.
И конечно же давайте закрепим эти алгоритмы на практике:
Теперь вы умеете решать задания на поиск площади сектора. Согласитесь, что с алгоритмом всё намного понятнее и проще?
Что нужно иметь в виду для ЕГЭ и ОГЭ
На самом деле это всё, что я хотела вам рассказать в данной статье. Давайте ещё раз повторим, что вы узнали.
- Сначала мы познакомились с понятием окружность, потом посмотрели, какие бывают углы в окружности.
- Затем увидели множество отрезков и прямых в окружности, записали их свойства, а также несколько теорем с ними.
- В завершение мы поговорили про длину окружности, площадь круга, а также поиск площади и длины дуги сектора.
Самое ценное, что всю теорию мы закрепили на реальных заданиях из ОГЭ и ЕГЭ. Конечно, это далеко не всё, что вам может встретиться. Если вы хотите хорошо разбираться в окружности и в других темах, которые встречаются на экзаменах, записывайтесь на наши курсы подготовки к ОГЭ и ЕГЭ. На них мы подробно изучаем всю теорию, решаем много заданий, запоминаем удобные лайфхаки и решаем пробные экзамены, чтобы не стрессовать на реальном. Присоединяйтесь!






.png)