Каталог заданий.
Уравнение окружности
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Найдите все значения параметра a, при каждом из которых система имеет ровно два решения.
2
Найдите все значения параметра a, при каждом из которых система
имеет единственное решение.
3
Найдите все значения параметра a, при каждом из которых система уравнений
имеет ровно два решения.
4
Найдите все значения параметра a, при каждом из которых система
имеет единственное решение.
5
Найдите все значения a, при каждом из которых система уравнений
имеет более двух решений.
Источник: ЕГЭ — 2015 по математике. Основная волна 04.06.2015. Вариант 1 (Часть С).
Пройти тестирование по этим заданиям
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Решение задач с окружностями
Задание
1
#3079
Уровень задания: Равен ЕГЭ
Найдите все значения (a), при каждом из которых система уравнений [begin{cases}
x(x^2+y^2-2y-8)=|x|cdot (2y-8)\
y=x+a end{cases}]
имеет ровно три решения.
(Задача от подписчиков)
1) Изобразим график первого уравнения.
а) При (x>0) уравнение принимает вид: [x(x^2+y^2-2y-8)=x(2y-8) quadRightarrowquad x^2+(y-2)^2=4] Мы получили уравнение окружности (назовем ее (s)) с центром в точке ((0;2)) и радиусом (2).
б) При (x=0) уравнение принимает вид: [0cdot (0+y^2-2y-8)=0cdot (2y-8) quadRightarrowquad 0=0] Таким образом, мы получили верное равенство. Следовательно, мы получили множество точек, абсцисса (x) которых равна нулю.
в) При (x<0) уравнение принимает вид: [x(x^2+y^2-2y-8)=-x(2y-8) quadRightarrowquad x^2+y^2=16] Мы получили уравнение окружности (назовем ее (S)) с центром в точке ((0;0)) и радиусом (4).
2) Уравнение (y=x+a) задает множество прямых, параллельных прямой (y=x) (это прямые, угол наклона которых к положительному направлению оси (Ox) равен (45^circ)).
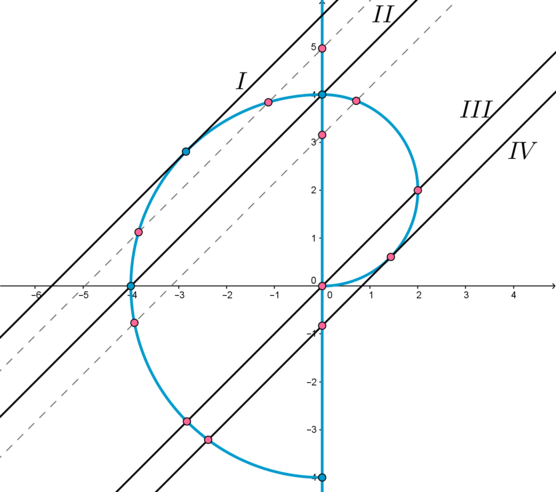
Таким образом, получаем такую картинку (голубым цветом изображен график первого уравнения):
3) Для того, чтобы система имела 3 решения, нужно, чтобы при некотором фиксированном (a) прямая (y=x+a) пересекала “голубой график” ровно в трех точках.
Таким образом, нам подходят следующие случаи:
— когда прямая (y) находится между (I) и (II) (не включая эти случаи). Случай (I) – касание прямой (y) и окружности (S). Случай (II) – прохождение прямой (y) через точку пересечения окружности (S) и прямой (x=0).
— когда прямая (y) находится между (II) и (III) (не включая (II) и включая (III)). Случай (III) – прохождение прямой (y) через точку пересечения окружности (s) и прямой (x=0).
— когда прямая (y) находится в положении (IV) – касается окружности (s).
Рассмотрим каждый из этих случаев по отдельности.
Между (I) и (II).
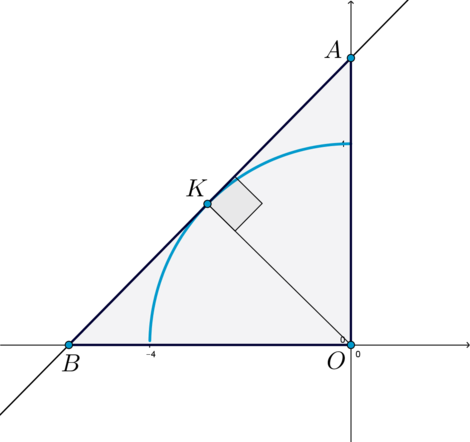
– Найдем значение (a), при котором прямая (y) находится в положении (I). В этом случае (a>0).
Пусть (A(0;a), B(-a;0)) – точки пересечения (y) с осями координат, (K) – точка касания. Тогда (OKperp AB) (как радиус, проведенный в точку касания). Длина (OA=a), (OB=a), (OK=4), (triangle AOB) прямоугольный. Тогда (AB=asqrt2). Тогда [S_{triangle AOB}=dfrac12 OKcdot AB=dfrac12 OBcdot OA
quadRightarrowquad a=4sqrt2.] – Найдем значение (a), при котором прямая (y) находится в положении (II). В этом случае (y) проходит через точку ((0;4)), следовательно, [4=0+a quadRightarrowquad a=4]
Таким образом, нам подходят значения (ain (4;4sqrt2)).
Между (II) и (III).
– Найдем (a), при котором прямая (y) находится в положении (III). В этом случае она проходит через точку ((0;0)), то есть (a=0).
Таким образом, нам подходят (ain [0;4)).
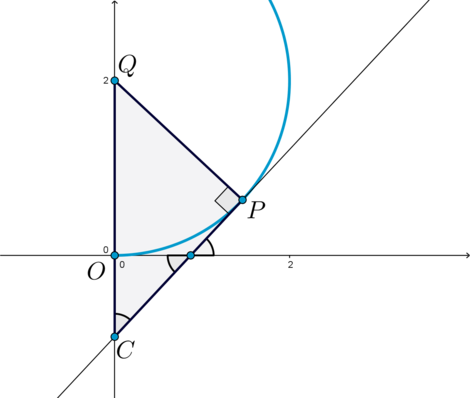
Положение (IV).
В этом случае (a<0). Пусть (Q) – центр окружности (s), (P) – точка касания, (C) – точка пересечения (y) с осью ординат. Тогда (triangle QPC) – прямоугольный. Ранее мы говорили, что прямая (y) наклонена к положительному направлению оси (Ox) под углом (45^circ), откуда будет следовать, что и (angle QCP=45^circ). Радиус (QP=2), отрезок (OC=-a) (так как (a<0)), (QO=2). Следовательно, [sinangle QCP=sin 45^circ=dfrac{sqrt2}2=dfrac{QP}{QC}=
dfrac{2}{2-a}
quadRightarrowquad a=-2sqrt2+2.]
Таким образом, обобщая все решение, находим ответ: [ain {-2sqrt2+2}cup[0;4)cup(4;4sqrt2).]
Ответ:
({-2sqrt2+2}cup[0;4)cup(4;4sqrt2))
Задание
2
#3202
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при каждом из которых система [begin{cases}
(x-2a+3)^2+(y-a)^2=2,25\
(x+3)^2+(y-a)^2=a^2+2a+1 end{cases}]
имеет единственное решение.
(Задача от подписчиков)
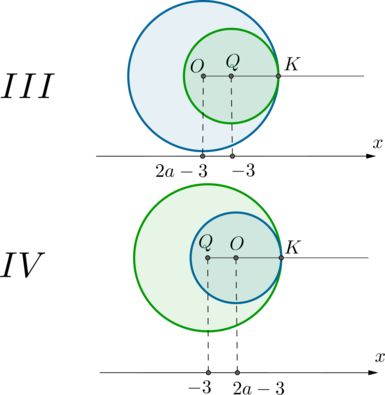
Оба уравнения системы при (ane -1) задают окружности: первое уравнение – окружность с центром в точке (O(2a-3; a)) и радиуса (R_1=1,5); второе – окружность с центром в точке (Q(-3;a)) и радиуса (R_1=|a+1|).
При (a=-1) второе уравнение задает точку (A(-3;-1)), которая не является решением первого уравнения. Следовательно, при (a=-1) система не имеет решений, значит, (a=-1) – не подходит.
Рассмотрим случай, когда (ane-1).
Система будет иметь единственное решение, когда окружности будут касаться друг друга (внутренним или внешним образом). Заметим, что центры обеих окружностей находятся на прямой (y=a). То есть линия центров окружностей параллельна оси абсцисс.
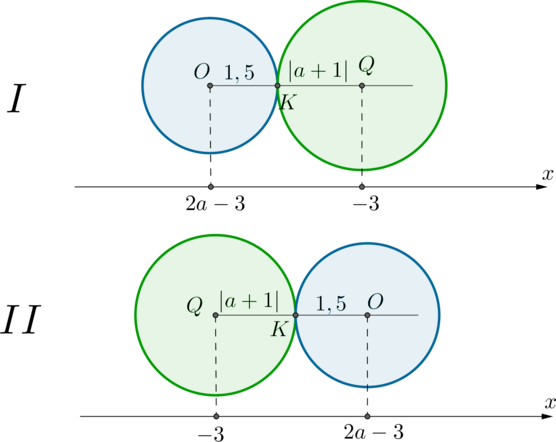
1) Пусть окружности касаются внешним образом в точке (K). Это одна из двух картинок:
Заметим, что, с одной стороны, расстояние между центрами окружностей равно сумме радиусов: (OQ=|a+1|+1,5), а с другой стороны, равно (|-3-(2a-3)|=2|a|). Получаем уравнение: [|a+1|+1,5=2|a|quadLeftrightarrowquad
left[begin{gathered}begin{aligned} &begin{cases} a< -1\
-2a=-a-1+1,5end{cases}\
&begin{cases} -1<a<0\
-2a=a+1+1,5 end{cases}\
&begin{cases} ageqslant 0\
2a=a+1+1,5 end{cases} end{aligned}end{gathered}right. quad
Leftrightarrowquad a=-dfrac56; dfrac52]
2) Пусть окружности касаются внутренним образом в точке (K). Это также одна из двух картинок (а также симметричные картинки, то есть когда точка касания находится слева):
В этих случаях длина отрезка (OQ), с одной стороны, равна (|-3-(2a-3)|=2|a|), а с другой стороны, она равна разности радиусов: (big|1,5-|a+1|big|) (ставим модуль, потому что неизвестно, какой радиус больше, то есть как окружность с центром (O) может быть вписана в окружность с центром (Q), так и наоборот). Получаем уравнение: [2|a|=big|1,5-|a+1|big| quadLeftrightarrowquad
left[begin{gathered}begin{aligned} & 2a=|a+1|-1,5\
&2a=1,5-|a+1| end{aligned}end{gathered}right.
quadLeftrightarrowquad a=-dfrac12; dfrac16]
Таким образом, окончательный ответ: [ain left{-dfrac56;
-dfrac12; dfrac16; dfrac52right}]
Ответ:
(left{-dfrac56; -dfrac12; dfrac16; dfrac52right})
Задание
3
#3977
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при которых система [begin{cases} (2x^2-4x+3y^2+6y+5)(8-|2x+y|)leqslant 0\
x^2-4x+y^2=a end{cases}]
имеет единственное решение.
(Задача от подписчиков)
1) Преобразуем неравенство системы:
((2x^2-4x+2+3y^2+6y+3-2-3+5)(8-|2x+y|)leqslant 0
quadLeftrightarrow)
(Leftrightarrowquad (2(x-1)^2+3(y+1)^2)(8-|2x+y|)leqslant
0quadLeftrightarrow)
(Leftrightarrowquad left[begin{gathered}begin{aligned}
&begin{cases} 2(x-1)^2+3(y+1)^2leqslant 0\
8-|2x+y|geqslant 0end{cases}\[2ex]
&begin{cases} 2(x-1)^2+3(y+1)^2geqslant 0\
8-|2x+y|leqslant 0end{cases} end{aligned}end{gathered}right.)
Т.к. сумма квадратов всегда неотрицательна, то данная совокупность равносильна:
[left[begin{gathered}begin{aligned}
&begin{cases}
2(x-1)^2+3(y+1)^2=0\
|2x+y|leqslant 8
end{cases}\[2ex]
&begin{cases}
2(x-1)^2+3(y+1)^2geqslant 0\
|2x+y|geqslant 8
end{cases}
end{aligned}end{gathered}right.
quadLeftrightarrowquad
left[begin{gathered}begin{aligned} &begin{cases}
x=1\
y=-1\
|2cdot 1+1|leqslant 8
end{cases}\[2ex]
&begin{cases}
x,yinmathbb{R}\
|2x+y|geqslant 8
end{cases}
end{aligned}end{gathered}right.
quadLeftrightarrowquad
left[begin{gathered}begin{aligned}
&begin{cases}
x=1\
y=-1
end{cases}\[2ex]
&|2x+y|geqslant 8
end{aligned}end{gathered}right.]
Т.к. (|2x+y|geqslant 

2) Преобразуем уравнение системы: [x^2-4x+y^2=aquadLeftrightarrowquad x^2-4x+4+y^2=a+4quadLeftrightarrowquad
(x-2)^2+y^2=a+4]
Данное уравнение при (a+4>0) задает окружность с центром в точке (O(2;0)) и радиусом (R=sqrt{a+4}); при (a+4=0) задает точку ((2;0)); при (a+4<0) – пустое множество.
Т.к. точка ((2;0)) не попадает в область, заданную неравенством, то при (a+4leqslant 0) система точно не будет иметь решений.
3) Рассмотрим случай (a+4>0).
Система будет иметь единственное решение тогда и только тогда, когда окружность будет иметь ровно одну общую точку с областью. Это возможно в одном из двух случаев:
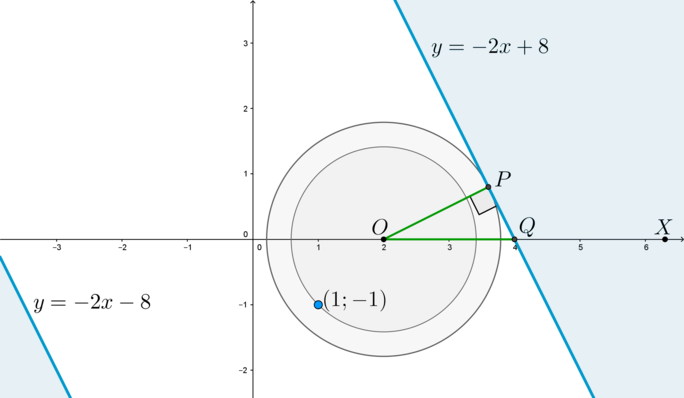
(1) Если окружность коснется границы области (y=-2x+8).
Пусть (P) – точка касания (то есть (OPperp y=-2x+8)). Рассмотрим прямоугольный (triangle OPQ), где (Q=(4;0)) – точка пересечения прямой (y=-2x+8) с осью абсцисс.
Т.к. угловой коэффициент прямой (y=-2x+8) равен (-2), то (mathrm{tg},angle PQX=-2), следовательно, (mathrm{tg},angle
PQO=2). Тогда [sin angle PQO=dfrac{2}{sqrt5}
quadRightarrowquad dfrac{OP}{OQ}=dfrac2{sqrt5} quad
Rightarrowquad OP=OQcdot dfrac2{sqrt5}=dfrac4{sqrt5}.]
Т.к. (OP) и есть радиус окружности, то [dfrac4{sqrt5}=sqrt{a+4} quad Rightarrowquad a=-dfrac45.]
(2) Если окружность проходит через точку ((1;-1)).
Это значит, что расстояние между точками (O) и ((1;-1)) равно радиусу окружности, следовательно, [sqrt{a+4}=sqrt{(2-1)^2+(0+1)^2}quad Leftrightarrowquad a=-2.]
Ответ:
(big{-2;-frac45big})
Задание
4
#3980
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при которых система [begin{cases}
left(|x|-3right)^2+left(|y|-2right)^2=1\
y=ax+1\xy<0end{cases}] имеет ровно два решения.
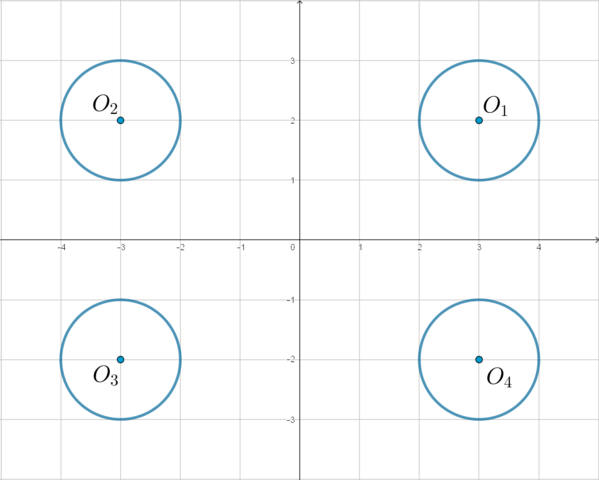
Рассмотрим первое уравнение системы. Оно задает 4 окружности. Действительно, пусть (x>0, y>0). Тогда уравнение примет вид ((x-3)^2+(y-2)^2=1) – это окружность с центром в точке (O_1(3;2)) и (r=1).
Если (x<0, y>0), то уравнение примет вид ((x+3)^2+(y-2)^2=1) – и это уравнение окружности с центром (O_2(-3;2)) и (r=1). И т.д.
Таким образом, получаем:
Рассмотрим третье неравенство системы (xy<0). Следовательно, либо (x>0, y<0), либо (x<0, y>0). Таким образом, учитывая это неравенство, остаются только две окружности: в (IV) и (II) четвертях. Уравнение (y=ax+1) задает прямую, у которой неизвестен угловой коэффициент, и которая проходит через точку ((0;1)):
Какие у нас могут быть случаи пересечения прямой с этими окружностями так, чтобы в итоге было ровно две точки пересечения?
а) прямая пересекает одну окружность, а вторую – нет;
б) прямая касается обеих окружностей.
Заметим, что так как окружности расположены симметрично относительно начала координат, то для того, чтобы прямая могла одновременно касаться обеих окружностей, она должна проходить через начало координат (то есть она тоже должна быть симметрична относительно начала координат). Наша прямая через начало координат не проходит. Следовательно, она не может касаться обеих окружностей сразу. Значит, случай б) невозможен. Остается только случай а).
Таким образом, нам нужно для начала рассмотреть все ситуации, когда прямая будет касаться какой-то из окружностей.
((1)) и ((2)) – случаи, когда прямая касается второй окружности (будем ее так называть, потому что у нее центр в (O_2)); ((3)) и ((4)) – случаи, когда прямая касается четвертой окружности.
Заметим, что эти случаи по возрастанию параметра (a) можно упорядочить так: ((4)rightarrow(1)rightarrow(3)rightarrow(2)).
Таким образом, нам нужны будут значения параметра, принадлежащие ((a_{4}; a_{1})) и ((a_{3}; a_{2})) (здесь (a_{i}) – значения параметра (a), которое соответствует расположению прямой в случае ((i))).
Значит, найдем (a_{1}, a_{2}, a_{3}, a_{4}).
Найдем значения (a), когда прямая (y=ax+1) касается второй окружности: [begin{cases} (x+3)^2+(y-2)^2=1\
y=ax+1end{cases}quadRightarrowquad (a^2+1)x^2+2(3-a)x+9=0] Так как прямая и окружность касаются, то есть имеют одну точку пересечения, то полученное уравнение должно иметь один корень, следовательно, его дискриминант должен быть равен нулю: [D=0quadRightarrowquad a=-dfrac34; 0] Значит, (a_2=0; a_1=-frac34).
Аналогично найдем, что (a_3=frac{-9+sqrt{17}}8), (a_4=frac{-9-sqrt{17}}8).
Следовательно, ответ: [ain left(dfrac{-9-sqrt{17}}8; -dfrac34right)cupleft(dfrac{-9+sqrt{17}}8;
0right)]
Ответ:
(ain left(frac{-9-sqrt{17}}8;
-frac34right)cupleft(frac{-9+sqrt{17}}8; 0right))

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Автор материала — Анна Малкова
Какими были задачи с параметрами на ЕГЭ-2022? На этой странице — обзор всех типов задач №17, предложенных на ЕГЭ по математике в этом году, с полным решением и оформлением.
Напомним, что «параметры» — одна из дорогостоящих задач ЕГЭ. Она оценивается в 4 первичных балла.
Основной темой задач с параметрами на ЕГЭ этого года были модули.
Если вы не помните, что такое модуль числа, — вам сюда.
Способы решения — разные. В одних задачах удобнее графический способ, в других — аналитический.
Мы начнем с тех задач, которые решаются графическим способом. В первых трех, которые мы здесь разбираем, нам встретится уравнение окружности.
Почитать о нем подробно можно здесь.
1. При каких значениях параметра уравнение
имеет ровно 4 решения?
Решение:
Вспомним, как решать уравнения вида
Поэтому исходное уравнение равносильно системе:
Получим:
Изобразим решения системы в координатах
Уравнение задает окружность
с центром
и радиусом 5; уравнение
задает окружность
с центром
и радиусом
; при этом должно выполняться условие
Заметим, что обе окружности проходят через точки и
Найдем, при каких значениях параметра исходное уравнение имеет ровно 4 решения.
При прямая
проходит через точку
общую для двух окружностей; уравнение имеет ровно 3 решения.
Если прямая проходит через точку
(нижнюю точку окружности
), уравнение также имеет 3 решения.
При этом поскольку разность ординат точек Q и A равна
то есть радиусу окружности
При уравнение имеет 4 решения.
Если решений меньше 4.
Если уравнение имеет ровно 3 решения, т.к. точка O(0; 0) общая для обеих окружностей.
Если прямая проходит через B — верхнюю точку окружности
уравнение имеет ровно 3 решения.
В этом случае
При уравнение имеет ровно 4 решения.
Если решений меньше, чем 4.
Объединив случаи, получим ответ.
Ответ:
2. При каких значениях параметра уравнение
имеет ровно 2 решения?
Решение:
Раскроем модуль по определению.
Уравнение (1) задает окружность с центром в точке Р (4; 3) и радиусом 5,
уравнение (2) задает окружность с центром в точке Q(-3; 4) и радиусом 5.
Изобразим график совокупности двух систем в системе координат (x;a).
При получаем часть окружности (1), лежащую ниже прямой a = 7x;
при получаем часть окружности (2), лежащую выше прямой a = 7x.
Исходное уравнение имеет ровно два различных решения, если прямая пересекает график совокупности двух систем ровно два раза.
Прямая проходящая через точку С, пересекает график совокупности двух систем один раз.
Найдем координаты С — самой нижней точки и Е — самой верхней точки правой окружности.
Для этих точек x = 4. Найдем координату a:
или
Координаты точек С (4; и Е (4; 8).
Найдем координаты D — самой нижней точки и F — самой верхней точки левой окружности
Для этих точек x = — 3, найдем координату a.
или
Координаты точек: D (3;
1), F(
3; 9).
Точки А и В, в которых пересекаются две окружности, лежат на прямой
a = 7x (так как при a = 7x выражение под модулем равно нулю).
Подставив a = 7x в уравнение окружности (1) получим:
x = 0 или x = 1.
Получили точки В (0; 0) и А (1; 7).
Прямая пересекает график совокупности двух систем ровно два раза в следующих случаях:
1) если прямая проходит выше точки С, но ниже точки D:
2) если прямая проходит выше точки В, но ниже точки А:
3) если прямая проходит выше точки Е, но ниже точки F:
Если или
то решений нет.
Если или a = 9, уравнение имеет ровно одно решение.
Если или a = 8, ровно три решения.
Если или
ровно четыре решения. Эти случаи нам не подходят.
Ответ: a
3. При каких значениях параметра уравнение
имеет ровно 2 корня?
Решение:
Раскрыв модуль, получим:
Решим систему графически в координатах
Прямая — это биссектриса первого и третьего координатных углов.
Неравенство задает полуплоскость, расположенную ниже прямой
Уравнение задает окружность
1 с центром в точке
и радиусом
Уравнение задает окружность
2 с центром в точке
и радиусом
Заметим, что обе окружности проходят через точки О(0; 0) и М(1; 1). В этом легко убедиться, подставив координаты этих точек в уравнения окружностей.
Исходное уравнение имеет ровно 2 корня, если прямая пересекает совокупность двух окружностей ровно в двух точках, лежащих не выше прямой a = x.
Это происходит в следующих случаях:
1) Прямая проходит выше точки А и ниже точки В на рисунке, где А — нижняя точка окружности
2, В — нижняя точка окружности
1.
2) Прямая проходит выше точки С и ниже точки D на рисунке, где D — верхняя точка окружности
2, С — верхняя точка окружности
1.
3) Прямая проходит выше точки О(0; 0) и ниже точки М(1;1).
Найдем координаты точек А, В, С, D.
Получим, что
Ответ:
Заметим, что в каждом из уравнений присутствовало выражение — как в уравнении окружности. Именно поэтому становилось понятно, что их можно решить графически в координатах x; a.
Теперь — следующий тип задач. Здесь окружностей уже не будет. Зато будет разложение на множители.
4. При каких значениях параметра уравнение
имеет ровно 4 решения?
Решение:
Раскроем модуль. Уравнение равносильно совокупности двух систем:
Упростим по очереди каждую из них.
1) Случай
Найдем дискриминант и корни этого квадратного уравнения.
2) Случай
В этом случае также найдем дискриминант и корни квадратного уравнения.
Получим:
или
.
Решим совокупность двух систем графически в координатах
Если уравнение имеет меньше 4 решений.
Если также меньше 4 решений.
Если прямая проходит через точку A или точку B, уравнение имеет ровно 3 решения.
В точке A пересекаются прямые и
, значит, для этой точки
В точке B пересекаются прямые и
, то для точки B:
.
Уравнение имеет ровно 4 решения, если или
или
.
Ответ:
Следующие две задачи мы решим (для разнообразия) аналитическим способом.
5. При каких значениях параметра уравнение
имеет меньше 4 решений?
Решение:
Уравнение равносильно совокупности:
Рассмотрим каждый случай отдельно
1)
2)
Каждое из уравнений — квадратное и не может иметь больше 2 корней.
Если уравнение (1) имеет 2 неотрицательных корня, а уравнение (2) имеет 2 отрицательных корня, исходное уравнение имеет ровно 4 решения. Найдем, при каких значениях это происходит, а затем исключим эти значения. Получим случай, когда исходное уравнение имеет менее 4 корней.
Исходное уравнение имеет ровно 4 решения, если уравнение имеет два неотрицательных корня, а уравнение
имеет два отрицательных корня.
1 уравнение:
По теореме Виета,
для уравнения

При этом
Оценим и
Сравним т.к.
также
Получим:
2 уравнение:
При этом т.е.
— верно при всех a.
Получим:
Исходное уравнение имеет ровно 4 решения, если выполняется система условий:
При всех остальных значениях a — меньше четырёх решений. Значит, подходят значения
Ответ:
6. Найдите все положительные значения a, при каждом из которых уравнение
имеет ровно 4 корня.
Решение:
Раскроем модуль по определению.
Мы получили совокупность двух систем. Чтобы исходное уравнение имело ровно 4 корня, нужно, чтобы каждая система имела ровно два решения. Решим каждую из систем отдельно.
1) Первая система:
Чтобы квадратное уравнение имело два неотрицательных корня, необходимо и достаточно выполнения условий:
Другой способ: можно рассмотреть квадратичную функцию
и воспользоваться условиями:
Найдем дискриминант соответствующего квадратного уравнения.
при этом
Получим:
Корни уравнения
Отсюда
2) Вторая система:
Чтобы система имела ровно 2 решения, для квадратичной функции
необходимо и достаточно выполнения условий:
— верно для всех
Решение второй системы:
Исходное уравнение имеет ровно 4 различных решения, если
Ответ:
Как всему этому научиться? Если вы решили освоить тему «Параметры» — не нужно начинать со сложных задач. Вначале — подготовительная работа. Элементарные функции и их графики, базовые элементы для решения задач с параметрами. Кроме того, надо отлично знать методы алгебры: разложение выражений на множители, выделение полных квадратов, решение уравнений и неравенств всех типов и многое другое.
Изучить все это можно на Онлайн-курсе подготовки к ЕГЭ по математике. На нем мы решаем и такие задачи, и более сложные. Изучаем не менее 11 методов решения задач с параметрами. Выпускники Онлайн-курса отлично справились с «параметрами» на ЕГЭ-2022.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задачи с параметрами на ЕГЭ-2022: модули, окружности, квадратные уравнения» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
Графический метод решения задач с параметрами
Теперь вы узнали, что такое параметр, и увидели решение самых простых задач.
Но подождите — рано успокаиваться и говорить, что вы все знаете. Есть множество типов задач с параметрами и приемов их решения. Чтобы чувствовать себя уверенно, мало посмотреть решения трех незатейливых задач.
Вот список тем, которые стоит повторить:
1. Элементарные функции и их графики. Парабола, синус, логарифм, арктангенс и все остальные — всех их надо знать «в лицо».
Только после этого можно переходить к самому простому и наглядному способу решения задач с параметрами — графическому. Конечно, он не единственный. Но начинать лучше всего именно с него.
Мы разберем несколько самых простых задач, решаемых графическим методом. Больше задач — в видеокурсе «Графический метод решения задач с параметрами» (бесплатно).
1. При каких значениях параметра a уравнение имеет ровно 2 различных решения?
Дробь равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель не равен нулю.
В первом уравнении выделим полный квадрат:
Это уравнение окружности с центром в точке и радиусом равным 2. Обратите внимание — графики будем строить в координатах х; а.
Уравнение задает прямую, проходящую через начало координат. Нам нужны ординаты точек, лежащих на окружности и не лежащих на этой прямой.
Для того чтобы точка лежала на окружности, ее ордината а должна быть не меньше 0 и не больше 4.
Кроме того, точка не должна лежать на прямой , которая пересекает окружность в точках и Координаты этих точек легко найти, подставим в уравнение окружности.
Точка С также не подходит нам, поскольку при мы получим единственную точку, лежащую на окружности, и единственное решение уравнения.
2. Найдите все значения a, при которых уравнение имеет единственное решение.
Уравнение равносильно системе:
Мы возвели обе части уравнения в квадрат при условии, что (смотри тему «Иррациональные уравнения»).
Раскроем скобки в правой части уравнения, применяя формулу квадрата трехчлена. Получаем систему.
Приводим подобные слагаемые в уравнении.
Заметим, что при прибавлении к правой и левой части числа 49 можно выделить полные квадраты:
Решим систему графически:
Уравнение задает окружность с центром в точке , где радиус
Неравенство задает полуплоскость, которая расположена выше прямой , вместе с самой этой прямой.
Исходное уравнение имеет единственное решение, если окружность имеет единственную общую точку с полуплоскостью. Другими словами, окружность касается прямой, заданной уравнением
Пусть С — точка касания.
На координатной плоскости отметим точки и , в которых прямая пересекает оси Y и Х.
Рассмотрим треугольник ABP. Он прямоугольный, и радиус окружности PC является медианой этого треугольника. Значит по свойству медианы прямоугольного треугольника, проведенной к гипотенузе.
Из треугольника ABP найдем длину гипотенузы AB по теореме Пифагора.
Решая это уравнение, получаем, что
3. Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение.
График уравнения — окружность с центром и радиусом равным 2.
График уравнения — две симметричные окружности и радиуса 2 c центрами в точках и
Второе уравнение при задает окружность с центром в точке и радиусом a.
Вот такая картинка, похожая на злую птицу. Или на хрюшку. Кому что нравится.
Система имеет единственное решение в случаях, когда окружность , задаваемая вторым уравнением, касается только левой окружности или только правой
Если a — радиус окружности , то это значит, что (только правая) или (только левая).
Пусть А — точка касания окружности и окружности
, (как гипотенуза прямоугольного треугольника МNР с катетами 3 и 4),
В — точка касания окружности и окружности
длину MQ найдем как гипотенузу прямоугольного треугольника KMQ с катетами 7 и 4; Тогда для точки В получим:
Есть еще точки С и D, в которых окружность касается окружности или окружности соответственно. Однако эти точки нам не подходят. В самом деле, для точки С:
, но и это значит, что окружность с центром в точке М, проходящая через точку С, будет пересекать левую окружность и система будет иметь не одно, а три решения.
Аналогично, для точки D:
и значит, окружность с центром М, проходящая через точку D, будет пересекать правую окружность и система будет иметь три решения.
4. При каких значениях a система уравнений имеет 4 решения?
Конечно же, решаем графически. Только непуганый безумец возьмется решать такую систему аналитически : -)
И в первом, и во втором уравнении системы уже можно разглядеть известные «базовые элементы» (ссылка) — в первом ромбик, во втором окружность. Видите их? Как, еще нет? — Сейчас увидите!
Просто выделили полный квадрат во втором уравнении.
Сделаем замену Система примет вид:
Вот теперь все видно! Рисовать будем в координатах
Графиком первого уравнения является ромб, проходящий через точки с координатами и
Графиком второго уравнения является окружность с радиусом и центром в начале координат.
Когда же система имеет ровно 4 решения?
1) В случае, когда окружность вписана в ромб, то есть касается всех сторон ромба.
Запишем площадь ромба двумя способами — как произведение диагоналей пополам и как произведение стороны на высоту, проведенную к этой стороне.
Диагонали нашего ромба равны 8 и 6. Значит,
Сторону ромба найдем по теореме Пифагора. Видите на рисунке прямоугольный треугольник со катетами 3 и 4? Да, это египетский треугольник, и его гипотенуза, то есть сторона ромба, равна 5. Если h — высота ромба, то

Мы получили ответ:
2) Есть второй случай, и мы его найдем.
Давайте посмотрим — если уменьшить радиус окружности, сделав , окружность будет лежать внутри ромба, не касаясь его сторон. Система не будет иметь решений, и нам это не подходит.
Пусть радиус окружности больше, чем , но меньше 3. Окружность дважды пересекает каждую из четырех сторон ромба, и система имеет целых 8 решений. Опять не то.
Пусть радиус окружности равен 3. Тогда система имеет 6 решений.
А что, если ? Окружность пересекает каждую сторону ромба ровно 1 раз, всего 4 решения. Подходит!
Значит, Объединим случаи и запишем ответ:
Больше задач и методов решения — на онлайн-курсе Анны Малковой. И на интенсивах ЕГЭ-Студии в Москве.
Задания по теме «Системы уравнений с параметром»
Открытый банк заданий по теме системы уравнений с параметром. Задания C6 из ЕГЭ по математике (профильный уровень)
Задание №1227
Условие
Найдите все значения a > 0, при каждом из которых система begin(x-4)^2+(|y|-4)^2=9,\ x^2+(y-4)^2=a^2end имеет ровно 2 решения.
Решение
Если y geqslant 0, то первое уравнение задаёт окружность phi _1 с центром в точке C_1 (4; 4) радиуса 3 , а если y то оно задаёт окружность phi _2 с центром в точке C_2 (4; -4) того же радиуса.
При a > 0 второе уравнение задаёт окружность phi с центром в точке C(0; 4) радиуса a . Поэтому задача состоит в том, чтобы найти все значения параметра a , при каждом из которых окружность phi имеет ровно две общие точки с объединением окружностей phi _1 и phi _2.
Координаты точки касания окружностей phi и phi _1 явно видны на чертеже — точки A_1 (1; 4) и B_1 (7; 4) . То есть при a=CA_1=1 и a=CB_1=7 окружности phi и phi _1 касаются. При a > 7 и a окружности phi и phi _1 не пересекаются, при 1 окружности phi и phi _2 имеют 2 общие точки.
Далее, из точки C проведём луч CC_2 и обозначим A_2 и B_2 точки его пересечения с окружностью phi_2 , где A_2 лежит между C и C_2. Заметим, что длина отрезка CC_2= sqrt <4^2+(4-(-4))^<2>>= sqrt <80>= 4sqrt 5.
При a или a > CB_2 окружности phi и phi_2 не пересекаются. При CA_2 окружности phi и phi _2 имеют 2 общие точки. При a =CA_2=4sqrt 5-3 или a=CB_2=4sqrt 5+3, окружности phi и phi _2 касаются.
Исходная система имеет ровно 2 решения тогда и только тогда, когда окружность phi с одной из окружностей phi _1 и phi _2 имеет 2 общие точки, а с другой не пересекается, либо касается одновременно двух окружностей.
Так как 1 то условию задачи удовлетворяют значения ain (1;4sqrt 5-3) cup (7; 4sqrt 5+3).
Система уравнений с параметром.
Задача 1
Найти все значения параметра a, при каждом из которых система уравнений [left< begin ((x+5)^2+y^2-a^2)ln <(9-x^2-y^2)>= 0; \ ((x+5)^2+y^2-a^2)(x+y+5-a) = 0 \ endright. ] имеет два различных решения.
Условие получено от пользователей сайта alexlarin.net.
Задача хорошо решается графическим методом. Мне она показалась интересной тем, что, в отличие от обычной практики, в процессе размышлений здесь графики лучше размещать на отдельных рисунках. Привожу полное решение этой задачи в качестве очередного примера заданий ЕГЭ на параметр.
Подробное решение
Решение любой задачи, содержащей алгебраические выражения, должно начинаться с анализа области допустимых значений (ОДЗ) этих выражений. Особенно важно не забывать об этом при решении заданий второй части ЕГЭ профильного уровня.

Начнем с сомножителя, общего для обоих уравнений.
[ (x+5)^2+y^2-a^2 = 0; \ (x+5)^2+y^2=a^2 ]
Получили уравнение окружности на координатной плоскости. Радиус окружности равен абсолютному значению параметра а. В случае, когда а = 0, окружность вырождается в точку. (Не забываем, что r = |а| потому, что нужно рассмотреть все возможные значения параметра, в том числе и отрицательные, которые при возведении в квадрат удовлетворяют уравнению окружности.) Центр окружности расположен в точке с координатами <−5;0>. Изобразим несколько таких окружностей для различных значений параметра а.
Так как рассматриваемый сомножитель входит в оба уравнения системы, то все точки этих окружностей могут быть искомыми решениями системы. Но реально являются таковыми только те из них, которые входят в ОДЗ, т.е. те участки окружностей, которые пересекают упомянутый выше круг радиуса 3.
Анализируем рисунок:
— (красные) окружности, радиусы которых меньше 2 или больше 8 не имеют общих точек с (голубым) кругом, т.е. при (|a| in [0;2) cup (8;+infty)) рассматриваемый сомножитель не дает вклада в решение системы,
— окружности c r = 2 и r = 8 касаются границы голубого круга, но она не входит в ОДЗ, поэтому при (|a| = 2) и (|a| = 
— в случае, когда радиус окружности принадлежит промежутку (2;8), она пересекается с кругом ОДЗ в двух точках и решением системы являются все точки дуги (красной) окружности, лежащей внутри этого (голубого) круга. Таких точек, а следовательно и решений системы, бесконечное множество.
Выводы:
1) при (a in (-8; -2)cup (2;8)) система уравнений имеет бесконечное множество решений;
2) при (a in (-infty; -8] cup [-2;2] cup[8;+infty)) сомножитель (((x+5)^2+y^2-a^2)) не дает вклада в решения системы, поэтому при некоторых значениях параметра а из этого диапазона система может иметь два различных решения, если таковые будут получены из анализа оставшихся двух сомножителей.
Итак, продолжаем искать решения заданной системы уравнений среди решений следующей системы, содержащей оставшиеся два сомножителя [left< begin ln <(9-x^2-y^2)>= 0; \ (x+y+5-a) = 0. \ endright. ] Последняя равносильна заданной при условии, что нас не интересует случай, когда ((x+5)^2+y^2-a^2 = 0). В дальнейшем эту систему я буду называть сокращенной.

Решением сокращенной системы уравнений будут точки пересечения окружности (r = sqrt<8>) с этими прямыми. Прямые могут пересекать окружность в двух точках, касаться её в одной точке или вообще не иметь общих точек с окружностью. Нас интересуют те из них, которые имеют по два пересечения, что будет соответствовать двум различным решениям системы уравнений. Как видно по рисунку, такие прямые находятся между двумя касательными к окружности. Нужно уточнить их уравнения, чтобы найти соответствующие пределы изменения параметра a.

Например, для точки <2;2>применим первый способ:
— пусть x = 2 и y = 2, тогда (x^2+y^2 = 2^2+2^2 = 4+4=8), значит точка лежит на окружности;
— радиус, проведенный в эту точку, совпадает с диагональю квадрата 2×2, которая проходит под углом 45° к положительному направлению оси Ох и поэтому перпендикулярна к рассматриваемым (зелёным) прямым. Таким образом, выполняется условие: радиус окружности перпендикулярен касательной.
(Примечания: I.Имелся в виду квадрат с вершинами в точках <0;0>, <0;2> <2;2>и <2;0>). II.Тангенс угла наклона наших прямых равен −1, следовательно они проходят под углом 135° к положительному направлению оси Ох.)
В качестве второго примера, левую точку касания полностью найдём через производную и уравнение касательной. Нижняя часть окружности соответствует графику функции [ y = — sqrt <8-x^2>] Вычислим производную этой функции [ y’ = (- sqrt<8-x^2>)’ = -dfrac<1cdot(8-x^2)’><2sqrt<8-x^2>> = -dfrac<-2x><2sqrt<8-x^2>> = dfrac<sqrt<8-x^2>> ] Приравняем производную к тангенсу угла наклона искомой касательной, т.е. в нашем случае к −1 и решим уравнение относительно x. [dfrac<sqrt<8-x^2>> = -1;\ x = — sqrt<8-x^2>; ; x^2 = 8-x^2; \ 2x^2 = 8; ; x^2 = 4; ; x = pm2.] Нашли абсциссы точек касания. Подстановкой в уравнение окружности находим ординаты этих точек [ y = — sqrt<8-x^2>; ; y(-2) = — sqrt <8-(-2)^2>= — sqrt <8-4>= -2;]
Итак, точки касания найдены и обоснованы. Определим соответствующие им значения параметра a.
[ y = -x + (a-5) \ при ; x=2, ; y = 2 ;имеем\ 2 = -2 + (a-5) \ a-5=4;; a = 9 \ при ; x=-2,; y = -2 ; имеем \ -2 = 2 + (a-5) \ a-5=-4; ; a = 1 ] Следовательно, при (a in (1; 9) ) сокращённая система уравнений имеет ровно два различных решения.
Вернёмся к заданной системе уравнений. Чтобы она имела два различных решения, параметр a должен находиться в таком диапазоне, где первый из рассмотренных нами сомножителей не дает решений (иначе, как мы выяснили, их будет бесконечно много), а система из оставшихся двух сомножителей, сокращенная система, дает ровно два решения. Чтобы определить этот диапазон, найдем пересечение полученных ранее интервалов для параметра а с помощью числовой оси.
Как видно оба условия выполняюися для (a in (1; 2]cup [8; 9))
Ответ: (a in (1; 2]cup [8; 9))
Конечно, в итоговое решение, которое будет переписано на бланк, вы можете поместить один рисунок, который выглядит примерно так:
В качестве решения приведите все алгебраические выкладки с кратким обоснованием.
Задача для самостоятельного решения.
Задача 2
Найдите все значения параметра a, при каждом из которых система уравнений [left< begin (x+y-2a)sqrt <8x-y^2-x^2>= 0; \ (x+y-2a) Large (normalsize x^2+(y+3)^2-a^2 Large )normalsize = 0 \ endright. ] имеет ровно два различных решения.
1) ОДЗ: ( 8x-y^2-x^2 ge 0 )

2) Система равносильна совокупности [ left[ begin x+y-2a = 0; \ <left< begin sqrt <8x-y^2-x^2>= 0; \ x^2+(y+3)^2-a^2 = 0. end right.> end right. ] 3) Первое уравнение совокупности [x+y-2a = 0; \ y=-x+2a ] является уравнением прямых на координатной плоскости.
Находим точки касания этих прямых и окружности ОДЗ: [ (x-4)^2+y^2 = 4^2 \ y = pm sqrt <16 — (x-4)^2>\ y’ = pm dfrac<1cdot (16 — (x-4)^2)’><2sqrt<16 — (x-4)^2>> = mp dfrac<sqrt<16 — (x-4)^2>> \ mp dfrac<sqrt<16 — (x-4)^2>> = -1 \ pm (x-4) = sqrt <16 — (x-4)^2>\ (x-4)^2 = 16 — (x-4)^2 \ (x-4)^2 = 8\ x = pm sqrt <8>+ 4 = 4 pm 2sqrt<2>. \ y = pm sqrt <16 — (x-4)^2>= pm sqrt <16 — 8>= pm 2sqrt<2>. \ ] При каких (a) через точки касания проходят прямые? [ x+y-2a= 0;\ 4+2sqrt<2>+2sqrt <2>= 2a;\ a=2+2sqrt<2>.] [ x+y-2a = 0;\ 4-2sqrt<2>-2sqrt<2>=2a;\ a=2-2sqrt<2>. ]
Вывод:
— при ( a in (2-2sqrt<2>;; 2+2sqrt<2>) ) бесконечное множество решений;
— при ( a = 2-2sqrt<2>) и (a = 2+2sqrt <2>) уравнение имеет единственное решение;
— при ( a in (-infty; 2-2sqrt<2>)cup (2+2sqrt<2>; + infty) ) уравнение не даёт вклада в решения исходной системы.
4) Рассматриваем систему совокупности (сокращенную систему): [ <left< begin sqrt <8x-y^2-x^2>= 0; \ x^2+(y+3)^2-a^2 = 0. end right.> ] [sqrt <8x-y^2-x^2>= 0 LeftarrowRightarrow 8x-y^2-x^2=0 LeftarrowRightarrow (x-4)^2+y^2 = 4^2 ] Решениями первого уравнения этой системы являются все точки окружности — границы ОДЗ.
[x^2+(y+3)^2-a^2 =0 LeftarrowRightarrow x^2+(y+3)^2= a^2 ] Решениями второго уравнения этой системы являются все точки окружностей радиуса (а) центром в точке О2<0;-3>.
Решением системы — пересечение этих множеств.
При каких (a) окружности касаются друг друга?
Из геометрии — точки касания окружностей лежат на одной прямой с их центрами. [O_1O_2 = sqrt <4^2+3^2>= 5] Следовательно, (|a|=5-4=1) радиус меньшей касательной окружности, (|a|=5+4=9) радиус большей.
Вывод:
— при ( |a| in (1;;9) ) по 2 решения;
— при ( |a| = 1) и (|a| = 9 ) по 1-му решению;
— при ( |a| in [0;; 1)cup (9;; + infty) ) решений нет.
5) Общий вывод:
— при ( a in (-infty;; -9)cup (-1;; 2-2sqrt<2>) cup (9;; +infty ) ) система уравнений, заданная в условии задачи, не имеет решений;
— при ( a = <-9;;-1;;2-2sqrt<2>;;9;> ) она имеет единственное решение;
— при ( a in (-9;;-1)cup (2+2sqrt<2>;;9) ) два решения;
— при ( a = 2+2sqrt <2>) три решения;
— при ( a in (2-2sqrt<2>;; 2+2sqrt<2>) ) бесконечное множество решений.
Ответ: ( a in (-9;; -1)cup (2+2sqrt<2>;; 9) )
Перейдите по стрелке, чтобы найти ссылки на другие задачи ЕГЭ 2018.
источники:
http://academyege.ru/theme/sistemy-uravnenij-s-parametrom.html
http://mathematichka.ru/ege/C_problems/problem18_1_2018.html
9 мая 2014
Задачи C5, которая содержит в себе сразу два параметра, многими учениками воспринимается как что-то очень сложное и нестандартное. А на самом деле это одни из самых легкий и быстрых задач, которые вообще бывают в ЕГЭ по математике.
Смотрите также:
- Аналитическое решение задачи 18 с перебором различных вариантов
- Задачи 18: Аналитическое решение
- Приведение дробей к общему знаменателю
- Сводный тест по задачам B12 (2 вариант)
- Задача B2: лекарство и таблетки
- Задача C1: тригонометрия и показательная функция — 1 вариант
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Задачи с параметром»
Открытый банк заданий по теме задачи с параметром. Задания C6 из ЕГЭ по математике (профильный уровень)
Задание №1227
Условие
Найдите все значения a > 0, при каждом из которых система begin{cases}(x-4)^2+(|y|-4)^2=9,\ x^2+(y-4)^2=a^2end{cases} имеет ровно 2 решения.
Показать решение
Решение
Если y geqslant 0, то первое уравнение задаёт окружность phi _1 с центром в точке C_1(4; 4) радиуса 3, а если y < 0, то оно задаёт окружность phi _2 с центром в точке C_2(4; -4) того же радиуса.
При a > 0 второе уравнение задаёт окружность phi с центром в точке C(0; 4) радиуса a. Поэтому задача состоит в том, чтобы найти все значения параметра a, при каждом из которых окружность phi имеет ровно две общие точки с объединением окружностей phi _1 и phi _2.
Координаты точки касания окружностей phi и phi _1 явно видны на чертеже — точки A_1(1; 4) и B_1(7; 4). То есть при a=CA_1=1 и a=CB_1=7 окружности phi и phi _1 касаются. При a > 7 и a < 1 окружности phi и phi _1 не пересекаются, при 1 < a < 7 окружности phi и phi _2 имеют 2 общие точки.
Далее, из точки C проведём луч CC_2 и обозначим A_2 и B_2 точки его пересечения с окружностью phi_2 , где A_2 лежит между C и C_2. Заметим, что длина отрезка CC_2= sqrt {4^2+(4-(-4))^{2}}= sqrt {80}= 4sqrt 5.
При a < CA_2 или a > CB_2 окружности phi и phi_2 не пересекаются. При CA_2 < a < CB_2 окружности phi и phi _2 имеют 2 общие точки. При a =CA_2=4sqrt 5-3 или a=CB_2=4sqrt 5+3, окружности phi и phi _2 касаются.
Исходная система имеет ровно 2 решения тогда и только тогда, когда окружность phi с одной из окружностей phi _1 и phi _2 имеет 2 общие точки, а с другой не пересекается, либо касается одновременно двух окружностей.
Так как 1<4sqrt 5-3<7<4sqrt 5+3, то условию задачи удовлетворяют значения ain(1;4sqrt 5-3) cup (7; 4sqrt 5+3).
Ответ
(1;4sqrt 5-3) cup (7; 4sqrt 5+3).
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1226
Условие
При каких значениях параметра a система begin{cases} 15|x-2|+8|y+3|=120,\x^2 -4a^2 +2y+5=4(x-1)-(y+2)^2 end{cases} имеет ровно 4 решения?
Показать решение
Решение
Преобразуем второе уравнение системы, выделив полные квадраты:
begin{cases}15|x-2|+8|y+3|=120,\ x^2-4a^2+2y+5=4(x-1)-(y+2)^2 ;end{cases}
begin{cases}15|x-2|+8|y+3|=120,\ (x^2- 4x+4)+(y^2+6y+9)=(2a)^2 ;end{cases}
begin{cases}15|x-2|+8|y+3|=120,\ (x-2)^2 +(y+3)^2 =(2a)^2.end{cases}
Сделав замену переменных t=x-2 и omega=y+3, получим систему:
begin{cases}15|t|+8|omega |=120,enspace (1) \ t^2 +omega^2 =(2a)^2.enspace(2) end{cases}
При такой замене старая и новая система имеют одинаковое число решений.
Построим графики уравнений (1) и (2) в системе координат Otomega.
График уравнения (1) — ромб, диагонали которого, равные 16 и 30, лежат соответственно на осях Ot и Oomega , а графиком уравнения (2) является семейство окружностей с центром в начале координат и радиусом r=2|a|.
Графики уравнений системы имеют ровно 4 общие точки, и следовательно система имеет ровно 4 решения тогда и только тогда, когда окружность либо вписана в ромб, либо её радиус удовлетворяет условию: 8<r<15.
В первом случае радиус окружности является высотой прямоугольного треугольника с катетами 8 и 15, откуда
r=2|a|=frac{8cdot 15}{sqrt {8^2 +15^2 }}=frac{120}{17} ,
|a|=frac{60}{17}=3frac9{17} , тогда a=pm3frac9{17}.
Во втором случае получаем 8<2|a|<15, откуда -7,5<a<-4 или 4<a<7,5.
Ответ
a in (-7,5; -4) cup left{pm3frac9{17} right} cup (4; 7,5).
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1225
Условие
Найдите все значения a>0, при каждом из которых система begin{cases} (|x|-3)^2 +(y-3)^2=4,\ (x+3)^2 +y^2=a^2 end{cases} имеет единственное решение.
Показать решение
Решение
Если x geqslant 0, то первое уравнение задаёт окружность phi _1 с центром в точке C_1(3; 3) радиуса 2, а если x<0, то оно задаёт окружность phi _2 с центром в точке C_2(-3; 3) того же радиуса.
При a>0 второе уравнение задаёт окружность phi с центром в точке C(-3; 0) радиуса a. Поэтому задача состоит в том, чтобы найти все значения параметра a, при каждом из которых окружность phi имеет единственную общую точку с объединением окружностей phi _1 и phi _2.
Из точки C проведём луч CC_1 и обозначим A_1 и B_1 точки его пересечения с окружностью phi _1, где A_1 лежит между C и C_1.
Так как CC_1=sqrt {6^2 +3^2 }=sqrt {45} =3sqrt 5, то CA_1=3sqrt 5-2, CB_1=3sqrt 5+2.
При a < CA_1 или a > CB_1 окружности phi и phi _1 касаются. При CA_1 < a < CB_1 окружности phi и phi _1 имеют 2 общие точки. При a=CA_1=3sqrt 5-2 или a=CB_1=3sqrt 5+2, окружности phi и phi _1 касаются.
Координаты точки касания окружностей phi и phi _2 явно видны на чертеже: это точки A_2(-3; 1) и B_2(-3; 5). То есть при a=1 и a=5 окружности phi и phi _2 касаются. При остальных значениях параметра a окружности phi и phi _2 либо имеют 2 общие точки, либо не имеют общих точек.
Исходная система имеет единственное решение тогда и только тогда, когда окружность phi касается ровно одной из двух окружностей phi _1 и phi _2 и не пересекается с другой.
Так как 1<3sqrt 5-2<5<3sqrt 5+2, то условию задачи удовлетворяют только числа a=1 и a=3sqrt 5+2.
Ответ
1; 3sqrt 5+2.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1224
Условие
Найдите все неотрицательные значения a, при каждом из которых система уравнений begin{cases} sqrt {(x-3)^2 +y^2 }+sqrt {x^2 +(y-a)^2 }=sqrt {a^2 +9}, \ y=|2-a^2 | end{cases} имеет единственное решение.
Показать решение
Решение
Рассмотрим первое уравнение системы. Выражение AB=sqrt {(x-3)^2 +y^2 } определяет расстояние между точками A(x; y) и B(3; 0). Аналогично выражение AC=sqrt {x^2+(y-a)^2 } определяет расстояние между точками A(x; y) и C(0; a), а выражение BC=sqrt {a^2 +9} определяет расстояние между точками B(3;0) и C(0; a).
По неравенству треугольника AB+AC geqslant BC, причём равенство достигается тогда и только тогда, когда точка A принадлежит отрезку BC. Это значит, что для координат точки A(x; y) справедливы неравенства: 0 leqslant x leqslant 3, 0 leqslant y leqslant a.
Тогда из второго уравнения системы имеем:
0leqslant |2-a^2 |leqslant a, |2-a^2 |leqslant a, -aleqslant 2-a^2 leqslant a,begin{cases} 2-a^2 geqslant -a,\2-a^2 leqslant a, end{cases} enspace begin{cases} a^2 -a-2leqslant 0,\a^2+a-2geqslant 0, end{cases} enspace begin{cases} -1leqslant aleqslant 2,\aleqslant -2, ageqslant 1, end{cases}enspace ain[1;2].
Итак, первое уравнение системы определяет на плоскости xOy отрезок с концами в точках B и C, не параллельный оси Ox; второе уравнение системы определяет прямую, параллельную оси Ox. При a in [1; 2] они имеют одну точку пересечения, то есть исходная система уравнений имеет единственное решение.
Ответ
[1; 2].
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1223
Условие
При каких значениях параметра a система begin{cases} x-sqrt 3|y|=0,\ (x-2a)^2+(y-cos pi a)^2 leqslant (5a-21)^2 end{cases} имеет ровно два решения?
Показать решение
Решение
Решим задачу графически. Если |5-2a|=0, то неравенство системы задаёт круг с центром в точке (2a; cos pi a) и радиусом |5a-21|. Если |5a-21|=0, то решением
неравенства будет единственная точка: x=2a=frac{42}5 , y=cos pi a=cos frac{21pi }5 , а тогда у системы не может быть более одного решения.
Уравнение системы задаёт угол, биссектрисой которого является ось Ox. Сторона этого угла проходит через точки (0; 0) и left(1; frac1{sqrt 3}right), и поэтому образует угол 30^{circ} с положительным направлением оси Ox.
Ровно два решения будет, если круг касается обеих сторон угла. Тогда центр круга должен лежать на биссектрисе угла, то есть на луче Ox. Следовательно, ордината центра круга должна равняться нулю, а абсцисса быть больше нуля. Ордината равна нулю, если cos pi a=0, pi a=frac pi 2+pi k, k in mathbb Z, a=frac12+k, k ∈ Z.
Абсцисса центра круга равна 2a и равна 2k+1, она больше нуля, если k geqslant 0. Рассмотрим triangle O_1OM , где O_1 — центр круга, M — одна из точек касания. Тогда O_1M=|5a-21|, OO_1=2a, angle O_1MO =90^{circ}, angle MOO_1 =30^{circ}. Тогда O_1M= O_1Ocdot sin angle O_1OM= 2asin 30^{circ}= a. Значит, a=|5a-21|, k+frac12= left|5k+frac52 -21right|, k+frac12=left|5k-frac{37}2 right|; отсюда либо k+frac12 =5k-frac{37}{2,} то есть 4k=19,, k=frac{19}4 ; либо k+frac12 =frac{37}2-5k,, 6k=18, k=3. k — целое число, frac{19}4 notin Z. 3in mathbb Z и 3geqslant 0. Таким образом, k=3, a=frac12+k=3,5.
Ответ
3,5
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1222
Условие
Найдите все значения параметра a, при каждом из которых уравнение frac{x^2+ax+2}2=sqrt {4x^2+ax+1} имеет ровно три различных корня.
Показать решение
Решение
Уравнение frac{x^2+ax+2}2=sqrt {4x^2+ax+1} при frac{x^2+ax+2}2<0 не имеет корней. При x^2+ax+2 geqslant 0 обе части уравнения можно возвести в квадрат.
(x^2+ax+2)^2 =4(4x^2+ax+1),
x^4+ax^3+2x^2+ax^3+a^2x^2,+ 2ax+2x^2+2ax+4= 16x^2+4ax+4,
x^4+2ax^3+x^2(a^2-12)=0,
x^2(x^2+2ax+a^2-12)=0,
x^2((x+a)^2-12) =0,
x_1=0, (x+a-sqrt {12})(x+a+sqrt {12})=0,
x_2=-a+sqrt {12},
x_3=-a-sqrt {12}.
Чтобы исходное уравнение имело три различных корня, необходимо, чтобы числа x_{1,} x_{2,} x_3 были различными и для каждого из этих чисел выполнялось условие x^2 +ax+2 geqslant 0.
x_2 neq 0 и x_3 neq 0, если a neq sqrt {12}=2sqrt 3 и a neq -sqrt {12}=-2sqrt 3.
Обозначим g(x)=x^2+ax+2. g(0)=2>0. Числа x_2=-a+2sqrt 3 и x_3=-a-2sqrt 3 будут корнями исходного уравнения, если выполняются условия:
begin{cases} g(x_2)geqslant 0,\g(x_3)geqslant 0; end{cases}enspace begin{cases} (-a+2sqrt 3)^2+a(-a+2sqrt 3)+2geqslant 0,\( -a-2sqrt 3)^2+a(-a-2sqrt 3)+2geqslant 0; end{cases}
begin{cases} -2asqrt 3+14geqslant 0,\2asqrt 3+14geqslant 0; end{cases}enspace begin{cases} aleqslant frac7{sqrt 3} ,\ageqslant -frac7{sqrt 3}. end{cases}
Таким образом, ainleft[-frac7{sqrt3};-2sqrt3right),cup (-2sqrt 3;2sqrt3),,,cup left( 2sqrt3;frac7{sqrt3}right].
Ответ
left[-frac7{sqrt3};-2sqrt3right),cup (-2sqrt3;2sqrt3),,,cup left(2sqrt3;frac7{sqrt3}right].
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1221
Условие
Найдите все значения a, при каждом из которых система уравнений begin{cases} frac{xy^2-5xy-5y+25}{sqrt {x+5}}=0, \ y=ax end{cases} имеет ровно два различных решения.
Показать решение
Решение
Решим задачу графически. Построим графики первого и второго уравнения и определим, сколько точек пересечения они имеют при различных значениях параметра.
Первое уравнение frac{xy^2-5xy-5y+25}{sqrt {x+5}}=0 параметра не содержит и представляет собой равенство дроби нулю. Это выполняется, если числитель равен нулю, а знаменатель не равен нулю, при этом оба выражения имеют смысл.
Запишем уравнение в виде frac{(y-5)(xy-5)}{sqrt {x+5}}=0, разложив числитель на множители. При x leqslant -5 левая часть не имеет смысла. При x>-5 уравнение задаёт прямую y=5 и гиперболу y=frac5x.
Найдём координаты точек A, B и C. B — точка пересечения прямой y=5 и гиперболы y=frac5x , чтобы найти её координаты, нужно решить систему уравнений begin{cases} y=5,\y=frac5x. end{cases}
Получаем B(1; 5).
У точек A и C абсцисса равна -5, ординаты находим из уравнений прямой и гиперболы. A(-5;5) и C(-5;-1).
При каждом значении a уравнение y=ax задаёт прямую с угловым коэффициентом a, проходящую через начало координат. Чтобы найти значение a, при котором такая прямая проходит через точку с указанными координатами, нужно подставить координаты в уравнение прямой.
Например, для точки A(-5; 5) получаем x=-5, y=5, 5=acdot (-5), a=-1.
Аналогично для B(1;5),, a=5 и для C(-5;-1), a=frac15.
При x>-5 прямая y=ax пересекает прямую y=5 при a<-1 и a>0, пересекает правую ветвь гиперболы y=frac5x при a>0, пересекает левую ветвь гиперболы y=frac5x при a>frac15. При этом прямая y=ax проходит через точку пересечения прямой y=5 и гиперболы y=frac5x при a=5.
Число решений исходной системы равно числу точек пересечения прямой y=5 и гиперболы y=frac5x с прямой y=ax при условии x>-5.
Таким образом, исходная система имеет ровно два решения при 0 < a leqslant 0,2; a=5.
Ответ
(0; 0,2]; {5}.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1220
Условие
Найдите все значения a, при каждом из которых уравнение frac{x-3a}{x+3}+frac{x-2}{x-a}=1 имеет единственный корень.
Показать решение
Решение
frac{(x-3a)(x-a)+(x+3)(x-2)-(x+3)(x-a)}{(x+3)(x-a)}=0,
frac{x^2-ax-3ax+3a^2+x^2+x-6-x^2+ax-3x+3a}{(x+3)(x-a)}=0,
frac{x^2-x(3a+2)+3a^2+3a-6}{(x+3)(x-a)}=0,
begin{cases} x^2-x(3a+2)+3a^2+3a-6=0,\(x+3)(x-a)neq 0 end{cases}
Решим уравнение x^2-x(3a+2)+3a^2+3a-6=0,
x_{1,2}=frac{(3a+2)pmsqrt {-3a^2+28}}2.
1. При D<0 уравнение корней не имеет.
2. При D=0,enspace -3a^2+28=0, a=pm 2sqrt frac73. Уравнение имеет единственный корень x =frac{3a+2}2 при a=pm 2 sqrt frac73.
Проверим условие x neq -3,, x neq a.
frac{3a+2}2 =-3, a=-frac83 neq pm2sqrt frac73 ,
frac{3a+2}2 =a, a=-2neq pm2sqrt frac73.
Значит, a=pm 2sqrt frac73 удовлетворяет условию.
3. При D>0 уравнение имеет два корня x_{1,2}=frac{(3a+2) pm sqrt {28-3a^2}}2. Проверим, при каких значениях a значения x=-3 и x=a являются корнями уравнения x^2-x(3a+2)+3a^2+3a-6=0.
При x=-3 должно выполняться равенство 9+3(3a+2)+3a^2+3a-6=0,
3a^2+12a+9=0, a^2+4a+3=0, a=-1, a=-3.
При x=a должно выполняться равенство a^2-2a+3a-6=0,
a^2+a-6=0, a_1=-3, a_2=2.
При a=-3, a=-1 и a=2 исходное уравнение имеет единственный корень.
Ответ
-3; −1; pm 2sqrt frac73 ; 2.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1019
Условие
При каких значениях параметра a система
begin{cases} 5|x|+12|y-2|=60, \ y^2-a^2=4(y-1)-x^2end{cases}
имеет ровно 4 решения?
Показать решение
Решение
Преобразуем второе уравнение системы, выделив полный квадрат y^2-4y+4=(y-2)^2.
begin{cases} 5|x|+12|y-2|=60, \ y^2-a^2=4(y-1)-x^2;end{cases} Leftrightarrow begin{cases}5|x|+12|y-2|=60, \ x^2+(y-2)^2=a^2. end{cases}
Сделав замену переменных t=y-2, получим систему
begin{cases} 5|x|+12|t|=60,enspace(1)\ x^2+t^2=a^2.enspace(2)end{cases}
При такой замене число решений новой и старой системы одинаково. Построим графики уравнений (1) и (2) в системе координат Oxt.
График уравнения (1) — ромб, диагнали которого, равные 24 и 10, лежат соответственно на осях Ox и Ot, а графиком уравнения (2) является семейство окружностей с центром в начале координат и радиусом r=|a|.
Графики уравнений системы имеют ровно 4 общие точки, и следовательно, система имеет ровно 4 решения тогда и только тогда, когда окружность либо вписана в ромб, либо её радиус удовлетворяет условию 5 < r < 12.
В первом случае радиус окружности является высотой прямоугольного треугольника с катетами 5 и 12, откуда
r=|a|=frac{5 cdot 12}{sqrt{5^2+12^2}}=frac{60}{13}=4frac{8}{13}, a=pm 4frac{8}{13}.
Во втором случае получаем 5 < |a| < 12, откуда -12 < a < -5 или 5 < a < 12.
Ответ
a in (-12;-5) cup left { pm 4frac{8}{13}right } cup (5;12).
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1018
Условие
Найдите все значения параметра a, при каждом из которых уравнение x^3+3x^2-xlog_{3}(a+1)+5=0 имеет единственное решение на отрезке [0;2]
Показать решение
Решение
Уравнение x^3+3x^2-xlog_{3}(a+1)+5=0 имеет единственное решение на отрезке [0;2], если графики функций y=x^3+3x^2 и y=xlog_{3}(a+1)-5 имеют единственную точку пересечения на отрезке [0;2].
Построим графики этих функций.
1) y=x^3+3x^2.
Найдём стационарные точки: y’=3x^2+6x=3x(x+2). y’=0 при x=0, x=-2
y(-2)=-8+3(-2)^2=-8+12=4, y(0)=0. Отсюда получаем график y=x^3+3x^2.
2) y=xlog_{3}(a+1)-5. Графиком функции является прямая, угловой коэффициент которой k=log_{3}(a+1). Прямая y=kx-5 проходит через точку (0;-5).
Найдём точку x_{0}, в которой прямая y=kx-5 является касательной к графику функции y=x^3+3x^2.
Уравнение касательной y=(x_{0}^3+3x_{0}^2)+(3x_{0}^2+6x_{0})(x-x_{0}) проходит через точку (0;-5), следовательно, -5=(x_{0}^3+3x_{0}^2)-x_{0}(3x_{0}^2+6x_{0}),
2x_{0}^3+3x_{0}^2-5=0. x_{0}=1 — точка касания.
2x_{0}^3+3x_{0}^2-5=(x_{0}-1)(2x_{0}^2+5x_{0}+5).
Других точек касания нет, так как уравнение 2x_{0}^2+5x_{0}+5=0 корней не имеет.
Если x=1, то y=4, тогда 4=k-5, откуда k=9.
Найдем значение k, при котором прямая y=kx-5 проходит через точку (2;20). 20=2k-5, k=12,5, y=12,5x-5.
Для k=9 и k > 12,5 графики функций y=x^3+3x^2 и y=kx-5 имеют на отрезке [0;2] единственную общую точку. Найдем значения параметра a.
log_{3}(a+1)=9, a+1=3^9, a=3^9-1.
log_{3}(a+1) > 12,5, a+1 > 3^{tfrac{25}{2}}. a > 3^{12,5}-1.
Итак, если a=3^9-1 или a > 3^{12,5}-1, то уравнение x^3+3x^2-xlog_{3}(a+1)+5=0 имеет единственное решение на отрезке [0;2].
Ответ
a=3^9-1,, a > 3^{12,5}-1
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928
Задача с параметром: прямая и окружности
Систему из двух окружностей пересекает прямая. Прямая меняет свой коэффициент наклона, и нужно найти все такие коэффициенты наклона этой прямой, чтобы пересечений с окружностями было бы три или более.
Задача. При каком значении параметра система имеет больше двух решений?
Раскроем модуль. Он будет сниматься с положительным знаком, если подмодульное выражение неотрицательно, и с отрицательным, если подмодульное выражение меньше 0:
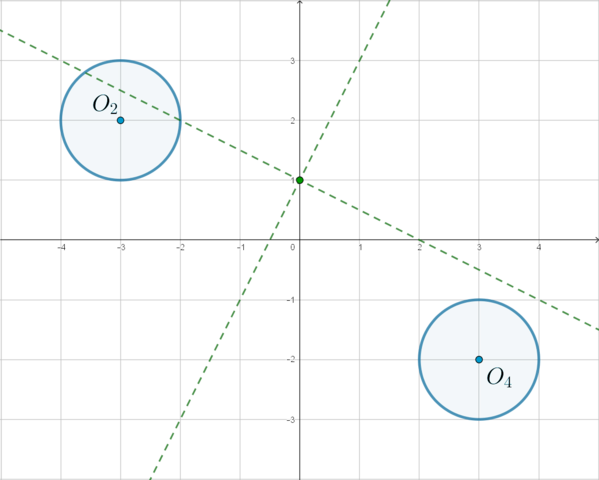
Таким образом, выделив полный квадрат, получили две окружности (вернее, их части). Одна из окружностей существует выше прямой , а вторая – ниже. Части наших окружностей стыкуются в точках с координатами O(0;0) и C(-2;-4) – это легко проверяется подстановкой.
Рисунок 1 — окружности и прямая разграничения
Окружности будет пересекать прямая. Что это за прямая и как она себя ведет, сразу не очевидно, и решила вопрос обычной подстановкой произвольно выбранного значения параметра. Выяснилось, что при любых обстоятельствах (любом параметре) коэффициент наклона меняется, а точка
— всегда принадлежит этой прямой, то есть прямая будет вращаться, и центр вращения – точка С. Это обстоятельство сразу облегчило мою задачу. Осталось определить такие коэффициенты наклона прямой, когда она пересечет систему из двух окружностей трижды.
Если прямая задана уравнением и проходит через точки
и
, то мы имеем два решения и это нас устраивать не может. Значение параметра при этом равно:
Методом неопределенных коэффициентов находим, что . На рисунке показaн случай, когда
, и пересечений по-прежнему 2.
Рисунок 2 — значение параметра равно 4
Так будет продолжаться вплоть до того момента, пока прямая не станет касательной к правой окружности, это будет соответствовать .
Продолжаем вращать нашу прямую против часовой стрелки. Начинаем с положения, когда она совпадает с осью — почти совпадает, имея, тем не менее, отрицательный коэффициент наклона – то есть стремится прижаться к оси слева – это соответствует коэффициенту наклона – и значению параметра – равным
. Продолжая вращать прямую вокруг точки
, понимаем, что три корня мы будем иметь при всех отрицательных коэффициентах наклона (на рисунке показано положение прямой для
и
), при коэффициенте, равном 0, то есть когда наша прямая параллельна оси
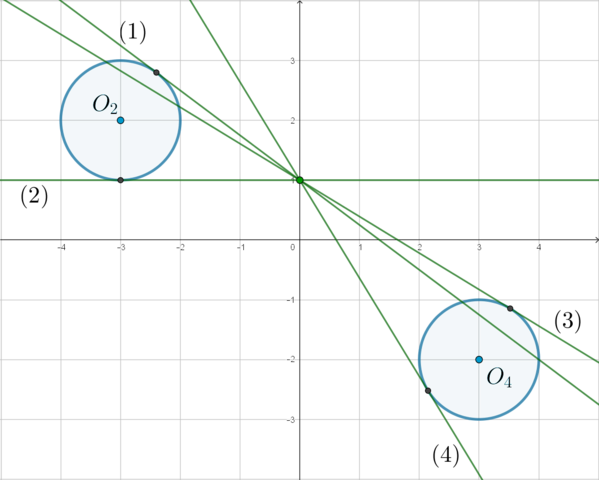
, и далее, при переходе значения параметра в положительную область значений – вплоть до момента, когда прямая не станет касательной к левой окружности.
Рисунок 3 — значение параметра равно -20
Рисунок 4 — значение параметра равно -2
Рисунок 5 — прямая стала касательной к левой окружности
Разберемся, какой коэффициент наклона будет у прямой, когда она станет касательной к левой окружности. Так как радиус обязан быть перпендикулярен нашей прямой, найдем коэффициент наклона прямой, проходящей через точки
и
, а потом воспользуемся свойством произведения коэффициентов наклона двух перпендикулярных прямых:
Итак, уравнение прямой:
Чтобы найти коэффициенты, подставим в него координаты точек и
:
Вычтем одно уравнение из другого:
Откуда
Тогда искомый коэффициент наклона будет равен:
При данном коэффициенте будем иметь два корня, поэтому в ответ эта точка уже не войдет.
Итак, мы изменяли наклон прямой, и коэффициент наклона принимал значения от — это ответ.
Ответ:

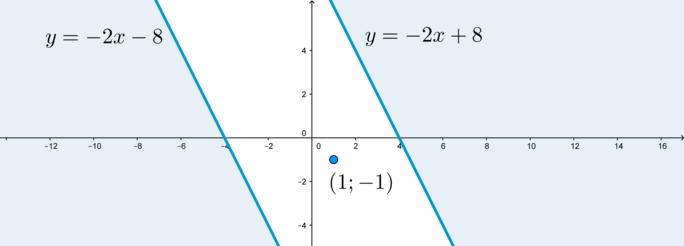
























.png)






