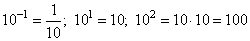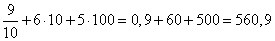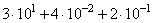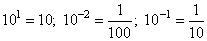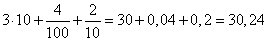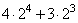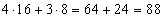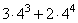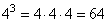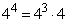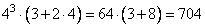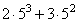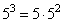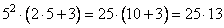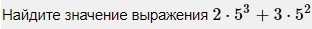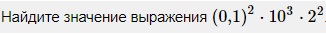Операции со степенями
[su_box title=”Описание задания” style=”soft” box_color=”#c1e8cc” title_color=”#0c0a0a”]
Во задании №2 ЕГЭ по математике необходимо продемонстрировать знания работы со степенными выражениями.
Тематика заданий: операции со степенями
Бал: 1 из 20
Сложность задания: ♦◊◊
Примерное время выполнения: 3 мин.
[/su_box]
Теория к заданию №2
Правила обращения со степенями можно представить следующим образом:
Кроме этого, следует напомнить об операциях с дробями:
Теперь можно перейти к разбору типовых вариантов! 🙂
Разбор типовых вариантов заданий №2 ЕГЭ по математике базового уровня
Во всех заданиях, аналогично первому заданию, нам необходимо найти значение выражения.
Вариант 2МБ1
Алгоритм выполнения:
- Представить число с отрицательным показателем в виде правильной дроби.
- Выполнить первое умножение.
- Представить степени чисел в виде простых чисел, заменив степени их умножением.
- Выполнить умножение.
- Выполнить сложение.
Решение:
Чтобы представить отрицательную степень числа в виде обыкновенной дроби, необходимо 1 разделить на это число, но уже в положительной степени.
То есть: 10-1 = 1/101 = 1/10
Выполним первое умножение, то есть умножение целого числа на правильную дробь. Для этого числитель дроби умножим на целое число, а знаменатель оставим без изменения.
9 · 1/10 = (9 · 1)/10 = 9/10
Первая степень числа всегда есть само число.
101 = 10
Вторая степень числа – это число умноженное само на себя.
102 = 10 · 10 = 100
Вычислим значение выражения, учитывая, что
получим:
Ответ: 560,9
Вариант 2МБ2
Алгоритм выполнения:
- Представить первую степень числа в виде целого числа.
- Представить отрицательные степени чисел в виде правильных дробей.
- Выполнить умножение целых чисел.
- Выполнить умножение целых чисел на правильные дроби.
- Выполнить сложение.
Решение:
Первая степень числа всегда есть само число. (101 = 10)
Чтобы представить отрицательную степень числа в виде обыкновенной дроби, необходимо 1 разделить на это число, но уже в положительной степени.
То есть:
10-1 = 1/101 = 1/10
10-2 = 1/102 = 1/(10 · 10) = 1/100
Выполним умножение целых чисел.
3 · 101 = 3 · 10 = 30
Выполним умножение целых чисел на правильные дроби.
4 · 10-2 = 4 · 1/100 = (4 ·1)/100 = 4/100
2 · 10-1 = 2 · 1/10 = (2 · 1)/10 = 2/10
Вычислим значение выражения, учитывая, что
получим:
Ответ: 30,24
Вариант 2МБ3
Алгоритм выполнения:
- Представить степени чисел в виде умножения и вычислить значение степеней чисел.
- Выполнить умножение.
- Выполнить сложение.
Решение:
Представим степени чисел в виде умножения. Для того чтобы представить степень числа в виде умножения, нужно это число умножить само на себя столько раз сколько содержится в показателе степени.
24 = 2 · 2 · 2 · 2 = 16
23 = 2 · 2 · 2 = 8
Выполним умножение:
4 · 24 = 4 · 16 = 64
3 · 23 = 3 · 8 = 24
Вычислим значение выражения:
Ответ: 88
Вариант 2МБ4
Алгоритм выполнения:
- Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.
- Вынести общий множитель за скобку.
- Выполнить действие в скобках.
- Представить степень числа в виде умножения и вычислить значение степени числа.
- Выполнить умножение.
Решение:
Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.
44 = 4 · 43
Вынесем общий множитель за скобку
3 · 43 + 2 · 44 = 43 · (3 + 2 · 4)
Выполним действие в скобках.
(3 + 2 · 4) = (3 + 
Представим степень числа в виде умножения. Для того чтобы представить степень числа в виде умножения, нужно это число умножить само на себя столько раз сколько содержится в показателе степени.
43 = 4 · 4 · 4 = 64
Вычислим значение выражения, учитывая, что
получим:
Ответ: 704
Вариант 2МБ5
Алгоритм выполнения:
- Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.
- Вынести общий множитель за скобку.
- Выполнить действие в скобках.
- Представить степень числа в виде умножения и вычислить значение степени числа.
- Выполнить умножение.
Решение:
Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.
53 = 5 · 52
Вынесем общий множитель за скобку
2 · 53 + 3 · 52 = 52 · (2 · 5 + 3)
Выполним действие в скобках.
(2 · 5 + 3) = (10 + 3) = 13
Представим степень числа в виде умножения. Для того чтобы представить степень числа в виде умножения, нужно это число умножить само на себя столько раз сколько содержится в показателе степени.
52 = 5 · 5 = 25
Вычислим значение выражения, учитывая, что
, а
получим:
Выполняем умножение в столбик, имеем:
Ответ: 325
Вариант 2МБ6
Решение:
В данном задании удобней привести значения к более привычному виду, а именно записать числа в числителе и знаменателе в стандартном виде:
После этого можно выполнить деление 24 на 6, в результате получим 4.
Десять в четвертой степени при делении на десять в третьей степени даст десять в первой, или просто десять, поэтому мы получим:
4 • 10 = 40
Ответ: 40
Вариант 2МБ6
Решение:
В данном случае мы должны заметить, что число 6 в знаменателе раскладывается на множители 2 и 3 в степени 5:
После этого можно выполнить сокращения степеней у двойки: 6-5=1, у тройки: 8-5=3.
Теперь возводим 3 в куб и умножаем на 2, получая 54.
Ответ: 54
Вариант 2МБ6
Алгоритм выполнения
- Применяем к числителю св-во степеней (ах)у=аху. Получаем 3–6.
- Применяем к дроби св-во степеней ax/ay=ax–y.
- Возводим 3 в полученную степень.
Решение:
(3–3)2 /3–8 = 3–6 /3–8= 3–6–(–8)) = 3–6+8 = 32 = 9
Ответ: 9
Вариант 2МБ7
Алгоритм выполнения
- Используем для степени в числителе (149) св-во (аb)х=ax·bx. 14 разложим на произведение 2 и 7. Получим произведение степеней с основаниями 2 и 7.
- Преобразуем выражение в 2 дроби, каждая из которых будет содержать степени с одинаковыми основаниями.
- Применяем к дробям св-во степеней ax/ay=ax–y.
- Находим полученное произведение.
Решение:
149 / 27·78 = (2·7)9 / 27·78 = 29·79 / 27 78 = 29–7·79–8 = 22·71 = 4·7 = 28
Ответ: 28
Вариант 2МБ8
Алгоритм выполнения
- Выносим за скобки общий множитель 52=25.
- Выполняем в скобках умножение чисел 2 и 5. Получаем 10.
- Выполняем в скобках сложение 10 и 3. Получаем 13.
- Выполняем умножение общего множителя 25 и 13.
Решение:
2·53+3·52 = 52·(2·5+3) = 25·(10+3) = 25·13 = 325
Ответ: 325
Вариант 2МБ9
Алгоритм выполнения
- Возводим в квадрат (–1). Получим 1, поскольку происходит возведение в четную степень.
- Возводим (–1) в 5-ю степень. Получим –1, т.к. происходит возведение в нечетную степень.
- Выполняем действия умножения.
- Получаем разность двух чисел. Находим ее.
Решение:
6·(–1)2+4·(–1)5 = 6·1+4·(–1) = 6+(–4) = 6–4 = 2
Ответ: 2
Вариант 2МБ10
Алгоритм выполнения
- Преобразуем множители 103 и 102 в целые числа.
- Находим произведения путем переноса десят.запятой вправо на соответствующее число знаков.
- Находим результирующую сумму.
Решение:
9,4·103+2,2·102 = 9,4·1000+2,2·100 = 9400+220 = 9620
Ответ: 9620
Вариант 2МБ11
Алгоритм выполнения
- Преобразуем 102 в целое число и выполняем умножение в числителе путем переноса деся.запятой.
- Преобразуем 10–2 в десят.дробь и выполняем умножение в знаменателе путем переноса десят.запятой влево.
- Домножаем числитель и знаменатель на 100, чтобы избавиться от десят.запятой в знаменателе.
- Находим результат путем деления числителя дроби на ее знаменатель.
Решение:
1,6·102 / 4·10–2 = 1,6·100 / 4·0,01 = 160/ 0,04 = 160·100 / 0,04·100 = 16000 / 4 = 4000
Ответ: 40000
Вариант 2МБ12
Алгоритм выполнения
- Применяем к дроби св-ва степеней ax·ay=ax+y и ax/ay=ax–y.
- Возводим 3 в полученную степень.
Решение:
3–10·35 / 3–7 = 3–10+5 /3–7 = 3–5 / 3–7 = 3–5–(–7)) = 3–5+7 = 32 = 9
Ответ: 9
Вариант 2МБ13
Алгоритм выполнения
- Представляем выражение в знаменателе как степень с основанием 8. Далее применяем св-во степеней (ах)у=аху, получаем 812.
- Применяем к дроби св-во степеней ax/ay=ax–y.
Решение:
813 /646 =813 / (82)6 =813 /812 = 813–12 = 81 = 8
Ответ: 8
Вариант 2МБ14
Алгоритм выполнения
- Преобразуем степени в числителе дроби и в делителе (число 92) так, чтобы получились степени с основанием 3.
- Используем св-во степеней (ах)у=аху для преобразованных степеней.
- Используем св-во степеней ax/ay=ax–y.
- Возводим 3 в полученную степень.
Решение:
274 /36 : 92 =(33)4 / 36 : (32)2 = 312/36 : 34 = 312–6–4 = 32 = 9
Ответ: 9
Вариант 2МБ15
Алгоритм выполнения
- Возводим каждый из множителей в соответствующую степень. Получим соответственно: 0,01, 1000, 4.
- Перемножаем 0,01 и 1000 путем переноса десят.запятой вправо на 3 знака. Получим 10.
- Умножаем 10 на 4.
Решение:
(0,1)2·103·22 = 0,01·1000·4 = 10·4 = 40
Ответ: 40
Даниил Романович | Просмотров: 18.6k
Найдите значения выражений
| 1 | 2cdot8^2+3cdot8^2 | Смотреть видеоразбор >> |
| 2 | frac{1,6cdot10^2}{4cdot10^{-2}} | Смотреть видеоразбор >> |
| 3 | frac{6^{-3}cdot6^7}{6^2} | Смотреть видеоразбор >> |
| 4 | frac{(4^{-4})^2}{4^{-10}} | Смотреть видеоразбор >> |
| 5 | frac{4^3}{2^5} | Смотреть видеоразбор >> |
| 6 | frac{2^4cdot6^6}{12^5} | Смотреть видеоразбор >> |
| 7 | 6cdot(-1)^2+4cdot(-1)^5 | Смотреть видеоразбор >> |
| 8 | (5cdot10^5 )cdot(1,7cdot10^{-3}) | Смотреть видеоразбор >> |
| 9 | frac{3^{-10}cdot3^5}{3^{-7}} | Смотреть видеоразбор >> |
| 10 | frac{3^{-13}}{(3^5)^{-3}} | Смотреть видеоразбор >> |
| 11 | frac{3^{10}}{27^3} | Смотреть видеоразбор >> |
| 12 | frac{4^{12}cdot2^7}{8^{10}} | Смотреть видеоразбор >> |
| 13 | 9cdot10^3+5cdot10^2+3cdot10^1 | Смотреть видеоразбор >> |
| 14 | (5,7cdot10^3):(1,9cdot10^{-2}) | Смотреть видеоразбор >> |
| 15 | frac{2^{-8}cdot2^8}{2^{-3}} | Смотреть видеоразбор >> |
| 16 | frac{5^{-2}cdot5^7}{5^3} | Смотреть видеоразбор >> |
| 17 | frac{9^{10}cdot3^2}{27^7} | Смотреть видеоразбор >> |
| 18 | 9,4cdot10^3+2,2cdot10^2 | Смотреть видеоразбор >> |
| 19 | (0,1)^2cdot10^3cdot2^2 | Смотреть видеоразбор >> |
| 20 | frac{2^5}{2^3cdot2^{-1}} | Смотреть видеоразбор >> |
| 21 | frac{4^{-2}cdot4^3}{4^{-1}} | Смотреть видеоразбор >> |
| 22 | frac{8^3}{2^4}:2^2 | Смотреть видеоразбор >> |
| 23 | 38cdot10-1,3cdot10^2 | Смотреть видеоразбор >> |
| 24 | frac{(0,1)^2}{10^{-3}}cdot10^2 | Смотреть видеоразбор >> |
| 25 | frac{2^7}{2^5cdot2} | Смотреть видеоразбор >> |
| 26 | frac{2^6cdot2^{-2}}{2^2} | Смотреть видеоразбор >> |
| 27 | frac{3^5cdot4^6}{12^5} | Смотреть видеоразбор >> |
Корни и степени
-
Степень с натуральным показателем
-
Степень с целым показателем
-
Кубический корень
-
Корень -ной степени
-
Сравнение арифметических корней
-
Как избавиться от иррациональности в знаменателе
-
Как упрощать иррациональные выражения, пользуясь формулами сокращенного умножения
Степенью называется выражение вида .
Здесь — основание степени,
— показатель степени.
к оглавлению ▴
Степень с натуральным показателем
Проще всего определяется степень с натуральным (то есть целым положительным) показателем.
По определению, .
Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.
.
Возвести число в куб — значит умножить его само на себя три раза.
.
Возвести число в натуральную степень — значит умножить его само на себя
раз:
к оглавлению ▴
Степень с целым показателем
Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным.
По определению,
.
Это верно для . Выражение 00 не определено.
Определим также, что такое степень с целым отрицательным показателем.
Конечно, все это верно для , поскольку на ноль делить нельзя.
Например,
Заметим, что при возведении в минус первую степень дробь переворачивается.
Показатель степени может быть не только целым, но и дробным, то есть рациональным числом. В статье «Числовые множества» мы говорили, что такое рациональные числа. Это числа, которые можно записать в виде дроби , где
— целое,
— натуральное.
Здесь нам понадобится новое понятие — корень -степени. Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.
Определение.
Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен
.
Согласно определению,
В школьной математике мы извлекаем корень только из неотрицательных чисел. Выражение для нас сейчас имеет смысл только при
.
Выражение всегда неотрицательно, т.е.
. Например,
.
Свойства арифметического квадратного корня:
Запомним важное правило:
По определению, 
к оглавлению ▴
Кубический корень
Аналогично, кубический корень из — это такое число, которое при возведении в третью степень дает число
.
Например, , так как
;
, так как
;
, так как
.
Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел.
Теперь мы можем дать определение корня -ной степени для любого целого
.
к оглавлению ▴
Корень  -ной степени
-ной степени
Корень -ной степени из числа
— это такое число, при возведении которого в
-ную степень получается число
.
Например,
Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел.
Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.
Итак, — такое число, что
. Оказывается, корни можно записывать в виде степеней с рациональным показателем. Это удобно.
По определению,
в общем случае .
Сразу договоримся, что основание степени больше 0.
Например,
Выражение по определению равно
.
При этом также выполняется условие, что больше 0.
Например,
Запомним правила действий со степенями:
— при перемножении степеней показатели складываются;
— при делении степени на степень показатели вычитаются;
— при возведении степени в степень показатели перемножаются;
Покажем, как применяются эти формулы в заданиях ЕГЭ по математике:
1.
Внесли все под общий корень, разложили на множители, сократили дробь и извлекли корень.
2.
3.
Здесь мы записали корни в виде степеней и использовали формулы действий со степенями.
4. Найдите значение выражения при
Решение:
При получим
Ответ: -0,5.
5. Найдите значение выражения при
Решение:
При a = 12 получим
Мы воспользовались свойствами степеней.
Ответ: 144.
6. Найдите значение выражения при b = — 5.
Решение:
При b = — 5 получим:
Ответ: -125.
7. Расположите в порядке возрастания:
Решение:
Запишем выражения как степени с положительным показателем и сравним.
Так как
то
Так как
то
Сравним и
для этого оценим их разность:
значит
Получим : поэтому
Ответ:
8. Представьте выражение в виде степени:
Решение:
Вынесем за скобку степень с меньшим показателем:
Ответ:
9. Упростите выражение:
Решение:
Приведем основания 6 и 12 к основаниям 2 и 3:
(выполним деление степеней с одинаковыми основаниями)
Ответ: 0,25.
10. Чему равно значение выражения при
?
Решение:
При получим
Ответ: 9.
к оглавлению ▴
Сравнение арифметических корней
11. Какое из чисел больше: или
?
Решение:
Возведем в квадрат оба числа (числа положительные):
Найдем разность полученных результатов:
так как
Значит, первое число больше второго.
Ответ:
к оглавлению ▴
Как избавиться от иррациональности в знаменателе
Если дана дробь вида то нужно умножить числитель и знаменатель дроби на
:
Тогда знаменатель станет рациональным.
Если дана дробь вида или
то нужно умножить числитель и знаменатель дроби на сопряженное выражение, чтобы получить в знаменателе разность квадратов.
Сопряженные выражения — это выражения, отличающиеся только знаками. Например,
и
и
— сопряженные выражения.
Пример:
12. Вот несколько примеров — как избавиться от иррациональности в знаменателе:
Пример 1.
Пример 2.
Пример 3.
Пример 4.
Совет. Если в знаменателе дана сумма двух корней, то в разности первым числом пишите то, которое больше, и тогда разность квадратов корней будет положительным числом.
Пример 5.
13. Сравните и
1)
2) Сравним и 14.
то и
а значит,
Ответ: меньше.
к оглавлению ▴
Как упрощать иррациональные выражения, пользуясь формулами сокращенного умножения
Покажем несколько примеров.
14. Упростите: выражения:
Пример 5.
т.к.
Пример 6.
Пример 7.
так как
Следующие несколько задач решаются с помощью формулы:
Решение:
Получим уравнение
Ответ:
19. Вычислите значение выражения:
Решение:
Ответ: 1.
20. Вычислите значение выражения:
Решение:
Ответ: 1.
21. Вычислите значение выражения: если
Решение.
Если то
следовательно
Ответ: — 1.
22. Вычислите:
Решение:
Ответ: 1.
Рассмотрим уравнение вида где
Это равенство выполняется, только если
Подробно об таких уравнениях — в статье «Показательные уравнения».
При решении уравнений такого вида мы пользуемся монотонностью показательной функции.
23. Решите уравнение:
а)
б)
в)
Решение.
23. Решите уравнение:
Решение:
тогда
Ответ: -1.
24. Решите уравнение:
Решение:
Ответ: 4.
25. Решите уравнение:
Решение:
Значит,
Ответ: -0,2.
Если вы хотите разобрать большее количество примеров — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Корни и степени» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
Во задании №2 ЕГЭ по математике необходимо продемонстрировать знания работы со степенными выражениями.
Тематика заданий: операции со степенями
Бал: 1 из 20
Сложность задания: ♦◊◊
Примерное время выполнения: 3 мин.
Теория к заданию №2
Правила обращения со степенями можно представить следующим образом:
Кроме этого, следует напомнить об операциях с дробями:
Теперь можно перейти к разбору типовых вариантов!
Разбор типовых вариантов заданий №2 ЕГЭ по математике базового уровня
Во всех заданиях, аналогично первому заданию, нам необходимо найти значение выражения.
Вариант 2МБ1
 Алгоритм выполнения:
Алгоритм выполнения:
- Представить число с отрицательным показателем в виде правильной дроби.
- Выполнить первое умножение.
- Представить степени чисел в виде простых чисел, заменив степени их умножением.
- Выполнить умножение.
- Выполнить сложение.
Решение:
Чтобы представить отрицательную степень числа в виде обыкновенной дроби, необходимо 1 разделить на это число, но уже в положительной степени.
То есть: 10-1 = 1/101 = 1/10
Выполним первое умножение, то есть умножение целого числа на правильную дробь. Для этого числитель дроби умножим на целое число, а знаменатель оставим без изменения.
9 · 1/10 = (9 · 1)/10 = 9/10
Первая степень числа всегда есть само число.
101 = 10
Вторая степень числа – это число умноженное само на себя.
102 = 10 · 10 = 100
Вычислим значение выражения, учитывая, что
получим:
Ответ: 560,9
Вариант 2МБ2
Алгоритм выполнения:
- Представить первую степень числа в виде целого числа.
- Представить отрицательные степени чисел в виде правильных дробей.
- Выполнить умножение целых чисел.
- Выполнить умножение целых чисел на правильные дроби.
- Выполнить сложение.
Решение:
Первая степень числа всегда есть само число. (101 = 10)
Чтобы представить отрицательную степень числа в виде обыкновенной дроби, необходимо 1 разделить на это число, но уже в положительной степени.
То есть:
10-1 = 1/101 = 1/10
10-2 = 1/102 = 1/(10 · 10) = 1/100
Выполним умножение целых чисел.
3 · 101 = 3 · 10 = 30
Выполним умножение целых чисел на правильные дроби.
4 · 10-2 = 4 · 1/100 = (4 ·1)/100 = 4/100
2 · 10-1 = 2 · 1/10 = (2 · 1)/10 = 2/10
Вычислим значение выражения, учитывая, что
получим:
Ответ: 30,24
Вариант 2МБ3
Алгоритм выполнения:
- Представить степени чисел в виде умножения и вычислить значение степеней чисел.
- Выполнить умножение.
- Выполнить сложение.
Решение:
Представим степени чисел в виде умножения. Для того чтобы представить степень числа в виде умножения, нужно это число умножить само на себя столько раз сколько содержится в показателе степени.
24 = 2 · 2 · 2 · 2 = 16
23 = 2 · 2 · 2 = 8
Выполним умножение:
4 · 24 = 4 · 16 = 64
3 · 23 = 3 · 8 = 24
Вычислим значение выражения:
Ответ: 88
Вариант 2МБ4
Алгоритм выполнения:
- Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.
- Вынести общий множитель за скобку.
- Выполнить действие в скобках.
- Представить степень числа в виде умножения и вычислить значение степени числа.
- Выполнить умножение.
Решение:
Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.
44 = 4 · 43
Вынесем общий множитель за скобку
3 · 43 + 2 · 44 = 43 · (3 + 2 · 4)
Выполним действие в скобках.
(3 + 2 · 4) = (3 + 
Представим степень числа в виде умножения. Для того чтобы представить степень числа в виде умножения, нужно это число умножить само на себя столько раз сколько содержится в показателе степени.
43 = 4 · 4 · 4 = 64
Вычислим значение выражения, учитывая, что
получим:
Ответ: 704
Вариант 2МБ5
Алгоритм выполнения:
- Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.
- Вынести общий множитель за скобку.
- Выполнить действие в скобках.
- Представить степень числа в виде умножения и вычислить значение степени числа.
- Выполнить умножение.
Решение:
Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.
53 = 5 · 52
Вынесем общий множитель за скобку
2 · 53 + 3 · 52 = 52 · (2 · 5 + 3)
Выполним действие в скобках.
(2 · 5 + 3) = (10 + 3) = 13
Представим степень числа в виде умножения. Для того чтобы представить степень числа в виде умножения, нужно это число умножить само на себя столько раз сколько содержится в показателе степени.
52 = 5 · 5 = 25
Вычислим значение выражения, учитывая, что
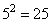
получим:
Выполняем умножение в столбик, имеем:
Ответ: 325
Вариант 2МБ6
Решение:
В данном задании удобней привести значения к более привычному виду, а именно записать числа в числителе и знаменателе в стандартном виде:
После этого можно выполнить деление 24 на 6, в результате получим 4.
Десять в четвертой степени при делении на десять в третьей степени даст десять в первой, или просто десять, поэтому мы получим:
4 • 10 = 40
Ответ: 40
Вариант 2МБ6
Решение:
В данном случае мы должны заметить, что число 6 в знаменателе раскладывается на множители 2 и 3 в степени 5:
После этого можно выполнить сокращения степеней у двойки: 6-5=1, у тройки: 8-5=3.
Теперь возводим 3 в куб и умножаем на 2, получая 54.
Ответ: 54
Вариант 2МБ6
Алгоритм выполнения
- Применяем к числителю св-во степеней (ах)у=аху. Получаем 3–6.
- Применяем к дроби св-во степеней ax/ay=ax–y.
- Возводим 3 в полученную степень.
Решение:
(3–3)2 /3–8 = 3–6 /3–8= 3–6–(–8)) = 3–6+8 = 32 = 9
Ответ: 9
Вариант 2МБ7
Алгоритм выполнения
- Используем для степени в числителе (149) св-во (аb)х=ax·bx. 14 разложим на произведение 2 и 7. Получим произведение степеней с основаниями 2 и 7.
- Преобразуем выражение в 2 дроби, каждая из которых будет содержать степени с одинаковыми основаниями.
- Применяем к дробям св-во степеней ax/ay=ax–y.
- Находим полученное произведение.
Решение:
149 / 27·78 = (2·7)9 / 27·78 = 29·79 / 27 78 = 29–7·79–8 = 22·71 = 4·7 = 28
Ответ: 28
Вариант 2МБ8
Алгоритм выполнения
- Выносим за скобки общий множитель 52=25.
- Выполняем в скобках умножение чисел 2 и 5. Получаем 10.
- Выполняем в скобках сложение 10 и 3. Получаем 13.
- Выполняем умножение общего множителя 25 и 13.
Решение:
2·53+3·52 = 52·(2·5+3) = 25·(10+3) = 25·13 = 325
Ответ: 325
Вариант 2МБ9
Алгоритм выполнения
- Возводим в квадрат (–1). Получим 1, поскольку происходит возведение в четную степень.
- Возводим (–1) в 5-ю степень. Получим –1, т.к. происходит возведение в нечетную степень.
- Выполняем действия умножения.
- Получаем разность двух чисел. Находим ее.
Решение:
6·(–1)2+4·(–1)5 = 6·1+4·(–1) = 6+(–4) = 6–4 = 2
Ответ: 2
Вариант 2МБ10
Алгоритм выполнения
- Преобразуем множители 103 и 102 в целые числа.
- Находим произведения путем переноса десят.запятой вправо на соответствующее число знаков.
- Находим результирующую сумму.
Решение:
9,4·103+2,2·102 = 9,4·1000+2,2·100 = 9400+220 = 9620
Ответ: 9620
Вариант 2МБ11
Алгоритм выполнения
- Преобразуем 102 в целое число и выполняем умножение в числителе путем переноса деся.запятой.
- Преобразуем 10–2 в десят.дробь и выполняем умножение в знаменателе путем переноса десят.запятой влево.
- Домножаем числитель и знаменатель на 100, чтобы избавиться от десят.запятой в знаменателе.
- Находим результат путем деления числителя дроби на ее знаменатель.
Решение:
1,6·102 / 4·10–2 = 1,6·100 / 4·0,01 = 160/ 0,04 = 160·100 / 0,04·100 = 16000 / 4 = 4000
Ответ: 40000
Вариант 2МБ12
Алгоритм выполнения
- Применяем к дроби св-ва степеней ax·ay=ax+y и ax/ay=ax–y.
- Возводим 3 в полученную степень.
Решение:
3–10·35 / 3–7 = 3–10+5 /3–7 = 3–5 / 3–7 = 3–5–(–7)) = 3–5+7 = 32 = 9
Ответ: 9
Вариант 2МБ13
Алгоритм выполнения
- Представляем выражение в знаменателе как степень с основанием 8. Далее применяем св-во степеней (ах)у=аху, получаем 812.
- Применяем к дроби св-во степеней ax/ay=ax–y.
Решение:
813 /646 =813 / (82)6 =813 /812 = 813–12 = 81 = 8
Ответ: 8
Вариант 2МБ14
Алгоритм выполнения
- Преобразуем степени в числителе дроби и в делителе (число 92) так, чтобы получились степени с основанием 3.
- Используем св-во степеней (ах)у=аху для преобразованных степеней.
- Используем св-во степеней ax/ay=ax–y.
- Возводим 3 в полученную степень.
Решение:
274 /36 : 92 =(33)4 / 36 : (32)2 = 312/36 : 34 = 312–6–4 = 32 = 9
Ответ: 9
Вариант 2МБ15
Алгоритм выполнения
- Возводим каждый из множителей в соответствующую степень. Получим соответственно: 0,01, 1000, 4.
- Перемножаем 0,01 и 1000 путем переноса десят.запятой вправо на 3 знака. Получим 10.
- Умножаем 10 на 4.
Решение:
(0,1)2·103·22 = 0,01·1000·4 = 10·4 = 40
Ответ: 40
Вариант 1 2. Вычисления. Действия со степенями.
1. Найдите значение выражения
2. Найдите значение выражения
3. Найдите значение выражения
4. Найдите значение выражения
5. Найдите значение выражения
6. Найдите значение выражения 4 · 72 + 6 · 72.
7.Найдите значение выражения .
8. Найдите значение выражения .
9. Найдите значение выражения 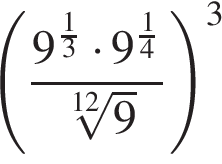
10.Найдите значение выражения .
Вариант 2 2. Вычисления. Действия со степенями.
1. Найдите значение выражения .
2. Найдите значение выражения .
3. Найдите значение выражения .
4. Найдите частное от деления на
.
5. Найдите значение выражения
6. Найдите значение выражения .
7.Найдите значение выражения
8. Найдите произведение чисел и
.
9. Найдите значение выражения
10. Найдите значение выражения
Вариант 3 2. Вычисления. Действия со степенями.
1. Найдите значение выражения .
2. Найдите значение выражения
3. Найдите значение выражения .
4. Найдите значение выражения
5. Найдите значение выражения .
6. Найдите значение выражения
7. Найдите значение выражения .
8. Найдите частное от деления 0,8 · 10−1 на 4 · 102.
9. Найдите значение выражения
10. Найдите значение выражения .
Вариант 4 2. Вычисления. Действия со степенями.
1. Найдите значение выражения .
2. Найдите значение выражения
3. Найдите значение выражения .
4. Найдите значение выражения
5. Найдите значение выражения .
6. Найдите значение выражения
7. Найдите значение выражения .
8. Найдите частное от деления 0,8 · 10−1 на 4 · 102.
9. Найдите значение выражения
10. Найдите значение выражения
Вариант 5 2. Вычисления. Действия со степенями.
1. Найдите значение выражения
2. Найдите сумму чисел и
3. Найдите значение выражения
4. Найдите произведение чисел и .
5. Найдите значение выражения .
6. Найдите значение выражения 3,4 · 102 + 1,8 · 103.
7. Найдите значение выражения
8. Найдите значение выражения .
9. Найдите значение выражения .
10. Найдите значение выражения
Вариант 6 2. Вычисления. Действия со степенями.
1. Найдите значение выражения .
2. Найдите значение выражения .
3. Найдите значение выражения 4 · 10-3 + 8 · 10-2 + 5 · 10-1.
4. Найдите значение выражения 3 · 101 + 5 · 102 + 9 · 103.
5. Найдите значение выражения
6. Найдите произведение чисел и
.
7. Найдите значение выражения
8. Найдите значение выражения .
9. Найдите значение выражения
10. Найдите значение выражения
Вариант 7 2. Вычисления. Действия со степенями.
1. Найдите значение выражения .
2. Найдите значение выражения
3. Найдите значение выражения (0,01)2 · 105 : 4−2
4. Найдите значение выражения .
5. Найдите значение выражения .
6. Найдите значение выражения:
7. Найдите значение выражения 3 · 43 + 2 · 43.
8. Найдите частное от деления на .
9. Найдите значение выражения
10. Найдите значение выражения
Вариант 8 2. Вычисления. Действия со степенями.
1. Найдите значение выражения
2. Найдите значение выражения
3. Найдите значение выражения .
4. Найдите значение выражения .
5. Найдите значение выражения .
6. Найдите значение выражения
7. Найдите значение выражения .
8. Найдите произведение чисел и .
9. Найдите значение выражения .
10. Найдите значение выражения
Вариант 9 2. Вычисления. Действия со степенями.
1. Найдите значение выражения .
2. Найдите значение выражения
3. Найдите значение выражения
4. Найдите значение выражения
5. Найдите значение выражения
6. Найдите значение выражения
7. Найдите значение выражения
8. Найдите значение выражения
9. Найдите значение выражения .
10. Найдите значение выражения .
Вариант 10 2. Вычисления. Действия со степенями.
1. Найдите значение выражения .
2. Найдите значение выражения .
3. Найдите значение выражения .
4. Найдите значение выражения .
5. Найдите значение выражения .
6. Найдите значение выражения 3,4 · 102 + 1,8 · 103.
7. Найдите произведение чисел и .
8. Найдите значение выражения 7,9 · 10-2 + 4,5 · 10-1.
9. Найдите значение выражения
10. Найдите значение выражения (0,01)2 · 105 : 4−2
|
2. Вычисления. Действия со степенями. |
||||
|
Вариант 1 1.300000 2. 0,25 3. 4560 4. 40 5. 280 6. 490 7. 32 8. 8 9. 27 10. 2 |
Вариант 2 1. 243 2. 121 3. 7 4. 5000 5. 0,25 6. 5 7.4 8. 0,0075 9. 0,5 10. 5 |
Вариант 3 1. 1 2. 5 3. 5 4. 9000 5. 7 6. 81 7. 15 8. 0,0002 9. 81 10. 2 |
Вариант 4 1. 1 2. 5 3. 5 4. 9000 5. 7 6. 81 7. 15 8. 0,0002 9. 81 10. 2 |
Вариант 5
|
|
Вариант 6
|
Вариант 7
10.40 |
Вариант 8
|
Вариант 9
|
Вариант 10
|
Инфоурок
›
Алгебра
›Другие методич. материалы›Карточки-тренажеры по теме «Степени» (подготовка к ЕГЭ)
Карточки-тренажеры по теме «Степени» (подготовка к ЕГЭ)
Скачать материал
Скачать материал


- Сейчас обучается 28 человек из 12 регионов


- Сейчас обучается 20 человек из 12 регионов


- Сейчас обучается 54 человека из 30 регионов


Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 154 790 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
-
«Алгебра и начала математического анализа. Базовый и углубленный уровни», Алимов А.Ш., Колягин Ю.М. и др.
Тема
§ 5. Степень с рациональным и действительным показателями
Больше материалов по этой теме
Другие материалы

Выражения: степени, корни (подготовка к ЕГЭ)
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (углублённый уровень)», Муравин Г.К., Муравина О.В.
- Тема: 5. Степенная функция у = хn при натуральном n
Рейтинг:
4 из 5
- 11.05.2018
- 50793
- 430

Презентация по математике «Степень числа»
- Учебник: «Алгебра и начала математического анализа. Базовый и углубленный уровни», Алимов А.Ш., Колягин Ю.М. и др.
- Тема: § 5. Степень с рациональным и действительным показателями
- 23.04.2018
- 1154
- 5


Кроссворд по математике по теме «Степень числа»
- Учебник: «Алгебра и начала математического анализа. Базовый и углубленный уровни», Алимов А.Ш., Колягин Ю.М. и др.
- Тема: § 5. Степень с рациональным и действительным показателями
Рейтинг:
3 из 5
- 19.03.2018
- 4940
- 29

Контрольная работа «Степени и корни»
- Учебник: «Алгебра и начала математического анализа. Базовый и углубленный уровни», Алимов А.Ш., Колягин Ю.М. и др.
- Тема: § 5. Степень с рациональным и действительным показателями
Рейтинг:
5 из 5
- 01.03.2018
- 6086
- 22


Подготовка к ОГЭ по теме «Степень»
- Учебник: «Алгебра и начала математического анализа. Базовый и углубленный уровни», Алимов А.Ш., Колягин Ю.М. и др.
- Тема: § 5. Степень с рациональным и действительным показателями
- 22.02.2018
- 489
- 4

Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Экскурсоведение: основы организации экскурсионной деятельности»
-
Курс профессиональной переподготовки «Логистика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Этика делового общения»
-
Курс профессиональной переподготовки «Организация менеджмента в туризме»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Организация маркетинга в туризме»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс повышения квалификации «Мировая экономика и международные экономические отношения»
-
Курс повышения квалификации «Актуальные вопросы банковской деятельности»
-
Курс профессиональной переподготовки «Эксплуатация и обслуживание общего имущества многоквартирного дома»
-
Скачать материал
-
04.10.2018
10033
-
DOCX
586.2 кбайт -
1298
скачиваний -
Рейтинг:
4 из 5 -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Катаева Наталия Ивановна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 5 лет и 1 месяц
- Подписчики: 0
- Всего просмотров: 15522
-
Всего материалов:
9



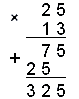
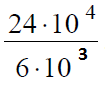
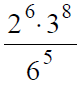
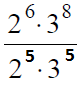
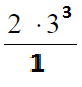





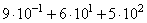 Алгоритм выполнения:
Алгоритм выполнения: