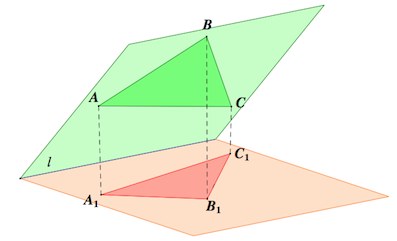
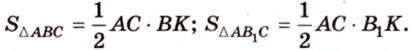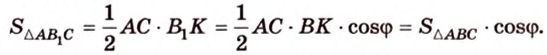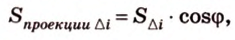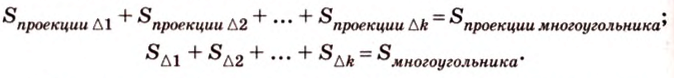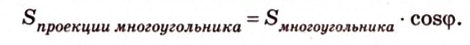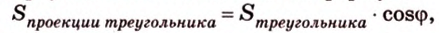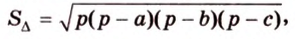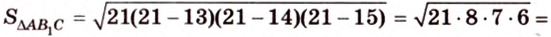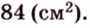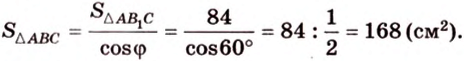22. C 2 № 485966. (Гущин) В правильной
четырехугольной призме высота равна
а сторона основания равна
Точка
— середина
ребра Найдите
расстояние от точки до плоскости
Решение.
Рассмотрим треугольную пирамиду Ее объем можно выразить двумя
способами:
1)
.
2) ,
где искомое
расстояние.
Приравняем выражения для объемов и выразим его:
Найдем площадь равнобедренного треугольника Проведем в нем высоту
.
.
Следовательно, искомое расстояние
Ответ:
C 2 № 504416. В правильной треугольной пирамиде SABC боковое ребро SA = 5, а сторона основания AB = 4. Найдите площадь сечения пирамиды
плоскостью, проходящей через ребро AB перпендикулярно ребру SC .
Решение.

высоту BK , тогда искомое сечение — треугольник ABK .
Пусть Q — площадь треугольника ABK . Сечение
из условия разбивает пирамиду на тетраэдры CAKB и SAKB .
Их суммарный объём
равен
объёму пирамиды.
Пусть — SO высота пирамиды. В треугольникеSCO имеем:
Объём пирамиды SABC равен
Приравнивая два найденных значения для объёма, получаем
Ответ: .
C 2 № 504437. В правильной
треугольной пирамиде SABC боковое ребро SA =
6, а сторона основания AB = 4. Найдите площадь сечения
пирамиды плоскостью, проходящей через ребро AB перпендикулярно
ребру SC .
Решение.

высоту BK, тогда искомое сечение — треугольник ABK.
Пусть Q — площадь треугольника ABK. Сечение
из условия разбивает пирамиду на тетраэдры CAKB и SAKB .
Их суммарный объём
равен
объёму пирамиды.
Пусть — SO высота пирамиды. В треугольникеSCO имеем:
Объём пирамиды SABC равен
Приравнивая два найденных значения для объёма, получаем
Ответ: .
ЕГЭ
2015. Математика. Тип. экзам. вар. 36 вар._
Ященко_2015 -272с
2 способ (метод проекций)
C 2 (Гушин) № 484562. В кубе найдите косинус
угла между плоскостями и
Решение.
Пусть точка — центр куба, а
— середина
а
— средняя линия треугольника
, поэтому
Треугольник
— равносторонний,
следовательно, искомый
угол равен углу
Примем длины ребер куба за . Найдем стороны треугольника
Из треугольника
находим
из равностороннего
треугольника находим
поскольку — середина диагонали
то
Теперь применим к треугольнику
теорему косинусов:
Ответ:
.
C 2 № 484565. В правильной четырехугольной пирамиде SABCD,
все ребра которой равны 1, найдите синус угла между плоскостью SAD и
плоскостью, проходящей через точку A перпендикулярно
прямой BD.
Решение.
Пусть точка — центр основания, а
— середина ребра
Поскольку
и
плоскость
перпендикулярна прямой
Это значит, что плоскость
и есть плоскость, проходящая
через точку перпендикулярно
Проведем отрезки и
Так как треугольник
правильный,
Так как треугольник
— равнобедренный,
Следовательно, искомый
угол равен углу Найдем
стороны треугольника
По теореме косинусов:
Отсюда
Ответ:
Примечание.
Решение существенно упрощается, если заметить, что треугольник — прямоугольный:
(2
способ )
треугольник
АОS проекция
треугольника ASD на плоскость АSС.
S AOS
= 1/2 AO · SO S AOS = 1/4
SH —высота боковой
грани
Воспользуемся
отношением 
Ответ:
10. C 2 № 500347. В правильной
треугольной призме стороны
основания равны 1, боковые ребра равны 2, точка — середина ребра
Найдите угол между
плоскостями и
Решение.

пересекает прямую
в точке
. Плоскости
и
пересекаются по прямой
. Из точки
опустим перпендикуляр
на прямую
, тогда отрезок
(проекция
) перпендикулярен прямой
. Угол
является линейным углом двугранного
угла, образованного плоскостями и
Точка —
середина ребра ,
поэтому .
Из равенства треугольников и
получаем:
В равнобедренном треугольнике угол
равен
,
высота
является биссектрисой, откуда
.
Из прямоугольного треугольника с прямым углом
получаем:
,
тогда .
Ответ может быть представлен и в другой форме:
Ответ:
C 2 № 500064. В правильной
треугольной призме стороны
основания равны 2, боковые ребра равны 3, точка — середина ребра
Найдите угол между
плоскостями и
Решение.
Прямая пересекает
прямую в
точке Плоскости
и
пересекаются по прямой
Из точки
опустим перпендикуляр
на прямую
тогда отрезок
(проекция
), по теореме о трех перпендикулярах,
перпендикулярен прямой Угол
является линейным углом двугранного
угла, образованного плоскостями и
Точка —
середина ребра поэтому
Из равенства треугольников и
получаем:
В равнобедренном треугольнике угол
равен
,
высота
является высотой и биссектрисой, откуда
Из прямоугольного треугольника с прямым углом
получаем:
,
тогда .
Ответ:
Замечание: Ответ
может быть представлен и в другой форме:
Использованные материалы:
ЕГЭ-2013. Решения заданий С2_Корянов А.Г,
Прокофьев А.А_2013 -102с
http://reshuege.ru/
ЕГЭ 2015. Математика. 50 вар. заданий_ред.
Ященко_2015 -248с
ЕГЭ 2015. Математика. Тип. экзам. вар. 36
вар._Ященко_2015 -272с
Всего: 9 1–9
Добавить в вариант
В правильной четырёхугольной призме ABCDA1B1C1D1 сторона основания AB равна 3, а боковое ребро На рёбрах AB, A1D1 и C1D1 отмечены точки M, N и K соответственно, причём AM = A1N = C1K = 1.
а) Пусть L — точка пересечения плоскости MNK с ребром BC. Докажите, что MNKL — квадрат.
б) Найдите площадь сечения призмы плоскостью MNK.
Источник: ЕГЭ по математике 28.03.2016. Досрочная волна, вариант 101
Источник: А. Ларин: Тренировочный вариант № 35.
Источник: А. Ларин: Тренировочный вариант № 255.
В прямоугольном параллелепипеде ABCDA1B1C1D1 AB = AA1 = 6, BC = 4. Точка P — середина ребра AB, точка M лежит на ребре DD1 так, что DM : D1D = 2 : 3.
а) Докажите, что прямая ВD1 параллельна плоскости MPC.
б) Найдите площадь сечения параллелепипеда плоскостью MPC.
Источник: А. Ларин: Тренировочный вариант № 162.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 на ребре CC1 отмечена точка М так, что СМ : С1М = 1 : 3. Плоскость АЕМ пересекает ребро ВВ1 в точке К.
А) Докажите, что ВК : В1К = 1 : 5.
Б) Найдите площадь сечения призмы плоскостью АЕМ, если АВ = 3, СС1 = 8.
Источник: А. Ларин: Тренировочный вариант № 171.
Сечением прямоугольного параллелепипеда ABCDA1B1C1D1 плоскостью α содержащей прямую BD1 и параллельной прямой AC, является ромб.
а) Докажите, что грань ABCD — квадрат.
б) Найдите угол между плоскостями α и BCC1, если AA1 = 6, AB = 4.
Источник: ЕГЭ по математике 31.03.2017. Досрочная волна.
В правильной треугольной пирамиде ABCD сторона основания ABC равна 12, В треугольнике ABD проведена биссектриса
а в треугольнике BCD проведены медиана
и высота
а) Найдите объем пирамиды
б) Найдите площадь проекции треугольника на плоскость ABC.
Источник: А. Ларин. Тренировочный вариант № 261.
Дан куб ABCDA1B1C1D1. Точка K — середина ребра C1D1.
а) Докажите, что расстояние от вершины A1 до прямой BK равно ребру куба.
б) Найдите угол между плоскостями KBA1 и BCC1.
Дан куб ABCDA1B1C1D1. Точка K — середина ребра C1D1.
а) Докажите, что расстояние от вершины A1 до прямой BK равно ребру куба.
б) Найдите угол между плоскостями KBA1 и ADD1.
Всего: 9 1–9
19
Фев 2014
Категория: Справочные материалы
Площадь ортогональной проекции многоугольника
2014-02-19
2014-02-19
Площадь ортогональной проекции многоугольника на плоскость равна площади проектируемого многоугольника, умноженной на косинус угла между плоскостью многоугольника и плоскостью проекций.
Докажем теорему для треугольника. Поскольку многоугольник разбивается на треугольники, сумма площадей которых есть площадь многоугольника, то и для многоугольника теорема будет верна.
Доказательство:
Пусть треугольник – проекция треугольника
на проецируемую плоскость.
Докажем, что
,
где – угол между плоскостями
Для этого разобьем треугольник на два треугольника c общей стороной
, параллельной прямой
пересечения плоскостей
. (Частный случай, когда одна из сторон треугольника
параллельна линии пересечения плоскостей
, можно рассмотреть отдельно (самостоятельно)).
Проекция треугольника – треугольник
. Причем
.
Пусть – перпендикуляр к
. Тогда по т. о трех перпендикулярах и
– перпендикуляр к
. Стало быть,
– угол между плоскостями треугольников (проецируемого и проекции).
Пусть – точка пересечения
и
,
– проекция т.
на плоскость
. Очевидно,
– высота треугольника
(
– высота треугольника
).
Из треугольника
Но и
Тогда
Имеем:
Аналогичные рассуждения – для пары треугольников и
:
(где – высота треугольника
,
– ее проекция)
Итак, суммируя площади треугольников и
соответственно, получаем
или
Что и требовалось доказать.
Пример.
Ребро куба равно 2 см. Через диагональ основания под углом к плоскости основания проведена плоскость, пересекающая боковое ребро. Найти площадь сечения.
Решение:
Пусть плоскость сечения проведена через диагональ и пересекает боковое ребро (
) в точке
.
По вышеуказанной теореме
где треугольник – проекция треугольника
на плоскость основания,
– угол между плоскостями
Ответ:
Применение теоремы можно также посмотреть, например, в этой задаче.
Автор: egeMax |
Нет комментариев
Печать страницы
Министерство образования и науки Республики Бурятии
МКУ «Закаменское районное управление образования»
МАОУ «Закаменская СОШ №1»
Ортогональная проекция при решении задач С2 ЕГЭ по математике
/ Исследовательская работа /
Выполнил: Анастасия Злягостева, ученица 11 класса
Руководитель: Зомонова Л.Г., учитель математики
Содержание
I.Введение…………………………………………………….…..………..2
§1. Основные понятия ортогональной проекции ……………….………4
1.1 Метод параллельного проецирования.
1.2 Ортогональное проектирование.
§2. Вычисление расстояний и углов……………………………………9
2.1 Расстояние между скрещивающимися прямыми .
2.2 Угол между скрещивающимися прямыми.
II.Заключение………………………………………………………….….15
III. Список используемой литературы………………………………….16
IV. Приложения……………………………………………………..…..17
Введение
Задача С2, или задача №14 ЕГЭ по математике часто вызывает затруднения у многих выпускников. Это связано с тем, что у большинства детей слабо развито пространственное воображение и, кроме этого, приобретенных умений и навыков в школе часто не хватает для решения таких задач.
Решению задач С2 посвящено большое количество учебно-методической литературы и имеется множество способов решения. В данной работе рассматривается решение задач на нахождение расстояния и угла между скрещивающимися прямыми с использованием ортогонального проектирования. Этот метод, в некоторых случаях является довольно рациональным, значительно упрощает решение и ведет к более быстрому получению ответа.
Мы постоянно встречаемся с различными способами проектирования (или, как еще говорят, проецирования) как в математике, так и в быту: оно применяется при изображении пространственных фигур на плоскости, в частности, при фотографировании и в кино; тени от предметов являются их проекциями; на проектировании основано введение координат как на плоскости, так и в пространстве, изготовление чертежей, планов и т.д.
На ортогональном проектировании основан такой важный для инженеров раздел прикладной математики, как начертательная геометрия, которая была создана знаменитым французским математиком Гаспаром Монжем (1746-1818). В ее основе лежит идея о том, что положение любой точки пространства можно задать ее ортогональными проекциями на две взаимно перпендикулярные плоскости.
Цель работы: изучить метод ортогонального проектирования и научиться применять его при решении задач на нахождения расстояния и угла между скрещивающимися прямыми.
Задачи:
- подобрать и изучить соответствующую литературу;
- изучить метод решения задач с помощью ортогональной проекции;
- применить на практике метод решения задач с помощью ортогональной проекции.
Объект исследования — задачи С2 (№14) ЕГЭ по математике профильного уровня.
Предмет исследования – метод ортогонального проектирования.
Методы исследования:
- изучение справочной и учебной литературы;
- анализ полученной информации;
- применение ортогональной проекции при решении задач на скрещивающиеся прямые.
§1. Основные понятия ортогональной проекции.
1.1. Метод параллельного проецирования.
В стереометрии изучаются пространственные фигуры, однако на чертеже они изображаются в виде плоских фигур. Каким же образом следует изображать пространственную фигуру на плоскости? Обычно в геометрии для этого используется параллельное проектирование.
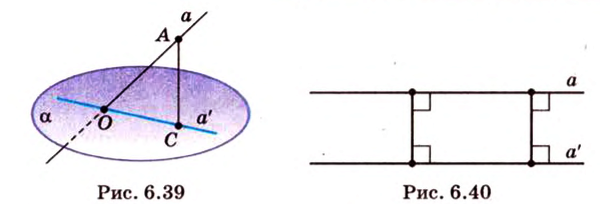
Пусть р — некоторая плоскость, l — пересекающая ее прямая (рис.1). Через произвольную точку А, не принадлежащую прямой l, проведем прямую, параллельную прямой l. Точка пересечения этой прямой с плоскостью р называется параллельной проекцией точки А на плоскость р в направлении прямой l. Обозначим ее А´. если точка А принадлежит прямой l, то параллельной проекцией А на плоскость р считается точка пересечения прямой l с плоскость р.
Таким образом, каждой точке А пространства сопоставляется ее проекция А´ на плоскость р. Это соответствие называется параллельным проектирование на плоскость р в направлении прямой l.
Пусть некоторая фигура в пространстве. Проекция ее точек на плоскость р образуют фигуру
´, которая называется параллельной проекцией фигуры
на плоскость р в направлении прямой l. Говорят также, что фигура Ф´ получена из фигуры Ф параллельным проектированием.
1.2.Ортогональное проектирование.
Определение. Ортогональное проектирование является частным случаем параллельного проектирования, при котором проектирующие прямые перпендикулярны к плоскости проекции, и обладает всеми свойствами параллельного проектирования.
Ортогональное проецирование обладает рядом преимуществ перед центральным и параллельным (косоугольным) проецированием.
Это:
— простота геометрических построений для определения ортогональных проекций точек;
— возможность при определенных условиях сохранить на проекциях форму и размеры проецируемой фигуры. При ортогональном проецировании если проецируемая фигура параллельна плоскости проекций, то ее проекция на данную плоскость не искажена или конгруэнтна проецируемой фигуре.
Определение 1.
Ортогональной проекцией точки на плоскость называют основание перпендикуляра, опущенного из этой точки на плоскость.
Рассмотрим рисунок 1, на котором изображены прямая p, перпендикулярная к плоскости α и пересекающая плоскость α в точке O.
Точка O является ортогональной проекцией на плоскость α каждой точки прямой p.
Замечание 1. Рассматриваемый в данном разделе случай ортогонального проектирования точки на плоскость α представляет собой частный случай более общего понятия проектирования точки на плоскость параллельно некоторой прямой, необязательно перпендикулярной к плоскости. Такое проектирование используется в нашем справочнике при определении понятия «призма».
Замечание 2. Если это не приводит к разночтениям, для упрощения формулировок термин «ортогональная проекция на плоскость» часто сокращают до термина «проекция на плоскость».
Определение 2. Проекцией фигуры a на плоскость α называют фигуру a’, образованную проекциями всех точек фигуры a на плоскость α.
Определение 3. Прямую, пересекающую плоскость и не являющуюся перпендикуляром к плоскости, называют наклонной к этой плоскости (рис. 2).
Все возможные случаи, возникающие при ортогональном проектировании прямой на плоскость представлены в следующей таблице:
|
Фигура |
Рисунок |
Свойство проекции |
|
Наклонная к плоскости α |
|
Если прямая PO пересекает плоскость α в точке O и является наклонной к плоскости α, а точка P’ является проекцией произвольной точки P этой прямой на плоскость α, то прямая P’O, лежащая в плоскости α, является проекцией прямой PO на плоскость α. |
|
Прямая, параллельная плоскости |
|
На рисунке прямая PO, где P – любая точка прямой a, является перпендикуляром к плоскости α. Если прямая a параллельна плоскости α, то проекцией прямой a является прямая a’, лежащая в плоскости α, параллельная прямой a и проходящая через основание O перпендикуляра PO. |
|
Прямая, лежащая на плоскости |
|
Если прямая a лежит в плоскости, то ее проекция a’, совпадает с прямой a. |
|
Прямая, перпендикулярная к плоскости |
|
Если прямая перпендикулярна плоскости α и пересекает плоскость α в точке O, то точка O и является проекцией этой прямой на плоскость α. |
§2. Вычисление расстояний и углов.
2.1. Расстояние между скрещивающимися прямыми.
Определение. Скрещивающиеся прямые – это непараллельные прямые линии, не лежащие в одной плоскости.
Расстояние между скрещивающимися прямыми равно расстоянию от точки, являющейся проекцией одной из данных прямых на перпендикулярную ей плоскость, до проекции другой прямой на эту же плоскость. Угол между второй прямой и указанной ей проекцией дополняет до 90⁰ угол между данными скрещивающимися прямыми.
Доказательство. Рассмотрим скрещивающиеся прямые a и b. Пусть плоскость α перпендикулярна прямой a и пересекает ее в точке А. Тогда а = А,
b=b´, b´
α (рис.1).
Пусть AH перепендикулярна b/. , что длина АН равна длине общего перпендикуляра данных скрещивающихся прямых. Т.к. , то Н – проекция некоторой точки Р прямой b и РН// a. В плоскости АНР проведем прямую PQ, параллельную прямой АН. Т.к. РН // a, то
Ясно, что HQ=AH. По теореме о трех перпендикулярах
перпендинулярна b. Т.к. PQ//AH, то PQ ┴a, PQ ┴b, то PQ – общий перпендикуляр двух скрещивающихся прямых. Угол НРВ является углом между скрещивающимися прямыми а и b и дополняет угол между прямыми b и b/ до 900. Что и требовалось доказать.
Для нахождения расстояния между скрещивающимися прямыми можно использовать следующий план:
- Найти плоскость, перпендикулярную одной из скрещивающихся прямых;
- Ортогонально спроектировать вторую прямую на эту плоскость;
- Из точки пересечения плоскости первой прямой опустить перпендикуляр на проекцию второй прямой;
Пример 1. Дан куб A…D1 с ребром a. Точка K — середина ребра BC. Найти расстояние между прямыми AC и C1K.
Решение: Проведем ортогональную плоскость (DD₁B₁), перпендикулярную пр. AC.
Построим проекции прямых AC и C₁K на орт.плоскость, пользуясь некоторыми свойствами . (Проекции пр.AC и ВD- т. О; пр. А₁С₁ и В₁С – т.О₁ пр.C₁К-О₁К₁).Расстояние от точки О до О₁К₁, то есть высота треугольника ОО₁К₁, опущенная на сторону О₁К₁, будет искомым расстояние h. Треугольник ОО₁К₁, — прямоугольный, в котором
следовательно,
Ответ:
Пример 2. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найти расстояние между прямыми AB и CB1.
Решение: В качестве ортогональной плоскости рассмотрим плоскость СС₁М, где М- середина АВ. Проекции: АВ на пл.(СС₁М) – т.М; СВ₁ — СР; МН – искомое расстояние , треугольник СМР- прямоугольный , поэтому
Ответ: .
2.2. Угол между скрещивающимися прямыми.
Угол между скрещивающимися прямыми – это угол между двумя пересекающимися прямыми которые соответственно параллельны заданным скрещивающимся прямым.
При решении задач на нахождение угла между скрещивающимися прямыми а и b в общем случае можно поступить следующим образом:
- Через одну из данных прямых, например через а, и через какую-нибудь точку W, взятую на другой прямой, проведем плоскость
.
- В плоскости
через точку W проведем прямую а₁
а. угол между прямыми а₁ и b равен искомому углу
(если угол
между прямыми 0
⁰.)
- Выбрав на прямой а₁ какую-нибудь точку К и на прямой b – точку L, получим треугольник WKL. Если этот треугольник не прямоугольный, то, подсчитав все его стороны. По теореме косинусов находим cosKWL. Понятно, что если cosKWL
, то угол острый, т.е cos
= cosKWL. Если же cosKWL
0, то угол KWL тупо, т.е .
= 180⁰— KWL. Но cos(180⁰-KWL) = — cosKWL. Таким образом, в этом случае cos
= cosKWL.
Пример 3. В основании пирамиды SABC лежит равносторонний треугольник ABC, длина стороны которого равна .Боковое ребро перпендикулярно
плоскости основания и имеет длину 2. Найти величину угла и расстояние между скрещивающимися прямыми, одна из которых проходит через точку S и середину ребра BC, а другая — через точку C и середину ребра AB.
Решение: Пусть D и E соответственно середины ребер АВ и СВ данной пирамиды. Спроектируем пирамиду на пл., перпендикулярную СD. При этом CD проектируется в точку D´, точка Е – в точку Е´, середину отрезка В´D´ .Очевидно,
Искомое расстояние равно расстоянию от точки D´ до прямой S´Е´, то есть равно высоте прямоугольного треугольника S´Е´D´, проведенной к гипотенузе S´Е´. Имеем :
Итак, искомое расстояние равно:
Поскольку SE ==
, то можем найти угол между прямыми SE и CD :
Итак, угол между прямыми SE и CD равен
Ответ:.
Заключение
В данной работе рассмотрен метод ортогонального проектирования и его применение при решении некоторых стереометрических задач на нахождение расстояния и угла между скрещивающимися прямыми, наиболее часто встречающихся во второй части ЕГЭ по математике профильного уровня. Своей распространенностью они обязаны тому, что вызывают наибольшие затруднения. Порой очень трудно развить пространственное воображение, но тщательно готовясь и используя некоторые упрощения можно достичь успеха. Изучив метод ортогональной проекции, и найдя ему обоснованное применение при решении задач по геометрии, мы с уверенностью можем сказать, что он определенно упрощает процесс представления и понимания условия, а следовательно и процесс решения, позволяет потратить меньшее количество времени, которое очень цениться в условиях экзамена.
Решая задачи указанного типа, наблюдаем, с одной стороны, абстрактный характер математических понятий, а с другой – большую эффективную их применимость к решениям стереометрических задач.
Изучение ортогональной проекции способствовало углублению и обогащению моих знаний. Задания №14 ЕГЭ по математике, ранее казавшиеся невероятно трудными, теперь не представляют для меня особой сложности. Я считаю, что выпускникам, стремящимся к отличному результату и высоким баллам необходимо изучить и освоить данный метод.
Список литературы
- http://fizmatinf.blogspot.ru/2013/12/blog-post_6943.html
- Василенко Е.А. Начертательная геометрия.- М.,1990.
- Гордон В.О.,Симинцев М.А.,Агневских М.А. Курс начертательной геометрии.-М.,1963.
- Сагателова Л. Задание С2: метод ортогонального проектирования// Математика. – 2012.- №4. – С. 18-22.
Приложение
Задача №1. Сторона основания правильной четырехугольной призмы равна 15, высота равно 20. Найти кратчайшее расстояние от стороны основания до не пересекающей ее диагонали призмы.
Решение:
Будем искать расстояние между АВ и и диагональю А₁С. Так как грань ВВ₁С₁С перпендикулярна АВ, то построим проекции АВ и А₁С на эту грань: Пр. (на пл. ВВ₁С₁С): АВ – т.А; А₁С- В₁С. Следовательно, расстояние от точки В до В₁С является искомым.
Рассмотрим выносной чертеж: ВН – перпендикуляр к В₁С и является искомым расстоянием. Так как треугольник ВВ₁С – прямоугольный, то
Ответ: 12
Задача №2. А…D₁ с ребром а. точка К – середина ребра ВС. Найти расстояние между прямыми АС и С₁К.
Решение:
Построим плоскость ВDD₁B₁, перпендикулярную прямой АС. Пусть т.О – проекция пр.ВD и АС, т.О₁— А₁С₁ и В₁ D₁, К₁ — принадлежит ВD и КК₁
параллельна АС. Тогда О- проекция прямой АС, О₁К₁ — проекция С₁К на плоскость D₁ В₁В. Следовательно, расстояние от точки О до О₁К₁, то есть высота треугольника О О₁К₁, опущенная на сторону О₁К₁, будет искомым расстоянием h. Треугольник ОО₁К₁, — прямоугольный, в котором
ОО₁ = а, ОК= , О₁К₁ =
Следовательно,
h = =
Ответ:
Задача №3. В правильной четырехугольной пирамиде со стороной основания а и боковым ребром найти расстояние и угол между апофемой и диагональю основания.
Решение: Пусть SADCD – данная пирамида, К- середина DC
Надо найти расстояние и угол между апофемой SК и диагональной основания АС. Плоскость SВD и перпендикулярна диагонали АС.
Следовательно, т.О – точка пересечения диагоналей АС и ВD- является проекцией диагонали АС на плоскость SВD. Проекцией апофемы SК будет прямая SК₁, где К₁ принадлежит ВD и КК₁ параллельно АС. Искомое расстояние будет равно высоте прямоугольного треугольника SОК₁, опущенной на гипотенузу SК₁. Из треугольника SОО₁ найдем:
Из треугольника SОК₁ найдем:
И
Угол между АС и SК = )=
Ответ:
Задача№4. Найти расстояние между скрещивающимися диагоналями соседних граней куба ребром1.
Решение: Способ1. Рассмотрим куб А…D₁.Найдем расстояние между прямыми А₁В и В₁
В качестве ортогональной плоскости рассмотрим плоскость АВ₁С₁, тогда проекции: А₁В –т.О, В₁ принадлежит АВ₁С₁, пр.СD₁ — т.О₁. искомое расстояние – высота ОН прямоугольного треугольника ОВ₁О₁:
Ответ: .
Задача №5. В основании пирамиды SABC лежит равносторонний треугольник ABC, длина стороны
которого равна .Боковое ребро перпендикулярно
плоскости основания и имеет длину 2. Найти величину угла и расстояние между скрещивающимися прямыми, одна из которых проходит через точку S и середину ребра BC, а другая — через точку C и середину ребра AB.
Решение:
Пусть D и E соответственно середины ребер АВ и СВ данной пирамиды. Спроектируем пирамиду на пл., перпендикулярную СD.
При этом CD проектируется в точку D´, точка Е – в точку Е´, середину отрезка В´D´
Очевидно, В´D´=,
S´D ´ А´В´ и S´D ´ = SC = 2.
Искомое расстояние равно расстоянию от точки D´ до прямой S´Е´, то есть равно высоте прямоугольного треугольника S´Е´D´, проведенной к гипотенузе S´Е´. Имеем :
Итак, искомое расстояние равно:
Поскольку SE = =
,
то можем найти угол между прямыми SE и CD :
Итак, угол между прямыми SE и CD равен
Ответ:.
Задача №6. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найти расстояние между прямыми AB и CB1.
Решение: В качестве ортогональной плоскости рассмотрим плоскость СС₁М, где М- середина АВ.
Проекции: АВ на пл.(СС₁М) – т.М; СВ₁ — СР;
МН – искомое расстояние , треугольник СМР- прямоугольный , поэтому
.
Ответ: .
Задача №7. Пример 7. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найти расстояние между прямыми SB и SD.
Решение:
В качестве ортогональной плоскости рассмотрим плоскость SMР, где М и Р – середины отрезков AD и ВС соответственно. Проекцией пр. AD (на пл. SMР) – т.М, SВ – пр. SР. Искомое расстояние – высота МН треугольника SMР.
Пусть НР=х, тогда для прямоугольных треугольников МРН и МSН имеем:
или
Решив уравнение =
,
Получаем: . Итак,
.
Ответ:.
Задача№8. К диагонали A1C куба A…D1 провели перпендикуляры из вершин A и B. Найти угол между этими перпендикулярами.
Решение: проведем плоскость так, чтобы
Проекция куба на плоскость — правильный шестиугольник А´В´С´D´ABCD. Перпендикуляры к А₁С параллельны плоскости
, поэтому угол между их проекциями равен искомому углу:
А
А₁´В = 60⁰.
Ответ: 60⁰
Задача №9.
Две противоположные вершины единичного куба совпадают с центрами оснований цилиндра, а остальные расположены на его боковой поверхности. Найти высоту и радиус основания этого цилиндра.
Решение: очевидно, что высота цилиндра равна диагонали куба, то сеть равна . Для определения радиуса цилиндра спроектируем всю конструкцию на плоскость основания цилиндра. Куб проектируется в правильный шестиугольник. Плоскость, проходящая через концы ребер куба, выходящих из одного из центров оснований цилиндра, параллельна основанию цилиндра, как например, плоскость АВ₁D₁ (AB₁D₁
А₁С).
Треугольник АВ₁D₁ — правильный, со стороной , его проекция будет правильным треугольником со стороной
, вписанным в основание цилиндра. Следовательно , радиус цилиндра равен R=
.
Ответ: ;
.
Преподаватель который помогает студентам и школьникам в учёбе.
Ортогональное проецирование — определение и вычисление с примерами решения
Ортогональное проецирование:
Параллельное проецирование, направление которого перпендикулярно плоскости проекции, называется ортогональным проецированием. Проекция фигуры, образующаяся при ортогональном проецировании, называется ортогональной проекцией, или просто проекцией этой фигуры.
Поскольку ортогональное проецирование является особым видом параллельного проецирования, то для него выполняются все свойства последнего. Ортогональной проекцией прямой
Отметим, что прямые, перпендикулярные одной из параллельных плоскостей, перпендикулярны и остальным, поэтому ортогональное проецирование на одну из таких плоскостей будет ортогональным и на остальные плоскости. Очевидно, что ортогональные проекции фигуры на параллельные плоскости равны между собой.
Ортогональное проецирование также имеет только ему присущие свойства. Одно из них выражает теорема о площади ортогональной проекции многоугольника.
Площадь ортогональной проекции
Теорема 5
Площадь ортогональной проекции произвольного многоугольника на плоскость равна произведению площади самого многоугольника на косинус угла между плоскостью многоугольника и плоскостью проекции.
Доказательство:
Как пример многоугольника возьмем 
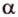
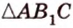
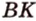
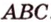
о трех перпендикулярах 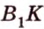
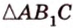
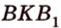
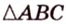
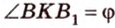
Учитывая, что 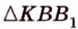
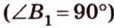
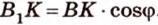
Итак, 
Чтобы доказать теорему для произвольного многоугольника, его разбивают на треугольники. Тогда для каждого треугольника и его проекции можно записать равенство
где 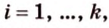
Получим в левой части равенства площадь проекции многоугольника, а в правой — площадь самого многоугольника, умноженную на косинус угла между их плоскостями. Отсюда
Т.е. и для этого случая теорема истинна.
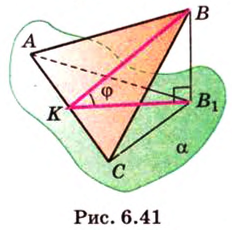
Пример:
Ортогональной проекцией треугольника является треугольник со сторонами 13 см, 14 см и 15 см. Плоскость треугольника образует с плоскостью проекции угол 60°. Вычислите площадь данного треугольника.
Решение:
Воспользуемся рисунком 6.41. Известно, что площадь проекции треугольника вычисляют по формуле:
где 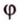
По формуле Герона найдем площадь 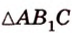
где 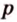
Тогда
Ответ: 168 см2.
- Декартовы координаты на плоскости
- Декартовы координаты в пространстве
- Геометрические преобразования в геометрии
- Планиметрия — формулы, определение и вычисление
- Параллельность прямых и плоскостей
- Перпендикулярность прямой и плоскости
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Перпендикулярность прямых и плоскостей в пространстве
1
Решение заданий С2 при подготовке к ЕГЭ 2014 г.
2
Применение ортогонального проекцирования
3
Задача 1. Условие: Изобразите сечение единичного куба A…D 1, проходящее через вершину D 1 и середины ребер AB; BC. Найти его S сеч.
4
K L M Решение: Ответ:
5
Задача 2. Условие: Изобразите сечение единичного куба A…D 1, проходящее через середины ребер AA 1, CC 1 и точку на ребре AB, отстоящую от вершины A на 0,75. Найдите его площадь.
6
Искомым сечением будет шестиугольник. Площадь его ортогональной проекции на плоскость ABC равна,косинус угла между плоскостью сечения и плоскостью ABC равен. Площадь сечения равна. Ответ:
7
Задача 3. Условие: В прямой призме ABCA 1 B 1 C 1 BK- биссектриса основания ABC. Через биссектрису и вершину А 1 проведена плоскость, составляющая с плоскостью основания 60°. Найти S сеч., если AB=3, BC=6, угол ABC=30°.
8
. AK=t; KC=2t. Ответ: 3.
9
Если ортогональная проекция на плоскость α переводит прямую a в точку A, а прямую b в прямую b 1, то расстояние между скрещивающимися прямыми a и b равно расстоянию от А до прямой b 1. Расстояние между скрещивающимися прямыми равно расстоянию от любой точки одной из этих прямых до плоскости, проходящей через вторую прямую параллельно первой прямой.
10
Задача 4. Условие: Дан правильный тетраэдр МАВС с ребром 1. Найдите расстояние между прямыми АL и МО, если L – середина МС, О – центр грани АВС. В С А M L 1 О Р Н Q
11
Решение: 1. LН (ABC), Н СО. 5. Вычислим ОQ. 2. СН = НО. Расстояние между скрещивающимися прямыми МО и АL равно расстоянию от точки О до прямой АН. ОQ- искомое расстояние. 4. ОQ АН, 3. Точка О и прямая АН – ортогональные проекции соответственно прямых МО и АL на (АВС). В С А M L 1 О Р Н Q
12
В С А M Ответ:. 1 О Р L Н Решение: Q
13
В правильной усеченной четырехугольной пирамиде A…D 1 со сторонами оснований а и b (a>b) и высотой h найти расстояние между диагональю BD 1 и диагональю большего основания AC. Задача 5. Условие:
14
15
В правильной четырехугольной пирамиде SАВСD, все ребра которой равны 1. Найдите угол между прямой DЕ, где Е — середина апофемы SF грани АSВ, и плоскостью АSC. А В С D S F Е Задача 6. Условие:
16
А В С D S F Введем прямоугольную систему координат. О Х У Z Н К Е Ответ:. направляющий вектор прямой DE.
17
Задача 7. Условие: В основании прямой призмы ABCDA1B1C1D1 лежит ABCD со стороной 21 и углом A, равным 60°. На ребрах AB, B1C1 и DC взяты соответственно точки E, F и G так, что AE=EB, B1F=FC1 и DG=3GC. Найти косинус угла между плоскостями EFG, если высота призмы равна 4,5. F E
18
1 способ решения:
19
Решение 2 (угол между прямой и плоскостью) F (ABC) F 1 -ортогональная проекция точки F на плоскость и основание BF 1 =F 1 C, FF 1 ll BB 1 G 1 -точка пересечения прямых EG и BC. Треугольник EF 1 G 1, лежащий в плоскости ABC,- ортогональная проекция треугольника EF 1 G 1, лежащего в плоскости EFG Из подобия треугольников EBG 1 и GCG 1 => EB ll GC, CG 1 =BC, т.к. GC=¼DC=½EB По теореме косинусов для треугольника EBF 1 : EF 1 ^2=EB^2+BF^2-2*EB*BF 1 *cos120°=63/4 EF=(37)/2 Из прямоугольных треугольников EFF 1 и F 1 FG 1 : EF^2=EF 1 ^2+F 1 F^2 =36 EF=6 FG 1 ^2=F1G1^2+F1F^2=270/4 FG 1 =(330)/2
20
По теореме косинусов для треугольника EBG 1 : EG 1 ^2=EB^2+BG^2-2*EB*BG 1 *cos120°=441/4 EG 1 =21/2 Используя теорему косинусов для треугольника EFG 1 : cos L EFG 1 =(EF^2+FG 1 ^2-EG 1 ^2)/(2*EF*FG 1 )=-3/(830) sin L EFG 1 =(1-(- 3/(830)^2=637/(810) Находим площадь треугольника EFG 1 S EFG1 =½*EF*FG1*sin L EFG 1 =((93)/16)*637 Находим площадь треугольника EF 1 G 1 : S EF1G1 =½*EF 1 *F 1 G 1 *sin150 °=(633)/16 Находим косинус угла Y между плоскостями EFG 1 и ABC по формуле: cos Y= S EF 1 G 1 /S EFG 1 =1/13 Ответ:1/13
21
Задача 8 Дана правильная четырехугольная пирамида MABCD, стороны основания которой равны 7. Угол между прямыми DM и AL, L- середина ребра MB, равен 60°.Найдите высоту пирамиды.
22
AB=BC=CD=AD=7 DM и AL скрещивающиеся прямые DM||OL в плоскости DMB OL||MD, так как OL-средняя линия треугольника BMD (по построению) L ALO=60° Докажем, что треугольник AOL- прямоугольный (AC BD, AC OM, тогда => AC (BMD) AC любой прямой, лежащей в этой плоскости, т.е. AC OL, треугольник AOL-прямоугольный, L AOL=90°, L LAD=30° tg L LAO=OL/OA=tg30 ° =3/3 OL/((7*2)/2)= 3/3 OL=((72)/2)* (3/3)=(76)/6 DM=2OL DM=2*((76)/6)=(76)/3 Треугольник OMD: OM=(DM^2-OD^2)= =(76)/6 Ответ: (76)/6
23
Задача 9 В правильной четырехугольной пирамиде PABCD с основанием ABCD точка M — середина ребра РA, точка K — середина ребра РB. Найдите расстояние от вершины A до плоскости CMK, если РC = 6, AB = 4.
24
МК — средняя линия треугольника АРВ МК || АВ=> АВ плоскости || сечения (по признаку параллельности прямой и плоскости) Расстояние L от точки А до сечения равно расстоянию от прямой АВ до сечения, L равно расстоянию от любой точки прямой АВ до сечения.
25
АН = НВ DMKC симметрична относительно HPT DT=TC Плоскость симметрии перпендикулярна плоскости сечения. Плоскость сечения проходит через прямую DC, которая перпендикулярна плоскости симметрии НРТ Плоскость симметрии перпендикулярна сечению и они пересекаются по прямой РТ.
26
По свойству перпендикулярных плоскостей перпендикуляр, опущенный из т. Н на сечение, попадает точно на прямую РТ, то есть найти нам надо длину именно этого перпендикуляра. Найдем высоту треугольника НРТ, проведённой к стороне РТ. X- искомое расстояние. Найдем через S: S=½*HT*PL*x
27
X- искомое расстояние. Найдем через S: S=(1/2)*HT*PL*x 1) PL = 0,5·РО, т.к. PL — ср. линия треугольника НРО. Найдём высоту пирамиды. В прямоугольном треугольнике PОС: PС = 6 и ОС = 0,5·АС = 0,5·42 = 22. По теореме Пифагора находим РО = =28 = 27. Значит, PL = 7. 2) НТ = ВС = АВ = 4. HL = 0,5·HO = 0,5·2 = 1, LT = HT — HL = = 3. 3) PT найдём по теореме Пифагора из треугольника PLT: PT = = 4. Теперь можно искать высоту х, проведённую к стороне РТ треугольника PTL: HT·PL = PT·x 4·7 = 4·x x = 7 Ответ: 7
28
Задача 10 В прямоугольном параллелепипеде A…D 1, AB=BC=102, AA1=27. Сечение параллелепипеда проходит через точки B и D и образует с плоскостью ABC угол. Найдите площадь сечения.
29
Сначала нам нужно построить это сечение. Очевидно, что отрезок принадлежит плоскости сечения и плоскости основания, то есть принадлежит линии пересечения плоскостей. Угол между двумя плоскостями – это угол между двумя перпендикулярами, которые проведены к линии пересечения плоскостей и лежат в этих плоскостях. BD AC. Пусть точка – точка пересечения диагоналей основания. – перпендикуляр к линии пересечения плоскостей, который лежит в плоскости основания:
30
Определим положение перпендикуляра, который лежит в плоскости сечения. (Помним, что если прямая перпендикулярна проекции наклонной, то она перпендикулярна и самой наклонной. Ищем наклонную по ее проекции (OC) и углу между проекцией и наклонной). Найдем тангенс угла COC 1 между OC 1 и OC : => между плоскостью сечения и плоскостью основания больше, чем между OC 1 и OC. То есть сечение расположено как-то так: K- точка пересечение OP и A 1 C 1. LM ll B 1 D 1.
31
Найдем проекцию сечения BLMD на плоскость основания. Для этого найдем проекции точек L и M. Четырехугольник BL 1 M 1 D– проекция сечения BLMD на плоскость основания. Найдем площадь четырехугольника BL 1 M 1 D. Для этого из площади треугольника BCD вычтем площадь треугольника L 1 CM 1 Найдем площадь треугольника L 1 CM 1. Треугольник L 1 CM 1 подобен треугольнику BCD. Найдем коэффициент подобия. Для этого рассмотрим треугольники OPC и OKK 1 : =>
32
S L1CM1 равен S BCD (отношение площадей подобных фигур равно квадрату коэффициента подобия). Тогда площадь четырехугольника BL 1 M 1 D равна площади треугольника BCD и равна: Найдем Ответ: 112
Презентация на тему «ортогональная проекция в задачахЕГЭ» 11 класс
-
Скачать презентацию (0.37 Мб)
-
1 загрузок -
0.0 оценка
Ваша оценка презентации
Оцените презентацию по шкале от 1 до 5 баллов
- 1
- 2
- 3
- 4
- 5
Комментарии
Добавить свой комментарий
Аннотация к презентации
Презентация для 11 класса на тему «ортогональная проекция в задачахЕГЭ» по математике. Состоит из 23 слайдов. Размер файла 0.37 Мб. Каталог презентаций в формате powerpoint. Можно бесплатно скачать материал к себе на компьютер или смотреть его онлайн с анимацией.
-
Формат
pptx (powerpoint)
-
Количество слайдов
23
-
Аудитория
-
Слова
-
Конспект
Отсутствует
Содержание
-
Слайд 1
Решение заданий С2 при подготовке к ЕГЭ 2014 г.
Презентацию подготовила:
Учитель по математике
высшей категории
МАОУ «Лицей №3 им. А. С. Пушкина»
Попова Н.Ф.г. Саратов,2014
-
Слайд 2
Задача 1. Условие:
Изобразите сечение единичного куба A…D1, проходящее через вершину D1 и середины ребер AB; BC. Найти его Sсеч.
-
Слайд 3
Решение:
K
L
MОтвет:
-
Слайд 4
Задача 2. Условие:
Изобразите сечение единичного куба A…D1, проходящее через середины ребер AA1, CC1 и точку на ребре AB, отстоящую от вершины A на 0,75. Найдите его площадь.
-
Слайд 5
Искомым сечением будет шестиугольник. Площадь его ортогональной проекции на плоскость ABC равна ,косинус угла между плоскостью сечения и плоскостью ABC равен . Площадь сечения равна .
Ответ:
-
Слайд 6
Задача 3. Условие:
В прямой призме ABCA1B1C1 BK-биссектриса основания ABC. Через биссектрису и вершину А1 проведена плоскость, составляющая с плоскостью основания 60°. Найти Sсеч., если AB=3, BC=6, угол ABC=30°.
-
Слайд 7
. AK=t; KC=2t.
Ответ: 3.
-
Слайд 8
Если ортогональная проекция на плоскость α переводит прямуюaв точку A, а прямую b в прямую b1, то расстояние между скрещивающимися прямыми a и bравно расстоянию от А до прямой b1.
Расстояние между скрещивающимися прямыми равно расстоянию от любой точки одной из этих прямых до плоскости, проходящей через вторую прямую параллельно первой прямой. -
Слайд 9
Задача 4. Условие:
Дан правильный тетраэдр МАВС с ребром 1. Найдите расстояние между прямыми АL и МО, если L – середина МС, О – центр грани АВС.
В
С
А
ML
1
О
РН
Q
-
Слайд 10
Решение:
LН(ABC), Н СО.
5. Вычислим ОQ.
2.СН = НО.
Расстояние между скрещивающимися прямыми МО и АL равно расстоянию от точки О до прямой АН.
ОQ- искомое расстояние.4. ОQ АН,
3. Точка О и прямая АН – ортогональные проекции соответственно прямых МО и АL на (АВС).В
С
А
ML
1
О
РН
Q
-
Слайд 11
В
С
А
MОтвет: .
1
О
Р
LН
Решение:
Q
-
Слайд 12
Задача 5. Условие:
В правильной усеченной четырехугольной пирамиде A…D1 со сторонами оснований а и b (a>b) и высотой h найти расстояние
между диагональю BD1 и диагональю большего основания AC. -
Слайд 13
-
Слайд 14
Задача 6. Условие:
В правильной четырехугольной пирамиде SАВСD, все ребра которой равны 1. Найдите угол между прямой DЕ, где Е — середина апофемы SF грани АSВ, и плоскостью АSC.
А
В
С
D
SF
Е
-
Слайд 15
А
В
С
D
SF
Введем прямоугольную систему координат.
О
Х
У
Z
НК
Е
Ответ: .
направляющий вектор прямой DE. -
Слайд 16
Задача 6. Условие:
В основании прямой призмы ABCDA1B1C1D1 лежит ABCD со стороной √21 и углом A, равным 60°. На ребрах AB, B1C1 и DC взяты соответственно точки E, F и G так, что AE=EB, B1F=FC1 и DG=3GC. Найти косинус угла между плоскостями EFG, если высота призмы равна 4,5.
-
Слайд 17
1 способ решения:
-
Слайд 18
Решение 1(угол между прямой и плоскостью)
F ⊥ (ABC)
F1-ортогональная проекция точки F на плоскость и основание
BF1=F1C, FF1ll BB1
G1-точка пересечения прямых EG и BC. Треугольник EF1G1, лежащий в плоскости ABC,- ортогональная проекция треугольника EF1G1, лежащего в плоскости EFG
Из подобия треугольников EBG1и GCG1=>EB ll GC, CG1=BC, т.к. GC=¼DC=½EB
По теореме косинусов для треугольника
EBF1:EF1^2=EB^2+BF^2-2*EB*BF1*cos120°=63/4
EF=(3√7)/2
Из прямоугольных треугольников EFF1
и F1FG1:EF^2=EF1^2+F1F^2 =36
EF=6
FG1^2=F1G1^2+F1F^2=270/4
FG1=(3√30)/2 -
Слайд 19
По теореме косинусов для треугольника EBG1:
EG1^2=EB^2+BG^2-2*EB*BG1*cos120°=441/4
EG1=21/2
Используя теорему косинусов для треугольника EFG1:
cosLEFG1=(EF^2+FG1^2-EG1^2)/(2*EF*FG1)=-3/(8√30)
sinLEFG1=√(1-(-3/(8√30)^2=√637/(8√10)
Находим площадь треугольника EFG1
SEFG1=½*EF*FG1*sinLEFG1=((9√3)/16)*√637
Находим площадь треугольника EF1G1:
SEF1G1=½*EF1*F1G1*sin150 °=(63√3)/16
Находим косинус угла Y между
плоскостями EFG1и ABC по формуле:
cos Y= SEF1G1/SEFG1=1/√13Ответ:1/√13
-
Слайд 20
-
Слайд 21
-
Слайд 22
-
Слайд 23
Посмотреть все слайды
Сообщить об ошибке
Похожие презентации










Спасибо, что оценили презентацию.
Мы будем благодарны если вы поможете сделать сайт лучше и оставите отзыв или предложение по улучшению.
Добавить отзыв о сайте