Основная волна егэ 2016 математика профиль - Помощь в подготовке к экзаменам и поступлению

ЕГЭ — 2016. Основная волна по математике 06.06.2016. Вариант 437. Юг

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Версия для печати и копирования в MS Word

В летнем лагере 164 ребёнка и 23 воспитателя. Автобус рассчитан не более чем на 45 пассажиров. Какое наименьшее количество автобусов понадобится, чтобы за один раз перевезти всех из лагеря в город?

Ответ:

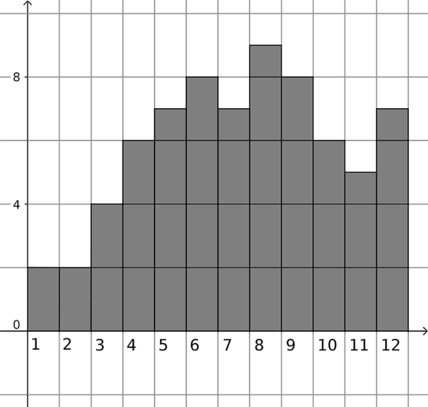
На диаграмме показана среднемесячная температура воздуха в Симферополе за каждый месяц 1988 года. По горизонтали указываются месяцы, по вертикали  — температура в градусах Цельсия. Определите по приведённой диаграмме, сколько месяцев среднемесячная температура превышала 20 градусов Цельсия.

Ответ:

На клетчатой бумаге с размером клетки 1×1 изображен параллелограмм. Найдите его площадь.

Ответ:

Научная конференция проводится в 4 дня. Всего запланировано 30 докладов: в первые два дня по 9 докладов, остальные распределены поровну между третьим и четвёртыми днями. На конференции планируется доклад профессора М. Порядок докладов определяется жеребьёвкой. Какова вероятность того, что доклад профессора М. окажется запланированным на последний день конференции?

Ответ:

Найдите корень уравнения

Ответ:

Отрезки AC и BD  — диаметры окружности с центром O. Угол AOD равен 66°. Найдите вписанный угол ACB. Ответ дайте в градусах.

Ответ:

На рисунке изображён график   — производной функции определённой на отрезке (−11; 2). Найдите абсциссу точки, в которой касательная к графику функции параллельна оси абсцисс или совпадает с ней.

Ответ:

Объём треугольной пирамиды равен 94. Через вершину пирамиды и среднюю линию её основания проведена плоскость (см. рис.). Найдите объём отсечённой треугольной пирамиды.

Ответ:

Найдите значение выражения

Ответ:

Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в кельвинах) от времени работы:где t  — время (в мин.), T₀  =  680 К, а  =  −16 К/мин², b  =  224 К/мин. Известно, что при температуре нагревательного элемента свыше 1400 К прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ дайте в минутах.

Ответ:

Имеется два сплава. Первый сплав содержит 5% меди, второй  — 14% меди. Масса второго сплава больше массы первого на 10 кг. Из этих двух сплавов получили третий сплав, содержащий 12% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

Ответ:

Найдите точку минимума функции

Ответ:

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащего отрезку

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

В правильной четырёхугольной пирамиде SABCD сторона AB основания равна 16, а высота пирамиды равна 4. На рёбрах AB, CD и AS отмечены точки M, N и K соответственно, причём AM  =  DN  =  4 и AK  =  3.

а)  Докажите, что плоскости MNK и SBC параллельны.

б)  Найдите расстояние от точки M до плоскости SBC.

Решите неравенство

В трапеции ABCD точка E  — середина основания AD, точка M  — середина боковой стороны AB. Отрезки CE и DM пересекаются в точке O.

а)  Докажите, что площади четырёхугольника AMOE и треугольника COD равны.

б)  Найдите, какую часть от площади трапеции составляет площадь четырёхугольника AMOE, если BC  =  3, AD  =  4.

В июле 2016 года планируется взять кредит в банке на четыре года в размере S млн рублей, где S  — целое число. Условия его возврата таковы:

— каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга;

— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.

Месяц и год	Июль 2016	Июль 2017	Июль 2018	Июль 2019	Июль 2020
Долг (в млн рублей)	S	0,8S	0,5S	0,1S	0

Найдите наибольшее значение S, при котором общая сумма выплат будет меньше 50 млн рублей.

Найдите все значение a, при каждом из которых уравнение

имеет ровно один корень.

На доске написано 10 неотрицательных чисел. За один ход стираются два числа, а вместо них записывается сумма, округлённая до целого числа (например, вместо 5,5 и 3 записывается 9, а вместо 3,3 и 5 записывается 8).

а)  Приведите пример 10 нецелых чисел и последовательности 9 ходов, после которых на доске будет записано число, равное сумме исходных чисел.

б)  Может ли после 9 ходов на доске быть написано число, отличающееся от суммы исходных чисел на 7?

в)  На какое наибольшее число могут отличаться числа, записанные на доске после 9 ходов, выполненных с одним и тем же набором исходных чисел в различном порядке?

Завершить тестирование, свериться с ответами, увидеть решения.

Источник

Подробные решения контрольных измерительных материалов Единого государственного экзамена по МАТЕМАТИКЕ от 06.06.2016. Профильный уровень. Основная волна

Условия КИМов реального ЕГЭ 2016 по математике (тип 1)
Часть 1

1. В квартире установлен прибор учёта расхода холодной воды (счётчик). Показания счётчика 1 сентября составляли 103 куб, м воды, а 1 октября — 114 куб. м. Сколько нужно заплатить за холодную воду за сентябрь, если стоимость 1 куб, м холодной воды составляет 19 руб. 20 коп.? Ответ дайте в рублях.
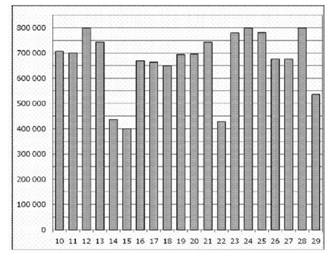
2. На диаграмме показано количество посетителей сайта РИА Новости во все дни с 10 по 29 ноября 2009 года. По горизонтали указываются дни месяца, по вертикали — количество посетителей сайта за данный день. Определите по диаграмме, во сколько раз наибольшее количество посетителей больше, чем наименьшее количество посетителей за день.

3. Найдите площадь треугольника, изображенного на рисунке.

4. В соревнованиях по толканию ядра участвуют 8 спортсменов из Великобритании, 6 спортсменов из Франции, 5 спортсменов из Германии и 5 — из Италии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется из Франции.
5. Наидите корень уравнения: $displaystyle 2^{4x-14}=frac{1}{64}$ .
6. В четырехугольник ABCD , периметр которого равен 48 вписана окружность, AB=15 . Найдите .

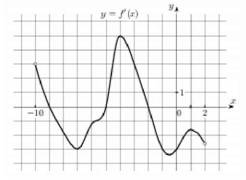
7. На рисунке изображён график displaystyle y=f'(x) производной функции displaystyle f(x) , определенной на интервале (-10; 2). Найдите количество точек, в которых касательная к графику функции параллельна прямой displaystyle y=-2x-11 или совпадает с ней.

8. Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.

Часть 2

9. Найдите значение выражений $displaystyle frac{log_{8}20}{log_{8}5}+log_{5}0,05$ .
10. Груз массой 0,8 кг колеблется на пружине. Его скорость displaystyle v меняется по закону $displaystyle v=v_{0}sin frac{2pi t}{T}$ . где displaystyle t — время с момента начала колебаний, displaystyle T=16 — период колебаний, $displaystyle v_{0}=0,5$ м/с. Кинетическая энергия (в джоулях) груза вычисляется по формуле $displaystyle E=frac{mv^{2}}{2}$ , где — масса груза в килограммах, — скорость груза в м/с.
Найдите кинетическую энергию груза через 10 секунд после начала колебаний. Ответ дайте в джоулях
11. Шесть одинаковых рубашек дешевле куртки на 2%. На сколько процентов девять таких же рубашек дороже куртки?
12. Найдите точку минимума функции $displaystyle y=2x-ln(x+8)^{2}.$

Тип 1

13. а) Решите уравнение $displaystyle 2log_{2}^{2}(2sin x)-7log_{2}(2sin x)+3=0.$
б) Укажите корни этого уравнения, принадлежащие отрезку $displaystyle left [ frac{pi }{2};2pi right ]$ .
14. В правильной треугольной призме $displaystyle ABCA_{1}B_{1}C_{1}$ сторона основания равна 6, а боковое ребро $displaystyle AA_{1}$ равно 3 . На ребре $displaystyle B_{1}C_{1}$ отмечена точка так, что $displaystyle B_{1}L=1$ . Точки и — середины ребер и $displaystyle A_{1}C_{1}$ соответственно. Плоскость displaystyle gamma параллельна прямой и содержит точки и .
а) Докажите, что прямая перпендикулярна плоскости ;
б) Найдите объем пирамиды, вершина которой — точка , а основание — сечение данной призмы плоскостью displaystyle gamma .
15. Решите неравенство: $displaystyle frac{49^{x}-6cdot 7^{x}+3}{7^{x}-5}+frac{6cdot 7^{x}-39}{7^{x}-7}leq 7^{x}+5.$
16. В трапеции ABCD боковая сторона перпендикулярна основаниям. Из точки на сторону опустили перпендикуляр . На стороне отмечена точка так, что прямые и перпендикулярны.
а) Докажите, что прямые и параллельны.
б) Найдите отношение BH:ED , если угол $displaystyle BCD=135^{circ}$ .
17. 15-го января планируется взять кредит в банке на сумму 1 млн рублей на 6 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на целое число процентов по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.

Найдите наименьшее значение , при котором общая сумма выплат будет составлять более 1,25 млн рублей.
18. Найдите все значения параметра , при каждом из которых уравнение
$displaystyle sqrt{15x^{2}+6ax+9}=x^{2}+ax+3$
имеет ровно три различных решения
19. На доске написаны числа 1, 2, 3, …,30. За один ход разрешается стереть произвольные три числа, сумма которых меньше 35 и отлична от каждой из сумм троек числа, стёртых на предыдущих ходах.
а) Приведите пример последовательности 5 ходов, б (Можно ли сделать 10 ходов?
в) Какое наибольшее число ходов можно сделать?

Подробные решения КИМов ЕГЭ №№1-12 и №№13-19(тип 1)

Условия КИМов основного ЕГЭ 2016 по математике (тип 2)

13. а) Решите уравнение $displaystyle 2cos ^{2}x+1=2sqrt{2}cos left ( frac{3pi }{2}-x right ).$
б) Укажите корни этого уравнения, принадлежащие промежутку $displaystyle left [ frac{3pi }{2};7pi right ].$
14. В правильной четырехугольной пирамиде SABCD сторона основания равна 16, а высота равна 4. На ребрах AB, CD и отмечены точки M, N и соответственно, причем AM=DN=4 и AK=3 .
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки до плоскости SBC .
15. Решите неравенство $displaystyle frac{4^{x}-2^{x+3}+7}{4^{x}-5cdot 2^{x}+4}leq frac{2^{x}-9}{2^{x}-4}+frac{1}{2^{x}-6}.$
16. В трапеции ABCD точка — середина основания , точка — середина боковой стороны . Отрезки и пересекаются в точке .
а) Докажите, что площади четырехугольника AMOE и треугольника COD равны
б) Найдите, какую часть от площади трапеции составляет площадь четырехугольника AMOE , если BC=3, AD=4.
17. В июле 2016 года планируется взять кредит в банке на млн рублей, где — целое число, на 4 года. Условия его возврата таковы:
— каждый январь долг возрастает на 15% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей

Найдите наибольшее значение , чтобы общая сумма выплат была меньше 50 млн рублей?
18. Найдите все значения , при каждом из которых уравнение $displaystyle frac{x-2a}{x+2}+frac{x-1}{x-a}=1$
имеет единственный корень.
19. На доске написаны числа 2 и 3. За один ход разрешено заменить написанные на доске числа и числами 2a-1 и a+b (например, из чисел 2 и 3 можно получить либо 3 и 5, либо 5 и 5).
а) Может ли после нескольких ходов на доска появиться число 19?
б) может ли через 100 ходов на доске быть написано число 200?
в) укажите наименьшую разность чисел через 1007 ходов.

Условия КИМов основного ЕГЭ 2016 по математике (тип 3)

13. а) Решите уравнение $displaystyle 2log_{3}^{2}(2cos x)-5log_{3}(2cos x)+2=0.$
б) Укажите корни этого уравнения, принадлежащие промежутку $displaystyle left [ pi ;frac{5pi }{2} right ].$
14. В правильной треугольной призме $displaystyle ABCA_{1}B_{1}C_{1}$ сторона основания равна 6, а боковое ребро $displaystyle AA_{1}$ равно 3. На ребре отмечена точка так, что AK=1 . Точки и — середины ребер $displaystyle A_{1}C_{1}$ и $displaystyle B_{1}C_{1}$ соответственно. Плоскость у параллельна прямой и содержит точки и .
а) Докажите, что прямая перпендикулярна плоскости displaystyle gamma .
б) Найдите расстояние от точки до плоскости .
15. Решите неравенство $displaystyle frac{25^{x}-5^{x+2}+26}{5^{x}-1}+frac{25^{x}+7cdot 5^{x}+1}{5^{x}-7}leq 2cdot 5^{x}-24.$
16. В треугольнике ABC проведены высоты и . На них из точек и опущены перпендикуляры и соответственно
а) Докажите, что прямые и параллельны.
б) Найдите отношение EH:AC , если угол ABC равен $displaystyle 30^{circ}$ .
17. 15-го января планируется взять кредит в банке на 1 млн рублей на 6 месяцев. Условия его возврата таковы:
-1-го числа каждого месяца долг возрастает на целое число процентов по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей

Найдите наибольшее значение , при котором общая сумма выплат будет составлять менее 1,2 млн. рублей.
18. Найдите все значения , при каждом из которых уравнение
$displaystyle sqrt{x^{4}-x^{2}+a^{2}}=x^{2}+x-a$
имеет ровно три различных решения.

Подробные решения КИМов ЕГЭ №№13-19(тип 2 и 3)

Условия КИМов основного ЕГЭ 2016 по математике (тип 4)

13. а) Решите уравнение $displaystyle 2cos 2x=4sin left ( frac{pi }{2}+x right )+1.$
б) Укажите корни этого уравнения, принадлежащие промежутку $displaystyle left [ -frac{5pi }{2};-pi right ].$
14. В правильной треугольной пирамиде SABC сторона основания равна 12, а высота равна 1. На ребрах AB,AC и отмечены точки M,N и соответственно, причем AM=AN=3 и $displaystyle AK=frac{7}{4}.$
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки до плоскости SBC .
15. Решите неравенство $displaystyle frac{9^{x+frac{1}{2}}-4cdot 3^{x}+5}{9^{x+frac{1}{2}}-4cdot 3^{x}+1}+frac{5cdot 3^{x}-19}{3^{x}-4}leq frac{2cdot 3^{x+2}-12}{3^{x+1}-1}$ .
16. Один из двух отрезков, соединяющих середины противоположных сторон четырехугольника, делит его площадь пополам, а другой в отношении 11:17
а) Докажите, что данный четырехугольник — трапеция
б) Найдите отношение оснований этой трапеции
17. В июле 2016 года планируется взять кредит в банке на млн рублей, где — целое число, на 4 года. Условия его возврата таковы:
— каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей

Найдите наименьшее значение , чтобы общая сумма выплат была больше 10 млн рублей?
18. Найдите все значения , при каждом из которых уравнение
$displaystyle frac{x^{3}+x^{2}-9a^{2}x-2x+a}{x^{3}-9a^{2}x}=1$
имеет единственный корень.

Подробные решения КИМов ЕГЭ №№13-19(тип 4)

Источник

Все варианты 2016 из открытых источников в интернете.

Досрочный период

Все предметы → от фипи.
Математика → 1 вариант профильного уровня.
Русский язык → 3 текста (задание 25).
Физика → задания 28-32.

Основной период

Математика (6 июня) → несколько вариантов второй части + 1 первая.
Математика (28 июня) → вторая часть.

Варианты 2015, 2014, 2013.

Источник

Категория: ЕГЭ (диагностич. работы)

Решения отдельных заданий ЕГЭ по математике от 6 июня 2016 года

Задания вариантов можно найти здесь и здесь.

13.1.

а) Решите уравнение:

б) Укажите корни этого уравнения, принадлежащие отрезку $[frac{pi}{2};2pi].$

Решение: + показать

14.1. В правильной треугольной призме сторона основания равна , а боковое ребро равно . На ребре отмечена точка так, что . Точки и – середины ребер и соответственно. Плоскость параллельна прямой и содержит точки и .
а) Докажите, что прямая перпендикулярна плоскости .

б) Найдите расстояние от точки до плоскости

Решение: + показать

15.1. Решите неравенство:

$frac{25^x-5^{x+2}+26}{5^x-1}+frac{25^x-7cdot 5^{x}+1}{5^x-7}leq 2cdot 5^x-24.$

Решение: + показать

16.1. В трапеции боковая сторона перпендикулярна основаниям. Из точки на сторону опустили перпендикуляр . На стороне отмечена точка так, что прямые и перпендикулярны.
а) Докажите, что прямые и параллельны.

б) Найдите отношение если угол равен $135^{circ}.$

Решение: + показать

16.2. В треугольнике проведены высоты и . На них из точек и опущены

перпендикуляры
а) Докажите, что прямые и параллельны.
б) Найдите отношение , если угол равен $30^{circ}.$

Решение: + показать

16.3. В трапеции точка – середина основания , точка – середина боковой стороны . Отрезки и пересекаются в точке .
а) Докажите, что площади четырёхугольника и треугольника равны.
б) Найдите, какую часть от площади трапеции составляет площадь четырёхугольника , если

Решение: + показать

17.1. 15‐го января планируется взять кредит в банке на сумму млн рублей на месяцев. Условия его возврата таковы:
‐ 1‐го числа каждого месяца долг возрастает на целое число процентов по сравнению с концом предыдущего месяца;

‐ со 2‐го по 14‐е число каждого месяца необходимо выплатить часть долга;
‐ 15‐го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.

Найдите наименьшее значение , при котором общая сумма выплат будет составлять более млн. рублей.

Решение: + показать

18.1. Определите, при каких значениях параметра уравнение

$sqrt{2^x-a}+frac{a-2}{sqrt{2^x-a}}=1$

имеет ровно два различных решения.

Решение: + показать

18.2. Определите, при каких значениях параметра уравнение

$sqrt{15x^2+6ax+9}=x^2+ax+3$

имеет ровно три различных решения.

Решение: + показать

18.3. Определите, при каких значениях параметра уравнение

$frac{x-2a}{x+2}+frac{x-1}{x-a}=1$

имеет ровно один корень.

Решение: + показать

18.4. Определите, при каких значениях параметра система уравнений

$begin{cases} x(x^2+y^2+y-2)=|x|(y+2),& &y=x+a& end{cases}$

имеет ровно три различных решения.

Решение: + показать

19.1. На доске написаны числа 1, 2, 3, …, 30. За один ход разрешается стереть произвольные три числа, сумма которых меньше 35 и отлична от каждой из сумм троек числа, стёртых на предыдущих ходах.
а) Приведите пример последовательности 5 ходов.

б) Можно ли сделать 10 ходов?
в) Какое наибольшее число ходов можно сделать?

Решение: + показать

Задания (часть С) резервного дня сдачи ЕГЭ по математике 2016 можно найти здесь.

Источник

13. а) Решите уравнение $$2log_3^2(2cos x) — 5 log_3(2cos x) + 2 = 0.$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $left[ pi; dfrac{5pi}{2}right]$.

14. В правильной треугольной призме $ABCA_1B_1C_1$ сторона основания $AB$ равна 6, а боковое ребро $AA_1$ равно 3. На ребре $AB$ отмечена точка $K$ так, что $AK = 1$. Точки $M$ и $L$ — середины ребер $A_1C_1$ и $B_1C_1$ соответственно. Плоскость $gamma$ параллельна прямой $AC$ и содержит точки $K$ и $L$.
а) Докажите, что прямая $BM$ перпендикулярна плоскости $gamma$;
б) Найдите расстояние от точки $C$ до плоскости $gamma$.

15. Решите неравенство $$frac{25^x — 5^{x+2} + 26}{5^x — 1} + frac{25^x — 7cdot5^x + 1}{5^x — 7} leqslant 2cdot5^x — 24.$$

16. В треугольнике $ABC$ проведены высоты $AK$ и $CM$. На них из точек $M$ и $K$ опущены перпендикуляры $ME$ и $KH$ соответственно.
а) Докажите, что прямые $EH$ и $AC$ параллельны;
б) Найдите отношение $EH : AC$, если угол $ABC$ равен $30^{circ}$.

17. 15-го января планируется взять кредит в банке на 1 млн рублей на 6 месяцев. Условия его возврата таковы:
− 1-го числа каждого месяца долг возрастает на целое число $r$ процентов по сравнению с концом предыдущего месяца;
− со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
− 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг (в млн рублей)	1	0,6	0,4	0,3	0,2	0,1	0

Найдите наибольшее значение $r$, при котором общая сумма выплат будет составлять менее 1,2 млн рублей.

18. Найдите все значения $a$, при каждом из которых уравнение $$sqrt{x^4 — x^2 + a^2} = x^2 + x — a$$ имеет ровно три различных решения.

19. На доске написаны числа 2 и 3. За один ход из них можно получить числа $a + b$ и $2a — 1$ или числа $a + b$ и $2b — 1$ (например, из чисел 2 и 3 можно получить числа 5 и 3 или 5 и 5).
а) Приведите пример последовательности ходов, после которых одно из чисел, написанных на доске окажется числом 19.
б) Может ли после 100 ходов одно из двух чисел, написанных на доске, оказаться числом 200?
в) Сделали 1007 ходов, причем на доске никогда не было равных чисел. Какое наименьшее значение может принимать разность большего и меньшего из полученных чисел?

Посмотреть полную версию с чатом

Источник

Реальные варианты ЕГЭ 2016

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Показания счётчика электроэнергии (1) сентября составляли (29 947) кВ(cdot )ч, а (1) октября — (30 047) кВ(cdot )ч. Сколько нужно заплатить за электроэнергию за сентябрь, если (1) кВ(cdot )ч электроэнергии стоит (4) рубля (28) копеек? Ответ дайте в рублях.

Вычислим, сколько кВ(cdot )ч электроэнергии было израсходовано за сентябрь: (30 047 — 29 947 = 100) кВ(cdot )ч. Таким образом, необходимо заплатить: (100cdot4,28 = 428) руб.

Ответ: 428

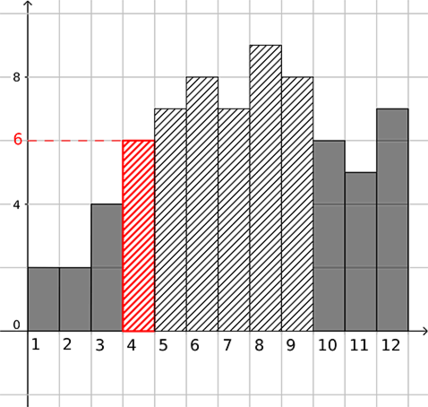
На диаграмме показана среднемесячная температура в Брянске за каждый месяц (1994) года. По горизонтали указывается номер месяца ((1) — январь, (2) — февраль и т.д.), по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру в Брянске в период с апреля по сентябрь (1994) года.
Ответ дайте в градусах Цельсия.

Наименьшая среднемесячная температура в период с апреля по сентябрь – это наименьшая температура с (4) по (9) месяц. По диаграмме видно, что в (4)-ом месяце температура в этом периоде была минимальна и равна (6^circ C).

Ответ: 6

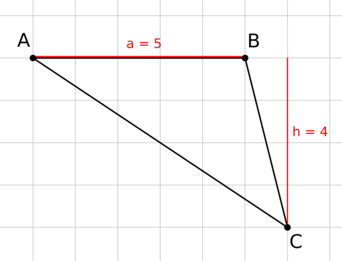
На клетчатой бумаге с размером клетки (1times1) изображён треугольник (ABC). Найдите его площадь.

Проведем высоту из точки (C) на прямую (AB). Так как треугольник тупоугольный, высота упадет на продолжение (AB) и будет равна (4), (AB = 5).

Тогда (S = frac{1}{2}cdot4cdot5 = 10).

Ответ: 10

В чемпионате по гимнастике участвуют (40) спортсменов, включая (8) спортсменов из Кореи и (10) — из России. Порядок, в котором выступают гимнасты, определяется жребием. Найдите вероятность того, что спортсмен из России будет выступать тридцать девятым.

В чемпионате принимают участие (10) спортсменов из России. Тогда вероятность того, что спортсмен, выступающий тридцать девятым, окажется из России, равна (dfrac{10}{40} = 0,25).

Ответ: 0,25

Найдите корень уравнения ( sqrt {3x+49} = 10)

Возведя в квадрат обе части равенства, получим:

[3x+49 = 100 quad Rightarrow quad 3x = 51 quad Rightarrow quad x = 17]

Т.к. возведение в квадрат может добавить лишние корни, то сделаем проверку: (sqrt{3cdot 17+49}=10) – верно.

Ответ: 17

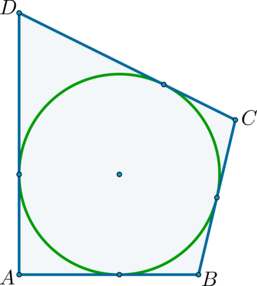
Стороны (AB) и (CD) четырёхугольника (ABCD), описанного около окружности, равны (28) и (24) соответственно. Найдите периметр этого четырёхугольника.

Так как в четырёхугольник (ABCD) можно вписать окружность, значит суммы его противоположных сторон равны: (AD+BC = AB+CD = 28+24 = 52).
Периметр четырёхугольника равен (AB+CD+AD+CB = 52+52 = 104).

Ответ: 104

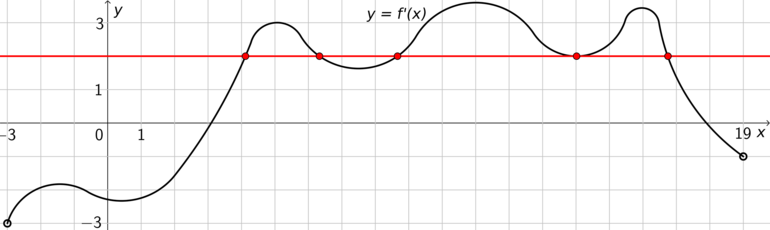
На рисунке изображён график (y = f'(x)) — производной функции (f(x)), определенной на интервале ((-3;19)). Найдите все точки, в которых касательная к графику функции (f(x)) параллельна прямой (y =
2x-11) или совпадает с ней. В ответ запишите их количество.

В уравнении касательной коэффициент перед (x) и есть значение производной в точке касания: (f'(x_0)=2). На рисунке изображен график производной, значит, задача сводится к тому, чтобы найти количество точек (x_0) с ординатой (2). Для этого проведем прямую (y = 2). Из рисунка видно, что таких точек (5).

Ответ: 5

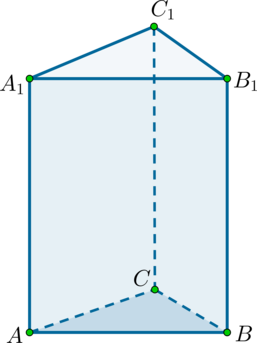
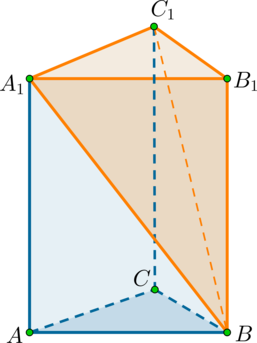
Найдите объем многогранника, вершинами которого являются точки (A_1
,B_1 ,C_1 ,B) прямой треугольной призмы (ABCA_1B_1C_1), площадь основания которой равна (5), а боковое ребро равно (9).

Необходимо вычислить объём треугольной пирамиды (см. рисунок), высота которой равна (9), а площадь основания — (5).

(V = dfrac{1}{3}cdot S_{осн} cdot h = dfrac{1}{3} cdot5cdot9 =
15).

Ответ: 15

Найдите значение выражения [dfrac {log_{4}{0,45}}{log_{4}{3}} +
log_{3}{20}]

Выполним преобразования: [dfrac {log_{4}{0,45}}{log_{4}{3}} +
log_{3}{20} = log_{3}{0,45}+log_{3}{20} = log_{3}{0,45cdot20} =
log_{3}{9} = 2]

Ответ: 2

Груз массой (0,25) кг колеблется на пружине. Его скорость (v) меняется по закону (v = v_0 sinfrac{2pi t}{T}) где (t) — время с момента начала колебаний, (T = 12) с — период колебаний, (v_0 = 1,6) м/с. Кинетическая энергия (E) (в джоулях) груза вычисляется по формуле (E = frac{mv^2}{2}), где (m) — масса груза в килограммах, (v) — скорость груза в м/с. Найдите кинетическую энергию груза через (10) секунд после начала колебаний.
Ответ дайте в джоулях.

Найдем скорость груза через (10) секунд после начала колебаний: [v
= v_0 sindfrac{2pi t}{T} = 1,6cdot sindfrac{2pi 10}{12} =
1,6cdot sindfrac{5pi}{3} =
1,6cdotleft(-dfrac{sqrt{3}}{2}right) = -dfrac{4sqrt{3}}{5}]

Найдем кинетическую энергию груза через (10) секунд после начала колебаний:

(E = dfrac{mv^2}{2} = dfrac{0,25 cdot
left(-frac{4sqrt{3}}{5}right)^2}{2} = 0,24 ).

Ответ: 0,24

Смешав (41)–процентный и (63)–процентный растворы кислоты и добавив (10) кг чистой воды, получили (49)–процентный раствор кислоты. Если бы вместо (10) кг воды добавили (10) кг (50)–процентного раствора той же кислоты, то получили бы (54)–процентный раствор кислоты. Сколько килограммов (41)–процентного раствора использовали для получения смеси?

Пусть масса (41)–процентного раствора кислоты — (x) кг, а масса (63)–процентного — (y) кг. Если смешать (41)–процентный и (63)–процентный растворы кислоты и добавить (10) кг чистой воды, получится (49)–процентный раствор кислоты. Значит, уравнение относительно массы кислоты будет выглядеть так: [0,41x+0,63y =
0,49(x+y+10)]

Если бы вместо (10) кг воды добавили (10) кг (50)–процентного раствора той же кислоты, то получили бы (54)–процентный раствор кислоты:

[0,41x+0,63y+0,5cdot10 =
0,54(x+y+10)]

Получили следующую систему уравнений:

[begin{cases}
0,41x+0,63y = 0,49(x+y+10) \
0,41x+0,63y+5 = 0,54(x+y+10)
end{cases} Leftrightarrow begin{cases}
0,08x-0,14y = -4,9 \
0,13x-0,09y = -0,4 end{cases}]

Решив систему, получим (x = 35, y = 55). Требовалось найти (x).

Ответ: 35

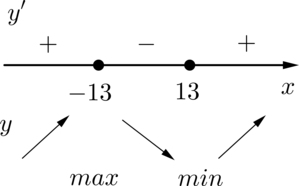
Найдите точку минимума функции (y=-dfrac{x}{x^2+169}).

Найдем производную заданной функции: [y’ = left(- dfrac{x}{x^2+169}right)’ = —
dfrac{1cdot(x^2+169)-xcdot(2x)}{(x^2+169)^2} =
dfrac{x^2-169}{(x^2+169)^2}]

Найдем критические точки функции (точки, в которых производная равна нулю или не существует):

[y’ = 0 quad Leftrightarrow quad x = -13 text{ или } x =
13]

Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка минимума (x=13).

Ответ: 13

а) Решите уравнение [2log^2_2{(2sin x)}-7log_2{(2sin x)}+3=0.]

б) Укажите корни этого уравнения, принадлежащие промежутку (left[dfrac{pi}2;2piright]).

а) ОДЗ уравнения: (2sin x>0 Rightarrow sin x>0).

Решим данное уравнение на ОДЗ. Сделаем замену (log_2{(2sin x)}=t). Тогда уравнение примет вид:

[2t^2-7t+3=0 Rightarrow t_1=3, t_2=dfrac12]

Сделаем обратную замену:

[left[begin{gathered}
begin{aligned}
& log_2{(2sin x)}=3\
& log_2{(2sin x)}=dfrac12
end{aligned}end{gathered} right. Rightarrow
left[begin{gathered}
begin{aligned}
& sin x=4\
& sin x=dfrac{sqrt2}2
end{aligned}end{gathered} right.]

Первое уравнение не имеет решений, т.к. (-1leqslant sin xleqslant
1). Второе уравнение имеет решения и удовлетворяет ОДЗ, следовательно, (x_1=dfrac{pi}4+2pi n, x_2=dfrac{3pi}4+2pi m,
n,minmathbb{Z}).

б) Отберем корни, решив два неравенства:

[dfrac{pi}2leqslant dfrac{pi}4+2pi nleqslant 2pi quad text{и} quad
dfrac{pi}2leqslant dfrac{3pi}4+2pi mleqslant 2pi]

Корень, принадлежащий отрезку (left[dfrac{pi}2;2piright]) — это (x=dfrac{3pi}4).

Ответ:

а) (dfrac{pi}4+2pi n, dfrac{3pi}4+2pi m, n,
minmathbb{Z})

б) (dfrac{3pi}4)

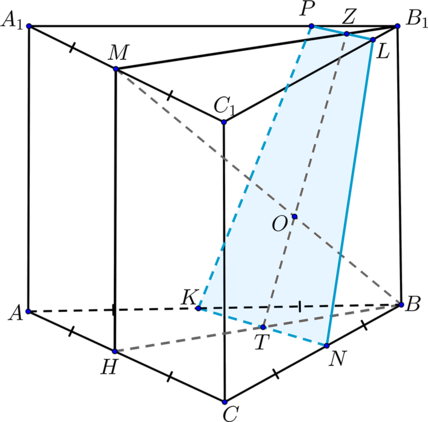
В правильной треугольной призме (ABCA_1B_1C_1) сторона основания (AB) равна (12), а боковое ребро (AA_1) равно (6). На ребре (B_1C_1) отмечена точка (L) так, что (B_1L=2). Точки (K, M) – середины ребер (AB) и (A_1C_1) соответственно. Плоскость (alpha) параллельна прямой (AC) и содержит точки (K) и (L).

а) Докажите, что прямая (BM) перпендикулярна плоскости (alpha).

б) Найдите объем пирамиды, вершины которой – точка (M), а основание – сечение данной призмы плоскостью (alpha).

а)

Построим сечение пирамиды плоскостью (alpha). Т.к. плоскость (alpha) параллельна прямой (AC), то она будет пересекать основания призмы по прямым, параллельным прямой (AC). Следовательно, прямая пересечения плоскости (alpha) с плоскостью (A_1B_1C_1) – прямая (LPparallel A_1C_1parallel AC). Таким образом, сечение призмы плоскостью (alpha) – равнобокая трапеция (KNLP).

Для того, чтобы прямая была перпендикулярна плоскости, она должна быть перпендикулярна двум пересекающимся прямым из этой плоскости.
Проведем (MHperp ABC Rightarrow ) по теореме о трех перпендикулярах (BM) (наклонная) (perp KN), т.к. (BH) (проекция) (perp
KN).

(BM) пересекает плоскость (alpha) на прямой (TZ), где (T, Z) – середины (KN) и (PL) соответственно. Докажем, что (BMperp TZ). Для этого докажем, что (angle OTB=angle HMB).
Рассмотрим сечение (MHBB_1). (BH) – высота правильного треугольника, следовательно, (BH=dfrac{12sqrt3}{2}=6sqrt3
Longrightarrow BT=3sqrt3.) (B_1Z=sqrt3 Longrightarrow TZ’=2sqrt3).

Таким образом, (mathrm{tg},angle OTB =
dfrac{6}{2sqrt3}=sqrt3=dfrac{BH}{MH}=mathrm{tg},angle MHB).

Следовательно, (bigtriangleup OTB~bigtriangleup MHB) по двум углам (Longrightarrow angle TOB=angle MHB =90^{circ}).
Таким образом, (BMperp KN) и (BMperp OT Longrightarrow BMperp
alpha).

б) Найдем (MO) – высоту пирамиды (MKNLP).
Т.к. (mathrm{tg},angle OTB=sqrt3 Longrightarrow angle
OTB=60^{circ} Longrightarrow sinangle OTB =
dfrac{sqrt3}{2}=dfrac{OB}{TB}
Longrightarrow OB=dfrac{9}{2}).

Аналогично, (dfrac{sqrt3}{2}=dfrac{BH}{MB} Longrightarrow MB=12
Longrightarrow MO=MB-OB=dfrac{15}{2}).

Найдем высоту (ZT) трапеции (KNLP).

Из прямоугольного (triangle ZZ’T) по теореме Пифагора (ZT=sqrt{6^2+(2sqrt3)^2}=4sqrt3)

(KN=dfrac12 AC=6, quad LP=dfrac 16 A_1C_1=2). Значит: [V_{MKNLP}=dfrac MOcdot dfrac{KN+LP}2cdot ZT=dfrac{1}{3}cdot dfrac{15}{2}cdot
dfrac{6+2}{2}cdot 4sqrt3=40sqrt3]

Ответ:

б)(40sqrt3)

Решите неравенство

[dfrac{49^x-6cdot 7^x+3}{7^x-5}+dfrac{6cdot 7^x-39}{7^x-7}leqslant 7^x+5]

Сделаем замену (7^x=t) и приведем правую и левую части неравенства к общему знаменателю:

[dfrac{t^3-7t^2-6t^2+42t+3t-21+6t^2-30t-39t+195}{(t-5)(t-7)}
leqslant dfrac{t^3-7t^2-25t+175}{(t-5)(t-7)} Leftrightarrow]

[Leftrightarrow dfrac{t-1}{(t-5)(t-7)}leqslant 0]

Решим полученное неравенство методом интервалов:

Нам подходят те значения (t), над которыми стоит знак “(-)”:

[left[
begin{gathered}
begin{aligned}
&tleqslant 1\
& 5<t<7 end{aligned} end{gathered} right. Rightarrow left[
begin{gathered}
begin{aligned}
&7^xleqslant 1\
& 5<7^x<7 end{aligned} end{gathered} right. Rightarrow left[
begin{gathered}
begin{aligned}
& xleqslant0\
& log_75<x<1 end{aligned} end{gathered} right.]

Ответ:

((-infty;0]cup(log_75;1))

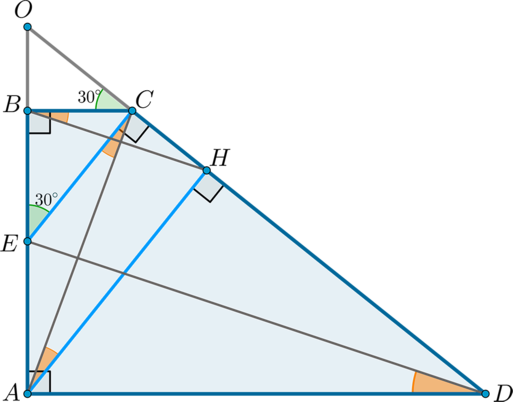
В трапеции (ABCD) боковая сторона (AB) перпендикулярна основаниям. Из точки (A) на сторону (CD) опустили перпендикуляр (AH). На стороне (AB) отмечена точка (E) так, что прямые (CD) и (CE) перпендикулярны.

а) Докажите, что прямые (BH) и (ED) параллельны.

б) Найдите отношение (BH:ED), если (angle BCD=150^circ).

а) Рассмотрим четырехугольник (AECD): т.к. (angle ECD+angle
EAD=180^circ), то около него можно описать окружность. Следовательно, (angle ECA=angle EDA) как вписанные и опирающиеся на одну хорду (EA). Около четырехугольника (ABCH) также можно описать окружность, следовательно, (angle CBH=angle CAH).

Но (angle CAH=angle ECA) как накрест лежащие при (ECparallel AH) и (AC) – секущей. Следовательно, (angle CBH=angle ADE).

Таким образом, (angle AED=90^circ-angle ADE=90^circ -angle
CBH=angle EBH) – соответственные при прямых (BH) и (ED) и секущей (AB). Значит (BHparallel ED).

б) Достроим трапецию (ABCD) до треугольника (AOD). Т.к. (BHparallel
ED Rightarrow triangle OBHsim triangle OED).

Значит, (dfrac{BH}{ED}=dfrac{OB}{OE}).

Т.к. (angle BCD=150^circ Rightarrow angle BCE=angle
BOC=60^circ, angle OCB=angle BEC=30^circ).

Пусть (OB=x Rightarrow BC=sqrt3 x Rightarrow BE=3x Rightarrow
OE=4x). Таким образом, [dfrac{BH}{ED}=dfrac{OB}{OE}=dfrac14]

Ответ:

б) (1:4)

(15)-ого января планируется взять кредит в банке на сумму (1) млн рублей на (6) месяцев. Условия его возврата таковы:
(bullet) (1)-ого числа каждого месяца долг возрастает на целое число (r) процентов по сравнению с концом предыдущего месяца;
(bullet) со (2)-ого по (14)-е числа каждого месяца необходимо выплатить часть долга;
(bullet) (15)-ого числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
[begin{array}{|l|c|c|c|c|c|c|c|} hline
text{Дата} & 15.01 & 15.02 & 15.03 & 15.04 & 15.05 & 15.06 & 15.07\
hline text{Долг (в млн руб.)} & 1 & 0,9 & 0,8 & 0,7 &
0,6 & 0,5 &
0\
hline
end{array}]
Найдите наименьшее значение (r), при котором общая сумма выплат будет составлять более (1,3) млн рублей.

Составим таблицу, где (dfrac{100+r}{100}=t.)

[begin{array}{|l|c|c|c|c|} hline text{Месяц} & text{Долг в млн
руб.} & text{Долг в млн руб.} & text{Долг в млн руб.} &
text{Выплата в млн руб.}\
& text{до начисления} & text{после начисления} & text{после выплаты} & \
& text{процентов} & text{процентов} & & \
hline
1&1 &t &0,9 & t-0,9\
hline
2&0,9 &0,9t &0,8 & 0,9t-0,8\
hline
3&0,8 &0,8t &0,7 & 0,8t-0,7\
hline
4&0,7 &0,7t &0,6 & 0,7t-0,6\
hline
5&0,6 &0,6t &0,5 & 0,6t-0,5\
hline
6&0,5 &0,5t &0 & 0,5t\
hline
end{array}]
Тогда общая сумма выплат составляет:
(0,1tcdot (10+9+8+7+6+5)-0,1(9+8+7+6+5)=4,5t-3,5)
Т.к. общая сумма выплат должна быть более 1,3 млн, то имеем неравенство:
(4,5t-3,5>1,3 Leftrightarrow t>dfrac{16}{15})

Таким образом, (r>dfrac{100}{15})
Т.к. (r) – целое, то наименьшее (r), удовлетворяющее неравенству — это (r=7).

Ответ:

(7%)

Найдите все значения параметра (a), при каждом из которых уравнение [sqrt{8x^2+4ax+4}=x^2+ax+2]

имеет ровно три различных решения.

Сделаем преобразования:

(sqrt{8x^2+4ax+4}=x^2+ax+2 quad Leftrightarrowquad
begin{cases}
8x^2+4ax+4=(x^2+ax+2)^2\
x^2+ax+2geqslant 0 end{cases} quad Leftrightarrow)

(Leftrightarrowquad
begin{cases}
x^4+2ax^3+a^2x^2-4x^2=0\
x^2+ax+2geqslant 0 end{cases}quad Leftrightarrowquad
begin{cases}
left[ begin{gathered}
begin{aligned}
&x_1=0\
&x_2=2-a\
&x_3=-2-a
end{aligned}
end{gathered}
right.\
x^2+ax+2geqslant 0
end{cases}
)

Для того, чтобы система имела три различных решения, необходимо, чтобы все три корня были различны и удовлетворяли неравенству (x^2+ax+2geqslant 0).

Заметим, что при всех (ane pm 2) все три корня различны, значит, необходимо, чтобы:

[begin{cases}
0^2+acdot 0+2geqslant 0\
(2-a)^2+a(2-a)+2geqslant 0\
(-2-a)^2+a(-2-a)+2geqslant 0\
ane pm 2 end{cases} Rightarrow
begin{cases}
aleqslant 3\
ageqslant -3\
ane pm 2
end{cases}]

Значит, (ain [-3;-2)cup(-2;2)cup(2;3]).

Ответ:

(ain [-3;-2)cup(-2;2)cup(2;3])

Дана последовательность, состоящая из (n) целых чисел, причем (a_1=1, a_n=235). Сумма любых соседних членов данной последовательности равна либо (3), либо (5), либо (25).

а) Приведите пример такой последовательности.

б) Может ли в такой последовательности (n=1000)?

в) Какое наименьшее количество чисел может быть в такой последовательности?

а) Пример последовательности при (n=23):

( 1, 2, 23, -18, 43, -38, 63,-58,83,-78,103,-100,125,-122,147,-144,
169,-166,191,-188,213,-210,235. )

б) Исходя из условия, любые соседние числа данной последовательности будут разной четности. Следовательно, если бы такая последовательность существовала, то (a_{1000}) было бы четным, а (235) – нечетное число, следовательно, такой последовательности не существует.

в) Наименьшее (n) равно (23) (пример из пункта а).

Т.к. из пункта б) следует, что количество членов последовательности должно быть нечетным, нам нужно доказать, что (n>21). Докажем от противного. Предположим, что существует такая последовательность, где (nleqslant 21). Будем рассматривать последовательность справа налево. Заметим, что если какой-то член последовательности больше (25), то слева от него стоит отрицательное число. Также заметим, что слева от отрицательного числа обязано стоять положительное число. Поэтому до тех пор, пока, идя справа налево, мы не встретим первое положительное число (leqslant 25) (назовем его (a_i)), числа будут образовывать знакопеременную последовательность.

Среди чисел, стоящих правее (a_i), любые числа, стоящие через один, отличаются по модулю либо на (0), либо на (2), либо на (20), либо на (22):

пусть (a,b,c) – три подряд идущих члена последовательности, стоящие правее (a_i). Тогда (a+b=p, b+c=q Rightarrow |a-c|=|p-q|), где (p, q) принимают значения (3, 5, 25) (из условия). Следовательно, (|p-q|) принимает значения (0,2,20,22).

Таким образом, правее (a_i) стоит не менее (20) чисел, т.к. (235-22cdot 9=37>25). То есть мы максимально быстро уменьшаем положительные числа: [235,*213,*,191,*,169,*,dots qquad qquad
({small{text{* — отрицательные числа}}})]

Итак, мы имеем последовательность (1, dots, a_i, a_{i+1}, dots,
235), в которой как минимум (22) члена последовательности (т.к. (a_ine 1)). Но по предположению (nleqslant 21), следовательно, мы получили противоречие.

Ответ:

б) нет

в) (23)

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Условия КИМов реального ЕГЭ 2016 по математике (тип 1)

Часть 1

1. В квартире установлен прибор учёта расхода холодной воды (счётчик). Показания счётчика 1 сентября составляли 103 куб, м воды, а 1 октября — 114 куб. м.

Сколько нужно заплатить за холодную воду за сентябрь, если стоимость 1 куб, м холодной воды составляет 19 руб. 20 коп.? Ответ дайте в рублях.
2. На диаграмме показано количество посетителей сайта РИА Новости во все дни с 10 по 29 ноября 2009 года. По горизонтали указываются дни месяца, по вертикали — количество посетителей сайта за данный день. Определите по диаграмме, во сколько раз наибольшее количество посетителей больше, чем наименьшее количество посетителей за день.

3. Найдите площадь треугольника, изображенного на рисунке.

4. В соревнованиях по толканию ядра участвуют 8 спортсменов из Великобритании, 6 спортсменов из Франции, 5 спортсменов из Германии и 5 — из Италии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется из Франции.
5. Наидите корень уравнения: 24x−14=164.
6. В четырехугольник ABCD, периметр которого равен 48 вписана окружность, AB=15. Найдите CD.

7. На рисунке изображён график y=f′(x) производной функции f(x), определенной на интервале (-10; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y=−2x−11 или совпадает с ней.

8. Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.

Часть 2

9. Найдите значение выражений log820log85+log50,05.
10. Груз массой 0,8 кг колеблется на пружине. Его скорость v меняется по закону v=v0sin2πtT. где t — время с момента начала колебаний, T=16 — период колебаний, v0=0,5 м/с. Кинетическая энергия E(в джоулях) груза вычисляется по формуле E=mv22, где m- масса груза в килограммах, v — скорость груза в м/с.
Найдите кинетическую энергию груза через 10 секунд после начала колебаний. Ответ дайте в джоулях
11. Шесть одинаковых рубашек дешевле куртки на 2%. На сколько процентов девять таких же рубашек дороже куртки?
12. Найдите точку минимума функции y=2x−ln(x+8)2.

Тип 1

13. а) Решите уравнение 2log22(2sinx)−7log2(2sinx)+3=0.
б) Укажите корни этого уравнения, принадлежащие отрезку [π2;2π].
14. В правильной треугольной призме ABCA1B1C1 сторона основания AB равна 6, а боковое ребро AA1 равно 3 . На ребре B1C1 отмечена точка L так, что B1L=1. Точки K и M — середины ребер AB и A1C1 соответственно. Плоскость γ параллельна прямой AC и содержит точки K и L.
а) Докажите, что прямая BM перпендикулярна плоскости γ;
б) Найдите объем пирамиды, вершина которой — точка M, а основание — сечение данной призмы плоскостью γ.
15. Решите неравенство: 49x−6⋅7x+37x−5+6⋅7x−397x−7≤7x+5.
16. В трапеции ABCD боковая сторона AB перпендикулярна основаниям. Из точки A на сторону CDопустили перпендикуляр AH. На стороне AB отмечена точка E так, что прямые CD и CEперпендикулярны.
а) Докажите, что прямые BH и ED параллельны.
б) Найдите отношение BH:ED, если угол BCD=135∘.
17. 15-го января планируется взять кредит в банке на сумму 1 млн рублей на 6 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на целое число r процентов по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.

Найдите наименьшее значение r, при котором общая сумма выплат будет составлять более 1,25 млн рублей.
18. Найдите все значения параметра a, при каждом из которых уравнение
15×2+6ax+9−−−−−−−−−−−−√=x2+ax+3
имеет ровно три различных решения
19. На доске написаны числа 1, 2, 3, …,30. За один ход разрешается стереть произвольные три числа, сумма которых меньше 35 и отлична от каждой из сумм троек числа, стёртых на предыдущих ходах.
а) Приведите пример последовательности 5 ходов, б (Можно ли сделать 10 ходов?
в) Какое наибольшее число ходов можно сделать?

(тип 2)

13. а) Решите уравнение 2cos2x+1=22√cos(3π2−x).
б) Укажите корни этого уравнения, принадлежащие промежутку [3π2;7π].
14. В правильной четырехугольной пирамиде SABCD сторона основания AB равна 16, а высота равна 4. На ребрах AB,CD и AS отмечены точки M,N и K соответственно, причем AM=DN=4 и AK=3.
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки K до плоскости SBC.
15. Решите неравенство 4x−2x+3+74x−5⋅2x+4≤2x−92x−4+12x−6.
16. В трапеции ABCD точка E — середина основания AD, точка M — середина боковой стороны AB. Отрезки CE и DM пересекаются в точке O.
а) Докажите, что площади четырехугольника AMOE и треугольника COD равны

б) Найдите, какую часть от площади трапеции составляет площадь четырехугольника AMOE, если BC=3,AD=4.
17. В июле 2016 года планируется взять кредит в банке на S млн рублей, где S — целое число, на 4 года. Условия его возврата таковы:
— каждый январь долг возрастает на 15% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей

Найдите наибольшее значение S, чтобы общая сумма выплат была меньше 50 млн рублей?
18. Найдите все значения a, при каждом из которых уравнение x−2ax+2+x−1x−a=1
имеет единственный корень.
19. На доске написаны числа 2 и 3. За один ход разрешено заменить написанные на доске числа a и bчислами 2a−1 и a+b (например, из чисел 2 и 3 можно получить либо 3 и 5, либо 5 и 5).
а) Может ли после нескольких ходов на доска появиться число 19?
б) может ли через 100 ходов на доске быть написано число 200?
в) укажите наименьшую разность чисел через 1007 ходов.

(тип 3)

13. а) Решите уравнение 2log23(2cosx)−5log3(2cosx)+2=0.
б) Укажите корни этого уравнения, принадлежащие промежутку [π;5π2].
14. В правильной треугольной призме ABCA1B1C1 сторона основания AB равна 6, а боковое ребро AA1 равно 3. На ребре AB отмечена точка K так, что AK=1. Точки M и L — середины ребер A1C1 и B1C1 соответственно. Плоскость у параллельна прямой AC и содержит точки K и L.
а) Докажите, что прямая BM перпендикулярна плоскости γ.
б) Найдите расстояние от точки C до плоскости γ.
15. Решите неравенство 25x−5x+2+265x−1+25x+7⋅5x+15x−7≤2⋅5x−24.
16. В треугольнике ABC проведены высоты AK и CM. На них из точек M и K опущены перпендикулярыME и KH соответственно
а) Докажите, что прямые EH и AC параллельны.
б) Найдите отношение EH:AC, если угол ABC равен 30∘.
17. 15-го января планируется взять кредит в банке на 1 млн рублей на 6 месяцев. Условия его возврата таковы:
-1-го числа каждого месяца долг возрастает на целое число r процентов по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей

Найдите наибольшее значение r, при котором общая сумма выплат будет составлять менее 1,2 млн. рублей.
18. Найдите все значения a, при каждом из которых уравнение
x4−x2+a2−−−−−−−−−−√=x2+x−a
имеет ровно три различных решения.

(тип 4)

13. а) Решите уравнение 2cos2x=4sin(π2+x)+1.
б) Укажите корни этого уравнения, принадлежащие промежутку [−5π2;−π].
14. В правильной треугольной пирамиде SABC сторона основания AB равна 12, а высота равна 1. На ребрах AB,AC и AS отмечены точки M,N и K соответственно, причем AM=AN=3 и AK=74.
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки K до плоскости SBC.
15. Решите неравенство 9x+12−4⋅3x+59x+12−4⋅3x+1+5⋅3x−193x−4≤2⋅3x+2−123x+1−1.
16. Один из двух отрезков, соединяющих середины противоположных сторон четырехугольника, делит его площадь пополам, а другой в отношении 11:17
а) Докажите, что данный четырехугольник — трапеция
б) Найдите отношение оснований этой трапеции
17. В июле 2016 года планируется взять кредит в банке на S млн рублей, где S — целое число, на 4 года. Условия его возврата таковы:
— каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей

Найдите наименьшее значение S, чтобы общая сумма выплат была больше 10 млн рублей?
18. Найдите все значения a, при каждом из которых уравнение
x3+x2−9a2x−2x+ax3−9a2x=1
имеет единственный корень.

Источник