Пробный ОГЭ 2022 по математике 9 класс региональная оценка качества образования у 9 классов 4 варианта для проведения пробного экзамена с ответами и решением, работа прошла в Тюменской области 72 регионе: 14 декабря 2021 года.
-
Скачать вариант 9051
-
Скачать вариант 9052
-
Скачать вариант 9053
-
Скачать вариант 9054
-
Скачать ответы для 1 варианта
-
Скачать ответы для 2 варианта
-
Скачать ответы для 3 варианта
-
Скачать ответы для 4 варианта
-
Скачать ответы на тестовую часть
Пробное ОГЭ 2022 по математике 9 класс вариант №9051
Пробное ОГЭ 2022 по математике 9 класс вариант №9052
Пробное ОГЭ 2022 по математике 9 класс вариант №9053
Пробное ОГЭ 2022 по математике 9 класс вариант №9054
Сложные задания и ответы с 1 варианта:
На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме. Сторона одной клетки на плане соответствует 0,4 м, а условные обозначения двери и окна приведены в правой части рисунка. Вход в квартиру находится в коридоре. Слева от входа в квартиру находится санузел, а в противоположном конце коридора – дверь в кладовую. Рядом с кладовой находится спальня, из которой можно пойти на одну из застекленных лоджий. Самое большое по площади помещение – гостиная, откуда можно попасть в коридор и на кухню. Из кухни также можно попасть на застекленную лоджию.
1)Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр.
Ответ: 6172
2)Паркетная доска размером 20 см на 80 см продается в упаковках по 12 штук. Сколько упаковок паркетной доски понадобилось, чтобы выложить пол в спальне?
Ответ: 9
3)Найдите площадь гостиной. Ответ дайте в квадратных метрах.
Ответ: 24,96
4)На сколько процентов площадь коридора больше площади кладовой?
Ответ: 525
5)В квартире планируется установить стиральную машину. Характеристики стиральных машин, условия подключения и доставки приведены в таблице. Планируется купить стиральную машину с фронтальной загрузкой, по глубине не превосходящую 42 см. Сколько рублей будет стоить наиболее дешёвый подходящий вариант вместе с подключением и доставкой?
Ответ: 28800
6)На координатной прямой отмечены точки A, B. C и D соответствуют числам – 0,032; 0,023; 0,302; – 0,203. Какой точке соответствует число – 0,203?
Ответ: 2,05
9)Решите уравнение – 2x–7= – 4x.
Ответ: 3,5
10)В лыжных гонках участвуют 7 спортсменов из России, 1 спортсмена из Швеции и 2 спортсмена из Норвегии. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из Швеции.
Ответ: 0,1
12)В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) длительностью более 5 минут рассчитывается по формуле C = 150+11 ⋅ (t − 5), где t — длительность поездки, выраженная в минутах. Пользуясь этой формулой, рассчитайте стоимость 13-минутной поездки. Ответ дайте в рублях.
Ответ: 238
14)В амфитеатре 14 рядов. В первом ряду 18 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в девятом ряду амфитеатра?
Ответ: 34
15)В треугольнике ABC известно, что угол BAC равен 84º, AD – биссектриса. Найдите угол BAD. Ответ дайте в градусах.
Ответ: 42
16)В треугольнике ABC известно, что AC=8, BC=15, угол C равен 90º. Найдите радиус описанной около этого треугольника окружности.
Ответ: 8,5
17)Диагонали AC и BD прямоугольника ABCD пересекаются в точке O, BO=24, AB=45. Найдите AC.
Ответ: 48
18)На клетчатой бумаге с размером клетки 1*1 изображён ромб. Найдите площадь этого ромба.
Ответ: 6
19)Какое из следующих утверждений верно? 1) Диагонали равнобедренной трапеции равны. 2) Если три угла одного треугольника равны соответственно трем углам другого треугольника, то такие треугольника равны. 3) Тангенс любого острого угла меньше единицы.
Ответ: 1
21)Теплоход проходит по течению реки до пункта назначения 80 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 5 км/ч, стоянка длится 23 часа, а в пункт отправления теплоход возвращается через 35 часов после отплытия из него.
Ответ: 15 км/ч
23)Точка H является основанием высоты BH , проведённой из вершины прямого угла B прямоугольного треугольника ABC . Окружность с диаметром BH пересекает стороны A B и CB в точках P и K соответственно. Найдите PK , если BH 14 .
Ответ: 14
24)На средней линии трапеции ABCD с основаниями A D и BC выбрали произвольную точку K . Докажите, что сумма площадей треугольников BKC и AKD равна половине площади трапеции.
25)На стороне BC остроугольного треугольника ABC как на диаметре построена полуокружность, пересекающая высоту A D в точке M , A D 16 , MD 4 , H — точка пересечения высот треугольника ABC . Найдите A H .
Ответ: 15
Сложные задания и ответы с 2 варианта:
2)Паркетная доска размером 20 см на 80 см продается в упаковках по 12 штук. Сколько упаковок паркетной доски понадобилось, чтобы выложить пол в кладовой?
Ответ: 2
3)Найдите площадь гостиной. Ответ дайте в квадратных метрах.
Ответ: 24,96
4)На сколько процентов площадь кухни больше площади санузла?
Ответ: 200
5)В квартире планируется установить стиральную машину. Характеристики стиральных машин, условия подключения и доставки приведены в таблице. Планируется купить стиральную машину с фронтальной загрузкой, вместимостью не менее 6 кг.
Ответ: 29300
10)В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
Ответ: 0.35
12)В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) длительностью более 5 минут рассчитывается по формуле C = 150+11 ⋅ (t − 5), где t — длительность поездки, выраженная в минутах. Пользуясь этой формулой, рассчитайте стоимость 16-минутной поездки. Ответ дайте в рублях.
Ответ: 271
14)В амфитеатре 15 рядов. В первом ряду 20 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в десятом ряду амфитеатра?
Ответ: 38
15)В треугольнике ABC известно, что угол BAC равен 64º, AD – биссектриса. Найдите угол BAD. Ответ дайте в градусах.
Ответ: 32
16)В треугольнике ABC известно, что AC=16, BC=12, угол C равен 90º. Найдите радиус описанной около этого треугольника окружности.
Ответ: 10
17)Диагонали AC и BD прямоугольника ABCD пересекаются в точке O, BO=11, AB=10. Найдите AC.
Ответ: 22
19)Какие из следующих утверждений верны? 1) Если диагонали параллелограмма равны, то этот параллелограмм является ромбом. 2) Сумма острых углов прямоугольного треугольника равна 90 градусам. 3) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
Ответ: 23
21)Теплоход проходит по течению реки до пункта назначения 165 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 26 км/ч, стоянка длится 5 часов, а в пункт отправления теплоход возвращается через 18 часов после отплытия из него.
Ответ: 4 км/ч
23)Точка H является основанием высоты BH , проведённой из вершины прямого угла B прямоугольного треугольника ABC . Окружность с диаметром BH пересекает стороны A B и CB в точках P и K соответственно. Найдите BH , если PK 13.
Ответ: 13
24)На средней линии трапеции ABCD с основаниями A D и BC выбрали произвольную точку K . Докажите, что сумма площадей треугольников BKC и AKD равна половине площади трапеции.
25)На стороне BC остроугольного треугольника ABC как на диаметре построена полуокружность, пересекающая высоту A D в точке M , A D 80 , MD 64, H — точка пересечения высот треугольника ABC . Найдите A H .
Ответ: 28,8
Сложные задания и ответы с 3 варианта:
Полина летом отдыхает у дедушки в деревне Ясной. В четверг они собираются съездить на велосипедах в село Майское в магазин. Из деревни Ясная в село Майское можно проехать по прямой лесной дорожке. Есть более длинный путь: по прямолинейному шоссе через деревню Камышёвку до деревни Хомяково, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в село Майское. Есть и третий маршрут: в деревне Камышёвке можно свернуть на прямую тропинку в село Майское, которая идёт мимо пруда. Лесная дорожка и тропинка образуют с шоссе прямоугольные треугольники. По шоссе Полина с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке — со скоростью 15 км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна 2 км.
1)Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других символов.
Ответ: 213
2)Сколько километров проедут Полина с дедушкой от деревни Камышёвка до села Майское, если они поедут по шоссе через деревню Хомяково?
Ответ: 34
3)Найдите расстояние от деревни Камышёвка до села Майское по прямой. Ответ дайте в километрах.
Ответ: 26
4)Сколько минут затратят на дорогу из деревни Ясная в село Майское Полина с дедушкой, если они поедут сначала по шоссе, а затем свернут в Камышёвке на прямую тропинку, которая проходит мимо пруда?
Ответ: 170
5)В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Ясная, селе Майское, деревне Камышёвка и деревне Хомяково. Полина с дедушкой хотят купить 2 л молока, 3 кг говядины и 2 кг картофеля. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Ответ: 1134
6)Найдите значение выражения 9,8 8,6 .
Ответ: 18,4
10)Родительский комитет закупил 10 пазлов для подарков детям в связи с окончанием учебного года, из них 4 с машинами и 6 с видами городов. Подарки распределяются случайным образом между 10 детьми, среди которых есть Володя. Найдите вероятность того, что Володе достанется пазл с машиной.
Ответ: 0,4
12)Перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, позволяет формула 1,8 32 F c t t , где t C — температура в градусах Цельсия, t F — температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует – 35 градусов по шкале Цельсия?
Ответ: -31
13)В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой 3 мг. Каждые 20 минут масса колонии увеличивается в 3 раза. Найдите массу колонии микроорганизмов через 80 минут после начала эксперимента. Ответ дайте в миллиграммах.
Ответ: 4
17)Диагональ прямоугольника образует угол 74º с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах
Ответ: 32
19)Какое из следующих утверждений верно? 1) Диагонали прямоугольника точкой пересечения делятся пополам. 2) Точка пересечения двух окружностей равноудалена от центров этих окружностей. 3) Площадь любого параллелограмма равна произведению длин его сторон.
Ответ: 1
21)Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 51 минуту, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 251 км, скорость первого велосипедиста равна 10 км/ч, скорость второго — 20 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
Ответ: 173 км
24)Внутри параллелограмма ABCD выбрали произвольную точку F . Докажите, что сумма площадей треугольников BFC и AFD равна половине площади параллелограмма.
25)Окружности радиусов 12 и 20 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD .
Ответ: 30
Сложные задания и ответы с 4 варианта:
Серёжа летом отдыхает с папой в деревне Пирожки. В среду они собираются съездить на машине в село Княжеское. Из деревни Пирожки в село Княжеское можно проехать по прямой грунтовой дороге. Есть более длинный путь: по прямолинейному шоссе через деревню Васильево до деревни Рябиновка, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в село Княжеское. Есть и третий маршрут: в деревне Васильево можно свернуть на прямую грунтовую дорогу в село Княжеское, которая идёт мимо пруда. Шоссе и грунтовые дороги образуют прямоугольные треугольники.
По шоссе Серёжа с папой едут со скоростью 60 км/ч, а по грунтовой дороге — со скоростью 40 км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна 2 км.
1)Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других символов.
Ответ: 423
2)Сколько километров проедут Серёжа с папой от деревни Васильево до села Княжеское, если они поедут по шоссе через деревню Рябиновку?
Ответ: 28
3)Найдите расстояние от деревни Васильево до села Княжеское по прямой. Ответ дайте в километрах.
Ответ: 20
4)Сколько минут затратят на дорогу из деревни Пирожки в село Княжеское Серёжа с папой, если они поедут сначала по шоссе, а затем свернут в деревне Васильево на прямую грунтовую дорогу, которая проходит мимо пруда?
Ответ: 48
5)В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Пирожки, селе Княжеском, деревне Васильево и деревне Рябиновке.
Ответ: 438
6)Серёжа с папой хотят купить 2 л молока, 3 батона хлеба и 1 кг сыра «Российский». В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Ответ: 12,1
10)Родительский комитет закупил 25 пазлов для подарков детям в связи с окончанием учебного года, из них 22 с машинами и 3 с видами городов. Подарки распределяются случайным образом между 25 детьми, среди которых есть Коля. Найдите вероятность того, что Коле достанется пазл с машиной.
Ответ: 0,88
14)В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой 14 мг. За каждые 30 минут масса колонии увеличивается в 3 раза. Найдите массу колонии микроорганизмов через 90 минут после начала эксперимента. Ответ дайте в миллиграммах.
Ответ: 378
17)Диагональ прямоугольника образует угол 86º с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Ответ: 8
19)Какое из следующих утверждений верно? 1) Отношение площадей подобных треугольников равно коэффициенту подобия. 2) Диагонали прямоугольника точкой пересечения делятся пополам. 3) Биссектриса треугольника делит пополам сторону, к которой проведена. В ответ запишите номер выбранного утверждения.
Ответ: 2
21)Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 48 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 168 км, скорость первого велосипедиста равна 15 км/ч, скорость второго — 30 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
Ответ: 120 км
23)Найдите боковую сторону AB трапеции ABCD , если углы ABC и BCD равны соответственно 60 и 135 , а CD 24 .
Ответ: 8 корень из 6
24)Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.
25)Окружности радиусов 45 и 90 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD .
Ответ: 120
Тренировочные варианты ОГЭ 2022 по математике 9 класс:
-
Математика 9 класс работа статград ОГЭ 2022 варианты МА2190201-МА2190204
-
08.12.2021 Математика 9 класс ОГЭ 2022 2 варианта и ответы контрольной работы
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Диагностический вариант СтатГрад ОГЭ по математике 90502-14.05.2018 с ответами
Региональная оценка качества образования 2022 математика 9 класс вариант 9051
С изменениями в КИМ ЕГЭ-2022 можно ознакомиться в демоверсиях на сайте ФИПИ
В разделе «Документы» размещены расписания ЕГЭ, ОГЭ и ГВЭ, утвержденные министерством просвещения
Размещены результаты КР9 по обществознанию
Результаты ГВЭ-11 размещены на сайте. Уточнённые даты подачи и рассмотрения апелляций смотрите в протоколе ГЭК
Размещены и направлены в муниципалитеты результаты КР-9 по информатике, биологии, литературе, ГВЭ-9 по русскому, ГВЭ-11 по русскому и математике
Ура. Дождались. Результаты ОГЭ по русскому языку размещены для индивидуального просмотра по коду регистрации на нашем сайте, а также направлены в муниципалитеты
В личном кабинете ОО размещены Выдержка из МР по организации видеонаблюдения ГИА 2021 для использования при установке видеокамер в ППЭ 9 классов
29 апреля состоится акция «Диктант Победы»
Полезная информация
18 апреля стартует онлайн-марафон «ЕГЭ — это про100!» для выпускников 2022 года. Трансляции будут проходить в официальных аккаунтах Рособрнадзора:
В разделе Документы размещены расписания ЕГЭ, ОГЭ и ГВЭ, утвержденные министерством просвещения.
Www. ege-kostroma. ru
22.05.2020 20:39:21
2020-05-22 20:39:21
Источники:
Https://www. ege-kostroma. ru/
14.12.2021 Пробный ОГЭ 2022 по математике 9 класс 4 варианта с ответами | ЕГЭ ОГЭ СТАТГРАД ВПР 100 баллов » /> » /> .keyword { color: red; } Региональная оценка качества образования 2022 математика 9 класс вариант 9051
14.12.2021 Пробный ОГЭ 2022 по математике 9 класс 4 варианта с ответами
14.12.2021 Пробный ОГЭ 2022 по математике 9 класс 4 варианта с ответами
Пробный ОГЭ 2022 по математике 9 класс региональная оценка качества образования у 9 классов 4 варианта для проведения пробного экзамена с ответами и решением, работа прошла в Тюменской области 72 регионе: 14 декабря 2021 года.
Скачать вариант 9051
Скачать вариант 9052
Скачать вариант 9053
Скачать вариант 9054
Скачать ответы для 1 варианта
Скачать ответы для 2 варианта
Скачать ответы для 3 варианта
Скачать ответы для 4 варианта
Скачать ответы на тестовую часть
Пробное ОГЭ 2022 по математике 9 класс вариант №9051
Пробное ОГЭ 2022 по математике 9 класс вариант №9052
Пробное ОГЭ 2022 по математике 9 класс вариант №9053
Пробное ОГЭ 2022 по математике 9 класс вариант №9054
Сложные задания и ответы с 1 варианта:
На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме. Сторона одной клетки на плане соответствует 0,4 м, а условные обозначения двери и окна приведены в правой части рисунка. Вход в квартиру находится в коридоре. Слева от входа в квартиру находится санузел, а в противоположном конце коридора – дверь в кладовую. Рядом с кладовой находится спальня, из которой можно пойти на одну из застекленных лоджий. Самое большое по площади помещение – гостиная, откуда можно попасть в коридор и на кухню. Из кухни также можно попасть на застекленную лоджию.
1)Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр.
Ответ: 6172
2)Паркетная доска размером 20 см на 80 см продается в упаковках по 12 штук. Сколько упаковок паркетной доски понадобилось, чтобы выложить пол в спальне?
Ответ: 9
3)Найдите площадь гостиной. Ответ дайте в квадратных метрах.
Ответ: 24,96
4)На сколько процентов площадь коридора больше площади кладовой?
Ответ: 525
5)В квартире планируется установить стиральную машину. Характеристики стиральных машин, условия подключения и доставки приведены в таблице. Планируется купить стиральную машину с фронтальной загрузкой, по глубине не превосходящую 42 см. Сколько рублей будет стоить наиболее дешёвый подходящий вариант вместе с подключением и доставкой?
Ответ: 28800
6)На координатной прямой отмечены точки A, B. C и D соответствуют числам – 0,032; 0,023; 0,302; – 0,203. Какой точке соответствует число – 0,203?
Ответ: 2,05
9)Решите уравнение – 2x–7= – 4x.
Ответ: 3,5
10)В лыжных гонках участвуют 7 спортсменов из России, 1 спортсмена из Швеции и 2 спортсмена из Норвегии. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из Швеции.
Ответ: 0,1
12)В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) длительностью более 5 минут рассчитывается по формуле C = 150+11 ⋅ (t − 5), где t — длительность поездки, выраженная в минутах. Пользуясь этой формулой, рассчитайте стоимость 13-минутной поездки. Ответ дайте в рублях.
Ответ: 238
14)В амфитеатре 14 рядов. В первом ряду 18 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в девятом ряду амфитеатра?
Ответ: 34
15)В треугольнике ABC известно, что угол BAC равен 84º, AD – биссектриса. Найдите угол BAD. Ответ дайте в градусах.
Ответ: 42
16)В треугольнике ABC известно, что AC=8, BC=15, угол C равен 90º. Найдите радиус описанной около этого треугольника окружности.
Ответ: 8,5
17)Диагонали AC и BD прямоугольника ABCD пересекаются в точке O, BO=24, AB=45. Найдите AC.
Ответ: 48
18)На клетчатой бумаге с размером клетки 1*1 изображён ромб. Найдите площадь этого ромба.
Ответ: 6
19)Какое из следующих утверждений верно? 1) Диагонали равнобедренной трапеции равны. 2) Если три угла одного треугольника равны соответственно трем углам другого треугольника, то такие треугольника равны. 3) Тангенс любого острого угла меньше единицы.
Ответ: 1
21)Теплоход проходит по течению реки до пункта назначения 80 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 5 км/ч, стоянка длится 23 часа, а в пункт отправления теплоход возвращается через 35 часов после отплытия из него.
Ответ: 15 км/ч
23)Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны A B и CB в точках P и K соответственно. Найдите PK, если BH 14 .
Ответ: 14
24)На средней линии трапеции ABCD с основаниями A D и BC выбрали произвольную точку K. Докажите, что сумма площадей треугольников BKC и AKD равна половине площади трапеции.
25)На стороне BC остроугольного треугольника ABC как на диаметре построена полуокружность, пересекающая высоту A D в точке M, A D 16 , MD 4 , H — точка пересечения высот треугольника ABC. Найдите A H.
Ответ: 15
Сложные задания и ответы с 2 варианта:
2)Паркетная доска размером 20 см на 80 см продается в упаковках по 12 штук. Сколько упаковок паркетной доски понадобилось, чтобы выложить пол в кладовой?
Ответ: 2
3)Найдите площадь гостиной. Ответ дайте в квадратных метрах.
Ответ: 24,96
4)На сколько процентов площадь кухни больше площади санузла?
Ответ: 200
5)В квартире планируется установить стиральную машину. Характеристики стиральных машин, условия подключения и доставки приведены в таблице. Планируется купить стиральную машину с фронтальной загрузкой, вместимостью не менее 6 кг.
Ответ: 29300
10)В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
Ответ: 0.35
12)В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) длительностью более 5 минут рассчитывается по формуле C = 150+11 ⋅ (t − 5), где t — длительность поездки, выраженная в минутах. Пользуясь этоЙ формулой, рассчитайте стоимость 16-минутной поездки. Ответ дайте в рублях.
Ответ: 271
14)В амфитеатре 15 рядов. В первом ряду 20 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в десятом ряду амфитеатра?
Ответ: 38
15)В треугольнике ABC известно, что угол BAC равен 64º, AD – биссектриса. Найдите угол BAD. Ответ дайте в градусах.
Ответ: 32
16)В треугольнике ABC известно, что AC=16, BC=12, угол C равен 90º. Найдите радиус описанной около этого треугольника окружности.
Ответ: 10
17)Диагонали AC и BD прямоугольника ABCD пересекаюТся в точке O, BO=11, AB=10. Найдите AC.
Ответ: 22
19)Какие из следующих утверждений верны? 1) Если диагонали параллелограмма равны, то этот параллелограмм является ромбом. 2) Сумма острых углов прямоугольного треугольника равна 90 градусам. 3) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
Ответ: 23
21)Теплоход проходит по течению реки до пункта назначения 165 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 26 км/ч, стоянка длится 5 часов, а в пункт отправления теплоход возвращается через 18 часов после отплытия из него.
Ответ: 4 км/ч
23)Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны A B и CB в точках P и K соответственно. Найдите BH, если PK 13.
Ответ: 13
24)На средней линии трапеции ABCD с основаниями A D и BC выбрали произвольную точку K. Докажите, что сумма площадей треугольников BKC и AKD равна половине площади трапеции.
25)На стороне BC остроугольного треугольника ABC как на диаметре построена полуокружность, пересекающая высоту A D в точке M, A D 80 , MD 64, H — точка пересечения высот треугольника ABC. Найдите A H.
Ответ: 28,8
Сложные задания и ответы с 3 варианта:
Полина летом отдыхает у дедушки в деревне Ясной. В четверг они собираются съездить на велосипедах в село Майское в магазин. Из деревни Ясная в село Майское можно проехать по прямой лесной дорожке. Есть более длинный путь: по прямолинейному шоссе через деревню Камышёвку до деревни Хомяково, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в село Майское. Есть и третий маршрут: в деревне Камышёвке можно свернуть на прямую тропинку в село Майское, которая идёт мимо пруда. Лесная дорожка и тропинка образуют с шоссе прямоугольные треугольники. По шоссе Полина с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке — со скоростью 15 км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна 2 км.
1)Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других символов.
Ответ: 213
2)Сколько километров проедут Полина с дедушкой от деревни Камышёвка до села Майское, если они поедут по шоссе через деревню Хомяково?
Ответ: 34
3)Найдите расстояние от деревни Камышёвка до села Майское по прямой. Ответ дайте в километрах.
Ответ: 26
4)Сколько минут затратят на дорогу из деревни Ясная в село Майское Полина с дедушкой, если они поедут сначала по шоссе, а затем свернут в Камышёвке на прямую тропинку, которая проходит мимо пруда?
Ответ: 170
5)В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Ясная, селе Майское, деревне Камышёвка и деревне Хомяково. Полина с дедушкой хотят купить 2 л молока, 3 кг говядины и 2 кг картофеля. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Ответ: 1134
6)Найдите значение выражения 9,8 8,6 .
Ответ: 18,4
10)Родительский комитет закупил 10 пазлов для подарков детям в связи с окончанием учебного года, из них 4 с машинами и 6 с видами городов. Подарки распределяются случайным образом между 10 детьми, среди которых есть Володя. Найдите вероятность того, что Володе достанется пазл с машиной.
Ответ: 0,4
12)Перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, позволяет формула 1,8 32 F c t t , где t C — температура в градусах Цельсия, t F — температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует – 35 градусов по шкале Цельсия?
Ответ: -31
13)В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой 3 мг. Каждые 20 минут масса колонии увеличивается в 3 раза. Найдите массу колонии микроорганизмов через 80 минут после начала эксперимента. Ответ дайте в миллиграммах.
Ответ: 4
17)Диагональ прямоугольника образует угол 74º с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах
Ответ: 32
19)Какое из следующих утверждений верно? 1) Диагонали прямоугольника точкой пересечения делятся пополам. 2) Точка пересечения двух окружностей равноудалена от центров этих окружностей. 3) Площадь любого параллелограмма равна произведению длин его сторон.
Ответ: 1
21)Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 51 минуту, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 251 км, скорость первого велосипедиста равна 10 км/ч, скорость второго — 20 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
Ответ: 173 км
24)Внутри параллелограмма ABCD выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади параллелограмма.
25)Окружности радиусов 12 и 20 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
Ответ: 30
Сложные задания и ответы с 4 варианта:
Серёжа летом отдыхает с папой в деревне Пирожки. В среду они собираются съездить на машине в село Княжеское. Из деревни Пирожки в село Княжеское можно проехать по прямой грунтовой дороге. Есть более длинный путь: по прямолинейному шоссе через деревню Васильево до деревни Рябиновка, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в село Княжеское. Есть и третий маршрут: в деревне Васильево можно свернуть на прямую грунтовую дорогу в село Княжеское, которая идёт мимо пруда. Шоссе и грунтовые дороги образуют прямоугольные треугольники.
По шоссе Серёжа с папой едут со скоростью 60 км/ч, а по грунтовой дороге — со скоростью 40 км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна 2 км.
1)Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других символов.
Ответ: 423
2)Сколько километров проедут Серёжа с папой от деревни Васильево до села Княжеское, если они поедут по шоссе через деревню Рябиновку?
Ответ: 28
3)Найдите расстояние от деревни Васильево до села Княжеское по прямой. Ответ дайте в километрах.
Ответ: 20
4)Сколько минут затратят на дорогу из деревни Пирожки в село Княжеское Серёжа с папой, если они поедут сначала по шоссе, а затем свернут в деревне Васильево на прямую грунтовую дорогу, которая проходит мимо пруда?
Ответ: 48
5)В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Пирожки, селе Княжеском, деревне Васильево и деревне Рябиновке.
Ответ: 438
6)Серёжа с папой хотят купить 2 л молока, 3 батона хлеба и 1 кг сыра «Российский». В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Ответ: 12,1
10)Родительский комитет закупил 25 пазлов для подарков детям в связи с окончанием учебного года, из них 22 с машинами и 3 с видами городов. Подарки распределяются случайным образом между 25 детьми, среди которых есть Коля. Найдите вероятность того, что Коле достанется пазл с машиной.
Ответ: 0,88
14)В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой 14 мг. За каждые 30 минут масса колонии увеличивается в 3 раза. Найдите массу колонии микроорганизмов через 90 минут после начала эксперимента. Ответ дайте в миллиграммах.
Ответ: 378
17)Диагональ прямоугольника образует угол 86º с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Ответ: 8
19)Какое из следующих утверждений верно? 1) Отношение площадей подобных треугольников равно коэффициенту подобия. 2) Диагонали прямоугольника точкой пересечения делятся пополам. 3) Биссектриса треугольника делит пополам сторону, к которой проведена. В ответ запишите номер выбранного утверждения.
Ответ: 2
21)Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 48 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 168 км, скорость первого велосипедиста равна 15 км/ч, скорость второго — 30 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
Ответ: 120 км
23)Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60 и 135 , а CD 24 .
Ответ: 8 корень из 6
24)Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.
25)Окружности радиусов 45 и 90 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
12.2021 Пробный ОГЭ 2022 по математике 9 класс 4 варианта с ответами
Пробный ОГЭ 2022 по математике 9 класс региональная оценка качества образования у 9 классов 4 варианта для проведения пробного экзамена с ответами и решением, работа прошла в Тюменской области 72 регионе: 14 декабря 2021 года.
На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме. Сторона одной клетки на плане соответствует 0,4 м, а условные обозначения двери и окна приведены в правой части рисунка. Вход в квартиру находится в коридоре. Слева от входа в квартиру находится санузел, а в противоположном конце коридора – дверь в кладовую. Рядом с кладовой находится спальня, из которой можно пойти на одну из застекленных лоджий. Самое большое по площади помещение – гостиная, откуда можно попасть в коридор и на кухню. Из кухни также можно попасть на застекленную лоджию.
1)Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр.
Ответ: 6172
2)Паркетная доска размером 20 см на 80 см продается в упаковках по 12 штук. Сколько упаковок паркетной доски понадобилось, чтобы выложить пол в спальне?
Ответ: 9
3)Найдите площадь гостиной. Ответ дайте в квадратных метрах.
Ответ: 24,96
4)На сколько процентов площадь коридора больше площади кладовой?
Ответ: 525
5)В квартире планируется установить стиральную машину. Характеристики стиральных машин, условия подключения и доставки приведены в таблице. Планируется купить стиральную машину с фронтальной загрузкой, по глубине не превосходящую 42 см. Сколько рублей будет стоить наиболее дешёвый подходящий вариант вместе с подключением и доставкой?
Ответ: 28800
6)На координатной прямой отмечены точки A, B. C и D соответствуют числам – 0,032; 0,023; 0,302; – 0,203. Какой точке соответствует число – 0,203?
Ответ: 2,05
9)Решите уравнение – 2x–7= – 4x.
Ответ: 3,5
10)В лыжных гонках участвуют 7 спортсменов из России, 1 спортсмена из Швеции и 2 спортсмена из Норвегии. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из Швеции.
Ответ: 0,1
12)В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) длительностью более 5 минут рассчитывается по формуле C = 150+11 ⋅ (t − 5), где t — длительность поездки, выраженная в минутах. Пользуясь этой формулой, рассчитайте стоимость 13-минутной поездки. Ответ дайте в рублях.
Ответ: 238
14)В амфитеатре 14 рядов. В первом ряду 18 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в девятом ряду амфитеатра?
Ответ: 34
15)В треугольнике ABC известно, что угол BAC равен 84º, AD – биссектриса. Найдите угол BAD. Ответ дайте в градусах.
Ответ: 42
16)В треугольнике ABC известно, что AC=8, BC=15, угол C равен 90º. Найдите радиус описанной около этого треугольника окружности.
Ответ: 8,5
17)Диагонали AC и BD прямоугольника ABCD пересекаются в точке O, BO=24, AB=45. Найдите AC.
Ответ: 48
18)На клетчатой бумаге с размером клетки 1*1 изображён ромб. Найдите площадь этого ромба.
Ответ: 6
19)Какое из следующих утверждений верно? 1) Диагонали равнобедренной трапеции равны. 2) Если три угла одного треугольника равны соответственно трем углам другого треугольника, то такие треугольника равны. 3) Тангенс любого острого угла меньше единицы.
Ответ: 1
21)Теплоход проходит по течению реки до пункта назначения 80 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 5 км/ч, стоянка длится 23 часа, а в пункт отправления теплоход возвращается через 35 часов после отплытия из него.
Ответ: 15 км/ч
23)Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны A B и CB в точках P и K соответственно. Найдите PK, если BH 14 .
Ответ: 14
24)На средней линии трапеции ABCD с основаниями A D и BC выбрали произвольную точку K. Докажите, что сумма площадей треугольников BKC и AKD равна половине площади трапеции.
25)На стороне BC остроугольного треугольника ABC как на диаметре построена полуокружность, пересекающая высоту A D в точке M, A D 16 , MD 4 , H — точка пересечения высот треугольника ABC. Найдите A H.
Ответ: 15
16 В треугольнике ABC известно, что AC 8, BC 15, угол C равен 90º.
100ballnik. com
06.08.2020 7:59:46
2020-08-06 07:59:46
Источники:
Https://100ballnik. com/14-12-2021-%D0%BF%D1%80%D0%BE%D0%B1%D0%BD%D1%8B%D0%B9-%D0%BE%D0%B3%D1%8D-2022-%D0%BF%D0%BE-%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B5-9-%D0%BA%D0%BB%D0%B0%D1%81%D1%81-4-%D0%B2%D0%B0/
Наталья Ефимова | ВКонтакте » /> » /> .keyword { color: red; } Региональная оценка качества образования 2022 математика 9 класс вариант 9051
Наталья Ефимова
Наталья Ефимова
Как считал Александр Куприн, «не в силе, не в ловкости, не в уме, не в таланте, не в творчестве выражается индивидуальность. Но в любви!». Самое известное произведение о любви — повесть «Гранатовый браслет» и экранизация.
Наталья Ефимова запись закреплена
Открытый банк заданий по математике. ОГЭ
Наталья Ефимова запись закреплена
Математика Онлайн | ОГЭ, ЕГЭ по математике
Карточки из Конструктора на 4 четверть для 7 и 8 классов!
Бесплатно доступны (прикреплены к этому посту):
7 кл: задания на тему «Линейная функция»
Показать полностью.
7 кл: задания на тему «Системы линейных уравнений»
8 кл: задания на тему «Разложение квадратного трёхчлена на множители»
8 кл: задания на тему «Рациональные уравнения»
8 кл: задания на тему «Решение задач с помощью квадратных и рациональных уравнений, задач из ЕГЭ/ОГЭ»
видеоразборы к каждому заданию.
В платной версии:
возможность учителю самому создать карточки с уникальным набором заданий, которые ученики не смогут найти в решебниках;
возможность создавать карточки с ответами.
Ссылка на двухминутное видео о Конструкторе: https://mat-ege. ru/constructor/about. php
Карточки из Конструктора на 4 четверть для 7 и 8 классов!
В платной версии:
7 кл задания на тему Системы линейных уравнений 8 кл задания на тему Разложение квадратного трёхчлена на множители 8 кл задания на тему Рациональные уравнения 8 кл задания на тему Решение задач с помощью квадратных и рациональных уравнений, задач из ЕГЭ ОГЭ видеоразборы к каждому заданию.
Vk. com
17.06.2020 1:20:20
2020-06-17 01:20:20
Источники:
Https://vk. com/id76069100
- ОГЭ по математике
Подборка тренировочных вариантов по математике для 9 класса в формате ОГЭ 2023 с ответами и критериями оценивания.
Изменений относительно 2022 года нет, потому актуальны и варианты прошлого года.
Тренировочные варианты ОГЭ 2023 по математике
| alexlarin.net | уровень 1 | уровень 2 |
| вариант 327 | larin22-oge-327-1 | larin22-oge-327 |
| вариант 328 | larin22-oge-328-1 | larin22-oge-328 |
| вариант 329 | larin23-oge-329-1 | larin23-oge-329 |
| вариант 330 | larin23-oge-330-1 | larin23-oge-330 |
| вариант 331 | larin23-oge-331-1 | larin23-oge-331 |
| вариант 332 | larin23-oge-332-1 | larin23-oge-332 |
| вариант 333 | larin23-oge-333-1 | larin23-oge-333 |
| вариант 334 | larin23-oge-334-1 | larin23-oge-334 |
| вариант 335 | larin23-oge-335-1 | larin23-oge-335 |
| вариант 336 | larin23-oge-336-1 | larin23-oge-336 |
| вариант 337 | larin23-oge-337-1 | larin23-oge-337 |
| вариант 338 | larin23-oge-338-1 | larin23-oge-338 |
| вариант 339 | larin23-oge-339-1 | larin23-oge-339 |
| вариант 340 | larin23-oge-340-1 | larin23-oge-340 |
| вариант 341 | larin23-oge-341-1 | larin23-oge-341 |
| вариант 342 | larin23-oge-342-1 | larin23-oge-342 |
| вариант 343 | larin23-oge-343-1 | larin23-oge-343 |
| вариант 344 | larin23-oge-344-1 | larin23-oge-344 |
| вариант 345 | larin23-oge-345-1 | larin23-oge-345 |
| вариант 346 | larin23-oge-346-1 | larin23-oge-346 |
| вариант 347 | larin23-oge-347-1 | larin23-oge-347 |
| вариант 348 | larin23-oge-348-1 | larin23-oge-348 |
| вариант 349 | larin23-oge-349-1 | larin23-oge-349 |
| вариант 350 | larin23-oge-350-1 | larin23-oge-350 |
| вариант 351 | larin23-oge-351-1 | larin23-oge-351 |
| вариант 352 | larin23-oge-352-1 | larin23-oge-352 |
| math100.ru | |
| Вариант 54 | math100-oge-54 |
| Вариант 55 | math100-oge-55 |
| Вариант 56 | math100-oge-56 |
| Вариант 57 | math100-oge-57 |
| Вариант 58 | math100-oge-58 |
| Вариант 59 | math100-oge-59 |
| Вариант 60 | math100-oge-60 |
| Вариант 61 | math100-oge-61 |
| Вариант 62 | math100-oge-62 |
| Вариант 63 | math100-oge-63 |
| Вариант 64 | math100-oge-64 |
| Вариант 65 | math100-oge-65 |
| Вариант 66 | math100-oge-66 |
| Вариант 67 | math100-oge-67 |
| Вариант 68 | math100-oge-68 |
| Вариант 69 | math100-oge-69 |
| Вариант 70 | math100-oge-70 |
| Вариант 71 | math100-oge-71 |
| Вариант 72 | math100-oge-72 |
| Вариант 73 | math100-oge-73 |
| Вариант 74 | math100-oge-74 |
| Вариант 75 | math100-oge-75 |
| Вариант 76 | math100-oge-76 |
| Вариант 77 | math100-oge-77 |
| Вариант 78 | math100-oge-78 |
| Вариант 79 | math100-oge-79 |
| Вариант 80 | math100-oge-80 |
| time4math.ru | |
| Варианты 1-2 | ответы |
| Варианты 3-4 | ответы |
| Варианты 5-6 | ответы |
| Варианты 7-8 | ответы |
| Варианты 9-10 | ответы |
| Варианты 11-12 | ответы |
| Варианты 13-14 | ответы |
| Варианты 15-16 | ответы |
| vk.com/pezhirovschool | |
| Вариант 1 (с решением) | скачать |
| Вариант 2 (с решением) | скачать |
| Вариант 3 (с решением) | скачать |
| Вариант 4 (с решением) | скачать |
| Вариант 5 (с ответами) | скачать |
| Вариант 6 | скачать |
| vk.com/oge100ballov | |
| variant 1 | скачать |
| variant 2 | скачать |
| variant 3 | скачать |
| variant 4 | скачать |
| yagubov.ru | |
| вариант 33 (сентябрь) | скачать |
| вариант 34 (октябрь) | скачать |
| вариант 35 (ноябрь) | скачать |
| вариант 36 (декабрь) | скачать |
| вариант 37 (январь) | скачать |
| вариант 38 (февраль) | скачать |
| вариант 39 (март) | скачать |
| vk.com/math.studying | |
| вариант 1 | ответы |
| вариант 2 | ответы |
| vk.com/matematicalate | |
| variant 1 | скачать |
| variant 2 | скачать |
| variant 3 | скачать |
Характеристика структуры и содержания КИМ ОГЭ 2023 по математике
Работа содержит 25 заданий и состоит из двух частей.
Часть 1 содержит 19 заданий с кратким ответом; часть 2 – 6 заданий с развёрнутым ответом. При проверке базовой математической компетентности экзаменуемые должны продемонстрировать владение основными алгоритмами, знание и понимание ключевых элементов содержания (математических понятий, их свойств, приёмов решения задач и проч.), умение пользоваться математической записью, применять знания к решению математических задач, не сводящихся к прямому применению алгоритма, а также применять математические знания в простейших практических ситуациях.
Задания части 2 направлены на проверку владения материалом на повышенном и высоком уровнях. Их назначение – дифференцировать хорошо успевающих школьников по уровням подготовки, выявить наиболее подготовленных обучающихся, составляющих потенциальный контингент профильных классов.
Эта часть содержит задания повышенного и высокого уровней сложности из различных разделов математики.
Все задания требуют записи решений и ответа. Задания расположены по нарастанию трудности: от относительно простых до сложных, предполагающих свободное владение материалом и высокий уровень математической культуры.
Связанные страницы:
Тренировочные варианты по математике в формате ОГЭ 2021 с ответами.
Источник — time4math.ru
Автор: Ширяева Елена Алексеевна (математик, профессиональный репетитор)
Варианты соответствуют новой демоверсии ОГЭ 2021 года по математике.
→ варианты 1-2
→ варианты 3-4
→ варианты 5-6
→ варианты 7-8
→ Скачать ответы
→ варианты 9-10
→ варианты 11-12
→ варианты 13-14
→ варианты 15-16
→ Скачать ответы
Варианты от oge100ballov
→ Вариант 1 с ответами
→ Вариант 2 с ответами
→ Вариант 3 с ответами
→ Вариант 4 с ответами
→ Вариант 5 с ответами
Изменения в КИМ 2021 года по сравнению с 2020 годом:
В рамках усиления акцента на проверку применения математических знаний в различных ситуациях количество заданий уменьшилось на одно за счет объединения заданий на преобразование алгебраических (задание 13 в КИМ 2020 г.) и числовых выражений (задание 8 в КИМ 2020 г.) в одно задание на преобразование выражений на позиции 8 в КИМ 2021 г.
Задание на работу с последовательностями и прогрессиями (задание 12 в КИМ 2020 г.) заменено на задание с практическим содержанием, направленное на проверку умения применять знания о последовательностях и прогрессиях в прикладных ситуациях (задание 14 в КИМ 2021 г.).
Скорректирован порядок заданий в соответствии с тематикой и сложностью.
Связанные страницы:
Математика ОГЭ Действия с корнями Задание 8 Практика
Площадь треугольника — ОГЭ по математике (задания для тренировки)
Карточки по теме «Действия с обыкновенными дробями» Задание 6 ОГЭ по математике
Графики функций — подготовка к ОГЭ по математике
- ОГЭ по математике
Подборка тренировочных вариантов по математике для 9 класса в формате ОГЭ 2022 с ответами и критериями оценивания.
Соответствуют демоверсии ОГЭ 2022 по математике
Характеристика структуры и содержания КИМ ОГЭ 2022 по математике
Работа содержит 25 заданий и состоит из двух частей.
Часть 1 содержит 19 заданий с кратким ответом; часть 2 – 6 заданий с развёрнутым ответом.
При проверке базовой математической компетентности экзаменуемые должны продемонстрировать владение основными алгоритмами, знание и понимание ключевых элементов содержания (математических понятий, их свойств, приёмов решения задач и проч.), умение пользоваться математической записью, применять знания к решению математических задач, не сводящихся к прямому применению алгоритма, а также применять математические знания в простейших практических ситуациях.
Задания части 2 направлены на проверку владения материалом на повышенном и высоком уровнях. Их назначение – дифференцировать хорошо успевающих школьников по уровням подготовки, выявить наиболее подготовленных обучающихся, составляющих потенциальный контингент профильных классов.
Эта часть содержит задания повышенного и высокого уровней сложности из различных разделов математики. Все задания требуют записи решений и ответа. Задания расположены по нарастанию трудности: от относительно простых до сложных, предполагающих свободное владение материалом и высокий уровень математической культуры.
Смотрите также:
Sorry, your request has been denied.
Решение заданий Варианта №2 из сборника ОГЭ 2022 по математике Ф.Ф. Лысенко, С.О. Иванова 40 тренировочных вариантов. ГДЗ решебник для 9 класса. Ответы с решением. Полный разбор всех заданий.
ЧАСТЬ 1
Задание 1-5.
Автомобильное колесо, как правило, представляет из себя металлический диск, с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине.
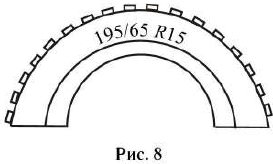
Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65R15 (см. рис. 8).
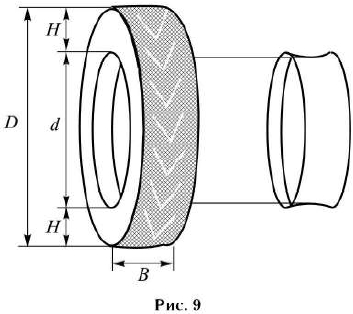
Первое число (число 195 в приведённом примере) обозначает ширину шины в миллиметрах (параметр В на рисунке 9).
Второе число (число 65 в приведённом примере) – процентное отношение высоты боковины (параметр Н на рисунке 9) к ширине шины, то есть 100·frac{H}{B}.
Последующая буква обозначает тип конструкции шины. В данном примере буква R обозначает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяется шины радиальной конструкции.
За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса d в дюймах (в одном дюйме 25,4 мм). Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины.
Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры.
Завод производит легковые автомобили определённой модели и устанавливает на них колёса с шинами маркировки 175/65R13.
Задание 6.
Найдите значение выражения frac{4}{35}+frac{13}{70}.
Задание 7.
Какое из данных чисел принадлежит отрезку [8; 9]?
1) frac{32}{6}
2) frac{47}{6}
3) frac{55}{6}
4) frac{53}{6}
Задание 8.
Найдите значение выражения (с–3)2·с8 при с = –18.
Задание 9.
Решите уравнение 5 – 2х = –3х.
Задание 10.
В коробке находятся фломастеры: 8 красных, 12 синих и 5 зелёных. Найдите вероятность того, что наудачу взятый фломастер окажется красным.
Задание 11.
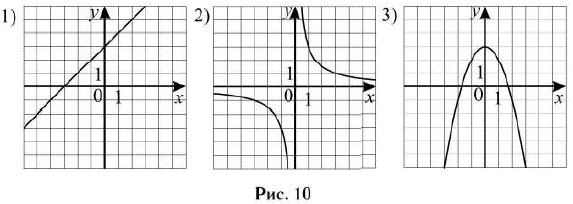
Установите соответствие между функциями и их графиками (см. рис. 10).
ФУНКЦИИ
А) у = х + 3
Б) у = 3 – х2
В) y=frac{3}{x}
ГРАФИКИ
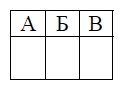
В таблице под каждой буквой укажите соответствующий номер.
Задание 12.
Расстояние S (в километрах), пройденное спортсменом, можно приближённо вычислить по формуле S = 6t, где t – количество часов в пути. Определите, через какое время спортсмен пройдёт 14 км. Ответ дайте в минутах.
Задание 13.
Укажите решение неравенства 15 – 6(х + 3) < 13 – 2x.
1) (–∞; -frac{1}{4})
2) (–4; +∞)
3) (–∞; -frac{1}{4})
4) (-frac{1}{4}; +∞)
Задание 14.
Регина написала на доске последовательность чисел. Первое число равно 13, а каждое следующее на 13 меньше, чем предыдущее. Найдите сумму первых 82 членов этой последовательности.
Задание 15.
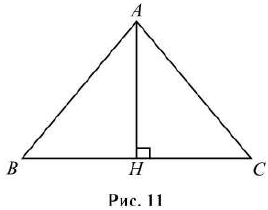
В остроугольном треугольнике АВС проведена высота АН, ∠АСВ = 64° (см. рис. 11). Найдите угол САН. Ответ дайте в градусах.
Задание 16.
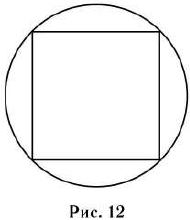
Радиус окружности, описанной около квадрата, равен 5√2 (см. рис. 12). Найдите длину стороны этого квадрата.
Задание 17.
Найдите площадь прямоугольника, если его периметр равен 32 и одна из его сторон на 4 больше другой (см. рис. 13).
Задание 18.
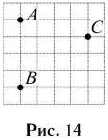
На клетчатой бумаге с размером клетки 1см х 1 см отмечены точки А, В и С (см. рис. 14). Найдите расстояние от точки С до прямой АВ. Ответ дайте в сантиметрах.
Задание 19.
Какие из следующих утверждений верны?
1) Диагонали прямоугольника равны.
2) Все равнобедренные треугольники подобны.
3) Если диагонали параллелограмма перпендикулярны, то это ромб.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
ЧАСТЬ 2
Задание 20.
Решите уравнение х3 + 3х2 = 9х + 27.
Задание 21.
Два мотоциклиста одновременно отправились в 420-километровый мотопробег. Первый едет со скоростью на 10 км/ч больше, чем второй, и прибывает к финишу на 1 час раньше второго. Найдите скорость (в км/ч) первого мотоциклиста.
Задание 22.
Постройте график функции y=-4-frac{x^{4}-2x^{3}}{2x-x^{2}} и определите, при каких значениях p прямая у = р имеет с графиком две общие точки.
Задание 23.
Высота треугольника разбивает его основание на два отрезка с длинами 4 и 7. Найдите длину этой высоты, если известно, что другая высота треугольника делит её в отношении 2:7, считая от вершины.
Задание 24.
Дан правильный шестиугольник. Докажите, что если середины его сторон последовательно соединить отрезками, то получится правильный шестиугольник.
Задание 25.
Через середину D медианы АК треугольника АВС и вершину В проведена прямая, пересекающая сторону АС в точке Т. Найдите отношение площади треугольника АDТ к площади четырёхугольника СКDТ.
Источник варианта: Сборник ОГЭ 2022 по математике под редакцией Ф.Ф. Лысенко, С.О. Иванова, 40 тренировочных вариантов по новой демоверсии 2022, Легион.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.2 / 5. Количество оценок: 5
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.
Тест «Виды потребления»
Проверочная работа по обществознанию.
Календарь диктантов 2022
Общие материалы | Вчера, 20:46
Расписание Всероссийских диктантов на 2022 год.
ОГЭ по математике
-
20.02.2023Тренировочный варианта №4 ОГЭ по математике
(3685)
-
03.02.2023Тренировочная работа №3 Статград ОГЭ 2023 по математике от 31.01.2023
(8503)
-
10.12.2022Тренировочный вариант №3 ОГЭ 2023 по математике с ответами
(13186)
-
09.12.2022Тренировочный вариант Статград №2 ОГЭ 2023 по математике от 29.11.2022
(7661)
-
09.12.2022Тренировочный вариант №2 ОГЭ 2023 по математике с ответами
(5380)
-
21.11.2022Тренировочный вариант №1 ОГЭ 2023 по математике с ответами
(9392)
-
12.10.2022Тренировочная работа №1 Статград ОГЭ 2023 по математике от 05.10.2022
(16657)
-
23.04.2022Тренировочная работа №5 ОГЭ 2022 по математике СТАТГРАД от 18.04.2022
(27473)
-
23.04.2022Реальный ОГЭ 2022 по математике
(108944)
-
23.04.2022Досрочный ОГЭ 2022 по математике от 21.04.2022
(121197)
-
14.03.2022Тренировочный вариант №6 ОГЭ 2022 по математике с ответами
(25878)
-
11.03.2022Тренировочная работа ОГЭ 2022 по математике №4 СтатГрад от 11.03.2022
(29404)
-
25.01.2022Тренировочная работа №3 Статград ОГЭ по математике от 20.01.22 9 класс
(28885)
-
25.12.2021Тренировочный вариант №5 ОГЭ 2022 по математике с ответами
(26767)
-
28.11.2021Тренировочный вариант №4 ОГЭ 2022 по математике с ответами
(27332)
-
27.11.2021Тренировочная работа №2 Статград ОГЭ 2022 по математике от 17.11.21 с ответами
(23448)
-
05.11.2021Тренировочная работа №3 ОГЭ 2022 по математике
(19004)
-
14.10.2021Тренировочная работа №1 СТАТГРАД ОГЭ 2022 по математике от 05.10.21
(29534)
-
09.10.2021Тренировочный вариант №2 ОГЭ 2022 по математике с ответами
(20534)
-
11.09.2021Тренировочный вариант №1 ОГЭ 2022 по математике с ответами
(33644)
-
11.05.2021Тренировочный вариант №13 ОГЭ 2021 по математике с ответами
(54038)
-
21.04.2021Тренировочный вариант №12 ОГЭ 2021 по математике с ответами
(34398)
-
13.04.2021Тренировочный вариант №11 ОГЭ 2021 по математике с ответами
(22461)
-
06.04.2021Тренировочный вариант №10 ОГЭ 2021 по математике с ответами
(27284)
-
29.03.2021Тренировочный вариант №9 ОГЭ 2021 по математике с ответами
(20459)
-
19.02.2021Тренировочный вариант №8 ОГЭ 2021 по математике с ответами
(44317)
-
28.01.2021Тренировочный вариант №7 ОГЭ 2021 по математике с ответами
(56041)
-
02.01.2021Пробный ОГЭ 2021 №6 по математике с ответами
(54668)
-
11.12.2020Пробный ОГЭ 2021 №5 по математике с ответами
(44992)
-
01.12.2020Тренировочная работа Статград ОГЭ по математике №2 от 25.11.20
(26897)
-
30.10.2020Пробный ОГЭ 2021 №4 по математике с ответами
(71435)
-
10.10.2020Тренировочная работа ОГЭ 2021 по математике №3
(33655)
-
07.10.2020Тренировочная работа №1 Статград ОГЭ 2021 по математике от 02.10.20
(52976)
-
17.09.2020Тренировочный вариант ОГЭ 2021 по математике №2
(44045)
-
13.09.2020Пробный ОГЭ 2021 по математике №1
(66655)
-
23.04.2020Досрочный ОГЭ 2020 по математике с ответами
(46948)
-
19.04.2020Пробный ОГЭ 2020 №18 по математике с ответами
(28774)
-
29.03.2020Пробный ОГЭ 2020 №17 по математике с ответами
(35183)
-
24.03.2020Тренировочная работа №4 Статград ОГЭ по математике от 05.03.20
(19888)
-
23.03.2020Пробный ОГЭ 2020 №16 по математике с ответами
(21449)
-
14.03.2020Пробный ОГЭ 2020 №15 по математике с ответами
(29475)
-
09.03.2020Тренировочная работа №4 ОГЭ 2020 по математике Статград 05.03.2020
(26187)
-
19.02.2020Пробный ОГЭ 2020 №14 по математике с ответами
(44034)
-
15.02.2020Пробный ОГЭ 2020 №13 по математике с ответами
(34463)
-
09.02.2020Пробный ОГЭ 2020 №12 по математике с ответами
(35551)
-
08.02.2020Тренировочная работа №3 СтатГрад ОГЭ математике от 4.02.20
(45838)
-
04.02.2020Пробный ОГЭ 2020 №11 по математике с ответами
(41967)
-
20.01.2020Пробный ОГЭ 2020 №10 по математике с ответами
(54193)
-
13.01.2020Пробный ОГЭ 2020 №9 по математике с ответами
(34404)
-
24.12.2019Пробный ОГЭ 2020 №8 по математике
(38667)
-
17.12.2019Пробный ОГЭ 2020 №7 по математике с ответами
(64700)
-
06.12.2019Пробный ОГЭ 2020 №6 по математике с ответами
(45246)
-
26.11.2019Пробный ОГЭ 2020 №5 по математике с ответами
(48817)
-
16.11.2019Тренировочная работа №2 Статград ОГЭ по математике от 12.11.19
(61339)
-
08.11.2019Пробный ОГЭ 2020 №4 по математике с ответами
(69715)
-
07.10.2019Тренировочный вариант Статград ОГЭ математике от 3.10.19
(88362)
-
23.09.2019Пробный ОГЭ 2020 №3 по математике с ответами
(91290)
-
20.09.2019Пробный ОГЭ 2020 №2 по математике с ответами
(99845)
-
19.09.2019Пробный ОГЭ 2020 №1 по математике с ответами
(112231)
-
16.05.2019Тренировочная работа ОГЭ 2019 по математике №9 с ответами
(47122)
-
16.05.2019Тренировочная работа №5 Статград ОГЭ 2019 по математике от 15.05.19
(33575)
-
08.04.2019Пробный ОГЭ 2019 по математике №8 с ответами
(52948)
-
08.04.2019Пробный ОГЭ 2019 по математике №7 с ответами
(29384)
-
22.03.2019Пробный ОГЭ 2019 по математике №6 с ответами
(33172)
-
21.03.2019Диагностическая работа №1 ОГЭ по математике СтатГрад от 19.03.19
(41983)
-
13.03.2019Пробный ОГЭ 2019 по математике №5 с ответами
(30992)
-
13.03.2019Пробный ОГЭ 2019 по математике №4 с ответами
(28342)
-
13.03.2019Пробный ОГЭ 2019 по математике №3 с ответами
(24376)
-
13.03.2019Пробный ОГЭ 2019 по математике №2 с ответами
(41106)
-
17.02.2019Тренировочная работа №3 СтатГрад ОГЭ по математике от 12.02.19
(42953)
-
16.11.2018Тренировочный вариант Статград №2 ОГЭ по математике от 8.11.18
(51949)
-
27.09.2018Тренировочная работа ОГЭ 2019 Статград по математике от 27.09.18
(83457)
-
09.09.2018Пробный ОГЭ 2019 по математике №1 с ответами
(172725)
-
24.05.2018Тренировочная работа Статград ОГЭ по математике 14.05.18
(31967)
-
25.03.2018Тренировочная работа Статград ОГЭ по математике от 21.03.18
(44533)
-
21.02.2018Тренировочная работа Статград ОГЭ по математике от 13.02.2018
(54582)
-
19.01.2018Пробный вариант ОГЭ 2018 по математике с решениями и ответами
(49249)
-
13.11.2017Тренировочная работа Статград по математике 9 класс от 9.11.2017
(108251)
-
15.10.2017Пробный ОГЭ 2018 по математике №1 с ответами
(118766)
-
30.09.2017Тренировочная работа ОГЭ 2018 СтатГрад по математике от 27.09.2017
(61344)
-
29.04.2017Пробный ОГЭ 2017 по математике №17 с ответами
(72262)
-
29.04.2017Пробный ОГЭ 2017 по математике №16 с ответами
(39276)
-
23.04.2017Пробный вариант ОГЭ 2017 по математике №15 с ответами
(18303)
-
23.04.2017Пробный вариант ОГЭ 2017 по математике №14 с ответами
(12925)
-
23.04.2017Пробный вариант ОГЭ 2017 по математике №13 с ответами
(12789)
-
23.04.2017Пробный вариант ОГЭ 2017 по математике №12 с ответами
(12169)
-
23.04.2017Пробный вариант ОГЭ 2017 по математике №11 с ответами
(12431)
-
23.04.2017Пробный вариант ОГЭ 2017 по математике №10
(10355)
-
23.04.2017Пробный вариант ОГЭ 2017 по математике №9
(28235)
-
23.04.2017Пробный вариант ОГЭ 2017 по математике №8
(9309)
-
23.04.2017Пробный вариант ОГЭ 2017 по математике №7
(11901)
-
23.04.2017Пробный вариант ОГЭ 2017 по математике №6
(3359)
-
14.03.201610 тренировочных вариантов ОГЭ 2016 по математике (с ответами)
(24721)
-
05.02.2016Пробный ОГЭ 2016 по математике №3
(12745)
-
05.02.2016Пробный ОГЭ 2016 по математике №2 с ответами и решениями
(13438)
-
05.02.2016Пробный ОГЭ 2016 по математике №1 с ответами и решениями
(11294)
-
22.01.2016Пробный вариант ОГЭ 2016 по математике с ответами
(32541)
-
19.04.2015Пробные варианты ОГЭ 2015 по математике
(30802)
-
01.08.2014Реальные варианты ГИА 2014 по математике
(19499)
-
07.01.201410 вариантов тренировочных работ ГИА по математике 2014 года с ответами и критериями оценки
(19531)
Обновлено: 10.03.2023
Тренировочный вариант предназначен для того, чтобы дать возможность участнику экзамена составить представление о структуре будущей экзаменационной работы, количестве и форме заданий, а также об их уровне сложности.
Тренировочный вариант №1: скачать
Тренировочный вариант №2: скачать
Тренировочный вариант №3: скачать
Тренировочный вариант №4: скачать
Решать тренировочный вариант №1 ОГЭ 2022 по математике:
Решать тренировочный вариант №2 ОГЭ 2022 по математике:
Решать тренировочный вариант №3 ОГЭ 2022 по математике:
Решать тренировочный вариант №4 ОГЭ 2022 по математике:
P.S кому нужен видео разбор вариантов напишите в комментарии.
Сложные задания и ответы 1 варианта:
На плане изображён дачный участок по адресу: п. Сосновка, ул. Зелёная, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота. При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв. м, а чуть подальше — жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведёт дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1 м×1 м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой. К участку подведено электричество. Имеется магистральное газоснабжение.
2)Плитки для садовых дорожек продаются в упаковках по 4 штуки. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки?
3)Найдите площадь, которую занимает гараж. Ответ дайте в квадратных метрах.
4)На сколько процентов площадь, которую занимает теплица, меньше площади, которую занимает гараж?
5)Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв. м, а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице. Во сколько рублей обойдётся наиболее дешёвый вариант покупки с доставкой?
6)Найдите значение выражения 6,4 – 4,8.
9)Решите уравнение 4(𝑥 + 1) = 9
10)В фирме такси в данный момент свободно 20 машин: 8 чёрных, 7 жёлтых и 5 зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.
12)Перевести значение температуры по шкале Фаренгейта в шкалу Цельсия позволяет формула tC = 5 9 (tF − 32), где tС — температура в градусах Цельсия, tF — температура в градусах Фаренгейта. Скольким градусам по шкале Цельсия соответствует 167 градусов по шкале Фаренгейта?
14)У Кати есть теннисный мячик. Она со всей силы бросила его об асфальт. После первого отскока мячик подлетел на высоту 540 см, а после каждого следующего отскока от асфальта подлетал на высоту в три раза меньше предыдущей. После какого по счёту отскока высота, на которую подлетит мячик, станет меньше 10 см?
15)Диагонали AC и BD прямоугольника ABCD пересекаются в точке O, BO = 37, AB = 56. Найдите AC.
16)Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 42, сторона BC равна 44, сторона AC равна 62. Найдите MN.
19)Какое из следующих утверждений верно? 1) Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники равны. 2) Все диаметры окружности равны между собой. 3) Площадь параллелограмма равна половине произведения его диагоналей. В ответ запишите номер выбранного утверждения.
21)Первая труба пропускает на 6 литров воды в минуту меньше, чем вторая труба. Сколько литров воды в минуту пропускает первая труба, если резервуар объёмом 140 литров она заполняет на 3 минуты дольше, чем вторая труба?
22)Постройте график функции y = 3|x + 2| − x 2 − 3x − 2 . Определите, при каких значениях m прямая y = m имеет с графиком ровно три общие точки.
23)Углы B и C треугольника ABC равны соответственно 71° и 79°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 8.
24)Биссектрисы углов B и C параллелограмма ABCD пересекаются в точке M, лежащей на стороне AD. Докажите, что M — середина AD.
25)Биссектриса CM треугольника ABC делит сторону AB на отрезки AM = 4 и MB = 8. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Сложные задания и ответы 2 варианта:
1)Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк перенесите последовательность четырёх цифр без пробелов, запятых и других дополнительных символов.
2)Плитка для пола размером 20 см на 40 см продаётся в упаковках по 8 штук. Сколько упаковок плитки понадобилось, чтобы выложить пол санузла?
3)Найдите площадь большей лоджии. Ответ дайте в квадратных метрах.
4)На сколько процентов площадь санузла больше площади кладовой?
5)В квартире планируется подключить интернет. Предполагается, что трафик составит 650 Мб в месяц, и исходя из этого выбирается наиболее дешёвый вариант. Интернет-провайдер предлагает три тарифных плана. Сколько рублей нужно будет заплатить за интернет за месяц, если трафик действительно будет равен 650 Мб?
9)Решите уравнение 8𝑥 2 = 72𝑥 Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
10)На тарелке лежат одинаковые на вид пирожки: 4 с мясом, 9 с капустой и 3 с вишней. Петя наугад выбирает один пирожок. Найдите вероятность того, что этот пирожок окажется с мясом.
11)На рисунке изображены графики функций вида y = kx + b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
13)Укажите решение неравенства −3 − 3𝑥 > 7𝑥 − 9
14)При проведении опыта вещество равномерно охлаждали в течение 10 минут. При этом каждую минуту температура вещества уменьшалась на 7° C. Найдите температуру вещества (в градусах Цельсия) через 6 минут после начала проведения опыта, если его начальная температура составляла − 8° C .
15)В треугольнике ABC угол C равен 90°, BC = 16, AB = 25. Найдите cosB.
16)Радиус окружности, описанной около квадрата, равен 32√2. Найдите длину стороны этого квадрата.
17)Сумма двух углов равнобедренной трапеции равна 218°. Найдите меньший угол трапеции. Ответ дайте в градусах
19)Какое из следующих утверждений верно? 1) Диагонали прямоугольника точкой пересечения делятся пополам. 2) Точка пересечения двух окружностей равноудалена от центров этих окружностей. 3) Площадь любого параллелограмма равна произведению длин его сторон. В ответ запишите номер выбранного утверждения.
20)Решите уравнение (𝑥 − 1)(𝑥 2 + 4𝑥 + 4) = 4(𝑥 + 2).
21)Поезд, двигаясь равномерно со скоростью 141 км/ч, проезжает мимо пешехода, идущего в том же направлении параллельно путям со скоростью 6 км/ч, за 12 секунд. Найдите длину поезда в метрах.
23)Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F . Найдите AB, если AF = 24, BF = 7 .
24)Через точку О пересечения диагоналей параллелограмма АВСD проведена прямая, пересекающая стороны AB и CD в точках E и F соответственно. Докажите, что отрезки AE и CF равны.
25)В треугольнике ABC известны длины сторон AB = 84, AC = 98, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.
Сложные задания и ответы 3 варианта:
2)Сколько рублей потратил абонент на услуги связи в декабре?
3)Сколько месяцев в 2019 году абонент превысил лимит по пакету исходящих минут?
5)Абонент решает, перейти ли ему на новый тариф, посчитав, сколько бы он потратил на услуги связи за 2019 г., если бы пользовался им. Если получится меньше, чем он потратил фактически за 2019 г., то абонент примет решение сменить тариф. Перейдёт ли абонент на новый тариф? В ответе запишите ежемесячную абонентскую плату по тарифу, который выберет абонент на 2020 год.
9)Решите уравнение 𝑥 2 − 121 = 0 Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
10)У бабушки 10 чашек: 4 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
12)Мощность постоянного тока (в ваттах) вычисляется по формуле P = 𝐼 2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 224 Вт, а сила тока равна 4 А. Ответ дайте в омах.
14)В амфитеатре 23 ряда, причём в каждом следующем ряду на одно и то же число мест больше, чем в предыдущем. В седьмом ряду 26 мест, а в одиннадцатом ряду 34 места. Сколько мест в последнем ряду амфитеатра?
15)В треугольнике ABC известно, что AB = BC, ∠ABC = 148°. Найдите угол BCA. Ответ дайте в градусах.
16)Сторона равностороннего треугольника равна 4√3. Найдите радиус окружности, описанной около этого треугольника.
17)Один из углов параллелограмма равен 74°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
19)Какое из следующих утверждений верно? 1) Площадь параллелограмма равна половине произведение его диагоналей. 2) Сумма углов прямоугольного треугольника равна 90 градусам. 3) Биссектрисы треугольника пересекаются в точке, которая является центром окружности, вписанной в треугольник. В ответ запишите номер выбранного утверждения.
20)Решите неравенство (𝑥 − 3) 2 Сложные задания и ответы 4 варианта:
2)Найдите расстояние от Антоновки до Егорки по шоссе. Ответ дайте в километрах.
3)Найдите расстояние от Егорки до Жилино по прямой. Ответ дайте в километрах.
4)Сколько минут затратят на дорогу Таня с дедушкой из Антоновки в Богданово, если поедут мимо пруда через Горюново?
5)На просёлочных дорогах машина дедушки расходует 9,2 литра бензина на 100 км. Известно, что на путь из Антоновки до Богданово через Ванютино и путь через Доломино и Горюново мимо конюшни ей необходим один и тот же объём бензина. Сколько литров бензина на 100 км машина дедушки расходует на шоссе?
7)На координатной прямой точки A, B, C и D соответствуют числам 0,1032; − 0,031; − 0,01; − 0,104.
9)Решите уравнение (x − 6)(− 5x − 9) = 0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
10)Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,07. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
12)Центростремительное ускорение при движении по окружности ( в м/с2 ) вычисляется по формуле a = ω 2 R, где ω — угловая скорость ( в с-1 ), R — радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус R, если угловая скорость равна 9 с-1 , а центростремительное ускорение равно 405 м/с2 . Ответ дайте в метрах.
13)Укажите решение неравенства x 2 > 36
14)У Яны есть попрыгунчик (каучуковый шарик). Она со всей силы бросила его об асфальт. После первого отскока попрыгунчик подлетел на высоту 240 см, а после каждого следующего отскока от асфальта подлетал на высоту в два раза меньше предыдущей. После какого по счёту отскока высота, на которую подлетит попрыгунчик, станет меньше 5 см?
15)В треугольнике два угла равны 27° и 79°. Найдите его третий угол. Ответ дайте в градусах.
16)Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 5, AC = 45. Найдите AK.
17)Найдите площадь квадрата, описанного около окружности радиуса 7.
19)Какие из следующих утверждений верны? 1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой. 2) Если диагонали параллелограмма равны, то этот параллелограмм является ромбом. 3) Расстояние от точки, лежащей на окружности, до центра окружности равно радиусу.
21)Первый рабочий за час делает на 9 деталей больше, чем второй, и выполняет заказ, состоящий из 216 деталей, на 4 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
23)Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH = 10, AC = 40.
24)Окружности с центрами в точках E и F пересекаются в точках C и D, причём точки E и F лежат по одну сторону от прямой CD. Докажите, что прямые CD и EF перпендикулярны.
25)Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC = 7, а расстояние от точки K до стороны AB равно 4.
Пробный ОГЭ 2021 по математике №1 с ответами. Школа Пифагора. Тренировочные варианты ОГЭ 2021 по математике с ответами.
Примеры некоторых заданий из варианта
10. В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
Ответ: ___________________________.
12. Мощность постоянного тока (в ваттах) вычисляется по формуле 𝑃=𝐼 2 𝑅, где 𝐼− сила тока (в амперах), 𝑅− сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление 𝑅, если мощность составляет 224 Вт, а сила тока равна 4 А. Ответ дайте в омах.
Ответ: ___________________________.
14. Улитка ползет от одного дерева до другого. Каждый день она проползает на одно и то же расстояние больше, чем в предыдущий день. Известно, что за первый и последний дни улитка проползла в общей сложности 11 метров. Определите, сколько дней улитка потратила на весь путь, если расстояние между деревьями равно 33 метрам.
Ответ: ___________________________.
Тренировочный вариант №19 ОГЭ 2021 по математике с ответами Школа Пифагора. Пробные варианты ОГЭ 2021 по математике с ответами.
Примеры некоторых заданий из варианта
10. Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,19. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Ответ: ___________________________.
14. Турист идет из одного города в другой, каждый день проходя больше, чем в предыдущий день, на одно и то же расстояние. Известно, что за первый день турист прошел 8 километров. Определите, сколько километров прошел турист за четвертый день, если весь путь он прошел за 10 дней, а расстояние между городами составляет 215 километров.
Ответ: ___________________________.
19. Какое из следующих утверждений верно?
1) Средняя линия трапеции параллельна её основаниям.
2) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
3) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
В ответ запишите номер выбранного утверждения.
Ответ: ___________________________.
Пробный ОГЭ 2022 по математике 9 класс региональная оценка качества образования у 9 классов 4 варианта для проведения пробного экзамена с ответами и решением, работа прошла в Тюменской области 72 регионе: 14 декабря 2021 года.
Пробное ОГЭ 2022 по математике 9 класс вариант №9051
Пробное ОГЭ 2022 по математике 9 класс вариант №9052
Пробное ОГЭ 2022 по математике 9 класс вариант №9053
Пробное ОГЭ 2022 по математике 9 класс вариант №9054
Сложные задания и ответы с 1 варианта:
Ответ: 6172
2)Паркетная доска размером 20 см на 80 см продается в упаковках по 12 штук. Сколько упаковок паркетной доски понадобилось, чтобы выложить пол в спальне?
Ответ: 9
3)Найдите площадь гостиной. Ответ дайте в квадратных метрах.
Ответ: 24,96
4)На сколько процентов площадь коридора больше площади кладовой?
Ответ: 525
5)В квартире планируется установить стиральную машину. Характеристики стиральных машин, условия подключения и доставки приведены в таблице. Планируется купить стиральную машину с фронтальной загрузкой, по глубине не превосходящую 42 см. Сколько рублей будет стоить наиболее дешёвый подходящий вариант вместе с подключением и доставкой?
Ответ: 28800
6)На координатной прямой отмечены точки A, B. C и D соответствуют числам – 0,032; 0,023; 0,302; – 0,203. Какой точке соответствует число – 0,203?
Ответ: 2,05
9)Решите уравнение – 2x–7= – 4x.
Ответ: 3,5
10)В лыжных гонках участвуют 7 спортсменов из России, 1 спортсмена из Швеции и 2 спортсмена из Норвегии. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из Швеции.
Ответ: 0,1
Ответ: 238
14)В амфитеатре 14 рядов. В первом ряду 18 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в девятом ряду амфитеатра?
Ответ: 34
15)В треугольнике ABC известно, что угол BAC равен 84º, AD – биссектриса. Найдите угол BAD. Ответ дайте в градусах.
Ответ: 42
16)В треугольнике ABC известно, что AC=8, BC=15, угол C равен 90º. Найдите радиус описанной около этого треугольника окружности.
Ответ: 8,5
17)Диагонали AC и BD прямоугольника ABCD пересекаются в точке O, BO=24, AB=45. Найдите AC.
Ответ: 48
18)На клетчатой бумаге с размером клетки 1*1 изображён ромб. Найдите площадь этого ромба.
Ответ: 6
19)Какое из следующих утверждений верно? 1) Диагонали равнобедренной трапеции равны. 2) Если три угла одного треугольника равны соответственно трем углам другого треугольника, то такие треугольника равны. 3) Тангенс любого острого угла меньше единицы.
Ответ: 1
21)Теплоход проходит по течению реки до пункта назначения 80 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 5 км/ч, стоянка длится 23 часа, а в пункт отправления теплоход возвращается через 35 часов после отплытия из него.
Ответ: 15 км/ч
23)Точка H является основанием высоты BH , проведённой из вершины прямого угла B прямоугольного треугольника ABC . Окружность с диаметром BH пересекает стороны A B и CB в точках P и K соответственно. Найдите PK , если BH 14 .
Ответ: 14
24)На средней линии трапеции ABCD с основаниями A D и BC выбрали произвольную точку K . Докажите, что сумма площадей треугольников BKC и AKD равна половине площади трапеции.
25)На стороне BC остроугольного треугольника ABC как на диаметре построена полуокружность, пересекающая высоту A D в точке M , A D 16 , MD 4 , H — точка пересечения высот треугольника ABC . Найдите A H .
Ответ: 15
Сложные задания и ответы с 2 варианта:
2)Паркетная доска размером 20 см на 80 см продается в упаковках по 12 штук. Сколько упаковок паркетной доски понадобилось, чтобы выложить пол в кладовой?
Ответ: 2
3)Найдите площадь гостиной. Ответ дайте в квадратных метрах.
Ответ: 24,96
4)На сколько процентов площадь кухни больше площади санузла?
Ответ: 200
5)В квартире планируется установить стиральную машину. Характеристики стиральных машин, условия подключения и доставки приведены в таблице. Планируется купить стиральную машину с фронтальной загрузкой, вместимостью не менее 6 кг.
Ответ: 29300
10)В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
Ответ: 0.35
Ответ: 271
14)В амфитеатре 15 рядов. В первом ряду 20 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в десятом ряду амфитеатра?
Ответ: 38
15)В треугольнике ABC известно, что угол BAC равен 64º, AD – биссектриса. Найдите угол BAD. Ответ дайте в градусах.
Ответ: 32
16)В треугольнике ABC известно, что AC=16, BC=12, угол C равен 90º. Найдите радиус описанной около этого треугольника окружности.
Ответ: 10
17)Диагонали AC и BD прямоугольника ABCD пересекаются в точке O, BO=11, AB=10. Найдите AC.
Ответ: 22
19)Какие из следующих утверждений верны? 1) Если диагонали параллелограмма равны, то этот параллелограмм является ромбом. 2) Сумма острых углов прямоугольного треугольника равна 90 градусам. 3) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
Ответ: 23
21)Теплоход проходит по течению реки до пункта назначения 165 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 26 км/ч, стоянка длится 5 часов, а в пункт отправления теплоход возвращается через 18 часов после отплытия из него.
Ответ: 4 км/ч
23)Точка H является основанием высоты BH , проведённой из вершины прямого угла B прямоугольного треугольника ABC . Окружность с диаметром BH пересекает стороны A B и CB в точках P и K соответственно. Найдите BH , если PK 13.
Ответ: 13
24)На средней линии трапеции ABCD с основаниями A D и BC выбрали произвольную точку K . Докажите, что сумма площадей треугольников BKC и AKD равна половине площади трапеции.
25)На стороне BC остроугольного треугольника ABC как на диаметре построена полуокружность, пересекающая высоту A D в точке M , A D 80 , MD 64, H — точка пересечения высот треугольника ABC . Найдите A H .
Ответ: 28,8
Сложные задания и ответы с 3 варианта:
Полина летом отдыхает у дедушки в деревне Ясной. В четверг они собираются съездить на велосипедах в село Майское в магазин. Из деревни Ясная в село Майское можно проехать по прямой лесной дорожке. Есть более длинный путь: по прямолинейному шоссе через деревню Камышёвку до деревни Хомяково, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в село Майское. Есть и третий маршрут: в деревне Камышёвке можно свернуть на прямую тропинку в село Майское, которая идёт мимо пруда. Лесная дорожка и тропинка образуют с шоссе прямоугольные треугольники. По шоссе Полина с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке — со скоростью 15 км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна 2 км.
Ответ: 213
2)Сколько километров проедут Полина с дедушкой от деревни Камышёвка до села Майское, если они поедут по шоссе через деревню Хомяково?
Ответ: 34
3)Найдите расстояние от деревни Камышёвка до села Майское по прямой. Ответ дайте в километрах.
Ответ: 26
4)Сколько минут затратят на дорогу из деревни Ясная в село Майское Полина с дедушкой, если они поедут сначала по шоссе, а затем свернут в Камышёвке на прямую тропинку, которая проходит мимо пруда?
Ответ: 170
5)В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Ясная, селе Майское, деревне Камышёвка и деревне Хомяково. Полина с дедушкой хотят купить 2 л молока, 3 кг говядины и 2 кг картофеля. В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.
Ответ: 1134
6)Найдите значение выражения 9,8 8,6 .
Ответ: 18,4
10)Родительский комитет закупил 10 пазлов для подарков детям в связи с окончанием учебного года, из них 4 с машинами и 6 с видами городов. Подарки распределяются случайным образом между 10 детьми, среди которых есть Володя. Найдите вероятность того, что Володе достанется пазл с машиной.
Ответ: 0,4
12)Перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, позволяет формула 1,8 32 F c t t , где t C — температура в градусах Цельсия, t F — температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует – 35 градусов по шкале Цельсия?
Ответ: -31
13)В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой 3 мг. Каждые 20 минут масса колонии увеличивается в 3 раза. Найдите массу колонии микроорганизмов через 80 минут после начала эксперимента. Ответ дайте в миллиграммах.
Ответ: 4
17)Диагональ прямоугольника образует угол 74º с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах
Ответ: 32
19)Какое из следующих утверждений верно? 1) Диагонали прямоугольника точкой пересечения делятся пополам. 2) Точка пересечения двух окружностей равноудалена от центров этих окружностей. 3) Площадь любого параллелограмма равна произведению длин его сторон.
Ответ: 1
21)Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 51 минуту, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 251 км, скорость первого велосипедиста равна 10 км/ч, скорость второго — 20 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
Ответ: 173 км
24)Внутри параллелограмма ABCD выбрали произвольную точку F . Докажите, что сумма площадей треугольников BFC и AFD равна половине площади параллелограмма.
25)Окружности радиусов 12 и 20 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD .
Ответ: 30
Сложные задания и ответы с 4 варианта:
Серёжа летом отдыхает с папой в деревне Пирожки. В среду они собираются съездить на машине в село Княжеское. Из деревни Пирожки в село Княжеское можно проехать по прямой грунтовой дороге. Есть более длинный путь: по прямолинейному шоссе через деревню Васильево до деревни Рябиновка, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в село Княжеское. Есть и третий маршрут: в деревне Васильево можно свернуть на прямую грунтовую дорогу в село Княжеское, которая идёт мимо пруда. Шоссе и грунтовые дороги образуют прямоугольные треугольники.
По шоссе Серёжа с папой едут со скоростью 60 км/ч, а по грунтовой дороге — со скоростью 40 км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна 2 км.
Ответ: 423
2)Сколько километров проедут Серёжа с папой от деревни Васильево до села Княжеское, если они поедут по шоссе через деревню Рябиновку?
Ответ: 28
3)Найдите расстояние от деревни Васильево до села Княжеское по прямой. Ответ дайте в километрах.
Ответ: 20
4)Сколько минут затратят на дорогу из деревни Пирожки в село Княжеское Серёжа с папой, если они поедут сначала по шоссе, а затем свернут в деревне Васильево на прямую грунтовую дорогу, которая проходит мимо пруда?
Ответ: 48
5)В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Пирожки, селе Княжеском, деревне Васильево и деревне Рябиновке.
Ответ: 438
Ответ: 12,1
10)Родительский комитет закупил 25 пазлов для подарков детям в связи с окончанием учебного года, из них 22 с машинами и 3 с видами городов. Подарки распределяются случайным образом между 25 детьми, среди которых есть Коля. Найдите вероятность того, что Коле достанется пазл с машиной.
Ответ: 0,88
14)В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой 14 мг. За каждые 30 минут масса колонии увеличивается в 3 раза. Найдите массу колонии микроорганизмов через 90 минут после начала эксперимента. Ответ дайте в миллиграммах.
Ответ: 378
17)Диагональ прямоугольника образует угол 86º с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Ответ: 8
19)Какое из следующих утверждений верно? 1) Отношение площадей подобных треугольников равно коэффициенту подобия. 2) Диагонали прямоугольника точкой пересечения делятся пополам. 3) Биссектриса треугольника делит пополам сторону, к которой проведена. В ответ запишите номер выбранного утверждения.
Ответ: 2
21)Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 48 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 168 км, скорость первого велосипедиста равна 15 км/ч, скорость второго — 30 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
Ответ: 120 км
23)Найдите боковую сторону AB трапеции ABCD , если углы ABC и BCD равны соответственно 60 и 135 , а CD 24 .
Ответ: 8 корень из 6
24)Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.
25)Окружности радиусов 45 и 90 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD .
Читайте также:
- Дисциплина в школе ссср
- Краткое содержание органы цветковых растений
- Добро пожаловать в рай краткое содержание вербер
- История мвд ссср краткое содержание
- Бадж египетская книга мертвых краткое содержание