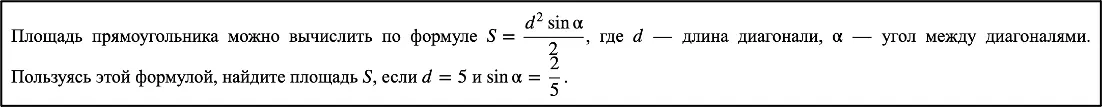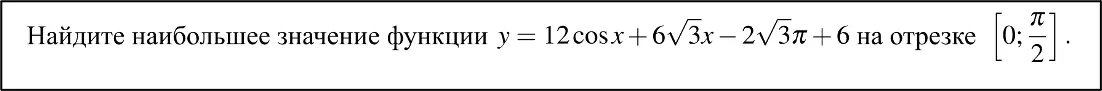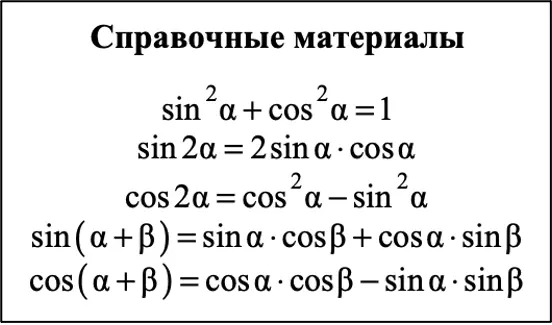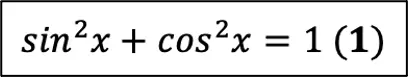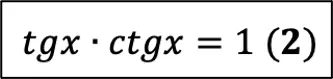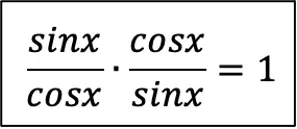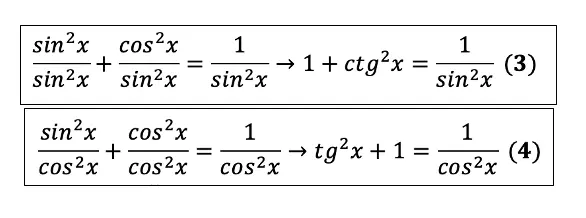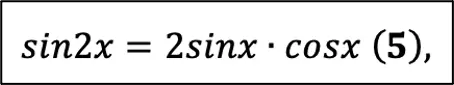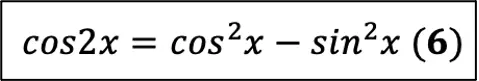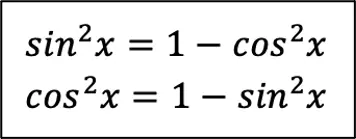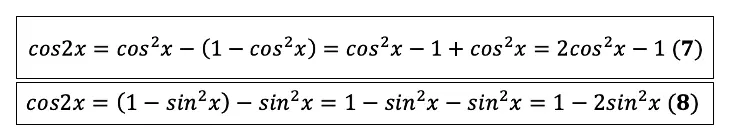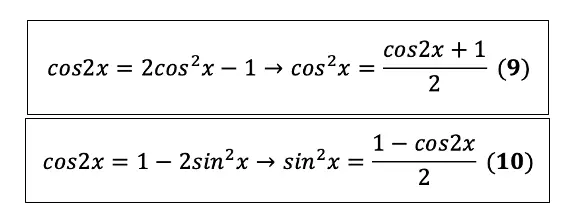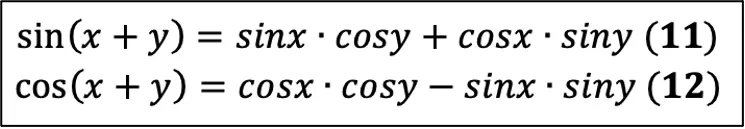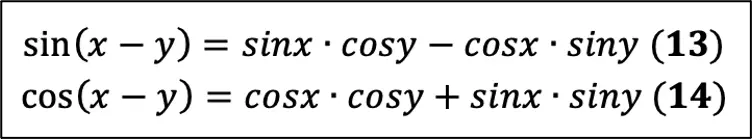Основные формулы тригонометрии для егэ профиль

Самые необходимые тригонометрические формулы

Для того чтобы сдать ЕГЭ по математике, вам понадобится около 20 формул тригонометрии. Это не много. Но их надо знать наизусть!

Вот таблица, в которой собраны основные тригонометрические формулы. Здесь все самое необходимое. Их легко выучить и применять.

Эти формулы применяются и в заданиях 1 части ЕГЭ по математике, и в заданиях 2 части.

Эта полезная табличка – только одна из многих страниц Справочника Анны Малковой для подготовки к ЕГЭ. Скачай Справочник бесплатно здесь.

Кроме того, надо знать определения синуса, косинуса и тангенса, а также значения этих функций для основных углов.

Первые 3 блока формул из нашей таблицы часто встречаются в заданиях 1 части ЕГЭ и в задаче из второй части, где надо решить тригонометрическое уравнение.

В первую очередь это основное тригонометрическое тождество:

sin{}^2 alpha +cos{}^2 alpha =1.

Это формулы, которые показывают, как выразить тангенс через косинус и котангенс через синус угла.

tg {}^2alpha +1=displaystyle frac{1}{{{cos}^2 alpha }};

1 + ctg{}^2alpha =displaystyle frac{1}{{{sin}^2 alpha }}.

Формулы синуса и косинуса двойного угла, формулы синуса суммы, косинуса разности, – все это надо знать, чтобы без ошибок решать тригонометрические уравнения.

А вот формулы суммы синусов и косинусов, а также преобразование произведения в сумму могут пригодиться при решении задач с параметрами.

Где же могут встретиться формулы из двух последних блоков, внизу таблицы?

Формулы понижения степени могут присутствовать и в тригонометрических уравнениях, и в «параметрах». И даже в задачах с физическим содержанием из 1 части ЕГЭ, если там вдруг попадется тригонометрия.

А универсальная тригонометрическая замена, когда мы выражаем синус и косинус угла альфа через тангенс половинного угла? А формулы синуса и косинуса тройных углов? Где же они применяются? Оказывается, они помогают решать задачи по геометрии из 2 части ЕГЭ. Так что их тоже стоит знать, если хотите сдать на высокий балл.

Обратите внимание, что в этой таблице нет формул приведения. О них мы рассказываем в отдельной статье нашего сайта.

Как же выучить тригонометрические формулы?

1. Учите формулы сразу. Не рассказывайте себе сказки о том, что в последнюю ночь перед ЕГЭ все выучите. Каждый день – один блок, то есть три-четыре формулы из нашей таблицы.

2. Тренируйтесь. Выучить иностранный язык проще всего тому, кто вынужден постоянно на нем говорить. Так и здесь. Для тренировки можно из классического задачника Сканави выбрать 20-50 заданий на преобразование тригонометрических выражений и доказательство тождеств.

3. Универсальный способ: ежедневно, садясь за уроки, берите чистый листок и выписывайте наизусть все тригонометрические формулы, какие помните. Когда всё готово — сверяете. И к экзамену вы будете помнить всё.

4. Еще один отличный способ. Вырежьте из плотной бумаги карточки. На одной пишете левую часть формулы. На другой – правую. Перемешиваете. И собираете. Любые формулы запоминаются легко и быстро!

5. И конечно, решаем задания ЕГЭ на применение этих формул. Начнем с задач 1 части, преобразование тригонометрических выражений.

Задача 1.

Найдите tgalpha , если cosalpha =displaystyle frac{sqrt{10}}{10} и alpha in left(displaystyle frac{3pi }{2};2pi right).

Решение:

Воспользуемся формулой:

tg{}^2x+1=displaystyle frac{1}{{cos}^2x} Rightarrow tg x =pm sqrt{displaystyle frac{1}{{cos}^2x}-1}.

Какой знак будет у тангенса, «плюс» или «минус»?

В условии дано, что alpha in left(displaystyle frac{3pi }{2};2pi right), то есть это угол из четвертой четверти, значит tgxtextless 0.

tgx =-sqrt{displaystyle frac{100}{10}-1}=-3.

Ответ: -3.

Задача 2.

Найдите displaystyle frac{10{sin 6alpha }}{3{cos 3alpha }}, если sin 3alpha =0,6.

Решение:

Воспользуемся формулой синуса двойного угла: sin2alpha = 2sinalphacosalpha :

displaystyle frac{10{sin 6alpha }}{3{sin 3alpha }}=displaystyle frac{10cdot 2{sin 3alpha }{cos 3alpha }}{3{sin 3alpha }}=displaystyle frac{20cdot {cos 3alpha }}{3}=displaystyle frac{20cdot 0,6}{3}=4.

Ответ: 4.

Задача 3.

Найдите 24cos2alpha , если sin alpha =-0,2.

Решение:

Воспользуемся формулой косинуса двойного угла: cos 2alpha = 1 — 2sin{}^2 alpha :

24cos2alpha = 24(1 — 2sin{}^2 alpha )=24left(1-2{left(-0,2right)}^2right)=

=24cdot left(1-0,08right)=24cdot 0,92=22,08.

Ответ: 22,08.

Задача 4.

Найдите displaystyle frac{3{cos alpha }-4{sin alpha }}{2{sin alpha }-5{cos alpha }}, если tgalpha=3.

Решение:

Вынесем косинус альфа за скобки в числителе и знаменателе:

displaystyle frac{3{cos alpha }-4{sin alpha }}{2{sin alpha }-5{cos alpha }}=displaystyle frac{{cos alpha }left(3-4tgalpha right)}{{cos alpha }left(2tgalpha -5right)}=displaystyle frac{3-4cdot 3}{2cdot 3-5}=displaystyle frac{-9}{1}=-9.

Ответ: -9.

Задача 5.

Найдите значение выражения: displaystyle frac{5{sin 98{}^circ }}{{sin 49{}^circ }cdot {sin 41{}^circ }}.

Решение:

Воспользуемся формулой синуса двойного угла:

sin2alpha = 2sinalphacosalpha ; тогда sinalpha cosalpha = displaystyle frac{1}{2}{sin 2alpha } .

displaystyle frac{5{sin 98{}^circ }}{{sin 49{}^circ cdot {sin 41{}^circ } }}=displaystyle frac{10{sin 49{}^circ }cdot {cos 49{}^circ }}{{sin 49{}^circ cdot {sin 41{}^circ } }}=displaystyle frac{10{sin 41{}^circ }}{{sin 41{}^circ }}=10.

Ответ: 10.

Задача 6.

Найдите значение выражения: sqrt{3}cos{}^2 displaystyle frac{5pi }{12}-sqrt{3}sin{}^2 displaystyle frac{5pi }{12} .

Решение:

Вынесем общий множитель за скобки и воспользуемся формулой косинуса двойного угла:

cos2alpha = cos{}^2 alpha — sin{}^2 alpha.

sqrt{3}{{cos}^2 displaystyle frac{5pi }{12} }-sqrt{3}{{sin}^2 displaystyle frac{5pi }{12}=sqrt{3}left({{cos}^2 displaystyle frac{5pi }{12} }-{{sin}^2 displaystyle frac{5pi }{12} }right) }=

=sqrt{3}cdot cos displaystyle frac{5pi }{6}=sqrt{3}cdot left(-displaystyle frac{sqrt{3}}{2}right)=-1,5.

Ответ: -1,5.

Задача 7.

Найдите значение выражения: -50tg 9{}^circ cdot tg 81{}^circ +31.

Решение:

Используя формулы приведения, получим: tg81{}^circ = tgleft(90{}^circ -9{}^circ right) = ctg9{}^circ.

Пользуемся также тем, что тангенс и котангенс угла альфа — взаимно обратные величины, tgalpha cdot ctgalpha =1.

Получим:

-50tg 9{}^circ cdot ctg 9{}^circ +31=-50+31 = - 19.

Ответ: -19.

Задача 8.

Найдите значение выражения: sqrt{72}-sqrt{288} sin {}^2 displaystyle frac{21pi }{8}.

Решение:

sqrt{72}-sqrt{288} sin{}^2 displaystyle frac{21pi }{8}=6sqrt{2}-12sqrt{2}sin{}^2 displaystyle frac{21pi }{8}=6sqrt{2}cdot left(1-2{}^2 displaystyle frac{21pi }{8} right)=

=6sqrt{2}cos (2cdot displaystyle frac{21pi }{8})=6sqrt{2}cos displaystyle frac{21pi }{4}=6sqrt{2}cosdisplaystyle frac{5pi }{4}=6sqrt{2}cdot displaystyle frac{sqrt{2}}{2}=6.

Мы вынесли за скобки множитель 6sqrt{2} и применили формулу косинуса двойного угла, выразив его через квадрат синуса угла.

Ответ: 6.

Задача 9.

Найдите значение выражения: 5sin displaystyle frac{11pi }{12}cdot cos displaystyle frac{11pi }{12}.

Решение:

Воспользуемся формулой синуса двойного угла: sin2alpha = 2sinalphacosalpha . Также применим одну из формул приведения: sinleft(2pi -alpha right) = -sin alpha .

5sin displaystyle frac{11pi }{12} cos displaystyle frac{11pi }{12}=displaystyle frac{5}{2}cdot sin displaystyle frac{11pi }{6}=displaystyle frac{5}{2}cdot sin left(2pi -displaystyle frac{pi }{6}right)=-displaystyle frac{5}{2}cdot sin displaystyle frac{pi }{6}=-displaystyle frac{5}{2}cdot displaystyle frac{1}{2}=-1,25.

Ответ: -1,25.

Задача 10.

Найдите значение выражения: 2sqrt{3}-4sqrt{3}{{sin}^2 displaystyle frac{7pi }{12}}.

Решение:

Вынесем общий множитель за скобки и воспользуемся формулой косинуса двойного угла:

cos2alpha = 1 — 2{sin}^2 alpha.

2sqrt{3}-4sqrt{3}{{sin}^2 displaystyle frac{7pi }{12}= }2sqrt{3}(1-2{{sin}^2 displaystyle frac{7pi }{12})= }

=2sqrt{3}cdot cos displaystyle frac{7pi }{6}=2sqrt{3}cdot cos left(pi +displaystyle frac{pi }{6}right)=-2sqrt{3}cdot cos displaystyle frac{pi }{6}=-2sqrt{3}cdot displaystyle frac{sqrt{3}}{2}=-3.

Ответ: -3.

Задача 11.

Найдите значение выражения: sqrt{108}{{cos}^2 displaystyle frac{pi }{12} }-sqrt{27}.

Решение:

Вынесем общий множитель за скобки и воспользуемся формулой косинуса двойного угла:

cos2alpha = {cos}^2 alpha -sin{}^2 alpha = 2cos{}^2 alpha -1.

sqrt{108}cos{}^2 displaystyle frac{pi }{12}-sqrt{27}=6sqrt{3}cos{}^2 displaystyle frac{pi }{12}-3sqrt{3}=3sqrt{3}left(2{{cos}^2 displaystyle frac{pi }{12} }-1right)=3sqrt{3}cdot cos displaystyle frac{pi }{6}=

=3sqrt{3}cdot displaystyle frac{sqrt{3}}{2} =4,5.

Ответ: 4,5.

Задача 12.

Найдите значение выражения: -displaystyle frac{6{sin 374{}^circ }}{{sin 14{}^circ }}.

displaystyle frac{-6{sin 374{}^circ }}{{sin 14{}^circ }}=displaystyle frac{-6{sin 14{}^circ }}{{sin 14{}^circ }}=-6.

Мы воспользовались периодичностью функции синус: sinleft(360^circ +alpha right)=sin alpha . В нашей задаче 374 = 360 + 14.

Ответ: — 6.

Задача 13.

Найдите значение выражения: 7sqrt{2}{sin displaystyle frac{15pi }{8}cdot {cos displaystyle frac{15pi }{8} } }.

Решение:

Воспользуемся формулой синуса двойного угла: sin2alpha = 2sinalpha cosalpha.

7sqrt{2} sin displaystyle frac{15pi }{8}cdot cos displaystyle frac{15pi }{8}=displaystyle frac{7sqrt{2}}{2}cdot sin displaystyle frac{15pi }{4}=displaystyle frac{7sqrt{2}}{2}cdot sin left(4pi -displaystyle frac{pi }{4}right)=displaystyle frac{7sqrt{2}}{2}cdot sin displaystyle frac{pi }{4}=displaystyle frac{7sqrt{2}}{2}cdot displaystyle frac{sqrt{2}}{2}=3,5.

Ответ: 3,5.

Заметим, что если в задаче нам встретилось произведение синуса альфа на косинус альфа, то, скорее всего, нужно будет применять формулу синуса двойного угла.

Задача 14.

Найдите tgalpha , если cosalpha =-displaystyle frac{5sqrt{41}}{41} и alpha in left(pi ;displaystyle frac{3pi }{2}right).

Решение:

Вспомним основное тригонометрическое тождество: {{cos}^2 alpha }+ {{sin}^2 alpha }=1. Выразим из этой формулы синус альфа:

sinalpha =pm sqrt{1-{{cos}^2 alpha }}.

Какой же знак выбрать, «плюс» или «минус»?

Угол альфа в третьей четверти, значит, его синус отрицателен.

sinalpha =-sqrt{1-{left(-displaystyle frac{5sqrt{41}}{41}right)}^2}=-sqrt{1-displaystyle frac{25}{41}}=-sqrt{displaystyle frac{16}{41}}=-displaystyle frac{4}{sqrt{41}}.

tgalpha =displaystyle frac{{sin alpha }}{{cos alpha }}=left(-displaystyle frac{5sqrt{41}}{41}right):left(-displaystyle frac{4}{sqrt{41}}right)=displaystyle frac{5}{4}=1,25.

Ответ: 1,25.

Задача 15.

Найдите sinalpha , если cosalpha =-displaystyle frac{sqrt{19}}{10} и alpha in left(displaystyle frac{pi }{2};pi right).

Решение:

Как и в предыдущей задаче, выразим синус альфа из основного тригонометрического тождества:

sinalpha =pm sqrt{1-{{cos}^2 alpha }}.

Дан угол альфа, принадлежащий второй четверти, значит, его синус положителен.

sinalpha =sqrt{1-{left(displaystyle frac{sqrt{19}}{10}right)}^2}=sqrt{displaystyle frac{81}{100}}=0,9.

Ответ: 0,9.

Задача 16.

Найдите tgalpha , если sinalpha =-displaystyle frac{4sqrt{41}}{41} и alpha in left(pi ;displaystyle frac{3pi }{2}right).

Решение:

Аналогично предыдущим задачам, выразим косинус альфа из основного тригонометрического тождества:

cosalpha =pm sqrt{1-{{sin}^2 alpha }}.

Угол альфа в третьей четверти, значит, его косинус отрицателен.

cosalpha =-sqrt{1-displaystyle frac{16}{41}}=-sqrt{displaystyle frac{25}{41}}=-displaystyle frac{5}{sqrt{41}}, тогда tgalpha =displaystyle frac{{sin alpha }}{{cos alpha }}=-displaystyle frac{4}{sqrt{41}}div left(-displaystyle frac{5}{sqrt{41}}right)=displaystyle frac{4}{5}=0,8.

Ответ: 0,8.

Задача 17.

Найдите значение выражения: — 42tg34{}^circ cdot tg 56{}^circ +6.

Решение:

-42tg34{}^circ cdot tg {56}^circ =-42tg 34{}^circ cdot tg left(90{}^circ -34{}^circ right)=-42tg34{}^circ cdot ctg 34{}^circ =-42.

Мы применили формулу приведения, а также то, что тангенс и котангенс угла альфа — взаимно обратные величины, и их произведение равно единице.

Ответ: -42.

Задача 18.

Найдите значение выражения: displaystyle frac{24}{{{sin}^2 127{}^circ }}+4+sin{}^2 217{}^circ .

Решение:

Воспользуемся формулами приведения:

displaystyle frac{24}{{{sin}^2 127+4+sin{}^2 217}}=displaystyle frac{24}{{{sin}^2 left(90{}^circ +37{}^circ right)+4+{{sin}^2 left(180{}^circ +37{}^circ right) } }}=

=displaystyle frac{24}{{{cos}^2 37{}^circ +4+{{sin}^2 37{}^circ } }}=displaystyle frac{24}{5}=4,8.

Также мы применили основное тригонометрическое тождество. Сумма квадратов синуса и косинуса угла альфа равна единице.

Ответ: 4,8.

Задача 19.

Найдите значение выражения: displaystyle frac{2{sin 136{}^circ }}{{sin 68{}^circ }cdot {sin 22{}^circ }}.

Решение:

Так как 68{}^circ +22{}^circ =90{}^circ , то заменим {sin 68{}^circ } на {cos 22 }^circ по формуле приведения и воспользуемся формулой синуса двойного угла:

sin2alpha = 2sinalphacosalpha.

displaystyle frac{2{sin 136{}^circ }}{{sin 68{}^circ }{sin 22{}^circ }}=displaystyle frac{2{sin 136{}^circ }}{{cos 22{}^circ }{sin 22{}^circ }}=displaystyle frac{4{sin left(180{}^circ -44{}^circ right) }}{{sin 44{}^circ }}=

=displaystyle frac{4{sin 44{}^circ }}{{sin 44{}^circ }}=4.

Ответ: 4.

Задача 20.

Найдите значение выражения: displaystyle frac{21left({{sin}^2 66{}^circ }-{{cos}^2 66{}^circ }right)}{{cos 132{}^circ }}.

Решение:

Воспользуемся формулой косинуса двойного угла:

{cos 2alpha ={{cos}^2 alpha }-{{sin}^2 alpha } }.

displaystyle frac{21left({{sin}^2 66{}^circ }-{{cos}^2 66{}^circ }right)}{{cos 132{}^circ }}=displaystyle frac{-21{cos 132{}^circ }}{{cos 132{}^circ }}=-21.

Ответ: -21.

Задача 21.

Найдите значение выражения: sqrt{2}{sin displaystyle frac{7pi }{8}cdot {cos displaystyle frac{7pi }{8}} }.

Решение:

Воспользуемся формулой синуса двойного угла:

{sin 2alpha =2{sin alpha }{cos alpha } }.

sqrt{2}{sin displaystyle frac{7pi }{8} }cdot {cos displaystyle frac{7pi }{8}=displaystyle frac{sqrt{2}}{2}{sin displaystyle frac{7pi }{4} } }=displaystyle frac{sqrt{2}}{2}{sin left(2pi -displaystyle frac{pi }{4}right) }=-displaystyle frac{sqrt{2}}{2}sin displaystyle frac{pi }{4}=

= -displaystyle frac{sqrt{2}}{2}cdot displaystyle frac{sqrt{2}}{2}=-0,25.

Ответ: -0,25.

Задача 22.

Найдите значение выражения: 3sqrt{2}{{cos}^2 displaystyle frac{9pi }{8} }-3sqrt{2}{{sin}^2 displaystyle frac{9pi }{8} }.

Решение:

3sqrt{2}{cos}^2 displaystyle frac{9pi }{8} -3sqrt{2}{{sin}^2 displaystyle frac{9pi }{8} }=3sqrt{2}left({{cos}^2 displaystyle frac{9pi }{8} }-{{sin}^2 displaystyle frac{9pi }{8} }right)=3sqrt{2}{cos displaystyle frac{9pi }{4} }=

=3sqrt{2}cos left(2pi +displaystyle frac{pi }{4}right)=3sqrt{2}cos displaystyle frac{pi }{4}=3sqrt{2}cdot displaystyle frac{sqrt{2}}{2}=3.

И здесь тоже была формула косинуса двойного угла, но только в другой форме.

Ответ: 3.

Задача 23.

Найдите значение выражения: 26sqrt{2}{cos displaystyle frac{pi }{4} }{cos displaystyle frac{4pi }{3} }.

Решение:

26sqrt{2}{cos displaystyle frac{pi }{4} }{cos displaystyle frac{4pi }{4} }=26sqrt{2}cdot displaystyle frac{sqrt{2}}{2}cdot left(-displaystyle frac{1}{2}right)=-13.

А здесь мы просто вычислили косинус и синус табличного угла displaystyle frac{pi }{4}.

Ответ: -13.

Задача 24.

Найдите значение выражения: 18sqrt{2}tgdisplaystyle frac{pi }{4}{sin displaystyle frac{pi }{4} }.

Решение:

18sqrt{2}cdot tgdisplaystyle frac{pi }{4}{cdot sin displaystyle frac{pi }{4}= }18sqrt{2}cdot 1cdot displaystyle frac{sqrt{2}}{2}=18.

Это задача на вычисление тригонометрических функций для табличного угла displaystyle frac{pi }{4}. Если этот угол выразить в градусах, то он равен 45 градусов.

Ответ: 18.

Задача 25.

Найдите значение выражения: displaystyle frac{2{cos left(2pi -beta right) }-3{sin left(-displaystyle frac{pi }{2}+beta right) }}{2{cos left(beta -3pi right) }}.

Решение:

Используя формулы приведения, получим:

displaystyle frac{2{cos left(2pi -beta right) }-3{sin left(-displaystyle frac{pi }{2}+beta right) }}{2{cos left(beta -3pi right) }}=displaystyle frac{2{cos beta }+3{cos beta }}{-2{cos beta }}=

=-displaystyle frac{5{cos beta }}{2{cos beta }}=-2,5.

Лайфхак: если вам сложно запомнить формулы приведения, вы можете вместо них использовать формулы косинуса разности и синуса суммы.

Ответ: -2,5.

Посмотрим, как формулы тригонометрии применяются при решении уравнений.

Задача 26.

Решите уравнение: {{sin}^2 left(displaystyle frac{pi }{4}-xright) }={{sin}^2 left(displaystyle frac{pi }{4}+xright) }.

Решение:

Воспользуемся формулой понижения степени: sin{}^2 x=displaystyle frac{1-{cos 2x }}{2}.

displaystyle frac{1-{cos left(displaystyle frac{pi }{2}-2xright) }}{2}=displaystyle frac{1-{cos left(displaystyle frac{pi }{2}+2xright) }}{2}Leftrightarrow {cos left(displaystyle frac{pi }{2}-2xright) }={cos left(displaystyle frac{pi }{2}+2xright)Leftrightarrow }

Leftrightarrow {cos 2x=-{cos 2xLeftrightarrow 2 } }{cos 2x=0 }Leftrightarrow 2x=displaystyle frac{pi }{2}+pi kLeftrightarrow x=displaystyle frac{pi }{4}+displaystyle frac{pi k}{2}; kin Z.

Ответ: x=displaystyle frac{pi }{4}+displaystyle frac{pi k}{2}; kin Z.

Задача 27.

Решите уравнение: {{cos}^2 3x }+{{cos}^2 4x }+{{cos}^2 5x }=displaystyle frac{3}{2}.

Решение:

Воспользуемся формулой понижения степени: {{cos}^2 x }=displaystyle frac{1+{cos 2x }}{2}.

{cos}^2 3x+{cos}^2 4x+{cos}^2 5x=displaystyle frac{3}{2}Leftrightarrow displaystyle frac{1+{cos 6x }}{2}+

+displaystyle frac{1+{cos 8x }}{2}+displaystyle frac{1+{cos 10x }}{2}=displaystyle frac{3}{2}.

Умножим обе части на два:

1 + cos6x + 1 + cos8x + 1 + cos10x = 3 Leftrightarrow cos6x + cos8x + cos 10x = 0.

Воспользуемся формулой суммы косинусов: cosalpha + cos beta = 2cos displaystyle frac{alpha +beta }{2} cosdisplaystyle frac{alpha -beta }{2};

cos6x + cos10x = 2cos8x cos2x.

Уравнение примет вид:

2cos8x cos2x + cos8x =0.

Вынесем общий множитель за скобки. Теперь произведение двух множителей равно нулю, а с этим мы умеем работать.

{cos 8xleft(2{cos 2x+1 }right)=0Leftrightarrow left[ begin{array}{c}{cos 8x=0 } \{cos 2x=-displaystyle frac{1}{2} } end{array}Leftrightarrow left[ begin{array}{c}8x=displaystyle frac{pi }{2}+pi k \2x=pm displaystyle frac{2pi }{3}+2pi k;kin Z end{array}right.right. }Leftrightarrow left[ begin{array}{c}x=displaystyle frac{pi }{16}+displaystyle frac{pi k}{8} \x=pm displaystyle frac{pi }{3}+pi k;kin Z end{array}right. .

Ответ: left[ begin{array}{c}x=displaystyle frac{pi }{16}+displaystyle frac{pi k}{8} \x=pm displaystyle frac{pi }{3}+pi k;kin Z end{array}right. .

Все о решении тригонометрических уравнений здесь.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Самые необходимые тригонометрические формулы» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник
Геометрия

  • Треугольник
  • Четырехугольники
  • Окружность и круг
  • Призма
  • Пирамида
  • Усеченная пирамида
  • Цилиндр
  • Конус
  • Усеченный конус
  • Сфера и шар

1. Формулы сокращённого умножения

левая круглая скобка a плюс b правая круглая скобка в квадрате =a в квадрате плюс 2ab плюс b в квадрате

левая круглая скобка a минус b правая круглая скобка в квадрате =a в квадрате минус 2ab плюс b в квадрате

левая круглая скобка a плюс b правая круглая скобка в кубе =a в кубе плюс 3a в квадрате b плюс 3ab в квадрате плюс b в кубе

левая круглая скобка a минус b правая круглая скобка в кубе =a в кубе минус 3a в квадрате b плюс 3ab в квадрате минус b в кубе

a в квадрате минус b в квадрате = левая круглая скобка a минус b правая круглая скобка левая круглая скобка a плюс b правая круглая скобка

a в кубе плюс b в кубе = левая круглая скобка a плюс b правая круглая скобка левая круглая скобка a в квадрате минус ab плюс b в квадрате правая круглая скобка

a в кубе минус b в кубе = левая круглая скобка a минус b правая круглая скобка левая круглая скобка a в квадрате плюс ab плюс b в квадрате правая круглая скобка

Наверх

2. Модуль числа

Определение: left| a |= система выражений новая строка a,a больше или равно 0, новая строка минус a,a меньше 0. конец системы .

Основные свойства модуля:

|a| больше или равно 0;

|a|=| минус a|;

система выражений новая строка |a| больше или равно a, новая строка |a| больше или равно минус a; конец системы .

|a|=a равносильно a больше или равно 0;

|a|= минус a равносильно a меньше или равно 0.

Наверх

3. Степень с действительным показателем

Свойства степени с действительным показателем

Пусть a больше 0,b больше 0,x принадлежит R ,y принадлежит R . Тогда верны следующие соотношения:

Наверх

4. Корень n-ой степени из числа

Корнем n-ой степени левая круглая скобка n принадлежит N ,n больше или равно 2 правая круглая скобка из числа a называется число, n-ая степень которого равна a.
Арифметическим корнем четной степени n левая круглая скобка n=2k,k принадлежит N правая круглая скобка из неотрицательного числа a называется неотрицательное число, n-ая степень которого равна a.

Основные свойства арифметического корня:

a больше или равно 0: левая круглая скобка корень n степени из левая круглая скобка a правая круглая скобка правая круглая скобка в степени левая круглая скобка n правая круглая скобка =a, корень n степени из левая круглая скобка a правая круглая скобка в степени левая круглая скобка n правая круглая скобка =a, корень n степени из левая круглая скобка a правая круглая скобка в степени левая круглая скобка m правая круглая скобка = левая круглая скобка корень n степени из левая круглая скобка a правая круглая скобка правая круглая скобка в степени левая круглая скобка m правая круглая скобка , корень m степени из левая круглая скобка корень n степени из левая круглая скобка a правая круглая скобка правая круглая скобка = корень mn степени из левая круглая скобка a правая круглая скобка ;

a принадлежит R : корень n степени из левая круглая скобка a правая круглая скобка в степени левая круглая скобка n правая круглая скобка = |a|;

a больше или равно 0,b больше или равно 0: корень n степени из левая круглая скобка ab правая круглая скобка = корень n степени из левая круглая скобка a правая круглая скобка умножить на корень n степени из левая круглая скобка b правая круглая скобка , корень n степени из левая круглая скобка дробь: числитель: a, знаменатель: b конец дроби правая круглая скобка = дробь: числитель: корень n степени из левая круглая скобка a правая круглая скобка , знаменатель: корень n степени из левая круглая скобка b правая круглая скобка конец дроби левая круглая скобка b не равно 0 правая круглая скобка ;

a меньше 0,b меньше 0: корень n степени из левая круглая скобка ab правая круглая скобка = корень n степени из левая круглая скобка минус a правая круглая скобка умножить на корень n степени из левая круглая скобка минус b правая круглая скобка , корень n степени из левая круглая скобка дробь: числитель: a, знаменатель: b конец дроби правая круглая скобка = дробь: числитель: корень n степени из левая круглая скобка минус a правая круглая скобка , знаменатель: корень n степени из левая круглая скобка минус b правая круглая скобка конец дроби ;

a больше или равно 0,b больше или равно 0:a корень n степени из левая круглая скобка b правая круглая скобка = корень n степени из левая круглая скобка a правая круглая скобка в степени левая круглая скобка n правая круглая скобка b;

a меньше 0,b больше или равно 0:a корень n степени из левая круглая скобка b правая круглая скобка = минус корень n степени из левая круглая скобка a правая круглая скобка в степени левая круглая скобка n правая круглая скобка b.

Наверх

5. Логарифмы

Определение логарифма: log _ab=cunderseta больше 0,a не равно 1mathop равносильно a в степени левая круглая скобка c правая круглая скобка =b.

Основное логарифмическое тождество: a в степени левая круглая скобка log правая круглая скобка _ab=b.

Основные свойства логарифмов

Пусть a больше 0, a не равно 1, b больше 0, b не равно 1, x больше 0, y больше 0, p принадлежит R . Тогда верны следующие соотношения:

Наверх

6. Арифметическая прогрессия

Формула n-го члена арифметической прогрессии: a_n=a_1 плюс d левая круглая скобка n минус 1 правая круглая скобка .

Характеристическое свойство арифметической прогрессии: a_n= дробь: числитель: a_n минус 1 плюс a_n плюс 1, знаменатель: 2 конец дроби ,n больше или равно 2.

Сумма n первых членов арифметической прогрессии: S_n= дробь: числитель: a_1 плюс a, знаменатель: 2 конец дроби n.

При решении задач, связанных с арифметической прогрессией, могут оказаться полезными также следующие формулы:

S_n= дробь: числитель: 2a_1 плюс d левая круглая скобка n минус 1 правая круглая скобка , знаменатель: 2 конец дроби n;

S_n= дробь: числитель: 2a_n минус d левая круглая скобка n минус 1 правая круглая скобка , знаменатель: 2 конец дроби n;

a_n= дробь: числитель: a_n минус k плюс a_n плюс k, знаменатель: 2 конец дроби ,k меньше n;

a_k плюс a_n=a_k минус m плюс a_n плюс m,m меньше k;

d= дробь: числитель: a_n минус a_k, знаменатель: n минус k конец дроби .

Наверх

7. Геометрическая прогрессия

Формула n-го члена геометрической прогрессии: a_n=a_1q в степени левая круглая скобка n минус 1 правая круглая скобка .

Характеристическое свойство геометрической прогрессии: a_n в квадрате =a_n минус 1a_n плюс 1,n больше или равно 2.

Сумма n первых членов геометрической прогрессии: S_n= дробь: числитель: a_1 минус a_nq, знаменатель: 1 минус q конец дроби , q не равно 1.

При решении задач, связанных с геометрической прогрессией, могут оказаться полезными также следующие формулы:

S_n= дробь: числитель: a_1 левая круглая скобка 1 минус q в степени левая круглая скобка n правая круглая скобка правая круглая скобка , знаменатель: 1 минус q конец дроби ;

a_n в квадрате =a_n минус ka_n плюс k,k меньше n;

a_ka_n=a_k минус ma_n плюс m,m меньше k;

|q|= корень n минус k степени из левая круглая скобка дробь: числитель: a правая круглая скобка _n, знаменатель: a_k конец дроби .

Наверх

8. Бесконечно убывающая геометрическая прогрессия

Сумма бесконечно убывающей геометрической прогрессии: S= дробь: числитель: a_1, знаменатель: 1 минус q конец дроби .

Наверх

9. Основные формулы тригонометрии

Зависимость между тригонометрическими функциями одного аргумента:

синус в квадрате альфа плюс косинус в квадрате альфа =1;

тангенс альфа = дробь: числитель: синус альфа , знаменатель: косинус альфа конец дроби ;

ctg альфа = дробь: числитель: косинус альфа , знаменатель: синус альфа конец дроби ;

тангенс альфа ctg альфа =1;

1 плюс тангенс в квадрате альфа = дробь: числитель: 1, знаменатель: косинус в квадрате альфа конец дроби ;

1 плюс ctg в квадрате альфа = дробь: числитель: 1, знаменатель: синус в квадрате альфа конец дроби .

Формулы сложения:

косинус левая круглая скобка альфа плюс бета правая круглая скобка = косинус альфа косинус бета минус синус альфа синус бета ;

косинус левая круглая скобка альфа минус бета правая круглая скобка = косинус альфа косинус бета плюс синус альфа синус бета ;

синус левая круглая скобка альфа плюс бета правая круглая скобка = синус альфа косинус бета плюс косинус альфа синус бета ;

синус левая круглая скобка альфа минус бета правая круглая скобка = синус альфа косинус бета минус косинус альфа синус бета ;

тангенс левая круглая скобка альфа плюс бета правая круглая скобка = дробь: числитель: тангенс альфа плюс тангенс бета , знаменатель: 1 минус тангенс альфа тангенс бета конец дроби ;

тангенс левая круглая скобка альфа минус бета правая круглая скобка = дробь: числитель: тангенс альфа минус тангенс бета , знаменатель: 1 плюс тангенс альфа тангенс бета конец дроби ;

ctg левая круглая скобка альфа плюс бета правая круглая скобка = дробь: числитель: ctg альфа ctg бета минус 1, знаменатель: ctg бета плюс ctg альфа конец дроби ;

ctg левая круглая скобка альфа минус бета правая круглая скобка = дробь: числитель: ctg альфа ctg бета плюс 1, знаменатель: ctg бета минус ctg альфа конец дроби .

Формулы тригонометрических функций двойного аргумента: синус 2 альфа =2 синус альфа косинус альфа ;

синус 2 альфа = дробь: числитель: 2 тангенс альфа , знаменатель: 1 плюс тангенс в квадрате альфа конец дроби ;

косинус 2 альфа = косинус в квадрате альфа минус синус в квадрате альфа ;

косинус 2 альфа =2 косинус в квадрате альфа минус 1;

косинус 2 альфа =1 минус 2 синус в квадрате альфа ;

косинус 2 альфа = дробь: числитель: 1 минус тангенс в квадрате альфа , знаменатель: 1 плюс тангенс в квадрате альфа конец дроби ;

тангенс 2 альфа = дробь: числитель: 2 тангенс альфа , знаменатель: 1 минус тангенс в квадрате альфа конец дроби ;

ctg2 альфа = дробь: числитель: ctg в квадрате альфа минус 1, знаменатель: 2ctg альфа конец дроби .

Формулы понижения степени:

синус в квадрате альфа = дробь: числитель: 1 минус косинус 2 альфа , знаменатель: 2 конец дроби ;

косинус в квадрате альфа = дробь: числитель: 1 плюс косинус 2 альфа , знаменатель: 2 конец дроби ;

тангенс в квадрате альфа = дробь: числитель: 1 минус косинус 2 альфа , знаменатель: 1 плюс косинус 2 альфа конец дроби ;

ctg в квадрате альфа = дробь: числитель: 1 плюс косинус 2 альфа , знаменатель: 1 минус косинус 2 альфа конец дроби .

Формулы приведения

Все формулы приведения получаются из соответствующих формул сложения. Например:

косинус левая круглая скобка дробь: числитель: Пи , знаменатель: 2 конец дроби плюс альфа правая круглая скобка = косинус дробь: числитель: Пи , знаменатель: 2 конец дроби косинус альфа минус синус дробь: числитель: Пи , знаменатель: 2 конец дроби синус альфа = минус синус альфа .

Применение формул приведения укладывается в следующую схему:

— определяется координатная четверть, в которой лежит аргумент приводимой функции, считая, что альфа принадлежит левая круглая скобка 0; дробь: числитель: Пи , знаменатель: 2 конец дроби правая круглая скобка ;

— определяется знак приводимой функции;

— определяется название приведенной функции по следующему правилу: если аргумент приводимой функции имеет вид левая круглая скобка дробь: числитель: Пи , знаменатель: 2 конец дроби pm альфа правая круглая скобка или левая круглая скобка дробь: числитель: 3 Пи , знаменатель: 2 конец дроби pm альфа правая круглая скобка , то функция меняется на сходственную функцию, если аргумент приводимой функции имеет вид левая круглая скобка Пи pm альфа правая круглая скобка , то функция названия не меняет.

Например, получим формулу тангенс левая круглая скобка дробь: числитель: 3 Пи , знаменатель: 2 конец дроби плюс альфа правая круглая скобка :

— дробь: числитель: 3 Пи , знаменатель: 2 конец дроби плюс альфа принадлежит левая круглая скобка дробь: числитель: 3 Пи , знаменатель: 2 конец дроби ;2 Пи правая круглая скобка — IV четверть;

— в IV четверти тангенс отрицательный;

— аргумент приводимой функции имеет вид дробь: числитель: 3 Пи , знаменатель: 2 конец дроби плюс альфа , следовательно, название функции меняется. Таким образом, тангенс левая круглая скобка дробь: числитель: 3 Пи , знаменатель: 2 конец дроби плюс альфа правая круглая скобка = минус ctg альфа .

Формулы преобразования суммы тригонометрических функций в произведение:

синус альфа плюс синус бета =2 синус дробь: числитель: альфа плюс бета , знаменатель: 2 конец дроби косинус дробь: числитель: альфа минус бета , знаменатель: 2 конец дроби ;

синус альфа минус синус бета =2 синус дробь: числитель: альфа минус бета , знаменатель: 2 конец дроби косинус дробь: числитель: альфа плюс бета , знаменатель: 2 конец дроби ;

косинус альфа плюс косинус бета =2 косинус дробь: числитель: альфа плюс бета , знаменатель: 2 конец дроби косинус дробь: числитель: альфа минус бета , знаменатель: 2 конец дроби ;

косинус альфа минус косинус бета = минус 2 синус дробь: числитель: альфа плюс бета , знаменатель: 2 конец дроби синус дробь: числитель: альфа минус бета , знаменатель: 2 конец дроби ;

тангенс альфа плюс тангенс бета = дробь: числитель: синус левая круглая скобка альфа плюс бета правая круглая скобка , знаменатель: косинус альфа косинус бета конец дроби ;

тангенс альфа минус тангенс бета = дробь: числитель: синус левая круглая скобка альфа минус бета правая круглая скобка , знаменатель: косинус альфа косинус бета конец дроби ;

ctg альфа плюс ctg бета = дробь: числитель: синус левая круглая скобка альфа плюс бета правая круглая скобка , знаменатель: синус альфа синус бета конец дроби ;

ctg альфа минус ctg бета = дробь: числитель: синус левая круглая скобка бета минус альфа правая круглая скобка , знаменатель: синус альфа синус бета конец дроби .

Формулы преобразования произведения тригонометрических функций в сумму:

косинус альфа косинус бета = дробь: числитель: 1, знаменатель: 2 конец дроби левая круглая скобка косинус левая круглая скобка альфа минус бета правая круглая скобка плюс косинус левая круглая скобка альфа плюс бета правая круглая скобка правая круглая скобка ;

синус альфа синус бета = дробь: числитель: 1, знаменатель: 2 конец дроби левая круглая скобка косинус левая круглая скобка альфа минус бета правая круглая скобка минус косинус левая круглая скобка альфа плюс бета правая круглая скобка правая круглая скобка ;

синус альфа косинус бета = дробь: числитель: 1, знаменатель: 2 конец дроби левая круглая скобка синус левая круглая скобка альфа плюс бета правая круглая скобка плюс синус левая круглая скобка альфа минус бета правая круглая скобка правая круглая скобка .

Наверх

10. Производная и интеграл

Таблица производных некоторых элементарных функций

Правила дифференцирования:

1. левая круглая скобка f левая круглая скобка x правая круглая скобка плюс g левая круглая скобка x правая круглая скобка правая круглая скобка в степени левая круглая скобка prime правая круглая скобка =f' левая круглая скобка x правая круглая скобка плюс g' левая круглая скобка x правая круглая скобка ;

2. левая круглая скобка cf левая круглая скобка x правая круглая скобка правая круглая скобка в степени левая круглая скобка prime правая круглая скобка =cf' левая круглая скобка x правая круглая скобка ;

3. левая круглая скобка f левая круглая скобка x правая круглая скобка g левая круглая скобка x правая круглая скобка правая круглая скобка в степени левая круглая скобка prime правая круглая скобка =f' левая круглая скобка x правая круглая скобка g левая круглая скобка x правая круглая скобка плюс f левая круглая скобка x правая круглая скобка g' левая круглая скобка x правая круглая скобка ;

4. левая круглая скобка дробь: числитель: f левая круглая скобка x правая круглая скобка , знаменатель: g левая круглая скобка x правая круглая скобка конец дроби правая круглая скобка в степени левая круглая скобка prime правая круглая скобка = дробь: числитель: f' левая круглая скобка x правая круглая скобка g левая круглая скобка x правая круглая скобка минус f левая круглая скобка x правая круглая скобка g' левая круглая скобка x правая круглая скобка , знаменатель: g в квадрате левая круглая скобка x правая круглая скобка конец дроби ;

5. левая квадратная скобка f левая круглая скобка g левая круглая скобка x правая круглая скобка правая круглая скобка правая квадратная скобка в степени левая круглая скобка prime правая круглая скобка =f' левая круглая скобка g левая круглая скобка x правая круглая скобка правая круглая скобка g' левая круглая скобка x правая круглая скобка .

Уравнение касательной к графику функции y=f левая круглая скобка x правая круглая скобка в его точке левая круглая скобка x_0;f левая круглая скобка x_0 правая круглая скобка правая круглая скобка :

y=f' левая круглая скобка x_0 правая круглая скобка левая круглая скобка x минус x_0 правая круглая скобка плюс f левая круглая скобка x_0 правая круглая скобка .

Таблица первообразных для некоторых элементарных функций

Правила нахождения первообразных

Пусть F левая круглая скобка x правая круглая скобка ,G левая круглая скобка x правая круглая скобка ― первообразные для функций f левая круглая скобка x правая круглая скобка и g левая круглая скобка x правая круглая скобка соответственно, a, b, k ― постоянные, k не равно 0. Тогда:

— F левая круглая скобка x правая круглая скобка плюс G левая круглая скобка x правая круглая скобка ― первообразная для функции f левая круглая скобка x правая круглая скобка плюс g левая круглая скобка x правая круглая скобка ;

— aF левая круглая скобка x правая круглая скобка ― первообразная для функции af левая круглая скобка x правая круглая скобка ;

— дробь: числитель: 1, знаменатель: k конец дроби F левая круглая скобка kx плюс b правая круглая скобка ― первообразная для функции f левая круглая скобка kx плюс b правая круглая скобка ;

— Формула Ньютона-Лейбница: принадлежит t пределы: от a до b, f левая круглая скобка x правая круглая скобка dx=F левая круглая скобка b правая круглая скобка минус F левая круглая скобка a правая круглая скобка .

1. Треугольник

Пусть a,b,c ― длины сторон BC, AC, AB треугольника ABC соответственно; p= дробь: числитель: a плюс b плюс c, знаменатель: 2 конец дроби ― полупериметр треугольника ABC; A, B, C ― величины углов BAC, ABC, ACB треугольника ABC соответственно; h_a,h_b,h_c ― длины высот AA2, BB2, CC2 треугольника ABC соответственно; R ― радиус окружности, описанной около треугольника ABC; r — радиус окружности, вписанной в треугольник ABC; S_vartriangle ABC ― площадь треугольника ABC. Тогда имеют место следующие соотношения:

дробь: числитель: a, знаменатель: синус A конец дроби = дробь: числитель: b, знаменатель: синус B конец дроби = дробь: числитель: c, знаменатель: синус C конец дроби =2R (теорема синусов);

c в квадрате =a в квадрате плюс b в квадрате минус 2ab косинус C (теорема косинусов);

S_vartriangle ABC= дробь: числитель: 1, знаменатель: 2 конец дроби ah_a;

S_vartriangle ABC= дробь: числитель: 1, знаменатель: 2 конец дроби ab синус C;

S_vartriangle ABC= дробь: числитель: abc, знаменатель: 4R конец дроби ;

S_vartriangle ABC=pr;

S_vartriangle ABC= корень из p левая круглая скобка p минус a правая круглая скобка левая круглая скобка p минус b правая круглая скобка левая круглая скобка p минус c правая круглая скобка .

Наверх
2. Четырёхугольники

Параллелограмм

Параллелограммом называется четырехугольник, противоположные стороны которого попарно параллельны.

Прямоугольником называется параллелограмм, у которого все углы прямые.

Ромбом называется параллелограмм, все стороны которого равны.

Квадратом называется прямоугольник, все стороны которого равны. Из определения следует, что квадрат является ромбом, следовательно, он обладает всеми свойствами прямоугольника и ромба.

Трапецией называется четырехугольник, две стороны которого параллельны, а две другие не параллельны.

Площадь четырехугольника

Площадь параллелограмма равна произведению его основания на высоту.

Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними.

Площадь трапеции равна произведению полусуммы ее оснований на высоту.

Площадь четырехугольника равна половине произведения его диагоналей на синус угла между ними.

Наверх

3. Окружность и круг

Соотношения между элементами окружности и круга

Пусть r — радиус окружности, d — ее диаметр, C — длина окружности, S — площадь круга, l_n градусов  — длина дуги в n градусов, l_ альфа  — длина дуги в альфа радиан, S_n градусов  — площадь сектора, ограниченного дугой в n градусов, S_ альфа  — площадь сектора, ограниченного дугой в альфа радиан. Тогда имеют место следующие соотношения:

Вписанный угол

Вписанный угол измеряется половиной дуги, на которую он опирается.

Вписанные углы, опирающиеся на одну и ту же дугу, равны.

Вписанный угол, опирающийся на полуокружность, — прямой.

Вписанная окружность

Центр окружности, вписанной в многоугольник, есть точка равноудаленная от всех сторон этого многоугольника, ― точка пересечения биссектрис углов этого многоугольника. Таким образом, в многоугольник можно вписать окружность, и притом только одну, тогда и только тогда, когда биссектрисы его углов пересекаются в одной точке.

В четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.

Описанная окружность

Центр окружности, вписанной в многоугольник, есть точка равноудаленная от всех вершин этого многоугольника, ― точка пересечения серединных перпендикуляров к сторонам этого многоугольника. Таким образом, около многоугольника можно описать окружность, и притом только одну, тогда и только тогда, когда серединные перпендикуляры к сторонам этого многоугольника пересекаются в одной точке.

Около четырехугольника можно описать окружность тогда и только тогда, когда суммы его противоположных углов равны 180 градусов.

Наверх

4. Призма

Пусть H ― высота призмы, AA1 ― боковое ребро призмы, P_осн ― периметр основания призмы, S_осн ― площадь основания призмы, S_бок ― площадь боковой поверхности призмы, S_полн ― площадь полной поверхности призмы, V ― объем призмы, P_bot  ― периметр перпендикулярного сечения призмы, S_bot  ― площадь перпендикулярного сечения призмы. Тогда имеют место следующие соотношения:

S_бок=P_bot AA_1;

S_полн=2S_осн плюс S_бок;

V=S_bot AA_1;

V=S_оснH.

Свойства параллелепипеда:

— противоположные грани параллелепипеда равны и параллельны;

— диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам;

— квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

Наверх

5. Пирамида

Пусть H ― высота пирамиды, P_осн ― периметр основания пирамиды, S_осн ― площадь основания пирамиды, S_бок ― площадь боковой поверхности пирамиды, S_полн ― площадь полной поверхности пирамиды, V ― объем пирамиды. Тогда имеют место следующие соотношения:

S_полн=S_осн плюс S_бок;

V= дробь: числитель: 1, знаменатель: 3 конец дроби S_оснH .


Замечание. Если все двугранные углы при основании пирамиды равны бета , а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны h_бок, то S_бок= дробь: числитель: 1, знаменатель: 2 конец дроби P_оснh_бок= дробь: числитель: S_осн, знаменатель: косинус бета конец дроби .

Наверх

6. Усечённая пирамида

Пусть H ― высота усеченной пирамиды, P_1 и P_2 ― периметры оснований усеченной пирамиды, S_1 и S_2 ― площади оснований усеченной пирамиды, S_бок ― площадь боковой поверхности усеченной пирамиды, S_полн ― площадь полной поверхности усеченной пирамиды, V ― объем усеченной пирамиды.

Тогда имеют место следующие соотношения:

S_полн=S_1 плюс S_2 плюс S_бок;

V= дробь: числитель: 1, знаменатель: 3 конец дроби H левая круглая скобка S_1 плюс S_2 плюс корень из S_1S_2 правая круглая скобка .

Замечание. Если все двугранные углы при основании пирамиды равны бета , а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны h_бок, то: S_бок= дробь: числитель: 1, знаменатель: 2 конец дроби левая круглая скобка P_1 плюс P_2 правая круглая скобка h_бок= дробь: числитель: |S_1 минус S_2|, знаменатель: косинус бета конец дроби .

Наверх

7. Цилиндр

Пусть h ― высота цилиндра, r ― радиус цилиндра, S_бок ― площадь боковой поверхности цилиндра, S_полн ― площадь полной поверхности цилиндра, V ― объем цилиндра.

Тогда имеют место следующие соотношения:

S_бок=2 Пи rh;

S_полн=2 Пи r левая круглая скобка r плюс h правая круглая скобка ;

V= Пи r в квадрате h.

Наверх

8. Конус

Пусть h ― высота конуса, r ― радиус основания конуса, l ― образующая конуса, S_бок ― площадь боковой поверхности конуса, S_полн ― площадь полной поверхности конуса, V ― объем конуса.

Тогда имеют место следующие соотношения:

S_бок= Пи rl;

S_полн= Пи r левая круглая скобка r плюс l правая круглая скобка ;

V= дробь: числитель: 1, знаменатель: 3 конец дроби Пи r в квадрате h.

Наверх

9. Усечённый конус

Пусть h ― высота усеченного конуса, r и r_1 ― радиусы основания усеченного конуса, l ― образующая усеченного конуса, S_бок ― площадь боковой поверхности усеченного конуса, V ― объем усеченного конуса. Тогда имеют место следующие соотношения:

S_бок= Пи левая круглая скобка r плюс r_1 правая круглая скобка l;

V= дробь: числитель: 1, знаменатель: 3 конец дроби Пи h левая круглая скобка r в квадрате плюс rr_1 плюс r_1 в квадрате правая круглая скобка .

Наверх

10. Сфера и шар

Пусть R ― радиус шара, D ― его диаметр, S ― площадь ограничивающей шар сферы, S_h ― площадь сферической поверхности шарового сегмента (шарового слоя), высота которого равна h, V ― объем шара, V_сегм ― объем сегмента, высота которого равна h, V_сект ― объем сектора, ограниченного сегментом, высота которого равна h. Тогда имеют место следующие соотношения:

Наверх

Источник

Чуть больше 30% выпускников справляется с тригонометрией на ЕГЭ по математике. И неудивительно: для решения заданий из базы и профиля надо знать очень много формул, которые сложно освоить за 1-2 года. На самом деле, это миф! Чтобы решить задания по тригонометрии, нужно знать всего 5 формул — и просто уметь ими пользоваться.

тригонометрия егэ

Тригонометрия на ЕГЭ: 5 формул для базы и профиля

Тригонометрия на ЕГЭ: основные проблемы темы

Чаще всего тригонометрию начинают изучать в 10 классе — но в некоторых школах оставляют до 11. В первом случае у учеников есть 2 года, чтобы освоить новую тему. А во втором, к сожалению, всего год. И это проблема. Дело в том, что в тригонометрии очень много формул, которые нужно знать, чтобы успешно решать задания. Если за 2 года их можно успеть выучить, то за год это будет сделать проблематично.

Ситуация осложняется ещё двумя факторами. Во-первых, в самой математике много формул, признаков, теорем и т.д. Во-вторых, кроме математики есть и другие экзамены, для которых нужно выучить большой объём информации.

Именно поэтому я всегда советую своим ученикам не учить формулы для тригонометрии на ЕГЭ, а выводить! Но об этом мы поговорим чуть позже, а сейчас давайте обсудим, почему тригонометрия так важна и где в ЕГЭ ее можно встретить.

Задания по тригонометрии в базе и профиле на ЕГЭ

Так как ЕГЭ по математике делится на базовый и профильный, а тригонометрия встречается в обоих, то давайте рассмотрим оба уровня экзамена.

Тригонометрия в базе

Что касается Базового уровня, то в нём всего 3 задания, в которых можно столкнуться с тригонометрией:

В № 7 в виде простейшего выражения

Как правило, для успешного решения таких заданий достаточно воспользоваться формулами из справочного материала.

тригонометрия в егэ база

Пример задания № 7 по тригонометрии, демоверсия ЕГЭ

В № 8 в виде формулы прикладной задачи

Стоит отметить, что в базовом ЕГЭ в прикладных задачах тригонометрия попадается редко, но нужно быть готовыми.

тригонометрия в егэ база

Пример задания № 8 по тригонометрии, демоверсия ЕГЭ

В № 15 как тригонометрия в геометрии

В справочном материале есть вся необходимая информация для успешного решения данного задания, а именно определение всех тригофункций в прямоугольном треугольнике.

тригонометрия в егэ база

Пример задания № 15 по тригонометрии, демоверсия ЕГЭ

Тригонометрия в профиле

Базовый уровень мы рассмотрели, теперь перейдём к профильному. Здесь уже больше вариантов, в которых можно встретиться с тригонометрией. Давайте посмотрим на Части 1 и 2.

В № 3 как тригонометрия в геометрии (Часть 1)

То же самое задание, как в базовом ЕГЭ, вот только в справочном материале уже нет необходимой информации.

тригонометрия егэ профиль задания

Пример задания № 3 по тригонометрии, демоверсия ЕГЭ

В № 4 в виде выражения (Часть 1)

То же самое задание, как в базовом ЕГЭ.

тригонометрия егэ профиль задания

Пример задания № 4 по тригонометрии, демоверсия ЕГЭ

В № 7 в виде формулы прикладной задачи (Часть 1)

То же самое задание, как в базовом ЕГЭ. Для успешного решения подойдут базовые навыки работы с тригонометрией.

тригонометрия егэ профиль задания

Пример задания № 7 по тригонометрии, демоверсия ЕГЭ

В № 11 как часть функции (Часть 1)

Функцию нужно проанализировать для поиска наибольшего/наименьшего значения или точек максимума/минимума.

тригонометрия егэ профиль задания

Пример задания № 11 по тригонометрии, демоверсия ЕГЭ

Если с Частью 1 профиля всё более-менее очевидно, то во второй части бывают сюрпризы, о которых ученики даже не подозревают. Да-да, тригонометрия на ЕГЭ умеет прятаться и в Части 2. Давайте посмотрим на эти задания.

В № 12 (Часть 2)

Тут сюрпризов нет. Это уравнение второй части, в котором ученики как раз ожидают увидеть тригонометрию, хотя она там бывает не всегда!

тригонометрия егэ профиль задания

Пример задания № 12 по тригонометрии, демоверсия ЕГЭ

В № 13 — стереометрия (Часть 2)

Да, тригонометрия может встретиться здесь в виде теоремы синусов или теоремы косинусов, а ещё в виде формул в методе координат (для любителей решать этим методом).

В № 16 — планиметрия (Часть 2)

Здесь всё аналогично стереометрии: есть геометрические формулы, в которых прячется тригонометрия. Ведь, как я и сказала выше, в геометрии она тоже бывает!

5 формул тригонометрии: теория для ЕГЭ

А теперь предлагаю перейти к самому интересному — а именно к формулам. К сожалению, их действительно много. А ещё они похожи, и если их просто учить (или бездумно зубрить), то велик риск перепутать «+» с «–» или забыть какую-нибудь единичку.

Именно поэтому я рекомендую не учить формулы, а выводить. Это очень удобно тем более, что в профильном ЕГЭ по математике весь справочный материал состоит из 5-ти формул тригонометрии, из которых очень легко выводятся все остальные.

Но прежде чем я расскажу вам, как выводятся тригонометрические формулы, пообещайте, что обязательно отработаете все правила выведения! Для этого нужно будет регулярно выводить формулы по указанным ниже схемам.

Вот формулы, которые будут у вас в справочном материале:

тригонометрия теория для егэ

Тригонометрия: теория для ЕГЭ — 5 основных формул

Формула № 1 и как она пригодится в поиске котангенса и тангенса

Первая формула — основное тригонометрическое тождество (ОТТ):

тригонометрия теория для егэ

Тригонометрия: теория для ЕГЭ — формула № 1

Обычно ученики знают ее очень хорошо. Она связывает синус и косинус и помогает найти одну функцию через другую.

С этой формулой косвенно связана другая (ее нет в справочном материале), которая тоже легко дается школьникам:

тригонометрия теория для егэ

Тригонометрия: теория для ЕГЭ

Эту формулу очень легко запомнить, если знать, как можно расписать тангенс и котангенс через синус и косинус:

тригонометрия теория для егэ

Тригонометрия: теория для ЕГЭ

Эти 2 формулы связывают по отдельности синус с косинусом и тангенс с котангенсом. Но иногда требуется, чтобы были связаны все 4 функции, и здесь на помощь приходят следствия из ОТТ (как раз та самая формула № 1).

Чтобы вывести следствия нужно всего лишь разделить ОТТ на sin2 и cos2:

тригонометрия теория для егэ

Тригонометрия: теория для ЕГЭ — что выводится из формулы № 1

Теперь можно легко найти:

  • котангенс, зная синус,
  • или тангенс, зная косинус.

Формула № 2 и что из нее можно вывести

С тождествами разобрались, давайте перейдём к формулам двойного угла. Что касается синуса двойного угла (вторая формула в справочном материале):

тригонометрия теория для егэ

Тригонометрия: теория для ЕГЭ — формула № 2

Здесь всё просто, берёте и применяете формулу, если видите, что она нужна для задания.

Формула № 3 и что из нее можно вывести

А вот с косинусом двойного угла (третья формула в справочном материале) всё интереснее. Безусловно, косинус двойного угла:

тригонометрия теория для егэ

Тригонометрия: теория для ЕГЭ — формула № 3

в чистом виде встречается, и тогда вы делаете всё тоже самое, что с синусом. Но на самом деле есть ещё 2 формулы, которые очень просто вывести, используя ОТТ (формулу № 1). Для начала нужно выразить квадрат синуса и квадрат косинуса из ОТТ (Шаг 1):

тригонометрия теория для егэ

Тригонометрия: теория для ЕГЭ — как еще найти косинус двойного угла (Шаг 1)

А потом нужно подставить эти значения в формулу (6, или третья формула справочного материала) (Шаг 2):

тригонометрия теория для егэ

Тригонометрия: теория для ЕГЭ — как еще найти косинус двойного угла (Шаг 2)

Вот мы вывели ещё 2 формулы! А сейчас я покажу вам как практически ничего не делая получить ещё 2. Мы будем выводить формулы понижения степени из формул двойного угла. Смотрите, нужно всего лишь выразить одно из другого:

тригонометрия теория для егэ

Тригонометрия: теория для ЕГЭ — что выводится из формулы № 3

Формулы № 4 и 5 и что из них можно вывести

Давайте посмотрим на справочный материал, у нас там ещё целых 2 формулы, из которых мы получим конечно же ещё 2! Сейчас вообще ничего удивительного не будет. Вот формулы, которые уже даны:

тригонометрия теория для егэ

Тригонометрия: теория для ЕГЭ — формулы № 4 и 5

Как вы заметили, они для суммы углов, а чтобы получить формулы для разности углов, нам нужно всего лишь поменять знаки в формуле на противоположные (разумеется, я говорю про «+» и «–»):

тригонометрия теория для егэ

Тригонометрия: теория для ЕГЭ — что выводится из формул № 4 и 5

Вот так при помощи нехитрых преобразований из 5-ти формул справочного материала мы получили целых 14!

Все скриншоты взяты из открытого банка заданий ФИПИ или из демоверсий ЕГЭ по математике 2022.

Что еще пригодится вам для тригонометрии на ЕГЭ

Скажу по секрету, что это далеко не все формулы тригонометрии, которые существуют. Есть и другие:

  • некоторые можно вывести из вышеуказанных,
  • некоторые можно обобщить и вместо огромного количества формул использовать короткое правило.

Но мне кажется, что пока этого и так много!

Советую сначала хорошо отработать формулы, которые я перечислила в этой статье, и только потом браться за другие. Так вы не загрузите свою память и будете быстрее решать сложные задания по тригонометрии из ЕГЭ. Это, кстати, касается любой темы на экзамене по математике: а в ЕГЭ их очень много. Поэтому чтобы получить высокий балл, надо правильно и системно отработать их все.

Именно так я и строю подготовку к ЕГЭ по математике вместе со своими учениками: строгая система подготовки — ключ к успеху на экзамене. Сначала мы разбираем простые темы и задания и учимся решать их самыми удобными способами — почти на автомате. А после я добавляю более хитрые и сложные задания. В итоге ребята и имеют хорошую базу знаний по математике, и умеют решать самые разные типы задач. Так что если вы хотите по-настоящему знать математику, а не зазубривать формулы, приходите на мои уроки!

А чтобы отрабатывать выведение было не так скучно, держите моего котика, который любезно согласился позировать в позе котангенса:

тригонометрия егэ

Тригонометрия ЕГЭ: КОТангенс
Источник

Лобышева Ирина Сергеевна

Опубликовано 04.12.2014 — 11:35 — Лобышева Ирина Сергеевна

  каждый год выпускаю классы и имею подборку тригонометрических формул используемых в обеих частях ЕГЭ, которыми хочу поделиться с Вами. 

Скачать:

Вложение Размер
Файл trigonometriya.docx 1.28 МБ

Предварительный просмотр:

По теме: методические разработки, презентации и конспекты

Разработка урока алгебры в 10 классе по теме «Формулы тригонометрии»

Данный урок является обобщающим по теме «Тригонометрические формулы»…

Формулы тригонометрии

Обобщающий урок по теме в 10 классе по учебнику А.Г. Мордкович…

Основные формулы по тригонометрии

Приведены основные формулы по тригонометрии для 10 класса….

Тригонометрия. Сборник формул

Тригонометрия. Сборник формул…

Основные формулы тригонометрии

Основные формулы тригонометрии, которые необходимы при подготовке к ЕГЭ по математике…

Формулы тригонометрии

В  презентации  содержится  материал  о  различных  формулах  по  тригонометрии.  Содержание  презентации  можно  использовать  как…

Тригонометрия учебник с формулами

Учебник по тригонометрии включает теоретический материал с формулами…

  • Мне нравится 

 

Источник

Тригонометрическими уравнениями называют уравнения, в которых переменная содержится под знаком тригонометрических функций. К их числу прежде всего относятся простейшие тригонометрические уравнения, т.е. уравнения вида $sin x=a, cos x=a, tg x=a$, где $а$ – действительное число.

Перед решением уравнений разберем некоторые тригонометрические выражения и формулы.

$1$ радиан $={180}/{π}≈57$ градусов

$1$ градус $={π}/{180}$ радиан

Значения тригонометрических функций некоторых углов

$α$ $ 0$ ${π}/{6}$ ${π}/{4}$ ${π}/{3}$ ${π}/{2}$ $π$
$sinα$ $ 0$ $ {1}/{2}$ $ {√2}/{2}$ $ {√3}/{2}$ $ 1$ $ 0$
$cosα$ $ 1$ $ {√3}/{2}$ $ {√2}/{2}$ $ {1}/{2}$ $ 0$ $ -1$
$tgα$ $ 0$ $ {√3}/{3}$ $ 1$ $ √3$ $ -$ $ 0$
$ctgα$ $ -$ $ √3$ $ 1$ $ {√3}/{3}$ $ 0$ $ -$

Периоды повтора значений тригонометрических функций

Период повторения у синуса и косинуса $2π$, у тангенса и котангенса $π$

Знаки тригонометрических функций по четвертям

Эта информация нам пригодится для использования формул приведения. Формулы приведения необходимы для понижения углов до значения от $0$ до $90$ градусов.

Чтобы правильно раскрыть формулы приведения необходимо помнить, что:

  1. если в формуле содержатся углы $180°$ и $360°$ ($π$ и $2π$), то наименование функции не изменяется; (если же в формуле содержатся углы $90°$ и $270°$ (${π}/{2}$ и ${3π}/{2}$), то наименование функции меняется на противоположную (синус на косинус, тангенс на котангенс и т. д.);
  2. чтобы определить знак в правой части формулы ($+$ или $-$), достаточно, считая угол $α$ острым, определить знак преобразуемого выражения.

Преобразовать $сos(90° + α)$. Прежде всего, мы замечаем, что в формуле содержится угол $90$, поэтому $cos$ измениться на $sin$.

$сos(90° + α)=sinα$

Чтобы определить знак перед $sinα$, предположим, что угол $α$ острый, тогда угол $90° + α$ должен оканчиваться во 2-й четверти, а косинус угла, лежащего во 2-й четверти, отрицателен. Поэтому, перед $sinα$ нужен знак $-$.

$сos(90° + α)= — sinα$ — это конечный результат преобразования

Четность тригонометрических функций

Косинус четная функция: $cos(-t)=cos t$

Синус, тангенс и котангенс нечетные функции: $sin(-t)= — sin t; tg(-t)= — tg t; ctg(-t)= — ctg t$

Тригонометрические тождества

  1. $tgα={sinα}/{cosα}$
  2. $ctgα={cosα}/{sinα}$
  3. $sin^2α+cos^2α=1$ (Основное тригонометрическое тождество)

Из основного тригонометрического тождества можно выразить формулы для нахождения синуса и косинуса

$sinα=±√{1-cos^2α}$

$cosα=±√{1-sin^2α}$

  1. $tgα·ctgα=1$
  2. $1+tg^2α={1}/{cos^2α}$
  3. $1+ctg^2α={1}/{sin^2α}$

Вычислить $sin t$, если $cos t = {5}/{13} ; t ∈({3π}/{2};2π)$

Найдем $sin t$ через основное тригонометрическое тождество. И определим знак, так как $t ∈({3π}/{2};2π)$ -это четвертая четверть, то синус в ней имеет знак минус

$sin⁡t=-√{1-cos^2t}=-√{1-{25}/{169}}=-√{{144}/{169}}=-{12}/{13}$

Источник

3621

На ЕГЭ по профильной математике с собой можно взять только черные гелевые ручки и линейку. На экзамене профильного уровня, в отличие от базового, не выдаются справочные материалы – выпускникам не предоставляются формулы, необходимые для решения задач. Исключение составляют лишь 5 формул по тригонометрии, но, естественно, они не помогут набрать максимальные баллы, если экзаменуемые не будут знать об остальных важных сведениях и математических свойствах.

Содержание

Формулы для ЕГЭ по профильной математике. Алгебра

Формулы сокращенного умножения

Квадрат суммы: (a + b)² = a² + 2ab + b²

Квадрат разности: (a – b)² = a² – 2ab + b²

Разность квадратов: a² – b² = (a + b)(a – b)

Сумма кубов: a³ + b³ = (a + b)(a² – ab + b²)

Разность кубов: a³ – b³ = (a – b)(a² + ab + b²)

Прогрессия

Арифметическая

Геометрическая

Таблица степеней

Скриншот 11-11-2022 034403

Свойства степеней

Скриншот 11-11-2022 034826

Таблица квадратов

Скриншот 11-11-2022 035150

Интенсивы по подготовке к региональному этапу ВсОШ

Все, что нужно знать
для победы, за 7 дней!

Свойства корней

Скриншот 11-11-2022 035515

Тригонометрия

Таблица значений тригонометрических функций

Скриншот 11-11-2022 035849

Тригонометрическая окружность

Скриншот 11-11-2022 040226

Тригонометрические формулы

Скриншот 11-11-2022 040507

Обратные тригонометрические функции

Преобразование суммы и разности в произведение

Регулярные курсы по подготовке к олимпиадам и ЕГЭ

Поступаем в вуз мечты без проблем!

Вероятность

Вероятность события А: m – благоприятные, n – общее число событий

 P(A) = m/n

События А и В происходят одновременно: A · B

Независимые события: P(A · B) = P(A) · P(B)

Зависимые события: P(A · B) = P(A) · P(B | A)

Происходит или А, или В: A + B

Несовместные события: P(A + B) = P(A) + P(B)

Совместные события: P(A + B) = P(A) + P(B) – P(A · B)

Свойства модуля

Производные

Основные правила дифференцирования

Таблица производных

Первообразные

Логарифмы

Квадратные уравнения

Дискриминант

Теорема Виета

Разложение на множители

3528

Формулы для ЕГЭ по профильной математике. Геометрия

Планиметрия

Треугольник

Следствие из теоремы косинусов:

Длина биссектрисы (через угол):

Длина биссектрисы (через отрезки):

Прямоугольный треугольник

24 декабря – 20 января

5-11 классы

Онлайн-олимпиада Коалиции

Равносторонний треугольник

Аргументы для итогового сочинения

Подборка лучших аргументов

Равносторонний шестиугольник

Площадь внутреннего треугольника:

Площадь внутреннего прямоугольника:

Ромб

Трапеция

Произвольный четырёхугольник

Окружность

Стереометрия

27f77fef-868e-4746-af5a-ff3f5d564738

Выводы

Не заучивайте формулы без осознания того, откуда берутся числа. Как можно чаще применяйте формулы при решении задач, тренируйте гибкость мышления, чтобы на ЕГЭ по профильной математике справиться со всеми заданиями.

А чтобы в разы повысить шансы на успех и разобраться в тонкостях непростой науки, можно обратиться за помощью к преподавателю онлайн-курса по подготовке к ЕГЭ.

Поделиться в социальных сетях

Какими формулами вам приходится пользоваться чаще всего?

Межтекстовые Отзывы

Посмотреть все комментарии

Читайте также

Источник

На странице вы найдете все формулы тригонометрии в удобном для использования оформлении. Формулы структурированы в блоки по количеству аргументов, степеням, арифметическим операциям над ними.

Содержание:
  1. Основные тригонометрические тождества
  2. Формулы двойного угла
  3. Формулы тройного угла
  4. Формулы понижения степени
    1. Вторая степень
    2. Третья степень
    3. Четвертая степень
    4. Пятая степень
  5. Формулы половинного угла
  6. Формулы понижения степени половинного угла
  7. Формулы сложения аргументов
  8. Формулы вычитания аргументов
  9. Формулы суммы
  10. Формулы разности
  11. Формулы произведения
  12. Формулы произведения в степени
  13. Все формулы на одном листе

Все формулы тригонометрии

Основные тригонометрические тождества

tg alpha = dfrac {sin alpha}{ cos alpha} = dfrac{1}{ctg alpha}

ctg alpha = dfrac {cos alpha}{ sin alpha} = dfrac{1}{tg alpha}

sin ^2 alpha + cos ^2 alpha = 1

1+tg^2alpha=dfrac{1}{cos^2alpha}

1+ctg^2alpha=dfrac{1}{sin^2alpha}

tgalpha cdot ctgalpha=1

Формулы двойного угла (аргумента)

sin(2alpha)=2 cdot cos alpha cdot sin alpha

sin(2alpha)=dfrac{2 cdot tg alpha}{1+tg ^2 alpha}=dfrac{2 cdot ctg alpha}{1+ctg ^2 alpha}=dfrac{2}{tg alpha + ctg alpha}

cos(2alpha)=cos ^2 alpha- sin ^2 alpha = 2 cdot cos ^2 alpha- 1 = 1- 2 cdot sin ^2 alpha

cos(2alpha)=dfrac{1 -tg ^2 alpha}{1+tg ^2 alpha}=dfrac{ctg ^2 alpha- 1}{ctg ^2 alpha +1}=dfrac{ctg alpha-tg alpha}{ctg alpha + tg alpha}

tg(2alpha) = dfrac{2 cdot tg alpha}{1-tg ^2 alpha}=dfrac{2 cdot ctg alpha}{ctg ^2 alpha- 1}=dfrac{2}{ctg alpha- tg alpha}

ctg(2alpha) = dfrac{ctg ^2 alpha-1}{2 cdot ctg alpha}=dfrac{ctg alpha- tg alpha}{2}

Формулы тройного угла (аргумента)

sin(3alpha)=3 cdot sin alpha- 4 cdot sin ^3 alpha

cos(3alpha)= 4 cdot cos ^3 alpha- 3 cdot cos alpha

tg(3alpha)= dfrac{3 cdot tg alpha- tg ^3 alpha}{1-3 cdot tg ^2 alpha}

ctg(3alpha)= dfrac{ctg ^3 alpha- 3 cdot ctg alpha}{3 cdot ctg ^2 alpha -1}

Формулы понижения степени тригонометрических функций

Вторая степень

sin ^2 alpha = dfrac{1-cos(2alpha)}{2}

cos ^2 alpha = dfrac{1+cos(2alpha)}{2}

tg ^2 alpha = dfrac{1-cos(2alpha)}{1+cos(2alpha)}

ctg ^2 alpha = dfrac{1+cos(2alpha)}{1-cos(2alpha)}

(sin alpha- cos alpha)^2=1-sin(2 alpha)

(sin alpha+ cos alpha)^2=1+sin(2 alpha)

Третья степень

sin ^3 alpha = dfrac{3 cdot sin(alpha)-sin(3 alpha)}{4}

cos ^3 alpha = dfrac{3 cdot cos(alpha)+cos(3 alpha)}{4}

tg ^3 alpha = dfrac{3 cdot sin (alpha)-sin(3 alpha)}{3 cdot cos (alpha)+cos(3 alpha)}

ctg ^3 alpha = dfrac{3 cdot cos (alpha)+cos(3 alpha)}{3 cdot sin (alpha)-sin(3 alpha)}

Четвёртая степень

sin ^4 alpha = dfrac{3-4 cdot cos(2 alpha)+cos(4 alpha)}{8}

cos ^4 alpha = dfrac{3+4 cdot cos(2 alpha)+cos(4 alpha)}{8}

Пятая степень

sin ^5 alpha = dfrac{10 cdot sin(alpha)-5 cdot sin(3 alpha)+sin(5 alpha)}{16}

cos ^5 alpha = dfrac{10 cdot cos(alpha)+5 cdot cos(3 alpha)+cos(5 alpha)}{16}

Формулы половинного угла (аргумента)

sin Big( dfrac{alpha}{2} Big)=pm sqrt{dfrac{1-cos alpha}{2}}

cos Big( dfrac{alpha}{2} Big)=pm sqrt{dfrac{1+cos alpha}{2}}

tg Big( dfrac{alpha}{2} Big)= dfrac{1-cos alpha}{sin alpha}= dfrac{sin alpha}{1+cos alpha}

ctg Big( dfrac{alpha}{2} Big)= dfrac{1+cos alpha}{sin alpha}= dfrac{sin alpha}{1-cos alpha}

Формулы понижения степени половинного угла (аргумента)

sin ^2 Big( dfrac{alpha}{2} Big)=dfrac{1-cos alpha}{2}

cos ^2 Big( dfrac{alpha}{2} Big)=dfrac{1+cos alpha}{2}

tg ^2 Big( dfrac{alpha}{2} Big)=dfrac{1-cos alpha}{1+cos alpha}

ctg ^2 Big( dfrac{alpha}{2} Big)=dfrac{1+cos alpha}{1-cos alpha}

Формулы сложения аргументов

sin(alpha + beta)=sin alpha cdot cos beta + cos alpha cdot sin beta

cos(alpha + beta)=cos alpha cdot cos beta- sin alpha cdot sin beta

tg(alpha + beta)= dfrac{tg alpha + tg beta}{1-tg alpha cdot tg beta}

ctg(alpha + beta)= dfrac{ctg alpha cdot ctg beta-1}{ctg alpha + ctg beta}

Формулы вычитания аргументов

sin(alpha- beta)=sin alpha cdot cos beta- cos alpha cdot sin beta

cos(alpha- beta)=cos alpha cdot cos beta+ sin alpha cdot sin beta

tg(alpha- beta)= dfrac{tg alpha- tg beta}{1+tg alpha cdot tg beta}

ctg(alpha- beta)= dfrac{ctg alpha cdot ctg beta+1}{ctg beta — ctg alpha}

Формулы суммы тригонометрических функций

sin alpha+ sin beta=2 cdot sin big( dfrac{alpha + beta}{2} big) cdot cos big( dfrac{alpha- beta}{2} big)

cos alpha+ cos beta=2 cdot cos big( dfrac{alpha + beta}{2} big) cdot cos big( dfrac{alpha- beta}{2} big)

tg alpha + tg beta = dfrac{sin(alpha + beta)}{cos alpha cdot cos beta}

ctg alpha + ctg beta = dfrac{sin(alpha + beta)}{cos alpha cdot cos beta}

sin (alpha)+cos(alpha)=sqrt{2} cdot sin Big( alpha+ dfrac{pi}{4} Big)

Формулы разности тригонометрических функций

sin alpha- sin beta=2 cdot sin big( dfrac{alpha- beta}{2} big) cdot cos big( dfrac{alpha+ beta}{2} big)

cos alpha- cos beta=-2 cdot sin big( dfrac{alpha + beta}{2} big) cdot sin big( dfrac{alpha- beta}{2} big)

tg alpha- tg beta = dfrac{sin(alpha- beta)}{cos alpha cdot cos beta}

ctg alpha- ctg beta = dfrac{sin(alpha + beta)}{sin alpha cdot sin beta}

sin (alpha)-cos(alpha)=sqrt{2} cdot sin Big( alpha- dfrac{pi}{4} Big)

Формулы произведения тригонометрических функций

sin alpha cdot sin beta = dfrac{cos (alpha- beta)-cos(alpha + beta)}{2}

sin alpha cdot cos beta = dfrac{sin (alpha- beta)+sin(alpha + beta)}{2}

cos alpha cdot cos beta = dfrac{cos (alpha- beta)+cos(alpha + beta)}{2}

tg alpha cdot tg beta = dfrac{cos(alpha- beta)- cos(alpha+beta)}{cos(alpha- beta)+ cos(alpha+beta)}=dfrac{tg alpha + tg beta}{ctg alpha + ctg beta}

ctg alpha cdot ctg beta = dfrac{cos(alpha- beta)+ cos(alpha+beta)}{cos(alpha- beta)- cos(alpha+beta)}=dfrac{ctg alpha + ctg beta}{tg alpha + tg beta}

tg alpha cdot ctg beta = dfrac{sin(alpha- beta)+ sin(alpha+beta)}{sin(alpha+ beta)- sin(alpha-beta)}

Формулы произведения тригонометрических функций в степени

sin ^2 (alpha) cdot cos ^2 (alpha) = dfrac{1-cos(4 alpha)}{8}

sin ^3 (alpha) cdot cos ^3 (alpha) = dfrac{3 cdot sin(2 alpha)- sin(6 alpha)}{32}

sin ^4 (alpha) cdot cos ^4 (alpha) = dfrac{3-4 cdot cos(4 alpha)+ cos(8 alpha)}{128}

sin ^5 (alpha) cdot cos ^5 (alpha) = dfrac{10 cdot sin (2 alpha)-5 cdot sin(6 alpha)+sin (10 alpha)}{512}

Все формулы тригонометрии на одном листе

На этой картинке собраны все формулы тригонометрии для печати. Лист можно распечатать и использовать при решении задач ЕГЭ или вырезать таблицы и использовать как шпаргалку. Распечатанный лист можно применять как справочный материал при решении задач по тригонометрии в 10 и 11 классе.

Формулы тригонометрии на листе А4

Источник

Понравилась статья? Поделить с друзьями:
  • Основные формулы по физике егэ 11 класс
  • Основные формулы планиметрии для егэ профиль
  • Основные формулы по физике для егэ шпаргалка
  • Основные формулы логарифмов шпаргалка для егэ
  • Основные формулы по физике для егэ 2023