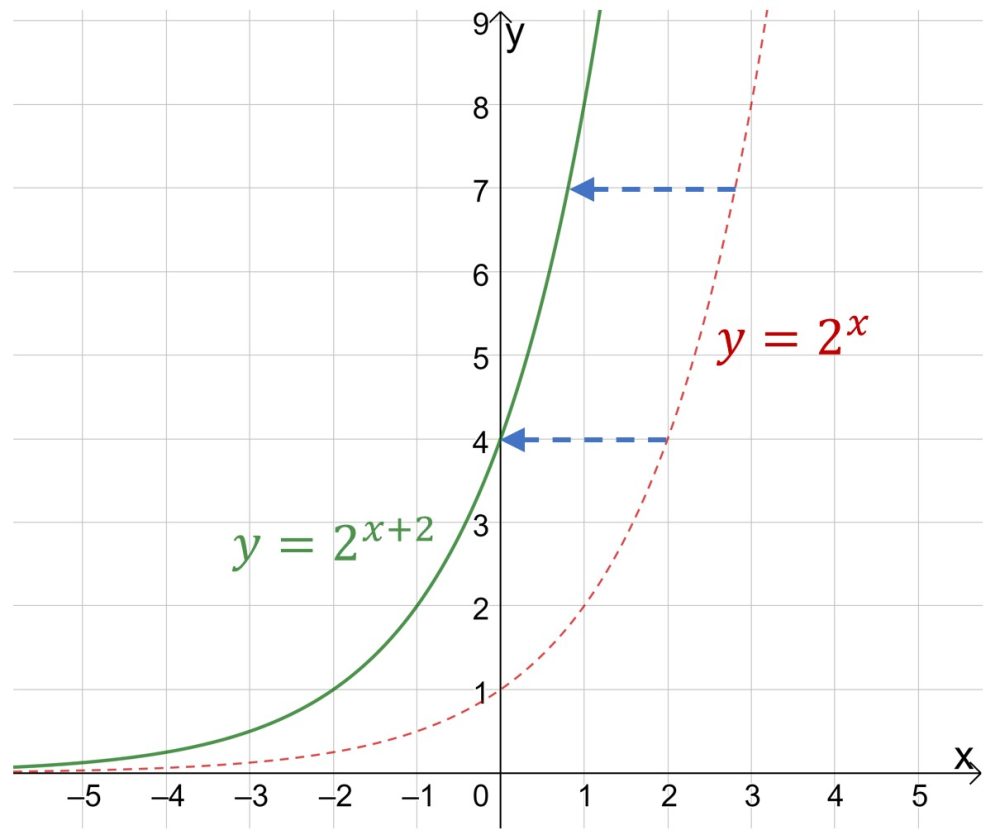
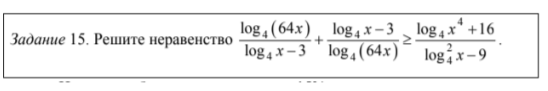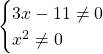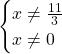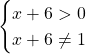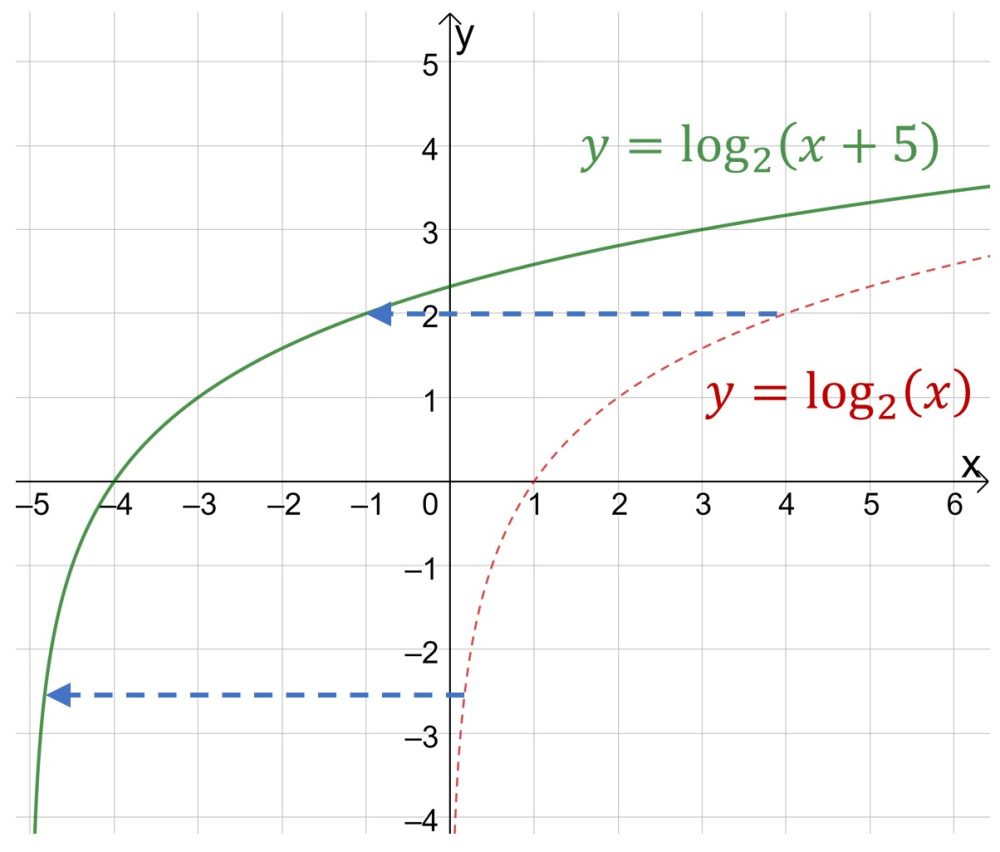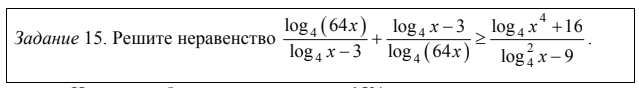Основные ошибки егэ математика профиль - Помощь в подготовке к экзаменам и поступлению

Чтобы успешно сдать экзамен, подготовку нужно начинать заранее. И если вы не можете самостоятельно определить свои слабые места и проблемы, рекомендуем начать с разбора типичных ошибок ЕГЭ и ОГЭ по математике.

Здесь мы приведем анализ типичных ошибок 2023 и дадим советы, как их не допустить при сдаче ОГЭ/ЕГЭ по математике. Следите за нашим телеграм-каналом – там мы будем разбирать и другие дисциплины, чтобы помочь вам в поступлении.

Базовый уровень математики

Ошибки в задачах на проценты

Чаще всего их допускают, так как не разбираются в сути процента.

Возьмем пример задачи, когда нужно сначала снизить цену на 25%, а потом повысить ее на 25%. Самая частая ошибка – полагать, что эти проценты будут равны одной и той же сумме. На самом же деле база их зачисления будет совершенно разной.

В этом примере 6% участников допустили вариант, что новую цену нужно понизить на 25%. На самом же деле новая цена – это 125% от старой. И вопрос в этой задаче – узнать, сколько будет 100% от старой цены.

Совет: повторить основы расчета процентов, повторить взаимосвязи величин, подумать над способом решения таких задач.

Невнимательное прочтение условия задания

Волнение и психологическое напряжение приводят к тому, что участники часто неправильно понимают условие задания. В итоге – снижение итогового балла по невнимательности, а не по незнанию.

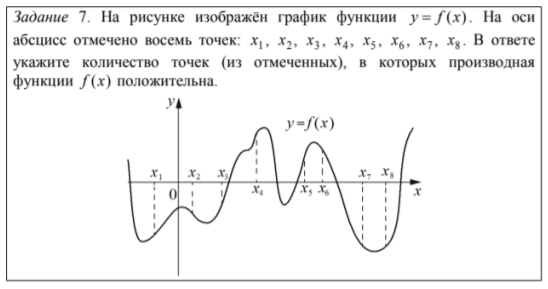
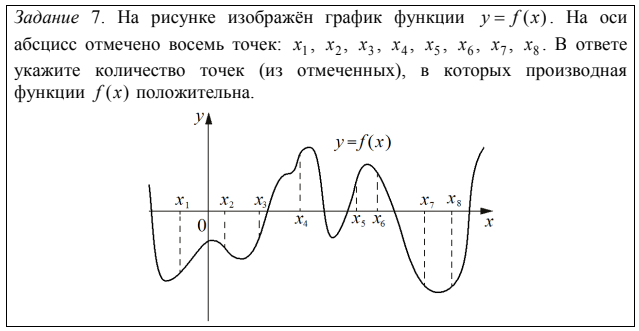
Например:

В 24% участников упомянули те точки, где значение функции (а не производной) положительное. Еще 2% указали номера точек, где производная принимает положительное значение.

Совет: вдумчиво, медленно и несколько раз читайте задание.

Непонимание текста задачи (на повышенном уровне и в практико-ориентированных заданиях)

Учащиеся могут не только неправильно понять, но и вовсе не понять условия. Иногда это происходит из-за незнания величин, единиц их измерения или плохой работы с формулами. Многие просто пропускают эту часть тестирования.

Вот пример задачи:

Её выполнило только 57% участников тестирования. 8% вообще не дали ответа, 6% дали ответ «чем ближе, тем лучше», 4% – «лампочку необходимо поместить в середину разрешенного интервала», еще 4,5% приняли фокус за основной параметр.

Совет: изучайте задания прошлых лет, просите учителя практиковать как можно более разные задачи.

Ошибки в вычислениях

Школьная привычка использовать даже в самых легких примерах калькулятор приводит к плачевному результату на экзамене. Если учащийся не научиться быстро считать в уме или хотя бы на бумаге, во время тестирования он может ошибиться даже в самых простых заданиях.

Особенно сложно участникам тестирования даются дроби, отрицательные числа, элементарные преобразования выражений и другие проблемы, копившиеся еще с 5 класса.

Совет: если в чем-то не разбираетесь, обязательно отработайте эту тему до автоматизма перед экзаменом, потому что она обязательно попадется.

Ошибки теоретического характера

Это касается фактов по геометрии и алгебре, незнание которых приводит к снижению процента выполнения заданий и базового, и профильного уровней.

Например:

В этой задаче около 8% участников вообще не ответили на поставленное условие, 38% дали ответ с ошибками относительно боковой поверхности конуса, а 12% совершили ошибки в расчёте объёма.

Статистика показывает, что в таких заданиях ошибок гораздо больше, чем в гораздо более сложных профильных заданиях.

Совет: потренируйтесь перед тестированием. Если ответы не сходятся с ключами, обратитесь за помощью к стороннему специалисту (репетитору или сервису студенческой помощи), чтобы они указали, где вы ошибаетесь.

Ошибки в алгоритмах и методах решения

Этот тип ошибок встречается во всех заданиях.

Например:

Около 15% участников получили нулевые баллы из-за проблем с невнимательным чтением неравенства, непониманием алгоритма решения совокупностей и систем логарифмических неравенств.

Хватает ошибок и в решении дробнорациональных неравенств, когда ученики забывают про знаменатель.

Совет: всегда проверяйте решение. Научитесь правильно находить последовательность в решении алгоритмов.

Ошибки в чтении и построении чертежа

Такое случается, когда ученик не понимает взаимосвязь элементов геометрических конструкций, а также не обладает основными пространственными представлениями.

Например:

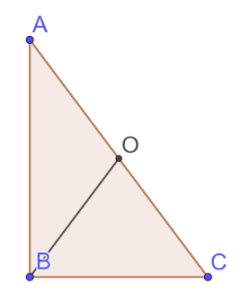
Около 10% участников экзамена сделали ошибки в вычислении углов по их записи, просто перепутав буквы или не понимая, где расположены вершины всех углов. Еще 5% решили, что угол ACD прямой. А 3% увидели в угле ABD равносторонний треугольник.

Совет: тренируйтесь находить взаимосвязь элементов геометрических конструкций.

Неумение обосновывать и доказывать

14 и 16 задания по стереометрии и планиметрии отличаются повышенным уровнем сложности и требуют развернутого ответа. В каждом по 2 пункта: в первом нужно доказать, во втором – произвести вычисления.

Самые распространенные ошибки касаются первого пункта, так как у участников выявились проблемы с умением доказывать.

Есть проблемы и в оформлении доказательств. Например:

Основная трудность в отсутствии понимания логики построения доказательства.

Совет: тренируйтесь в доказательной базе, повышайте математическую культуру, учитесь обосновывать выбранные методы и способы их решения.

Ошибки в заданиях по тригонометрии

Из-за невнимательности и неаккуратности, а также отсутствия знаний по большому количеству теоретических фактов и способности их применять на практике, участники совершают частые ошибки в решении тригонометрических заданий.

Например:

Только 34% участников выполнили его. Самые частые ошибки (около 12%) связаны в первую очередь с нахождением тригонометрического знака – чаще всего потеря знака «минус». Еще 22% ждут «красивого» ответа, равного 1 или 2.

Ошибки математического моделирования

В 11 и 17 заданиях проверяют способность учащихся к построению и исследованию простейших математических моделей.

В текстовых задачах основную роль играет сюжетная часть – она имеет практическую ориентацию. И часто из-за непонимания взаимосвязи величин в этих заданиях допускают ошибки.

Например, в задачах на движение примерно 10% не понимают принципы движения по реке – они умножают собственную скорость на время движения.

Совет: тренируйте текстовые задачи, внимательно читайте условие задачи.

Профильный уровень

Здесь приведем краткий список трудностей и ошибок участников ЕГЭ по математике:

Задание 2 – учащиеся не понимают разницу в сравнении отрицательных чисел и их моделей.
Задание 6 – не понимают геометрический рисунок (относятся к нему как к чертежу, где соблюдены все размеры).
Задание 7 – отвечают наугад в решениях производных и попытках увидеть ее на чертеже.
Задание 8 – ошибаются в наглядном решении.
Задание 9 – неправильно применяют свойства степеней, ошибаются в решении логарифмов из-за отсутствия практики.
Задание 12 – ошибаются в задачах с нулями производной.

Как правильно читать задание, чтобы не совершать ошибок по невнимательности

Есть несколько рекомендаций, чтобы избежать ошибок из-за невнимательного прочтения задания. Это и будет алгоритмом решения задачи:

прочтите условие;
выпишите данные величины, сделайте рисунок в геометрическом задании;
установите и запишите отношения и взаимосвязи между известными данными;
выпишите что найти, ответ на какой вопрос нужно дать;
определите тип задания;
сформулируйте содержание и последовательность действий.

Это будет ваш своеобразный чек-лист, который обязательно нужно соблюдать при решении любой задачи, чтобы не допустить обидных ошибок.

Данные условия важно именно выписывать, а не иметь в виду. Фиксация их в уме чаще всего приводит к записи неправильного ответа.

И еще момент: не приступайте к решению задачи сразу же после ее прочтения. Психологи утверждают, что важно выдержать паузу между стимулом и реакцией – именно при этом условии удастся добиться оптимальных результатов:

сориентироваться в условии,
обдумать и спланировать ее решение,
понять уровень ее сложности и решить, откладывать ли ее решение напоследок.

Кроме сложности задачи оцените, сколько баллов она принесет и насколько она утомительна. Важно оставить энергию для решения других заданий при сдаче единого государственного экзамена.

Начинайте с самой простой задачи, постепенно продвигаясь к самой сложной. На экзамене важно количество решенных заданий, а не их сложность.

Знание типичных ошибок ЕГЭ и ОГЭ по математике даст вам полную картину того, к каким заданиями нужно готовиться с большим усилием. А чтобы не отвлекаться на другие учебные дела, не забывайте: рядом есть сервис студенческой помощи, который подставит плечо в трудную минуту.

Источник

Это статья написана в первую очередь для выпускников, которые совсем скоро пойдут на важный и ответственный бой, называемый единым государственным экзаменом. От исхода этого поединка зависит дальнейший вектор развития. Но прошу Вас, не думайте, что от результатов зависит вся ваша жизнь. Экзамен – это лишь рубеж, испытание, которое нужно пройти с высоко поднятой головой.

Я достаточно давно и интенсивно занимаюсь подготовкой абитуриентов к единому государственному экзамену по математике и физике. После экзамена ребята активно делятся впечатлениями, когда приходят результаты – отправляют сканы работ, которые я внимательно изучаю. И я вижу, что из года в год ребята теряют баллы на вполне конкретных заданиях. И чтобы Ваши потери на экзамене на фоне волнения были минимальными, давайте разберем типичные ошибки ученика на ЕГЭ.

1) Уравнения с квадратным корнем

Не забывайте про ограничения!!! Вообще говоря можно наложить ограничения и на подкоренное выражение и на правую часть:

$begin{cases} 2x+6geq0 \ -xgeq0 end{cases}$

$begin{cases} xgeq-3 \ xle0 end{cases}$

… но если решаете возведением обеих частей в квадрат, то первое неравенство избыточно.
Как альтернатива, выполните проверку, подставив полученные корни в уравнение. Составители очень часто ловят на этом задании, провоцируют указать именно тот корень, который не удовлетворяет ограничениям.
Ограничения актуальны и для обычных дробных уравнений такого вида:

$frac{2x-8}{3x-11}=frac{6}{x^2}$

$begin{cases} 3x-11neq0 \ x^2neq0 end{cases}$

$begin{cases} xneqfrac{11}{3} \ xneq0 end{cases}$

Ну и конечно, куда без ограничений при решении логарифмических уравнений:

$log_7{left(x^2+3xright)}=log_7{left(49right)}$

Напоминаю, что аргумент логарифма должен быть СТРОГО БОЛЬШЕ НУЛЯ:

Ну а если Вы имеете дело с логарифмом с переменным основанием

$log_{x+6}{left(32right)}=5$

то не забудьте, что основание должно быть положительным и не равняться единице.

$begin{cases} x+6>0 \ x+6neq1 end{cases}$

2) Планиметрия
Что касается планиметрии, советую повторить:
1. Формулы для расчета площадей все фигур. Не забудьте повторить, как находится длина дугового сектора и площадь сектора, на всякий случай. Хотя встречаются на ЕГЭ они не так часто.
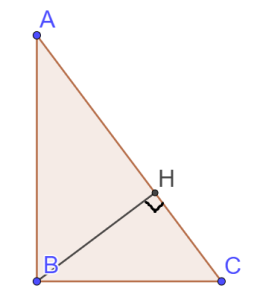
2. Помните, что медиана в прямоугольном треугольнике не только делит гипотенузу пополам, но и равна половине гипотенузы.

$BO=frac{AC}{2}$

3. Повторите свойства пропорциональных отрезков в прямоугольном треугольнике. Высота, проведенная из вершины прямого угла делит прямоугольный треугольник на два подобных. Расписав отношения сторон всех подобных треугольников Вы придете к формулам:

${AB}^2=AHcdot AC$

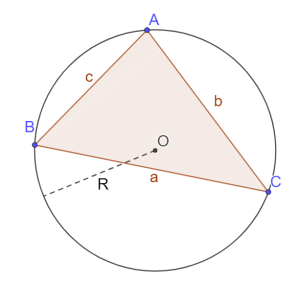
4. Повторите теоремы синусов и косинусов. Теорема синусов бывает весьма полезна для нахождения радиуса описанной окружности

Теорема синусов:

$frac{a}{sin{left(angle Aright)}}=frac{b}{sin{left(angle Bright)}}=frac{C}{sin{left(angle Cright)}}=2R$

Теорема косинусов:

$a^2=b^2+c^2-2bc cdot cos{left(angle BACright)}$

5. Из года в год найдется ученик, который забудет формулу для расчета радиуса вписанной окружности. А она ведь такая простая!

И работает не только для треугольников, но и для четырехугольников, пятиугольников и так далее. Не забудьте, что в формуле берется ПОЛУПЕРИМЕТР, а S – это площадь фигуры, а не круга!

3) Немного поговорим про преобразование выражений. Чаще всего ребята ошибаются именно в тригонометрии при использовании формул приведения.

Напоминаю алгоритм:

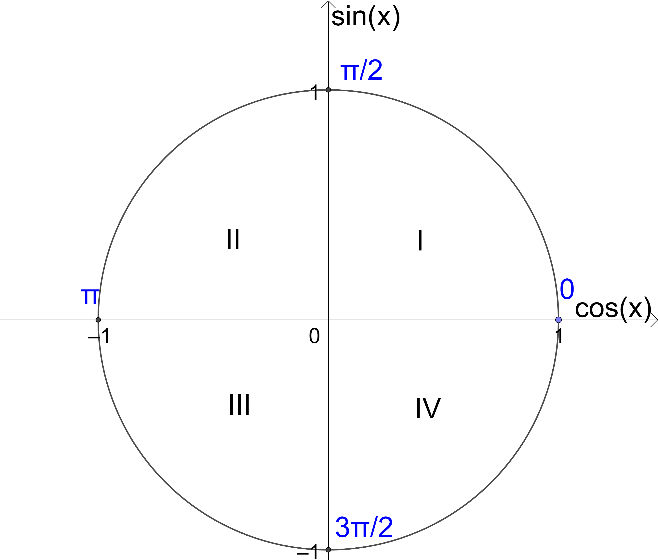
1. Определяем номер четверти, в которой лежит угол.

2. Определяем знак функции. Напоминаю, что знак смотрится по исходной функции.

3. Не забываем, что в точках $frac{pi}{2}$ и $frac{3pi}{2}$ функция меняется на ко-функцию, то есть синус на косинус, косинус на синус, тангенс на котангенс и т.д.

Для лучшего понимания приведу пример

Упростить $ctg{left(frac{3pi}{2}+alpharight)}$ , где $alphainleft(0;frac{pi}{2}right)$

Шаг 1: Определяем четверть
$left(frac{3pi}{2}+alpharight) epsilon IV$ четв.

Шаг 2: Определяем знак исходной функции в данной четверти. Знак в IV четв. будет отрицательным.
Шаг 3: Так как в выражении есть $frac{3pi}{2},$ то заменим на . В итоге получим $ctg{left(frac{3pi}{2}+alpharight)}=-tgleft(alpharight)$

4) Переходим к стереометрии. Тут советы будут аналогичны советам по планиметрии. Повторите все формулы объемов фигур и площадей поверхностей, особенно шара. Легче всего эта формула запоминается, если вы запомните, что площадь поверхности шара – это производная от его объема.

$V=frac{4}{3}pi r^3$

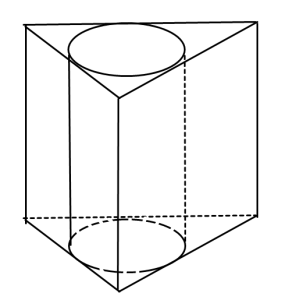
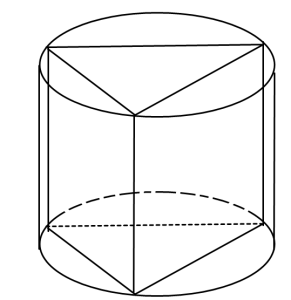
Если Вы имеете дело с комбинацией тел, то внимательно несколько раз прочитайте условие задачи. Цилиндр вписан в призму или описан около призмы, параллелепипед вписан в цилиндр или описан около цилиндра и так далее. Советую держать в голове картинки:
Это – пример призмы, описанной около цилиндра

А это – пример призмы, вписанной в цилиндр

Ну а теперь поговорим о самых распространенных ошибках в стереометрии первой части:
1. Угол между двумя прямыми всегда не более 90 градусов.
Пример:

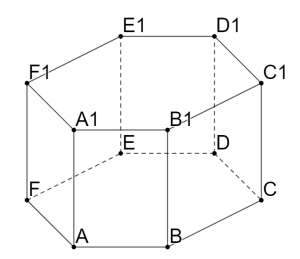
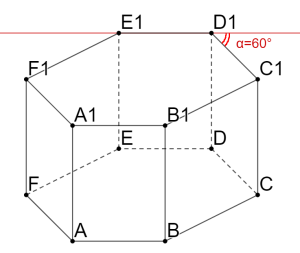
В правильной шестиугольной призме $ABCDEFA_{1}B_{1}C_{1}D_{1}E_{1}F_{1}$ , все рёбра которой равны 8, найдите угол между прямыми FA и $D_{1}E_{1}$ . Ответ дайте в градусах.

Большая часть ребят проводит прямую $D_{1}C_{1}$ , параллельную FA и берут угол $E_{1}D_{1}C_{1}$ , тем самым получая ответ в 120 градусов. Но это не правильно. Брать нужно смежный угол, который будет равен 60 градусов.

2. Ошибки в применении коэффициента подобия

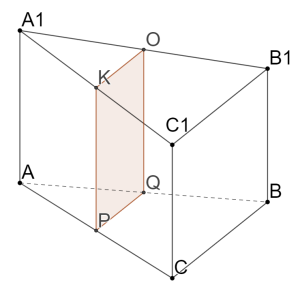
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объем этой призмы, если объём отсеченной призмы равен 20.

Классический пример – призма и плоскость проведенная через среднюю линию треугольника, лежащего в основании. Ребята полагают, что отношение объемов малой призмы к большой призме равно кубу коэффициента подобия, который в нашем случае равен ½. Но это не так. Отличаются эти призмы только основанием, а вот высоты одинаковы. Следовательно, отношение объемов будет равно отношению площадей оснований. А это квадрат коэффициента подобия.

3. Ошибки в расчете площадей поверхностей составных многогранников.
Классическая проблема в данном случае заключается в том, что ребята достраивают фигуру до куба или параллелепипеда. В этом случае возникает опасность либо посчитать лишнюю поверхность, либо потерять нужную.
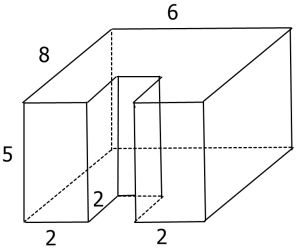
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Возможно это немного дольше, но я советую посчитать площадь каждого прямоугольника по отдельности и сложить все значения.

5) График функции и её производной. Наше счастье и наша боль. Мне кажется, эта задача напоминает квест на внимательность. Прежде чем записывать ответ в бланк, советую внимательно несколько раз прочитать задание и для себя ответить на вопрос: я имею дело с графиком функции или ее производной.
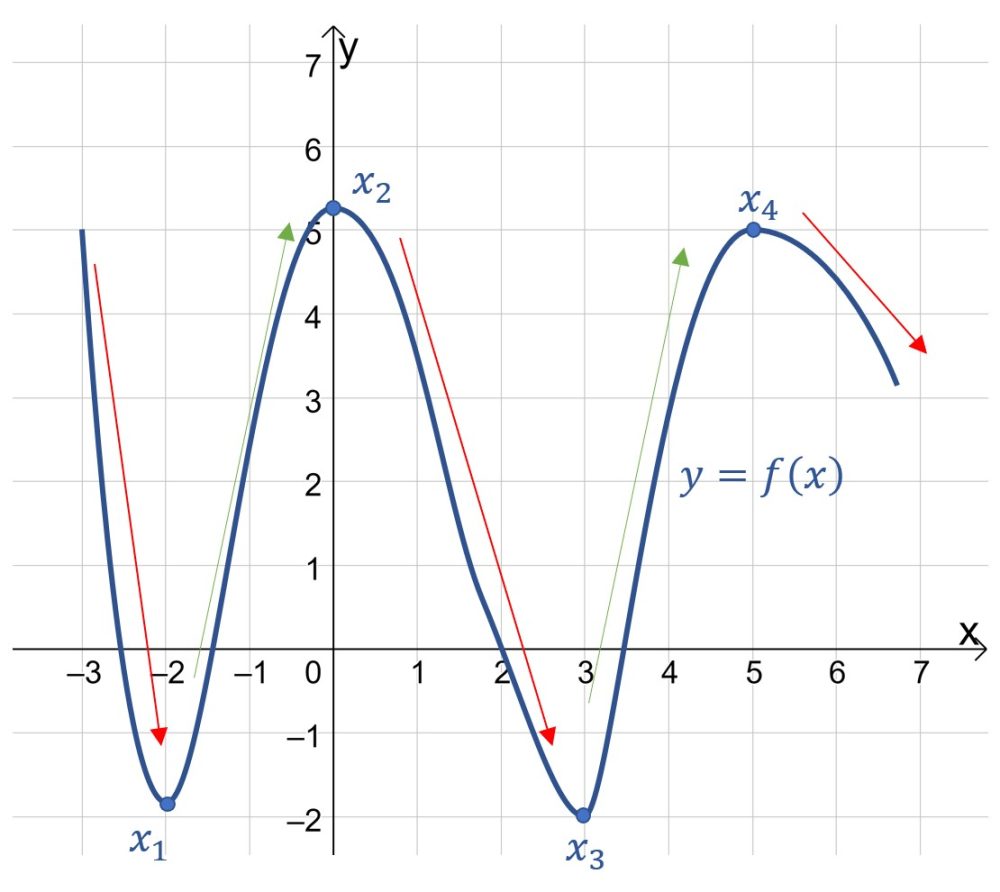
1. Если Вы имеете дело с графиком самой функции, то помните, что точки экстремума – это точки, где функция переходит с возрастания на убывание или с убывания на возрастание. Точки пересечения графика с осью х ничего не означают.
Для примера предлагаю рассмотреть следующую функцию:

Там, где функция возрастает (зелёные стрелки), производная функции положительна, а там, где функция убывает (красные стрелки), производная функции отрицательная. Производная равна нулю в точках экстремума .

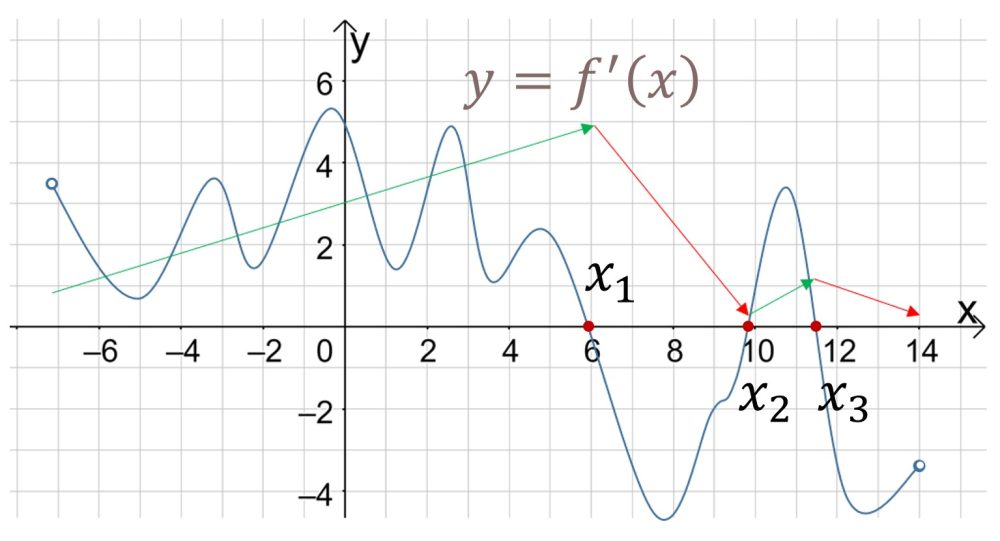
2. Если на экзамене Вам попалась производная функции, то помните: там, где график лежит выше оси х, функция возрастает, там, где график лежит ниже оси х – функция убывает, а точки пересечения графика с осью х-это точки экстремума.

– т. экстремума, – т. max, – т. min

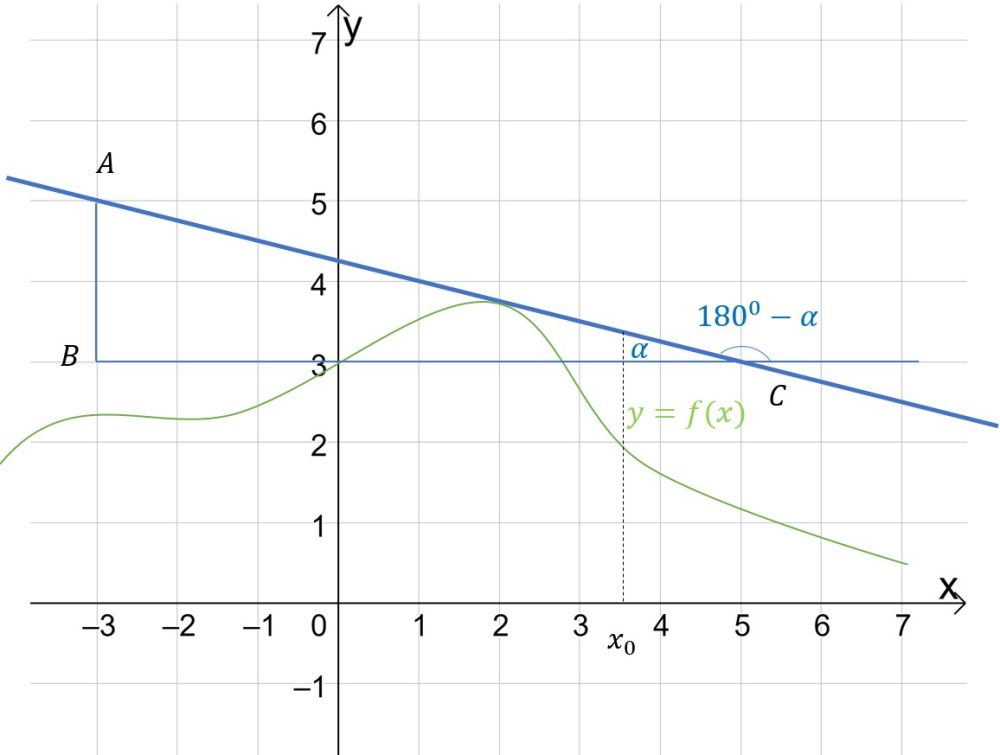
3. Внимательно посмотрите на касательную к графику функции. Если она возрастает, значит значение производной положительно, если убывает-отрицательно.

$tgleft({180}^0-alpharight)=-tg{left(alpharight)}=-frac{AB}{BC}=-frac{2}{8}=-0,25$

НЕ ТЕРЯЙТЕ МИНУС В ОТВЕТЕ!

6) Текстовые задачи тоже довольно часто становятся камнем преткновения у выпускников. Советую повторить формулы для суммы арифметической прогрессии, связь концентрации и массы раствора, производительности и работы.
Любимая ошибка выпускников находить среднюю скорость как среднее арифметическое. Не делайте так! Средняя скорость – это общий путь, деленный на общее время.

$v_{cp}=s_{общ}/t_{общ}=(s_1+s_2)/(frac{s_1}{v_1} +frac{s_2}{v_2} )$

(Работа = Производительность Время)

(Путь = Скорость Время)

M_{кислоты}=n∙M_{раствора}

Формула n-го члена арифметической прогрессии:

Сумма первых n членов арифметической прогрессии вычисляется по формуле: $s_n=frac{left(a_1+a_nright)}{2}cdot n=frac{2a_1+left(n-1right)d}{2}cdot n$

Достаточно тяжело идут у ребят задачи на проценты такого вида:

В 2000 году диван подешевел на 7 процентов, в 2001 подорожал на 8 процентов. Конечная цена 25000 рублей. Найти начальную стоимость.

Советую начальную стоимость обозначить за х, тогда в 2000 году стоимость дивана станет (х-0.07х) =0.93 х рублей, а в 2001 году стоимость будет равна 0.93х*1.08 рублей, которая будет равна 25000 рублей. Можно, конечно, идти с конца, но тогда у ребят возникают сложности, что какую величину обозначить за 100 процентов, что за 107 процентов или может быть за 93 процента.

7) Графики функций. Для правильного выполнения данного номера я советую Вам повторить , какие коэффициенты в функции отвечают за смещение графика вправо или влево, какие вверх или вниз, повторить формулу для расчета вершины параболы $x_0=frac{-b}{2a}$ .
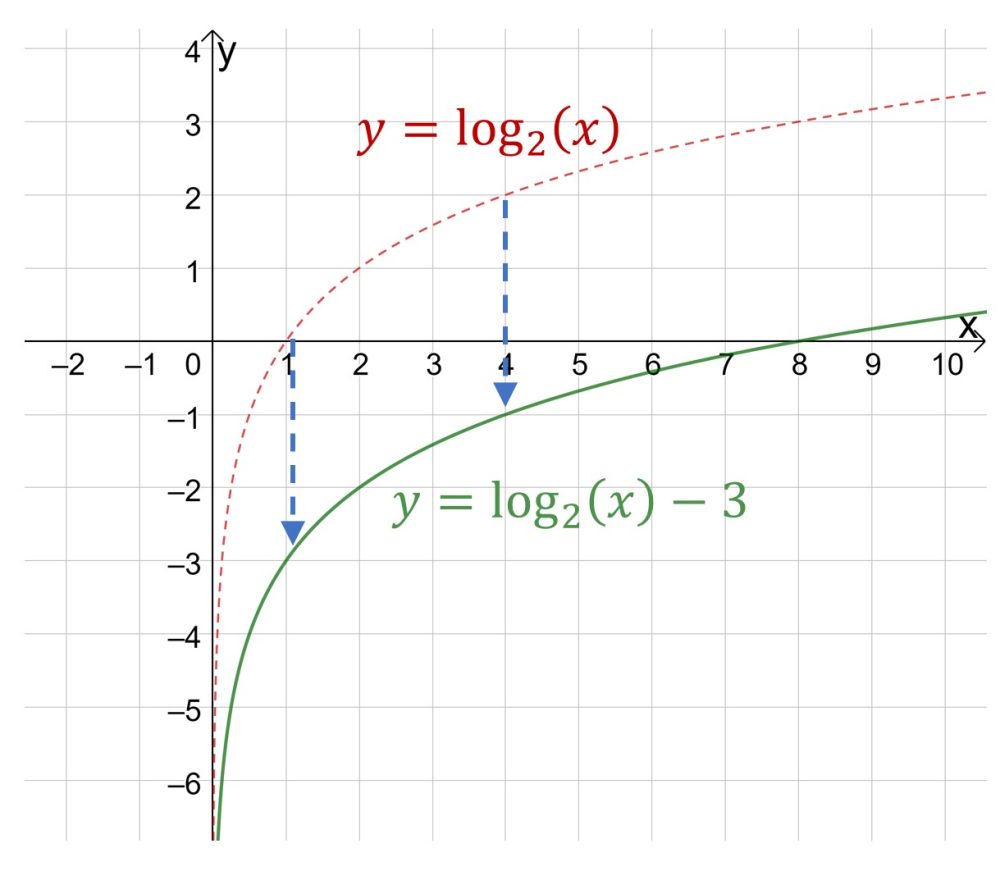
Если у Вас функция вида $fleft(xright)=b+log_a{left(xright)}$ , то коэффициент b отвечает за смещение графика функции вверх или вниз.

А здесь – график с положительным коэффициентом b, равным 2:

Если же Ваш график имеет вид $fleft(xright)=log_a{left(x+bright)}$ , то вы должны понимать, что при положительном значении b ваш график смещается влево, а при отрицательном значении b вправо.

Абсолютно аналогично и с графиками показательной функции.
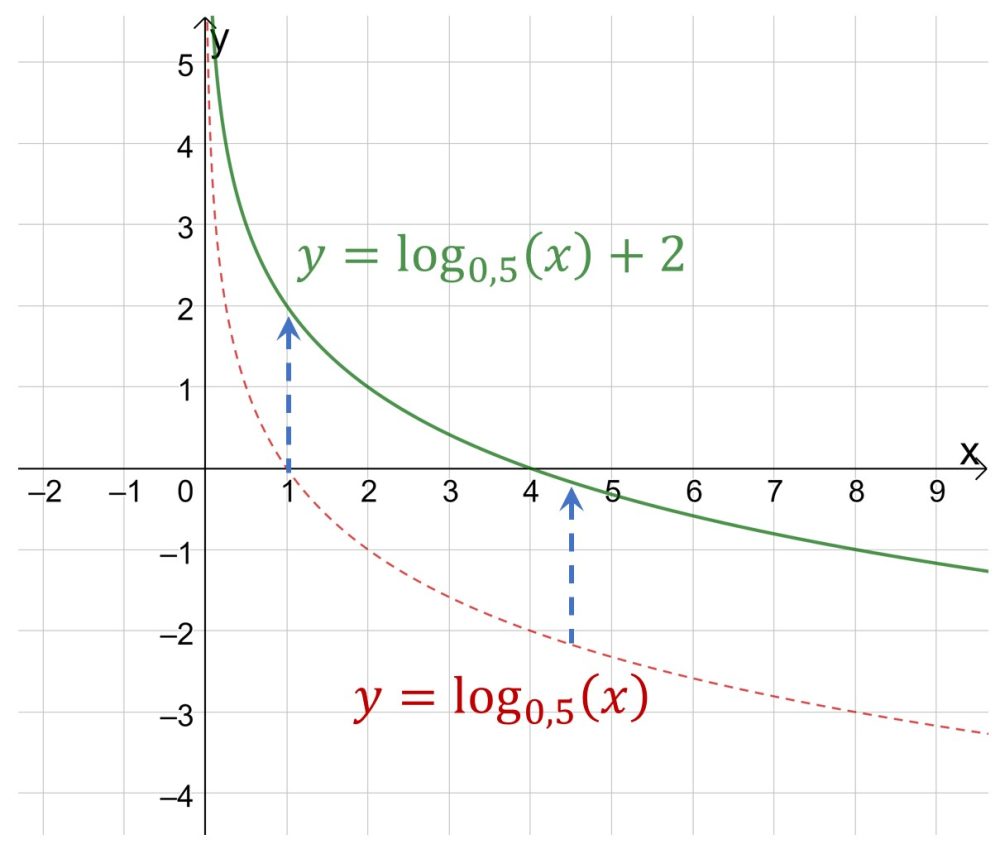
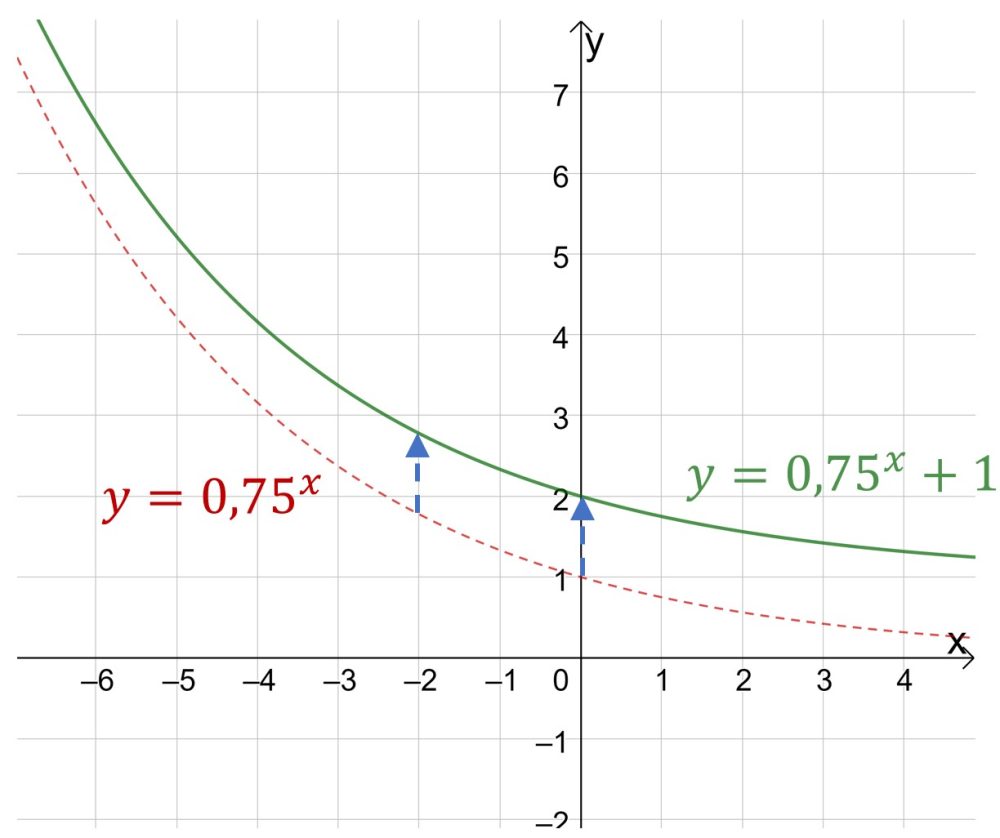
Если вы имеете дело с графиком вида , то при положительном b график смещается вверх, при отрицательном b вниз.
На первом графике пример отрицательного коэффициента b, на втором графике пример положительного b.

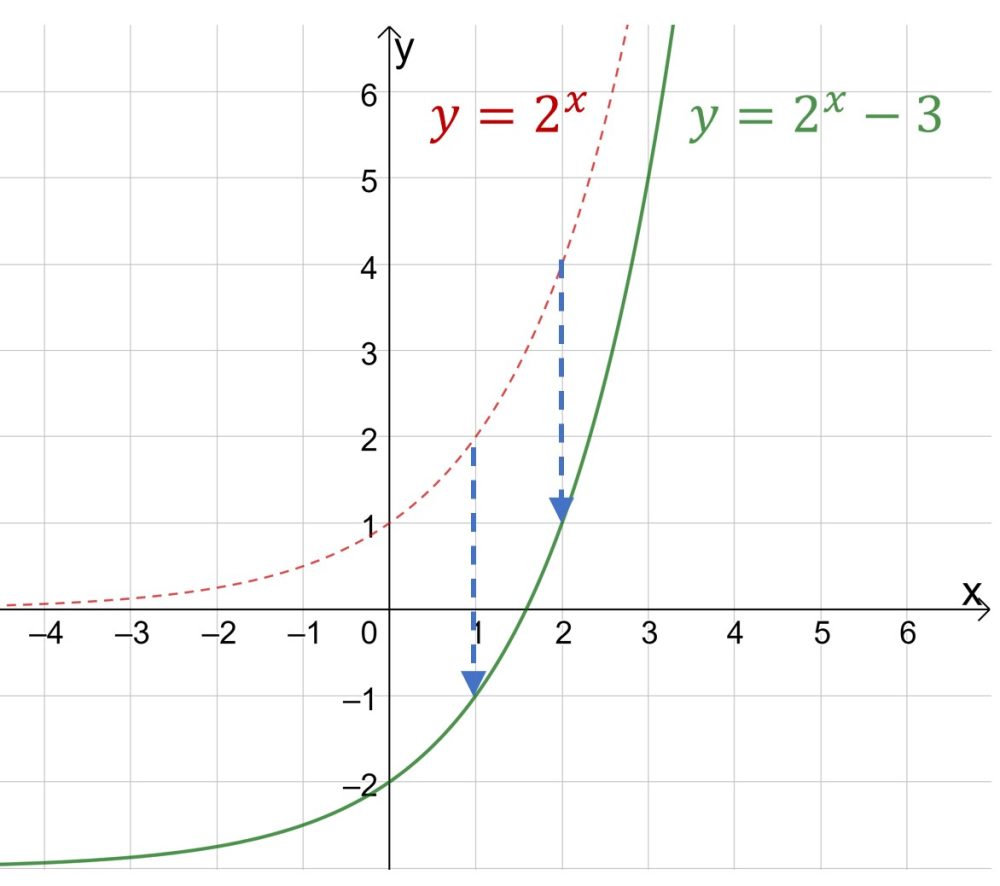
Ну и не забывайте о графиках показательной функции вида $fleft(xright)=a^{x+b}$ . Здесь коэффициент b отвечает за смещение графика функции вправо или влево.

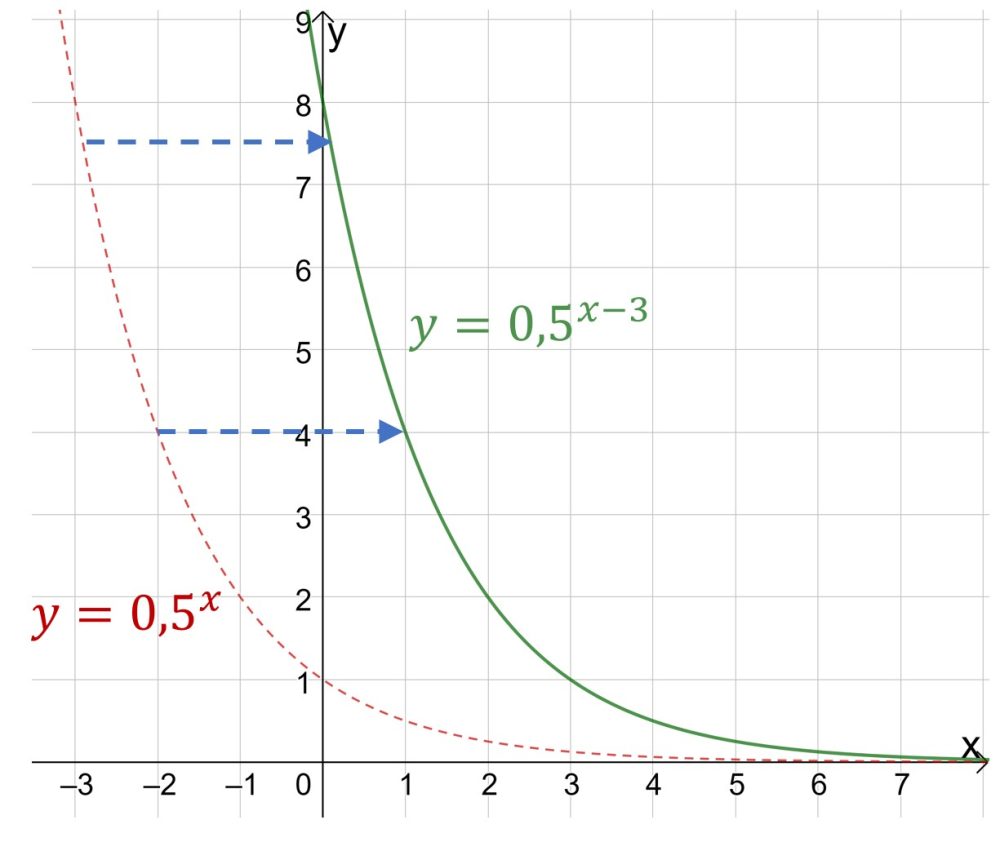
Если вдруг у Вас на экзамене все эти смещения туда-сюда вылетели их головы, то берите одну-две-три точки (по ситуации), подставляйте в уравнение функции и находите нужные Вам коэффициенты.

И хотелось бы напомнить , что основание логарифма и основание показательной функции МОГУТ БЫТЬ ТОЛЬКО ПОЛОЖИТЕЛЬНЫМИ.

Ну и нельзя оставить без внимания задания на нахождение точек максимума и минимума и на нахождение наибольшего и наименьшего значения функции. Тут советов будет несколько:

1) Повторите таблицу производных функций и вспомните формулы для производной частного и произведения.

2) Если Вам нужно найти наибольшее или наименьшее значение функции, содержащей логарифм, например $y=ln{left(x+5right)^5}-5x$ , то в большинстве случаев это значение достигается при таком х, когда логарифм обращается в нуль, а число под логарифмом рано единице. В данном случае точка экстремума равна -4. Именно в этой точке достигается наименьшее значение функции.

3) Если Вы имеете дело с иррациональной функцией, например $y=sqrt{x^2-6x+11}$ , то точка экстремума может быть найдена с помощью формулы для расчета вершины параболы. Одним словом, координата вершины параболы это и есть точка экстремума.

4) Теперь поговорим о показательных и логарифмических функциях. Если график возрастающий, то есть основание больше единицы, например $y=2^{x^2+2x+5}$ , то экстремум (в данном случае минимум) достигается в вершине квадратичной функции . Ну а подставив точку минимума в саму функцию, Вы имеете все шансы быстро и легко найти наименьшее значение.

С логарифмической функцией дела обстоят аналогичным образом. Давайте рассмотрим функцию вида $y=log_5{left(4-2x-x^2right)}+3$ . Основание больше единицы и равно 5. Значит функция возрастающая. Смотрим внимательно на аргумент под логарифмом. Он представляет собой квадратичную функцию, графиком является парабола с ветвями вниз. Найдя вершину параболы по формуле x_верш=-b/(2a), вы найдете точку экстремума, в данном случае максимума, ну а подставив ее в саму функцию, вы найдите ее наибольшее значение. И для полноты картины, предлагаю рассмотреть убывающую логарифмическую функцию $y=log_frac{1}{3}{left(x^2+6x+12right)}$ с основанием меньше единицы и равным 1/3. Подлогарифмическое выражение также представляет собой параболу с ветвями вверх. Найдя вершину параболы, вы найдите точку минимума, а подставив ее в саму функцию, вы получите наибольшее значение функции.

PS: Наверное, многие задумались, почему, подставляя точки минимума, мы получаем наибольшее значение. Ответ прост – если Ваша функция убывающая, то чем больше аргумент, тем меньше значение самой функции.

9) В своей статье я совсем не затронула задачи на вероятность. Думаю, со вторым номером из кимов справляются практически все. А вот 10 номер такой непредсказуемый, столько интересных и новых задач. И каждая задача не похожа на предыдущую… Здесь сложно дать какой-либо совет. Проработайте задачи из открытого банка ФИПИ, с сайта Решу ЕГЭ, посмотрите свежие сборники 2022 года, варианты Статграда.

Я постаралась очень кратко пробежаться по основным ошибкам выпускников. Если Вам эта статья будет хоть на 0,01 процента будет полезна, то значит, писалась она не зря.

PS: Хотелось бы выразить благодарность Филину Арсению Андреевичу за ценные замечания и помощь в публикации. Он опытный преподаватель, выпускник Физфака МГУ, в прошлом призер олимпиад Физтех и Ломоносов.
Ну а если Вы хотите повторить все темы перед экзаменом, обобщить знания, проработать свои ошибки и узнать еще больше подводных камней, смело могу порекомендовать финальный курс по математике, который будет проводить сам Арсений. Старт 17 мая.

Источник

10 основных ошибок, допускаемых в ЕГЭ по математике

Совет учиться на ошибках других бесполезен; научиться чему-либо можно только на собственных ошибках.

Б. Шоу

Обзор основных ошибок

Обзор составлен на основе материалов ФИПИ за 2016, 2017 гг.

https://drive.google.com/file/d/0B8MkXVdvfYcrZUdvcmk0TEpia1k/view

http://www.fipi.ru/sites/default/files/document/1476454097/matematika.pdf

Профильный уровень

Задание	Процент выполнения	Типичные ошибки
1	90%	Неумение читать условие и непонимание процентов
2	95%	Невнимательное чтение условия и непонимание единиц измерения
3	88%	Невнимательное чтение условия
4	89%	Невнимательное чтение условия
5	91%	Ошибки в свойствах степеней
6	65%	Непонимание математической записи угла и неверное чтение чертежа
7	54%	Невнимательное чтение условия
8	57%	Отсутствие базовых пространственных представлений и знаний соотношений
9	47%	Ошибки в определении знака тригонометрической функции
10	65%	Невнимательное чтение условия или непонимание текста
11	36%	Невнимательное чтение условия
12	38%	Непонимание алгоритма исследования функции с помощью производной
13	36%	Неумение и небрежность отбора корней тригонометрического уравнения с помощью единичной окружности
14	6%	Неумение доказывать, непонимание взаимосвязи элементов геометрической конструкции, ошибки в теоретических фактах
15	15%	Невнимательное чтение математической записи неравенства, непонимание алгоритма решения совокупностей и систем логарифмических неравенств, забыт знаменатель при решении дробно-рационального неравенства, небрежность при изображении множества решений на координатной прямой
16	3%	Неверное понимание логики построения доказательства, ошибки в построении чертежа
17	11%	Неверное составление модели задачи (непонимание взаимосвязи величин) и вычислительные ошибки
18	3,5%	Недостаточная сформированность графического метода решения – отсутствие объяснений и обоснований, отсутствие ответа на поставленный вопрос
19	3,5%	Непонимание того, что на вопрос «Может ли…?» нужно давать аргументированное решение, а не ответ «да» или «нет»

Базовый уровень

Основные факторы, вызывающие ошибки:

недостаточный уровень понимания условия при чтении задания,
вычислительные ошибки,
недостаточная развитость наглядных геометрических представлений.

Анализ 10 типичных ошибок на примерах заданий ЕГЭ

Задачи на проценты – непонимание механизма начисления процентов.

В большинстве случаев причина ошибок – непонимание сущности процента. Например, если в условии сказано, что цена товара сначала была повышена на 25%, а затем понижена на 25%, то эти проценты не будут одной и той же суммой денег, т.к. база начисления этих процентов разная.

Пример:

При решении этого задания 6% участников экзамена посчитали, что если цена была повышена на 25%, то для нахождения старой цены нужно новую цену понизить на 25%. В действительности же новая цена составляет 125% от старой цены, а узнать нужно, сколько рублей соответствуют 100%.

В более сложной экономической задаче требуется понимание механизма начисления простых и сложных процентов, обоснованное применение формул, выбор правильного способа решения. Типичные ошибки здесь связаны с неверным составлением модели задачи, непониманием взаимосвязи величин, непониманием того, что важен не только ответ, но и способ решения задачи.

Невнимательное чтение условия.

К сожалению, это самая распространенная ошибка согласно анализу типичных ошибок ЕГЭ, проведенному ФИПИ.

Конечно, многое здесь можно списать на волнение и психологическое напряжение. Даже самые подготовленные ученики на экзамене могут растеряться, переволноваться или поспешить в решении более простых заданий. Однако факт остается фактом, и при подготовке к экзаменам на него нужно обратить внимание.

Примеры:

Почти 24% участников экзамена указали количество точек, в которых значение функции (а не ее производной) положительно, а еще около 2% участников пытались перечислить номера точек, в которых производная принимает положительное значение.

Около 2,5% участников экзамена нашли вероятность выбора подтекающего насоса, не обратив внимания на частицу «не» в условии.

Практико-ориентированные задания базового и повышенного уровня – непонимание текста задачи.

Кроме ошибок, связанных с невнимательным чтением условия, на первое место здесь выходит непонимание текста задачи, незнание единиц измерения величин, неумение работать с формулами. Многие выпускники даже не приступают к технически не сложным практико-ориентированным задачам повышенного уровня.

Пример:

Выполнение задания – около 57%. Отмечается, что 8% участников не дали никакого ответа; 6% решили, что чем ближе, тем лучше; 4% решили, что лампочку нужно поместить в середину разрешенного интервала, а еще 4,5% решили, что самый главный параметр – это фокус.

Вычислительные ошибки.

Привычка вычислять все с помощью калькулятора, вплоть до таблицы умножения и действий с круглыми числами доставляет учащимся немало проблем на экзамене. Отсутствие навыков быстрого счета в уме или на бумаге часто приводит к тому, что участники экзамена допускают грубые ошибки в элементарных примерах. «Слабые» места многих старшеклассников – это дроби, отрицательные числа, элементарные преобразования выражений, т.е. проблемы, накопившиеся с 5 класса.

Ошибки в теоретических фактах.

Незнание необходимых для решения задач теоретических фактов, как по алгебре, так и по геометрии, существенно снижает процент выполнения большинства заданий как базового, так и повышенного уровня сложности.

Примеры:

Около 8% выпускников не дали никакого ответа; 38% ошиблись в формуле боковой поверхности конуса, а еще 12% в формуле его объема. Отмечается, что процент выполнения этого задания существенно ниже, чем, например, формально гораздо более сложного задания с полным решением на решение уравнения и осуществление отбора корней. Это означает, что низкий процент выполнения заданий по стереометрии вызван именно существенными проблемами в ее преподавании.

В задании 5 проверялось умение решать показательные и логарифмические уравнения. Из семи процентов выпускников, не справившихся с заданием, 2% ошиблись в свойствах степеней.

Незнание алгоритмов и методов решения.

Знание алгоритмов и методов решения проверялось во многих заданиях экзаменационной работы. Например, в задании 12 требовалось продемонстрировать понимание алгоритма исследования функции с помощью производной, а в заданиях 5,13,15 знание общих и частных методов решения уравнений и неравенств.

Пример:

Ненулевые баллы получило около 15% участников экзамена. Типичные ошибки связаны с невнимательным чтением математической записи неравенства, непониманием алгоритма решения совокупностей и систем логарифмических неравенств. Очень много ошибок при решении дробно-рационального неравенства (забыт знаменатель).

Неверное чтение чертежей, непонимание взаимосвязи элементов геометрической конструкции, отсутствие базовых пространственных представлений, ошибки в построении чертежа.

В преподавании геометрии очень важным является не только умение решать вычислительные задачи с геометрическим содержанием (по формулам), но и формировать геометрические представления о фигурах (телах). При отсутствии базовых пространственных представлений сложно ожидать высокого процента выполнения стереометрического задания с полным решением.

Пример:

Отмечается, что около 10% участников экзамена при решении этой задачи неверно определили углы по их записи (перепутали буквы или не понимают, какая из букв в записи угла соответствует его вершине). Около 5% участников «увидели» прямоугольный треугольник ACD, а еще 3% — равносторонний треугольник ABD.

Процент выполнения экзаменующимися геометрических заданий традиционно ниже, чем процент выполнения заданий алгебраических. В целом при решении геометрических задач более половины выпускников продемонстрировали отсутствие знания взаимосвязей элементов геометрической конструкции и соотношений между величинами пространственных фигур.

Неумение доказывать, обосновывать.

К заданиям повышенного уровня относились задания второй части 14 (стереометрия) и 16 (планиметрия) с развернутым ответом. Оба задания содержали два пункта. В первом пункте задание доказать, а во втором пункте вычислить. Основной проблемой оказалось выполнение первого пункта. Участники экзамена продемонстрировали неумение доказывать. При этом много встречается различного рода логических ошибок. Наибольшие затруднения участники испытывали при оформлении доказательства.

Пример:

Типичные ошибки связаны с непониманием логики построения доказательства. Например, доказательство начинается так: «Пусть точка О является серединой отрезка СК…». Т.е. в начале доказательства уже допускается факт, который и требуется доказать.

Задания 18 и 19 высокого уровня сложности предназначены для конкурсного отбора в ВУЗы с повышенными требованиями к математической подготовке абитуриентов. Это задания на комбинацию различных методов. Для успешного их выполнения, кроме прочих математических знаний, необходим высокий уровень математической культуры, который предполагает, в частности, умение обосновывать выбранные методы и способы решения.

Примеры:

Ненулевые баллы при решении этого задания получило около 17% участников экзамена. Многие выпускники попробовали исследовать несколько примеров, а потом обобщить полученный результат. Типичным заблуждением для многих оказалось, что на вопрос «Может ли?» нужно давать аргументированное решение, а не качественный ответ «да» или «нет».

Ненулевые баллы при решении этого задания получило около 3% участников экзамена. Основной проблемой оказалось применение графического метода, который, как показали работы участников экзамена, не достаточно сформирован. Без объяснений и обоснований на координатной плоскости отмечаются графики, и считывается множество значений параметра. Во многих случаях на координатной плоскости обозначено много верных объектов, а ответа на поставленный вопрос так и не последовало.

Задания по тригонометрии требуют тщательности решения.

Представленные в экзаменационной работе задания по тригонометрии не относятся к числу самых сложных, однако их выполнение требует тщательности решения, аккуратности, внимания, знания большого количества теоретических фактов и умения их применять на практике.

Примеры:

Выполнение задания – около 34%. Типичные ошибки связаны в первую очередь с определением знака тригонометрической функции – почти 12% участников экзамена потеряли знак «минус». Еще 22% решили, что ответ ожидается «хорошим» — 1 или 2.

Задание 13 проверяло умение решать тригонометрические уравнения и производить отбор корней. Основной проблемой первого пункта оказалось неумение вводить новую переменную (ошибки в свойствах степеней), незнание формул решения простейшего тригонометрического уравнения. При выполнении второго пункта участники продемонстрировали неумение или небрежность отбора корней.

Отсутствие навыков математического моделирования.

Способность к построению и исследованию простейших математических моделей проверяется в заданиях 11 (текстовая задача) и 17 (текстовая задача с экономическим содержанием). Текстовые задачи, как правило, являются стандартными задачами на составление уравнений курса алгебры 8 класса. В экономической задаче требуется верно построить математическую модель и исследовать ее. Важную роль при этом играет сюжетная, практико-ориентированная часть условия. При составлении математических моделей основные ошибки являются следствием непонимания взаимосвязи величин. Так, например, в задачах на движение около 10% участников экзамена продемонстрировали непонимание движения по реке – собственную скорость умножили на время движения.

Задачи с ошибками как форма работы на уроке.

Одной из форм работы на уроках является поиск и исправление ошибок. «Задачи с ошибками» являются заданиями творческого типа, они приучают обращать внимание на особо тонкие места в логических рассуждениях, помогают различать во многом сходные понятия, приучают к точности суждений и математической строгости и т. д.

Мой опыт преподавания показывает, что такие задания нравятся учащимся и являются достаточно эффективным способом совершенствования навыков решения задач.

Методика работы с задачами с ошибками может быть следующей:

1 этап: Индивидуальная, парная или групповая работа, в зависимости от уровня подготовленности учащихся, по поиску и исправлению ошибок. Задачи с ошибками могут быть представлены в раздаточном материале (карточки) или на слайдах презентации.

2 этап: Совместное обсуждение ошибок.

3 этап: Снова индивидуальная или парная работа – составление памятки «Советы ученику, решающему задачу».

4 этап: Проверка результатов и подведение итогов учителем.

Примеры заданий с ошибками по многим темам можно составить самим или найти в литературных и интернет-источниках.

Мои рекомендации:

Черкасов О.Ю., Якушев А.Г. Математика для поступающих в ВУЗы.

У меня старое издание 1996 года, но есть и более поздние издания этой книги.

Раздел 7 этого пособия так и называется: «Учимся на чужих ошибках».

http://math4school.ru/rabota_nad_oshibkami.html

Раздел сайта «Мath4school» называется «Работа над ошибками», содержит большое количество примеров с решениями и подробным анализом ошибок.

Источник

В этой статье собрали распространённые ошибки, которые допускают выпускники при сдаче ЕГЭ по профильной математике.

Причины ошибок в ЕГЭ по профильной математике

Мы попросили наставников онлайн-школы Вебиума проанализировать работы школьников по профильной математике, чтобы выделить самые частые причины, из-за которых теряются баллы на ЕГЭ.

Среди таких ошибок:

отсутствие ограничений;
неправильное составление формул приведения;
непонимание тригонометрии;
оформление;
невнимательность.

Шпаргалка: Полезные материалы для подготовки к ЕГЭ по профильной математике

Отсутствие ограничений

Эту ошибку ребята допускают как и в первой, так и во второй части. Ограничения необходимо прописывать в ходе решения задачи, иначе большая вероятность, что вы забудете это сделать.

Как избежать ошибку: выучить, что корни, логарифмы, тангенсы, котангенсы вызывают ОДЗ (область допустимых значений).

Лайфхаки для первой части ЕГЭ по математике

Неправильное составление формул приведения

Самая распространённая ошибки в формуле — sin(3pi/2 + A) = -cosA. Знак у косинуса смотрится по синусу, а не наоборот.

Как избежать ошибку: выучить формулы приведения. Как их запомнить, рассказываем в видео.

Непонимание тригонометрии

В школах курсу тригонометрии уделяют мало времени, поэтому ребята не умеют работать с окружностью и не понимают её в целом. Все знаки преобразования обычно выбирают на окружности без определения четвертей и чётности — а это неправильно.

Лучшие ресурсы и пособия для подготовки к ЕГЭ по профильной математике

Как избежать ошибку: научиться самостоятельно чертить тригонометрическую окружность, запомни все оси (тангенс, котангенс) и углы, чтобы не путаться со знаками и аргументами.

Шпаргалка: Основные формулы тригонометрии

Оформление

Чаще всего на ЕГЭ по профильной математике снижают баллы за оформление задания.

Роман Махмутов, наставник по профильной математике в команде Вебиума, рассказал, как избежать эту ошибку: «Если говорить про недочёты в оформлении, то для большинства важно дойти до правильного ответа, поэтому не все реагируют на мои комментарии по этому поводу. Чтобы это исправить, могу дать несколько советов:

Чаще обсуждайте решения заданий с наставником;
Не только смотреть на правильность/неправильность ответа, но и на советы по оформлению, так как это тоже играет очень важную роль.

Я часто сталкивался со студентами, у которых такая логика мышления: «Самое главное — получить правильный ответ, а красиво оформлять на экзамене буду». Если вы не хотите потерять баллы на экзамене, научитесь учитывать все критерии оценивания работы как можно раньше».

Техники запоминания чисел

Невнимательность

Наставники команды Вебиума отмечают, что школьники часто невнимательно читают условие задачи. Из-за этого ход решения сразу становится неверным: приходится переделывать задание полностью.

Чтобы сдать ЕГЭ по профильной математике на высокий балл, нужно ознакомиться с темами, которые попадутся на экзамене. А также познакомиться со всеми изменениями в демоверсии — демонстрационном варианте ЕГЭ, по которому составляются реальные варианты экзамена.

Частые ошибки в ЕГЭ по профильной математике

Научиться решать все виды уравнений — рациональные, показательные, логарифмические, тригонометрические, смешанные — можно на курсе «Задание 12 — уравнения». Также курс можно взять с проверкой задач от наставника.

Не ошибаться — это навык, который можно проработать путём многочисленной практики. Рассмотренные нами ошибки в большей степени зависят от внимательности и ответственного подхода к заданию. Рекомендуем несколько раз проверять домашнюю работу перед сдачей и выписывать, в каких заданиях были допущены ошибки, чтобы их проанализировать.

Теорию, которая нужна для ЕГЭ по профильной математике, объясняем на наших курсах. А практику можно отработать на бесплатных пробниках.

А если вы готовитесь к ЕГЭ по базовой математике, то набрать нужные баллы и сэкономить время для подготовки к другим предметам наш спецкурс.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!

Источник

Скачать материал

Сейчас обучается 265 человек из 63 регионов

Описание презентации по отдельным слайдам:

1 слайд

Типичные ошибки в ЕГЭ по математике
Советы по подготовке
2 слайд

1 часть:
8 заданий с кратким ответом базового уровня
2 часть:
4 задания с кратким ответом повышенного уровня сложности
7 заданий с развернутым ответом повышенного и высокого уровня сложности
Полученные баллы суммируются
Структура работы
3 слайд

Выполняем внимательно
Не пишем в бланке ответов после числа единицы измерений
Не пишем карандашом (после сканирования записи исчезнут)
Исключаем возможность арифметической ошибки (делаем обязательную проверку)
Для экономии времени пропускаем задание, которое не удается решить сразу, а переходим к следующему
К выполнению пропущенных заданий можно вернуться, если останется время
Основное количество баллов можно и нужно получить за 12 первых заданий
4 слайд

Минимум записей, но достаточный для того, чтобы контролировать решение, выполняя обратное действие, найти ошибку.
Устный счет создает лишь видимость экономии времени, при этом возникает риск допустить неустранимую ошибку. Даже если возникает подозрение в неправильности полученного ответа, как обнаружить ошибку в незаписанных выкладках? Все вычисления следует проводить на бумаге аккуратно и неторопливо, четко оформляя решение и ответ задачи.
Если вы будете решать устно, то каждый раз будете безуспешно ловить ускользающие от вас мысли «за хвост».
Вред от пристрастия к устному счету
5 слайд

Знание приемов решения разных задач
Знание алгоритмов решения различных уравнений:
Линейные уравнения
Квадратные уравнения
Рациональные уравнения
Дробно-рациональные уравнения
Показательные уравнения
Логарифмические уравнения
Иррациональные уравнения
Тригонометрические уравнения

Знание общих методов решения уравнений
Замена уравнения h(f(x))=h(g(x)) уравнением f(x)=g(x)
Метод разложения на множители
Метод введения новой переменной
Функционально- графический метод
Знание общих методов решения неравенств
Знание специальных методов решения уравнений и неравенств.
6 слайд

О потере корней
-деление обеих частей уравнения на одно и то же выражение
-сужение ОДЗ в процессе решения уравнения
Замена уравнения h(f(x))=h(g(x)) уравнением f(x)=g(x) в случае . если у=h(x) –немонотонная функция

Рекомендуется следить за равносильностью уравнений и неравенств, полученных в результате преобразований
Правильное определение области допустимых значений – необходимое условие получения верного решения
ОДЗ, как правило, громоздка, ее вовсе не обязательно решать, лучше проверить решение подстановкой в ОДЗ
7 слайд

Уметь задать себе вопрос «Что не нравится?»,
– думать на шаг вперед
Помечтать:
А что бы было, если…
На что похоже?
Примеры:
Вычислить 108 cos 2 23π /12 — 27
Знать формулы
8 слайд

8−7𝑥 =𝑥
Если уравнение имеет несколько корней, в ответ запишите меньший
Ответ: 1
log 2 (−х) = log 2 ( х 2 −12)
Если уравнение имеет несколько корней, в ответ запишите больший
Ответ: -4
log х (4х) = 3
Если корней несколько, то в ответ запишите их произведение
Ответ: -4

Задачи-ловушки
9 слайд

Правило за 100% брать ту величину, с которой мы сравниваем
Пример. Шесть одинаковых рубашек дешевле куртки на 2%. На сколько процентов девять таких рубашек дороже куртки?
Стоимость куртки возьмем за 100%
1) 100 – 2 = 98 (%) — 3 рубашки
2) 98 : 6 х 9 = 147 (%) — 9 рубашек
3) 147 – 100 = 47 (%)
Ответ: 47
Много ошибок при решении задач на проценты
10 слайд

Быстрее по формуле:
А = А 0 1+ р 100 увеличение на р%
А = А 0 ( 1− р 100 ) уменьшение на р%
Пример решения задачи:
Телевизор стоил 11400 руб. На распродаже скидка на телевизор составила р% (р — целое число). Оказалось, что для покупки телевизора достаточно было 10000 руб. Найти наименьшее значение р.
А= А 0 1− р 100 ; А= 11400 1− р 100 ; А≤10000;
11400 1− р 100 ≤ 10000 ; р = 13
Формулы для решения задач на проценты
11 слайд

Решаем 1 часть максимально быстро.
На чем можно сэкономить?
При решении задачи на движение
720 х − 720 х+10 =1
Х=10z
720 10𝑧 − 720 10𝑧+10 =1
72 𝑧 − 72 𝑧+1 =1
Ответ подбираем z=8
При решении задачи на смеси 0,3х+0.6у+5=0,41(х+у+10);
0,3х+0,6у=0,36(х+у+10)

30х+60у+500=41(х+у+10);
30х+60у=36(х+у+10)
12 слайд

Задание №13
ОТНОСИТЕЛЬНО НЕТРУДНОЕ УРАВНЕНИЕ
Может содержать тригонометрические функции, логарифмы, степени, корни, показательную функцию
Как правило, требует замены переменной, позволяющей свести уравнение к квадратному, и отбора корней на заданном отрезке, обусловленного ограниченностью новой переменной, наличием выражений с переменной в знаменателях дробей, а также под знаками корней четной степени и логарифмов
13 слайд

Типичные ошибки в задании №13
Использование формулы корней для простейшего тригонометрического уравнения относительно синуса – к уравнению относительно косинуса и, наоборот, неверная периодичность корней, описки и другие ошибки в записи корня
14 слайд

Типичные ошибки в задании № 13
По-прежнему, как и в прошлых годах, учащиеся теряют баллы в пункте б) решения задачи 13 по причине отсутствия обоснования отбора корней из промежутка
1 балл за решение пункта б) выставляется при условии присутствия «следов» отбора корней
Много ошибок связано с незнанием множества значений тригонометрических функций синус и косинус. В работах учащихся довольно часто в формуле корней тригонометрического уравнения встречались несуществующие значения обратных тригонометрических функций:
15 слайд

Различные способы отбора корней
1. Арифметический способ:
а) непосредственная подстановка полученных корней в уравнение и имеющиеся ограничения;
б) перебор значений целочисленного параметра и вычисление корней.
2. Алгебраический способ:
а) решение неравенства относительно неизвестного целочисленного параметра и вычисление корней;
б) исследование уравнения с двумя целочисленными параметрами.
3. Геометрический способ:
а) изображение корней на тригонометрической окружности с последующим отбором и учетом имеющихся ограничений;
б) изображение корней на числовой прямой с последующим отбором и учетом имеющихся ограничений.
4. Функционально-графический способ:
выбор корней с помощью графика простейшей тригонометрической функции.
16 слайд

Задания №14 и №16
Проверяют умения выполнять действия с геометрическими фигурами
В первом пункте – доказать
Во втором пункте – вычислить
Затруднения в оформлении доказательства
Неверное применение теоретического материала
Большое количество вычислительных ошибок
17 слайд

Задание №15
Неравенство, содержащее степени, дроби, корни, логарифмы (в том числе, с переменным основанием).
Традиционно выполняемые задания
Основные проблемы:
Неумение решать логарифмические неравенства
Арифметические ошибки
Незнание свойств логарифмов
Неумение использовать замену переменных
18 слайд

Задание №17
Задача с экономическим содержанием
Проблемы
Неумение работать с процентами
Неумение правильно считывать условие
Неумение составлять математическую модель по условию задачи
Вычислительные ошибки
19 слайд

Задание №18
Задача с параметром
Нужно постараться решить эту задачу или хотя бы продвинуться в ее решении как можно дальше
Для успешного решения важно умение анализировать условие и находить возможные пути решения
Владеть функционально-графическими способами решения
Наибольшие проблемы:
Понимание логики задачи и анализ условия
Неумение искать ключевые факты и делать необходимые обоснования
20 слайд

Задание №19
Задание олимпиадного типа
Для ее решения не требуется никаких специальных знаний, выходящих за рамки стандарта математического образования. Однако нужно проявить определенный уровень математической культуры, логического мышления.
Наибольшие проблемы:
Непонимание логики задачи
Неверный анализ условия
Неумение делать необходимые обоснования и выводы
21 слайд

ЕГЭ 2017 (досрочный)
19. На доске написано несколько различных чисел, произведение любых двух из которых
больше 40 и меньше 100.
А) Может ли на доске быть 5 чисел?
Б) Может ли на доске быть 6 чисел?
В)Какое наибольшее значение может принимать сумма чисел на доске, если их четыре?

А) Да
Например, 6;7;8;9; 10
Б) нет
В) 35
22 слайд

О проверке работ и об апелляции
Каждая работа проверяется
2 независимыми экспертами
При расхождении оценки двух экспертов по конкретному заданию на 1 балл выпускнику этот балл засчитывается
Если расхождение в оценке более 1 балла, то работу проверяет третий эксперт
При подаче апелляции вся ваша работа будет перепроверяться (а не только тот номер, с оценкой которого вы не согласны)
23 слайд

Успешнее сдают ЕГЭ
— кто оказывается более внимательным и собранным;
— меньше делает ошибок в первой части;
— внимательно читает задания;
— не теряется увидев незнакомый или не типичный текст, а пытается соотнести его со своими знаниями;

— использует рациональные приемы решений, счёта.
Умеет четко планировать своё время, расставлять приоритеты;

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 154 818 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

12.11.2020
369
1

13.09.2020
382
3

11.09.2020
450
1

10.09.2020
223
0

27.07.2020
222
6

15.06.2020
162
0

08.06.2020
414
0

01.06.2020
138
1

Вам будут интересны эти курсы:

Курс повышения квалификации «Подростковый возраст — важнейшая фаза становления личности»
Курс повышения квалификации «Правовое обеспечение деятельности коммерческой организации и индивидуальных предпринимателей»
Курс повышения квалификации «Основы туризма и гостеприимства»
Курс повышения квалификации «Методика написания учебной и научно-исследовательской работы в школе (доклад, реферат, эссе, статья) в процессе реализации метапредметных задач ФГОС ОО»
Курс повышения квалификации «Управление финансами: как уйти от банкротства»
Курс повышения квалификации «Источники финансов»
Курс профессиональной переподготовки «Риск-менеджмент организации: организация эффективной работы системы управления рисками»
Курс профессиональной переподготовки «Политология: взаимодействие с органами государственной власти и управления, негосударственными и международными организациями»
Курс профессиональной переподготовки «Уголовно-правовые дисциплины: теория и методика преподавания в образовательной организации»
Курс профессиональной переподготовки «Методика организации, руководства и координации музейной деятельности»
Курс профессиональной переподготовки «Техническая диагностика и контроль технического состояния автотранспортных средств»
Курс профессиональной переподготовки «Управление качеством»

Источник