Подготовка к ЕГЭ с преподавателем
Теорема Пифагора
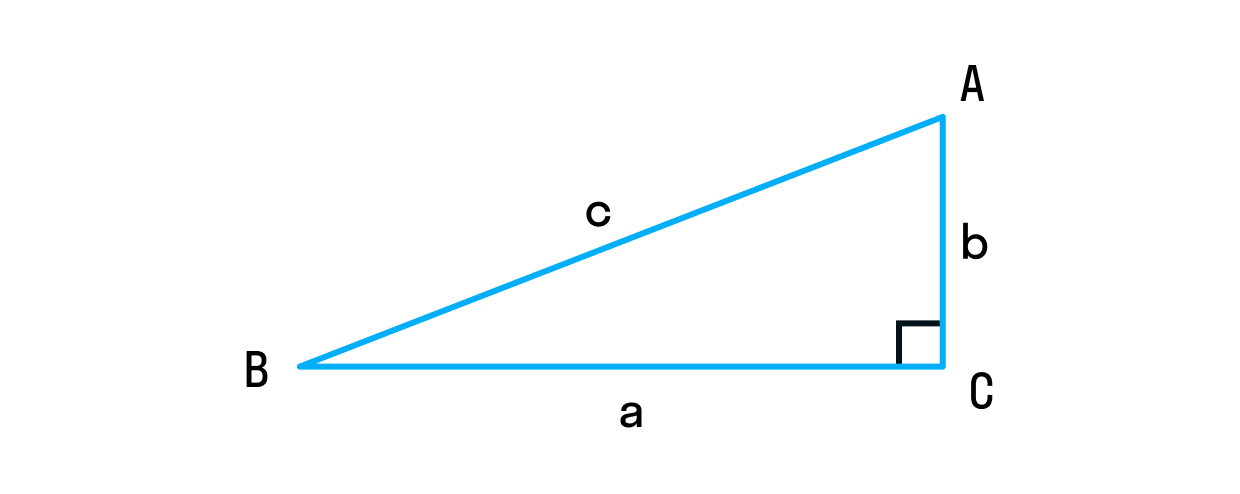
Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии. Она устанавливает соотношение между сторонами прямоугольного треугольника. И звучит так:
В прямоугольном треугольнике сумма квадратов длин катетов равна квадрату длины гипотенузы.
c2 = a2 + b2.
Теорема Пифагора — это частный случай теоремы косинусов. Это объясняется тем, что косинус 90 градусов равен нулю.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Демоурок по подготовке к экзаменам
Составим ваш личный путь к высоким баллам — учтем сроки, уровень знаний и цель.
Теорема Фалеса
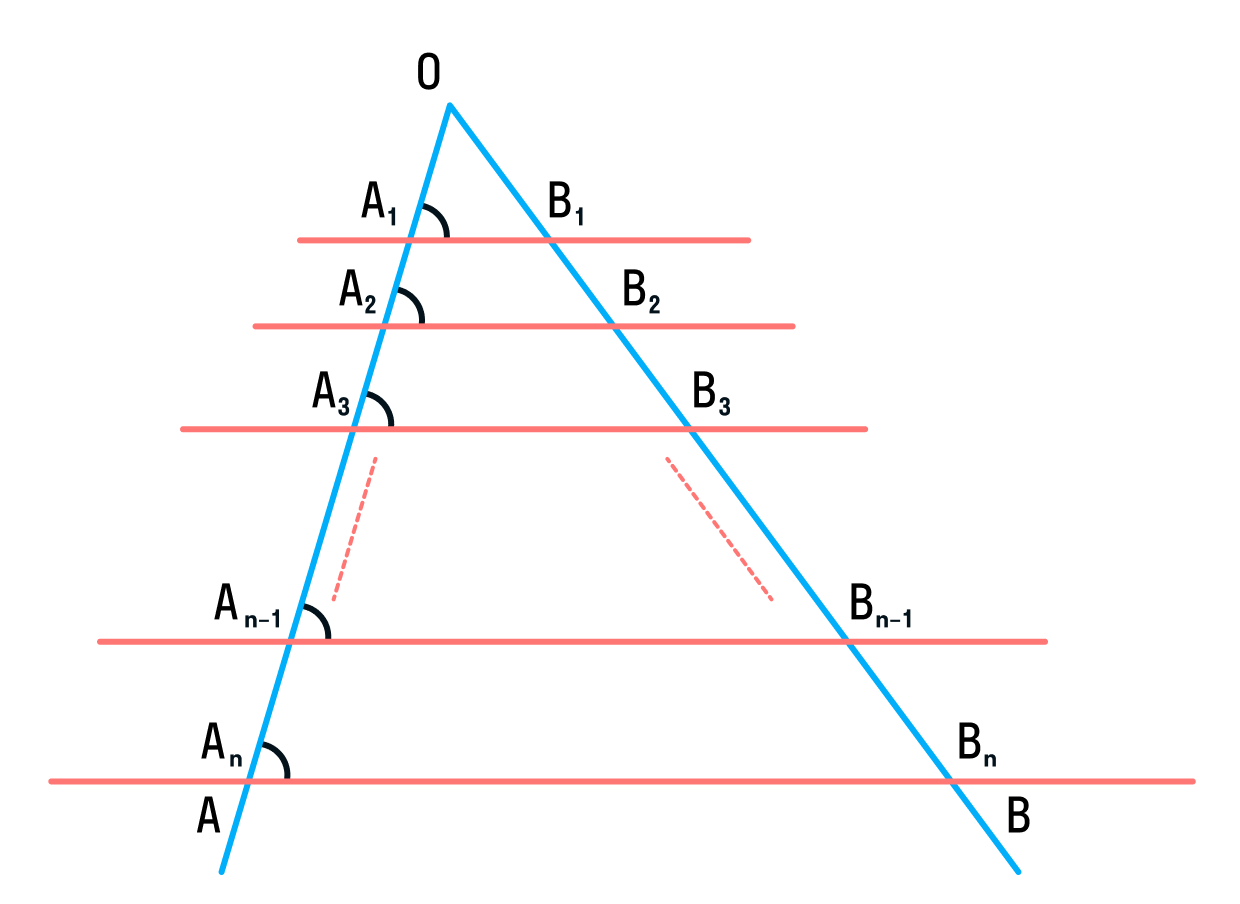
Теорема Фалеса — это свойство параллельных прямых, которые пересекают две секущие с общей точкой.
Вообще, есть две теоремы Фалеса — общая, на все случаи жизни, и частная — то, что нужно для решения задач на ЕГЭ по математике.
Через произвольные точки A1, A2, … An–1, An, лежащие на стороне AO угла AOB, проведены параллельные прямые, пересекающие сторону угла OB в точках B1, B2, … Bn–1, Bn, соответственно. Тогда справедливы равенства:
В ЕГЭ по математике теорема Фалеса встречается чаще всего в параллелограмме, у которого проведена диагональ, — будьте начеку.
Теорема косинусов
Теорема Пифагора — кайф, легко запомнить, часто встречается, применяем только тогда, когда у нас есть прямоугольный треугольник. Но на самом деле теорема Пифагора работает для любого треугольника, только называется она в этом случае теоремой косинусов.
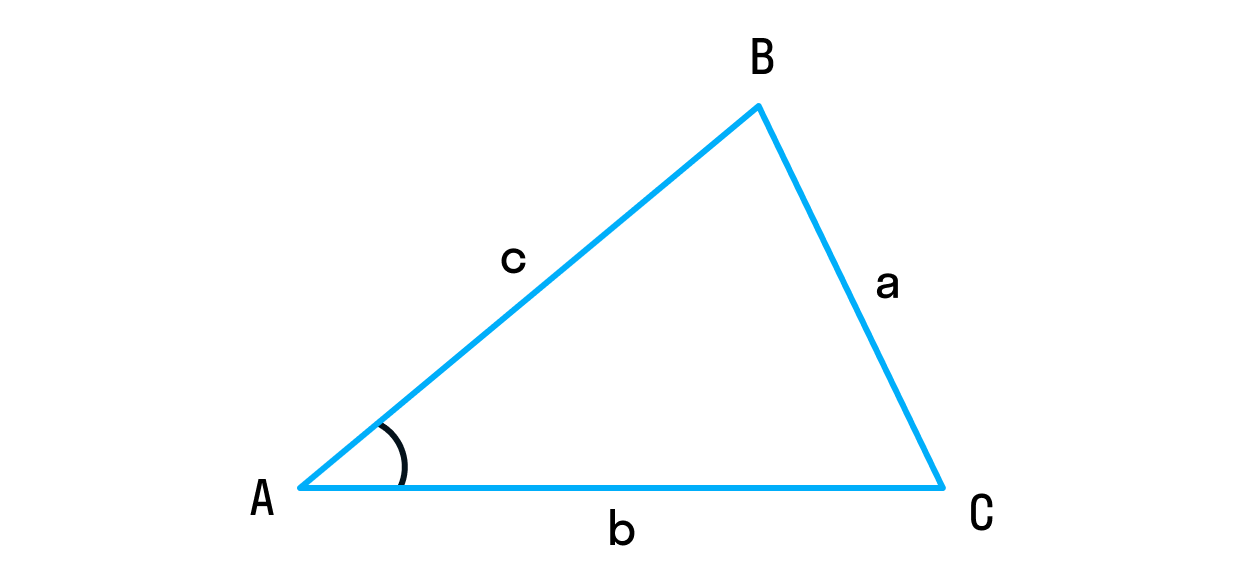
Квадрат длины стороны треугольника равен сумме квадратов длин других сторон минус удвоенное произведение длин этих сторон на косинус угла между ними.
a2 = b2 + c2 – 2bc cos A
Собственно, по формуле сразу становится понятно, почему это соотношение называется теоремой косинусов. Ещё она крайне похожа на разность квадратов с учётом косинуса, поэтому запомнить её не очень сложно. И если вспомнить, что косинус 90 градусов — это 0, то мы увидим знакомую теорему Пифагора.
Теорема синусов
Казалось бы, синус — это что-то про тригонометрию, но на самом деле совсем не только. Планиметрия может с этим смело поспорить, и теорема синусов — явный аргумент в этом воображаемом споре. Если коротко, теорема синусов — это формула связи угла с противолежащей ему стороной в треугольнике.
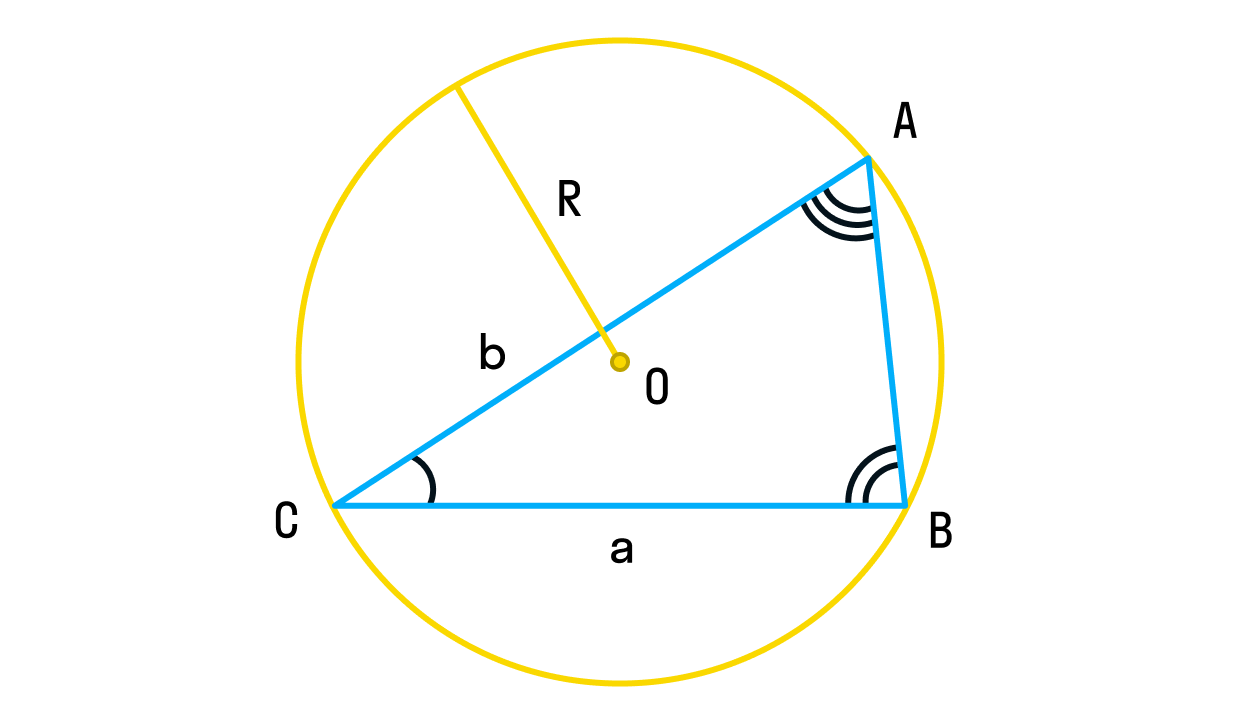
Для любого треугольника справедливы равенства:
,
где R — радиус описанной около треугольника окружности.
По теореме синусов, во-первых, можно быстро найти радиус описанной окружности по известной стороне и противолежащему ей углу. Во-вторых, если треугольник не прямоугольный, то в нём можно просто найти синус угла по известным стороне и радиусу описанной окружности. Ну и в конце концов, можно использовать отношение двух любых сторон и углов. Формула синусов в ЕГЭ по математике используется нечасто, но иметь её в своем арсенале полезно и обязательно.
Теорема Менелая
Её также называют теоремой о треугольнике и секущей, и звучит она так:
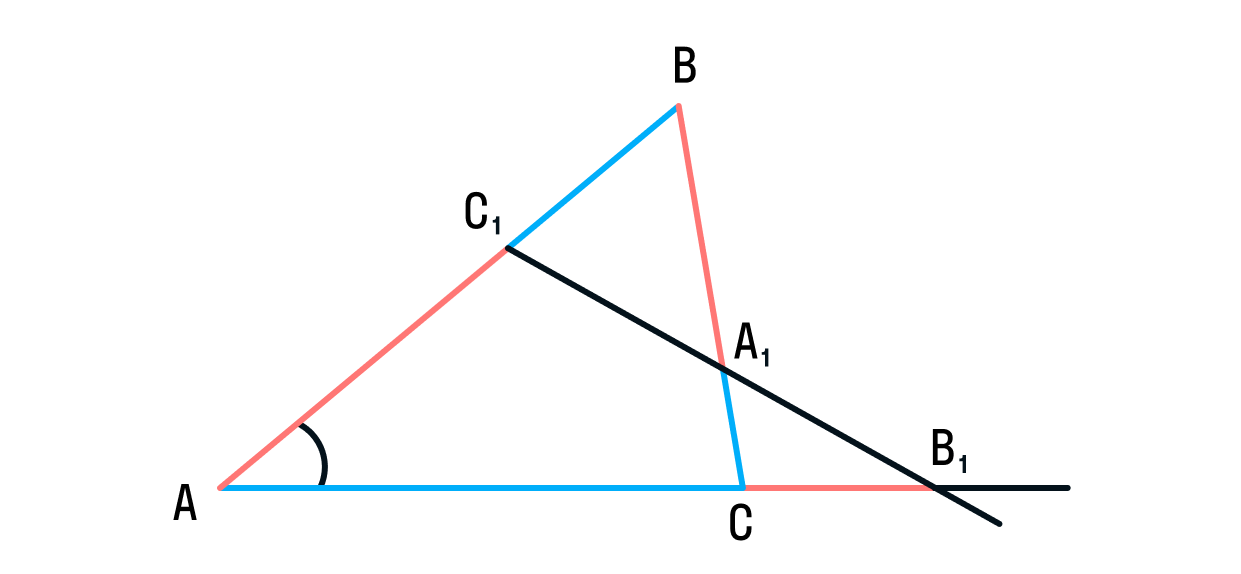
Если на сторонах AB и BC треугольника ABC взяты соответственно точки C1 и A1, а точка B1 взята на продолжении стороны AC за точку C, то точки C1, A1 и B1 лежат на одной прямой тогда и только тогда, когда выполнено равенство:
Теорема Менелая пригодится для решения 2-й части ЕГЭ по математике. Она поможет уменьшить огромную кучу исписанных листочков при решении и сохранить время на экзамене, ведь помогает решать в несколько действий.
Чтобы с лёгкостью запомнить все основные теоремы из геометрии для ЕГЭ по математике, скачайте и распечатайте удобную шпаргалку. Кроме теорем из этой статьи, там есть ещё две редкие — теоремы Чевы и Вариньона, а также задачи на доказательства.
Математика — обязательный для сдачи на ЕГЭ предмет, без которого не получишь аттестат. Это также один из самых сложных экзаменов для выпускников. Делимся типичными ошибками в ЕГЭ по математике, а также ресурсами, которые помогут отработать теорию на практике.
Справочник
«ОСНОВНЫЕ ТЕОРЕМЫ
ГЕОМЕТРИИ»
Содержание:
1.
Теоремы базового уровня……………………………………….3 – 11 стр.
1.1.
Теорема Фалеса Милетского……………………………..……3 стр. 1.2. Теорема
Пифагора………………………………………………3 стр. 1.3.
Теорема синусов………………………………………………..4 стр. 1.4. Теорема косинусов……………………………………………..4 стр.
1.5.
Теорема биссектрис…………………………………………….5 стр.
1.6.
Теорема о пересечении медиан треугольника……………..…5 стр. 1.7. Теорема о высотах
треугольника………………………………5 стр. 1.8.
Площади треугольников……………………………….………6 стр.
1.9.
Вписанный и центральный углы……………………………….7 стр.
1.10.
Вписанная окружность треугольника………………………..8 стр.
1.11.
Описанная окружность треугольника……………………..…8 стр.
1.12.
Вневписанная окружность треугольника……………………..8 стр. 1.13. Площади
четырехугольников……….……………………..….9 стр.
1.14.
Вписанный четырехугольник………………..………………10 стр.
1.15.
Описанный четырехугольник…………..……………………10 стр.
1.16.
Теорема о двух секущих……..………………………………11 стр. 1.17. Теорема о касательной и
секущей……………………………11 стр.
1.18. Теорема
о двух хордах………………………………………..11 стр.
2.
Теоремы профильного уровня…………………………………12 – 13 стр.
2.1.
Теорема Менелая………………………………………………12 стр. 2.2. Теорема
Чевы…………………………………………………..12 стр.
2.3.
Теорема Ван – Обеля………………………………………….12 стр.
2.4.
Теорема Стюарта………………………………………………13 стр.
2.5.
Теорема Птолемея…………………………………………….13 стр.
2.6.
Теорема Аполлония……………………………………………13 стр.
Теорема Фалеса
Милетского «Несколько параллельных прямых a║b║c║d и т.д., отсекающие на
одной из сторон угла равные отрезки, и на другой стороне угла также отсекающие
на одной из сторон угла равные отрезки, и на другой стороне угла также отсекают
равные отрезки»

Теорема Пифагора
1. Квадрат
гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
2. Если
квадрат стороны треугольника равен сумме квадратов двух других его сторон, то
треугольник – прямоугольный.

Теорема синусов
Пусть a, b, c – стороны треугольника; α, β, γ –
противолежащие им углы; R – радиус описанной окружности. Тогда:
Теорема косинусов
Пусть a, b, c – стороны треугольника; α – угол,
противолежащий стороне a. Тогда:
α
Теорема биссектрис
Биссектриса треугольника делит противоположную сторону на два
отрезка, длины которых относятся так же, как длины соответствующих сторон.
Теорема о пересечении медиан треугольника
В треугольнике три медианы пересекаются в одной точке. Точка
пересечения делит каждую медиану в отношении 2:1, если считать от вершины, из
которой проведена медиана.

Теорема о высотах треугольника
В треугольнике высоты пересекаются в одной точке.
Площади треугольников
;
;
;
(формула
Герона)
где:
•
a,b,c – стороны треугольника
•
ha – высота треугольника
•
p – полупериметр треугольника
•
r – радиус вписанной окружности
•
R – радиус описанной окружности
•
β – угол между сторонами
Вписанный и центральный углы
Угол называется вписанным в окружность, если его вершина
лежит на окружности, а стороны пересекают эту окружность.
На рисунке вписанным углом является ABC.
Центральным называется угол вершиной в центре окружности. На
рисунке центральным углом является угол AOC.
Вписанная окружность треугольника

вписать единственную окружность. Центр окружности, вписанной в треугольник, совпадает
с точной пересечения его биссектрис.
Описанная окружность треугольника
Около любого треугольника можно описать
единственную окружность. Центр окружности, описанной около треугольника,
совпадает с точкой пресечения серединных перпендикуляров к его сторонам

Вневписанная окружность треугольника
В любом треугольнике биссектрисы двух
внешних углов и биссектриса внутреннего угла, не смежного с ними, пересекаются
в одной точке.
Площади четырехуголников
— площадь любого четырехугольника, где
•
d1 – первая диагональ
•
d2 – вторая диагональ
•
α – угол между диагоналями
— площадь четырехугольника,
вписанного в окружность (формула Герона), где
•
p – полупериметр четырехугольника
•
a, b, c и d – стороны четырехугольника
S = aha – площадь паралелограмма, где
•
a – основание паралелограмма
•
ha – высота, проведенная к основанию
S = ab sinβ – площадь параллелограмма, где
•
a и b – стороны паралелограмма
•
β – угол между смежными сторонами
S = ab – площадь прямоугольника, где
a и b – стороны квадрата
S = – площадь квадрата, где
a – сторона квадрата
S = aha – площадь ромба, где
•
a – сторона ромба
•
ha – высота, проведенная к стороне
S = – площадь ромба, где
•
a – сторона ромба
•
β – угол между сторонами ромба
Вписанный четырехугольник
Четырехугольник можно вписать в окружность тогда и только
тогда, когда суммы его противоположных углов равны 180.

Описанный четырехугольник
Четырехугольник можно описать вокруг окружности тогда и
только тогда, когда суммы длин его противоположных сторон равны.

DC
+ AB = DA + BC
Теорема о двух секущих
Если из точки, лежащей вне окружности, проведены две секущие,
то произведение одной секущей на ее внешнюю часть равно произведению другой
секущей на ее внешнюю часть:

MAMB = MC
MD
Теорема о касательной и секущей
Если из точки, лежащей вне окружности
проведены касательная и секущая, то квадрат длины касательной равен
произведению секущей на ее внешнюю часть

= MA MB
M
B
Теорема о двух
хордах Если две хорды окружности AB и CD пересекаются в точке S, то
произведение отрезков одной хорды равно произведению отрезков другой хорды. AS SD = CS
SB
D

SD = CS
SB
A
Теорема Менелая

Теорема Чевы
Отрезок, соединяющий вершину треугольника с точкой на
противоположной стороне или ее продолжении, называется чевианой.

Теорема Ван-Обеля

Теорема Стюарта

py
a
Теорема
Птолемея
Если
четырехугольник вписан в окружность, то
 AB
AB + AD
+ AD = AC
= AC
Теорема Аполлония
A
Если AD – медиана треугольника ABC, то
Желаем вам успехов!
Эта удобная шпаргалка поможет с лёгкостью запомнить все основные теоремы из геометрии для ЕГЭ по математике. В ней вы найдёте все нужные формулы и теоремы, а именно:
- Теорема Фалеса;
- Теорема Птолемея;
- Теорема Чевы через треугольник;
- Теорема Менелая через треугольник;
- Теорема Чевы для линий треугольника;
- Теорема Менелая для линий через треугольник;
- Теорема Вариньона;
- Задачи на доказательства.
Также в конце шпаргалки — видео от Эйджея с объяснениями этих теорем.






Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
Планиметрия
Подобие треугольников
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.
Число $k$ — коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)
- Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
- Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Признаки подобия треугольников:
- Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Площади фигур
Площадь треугольника
- $S={a·h_a}/{2}$, где $h_a$ — высота, проведенная к стороне $а$
- $S={a·b·sinα}/{2}$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
- Формула Герона $S=√{p(p-a)(p-b)(p-c)}$, где $р$ — это полупериметр $p={a+b+c}/{2}$
- $S=p·r$, где $r$ — радиус вписанной окружности
- $S={a·b·c}/{4R}$, где $R$ — радиус описанной окружности
- Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ — катеты прямоугольного треугольника.
- Для равностороннего треугольника $S={a^2 √3}/{4}$, где $а$ — длина стороны.
Площади четырехугольников
Прямоугольник
$S=a·b$, где $а$ и $b$ — смежные стороны.
Ромб
$S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ — диагонали ромба
$S=a^2·sinα$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.
Трапеция
$S={(a+b)·h}/{2}$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.
Квадрат
$S=a^2$, где $а$ — сторона квадрата.
Параллелограмм
$S=a·b·sinα$, где $а$ и $b$ — длины сторон параллелограмма, а $α$ — угол между этими сторонами.
Пропорциональные отрезки в прямоугольном треугольнике
В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:
Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.
$CD^2=DB·AD$
В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.
$CB^2=AB·DB$
$AC^2=AB·AD$
Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.
$AC·CB=AB·CD$
Метрические соотношения в окружности
1. Две касательные, проведенные к окружности из одной точки, равны, и центр окружности лежит на биссектрисе угла между ними.
2. Если хорды $АС$ и $BD$ пересекаются в некоторой точке $N$, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
$AN·NC=BN·ND$
Пример:
Хорды $АВ$ и $CD$ пересекаются в точке $Е$. Найдите $ЕD$, если $АЕ=16, ВЕ=9, СЕ=ED$.
Решение:
Если хорды $АВ$ и $СD$ пересекаются в некоторой точке $Е$, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
$AЕ·ЕВ=СЕ·ЕD$
Так как $СЕ=ED$, данное выражение можно записать в виде:
$ЕD^2=AЕ·ЕВ$
Подставим числовые значения
$ЕD^2=16·9$
$ЕD=√{16·9}=4·3=12$
Ответ: $12$
3. Если из одной точки к одной окружности проведены две секущие, то произведение первой секущей на ее внешнюю часть равно произведению второй секущей на свою внешнюю часть.
$АС·ВС=EC·DC$
4. Если из одной точки к окружности проведены секущая и касательная, то произведение секущей на ее внешнюю часть равно квадрату длины касательной.
$BD·СB=AB^2$
Вписанные и описанные окружности для четырехугольников.
1. Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
$АВ+CD=BC+AD$
2. Если сумма противоположных углов четырехугольника равна $180°$, то только тогда около него можно описать окружность.
$∠В+∠D=180°$
$∠A+∠C=180°$
Вневписанные окружности
Вневписанной окружностью треугольника называется окружность, касающаяся одной из его сторон и продолжений двух других.
Для каждого треугольника существует три вневписанных окружности, которые расположены вне треугольника, центрами вневписанных окружностей являются точки пересечения биссектрис внешних углов треугольника.
Точки $О_1, О_2$ и $О_3$ – центры вневписанных окружностей.
Связь площади треугольника с радиусами вневписанных окружностей.
Введем обозначения:
$S$ — площадь треугольника;
$p$ — полупериметр треугольника;
$a, b, c$ — стороны треугольника;
$r_a, r_b, r_c$ — радиусы вневписанных окружностей касающиеся соответственно сторон $a, b$ и $c$;
Для данных обозначений справедливы равенства:
$r_a={S}/{p-a};$
$r_b={S}/{p-b};$
$r_c={S}/{p-c}.$
Пример:
В прямоугольном треугольнике $АВС$ угол $С=90°, АС=6, ВС=8$. Найдите радиус вневписанной окружности, касающейся гипотенузы.
Решение:
Радиус вневписанной окружности, касающейся стороны $АВ$ равен:
$r_{АВ}={S}/{p-АВ}$, где $S$ — площадь треугольника, $р$ — полупериметр треугольника.
Чтобы подставить в формулу данные, найдем сначала площадь треугольника и его полупериметр.
Площадь прямоугольного треугольника равна половине произведения катетов:
$S={АС·АВ}/{2}={6·8}/{2}=24$
Нам неизвестна гипотенуза, найдем ее по теореме Пифагора:
$АВ=√{АС^2+СВ^2}=√{6^2+8^2}=√{100}=10$
Зная все стороны, вычислим полупериметр:
$р={6+8+10}/{2}=12$
Теперь можем все данные подставить в формулу нахождения радиуса вневписанной окружности:
$r_{АВ}={S}/{p-АВ}={24}/{12-10}={24}/{2}=12$
Ответ: $12$
Биссектриса
Биссектриса – это линия, которая делит угол пополам.
Свойства биссектрисы:
1. В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой.
2. Если точка лежит на биссектрисе, то расстояния от неё до сторон угла равны.
$AD=DC$
3. Три биссектрисы в треугольнике пересекаются в одной точке, эта точка является центром вписанной в треугольник окружности.
4. Биссектриса угла в параллелограмме отсекает равнобедренный треугольник.
5. Биссектрисы смежных углов перпендикулярны.
6. В треугольнике биссектриса угла делит противоположную сторону на отрезки, отношение которых такое же, как отношение сторон треугольника, между которыми эта биссектриса прошла.
${AB}/{AC}={BA_1}/{A_1C}$
7. Для нахождения длины биссектрисы справедлива формула:
$АА_1=√{АВ·АС-ВА_1·А_1 С}$
Медиана
Медиана — это линия, проведенная из вершины треугольника к середине противоположной стороны.
Свойства медиан:
1. Медиана делит треугольник на два равновеликих треугольника, т.е. на два треугольника, у которых площади равны.
$S_1=S_2$
2. Медианы пересекаются в одной точке и этой точкой делятся в отношении два к одному, считая от вершины.
3. В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы и радиусу описанной около этого треугольника окружности.
4. Для нахождения длины медианы, проведенной к стороне «с», справедлива формула:
$М_с={√{2(а^2+b^2)-c^2}}/{2}$
Высота
Высота в треугольнике — это линия, проведенная из вершины треугольника к противоположной стороне под углом в 90 градусов.
$BB_1$ — высота
Свойства высот:
1. Три высоты (или их продолжения) пересекаются в одной точке.
2. При пересечении двух высот получаются подобные треугольники:
$∆АА_1 В~∆СС_1В;$
$∆АС_1 М~∆СМА1$
3. Угол между высотами в остроугольном треугольнике равен углу между сторонами, к которым эти высоты проведены.
4. Высоты треугольника обратно пропорциональны его сторонам:
$h_a:h_b:h_c={1}/{a}:{1}/{b}:{1}/{c}$
Теорема синусов
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
${a}/{sinα}={b}/{sinβ} ={c}/{sinγ} =2R$, где $R$ — радиус описанной около треугольника окружности.
Пример:
В треугольнике $АВС ВС=16, sin∠A={4}/{5}$. Найдите радиус окружности, описанной вокруг треугольника $АВС$.
Решение:
Воспользуемся теоремой синусов:
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной окружности
${ВС}/{sinA} =2R$
Далее подставим числовые данные и найдем $R$
${16·5}/{4}=2R$
$R={16·5}/{4·2}=10$
Ответ: $10$
Теорема косинусов
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
$a^2=b^2+c^2-2·b·c·cosα.$
Формулы для профильного ЕГЭ-2022 по математике
Формулы сокращённого умножения
Арифметическая и геометрическая прогрессии
Вероятность
Свойства степеней
Свойства логарифмов
Тригонометрия
Производные
Первообразные
Геометрия
Формулы сокращённого умножения
| `(a + b)^2=a^2 + 2ab + b^2` | |
| `(a − b)^2=a^2 − 2ab + b^2` | |
| `a^2 − b^2=(a + b)(a − b)` | |
| `a^3 + b^3=(a + b)(a^2 − ab + b^2)` | |
| `a^3 − b^3=(a − b)(a^2 + ab + b^2)` | |
| `(a + b)^3=a^3 + 3a^2b + 3ab^2 + b^3` | |
| `(a − b)^3=a^3 − 3a^2b + 3ab^2 − b^3` |
Прогрессии
Арифметическая прогрессия:
| `a_n=a_(n-1)+d` |
| `a_n=a_1+(n-1)*d` |
| `S_n=((a_1+a_n)*n)/2` |
Геометрическая прогрессия:
| `b_n=b_(n-1)*q` |
| `b_n=b_1*q^(n-1)` |
| `S_n=((q^n-1)*b_1)/(q-1)` |
| Бесконечно убывающая: `S=b_1/(1-q)` |
Вероятность
| Вероятность события A: | `P(A)=m/n` | |
| События происходят A и B происходят одновременно | `A*B` | |
| Независимые события: | `P(A*B)=P(A)*P(B)` | |
| Зависимые события: | `P(A*B)=P(A)*P(B|A)` | |
| Происходит или событие A, или B | `A+B` | |
| Несовместные события: | `P(A+B)=P(A)+P(B)` | |
| Совместные события: | `P(A+B)=P(A)+P(B)-P(A*B)` |
Свойства степеней
| `a^0=1` | `a^1=a` |
| `a^(-1)=1/a` | `a^(-n)=1/a^n` |
| `a^(1/2)=sqrt(a)` | `a^(1/n)=root(n)(a)` |
| `a^m*a^n=a^(m+n)` | `a^m/a^n=a^(m-n)` |
| `(a*b)^n=a^n*b^n` | `(a/b)^n=a^n/b^n` |
| `(a^m)^n=a^(m*n)` | `a^(m/n)=root(n)(a^m)` |
Свойства логарифмов
| `log_ab=c``a^c=b` | |
| `log_a1=0` | |
| `log_aa=1` | |
| `log_a(b*c)=log_ab+log_ac` | |
| `log_a(b/c)=log_ab-log_ac` | |
| `log_ab^n=n*log_ab` | |
| `log_(a^m)b=1/m*log_ab` | |
| `log_ab=1/(log_ba)` | |
| `log_ab=(log_cb)/(log_ca)` | |
| `a^(log_cb)=b^(log_ca)` | |
| `a^(log_ab)=b` |
Тригонометрия
| `alpha` | `0` | `pi/6` | `pi/4` | `pi/3` | `pi/2` | `pi` | `(3pi)/2` | `2pi` |
|---|---|---|---|---|---|---|---|---|
| `0^circ` | `30^circ` | `45^circ` | `60^circ` | `90^circ` | `180^circ` | `270^circ` | `360^circ` | |
| `sinalpha` | `0` | `1/2` | `sqrt(2)/2` | `sqrt(3)/2` | `1` | `0` | `-1` | `0` |
| `cosalpha` | `1` | `sqrt(3)/2` | `sqrt(2)/2` | `1/2` | `0` | `-1` | `0` | `1` |
| `text(tg)alpha` | `0` | `sqrt(3)/3` | `1` | `sqrt(3)` | `infty` | `0` | `infty` | `0` |
| `text(ctg)alpha` | `infty` | `sqrt(3)` | `1` | `sqrt(3)/3` | `0` | `infty` | `0` | `infty` |
Основные соотношения
| `sin^2alpha+cos^2alpha=1` | |
| `text(tg)alpha=sinalpha/cosalpha=1/(text(ctg)alpha)` |
Формулы двойного угла
| `cos2alpha={(cos^2alpha-sin^2alpha),(1-2sin^2alpha),(2cos^2alpha-1):}` | |
| `sin2alpha=2sinalphacosalpha` | |
| `text(tg)2alpha=(2text(tg)alpha)/(1-text(tg)^2alpha)` |
Формулы суммы и разности аргументов
| `sin(alpha+-beta)=sinalphacosbeta+-cosalphasinbeta` |
| `cos(alpha+-beta)=cosalphacosbeta∓sinalphasinbeta` |
| `text(tg)(alpha+-beta)=(text(tg)alpha+-text(tg)beta)/(1∓text(tg)alpha*text(tg)beta)` |
Преобразование суммы и разности в произведение
| `sinalpha+-sinbeta=2sin((alpha+-beta)/2)cos((alpha∓beta)/2)` |
| `cosalpha+cosbeta=2cos((alpha+beta)/2)cos((alpha-beta)/2)` |
| `cosalpha-cosbeta=-2sin((alpha+beta)/2)sin((alpha-beta)/2)` |
Формулы половинного аргумента
| `sin(alpha/2)=+-sqrt((1-cosalpha)/2)` | |
| `cos(alpha/2)=+-sqrt((1+cosalpha)/2)` | |
| `text(tg)(alpha/2)=+-sqrt((1-cosalpha)/(1+cosalpha))=(1-cosalpha)/sinalpha=sinalpha/(1+cosalpha)` |
Обратные тригонометрические функции
| `sinx=A` | `x=(-1)^k*arcsinA + pik` или `{(x=arcsinA + 2pik),(x=pi-arcsinA+2pik):}` |
`kinZZ` |
| `cosx=A` | `x=±arccosA + 2pik` | `kinZZ` |
| `tg x=A` | `x=text(arctg) A + pik` | `kinZZ` |
| `ctg x=A` | `x=text(arcctg) A + pik` | `kinZZ` |
Также некоторые тригонометрические соотношения смотрите в разделе Геометрия.
Производные
Основные правила дифференцирования
| `(u+-v)’=u’+-v’` | |
| `(u*v)’=u’*v+u*v’` | |
| `(u/v)^’=(u’*v-u*v’)/v^2` | |
| `[f(g(x))]’=f'(g(x))*g'(x)` |
Уравнение касательной
| `y=f(x_0)+f'(x_0)*(x-x_0)` |
Производные элементарных функций
| `C’=0` | `(C*x)’=C` | |
| `(x^m)’=mx^(m-1)` | `(sqrtx)’=1/(2sqrtx)` | |
| `(1/x)^’=-1/x^2` | ||
| `(e^x)’=e^x` | `(lnx)’=1/x` | |
| `(a^x)’=a^x*lna` | `(log_ax)’=1/(xlna)` | |
| `(sinx)’=cosx` | `(cosx)’=-sinx` | |
| `(text(tg)x)’=1/cos^2x` | `(text(ctg)x)’=-1/sin^2x` | |
| `(arcsinx)’=1/sqrt(1-x^2)` | `(arccosx)’=-1/sqrt(1-x^2)` | |
| `(text(arctg))=1/(1+x^2)’` | `(text(arcctg))’=-1/(1+x^2)` |
Также некоторые сведения про производные смотрите в описании задач
№14 (база), №7 (профиль), №12 (профиль).
Первообразные
| Первообразная: | `F'(x)=f(x)` | |||
| Неопределённый интеграл: | `intf(x)dx=F(x)+C` | |||
| Определённый интеграл (формула Ньютона-Лейбница): | `int_a^bf(x)dx=F(b)-F(a)` |
Таблица первообразных
| `f(x)` | `F(x)` | `f(x)` | `F(x)` | |
|---|---|---|---|---|
| `a` | `ax` | |||
| `x^n` | `x^(n+1)/(n+1)` | `1/x` | `lnx` | |
| `e^x` | `e^x` | `a^x` | `a^x/lna` | |
| `sinx` | `-cosx` | `cosx` | `sinx` | |
| `1/cos^2x` | `text(tg)x` | `1/sin^2x` | `-text(ctg)x` | |
| `1/(x^2+a^2)` | `1/atext(arctg)x/a` | `1/(x^2-a^2)` | `1/(2a)ln|(x-a)/(x+a)|` | |
| `1/sqrt(a^2-x^2)` | `text(arcsin)x/a` | `1/sqrt(x^2+a)` | `ln|x+sqrt(x^2+a)|` |
Геометрия
Планиметрия (2D)
Площади фигур:
| Окружность: | `S=pir^2` | |
| Треугольник: | `S=1/2ah` | |
| Параллелограмм: | `S=ah` | |
| Четырёхугольник: | `S=1/2d_1d_2sinvarphi` | |
| Трапеция: | `S=(a+b)/2*h` |
Стереометрия (3D)
| Призма: | `V=S_(осн)h` | |
| Пирамида: | `V=1/3S_(осн)h` | |
| Конус: | `V=1/3S_(осн)h` | |
| `S_(бок)=pirl` | ||
| Цилиндр: | `V=pir^2h` | |
| `S_(бок)=2pirh` | ||
| Шар: | `V=4/3pir^3` | |
| `S=4pir^2` |
Этапы закрепощения крестьян в России
Крепостное право на Руси появилось позже, чем во многих средневековых европейских королевствах. Это было связано с объективными причинами – низкая плотность населения, зависимость от ордынского ига.
Задания 12-18 досрочного ЕГЭ по математике
3 примера по каждому заданию. Досрочный ЕГЭ по математике прошёл 28 марта.
ОГЭ по математике. Тренировочный вариант СтатГрад
Видеоуроки ОГЭ | Вчера, 21:46
Решение тестовой части (№1-19) тренировочной работы по математике от 18 апреля 2022 года.
Факт 1.
(bullet) Множество натуральных чисел (mathbb{N}) – это числа (1,
2, 3, 4 ) и т.д.
(bullet) Множество целых чисел (mathbb{Z}) состоит из натуральных чисел, противоположных им ((-1, -2, -3 ) и т.д.) и нуля (0).
(bullet) Рациональные числа (mathbb{Q}) – числа вида (dfrac ab), где (ain mathbb{Z}), (bin mathbb{N}).
Таким образом, существует включение: (mathbb{N}) содержится в (mathbb{Z}), а (mathbb{Z}) содержится в (mathbb{Q}).
Факт 2.
(bullet) Правила сложения дробей: [begin{aligned} &dfrac ab+dfrac cb=dfrac{a+c}b[2ex]
&dfrac ab+dfrac cd=dfrac{ad+bc}{bd}end{aligned}] Пример: (dfrac {31}6+dfrac {67}6=dfrac{31+67}6=dfrac{98}6)
(bullet) Правила умножения дробей: [dfrac abcdot dfrac cd=dfrac{ac}{bd}] Пример: (dfrac 47cdot dfrac{14}5=dfrac{4cdot 14}{7cdot 5})
(bullet) Правила деления дробей: [dfrac ab: dfrac cd=dfrac abcdot dfrac dc] Пример: (dfrac 45 :dfrac 67=dfrac 45cdot dfrac 76)
Факт 2.
(bullet) Сокращение дробей – деление числителя и знаменателя на одно и то же число, отличное от нуля.
Пример:
(begin{aligned} &dfrac{98}6=dfrac{49cdot
2llap{/}}{3cdot
2llap{/}}=dfrac{49}3[2ex]
&dfrac{4cdot 14}{7cdot 5}=dfrac{4cdot 2cdot
7llap{/}}{7llap{/}cdot
5}=dfrac 85[2ex]
&dfrac{4cdot 7}{5cdot 6}=dfrac {2llap{/}cdot 2cdot 7}{5cdot
3cdot
2llap{/}}=dfrac{14}{15}end{aligned})
(bullet) Если (dfrac ab) – несократимая дробь, то ее можно представить в виде конечной десятичной дроби тогда и только тогда, когда знаменатель (b) делится только на числа (2) и (5).
Пример: дробь (dfrac2{65}) нельзя представить в виде конечной десятичной дроби, так как (65=5cdot 13), то есть (dfrac2{65}=0,0307…)
дробь (dfrac3{160}) можно представить в виде конечной десятичной дроби, так как (160=2^5cdot 5), то есть (dfrac3{160}=0,01875).
Факт 3.
(bullet) Формулы сокращенного умножения:
(blacktriangleright) Квадрат суммы и квадрат разности: [(a+b)^2=a^2+2ab+b^2] [(a-b)^2=a^2-2ab+b^2]
(blacktriangleright) Куб суммы и куб разности: [(a+b)^3=a^3+3a^2b+3ab^2+b^3quad {small{text{или}}}quad
(a+b)^3=a^3+b^3+3ab(a+b)] [(a-b)^3=a^3-3a^2b+3ab^2-b^3quad {small{text{или}}}quad
(a-b)^3=a^3-b^3-3ab(a-b)]
Заметим, что применение данных формул справа налево часто помогает упростить вычисления:
(13^3+3cdot 13^2cdot 7+3cdot 13cdot 49+7^3=(13+7)^3=20^3=8000)
(blacktriangleright) Разность квадратов: [a^2-b^2=(a-b)(a+b)]
(blacktriangleright) Сумма кубов и разность кубов: [a^3+b^3=(a+b)(a^2-ab+b^2)] [a^3-b^3=(a-b)(a^2+ab+b^2)]
Заметим, что не существует формулы суммы квадратов (a^2+b^2).
Заметим, что применение данных формул слева направо часто помогает упростить вычисления:
(dfrac{7^6-2^6}{7^4+14^2+16}=
dfrac{(7^2-2^2)(7^4+7^2cdot2^2+2^4)}
{7^4+(7cdot2)^2+2^4}=7^2-2^2=45)
Факт 4.
(bullet) Квадрат суммы нескольких слагаемых равен сумме квадратов этих слагаемых и удвоенных попарных произведений: [begin{aligned}
&(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc[2ex]
&(a+b+c+d)^2=a^2+b^2+c^2+d^2+2ab+2ac+2ad+2bc+2bd+2cd[2ex]
&{small{text{и т.д.}}}end{aligned}]
Геометрия на профильном ЕГЭ по математике — одна из сложных тем для абитуриентов. Дело в том, что когда-то экзамен по геометрии в школе был обязательным, а сейчас — нет. В результате у большинства абитуриентов знания по геометрии близки к нулю.
Геометрия на профильном ЕГЭ — это три в части 1 (сюда входит и планиметрия, и стереометрия), а также задача 14 (стереометрия) и для многих недосягаемая 16 (геометрия) из второй части. Как же научиться их решать?
Начнем с планиметрии. Прежде всего, выучите основные формулы геометрии.
На нашем сайте вы найдете курс геометрии с нуля — основные определения, формулы и теоремы, а также разбор множества экзаменационных задач по геометрии из части 1.
Для решения задач по геометрии из части 2 нужна более серьезная подготовка.
Первый этап — теория. Необходимый материал есть в учебнике по геометрии за 7-9 класс (автор — А. В. Погорелов или Л. С. Атанасян). Выпишите в тетрадь определения и формулировки теорем. Сделайте чертежи. Доказывать теоремы старайтесь самостоятельно.
Программа по геометрии.
1. Треугольники. Элементы треугольника. Вершины и стороны. Высоты, медианы, биссектрисы (определения).
2. Построение треугольника: практические задания.
а) Три стороны треугольника равны
и
сантиметров соответственно. Постройте треугольник
с помощью циркуля и линейки.
б) В треугольнике угол
равен
градусов, сторона
равна двум,
равна
. Постройте треугольник
.
в) В треугольнике сторона
равна
, угол
равен
, угол
равен
. Постройте треугольник
.
3. Три признака равенства треугольников. Неравенство треугольника.
4. Постройте с помощью циркуля и линейки:
а) серединный перпендикуляр к отрезку;
б) биссектрису угла.
5. Углы при параллельных прямых и секущей. Вертикальные, смежные, соответственные, односторонние и накрест лежащие углы. Их определение и свойства.
6. Теорема о сумме углов треугольника.
7. Внешний угол треугольника.
8. Постройте в одном и том же треугольнике
а) три высоты. Рассмотрите также случаи тупоугольного и прямоугольного треугольника.
б) три биссектрисы.
в) три медианы.
9. Равнобедренный треугольник. Определение и свойства. Высота в равнобедренном треугольнике.
10. Средняя линия треугольника и ее свойства.
11. Прямоугольный треугольник. Теорема Пифагора.
12. Определения синуса, косинуса и тангенса
— для острого угла прямоугольного треугольника
— для произвольного угла.
13. Четырехугольники. Сумма углов четырехугольника.
14. Параллелограмм. Определение и свойства. Площадь параллелограмма.
15. Виды параллелограммов и их свойства. (ромб, прямоугольник, квадрат).
16. Трапеция. Средняя линия трапеции. Площадь трапеции.
17. Подобные треугольники. Три признака подобия треугольников.
18. Площадь треугольника. Формулы и
.
19. Теоремы синусов и косинусов.
20. Чему равно отношение площадей подобных фигур.
21. Свойство медианы (в каком отношении делятся медианы в точке пересечения?)
22. Свойство биссектрисы (в каком отношении биссектриса делит противоположную сторону?)
23. Окружность и круг. Длина окружности. Площадь круга. Длина дуги и площадь сектора.
24. Теорема о радиусе, проведенном в точку касания.
25. Центральный и вписанный углы. Связь между ними.
26. Теоремы о вписанных углах.
27. Теорема о пересекающихся хордах.
28. Теорема об отрезках длин касательных, проведенных из одной точки.
29. Теорема о секущей и касательной.
30. Дан треугольник . Постройте
а) окружность, вписанную в данный треугольник
б) окружность, описанную вокруг данного треугольника.
Где находятся центры этих окружностей?
31. Еще три формулы площади треугольника (через радиус вписанной окружности, через радиус описанной окружности и формула Герона).
32. Когда можно вписать окружность в четырехугольник? Когда — описать вокруг четырехугольника?
Программа по стереометрии
Разбирая и решая задания ЕГЭ по геометрии, вы заметите очень интересную вещь. Простые задачи из части 1, разобранные на нашем сайте, часто оказываются базовыми схемами, на которых строятся сложные задачи из части 2 профильного ЕГЭ.
Решая на ЕГЭ задачи по геометрии, обращайте особое внимание на оформление. Помните совет, который дал абитуриентам автор бестселлера «Математика — абитуриенту» В. В. Ткачук. Вот он, этот ценнейший совет:
«Подробность решения должна быть такова, чтобы его мог понять человек в 10 (десять) раз глупее вас».