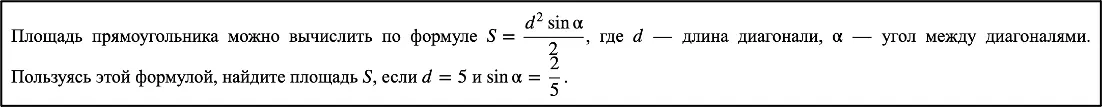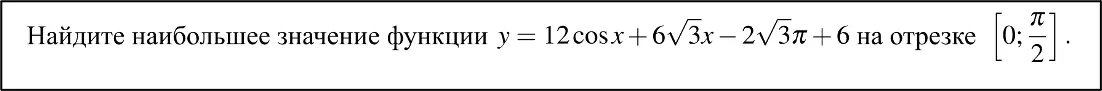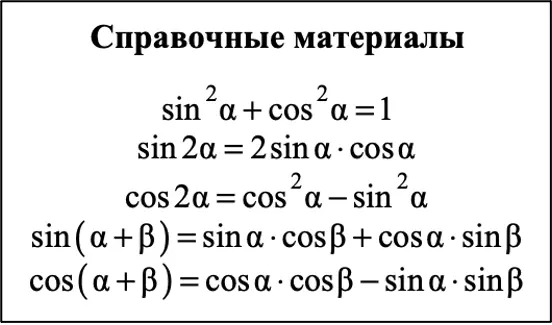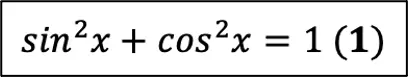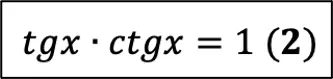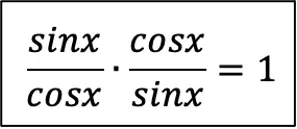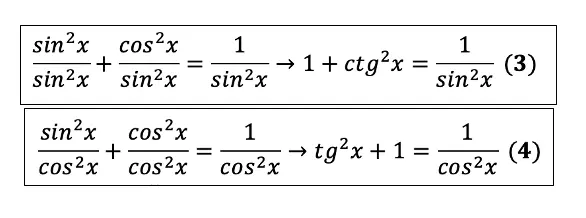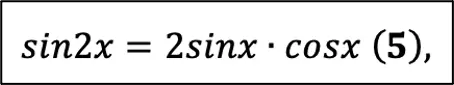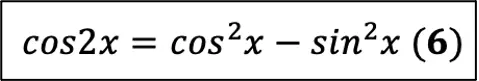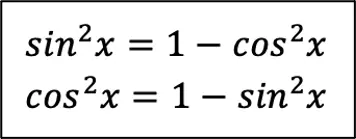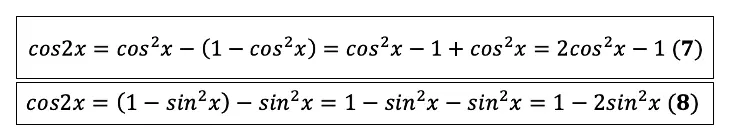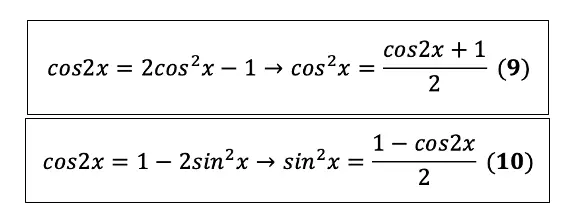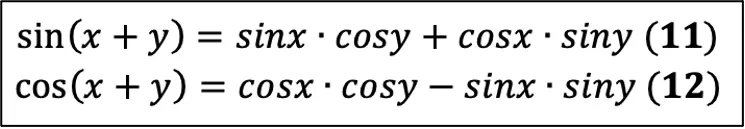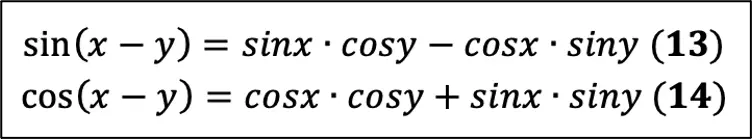Тригонометрическими уравнениями называют уравнения, в которых переменная содержится под знаком тригонометрических функций. К их числу прежде всего относятся простейшие тригонометрические уравнения, т.е. уравнения вида $sin x=a, cos x=a, tg x=a$, где $а$ – действительное число.
Перед решением уравнений разберем некоторые тригонометрические выражения и формулы.
$1$ радиан $={180}/{π}≈57$ градусов
$1$ градус $={π}/{180}$ радиан
Значения тригонометрических функций некоторых углов
| $α$ | $ 0$ | ${π}/{6}$ | ${π}/{4}$ | ${π}/{3}$ | ${π}/{2}$ | $π$ | |
| $sinα$ | $ 0$ | $ {1}/{2}$ | $ {√2}/{2}$ | $ {√3}/{2}$ | $ 1$ | $ 0$ | |
| $cosα$ | $ 1$ | $ {√3}/{2}$ | $ {√2}/{2}$ | $ {1}/{2}$ | $ 0$ | $ -1$ | |
| $tgα$ | $ 0$ | $ {√3}/{3}$ | $ 1$ | $ √3$ | $ -$ | $ 0$ | |
| $ctgα$ | $ -$ | $ √3$ | $ 1$ | $ {√3}/{3}$ | $ 0$ | $ -$ |
Периоды повтора значений тригонометрических функций
Период повторения у синуса и косинуса $2π$, у тангенса и котангенса $π$
Знаки тригонометрических функций по четвертям
Эта информация нам пригодится для использования формул приведения. Формулы приведения необходимы для понижения углов до значения от $0$ до $90$ градусов.
Чтобы правильно раскрыть формулы приведения необходимо помнить, что:
- если в формуле содержатся углы $180°$ и $360°$ ($π$ и $2π$), то наименование функции не изменяется; (если же в формуле содержатся углы $90°$ и $270°$ (${π}/{2}$ и ${3π}/{2}$), то наименование функции меняется на противоположную (синус на косинус, тангенс на котангенс и т. д.);
- чтобы определить знак в правой части формулы ($+$ или $-$), достаточно, считая угол $α$ острым, определить знак преобразуемого выражения.
Преобразовать $сos(90° + α)$. Прежде всего, мы замечаем, что в формуле содержится угол $90$, поэтому $cos$ измениться на $sin$.
$сos(90° + α)=sinα$
Чтобы определить знак перед $sinα$, предположим, что угол $α$ острый, тогда угол $90° + α$ должен оканчиваться во 2-й четверти, а косинус угла, лежащего во 2-й четверти, отрицателен. Поэтому, перед $sinα$ нужен знак $-$.
$сos(90° + α)= — sinα$ — это конечный результат преобразования
Четность тригонометрических функций
Косинус четная функция: $cos(-t)=cos t$
Синус, тангенс и котангенс нечетные функции: $sin(-t)= — sin t; tg(-t)= — tg t; ctg(-t)= — ctg t$
Тригонометрические тождества
- $tgα={sinα}/{cosα}$
- $ctgα={cosα}/{sinα}$
- $sin^2α+cos^2α=1$ (Основное тригонометрическое тождество)
Из основного тригонометрического тождества можно выразить формулы для нахождения синуса и косинуса
$sinα=±√{1-cos^2α}$
$cosα=±√{1-sin^2α}$
- $tgα·ctgα=1$
- $1+tg^2α={1}/{cos^2α}$
- $1+ctg^2α={1}/{sin^2α}$
Вычислить $sin t$, если $cos t = {5}/{13} ; t ∈({3π}/{2};2π)$
Найдем $sin t$ через основное тригонометрическое тождество. И определим знак, так как $t ∈({3π}/{2};2π)$ -это четвертая четверть, то синус в ней имеет знак минус
$sint=-√{1-cos^2t}=-√{1-{25}/{169}}=-√{{144}/{169}}=-{12}/{13}$
Чуть больше 30% выпускников справляется с тригонометрией на ЕГЭ по математике. И неудивительно: для решения заданий из базы и профиля надо знать очень много формул, которые сложно освоить за 1-2 года. На самом деле, это миф! Чтобы решить задания по тригонометрии, нужно знать всего 5 формул — и просто уметь ими пользоваться.
Тригонометрия на ЕГЭ: основные проблемы темы
Чаще всего тригонометрию начинают изучать в 10 классе — но в некоторых школах оставляют до 11. В первом случае у учеников есть 2 года, чтобы освоить новую тему. А во втором, к сожалению, всего год. И это проблема. Дело в том, что в тригонометрии очень много формул, которые нужно знать, чтобы успешно решать задания. Если за 2 года их можно успеть выучить, то за год это будет сделать проблематично.
Ситуация осложняется ещё двумя факторами. Во-первых, в самой математике много формул, признаков, теорем и т.д. Во-вторых, кроме математики есть и другие экзамены, для которых нужно выучить большой объём информации.
Именно поэтому я всегда советую своим ученикам не учить формулы для тригонометрии на ЕГЭ, а выводить! Но об этом мы поговорим чуть позже, а сейчас давайте обсудим, почему тригонометрия так важна и где в ЕГЭ ее можно встретить.
Задания по тригонометрии в базе и профиле на ЕГЭ
Так как ЕГЭ по математике делится на базовый и профильный, а тригонометрия встречается в обоих, то давайте рассмотрим оба уровня экзамена.
Тригонометрия в базе
Что касается Базового уровня, то в нём всего 3 задания, в которых можно столкнуться с тригонометрией:
В № 7 в виде простейшего выражения
Как правило, для успешного решения таких заданий достаточно воспользоваться формулами из справочного материала.
В № 8 в виде формулы прикладной задачи
Стоит отметить, что в базовом ЕГЭ в прикладных задачах тригонометрия попадается редко, но нужно быть готовыми.
В № 15 как тригонометрия в геометрии
В справочном материале есть вся необходимая информация для успешного решения данного задания, а именно определение всех тригофункций в прямоугольном треугольнике.
Тригонометрия в профиле
Базовый уровень мы рассмотрели, теперь перейдём к профильному. Здесь уже больше вариантов, в которых можно встретиться с тригонометрией. Давайте посмотрим на Части 1 и 2.
В № 3 как тригонометрия в геометрии (Часть 1)
То же самое задание, как в базовом ЕГЭ, вот только в справочном материале уже нет необходимой информации.
В № 4 в виде выражения (Часть 1)
То же самое задание, как в базовом ЕГЭ.
В № 7 в виде формулы прикладной задачи (Часть 1)
То же самое задание, как в базовом ЕГЭ. Для успешного решения подойдут базовые навыки работы с тригонометрией.
В № 11 как часть функции (Часть 1)
Функцию нужно проанализировать для поиска наибольшего/наименьшего значения или точек максимума/минимума.
Если с Частью 1 профиля всё более-менее очевидно, то во второй части бывают сюрпризы, о которых ученики даже не подозревают. Да-да, тригонометрия на ЕГЭ умеет прятаться и в Части 2. Давайте посмотрим на эти задания.
В № 12 (Часть 2)
Тут сюрпризов нет. Это уравнение второй части, в котором ученики как раз ожидают увидеть тригонометрию, хотя она там бывает не всегда!
В № 13 — стереометрия (Часть 2)
Да, тригонометрия может встретиться здесь в виде теоремы синусов или теоремы косинусов, а ещё в виде формул в методе координат (для любителей решать этим методом).
В № 16 — планиметрия (Часть 2)
Здесь всё аналогично стереометрии: есть геометрические формулы, в которых прячется тригонометрия. Ведь, как я и сказала выше, в геометрии она тоже бывает!
5 формул тригонометрии: теория для ЕГЭ
А теперь предлагаю перейти к самому интересному — а именно к формулам. К сожалению, их действительно много. А ещё они похожи, и если их просто учить (или бездумно зубрить), то велик риск перепутать «+» с «–» или забыть какую-нибудь единичку.
Именно поэтому я рекомендую не учить формулы, а выводить. Это очень удобно тем более, что в профильном ЕГЭ по математике весь справочный материал состоит из 5-ти формул тригонометрии, из которых очень легко выводятся все остальные.
Но прежде чем я расскажу вам, как выводятся тригонометрические формулы, пообещайте, что обязательно отработаете все правила выведения! Для этого нужно будет регулярно выводить формулы по указанным ниже схемам.
Вот формулы, которые будут у вас в справочном материале:
Формула № 1 и как она пригодится в поиске котангенса и тангенса
Первая формула — основное тригонометрическое тождество (ОТТ):
Обычно ученики знают ее очень хорошо. Она связывает синус и косинус и помогает найти одну функцию через другую.
С этой формулой косвенно связана другая (ее нет в справочном материале), которая тоже легко дается школьникам:
Эту формулу очень легко запомнить, если знать, как можно расписать тангенс и котангенс через синус и косинус:
Эти 2 формулы связывают по отдельности синус с косинусом и тангенс с котангенсом. Но иногда требуется, чтобы были связаны все 4 функции, и здесь на помощь приходят следствия из ОТТ (как раз та самая формула № 1).
Чтобы вывести следствия нужно всего лишь разделить ОТТ на sin2 и cos2:
Теперь можно легко найти:
- котангенс, зная синус,
- или тангенс, зная косинус.
Формула № 2 и что из нее можно вывести
С тождествами разобрались, давайте перейдём к формулам двойного угла. Что касается синуса двойного угла (вторая формула в справочном материале):
Здесь всё просто, берёте и применяете формулу, если видите, что она нужна для задания.
Формула № 3 и что из нее можно вывести
А вот с косинусом двойного угла (третья формула в справочном материале) всё интереснее. Безусловно, косинус двойного угла:
в чистом виде встречается, и тогда вы делаете всё тоже самое, что с синусом. Но на самом деле есть ещё 2 формулы, которые очень просто вывести, используя ОТТ (формулу № 1). Для начала нужно выразить квадрат синуса и квадрат косинуса из ОТТ (Шаг 1):
А потом нужно подставить эти значения в формулу (6, или третья формула справочного материала) (Шаг 2):
Вот мы вывели ещё 2 формулы! А сейчас я покажу вам как практически ничего не делая получить ещё 2. Мы будем выводить формулы понижения степени из формул двойного угла. Смотрите, нужно всего лишь выразить одно из другого:
Формулы № 4 и 5 и что из них можно вывести
Давайте посмотрим на справочный материал, у нас там ещё целых 2 формулы, из которых мы получим конечно же ещё 2! Сейчас вообще ничего удивительного не будет. Вот формулы, которые уже даны:
Как вы заметили, они для суммы углов, а чтобы получить формулы для разности углов, нам нужно всего лишь поменять знаки в формуле на противоположные (разумеется, я говорю про «+» и «–»):
Вот так при помощи нехитрых преобразований из 5-ти формул справочного материала мы получили целых 14!
Все скриншоты взяты из открытого банка заданий ФИПИ или из демоверсий ЕГЭ по математике 2022.
Что еще пригодится вам для тригонометрии на ЕГЭ
Скажу по секрету, что это далеко не все формулы тригонометрии, которые существуют. Есть и другие:
- некоторые можно вывести из вышеуказанных,
- некоторые можно обобщить и вместо огромного количества формул использовать короткое правило.
Но мне кажется, что пока этого и так много!
Советую сначала хорошо отработать формулы, которые я перечислила в этой статье, и только потом браться за другие. Так вы не загрузите свою память и будете быстрее решать сложные задания по тригонометрии из ЕГЭ. Это, кстати, касается любой темы на экзамене по математике: а в ЕГЭ их очень много. Поэтому чтобы получить высокий балл, надо правильно и системно отработать их все.
Именно так я и строю подготовку к ЕГЭ по математике вместе со своими учениками: строгая система подготовки — ключ к успеху на экзамене. Сначала мы разбираем простые темы и задания и учимся решать их самыми удобными способами — почти на автомате. А после я добавляю более хитрые и сложные задания. В итоге ребята и имеют хорошую базу знаний по математике, и умеют решать самые разные типы задач. Так что если вы хотите по-настоящему знать математику, а не зазубривать формулы, приходите на мои уроки!
А чтобы отрабатывать выведение было не так скучно, держите моего котика, который любезно согласился позировать в позе котангенса:
Опубликовано 04.12.2014 — 11:35 — Лобышева Ирина Сергеевна
каждый год выпускаю классы и имею подборку тригонометрических формул используемых в обеих частях ЕГЭ, которыми хочу поделиться с Вами.
Скачать:
| Вложение | Размер |
|---|---|
| 1.28 МБ |
Предварительный просмотр:
По теме: методические разработки, презентации и конспекты
Разработка урока алгебры в 10 классе по теме «Формулы тригонометрии»
Данный урок является обобщающим по теме «Тригонометрические формулы»…
Формулы тригонометрии
Обобщающий урок по теме в 10 классе по учебнику А.Г. Мордкович…
Основные формулы по тригонометрии
Приведены основные формулы по тригонометрии для 10 класса….
Тригонометрия. Сборник формул
Тригонометрия. Сборник формул…
Основные формулы тригонометрии
Основные формулы тригонометрии, которые необходимы при подготовке к ЕГЭ по математике…
Формулы тригонометрии
В презентации содержится материал о различных формулах по тригонометрии. Содержание презентации можно использовать как…
Тригонометрия учебник с формулами
Учебник по тригонометрии включает теоретический материал с формулами…
- Мне нравится
(blacktriangleright) Рассмотрим прямоугольную систему координат и в ней окружность с единичным радиусом и центром в начале координат.
Угол в (1^circ) — это такой центральный угол, который опирается на дугу, длина которой равна (dfrac1{360}) длины всей окружности.
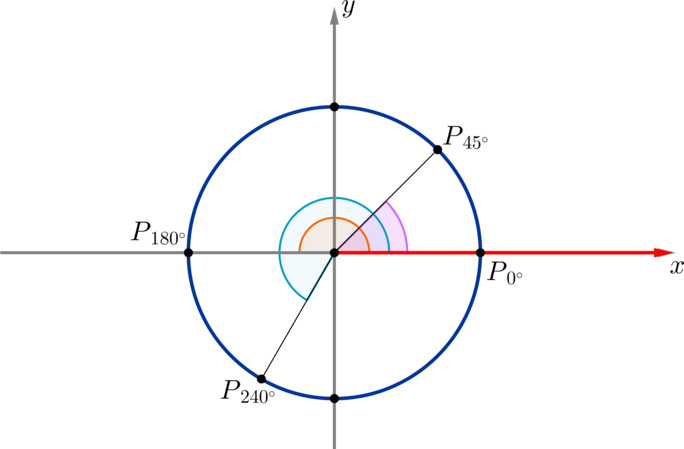
(blacktriangleright) Будем рассматривать на окружности такие углы, у которых вершина находится в центре окружности, а одна сторона всегда совпадает с положительным направлением оси (Ox) (на рисунке выделено красным).
На рисунке таким образом отмечены углы (45^circ, 180^circ,
240^circ):
Заметим, что угол (0^circ) — это угол, обе стороны которого совпадают с положительным направлением оси (Ox).
Точку, в которой вторая сторона такого угла (alpha) пересекает окружность, будет называть (P_{alpha}).
Положение точки (P_{0}) будем называть начальным положением.
Таким образом, можно сказать, что мы совершаем поворот по окружности из начального положения (P_0) до положения (P_{alpha}) на угол (alpha).
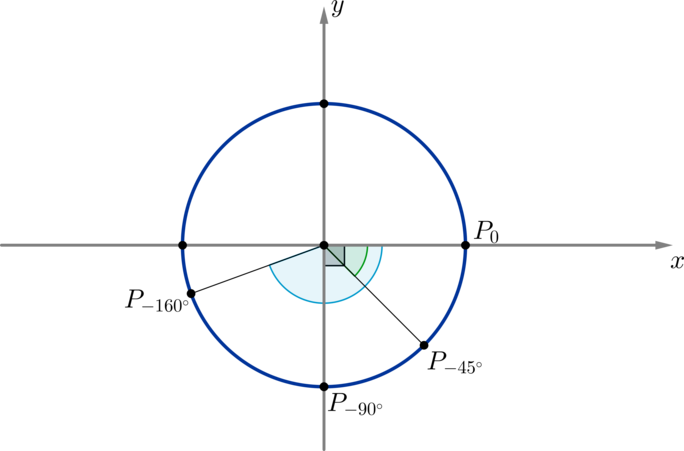
(blacktriangleright) Поворот по окружности против часовой стрелки — это поворот на положительный угол. Поворот по часовой стрелке — это поворот на отрицательный угол.
Например, на рисунке отмечены углы (-45^circ, -90^circ,
-160^circ):
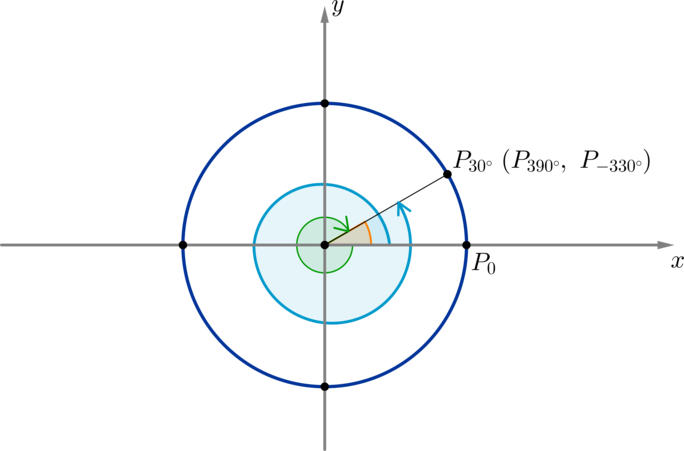
(blacktriangleright) Рассмотрим точку (P_{30^circ}) на окружности. Для того, чтобы совершить поворот по окружности из начального положения до точки (P_{30^circ}), необходимо совершить поворот на угол (30^circ) (оранжевый). Если мы совершим полный оборот (то есть на (360^circ)) и еще поворот на (30^circ), то мы снова попадем в эту точку, хотя уже был совершен поворот на угол (390^circ=360^circ+30^circ) (голубой). Также попасть в эту точку мы можем, совершив поворот на (-330^circ) (зеленый), на (750^circ=360^circ+360^circ+30^circ) и т.д.
Таким образом, каждой точке на окружности соответствует бесконечное множество углов, причем отличаются эти углы друг от друга на целое число полных оборотов ((ncdot360^circ, ninmathbb{Z})).
Например, угол (30^circ) на (360^circ) больше, чем угол (-330^circ), и на (2cdot 360^circ) меньше, чем угол (750^circ).
Все углы, находящиеся в точке (P_{30^circ}) можно записать в виде: (alpha=30^circ+ncdot 360^circ, ninmathbb{Z}).
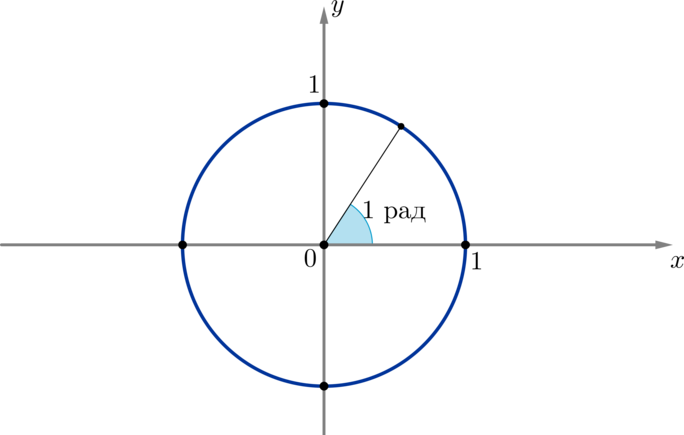
(blacktriangleright) Угол в (1) радиан — это такой центральный угол, который опирается на дугу, длина которой равна радиусу окружности:
Т.к. длина всей окружности радиусом (R) равна (2pi R), а в градусной мере — (360^circ), то имеем (360^circ=2pi cdot
1textbf{ рад}), откуда [180^circ=pi textbf{ рад}] Это основная формула, с помощью которой можно переводить градусы в радианы и наоборот.
Пример 1. Найти радианную меру угла (60^circ).
Т.к. (180^circ = pi Rightarrow 1^circ = dfrac{pi}{180}
Rightarrow 60^circ=dfrac{pi}3)
Пример 2. Найти градусную меру угла (dfrac34 pi).
Т.к. (pi=180^circ Rightarrow dfrac34 pi=dfrac34 cdot
180^circ=135^circ).
Обычно пишут, например, не (dfrac{pi}4 text{ рад}), а просто (dfrac{pi}4) (т.е. единицу измерения “рад” опускают). Обратим внимание, что обозначение градуса при записи угла не опускают. Таким образом, под записью “угол равен (1)” понимают, что “угол равен (1) радиану”, а не “угол равен (1) градусу”.
Т.к. (pi thickapprox 3,14 Rightarrow 180^circ thickapprox 3,14
textbf{ рад} Rightarrow 1 textbf{ рад} thickapprox 57^circ).
Такую приблизительную подстановку делать в задачах нельзя, но знание того, чему приближенно равен (1) радиан в градусах часто помогает при решении некоторых задач. Например, таким образом проще найти на окружности угол в (5) радиан: он примерно равен (285^circ).
(blacktriangleright) Из курса планиметрии (геометрии на плоскости) мы знаем, что для углов (0<alpha< 90^circ) определены синус, косинус, тангенс и котангенс следующим образом:
если дан прямоугольный треугольник со сторонами (a, b, c) и углом (alpha), то:
Т.к. на единичной окружности определены любые углы (alphain(-infty;+infty)), то нужно определить синус, косинус, тангенс и котангенс для любого угла.
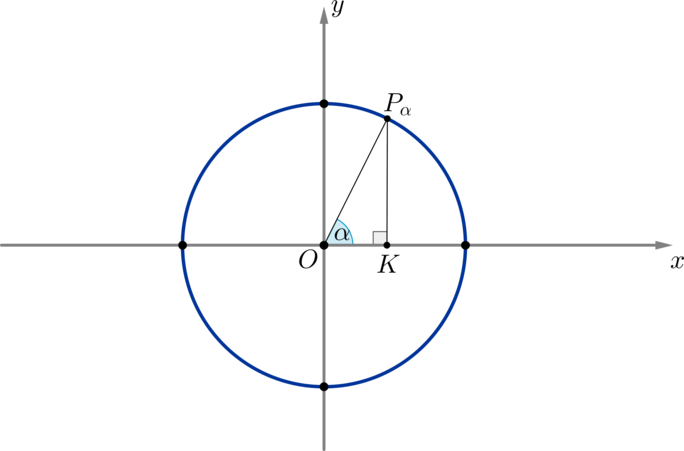
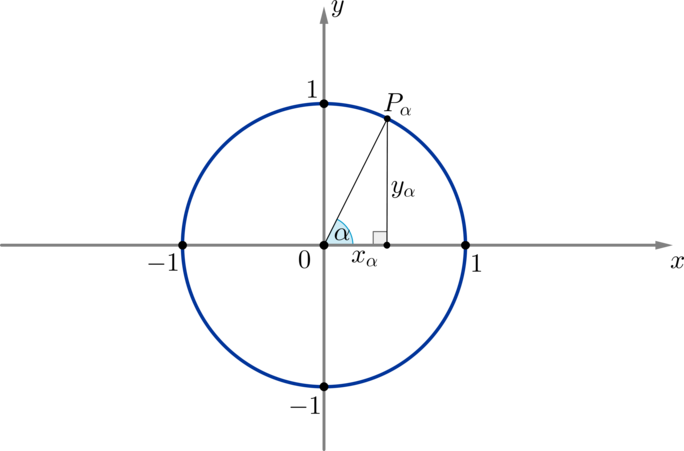
Рассмотрим единичную окружность и на ней угол (alpha) и соответствующую ему точку (P_{alpha}):
Опустим перпендикуляр (P_{alpha}K) из точки (P_{alpha}) на ось (Ox). Мы получим прямоугольный треугольник (triangle OP_{alpha}K), из которого имеем: [sinalpha=dfrac{P_{alpha}K}{P_{alpha}O} qquad cos alpha=dfrac{OK}{P_{alpha}O}] Заметим, что отрезок (OK) есть не что иное, как абсцисса (x_{alpha}) точки (P_{alpha}), а отрезок (P_{alpha}K) — ордината (y_{alpha}). Заметим также, что т.к. мы брали единичную окружность, то (P_{alpha}O=1) — ее радиус.
Таким образом, [sinalpha=y_{alpha}, qquad cos alpha=x_{alpha}]
Таким образом, если точка (P_{alpha}) имела координаты ((x_{alpha},;y_{alpha})), то через соответствующий ей угол ее координаты можно переписать как ((cosalpha,;sinalpha)).
Определение: 1. Синусом угла (alpha) называется ордината точки (P_{alpha}), соответствующей этому углу, на единичной окружности.
2. Косинусом угла (alpha) называется абсцисса точки (P_{alpha}), соответствующей этому углу, на единичной окружности.
Поэтому ось (Oy) называют осью синусов, ось (Ox) — осью косинусов.
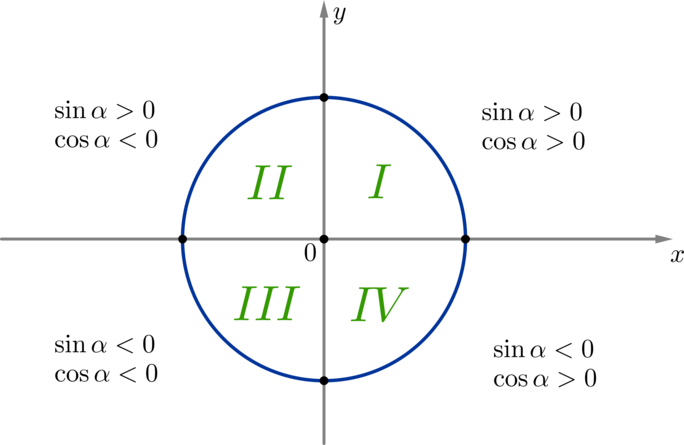
(blacktriangleright) Окружность можно разбить на (4) четверти, как показано на рисунке.
Т.к. в (I) четверти и абсциссы, и ординаты всех точек положительны, то косинусы и синусы всех углов из этой четверти также положительны.
Т.к. во (II) четверти ординаты всех точек положительны, а абсциссы — отрицательны, то косинусы всех углов из этой четверти — отрицательны, синусы — положительны.
Аналогично можно определить знак синуса и косинуса для оставшихся четвертей.
Пример 3. Так как, например, точки (P_{frac{pi}{6}}) и (P_{-frac{11pi}6}) совпадают, то их координаты равны, т.е. (sindfrac{pi}6=sin left(-dfrac{11pi}6right), cos
dfrac{pi}6=cos
left(-dfrac{11pi}6right)).
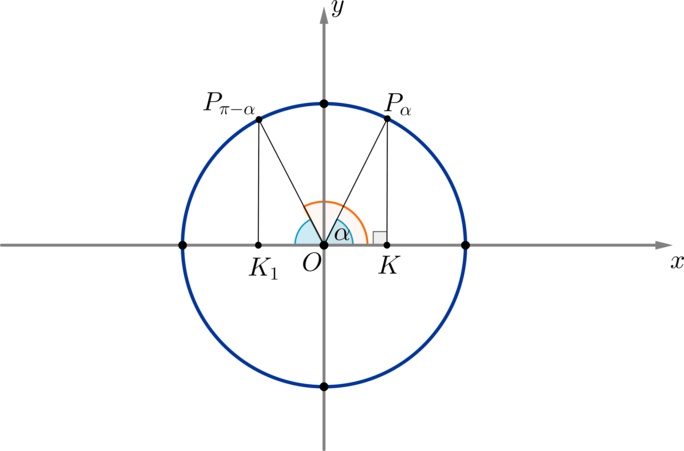
Пример 4. Рассмотрим точки (P_{alpha}) и (P_{pi-alpha}). Пусть для удобства (0<alpha<dfrac{pi}2).
Проведем перпендикуляры на ось (Ox): (OK) и (OK_1). Треугольники (OKP_{alpha}) и (OK_1P_{pi-alpha}) равны по гипотенузе и углу ((angle P_{alpha}OK=angle P_{pi-alpha}OK_1=alpha)).
Следовательно, (OK=OK_1, KP_{alpha}=K_1P_{pi-alpha}).
Т.к. координаты точки (P_{alpha}=(OK;KP_{alpha})=(cosalpha,;sinalpha)), а точки (P_{pi-alpha}=(-OK_1;K_1P_{pi-alpha})=(cos(pi-alpha),;sin(pi-alpha))), следовательно, [cos(pi-alpha)=-cosalpha, qquad sin(pi-alpha)=sinalpha]
Таким образом доказываются и другие формулы, называемые формулами приведения: [{large{begin{array}{l|r}
hline sin(pi-alpha)=sinalpha &
cos(pi-alpha)=-cosalpha\[2ex]
sin(pi+alpha)=-sinalpha &
cos(pi+alpha)=-cosalpha\[2ex]
sin(2pipmalpha)=pmsinalpha & cos
(2pipmalpha)=cosalpha\[2ex]
sin left(dfrac{pi}2pmalpharight)=cosalpha &
cosleft(dfrac{pi}2pmalpharight)=pmsinalpha\[2ex]
hline
end{array}}}]
С помощью этих формул можно найти синус или косинус любого угла, сведя это значение к синусу или косинусу угла из (I) четверти.
Таблица синусов, косинусов, тангенсов и котангенсов углов из первой четверти:
[{large{begin{array}{|c|c|c|c|c|c|}
hline &&&&&\[-17pt]
& quad 0 quad (0^ circ)& quad dfrac{pi}6 quad (30^circ)
& quad dfrac{pi}4
quad (45^circ) & quad dfrac{pi}3 quad (60^circ)& quad dfrac{pi}2 quad
(90^circ) \
&&&&&\[-17pt]
hline sin & 0 ½&frac{sqrt2}2&frac{sqrt3}2&1\[4pt]
hline cos &1&frac{sqrt3}2&frac{sqrt2}2½&0\[4pt]
hline mathrm{tg} &0 &frac{sqrt3}3&1&sqrt3&infty\[4pt]
hline mathrm{ctg} &infty &sqrt3&1&frac{sqrt3}3&0\[4pt]
hline
end{array}}}]
Заметим, что данные значения были выведены в разделе “Геометрия на плоскости (планиметрия). Часть II” в теме “Начальные сведения о синусе, косинусе, тангенсе и котангенсе”.
Пример 5. Найдите (sin{dfrac{3pi}4}).
Преобразуем угол: (dfrac{3pi}4=dfrac{4pi-pi}{4}=pi-dfrac{pi}4)
Таким образом, (sin{dfrac{3pi}4}=sinleft(pi-dfrac{pi}4right)=sindfrac{pi}4=dfrac{sqrt2}2).
(blacktriangleright) Для упрощения запоминания и использования формул приведения можно следовать следующему правилу.
Случай 1. Если угол можно представить в виде (ncdot pipm
alpha), где (ninmathbb{N}), то [sin(ncdot pipm
alpha)=bigodot sinalpha] где на месте (bigodot) стоит знак синуса угла (ncdot pipm alpha). [cos(ncdot pipm
alpha)=bigodot cosalpha] где на месте (bigodot) стоит знак косинуса угла (ncdot pipm alpha).
Знак угла можно найти, определив, в какой четверти он находится. Пользуясь таким правилом, предполагаем, что угол (alpha) находится в (I) четверти.
Случай 2. Если угол можно представить в виде (ncdot
pi+dfrac{pi}2pmalpha), где (ninmathbb{N}), то [sin(ncdot pi+dfrac{pi}2pm
alpha)=bigodot cosalpha] где на месте (bigodot) стоит знак синуса угла (ncdot pipm alpha). [cos(ncdot pi+dfrac{pi}2pm
alpha)=bigodot sinalpha] где на месте (bigodot) стоит знак косинуса угла (ncdot pipm alpha).
Знак определяется таким же образом, как и в случае (1).
Заметим, что в первом случае функция остается неизменной, а во втором случае — меняется (говорят, что функция меняется на кофункцию).
Пример 6. Найти (sin dfrac{13pi}{3}).
Преобразуем угол: (dfrac{13pi}{3}=dfrac{12pi+pi}{3}=4pi+dfrac{pi}3), следовательно, (sin dfrac{13pi}{3}=sin
left(4pi+dfrac{pi}3right)=sindfrac{pi}3=dfrac{sqrt3}2)
Пример 7. Найти (cos dfrac{17pi}{6}).
Преобразуем угол: (dfrac{17pi}{6}=dfrac{18pi-pi}{6}=3pi-dfrac{pi}6), следовательно, (cos dfrac{17pi}{6}=cos
left(3pi-dfrac{pi}6right)=-cosdfrac{pi}6=-dfrac{sqrt3}2)
(blacktriangleright) Область значений синуса и косинуса.
Т.к. координаты (x_{alpha}) и (y_{alpha}) любой точки (P_{alpha}) на единичной окружности находятся в пределах от (-1) до (1), а (cosalpha) и (sinalpha) — абсцисса и ордината соответственно этой точки, то [{large{-1leq cosalphaleq 1 ,qquad -1leqsinalphaleq 1}}]
Из прямоугольного треугольника по теореме Пифагора имеем: (x^2_{alpha}+y^2_{alpha}=1^2)
Т.к. (x_{alpha}=cosalpha, y_{alpha}=sinalpha Rightarrow) [{large{sin^2alpha+cos^2alpha=1}} — textbf{основное тригонометрическое тождество (ОТТ)}]
(blacktriangleright) Тангенс и котангенс.
Т.к. (mathrm{tg},alpha=dfrac{sinalpha}{cosalpha}, cosalphane 0)
(mathrm{ctg},alpha=dfrac{cosalpha}{sinalpha}, sinalphane 0), то:
1) ({large{mathrm{tg},alphacdot mathrm{ctg},alpha=1, cosalphane 0, sinalpha ne 0}})
2) тангенс и котангенс положительны в (I) и (III) четвертях и отрицательны в (II) и (IV) четвертях.
3) область значений тангенса и котангенса — все вещественные числа, т.е. (mathrm{tg},alphainmathbb{R},
mathrm{ctg},alphainmathbb{R})
4) для тангенса и котангенса также определены формулы приведения.
Случай 1. Если угол можно представить в виде (ncdot pipm
alpha), где (ninmathbb{N}), то [mathrm{tg},(ncdot pipm
alpha)=bigodot mathrm{tg},alpha] где на месте (bigodot) стоит знак тангенса угла (ncdot pipm alpha) ((cosalphane 0)). [mathrm{ctg},(ncdot pipm
alpha)=bigodot mathrm{ctg},alpha] где на месте (bigodot) стоит знак котангенса угла (ncdot pipm alpha) ((sinalphane 0)).
Случай 2. Если угол можно представить в виде (ncdot
pi+dfrac{pi}2pmalpha), где (ninmathbb{N}), то [mathrm{tg},(ncdot pi+dfrac{pi}2pm
alpha)=bigodot mathrm{ctg},alpha] где на месте (bigodot) стоит знак тангенса угла (ncdot pipm alpha) ((sinalphane 0)). [mathrm{ctg},(ncdot pi+dfrac{pi}2pm
alpha)=bigodot mathrm{tg},alpha] где на месте (bigodot) стоит знак котангенса угла (ncdot pipm alpha) ((cosalphane 0)).
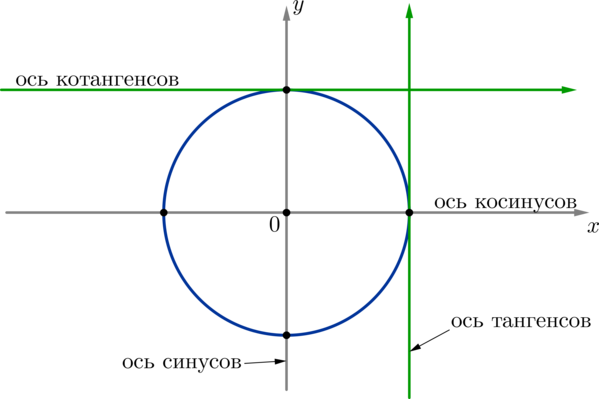
5) ось тангенсов проходит через точку ((1;0)) параллельно оси синусов, причем положительное направление оси тангенсов совпадает с положительным направлением оси синусов;
ось котангенсов — через точку ((0;1)) параллельно оси косинусов, причем положительное направление оси котангенсов совпадает с положительным направлением оси косинусов.
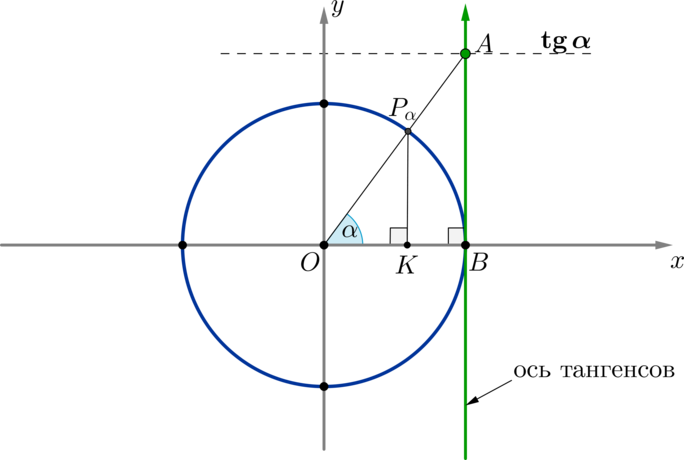
Доказательство этого факта приведем на примере оси тангенсов.
(triangle OP_{alpha}K sim triangle AOB Rightarrow
dfrac{P_{alpha}K}{OK}=dfrac{BA}{OB} Rightarrow
dfrac{sinalpha}{cosalpha}=dfrac{BA}1 Rightarrow
BA=mathrm{tg},alpha).
Таким образом, если точку (P_{alpha}) соединить прямой с центром окружности, то эта прямая пересечет линию тангенсов в точке, значение которой равно (mathrm{tg},alpha).
6) из основного тригонометрического тождества вытекают следующие формулы: [1+mathrm{tg},^2alpha=dfrac1{cos^2alpha},cosalphane 0 qquad qquad 1+mathrm{ctg},^2alpha=dfrac1{sin^2alpha}, sinalphane 0] Первую формулу получают делением правой и левой частей ОТТ на (cos^2alpha), вторую — делением на (sin^2alpha).
Обращаем внимание, что тангенс не определен в углах, где косинус равен нулю (это (alpha=dfrac{pi}2+pi n, ninmathbb{Z}));
котангенс не определен в углах, где синус равен нулю (это (alpha=pi+pi n, ninmathbb{Z})).
(blacktriangleright) Четность косинуса и нечетность синуса, тангенса, котангенса.
Напомним, что функция (f(x)) называется четной, если (f(-x)=f(x)).
Функция называется нечетной, если (f(-x)=-f(x)).
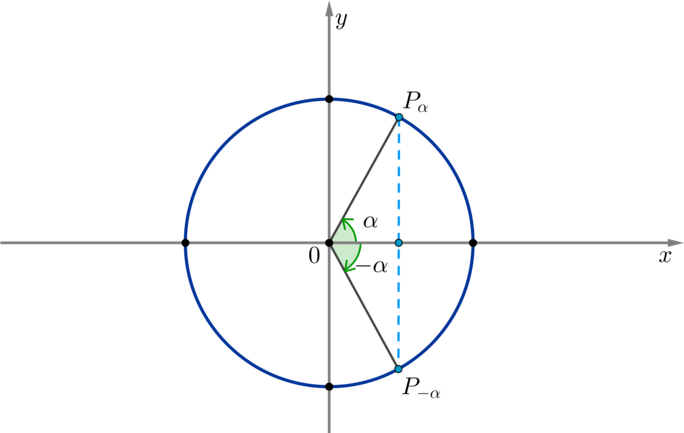
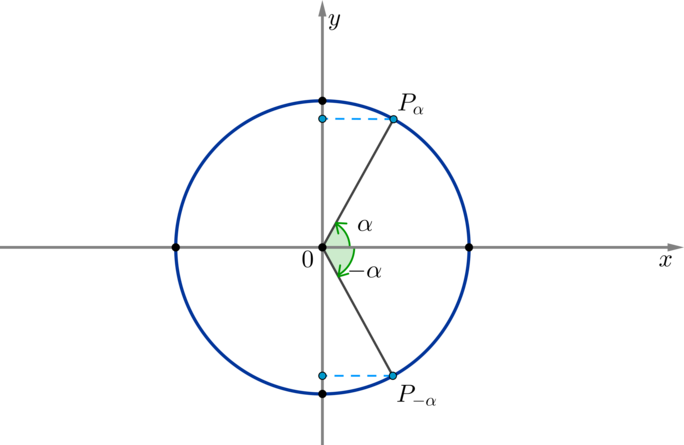
По окружности видно, что косинус угла (alpha) равен косинусу угла (-alpha) при любых значениях (alpha):
Таким образом, косинус — четная функция, значит, верна формула [{Large{cos(-x)=cos x}}]
По окружности видно, что синус угла (alpha) противоположен синусу угла (-alpha) при любых значениях (alpha):
Таким образом, синус — нечетная функция, значит, верна формула [{Large{sin(-x)=-sin x}}]
Тангенс и котангенс также нечетные функции: [{Large{mathrm{tg},(-x)=-mathrm{tg},x}}] [{Large{mathrm{ctg},(-x)=-mathrm{ctg},x}}]
Т.к. (mathrm{tg},(-x)=dfrac{sin (-x)}{cos(-x)}=dfrac{-sin
x}{cos x}=-mathrm{tg},x qquad mathrm{ctg},(-x)=dfrac{cos(-x)}{sin(-x)}=-mathrm{ctg},x))
- Материалы для подготовки к ЕГЭ
-
- Рубрики
- 01 Геометрия (13)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (78)
- 13 (С2) Стереометр. задачи (94)
- 14 (С3) Неравенства (89)
- 15 (С4) Практич. задачи (71)
- 16 (С5) Планиметр. задачи (86)
- 17 (С6) Параметры* (79)
- 18 (С7) Числа, их свойства (38)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
- II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (60)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (92)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
- Дружественные сайты
Сайт А. Ларина
ЕгэТренер – О. Себедаш
Математика?Легко!
Егэ? Ок! – И. Фельдман
- Свежие записи
- Тест «Гиперболы»
- Тест. Графики функций. Комбинированные задачи
- 10. Графики функций. Комбинированные задачи
- Тест. Тригонометрические функции
- 10. Тригонометрическая функция
- Тест. Кусочно-линейная функция
- 10. Кусочно-линейная функция
- Архивы Архивы
- Треугольник
- Четырехугольники
- Окружность и круг
- Призма
- Пирамида
- Усеченная пирамида
- Цилиндр
- Конус
- Усеченный конус
- Сфера и шар
1. Формулы сокращённого умножения
Наверх
2. Модуль числа
Определение:
Основные свойства модуля:
Наверх
3. Степень с действительным показателем
Свойства степени с действительным показателем
Пусть Тогда верны следующие соотношения:
Наверх
4. Корень n-ой степени из числа
Корнем n-ой степени из числа a называется число, n-ая степень которого равна a.
Арифметическим корнем четной степени n из неотрицательного числа a называется неотрицательное число, n-ая степень которого равна a.
Основные свойства арифметического корня:
Наверх
5. Логарифмы
Определение логарифма:
Основное логарифмическое тождество:
Основные свойства логарифмов
Пусть
Тогда верны следующие соотношения:
Наверх
6. Арифметическая прогрессия
Формула n-го члена арифметической прогрессии:
Характеристическое свойство арифметической прогрессии:
Сумма n первых членов арифметической прогрессии:
При решении задач, связанных с арифметической прогрессией, могут оказаться полезными также следующие формулы:
Наверх
7. Геометрическая прогрессия
Формула n-го члена геометрической прогрессии:
Характеристическое свойство геометрической прогрессии:
Сумма n первых членов геометрической прогрессии:
При решении задач, связанных с геометрической прогрессией, могут оказаться полезными также следующие формулы:
Наверх
8. Бесконечно убывающая геометрическая прогрессия
Сумма бесконечно убывающей геометрической прогрессии:
Наверх
9. Основные формулы тригонометрии
Зависимость между тригонометрическими функциями одного аргумента:
Формулы сложения:
Формулы тригонометрических функций двойного аргумента:
Формулы понижения степени:
Формулы приведения
Все формулы приведения получаются из соответствующих формул сложения. Например:
Применение формул приведения укладывается в следующую схему:
— определяется координатная четверть, в которой лежит аргумент приводимой функции, считая, что ;
— определяется знак приводимой функции;
— определяется название приведенной функции по следующему правилу: если аргумент приводимой функции имеет вид или
, то функция меняется на сходственную функцию, если аргумент приводимой функции имеет вид
, то функция названия не меняет.
Например, получим формулу :
— — IV четверть;
— в IV четверти тангенс отрицательный;
— аргумент приводимой функции имеет вид , следовательно, название функции меняется. Таким образом,
Формулы преобразования суммы тригонометрических функций в произведение:
Формулы преобразования произведения тригонометрических функций в сумму:
Наверх
10. Производная и интеграл
Таблица производных некоторых элементарных функций
Правила дифференцирования:
1.
2.
3.
4.
5.
Уравнение касательной к графику функции в его точке
:
Таблица первообразных для некоторых элементарных функций
Правила нахождения первообразных
Пусть ― первообразные для функций
и
соответственно, a, b, k ― постоянные,
Тогда:
— ― первообразная для функции
— ― первообразная для функции
— ― первообразная для функции
— Формула Ньютона-Лейбница:
1. Треугольник
Пусть ― длины сторон BC, AC, AB треугольника ABC соответственно;
― полупериметр треугольника ABC; A, B, C ― величины углов BAC, ABC, ACB треугольника ABC соответственно;
― длины высот AA2, BB2, CC2 треугольника ABC соответственно; R ― радиус окружности, описанной около треугольника ABC; r — радиус окружности, вписанной в треугольник ABC;
― площадь треугольника ABC. Тогда имеют место следующие соотношения:
(теорема синусов);
(теорема косинусов);
Наверх
2. Четырёхугольники
Параллелограмм
Параллелограммом называется четырехугольник, противоположные стороны которого попарно параллельны.
Прямоугольником называется параллелограмм, у которого все углы прямые.
Ромбом называется параллелограмм, все стороны которого равны.
Квадратом называется прямоугольник, все стороны которого равны. Из определения следует, что квадрат является ромбом, следовательно, он обладает всеми свойствами прямоугольника и ромба.
Трапецией называется четырехугольник, две стороны которого параллельны, а две другие не параллельны.
Площадь четырехугольника
Площадь параллелограмма равна произведению его основания на высоту.
Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними.
Площадь трапеции равна произведению полусуммы ее оснований на высоту.
Площадь четырехугольника равна половине произведения его диагоналей на синус угла между ними.
Наверх
3. Окружность и круг
Соотношения между элементами окружности и круга
Пусть r — радиус окружности, d — ее диаметр, C — длина окружности, S — площадь круга, — длина дуги в
градусов,
— длина дуги в
радиан,
— площадь сектора, ограниченного дугой в n градусов,
— площадь сектора, ограниченного дугой в
радиан. Тогда имеют место следующие соотношения:
Вписанный угол
Вписанный угол измеряется половиной дуги, на которую он опирается.
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Вписанный угол, опирающийся на полуокружность, — прямой.
Вписанная окружность
Центр окружности, вписанной в многоугольник, есть точка равноудаленная от всех сторон этого многоугольника, ― точка пересечения биссектрис углов этого многоугольника. Таким образом, в многоугольник можно вписать окружность, и притом только одну, тогда и только тогда, когда биссектрисы его углов пересекаются в одной точке.
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.
Описанная окружность
Центр окружности, вписанной в многоугольник, есть точка равноудаленная от всех вершин этого многоугольника, ― точка пересечения серединных перпендикуляров к сторонам этого многоугольника. Таким образом, около многоугольника можно описать окружность, и притом только одну, тогда и только тогда, когда серединные перпендикуляры к сторонам этого многоугольника пересекаются в одной точке.
Около четырехугольника можно описать окружность тогда и только тогда, когда суммы его противоположных углов равны
Наверх
4. Призма
Пусть H ― высота призмы, AA1 ― боковое ребро призмы, ― периметр основания призмы,
― площадь основания призмы,
― площадь боковой поверхности призмы,
― площадь полной поверхности призмы, V ― объем призмы,
― периметр перпендикулярного сечения призмы,
― площадь перпендикулярного сечения призмы. Тогда имеют место следующие соотношения:
Свойства параллелепипеда:
— противоположные грани параллелепипеда равны и параллельны;
— диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам;
— квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
Наверх
5. Пирамида
Пусть H ― высота пирамиды, ― периметр основания пирамиды,
― площадь основания пирамиды,
― площадь боковой поверхности пирамиды,
― площадь полной поверхности пирамиды, V ― объем пирамиды. Тогда имеют место следующие соотношения:
;
.
Замечание. Если все двугранные углы при основании пирамиды равны , а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны
, то
Наверх
6. Усечённая пирамида
Пусть H ― высота усеченной пирамиды, и
― периметры оснований усеченной пирамиды,
и
― площади оснований усеченной пирамиды,
― площадь боковой поверхности усеченной пирамиды,
― площадь полной поверхности усеченной пирамиды, V ― объем усеченной пирамиды.
Тогда имеют место следующие соотношения:
Замечание. Если все двугранные углы при основании пирамиды равны , а высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны
, то:
Наверх
7. Цилиндр
Пусть h ― высота цилиндра, r ― радиус цилиндра, ― площадь боковой поверхности цилиндра,
― площадь полной поверхности цилиндра, V ― объем цилиндра.
Тогда имеют место следующие соотношения:
Наверх
8. Конус
Пусть h ― высота конуса, r ― радиус основания конуса, l ― образующая конуса, ― площадь боковой поверхности конуса,
― площадь полной поверхности конуса, V ― объем конуса.
Тогда имеют место следующие соотношения:
Наверх
9. Усечённый конус
Пусть h ― высота усеченного конуса, r и ― радиусы основания усеченного конуса, l ― образующая усеченного конуса,
― площадь боковой поверхности усеченного конуса, V ― объем усеченного конуса. Тогда имеют место следующие соотношения:
Наверх
10. Сфера и шар
Пусть R ― радиус шара, D ― его диаметр, S ― площадь ограничивающей шар сферы, ― площадь сферической поверхности шарового сегмента (шарового слоя), высота которого равна h, V ― объем шара,
― объем сегмента, высота которого равна h,
― объем сектора, ограниченного сегментом, высота которого равна h. Тогда имеют место следующие соотношения:
Наверх