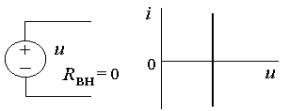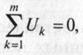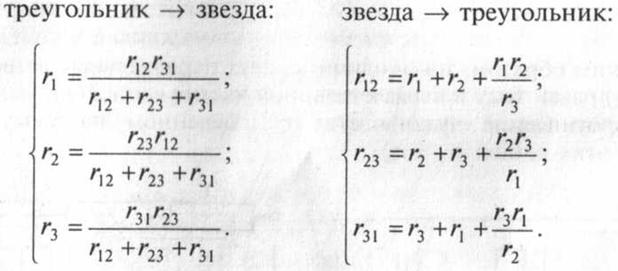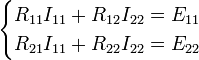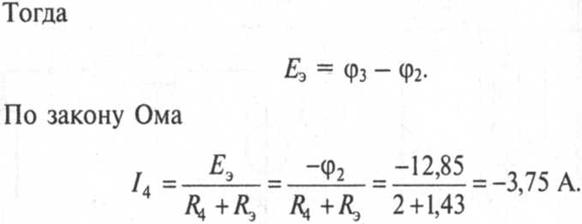Основы электротехники экзамен

198

Преимущества электрической энергии. Основные электротехнические понятия. Электрический ток. Электрическая цепь. Сила тока. ЭДС. Напряжение. Закон Ома. Работа и мощность в электрической цепи. Закон Джоуля-Ленца.

Ответ: Преимущества электрической энергии.

В настоящее время электрическая энергия – самый распространенный вид энергии и по сравнению с другими видами энергии обладает следующими преимуществами:

1.     Электрическая энергия – единственный вид энергии, который можно производить централизованно в больших количествах, что обеспечивает низкую её стоимость;

2.    быстро и экономично передается на большие расстояния;

3.    легко делится и распределяется между потребителями;

4.    легко преобразуется в другие виды энергии, что делает её универсальным энергоносителем;

5.     является единственным видом энергии, на использовании которой основана работа телекоммуникационных систем, электронно-вычислительной техники, современных систем управления и автоматики.

6.    Потребители электрической энергии отличаются высокой экономичностью и экологической чистотой.

 Несмотря на все эти достоинства электрической энергии свойственны и определенные недостатки:

1.     Электрическая энергия в промышленном масштабе не может быть запасена впрок в больших количествах;

2.     В природе нет естественных источников и запасов электрической энергии, пригодных для практического использования.

3.     специфические загрязнения окружающей среды: электромагнитные поля и электромагнитные излучения, действие которых на человека практически не исследованы.

 Электрическую энергию в промышленных масштабах получают в основном на тепловых электрических станциях за счет использования энергии первичных источников (уголь, газ, мазут).

1). Электрический ток. Сила тока

Упорядоченное направленное движение свободных электрических зарядов в пространстве под действием силы электрического поля называют электрическим током. Количественной мерой электрического тока является сила тока I [A]. Сила тока в электрической цепи определяется количеством электричества dQ [ Кл ], проходящего через поперечное сечение проводника в единицу времени (с): I = dQ /dt [ Кл/с ], [A]. При измерении количества электричества часто пользуются единицей измерения — Ампер-секунда (Q = 1 Кл = 1 А-с), а при измерении больших количеств – Ампер-час (1А-час = 3600 А-с ).

2). Электрическая цепь

Электрическая цепь – это совокупность соединённых между собой электротехнических устройств, обеспечивающих прохождение электрического тока и предназначенных для производства электрической энергии, а также её передачи, распределения и преобразования в требуемый вид энергии (работу).

 Чтобы по электрической цепи протекал электрический ток, эта цепь должна быть «замкнута». «Разрыв» электрической цепи в любом месте, т.е. появление в цепи непроводящего участка, приводит к прекращению электрического тока.

Простейшая электрическая цепь содержит следующие элементы:

1. Источник электрической энергии (генерирующее устройство) — преобразует какой-либо вид первичной энергии в электрическую;

2. Соединительные провода – соединяют зажимы источника электрической энергии и потребителя и служат для передачи электрической энергии;

3. Потребитель электрической энергии — служит для преобразования электрической энергии в требуемый вид энергии, т.е. в работу.

Кроме этих устройств электрическая цепь обычно содержит электроизмерительные приборы, различные сигнальные, регулирующие, коммутирующие, защитные и другие электротехнические устройства.

3.) Электродвижущая сила (ЭДС) и напряжение

При протекании электрического тока по электрической цепи совершается работа (механическая, тепловая и др.), на выполнение которой источник электрической энергии затрачивает некоторую энергию. Количественной мерой этой энергии источника является электродвижущая сила [Е] — ЭДС источника электрической [В] – это его полная энергия, которую он может израсходовать на получение работы, совершаемой при перемещении единицы количества электричества по замкнутому контуру электрической цепи (а — а): E аа = dW аа /dQ [B].

 Для характеристики работы, совершаемой источником электрической энергии на некотором участке электрической цепи, используется понятие разность потенциалов или напряжение [U]. Напряжение [U] характеризуется работой, совершаемой источником электрической энергии на некотором участке цепи (c — d): Ucd = dWcd /dQ [B].

4). Закон Ома

закон Ома : I = Y U ,здесь Y [1/ Ом ], [Сименс], [См] – коэффициент пропорциональности, значение которого зависит от свойств и параметров проводника и называется проводимостью.

 Для цепи постоянного тока закон Ома записывается в виде формулы: I = U/R , а для цепи переменного тока: I = U/Z , где Z — полное сопротивление электрической цепи переменного тока.

5). Работа и мощность в электрической цепи

При прохождении электрического тока по электрической цепи в ней происходит преобразование электрической энергии в другие виды энергии, т.е. совершается работа [dW] [Дж] или [Н∙м]. Из выражения для напряжения: U = dW /dQ можно записать: dW = U dQ = U I dt [Дж], или : W = U I t [Дж].

  Для характеристики скорости энергетического процесса преобразования и обмена электрической энергией в электрических цепях переменного тока используют понятие — полная мощность [S] [ВА]: S = dW /dt = U I .

Скорость процесса преобразования электрической энергии в другие виды энергии – характеризуется понятием — активная мощность Р [Вт]. В случае, когда проводник, по которому течёт электрический ток не перемещается (отсутствует механическая работа) и в проводнике не происходит химических превращений, то вся энергия электрического тока преобразуется во внутреннюю энергию, которая выделяется в виде тепла. В случае такого полного преобразования электрической энергии в тепловую для определения активной мощности используется формула Джоуля-Ленца: P = I² R [Вт]. По этой же формуле обычно определяют тепловые потери («джоулевы» потери) в различных электротехнических устройствах, машинах, аппаратах и др.

 Скорость процесса обмена электрической энергией между электромагнитными полями в электрических цепях переменного тока вводится понятие — реактивная мощность Q=I²X, единица измерения Вольт-Ампер реактивный [ВАр]

2. Электрическая цепь постоянного тока. Основные элементы и их условно-графические обозначения. Методы расчета цепей постоянного тока (правила Кирхгофа, метод эквивалентных преобразований).

Электрической цепью называют совокупность электротехнических устройств, образующих путь для прохождения электрического тока, электромагнитные процессы в которой могут быть описаны с помощью электрических величин — электродвижущей силы (E), тока (I) и напряжения (U).

Для расчета и анализа режимов работы реальных устройств электрических цепей используют эквивалентные схемы замещения. Чем точнее элементы схемы замещения отражают реальную цепь, тем точнее ее расчет и анализ режимов работы.

Схемы замещения линейных электрических цепей постоянного тока можно составить с помощью двух типов идеальных элементов (Рис.1):

идеального источника Э.Д.С. с параметром Е (Рис.1а) и идеального резистора (сопротивления) с параметром R (Рис.1б).

Электрические провода, соединяющие такие элементы, изображаются на схемах в виде отрезков прямых линий, электрическим сопротивлением этих проводов при анализе и расчете пренебрегают.

Ветвью называют участок цепи вдоль которого протекает один и тот же ток и который состоит из последовательно соединенных элементов.

Узлом называется место соединения трех и более ветвей.

Контуром называется любой замкнутый путь цепи, который можно обойти, двигаясь по ее ветвям.

Расчет и анализ электрических цепей производится с использованием закона Ома, первого и второго законов Кирхгофа.

Закон Ома для участка цепи

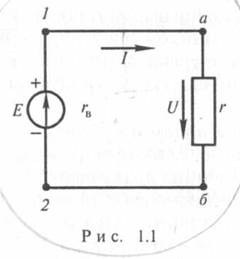
Соотношение между током I, напряжением U_R и сопротивлением R участка аb электрической цепи выражается законом Ома: или U_R = RI-падение напряжения на резисторе R

При расчете электрических цепей иногда удобнее пользоваться не сопротивлением R, а величиной обратной сопротивлению, т.е. электрической проводимостью:

Закон Ома для всей цепи

Этот закон определяет зависимость между ЭДС Е источника питания с внутренним сопротивлением r0 , током I электрической цепи и общим эквивалентным сопротивлением R_Э = r₀ + R всей цепи:

Сложная электрическая цепь содержит, как правило, несколько ветвей, в которые могут быть включены свои источники питания и режим ее работы не может быть описан только законом Ома. Но это можно выполнить на основании первого и второго законов Кирхгофа, являющихся следствием закона сохранения энергии.

Первый закон Кирхгофа

В любом узле электрической цепи алгебраическая сумма токов равна нулю: ,

где m-число ветвей подключенных к узлу.

При записи уравнений по первому закону Кирхгофа токи, направленные к узлу, берут со знаком «плюс», а токи, направленные от узла – со знаком «минус».

Второй закон Кирхгофа

В любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех его участках: , где n – число источников ЭДС в контуре; m – число элементов с сопротивлением Rк в контуре;

Uк = RкIк – напряжение или падение напряжения на к-м элементе контура.

Электротехника: вопросы к экзамену (с ответами)

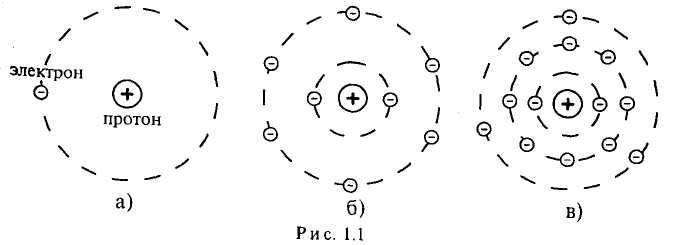
1 Электрическое поле (эп) и его основные характеристики: напряженность поля, электрическое напряжение, потенциал точки поля. Графическое изображение эп.

Каждый
химический элемент (вещество) состоит
из совокуп­ности
мельчайших материальных частиц —
атомов. В
состав атомов любого вещества входят
элементарные частицы,
часть которых обладает электрическим
зарядом.

Атом
пред­оставляет
собой систему, состоящую из ядра, вокруг
которого вра­щаются
электроны.

Если
нарушается равенство числа электронов
и протонов, то из электрически
нейтрального атом становится заряженным.
Заря­женный атом называется ионом.

Если
в силу каких-либо причин атом потеряет
один или не­сколько
электронов, то в нем нарушится равенство
зарядов и та­кой
атом становится положительным ионом,
поскольку в нем преобладает
положительный заряд протонов ядра. Если
атом приобретает
один или несколько электронов, то он
становится отрицательным
ионом, так как в нем преобладает
отрицатель­ный
заряд.

Вещество
(твердое тело, жидкость, газ) считается
электрически нейтральным,
если количество положительных и
отрицательных зарядов
в нем одинаково. Если же в нем преобладают
положи­тельные или отрицательные
заряды, то оно считается соответст­венно
положительно или отрицательно заряженным.

Электрический
заряд или заряженное тело создают
электриче­ское
поле.

Электрическое
поле
—
это
пространство вокруг заряженного тела
или
заряда, в котором обнаруживается действие
сил на пробный за­ряд,
помещенный в это пространство.

Электрическое
поле, создаваемое неподвижными зарядами,
называется
электростатическим.

Напряженность
поля:

Обнаружить
электрическое поле можно пробным
зарядом, если поместить
его в это поле. Пробным называется
положительный заряд,
внесение которого в исследуемое поле
не приводит к его изменению.
То есть пробный заряд не влияет ни на
силу, ни на энергию,
ни на конфигурацию поля.

Если
в точку А
электрического
поля (рис. 1.2), созданного за­рядом Q,
расположенную
на расстоянии r
от
него, внести пробный
заряд q,
то
на него будет дейст­вовать
сила F,
причем
если заряды Q
и
q
имеют
одинаковые знаки, то они отталкиваются
(как это изобра­жено на рис. 1.2), а если
разные, то притягиваются.

Величина
силы F,
действующей
на пробный заряд q,
помещен­ный
в точку А
электрического
поля, пропорциональна величине заряда
q
и
интенсивности электрического поля,
созданного заря­дом
Q
в
точке
А

F=qE_A, (1.1)

где
Ё_А
— напряженность
электрического поля, характеризующая
интенсивность
поля в точке А.
Из
(1.1) видно, что

. (1.2)

То
есть напряженность каждой тонки
электрического поля харак­теризуется
силой, с которой поле действует на
единицу заряда, по­мещенного
в эту точку. Таким
образом, напряженность является силовой
характеристикой каждой точки электрического
поля.

Измеряется
напряженность электрического поля в
вольтах на метр
[Е] = В/м.

Напряженность
электрического поля — величина векторная.

Направление
вектора напряженности в любой точке
электриче­ского поля совпадает с
направлением силы, действующей на
поло­жительный
пробный заряд, помещенный в эту точку
поля (см.
рис.
1.2).

Поскольку в
дальнейшем будут учитываться только
значения силы
и напряженности, будем обозначать их F
и
Е соответственно.

Напряженность
является параметром каждой точки
электриче­ского поля и не зависит от
величины пробного заряда q.
Измене­ние
величины q
приводит
к пропорциональному изменению си­лы
F‘(1.1),
а отношение F/q
(1.2),
т.е. напряженность Е_А,
остает­ся
неизменной.

Для
наглядности электрическое
поле изображают электриче­скими
линиями,
которые иногда называют линиями
напряжен­ности
электрического поля, или силовыми
линиями. Электриче­ские
линии направлены от положительного
заряда к отрицательному.
Линия проводится так, чтобы вектор
напряженности поля в
данной точке являлся касательной к ней
(рис. 1.3в).

Электрическое
поле называется однородным, если
напряжен­ность
его во всех точках одинакова по величине
и направлению. Однородное
электрическое поле изображается
параллельными ли­ниями,
расположенными на одинаковом расстоянии
друг от друга.

Однородное поле,
например, существует между пластинами
плоского конденсатора (рис. 1.3г).

Потенциал
и напряжение в (ЭП):

Для
энергетической характеристики каждой
точки электриче­ского поля вводится
понятие «потенциал». Обозначается
потен­циал
буквой φ.

Потенциал
в каждой точке электрического поля
характеризуется энергией
W,
которая затрачивается (или может быть
затрачена) полем
на перемещение единицы положительного
заряда q
из данной точки
за пределы поля, если поле создано
положительным зарядом, или
из-за пределов поля в данную точку, если
поле создано отрица­тельным зарядом
(рис.
1.7а).

Из
приведенного выше определения
следует, что потенциал
в точке А
равен
φ_A=W_A/q;
потенциал
в точке В
—
φ_В=
W_B/q,
а
по­тенциал в точке С
—
φ_С=
W_c/q.

Измеряется
потенциал в
вольтах

Величина потенциала
в каждой точке электрического поля
определяется выражением

(1.12)

Потенциал
— скалярная величина. Если электрическое
поле со­здано
несколькими зарядами, то потенциал в
каждой точке поля определяется
алгебраической суммой потенциалов,
созданных в этой точке каждым зарядом.

Так
как (рис. 1.7а) r_A<r_B<r_c,
то
из (1.12) следует, что φ_А>φ_г>φ_С,
если поле создано положительным зарядом.

Если
в точку А
(рис.
1.7а) электрического поля поместить
по­ложительный
пробный заряд q,
то
под действием сил поля он будет
перемещаться из точки А
в
точку В,
а
затем в точку С, т. е. в направлении поля.
Таким образом, положительный пробный
заряд
перемещается из точки с большим
потенциалом в точку с
меньшим потенциалом. Между двумя точками
с равными по­тенциалами
заряд перемещаться не будет. Следовательно,
для перемещения
заряда между двумя точками электрического
поля должна
быть разность потенциалов в этих точках.

Разность потенциалов
двух точек электрического поля
характеризует
напряжение U
между
этими точками

Напряжение
между двумя точками электрического
поля харак­теризуется
энергией, затраченной на перемещение
единицы положи­тельного
заряда между этими точками, т. е. U_AB=
W_AB/q.
;
Измеряется напряжение в вольтах (В).

Между
напряжением и напряженностью в од­нородном
электрическом поле (рис. 1.8) сущест­вует
зависимость

откуда
следует

Из
(1.13) видно, что напряженность однородного
электричес­кого поля определяется
отношением напряжения между двумя
точками
поля к расстоянию между этими точками.

В
общем случае для неоднородного
электрического поля значе­ние
напряженности определяется отношением

(1.14)

где
dU
— напряжение
между двумя точками поля на одной
элект­рической
линии на расстоянии di
между
ними.

Единица
напряженности электрического поля
определяется из выражения
(1.13)

Потенциалы
в точках электрического поля могут
иметь различные значения. Однако в
электрическом
поле можно выделить ряд точек
с одинаковым потенциалом. Поверхность,
проходящая через эти точки, называется
равнопотенциальной, или эквипотенциальной.
Равнопотенциальная
поверхность любой конфигурации
перпендикулярна к линиям Рис.
1.9 электрического
поля. Обкладки цилиндри­ческого
конденсатора (рис. 1.76) и плоского
конденсатора (рис. 1.9)
имеют одинаковый потенциал по всей
площади
каждой обкладки и являются равнопотенциальными
поверхностями.

1. ЭП
   точечного заряда. Закон Кулона. Теорема
   Гаусса.

Точечным
считается заряд, размерами которого
можно прене­бречь по сравнению с
расстоянием, на котором рассматривается
его
действие.

Сила
взаимодействия F
двух
точечных зарядов Q
и
q
(рис.
1.2) определяется
по закону Кулона:

(1.3)

где
г
—
расстояние между зарядами; £_а
— абсолютная диэлектри­ческая
проницаемость среды, в которой
взаимодействуют заряды. Из
(1.3) следует, что напряженность
электрического поля заряда Q
в
точке А
(рис.
1.2) равна

(1.4)

Таким
образом, напряженность поля Е_л,
созданная
зарядом Q
в
точке А
электрического
поля, зависит от величины заряда Q,
создающего
поле, расстояния точки А
от
источника поля r
и от абсолютной
диэлектрической проницаемости среды
ε_a,
в которой создается
поле. Диэлектрическая проницаемость
характеризует электрические свойства
среды, т. е. интенсивность поляризации.

Единицей
измерения абсолютной диэлектрической
проницае­мости среды является фарад
на метр

так как Кл/В = Ф.

Различные
среды имеют разные значения абсолютной
диэлект­рической
проницаемости. Абсолютная
диэлектрическая проницаемость вакуума

(1.5)
называется
электрической постоянной.

Абсолютную
диэлектрическую проницаемость любой
среды s_a
удобно
выражать через электрическую постоянную
£о и диэлектри­ческую
проницаемость е_г—
табличную величину (Приложение 2).

Диэлектрическая
проницаемость е„
которую
иногда называют относительной, показывает,
во сколько раз абсолютная диэлект­рическая
проницаемость среды больше, чем
электрическая по­стоянная,
т.е.

(1-6)
Из
(1.6) следует (1.7)

Таким
образом, напряженность электрического
поля, созданно­го зарядом Q
на
расстоянии г от него, определяется
выражением

(1.8)

Напряженность
электрического по­ля,
созданного несколькими зарядами
в какой-либо точке А
этого
поля,
определяется геометрической cуммой
напряженностей, созданных в
этой точке каждым точечным зарядом:
Е_л
=
Е_м
+ Е_А2
+…+
Е_Ак
(см. Q₃
^Aй,рис.
1.4).

1. Проводники
   и диэлектрики в
   электрическом
   поле.

2. Поляризация
   диэлектрика. Диэлектрическая
   проницаемость.

3. Понятие
   об электроемкости. Конденсаторы.
   Последовательное, параллельное и
   смешанное соединение
   конденсаторов.

Электрическая
емкость

Если
проводник А
получит
какой-либо заряд Q,
то
этот провод­ник создает электрическое
поле. Электрическое поле, созданное
проводником А,
обладает
энергией, которая и характеризует
по­тенциал проводника ф. Очевидно,
изменение заряда проводника вызывает
аналогичное изменение его потенциала.
Таким обра­зом,
между зарядом проводника и его потенциалом
существует прямая
пропорциональность, которую можно
записать следую­щим
уравнением:

где
С
—
коэффициент пропорциональности, который
и называет­ся
электрической емкостью проводника. Из
(6.1) следует, что электрическая емкость
проводника

То
есть электрическая
емкость проводника характеризуется
заря­дом
Q,
который необходимо сообщить проводнику,
чтобы его потен­циал
изменился на единицу. Единицей
измерения емкости является фарад.

Фарад
— большая единица. Например, электрическая
емкость проводника под названием «земля»
не превышает 0,7 Ф. Поэтому на
практике емкость измеряется в микрофарадах,
нанофарадах и пикофарадах.

Электрическая
емкость проводника характеризует
способность проводника
накапливать электрический заряд,
изменяющий его потенциал
на единицу (на 1 В).

Емкость
проводника не зависит от заряда Q,
сообщенного
про­воднику, так как изменение заряда
Q
вызовет
пропорциональное изменение потенциала
проводника φ,
а
их отношение остается неизменным (6.2).
(Емкость 5-литрового баллона не зависит
от количества
жидкости, заполняющей баллон.)

Емкость
проводника не зависит также от материала
и массы проводника.

Емкость проводника
зависит от:

1)
площади
поверхности проводника, так как заряды
располага­йся
на поверхности проводника;

2)
среды, в которой находится проводник.
Например, если проводник
перенести из воздуха в минеральное
масло, его емкость увеличится
в 2,2 раза, так как диэлектрическая
проницаемость минерального
масла ε_r=2,2
(см. Приложение 2); 3)
близости других проводников. Если рядом
с проводником в определенной
среде расположен еще один проводник,
то емкость системы
этих двух проводников будет гораздо
больше, чем сумма емкостей
каждого из этих проводников в этой
среде. На этом принципе
устроены электрические конденсаторы.

Профессия: «Электромонтер по ремонту и обслуживанию электрооборудования »

Дисциплина: «Электротехника»

1. Постоянный электрический ток: определение, источники, параметры и их единицы измерения.

2. Графическое изображение соединения фаз генератора и приемника по схемам:

«Звезда» и «Треугольник».

3. Напишите закон Ома для ветви и электрической цепи в целом.

4. Закон Ома и его применение.

5. Устройство и принцип действия однофазного трансформатора. Режимы работы.

6. Внутрь катушки вставили стальной сердечник. Как изменится индуктивность этой катушки?

7. Работа и мощность постоянного тока.

8. Предохранители устройства назначения, принцип действия.

9. Как соединить преемники электрической энергии параллельно?

10. Электрическая цепь постоянного тока. Из каких элементов состоит , для чего они нужны?

11. Явление электромагнитной индукции. Закон электромагнитной индукции. Правило Ленца.

12. Что произойдет, если в электрической цепи с последовательно соединенными лампами одна из ламп сгорит?

13. Электрическое сопротивление, электрическая проводимость. Удельное сопротивление.

14. Трехфазные трансформаторы соединения обмоток трехфазного трансформатора.

15. С какой целью источники электрической энергии включают параллельно?

16 Какое соединение приемников электрической цепи считается параллельным?

17. В чем суть закона электромагнитной индукции?

18. Электропаяльник включен в сеть напряжением 220В, потребляет ток 0,3А. Определить сопротивление электропаяльника.

19. Переменный ток. Характеристики синусоидально изменяющихся величин.

20. Что такое проводники второго рода?

21. Как влияет диэлектрик на емкость конденсатора?

22. Как выглядят силовые линии магнитного прямолинейного проводника?

23. В чем суть закона Фарадея?

24. Приведите примеры практического применения теплового действия электротока.

25. Магнитная индукция. Правило левой руки.

26. Какое включение в электрическую цепь источников электроэнергии считается согласным,

а какое встречным?

27. Что называется узлом, ветвью и контуром электрической цепи?

28. Электрический заряд, электрическое поле, характеристики электрического поля?

29. Коэффициент полезного действия. От каких энергетических показателей зависит КПД?

30. Как классифицируется нагрузка в трехфазной цепи?

31. Цепь переменного тока с резистором. График мгновенных значений напряжения и тока.

Векторная диаграмма.

32. От каких параметров зависит сила, действующая на проводник с током?

33. В чем суть закона Кулона?

34. Электрическая цепь переменного тока с индуктивным элементом. График мгновенных значений напряжения и тока. Векторная диаграмма.

35. Какие величины характеризуют каждую точку электрического поля?

36. С какой целью источники электрической энергии включаются последовательно?

37. Что такое электрическое сопротивление?

38. Какая мощность источника электроэнергии будет полезной, а какая потребляемой?

39. Каково соотношение сопротивления амперметра и шунта, если:

а) Rш RA; б) Rш RA; в) Rш = RA

40. Сформулируйте 1-ый закон Кирхгофа.

41. Техническое применение электролиза.

42.В какой линии передач при несимметричной нагрузке, соединенной звездой, фазные напряжения одинаковы?

43. Сформулируйте 2-ой закон Кирхгофа.

44. От каких параметров зависит удельное сопротивление металлического проводника?

45. Полезное применение вихревых токов.

46.Что такое последовательное соединение резисторов? Эквивалентное сопротивление?

47.Работа электрического тока. Единицы измерения работы электрического тока.

48. Однофазный трансформатор включен в сеть 220В. Первичная обмотка трансформатора имеет 800 витков, вторичная -40. Вычислите коэффициент трансформации и напряжение на вторичной обмотке.

49. Что такое параллельное соединение резисторов? Использование на практике этого соединения.

50. В чем состоит суть закона Джоуля-Ленца?

51. Может ли существовать магнитное поле независимо от электрического поля?

52. Характеристики магнитного поля. Магнитный поток и магнитодвижушая сила.

53. Что такое сдвиг фаз между напряжением и током?

54. Техническое применение электролиза.

55. Электрическая цепь электрического тока с емкостным элементом. График мгновенных значений напряжения и тока. Векторная диаграмма.

56. Какая линия электрического поля называется силовой?

57. В чем состоит суть принципа обратимости электрической машины?

58. Напряженность магнитного поля. Магнитная проницаемость.

59. При каких условиях возникает режим короткого замыкания в цепи?

60. Симметричная нагрузка трехфазной цепи соединена «звездой». Линейное напряжение 380В. Определите фазное напряжение.

61. От каких параметров зависит сила, действующая на проводник с током, помещенным в магнитное поле?

62. Назовите основные виды источников электрической энергии.

63. Симметричная нагрузка трехфазной цепи соединена «треугольником». Линейное напряжение 380В. Определите фазное напряжение.

64. Сформулируйте закон сохранения энергии (баланс мощностей).

65. Что такое мощность электрического тока? Каким прибором измеряется?

66. Можно ли проводить электродуговую сварку, используя источник постоянного тока?

67. Каким правилом определяется направление силовых магнитных линий?

68. В чем состоит суть принципа действия электрической печи?

69. В чем состоят преимущества и недостатки ламп накаливания?

70. Что называется электросбережением?

71. Как классифицируются нагрузки в 3-х фазной цепи?

72. Как определить направление индуцированной ЭДС в проводнике?

73. При каких условиях источник электрической энергии отдает приемнику наибольшую мощность?

74. Какое соединение резисторов называют смешанным?

75. Какие материалы называются диэлектриками?

Ответы на экзамен электроника электротехника

1.  
Основные элементы электрической цепи (активные,
пассивные). Обозначение тока, потенциалов и напряжения в  электрической цепи.

Электрическая цепь– совокупность
источников, приёмников электрической энергии и соединяющих их проводов. Кроме
этих элементов, в Э. ц. могут входить выключатели, переключатели,
предохранители и другие электрические аппараты защиты и коммутации, а также
измерит, и контрольные приборы.

 Активные
элементы
– источники электрической энергии, в которых неэлектрические виды энергии
преобразуются в электрическую.

Различают
два основных активных элемента: источник напряжения (ЭДС) и источник тока.

Пассивные
элементы
– приемники электромагнитной энергии. Электрическая энергия в них преобразуется
в неэлектрические виды энергии – активное сопротивление (проводимость), либо
накапливается в виде энергии электрического поля (емкость) или энергии
магнитного поля (индуктивность). Емкость и индуктивность являются реактивными
приемниками энергии или реактивными элементами.

Ток
обозначается
через I с направлением
течения.

На
схемах рядом с точкой более высокого потенциала ставится знак +, а рядом с
точкой более низкого – знак -. Разность потенциалов обозначается через U. Разность потенциалов
в двух точках a и b обозначается через U_ab.

Напряжение
обозначается
U.

2.  
Идеальные источники тока и ЭДС, обозначение и
основные характеристики.

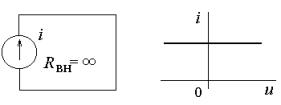
 Идеальный 
 источник 
 тока
(I),
величина тока, протекающего через который, не зависит от напряжения на его
зажимах. Внутреннее сопротивление такого источника можно условно принять равным
бесконечности. Обозначение идеального 
 источника 
 тока  и его
вольт-амперная характеристика приведены на рис.

Идеальный 
 источник 
напряжения (E),
напряжение на зажимах которого не зависит от величины  протекающего через
него  тока .
Внутреннее сопротивление  идеального 
 источника 
напряжения можно условно принять равным нулю. Обозначение такого источника и
его вольт-амперная характеристика приведены на рис.

1.  
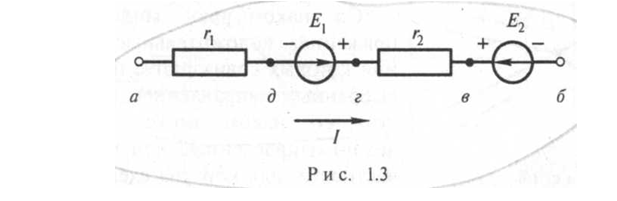
Закон Ома для участка цепи без источника ЭДС и закон
Ома для замкнутой цепи. Рисунок.  4. Закон Ома для участка цепи, содержащий
ЭДС. Рисунок.

5.  
Первый закон Кирхгофа. Пример его применения. 6.
Второй закон Кирхгофа. Пример его применения.

Кроме простых цепей существуют
сложные цепи. Сложной электрической цепью называют цепь, которая не может быть непо­средственно
рассчитана по закону Ома.

Сложная
цепь обычно содержит несколько источников ЭДС в разных ветвях. Число ветвей
электрической цепи обозначают через q, число узлов — через q, а число независимых контуров —
через п, где п = р — q + 1.

Для расчета сложных
цепей используют законы Кирхгофа, ко­торые формулируются для разветвленных и
сложных электриче­ских цепей; при их рассмотрении используют понятия ветви,
узла и контура.

Ветвью называют часть электрической
цепи, состоящую только из последовательно соединенных источников ЭДС (или тока)
и сопротивлений и имеющую два зажима для подключения ее к остальной
части цепи. На схемах электрических цепей каждую ветвь обычно изображают в виде
последовательного соединения одного эквивалентного источника ЭДС (или тока) и
одного экви­валентного сопротивления. Ветвь непосредственно соединяет два узла.
В ветви через все элементы протекает один и тот же ток.

Узлом называют точку электрической цепи, в которой соедине­но не
менее трех ветвей. На схемах узел обозначают точкой.

Контуром называют последовательность ветвей электрической цепи,
образующей замкнутый путь, в котором один из узлов одно­временно является
началом и концом пути, а остальные встречают­ся только один раз.

Первый закон Кирхгофа выражает тот факт, что ни в одной точке цепи
не происходит накопление электрических зарядов. Согласно этому закону (закону
Кирхгофа для токов) алгебраическая сумма токов в любом узле электрической цепи
равна нулю:

где со
знаком плюс записывают токи с положительными направле­ниями от узла, со знаком
минус — с положительными направле­ниями к узлу или наоборот. Иначе: сумма
токов, направленных от узла, равна сумме токов, направленных к узлу. Так,
например, для узла 1 (рис. 1.4) получим уравнение

I₁-I₂+I₃-I₄=0,

Второй
закон Кирхгофа устанавливает
связь между ЭДС, токами и сопротивлениями в любом замкнутом контуре. Согласно
этому закону (закону Кирхгофа для напряжений), алгебраическая сумма напряжений
участков любого контура электрической цепи равна нулю:

где т
— число участков контура.

Со
знаком плюс записывают на­пряжения, положительные направле­ния которых
совпадают с произвольно выбранным направлением обхода кон­тура, со знаком минус
— противопо­ложно направленные или наоборот. В частности, для контура схемы
замещения цепи, содержащего только источники ЭДС и резистивные эле­менты,
алгебраическая сумма напряжений на резистивных элементах равна алгебраической
сумме ЭДС:

Где
т
—
число резистивных элементов; п — число ЭДС в контуре.

Со
знаком плюс записывают ЭДС и токи, положительные на­правления которых совпадают
с произвольно выбранным направлением обхода контура, со знаком минус —
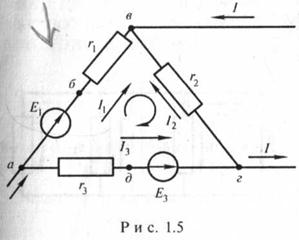
противоположно на­правленные или наоборот. Так, например, для контура, приведен­ного
на рис. 1.5,

7.  
Баланс мощностей в цепях постоянного тока.

8.  
Преобразование схем с последовательным, параллельным
и смешанным соединением сопротивлений.

9.
Преобразование треугольника сопротивлений в звезду и
наоборот.

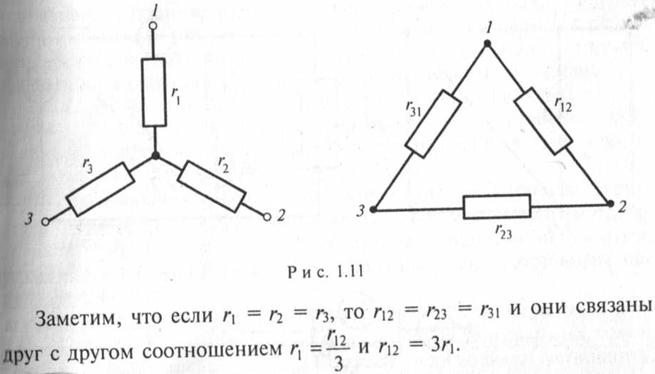
Элементы цепи часто соединяют
или треугольником, или звез­дой (рис. 1.11).

Для упрощения
расчета электрических цепей в ряде случаев целесообразно применять
преобразование треугольника сопротив­лений в эквивалентную звезду или звезды в
эквивалентный тре­угольник.

Условия
эквивалентного преобразования требуют, чтобы преоб­разования, производимые в
одной части цепи, не вызывали изме­нений в распределении токов и напряжений в
остальной части цепи. Согласно этим условиям, потенциалы одноименных точек
треугольника и звезды и подходящие к узлам токи должны быть одинаковы.

Формулы
перехода от сопротивлений треугольника к сопротив­лениям звезды и наоборот в
соответствии с обозначениями на рис. 1.11 имеют вид:

Используя эквивалентные
преобразования, сложную цепь ино­гда можно свести к простой. Часто
преобразования приводят к уменьшению числа ветвей и узлов сложной цепи и,
следовательно, к упрощению ее расчета.

6.  
Метод контурных токов. Пример его применения.

Ме́тод ко́нтурных то́ков — метод
сокращения размерности системы уравнений, описывающей электрическую цепь.

Основные принципы

Любая электрическая цепь, состоящая из Р
рёбер (ветвей, участков) и У узлов, может быть описана системой
уравнений в соответствии с 1-м
и 2-м законами Кирхгофа. Число уравнений в такой системе равно Р, из
них У–1 уравнений составляется по 1-му закону Кирхгофа для всех узлов,
кроме одного; а остальные Р–У+1 уравнений – по 2-му закону
Кирхгофа для всех независимых контуров. Поскольку независимыми переменными в
цепи считаются токи рёбер, число независимых переменных равно числу уравнений,
и система разрешима.

Существует несколько методов сократить число
уравнений в системе. Одним из таких методов является метод контурных токов.

Метод использует тот факт, что не все токи в рёбрах
цепи являются независимыми. Наличие в системе У–1 уравнений для узлов
означает, что зависимы У–1 токов. Если выделить в цепи Р–У+1
независимых токов, то систему можно сократить до Р–У+1 уравнений.
Метод контурных токов основан на очень простом и удобном способе выделения в
цепи Р–У+1 независимых токов.

Метод контурных токов основан на допущении, что в
каждом из Р–У+1 независимых контуров схемы циркулирует некоторый
виртуальный контурный ток. Если некоторое ребро принадлежит только одному
контуру, реальный ток в нём равен контурному. Если же ребро принадлежит
нескольким контурам, ток в нём равен сумме соответствующих контурных токов (с
учётом направления обхода контуров). Поскольку независимые контура покрывают
собой всю схему (т.е. любое ребро принадлежит хотя бы одному контуру), то ток в
любом ребре можно выразить через контурные токи, и контурные токи составляют
полную систему токов.

Построение системы уравнений

Для построения системы уравнений необходимо выделить
в цепи P – У + 1 независимых контуров. По
каждому из этих контуров будет составлено одно уравнение по 2-му закону
Кирхгофа. В каждом контуре необходимо выбрать направление обхода (например, по
часовой стрелке).

Ток во всех рёбрах схемы необходимо представить как
сумму (с учётом знаков) контурных токов, которые протекают по этим рёбрам.

При наличии в цепи источников тока, их
предварительно преобразовывают в источники напряжения.

Правило построения уравнения таково. Обходя контур в
соответствии с выбранным направлением, записываем в левую часть уравнений сумму
(с учётом знаков) токов в рёбрах, умноженных на сопротивление ребра. В правой
части уравнения записываем все источники ЭДС, имеющиеся в контуре (со знаком
«плюс», если направление обхода контура совпадает с направлением ЭДС, и
наоборот).

Составив уравнения для всех независимых контуров,
получаем совместную систему P – У + 1
уравнений относительно P – У + 1 неизвестных
контурных токов.

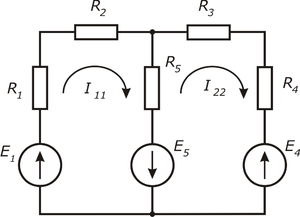
Пример

Метод
контурных токов

Положим, что в левом контуре по часовой стрелке
течет контурный ток I₁₁, а в правом (также по часовой
стрелке) — контурный ток I₂₂. Для каждого из контуров
составим уравнения по второму закону
Кирхгофа.
При этом учтем, что по смежной ветви (с сопротивлением R₅)
течет сверху вниз ток I₁₁–I₂₂. Направления
обхода контуров примем также по часовой стрелке.

Для первого контура

или

Для второго контура

или

Перепишем эти уравнения следующим образом:

Здесь

— полное сопротивление первого контура;

— полное сопротивление второго контура;

— сопротивления смежной ветви между первым и вторым
контурами, взятые со знаком минус;

—
контурная ЭДС первого контура;

— контурная ЭДС второго контура.

7.  Метод
эквивалентного генератора. Пример его применения.

8.
   Метод эквивалентного сопротивления. Пример его
применения.

9.
    Закон Джоуля-Ленца. Пример его применения.

Закон
Джоуля — Ленца — физический закон, дающий количественную оценку теплового действия электрического тока. Открыт в 1840 году независимо Джеймсом Джоулем и Эмилием Ленцом.

При прохождении электрического
тока через металлический проводник электроны сталкиваются то с нейтральными
молекулами, то с молекулами, потерявшими электроны. Движущийся электрон либо отщепляет
от нейтральной молекулы новый электрон, теряя свою кинетическую энергию и
образуя новый положительный ион, либо соединяется с молекулой, потерявшей
электрон (с положи­тельным ионом), образуя нейтральную молекулу. При столкнове­нии
электронов с молекулами расходуется энергия, которая пре­вращается в тепло.
Любое движение, при котором преодолевается сопротивление, требует затраты
определенной энергии. Так, напри­мер, для перемещения какого-либо тела
преодолевается сопротив­ление трения и работа, затраченная на это, превращается
в тепло.

Электрическое сопротивление проводника играет ту же
роль, чтя и сопротивление трения. Таким образом, для проведения тока через
проводник источник тока затрачивает некоторую энергию, которая превращается в
тепло. Переход электрической энергии в тепловую отражает закон Ленца — Джоуля
или закон теплового действия тока.

Русский ученый Ленц и английский физик Джоуль
одновремен­но и независимо один от другого установили, что при прохождении
электрического тока по проводнику количество теплоты, выделяемое проводником,
прямо пропорционально квадрату тока, сопротивлению проводника и времени, в
течение которого электрический ток протекал по проводнику. Это положение
называется законом Лен­ца — Джоуля.

 Если обозначить количество теплоты,
создаваемое током, буквой Q, силу тока, протекающего по
проводнику,— I, сопротивление проводника r и время, в
течение которого ток протекал по проводнику, t,  то
закону Ленца — Джоуля можно придать следующее выражение:

Пример 1. Определить
количество теплоты, выделенное в нагревательном приборе в течение 0,5 ч, если
он включен в сеть с напряжением 110 в и имеет сопротивление 24 ом.

Решение. Время прохождения в секундах:

t=0,5 ч =30 мин
=30х60=1800 сек.

 Количество теплоты, выделенное в приборе,

Примеры 2. В электрическом
кипятильнике вода, потребляя количество теплоты 400 000 дж,
закипает через 15 мин. Определить сопротивление нагрева­тельного
элемента этого кипятильника, а также мощность, если кипятильник ра­ботает под
напряжением 220 в и его к. п. д. равен 80%.

Решение. Так как к. п. д. кипятильника равен 80%,
выделенное нагрева­тельным элементом количество теплоты

Q = 400 000 : 0,8 = 500 000 дж.

Силу тока, протекающего через кипятильник, найдем из
слёлующей формулы

откуда

Сопротивление нагревательного элемента

Мощность, потребляемая кипятильником,

10.
Выделяемая и потребляемая мощность.

11.
Определение показаний приборов (амперметр и
вольтметр) при последовательном и параллельном соединении проводников.

12.
Режимы работы цепи (согласования, холостого хода и
т. д.)

· 
В режиме холостого хода источник питания отсоединен от нагрузки и работает ’’
вхолостую”. Сопротивление внешнего участка цепи , ток равен 0.

· 
В режиме короткого замыкания источник питания замкнут накоротко. Режим является
аварийным. Ток короткого замыкания Iк.з. во много раз превышает значение
номинального тока.

· 
Номинальным режимом называют такой режим, на который рассчитаны источник питания
и приемники электроэнергии заводом изготовителем. Процесс преобразования
электроэнергии в другие виды идет без постороннего нагрева, т.е. в допустимых
пределах по паспорту (U_н; I_н ; P_н и т.д.)
В этом режиме соблюдаются наилучшие условия работы: экономичность,
долговечность и т.д.

·  Под согласованным
режимом понимают такой режим, когда источник или приемник работают с
максимально возможной мощностью. На практике этот режим применяется в
радиотехнических установках и схемах, где низкий коэффициент .полезного
действия.

13.
Сила тока короткого замыкания.

Режим короткого замыкания (рис. 21). Коротким замыканием
(к. з.) называют такой режим работы источника, когда его зажимы замкнуты
проводником, сопротивление которого можно считать равным нулю. Практически к.
з. возникает при соединении друг с другом проводов, связывающих источник с
приемником, так как эти провода имеют обычно незначительное сопротивление и его
можно принять равным нулю. К. з. может происходить в результате неправильных
действий персонала, обслуживающего электротехнические установки (рис. 22, а),
или при повреждении изоляции проводов (рис. 22,б, в); в последнем случае эти
провода могут соединяться через землю, имеющую весьма малое сопротивление, или
через окружающие металлические детали (корпуса электрических машин и аппаратов,
элементы кузова локомотива и пр.).
При коротком замыкании ток

I_к.з = E
/ R₀ (15)

Ввиду того что внутреннее сопротивление источника Ro обычно очень мало,
проходящий через него ток возрастает до весьма больших значений. Напряжение же
в месте к. з. становится равным нулю (точка К на рис. 20), т. е. электрическая
энергия на участок электрической цепи, расположенный за местом к. з., поступать
не будет.

Если точки a и b замкнуть проводником, сопротивление
которого мало по сравнению с внутренним сопротивлением источника
(R << r), тогда в цепи потечет ток короткого замыкания

Сила
тока короткого замыкания – максимальная сила тока, которую можно получить от
данного источника с электродвижущей силой e
и внутренним сопротивлением r.

14.
Проводимость электрической цепи.

Всякий проводник можно характеризовать не только его сопротивлением, но и
так называемой проводимостью — способностью проводить электрический ток.
Проводимость есть величина, обратная сопротивлению. Единица проводимости
называется сименсом (См). 1 См равен 1/1 Ом. Проводимость обозначают буквой G
(g). Следовательно,

G = 1 / R (4)

Удельное электрическое сопротивление и проводимость. Атомы разных веществ
оказывают прохождению электрического тока неодинаковое сопротивление.