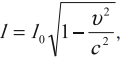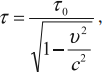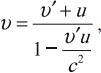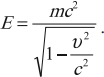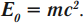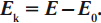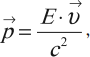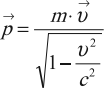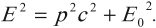Оглавление:
- Основные теоретические сведения
- Основы специальной теории относительности
- Фотон и его свойства
- Внешний фотоэффект
- Постулаты Бора
- Атомное ядро
- Радиоактивность. Закон радиоактивного распада
- Ядерные реакции
Основные теоретические сведения
Основы специальной теории относительности
К оглавлению…
Специальная теория относительности (СТО) базируется на двух постулатах:
- Принцип относительности: в любых инерциальных системах отсчета все физические явления при одних и тех же исходных условиях протекают одинаково, т.е. никакими опытами, проведенными в замкнутой системе тел, нельзя обнаружить покоится ли тело или движется равномерно и прямолинейно.
- Принцип постоянства скорости света: во всех инерциальных системах отсчета скорость света в вакууме одинакова и не зависит от скорости движущегося источника света.
Равное с постулатами СТО имеет значение положение СТО о предельном характере скорости света в вакууме: скорость любого сигнала в природе не может превосходить скорость света в вакууме: c = 3∙108 м/с. При движении объектов со скоростью сопоставимой со скоростью света, наблюдаются различные эффекты, описанные далее.
1. Релятивистское сокращение длины.
Длина тела в системе отсчета, где оно покоится, называется собственной длиной L0. Тогда длина тела движущегося со скоростью V в инерциальной системе отсчета уменьшается в направлении движения до длины:
где: c – скорость света в вакууме, L0 – длина тела в неподвижной системе отсчета (длина покоящегося тела), L – длина тела в системе отсчета, движущейся со скоростью V (длина тела, движущегося со скоростью V). Таким образом, длина тела является относительной. Сокращение тел заметно, только при скоростях, сопоставимых со скоростью света.
2. Релятивистское удлинение времени события.
Длительность явления, происходящего в некоторой точке пространства, будет наименьшей в той инерциальной системе отсчета, относительно которой эта точка неподвижна. Это означает, что часы, движущиеся относительно инерциальной системы отсчета, идут медленнее неподвижных часов и показывают больший промежуток времени между событиями. Релятивистское замедление времени становится заметным лишь при скоростях сопоставимых со скоростью света, и выражается формулой:
Время τ0, замеренное по часам, покоящимся относительно тела, называется собственным временем события.
3. Релятивистский закон сложения скоростей.
Закон сложения скоростей в механике Ньютона противоречит постулатам СТО и заменяется новым релятивистским законом сложения скоростей. Если два тела движутся навстречу друг другу, то их скорость сближения выражается формулой:
где: V1 и V2 – скорости движения тел относительно неподвижной системы отсчета. Если же тела движутся в одном направлении, то их относительная скорость:
4. Релятивистское увеличение массы.
Масса движущегося тела m больше, чем масса покоя тела m0:
5. Связь энергии и массы тела.
С точки зрения теории относительности масса тела и энергия тела – это практически одно и то же. Таким образом, только факт существования тела означает, что у тела есть энергия. Наименьшей энергией Е0 тело обладает в инерциальной системе отсчета относительно которой оно покоится и называется собственной энергией тела (энергия покоя тела):
Любое изменение энергии тела означает изменение массы тела и наоборот:
где: ∆E – изменение энергии тела, ∆m – соответствующее изменение массы. Полная энергия тела:
где: m – масса тела. Полная энергия тела Е пропорциональна релятивистской массе и зависит от скорости движущегося тела, в этом смысле важны следующие соотношения:
Кстати кинетическую энергию тела, движущегося с релятивистской скоростью, можно считать только по формуле:
С точки зрения теории относительности закон сохранения масс покоя несправедлив. Например, масса покоя атомного ядра меньше суммы масс покоя частиц, входящих в ядро. Однако, масса покоя частицы способной к самопроизвольному распаду больше суммы собственных масс составляющих ее.
Это не означает нарушения закона сохранения массы. В теории относительности справедлив закон сохранения релятивистской массы, так как в изолированной системе тел сохраняется полная энергия, а значит и релятивистская масса, что следует из формулы Эйнштейна, таким образом можно говорить о едином законе сохранения массы и энергии. Это не означает возможность перехода массы в энергию и наоборот.
Между полной энергией тела, энергией покоя и импульсом существует зависимость:
Фотон и его свойства
К оглавлению…
Свет – это поток квантов электромагнитного излучения, называемых фотонами. Фотон – это частица, переносящая энергию света. Он не может находиться в покое, а всегда движется со скоростью, равной скорости света. Фотон обладает следующими характеристиками:
1. Энергия фотонов равна:
где: h = 6,63∙10–34 Дж∙с = 4,14∙10–15 эВ∙с – постоянная Планка, ν – частота света, λ – длина волны света, c – скорость света в вакууме. Энергия фотона в Джоулях очень мала, поэтому для математического удобства ее часто измеряют во внесистемной единице – электрон-вольтах:
1 эВ = 1,6∙10–19 Дж.
2. Фотон движется в вакууме со скоростью света c.
3. Фотон обладает импульсом:
4. Фотон не обладает массой в привычном для нас смысле (той массой, которую можно измерить на весах, рассчитать по второму закону Ньютона и так далее), но в соответствии с теорией относительности Эйнштейна, обладает массой как мерой энергии (E = mc2). Действительно, любое тело, имеющее некоторую энергию, имеет и массу. Если учесть, что фотон обладает энергией, то он обладает и массой, которую можно найти как:
5. Фотон не обладает электрическим зарядом.
Свет обладает двойственной природой. При распространении света проявляются его волновые свойства (интерференция, дифракция, поляризация), а при взаимодействии с веществом – корпускулярные (фотоэффект). Эта двойственная природа света получила название корпускулярно-волнового дуализма.
Внешний фотоэффект
К оглавлению…
Фотоэлектрический эффект – явление, заключающееся в появлении фототока в вакуумном баллоне при освещении катода монохроматическим светом некоторой длины волны λ.
Когда напряжение на аноде отрицательно, электрическое поле между катодом и анодом тормозит электроны. Измеряя данное задерживающее напряжение при котором исчезает фототок, можно определить максимальную кинетическую энергию фотоэлектронов вырываемых из катода:
Многочисленными экспериментаторами были установлены следующие основные закономерности фотоэффекта:
- Фотоэффект безынерционен. Это значит, что электроны начинают вылетать из металла сразу же после начала облучения светом.
- Максимальная кинетическая энергия фотоэлектронов линейно возрастает с увеличением частоты света ν и не зависит от его интенсивности.
- Для каждого вещества существует так называемая красная граница фотоэффекта, то есть наименьшая частота νmin (или наибольшая длина волны λmax) при которой еще возможен внешний фотоэффект.
- Число фотоэлектронов, вырываемых светом из катода за 1 с, прямо пропорционально интенсивности света.
При взаимодействии с веществом фотон целиком передает всю свою энергию E = hν одному электрону. Часть этой энергии электрон может рассеять при столкновениях с атомами вещества. Кроме того, часть энергии электрона затрачивается на преодоление потенциального барьера на границе металл–вакуум. Для этого электрон должен совершить работу выхода Aвых, зависящую от свойств материала катода. Наибольшая кинетическая энергия, которую может иметь вылетевший из катода фотоэлектрон, в таком случае, определяется законом сохранения энергии:
Эту формулу принято называть уравнением Эйнштейна для внешнего фотоэффекта. С помощью уравнения Эйнштейна можно объяснить все закономерности внешнего фотоэффекта. Для красной границы фотоэффекта, согласно формуле Эйнштейна, можно получить выражение:
Постулаты Бора
К оглавлению…
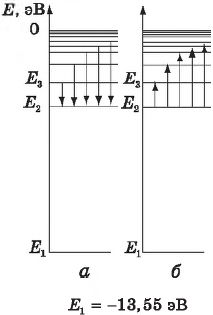
Первый постулат Бора (постулат стационарных состояний): атомная система может находится только в особых стационарных или квантовых состояниях, каждому из которых соответствует определенная номер n и энергия En. В стационарных состояниях атом не излучает и не поглощает энергию.
Состоянию с наименьшей энергией присваивается номер «1». Оно называется основным. Всем остальным состояниям присваиваются последовательные номера «2», «3» и так далее. Они называются возбужденными. В основном состоянии атом может находиться бесконечно долго. В возбужденном состоянии атом живет некоторое время (порядка 10 нс) и переходит в основное состояние.
Согласно первому постулату Бора, атом характеризуется системой энергетических уровней, каждый из которых соответствует определенному стационарному состоянию. Механическая энергия электрона, движущегося по замкнутой траектории вокруг положительно заряженного ядра, отрицательна. Поэтому всем стационарным состояниям соответствуют значения энергии En < 0. При En ≥ 0 электрон удаляется от ядра (происходит ионизация). Величина |E1| называется энергией ионизации. Состояние с энергией E1 называется основным состоянием атома.
Второй постулат Бора (правило частот): при переходе атома из одного стационарного состояния с энергией En в другое стационарное состояние с энергией Em излучается или поглощается квант, энергия которого равна разности энергий стационарных состояний:
Атом водорода
Простейший из атомов – атом водорода. Он содержит единственный электрон. Ядром атома является протон – положительно заряженная частица, заряд которой равен по модулю заряду электрона. Обычно электрон находится на первом (основном, невозбужденном) энергетическом уровне (электрон, как и любая другая система, стремится к состоянию с минимумом энергии). В этом состоянии его энергия равна E1 = –13,6 эВ. В атоме водорода выполняются следующие соотношения, связывающие радиус траектории вращающегося вокруг ядра электрона, его скорость и энергию на первой орбите с аналогичными характеристиками на остальных орбитах:
На любой орбите в атоме водорода кинетическая (К) и потенциальная (П) энергии электрона связаны с полной энергией (Е) следующими формулами:
Атомное ядро
К оглавлению…
В настоящее время твердо установлено, что атомные ядра различных элементов состоят из двух частиц – протонов и нейтронов, которые принято называть нуклонами. Для характеристики атомных ядер вводится ряд обозначений. Число протонов, входящих в состав атомного ядра, обозначают символом Z и называют зарядовым числом или атомным номером (это порядковый номер в периодической таблице Менделеева). Число нейтронов обозначают символом N. Общее число нуклонов (то есть протонов и нейтронов) называют массовым числом A, для которого можно записать следующую формулу:
Энергия связи. Дефект массы
Важнейшую роль в ядерной физике играет понятие энергии связи ядра. Энергия связи ядра равна минимальной энергии, которую необходимо затратить для полного расщепления ядра на отдельные частицы. Из закона сохранения энергии следует, что энергия связи равна той энергии, которая выделяется при образовании ядра из отдельных частиц.
Энергию связи любого ядра можно определить с помощью точного измерения его массы. Такие измерения показывают, что масса любого ядра Mя всегда меньше суммы масс входящих в его состав протонов и нейтронов: Mя < Zmp + Nmn. При этом разность этих масс называется дефектом масс, и вычисляется по формуле:
По дефекту массы можно определить с помощью формулы Эйнштейна E = mc2 энергию, выделившуюся при образовании данного ядра, то есть энергию связи ядра Eсв:
Но удобнее рассчитывать энергию связи по другой формуле (здесь массы берутся в атомных единицах, а энергия связи получается в МэВ):
Радиоактивность. Закон радиоактивного распада
К оглавлению…
Почти 90% из известных атомных ядер нестабильны. Нестабильное ядро самопроизвольно превращается в другие ядра с испусканием частиц. Это свойство ядер называется радиоактивностью.
Альфа-распад. Альфа-распадом называется самопроизвольное превращение атомного ядра с числом протонов Z и нейтронов N в другое (дочернее) ядро, содержащее число протонов Z – 2 и нейтронов N – 2. При этом испускается α-частица – ядро атома гелия 42He. Общая схема альфа-распада:
Бета-распад. При бета-распаде из ядра вылетает электрон (0–1e). Схема бета-распада:
Гамма-распад. В отличие от α— и β-радиоактивности γ-радиоактивность ядер не связана с изменением внутренней структуры ядра и не сопровождается изменением зарядового или массового чисел. Как при α-, так и при β-распаде дочернее ядро может оказаться в некотором возбужденном состоянии и иметь избыток энергии. Переход ядра из возбужденного состояния в основное сопровождается испусканием одного или нескольких γ-квантов, энергия которых может достигать нескольких МэВ.
Закон радиоактивного распада. В любом образце радиоактивного вещества содержится огромное число радиоактивных атомов. Так как радиоактивный распад имеет случайный характер и не зависит от внешних условий, то закон убывания количества N(t) нераспавшихся к данному моменту времени t ядер может служить важной статистической характеристикой процесса радиоактивного распада. Закон радиоактивного распада имеет вид:
Величина T называется периодом полураспада, N0 – начальное число радиоактивных ядер при t = 0. Период полураспада – основная величина, характеризующая скорость радиоактивного распада. Чем меньше период полураспада, тем интенсивнее протекает распад.
При α— и β-радиоактивном распаде дочернее ядро также может оказаться нестабильным. Поэтому возможны серии последовательных радиоактивных распадов, которые заканчиваются образованием стабильных ядер.
Ядерные реакции
К оглавлению…
Ядерная реакция – это процесс взаимодействия атомного ядра с другим ядром или элементарной частицей, сопровождающийся изменением состава и структуры ядра и выделением вторичных частиц или γ-квантов. В результате ядерных реакций могут образовываться новые радиоактивные изотопы, которых нет на Земле в естественных условиях.
При ядерных реакциях выполняется несколько законов сохранения: импульса, энергии, момента импульса, заряда. В дополнение к этим классическим законам сохранения при ядерных реакциях выполняется закон сохранения так называемого барионного заряда (то есть числа нуклонов – протонов и нейтронов). Например, в реакции общего вида:
Выполняются следующие условия (общее число нуклонов до и после реакции остается неизменным):
Энергетический выход ядерной реакции
Ядерные реакции сопровождаются энергетическими превращениями. Энергетическим выходом ядерной реакции называется величина:
где: MA и MB – массы исходных продуктов, MC и MD – массы конечных продуктов реакции. Величина ΔM называется дефектом масс. Ядерные реакции могут протекать с выделением (Q > 0) или с поглощением энергии (Q < 0). Во втором случае первоначальная кинетическая энергия исходных продуктов должна превышать величину |Q|, которая называется порогом реакции.
Для того чтобы ядерная реакция имела положительный энергетический выход, удельная энергия связи нуклонов в ядрах исходных продуктов должна быть меньше удельной энергии связи нуклонов в ядрах конечных продуктов. Это означает, что величина ΔM должна быть положительной.
Принципы СТО.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: принцип относительности Эйнштейна, инвариантность скорости света.
Принцип относительности Галилея, подробно рассмотренный в предыдущем листке, говорит о том, что никакие лабораторные опыты механики не помогут определить, покоится ли лаборатория или движется равномерно и прямолинейно.
Но возникает закономерный вопрос: а кто заставляет нас ограничиваться лишь механическими явлениями? Давайте перейдём в другие области физики: будем наблюдать в движущейся лаборатории распространение тепла или света, ставить опыты с электромагнитными колебаниями, изучать ядерные процессы. . . Раз уж механика нам не помощник, то, быть может, где-нибудь в молекулярной физике, электродинамике, оптике, атомной или ядерной физике найдутся явления, на протекании которых скажется равномерно-прямолинейное движение лаборатории? Тогда, сопоставив ход таких явлений в неподвижной и в движущейся системах отсчёта, мы зафиксируем факт движения и сможем измерить его скорость.
С развитием электродинамики поначалу казалось, что так оно и есть. Дело в том, что, в отличие от законов механики Ньютона, уравнения Максвелла оказались не инвариантными относительно преобразований Галилея.
Гипотеза о мировом эфире.
Из уравнений Максвелла следует, например, что свет в вакууме распространяется со скоростью c= 300000 км/с в любом направлении, причём эта скорость не зависит от того, покоится ли источник света или движется. Физиков данный факт ничуть не удивлял: свет рассматривался как колебания особой всепроникающей среды — неподвижного мирового эфира. Считалось, что электромагнитные волны распространяются в эфире аналогично звуковым волнам в воздухе, а со звуком ведь дело обстоит точно так же: сигнал от бибикнувшего автомобиля бежит в воздухе во все стороны со скоростью примерно 330 м/с вне зависимости от скорости, с которой движется автомобиль.
А теперь представьте себе, что вы находитесь в звездолёте, который мчится в космическом вакууме со скоростью v= 50000км/с относительно удалённых звёзд. Вы сидите лицом по ходу движения звездолёта и смотрите на лампочку, которая находится в его носовой части.
Свет от лампочки, не обращая внимания на её движение, перемещается относительно звёзд со скоростью c. Вы движетесь навстречу свету со скоростью v; стало быть, относительно вас свет имеет скорость
c+v= 350000 км/с. Вы измеряете эту скорость, сопоставляете её с известным значением c и приходите к выводу, что двигаетесь со скоростью 50000 км/с! Таким образом, электромагнитные явления вроде бы позволяют отличить покой от равномерного прямолинейного движения.
У вас, кстати, может возникнуть вопрос: а чем плох аналогичный эксперимент со звуком? Давайте бибикнем в носовой части длинного движущегося лимузина, измерим скорость звука относительно нас и опровергнем принцип относительности Галилея! Ничего не выйдет: если лимузин замкнутый (как и должно быть), то он увлекает свой воздух вместе с собой, и вы ничего не заметите. А вот в звездолёте вам никуда не деться от всепроникающего «эфирного ветра», который несётся вам в лицо и увеличивает тем самым скорость света в описанном выше эксперименте с лампочкой. (Пытаясь спасти принцип относительности Галилея применительно к электродинамике, Герц предположил, что эфир также увлекается движущимися телами. Из этой гипотезы следовало, однако, что струя воды, увлекая эфир, должна увлекать и луч света — а в экспериментах такого не наблюдалось.)
Соответственно, многие учёные (в том числе выдающийся голландский физик Х. Лоренц) считали, что инерциальные системы отсчёта, будучи равноправными с точки зрения механики, в электродинамике перестают быть таковыми. Имеется выделенная, привилегированная система отсчёта, связанная с неподвижным мировым эфиром. Остальные системы отсчёта движутся относительно неё, и возникающий «эфирный ветер» меняет в них величину скорости света.
С целью обнаружения эфирного ветра в 1881 году был поставлен один из самых знаменитых физических экспериментов — опыт Майкельсона. С помощью чувствительного интерферометра производились попытки измерить скорость Земли относительно эфира. А именно, исследовалась интерференционная картина, даваемая двумя когерентными пучками света, имеющими перпендикулярные направления. Интерферометр движется относительно эфира вместе с Землёй; при вращении интерферометра меняется направление эфирного ветра относительно интерферометра, что должно сказываться на скоростях пучков и давать сдвиги интерференционной картины.
Однако никаких сдвигов обнаружено не было! Наблюдения проводились в разное время года (когда скорость Земли ощутимо меняла направление) и неизменно давали отрицательный результат. Интерферометр был настолько точный, что списать отсутствие эфирного ветра на недостаточную чувствительность прибора было нельзя.
Почему же движение Земли относительно эфира не удаётся зафиксировать? Не сомневаясь в существовании эфира, Лоренц заметил, что результаты опыта Майкельсона полностью объясняются, если сделать невероятное предположение: размеры движущегося предмета сокращаются в направлении движения! Так, если стержень длины начинает двигаться вдоль своей оси со скоростью
, то его длина становится равной:
(1)
Эта гипотеза, названная лоренцевым сокращением, не вытекала на тот момент из каких-либо физических принципов и стояла особняком, будучи призвана лишь справиться с отрицательным результатом опыта. Но тем не менее формула (1) действительно оказалась верна! Её объяснение пришло позже, уже в рамках теории относительности Эйнштейна.
Постулаты Эйнштейна.
Альберт Эйнштейн — величайшая фигура в истории физики. Для разрешения трудностей, описанных выше, он отказался от некоторых сложившихся в физике устоев и предпринял весьма радикальные шаги. Сформулируем ещё раз те проблемы, с которыми столкнулась физика, и их решения, предложенные Эйнштейном.
1. Не удаётся обнаружить привилегированную систему отсчёта, связанную с неподвижным мировым эфиром.
Так её и нет вовсе. Никакого эфира не существует. Все инерциальные системы отсчёта полностью равноправны между собой, и никакими физическими опытами нельзя выделить одну из них среди остальных.
Таким образом, Эйнштейн обобщил принцип относительности Галилея с механических на вообще все физические явления.
Принцип относительности Эйнштейна. Всякое физическое явление при одних и тех же начальных условиях протекает одинаково в любой инерциальной системе отсчёта.
Следовательно, если ваша лаборатория находится внутри корабля, то не только механический, но и вообще никакой эксперимент не даст вам ответа на вопрос, покоится ли корабль или движется равномерно и прямолинейно. Вы можете ставить опыты с газами, изучать тепловые явления, наблюдать за распространением электромагнитных волн, следить за атомными и ядерными процессами, анализировать взаимодействия элементарных частиц — и нигде вам не удастся обнаружить каких-либо отклонений в протекании этих явлений, вызванных фактом равномерно-прямолинейного движения корабля.
В предыдущем разделе мы убедились в том, что законы механики имеют одинаковую математическую форму во всех инерциальных системах отсчёта: уравнения, выражающие эти законы, инвариантны относительно преобразований Галилея. Таков смысл принципа относительности Галилея. Обобщающий его принцип относительности Эйнштейна утверждает, что любой физический закон имеет одинаковую математическую форму во всех инерциальных системах отсчёта. Все уравнения, выражающие законы физики, должны быть инвариантны относительно перехода из одной инерциальной системы отсчёта в другую.
В частности, основные уравнения электродинамики — уравнения Максвелла — должны сохранять свою форму при таком переходе. Как же тогда быть со следующей трудностью?
2. Электродинамика противоречит механике в том, что уравнения Максвелла не инвариант-ны относительно преобразований Галилея.
Что ж, это проблема механики, а не электродинамики. Уравнения Максвелла блестяще работают в области электромагнитных явлений. Если преобразования Галилея не вяжутся с уравнениями Максвелла, то неверны преобразования Галилея, а не уравнения Максвелла.
Но легко сказать — преобразования Галилея неверны! Во-первых, они, казалось бы, совершенно очевидны — вам наверняка не составило труда в них разобраться. Чему там, собственно говоря, быть неверным?
А во-вторых — следствием преобразований Галилея, как мы видели, является закон сложения скоростей. Вы неоднократно пользовались им при решении задач. Что же получается — и закон сложения скоростей объявляется неверным?
Да, именно так — гласил ответ Эйнштейна. Классическая механика Ньютона нуждается в глубоком, коренном пересмотре своих основных принципов. И слабый пункт классической механики состоит в том, что механические законы предполагают мгновенность распространения взаимодействий между телами.
Рассмотрим, например, гравитационное притяжение двух тел. Если одно из тел сместить в сторону, то, согласно закону всемирного тяготения, второе тело «почувствует» этот факт мгновенно, как только изменится расстояние от него до первого тела. Получается, что взаимодействие передаётся от одного тела к другому с бесконечной скоростью.
Эксперименты, однако, показывают, что механизм передачи взаимодействий состоит в следующем: изменение состояния тела меняет поле около него; возникшее возмущение поля начинает бежать во все стороны с некоторой конечной скоростью и лишь спустя определённый промежуток времени достигает другого тела. Мгновенно передающихся взаимодействий ни в каких опытах не наблюдается.
Но если взаимодействия не могут передаваться в бесконечной скоростью, то в природе существует предельная, максимальная скорость распространения взаимодействий. Изменённые законы механики должны учитывать наличие этой предельной скорости и, соответственно, конечность времени передачи взаимодействий между телами.
Второй постулат Эйнштейна отводит исключительную роль скорости света.
Принцип инвариантности скорости света. В каждой инерциальной системе отсчёта свет движется в вакууме с одной и той же скоростью; величина этой скорости не зависит от того, покоится или движется источник света.
Таким образом, вышеописанный опыт с лампочкой в носовой части звездолёта нам провести не удастся: скорость света относительно наблюдателя в звездолёте будет равна c, а не c+v, и наблюдатель не может заметить факт движения звездолёта. Классический закон сложения скоростей применительно к скорости света не работает.
Мы увидим далее, что максимальная скорость распространения взаимодействий, присущая нашему миру, оказывается равной как раз скорости света в вакууме. Никакой сигнал, никакое тело, никакой вообще материальный объект в природе не может двигаться со скоростью, превышающей c. Величина c является фундаментальной константой, отражающей свойства мира, в котором мы живём.
Оба постулата Эйнштейна — принцип относительности и принцип инвариантности скорости света — легли в основу специальной теории относительности (СТО). Эта теория затрагивает глубокие свойства пространства-времени, радикально меняя наши представления об окружающем мире. Механика, построенная Эйнштейном на постулатах СТО, получила название релятивистской (от англ. relativity — относительность).
Новые и удивительные свойства пространства-времени и новые законы, устанавливаемые в СТО, проявляются при больших скоростях движения — и тем ярче, чем ближе мы подходим к скорости света. В повседневной жизни мы не замечаем этих релятивистских эффектов — по той простой причине, что привычные нам скорости чрезвычайно малы по сравнению со скоростью света. Во многих практических задачах можно считать скорость света бесконечной — и тогда прекрасно работает классическая механика.
Итак, классическая механика оказывается приближённой теорией и годится для небольших скоростей. Релятивистская механика используется тогда, когда скорости тел достаточно близки к скорости света — в таких ситуациях классическая механика отказывает совершенно. Классическая механика является предельным случаем релятивистской механики: формулы классической механики получаются из релятивистских формул предельным переходом .
 |
| Рис. 1. Кажущийся парадокс со световой вспышкой |
Какие же новые свойства пространства-времени и новые физические законы открыла теория относительности? Мы будем рассказывать о них в двух следующих разделах. Здесь мы покажем лишь, что из постулатов СТО следуют весьма неожиданные и, казалось бы, парадоксальные выводы.
Рассмотрим системы отсчёта и
— те же, что и в предыдущей теме (рис. 1). В момент времени
, когда их начала
и
находятся в одной точке, в этой точке происходит световая вспышка.
Где окажется волновой фронт вспышки к моменту времени ?
В системе свет распространяется во все стороны со скоростью
. Поэтому в системе
вспышка достигнет сферы
радиуса
с центром в точке
.
В системе скорость света также равна
. Значит, в системе
вспышка достигнет сферы
того же радиуса
, но с центром в точке
.
Однако точки и
к моменту
разойдутся на расстояние
. Получается, что волновой фронт в один и тот же момент времени находится на двух разных сферах
и
. Противоречие?
Противоречия на самом деле нет. Причина кажущегося парадокса кроется в понятии одновременности. На место нашего интуитивного понимания одновременности приходит чёткое определение этого термина, даваемое в СТО.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Принципы СТО.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
Постулаты Бора
Основу квантовой теории атома Бора составляют два постулата.
Первый постулат Бора гласит: атомная система может находиться только в особых стационарных, или квантовых, состояниях, каждому из которых соответствует определенная энергия $Е_n$; в стационарном состоянии атом не излучает энергию.
Этот постулат противоречит классической механике, согласно которой энергия движущихся электронов может быть любой. Он противоречит также и электродинамике Максвелла, так как допускает возможность ускоренного движения электронов без излучения электромагнитных волн.
Второй постулат Бора: излучение света происходит при переходе атома из стационарного состояния с большей энергией $Е_k$ в стационарное состояние с меньшей энергией $Е_n$. Энергия излученного фотона равна разности энергий стационарных состояний:
$hν_{kn}=E_k-E_n$
Отсюда можно получить частоту излучения:
$ν_{kn}={E_k-E_n}/{h}={E_k}/{h}-{E_n}/{h}$
При поглощении света атом переходит из стационарного состояния с меньшей энергией в стационарное состояние с большей энергией.
Модель атома водорода Бора
Для построения модели простейшей системы — атома водорода — Бор постулировал также правило определения стационарных значений энергии атома (уровней энергии) — так называемое правило квантования.
Правило квантования орбит Бора заключается в следующем.
Стационарным состояниям атома соответствуют разрешенные дискретные значения энергии электрона, такие, что при движении по стационарным круговым орбитам электрон должен иметь дискретные значения момента количества движения:
$m_{e}υr=n{h}/{2π}, n=1,2,3…,$
где $m_{e}$ — масса электрона, $υ$ — его скорость, $r$ — радиус орбиты, $h$ — постоянная Планка, $n$ называется главным квантовым числом (является номером орбиты в спектре атома водорода, в частности).
Используя законы механики Ньютона и правило квантования, Бор вычислил допустимые радиусы орбит и значения энергии стационарных состояний. Минимальный радиус орбиты определяет размер атома (он оказался равным $0.53·10^{-10}$м). Значения энергий стационарных состояний в электронвольтах отложены на вертикальной оси. (В атомной физике энергию выражают в электронвольтах, сокращенно — эВ. $1$ эВ — это энергия, приобретаемая электроном при прохождении разности потенциалов $1$ В. $1$ эВ$ = 1.6·10^{-19}$ Дж.)
Правило квантования орбит и постулаты Бора позволили ему самому и другим ученым объяснить наблюдавшиеся закономерности в оптическом спектре излучения атома водорода, а также в рентгеновских спектрах, и дать физическое истолкование Периодического закона элементов.
Поглощение света
Поглощение света — процесс, обратный излучению, при котором атом с нижних энергетических уровней переходит на верхние уровни. При этом он поглощает излучение тех же частот, которые излучает при переходе с верхних энергетических уровней на нижние.
Гипотеза Планка о квантах
Гипотеза Планка — предположение, что атомы испускают электромагнитную энергию (свет) не непрерывно, а отдельными порциями — квантами.
Энергия каждой порции пропорциональна частоте излучения:
$E=hν,$
где $h=6.63·10^{-34}$ $Дж·с$ — постоянная Планка, $ν$ — частота света.
Постоянная Планка (квант действия) — фундаментальная физическая константа. Введена М. Планком в 1900 г. Наиболее точное значение постоянной Планка $h = 6.626176(36) · 10^{-34}$ $Дж·с$. Чаще пользуются постоянной $h={h}/{2π}=1.0545887(57)·10^{-34}$ $Дж·с$, также называемой постоянной Планка. Формула $p↖{→}={mυ↖{→}}{√{1-{υ^2}/{c^2}}$ — это вторая из простых великих формул физики (первая — формула Эйнштейна, связывающая энергию покоя тела с его массой). После открытия Планка начала развиваться квантовая теория.
Основы специальной теории относительности
Специальная теория относительности (СТО) – физическая теория, рассматривающая пространственно-временные свойства физических процессов. Закономерности СТО проявляются при больших (сравнимых со скоростью света) скоростях. Законы классической механики в этом случае не работают. Причина этого заключается в том, что передача взаимодействий происходит не мгновенно, а с конечной скоростью (скоростью света).
Классическая механика является частным случаем СТО при небольших скоростях. Явления, описываемые СТО и противоречащие законам классической физики, называют релятивистскими. Согласно СТО одновременность событий, расстояния и промежутки времени являются относительными.
В любых инерциальных системах отсчета при одинаковых условиях все механические явления протекают одинаково (принцип относительности Галилея). В классической механике измерение времени и расстояний в двух системах отсчета и сравнение этих величин считаются очевидными. В СТО это не так.
События являются одновременными, если они происходят при одинаковых показаниях синхронизированных часов. Два события, одновременные в одной инерциальной системе отсчета, не являются одновременными в другой инерциальной системе отсчета.
Содержание
- Инвариантность скорости света. Принцип относительности Эйнштейна
- Полная энергия
- Энергия покоя
- Релятивистский импульс
- Основные формулы раздела «Основы специальной теории относительности»
Инвариантность скорости света. Принцип относительности Эйнштейна
В 1905 г. Эйнштейн создал специальную теорию относительности (СТО). В основе его теории относительности лежат два постулата:
- Любые физические явления во всех инерциальных системах отсчета при одинаковых условиях протекают одинаково (принцип относительности Эйнштейна).
- Скорость света в вакууме во всех инерциальных системах отсчета одинакова и не зависит от скорости источника и приемника света (принцип постоянства скорости света).
Первый постулат распространяет принцип относительности на все явления, включая электромагнитные. Проблема применимости принципа относительности возникла с открытием электромагнитных волн и электромагнитной природы света. Постоянство скорости света приводит к несоответствию с законом сложения скоростей классической механики. По мысли Эйнштейна, изменения характера взаимодействия при смене системы отсчета не должно происходить. Первый постулат Эйнштейна непосредственно вытекает из опыта Майкельсона–Морли, доказавшего отсутствие в природе абсолютной системы отсчета. В этом опыте измерялась скорость света в зависимости от скорости движения приемника света. Из результатов этого опыта следует и второй постулат Эйнштейна о постоянстве скорости света в вакууме, который вступает в противоречие с первым постулатом, если распространить на электромагнитные явления не только сам принцип относительности Галилея, но и правило сложения скоростей. Следовательно, преобразования Галилея для координат и времени, а также его правило сложения скоростей к электромагнитным явлениям неприменимы.
Следствия из постулатов СТО
Если проводить сравнение расстояний и показаний часов в разных системах отсчета с помощью световых сигналов, то можно показать, что расстояние между двумя точками и длительность интервала времени между двумя событиями зависят от выбора системы отсчета.
Относительность расстояний:
где ( I_0 ) – длина тела в системе отсчета, относительно которой тело покоится, ( l ) – длина тела в системе отсчета, относительно которой тело движется, ( v ) – скорость тела.
Это означает, что линейный размер движущегося относительно инерциальной системы отсчета уменьшается в направлении движения.
Относительность промежутков времени:
где ( tau_0 ) – промежуток времени между двумя событиями, происходящими в одной точке инерциальной системы отсчета, ( tau ) – промежуток времени между этими же событиями в движущейся со скоростью ( v ) системе отсчета.
Это означает, что часы, движущиеся относительно инерциальной системы отсчета, идут медленнее неподвижных часов и показывают меньший промежуток времени между событиями (замедление времени).
Закон сложения скоростей в СТО записывается так:
где ( v ) – скорость тела относительно неподвижной системы отсчета, ( v’ ) – скорость тела относительно подвижной системы отсчета, ( u ) – скорость подвижной системы отсчета относительно неподвижной, ( c ) – скорость света.
При скоростях движения, много меньших скорости света, релятивистский закон сложения скоростей переходит в классический, а длина тела и интервал времени становятся одинаковыми в неподвижной и движущейся системах отсчета (принцип соответствия).
Для описания процессов в микромире классический закон сложения неприменим, а релятивистский закон сложения скоростей работает.
Полная энергия
Полная энергия ( E ) тела в состоянии движения называется релятивистской энергией тела:
Полная энергия, масса и импульс тела связаны друг с другом – они не могут меняться независимо.
Закон пропорциональности массы и энергии – один из самых важных выводов СТО. Масса и энергия являются различными свойствами материи. Масса тела характеризует его инертность, а также способность тела вступать в гравитационное взаимодействие с другими телами.
Важно!
Важнейшим свойством энергии является ее способность превращаться из одной формы в другую в эквивалентных количествах при различных физических процессах – в этом заключается содержание закона сохранения энергии. Пропорциональность массы и энергии является выражением внутренней сущности материи.
Энергия покоя
Наименьшей энергией ( E_0 ) тело обладает в системе отсчета, относительно которой оно покоится. Эта энергия называется энергией покоя:
Энергия покоя является внутренней энергией тела.
В СТО масса системы взаимодействующих тел не равна сумме масс тел, входящих в систему. Разность суммы масс свободных тел и массы системы взаимодействующих тел называется дефектом масс – ( Delta m ). Дефект масс положителен, если тела притягиваются друг к другу. Изменение собственной энергии системы, т. е. при любых взаимодействиях этих тел внутри нее, равно произведению дефекта масс на квадрат скорости света в вакууме:
Экспериментальное подтверждение связи массы с энергией было получено при сравнении энергии, высвобождающейся при радиоактивном распаде, с разностью масс исходного ядра и конечных продуктов.
Это утверждение имеет разнообразные практические применения, включая использование ядерной энергии. Если масса частицы или системы частиц уменьшилась на ( Delta m ), то при этом должна выделиться энергия ( Delta E=Delta mcdot c^2 ).
Кинетическая энергия тела (частицы) равна:
Важно!
В классической механике энергия покоя равна нулю.
Релятивистский импульс
Релятивистским импульсом тела называется физическая величина, равная:
где ( E ) – релятивистская энергия тела.
Для тела массой ( m ) можно использовать формулу:
В экспериментах по исследованию взаимодействий элементарных частиц, движущихся со скоростями, близкими к скорости света, подтвердилось предсказание теории относительности о сохранении релятивистского импульса при любых взаимодействиях.
Важно!
Закон сохранения релятивистского импульса является фундаментальным законом природы.
Классический закон сохранения импульса является частным случаем универсального закона сохранения релятивистского импульса.
Полная энергия ( E ) релятивистской частицы, энергия покоя ( E_0 ) и импульс ( p ) связаны соотношением:
Из него следует, что для частиц с массой покоя, равной нулю, ( E_0 ) = 0 и ( E=pc ).
Основные формулы раздела «Основы специальной теории относительности»
Основы специальной теории относительности
3 (59.27%) 218 votes
Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.
Все материалы доступны по лицензии Creative Commons — «Attribution-NonCommercial»
Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.
Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.
Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.
© 2014-2023 Все права на дизайн сайта принадлежат С.Є.А.
1. Какой тип ответа: расчёт физической величины.
2. Какова структура содержания задания: физическая задача из разделов физики «Основы специальной теории относительности» и «Квантовая физика».
3. Какой уровень сложности задания: базовый.
4. Как оценивается задание: правильный ответ на задание оценивается (1) баллом (задание считается выполненным верно, если правильно указаны требуемые число или два числа).
Пример:
рассчитай импульс электрона, если его длина волны равна (10^{-8}) см. (Ответ представь в виде (p · 10^{24}).)
Как решить задание из примера?
| Дано | Решение |
|
(lambda = 10^{-8})(=) (= 10^{-10}) см; (h = 6,6 · 10^{-34}) Дж · с |
1. Физическая модель задачи: — свойство корпускулярно-волнового дуализма для объяснения поведения объектов в квантовой физике. 2. Физический закон: — длина волны де Бройля движущейся частицы (lambda = frac{h}{p}). ((1)) 3. Математическое решение задачи: — выразим импульс из формулы ((1)): (p_e = frac{h}{lambda}); ((2)) — проверим размерность формулы ((3)): ([p_e] = frac{Дж · с}{м} = frac{Н · м · с}{м} = frac{кг · м · с}{с^2} = кг · м/с); — проводим вычисления: (p_e · 10^{24} = frac{6,6 · 10^{-34} · 10^{24}}{10^{-10}} = 6,6) м |
| Найти: (p_e) | Правильный ответ: (6,6) м |
| Типичные ошибки |
1. Обрати внимание на математические действия со степенями |
Какова форма ответа: запиши в бланк ответов № (1) целое число или
конечную десятичную дробь без указания единиц измерения физических величин (без пробелов; каждый символ — цифра, запятая, «(-)», «(+)» — пишутся в отдельной клеточке).
Ответ: (6,6).