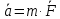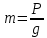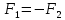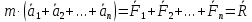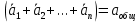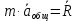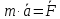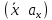Билет
№1.
-
Векторный
способ задания движения точки.
Траектория, скорость, ускорение точки. -
Эквивалентность
пар. Сложение пар. Условие равновесия
системы пар сил.
1.
Векторная система координат.
Положение
точки М определено, если радиус-вектор
r
из центра
О выражен функцией времени t
r=
r(t)
задан способ определения модуля
вектора и его направления, если имеется
система координат. Скорость и ускорение:
tr(t),
тогда
(t+Δt)r(t+Δt),
получаем
Δr=
r(t+Δt)-r(t)
Vср=Δr/Δt.
V=lim(Δr/Δt)=dr/dt.
aср=ΔV/Δt.
a=lim(Δv/Δt)=dV/dt=
d²r(t)/dt².
Переход
от векторной формы к координатной:
r(t)=x(t)i+y(t)j+z(t)k.
Обратно:
x=r(t)×i,
y=r(t)×j,
z=r(t)×k.
2.
Эквивалентность пар. Сложение пар.
Условия равновесия пар сил.
Эквивалентность:
А) 2 пары, имеющие равные моменты,
эквивалентны. Пару сил можно перемещать,
поворачивать в плоскости действия,
перемещать в параллельную плоскость,
менять одновременно силу и плечо.
Б)
2 пары, лежащие в одной плоскости, можно
заменить на одну пару, лежащую в той
же плоскости с моментом, равным сумме
моментов этих пар.
M=M(R,R’)=BA×R=BA×(F1+F2)=BA×F1+BA×F2.
При
переносе сил вдоль линии действия
момент пары не меняется
BA×F1=M1,
BA×F2=M2,
M=M1+M2.
СЛОЖЕНИЕ.
2 пары, лежащие в пересекающихся
плоскостях, эквивалентны 1 паре, момент
которой равен сумме моментов двух
данных пар.
Дано:
(F1,
F1’),
(F2,
F2’)
Доказательство:
Приведем
данные силы к плечу АВ – оси пересечения
плоскостей. Получим пары:
(Q1,Q1’)
и (Q2,Q2’).
При этом M1=M(Q1,Q1’)=M(F1,
F1’),
M2=M(Q2,Q2’)=M(F2,
F2’).
Сложим
силы R=Q1+Q2,
R’=Q1’+Q2’.
Т.
к.
Q1’=
—
Q1,
Q2’=
—
Q2
R=
—R’.
Доказано,
что
система
двух
пар
эквивалентна
системе
(R,R’).
M(R,R’)=BA×R=BA×(Q1+Q2)=
BA×Q1+BA×Q2=M(Q1,Q1’)+
M(Q2,Q2’)=M(F1,F1’)+
M(F2,F2’)
M=M1+M2.
УСЛОВИЯ
РАВНОВЕСИЯ:
Система
находится в равновесии, если суммарный
момент всех пар сил, действующих на
тело, равен нулю.
M1+
M2+…+
Mn=0.
Билет
№2.
-
Координатный
способ задания движения точки
(прямоугольная декартова система
координат). Траектория, скорость,
ускорение точки. -
Аксиомы
статики.
1.
Декартова система координат.
Вектор
r
можно разложить по базису I,
j,
k:
r=xi+yj+zk.
Движение
материальной точки полностью определено,
если заданы три непрерывные и однозначные
функции от времени t:
x=x(t),
y=y(t),
z=z(t),
описывающие изменение координат точки
со временем. Эти уравнение называются
кинематическими уравнениями движения
точки. Радиус-вектор r
является функцией переменных x,
y,
z,
которые, в свою очередь, являются
функциями времени t.
Поэтому производная r׳(t)
может быть вычислена по правилу
dr/dt=∂r/∂x∙dx/dt+∂r/∂y∙dy/dt+∂r/∂z∙dz/dt.
Отсюда
вытекает, что v=vxi+vyj+vzk.
V=√(vx²+vy²+vz²)
Ускорением
точки в данный момент времени назовем
вектор а,
равный производной от вектора скорости
v
по времени. А=x׳׳(t)I+y׳׳(t)j+z׳׳(t)k.
А=√((x׳׳(t))²+(y׳׳(t))²+(z׳׳(t))²)
2.
Аксиомы статики.
-
2
силы, приложенные к абс. твердому телу
будут эквивалентны 0 тогда и только
тогда, когда они равны по модулю,
действуют на одной прямой и направлены
в противоположные стороны. -
Действие
данной системы сил на абсолютно
твердое тело не изменится, если к ней
добавить или отнять систему сил,
эквивалентную 0 => точку приложения
силы можно переносить вдоль линии её
действия. -
Если
к телу приложены 2 силы, исходящие из
одной точки, то их можно заменить
равнодействующей (любую силу можно
разложить на составляющие бесконечное
число раз). -
Силы
взаимодействия двух тел равны по
модулю и противоположны по направлению.
Действие
связей можно заменить действием сил
– реакций связи.
Билет
№3.
-
Естественный
способ задания движения точки.
Траектория, скорость, ускорение точки. -
Алгебраический
и векторный момент силы относительно
точки.
1.
Естественный способ.
Если
задана траектория движения точки,
выбрано начало и положительное
направление отсчета и известна S=S(t)
зависимость пути от времени, то такой
способ задания движения точки называется
естественным. V=dr/dt∙dS/dS=S׳(t)∙dr/dS=S׳(t)∙τ=
=vτ∙τ.
Dr/dS=τ.
Τ
направлена всегда в «+» направлении
отсчета S.
A=dv/dt=S׳׳(t)∙τ+S׳(t)∙dτ/dt=S׳׳∙τ+
(S׳)²n/ρ.
Aτ=S׳׳-тангенциальное
ускорение, an=(S׳)²/ρ-нормальное
(центростремительное) ускорение,
ρ-радиус кривизны.
A=√((aτ)²+(an)²).
2.
Векторный и алгебраический момент
пары сил.
Алгебраический
момент M=F∙d
(пара). M=dF1=dF2=2SΔABC=
Sٱ.
Он не
меняется при перемещении сил вдоль
линии их действия (ни плечо, ни
направление вращения не меняются).
Векторный
момент – вектор M=M(F,F’),
направлен перпендикулярно плоскости
пары в ту сторону, откуда видно
стремление пары повернуть тело против
часовой хода стрелки, его модуль равен
алгебраическому моменту пары.
M(F1,F2)=BAxF1=ABxF2.
Моменты
относительно точки.
Алгебраическим
моментом силы F
относительно точки О называется взятое
со знаком «+» или «-» произведение |F|
на её плечо: MO(F)=Fh=2SΔOAB
∙ MO(F).
«+» — против часовой стрелки. Характеризует
вращательный эффект F.
Свойства:
А)
Не меняется при переносе точки
приложения вдоль линии действия силы.
(т.к. |F|sinα=
const).
Б)
Ь=0 если т. О лежит на линии действия
силы.
Плоскость
действия M
– через F
и O.
Векторный
момент силы F
относительно точки О – вектор MO(F)=rxF
(r
– радиус- вектор из А в О).
|MO(F)|=|F|∙|r|∙sinα=Fh.
i
j
k
MO(F)=
xA
yA
zA
=>
Fx
Fy
Fz
-
MOx(F)=yFz-zFy
-
MOy(F)=zFx-xFz
MOz(F)=xFy-yFx
Билет
№4.
-
Координатный
способ задания движения точки (полярная
система координат). Траектория,
скорость, ускорение точки. -
Пара
сил. Теорема о сумме моментов сил,
составляющих пару, относительно
произвольной точки.
1.
Полярные координаты
Ox
– полярная ось, φ – полярный угол, r
– полярный радиус. Если задан закон
r=r(t),
φ=φ(t),
то задано движение в полярной системе
координат. Пусть r=rºr,
rº
— единичный вектор, pº┴rº
— единичный
вектор. Тогда v=dr/dt=r׳rº+
rdrº/dt=r׳rº+rφ׳pº=vrrº+vppº.
vp
и vr
– трансверсальная и радиальная
составляющая скорости. A=dv/dt=d(r׳rº+rφ׳pº)/
dt=r׳׳rº+r׳drº/dt+r׳φ׳pº+rφ׳׳pº+rφ׳∙
dpº/dt=(r׳׳-(rφ׳)²)rº+(rφ׳׳+2r׳φ׳)pº=
ar∙rº+appº.
r²=x²+y²,
φ=arctg(y/x).
vr=r׳=(xvx+yvy)/r,
vp=rφ׳=(xvy-yvx)/r
2.
Т. о приведении произвольной системы
сил к силе и паре сил.
Теорема
Пуассо: Произвольная система сил,
действующих на твердое тело, можно
привести к какому-либо центру О, заменив
все действующие силы главным вектором
системы сил R,
приложенным к точке О, и главным
моментом MO
системы сил относительно точки О.
Доказательство:
Пусть
О – центр приведения. Переносим силы
F1,
F2,…,Fn
в точку О: FO=
F1
+F2+…+Fn=
∑Fk.
При этом получаем каждый раз
соответствующую пару сил (F1,F1”)…(Fn,Fn”),
Моменты этих пар равны моментам этих
сил относительно точки О.
M1=M(F1,F1”)=r1xF1=MO(F1).
На основании правила приведения систем
пар к простейшему виду MO=M1+…+M2=∑MO(Fk)=
∑rkxFk
=> (F1,
F2,…,Fn)
~ (R,MO)
(не зависит от выбора точки О).
Билет
№5.
-
Определение
скорости точки при задании ее движения
в криволинейных координатах. -
Момент
силы относительно оси.
1.
Скорость точки в криволинейных
координатах.
V=dr/dt=(∂r/∂q1)∙dq1/dt+(∂r/∂q2)∙dq2/dt+(∂r/∂q3)∙dq3/dt.
v=(dq1/dt)H1e1+(dq2/dt)H2e2+(dq3/dt)H3e3.
v=√(dq1/dt)²H1²+(dq2/dt)²H2²+(dq3/dt)²H3².
vq1=(dq1/dt)H1,
vq2=(dq2/dt)H2,
vq3=(dq3/dt)H3.
Пример:
1) скорость в цилиндрической системе.
Т.к.
x=ρcosφ,
y=ρsinφ,
z=z,
то
H1=1,
H2=ρ,
H3=1.
vρ=dρ/dt,
vφ=ρdφ/dt,
vz=dz/dt.
2)
Движение по винтовой.
ρ=R=const,
φ=kt,
z=ut.
vρ=0,
vφ=kR,
vz=u.
2.
Момент силы относительно оси.
Момент
силы относительно оси – алгебраический
момент проекции этой силы на ось,
перпендикулярную оси z,
взятого относительно точки A
пересечения оси с этой плоскостью.
Характеризует вращательный эффект
относительно оси.
Mz(F)=2SΔABC=F┴∙h.
Если
Mz(F)=0,
то сила F
либо параллельна оси z,
либо линия её действия пересекает ось
z.
Билет
№6.
-
Понятие
о криволинейных координатах.
Координатные линии и координатные
оси. -
Основные
виды связей и их реакции.
1.
Криволинейные координаты.
Устанавливают
закон выбора 3 чисел q1,
q2,
q3.
q1,
q2,
q3
– криволинейные координаты. Функция
координат: r=r(q1,q2,q3)
(из точки О).
Возьмем
точку М0
с координатами q1,q10,q20.
X=X(q1,q20,q30);
Y=Y(q1,q20,q30);
Z=Z(q1,q20,q30);
Определяют
кривую (переменная только q1).
Кривая – координатная линия,
соответствующая изменению q1
(аналогично q2
и q3).
Касательные к координатным линиям,
проведенные в точке M0
в сторону возрастания соответствующих
координат – координатные оси: [q1],
[q2],
[q3].
H1=
Коэффициент
Ламе.
e1=(∂r/∂q1)/H1.
Аналогично
Н2,
Н3,
е2,
е3.
2.
Виды связей и их реакции.
Связи
– ограничения, накладываемые на
свободное твердое тело (занимает
произвольное положение в пространстве).
Реакция связи направлена в сторону,
противоположную той, куда связь не
дает перемещаться телу.
-
Гладкая
поверхность – по общей нормали. -
Нить
– вдоль к точке закрепления. -
Сферический
шарнир – по любому радиусу. -
Сферический
шарнир – по любому радиусу. -
Подпятник,
подшипник – любое направление.
Дополнительно:
А)
Скользящий;
Б)
Внутренний.
Билет
№7.
-
Число
степеней свободы твердого тела в
общем и частных случаях его движения. -
Лемма
о параллельном переносе силы.
1. Число степеней
свободы твердого тела
n=3N-k,
где n-число
степеней свободы, N-число
точек, к-число связей. n
=6-для свободного тв.тела
Для
тела, кот-е совершает сферич.дв-е
достаточно 3 коор-ты, поскольку оно
имеет 3 степени свободы.
2.
Лемма о параллельном переносе силы.
Сила,
приложенная к какой-либо точке твердого
тела, эквивалентна такой же силе,
приложенной к любой другой точке тела,
и паре сил, момент которой равен моменту
данной силы относительно новой точки
приложения.
Доказательство:
пусть дана сила F.
Приложим к какой-либо точке В систему
F’
и F”.
|F|=|F’|=|F”|.
F~(F,F’,F”),
т.к. (F’,F”)
~ 0, то
F
~ (F,F’,F”)
~ (F,F’,F”)
~ (F’,M(F,F”)).
Но
M(F,F”)=BAxF=MB(F).
Получаем:
F
~ (F’,M(F,F”))
Ч.
т.
д.
Билет
№8.
-
Поступательное
движение твердого тела. Число степеней
свободы, уравнения движения. Скорости
и ускорения точек тела. -
Связь
векторного момента силы относительно
точки с моментом силы относительно
оси, проходящей через эту точку.
1.
Поступательное движение.
Существует
5 видов движения – поступательное,
вращательное вокруг неподвижной оси,
плоское (плоскопараллельное),
сферическое, общий случай. Поступательное
движение твердого тела – движение,
при котором любая прямая этого тела
при движении остается параллельной
самой себе.
Траектории
любой точки тела, совершающего
поступательное движение, одинаковы.
Радиус
– вектор любой точки движущегося
поступательно тела равен rB=rA+AB,
AB=const.
drB/dt=drA/dt+
dAB/dt=drA/dt
=> vB=vA,
aB=aA
2.
Связь между моментом относительно
оси и относительно точки.
Момент
силы F
относительно оси z
равен проекции на эту ось вектора
момента силы F
относительно
произвольной точки О на этой оси.
Доказательство:
Пусть
О – произвольная точка на оси z.
Момент силы F
относительно точки О перпендикулярен
плоскости ОАВ
MO(F)┴(OAB).
Пусть угол между
MO(F)
и осью z
равен α. Тогда ПрzMO(F)=2SΔO’A’B’=
2SΔOAB∙cosα
=> Mz(F)
= |MO(F)|cosα.
Ч.т.д.
Билет
№9.
-
Вращение
твердого тела вокруг неподвижной
оси. Векторные и скалярные формулы
для скоростей и ускорений точек тела. -
Теорема
о приведении произвольной системы
сил к силе и паре – основная теорема
статики.
1.
Вращение вокруг неподв. оси.
φ=φ(t)
– угол поворота, n=1
степень свободы. Для задания вращения
вокруг неподвижной оси необходимо
выбрать ось, начало отсчета угла
поворота и его положительное направление
и задать зависимость угла поворота
от времени. ω=dφ/dt
– угловая скорость. ε=dω/dt=
d²φ/dt²
— угловое ускорение. Скорость любой
точки тела, не лежащей на оси v=ωxr,
ускорение a=dv/dt=(dω/dt)xr+
ωxdr/dt=εxr+ωx(ωxr),
где aτ=εxr
Частные
случаи: 1) ω=const
– равномерное вращение (φ=φº+ωt
). 2) ε=const
– равноускоренное вращение (ω=ωº+εt,
φ=φº+ωt+
εt²/2)
2. Основная
теорема статики (теор. Пуансо):
При
приведении системы сил к заданому
центру возникает главный вектор R
равный сумме всех сил и главный момент
Мо,
равный сумме моментов всех сил
относительно центра приведения.
R=Fk
Lo=Mo(Fk)
Билет
№10.
-
Плоское
движение твердого тела. Уравнения
плоского движения. Разложение плоского
движения на поступательное движение
вместе с полюсом и вращательное вокруг
оси, проходящей через полюс. -
Инварианты
системы сил. Частные случаи приведения
системы сил к простейшему виду.
2.
Инварианты системы сил. Частные случаи
приведения.
Инвариант
системы сил – векторные и скалярные
величины, не зависящие от точки
приведения системы сил.
-
Главный
вектор R=∑Fi=const. -
Скалярное
произведение главного вектора и
главного момента LOR=const=FxMx+
FyMy+FzMz.
Доказательство:
Умножим обе части выражения (1) на R:
MO1R=
MOR+(O1OxR)R
ПрR(LO1)=
ПрR(LO)=
LO1R∙
∙cos(LO1^R)=
LO2Rcos(LO2^R).
LO1xRx+
LO1yRy
+LO1zRz
=LO2xRx
+LO2yRy
+LO2zRz
Приведение к
простейшему виду:
-
MO=0,
R0
к равнодействующей, равной R,
проходящей через О. -
R=0,
MO0
к паре с моментом MO
(независимо
от О).
R0,
MO0,
MO┴
R
к
равнодействующей, равной R,
проходящей через О1:
ОО1=d=
|MO|
/ |R|.
Доказательство: R
и пара сил с моментом MO
лежат в одной плоскости
силы
R
и R”
уравновешиваются, систему можно
заменить равнодействующей R’.
-
MOR0,
R0,
MO0,
R
не перпендикулярна MO
– приводится к динаме.
Доказательство:
Разложим MO
на 2 составляющих: M1
и M2.
M2
представим в виде пары сил R’
и R”.
Силы R
и R”
уравновешиваются, а M1
перенесем в точку O1
(свободы).
В
результате получили винт R’,
M1,
проходящий через точку О1.
Прямая,
проходящая через точку О1
– ось динамы.
Билет
№11.
-
Соотношение
между ускорениями двух точек плоской
фигуры при плоском движении твердого
тела. -
Равновесие
тела с учетом трения скольжения.
Законы Кулона.
1.
Соотн. между уск. 2-х точек при плоском
движении.
vB=vA+ωxAB.
aB=dvB/dt=dvA/dt+(dω/dt)xAB+
ωx(dAB/dt)=aA+εxAB+ωx(ωx
AB).
Считая,
что εхАВ=(aBA)τ;
(aBA)n=ω²∙AB,
окончательно получим:
aB=aA+(aBA)τ+(aBA)n
aA
– ускорение
полюса;
aBA
– ускорение движения вокруг полюса.
2.
Сила трения скольжения.
Законы
Кулона для Fтр.ск.:
1)Сила
трения скольжения лежит в интервале
0
Fтр
Fмах;
2) Сила трения
скольжения не зависит от площади
соприкасающихся тел, а зависит лишь
от силы давления этого тела на
поверхность
3)Сила
тр.скольжения опр-ся по ф-ле: Fтр=fN,
N-сила
реакции опоры =Р, f-коэф-т
трения скольжения
4)Коэф-т трения
скольжения завис.от шероховатостей
пов-тей трущихся тел, от температуры,
от физич.состояния материала.
Билет
№12.
-
Мгновенный
центр скоростей, способы нахождения
МЦС. -
Равновесие
тела с учетом трения качения. Коэффициент
трения качения.
1.
МЦС. Способы нахождения.
При
плоском движении твердого тела в
каждый момент времени существует
точка, скорость которой равна нулю.
vP=vO+vPO=0,
vO=ω∙OP=>OP=
vO/ω.
Способы
нахождения:
-
на
основе физического условия задачи. -
На
основе предваритель-ного определения
скорости двух точек.
2.
Трение качения. Коэффициент трения
качения.
Круглое
тело вдавливается в опорную поверхность
(дуга CD).
Трение качения – сопротивление,
возникающее при качении одного тела
по поверхности другого. Полная реакция
N’
опорной поверхности препятствует
качению.
Нам
нужен момент сопротивления качению
=> заменим N’
и представим в виде Fтр.
и N,
приложенных в точке В,
смещенной от центра на δ. Условия
равновесия: N=P,
F=Q.
QmaxR=δN.
Mтр.max=δ∙N.
Момент сопротивления качению 0<Mк<Mк.max
(не зависит от радиуса). Коэффициент
трения качения δ при предельном
состоянии равновесия (при Qmax)
N
(сила нормального давления) отстает
на δ от вертикального радиуса. δ не
зависит от материала, из которого
сделано тело. Определяется
экспериментально.
Билет
№13.
-
Вращение
твердого тела вокруг неподвижной
точки. Число степеней свободы, углы
Эйлера. -
Условия
равновесия произвольной системы сил
в векторной и аналитической формах.
Частные случаи.
1.
Вращение твердого тела вокруг
неподвижной точки. Углы Эйлера.
Движение
твердого тела, у которого одна точка
неподвижна, называется сферическим.
Количество степеней свободы n=3.
(XA,
YA,
ZA).
Положение
тела определяется с помощью углов
Эйлера. Определение: свяжем с телом
подвижную систему координат Oxyz.
Плоскость xOy
пересекает неподвижную плоскость
x1Oy1
по прямой ОК – линии узлов.
Ψ
– угол прецессии;
φ
– угол собственного вращения
θ
– угол нутации.
Все
углы против часовой стрелке.
Если
заданы функции Ψ=f1(t);
φ=f2(t);
θ=f3(t)
то движение полностью определено.
2. Условия
равновесия для произвольной
простр.системы сил, а также следствия
из этих уравнений.
R=0
и Lo=0
–ур-я равновесия. Им соотв-ют 6 скалярных
алгебраических ур-1 равновесия для
простр.системы сил:
Fkх=0
Fkу=0
Fkz=0
Мх(Fk)=0
Му(Fk)=0
Мz(Fk)=0
– аналитическое условие равновесия
для произвольной системы сил.
Пусть
все силы
пл-ти хоу, тогда: Fkх=0
Fkу=0
Мо(Fk)=0
условие равновесия для произвольной
плоской системы сил.
Условие
равновесия
для плоской системы параллельных
сил.
Пустьсилы
оси оу, тогда Fkх=0
Мо(Fk)=0
Условие
равновесия
для пространственной системы
параллельных
сил.
F1,
F2,
F3,…,Fn
оси оz,
тогда: Fkz=0
Мх(Fk)=0
Му(Fk)=0
Вторая
форма
условия равновесия для пороизвольной
плоской системы сил:
МА(Fk)=0
МВ(Fk)=0
МС(Fk)=0
– причем т.А, т,В, т.С
одной прямой.
— Докажем
необходимость этих условий:
Допустим,
система сил нах-ся в равновесии. Тогда
очевидно, что
моментов всех сил относительно любой
точки пл-ти=0, т.е. выполняются эти 3
условия.
— Докажем
достаточность этих условий:
Доказать
достоточность – это значит доказать,
что при выполнении этих усл-й система
нах-ся в равновесии. Доказывать будем
методом от противного, поэтому
предположим, что эти усл-я выполняются,
но система не нах-ся в равновесии, т.е.
существует R*0
эквив.данной сист.сил.
Рассмотрим
усл-е первое и 2-е: для того, чтобы они
выполнялись необходимо, чтобы R*
проходил через т.А и т.В. Согласно
третьему условию hR=0.
Поскольку т.С
прямой АВ это может выполняться только
в случае R*=0,
т.е. наше предположение не верно и
система действительно нах-ся в
равновесии.
Третья
форма усл-я равновесия
для произвольной плоской системы сил.
Fkz=0
МА(Fk)=0
МВ(Fk)=0
– причем ось ох не перпендикулярна
АВ.
— Необходимость
этого усл-я очевидна, т.к.если система
нах-ся в равновесии, то главный вектор
и главный момент =0 относительно любой
точки.
— Докажем
достаточность этих условий:
Предположим,
что система не нах-ся в равновесии и
сущ-ет, т.е. сущ-ет R*
и R*
0
является равнодействующей данной
системы сил. Для того, чтобы выполнялось
усл-е 2 и 3 необходимо, чтобы R*
проходил через АВ.
Потребуем
выполнения усл-я R*cos=0,
поскольку х не перпендикулярна АВ ,
то R*
должно быть равно 0, т.о. мы доказали,
что эти усл-я достаточны для того чтобы
система находилась в равновесии.
На основании двух
изложенных форм ур-й равновесия для
плоской системы параллельных сил
можно записать еще один вид ур-я
равновесия для плоской системы
параллельных сил:
МА(Fk)=0
МВ(Fk)=0,
АВ не параллельна F1,
F2,
F3,…,Fn
Билет
№14.
-
Определение
скоростей точек плоской фигуры с
помощью МЦС. -
Теорема
Вариньона о моменте равнодействующей
силы. Пример применения: распределенные
силы.
1.
Опред. v
2-х точек с пом. МЦС.
Зная
положение МЦС и скорость какой-либо
точки фигуры, можно найти скорости
всех точек плоской фигуры. Пусть P
– МЦС и известна скорость какой-либо
точки фигуры vА,
тогда ω= vА/AP.
vB=
vАPB/PA.
Соединив конец вектора vB
с точкой Р, получим распределение
скоростей вдоль отрезка РВ.
2.
Теорема Вариньона.
Если
данная система сил имеет равнодействующую,
то момент равнодействующей относительно
произвольной точки О равен сумме
моментов относительно той же точки.
Пусть
система сил (F1,
F2,…,Fn)
приводит к равнодействующей R,
проходящей через точку С пересечения
линий действия сил. Возьмем произвольную
точку О, тогда:
MO(R)=rxR=rx∑Fi=∑(rxFi)=
∑MOi(Fi).
Ч.
т. д..
Билет
№15.
-
Мгновенный
центр ускорений. Частные случаи. -
Лемма
о параллельном переносе силы.
1.
МЦУ. Способы нахождения.
МЦУ
– точка плоской фигуры, ускорение
которой в данный момент времени равно
нулю.
aQ=aA+aAQ=0.
Угол между aQA
и QA
tgα=aBAτ/aBAn=ε/ω²,
aAQ=√aAQτ+aAQn=AQ√
ε²+ω4
1
способ нахождения МЦУ:
Отложить
от точки А под углом α=arctg(ε/ω²)
к aA
отрезок AQ=aA/√(ε²+ω4
в направлении круговой стрелки ε.
2
способ нахождении МЦУ основан на
условии задачи – если ускорение
какой-либо точки по условию задачи
равно нулю, то эта точка является МЦУ.
2.
Лемма о параллельном переносе силы.
Сила,
приложенная к какой-либо точке твердого
тела, эквивалентна такой же силе,
приложенной к любой другой точке тела,
и паре сил, момент которой равен моменту
данной силы относительно новой точки
приложения.
Доказательство:
пусть дана сила F.
Приложим к какой-либо точке В систему
F’
и F”.
|F|=|F’|=|F”|.
F~(F,F’,F”),
т.к. (F’,F”)
~ 0, то
F
~ (F,F’,F”)
~ (F,F’,F”)
~ (F’,M(F,F”)).
Но
M(F,F”)=BAxF=MB(F).
Получаем:
F
~ (F’,M(F,F”))
Ч.
т.
д.
Билет
№16.
-
Векторные
и скалярные формулы для скоростей и
ускорений точек тела при его вращении
вокруг неподвижной точки. -
Аналитическое
выражение для моментов силы относительно
осей координат.
1.
Скорости и ускорения точек тела при
его вращении вокруг неподвижной точки.
VA=ω×rA.
Пусть точка М лежит на мгновенной оси
вращения.
i
j k
VM=ω×rM=
ωx
ωy
ωz
XM
YM
ZM
X/ωx=Y/ωy=Z/ωz
– мгновенная ось вращения.
aA=dv/dt=dω/dt×rA+ω×drA/dt=ε×rA+ω×vA=aAвр+aAос.
aAвр=
ε×rA
– вращательное ускорение точки.
aAос=
ω×vA
– осестремительное ускорение точки.
Формула
Ривальса: aAoc=ωvAsin(ω,
vA).
aвр
направлен перпендикулярно плоскости
(ε,r)
в сторону, откуда переход от ε к r
виден против часовой стрелки.
aвр
направлен по перпендикуляру к плоскости
(ω,v).
2.
Аналитические выражения для моментов
силы относительно осей координат.
i
j k
MO(F)=
xA
yA
zA
=>
Fx
Fy
Fz
-
MOx(F)=yFz-zFy
-
MOy(F)=zFx-xFz
MOz(F)=xFy-yFx
Билет
№17.
-
Свободное
движение твердого тела. Скорости и
ускорения его точек. -
Связь
векторного момента силы относительно
точки с моментом силы относительно
оси, проходящей через эту точку.
1.
Скорости и ускорения точек тела при
его свободном движении.
Разложение
общего вида движения на поступательное,
связанное с точкой О и вращательное
относительно О.
Поступательное:
X1o=f1(t);
Y1o=f2(t);
Z1o=f3(t).
Вращательное:
Ψ=f4(t);
φ=f5(t);
θ=f6(t).
Таким
образом, число степеней свободы при
свободном движении твердого тела
равно 6.
ρA=ρо+rvA=dρ/dt+dr/dt=vo+ω×r.
aA=dvA/dt=dvo/dt+dω/dt×r+ω×dr/dt=ao+ε×r+ω²r=
ao+aAвр+aAос.
2.
Связь между моментом относительно
оси и относительно точки.
Момент
силы F
относительно оси z
равен проекции на эту ось вектора
момента силы F
относительно
произвольной точки О на этой оси.
Доказательство:
Пусть
О – произвольная точка на оси z.
Момент силы F
относительно точки О перпендикулярен
плоскости ОАВ
MO(F)┴(OAB).
Пусть угол между
MO(F)
и осью z
равен α. Тогда ПрzMO(F)=2SΔO’A’B’=
2SΔOAB∙cosα
=> Mz(F)
= |MO(F)|cosα.
Ч.т.д.
Билет
№18.
-
Сложное
движение точки. Основные понятия и
определения. Примеры. -
Центр
системы параллельных сил. Формулы
для радиуса-вектора и координат центра
системы параллельных сил.
1.
Сложное движение точки. Основные
понятия.
Сложное
движение – движение по отношению к
системе координат, выбранной за
основную (абсолютную).
Относительное
движение – движение точки по отношению
к подвижной системе координат.
Переносное
движение – движение подвижной системы
координат относительно неподвижной.
Установление связи между этими
движениями позволяет решать различные
задачи.
2.
Центр системы параллельных сил. Формула
для радиус-вектора и координат центра
системы параллельных сил.
Дано
: F1
|| F2
.
R=F1+F2.
MC(R)=MC(F1)+MC(F2)=0
F1∙CA1=F2∙CA2.
Повернем F1
и F2
на угол α, при этом R
повернется тоже на угол α. С – центр
параллельных сил.
То
же самое, если сил несколько и не по
одной прямой. R=∑Fi,
R||Fi
(точка С принадлежит R)
MO(R)=∑MO(Fi),
rC×R=∑(ri×Fi).
Введем
единичный вектор e
Fk=Fk∙e
R=∑Fk∙e.
rC×∑Fi∙e=∑ri×(Fi∙e).
∑FirC×e=∑Firi×e.
(∑FirC-∑Firi)×e=0
rC=∑Firi/∑Fi.
Координаты
центра системы параллельных сил:
XC=∑Fixi/R;
YC=∑Fiyi/R;
ZC=∑Fizi/r
Билет
№19.
-
Сложное
движение точки. Теорема о сложении
скоростей. Примеры. -
Центр
тяжести тела. Методы нахождения центра
тяжести.
1.
Сложное движение точки. Основные
понятия.
Сложное
движение – движение по отношению к
системе координат, выбранной за
основную (абсолютную).
Относительное
движение – движение точки по отношению
к подвижной системе координат.
Переносное
движение – движение подвижной системы
координат относительно неподвижной.
Установление связи между этими
движениями позволяет решать различные
задачи.
Центр
тяжести тела. Методы нахождения центра
тяжести.
Центр
тяжести – центр системы параллельных
сил тяжести частиц тела. Его радиус-вектор
rC=∑Piri/P.
XC=∑Pixi/P;
Yc=∑Piyi/P;
ZC=∑Pizi/P
Вес
тела P=∑Pi,
Pi
– сила тяжести частицы.
Методы
определения координат центра тяжести
тела.
-
Свойства
симметрии: если тело имеет плоскость,
ось или центр симметрии, то центр
тяжести лежит на них. -
Разбиение:
Если известны центры тяжести отдельных
частей тела, то
rC=(V1rC1+V2rC2+…+VnrCn)/V
Отрицательные
массы:
rC=VсплrC-V1rC1-…-VnrCn,
где Vk,
rCk
– объемы и радиус-векторы пустот тела.
-
Интегрирование:
если тело нельзя разбить)
XC=(∫xdV)/V,
YC=(∫ydV)/V,
ZC=(∫zdV)/V
Билет
№20.
-
Сложное
движение точки. Теорема о сложении
ускорений – теорема Кориолиса.
Ускорение Кориолиса. -
Лемма
о параллельном переносе силы.
1.
Сложное движение точки. Основные
понятия.
Сложное
движение – движение по отношению к
системе координат, выбранной за
основную (абсолютную).
Относительное
движение – движение точки по отношению
к подвижной системе координат.
Переносное
движение – движение подвижной системы
координат относительно неподвижной.
Установление связи между этими
движениями позволяет решать различные
задачи.
Опр-е
ускорения точки
в сложном движении
VM=VO+[
ωr]+
Vr
WM=d
VM/dt=(d
VO/dt)+[
εr]+[
ω(dr/dt)]+d
Vr/dt
dr/dt=[
ωr]+
Vr
WM=Wo+[
εr]+
[ω[ωr]]+[
ω
Vr]+
[ ωVr]+Wr
d
Vr/dt=[
ω
Vr]+
Wr
Wk=2[ω
Vr]
WM=WL+Wr+WK
– кинематическая теорема Кариолиса
Абсолютное
ускорение точки –это есть сумма
переносного ускорения, относительного
ускорения и ускорения Кариолиса
Переносное
ускорение хар-ет измен-е переносной
скорости в переносном движении.
Относительное
ускорение хар-ет изм-е относительной
скоростив в относительном движении.
Ускорение Кариолиса хар-ет изм-е
относительной скорости в переносном
движении
Ускорение
Кариолиса.
Согласно
правилу векторного произведения,
вектор ускорения Кариолиса ┴ пл-ти,
в кот-й лежат вектора ω
и Vr
и направлена в ту сторону,что с конца
этого вектора кратчайшее совмещение
первого вектора ко второму ω
к Vr
кажется видным против хода часовой
стрелки.
2.
Лемма о параллельном переносе силы.
Сила,
приложенная к какой-либо точке твердого
тела, эквивалентна такой же силе,
приложенной к любой другой точке тела,
и паре сил, момент которой равен моменту
данной силы относительно новой точки
приложения.
Доказательство:
пусть дана сила F.
Приложим к какой-либо точке В систему
F’
и F”.
|F|=|F’|=|F”|.
F~(F,F’,F”),
т.к. (F’,F”)
~ 0, то
F
~ (F,F’,F”)
~ (F,F’,F”)
~ (F’,M(F,F”)).
Но
M(F,F”)=BAxF=MB(F).
Получаем:
F
~ (F’,M(F,F”))
Ч.
т.
д.
Билет
№21.
-
Сложное
движение точки. Ускорение Кориолиса.
Правило Жуковского. Примеры. -
Эквивалентность
пар. Сложение пар. Условие равновесия
системы пар сил.
1.
Сложное движение точки. Основные
понятия.
Сложное
движение – движение по отношению к
системе координат, выбранной за
основную (абсолютную).
Относительное
движение – движение точки по отношению
к подвижной системе координат.
Переносное
движение – движение подвижной системы
координат относительно неподвижной.
Установление связи между этими
движениями позволяет решать различные
задачи.
Ускорение
Кориолиса. Правило Жуковского.
Полное
ускорение точки А, участвующей в
сложном движении
aA=ar+ae+2ω×vr.
Слагаемое aК=2ω×vr
называется ускорением Кориолиса.
aK=2ωvrsin(ω,vr).
Частные случаи:
А)
ω0
– смена знака
Б)
vr0
– относительный покой (смена знака
движения).
В)
sin(ω,vr)0,
ω||vr.
Правило
Жуковского. Ускорение Кориолиса равно
проекции относительной скорости на
плоскость, перпендикулярную ω,
увеличенной в 2ω раз и повернутой на
90° в направлении круговой стрелки ω.
2.
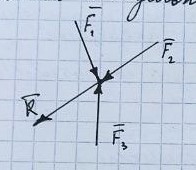
Пара сил. ∑ моментов сил, составляющих
пару.
Пара
сил – система 2-х равных по модулю и
противоположных по направлению сил,
действующих на твердое тело. ∑F=0;
∑M≠0.
Расстояние
между линиями действия – плечо d.
Пара сил характеризуется плоскостью
действия, моментом пары.
ТЕОРЕМА:
Векторный момент пары сил равен
векторному моменту одной из её сил
относительно другой.
Доказательство:
MO(F1)+
MO(F2)=rAxF1+
rAxF2=
rAxF1—
rBxF1=(rA—rB)
x
F1.
Из сложения треугольником OA+AB=OB
=>
AB=OB—OA
=> MO(F1)+
MO(F2)=ABxF1=MA(F1)
=> сумма моментов сил, составляющих
пару, не зависит от положения точки,
относительно которой берутся моменты.
Билет
№22.
-
Сложение
вращений твердого тела вокруг
пересекающихся осей. -
Зависимость
между главными моментами системы сил
относительно двух центров приведения.
1.
Сложение вращений твердого тела вокруг
пересекающихся осей.
В
случае вращательных относительного
и переносного движений твердого тела,
когда оси их вращений пересекаются в
точке О, абсолютное движение будет
сферическим движением вокруг точки
О.
ω=ωe+ωr.
Скорость любой точки, лежащей на линии
по которой направлен вектор ω
v=ω×r=0.
Скорость любой точки М тела в данном
случае можно определить так:
vM=ω×rM=(ωe+ωr)×rM=ve+vr.
ve=ωe∙he;
vr=ωr∙hr;
v=ω∙h;
где
he,
hr,
h
– кратчайшие расстояния от точки М
до соответствующих осей вращения.
2.
Зависимость между главными моментами
сил относительно 2 центров приведения.
Главный
момент системы сил относительно
второго центра приведения О1
равен вектору главного момента системы
сил относительно первого центра
приведения О, плюс векторный момент
главного вектора, приложенного в
первом центре приведения относительно
второго центра.
Доказательство:
Момент
относительно любой точки O1
MO1=∑(rO1ixFi).
Момент относительно первого центра
приведения О MO=∑(rOixFi).
Причем rO1i=O1O+rOi.
MO1=∑(O1O+rO1)xFi=O1O∑Fi+
∑(rOixFi)=MO+O1OxR=
MO+MO1(R).
MO1=
MO+MO1(R)
(1)
Билет
№23.
-
Определение
ускорений точек плоской фигуры при
известном положении МЦУ. -
Система
сходящихся сил. Условия равновесия.
1.
Определение ускорения точек плоской
фигуры с помощью МЦУ.
Зная
положение МЦУ и ускорение какой-либо
точки плоской фигуры можно найти
ускорение всех точек плоской фигуры.
Пусть
известна величина и направление точки
А aA
плоской фигуры и МЦУ – Q.
Тогда ускорение любой другой точки B
плоской фигуры будет лежать под углом
α, равным углу между aA
и QA
против направления круговой стрелки
ε.. Его величина aB=QB/√ε²+ωюбюб4=QBaA/
AQ.
2.
Система сходящихся сил. Условия
равновесия.
Система
сил называется сходящейся, если линии
всех сил пересекаются в одной точке.
Попарно поочередно сложим эти силы,
перенесенные к точке пересечения.
Тогда R=∑Fk
– главный вектор, так как R12=F1+F2,
R13=R12+F3
и т. д.
Rx=∑Fix
R=√(Rx²+Ry²+Rz²),
cos(x,R)=Rx/R
– аналитический способ задания.
Условия
равновесия.
Система
находится в равновесии когда главный
вектор R=0.
А)
Векторная форма: R=∑Fk=0;
Б)
Аналитическая форма: Rx=Fkx=0,
Ry=Fky=0,
Rz=Fkz=0;
В)
Графическая форма: замкнут многоугольник
сил.
Билет
№24.
-
Способы
определения углового ускорения при
плоском движении твердого тела. -
Равновесие
тела с учетом трения качения. Коэффициент
трения качения.
1.
Способы опред. угл. уск. При плоском
движении.
-
Если
задана зависимость ула поворота
плоского тела от времени φ=φ(t),
то ε=φ׳׳(t); -
Если
известна зависимость угловой скорости
от времени ω=ω(t),
то, так как ω=vτ/R,
то ε=ω׳(t)=d/dt(vτ/R)=1/R∙dvτ/dt=
aτ/R. -
Из
условия задачи.
Н
Y
B
C
A
X
Если
известны по модулю aA
и (aBA)n,
то, проецируя векторное равенство
aB=aA+(aBA)τ+(aBA)n
на ось Ох, получим:
εAB∙AB∙sinφ=aA+(ωAB)²∙AB∙cosφ
2.
Трение качения. Коэффициент трения
качения.
Круглое
тело вдавливается в опорную поверхность
(дуга CD).
Трение качения – сопротивление,
возникающее при качении одного тела
по поверхности другого. Полная реакция
N’
опорной поверхности препятствует
качению.
Нам
нужен момент сопротивления качению
=> заменим N’
и представим в виде Fтр.
и N,
приложенных в точке В,
смещенной от центра на δ. Условия
равновесия: N=P,
F=Q.
QmaxR=δN.
Mтр.max=δ∙N.
Момент сопротивления качению 0<Mк<Mк.max
(не зависит от радиуса). Коэффициент
трения качения δ при предельном
состоянии равновесия (при Qmax)
N
(сила нормального давления) отстает
на δ от вертикального радиуса. δ не
зависит от материала, из которого
сделано тело. Определяется
экспериментально.
Билет
№25.
-
Полная
и локальная производные вектора.
Формула Бура. -
Центр
тяжести тела. Методы определения
положения центра тяжести.
1.
Полная и локальная производная вектора.
Формула Бура.
Пусть
задан вектор b(t)=bxi+byj
+bzk
в подвижной системе отсчета. Орты i,
j,
k
не меняются в подвижной системе
отсчета. Поэтому локальная производная
d~b/dt=dbx/dt∙i+dby/dt∙j+dbz/dt∙k,
а полная производная с учетом изменения
также ортов i,
j,
k
примет вид:
db/dt=
dbx/dt∙i+dby/dt∙j+dbz/dt∙k+bxdi/dt+
bzdj/dt+
bzdk/dt.=
d~b/dt+ω×(bxi+
byj+bzk)=
d~b/dt+ω×b.
db/dt=d~b/dt+ω×b
– формула
Бура.
Частные
случаи:
А)
ω=0db/dt=
d~b;
Б)
Если вектор b
не меняется в подвижной системе
отсчета, то db/dt=
ω×b;
В)
Если b
все время параллелен вектору угловой
скорости (ω×b=0),
то db/dt=
d~b.
2.
Центр тяжести тела. Методы нахождения
центра тяжести.
Центр
тяжести – центр системы параллельных
сил тяжести частиц тела. Его радиус-вектор
rC=∑Piri/P.
XC=∑Pixi/P;
Yc=∑Piyi/P;
ZC=∑Pizi/P
Вес
тела P=∑Pi,
Pi
– сила тяжести частицы.
Методы
определения координат центра тяжести
тела.
-
Свойства
симметрии: если тело имеет плоскость,
ось или центр симметрии, то центр
тяжести лежит на них. -
Разбиение:
Если известны центры тяжести отдельных
частей тела, то
rC=(V1rC1+V2rC2+…+VnrCn)/V
Отрицательные
массы:
rC=VсплrC-V1rC1-…-VnrCn,
где Vk,
rCk
– объемы и радиус-векторы пустот тела.
-
Интегрирование:
если тело нельзя разбить)
XC=(∫xdV)/V,
YC=(∫ydV)/V,
ZC=(∫zdV)/V
Билет
№26.
-
Пара
вращений. -
Теорема
о приведении произвольной системы
сил к паре – основная теорема статики.
1.
Пара вращений.
При
противоположных направлениях векторов
ωe
и ωr
и равенстве
их модулей (ωe
= ωr),
если условие ωe=-ωr
выполняется на отрезке времени t2-t1,
абсолютное движение будет поступательным.
Такой случай сложения вращательных
движений называется парой вращений.
Действительно,
ω=ωe+ωr=
—ωr+ωr=0,
и для любой точки тела справедливы
соотношения: v=ωe×r1+ωr×r2=ωe×(r1—r2)=ωe×OeOr=ωr×OrOe;
Следовательно,
скорости всех точек тела в данном
случае одинаковы и равны скорости
поступательного движения.
2.
Т. о приведении произвольной системы
сил к силе и паре сил.
Теорема
Пуассо: Произвольная система сил,
действующих на твердое тело, можно
привести к какому-либо центру О, заменив
все действующие силы главным вектором
системы сил R,
приложенным к точке О, и главным
моментом MO
системы сил относительно точки О.
Доказательство:
Пусть
О – центр приведения. Переносим силы
F1,
F2,…,Fn
в точку О: FO=
F1
+F2+…+Fn=
∑Fk.
При этом получаем каждый раз
соответствующую пару сил (F1,F1”)…(Fn,Fn”),
Моменты этих пар равны моментам этих
сил относительно точки О.
M1=M(F1,F1”)=r1xF1=MO(F1).
На основании правила приведения систем
пар к простейшему виду MO=M1+…+M2=∑MO(Fk)=
∑rkxFk
=> (F1,
F2,…,Fn)
~ (R,MO)
(не зависит от выбора точки О).
Билет
№27.
-
Сложение
вращений твердого тела вокруг
параллельных осей. -
Инварианты
системы сил. Частные случаи приведения
системы сил к простейшему виду.
1.
Сложение вращений твердого тела
относительно параллельных осей.
Если
оси вращательных движений тела
параллельны, то вектор результирующей
угловой скорости ω
тела в неподвижной системе координат
будет коллинеарен ωе
и ωr.
Положение мгновенной оси вращения
тела как оси, проходящей в данный
момент времени через точку Р – МЦС в
плоскости П, перпендикулярной осям
вращений, можно определить из анализа:
vrP=ωr×OrP,
veP=
ωe×OeP,
Or,
Oe
– точки пересечений П с соответствующими
осями вращения. vP=veP+vrP=0
veP=
— vrP
veP=
vrP
ωrOrP=
ωeOeP.
В
зависимости от взаимного расположения
и численного значения векторов ωr
и ωe
можно выделить 3 случая сложения
вращательных движений:
А)
При совпадении направлений векторов
ωe
и ωr
абсолютное движение будет плоским.
Абсолютная угловая скорость в этом
случае будет иметь направление,
совпадающее с направлениями её
составляющих, а её модуль ω=ωr+ωe.
Положение точки Р можно найти из
пропорции ωe/OrP=ωrOeP=ω/OeOr.
Скорость любой точки тела может быть
найдена по формуле v=ω×PM.
Б)
При противоположных направлениях
векторов ωe
и ωr,
когда ωr≠ωe,
абсолютное движение будет плоским.
Абсолютная угловая скорость имеет
направление, совпадающее с направлением
большей по модулю составляющей угловой
скорости, а её модуль ω=|ωr-ωe|.
Пропорции для нахождения точки Р имеют
тот же вид, что и в пункте А.
2.
Инварианты системы тел. Частные случаи
приведения.
Инвариант
системы сил – векторные и скалярные
величины, не зависящие от точки
приведения системы сил.
-
Главный
вектор R=∑Fi=const. -
Скалярное
произведение главного вектора и
главного момента LOR=const=FxMx+
FyMy+FzMz.
Доказательство:
Умножим обе части выражения (1) на R:
MO1R=
MOR+(O1OxR)R
ПрR(LO1)=
ПрR(LO)=
LO1R∙
∙cos(LO1^R)=
LO2Rcos(LO2^R).
LO1xRx+
LO1yRy
+LO1zRz
=LO2xRx
+LO2yRy
+LO2zRz
Приведение к
простейшему виду:
-
MO=0,
R0
к равнодействующей, равной R,
проходящей через О. -
R=0,
MO0
к паре с моментом MO
(независимо
от О).
R0,
MO0,
MO┴
R
к
равнодействующей, равной R,
проходящей через О1:
ОО1=d=
|MO|
/ |R|.
Доказательство: R
и пара сил с моментом MO
лежат в одной плоскости
силы
R
и R”
уравновешиваются, систему можно
заменить равнодействующей R’.
-
MOR0,
R0,
MO0,
R
не перпендикулярна MO
– приводится к динаме.
Доказательство:
Разложим MO
на 2 составляющих: M1
и M2.
M2
представим в виде пары сил R’
и R”.
Силы R
и R”
уравновешиваются, а M1
перенесем в точку O1
(свободы).
В
результате получили винт R’,
M1,
проходящий через точку О1.
Прямая,
проходящая через точку О1
– ось динамы.
Билет
№28.
-
Теорема
о проекциях скоростей двух точек
твердого тела на прямую, проходящую
через эти точки. -
Главный
вектор и главный момент системы сил,
формулы для их вычисления.
1.
Теорема о проекциях двух точек на
линию, соединяющую эти точки.
При
любом движении проекции двух точек
на линию, их соединяющую, равны.
Док-во:
rB=rA+AB
=> drB/dt
= drA/dt+dAB/dt,
но dAB/dt
┴ AB.
Проецируем
на линию АВ, учитывая, что dAB/dt
┴ AB:
ПрАВ(vB)=ПрАВ(v)A+0.
2.
Главный вектор, момент.
Пусть
дана система сил (F1,
F2,…,Fn).
Главным
вектором системы сил называется
вектор, равный векторной сумме этих
сил.
R=∑Fk.
Rx=∑Fkx;
cos(x,R)=
Rx/R;
Ry=∑Fky;
cos(y,R)=
Ry/R;
Rz=∑Fkz;
cos(z,R)=
Rz/R;
Главный
момент системы сил – сумма моментов
сил относительно какого-либо полюса
(центра приведения).
Lx=∑Mx(Fk)
Билет
№29.
-
Векторные
и скалярные формулы для скоростей и
ускорений точек тела при его вращении
вокруг неподвижной точки. -
Связь
векторного момента силы относительно
точки с моментом силы относительно
оси, проходящей через эту точку.
1.
Скорости и ускорения точек тела при
его вращении вокруг неподвижной точки.
VA=ω×rA.
Пусть точка М лежит на мгновенной оси
вращения.
i
j k
VM=ω×rM=
ωx
ωy
ωz
XM
YM
ZM
X/ωx=Y/ωy=Z/ωz
– мгновенная ось вращения.
aA=dv/dt=dω/dt×rA+ω×drA/dt=ε×rA+ω×vA=aAвр+aAос.
aAвр=
ε×rA
– вращательное ускорение точки.
aAос=
ω×vA
– осестремительное ускорение точки.
Формула
Ривальса: aAoc=ωvAsin(ω,
vA).
aвр
направлен перпендикулярно плоскости
(ε,r)
в сторону, откуда переход от ε к r
виден против часовой стрелки.
aвр
направлен по перпендикуляру к плоскости
(ω,v).
2.
Связь между моментом относительно
оси и относительно точки.
Момент
силы F
относительно оси z
равен проекции на эту ось вектора
момента силы F
относительно
произвольной точки О на этой оси.
Доказательство:
Пусть
О – произвольная точка на оси z.
Момент силы F
относительно точки О перпендикулярен
плоскости ОАВ
MO(F)┴(OAB).
Пусть угол между
MO(F)
и осью z
равен α. Тогда ПрzMO(F)=2SΔO’A’B’=
2SΔOAB∙cosα
=> Mz(F)
= |MO(F)|cosα.
Ч.т.д.
Билет
№30.
-
Соотношение
между ускорениями двух точек плоской
фигуры при плоском движении твердого
тела. -
Главный
вектор и главный момент системы сил,
формулы для их вычисления.
1.
Соотн. между уск. 2-х точек при плоском
движении.
vB=vA+ωxAB.
aB=dvB/dt=dvA/dt+(dω/dt)xAB+
ωx(dAB/dt)=aA+εxAB+ωx(ωx
AB).
Считая,
что εхАВ=(aBA)τ;
(aBA)n=ω²∙AB,
окончательно получим:
aB=aA+(aBA)τ+(aBA)n
aA
– ускорение
полюса;
aBA
– ускорение движения вокруг полюса.
2.
Главный вектор, момент.
Пусть
дана система сил (F1,
F2,…,Fn).
Главным
вектором системы сил называется
вектор, равный векторной сумме этих
сил.
R=∑Fk.
Rx=∑Fkx;
cos(x,R)=
Rx/R;
Ry=∑Fky;
cos(y,R)=
Ry/R;
Rz=∑Fkz;
cos(z,R)=
Rz/R;
Главный
момент системы сил – сумма моментов
сил относительно какого-либо полюса
(центра приведения).
Lx=∑Mx(Fk)
Ставлю 10/10
Все нравится, очень удобный сайт, помогает в учебе. Кроме этого, можно заработать самому, выставляя готовые учебные материалы на продажу здесь. Рейтинги и отзывы на преподавателей очень помогают сориентироваться в начале нового семестра. Спасибо за такую функцию. Ставлю максимальную оценку.
Отлично
Лучшая платформа для успешной сдачи сессии
Познакомился со СтудИзбой благодаря своему другу, очень нравится интерфейс, количество доступных файлов, цена, в общем, все прекрасно. Даже сам продаю какие-то свои работы.
Отлично
Студизба ван лав ❤
Очень офигенный сайт для студентов. Много полезных учебных материалов. Пользуюсь студизбой с октября 2021 года. Серьёзных нареканий нет. Хотелось бы, что бы ввели подписочную модель и сделали материалы дешевле 300 рублей в рамках подписки бесплатными.
Отлично
Отличный сайт
Лично меня всё устраивает — и покупка, и продажа; и цены, и возможность предпросмотра куска файла, и обилие бесплатных файлов (в подборках по авторам, читай, ВУЗам и факультетам). Есть определённые баги, но всё решаемо, да и администраторы реагируют в течение суток.
Отлично
Маленький отзыв о большом помощнике!
Студизба спасает в те моменты, когда сроки горят, а работ накопилось достаточно. Довольно удобный сайт с простой навигацией и огромным количеством материалов.
Хорошо
Студ. Изба как крупнейший сборник работ для студентов
Тут дофига бывает всего полезного. Печально, что бывают предметы по которым даже одного бесплатного решения нет, но это скорее вопрос к студентам. В остальном всё здорово.
Отлично
Спасательный островок
Если уже не успеваешь разобраться или застрял на каком-то задание поможет тебе быстро и недорого решить твою проблему.
Отлично
Всё и так отлично
Всё очень удобно. Особенно круто, что есть система бонусов и можно выводить остатки денег. Очень много качественных бесплатных файлов.
Отлично
Отзыв о системе «Студизба»
Отличная платформа для распространения работ, востребованных студентами. Хорошо налаженная и качественная работа сайта, огромная база заданий и аудитория.
Хорошо
Отличный помощник
Отличный сайт с кучей полезных файлов, позволяющий найти много методичек / учебников / отзывов о вузах и преподователях.
Отлично
Отлично помогает студентам в любой момент для решения трудных и незамедлительных задач
Хотелось бы больше конкретной информации о преподавателях. А так в принципе хороший сайт, всегда им пользуюсь и ни разу не было желания прекратить. Хороший сайт для помощи студентам, удобный и приятный интерфейс. Из недостатков можно выделить только отсутствия небольшого количества файлов.
Отлично
Спасибо за шикарный сайт
Великолепный сайт на котором студент за не большие деньги может найти помощь с дз, проектами курсовыми, лабораторными, а также узнать отзывы на преподавателей и бесплатно скачать пособия.
Отлично
Экзамен по теоретической механике проходит в письменной форме и включает ответы на вопросы по теории и решение задач по темам изученного раздела.
Получить помощь на экзамене >
Сохранить и поделиться с друзьями
Здесь представлена информация и материалы для подготовки и успешной сдачи экзамена по теоретической механике для студентов очной, заочной и дистанционной форм обучения:
Материалы для сдачи экзамена
Здесь представлены экзаменационные вопросы, примеры билетов с ответами и решениями, теория, примеры решения задач и критерии оценок.
- Экзаменационные вопросы по курсу теории
Перечень вопросов для подготовки к экзамену по теоретической механике. - Экзаменационные билеты
Образец экзаменационного билета - Ответы на билет
Ответы на вопросы и решение задач экзаменационного билета - Критерии оценки знаний студентов
Критерии выставления экзаменационных оценок - Онлайн-помощь на экзаменах и зачетах
Профессиональная поддержка студентов в режиме онлайн - Краткий курс теоретической механики
Лекции для подготовки к экзаменам - Примеры решения задач
Решенные задачи теоретической механики с пояснениями
На экзамене студенту выдается экзаменационный билет с вопросами и задачами.
Для получения положительной оценки необходимо ответить на все теоретические вопросы и решить минимум одну задачу.
В некоторых случаях, преподаватель может задать экзаменуемому дополнительные вопросы для уточнения уровня знаний студента.
К итоговой аттестации допускаются студенты выполнившие и защитившие расчетно-графические, контрольные, курсовые и лабораторные работы по курсу.
Перечень необходимых заданий для выполнения расчетно-графических и контрольных работ устанавливает преподаватель.
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Шпаргалка: Ответы на
экзаменационные вопросы по теоретической механике
1.1)Предмет динамики. Основные
понятия и определения: масса, мат.точка, сила.
2) Дифф.ур-я движения мат.точки в
поле центральной силы. Формула Бине.
1) Массу Ньютон определяет как
количество материи, а кельвин как количество энергии.
Мат.точкой называется материальное
тело размерами которого при изучении данного движения можно пренебречь.
Мат.точка имеет массу.
Сила – векторная величена
определяющая меру взаимодействия между двумя телами.
2)
Дифференциальное уравнение
траектории точки в форме Бине.
2.1) З-ны механики
Галелея-Ньютона. Инерциальная система отсчета. Задачи динамики.
2) Движение мат.точки в поле
тяготения Земли.
1)
I-й з-н (З-н Инерции): Мат.точка сохраняет состояние покоя
или равномерного прямолинейного движения до тех пор пока действие других тел не
изменит этого состояния.
II-й з-н (Основной з-н движения): Модуль ускорения мат.точки
пропорционален модулю приложенной к ней силы, а направление ускорения совпадает
с направлением действия на неё силы.
III-й з-н (З-н дейтвия и противодействия): Две мат.точки
действуют друг на друга с силами равными по модулю и направленные вдоль прямой
соеденяющей эти точки – в противоположные стороны.
Согласно з-ну всемирного тяготения
сила тяготения пропорциональна силе тяжести, т.е. массе тяготеещей.
Галелей установил, если свободное
падение тел происходит в пустоте и не далеко от поверхности Земли, то оно
совершается с одним и тем же ускорением g-9,81
м/с^2 => из второго закона Ньютона.
P=mg, где P – вес тела
M – масса Земли; R –
радиус Земли; h<<R
Задачи динамики:
Первая задача динамики состоит в
том, что зная закон движения и массу мат.точки необходимо найти силы
действующие на свободную точку или реакции связей, если точка не свободна; в
последнем случае активно действующие силы должны быть заданы.
Вторая задача динамики: Зная
действующие на мат.точку силы, её массу, начальное положение и скорость
определить закон движения мат.точки.
2)Если на мат точку M действует центральная
сила P , то момент количества движения этой точки Lo относительно центра силы O
постоянен и точка движется в плоскости I,
перпендекулярной Lo. В этом случае Lo=const
3.1) Дифференциальные ур-я
движения свободной и несвободной точки в декартовых координатах и в проекциях
на оси естественного трёхгранника.
2) Сохранение момента количества
движения мат.точки в случае центральной силы. Секторная скорость. Закон
площадей.
1) Для свободной материальной
точки.
 |
В проекциях на оси
координат: На оси естественного трёхгранника:
 |
2) Моментом количества движения
материальной точки отоносительно центра называется вектор,модуль которого равен
произведению модуля количества движения на кратчайшее расстояние от центра до
линии действия вектора количества движения, перпендекулярного плоскости, в
которой лежат линии и направленный так, чтобы глядя от его конца видеть
движение, совершающееся против часовой стрелки.
ТЕОРЕМА: Производная по времени от
момента количества даижения материальной точки относительно некоторого центра
равна геометрической сумме моментов всех сил, действующих на точку.
4.1)Две основные задачи динамики
для мат.точки. Решение первой задачи динамики. Пример.
2)Теорема об изменении
кинетического момента механической системы по отнашению к неподвижному центру и
в её движении по отнашению к центру масс.
Первая задача динамики состоит в
том, что, зная закон движения и массу материальной точки необходимо найти силы
действующие на свободную точку или реакции связи, если точка несвободна. В
последнем случае активно действующие силы должны быть заданы.
Вторая задача динамики: зная
действующие на материальную точку силы, её массу, начальное положение и
скорость определить закон движения материальной точки.
Решение первой задачи.
Пусть задан закон движения
материальной точки в виде,
А так же её равнодействующая и
масса m.
Из дифференциального уравнения
движения материальной точки в
 |
 |
||
декартовой системе координат
следует, что:
 |
|||
Аналогично решается первая
задача для свободной точки, когда связи отсутствуют, а по известным уравнениям
движения необходимо найти действующие на точку силы. В этом случае:
 |
Пример.
Груз весом Р поднимается
вертикально вверх по закону
Определить натяжение тросса.
 |
 |
||
Дано: Решение.
 |
2)ТЕОРЕМА: Производная по
времени от кинетического момента механической системы относительно неподвижного
центра равен главному моменту всех внешних сил, действующих на систему
относительно того же центра.
5.1)Решение I-й задачи динамики. Пример.
2)Теорема об изменении количества
движения точки и система в дифф.и конечной формах.
1)Решение первой задачи.
 |
 |
||
Пусть задан закон движения
материальной точки в виде,
А так же её равнодействующая и
масса m.
Из дифференциального уравнения
движения материальной точки в
 |
декартовой системе координат
следует, что:
Аналогично решается первая
задача для свободной точки, когда связи отсутствуют, а по известным уравнениям движения
необходимо найти действующие на точку силы. В этом случае:
 |
 |
||
 |
Пример.
Груз весом Р поднимается
вертикально вверх по закону
Определить натяжение тросса.
 |
 |
||
Дано: Решение.
 |
2)ТЕОРЕМА: Производная по
времени от кинетического момента механической системы относительно неподвижного
центра равен главному моменту всех внешних сил, действующих на систему
относительно того же центра.
2)З-н сохранения количества
движения:
Если геометрическая сумма всех
внешних сил, приложенных к механической системе = 0, то её вектор количества
движения постоянен. Воспользуемся дифф.формой теоремы об изменении количества
движения механической системы.
.б) Если алгебраическая сумма
проекций на какую либо ось всех действующих сил системы = 0, то проекция её вектора
количества движения на эту ось есть величена постоянная.
6.1)Решение II-й задачи динамики. Постоянные интегрирования и их
определения по начальным условиям. Пример.
2)Кинетический момент механической
системы относительно центра и оси. Кинетический момент твёрдого тела
вращающегося относительно оси.
1)Для решения этой задачи
целесообразно воспользоваться дифф.ур-ми мат.точки в виде:
Поскольку действие силы
известны, то => известны и правые части этих ур-й. Интегрирование их дважды
по времени приводит их к 3-м ур-м содержащим 6 произвольным постонным:
Значе ния этих постоянных
могут быть просто найдены с помощью нач.усл., т.е. если известно:
Подставив найденные значения
в постоянные интегрирования в общее решение дифф-х ур-й получили закон движения
точки:
Отсюда => , что мат.точка под
действием одной и той же силы может совершать целый класс движений определённый
начальными условиями.
 |
|||
 |
|||
Например: движения свободной
мат.точки под силами тяжести – семейств кривых 2-го порядка.
Начальные условия позволяют учесть
влияние на движение мат.точки сил дейсвовавших на неё до того момента, который
принят за начальный.
2)Закон сохранения кинетического
момента механической системы:
1)Если сумма моментов относительно
данного центра всех внешних сил = 0, то кинетический момент механической
системы сохраняет модуль и направление в пространстве
2)Если сумма моментов всех
действующих на систему внешних сил относительно некоторой оси = 0, то
кинетический момент механической системы относительно этой оси есть величина
постоянная.
Частные случаи:
Система вращается вокруг
неподвижной оси в этом случае кинетический момент механической системы =
,и если сумма моментов
относительно этой оси равна нулю, то
7.1)Свободные колебания мат.точки.
Частота и период колебаний. Амплитуда и начальная фаза.
2)Потенциальное силовое поле и
силовая функция. Выражение проекций силы потенциального поля с помощью силовой
функции.
1)

8.1)Затухающие колебания
мат.точки. Случай апериодического движения.
2)Момент инерции твёрдого тела
относительно оси любого направления. Центробежные моменты инерции.
1)

2)
9.1)Вынужденные колебания
мат.точки. Резонанс.
2)Количество движения мат.точки и
механической системы. Выражение количества движения механической системы через массу
системы и скорость центра масс.
1)Движение мат.точки называется
вынужденным если на ряду с востанавливающей силой на неё действует возмущающая
сила.
С целью упрощения будем
считать, что возмущающая сила изменяется по гармоническому закону.
Явление сильного возрастания
амплитуды при совпадении частоты возмущающей силы с частотой собственных
колебаний называется резонансом.
2) Количеством движения мат точки
называется вектор, имеющий направление вектора скорости, и модуль, равный
произведению массы точки m на модуль скорости её движения v.
Количеством движения механической
системы называется вектор, равный геометрической сумме (главному вектору)
количеств движения всех мат точек этой системы.
10.1)Дифф.ур-я поступательного
движения судна при сопротивлении, пропорциональном скорости.
2)Момент количества движения
мат.точки относительно центра и оси.
1)При движении тел в
жидкости, сила трения пропорциональна первой степени скорости.
 |
2)Моментом количества движения
мат.точки относительно центра называется вектор, модуль которого = произведению
модуля количества движения на кратчайшее расстояние от центра до линии действия
вектора количества движения, I-й плоскости в которой лежат
упоминающиеся линии и направленный так, что бы глядя от его конца видеть
движение, совершающееся против часовой стрелки.
Моментом количества
движения мат.точки относительно оси называется скалярная величена =
произведению проекции количества движения мат.точки на плоскость
перпендикулярную данной оси и на кратчайшее расстояние от точки пересечения
данной оси с этой плоскостью до прямой, на которой лежит прямая вектора
количества движения.
11.1)Дифф.ур-я относительного
движения мат.точки. Переносная и Кориолисова силы инерции.
2)З-н сохранения кинетического
момента механической системы. Примеры.
1)Введем 2 вектора
численно равные
произведениям
и направленные
противоположно ускорениям
Эти векторы назовём переносной и
кориолисовой силами инерции.
Дифф.ур-я относительного
движения мат.точки.
2)а)Если сумма моментов
относительно данного центра всех внешних сил = 0, то кинетический момент
механической системы сохраняет модуль и направление в пространстве.
.б)Если сумма моментов всех
действующих на систему сил относительно некоторой оси = 0, то кинетический
момент механической системы относительно этой оси есть величина постоянная.
Частный случай:
Система вращается вокруг
неподвижной оси. В этом случае:
И если сумма моментов
относительно этой оси = 0, то:
Пример:
Платформа Жуковского
Изменяя положение рук можно
изменить угловую скорость вращения системы.
12.1)принцип относительности
классической механики. Случаи относительного покоя.
2)Работа силы на конечном
перемещении точки в потенциальном поле. Потенциальная энергия. Примеры
потенциальных силовых полей.
1)Никакие механические явления ,
происходящие в среде, не могут обнаружить её прямолинейного и равномерного
поступательного движения.
В том случае, когда мат точка
находится в состоянии относительного покоя, геометрическая сумма приложенных к
точке сил и переносной силы инерции равна 0.
2)ТЕОРЕМА. Работа постоянной силы
по модулю и направлению силы на результирующем перемещении = алгебраической
сумме работ этой силы на составляющих перемещениях.
Работа сил, действующих на точки
механической системы в потенциальном поле, равна разности значений силовой
функции в конечном и начальном положениях системы и не зависит от формы
траектории точек этой системы.
Потенциальная энергия системы в
любом данном её положении = сумме работ сил потенциального поля, приложенных к
её точкам на перемещении системы из данного положения в нулевое.
Примером потенциального силового
поля является гравитационное поле Земли.
13.1)Механическая система. Масса
системы, Центр масс и его координаты.
2)Мощность. Работа и мощность сил,
приложенных к твёрдому телу, вращающемуся вокруг неподвижной оси.
1)Механической системой или
системой материальных точек называется такая их совокупность, при которой
изменение положения одной из точек вызывает изменение положения всех остальных.
Примером механической системы может служить любая машина или механизм, где
движение от одних частей машины или механизма передаётся с помощью связей
другим частям. Твёрдое тело будем рассматривать как механическую систему,
расстояния между точками которой неизменны. Системы, отвечающие этому условию
называются неизменными. Системой свободных точек называется система
материальных точек, движение которой не ограничивается никакими связями, а
определяется только действующими на них силами. Пример- солнечная система.
Системой несвободных точек называется система материальных точек, движения
которых не ограничены связями. Пример- система блоков (полиспаст). Масса
системы это сумма масс всех точек, входящих в систему. Центром масс
механической системы называется точка радиус-вектор которой отвечает условию , где
— радиусы-векторы материальных точек
. Спроектировав обе части
этого равенства на оси OX, OY,
OZ прямоугольной системы координат, получим
выражение, определяющее координаты центра масс механической системы
, где
— координаты точек.
2)Предположим, что к твёрдому
телу, вращающемуся вокруг неподвижной оси Z,
приложены внешние силы .
Вычислим сначала элементарную работу отдельной силы , которая приложена в точке
, описывающей окружность радиусом
. Разложим эту силу на три
составляющие, направленные по естественным осям траектории точки
. Определим момент силы
относительно оси z
как сумму моментов её составляющих относительно этой оси. В общем момент силы относительно оси Z равен моменту силы
, которая лежит в плоскости, перпендикулярной оси
Z . При элементарном перемещении тела его угол
поворота φ получает приращение dφ, а
дуговая координата точки —
приращение . Вычислим работу силы
на этом перемещении как сумму работ трёх её
составляющих. Работа сил перпендикулярных
вектору скорости точки ,
равна 0, поэтому элементарная работа силы
. Элементарная работа всех сил, приложенных к
твёрдому телу , где
— Главный момент внешних сил
относительно оси вращения z. Таким образом , т.е. элементарная работа сил,
приложенных к твёрдому телу, вращающемуся вокруг неподвижной оси, равна
произведению главного момента внешних сил относительно оси вращения на
приращение угла поворота. Мощность вычисляется по следующей формуле:
14.1)Классификация сил,
действующих на механическую систему: силы внешние и внутренние, активные и
реакции связей.
2)Физический маятник. Опытное
определение моментов инерции тел.
1)Внешние силы- силы, действующие
на материальную точку системы со стороны тел не входящих в состав данной
механической системы.
Внутренние силы- силы, действующие
между материальными точками данной механической системы.
Силы заданные по условию задачи
принято называть- активными силами. А силы, обусловленные наличием связи-
реакциями связи.
2) Физический маятник- твёрдое
тело, совершающее колебания вокруг горизонтальной неподвижной оси под действием
только силы тяжести. Ось вращения физического маятника называется- осью
привеса. Обозначим φ угол между вертикальной осью, проходящей через ось привеса
линией, проходящей перпендикулярно оси привеса через центр тяжести точку С. G— вес тела. Дифференциальное уравнение физического маятника
знак «-» в правой части
поставлен потому, что при повороте маятника в положительном направлении (т.е.
против часовой стрелки) сила тяжести хочет повернуть маятник в обратном
направлении. — это
уравнение называется дифференциальным уравнением колебаний физического
маятника.
15.1)Моменты инерции системы и
твёрдого тела относительно оси, полюса и плоскости. Радиус инерции.
2)Законы Кеплера. Закон всемирного
тяготения.
1)Моментом инерции твердого тела
относительно оси называется скалярная величина, равная сумме произведений массы
каждой точки тела на квадрат расстояния от этой точки до оси.
Моментом инерции твёрдого тела
относительно плоскости называется скалярная величина, равная сумме произведений
массы каждой точки тела на квадрат расстояний от этой точки до плоскости.
Моментом инерции твёрдого тела
относительно полюса (полярным моментом инерции) называется скалярная величина,
равная сумме произведений массы каждой точки тела на квадрат расстояния от
точки до этого полюса. Радиусом инерции тела относительно данной оси z называется линейная величина , определяемая равенством
, где М- масса системы.
2)Законы Кеплера: 1. Все планеты
солнечной системы движутся по эллипсу, в одном из фокусов находится Солнце. 2.
Секторные скорости радиусов векторов планет, относительно Солнца не зависят от
времени. 3. Квадраты периодов обращения планет относятся как кубы больших
полуосей.
Закон всемирного тяготения
16. 1)Осевые моменты инерции
однородного стержня, цилиндра, шара.
2)Теорема об изменении момента
количества движения точки.
1)Момент инерции однородного
тонкого стержня Момент
инерции однородного круглого цилиндра Полого цилиндра
Момент однородного шара
— это соотношение выражает теорему об изменении
момента количества 2)движения материальной точки относительно центра:
производная по времени от момента количества движения материальной точки
относительно некоторого неподвижного центра равна геометрической сумме моментов
сил, действующих на точку, относительно того же центра.
17.1)Теорема о моментах инерции
относительно параллельных осей.
Момент инерции твёрдого тела
относительно некоторой оси равен моменту инерции тела относительно параллельной
оси, проходящей через его центр масс, сложенному с произведением массы тела на
квадрат расстояния между осями. Допустим, что задана ось. Для доказательства теоремы проведём 3
взаимно перпендикулярные оси, из которых ось параллельна заданной оси
, а ось
лежит в плоскости параллельных осей
и
. Для вычисления моментов инерции тела
относительно осей и
опустим из каждой точки
рассматриваемого тела
перпендикуляры и
на оси
и
. Выразим длины этих перпендикуляров через
координаты этих точек: ,
(зависимость а). Определим
моменты инерции тела относительно осей и
:
,
. Применим зависимость а)
(зависимость б),
из этой формулы получим
т.к.
=0 , то
. Подставляя это значение в равенство б),
получаем зависимость, установленную теоремой:

Эллипсоид инерции. Главные оси и главные моменты инерции.
2) Дифференциальные уравнения
поступательного движения и вращения тела вокруг неподвижной оси.
1)Момент инерции твёрдого тела
относительно оси v определяется по формуле
Рассмотрим изменение момента
инерции , происходящее
при изменении направления оси v т.е при изменении углов α, β, γ.
Для наглядного изображения этого изменения отложим по оси v от точки О отрезок ON,
длина которого Выразим
направляющие косинусы оси v через координаты x, y, z
точки N и длину отрезка ON: ;
;
. Подставим cosα, cosβ, cosγ в выражение
, подставили разделили на
получили
. Это уравнение определяет поверхность,
по которой перемещается точка N, при изменении направления оси v при условии(ф-ла 123). Это уравнение представляет собой
уравнение поверхности второго порядка. Эта поверхность является эллипсоидом,
т.к. расстояния от всех точек N до точки О, определяемые формулой
123 всегда конечны. Этот эллипсоид называется эллипсоидом инерции. Центр
эллипсоида находится в начале координат. Три оси эллипсоида называются главными
осями инерции тела в точке О, а моменты инерции относительно этих осей-
главными моментами инерции. Величины
называются центробежными моментами инерции
соответственно относительно осей y и z, z и x,
x и y.
2)При поступательном движении тела
все его точки движутся также как и и его центр масс. Поэтому дифференциальные
уравнения движения центра масс тела являются дифференциальными уравнениями
поступательного движения твёрдого тела: с y и z такие же уравнения m— масса
тела, — координаты
центра масс тела —
проекция внешней силы F на оси координат X,Y,Z
– проекции главного вектора внешних сил R на эти
оси. По дифференциальным уравнениям поступательного движения можно решать два
основных типа задач на поступательное движение твёрдого тела: 1) по заданному
движению твёрдого тела определить главный вектор, приложенных к нему сил 2) по
заданным внешним силам, действующим на тело, и начальным условиям движения
находить кинематические уравнения движения тела, если известно, что оно
движется поступательно.
Уравнение представляет собой дифференциальное уравнение
вращения твёрдого тела вокруг неподвижной оси. По дифференциальному уравнению
можно решать следующие задачи: 1) по заданному уравнению вращения тела и его моменту инерции
определять главный момент
внешних сил, действующих на тело : 2) по заданным внешним силам, приложенным к
телу, по начальным условиям вращения и по моменту инерции
находить уравнение вращения тела
3) определять момент инерции тела
относительно оси вращения,
зная величины и
19.1) Дифференциальные уравнения
движения механической системы. Т- ма о движении центра масс системы.
2)Движение тел в воздухе при
наличии сопротивления, пропорционального квадрату скорости.
1)
эти уравнения называются
уравнениями движения механ. сист. в вектр. ф – ме.
Теорема: Произведение массы
механической системы на ускор. ее центра масс = гл. вектору всех действ на
сист. внешних сил. Данная теорема позволяет глубже раскрыть значение матер.
точки и изучения динамики ее движения.
2)
При движении тел в газах в
частности в воздухе при скорости до 300 мс сила сопротивления пропорциональна
квадрату скорости, т.е. где x— const
20.1)Закон сохранения движения
центра масс. Примеры.
2)Решение задачи о движении тела, брошенного
под углом к горизонту.
1)
А) Если гл. вектор внешних сил,
прилож. к механ. сист. все время равен 0 то ее центр масс находится в покое или
движется равномерно и прямолинейно.
Б) Если проекция гл. вектора внеш.
сил на какую- нибудь неподвижную ось остается все время равным 0 то и проекция
ц. масс механ. сист на эту ось движется равномерно и прямолинейно.
Рассмотрим пример, который
позволяет применить т — му о движ. Центра масс: движение тела по горизонтальной
шероховатой пов — ти. Перемещение ц. масс тела происходит за счет сцепления
между обувью и поверхностью, т.е за счет внешних по отношению к человеку сил,
то возникают эти силы только при соотв. напряж. мускулов человека, что создает
позицию движения за счет них, однако если бы сцепление отсутствовало, то
человек не мог бы перемещаться наверх.
Fм
Fистр
21.1) Кинетическая энергия
материальной точки и механической системы. Вычисление кинетической энергии
твердого тела в различных случаях его движения.
2)Закон сохранения количества
движения механической системы. Примеры.
1)Кинетической энергией
метер. т-ки называется величина равная половине произведения ее массы на
квадрат скорости:
Кинетической энергией
механической системы называется сумма кинетических энергий всех входящих в нее
материальных точек:
2)
Если главный вектор всех
действующих на систему внешних сил равен 0, то вектор количества движения
системы есть величина постоянная.
Если алгебраическая сумма проекций
на какую-нибудь ось всех действующих на механическую систему внешних сил равна
0, то проекция вектора количества движения на эту ось есть величина постоянная.
22.1)Элементарная работа силы, ее
аналитическое выражение. Работа силы на конечном пути. Работа силы тяжести.
2)Главные оси и главные моменты инерции.
Свойства главных осей и главных центральных осей инерции.
1)Элементарной работой силы F называется скалярное произведение: A=(F∆r),
где ∆r вектор элементарного перемещения точки,
приложения силы, произошедшего в результате действия силы.
Работа силы на конечном
перемещении равна алгебраической сумме ее работ на отдельных элементарных
участках:
При движении тела по
непрерывной траектории можно перейти к пределу при стремлении числа участков к
бесконечности и получить:
2)Поскольку уравнение не содержит
координат первой степени, то его центр совпадает с началом координат. Три оси
симметрии эллипсоида инерции называются – главными осями инерции относительно
точки 0, а момент инерции относительно осей – главным моментом инерции.
Если выбрать систему координат
так, что бы оси совпадали с главными осями инерции механ. сист, то уравнение
эллипса примет вид: J*x X2* + J*y Y2* + J*z Z2* = 1
Каждой точке соотв. свой эллипс
инерции и если он известен, то можно найти момент инерции относительно любой
оси, проходящей через данную точку. Эллипсоид, соотв. центру масс тела
называется центральным эллипсоидом инерции, а его оси симметрии главными
центральными осями инерции.
Если известны главные центры
моментов инерции, то можно построить центр эллипсоид. инерции, а отсюда следует
определение: моментом инерции относительно любой оси, проходящей через центр
масс системы.
23.1) Работа силы упругости и силы
тяготения. Работа сил, приложенных к твёрдому телу, вращающемуся вокруг
неподвижной оси.
2)Теорема об изменении
кинетического момента механической системы по отношению к центру масс.
 |
Работа силы упругости.
 |
Работа силы тяготения.
Работа сил на конечном перемещении
равна произведению главного момента внешних сил относительно оси вращения на
конечное изменение угла поворота тела.
2)А) Относительно неподвижного
центра Производная по времени от кинетического момента относительно
неподвижного центра равна главному моменту всех внешних сил, действующих на
систему относительно того же центра. Б) Относительно центра системы координат,
движущимся поступательно вместе с центром масс. Производная по времени от
кинетического момента механической системы, относительно центра системы
координат, движущимся поступательно вместе с центром масс, равна главному
моменту всех внешних сил, относительно центра масс.
24.1)Теорема об изменении
кинетической энергии мат точки и механической системы в диффер и конечной
формах.
2)Потенциальная энергия мат точки
и механ системы. Поверхность равного потенциала.
1)ТЕОРЕМА. Изменение
кинетической энергии механ системы на некотором перемещении = сумме работ
внешних и внутренних сил, действующих на мат точки системы на этом перемещении.
Конечная форма.
2) Потенциальная энергия системы в
любом данном её положении = сумме работ сил потенциального поля, приложенных к
её точкам на перемещении системы из данного положения в нулевое.
Пусть U=U(x
,y ,z)-
силовая функция поля.
П=П(x,
y, z)-
потенциальная энергия точки.
Уравнение П( x, y, z)
определяет некоторую поверхность в пространстве, которая называется
поверхностью равного потенциала или эквипотенциальной поверхностью.
25.1)Закон сохранения механической
энергии системы при действии на неё потенциальных сил.
2)Количество движения точки и
механической системы. Элементарный импульс и импульс силы за конечный
промежуток времени.
1)При движении механической
системы в стационарном потенциальном поле полная механическая энергия системы
при движении остается неизменной.
2)Количеством движения мат точки
называется вектор, имеющий направление вектора скорости, и модуль, равный
произведению массы точки m на модуль скорости её движения v.
Количеством движения механической
системы называется вектор, равный геометрической сумме (главному вектору)
количеств движения всех мат точек этой системы.
Если постоянная по модулю и
направлению сила P действует течение промежутка
времени
то её импульсом за этот промежуток
времени является вектор
Подборка по базе: Лекция 1_РО_24.01.2022г_Геометрия. Фигуры. Аксиомы. Теоремы.pptx, Сухов А Ф Механика грунтов практическая работа 1.docx, ТЕСТ Механика. Электромагнетизм (4).docx, _айырбаев _._. Классикалы_ механика негіздері.pdf, Классикалы_ механика_а кіріспе. Н_кте кинематикасы.doc, Абай Мадина, механика практика 3 апта.pdf, Абай Мадина , 3 апта, механика (тест және суретке анықтама).pdf, 7 сын Бұйымды жасау. Материалдар мен бөлшектерді механикалық өң, Ответы — РОСДИСТАНТ — Механика грунтов.docx, Техническая механика.djvu
Теоретическая механика
1. Аксиомы статики.
- Аксиома инерции:
Под действием уравновешенной системы сил материальная точка (тело) находится в состоянии покоя или движется равномерно и прямолинейно.
- Аксиома равновесия 2-х сил:
Абсолютно твердое тело находится в равновесии под действием двух сил тогда и только тогда, когда эти силы равны по модулю, действуют по одной прямой в противоположные стороны.
- Аксиома присоединения и исключения уравновешивающих сил:
Не нарушая состояние абсолютно твердого тела, к нему можно прикладывать или отбрасывать от него уравновешивающую систему сил.
- Аксиома параллелограмма сил:
Две силы, приложенные к телу в одной точке, имеют равнодействующую, проходящую через эту же точку и равную их геометрической сумме.
- Аксиома равенства действия и противодействия:
Силы взаимодействия 2-х тел равны по модулю и направлены по одной прямой в противоположные стороны.
- Аксиома о сохранении равновесия сил, приложенных к деформированному телу:
Равновесие деформируемого тела не нарушится, если это тело отвердеет.
2. Определение равнодействующей и уравновешивающей произвольной системы сил.
- Если данная система сил эквивалентна одной силе, то эта сила называется равнодействующей данной системы сил.
- Силой, уравновешивающей систему сил, называют такую силу, которая будучи присоединенной к данной системе сил, оставляет вместе с ней новую систему сил, эквивалентную нулю.
3. Сходящаяся система сил.
Сходящаяся система сил – это система таких сил, линии действия которых полностью сходятся в одной точке.
Действие каждой силы на абсолютно твердое тело не меняется при переносе силы вдоль линии ее действия на иную точку тела.
4. Равнодействующая система сходящихся сил.
Сходящаяся система сил имеет равнодействующую, приложенную в точке пересечения линий действия сил системы и равную векторной сумме всех сил системы.
5. Условия равновесия системы сходящихся сил в векторной форме и в проекциях на оси декартовой системы координат.
Сходящаяся система сил является уравновешенной тогда и только тогда, когда векторная сумма всех сил системы равна нулю.
Если R – вектор, замыкающий силовой многоугольник:
Геометрическое условие равновесия системы сходящихся сил означает, что силовой многоугольник, построенный на векторах слагаемых сил данной системы, замкнут.
6. Теорема о трех уравновешенных силах.
Если под действием трех сил тело находится в равновесии, и линии двух действующих сил пресекаются, то все силы находятся в одной плоскости, и их линии действия пересекаются в одной точке.
7. Определение алгебраической величины момента силы относительно векторного центра.
Моментом силы относительно точки называется алгебраическая величина, равная произведению модуля силы на кратчайшее расстояние от точки до линии действия силы.
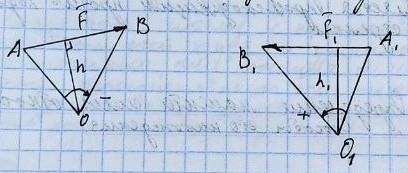
8. Сформулируйте и запищите векторное выражение момента силы относительно некоторого центра.
Моменты силы относительно некоторого центра равен векторному произведению радиус-вектора точки приложения силы на вектор силы.
9. Почему для плоской системы сил нет необходимости придавать векторный смысл моменту силы?
- В случае плоской системы сил силы относительно точки можно принимать за алгебраическую величину.
- Для пространственной системы сил момент – это вектор, который направлен перпендикулярно к плоскости, в которой лежат сила и точка, в ту сторону, откуда вращение тела сил представляется происходящим против хода часовой стрелки.
10. Определение моменты силы относительно оси. Способы его нахождения.
- Моментом силы относительно оси называется алгебраическая величина момента проекции этой силы на плоскость, перпендикулярно к данной оси, относительно точки пересечения этой плоскости с осью.
- Момент силы относительно оси равен проекции на эту ось вектора момента силы относительно произвольной точки, лежащей на этой оси.
Для определения знака момента удобно рассматривать систему с положительных направлений оcей x, y, z и принимать момент положительным, если проекция силы на плоскость, перпендикулярную оси, пытается создавать вращательный эффект вокруг этой же оси против хода часовой стрелки.
11. Определение пары сил и момента пары сил.
Система двух равных по величине, антинаправленных и не лежащих на одной прямой сил называется парой сил. Пара сил не имеет равнодействующей, то есть заменена эквивалентной силой.
Момент пары сил есть вектор, перпендикулярный к плоскости действия пары, направленной в сторону, откуда поворот тела данной парой виден происходящим против хода часовой стрелки.
12. Как направлен вектор момента пары сил?
Момент пары сил, то есть вектор M(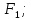
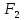
13. Определение главного вектора и главного момента произвольной пространственной системы сил.
- Сила R, равная геометрической сумме всех сил данной системы, называется главным вектором:
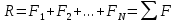
- Величина
, равная геометрической сумме моментов всех сил систем относительно центра произведения, называется главным моментом относительно этого центра:
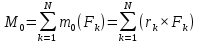
14. Чем отличаются главный вектор от равнодействующей произвольной системы сил?
Равнодействующая система сил эквивалентна системе сил, а главный вектор сам по себе не эквивалентен данной системе сил, но эквивалентен ей только в совокупности с главным моментов.
15. Определение центра тяжести. Способы определения координат центра тяжести.
Центром тяжести тела называется центр системы параллельных сил, которую приближенно образуют силы тяжести его элементарных частиц.
Способы:
- Аналитический (путем интегрирования)
- Метод симметрии:
Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно там.
- Экспериментальный (путем подвешивания)
16. Метод отрицательных масс и метод разбивания на части при определении координат центра тяжести.
- Дополнение (Метод отрицательных площадей и объектов) (отрицательных масс)
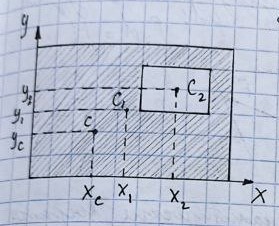
- Разбиение на части
Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести Cи площади Sизвестны.
17. Дайте определение момента пары сил. Как направлен вектор-момент пары?
Пара сил не имеет равнодействующей. Она стремится сообщить телу некоторое вращение.
Вращательный эффект пары сил характеризуется векторной величиной, называемой моментом пары сил.
Момент пары сил относительно точки O:
Момент пары сил перпендикулярен плоскости действия пары, направлен по правилу правого винта и равен по модулю произведению модуля любой из сил на плечо пары сил:
18. Напишите аналитические выражения для главного вектора и главного момента.
Выразим главный вектор сил через его проекции на координатной оси:
где: 
где: 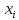
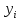
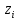
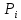
Модуль главного вектора определяется:
Главный момент:
где: 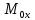
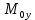
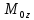
19. В чем состоит метод отрицательных масс и метод разбиения на части при определении координат центра тяжести?
Метод отрицательных масс:
«Частный случай метода разбиения»
Используется при определении положения центра масс фигуры, имеющей вырезы.
Массу удаленного участка считают отрицательной, а силу тяжести этого участка (—mg) направляют вверх.
В дальнейшем используют условие равновесия тела, находящегося под действием системы параллельных сил.
Метод разбиения на части:
Состоит в том, что рассматриваемое тело мысленно разбивается на части, центры тяжести которых известны либо могут быть легкоопределимы, после чего применяются формулы для определения координат центра системы параллельных сил.
20. Определение скорости и ускорения при векторном способе задания движения.
Скорость – вектор, характеризующий быстроту изменения положения точки по величине и направлению.
Ускорение – вектор, характеризующий быстроту изменения скорости точки по величине и направлению.
21. Поступательное движение тела. Определение скоростей и ускорений точки.
Поступательным называется такое движение тела, при котором прямая, соединяющая 2 любые точки этого тела, перемещается, оставаясь параллельной своему начальному направлению.
При поступательном движении точки тела могут двигаться по любым траекториям.
22. Вращательное движение твердого тела, угловая скорость, угловое ускорение.
Вращением твердого тела вокруг неподвижной оси называют такое движение тела, при котором хотя бы 2 его точки остаются неподвижными.
Неподвижная прямая проходящая через 2 неподвижные точки тела называется осью вращения тела.
Мера изменения угла поворота с течением времени называется угловой скоростью.
Величина, характеризующая изменение угловой скорости с течением времени, называется его угловым ускорением.
23. Плоское движение твердого тела.
Плоское движение твердого тела – это такое движение, при котором каждая точка движется в плоскости, которая параллельна некоторой неподвижной плоскости.
Такое движение совершает колеса или шатун в кривошипно-шатунном механизме.
24. Мгновенный центр скоростей. Частные случаи его определения.
Мгновенным центром скоростей называется точка сечения тела, скорость которой в данный момент времени равна 0.
Частные случаи МЦС:
- Если
: AB γ
, AB γ
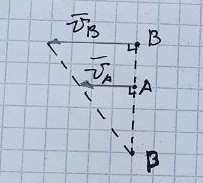
25. Сложное движение точки. Общие сведения.
В ряде случаев при решении задач по механике оказывается целесообразным рассматривать движения одновременно по отношению к двум системам отсчета, одна из которых является основной или условно-неподвижной.
Другая система отсчета (подвижная) движется определенным образом по отношению к первой. Движение, совершаемое при этом точками или телом, называется составным или сложным.
- Движения, совершаемые связанной точкой относительно неподвижной системы отсчета, называются абсолютным движением. Абсолютная скорость
равна геометрической сумме относительной и переносной скоростей.
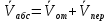
26. Лемма Пуансо
Всякая сила, приложенная к твердому телу эквивалентна такой же силе, но приложенной в другой точке тела, не лежащей на линии действия первой силы, и паре сил с моментом, равным моменту первой силы относительно точки приложения второй силы.
27. Теорема Вариньона.
Момент равнодействующей системы сил относительно какого-либо центра равен геометрической сумме моментов, составляющих систему сил относительно того же центра.
28. Центр параллельных сил.
Центром параллельных сил называется точка, при повороте вокруг которой всех сил системы на один и тот же угол, линия действия равнодействующей системы параллельных сил повернется в ту же сторону на тот же угол.
Свойства центра параллельных сил:
- Сумма моментов всех сил
относительно точки C равна нулю.
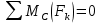
- Если все силы повернуть на некоторый угол α, не меняя точек приложенных сил, то центр новой системы параллельных сил будет той же точкой C.
29. Теорема о сложении скоростей.
При сложении движений абсолютная скорость точек равна геометрической сумме относительной и переносной скоростей.
30. Теорема о сложении ускорений.
Теорема Кориолиса:
При сложном движении ускорение точки равно геометрической сумме трех ускорений: относительного, переносного и поворотного (кориолисова).
31. Аксиомы динами точки.
- Закон инерции:
Изолированная материальная точка находится в состоянии покоя или совершает равномерное и прямолинейное движение.
Свойство тела сопротивляться изменению скорости тела называется инерцией.
Сила, с которой происходит сопротивление, называется силой инерции.
- Основной закон динамики:
Ускорение, сообщаемое телу, пропорционально действующей на тело силе и направлено по этой силе.
Масса является мерой инертности.
- Закон действия и противодействия сил:
Силы взаимодействия 2-х материальных точек равны по модулю и направлены в противоположную сторону по линии действия этих сил.
- Закон независимости действия сил:
Ускорение материальной точки, находящейся под действием нескольких сил равно геометрической сумме тех ускорений, которые точка могла бы получиться под действием каждой силы по отдельности.
32. Дифференциальные уравнения движения точки.
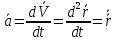
- Дифференциальное уравнения движения материальной точки в векторном пространстве.
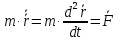
- Дифференциальное уравнения в Декартовой системе координат.
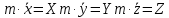
Ответы на экзаменационные вопросы по теоретической механике
[
·
Скачать
(16.17 Mb)
]
Ответы на экзаменационные вопросы по теоретической механике.
Содержание:
1. Аксиомы статики. Момент силы относительно центра и оси.
— III закон Ньютона.
— Принцип освобождаемости от связей.
— Принцип независимости действия сил.
— Система сил.
— Теоретическая механика.
— Аксиома 1,2,3.
2. Главный вектор и главный момент системы сил.
— Главный вектор системы сил.
— Теорема о приведении системы сил к одному центру.
3. Пара сил и ее момент.
— Определение.
— Теорема.
4. Содержание метода Пуансо о приведении системы сил к одному центру.
5. Необходимые условия равновесия системы сил.
— Теорема.
— Доказательство.
6. Теорема об эквивалентности системы сил.
— Доказательство.
— основные свойства пары сил.
7. Методы расчета усилий в стержнях фермы.
8. Законы Амонтона — Кулона о трении.
9. Центр параллельных сил. Методы применяемые при определении положения центра тяжести однородного тела.
10. Траектория, скорость, ускорение точки. Выявление векторов скорости и ускорение точки при координатном и естественном способе зад. движения.
11. Поступательное движение абсолютного твердого тела.
12. Вращение твердого тела вокруг неподвижной оси. Закон вращения, угловая скорость, угловое ускорения.
13. Выявление скорости и ускорения любой точки тела, вращающаяся вокруг неподвижной оси.
14. Плоскопараллельное движение твердого тела. Законы движения.
15. Способы выявления скорости плоской фигуры в данный момент времени.
16. Способы выявления ускорения точки плоской фигуры в данный момент времени.
17. Сложное движение точки. Теоремы сложения скоростей и ускорений при сп. движении точки.
18. основные законы механики. Две основные задачи динамики материальной точки.
— Аксиомы 1,2,3,4.
20. Относительное движение материальной точки.
21. Определение материальной точки, механической системы.
22. Дифференциальные уравнения движения точек М.С. Определение внешних и внутренних сил. Основные свойства внутренних сил мех. сист.
23. Центр масс механической системы. Способы выявления.
24. Теорема об изменении количества движения механической системы.
25. Теорема о движении у.м. механической системы.
26. Моменты количества движения материальной точки и механической системы относительного центра.
27. Теорема об изменений момента количества движения (кин. момента) М.С. относительно неподвижного центра оси.
29. Определение кинетической энергии материальной точки и мех. сист. Кинетическая энергия тела при поступательном, вращательном и плоскопараллельным движениях.
Год: 2014
Страниц: 22
Формат: JPEG
·
Скачать Ответы на экзаменационные вопросы по теоретической механике
(16.17 Mb)
Просмотров: 20249 / Загрузок: 2928 / Добавил: mgsu / Дата: 03.05.2014 / Комментарии: 0
- 1
- 2
- 3
- 4
- 5
Теоретическая механика
Преподаватели
Преподавателей не найдено
Учебные материалы
- Задачники
-
А.Б. Пименов — Методика решения задач по теоретической механике. 2016. -
А.Б. Пименов — Задачник по теоретической механике. 2015. -
А.Б. Пименов — Методика решения задач по теоретической механике. 2016. -
Коткин Г.Л., В.Г. Сербо — Сборник задач по классической механике - Контрольные работы
-
Контрольные работы по теоретической механике - Лекции
-
Написанные лекции по теоретической механике -
Конспекты лекций по теоретической механике. Лектор — Халилов В.Р. 2014. -
Лекции по теоретической механике -
Конспект лекций по теоретической механике - Материалы к зачёту экзамену
-
Билеты к экзамену по теоретической механике -
Вопросы и задачи билетов по теоретической механике. 2004 г. (зимний семестр). -
Билеты по теоретической механике. Часть 2 (еще часть билетов) -
Ответы на экзаменационные билеты по теоретической механике 2016 -
Билеты по теоретической механике. Часть 3 (еще часть билетов) -
Билеты по теоретической механике и оглавление ко всем этим частям -
Билеты по теоретической механике. Часть 1 (конспекты лекций и часть для билетов) -
Программа и список задач к экзамену (2-й поток, осень 2005) -
Подробный теормакс по теоретической механике -
Ответы к зачету по теоретической механике в группе Павловой -
Ещё одни ответы к экзамену по теоретической механике (с 10 по 23 билет) -
Ответы на экзаменационные билеты по теоретической механике, 5-й семестр -
Теормин по теоретической механике -
Вопросы и задачи для подготовки к экзамену по теоретической механике -
Много полезных материалов по теоретической механике - Полезные материалы
-
Дополненый файл — Решение задач по теоретической механике -
Задачи с решениями по теоретической механике -
Основные формулы по теоретической механике - Учебники
-
Г. Голдстейн — Классическая механика -
В.В. Петкевич — Теоретическая механика -
В.Ф. Журавлёв — Основы теоретической механики -
Л.Д. Ландау, Е.М. Лифшиц — Теоретическая физики (в 10 томах). Том 1. Механика. -
Л.С. Кузьменков — Теоретичсекая физика. Клaссическая механика. -
Методичка по теоретической механике -
В.Р. Халилов, Г.А. Чижов — Динамика классических систем -
Методичка по теоретической механике



















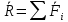
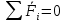
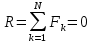
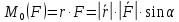
 , равная геометрической сумме моментов всех сил систем относительно центра произведения, называется главным моментом относительно этого центра:
, равная геометрической сумме моментов всех сил систем относительно центра произведения, называется главным моментом относительно этого центра: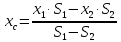
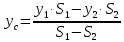
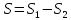
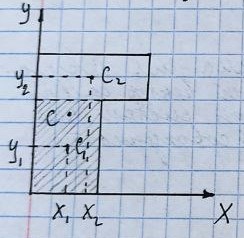
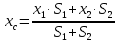
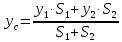
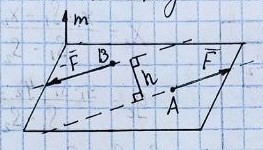
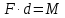
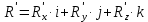
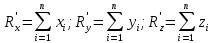
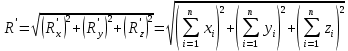
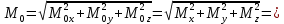
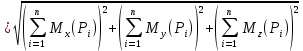
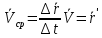
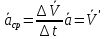
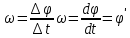
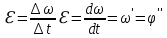
 : AB γ
: AB γ  , AB γ
, AB γ 
 равна геометрической сумме относительной и переносной скоростей.
равна геометрической сумме относительной и переносной скоростей.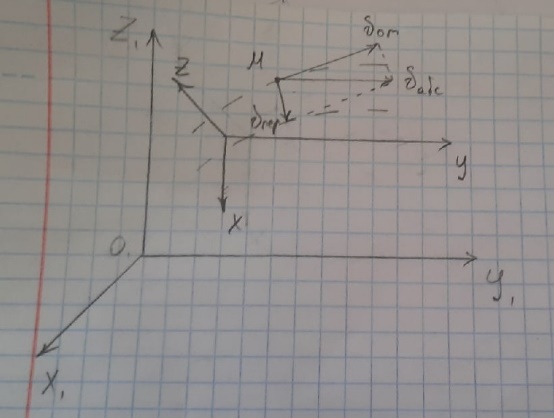
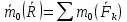
 относительно точки C равна нулю.
относительно точки C равна нулю.