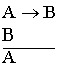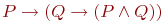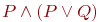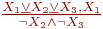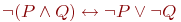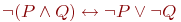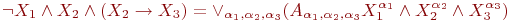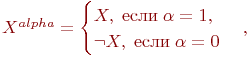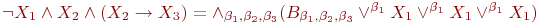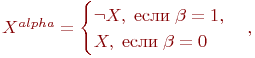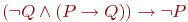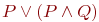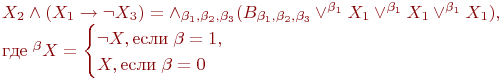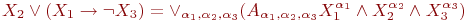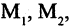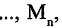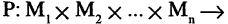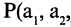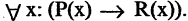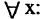|
Экзаменационные вопросы |
© Kovalenko Leonid |
||
|
по математической логике и теории алгоритмов |
|||
|
Весь материал взят с книг и научных работ. Ничего не придумано☺ |
|||
|
1. Определение формальной аксиоматической теории (ФАТ). Секвенции (выводы). |
|||
|
Формулы. Построение формул. 5 свойств выводов …………………………………………………… |
3 |
||
|
2. Исчисление высказываний. Построение ИВ как ФАТ. Алфавит, формулы, аксиомы, |
|||
|
выводы и правила вывода…………………………………………………………………………………………. |
4 |
||
|
3. Доказать, исходя из аксиом ИВ и правила вывода секвенцию ! — первое |
|||
|
свойство выводов ИВ……………………………………………………………………………………………….. |
5 |
||
|
4. Доказать, исходя из свойств выводов, аксиом ИВ и правила вывода ИВ следующие |
|||
|
свойства выводов ИВ ……………………………………………………………………………………………….. |
6 |
||
|
5. Теорема дедукции …………………………………………………………………………………………….. |
6 |
||
|
6. Свойство транзитивности импликации. Доказать секвенцию: , |
|||
|
………………………………………………………………………………………………………………………………. |
8 |
||
|
7. Противоречивые формулы ………………………………………………………………………………… |
9 |
||
|
8. Обоснование доказательства от противного: доказать, что если , ¬ , то 9 |
|||
|
9. Тождественность формул ИВ. Доказать тождество: ¬ ¬ ≡ ………….. |
11 |
||
|
10. |
Аксиоматическое введение в ИВ и …………………………………………………………… |
12 |
|
|
11. |
Теорема о том, что всякая выводимая в ИВ формула есть тавтология …………….. |
13 |
|
|
12. Доказательство леммы , , … , ……………………………………….. |
13 |
||
|
13. |
Теорема о том, что любая тавтология выводима в ИВ ……………………………………. |
16 |
|
|
14. |
Полнота и непротиворечивость ИВ ……………………………………………………………….. |
17 |
|
|
15. |
Предикаты. Кванторы. Свойства кванторов …………………………………………………… |
18 |
|
|
16. |
ИП — исчисление предикатов. Алфавит ИП. Формулы в ИП. Равносильность |
||
|
формул ИП. Приведённые и нормальные формулы ИП. Теоремы о приведённой и |
|||
|
нормальной форме формул ИП……………………………………………………………………………….. |
20 |
||
|
17. Выполнимость и общезначимость формул ИП. Общезначимость формул |
|||
|
, ……………………………………………………………………………………………………… |
21 |
||
|
18. Аксиомы ИП. Общезначимость аксиом ИП. Правила вывода ИП. Оформление ИП |
|||
|
как ФАТ …………………………………………………………………………………………………………………. |
23 |
||
|
19. |
Теорема об общезначимости формул ИП, получающихся из общезначимых по |
||
|
любому из 4-х правил вывода ИП …………………………………………………………………………… |
23 |
||
|
20. |
Полнота и непротиворечивость ИП. Теорема Гёделя. Тезис Чёрча …………………. |
24 |
|
|
21. |
Алгоритмы. Определение (интуитивное) алгоритма. Свойства алгоритмов. |
||
|
Направления поисков точного определения алгоритма. Вычислимые функции. |
|||
|
Проблема алгоритмической неразрешимости………………………………………………………….. |
25 |
||
|
22. Рекурсивные функции. 3 простейших ПРФ (примитивно-рекурсивных функций). |
|||
|
Оператор суперпозиции. Примеры………………………………………………………………………….. |
26 |
|
23. Оператор ПР (примитивной рекурсии). Доказать, что функции + , , − , |
|
|
− , − — ПРФ……………………………………………………………………………………………….. |
27 |
|
24. Оператор минимизации. Частично-рекурсивные функции. Доказать, что ÷ = |
|
|
− , ≥ не определена, < — ЧРФ. Точное определение алгоритма. Тезис |
|
|
Чёрча ……………………………………………………………………………………………………………………… |
29 |
|
25. Машина Тьюринга. Тьюринговая функциональная схема. Точное определение |
|
|
алгоритма. Тезис Тьюринга…………………………………………………………………………………….. |
31 |
|
26. Функции, вычислимые по Тьюрингу. Доказать, что 3 простейших ПРФ — |
|
|
вычислимы по Тьюрингу………………………………………………………………………………………… |
34 |
|
27. Геделева нумерация МТ. Примеры: по номеру найти МТ и по МТ записать номер |
|
|
………………………………………………………………………………………………………………………………. |
36 |
|
28. Самоприменимость МТ. Теорема об алгоритмической неразрешимости проблемы |
|
|
самоприменимости…………………………………………………………………………………………………. |
37 |
|
29. Нормальные алгоритмы Маркова. Точное определение алгоритма. Примеры…. |
38 |
|
Литература …………………………………………………………………………………………………………. |
41 |
1. Определение формальной аксиоматической теории (ФАТ). Секвенции (выводы). Формулы. Построение формул. 5 свойств выводов
Различают неформальную и формальную аксиоматические теории:
•Неформальная (интуитивная) аксиоматическая теория — теория, в которой правила логики явно не заданы (геометрия, арифметика, теория вероятностей и т. п.).
•Формальная аксиоматическая теория — теория, в которой правила логики явно заданы.
Формальная аксиоматическая теория (ФАТ) – теория, в которой определены:
•Выражения (конечные последовательности символов).
•Формулы (подмножество выражений — последовательность символов определенного вида; стержень теории; обычно количество формул в данной теории составляет счётное множество).
o Алфавит (счётное число символов, часто — латинские буквы).
o Связки между формулами и правила их записи. Число связок всегда конечно. Связки бывают 1-го порядка (связывающие одну формулу; например, sin в тригонометрии), 2-го порядка (связывающие две формулы; например,
+ в арифметике). Теоретически связки могут быть и -го порядка,
связывающие между собой формул.
oСкобки двух видов — правая и левая — нужны для того, чтобы определять порядок действий в формулах.
•Аксиомы данной теории (конечное число формул объявляются аксиомами).
•Правила вывода в рамках данной теории (правила вывода, позволяющие из одних формул получать другие — это действия с формулами; обычно количество правил вывода — конечное множество).
Построение формул:
1)Объявляются первичные (атомарные) формулы. Часто первичные формулы обозначаются заглавными буквами латинского алфавита.
2)Если — некоторая (уже построенная) формула и 1 — связка 1-го порядка, то 1
— тоже формула. Если и — две построенные формулы и 2 — связка 2-го порядка, то 2 — тоже формула, и, в общем случае, если 1, … , — построенных формул и — связка порядка , то (1, … , ) — тоже формула.
3)Любая формула данной теории либо сама является первичной, либо построена из первичных формул с помощью конечного числа применения правила №2.
Пусть («гамма») — произвольное конечное множество формул (возможно, пустое), используемых в качестве посылок вывода (гипотез).
Выводы (секвенции). Заметим, что слово секвенция означает «последовательность».
Далее следует считать, что вывод — это последовательный список формул, каждая из которых выводится из аксиом или предыдущих формул при помощи правил вывода.
Формула называется непосредственным следствием формул 1, … , −1, если
может быть получена из этих формул с помощью однократного применения какоголибо правила вывода .
Вывод (секвенция) — последовательность формул 1, … , , каждая из которых либо является аксиомой, либо выводится из одной или нескольких предыдущих формул этой последовательности по одному из правил вывода.
Теорема — последняя формула вывода. Иначе говоря, теорема аксиоматической теории — формула, которая может быть выведена при помощи правил вывода.
Формула называется следствием множества формул тогда и только тогда,
когда существует такая последовательность формул 1, … , −1 , каждая из которых либо аксиома, либо формула из , либо непосредственное следствие предыдущих формул. Эта последовательность формул называется выводом из ( — « есть следствие формул » или « можно вывести из формул »). Если — пустое множество формул, то есть следствие аксиом: — то есть теорема. Если из некоторых формул следует любая формула данной теории, то это значит, что формулы противоречивы: . Если состоит из формул 1, … , , то вывод из можно записать так: 1, … , . Формулы из множества называются посылками или предположениями.
Свойства выводов:
1), !
2)Если , , , то , , («порядок формул не имеет значения»).
3)Если и — любая формула, то , («лишняя формула не мешает»).
4)Если , и , то («удаление выводимой формулы»).
Пусть 1, … , — вывод формулы из , . То есть 1, … , .
Тогда если среди 1, … , встречается формула , то каждое её вхождение заменяем последовательностью формул, составляющих вывод из .
Таким образом, получаем вывод из .
5)Если из формул выводится , а из набора формул , выводится формула , то из набора формул , выводится формула .
Запишем вывод формулы из , . Каждое вхождение в этот вывод заменим выводом из . Получим вывод из , .
2. Исчисление высказываний. Построение ИВ как ФАТ. Алфавит, формулы, аксиомы, выводы и правила вывода
Наиболее употребительными являются 2 системы аксиом:
•Исчисление высказываний.
•Исчисление секвенций.
По существу, обе эти системы составляют одну теорию.
Символы ИВ:
•Алфавит: , , 1, 2, …
•Связки:
o Отрицание ¬ — связка первого порядка. ¬ — «не ».
o Импликация — связка второго порядка. — «из следует ».
o Тождественная истинность ≡ — связка второго порядка. ≡ — « то же самое, что и ».
o Скобки () — порядок действий.
o Знак вывода . — « есть следствие » или « можно вывести из ».
Формулы ИВ:
•Первичные формулы — заглавные буквы латинского алфавита (возможно, с
индексами): , , 1, 2, … Смысл первичных формул в ИВ — каждая буква заменяет высказывание, которое
может быть либо истинным, либо ложным.
•Если и — формулы, то ¬ , ¬ , , — тоже формулы.
•Все остальные формулы получаются из первичных с помощью применения конечного числа связок отрицания ¬ и импликации .
Внешние скобки можно опускать. Например, ((¬ ) ( )) → ¬ .
Отрицание относится непосредственно к наикратчайшей формуле, следующей за этим знаком. Например, ¬ означает (¬) .
Правило вывода формул ИВ только одно: modus ponens (. ., «модус поненс»,
переводится как «правило вывода») — которое состоит в следующем: , («если верно и из следует , то тоже должно быть истинным»).
Аксиомы ИВ (являются независимыми друг от друга): А1. ( ) (утверждение следствия).
А2. ( ( )) (( ) ( )) (самодистрибутивность импликации). А3. (¬ ¬) ((¬ ) ) (рассуждение от противного).
Вместо , и можно подставлять любые формулы ИВ.
(Можно ввести другие системы аксиом, равносильные этим трём.)
3. Доказать, исходя из аксиом ИВ и правила вывода секвенцию ! —
первое свойство выводов ИВ
(рефлексивность импликации). Это означает, что из приведённых выше трёх аксиом следует, что из любой формулы следует сама . Построим вывод:
1)Подставим в аксиому А2 вместо формулы формулу , а вместо — . То есть из этого:
( ( )) (( ) ( ))!
Получим:
( (( ) )) (( ( )) ( )) ! (1)
2)Подставим в аксиому А1 вместо формулы формулу . То есть из этого:
( )!
Получим:
(( ) )! (2)
3)По правилу . . из (1) и (2) непосредственно следует формула:
( ( )) ( )! (3)
4)Подставим в аксиому А1 вместо формулы формулу . То есть из этого:
( )!
Получим

( )! (4)
5)Тогда из формул (3) и (4) по правилу . . выводится нужная формула:
!
4.Доказать, исходя из свойств выводов, аксиом ИВ и правила вывода ИВ
следующие свойства выводов ИВ
2) Если , то , .
. . , !
По свойству №3 («лишняя формула не мешает») и №2 («порядок формул не имеет значения») — добавляем в начало:
, , !
По свойству №4 («удаление выводимой формулы») — так как по условию выводима из , то её можно убрать как выводимую:
, !
3) Если и , то .
. . , !
По свойству №3 («лишняя формула не мешает») и №2 («порядок формул не имеет значения») — добавляем в начало:
, , !
По свойству №4 («удаление выводимой формулы») — так как по условию ивыводимы из , то их можно убрать как выводимые:
!
4) Если и — любая формула ИВ, то .
. . , ( ) ( )!
По свойству №3 («лишняя формула не мешает») и №2 («порядок формул не имеет значения») — добавляем в начало:
, , ( ) ( )! (1)
Так как ( ) — аксиома А1, то (аксиома следует из любых формул):
( )!
По свойству №3 («лишняя формула не мешает») — добавляем :
( )!
Из (1) по свойству №4 («удаление выводимой формулы») — так как по условиюи ( ), то их можно убрать как выводимые:
!
5. Теорема дедукции
Если из формул и выводится формула , то из формул выводится формула
(«если , , то »). (Дедукция — переход от общего к частному.) Метод математической индукции (индукция — это переход от частного к общему):
1.Проверяют истинность утверждения для = 1 ( = 0) — база индукции.
2.Предполагают, что утверждение верно для = — индуктивное предположение.
3.Доказывают, что тогда оно верно и для = + 1 — индуктивный переход.
Доказательство (методом математической индукции по числу — длине вывода). Пусть 1, … , есть вывод из и (то есть 1, … , ).

База индукции. Пусть = 1. Тогда совпадает с 1. Согласно определению вывода возможны 3 случая:
|
1) — аксиома |
2) — формула из |
3) совпадает с |
|
Если 1 — аксиома, то по свойству №3 («лишняя |
Значит совпадает с . |
|
|
формула не мешает») — добавляем , а если 1 — |
По свойству ИВ №1 ( |
|
|
формула из , то ничего не добавляем: в любом из |
!) и свойству №3 («лишняя |
|
|
этих двух случаев можно вывести . |
формула не мешает»): |
|
|
! ( 1!) |
! |
|
|
Тогда, по свойству ИВ №4: |
То есть получили |
|
|
если и — любая формула ИВ, то |
(где совпадает с ). |
|
Допустим теперь, что если длина вывода формулы меньше , то утверждение теоремы верно, и докажем, что тогда теорема верна для длины вывода, равного . При этом возможны 4 случая:
|
1) — аксиома |
2) — формула из |
3) совпадает с |
|||||
|
Доказательство такое же, как при = 1 |
|||||||
|
4) получена по правилу . . из , ( ), где , < |
|||||||
|
то есть , |
( имеет вид ) |
||||||
Отбрасывая последние − формулы из 1, … , , получаем вывод , . Отбрасывая последние − формулы из 1, … , , получаем вывод , . Длины этих выводов меньше и мы имеем:
, ! (1)
, ! ( , )! (2)
Индуктивное предположение (верно для и ):
! (1)
! ( ( ))! (2)
Далее следует индуктивный переход к .
По аксиоме А2:
( ( )) (( ) ( ))!
Имеем ( → , → , свойство №3: «лишняя формула не мешает» — добавляем ):
( ( )) (( ) ( ))! (3) . . к секвенциям (2) и (3):
( ) ( )! (4)
После этого, применяя все то же правило . . к секвенциям (1) и (4) получаем:
!
То есть !
Таким образом, индукция проведена, и теорема дедукции доказана.
6.Свойство транзитивности импликации. Доказать секвенцию: ( ),
Транзитивность импликации (правило силлогизма).
, ?
По свойству ИВ №2 («если , то , ») и свойству №2 («порядок формул не имеет значения»):
, , ?
По свойству №5 («если из формул выводится , а из набора формул , выводится формула , то из набора формул , выводится формула »):
Получаем («если из формул , выводится , а из формул , выводится формула , то из формул , , выводится формула »):
По свойству №2 («порядок формул не имеет значения») и теореме дедукции («если
, , то »):
, !
Доказать секвенцию: ( ), .
( ), ?
По свойству ИВ №2 («если , то , »):
( ), , ?
По свойству №2 («порядок формул не имеет значения»):
( ), , ?
По теореме дедукции («если , , то »):
( ), ?
По теореме дедукции («если , , то »):
( ) ( )?
По свойству №1 (, или ):
( ) ( )!
По свойству ИВ №2 («если , то , »):
( ), !
По свойству ИВ №2 («если , то , »):
( ), , !
По свойству №2 («порядок формул не имеет значения»):
( ), , !
По теореме дедукции («если , , то »):
( ), !

7. Противоречивые формулы
Доказать:
1)Если и ¬ , то («из ложного следует всё, что угодно»).
Пусть — любая формула. Тогда из двух данных секвенций по свойству ИВ №4 («если и — любая формула ИВ, то ») следует, что ¬ и¬ ¬. По аксиоме А3 (заметим, что аксиома следует из любых формул):
(¬ ¬) ((¬ ) )!
По свойству №3 («лишняя формула не мешает») — добавляем :
(¬ ¬ ) ((¬ ) )!
Тогда применяя 2 раза свойство ИВ №2 («если , то , »), получим:
, (¬ ¬), (¬ ) !
По свойству №4 («удаление выводимой формулы») — так как ¬ ¬ и ¬ , то выводимые формулы (¬ ¬) и (¬ ) можно убрать:
!
2)Если , то , ¬ .
По условию:
!
По свойству №3 («лишняя формула не мешает») — добавляем ¬:
, ¬ !
Следующее утверждение также справедливо, так как по свойству №1 (¬ ¬) и по свойству №3 («лишняя формула не мешает») — добавляем :
, ¬ ¬ !
По уже доказанному выше утверждению («если и ¬, то ») — так как
, ¬ и , ¬ ¬, то получим: , ¬ !
8. Обоснование доказательства от противного: доказать, что если , ¬ , то
Доказательство «от противного» — вид доказательства, при котором «доказывание» некоторого суждения (тезиса доказательства) осуществляется через опровержение отрицания этого суждения — антитезиса.
Доказательство утверждения проводится следующим образом. Сначала принимают предположение, что утверждение неверно, а затем доказывают, что при таком предположении было бы верно некоторое утверждение , которое заведомо неверно.
Из определения импликации следует, что, если ложно, то формула ¬ истинна тогда и только тогда, когда ¬ ложно, следовательно утверждение истинно.
Полученное противоречие показывает, что исходное предположение было неверным, и поэтому верно утверждение ¬¬ , которое по закону двойного отрицания равносильно утверждению .
Доказательство №1 (если , ¬ , то ).
Так как , ¬ , то есть из и ¬ выводима любая формула, то, в частности, выводима и формула : , ¬ . Значит, ¬ по теореме дедукции.
По свойству ИВ №1 ( ) из любых формул (в частности, из формул ) выводится ¬ ¬, а по свойству №3: «лишняя формула не мешает»: ¬ ¬.
Сдругой стороны, по аксиоме А3:
(¬ ¬ ) ((¬ ) )!
Имеем ( → , свойство №3: «лишняя формула не мешает» — добавляем ):
(¬ ¬ ) ((¬ ) )!
Применяя 2 раза свойство ИВ №2 («если , то , »), получим:
, (¬ ¬ ), (¬ ) !
По свойству №4 («удаление выводимой формулы») — так как ¬ и ¬ ¬, то, удаляя выводимые формулы ¬ и ¬ ¬, получим: !
Доказательство №2 (если , , то ¬).
В самом начале докажем, что если — любая формула, то , ¬ . По свойству №1 ( ):
!
По свойству №3 («лишняя формула не мешает») — добавляем ¬:
¬ , !
Следующее утверждение также справедливо, так как по свойству №1 (¬ ¬) и по свойству №3 («лишняя формула не мешает») — добавляем :
¬ , ¬ !
То есть ¬ , и ¬ , ¬ — по уже доказанному в 7-ом вопросе утверждению («если и ¬, то ») и свойству №2 («порядок формул не имеет значения»):
, ¬ !
Теперь перейдём к основному доказательству («если , , то ¬»).
Так как по доказанному выше («если — любая формула, то , ¬ ») и свойству №2 («порядок формул не имеет значения»), то имеем:
¬¬ , ¬ !
Так как по доказательству №1 («если , ¬ , то »), то:
¬¬ !
Кроме того, формулы и по условию противоречивы (, ). Тогда по свойству №3 («лишняя формула не мешает») — будут противоречивы 3 формулы:
, ¬¬ !
Как уже было написано, ¬¬ ! — значит по свойству №4 («удаление выводимой формулы») можно удалить выводимую формулу :
, ¬¬ !
Тогда по доказательству №1 («если , ¬ , то ») получаем ¬.
На чтение 7 мин. Просмотров 86 Опубликовано 18.02.2013
Ответы на все модули по предмету математическая логика, для итогового тестирования.
Ответы на модуль 1 (МАТЕМАТИЧЕСКАЯ ЛОГИКА) по предмету математическая логика.
1) Какая из перечисленных функций называется предикатом? функция, переменные которой принимают значения из некоторого произвольного множества M или множеств, возможно, и бесконечных, а сама функция принимает два значения: «истина» и «ложь».
2) Как называется булева функция, если ее можно представить в виде полинома Жегалкина степени не выше первой? линейной.
3) Как называется прием, в результате которого из некоторых данных формул получают их частные случаи? подстановкой.
4) Какая операция называется сколемизацией? операция исключения квантора существования.
5) Что из перечисленного является одноместным предикатом? свойство.
6) Как называется формула , если существуют такие конкретные высказывания , которые превращают данную формулу в ложное высказывание? опровержимой.
7) Как называется логическая операция, соответствующая союзу «если, … то»? импликацией.

9) Как называется перевод высказывания естественного языка на символический язык? формализацией.
10) Как называется класс булевых функций, если он вместе со всеми своими функциями содержит любую их суперпозицию? замкнутым.
11) Какой из перечисленных модусов условно-категоричных силлогизмов является неправильным?
12) Какая из перечисленных операций является одноместной? дополнение.
13) При каком способе задания переключательная функция задается с помощью соответствующей отметки вершин n-мерного куба? при геометрическом способе задания.
14) Как называется предикат, у которого множество истинностей является пересечением множеств истинности исходных предикатов? конъюнкцией предикатов.
15) Как называются символы функций и предикатов? сигнатурой.
16) Укажите правило отыскания совершенной дизъюнктивной нормальной формы для формулы? нужно выбрать все те наборы значений переменных, на которых формула принимает значение 1; для каждого такого набора выписать совершенный конъюнктивный одночлен, принимающий значение 1 на этом наборе и только на нем; полученные совершенные конъюнктивные одночлены соединить знаками дизъюнкции.
17) Какая из перечисленных бинарных логических операций называется конъюнкцией? соединяющая две двоичные переменные a и b, принадлежащие множеству {0, 1}, в такую переключательную функцию c, которая равна 1 только тогда, когда равны 1 обе переменные.
18) Какая из перечисленных записей описывает второй закон Аристотеля — противоречия?
19) Как называют любую элементарную формулу или ее отрицание? литералом.
20) В каком случае дизъюнкция двух предикатов есть выполнимый предикат? тогда и только тогда, когда по меньшей мере один из данных предикатов выполним.
21) В каком случае силлогизм является условным? если обе посылки и вывод — условные высказывания.
22) Какие из перечисленных записей являются законами де Моргана? (x ∨ y)′ = x′ ∙ y′, (x ∙ y)′ = x′ ∨ y′.
23) Как называется множество, элементы которого являются элементами множеств A и B? пересечением множеств A и B.
24) В каком случае класс булевых функций называется собственным? если он не пуст и не совпадает с классом всех булевых функций.
25) Как называется возникающее исчисление предикатов, если в сигнатуре отсутствуют функциональные символы? чистым исчислением предикатов.
Ответы на модуль 2 (ЭЛЕМЕНТЫ ТЕОРИИ АЛГОРИТМОВ) по предмету математическая логика.
1) Какая из перечисленных записей называется формулой подстановки (P, Q)? P -> Q.
2) Как называется функция f, заданная на некотором множестве слов алфавита A? нормально вычислимой функцией.
3) Какое свойство алгоритма означает, что описываемый алгоритмом процесс и сам алгоритм не могут быть разбиты на отдельные элементарные этапы, возможность выполнения которых на ЭВМ у пользователя не вызывает сомнения? дискретность.
4) Какой символ, используемый в схемах алгоритмов, отображает выход во внешнюю среду и вход из внешней среды? терминатор.
5) Какое свойство алгоритма предполагает, что алгоритм может быть пригоден для решения всех задач данного типа? массовость.
6) Какое свойство алгоритма обеспечивает однозначность результата вычислительного процесса при заданных исходных данных? определенность.
7) Сколько входных и выходных лент имеет многоленточная машина Тьюринга? несколько входных лент и одну выходную.

9) Как называется операция получения новой функции по имеющимся функциям: по правилу ? суперпозицией.
10) Как называется правило построения последовательности слов в алфавите A, исходя из данного слова V в этом алфавите? нормальным алгоритмом (Маркова) в этом алфавите.
11) Что записывается на ленте машины Тьюринга? исходные данные и затем — результат.
12) Как называются свойства текстов, описывающих алгоритм? синтаксические свойства.
13) Какая из перечисленных операций называется минимизацией? операция построения новой функции по известной функции по правилу.
14) Какие из перечисленных классов функций (заданных на натуральных числах и принимающих натуральные значения) совпадают? класс всех функций, вычислимых по Тьюрингу, класс всех частично рекурсивных функций и класс всех нормально вычислимых функций.
15) Если A и B — два алфавита, причем , то: алфавит B называется расширением алфавита A.
16) В чем состоит смысл теоремы Райса? в том, что по описанию алгоритма, вычисляющего функцию, ничего нельзя узнать о свойствах функции, которую он вычисляет.
17) Кто является автором тезиса: «Класс интуитивно вычислимых функций совпадает с классом частично рекурсивных функций»? А. Чёрч.
18) Какой символ в схемах алгоритмов может быть использован для обозначения заголовка цикла? подготовка.
19) Какой схемой не может быть представлено предписание о последовательности действий алгоритма? эквивалентной схемой.
20) Какой фигурой обозначается вершина граф-схемы алгоритма операторного типа? прямоугольником.
21) Что из перечисленного является внутренней памятью машины Тьюринга? конечное множество состояний.
22) Для чего в схемах алгоритмов используется символ «процесс»? для обозначения операции присваивания.
23) Какой фигурой в схемах алгоритмов обозначается символ «решение»? ромбом.
24) Чем определяется каждая машина Тьюринга? своим алфавитом, состоянием внутренней памяти и программой.
25) Какая теорема устанавливает алгоритмическую неразрешимость вообще всякого нетривиального свойства вычислимых функций? теорема Райса.
Ответы на модуль 3 (МАТЕМАТИЧЕСКАЯ ЛОГИКА И ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ) по предмету математическая логика.
1) Какой из перечисленных радикалов является оперативной экспертной системой, предметно-ориентированной распределенной базой данных и знаний в форме сети локальных накопителей и преобразователей данных? У-радикал.
2) Какой процесс происходит на этапе эволюции интеллектуальной системы? фундаментальные научные исследования.
3) Что из перечисленного включает в себя оценивание предметной области, генерацию задач и выбор доминирующей задачи? целеполагание интеллектуальных систем.
4) Что из перечисленного является результатом оценивания систем предметной области интеллектуальной системы с точки зрения соответствия базовым требованиям интеллектуальной системы с учетом системного анализа предметной области? целеполагание интеллектуальных систем.
5) Какой характеристикой обладает интеллектуальная система? слабоформальность.
6) Как называется процесс реализации алгоритма решения задачи в форме системокванта в режиме самоорганизации среды радикалов рабочей подсистемы? создание опытного образца системокванта.
7) Как называется задача составления релейно-контактных схем с заданными условиями работы? задачей синтеза.

9) Как называется сенсорная область, в которой происходит сбор семантической информации и ее использование для воздействия на предметную область? терминальная среда.
10) Какое из перечисленных правил вывода описывается формулой ? правило условного оператора.
11) Как называется устройство, осуществляющие перевод чисел из десятичной системы в двоичную? шифратор.
12) Что из перечисленного характерно для кибернетических систем? детерминированное поведение.
13) Как называется логика процессов, в которой выразимы некоторые свойства программы, зависящие от процесса ее выполнения? пропозициональной динамической логикой.
14) Какое соединение реализует дизъюнкцию соответствующих данным контактам булевых переменных? параллельное соединение.
15) К какому классу интеллектуальных систем относятся спутниковая навигационная система, космическая межпланетная станция? к искусственным интеллектуальным системам.
16) Каковы две релейно-контактные схемы, составленные из одних и тех же реле, если они обладают одинаковыми функциями проводимости? схемы равносильны.
17) Что реализует последовательное соединение двух контактов? конъюнкцию соответствующих этим контактам булевых переменных.
18) Как называются системы изменения части объектов внешней или модельной предметной области, образующих опорные множества объектов данных исполнителей? интеллектуальные исполнители.
19) От какой модели алгоритма унаследовало свои основные конструкции современное структурное программирование? рекурсивные функции.
20) Как называется наблюдаемые параметры объекта управления управляющей системы? фазовыми координатами.
21) Какая из перечисленных формул описывает правило бесконечного цикла?
22) Как называется область локальных баз данных и локальных баз знаний, где хранится и преобразуется симантическая информация? ультасреда.
23) Какое правило вывода не преобразует, а лишь говорит о том, что то же f можно использовать и в более частной ситуации, чем A => B? правило релаксации.
24) На каком этапе функционирования интеллектуальной системы происходит серийное производство системокванта в форме радикала? самообучение.
25) Что можно получать в распределенной базе данных? гипертексты.
Ставлю 10/10
Все нравится, очень удобный сайт, помогает в учебе. Кроме этого, можно заработать самому, выставляя готовые учебные материалы на продажу здесь. Рейтинги и отзывы на преподавателей очень помогают сориентироваться в начале нового семестра. Спасибо за такую функцию. Ставлю максимальную оценку.
Отлично
Лучшая платформа для успешной сдачи сессии
Познакомился со СтудИзбой благодаря своему другу, очень нравится интерфейс, количество доступных файлов, цена, в общем, все прекрасно. Даже сам продаю какие-то свои работы.
Отлично
Студизба ван лав ❤
Очень офигенный сайт для студентов. Много полезных учебных материалов. Пользуюсь студизбой с октября 2021 года. Серьёзных нареканий нет. Хотелось бы, что бы ввели подписочную модель и сделали материалы дешевле 300 рублей в рамках подписки бесплатными.
Отлично
Отличный сайт
Лично меня всё устраивает — и покупка, и продажа; и цены, и возможность предпросмотра куска файла, и обилие бесплатных файлов (в подборках по авторам, читай, ВУЗам и факультетам). Есть определённые баги, но всё решаемо, да и администраторы реагируют в течение суток.
Отлично
Маленький отзыв о большом помощнике!
Студизба спасает в те моменты, когда сроки горят, а работ накопилось достаточно. Довольно удобный сайт с простой навигацией и огромным количеством материалов.
Хорошо
Студ. Изба как крупнейший сборник работ для студентов
Тут дофига бывает всего полезного. Печально, что бывают предметы по которым даже одного бесплатного решения нет, но это скорее вопрос к студентам. В остальном всё здорово.
Отлично
Спасательный островок
Если уже не успеваешь разобраться или застрял на каком-то задание поможет тебе быстро и недорого решить твою проблему.
Отлично
Всё и так отлично
Всё очень удобно. Особенно круто, что есть система бонусов и можно выводить остатки денег. Очень много качественных бесплатных файлов.
Отлично
Отзыв о системе «Студизба»
Отличная платформа для распространения работ, востребованных студентами. Хорошо налаженная и качественная работа сайта, огромная база заданий и аудитория.
Хорошо
Отличный помощник
Отличный сайт с кучей полезных файлов, позволяющий найти много методичек / учебников / отзывов о вузах и преподователях.
Отлично
Отлично помогает студентам в любой момент для решения трудных и незамедлительных задач
Хотелось бы больше конкретной информации о преподавателях. А так в принципе хороший сайт, всегда им пользуюсь и ни разу не было желания прекратить. Хороший сайт для помощи студентам, удобный и приятный интерфейс. Из недостатков можно выделить только отсутствия небольшого количества файлов.
Отлично
Спасибо за шикарный сайт
Великолепный сайт на котором студент за не большие деньги может найти помощь с дз, проектами курсовыми, лабораторными, а также узнать отзывы на преподавателей и бесплатно скачать пособия.
Отлично
2. Равносильность формул логики высказываний. Основные равносильности. Примеры.
3. Логическое следствие в логике высказываний. Способы доказательства логических следствий. Анализ правильности рассуждений. Примеры.
4. Нормальные формы формул логики высказываний. Распознавание вида формул (эффективные процедуры). Примеры.
5. Совершенные нормальные формы формул логики высказываний. Теоремы о существовании СКНФ и СДНФ. Примеры.
6. Формальные аксиоматические теории. Алфавит, формула, аксиомы, правила вывода. Понятия вывода и вывода из систем гипотез.
7. Исчисление высказываний (формальная теория L). Алфавит, формулы, аксиомы, правила вывода исчисления высказываний. Примеры.
8. Доказуемость и выводимость формул в исчислении высказываний. Теорема дедукции и ее следствия. Примеры.
9. Автоматическое доказательство теорем. Метод резолюций в исчислении высказываний. Привести пример.
10. Некоторые теоремы исчисления высказываний. Провести доказательство одной теоремы.
11. Проблемы полноты, разрешимости и непротиворечивости исчисления высказываний.
12. Независимость системы аксиом исчисления высказываний. Провести доказательство независимости одной из аксиом. Другие аксиоматизации исчисления высказываний.
13. Определение предиката. Множество истинности предиката (характеристическое множество). Классификация предикатов на множестве. Логические операции над предикатами. Геометрическая интерпретация этих операций на основе понятия
характеристических множеств. Примеры.
14. Кванторы общности и существования. Изменение местности предиката при связывании переменных кванторами. Свободные и связанные переменные. Формулы логики предикатов. Примеры.
15. Классификация формул в логике предикатов. Равносильные формулы логики предикатов. Основные равносильности. Проблема разрешения в логике предикатов. Примеры.
16. Исчисление предикатов. Общезначимость и полнота чистого исчисления предикатов. Метод резолюций в логике предикатов. Пример.
17. Понятие алгоритма. Основные требования. Необходимость уточнения понятия алгоритма. Формализация понятия алгоритма.
18. Формализация понятия алгоритма. Машина Тьюринга. Вычислимость по Тьюрингу. Тезис Черча.
19. Формализация понятия алгоритма. Рекурсивные функции. Примитивно рекурсивные, частично рекурсивные и общерекурсивные функции.
20. Меры сложности вычислений. Легко и трудноразрешимые задачи. Классы задач Р и NP. NP-полные задачи.
21. Основы нечеткой логики. Нечеткие множества. Алгебра нечетких множеств.
Правильные ответы выделены зелёным цветом.
Все ответы: Курс предназначен для знакомства будущих специалистов по информационным технологиям с основами науки о научном мышлении.
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Все кошки хищники. Собака хищник. Следовательно, собака кошка.
Даны значения логических переменных 
F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да — 1. Нет — 0.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
Переведите в десятичную форму записи двоичное число: 1001
Вычислить значение многочлена Жегалкина 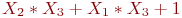
Задана функция 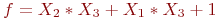
Проверьте, является ли она сохраняющей ноль.
Если да, то 1, если нет то 0.
Задана функция 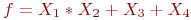
Проверьте, является ли она сохраняющей ноль.
Если да, то 1, если нет то 0.
Пусть латинские буквы обозначают высказывания:
A — общеутвердительное;
E — общеотрицательное;
O — частноотрицательное;
I — частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | A | 1 |
Пусть
 |
 |
|---|---|
| 0 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 0 |
Проверьте, истинно ли утверждение:
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:


 |
 |
 |
|---|---|---|
| 0 | 0 | 0 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Млекопитающие кормят детей своим грудным молоком. Человек — млекопитающее. Доцент Бояршинов — человек. Следовательно, он кормит детей своей грудью.
Даны значения логических переменных 
F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да — 1. Нет — 0.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Переведите в двоичную форму записи десятичное число: 31
Вычислить значение многочлена Жегалкина 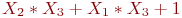
Задана функция 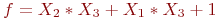
Проверьте, является ли она сохраняющей единицу.
Если да, то 1, если нет то 0.
Задана функция 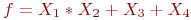
Проверьте, является ли она сохраняющей единицу.
Если да, то 1, если нет то 0.
Задана логическая функция:
Найти значение этой функции для случая:
Пусть латинские буквы обозначают высказывания:
A — общеутвердительное;
E — общеотрицательное;
O — частноотрицательное;
I — частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| E | A | 1 |
Как выглядит на языке кванторов утверждение: «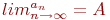
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Пусть
 |
 |
|---|---|
| 0 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 1 |
Проверьте, истинно ли утверждение:
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:


 |
 |
 |
|---|---|---|
| 0 | 0 | 1 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Первый и последний президент СССР — М.С. Горбачёв. Москва — столица СССР. Следовательно, М.С. Горбачёв не проживает в Москве.
Даны значения логических переменных 
F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да — 1. Нет — 0.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Переведите число 101102 в десятичное.
Вычислить значение многочлена Жегалкина 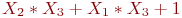
Задана функция 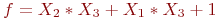
Проверьте, является ли она линейной.
Если да, то 1, если нет то 0.
Задана функция 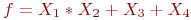
Проверьте, является ли она самодвойственной.
Если да, то 1, если нет то 0.
Задана логическая функция:
Найти значение этой функции для случая:
Пусть латинские буквы обозначают высказывания:
A — общеутвердительное;
E — общеотрицательное;
O — частноотрицательное;
I — частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | A | 2 |
Как выглядит на языке кванторов утверждение: «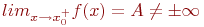
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:


 |
 |
 |
|---|---|---|
| 0 | 1 | 0 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
В Риме сохранились постройки времён Юлия Цезаря.
Даны значения логических переменных 
F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да — 1. Нет — 0.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проведите сложение двух пятизначных двоичных слагаемых: 
В ответе приведите значение второго слагаемого в десятичной форме.
Вычислить значение многочлена Жегалкина 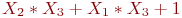
Задана функция 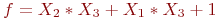
Проверьте, является ли она самодвойственной.
Если да, то 1, если нет то 0.
Задана функция 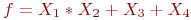
Проверьте, является ли она монотонной.
Если да, то 1, если нет то 0.
Задана логическая функция:
Найти значение этой функции для случая:
Пусть латинские буквы обозначают высказывания:
A — общеутвердительное;
E — общеотрицательное;
O — частноотрицательное;
I — частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| E | A | 2 |
Как выглядит на языке кванторов утверждение: «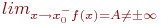
Пусть
 |
 |
|---|---|
| 1 | 1 |
Проверьте, истинно ли утверждение:
Проведите сложение двух пятизначных двоичных слагаемых: 
В ответе приведите значение второго слагаемого в десятичной форме.
Пусть
 |
 |
|---|---|
| 1 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 1 |
Проверьте, истинно ли утверждение:
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:


 |
 |
 |
|---|---|---|
| 0 | 1 | 1 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Шесть делится на два без остатка и 7 — простое число.
Даны значения логических переменных 
F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да — 1. Нет — 0.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проведите сложение двух пятизначных двоичных слагаемых: 
В ответе приведите значение суммы в двоичной форме.
Вычислить значение многочлена Жегалкина 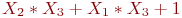
Задана функция 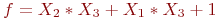
Проверьте, является ли она монотонной.
Если да, то 1, если нет то 0.
Задана функция 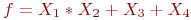
Проверьте, является ли она линейной.
Если да, то 1, если нет то 0.
Задана логическая функция:
Найти значение этой функции для случая:
Пусть латинские буквы обозначают высказывания:
A — общеутвердительное;
E — общеотрицательное;
O — частноотрицательное;
I — частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | A | 3 |
Как выглядит на языке кванторов утверждение: «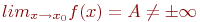
Пусть
 |
 |
|---|---|
| 0 | 0 |
Проверьте, истинно ли утверждение: 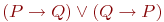
Вычислить значение многочлена Жегалкина 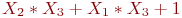
Пусть
 |
 |
|---|---|
| 0 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 0 |
Чему равно выражение 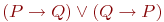
Пусть
 |
 |
|---|---|
| 0 | 0 |
Проверьте, истинно ли утверждение: 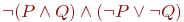
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:


 |
 |
 |
|---|---|---|
| 1 | 0 | 0 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
13 — простое число, как и его квадрат.
Даны значения логических переменных 
F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да — 1. Нет — 0.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проведите сложение двух пятизначных двоичных слагаемых: 
В ответе приведите значение суммы в десятичной форме.
Вычислить значение многочлена Жегалкина 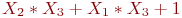
Заданы три функции:
f_1=X_2*X_3+X_1*X_3+1;\
f_2=X_1+X_2+X_2*X_3+1+X_1*X_2*X_3;\
f_3=X_1*X_2+X_3+1
Функция 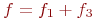
Проверьте, является ли она сохраняющей ноль.
Если да, то 1, если нет то 0.
Задана функция 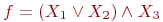
Проверьте, является ли она сохраняющей ноль.
Если да, то 1, если нет то 0.
Задана логическая функция:
Найти значение этой функции для случая:
Пусть латинские буквы обозначают высказывания:
A — общеутвердительное;
E — общеотрицательное;
O — частноотрицательное;
I — частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| E | A | 3 |
Как выглядит на языке кванторов утверждение: «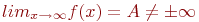
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Заданы три функции:
f_1=X_2*X_3+X_1*X_3+1;\
F_2=X_1+X_2+X_2*X_3+1+X_1*X_2*X_3;\
F_3=X_1*X_2+X_3+1.
Функция 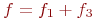
Проверьте, является ли она сохраняющей ноль.
Если да, то 1, если нет то 0.
Пусть
 |
 |
|---|---|
| 0 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 1 |
Проверьте, истинно ли утверждение:
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:


 |
 |
 |
|---|---|---|
| 1 | 0 | 1 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Байт — это 8 бит.
Даны значения логических переменных 
F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да — 1. Нет — 0.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проведите сложение двух пятизначных двоичных слагаемых: 
В ответе приведите значение суммы в двоичной форме, ограничившись пятью младшими разрядами.
Условия.
Вычислить значение многочлена Жегалкина 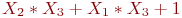
Заданы три функции:
f_1=X_2*X_3+X_1*X_3+1;\
f_2=X_1+X_2+X_2*X_3+1+X_1*X_2*X_3;\
f_3=X_1*X_2+X_3+1
Функция 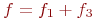
Проверьте, является ли она сохраняющей единицу.
Если да, то 1, если нет то 0.
Задана функция 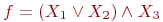
Проверьте, является ли она сохраняющей единицу.
Если да, то 1, если нет то 0.
Задана логическая функция:
Найти значение этой функции для случая:
Пусть латинские буквы обозначают высказывания:
A — общеутвердительное;
E — общеотрицательное;
O — частноотрицательное;
I — частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | A | 4 |
Как выглядит на языке кванторов утверждение: «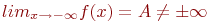
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:
где
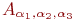
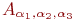
Задана функция 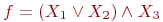
Проверьте, является ли она сохраняющей единицу.
Если да, то 1, если нет то 0.
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение: 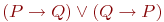
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:


 |
 |
 |
|---|---|---|
| 1 | 1 | 0 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
В логике любое высказывание либо истинно, либо ложно.
Даны значения логических переменных 
F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да — 1. Нет — 0.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проведите сложение двух пятизначных двоичных слагаемых: 
Вычислить значение многочлена Жегалкина 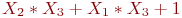
Заданы три функции:
f_1=X_2*X_3+X_1*X_3+1;\
f_2=X_1+X_2+X_2*X_3+1+X_1*X_2*X_3;\
f_3=X_1*X_2+X_3+1
Функция 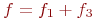
Проверьте, является ли она самодвойственной.
Если да, то 1, если нет то 0.
Задана функция 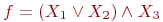
Проверьте, является ли она монотонной.
Если да, то 1, если нет то 0.
Задана логическая функция:
Найти значение этой функции для случая:
Пусть латинские буквы обозначают высказывания:
A — общеутвердительное;
E — общеотрицательное;
O — частноотрицательное;
I — частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| E | A | 4 |
Что означает записанное на языке кванторов утверждение: «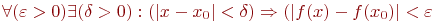
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:
где


Задана логическая функция:
Найти значение этой функции для случая:
 |
 |
 |
|---|---|---|
| 1 | 1 | 1 |
Пусть
 |
 |
|---|---|
| 1 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 1 |
Проверьте, истинно ли утверждение:
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:


 |
 |
 |
|---|---|---|
| 1 | 1 | 1 |
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Задана логическая функция:
Найти значение этой функции для случая:
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Все кошки хищники. Хищники питаются убитыми ими животными. Кошка, поедающая украденные со стола куриные окорока, убила всех этих птиц.
Даны значения логических переменных 
F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да — 1. Нет — 0.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
Переведите в десятичную форму записи двоичное число: 11001
Вычислить значение многочлена Жегалкина 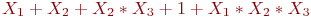
Задана функция 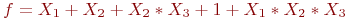
Проверьте, является ли она сохраняющей ноль.
Если да, то 1, если нет то 0.
Задана функция 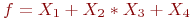
Проверьте, является ли она сохраняющей ноль.
Если да, то 1, если нет то 0.
Пусть латинские буквы обозначают высказывания:
A — общеутвердительное;
E — общеотрицательное;
O — частноотрицательное;
I — частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | E | 1 |
Пусть
 |
 |
|---|---|
| 0 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 0 |
Проверьте, истинно ли утверждение:
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:


 |
 |
 |
|---|---|---|
| 0 | 0 | 0 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Киты и львы млекопитающие. Киты пьют солёную воду, следовательно львы пьют пресную.
Даны значения логических переменных 
F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да — 1. Нет — 0.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Переведите в двоичную форму записи десятичное число: 27
Вычислить значение многочлена Жегалкина 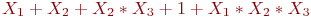
Задана функция 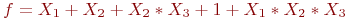
Проверьте, является ли она сохраняющей единицу.
Если да, то 1, если нет то 0.
Задана функция 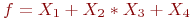
Проверьте, является ли она сохраняющей единицу.
Если да, то 1, если нет то 0.
Задана логическая функция:
Найти значение этой функции для случая:
Пусть латинские буквы обозначают высказывания:
A — общеутвердительное;
E — общеотрицательное;
O — частноотрицательное;
I — частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| E | I | 1 |
Как выглядит на языке кванторов утверждение: «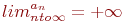
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Пусть
 |
 |
|---|---|
| 0 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 1 |
Проверьте, истинно ли утверждение:
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:


 |
 |
 |
|---|---|---|
| 0 | 0 | 1 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Алюминий плотнее свинца.
Даны значения логических переменных 
F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да — 1. Нет — 0.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Найти сумму: 110102+101112. В ответе приведите значение в десятичной форме.
Вычислить значение многочлена Жегалкина 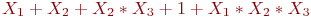
Задана функция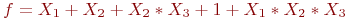
Проверьте, является ли она линейной.
Если да, то 1, если нет то 0.
Задана функция 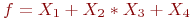
Проверьте, является ли она самодвойственной.
Если да, то 1, если нет то 0.
Задана логическая функция:
Найти значение этой функции для случая:
Пусть латинские буквы обозначают высказывания:
A — общеутвердительное;
E — общеотрицательное;
O — частноотрицательное;
I — частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | E | 2 |
Как выглядит на языке кванторов утверждение: «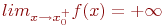
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение: 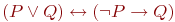
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:


 |
 |
 |
|---|---|---|
| 0 | 1 | 0 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.

Даны значения логических переменных 
F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да — 1. Нет — 0.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проведите сложение двух пятизначных двоичных слагаемых: 
В ответе приведите значение второго слагаемого в десятичной форме.
Вычислить значение многочлена Жегалкина 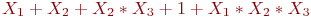
Задана функция 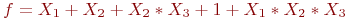
Проверьте, является ли она самодвойственной.
Если да, то 1, если нет то 0.
Задана функция 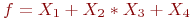
Проверьте, является ли она монотонной.
Если да, то 1, если нет то 0.
Задана логическая функция:
Найти значение этой функции для случая:
Пусть латинские буквы обозначают высказывания:
A — общеутвердительное;
E — общеотрицательное;
O — частноотрицательное;
I — частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| E | I | 2 |
Как выглядит на языке кванторов утверждение: «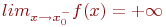
Пусть
 |
 |
|---|---|
| 1 | 1 |
Проверьте, истинно ли утверждение: 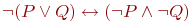
Проведите сложение двух пятизначных двоичных слагаемых: 
В ответе приведите значение второго слагаемого в десятичной форме.
Пусть
 |
 |
|---|---|
| 1 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 1 |
Проверьте, истинно ли утверждение:
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:


 |
 |
 |
|---|---|---|
| 0 | 1 | 1 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Шесть делится на три без остатка, поэтому оно простое число.
Условия.
Даны значения логических переменных 
F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да — 1. Нет — 0.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проведите сложение двух пятизначных двоичных слагаемых: 
В ответе приведите значение суммы в двоичной форме.
Вычислить значение многочлена Жегалкина 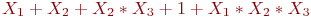
Задана функция 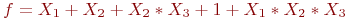
Проверьте, является ли она монотонной.
Если да, то 1, если нет то 0.
Задана функция 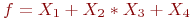
Проверьте, является ли она линейной.
Если да, то 1, если нет то 0.
Задана логическая функция:
Найти значение этой функции для случая:
Пусть латинские буквы обозначают высказывания:
A — общеутвердительное;
E — общеотрицательное;
O — частноотрицательное;
I — частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | E | 3 |
Как выглядит на языке кванторов утверждение: «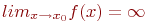
Пусть
 |
 |
|---|---|
| 0 | 0 |
Проверьте, истинно ли утверждение:
Вычислить значение многочлена Жегалкина 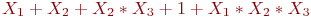
Пусть
 |
 |
|---|---|
| 0 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 0 |
Проверьте, истинно ли утверждение:
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:


 |
 |
 |
|---|---|---|
| 1 | 0 | 0 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
225 — это значение квадрата числа 15.
Даны значения логических переменных 
F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да — 1. Нет — 0.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проведите сложение двух пятизначных двоичных слагаемых: 
В ответе приведите значение суммы в десятичной форме.
Вычислить значение многочлена Жегалкина 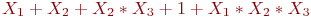
Заданы три функции:
f_1=X_2*X_3+X_1*X_3+1;\
f_2=X_1+X_2+X_2*X_3+1+X_1*X_2*X_3;\
f_3=X_1*X_2+X_3+1
Функция 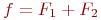
Проверьте, является ли она сохраняющей ноль.
Если да, то 1, если нет — 0.
Задана функция 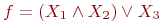
Проверьте, является ли она сохраняющей ноль.
Если да, то 1, если нет то 0.
Задана логическая функция:
Найти значение этой функции для случая:
Пусть латинские буквы обозначают высказывания:
A — общеутвердительное;
E — общеотрицательное;
O — частноотрицательное;
I — частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| E | I | 3 |
Как выглядит на языке кванторов утверждение: «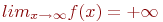
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Заданы три функции:
f_1=X_2*X_3+X_1*X_3+1;\
F_2=X_1+X_2+X_2*X_3+1+X_1*X_2*X_3;\
F_3=X_1*X_2+X_3+1.
Функция 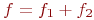
Проверьте, является ли она сохраняющей ноль.
Если да, то 1, если нет то 0.
Пусть
 |
 |
|---|---|
| 0 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 1 |
Проверьте, истинно ли утверждение:
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:


 |
 |
 |
|---|---|---|
| 1 | 0 | 1 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Волга впадает в Каспийское море.
Даны значения логических переменных 
F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да — 1. Нет — 0.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проведите сложение двух пятизначных двоичных слагаемых: 
В ответе приведите значение суммы в двоичной форме, ограничившись пятью младшими разрядами.
Вычислить значение многочлена Жегалкина 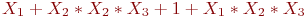
Заданы три функции:
f_1=X_2*X_3+X_1*X_3+1;\
f_2=X_1+X_2+X_2*X_3+1+X_1*X_2*X_3;\
f_3=X_1*X_2+X_3+1
Функция 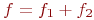
Проверьте, является ли она сохраняющей единицу.
Если да, то 1, если нет то 0.
Задана функция 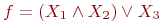
Проверьте, является ли она сохраняющей единицу.
Если да, то 1, если нет то 0.
Задана логическая функция:
Найти значение этой функции для случая:
Пусть латинские буквы обозначают высказывания:
A — общеутвердительное;
E — общеотрицательное;
O — частноотрицательное;
I — частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | E | 4 |
Как выглядит на языке кванторов утверждение: «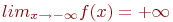
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:
где
X^{alpha}=begin{cases}X,; mbox{если};alpha=1,\
neg X, ; mbox{если}; alpha=0 end{cases},
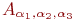
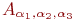
Задана функция 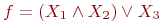
Проверьте, является ли она сохраняющей единицу.
Если да, то 1, если нет то 0.
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:


 |
 |
 |
|---|---|---|
| 1 | 0 | 0 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Если о высказывании нельзя однозначно сказать истинно оно или ложно, то это не высказывание.
Даны значения логических переменных 
F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да — 1. Нет — 0.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проведите сложение двух пятизначных двоичных слагаемых: 
Вычислить значение многочлена Жегалкина 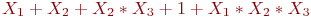
Заданы три функции:
f_1=X_2*X_3+X_1*X_3+1;\
f_2=X_1+X_2+X_2*X_3+1+X_1*X_2*X_3;\
f_3=X_1*X_2+X_3+1
Функция 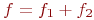
Проверьте, является ли она самодвойственной.
Если да, то 1, если нет то 0.
Задана функция 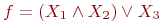
Проверьте, является ли она монотонной.
Если да, то 1, если нет то 0.
Задана логическая функция:
Найти значение этой функции для случая:
Пусть латинские буквы обозначают высказывания:
A — общеутвердительное;
E — общеотрицательное;
O — частноотрицательное;
I — частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| E | I | 4 |
Что означает записанное на языке кванторов утверждение: «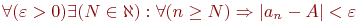
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:
где


Задана логическая функция:
Найти значение этой функции для случая:
 |
 |
 |
|---|---|---|
| 1 | 1 | 1 |
Пусть
 |
 |
|---|---|
| 1 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 1 |
Проверьте, истинно ли утверждение:
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:


 |
 |
 |
|---|---|---|
| 1 | 1 | 1 |
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Задана логическая функция:
Найти значение этой функции для случая:
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Все хищники убивают своих жертв. Лев убил антилопу. Значит он хищник.
Даны значения логических переменных 
F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да — 1. Нет — 0.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
Переведите в десятичную форму записи двоичное число: 10101
Вычислить значение многочлена Жегалкина 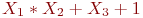
Задана функция 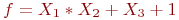
Проверьте, является ли она сохраняющей ноль.
Если да, то 1, если нет то 0.
Задана функция 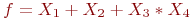
Проверьте, является ли она сохраняющей ноль.
Если да, то 1, если нет то 0.
Пусть латинские буквы обозначают высказывания:
A — общеутвердительное;
E — общеотрицательное;
O — частноотрицательное;
I — частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя, укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | I | 1 |
Пусть
 |
 |
|---|---|
| 0 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 0 |
Проверьте, истинно ли утверждение:
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:


 |
 |
 |
|---|---|---|
| 0 | 0 | 0 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0:
Первый и последний президент СССР — М.С. Горбачёв. Москва — столица СССР. Следовательно, М.С. Горбачёв проживает в Москве.
Даны значения логических переменных 
F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да — 1. Нет — 0.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Переведите в двоичную форму записи десятичное число: 29
Вычислить значение многочлена Жегалкина 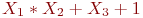
Задана функция 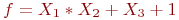
Проверьте, является ли она сохраняющей единицу.
Если да, то 1, если нет то 0.
Задана функция 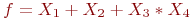
Проверьте, является ли она сохраняющей единицу.
Если да, то 1, если нет то 0.
Задана логическая функция:
Найти значение этой функции для случая:
Пусть латинские буквы обозначают высказывания:
A — общеутвердительное;
E — общеотрицательное;
O — частноотрицательное;
I — частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | O | 1 |
Как выглядит на языке кванторов утверждение: «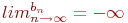
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Пусть
 |
 |
|---|---|
| 0 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 1 |
Проверьте, истинно ли утверждение:
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:


 |
 |
 |
|---|---|---|
| 0 | 0 | 1 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Золото дороже серебра.
Даны значения логических переменных 
F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да — 1. Нет — 0.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проведите сложение двух пятизначных двоичных слагаемых: 
В ответе приведите значение первого слагаемого в десятичной форме.
Вычислить значение многочлена Жегалкина 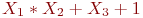
Задана функция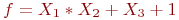
Проверьте, является ли она линейной.
Если да, то 1, если нет то 0.
Задана функция 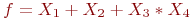
Проверьте, является ли она самодвойственной.
Если да, то 1, если нет то 0.
Задана логическая функция:
Найти значение этой функции для случая:
Пусть латинские буквы обозначают высказывания:
A — общеутвердительное;
E — общеотрицательное;
O — частноотрицательное;
I — частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | I | 2 |
Как выглядит на языке кванторов утверждение: «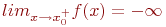
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:


 |
 |
 |
|---|---|---|
| 0 | 1 | 0 |
Оцените истинность или ложность высказывания:
2+2=4 или 2 * 2=5.
Если высказывание истинно, то введите ответ 1, если ложно, то введите 0.
Даны значения логических переменных 
F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да — 1. Нет — 0.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проведите сложение двух пятизначных двоичных слагаемых: 
В ответе приведите значение второго слагаемого в десятичной форме.
Вычислить значение многочлена Жегалкина 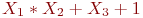
Задана функция 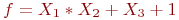
Проверьте, является ли она самодвойственной.
Если да, то 1, если нет то 0.
Задана функция 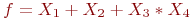
Проверьте, является ли она монотонной.
Если да, то 1, если нет то 0.
Задана логическая функция:
Найти значение этой функции для случая:
Пусть латинские буквы обозначают высказывания:
A — общеутвердительное;
E — общеотрицательное;
O — частноотрицательное;
I — частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | O | 2 |
Как выглядит на языке кванторов утверждение: «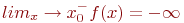
Пусть
 |
 |
|---|---|
| 1 | 1 |
Проверьте, истинно ли утверждение:
Проведите сложение двух пятизначных двоичных слагаемых: 
В ответе приведите значение второго слагаемого в десятичной форме.
Пусть
 |
 |
|---|---|
| 1 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 1 |
Проверьте, истинно ли утверждение:
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:


 |
 |
 |
|---|---|---|
| 0 | 1 | 1 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
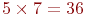
Даны значения логических переменных 
F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да — 1. Нет — 0.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проведите сложение двух пятизначных двоичных слагаемых: 
В ответе приведите значение суммы в двоичной форме.
Вычислить значение многочлена Жегалкина 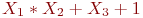
Задана функция 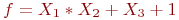
Проверьте, является ли она монотонной.
Если да, то 1, если нет то 0.
Задана функция 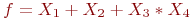
Проверьте, является ли она линейной.
Если да, то 1, если нет то 0.
Задана логическая функция:
Найти значение этой функции для случая:
Пусть латинские буквы обозначают высказывания:
A — общеутвердительное;
E — общеотрицательное;
O — частноотрицательное;
I — частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | I | 3 |
Как выглядит на языке кванторов утверждение: «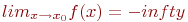
Пусть
Проверьте, истинно ли утверждение:
Вычислить значение многочлена Жегалкина 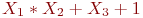
Пусть
 |
 |
|---|---|
| 0 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
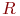 |
|---|---|---|
| 0 | 0 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 0 |
Проверьте, истинно ли утверждение:
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:


 |
 |
 |
|---|---|---|
| 1 | 0 | 0 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
1024 — это 2 в 10-й степени.
Даны значения логических переменных 
F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да — 1. Нет — 0.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проведите сложение двух пятизначных двоичных слагаемых: 
В ответе приведите значение суммы в десятичной форме.
Вычислить значение многочлена Жегалкина 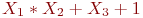
Заданы три функции:
f_1=X_2*X_3+X_1*X_3+1;\
f_2=X_1+X_2+X_2*X_3+1+X_1*X_2*X_3;\
f_3=X_1*X_2+X_3+1
Функция 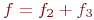
Проверьте, является ли она сохраняющей ноль.
Если да, то 1, если нет то 0.
Задана функция 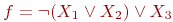
Проверьте, является ли она сохраняющей ноль.
Если да, то 1, если нет то 0.
Задана логическая функция:
Найти значение этой функции для случая:
Пусть латинские буквы обозначают высказывания:
A — общеутвердительное;
E — общеотрицательное;
O — частноотрицательное;
I — частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | O | 3 |
Как выглядит на языке кванторов утверждение: «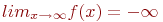
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Заданы три функции:
f_1=X_2*X_3+X_1*X_3+1;\
F_2=X_1+X_2+X_2*X_3+1+X_1*X_2*X_3;\
F_3=X_1*X_2+X_3+1.
Функция 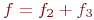
Проверьте, является ли она сохраняющей ноль.
Если да, то 1, если нет то 0.
Пусть
 |
 |
|---|---|
| 0 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
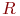 |
|---|---|---|
| 0 | 1 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 0 | 1 |
Проверьте, истинно ли утверждение:
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:


 |
 |
 |
|---|---|---|
| 1 | 0 | 1 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0:
Волга в сердце впадает моё
Даны значения логических переменных 
F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да — 1. Нет — 0.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проведите сложение двух пятизначных двоичных слагаемых: 
В ответе приведите значение суммы в двоичной форме, ограничившись пятью младшими разрядами.
Вычислить значение многочлена Жегалкина 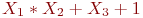
Заданы три функции:
f_1=X_2*X_3+X_1*X_3+1;\
f_2=X_1+X_2+X_2*X_3+1+X_1*X_2*X_3;\
f_3=X_1*X_2+X_3+1
Функция 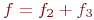
Проверьте, является ли она сохраняющей единицу.
Если да, то 1, если нет то 0.
Задана функция 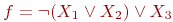
Проверьте, является ли она сохраняющей единицу.
Если да, то 1, если нет то 0.
Задана логическая функция:
Найти значение этой функции для случая:
Пусть латинские буквы обозначают высказывания:
A — общеутвердительное;
E — общеотрицательное;
O — частноотрицательное;
I — частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | I | 4 |
Как выглядит на языке кванторов утверждение: «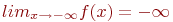
Представьте формулу алгебры высказываний в дизъюнктивной нормальной форме:
где
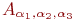
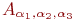
Задана функция 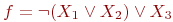
Проверьте, является ли она сохраняющей единицу.
Если да, то 1, если нет то 0.
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
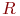 |
|---|---|---|
| 1 | 0 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 0 |
Проверьте, истинно ли утверждение:
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:


 |
 |
 |
|---|---|---|
| 1 | 1 | 0 |
Оцените истинность или ложность высказывания. Если высказывание истинно, то ответ 1, если ложно, то 0.
Следующее выражение является высказыванием: «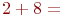
Даны значения логических переменных 
F1, F2, F3, F4, F5, F6, G. Можно ли утверждать, что функция G не следует из функций F1, F2, F3, F4, F5, F6 как из посылок. Да — 1. Нет — 0.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проведите сложение двух пятизначных двоичных слагаемых: 
Вычислить значение многочлена Жегалкина 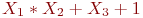
Заданы три функции:
f_1=X_2*X_3+X_1*X_3+1;\
f_2=X_1+X_2+X_2*X_3+1+X_1*X_2*X_3;\
f_3=X_1*X_2+X_3+1
Функция 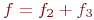
Проверьте, является ли она самодвойственной.
Если да, то 1, если нет то 0.
Задана функция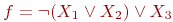
Проверьте, является ли она монотонной.
Если да, то 1, если нет то 0.
Задана логическая функция:
Найти значение этой функции для случая:
Пусть латинские буквы обозначают высказывания:
A — общеутвердительное;
E — общеотрицательное;
O — частноотрицательное;
I — частноутвердительное.
Пусть известно, какими высказываниями являются большая и малая посылки силлогизма. Также известна фигура силлогизма: 1; 2; 3 или 4. Укажите в ответе, каким высказыванием является заключение: A; E; O; I (буквы латинские). Если заключение сделать для заданной фигуры силлогизма нельзя укажите в ответе латинскую букву X.
| Большая посылка | Малая посылка | Фигура силлогизма |
|---|---|---|
| A | O | 4 |
Что означает записанное на языке кванторов утверждение: 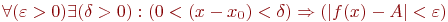
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:
где


Задана логическая функция:
Найти значение этой функции для случая:
 |
 |
 |
|---|---|---|
| 1 | 1 | 1 |
Пусть
 |
 |
|---|---|
| 1 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
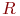 |
|---|---|---|
| 1 | 1 | 1 |
Проверьте, истинно ли утверждение:
Пусть
 |
 |
|---|---|
| 1 | 1 |
Проверьте, истинно ли утверждение:
Представьте формулу алгебры высказываний в конъюнктивной нормальной форме:


 |
 |
 |
|---|---|---|
| 1 | 1 | 1 |
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Проверьте справедливость утверждающе отрицающего модуса
Определите: выполняются ли условия посылки для случая:
Задана логическая функция:
Найти значение этой функции для случая:
Математическая логика — это раздел математики, изучающий математические обозначения, формальные системы, доказуемость математических суждений, природу математического доказательства в целом, вычислимость и прочие аспекты оснований математики.
Алгебра высказываний
Под высказыванием понимаем всякое утверждение (повествовательное предложение), про которое всегда определенно и объективно можно сказать, является оно истинным или ложным. Например, «5-3 = 2» или «В неделе семь дней» — истинные высказывания, а «5 > 8» или «В русском языке 35 букв» — ложные высказывания. Синонимами слова «высказывания» можно считать: логическое высказывание, булевское выражение, суждение, утверждение и т.п. Фразы: «Ура!», «Который час?» — не являются высказываниями.
Если высказывание истинное, то ему предписывается значение «истина» (другие обозначения: «1», «ДА» , «И», «+», «true»). Ложному высказыванию предписывается значение «ложь» (другие обозначения: «О», «НЕТ», «Л», «-«, «false»). Совокупность возможных значений высказывания образует множество истинности {0,1} и {И,Л}.
Есть два вида высказываний: простые и составные (сложные). Под простым будем понимать высказывание, которое не может быть разбито на более простые высказывания. Про него всегда однозначно можно сказать, что оно истинно или ложно, не интересуясь его структурой. Из простых высказываний при помощи логических операций можно строить сложные высказывания, которые всегда только истинны или только ложные. Высказывания обозначаются заглавными латинскими буквами: 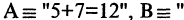
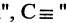
Логические операции
Операции над высказываниями задают в виде таблиц, называемых таблицами истинности.
Отрицание высказывания
Для каждого высказывания А может быть сформировано новое высказывание 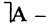
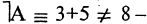
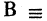
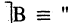
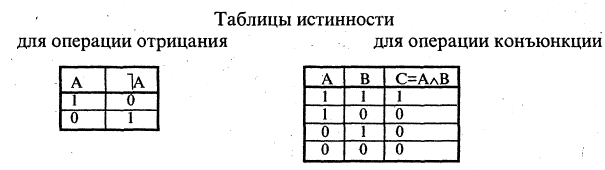
Конъюнкция высказываний
Конъюнкцией высказываний А и В называется высказывание 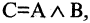

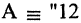
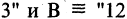

Операцию конъюнкции можно определить и для нескольких высказываний как связку высказываний, объединенных союзом «и». Конъюнкция из п высказываний — новое высказывание, причем высказывание
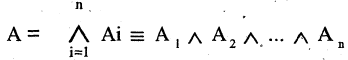
имеет значение «истина», если 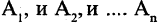
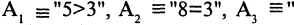
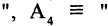
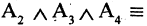
Мурманск севернее Смоленска») — ложное высказывание. В то время как 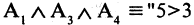
Дизъюнкция высказываний
Дизъюнкцией высказываний А и В называется высказывание 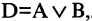

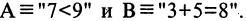
Операцию дизъюнкции можно определить для нескольких высказываний как связку высказываний, объединенных союзом «или»,
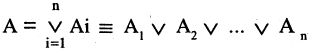
В этом случае высказывание А истинно, если истинно хотя бы одно из высказываний, входящих в связку.
Импликация высказываний
Импликацией высказываний А и В называется высказывание 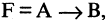
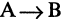
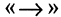


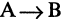

Пусть А и В истинны. Тогда папа, получив премию, покупает сыну велосипед. Естественно считать это истинным высказыванием. Когда же папа не купит сыну велосипед (В — ложно), получив премию (А — истинно), то это, мягко говоря, не логичный поступок, а импликация имеет значение «ложь». Если же папа не получит премию (А — ложно), но купит велосипед (В -истинно), то результат положителен. В том случае, если, не получив премии (А ложно), папа не купит велосипед (В — ложно) -обещание не нарушено, результат можно считать истинным.
Эквивалентность высказываний
Эквивалентностью высказываний А и В называется высказывание 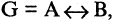
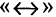






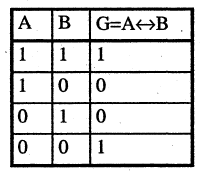
Замечание. Характерной особенностью операций над высказываниями является введение логических союзов с точно определенным смыслом, не допускающим никакой двусмысленности в толковании этих символов. Таким образом, математическая логика применима не для любых высказываний, а только для таких, которые допуск кают четкую оценку в двоичной системе «истина — ложь». Для преодоления такого рода ограничений в рамках нечеткой математики разрабатывается нечеткая логика.
Если в выражении встречаются различные логические операции, то в качестве естественного порядка (выполняемого поочередно слева направо) используется следующая последовательность: 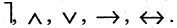
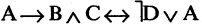
Введя скобки, получим формулу 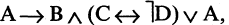
Если в выражении присутствуют арифметические операции, операции сравнения и логические операции, то порядок старшинства операций следующий:
Использование различных операций позволяет в удобной аналитической форме задавать различные множества.
Например, множество точек А, заштрихованное на рис. 1.16, может быть задано следующей формулой:
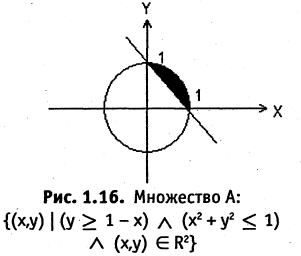
Система операций 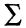
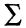
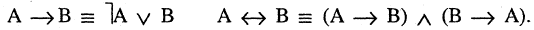
Булевы функции
Всякую формулу логики высказываний можно рассматривать как некоторую функцию: каждая буква (высказывание) может принимать одно из двух значений — «истина» или «ложь», при этом сложное высказывание, заданное этой формулой, также может быть истинным или ложным. Так формула
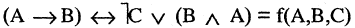
выражает функцию от переменных А, В и С.
Такого рода функции называются булевыми, а их аргументы — булевыми переменными. Аргументы булевых функций могут представлять собой, сокращенные обозначения некоторых конкретных высказываний. Тогда функция обозначает сокращенную запись некоторого сложного высказывания. Например, 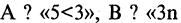
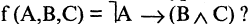
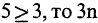
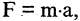
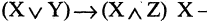
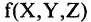
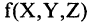
Целый ряд булевых функций обладает тем свойством, что они принимают одни и те же значения при любых значениях истинности аргументов. Такие формулы называются тождественно истинными. Например, при любых X и Y истинны формулы 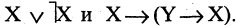
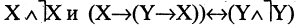
Наиболее важные тождественно истинные формулы получили название Основные законы математической логики.
Основные законы математической логики
1.Коммутативность
2.Ассоциативность
3.Дистрибутивность
4.Законы де Моргана
5.Закон поглощения
6.Закон идемпотентности
8.Закон противоречия
9.Закон исключения третьего
10.Закон двойного отрицания
Пример:
Упростить выражение, используя тождественны преобразования
Существует бесконечное множество тавтологий. Некоторы из них легли в основу методов доказательства.
Основные методы доказательств
При построении любой теории выделяется некоторый набор высказываний, так называемых аксиом, истинность которых постулируется. Из аксиом чисто логическим путем может был установлена истинность некоторых других высказываний называемых теоремами. Последовательность высказываний рассматриваемой теории, каждое из которых либо является аксиомой, либо выводится из одного или более предыдущих высказываний этой последовательности по логическим правилам вывода, называется доказательством. Высказывание, которое можно доказать, называется теоремой.
Формально каждая теорема может быть выражена в форме импликации 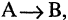
Метод цепочек импликаций
Метод цепочек импликаций состоит в том, что из посылки А страивается цепочка из 
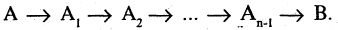
В основе этого метода лежит закон цепного высказывания или закон силлогизма
Метод от противного
Метод от противного. Используя этот метод, вместо доказательства прямого следствия «из А следует В» доказывают, что из «не В» следует «не А». Этот метод основан на законе контрапозиций, имеющем следующий вид:
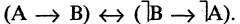
Метод необходимого и достаточного
Метод необходимого и достаточного. Теорема формулируется так: «Чтобы имело место А, необходимо и достаточно выполнение В». Доказательство такого вида теоремы распадается на две части:
а) доказывается, что если имеет место А, то справедливо В (В необходимо для А);
б) если имеет место В, то имеет место и А (В достаточно для А).
Доказательство таким методом базируется на законе тавтологии:
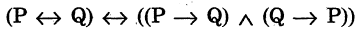
Алгебра предикатов
Предикатом 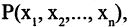
называется функция Р, отображающая их прямое произведение на двоичное множество, т. е. 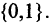
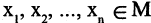
Рассмотрим примеры, 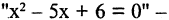
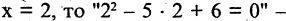
положив 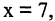
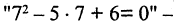
Всякий предикат 
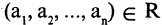
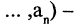

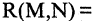
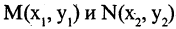
Если в 
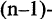
Логические операции над предикатами
Отрицание предиката
Пусть предикат 
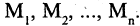


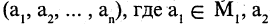
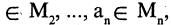
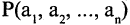
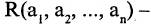
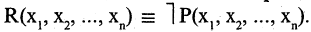
Например, предикат «

Конъюнкция предикатов
Пусть на множествах 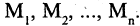

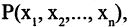

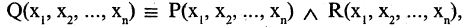
который истинен для одних и тех же кортежей только тогда, когда оба предиката — и 
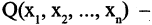
Например, конъюнкция предикатов 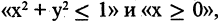
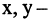
Дизъюнкция предикатов
Дизъюнкция предикатов 


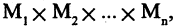


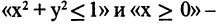
Импликация предикатов
Импликация предикатов 

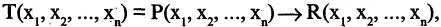
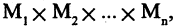


Например, импликация «



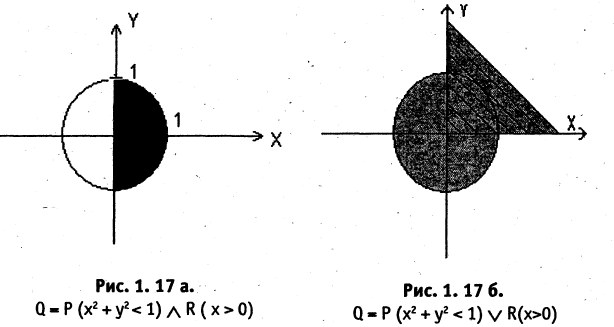
Эквивалентность предикатов
Эквивалентность предикатов 

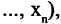



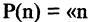
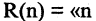

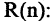


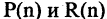
Наряду с логическими операциями важную роль играют операции, называемые кванторами. Квантор всеобщности есть операция, которая предикат 


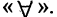



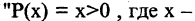



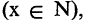

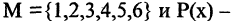

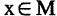
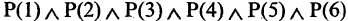
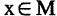
Квантор существования
Квантор существования есть операция, которая предикат 
из М, обладающий свойством 
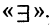







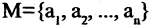
Кванторы обладают свойствами, являющимися аналогами законов де Моргана:
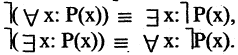
С помощью кванторов можно выражать ряд часто используемых на практике отношений между множествами. Например, высказывание «все объекты 

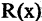
Переход от 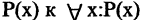



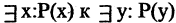
Рассмотрим пример. На множестве чисел задан двухместный предикат 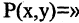


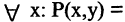

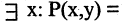

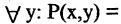

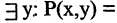

Связывая обе переменные данного предиката, получим высказывания:
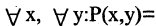
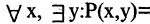
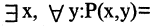
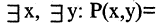
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Загрузка…