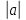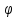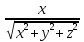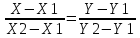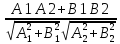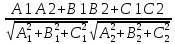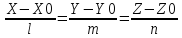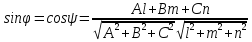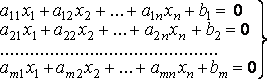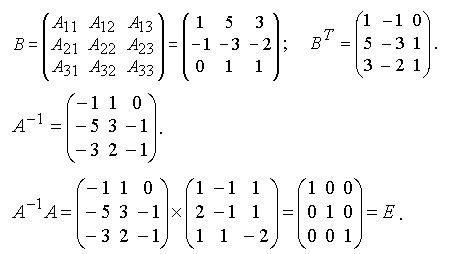Ответы на вопросы к экзамену по линейной алгебре

1.Матрица
– прямоугольная таблица размером m*n

2.
размер матрицы: прямоугольная таблица
из m
и n
чисел содержащая m
строк и n
столбцов

3.
элемент матрицы a_ij
находится
в 3 строке 4 столбце

4.
матрица называется квадратной, если
число строк = числу столбцов (m=n)

5.
число n
(если матрица квадратная) называется
порядком матрицы

6.
две квадратные матрицы( 4 и 5 порядков)
не могут быть равны

7.
диагональные — элементы квадратной
матрицы у которых номер строки равен
номеру столбца (образуют главную
диагональ)

8.
диагональная матрица – у которой все
недиагональные элементы =0

9.
равными называются матрицы одинаковой
размерности

10.
нулевая матрица – если все элементы её
равны 0

11.
единичная матрица — диагональная матрица
у которой все элементы главной диагонали
равны 1

12.
элементы равные единицы

13.единичная
матрица может быть прямоугольной

14.
транспонирование матрицы — замена
каждой её строки столбцом с тем же
номером

15.от
транспонирования размер не меняется

16.матица
столбец

17.матрица
строка

18.
суммой двух матриц (А и В) одинаковой
размерности
называется матрица С той же размерности
каждый элемент С_ij
которой равен сумме элементов А_ij+B_ij
стоящих
на одинаковых местах в слагаемых матрицах
А и В. Матрицы складываются поэлементно.

19.матрицы
одинаковой размерности

20.нет,нельзя

21.
произведением матрицы А на число

называется матрица λА с элементами
(λ_ij)
той же размерности что и исходная каждый
элемент которой равен произведению
соответствующего элемента исходной
матрицы на число λ

22.
свойства операции сложения матриц:
А+В=В+А , (А+В)+С=А+(В+С) ,если О нулевая
матрица то А+О=О+А=А, (А+В)^Т=А^Т+В^Т

23.
свойства операции умножения матрицы
на число:,,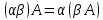
(,
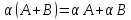
(^Т=α*А^Т

24.
свойства операции умножения матриц:
(АВ)С=А(ВС), α(АВ)=(αА)В=А(αВ), (А+В)С=АС+ВС,
(АВ)^Т=В^ТА^Т

25.перестановочными
матрицами называются 2 матрицы если
АВ=ВА

26.
произведение матрицы А на Е(единичная
матрица)= А

27.
операция умножения матриц коммутативна
АВВА
если существует АВ то ВА может не
существовать

28.
умножение матриц размером 3*7 и 7*5 возможно

29.
умножение матриц размером 4*6 и 4*8
невозможно

30.
размер матрицы при умножении матриц
размерами 12*9 и 9*5 = 12*5

31.да
отличаются

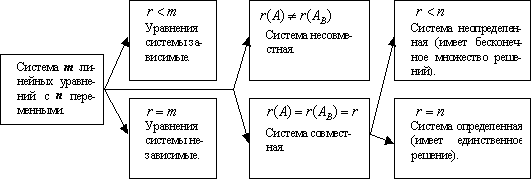
32.признаки
равенства определителя нулю: определитель
содержащий 2 одинаковые строки или 2
пропорциональные строки =0, если одна
из строк определителя целиком состоит
из нулей или является линейной комбинацией
его других строк, то определитель=0

33.
тоже самое

34.
определитель не меняется при
транспонировании, если к элементам
одной его строки прибавить соответствующие
элементы другой его строки умноженное
на одно и то же число.

35.
минором М_ij
элемента
а_ij
определителя
квадратной матрицы А=( а_ij)
n-ного
порядка называется определитель
(n-1)-ого
порядка, полученный из матрицы А
вычёркиванием i-строки
и j-столбца
на пересечении которых находится данный
элемент

36.
чтобы получить из матрицы А минор М₃₇
нужно вычеркнуть 3 строку и 7 столбец

37.
алгебраическим дополнением А_ij
элемента
а_ij
называется его минор М_ij,
взятый со знаком (-1)^i+j*
М_ij

38.
минор М₈₅
и
алгебраическое дополнение А₈₅
отличаются тем, что у минора будет знак
(-), а у алгебр. дополнения (+)

39.минор
М₂₆
и
алгебраическое дополнение А₂₆
ничем
не отличаются

40.
теорема о разложении определителя:
определитель n-ного
порядка равен сумме произведений
элементов любой его строки(столбца) на
их алгебраические дополнения

41.
сумма произведений элементов любой
строки(столбца) определителя на их
алгебраические дополнения равна
определителю

42.
сумма произведений элементов любой
строки(столбца) определителя на их
алгебраические дополнения соответствующих
эементов другой строки равна нулю

43.
матрица вырожденная
если её определитель равен нулю

44.
матрица невырожденная
если
её определитель отличен от нуля

45.
обратной для квадратной матрицы А
называется такая матрица А^-1,
что АА^-1=А^-1А=

46.
 Определитель произведения двух матриц равен
произведению их определителей
т.е.|AB|=|A||B| 

47.
Определитель произведения квадратных матриц одинакового
порядка равен произведению их определителей

48.
Для того, чтобы матрица А имела обратную,
необходимо, чтобы ее определитель был
отличен от нуля(была невырожденной)

49.для
нахождения обратной матрицы необходимо:
найти определитель исходной матрицы
А, если
,
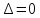
то обратной матрицы нет; находим
алгебраические дополнения А_ij
всех
элементов матрицы А и построить из них
новую А’; транспонировать матрицу А’ и
получить А*;разделить все элементы А*
на определитель матрицы А

50.вид
обратной матрицы:А^-1=

51.чтобы
матрица имела себе обратную необходимо,
чтоб определитель не равнялся 0

52.прямоугольная
матрица не имеет себе обратную матрицу

53.
вырожденная матрица не имеет себе
обратную матрицу

54.данная
матрица может иметь только 1 обратную
матрицу

55.ступенчатая
матрица – матрица вида 0 а_1к1….
а_1n
,
0 0 а_2к2….
А_2n
,
….., 0000 а_mкm….
А_mn

56.ступенчатая
матрица не может содержать нулевые
строки

57.высота
каждой ступеньки ступенчатой матрицы
одна строка

58.шириной
ступеньки называется число элементов
строки стоящих на ступеньке

59.нулевая
матрица не может быть ступенчатой

60.
единичная матрица будет ступенчатой

61.элементарные
преобразования строк матрицы: умножение
всех элементов какой либо строки отличное
от нуля, прибавление к каждому элементу
какой либо строки соответствующих
элементов другой строки умноженных на
некоторое число, перестановка строк,
вычеркивание нулевой строки,
транспонирование матрицы

62.
алгоритм приведения матрицы к ступенчатому
виду: найти первый из столбцов содержащий
не нулевые элементы, выбрать строку,
содержащую один из этих не нулевых
элементов, выбранную строку (если она
не первая) поменять местами с первой
строкой; сделать нулевыми все элементы
матриц под крайним элементом первой
строки, в первом не нулевом столбце
останется только один верхний не нулевой
элемент, так будет получена первая
ступень; сохраняя не изменой первую
строку полученной матрицы рассмотреть
матрицу из остальных строк и применить
к ней предыдущие шаги описанного
алгоритма

63.
минором порядка К матрицы А называется
определитель квадратной матрицы порядка
К, полученный из матрицы А вычеркиванием
каких либо строк и столбцов

64.ранг
матрицы- наивысший порядок отличных от
нуля миноров этой матрицы

65.минор
порядка 9 некоторой матрицы отличный
от нуля – ранг этой матрицы 9 или больше

66.размер
матрицы А 5*7 – наибольшее значение ранга
5

67.ранг
нулевой матрицы равен нулю

68.
ранг =0,когда матрица нулевая

69.ранг
квадратной невырожденной матрицы 5
порядка равен 5!

70.при
элементарных преобразованиях строк
или столбцов матриц ее ранг не изменится

71.ранг
ступенчатой матрицы=кол=ву ее ненулевых
строк

72.алгоритм
нахождения ранга матрицы: привести
данную матрицу к ступенчатому виду,
вычислить ранг полученной ступенчатой
матрицы, сосчитав количество ее строк
( ступенек), Ранг исходной матрицы равен
рангу полученной ступенчатой матрицы

73.
базисный минор матрицы – любой ненулевой
минор матрицы порядок которого совпадает
с рангом данной матрицы

74.
столбцы матрицы е₁
,
е₂
,
… , е_s

называются линейно зависимыми если
существуют такие числа к₁
,
к₂
, … , к_s

не равные нулю одновременно, что линейная
комбинация этих столбцов с данными
коэффициентами равна нулевому столбцу

75.
столбцы матрицы е₁
,
е₂
,
… , е_s

называются линейно не зависимыми если
линейная комбинация этих столбцов равна
нулю только при нулевом наборе
коэффициентов

76.
Строки
(столбцы) матрицы называются линейно зависимыми,
если существует их линейная комбинация,
не все коэффициенты в которой равны 0,
равная нулевой строке (столбцу).

77.
Строки (столбцы) матрицы называются линейно независимыми,
если существует их линейная комбинация,
и все коэффициенты в которой равны 0.

78.столбцы
и строки матрицы элементы которых входят
в базисный минор – линейно не зависимы
любой столбец (строка) матрицы является
линейной комбинацией этих столбцов(строк)

79.
Строки
и столбцы матрицы, элементы которых входят в базисный минор,
линейно независимы.

80.
вид СЛАУ: система m
линейных уравнений с n
неизвестными х₁,х₂,…,х_n
называется
система вида а₁₁х₁+а₁₂х₂+…+а_1nе_n=b₁

a₂₁х₁+а₂₂х₂+…+а_2nе_n=b_2
……

а_m1х₁+а_m2х₂+…+а_mnе_n=b_m

81.
коэффициенты при неизвестных образуют
прямоугольную таблицу – матрицу системы
а₁₁
а₁₂
… а_1n

а₂₁
а₂₂
…
а_2n

a_m1
a_m2
… a_mn

82.расширенная
матрица получается приписыванием к
матрице системы справа столбца свободных
членов (b₁
b₂
…
b_m)

83.
решением СЛАУ является упорядоченный
набор(к₁,к₂,…,к_n)
из n
чисел при подстановке которых вместо
соответствующих неизвестных каждое
уравнение системы превращается в верное
равенство.

84.
совместная матрица – имеющая хотя бы
одно решение

85.
несовместная матрица – не имеющая ни
одного решения

86.
определённая матрица – совместная
система имеющая одно решение

87.
неопределённая матрица — совместная
система имеющая более одного решения

88.
однородная матрица – все свободные
члены =0

89.
неоднородная матрица – не все свободные
члены =0

90.
общее решение СЛАУ – выражение для
неизвестных х₁,х₂,…,х_n,
из
которого может быть получено любое
конкретное решение системы

91.
частное решение СЛАУ — любое конкретное
решение системы

92.
равносильные или эквивалентные –
системы уравнений имеющие одно и то же
множество решений

93.СЛАУ
имеет единственное решение если
0,
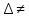
последняя ступенька имеет 2 шага в ширину

94.
метод обратной матрицы применяется к
СЛАУ если в системе число уравнений
совпадает с числом неизвестных и матрица
А является невырожденной.

95.
Метод Гаусса с помощью элементарных
преобразований строк расширенная
матрица Ặ приводится к ступенчатому
виду.

96.
теорема Крамера пусть
матрицы
А системы, а
_J
полученный
из матрицы А заменой J-того
столбца столбцом свободных членов.
тогда если
0
то система имеет единственное решение
определяемое по формулам Крамера:
х_J=J/
для любого j=1,n

97.
0

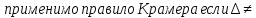
98.
система несовместна,
если
ранг основной и расширенной матриц
системы не равны r(A)≠r(A).

99.
СЛАУ совместна тогда и только тогда,
когда ранг расширенной матрицы системы
равен рангу основной матрицы.

100.
СЛАУ имеет единственное решение,
если матрица А является невырожденной, т.
е. ее определитель не равен нулю

101.СЛАУ
имеет бесконечно много решений если

102.количество
базисных неизвестных для СЛАУ, ступенчатой
матрицы, равно количеству первых
ненулевых элементов строк(сткпенек)

103.свободными
неизвестными для СЛАУ, ступенчатой
матрицы, являются остальные
неизвестные(т.е. все неизвестные кроме
базисных)

104.СЛАУ
у которой все свободные неизвестные
=0, не будет иметь нулевое решение

105.частный
способ решения матричных уравнений:
если А-квадр.и невырожд. матрица, то
Х=А^-1В

106.общий
способ решения матричных уравнений:
матрицу Х выписываем подробно с
неизвестными элементами, производим
умножение матриц А и Х и сравниваем
элементы матриц обеих частей уравнения,
в результате получится СЛАУ относительно
неизвестных элементов матрицы Х,эта
система распадается на подсистемы вида
АХ_J=B_J,
решая эти системы найдём все элементы
неизвестной матрицы Х, если хотя бы 1 из
этих подсистем является несовместной,
то данное матричное уравнение не имеет
решения

107.теорема
Кронекера — Капелли: СЛАУ совместна,
тогда и только тогда, когда ранг
расширенной матрицы Ặ системы равен
рангу матрицы системы А

108.
чтобы неоднородная система линейных
алгебраических уравнений была совместна,
необходимо и достаточно, чтобы
ранг расширенной матрицы системы совпадал
с рангом матрицы системы. 

109.связь
количества решений с рангом: если ранг
матрицы совместной системы равен числу
её переменных, т.е. r
=n,
то система имеет единственное решение
а если ранг меньше числа её переменных,
т.е. r
<n
то система неопределённая и имеет
бесконечное множество решений

110.базисной
подсистемой для данной системы, называется
подсистема, составленная из уравнения
системы на строках, их коэффициентов
которых, располагается базисный минор

111.базисными
неизвестными СЛАУ являются неизвестные
х₁,х₂,…,х_n,,
коэффициенты при которых входят в
базисный минор матрицы системы, а
остальные х_R+1,…,x_n
– свободные неизвестные

112.фундаментальная
система решений(фср) – любые n-r
линейно независимых решений однородной
СЛАУ

113.
нормальной ФСР называется ФСР однородной
СЛАУ в которой свободные неизвестные
задают по формулам

114.
свойства решений однородной СЛАУ: любое
решение однородной СЛАУ умноженное на
любое число также является решением
этой системы, сумма решений однородной
СЛАУ так же является её решением(из этих
свойств следует что любая линейная
комбинация решений однородной СЛАУ
также является решением этой системы)

115.
структура общего решения однородной
СЛАУ: запишем расширенную матрицу и
приведём её к ступенчатому виду, запишем
систему определяемую полученной
ступенчатой матрицей, определим базисные
и свободные неизвестные, найдем их
значения и запишем общее решение

116.свойства
решений неоднородной СЛАУ: сумма любого
решения неоднородной СЛАУ и любого
решения её приведённой однородной
системы является решением данной
неоднородной системы, разность любых
двух решений неоднородной СЛАУ является
решение ее приведенной однородной
системы

117.структура
общего решения неоднородной СЛАУ
представляет собой сумму общего решения
её приведённой однородной системы и
частного решения данной неоднородной
системы

118.
вектор — это направленный отрезок,
который имеет начало и конец

119.
коллинеарные векторы – лежат на одной
прямой или на параллельных прямых

120.
равные векторы — 2 вектора коллинеарные,
имеют одинаковую длину и одинаковое
направление

121.
суммой a+b
векторов называется вектор идущий из
начала вектора а в конец вектора b
если начало вектора b
совпадает с концом вектора а

122.
свойства сложения: a+b=b+a
, (a+b)+c=a+(b+c)
, для любого вектора а существует нулевой
вектор 0 такой что а+0=а , для каждого
вектора а существует противоположный
ему вектор а’ такой что а+а’=0

123.
разность а-b
векторов называется вектор с который
в сумме с вектором b
дает вектор а

124.
произведением ka
вектора на число называется вектор b
коллинеарный вектора а имеющий длину
равную

и направление совпадающее с направлением
а при k>0
и противоположное а при k<0

125.
свойства умножения вектора на число:
k(a+b)=ka+kb
, (k+m)a=ka+ma
, k(ma)=(km)a

126.
линейной комбинацией векторов а₁,а₂,…,а_n

называется выражение вида k₁a₁+k₂a₂+…+k_na_n
где k
числа

127.векторы

а₁,а₂,…,а_n

линейно зависимы если найдутся такие
числа k₁,k₂,…,k_n

не все равные нулю что соответствующая
линейная комбинация векторов =0, т.е.
k₁a₁+k₂a₂+…+k_na_n=0

128.
линейно не зависимые векторы если
равенство k₁a₁+k₂a₂+…+k_na_n=0
возможно только при всех k_i=0

129.
свойства линейно зависимых систем
векторов: если система векторов содержит
нулевой вектор то она линейно зависима,
если среди n
векторов какие либо (n-1)
линейно зависимы то и все n
векторов линейно зависимы, необходимым
и достаточным условием линейной
зависимости двух и трёх векторов является
их компланарность, любые четыре вектора
в трехмерном пространстве линейно
зависимы

130.
компланарные векторы – лежат либо в
одной плоскости либо в параллельных
плоскостях

131.
базис образуют два линейно независимых
вектора на плоскости (или 3 линейно
независимых вектора в пространстве),
если любой вектор плоскости (пространства)
может быть представлен в виде их линейной
комбинации

132.
координаты одного вектора – числовые
коэффициенты линейной комбинации в
рассматриваемом базисе, если a,b,c
– базис и d
= ka+mb+pc
то числа k,
m
, p
координаты вектора d
в базисе a,b,c

133.
свойства базиса: любые два неколлинеарных
вектора образуют базис на плоскости а
любые три некомпланарных вектора –
базис в пространстве, расположение
данного вектора по данному базису
единственно то есть координаты вектора
в данном базисе определяются единственным
образом, при сложение двух векторов их
одноименные координаты складываются,
при умножении вектора на число все его
координаты умножаются на это число

134.
проекция вектора АВ на ось U
– длинна направленного отрезка A’B’
оси U
где A’B’
– основание перпендикуляров опущенных
из точек А и В на ось U
(пр_uа
)

135.
свойства проекции: пр_uа
=

cos
где фи угол между а и осью U;
при сложении двух векторов их проекции
на любую ось складываются; при умножении
вектора на число его проекция на любую
ось умножается на это число

136.
декартовые координаты вектора d
– числа х у z

137.
направляющие косинусы – косинусы углов
образованных векторами с осями декартовой
системы координат

138.
свойства направляющих косинусов:
х=|d|cosα,
y=|d|cosβ.
z=|d|cosγ
α,β,γ
– углы которые данный вектор α образует
с осями координат

сosα
=

, аналогично;
cos²α+cos²β+cos²γ=1

139.
скалярное произведение двух векторов
– произведение их длин на косинус угла
между ними ab=|a||b|cos

140.
свойство скалярного произведения:
ab=|a|пр_ab;
ab=0
ab;
ab=ba;
(ka)b=k(ab);
(a+b)c=ac+bc;
a²=aa=|a|²;
если векторы a
и b
определены своими декартовыми координатами
то ab=x₁x₂
+
y₁y₂
+ z₁z₂;
cos=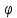

141.
тройка некомпланарных векторов abc
называется правой(левой) если после
приведения к общему началу вектор с
располагается по ту сторону от плоскости
определяемой векторами а и b
откуда кротчайший поворот от а и b
кажется совершающимся против часовой
стрелки (по часовой)

142.
векторное произведение векторов —
|c|=|a||b|sin;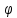
ca,
cb
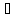
; тройка векторов abc
является правой

143.
сво1ства векторного произведения:
[ba]=-[ab];
[ab]=0

a||b;
длинна векторного произведения
равняется площади параллелограмма
построенного на приведенных к общему
началу векторов а и b

144.
орта (орт е_а
) произвольного вектора а – вектор
единичной длинны, коллиниарный а и
одинакового с ним направленный

145.векторное
произведение:с=,
c=a*b

146.с
мешанное произведение векторов a,b
и с называется результат скалярного
умножения векторного произведения
[ab]c

147.
свойства смешенного произведения:
скалярное произведение [ab]c
равно объему параллелепипеда построенного
на приведенных к общему началу векторов
a
b
с если они образуют правую тройку или
числу противоположному этому объему,
если a
b
с – левая тройка; если а b
с компланарны то [ab]c=0

148.abc=

149.
уравнение прямой проходящей через
данную точку перпендикулярно данному
вектору: A(x-x­­₀)
+ B(y-y₀)=0

150.
перпендикуляр проведенный из начала
координат к прямой называется нормалью
прямой

151.
общее уравнение прямой Ax+By+C=0

152.
каноническое уравнение прямой

153.
направляющий вектор прямой – вектор q

154.уравнение
прямой проходящей через две заданные
точки

155.
параметрическое уравнение прямой
х=x₀+lt,
y=y₀+mt

156.
угловой коэффициент прямой ?

157.
уравнение прямой с угловым коэффициентом
y=kx+b

158.
неполное уравнение прямой: с=0 – прямая
Ах+Ву=0 проходит через начало координат;
b=0
– прямая Ах+С=0 параллельна оси Оу; А=0
– прямая Ву+С=0 параллельна оси Ох ;
В=С=0 – уравнение Ах=0 определяет ось Оу
; А=С=0 – уравнение Ву=0 определяет ось
Ох

159.
уравнение прямой в отрезках х/а+у/b=1

160.угол
между прямыми – cos=
A=l,
B=m

161.
условия параллельности прямых А₁/А₂=В₁/В₂;
к₁=к₂;
l₁/l₂=m₁/m₂

162.
условия перпендикулярности двух прямых
А₁А₂+В₁В₂=0;
-к₂=-1/к₁;

163.
расстояние от точки до прямой ?

164.
нормальное уравнение прямой хcosα+ysinα=p

165.
отклонение прямой — если d
– расстояние от точки А до прямой L
то отклонение δ точки А от прямой L
есть число +d если точка А и начало
координат лежат по разные стороны от
прямой L
и число –d
если они лежат по одну сторону

166.
теорема отклонения прямой: отклонение
точки А от прямой L,
заданной нормальным уравнением
определяется: δ=х₁cosα+y₁sinα-p

167.
уравнение плоскости проходящей через
данную точку перпендикулярно данному
вектору: A(x-x₀)+B(y-y₀)+C(z-z₀)=0

168.
общее уравнение плоскости: Ax+By+Cz+D=0

169.
неполное уравнение плоскости: D=0
– плоскость Ax+By+Cz=0
проходит через начало координат, А=0,
В=0 – плоскость Ax+By+Cz=0
параллельна оси Оу, С=0 — плоскость
Ax+By+Cz=0
параллельна оси Оz,
А=В=0 – плоскость Сz+D=0
параллельно координатной плоскости
Оху , А=С=0 – плоскость Ву+D=0 параллельно
координатным плоскости Оуz, А=D=0 –
плоскость Ву+Сz=0 проходит через ось Ох,
В=D=0 – плоскость Ах+Сz=0 проходит через
ось Оу, С=D=0 – плоскость Ах+Ву=0 проходит
через ось Оz, А=В=D=0 – уравнение Cz=0 задает
координатную плоскость Оху, А=С=D=0
получаем Ву=0 уравнение координатной
плоскости Охz, B=C=D=0 плоскость Ах=0 является
координатной плоскостью Оуz

170.
уравнение плоскости в отрезках : х/а +
у/b + z/c = 1

171.
угол между плоскостями cos=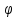

172.
условие параллельности плоскостей:
А₁/А₂=В₁/В₂=С₁/С₂

173.
условие перпендикулярности плоскостей
А₁А₂+В₁В₂
+С₁С₂=0

174.
уравнения плоскости проходящей через
три данные точки
=
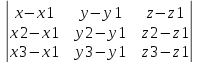
0

175.
нормальное уравнение плоскости :
хcosα+ycosβ+zcosγ-p=0

176.
расстояние от точки до плоскости
d=|хcosα+ycosβ+zcosγ-p|

177.
направляющий вектор прямой – любой не
нулевой вектор параллельный данной
прямой

178.
каноническое уравнение прямой

179.
уравнение прямой проходящей через две
данные точи (Х-Х1)/(Х2-Х1)=(У-У1)/(У2-У1)=(Z-Z1)/(Z2-Z1)

180.параметрическое
уравнение прямой

181.угол
между прямыми в пространстве равен
углу между их направляющими векторами

182.
условие параллельности прямых
l₁/l₂=m₁/m₂=n₁/n₂

183.
условие перпендикулярности прямых
l₁l₂+m₁m₂+n₁n₂=0

184.
угол между прямой и плоскостью

185.
Условие параллельности прямой и плоскости
Аl+Bm+Cn=0

186.
условие перпендикулярности прямой и
плоскости А/l=B/m=C/n

187.

188.
базисом в линейном пространстве
называется набор линейно независимых
векторов е₁,е₂,…,e_n,
такой, что любой вектор Х этого пространства

можно
представить в виде: Х=х₁е₁+х₂е₂+…+х_ne_n
=(
е₁,е₂,…,e_n)*(х₁)

(х₂)=
e(x)_e

(х_n)

189.
размерность-кол-во векторов в любом
базисе линейного пространства.

190.
Числа х₁,х₂,…,х_n
– координаты вектора Х в базисе Е.

191.
если размерность пространства n,
то его называют n-мерным.

192.
матрицей перехода от базиса е к базису
е’ называется матрица Т, столбцами
которой , являются координатные столбцы
векторов нового базиса е’ в старом
базисе е.

194.
линейным оператором(лин. преобразованием)
в линейном пространстве называется
отображение Ặ пространства на себя,
при котором для любых векторов х, у этого
пространства и для любого вещественного
числа α выполняется: Ặ(х+у)= Ặх+ Ặу,
Ặ(αх)=α(Ặх).

195.
матрица линейного оператора – матрица
А столбцами которой являются координатные
столбцы образов Ặ_еi
векторов базиса е в базисе е’:

Ặ_еi=а_1ie₁+
а_2ie₂+…+
а_nie_n

, A=(a_ij)

196.A-
матрица линейного оператора в базисе
е, а А’- в новом базисе е’, Т- матрица
перехода от базиса е к е’ : А’=Т^-1АТ

198.собственный
вектор матрицы А и оператора Ặ– ненулевой
вектор х, если выполняется одно из
равенств: Ặх=λх, Ах=λх, где λ действительное
число(собственное
число
матрицы оператора)

199.
собственные числа, это те числа, которые
получаются в решении, когда определитель
матрицы =0

200.
характеристическое уравнение – это
уравнение вида
=0

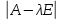
201.характеристический
многочлен – это многочлен определяющий
ее собственные значения

202.
1) A-𝝀E
2)

3)
=0
находим 𝝀(собственные
числа)

203.квадратичной
формой действительных переменных
х₁,х₂,…,х_n,,
называется многочлен второй степени
относительно этих переменных не
содержащий свободного члена и членов
первой степени

Тема: Ответы на экзамен по линейной алгебре

Раздел: Бесплатные рефераты по линейной алгебре

Тип: Шпаргалка | Размер: 113.35K | Скачано: 410 | Добавлен 19.04.15 в 13:12 | Рейтинг: 0 | Еще Шпаргалки

Вопросы к экзамену:

1.    Понятие матриц. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами.

2.    Определители второго порядка, третьего и n-го. Теорема Лапласа о разложении определителя по элементам строки или столбца.

3.    Квадратная матрица и ее определитель. Особенная и неособенная матрица. Присоединенная матрица. Матрица, обратной данной, и алгоритм ее вычисления.

4.    Понятие минора k-го порядка. Ранг матрицы. Вычисление ранга матрицы.

5.    Линейная независимость столбцов (строк) матрицы. Теорема о ранге матрицы.

6.    Векторы. Операция над векторами. N- мерный вектор. Понятие о векторном пространстве и его базисе.

7.    Собственные вектора и собственный значения матриц. Характеристическое уравнение матрицы.

8.    Система n линейных уравнений с n переменными и матричная форма ее записи. Решение системы. Совместные и несовместные, определенные и неопределенные системы линейных уравнений.

9.    Метод Гаусса решения систем n линейных уравнений с n переменными. Понятие о методе Жордана-Гаусса.

10.    Система m линейных уравнений с n переменными. Теорема Кронекера-Капелли. Условия определенности и неопределенности системы линейных уравнений.

11.    Базисные и свободные переменные. Базисное решение.

12.    Система линейных однородных уравнений и ее решения. Условия существования ненулевых решений систем.

13.    Векторы на плоскости и в пространстве. Линейные операции над векторами. Коллинеарные и компланарные вектора.

14.    Скалярное произведение двух векторов и его выражение в координатной форме. Угол между векторами.

15.    N-мерный вектор. Линейная комбинация, линейная зависимость и независимость векторов.

16.    Векторное пространство его размерность и базис. Теорема о существовании и единственности разложения вектора линейного пространства по векторам базиса.

17.    Скалярное произведение векторов в n-мерном пространстве. Евклидово пространство. Длина (норма) вектора.

18.    Ортогональный вектор. Ортогональный и ортонормированный базисы. Теорема и существовании ортонормированного базиса в евклидовом пространстве.

19.    Определение оператора. Понятие линейного оператора. Образ и прообраз векторов.

20.    Матрицы линейного оператора в заданном базисе: связь между вектором х и образом у. ранг оператора. Операции над линейными операторами. Нулевой и тождественный операторы.

21.    Собственные вектора и собственные значения оператора. Характеристический многочлен оператора и его характеристическое уравнение.

22.    Матрицы линейного оператора в базисе, состоящем из его собственных векторов.

23.    Квадратичная форма. Матрица квадратичной формы. Ранг квадратичной формы.

24.    Квадратичная форма (канонический вид). Приведение квадратичной формы к каноническому виду. Закон инерции квадратичных форм.

25.    Положительно и отрицательно определенная, знакоопределенная квадратичная формы. Критерии знакоопределенности квадратичной формы.

26.    Уравнение линии на плоскости. Точка пересечения двух линий. Основные виды уравнений прямой на плоскости.

27.    Общее уравнение прямой на плоскости, его исследование. Условия параллельности и перпендикулярности прямых.

28.    Кривые второго порядка, их общее уравнение. Нормальное уравнение окружности. Каноническое уравнение эллипса. Геометрический смысл параметров окружности и эллипса.

29.    Каноническое уравнение гиперболы и параболы, геометрический смысл их параметров. Уравнение асимптот гиперболы. График обратной пропорциональной зависимости и квадратного трехчлена.

30.    Общее уравнение плоскости в пространстве и его частные случаи. Нормальный вектор плоскости. Условия параллельности и перпендикулярности двух плоскостей.

31.    Уравнение прямой линии в пространстве как линии пересечения двух плоскостей. Каноническое уравнение прямой. Направляющий вектор прямой. Условия параллельности и перпендикулярности двух прямых в пространстве.

32.    Углы между двумя плоскостями, между двумя прямыми, между прямой и плоскостью. Условия параллельности и перпендикулярности двух плоскостей, двух прямых, прямой и плоскости.

0

19.04.15 в 13:12
Автор:surdul

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Шпаргалки на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Шпаргалки для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Шпаргалка, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---

Похожие работы

• Шпаргалка по линейной алгебре на экзамен

---

Подборка по базе: ОБЖТестовые вопросы к разделу 1_ просмотр попытки.pdf, englishТестовые вопросы к разделу 7_ просмотр попытки.pdf, Сборник вопросов Газоспасатели с литературой. С выделениями.(1)., Контрольная работа _Разделительные вопросы_ (1).doc, Самые популярные вопросы о Чичикове из поэмы.docx, Примерные вопросы к дифференцированному зачету_Психология общени, Тестовые вопросы к разделу 5_ просмотр попытки.pdf, Тестовые вопросы к разделу 8_ просмотр попытки.pdf, 13 вопросов.docx, Организация на рынке труда 42 вопроса — 1. Рынок труда представл

---

Вопрос №1

Матрицы и многомерные векторы. Матрицей называется прямоугольная таблица чисел, содержащая n строк и m столбцов.

Виды матриц.

Две матрицы называются равными, если их соответствующие элементы равны.

Если в матрице число строк равно числу столбцов (n=m), то матрица называется квадратной.

Матрица, у которой все элементы, стоящие вне главной диагонали равны 0, называется диагональной.

Диагональная матрица, у которой все диагональные элементы равны 1, называется единичной.

Матрица, состоящая из одних нулей, называется нулевой.

Если в квадратной матрице все элементы стоящие ниже (выше) главной диагонали равны 0, то она называется верхний (нижний) треугольник.

Если в матрице А строки записать столбцами с теми же номерами, то полученная матрица будет называться транспонированной к матрице А.

Если матрица А равна транспонированной, то она называется симметричной.

Действия над матрицами:

1) Умножение матрицы на число. В результате умножения матрицы на число получается матрица такой же размерности, что и исходная, каждый элемент которой является результатом произведения соответствующего элемента исходной матрицы на число. Мы получим одинаковый результат, умножая число на матрицу, или матрицу на число. Из определения следует, что общий множитель всех элементов матрицы можно выносить за знак матрицы.

2) Сложение и вычитание матриц. Складывать и вычитать можно только матрицы одинаковой размерности. Суммой (разностью) двух матриц называется матрица той же размерности, что и исходные, каждый элемент которой определяется как сумма (разность) соответствующих элементов матриц. Очевидно, результат сложения не изменится, если слагаемые матрицы поменять местами. Если к матрице прибавить или от нее отнять нулевую матрицу той же размерности, то получим исходную матрицу.

3) Умножение матрицы на матрицу. Умножать друг на друга можно только те матрицы, для которых число столбцов первого сомножителя равно числу строк второго сомножителя. Результатом умножения является матрица, у которой число строк равно числу строк первого сомножителя, а число столбцов совпадает с числом столбцов второго сомножителя. Иными словами, перемножать можно те матрицы, у которых совпадают средние индексы. Крайние индексы определяют размерность получаемого результата.

Свойства операций над матрицами.

1) В общем случае . Если то матрицы А и В называются перестановочными по отношению друг к другу.

2) Ассоциативность;

3) Дисрибутивность;

4) При умножении любой квадратной матрицы на единичную первоначальная матрица не меняется .
Вопрос №3

Перестановки. Расположение n элементов набора в произвольном порядке называется перестановка. Транспозицией называется перестановка двух каких либо элементов. Инверсией в перестановке называется наличие пары чисел, в которое большее число предшествует меньшему. Если число инверсий в перестановке честное, то она называется четной и наоборот.

Определитель произвольного порядка. Определителем квадратной матрицы n-го порядка, называется число равное алгебраической сумме n факториал слагаемых, каждый из которых является произведением n элементов матрицы взятых по одному из каждой строки и столбца, при этом каждое слагаемое умножается на (-1) в степени число инверсий в перестановке j если первые индексы взяты в порядке нарастания.

Вопрос №2

Определители 2-го и 3-го порядка и их свойства. Если квадратная матрица имеет определитель, отличный от нуля (Δ ≠ 0), то говорят, что матрица невырожденная, в противном случае — матрица вырожденная или особая.

Определителем квадратной матрицы 2-го порядка, называется число равное разности произведений элементов главной и побочной диагонали матрицы.

О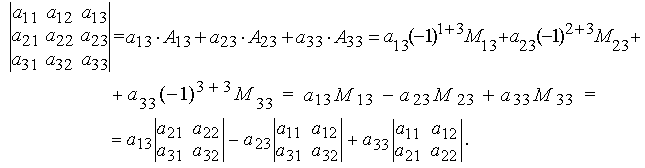пределителем квадратной матрицы 3-го порядка, называется число равное:

Таким образом, вычисление определителя третьего порядка сводится к вычислению определителей второго порядка.

Свойства определителей:

1) Если строка (столбец) матрицы состоит из 0, то ее определитель равен 0.

2) Если все элементы, какой либо строки (столбца) матрицы умножить на одно и тоже число, то и ее определитель умножится на это же число.

3) При транспонировании матрицы ее определитель не меняется.

4) При перестановки, каких либо двух строк (столбцов) матрицы знак матрицы меняется на противоположный. Доказательство вытекает из того, что при перестановке одной транспозиции четность инверсии меняется.

5) Если квадратная матрица содержит две одинаковые строки (столбца), то её определитель равен 0.

6) Сумма произведений элементов, какой либо строки (столбца) на алгебраические дополнения какой либо строки (столбца) равно 0.

7) Если элементы, какой либо строки (столбца) равны сумме двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы) кроме указанных, те же что и в исходном определителе, а рассматриваемая k-строка (столбец) в первом определителе содержит первые слагаемые, во втором вторые.

Определитель матрицы не изменится если к элементам какой либо строки (столбца) прибавить элемент какой либо строки (столбца) предварительно умноженные на одно и то же число.
Вопрос №4

Миноры и алгебраические дополнения. Минором элемента a_ij квадратной матрицы |A| n-ного порядка, называется определителем матрицы, полученной из матрицы |A| вычеркиванием i-той строки j-того столбца.

Алгебраическим дополнением A_ij элемента a_ij квадратной матрицы |A|, называется минор этого элемента, умноженный на (-1) в степени.

Вычисление определителей произвольного порядка (теорема Лапласа). Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения: (разложение по элементам i-й строки); (разложение по элементам j-го столбца).

Вопрос №5

Ранг матрицы, его нахождение. Рангом матрицы А (обозначается r(A)) называется наибольший порядок минора этой матрицы, отличного от нуля. Если все элементы матрицы равны нулю, то ранг такой матрицы принимают равным нулю.

Всякий отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы, называется базисным минором матрицы.

Ранг матрицы не изменится от следующих преобразований, называемых элементарными преобразованиями матрицы:

— замены строк столбцами, а столбцов соответствующими строками;

— перестановки строк матрицы;

— вычеркивания строки, все элементы которой равны нулю;

— умножения строки на число, отличное от нуля;

— прибавления к элементам строки соответствующих элементов другой строки, умноженной на одно и то же число.

Подчеркнем, что сама матрица при элементарных преобразованиях меняется, но ранг матрицы не изменится.

Пример. Определить ранг матрицы . Решение. Все миноры второго и третьего порядков данной матрицы равны нулю, т.к. элементы строк этих миноров пропорциональны. Миноры первого порядка (сами элементы матрицы) отличны от нуля. Следовательно, ранг матрицы равен единице.
Вопрос №6

Системы линейных уравнений. Уравнение называется линейным, если оно содержит неизвестные в первой степени и не содержит их произведений.

Запись в матричной форме.

— система линейных уравнений.

Обозначим, — матрица коэффициентов, — вектор неизвестных,

— вектор свободных членов. A_mn X_n1 + B_m1 = 0 — матричная запись системы уравнений.

Если система уравнений имеет решение, она называется совместной, не имеет – несовместной. Совместная система, имеющая одно решение, называется определенной, если много – неопределенной. Две системы уравнений называются равносильными или эквивалентными, если каждое решение является решением уравнения системы или наоборот.
Вопрос №8

Решение систем линейных уравнений с помощью определителей (формулы Крамера). Пусть Δ = |A| определитель матричной системы n линейных уравнений с n неизвестных, а Δ_j определитель матрицы, полученный из матричной системы заменой j-того столбца на столбец правых частей. Тогда если Δ ≠ 0, то система имеет единственное решение, определенное по формулам x_j = Δ_j / Δ (j = 1,2,…n) – формула Крамера.

Вопрос №7

Обратная матрица. Матрицей, обратной матрице А, называется матрица A^-1 такая, что A^-1A = A A^-1 = E.

Обратная матрица может существовать только для квадратной матрицы. Причем сама является той же размерности, что и исходная матрица.

Можно показать, что для того, чтобы квадратная матрица имела обратную, она должна быть невырожденной (т.е. Δ ≠ 0 ). Это условие является и достаточным для существования A^-1 матрице А. Итак, всякая невырожденная матрица имеет обратную, и, притом, единственную.

Сформулируем правило нахождения обратной матрицы на примере матрицы А.

1. Находим определитель матрицы. Если Δ ≠ 0, то матрица A^-1 существует.

2. Составим матрицу В алгебраических дополнений элементов исходной матрицы А. Т.е. в матрице В элементом i — ой строки и j — го столбца будет алгебраическое дополнение A_ij элемента a_ij исходной матрицы.

3. Транспонируем матрицу В и получим B^T.

Теорема существования и единственности обратной матрицы. Для квадратной матрицы А существует и при том единственная обратная матрица А^-1 тогда и только тогда, когда эта матрица не вырождена.

Решение систем линейных уравнений с помощью обратной матрицы. Матричным методом могут быть решены только те системы, у которых число уравнений совпадает с числом неизвестных и определитель матрицы коэффициентов отличен от нуля (матрица А невырожденная). Из этих условий следует, что и, следовательно, система совместна и определена. Решение системы можно получить так: . Используя свойства произведения матриц и свойство обратной матрицы . Т.е., для получения столбца неизвестных нужно обратную матрицу матрицы коэффициентов системы умножить на столбец свободных членов.

Пример. Решить систему матричным методом. Решение. Найдем обратную матрицу для матрицы коэффициентов системы .

Вычислим определитель, раскладывая по первой строке: . Поскольку Δ ≠ 0, то A^-1 существует.

Обратная матрица найдена верно.

Найдем решение системы .

Следовательно, x₁ = 1, x₂ = 2, x₃ = 3.

Матричный метод годится для решения любых систем, у которых матрица А квадратная и невырожденная.
Вопрос №10

Теорема Кронекера-Капелли. Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы. RgA = RgA*.

Доказательство.

1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А®А* не изменяют ранга.

2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.

Исследование системы линейных уравнений.

Вопрос №9

Решение и исследование систем линейных уравнений методом Гаусса. Этот метод решения систем линейных уравнений пригоден для решения систем с любым числом уравнений и неизвестных.

Суть метода Гаусса заключается в преобразовании заданной системы уравнений с помощью элементарных преобразований в эквивалентную систему ступенчатого треугольного вида.

Полученная система содержит все неизвестные в первом уравнении. Во втором уравнении отсутствует первое неизвестное, в третьем уравнении отсутствуют первое и второе неизвестные и т. д.

Если система совместна и определена (единственное решение), то последнее уравнение содержит одно неизвестное. Найдя последнее неизвестное, из предыдущего уравнения находим еще одно — предпоследнее. Подставляя полученные величины неизвестных, мы последовательно найдем решение системы.

Элементарными преобразованиями системы линейных уравнений, используемыми для приведения системы к треугольному виду, являются следующие преобразования:

— перестановка местами двух уравнений;

— умножение обеих частей одного из уравнений на любое число, отличное от нуля;

— прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число.

Элементарные преобразования переводят данную систему линейных алгебраических уравнений в эквивалентную систему.

Две системы называются эквивалентными, если всякое решение первой системы является решением другой системы и наоборот.
Вопрос №11

Базис и размерность пространства решений однородной системы линейных уравнений. Базисом линейного пространства L называется такая конечная упорядоченная линейно независимая система векторов, что любой вектор пространства L является линейной комбинацией этих векторов. В отличие от трехмерного пространства векторов, в некоторых линейных пространствах базис не существует.

В линейном пространстве любые два базиса содержат одинаковое число векторов.

Линейное пространство L, в котором существует базис, состоящий из n векторов, называется — n мерным линейным или векторным пространством. Число n называется размерностью пространства и обозначается dimL. Линейное пространство, в котором не существует базис, называется бесконечномерным.

Общее решение неоднородной системы линейных уравнений. Систему неоднородных уравнений запишем в матричном виде Ax = b, где матрица A имеет размеры mxn.

[T] Система линейных уравнений Ax = b может иметь либо бесконечно много решений, либо одно решение, либо не иметь решений.

[D] Пусть система имеет решение x⁽⁰⁾ . Если однородная система Ax = 0 имеет только одно решение, то из формулы общего решения будет следовать, что x⁽⁰⁾ — единственное решение неоднородной системы. Если однородная система имеет хотя бы одно ненулевое решение, то ее фундаментальная система решений будет состоять не менее, чем из одного решения. В формуле общего решения неоднородной системы будет произвольный коэффициент С1 , и при различных его значениях мы будем получать различные решения неоднородной системы.

Вопрос №12

Векторы на плоскости и в пространстве. Вектором называется направленный отрезок (упорядоченная пара точек). К векторам относится также и нулевой вектор, начало и конец которого совпадают.

Ортом вектора а называется вектор а⁰, который имеет единичную длину и то же направление, что и вектор а.

Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными.

Векторы, лежащие в одной плоскости или параллельные одной плоскости, называются компланарными.

Два вектора считаются равными, если они коллинеарные, одинаково направлены и равны по длине.

Пусть даны два вектора. Параллельным переносом приведем их к общему началу. Наименьший угол, на который надо повернуть один вектор до совпадения с другим, называется углом между векторами.

1) Базисом в пространстве называются любые 3 некомпланарных вектора, взятые в определенном порядке.

2) Базисом на плоскости называются любые 2 неколлинеарные векторы, взятые в определенном порядке.

3) Базисом на прямой называется любой ненулевой вектор.

Три вектора, a,b,c, называются линейно-независимыми, если они не лежат в одной плоскости.

Базисом в трехмерном пространстве R³ называется упорядоченная тройка любых линейно-независимых векторов.

Вопрос №1: «Матрицы и алгебра матриц».

Матрицы  и многомерные векторы. Матрицей называется
прямоугольная таблица чисел, содержащая n строк и m столбцов.

Виды матриц.

Две матрицы называются равными, если их
соответствующие элементы равны.

Если в матрице число строк равно числу столбцов (n=m), то матрица называется квадратной.

Матрица, у которой все элементы, стоящие вне главной
диагонали равны 0, называется диагональной.

Диагональная матрица, у которой все диагональные элементы
равны 1, называется единичной.

Матрица, состоящая из одних нулей, называется нулевой.

Если в квадратной матрице все элементы стоящие ниже (выше)
главной диагонали равны 0, то она называется верхний (нижний)
треугольник.

Если в матрице А строки записать столбцами с теми же
номерами, то полученная матрица будет называться транспонированной
к матрице А.

Если матрица А равна транспонированной, то она называется симметричной.

Действия над матрицами:

1) Умножение матрицы на число. В результате умножения
матрицы на число получается матрица такой же размерности, что и исходная,
каждый элемент которой является результатом произведения соответствующего
элемента исходной матрицы на число. Мы получим одинаковый результат, умножая
число на матрицу, или матрицу на число. Из определения следует, что общий
множитель всех элементов матрицы можно выносить за знак матрицы.

2) Сложение и вычитание матриц. Складывать и вычитать можно
только матрицы одинаковой размерности. Суммой (разностью) двух матриц
называется матрица той же размерности, что и исходные, каждый элемент которой
определяется как сумма (разность) соответствующих элементов матриц. Очевидно,
результат сложения не изменится, если слагаемые матрицы поменять местами. Если
к матрице прибавить или от нее отнять нулевую матрицу той же размерности, то получим
исходную матрицу.

3) Умножение матрицы на матрицу. Умножать друг на друга
можно только те матрицы, для которых число столбцов первого сомножителя равно
числу строк второго сомножителя. Результатом умножения является матрица, у
которой число строк равно числу строк первого сомножителя, а число столбцов
совпадает с числом столбцов второго сомножителя. Иными словами, перемножать
можно те матрицы, у которых совпадают средние индексы. Крайние индексы
определяют размерность получаемого результата.

Свойства операций над матрицами.

1) В общем случае . Если  то матрицы А и В называются перестановочными по
отношению друг к другу.

2)  Ассоциативность;

3)  Дистрибутивность;

4) При умножении любой квадратной матрицы на единичную
первоначальная матрица не меняется .

Вопрос №2: «Определители. Вычисление
определителей».

Определители 2-го и 3-го порядка и их
свойства. Если
квадратная матрица имеет определитель, отличный от нуля (Δ ≠ 0), то говорят,
что матрица невырожденная, в противном случае — матрица вырожденная или особая.

Определителем квадратной матрицы 2-го порядка,
называется число равное разности произведений элементов главной и побочной
диагонали матрицы.

Определителем квадратной матрицы 3-го
порядка, называется число равное:

Таким образом, вычисление определителя третьего порядка
сводится к вычислению определителей второго порядка.

Вопрос №3: «Свойства определителей».

Свойства определителей:

1) Если строка (столбец) матрицы состоит из 0, то ее
определитель равен 0.

2) Если все элементы, какой либо строки (столбца) матрицы
умножить на одно и тоже число, то и ее определитель умножится на это же число.

3) При транспонировании матрицы ее определитель не
меняется.

4) При перестановки, каких либо двух строк (столбцов)
матрицы знак матрицы меняется на противоположный. Доказательство вытекает из
того, что при перестановке одной транспозиции четность инверсии меняется.

5) Если квадратная матрица содержит две одинаковые строки
(столбца), то её определитель равен 0.

6) Сумма произведений элементов, какой либо строки
(столбца) на алгебраические дополнения какой либо строки (столбца) равно 0.

7) Если элементы, какой либо строки (столбца) равны сумме
двух слагаемых, то определитель равен сумме двух определителей, у которых все
строки (столбцы) кроме указанных, те же что и в исходном определителе, а рассматриваемая
k-строка (столбец) в первом определителе
содержит первые слагаемые, во втором вторые.

Определитель матрицы не изменится если к элементам какой
либо строки (столбца) прибавить элемент какой либо строки (столбца)
предварительно умноженные на одно и то же число.

Вопрос №4: «Обратная матрица и её
вычисление».

Обратная матрица. Матрицей, обратной матрице А,
называется матрица A^-1 такая, что A^-1A = A A^-1
= E.

Обратная матрица может существовать только для квадратной
матрицы. Причем сама является той же размерности, что и исходная матрица.

Можно показать, что для того, чтобы квадратная матрица
имела обратную, она должна быть невырожденной (т.е. Δ ≠ 0 ). Это условие
является и достаточным для существования A^-1 матрице А. Итак, всякая
невырожденная матрица имеет обратную, и, притом, единственную.

Сформулируем правило нахождения обратной матрицы на примере
матрицы А.

1. Находим определитель матрицы. Если Δ ≠ 0, то матрица A^-1
существует.

2. Составим матрицу В алгебраических дополнений элементов
исходной матрицы А. Т.е. в матрице В элементом i — ой строки и j — го столбца
будет алгебраическое дополнение A_ij элемента a_ij исходной
матрицы.

3. Транспонируем матрицу В и получим B^T.

Теорема существования и единственности обратной матрицы. Для
квадратной матрицы А существует и при том единственная обратная матрица А^-1
тогда и только тогда, когда эта матрица не вырождена. 

Вопрос №5: «Системы линейных уравнений,
их решение матричная запись».

Системы линейных уравнений. Уравнение называется линейным,
если оно содержит неизвестные в первой степени и не содержит их произведений.

Запись в матричной форме.

— система линейных уравнений.

Обозначим, — матрица коэффициентов,   —
вектор неизвестных,

— вектор свободных членов. A_mn
X_n1 + B_m1 = 0 — матричная запись системы уравнений.

Если система уравнений имеет решение, она называется совместной,
не имеет – несовместной. Совместная система, имеющая одно
решение, называется определенной, если много – неопределенной.
Две системы уравнений называются равносильными или эквивалентными,
если каждое решение является решением уравнения системы или наоборот.

Вопрос №6: «Решение систем линейных
уравнений с помощью обратной матрицы». Матричным методом могут быть решены
только те системы, у которых число уравнений совпадает с числом неизвестных и
определитель матрицы коэффициентов отличен от нуля (матрица А невырожденная). Из
этих условий следует, что  и,
следовательно, система совместна и определена. Решение системы можно получить
так: . Используя
свойства произведения матриц и свойство обратной матрицы . Т.е., для получения столбца
неизвестных нужно обратную матрицу матрицы коэффициентов системы умножить на
столбец свободных членов.

Пример. Решить систему  матричным методом. Решение. Найдем
обратную матрицу для матрицы коэффициентов системы .

Вычислим определитель, раскладывая по первой строке: . Поскольку Δ ≠ 0, то A^-1
существует.

Обратная матрица найдена верно.

Найдем решение системы .

Следовательно, x₁ = 1, x₂ = 2, x₃
= 3.

Матричный метод годится для решения любых систем, у которых
матрица А квадратная и невырожденная.

Вопрос №7: «Теорема Крамера, формулы
Крамера».

Пусть Δ = |A| определитель матричной системы
n линейных уравнений с n
неизвестных, а Δ_j определитель матрицы,
полученный из матричной системы заменой j-того
столбца на столбец правых частей. Тогда если Δ ≠ 0, то система имеет
единственное решение, определенное по формулам.

Вопрос №8: «Решение систем линейных
уравнений методом Гаусса».

Решение и исследование систем линейных
уравнений методом Гаусса.
Этот метод решения систем линейных уравнений пригоден для решения систем с
любым числом уравнений и неизвестных.

Суть метода Гаусса заключается в преобразовании заданной
системы уравнений с помощью элементарных преобразований в эквивалентную систему
ступенчатого треугольного вида.

Полученная система содержит все неизвестные в первом
уравнении. Во втором уравнении отсутствует первое неизвестное, в третьем
уравнении отсутствуют первое и второе неизвестные и т. д.

Если система совместна и определена (единственное решение),
то последнее уравнение содержит одно неизвестное. Найдя последнее неизвестное,
из предыдущего уравнения находим еще одно — предпоследнее. Подставляя
полученные величины неизвестных, мы последовательно найдем решение системы.

Элементарными преобразованиями системы линейных уравнений,
используемыми для приведения системы к треугольному виду, являются следующие
преобразования:

— перестановка местами двух уравнений;

— умножение обеих частей одного из уравнений на любое
число, отличное от нуля;

— прибавление к обеим частям одного уравнения
соответствующих частей другого уравнения, умноженных на любое число.

Элементарные преобразования переводят данную систему
линейных алгебраических уравнений в эквивалентную систему.

Две системы называются эквивалентными, если
всякое решение первой системы является решением другой системы и наоборот.

Вопрос №9: «Понятие вектора. Сложение
векторов, умножение вектора на скаляр».

Векторы на плоскости и в пространстве. Вектором
называется направленный отрезок (упорядоченная пара точек). К векторам
относится также и нулевой вектор, начало и конец которого совпадают.

Векторы и линейные операции над ними. Линейными операциями над
векторами называется сложение и умножение на число.

Суммой двух векторов a и b называется вектор c, направленный из начала вектора a в конец вектора b при условии, что начало b совпадет с концом вектора a.
Если векторы заданы их разложениями по базисным ортам, то при сложении векторов
складываются их соответствующие координаты.

Сумма любого конечного числа векторов может быть найдена по
правилу многоугольника: чтобы построить сумму конечного числа
векторов, достаточно совместить начало каждого последующего вектора с концом
предыдущего и построить вектор, соединяющий начало первого вектора с концом
последнего.

Вопрос №10: «Декартова и полярная
система координат на плоскости».

Декартовы прямоугольные координаты на
плоскости и в пространстве.

Системы координат на плоскости.

Декартовы прямоугольные координаты (рис.
4.1). О — начало координат, Ох — ось абсцисс, Оy — ось ординат,  — базисные векторы,  — абсцисса точки M ( — проекция точки M на ось Ох
параллельно оси Оy),  —
ордината точки M ( —
проекция точки M на ось Oy параллельно оси Ox).

Системы координат в пространстве.

Декартовы прямоугольные координаты (рис.
4.4). О — начало координат, Ох — ось абсцисс, Оy — ось ординат, Оz — ось
аппликат , — базисные
векторы. Oxy, Oxz, Oyz — координатные плоскости,  — абсцисса точки M ( — проекция точки M на ось Ох параллельно
плоскости Оyz),  —
ордината точки M ( —
проекция точки M на ось Oy параллельно плоскости Oxz),  — ордината точки M ( — проекция точки M на ось Oz параллельно
плоскости Oxy).

Полярные координаты на плоскости.  О — полюс, Ox — полярная ось,  — полярный радиус,  — полярный угол. Главные
значения  и :  (иногда ).

Выражение декартовых прямоугольных координат через полярные:

  

Выражение полярных координат через декартовы прямоугольные:

                              

Вопрос 11: «Цилиндрическая и сферическая
системы координат в пространстве».

Сферические и цилиндрические координаты
в пространстве.

Цилиндрические координаты. Главные значения , , :

Связь между декартовыми прямоугольными и цилиндрическими
координатами:

Сферические координаты. Главные значения , , θ:

Иногда вместо θ  рассматривают :

Вопрос №12: «Скалярное произведение
векторов и его свойства».

Скалярное произведение и его свойства.

Скалярным произведением двух векторов называется число,
равное произведению длин этих векторов на косинус угла между ними, т.е.  Из определения следует  где φ — угол между векторами.

В зависимости от значения угла между векторами, проекция
может принимать отрицательные, положительные или нулевые значения.

Свойства скалярного произведения.

Вопрос №13: «Векторное произведение
векторов и его свойства».

Векторным произведением вектора  на вектор  называется третий вектор , определяемый следующим образом:

1) длина его равна площади параллелограмма, построенного на
векторах  и , т.е.  где φ — угол между векторами  и ;

2) вектор  перпендикулярен векторам  и ;

3) векторы  после приведения к общему началу образуют правую
тройку векторов.

Свойства векторного произведения

Вопрос №14: «Смешанное произведение
векторов и его свойства».

Смешанным произведением трех векторов  называется число

Модуль смешанного произведения трех векторов численно равен
объему параллелепипеда, построенного на этих векторах.

Свойства смешанного произведения:

Вопрос №15: Двойное векторное
произведение».

Вопрос №16: «Уравнение прямой с угловым
коэффициентом».

 

Вопрос №17: «Угол между прямыми. Условия
параллельности и перпендикулярности двух прямых.

Определение. Если заданы две прямые y = k₁x
+ b₁,  y = k₂x + b₂, то острый угол между
этими прямыми будет определяться как . Две прямые параллельны, если k₁ = k₂.
Две прямые перпендикулярны, если k₁ = -1/k₂.

Теорема. Прямые Ах + Ву + С = 0 и А₁х
+ В₁у + С₁ = 0 параллельны, когда пропорциональны
коэффициенты А₁ = lА,  В₁ = lВ. Если еще и С₁
= lС, то прямые совпадают.

Координаты точки пересечения двух прямых находятся как
решение системы  уравнений этих прямых.

Вопрос №18: «Общее уравнение прямой».

 

Вопрос №19: «Общее уравнение плоскости.
Нормальный вектор плоскости».

Вопрос №20: «Угол между двумя
плоскостями. Условия параллельности и перпендикулярности двух плоскостей».

Вопрос №21: «Канонические уравнения
прямой в пространстве».

Вопрос №22: «Угол между прямыми в
пространстве. Условия параллельности и перпендикулярности двух плоскостей.

Вопрос №23: «Условие параллельности
прямой и плоскости в пространстве».

Вопрос №24: « Условие перпендикулярности
прямой и плоскости в пространстве».

Вопрос №25: «Угол между прямой и
плоскостью».

Вопрос №26: «Каноническое уравнение
эллипса. Исследование формы эллипса».

  

                                                                                 
                   

Вопрос №27: «Каноническое
уравнение гиперболы. Исследование формы гиперболы».

Вопрос №28: «Каноническое
уравнение параболы. Исследование формы параболы».

Вопрос №29: «Общее уравнение
линии второго порядка. Понятие типа линии второго порядка».

 

Уравнение такого вида может определять: 1) эллипс (в
частности, окружность), 2) гиперболу, 3) параболу, 4) пару прямых
(параллельных, пересекающихся либо совпадающих), 5) точку или не определять
никакой линии.

В простейшем случае, при В = 0, тип кривой можно
определить, выделив полные квадраты переменных.

Вопрос №30:
«Числовые последовательности и операции над ними, ограниченные и неограниченные
последовательности».

Вопрос №31: «Бесконечно большие
и бесконечно малые последовательности, основные свойства бесконечно малых последовательностей».

Вопрос №32: «Сходящиеся
последовательности: предел последовательности, основные свойства сходящихся
последовательностей».

Вопрос №33: «Монотонные
последовательности, число е».

Вопрос №34: «Определение
функции. Способы задания функций».

Вопрос №35: «Предел функции.
Односторонние пределы. Свойства пределов. Два замечательных предела».

Предел функции (предельное
значение функции) в заданной точке, предельной для области определения функции, —
такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной
точке.

Односторонний предел числовой функции в точке — это специфический предел,
подразумевающий, что аргумент функции приближается к указанной точке с
определённой стороны (слева или справа). Числовая функция имеет предел в точке
тогда и только тогда, когда она имеет в этой точке совпадающие левый и правый
пределы.

      

 

Вопрос №36: «Непрерывность и
разрывы и функций».

Вопрос №37: «Обратные функции».

Пусть X и Y – некоторые
множества и пусть задана функция f, т.е. множество пар чисел (x;y) (x ϵ X; y ϵ Y), в котором каждое
число x входит в
одну и только одну пару, а каждое число y – по крайней мере в одну пару.
Если в каждой паре этого множества числа x и y поменять
местами, то получим множество пар чисел (y;x), которое называется обратной функцией φ к
функции f.

Вопрос №38: «Сложные функции».

Если на некотором множестве X определена
функция z = φ(x) со множеством
значений Z, а на
множестве Z – функций
y = f [φ(x)] называется сложной
функцией от x [или
суперпозицией (иногда композицией) функций φ(x) и f(z)], а переменная z – промежуточной переменной
сложной функции.

Вопрос №39: «Производная. Ее
физический и геометрический смысл».

                                

Вопрос №40: «Правила
дифференцирования».

Вопросы 41: «Производные от
элементарных функций. Таблица производных».

Вопрос №42: «Дифференциал.
Определение и геометрический смысл».

Вопрос №43: «Производные и
дифференциалы высших порядков».

Вопрос №44: «Раскрытие
неопределенностей. Правило Лопиталя».

Вопрос №45: «Формулы Тейлора и
Маклорена».

Вопрос №46: «Разложение в ряд
Маклорена элементарных функций, вычисление числа е».