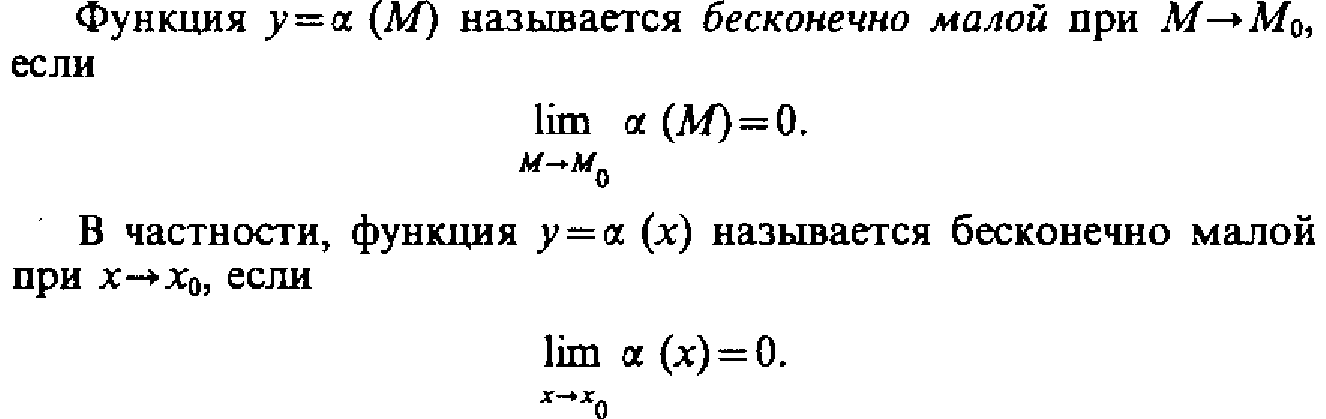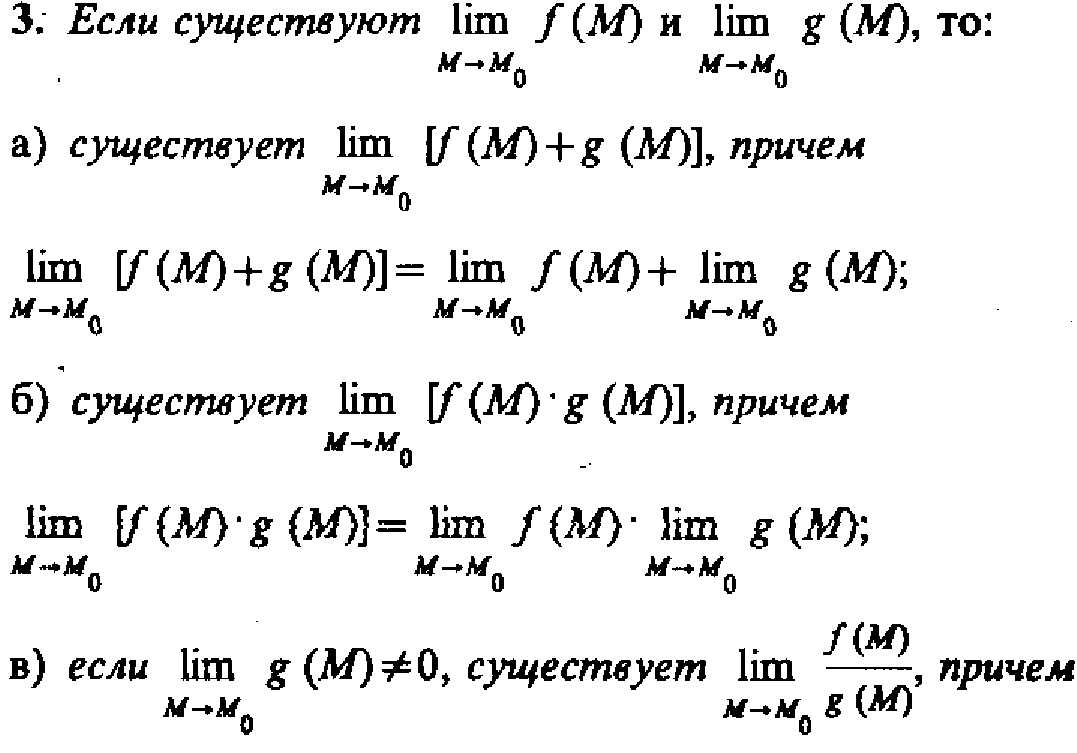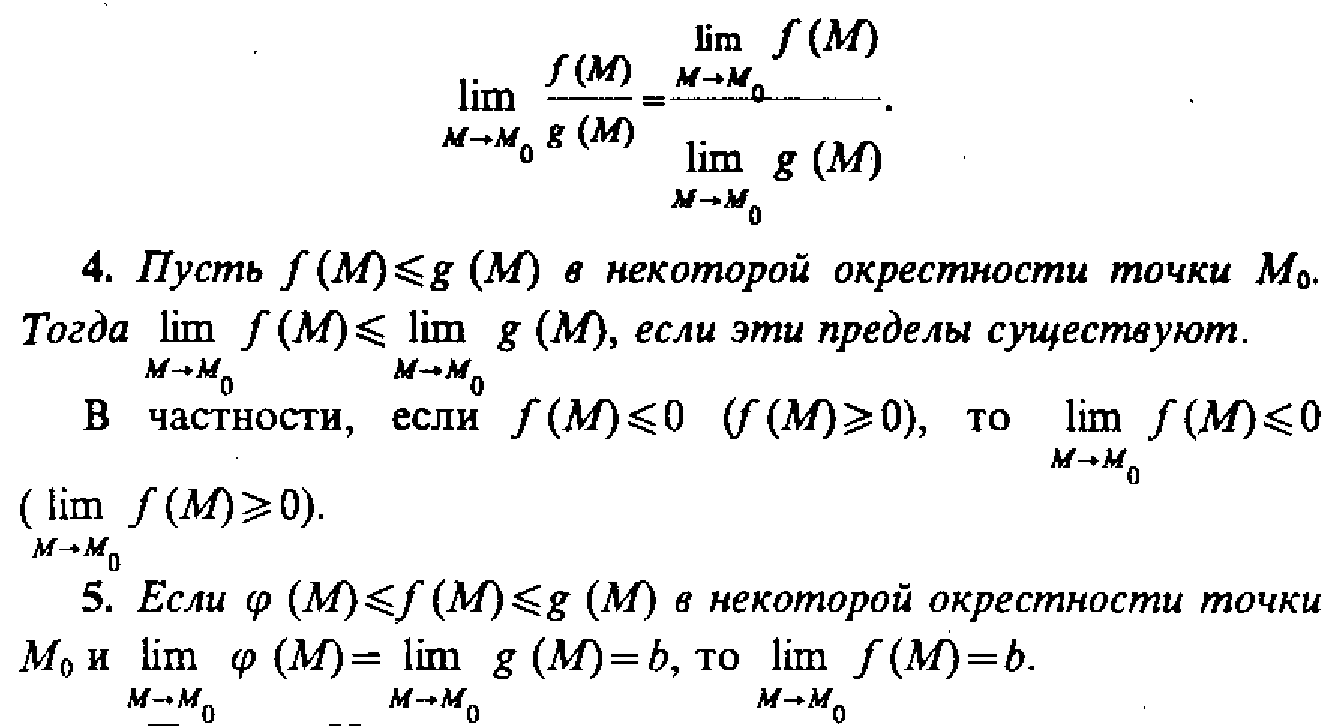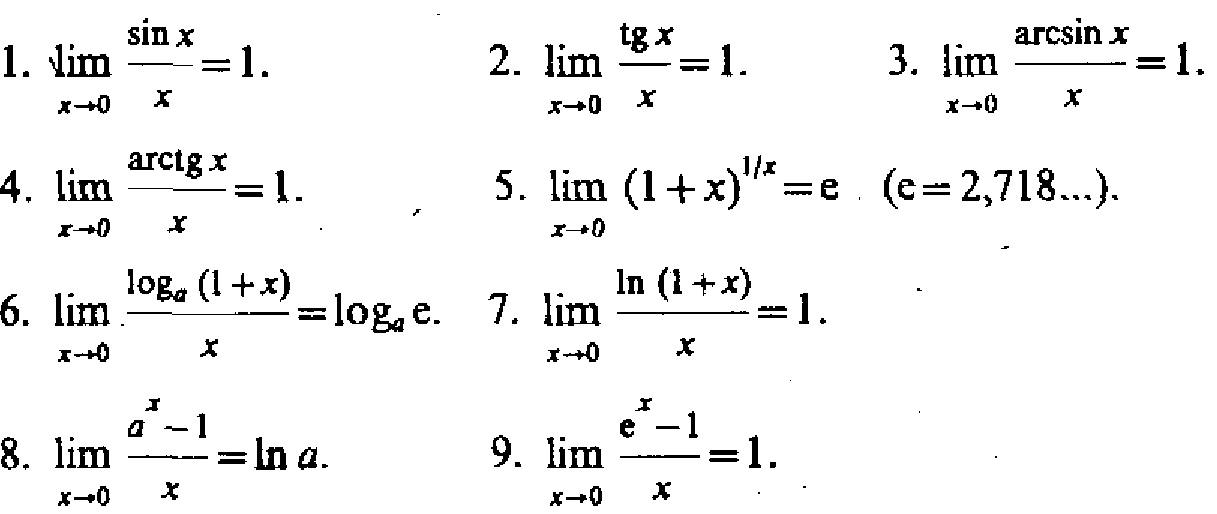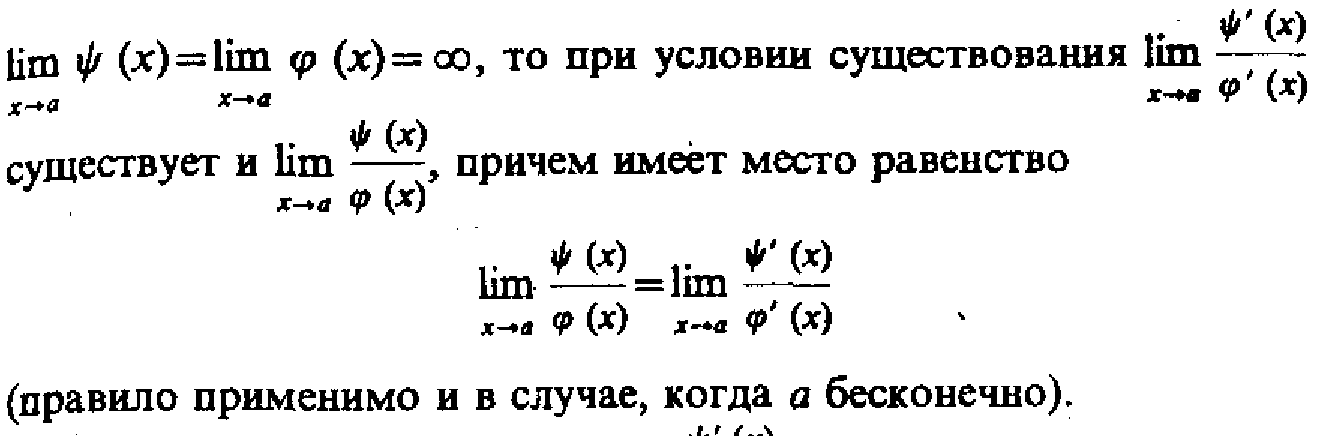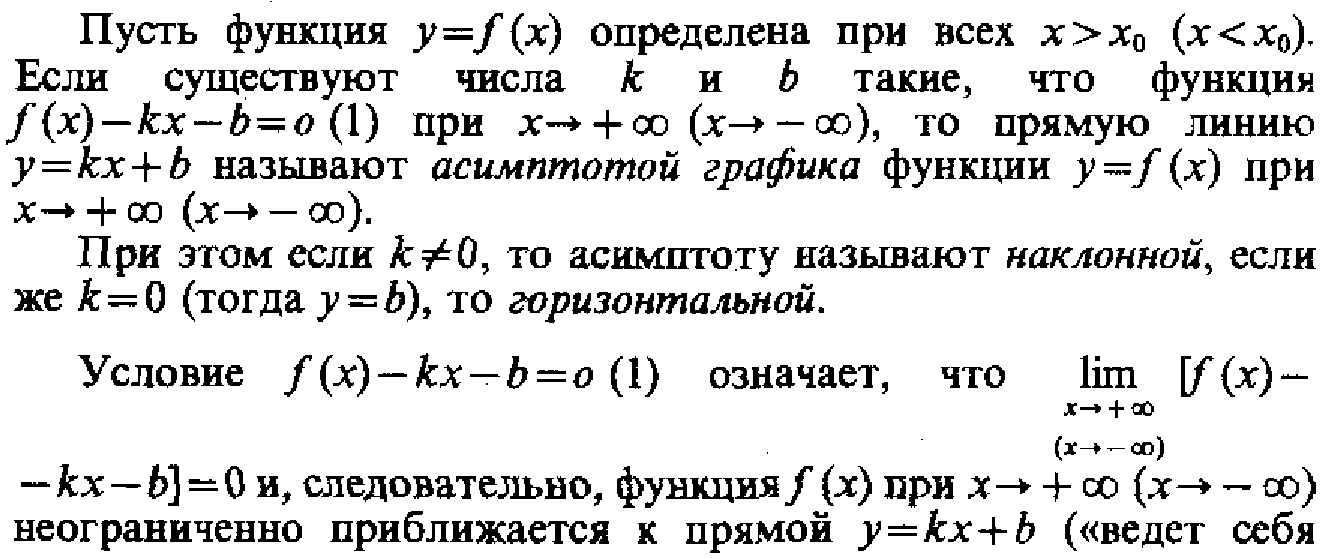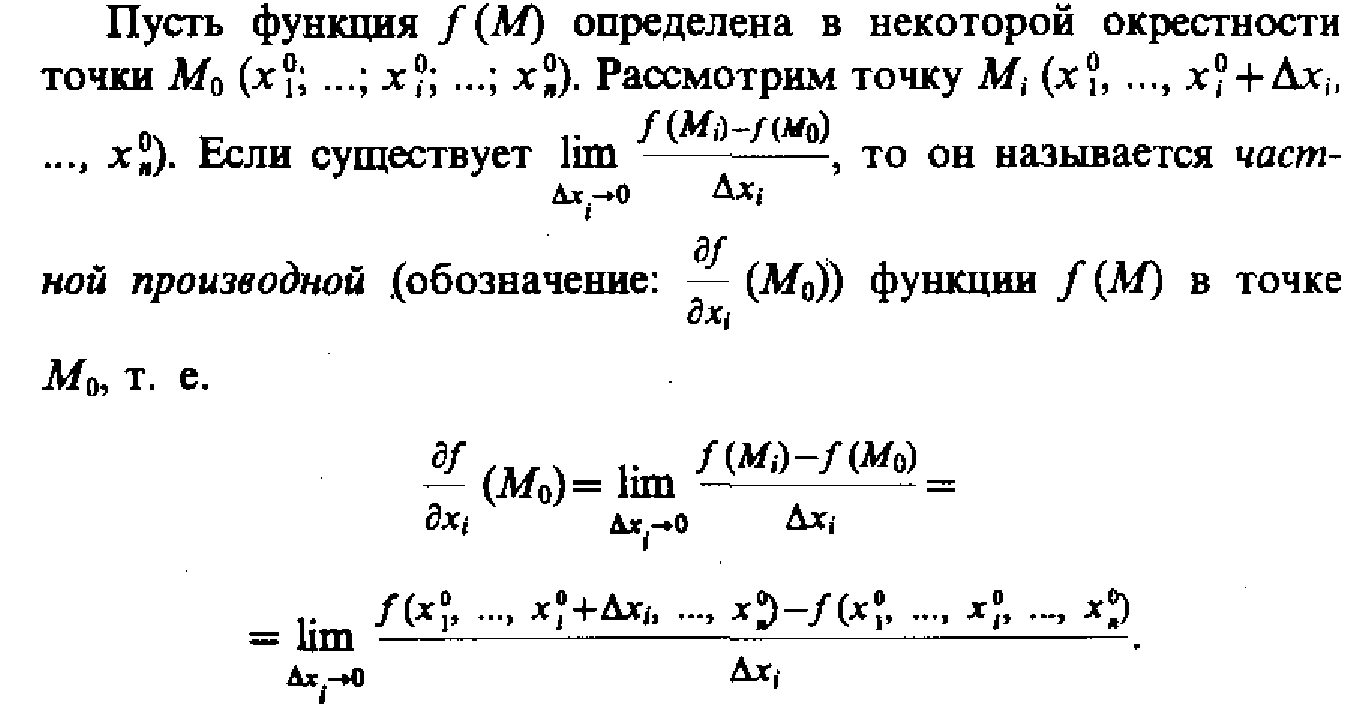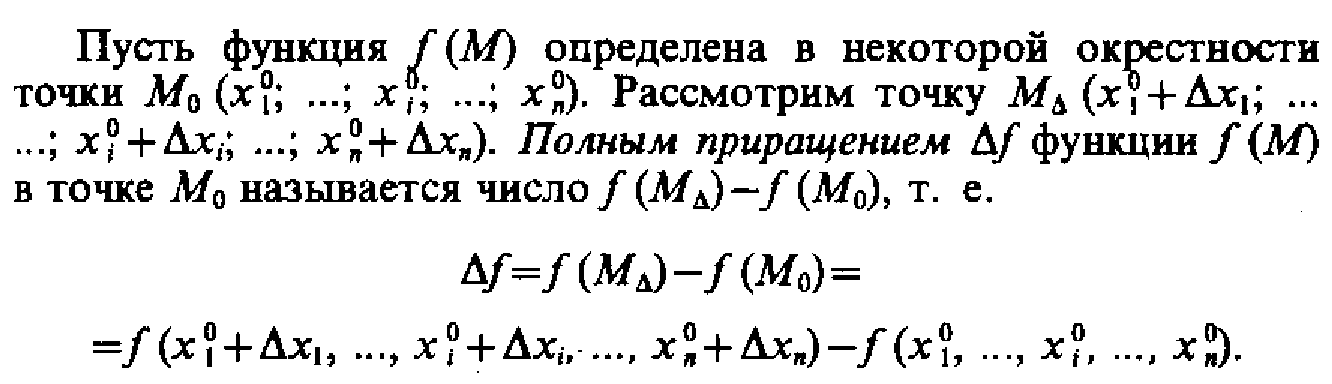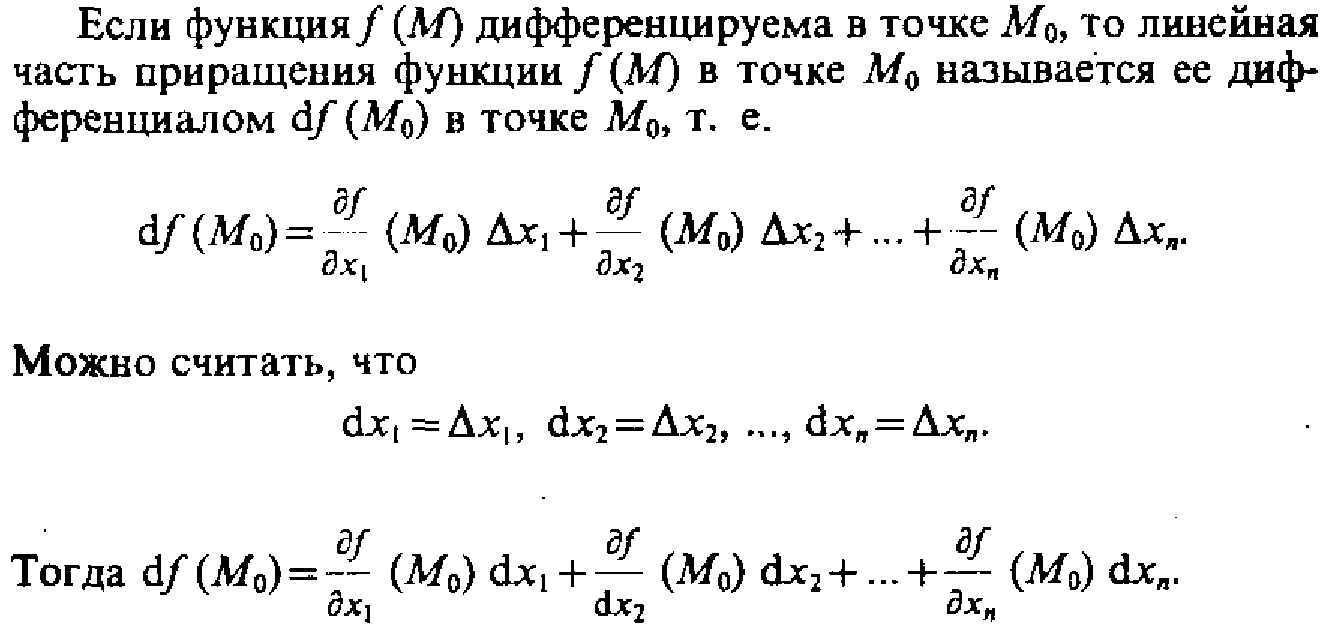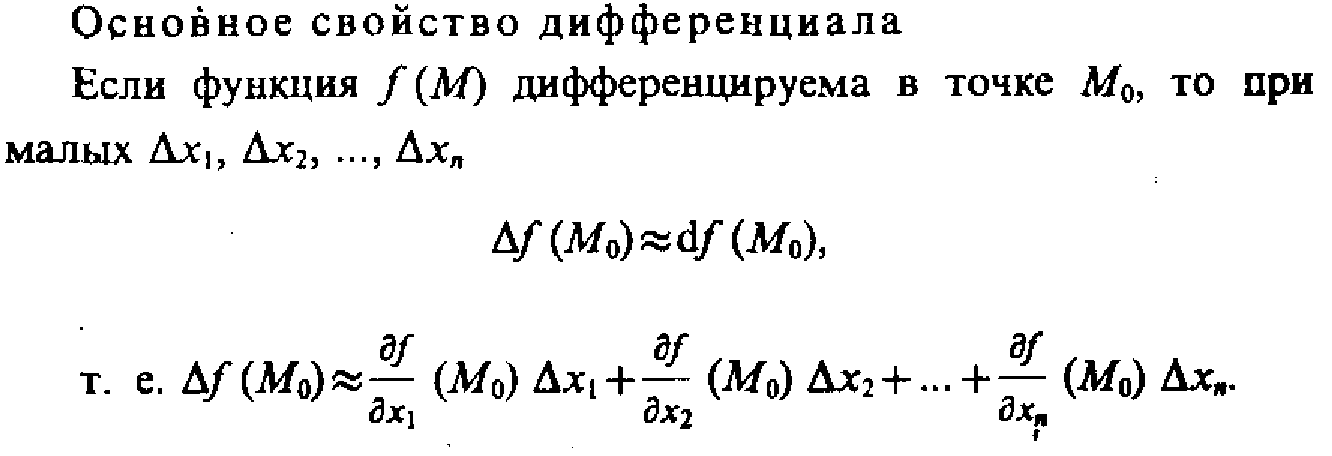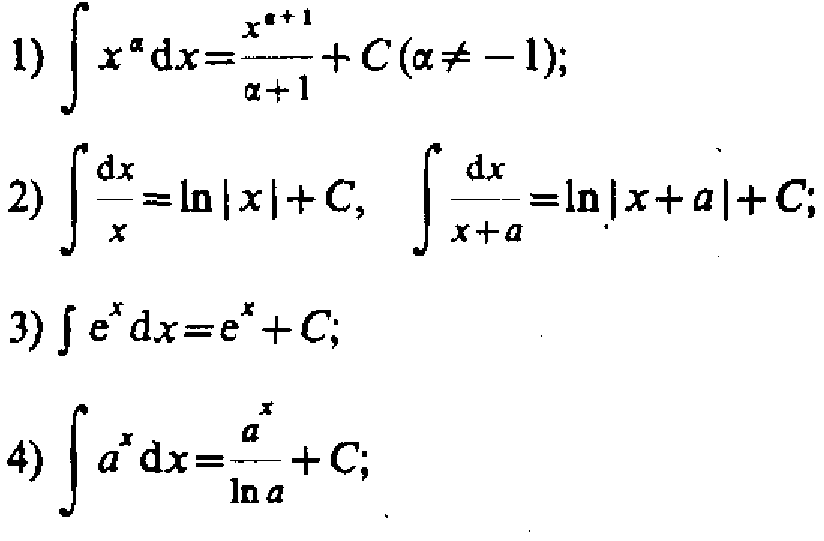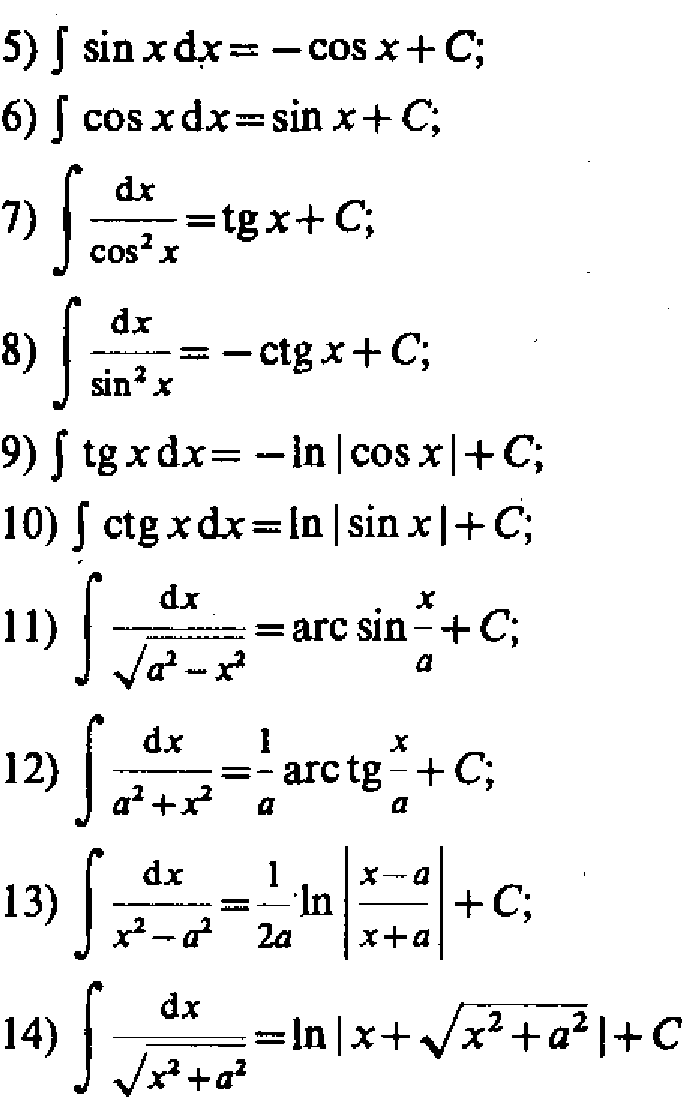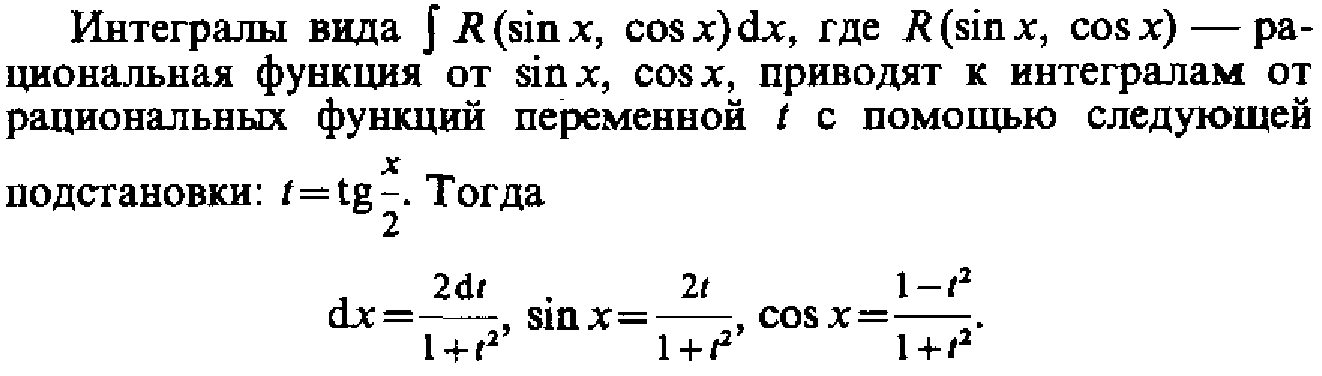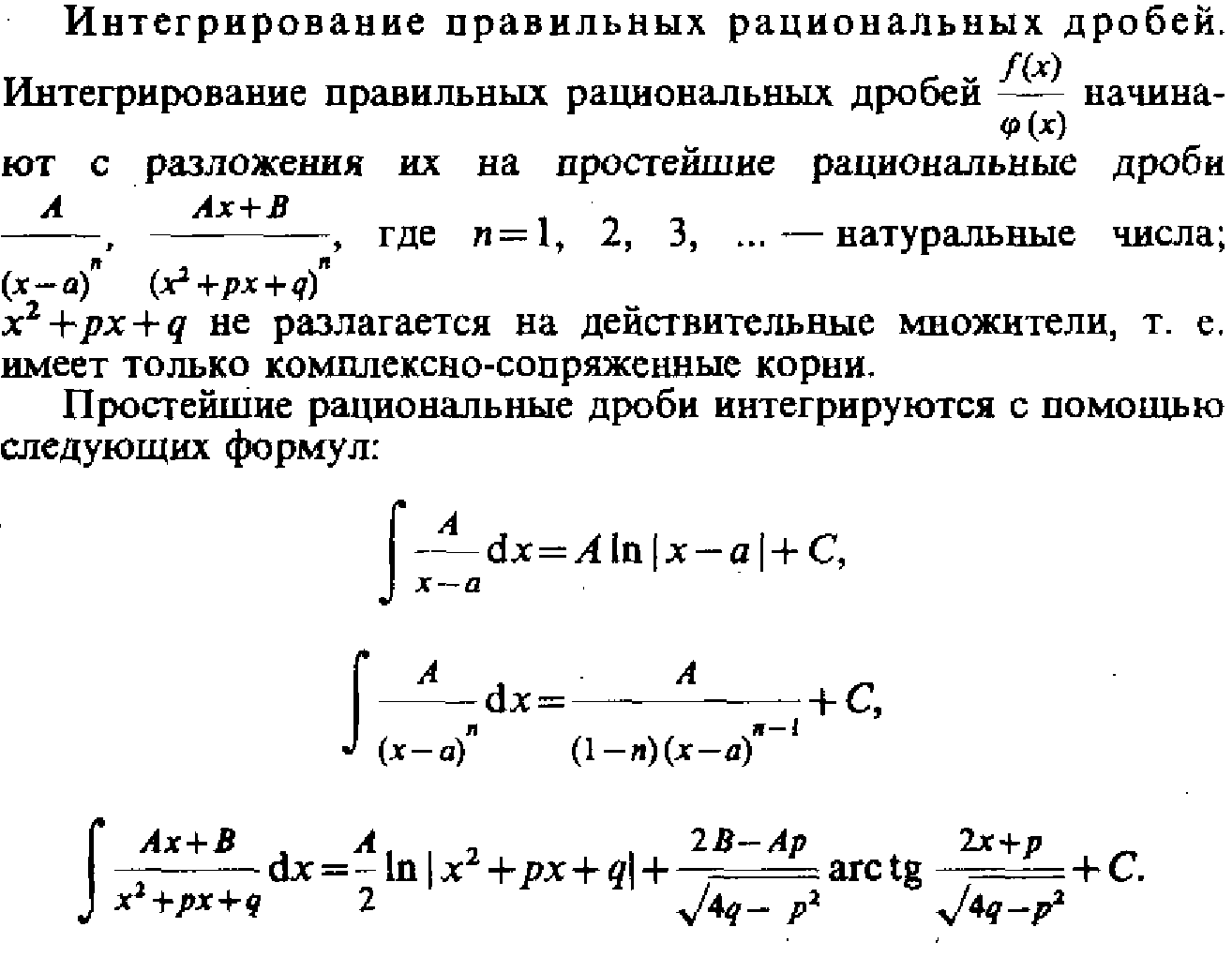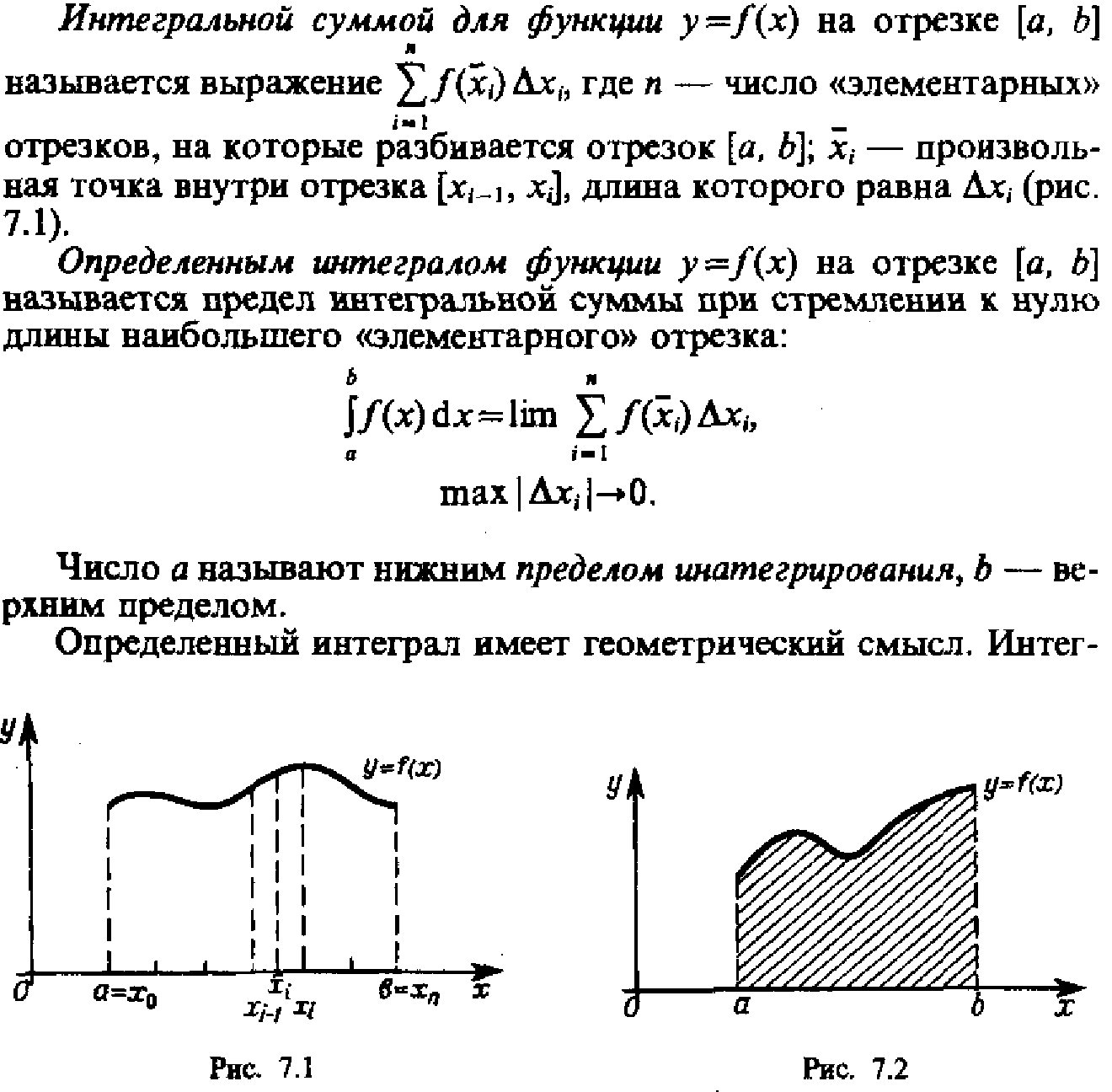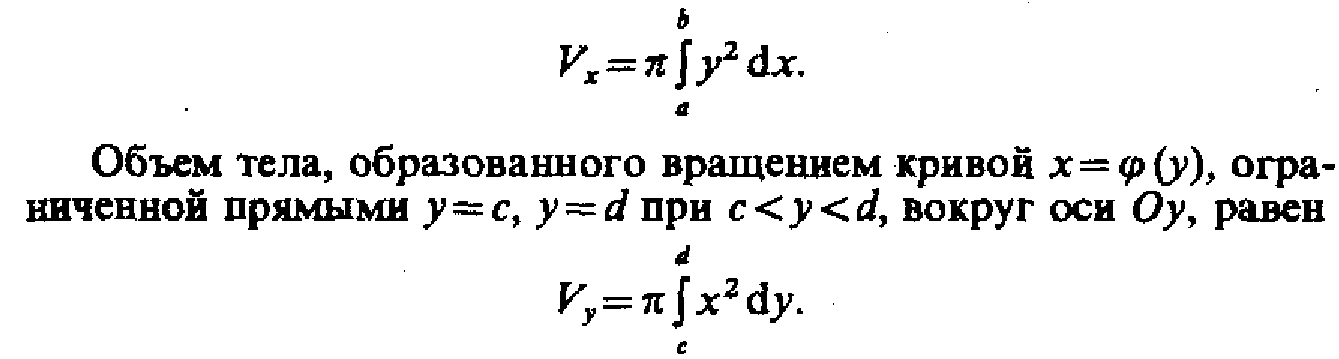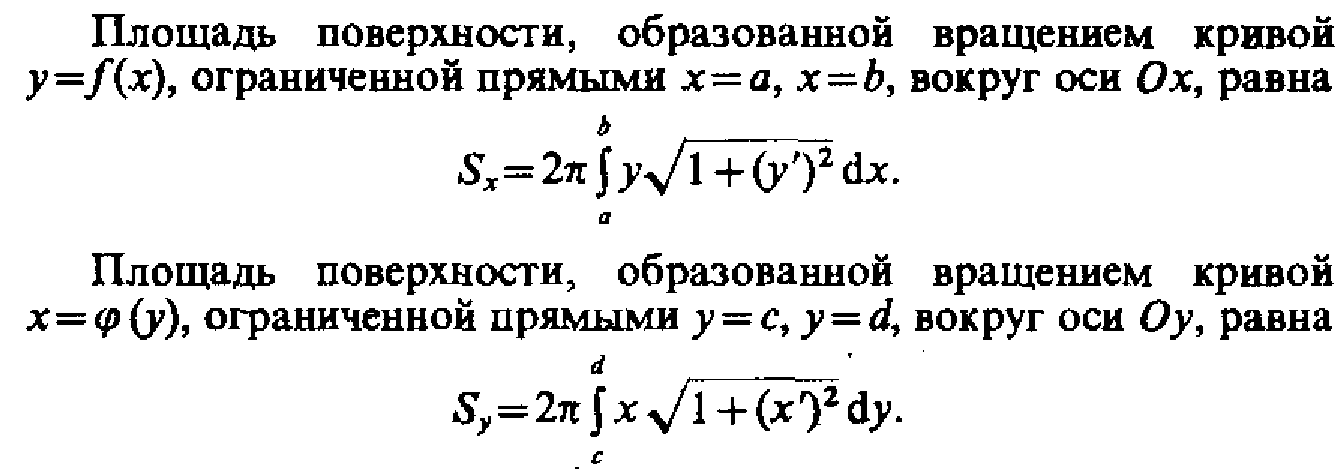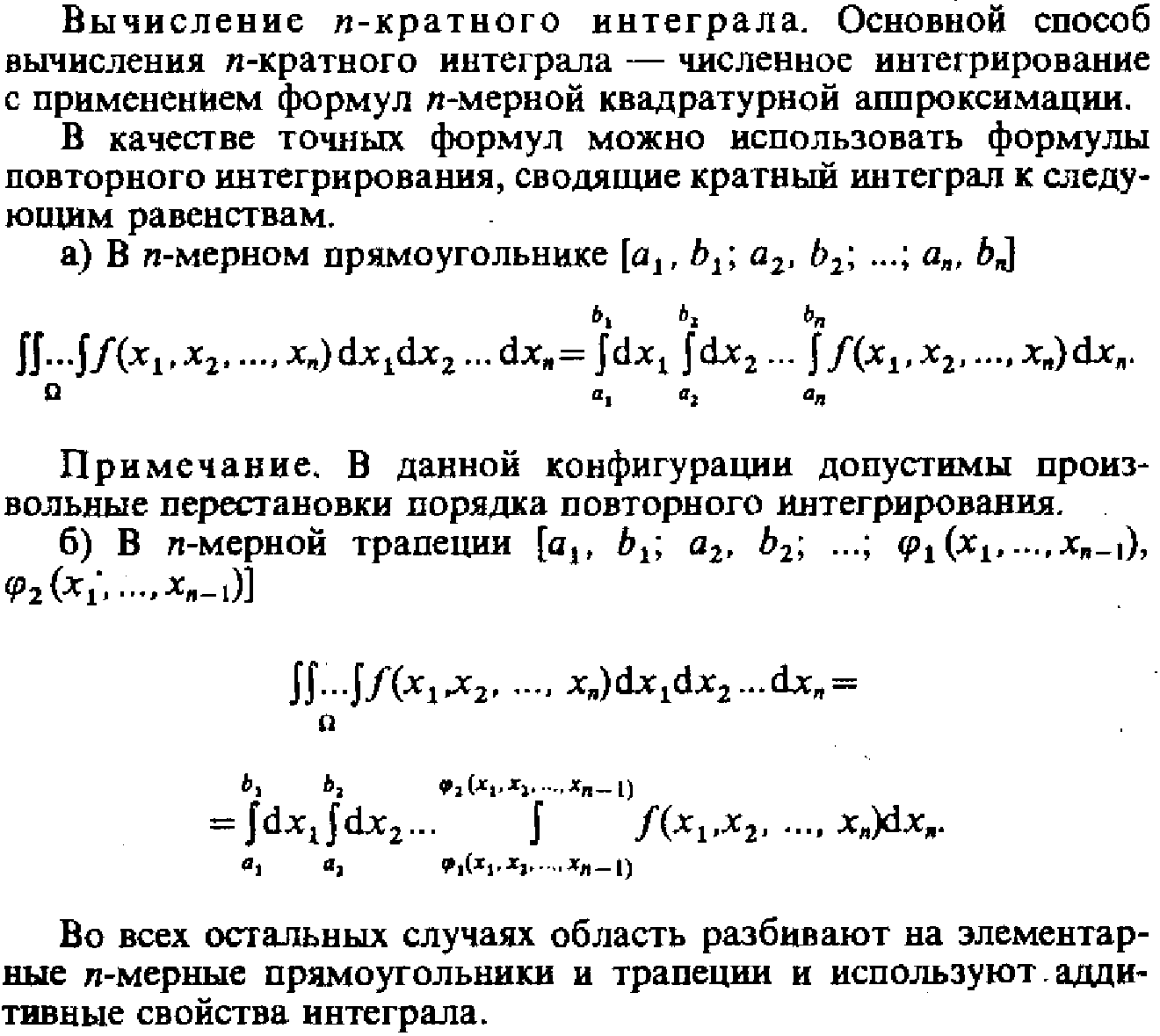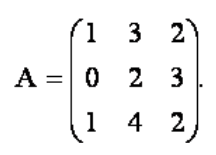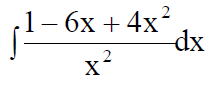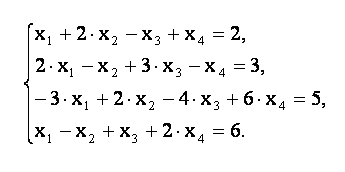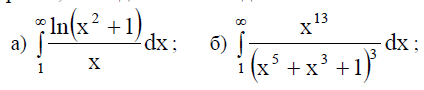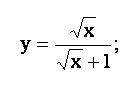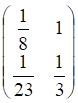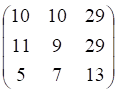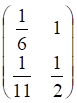Ответы на вопросы на экзамен по высшей математике

1. Понятие
   о функциях и способах их задания:

у
наз.ф-цией от х , если каж.рассматр знач-ю
х соотв.опред.знач-е величины у

х-аргумент,у-ф-ция.
Способы задания:а)аналитический
б)графический в)табличный

1. Классификация
   функций

Заданные
аналитически:1)алгебраические-получены
в рез-те алгебраич.действий над знач-ми
аргумента(многочлен) 2)неалгебраические(логафифм,
тригонометрические)

Обратные
ф-ции-получ.ф-ной зависимостью у=f(х)
но у-аргумент, х-ф-ция

1. Пределы.
   Понятия о пределах послед-тей и ф-ций

1. Непрерывность
   и разрыв ф-ций

1. Бесконечно
   малые ф-ции

1. Теоремы
   о пределах

1. Замечательные
   пределы

Рассмотрим
сектор АОС

S_кр=πr^2=π
(т.к r
=1)→2π радиан, S_сек=у
→х радиан

У=S_сек=πх/2π=х/2

S_АOC<S_секАОС<S_BOC

1/2*1*sinx≤x/2≤1/2*1*1*tgx

(*)1<x/sinx<1/cosx,х
є (0;2π) х=-у след-но у є (-π/2;0) 1<-y/sin(-y)
< 1/cos(-y)
1<y/siny<1/cosy
y
є(-π/2; 0)

Отсюда
с учетом нер-ва(*) получаем (**)
1<x/sinx<1/cosx,х
є (-π/2;0)υ(0;π/2). Т.к 1/cosx
стремится к 1/cosx=1,то
из нер-ва(**) по теореме о пределе пром
ф-ии lim_x→0
x/sinx=1

1. Понятие
   о производной.Механич. и геометрич.смыслы

1. Теоремы
   о произв.пост.величины,суммы, произвед,дроби

(10,11,12,13,14,15,16,17)

18.
Производные высших порядков ф-ций с
одной переменной

19.
Теорема о корнях производных(Ролля)

20.
Теорема о конечном приращении
ф-ции(Лагранжа)

21
Правило Лопиталя

22.
max
и min
ф-ций

23.
Необходимое условие существования
экстремума ф-ции с одной перем.

24.
Достаточное условие существования
экстремума ф-ции с одной перем.

25.
Асимптоты

26.
Дифференциал ф-ции с одной переменной

27.
Функции многих переменных. Частные и
полные приращения(28)

29.
Частные производные высших порядков

30.
Дифференциал ф-ции многих переменных

31.
Экстремум ф-ции многих перем. Необходимое
условие существования

32.
Достаточное условие экстремума ф-ции
многих переменных

все
частные производные равны 0

33.Условный
экстремум. Ф-ция Лагранжа

34.
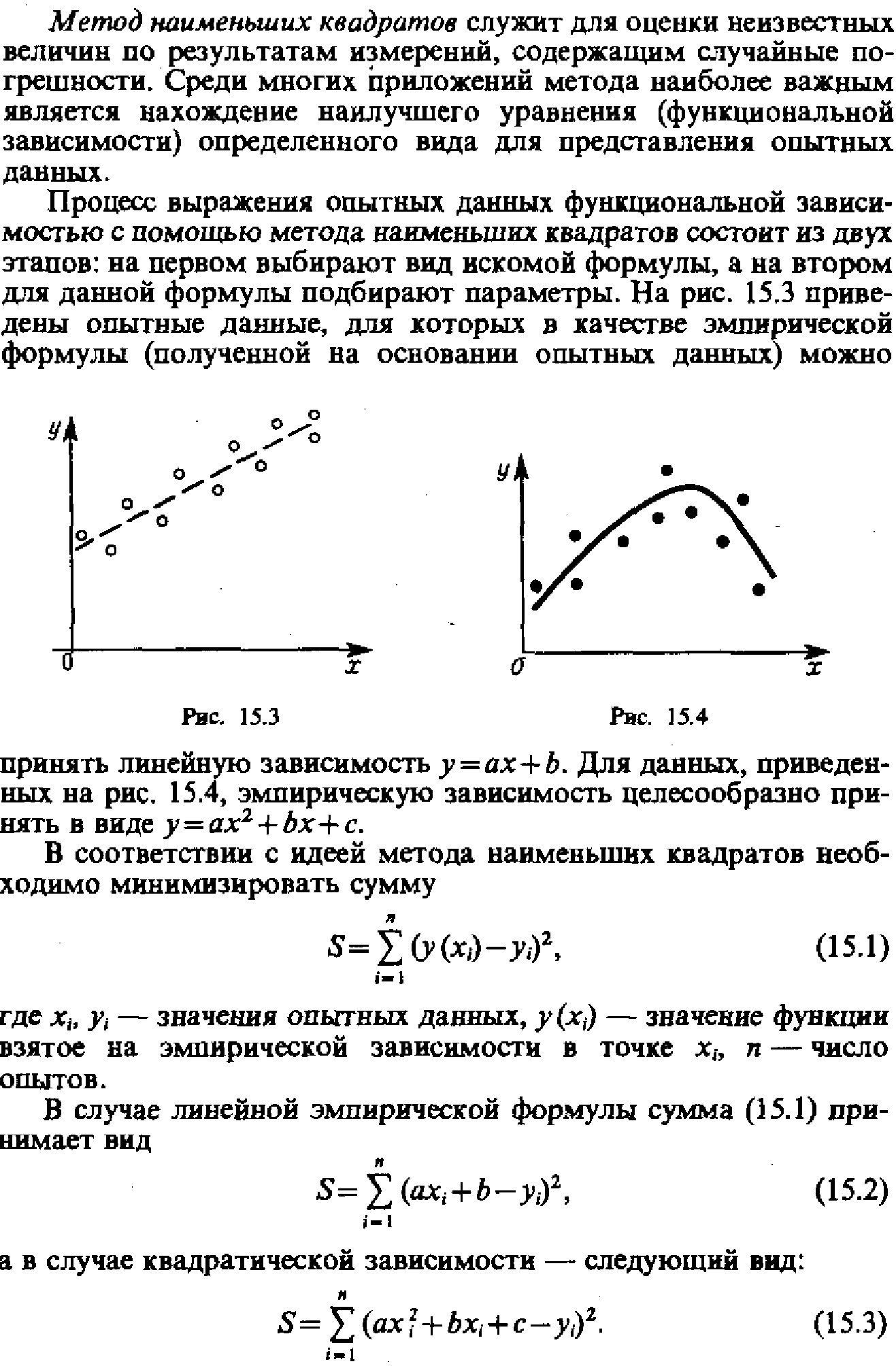
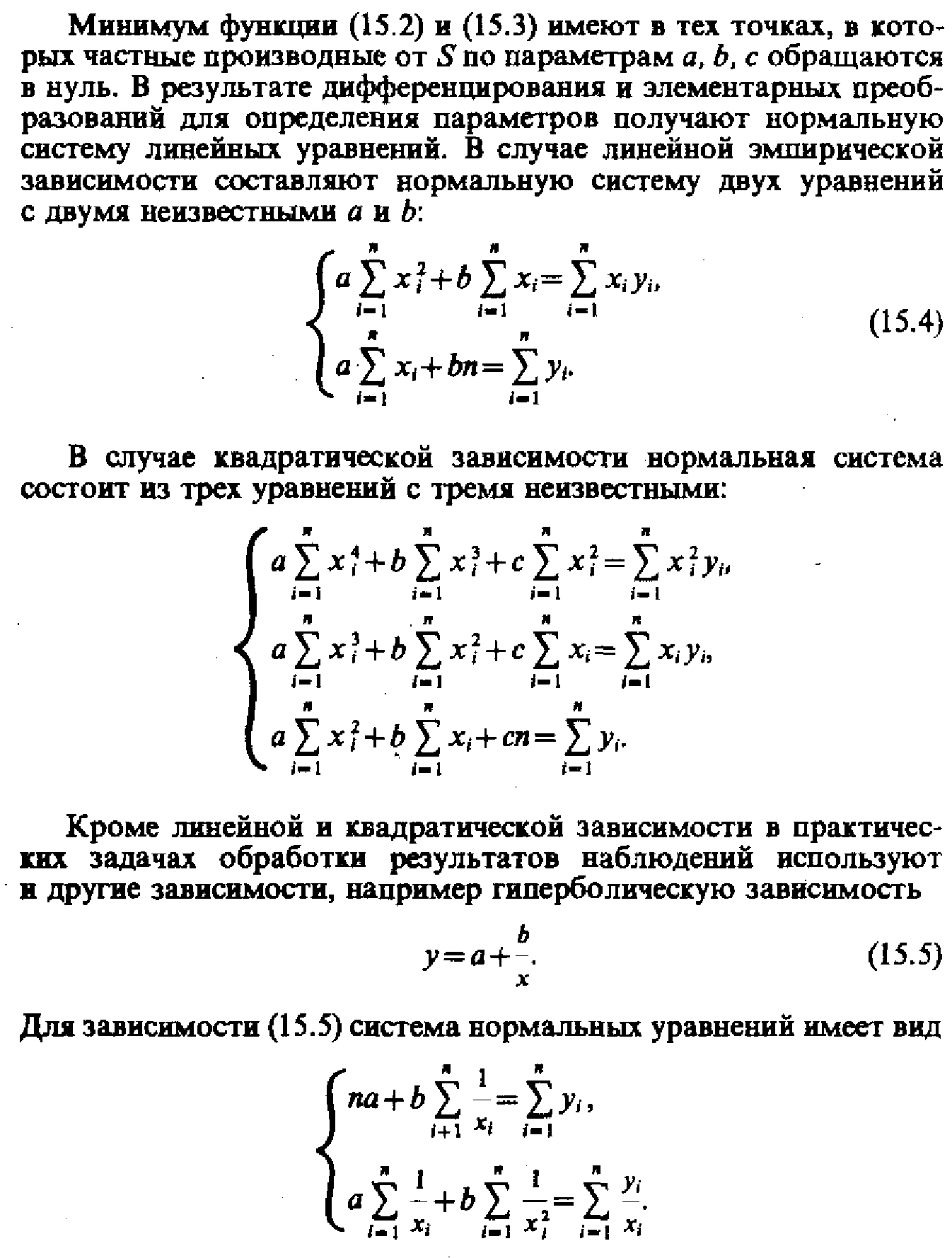
Метод наименьших квадратов

35.
Первообразная и неопределённый интеграл.
Таблица интегралов.

36.
Метод замены переменных при интегрировании

37.
Интегрирование по частям

38.
Интегрирование тригонометрических
функций

39.
Интегрирование рациональных дробей

40.
Определённый интеграл как предел
интегральной суммы. Формула Ньютона-Лейбница.

41.
Вычисление площадей плоских фигур с
пом.опред.интеграла

42.
Вычисление объёмов тел вращения

43.
Вычисление длины кривой

44.
Приближённые методы вычисления
определённого интеграла

45.
Несобственные интегралы

46.
Кратные интегралы

9

Соседние файлы в предмете Математический анализ

• #
• #
• #

  03.10.201322.36 Кб7Гетман Рыклин лаб 3.xlsx

• #
• #

  03.10.201327.36 Кб13множетсвенная регрессия Друж.xlsx

• #
• #
• #
• #
• #
• #

Экзаменационные билеты, вопросы и задачи по курсу высшей математики для студентов 1 курса (1 и 2 учебный семестр) и 2 курса (3 и 4 семестр) очной и заочной форм обучения технических и гуманитарных специальностей ВУЗов.

Допуск к экзамену получают учащиеся, выполнившие и сдавшие все контрольные и расчетные работы, предусмотренные учебным планом кафедры математики.

Для успешной сдачи экзамена необходимо выполнить 60 или более процентов заданий указанных в билете, решив минимум одну задачу.

Ответы на теоретические вопросы экзамена должны включать точные определения и основные положения рассматриваемой темы с выводами соответствующих формул.

Если Вам требуется помощь в решении задач, наши специалисты готовы ответить на все вопросы по математике.

Экзаменационный билет по высшей математике

Билет для сдачи экзамена по высшей математике включает решение задач и ответы на вопросы по темам, изучавшимся в пройденном учебном семестре, и может содержать от трех до 5, а в некоторых случаях и до 10 пунктов.

Например, в билете могут быть три теоретических вопроса и две задачи, либо задание в виде теста.

Пример экзаменационного билета

Примерный билет содержит задачи и вопросы по разделам высшей математики:

1. Определители. Свойства определителей.

2. Угол между векторами. Проекция вектора на ось.

3. Векторное произведение двух векторов и его свойства.

4. Найти обратную матрицу A^-1, если:

5. Вычислить неопределенный интеграл

Вопросы к экзаменам по математике

Примерный перечень экзаменационных вопросов по теории курса высшей математики, включаемых в билет:

Раздел матрицы и векторы

1. Матрицы. Виды матриц. Действия над матрицами.
2. Алгебраические дополнения и миноры.
3. Вычисление определителей методом треугольников и разложением по элементам строки или столбца.
4. Невырожденная матрица. Обратная матрица. Нахождение обратной матрицы.
5. Матричный метод решения систем линейных уравнений. Формулы Крамера.
6. Метод Гаусса решения систем алгебраических линейных уравнений.
7. Действия над векторами.
8. Линейная зависимость и независимость векторов.
9. Векторный базис. Координаты вектора.
10. Прямоугольная декартова система координат. Деление отрезка в заданном отношении. Определение расстояния между точками.
11. Скалярное произведение двух векторов и его свойства.
12. Смешанное произведение трех векторов и его свойства.

Неопределённый интеграл

1. Первообразная функция и неопределенный интеграл.
2. Простейшие свойства неопределенного интеграла и его геометрический смысл.
3. Интегрирование методом разложения и методом замены переменной.
4. Метод интегрирования по частям.
5. Интегрирование простейших дробей.
6. Интегрирование дробно-рациональной функции.
7. Интегрирование тригонометрических функций.
8. Интегрирование иррациональных функций.

Определённый интеграл

1. Определение определенного интеграла. Свойства определенного интеграла.
2. Определенный интеграл с переменным верхним пределом интегрирования. Формула Ньютона-Лейбница.
3. Замена переменной и интегрирование по частям в определенном интеграле.
4. Несобственные интегралы с бесконечными пределами интегрирования и от неограниченных функций.
5. Геометрические приложения определенного интеграла. Вычисление площадей фигур в декартовых и полярных координатах.
6. Длина дуги плоской кривой в декартовых и полярных координатах, объем тела вращения.
7. Решение физических задач с помощью определенных интегралов.

Кратные интегралы

1. Определение двойного интеграла. Его геометрический смысл
2. Свойства двойного интеграла
3. Понятие о правильных областях. Двукратный интеграл
4. Сведение двойного интеграла к двукратному
5. Замена переменных в двойном интеграле. Вычисление двойного интеграла полярных координатах
6. Вычисление объемов тел и площадей плоских областей
7. Задачи механики
8. Определение тройного интеграла. Его механический смысл. Свойства
9. Вычисление тройного интеграла
10. Вычисление тройного интеграла в декартовых координатах
11. Замена переменных в тройном интеграле. Тройной интеграл в цилиндрических и сферических координатах
12. Приложения тройных интегралов к задачам геометрии и механики
13. Вычисление объемов тел
14. Задачи механики

Криволинейные и поверхностные интегралы

1. Криволинейные интегралы первого рода (или по длине дуги)
2. Определение и физический смысл криволинейного интеграла первого рода. Свойства
3. Вычисление криволинейного интеграла первого рода
4. Криволинейный интеграл для пространственного случая
5. Некоторые применения криволинейного интеграла первого рода
6. Криволинейный интеграл второго рода (или по координатам)
7. Задача о работе силового поля. Определение криволинейного интеграла второго рода
8. Существование и вычисление криволинейного интеграла второго рода
9. Связь между криволинейными интегралами первого и второго рода
10. Формула Грина
11. Условия независимости интеграла от пути интегрирования
12. Поверхностный интеграл первого рода (или по площади поверхности). Теорема существования
13. Вычисление поверхностного интеграла первого рода
14. Некоторые применения поверхностного интеграла первого рода
15. Поверхностный интеграл второго рода или по координатам. Физический смысл
16. Применение поверхностного интеграла второго рода

Экзаменационные задачи по математике

Примеры экзаменационных задач по курсу высшей математики, которые могут быть включены в билет для сдачи экзамена:

1. Решить систему уравнений методом Гаусса

2. Используя признаки сходимости несобственных интегралов, исследовать на сходимость

3. Применяя основные правила дифференцирования, найти производную функции

Ответы на экзаменационные вопросы по математике

Ответы на некоторые теоретические вопросы в экзаменационных билетах по высшей математике:

• Однородные функции, однородные дифференциальные уравнения
• Линейное дифференциальное уравнение первого порядка
• Уравнение Бернулли
• Уравнение в полных дифференциалах
• Интегрирующий множитель
• Дифференциальные уравнения высших порядков. Задача Коши
• Числовые ряды. Основные понятия
• Ряд геометрической прогрессии со знаменателем
• Остаток ряда
• Свойства, сходящихся числовых рядов
• Необходимый признак сходимости числового ряда
• Признак сравнения рядов с неотрицательными членами
• Признак Даламбера
• Признак Коши

Другие ответы можно найти, воспользовавшись поиском на нашем сайте.

Наш коллектив математиков желает Вам успешной подготовки и сдачи экзамена, и в случае необходимости готов оказать студентам всю необходимую помощь.

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Ответы на экзаменационные билеты по высшей математики

№1 Функциональные
ряды

Членами являются
функции, определенные в некоторой области изменения аргумента х: U₁(x)+U₂(x)+…+U_n(x)+… Придавая х какое-либо значение
х₀ из области определения функций U_n(x), получим числовой ряд U₁(x₀)+ U₂(x₀)+…+ U_n(x₀)+… Этот ряд может сходиться или
расходиться. Если он сходится, то точка х₀ называется точкой
сходимости функционального ряда. Если при х=х₀ ряд
расходится, то точка х₀ называется точкой расходимости
функционального ряда. Совокупность всех точек сходимости функционального
ряда называется областью его сходимости.

Функциональный
ряд называется правильно сходящимся на сегменте [a, b], если существует такой
знакоположительный сходящийся ряд b₁+ b₂ +…+ b_n +…, что абсолютные величины членов
данного ряда для любого значения х, принадлежащего сегменту [a, b], не превосходят соответствующих
членов знакоположительного ряда, т. е. |U_n(x)| ≤ b_n (n=1, 2, …)

№2 Неопределенный
интеграл и его свойства

Интегральное
исчисление решает обратную задачу: найти F(x), зная ее производную f(x).

Функция F(x) называется первообразной, если выполняется равенство F’(x)=f(x).

Если F(x) одна из первообразных функции f(x), то любая первообразная
функции f(x) на этом промежутке имеет вид F(x)+C, где С€R.

Множество всех
первообразных функции f(x) называется неопределенным интегралом

Свойства:

– неопределенный
интеграл от алгебраической суммы конечного числа функций равен алгебраической
сумме неопределенных интегралов от каждого слагаемого в отдельности;

– постоянный
множитель можно выносить за знак неопределенного интеграла.

№3 Асимптоты

Асимптотой кривой
называется прямая, расстояние до которой от точки, лежащей на кривой, стремится
к 0 при неограниченном удалении от начала координат этой точки по кривой.

Асимптоты бывают
вертикальными, горизонтальными и наклонными.

Прямая х=a является вертикальной асимптотой
графика функции y=f(x), если lim f(x)=∞ ,

                   
 ^x→0±a

Уравнение
наклонной асимптоты будем искать в виде y=Rx+b

R = lim(y/x) ;   b = lim
(y – Rx)

      ^{x→0                             x→0}

№4 Экстремум
функции (для одной переменной)

Если функция  f(x) дифференцируема на интервале (a;b) и f’(x)>0 (f’(x)<0), то f(x) возрастает (убывает) на этом промежутке. Точка х₀ называется
точкой максимума функции f(x), если существует такая окрестность
точки х_0, что для всех х, не равных х₀ из этой окрестности,
выполняется неравенство f(x) < f(х₀), где х₀ – точка максимума. 
Значение функции в точке максимума (минимума) называется максимумом (минимумом)
функции. Максимум (минимум) функции называется экстремумом.

Необходимое
условие экстремума: если дифференцируемая функция f(x) имеет экстремум в точке х₀, то ее производная в этой точке
равна 0.

Достаточное
условие экстремума: если производная меняет знак на минус, то х₀ –
точка максимума; если с минуса на плюс, то точка х₀ – точка
минимума.

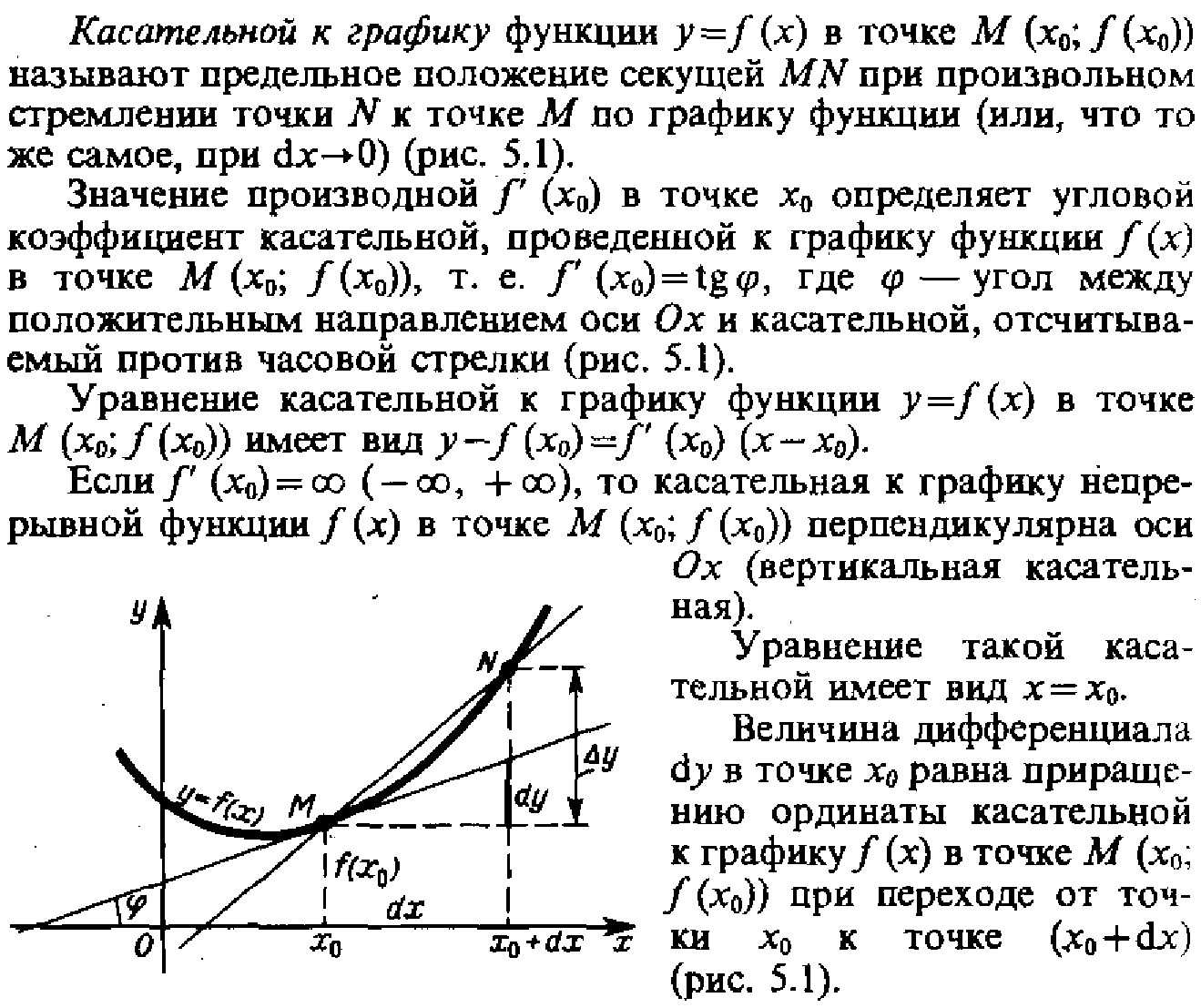
№5 Производная.
Ее геометрический и физический смысл.

Физический:
производной функции y=f(x) в точке х₀ называется предел отношения приращения функции ∆y в этой точке к вызвавшему его
приращению аргумента ∆х при произвольном стремлении ∆х к 0.

Геометрический:
угловой коэффициент касательной к графику функции в точке с абсциссой х₀
равен значению производной этой функции в точке х₀.

№6 Замечательные
пределы

lim (1+1/x)^x=e;   lim
(1+x)^1/x=e  (e – экспонент)

^{x→∞         
                           x→0}

№7 Точки разрыва
функции, классификация

Точка х₀
называется точкой разрыва функции y=f(x), если она принадлежит области
определения функции или ее границе и не является точкой непрерывности. В этом
случае говорят, что при        х = х₀ функция разрывна. Это может
произойти,  если в точке х₀ функция не определена, или не существует
предел функции при х → х₀ , или, если предел функции
существует, но не равен значению функции в точке х₀:  lim f(x) ≠ f(х₀).  Точку х0 называют точкой
разрыва первого рода,

                                                    
^x→x0

если существуют
конечные односторонние пределы f(x0-0)=lim f(x) и f(x0+0)=lim f(x), но         f(x0-0)≠f(x0+0).                                                                                     
^x→x0^{-0                                                                  
x→x}0⁺⁰

Точку х0 называют
точкой разрыва второго рода, если хотя бы один из односторонних пределов f(x0-0) и f(x0+0) не существует (в частности,
бесконечен).

№8 Непрерывность
функции на отрезке

Функция  y=f(x) называется непрерывной,
если:

– функция
определена в точке х₀ и в некоторой окрестности, содержащей эту
точку;

– функция имеет
предел при x→x₀,

– предел функции
при x→x₀ равен значению функции в точке x₀:    lim f(x) = f(х₀)

                                                                                                                   
^x→x0

Если  в точке х₀
функция непрерывна, то точка х₀ называется точкой непрерывности
данной функции. Часто приходится рассматривать непрерывность функции в точке х₀
справа или слева (т.е. одностороннюю непрерывность). Пусть функция y=f(x) определена в точке х₀
. Если                    lim f(x) = f(х₀), то говорят,
что функция y=f(x) непрерывна в точке x₀ справа; если lim f(x) = f(х₀),

^x→x0^{+0                                                                               
                                                                                                                   x→x}0^—0

то функция
называется непрерывной в точке x₀ слева.

№9 Предел функции
по Гейне

Число А
называется пределом функции f(x) в точке x₀ если для любой последовательности { x_n} сходящейся к x₀ , последовательность F({ x_n}) соответствующих значений функции сходится к А:

lim f(x) =A

^x→x0

№10 Предел
функции по Коши

Число А
называется пределом функции f(x) в точке x₀ если для любого сколь угодно малого
числа E>0 (эпселон больше 0)
найдется такое число δ>0 (дельта больше 0), что для всех х таких,
что          | x-x₀|< δ, x≠x₀ выполняется неравенство |f(x)-A|<E.

№11 Предел
числовой последовательности

Число а
называется пределом последовательности x_n, если для любого положительного E>0 найдется такое число n, где n<N выполняется неравенство | x_n-a|<E. В этом случае обозначают
так   lim x_n = a

^n→∞

Если
последовательность имеет предел, равный а, то она сходится к а.   Теорема:
сходящаяся последовательность имеет только один предел. Последовательность, не
имеющая предела, называется расходящейся.

Операции над
пределами последовательностей:

Пусть lim x_n = a;          lim у_n = b, тогда

                 ^{n→∞                             
n→∞}

– lim (x_n± у_n) = a±b;

    ^n→∞

– lim (x_n* у_n) = a*b;

    ^n→∞

– lim (c* x_n)
= c*a;

    ^n→∞

– lim (x_n)^R =
(lim x_n)^R=a^R;

    ^n→∞

– lim (x_n)^1/R
= a^1/R;

    ^n→∞

– lim a = a.

Бесконечно
большие последовательности:

– lim x_n= ±∞;

    ^n→∞

Правила
вычисления пределов ЧП:

– lim x_n= а;       lim y_n= ±∞, тогда      lim x_n/ lim y_n = а/±∞=0;

    ^{n→∞                         
n→∞                                           
n→∞        n→∞}

– lim x_n= 0;       lim y_n= ±∞, тогда     lim y_n=0, lim (x_n/ y_n)= ±∞

   ^{n→0                  n→∞                                          
n→∞              n→∞}

№12 Общее
уравнение плоскости, проходящей через три точки.

Если точки М₀
(x₀ ; y₀ ; z₀ ), М₁ (x₁ ; y₁ ; z₁ ), М₂ (x₂ ; y₂ ; z₂ ) не лежат на одной прямой, то
проходящая через них плоскость представляется уравнением

    x – x₀       y – y₀     z – z₀

    x₁ – x₀    
y₁ – y₀    z₁ – z₀   =  0

    x₂ – x₀    
y₂ – y₀    z₂ – z₀

№14 Уравнение
прямой в пространстве (общее и каноническое).

Прямая L, проходящая через точку М₀
(x₀ ; y₀ ; z₀ ) и имеющая направляющий вектор a {l,m,n}, представляется уравнениями   x – x₀         y – y₀        z – z₀

                                                                
=               
=                ,

                                          
  l                  m              
n

№15 Уравнение
прямой на плоскости.

Ax + By + C = 0, где А, В, С – постоянные
коэффициенты.

Заметим, что  n (А; В) – нормальный вектор (n  ┴ прямой).

Частные случаи
этого уравнения:

–  Ах + By = 0 (C=0) – прямая проходит через начало координат;

–  Ах + С = 0
(В=0) – прямая параллельна оси Оу;

–  Ву + С = 0
(А=0) – прямая параллельна оси Ох;

–  Ах = 0 –
прямая совпадает с осью Оу;

–  Ву = 0 –
прямая совпадает с осью Ох.

№16 Векторы.
Операции над векторами.

Вектор –
направленный отрезок прямой.

I. Правила треугольника.   Правила
параллелограмма.   II. Разность векторов.      Параллелограмма.

а           b                                   
а            b                             
а                a        c

а           b          a + b = c            

                                                   
a                                                b             b                   а

Равенство
векторов:

Два (ненулевых)
вектора равны, если они равнонаправлены и имеют один и тот же модуль. Все
нулевые векторы считаются равными. Во всех остальных случаях векторы не равны.

Сложение
векторов:

Суммой векторов
называется третий вектор

Сумма нескольких
векторов: Суммой векторов а1, а2, а3, …, аn называется вектор, получающийся после ряда последовательных сложений: к
вектору а1 прибавляется вектор а2, к полученному прибавляется вектор а3 и т.д.

Коллинеарность
векторов:

Векторы, лежащие
на параллельных прямых, называются коллинеарными.

Скалярное
произведение:

Скалярным
произведением вектора а на вектор b называется произведение их модулей на косинус угла между ними

Угол между
векторами:

cos(a^b)=(a*b)/(|a|*|b|)=(x1x2+y1y2+z1z2)/((x1^2+y1^2+z1^2)*(x2^2+y2^2+z2^2))^1/2

№17 Система
линейных уравнений. Формулы Крамера.

x = ∆1/∆;  x2
= ∆2/∆; … xn = ∆n/∆

№18 Система
линейных уравнений. Метод Гауса.

Системой линейных
уравнений, содержащей m-уравнений и n-неизвестных, называется система
вида    а11х1 + а12х2 + а13х3+…+аnxn = b1;

         { а21х1
+ а22х2 + а23х3+…+аnxn = b2;       },  где а_ij – коэффициенты системы, b_i – свободные

         am1x1 + am2x2 + am3x3+…+amnxn =
bm                     члены

№19 Обратная
матрица. Ранг матрицы.

Матрица А^-1
называется обратной к матрице А, если выполняется условие  А* А^-1 =
А^-1*А = Е

Всякая
невырожденная матрица (т.е. ∆≠0) имеет обратную.

Алгоритм вычисления
обратной матрицы:

1.  
вычисляем
определитель, составленный по данной матрице;

2.  
находим
матрицу А^Т, транспонированную к А;

3.  

составляем
союзную матрицу (А^*);

4.  
вычисляем
обратную матрицу по формуле А^-1 = А^*/∆А = 1/∆А*
(                               )

Ранг м-цы:

Минором R-го порядка произвольной м-цы А
называется определитель, составленный из элементов м-цы, расположенных на
пересечении каких-либо R-строк и R-столбцов.

Рангом м-цы А
называется наибольший из порядков ее миноров, неравных 0.

Базисным минором
называется любое из миноров м-цы А, порядок которого равен рангу А.

При элементарных
преобразованиях ранг м-цы не изменяется.

Ранг ступенчатой
м-цы равен количеству ее не нулевых строк.

Свойства:

– при
транспонировании м-цы ее ранг не меняется;

– если вычеркнуть
из м-цы нулевой ряд, то ранг не изменится.

Матрицей размера m*n называется прямоугольная таблица чисел, содержащая m-строк и n-столбцов. Числа, составляющие м-цу,
называются элементами м-цы.

Две м-цы А и В
одного размера называются равными, если они совпадают поэлементно.

Виды:
м-ца-строка; м-ца-столбец.

М-ца называется
квадратной n-го порядка, если число ее
строк равно числу столбцов и равно n.

Квадратная м-ца,
у которой все элементы, кроме элементов главной диагонали, равны 0, называется
диагональной.

Если у
диагональной м-цы n-го порядка все элеметы
главной диагонали равны 1, то м-ца называется единичной n-го порядка и обозначается Е.

Если все элементы
м-цы равны 0, то она называется нулевой.

Операции над
матрицами:

Умножение м-цы на
число. Произведением м-цы А на число λ называется матрица В= λ*А,
элементы которой b_ij = λ* a_ij (i=1,…,m, j=1,…,n)

Сложение м-ц.
Суммой двух м-ц А и В одинакового размера m на n называется м-ца С=А+В,
элементы которой Сij=aij+bij.

Аналогично
находится разность.

Умножение м-ц.
Умножение м-цы А на м-цу В возможно когда число столбцов первой м-цы равно
числу строк второй. Тогда произведением м-цы А и В называется м-ца С, каждый
элемент которой находится по формуле  

Сij=ai1*b1j+ai2*b2j+…+aiR*bR 
= ∑ais*bsj

 

Возведение в
степень.

А^2=A*A

Транспонирование
м-цы – переход от м-цы А к м-це А^Т, в которой строки и столбцы
меняются местами с сохранением порядка.

№21 Определители n-го порядка. Свойства определителей.

Квадратной м-це А
порядка n можно сопоставить число
дельта А(|А|, ∆), которое называется определителем, если:

– n=1, A=(a1), ∆A=a1;

 

– n=2,
A=                    ,    ∆=                  
=a11a22-a12a21;

	a11  a12  a13 a21  a22  a23 a31  a32  a33		a11  a12  a13 a21  a22  a23 a31  a32  a33

 

–n=3,
A=                            ;   ∆A=

Свойства
определителей:

1.  
Если у
определителя какая-л строка (столбец) состоит только из нулей, то ∆=0;

2.  
Если
какие-л две строки (столбца) определителя пропорциональны, то ∆=0;

3.  
Если
какую-л строку (столбец) определителя умножить на произвольное число, то и весь
определитель умножится на это число;

4.  
Если две
строки (столбца) определителя поменять местами, то определитель изменит знак;

5.  
Если к
какой-л строке (столбцу) определителя прибавить  какую-л другую строку
(столбец), умноженное на произвольное число, то определитель не изменится;

6.  
Определитель
произведения матриц равен произведению их определителей.

№22 Признаки
сравнения положительных рядов.

Для исследования
сходимости данного положительного ряда U0+U1+U2+…  его часто сравнивают с другим
положительным рядом  V0+V1+V2+…, о котором известно, что он сходится или расходится.

Если ряд 2
сходится и сумма его равна V, а члены
данного ряда не превосходят соответствующих членов ряда 2, то данный ряд
сходится, и сумма его не превосходит V. При этом остаток данного ряда не превосходит остатка ряда 2.

Если ряд 2
расходится, а члены данного ряда не меньше соответствующих членов ряда 2, то
данный ряд расходится.

№23 Признаки
Даламбера и Коши сходимости ряда

Признак
Даламбера:

Пусть в
положительном ряде U1+U2+…+Un+… отношение U_n+1/U_n последующего члена к
предыдущему при n→∞ имеет предел q. Возможны три случая:

q<1 –ряд сходится; q>1 – ряд расходится; q=1 – ряд может сходиться, а может и
расходиться.

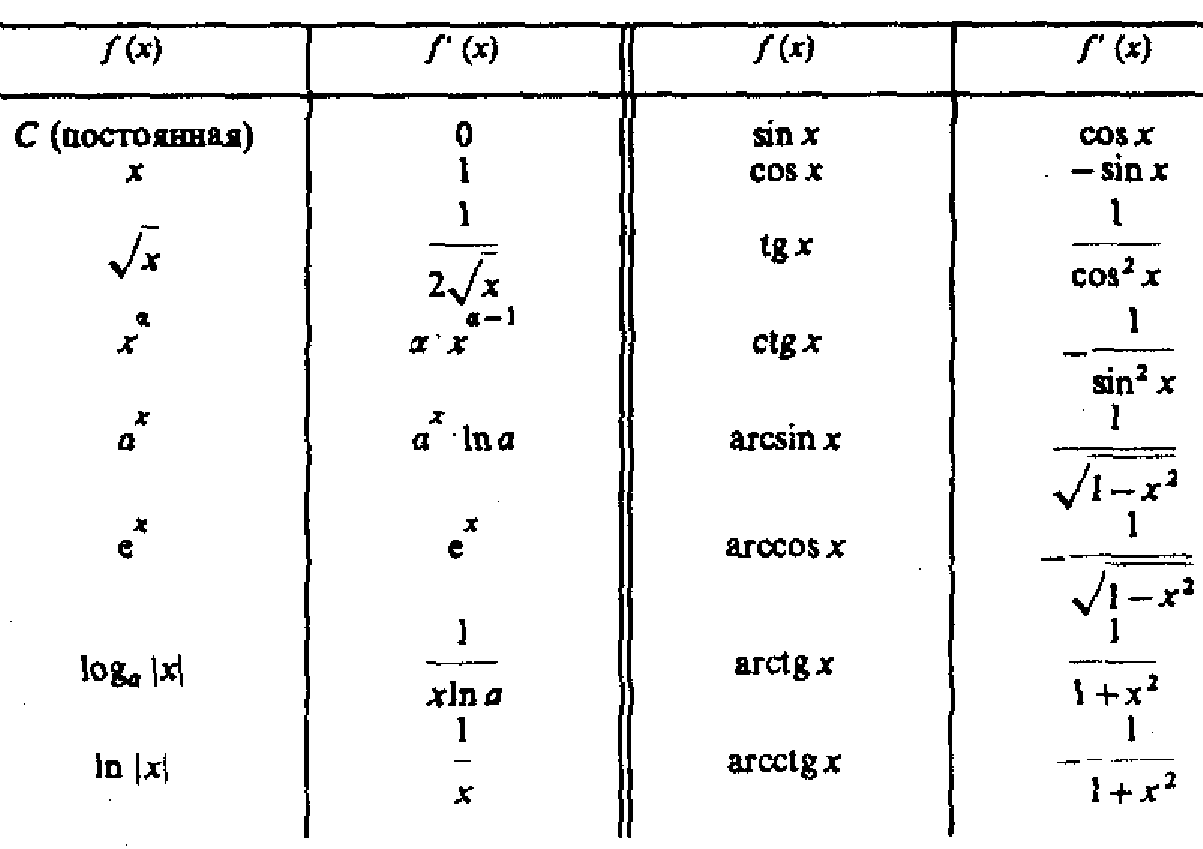
№24 Производные
обратных тригонометрических функций.

I.   d arcsin x = dx/(1-x^2)^1/2, d/dx
arcsin x = 1/(1-x^2)^1/2

II. d arccos x = — dx/(1-x^2)^1/2, d/dx
arccos x= — 1/(1-x^2)^1/2

III.
d arctg x =
dx/(1+x^2), d/dx arctg x = 1/(1+x^2)

IV.
d arcctg x = —
dx/(1+x^2), d/dx arcctg x = — 1/(1+x^2)

№25
Дифференцирование функций, заданных неявно.

Пусть уравнение,
связывающее x и y и удовлетворяющееся значениями x=x0 и y=y0, определяет y как неявную функцию от x. Для разыскания производной dy/dx в точке x=x0, y=y0 нет нужды искать явное
выражение функции. Достаточно приравнять дифференциалы обеих частей уравнения и
из полученного равенства найти отношение dy к dx.

№26
Дифференцирование функций, заданных параметрически.

Предположим, что
функция y от х задана параметрически
уравнениями x=x(t), y=y(t), причем в некоторой области изменения параметра  t  функции x(t) и y(t) дифференцируемы и x’(t)≠0.

Найдем
производную у’_x. Как мы знаем у’_x = dy/dx. Так как dx = x’(t)dt, dy = y’(t)dt, то

y’_x = dy/dx = y’(t)dt/x’(t)dt = y’(t)/x’(t) = y’t/x’t.

Таким образом, dy/dx = y’t/x’t.   Эта формула позволяет
находить производную функции, заданной параметрически.

№28 Дифференциал
функции.

Пусть приращение
функции y=f(x) разбито на сумму двух членов: ∆y = A ∆x+α, где А не зависит от ∆x (т.е. постоянно при данном значении
аргумента x) и α имеет высший порядок
относительно ∆x (при ∆x → 0).

Тогда первый
член, пропорциональный ∆x,
называется дифференциалом функции f(x) и обозначается dy или df(x).

№29
Дифференциальные уравнения с разделяющимися переменными.

Уравнение вида X1Y1dx +X2Y2dy = 0, где функции X1 и  X2 зависят только от x (одна из них или обе могут быть постоянными; то же для функций Y1, Y2), а функции Y1, Y2 – только от y, приводится к виду ydx – xdy = 0 делением на  Y1X2. Процесс произведения
называется разделением переменных.

№30 Площадь
криволинейной трапеции.

Фигура,
ограниченная прямыми y=P; x=a, x=b и графиком непрерывной и неотрицательной на     [a, b] функции f(x), называется криволинейной
трапецией. Площадь криволинейной трапеции

равна

             ∫f(x)dx;    ∫f(x)dx –  ∫g(x)dx

№31
Дифференциальные однородные уравнения первого порядка.

ДУ первого
порядка называется однородным, если оно может быть представлено в
виде                y’ = g (y/x).

Однородное ДУ
преобразуется в уравнение с разделяющимися переменными при помощи замены z=y/x;  y=z*x, то y’=z’x+z, поэтому уравнение y’=g(y/x) преобразуем к виду z’x+z=g(z); dz*x/dx=g(z)-z; dz(g(z)-z)=dx/x.

Найдя его общее
решение следует заметить в нем z на y/x.

Однородное ДУ
часто задается в дифференциальной форме: P(x;y)dx+Q(x;y)dy=0.

ДУ будет
однородным, если P(x;y) и Q(x;y) – однородные функции одинакового порядка.

Переписав
уравнение в виде dy/dx=-P(x;y)/Q(x;y) и переменив в правой части рассмотренное
выше преобразование получим уравнение y’=g(y/x).

При
интегрировании уравнения P(x;y)dx+Q(x;y)dy=0 нет необходимости предварительно
приводить их к виду y’=g(y/x): подстановка z=y/x сразу преобразует уравнение P(x;y)dx+Q(x;y)dy=0 в уравнение с разделяющимися переменными.

№32 Степенные
ряды

Степенным рядом
называется ряд вида а₀+а₁х+а₂х²+…+a_nxⁿ+…, а также ряд более общего
вида а₀+а1(х-х₀)+а₂(х-х₀)²+…+a_n(x-х₀)ⁿ+…,
где х₀ – постоянная величина. О первом ряде говорят, что он
расположен по степеням х, во втором – что он расположен по степеням х-х_0.

Постоянные а₀,
а₁, …, а_n, … называются коэффициентами
степенного ряда.

Степенной ряд
всегда сходится при х=0.

№33 Кривые
второго порядка на плоскости (эллипс, гипербола, парабола).

Линии,
определяемые уравнениями второй степени относительно переменных x и y, т.е. уравнениям вида Ах²+2Вху+Су²+2Вх+2Еу+F=0 (А²+В²+С²≠0),
называются кривыми 2-го порядка.

Эллипс.

х²/а²+у²/b²=1

Гипербола.

х²/а²-у²/b²=1

Парабола.

№34
Дифференциальные уравнения, приводимые к уравнениям однородной функции.

№35 Эллипсоид
(уравнение и чертеж).

№36 Гиперболоид
(уравнение, чертеж).

x²/a²+y²/b²-z²/c²=1

№37 Параболоид эллиптический (уравнение, чертеж)

№38 Параболоид
гиперболический (уравнение, чертеж)

x²/a²-y²/b²=2pz

№39 Уравнение в
полных дифференциалах

Если коэффициенты
P(x,y), Q(x,y) в уравнении

P (x,y)dx+Q(x,y)dy=0 (1)удовлетворяют условию

δP/δy=δQ/δx,  то левая часть (1) есть полный
дифференциал

 некоторой
функции F (x,y). Общий интеграл уравнения (1)

будет:  F (x,y) = C.

№1 Функциональные ряды

Членами являются функции, определенные в некоторой области изменения аргумента х: U₁(x)+U₂(x)+…+U_n(x)+… Придавая х какое-либо значение х₀ из области определения функций U_n(x), получим числовой ряд U₁(x₀)+ U₂(x₀)+…+ U_n(x₀)+… Этот ряд может сходиться или расходиться. Если он сходится, то точка х₀ называется точкой сходимости функционального ряда. Если при х=х₀ ряд расходится, то точка х₀ называется точкой расходимости функционального ряда. Совокупность всех точек сходимости функционального ряда называется областью его сходимости.

Функциональный ряд называется правильно сходящимся на сегменте [a, b], если существует такой знакоположительный сходящийся ряд b₁+ b₂ +…+ b_n +…, что абсолютные величины членов данного ряда для любого значения х, принадлежащего сегменту [a, b], не превосходят соответствующих членов знакоположительного ряда, т. е. |U_n(x)| ≤ b_n (n=1, 2, …)

№2 Неопределенный интеграл и его свойства

Интегральное исчисление решает обратную задачу: найти F(x), зная ее производную f(x).

Функция F(x) называется первообразной, если выполняется равенство F’(x)=f(x).

Если F(x) одна из первообразных функции f(x), то любая первообразная функции f(x) на этом промежутке имеет вид F(x)+C, где С€R.

Множество всех первообразных функции f(x) называется неопределенным интегралом

Свойства:

– неопределенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме неопределенных интегралов от каждого слагаемого в отдельности;

– постоянный множитель можно выносить за знак неопределенного интеграла.

№3 Асимптоты

Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к 0 при неограниченном удалении от начала координат этой точки по кривой.

А симптоты бывают вертикальными, горизонтальными и наклонными.

Прямая х=a является вертикальной асимптотой графика функции y=f(x), если lim f(x)=∞ ,

^x→0±a

Уравнение наклонной асимптоты будем искать в виде y=Rx+b

R = lim(y/x) ; b = lim (y – Rx)

^{x→0 x→0}

Если y = b, то это уравнение горизонтальной асимптоты.

№4 Экстремум функции (для одной переменной)

Если функция f(x) дифференцируема на интервале (a;b) и f’(x)>0 (f’(x)<0), то f(x) возрастает (убывает) на этом промежутке. Точка х₀ называется точкой максимума функции f(x), если существует такая окрестность точки х_0, что для всех х, не равных х₀ из этой окрестности, выполняется неравенство f(x) < f(х₀), где х₀ – точка максимума. Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Максимум (минимум) функции называется экстремумом.

Необходимое условие экстремума: если дифференцируемая функция f(x) имеет экстремум в точке х₀, то ее производная в этой точке равна 0.

Достаточное условие экстремума: если производная меняет знак на минус, то х₀ – точка максимума; если с минуса на плюс, то точка х₀ – точка минимума.

№5 Производная. Ее геометрический и физический смысл.

Физический: производной функции y=f(x) в точке х₀ называется предел отношения приращения функции ∆y в этой точке к вызвавшему его приращению аргумента ∆х при произвольном стремлении ∆х к 0.

Геометрический: угловой коэффициент касательной к графику функции в точке с абсциссой х₀ равен значению производной этой функции в точке х₀.

№6 Замечательные пределы

lim (1+1/x)^x=e; lim (1+x)^1/x=e (e – экспонент)

^{x→∞ x→0}

№7 Точки разрыва функции, классификация

Точка х₀ называется точкой разрыва функции y=f(x), если она принадлежит области определения функции или ее границе и не является точкой непрерывности. В этом случае говорят, что при х = х₀ функция разрывна. Это может произойти, если в точке х₀ функция не определена, или не существует предел функции при х → х₀ , или, если предел функции существует, но не равен значению функции в точке х₀: lim f(x) ≠ f(х₀). Точку х0 называют точкой разрыва первого рода,

^x→x0

если существуют конечные односторонние пределы f(x0-0)=lim f(x) и f(x0+0)=lim f(x), но f(x0-0)≠f(x0+0). ^x→x0^{-0 x→x}0⁺⁰

Точку х0 называют точкой разрыва второго рода, если хотя бы один из односторонних пределов f(x0-0) и f(x0+0) не существует (в частности, бесконечен).

№8 Непрерывность функции на отрезке

Функция y=f(x) называется непрерывной, если:

– функция определена в точке х₀ и в некоторой окрестности, содержащей эту точку;

– функция имеет предел при x→x₀,

– предел функции при x→x₀ равен значению функции в точке x₀: lim f(x) = f(х₀)

^x→x0

Если в точке х₀ функция непрерывна, то точка х₀ называется точкой непрерывности данной функции. Часто приходится рассматривать непрерывность функции в точке х₀ справа или слева (т.е. одностороннюю непрерывность). Пусть функция y=f(x) определена в точке х₀ . Если lim f(x) = f(х₀), то говорят, что функция y=f(x) непрерывна в точке x₀ справа; если lim f(x) = f(х₀),

^x→x0^{+0 x→x}0^—0

то функция называется непрерывной в точке x₀ слева.

№9 Предел функции по Гейне

Число А называется пределом функции f(x) в точке x₀ если для любой последовательности { x_n} сходящейся к x₀ , последовательность F({ x_n}) соответствующих значений функции сходится к А:

lim f(x) =A

^x→x0

№10 Предел функции по Коши

Число А называется пределом функции f(x) в точке x₀ если для любого сколь угодно малого числа E>0 (эпселон больше 0) найдется такое число δ>0 (дельта больше 0), что для всех х таких, что | x-x₀|< δ, x≠x₀ выполняется неравенство |f(x)-A|

№11 Предел числовой последовательности

Число а называется пределом последовательности x_n, если для любого положительного E>0 найдется такое число n, где nn-a|n = a

^n→∞

Если последовательность имеет предел, равный а, то она сходится к а. Теорема: сходящаяся последовательность имеет только один предел. Последовательность, не имеющая предела, называется расходящейся.

Операции над пределами последовательностей:

Пусть lim x_n = a; lim у_n = b, тогда

^{n→∞ n→∞}

– lim (x_n± у_n) = a±b;

^n→∞

– lim (x_n* у_n) = a*b;

^n→∞

– lim (c* x_n) = c*a;

^n→∞

– lim (x_n)^R = (lim x_n)^R=a^R;

^n→∞

– lim (x_n)^1/R = a^1/R;

^n→∞

– lim a = a.

^n→∞

Бесконечно большие последовательности:

– lim x_n= ±∞;

^n→∞

Правила вычисления пределов ЧП:

– lim x_n= а; lim y_n= ±∞, тогда lim x_n/ lim y_n = а/±∞=0;

^{n→∞ n→∞ n→∞ n→∞}

– lim x_n= 0; lim y_n= ±∞, тогда lim y_n=0, lim (x_n/ y_n)= ±∞

^{n→0 n→∞ n→∞ n→∞}

№12 Общее уравнение плоскости, проходящей через три точки.

Если точки М₀ (x₀ ; y₀ ; z₀ ), М₁ (x₁ ; y₁ ; z₁ ), М₂ (x₂ ; y₂ ; z₂ ) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением

x – x₀ y – y₀ z – z₀

x₁ – x₀ y₁ – y₀ z₁ – z₀ = 0

x₂ – x₀ y₂ – y₀ z₂ – z₀

№14 Уравнение прямой в пространстве (общее и каноническое).

Прямая L, проходящая через точку М₀ (x₀ ; y₀ ; z₀ ) и имеющая направляющий вектор a {l,m,n}, представляется уравнениями x – x₀ y – y₀ z – z₀

= = ,

l m n

в ыражающими коллинеарность векторов a {l,m,n} и М₀М { x – x₀ , y – y₀ , z – z₀ }. Они называются каноническими.

№15 Уравнение прямой на плоскости.

Ax + By + C = 0, где А, В, С – постоянные коэффициенты.

З аметим, что n (А; В) – нормальный вектор (n ┴ прямой).

Частные случаи этого уравнения:

– Ах + By = 0 (C=0) – прямая проходит через начало координат;

– Ах + С = 0 (В=0) – прямая параллельна оси Оу;

– Ву + С = 0 (А=0) – прямая параллельна оси Ох;

– Ах = 0 – прямая совпадает с осью Оу;

– Ву = 0 – прямая совпадает с осью Ох.

№16 Векторы. Операции над векторами.

Вектор – направленный отрезок прямой.

I. Правила треугольника. Правила параллелограмма. II. Разность векторов. Параллелограмма.

а b а b а a c

а b a + b = c

a b b а

Равенство векторов:

Два (ненулевых) вектора равны, если они равнонаправлены и имеют один и тот же модуль. Все нулевые векторы считаются равными. Во всех остальных случаях векторы не равны.

Сложение векторов:

Суммой векторов называется третий вектор

Сумма нескольких векторов: Суммой векторов а1, а2, а3, …, аn называется вектор, получающийся после ряда последовательных сложений: к вектору а1 прибавляется вектор а2, к полученному прибавляется вектор а3 и т.д.

Коллинеарность векторов:

Векторы, лежащие на параллельных прямых, называются коллинеарными.

Скалярное произведение:

Скалярным произведением вектора а на вектор b называется произведение их модулей на косинус угла между ними

Угол между векторами:

cos(a^b)=(a*b)/(|a|*|b|)=(x1x2+y1y2+z1z2)/((x1^2+y1^2+z1^2)*(x2^2+y2^2+z2^2))^1/2

№17 Система линейных уравнений. Формулы Крамера.

x = ∆1/∆; x2 = ∆2/∆; … xn = ∆n/∆

№18 Система линейных уравнений. Метод Гауса.

Системой линейных уравнений, содержащей m-уравнений и n-неизвестных, называется система вида а11х1 + а12х2 + а13х3+…+аnxn = b1;

{ а21х1 + а22х2 + а23х3+…+аnxn = b2; }, где а_ij – коэффициенты системы, b_i – свободные

am1x1 + am2x2 + am3x3+…+amnxn = bm члены

№19 Обратная матрица. Ранг матрицы.

Матрица А^-1 называется обратной к матрице А, если выполняется условие А* А^-1 = А^-1*А = Е

Всякая невырожденная матрица (т.е. ∆≠0) имеет обратную.

Алгоритм вычисления обратной матрицы:

1. вычисляем определитель, составленный по данной матрице;

2. находим матрицу А^Т, транспонированную к А;

3. с

   A11 A21 … An1

   A12 A22 … An2

   оставляем союзную матрицу (А^*);

4. вычисляем обратную матрицу по формуле А^-1 = А^*/∆А = 1/∆А* ( )

Ранг м-цы:

Минором R-го порядка произвольной м-цы А называется определитель, составленный из элементов м-цы, расположенных на пересечении каких-либо R-строк и R-столбцов.

Рангом м-цы А называется наибольший из порядков ее миноров, неравных 0.

Базисным минором называется любое из миноров м-цы А, порядок которого равен рангу А.

При элементарных преобразованиях ранг м-цы не изменяется.

Ранг ступенчатой м-цы равен количеству ее не нулевых строк.

Свойства:

– при транспонировании м-цы ее ранг не меняется;

– если вычеркнуть из м-цы нулевой ряд, то ранг не изменится.

№20 Матрицы. Операции над матрицами.

Матрицей размера m*n называется прямоугольная таблица чисел, содержащая m-строк и n-столбцов. Числа, составляющие м-цу, называются элементами м-цы.

Две м-цы А и В одного размера называются равными, если они совпадают поэлементно.

Виды: м-ца-строка; м-ца-столбец.

М-ца называется квадратной n-го порядка, если число ее строк равно числу столбцов и равно n.

Квадратная м-ца, у которой все элементы, кроме элементов главной диагонали, равны 0, называется диагональной.

Если у диагональной м-цы n-го порядка все элеметы главной диагонали равны 1, то м-ца называется единичной n-го порядка и обозначается Е.

Если все элементы м-цы равны 0, то она называется нулевой.

Операции над матрицами:

Умножение м-цы на число. Произведением м-цы А на число λ называется матрица В= λ*А, элементы которой b_ij = λ* a_ij (i=1,…,m, j=1,…,n)

Сложение м-ц. Суммой двух м-ц А и В одинакового размера m на n называется м-ца С=А+В, элементы которой Сij=aij+bij.

Аналогично находится разность.

У

R

множение м-ц. Умножение м-цы А на м-цу В возможно когда число столбцов первой м-цы равно числу строк второй. Тогда произведением м-цы А и В называется м-ца С, каждый элемент которой находится по формуле

Сij=ai1*b1j+ai2*b2j+…+aiR*bR = ∑ais*bsj

S=1

Возведение в степень.

А^2=A*A

Транспонирование м-цы – переход от м-цы А к м-це А^Т, в которой строки и столбцы меняются местами с сохранением порядка.

№21 Определители n-го порядка. Свойства определителей.

Квадратной м-це А порядка n можно сопоставить число дельта А(|А|, ∆), которое называется определителем, если:

– n=1, A=(a1), ∆A=a1;

a11 a12

a21 a22

a11 a12

a21 a22

– n=2, A= , ∆= =a11a22-a12a21;

a11 a12 a13

a21 a22 a23

a31 a32 a33

a11 a12 a13

a21 a22 a23

a31 a32 a33

–n=3, A= ; ∆A=

Свойства определителей:

1. Если у определителя какая-л строка (столбец) состоит только из нулей, то ∆=0;

2. Если какие-л две строки (столбца) определителя пропорциональны, то ∆=0;

3. Если какую-л строку (столбец) определителя умножить на произвольное число, то и весь определитель умножится на это число;

4. Если две строки (столбца) определителя поменять местами, то определитель изменит знак;

5. Если к какой-л строке (столбцу) определителя прибавить какую-л другую строку (столбец), умноженное на произвольное число, то определитель не изменится;

6. Определитель произведения матриц равен произведению их определителей.

№22 Признаки сравнения положительных рядов.

Для исследования сходимости данного положительного ряда U0+U1+U2+… его часто сравнивают с другим положительным рядом V0+V1+V2+…, о котором известно, что он сходится или расходится.

Если ряд 2 сходится и сумма его равна V, а члены данного ряда не превосходят соответствующих членов ряда 2, то данный ряд сходится, и сумма его не превосходит V. При этом остаток данного ряда не превосходит остатка ряда 2.

Если ряд 2 расходится, а члены данного ряда не меньше соответствующих членов ряда 2, то данный ряд расходится.

№23 Признаки Даламбера и Коши сходимости ряда

Признак Даламбера:

Пусть в положительном ряде U1+U2+…+Un+… отношение U_n+1/U_n последующего члена к предыдущему при n→∞ имеет предел q. Возможны три случая:

q<1 –ряд сходится; q>1 – ряд расходится; q=1 – ряд может сходиться, а может и расходиться.

№24 Производные обратных тригонометрических функций.

1. d arcsin x = dx/(1-x^2)^1/2, d/dx arcsin x = 1/(1-x^2)^1/2

2. d arccos x = — dx/(1-x^2)^1/2, d/dx arccos x= — 1/(1-x^2)^1/2

3. d arctg x = dx/(1+x^2), d/dx arctg x = 1/(1+x^2)

4. d arcctg x = — dx/(1+x^2), d/dx arcctg x = — 1/(1+x^2)

№25 Дифференцирование функций, заданных неявно.

Пусть уравнение, связывающее x и y и удовлетворяющееся значениями x=x0 и y=y0, определяет y как неявную функцию от x. Для разыскания производной dy/dx в точке x=x0, y=y0 нет нужды искать явное выражение функции. Достаточно приравнять дифференциалы обеих частей уравнения и из полученного равенства найти отношение dy к dx.

№26 Дифференцирование функций, заданных параметрически.

Предположим, что функция y от х задана параметрически уравнениями x=x(t), y=y(t), причем в некоторой области изменения параметра t функции x(t) и y(t) дифференцируемы и x’(t)≠0.

Найдем производную у’_x. Как мы знаем у’_x = dy/dx. Так как dx = x’(t)dt, dy = y’(t)dt, то

y’_x = dy/dx = y’(t)dt/x’(t)dt = y’(t)/x’(t) = y’t/x’t.

Таким образом, dy/dx = y’t/x’t. Эта формула позволяет находить производную функции, заданной параметрически.

№28 Дифференциал функции.

Пусть приращение функции y=f(x) разбито на сумму двух членов: ∆y = A ∆x+α, где А не зависит от ∆x (т.е. постоянно при данном значении аргумента x) и α имеет высший порядок относительно ∆x (при ∆x → 0).

Тогда первый член, пропорциональный ∆x, называется дифференциалом функции f(x) и обозначается dy или df(x).

№29 Дифференциальные уравнения с разделяющимися переменными.

Уравнение вида X1Y1dx +X2Y2dy = 0, где функции X1 и X2 зависят только от x (одна из них или обе могут быть постоянными; то же для функций Y1, Y2), а функции Y1, Y2 – только от y, приводится к виду ydx – xdy = 0 делением на Y1X2. Процесс произведения называется разделением переменных.

№30 Площадь криволинейной трапеции.

Ф

b

b

b

игура, ограниченная прямыми y=P; x=a, x=b и графиком непрерывной и неотрицательной на [a, b] функции f(x), называется криволинейной трапецией. Площадь криволинейной трапеции

равна

a

a

a

∫f(x)dx; ∫f(x)dx – ∫g(x)dx

№31 Дифференциальные однородные уравнения первого порядка.

ДУ первого порядка называется однородным, если оно может быть представлено в виде y’ = g (y/x).

Однородное ДУ преобразуется в уравнение с разделяющимися переменными при помощи замены z=y/x; y=z*x, то y’=z’x+z, поэтому уравнение y’=g(y/x) преобразуем к виду z’x+z=g(z); dz*x/dx=g(z)-z; dz(g(z)-z)=dx/x.

Найдя его общее решение следует заметить в нем z на y/x.

Однородное ДУ часто задается в дифференциальной форме: P(x;y)dx+Q(x;y)dy=0.

ДУ будет однородным, если P(x;y) и Q(x;y) – однородные функции одинакового порядка.

Переписав уравнение в виде dy/dx=-P(x;y)/Q(x;y) и переменив в правой части рассмотренное выше преобразование получим уравнение y’=g(y/x).

При интегрировании уравнения P(x;y)dx+Q(x;y)dy=0 нет необходимости предварительно приводить их к виду y’=g(y/x): подстановка z=y/x сразу преобразует уравнение P(x;y)dx+Q(x;y)dy=0 в уравнение с разделяющимися переменными.

№32 Степенные ряды

Степенным рядом называется ряд вида а₀+а₁х+а₂х²+…+a_nxⁿ+…, а также ряд более общего вида а₀+а1(х-х₀)+а₂(х-х₀)²+…+a_n(x-х₀)ⁿ+…, где х₀ – постоянная величина. О первом ряде говорят, что он расположен по степеням х, во втором – что он расположен по степеням х-х_0.

Постоянные а₀, а₁, …, а_n, … называются коэффициентами степенного ряда.

Степенной ряд всегда сходится при х=0.

№33 Кривые второго порядка на плоскости (эллипс, гипербола, парабола).

Линии, определяемые уравнениями второй степени относительно переменных x и y, т.е. уравнениям вида Ах²+2Вху+Су²+2Вх+2Еу+F=0 (А²+В²+С²≠0), называются кривыми 2-го порядка.

Эллипс.

х ²/а²+у²/b²=1

Гипербола.

х²/а²-у²/b²=1

Парабола.

y²=2px, где p>0

№

z

34 Дифференциальные уравнения, приводимые к уравнениям однородной функции.

№35 Эллипсоид (уравнение и чертеж).

x²/a²+y²/b²+z²/c²=1

№36 Гиперболоид (уравнение, чертеж).

x²/a²+y²/b²-z²/c²=1

гиперболоид

№ 37 Параболоид эллиптический (уравнение, чертеж)

x²/a²+y²/b²=2pz

№38 Параболоид гиперболический (уравнение, чертеж)

x²/a²-y²/b²=2pz

№39 Уравнение в полных дифференциалах

Если коэффициенты P(x,y), Q(x,y) в уравнении

P (x,y)dx+Q(x,y)dy=0 (1)удовлетворяют условию

δP/δy=δQ/δx, то левая часть (1) есть полный дифференциал

некоторой функции F (x,y). Общий интеграл уравнения (1)

будет: F (x,y) = C.

20

Комплексный сборник тестов с ответами по Высшей математике

Кривые второго порядка

Правильный ответ подчёркнут.

1. Кривой II порядка является

— эллипс, не вырожденный в окружность

— гипербола

— парабола

— окружность

2. Кривой II порядка является

— эллипс, не вырожденный в окружность

— гипербола

— парабола

— окружность

3. Кривой II порядка является

— эллипс, не вырожденный в окружность

— гипербола

— парабола

— окружность

4. Кривой II порядка является

— эллипс, не вырожденный в окружность

— гипербола

— парабола

— окружность

Прямые и плоскости в пространстве

Правильный ответ выделен и подчёркнут.

1. Уравнением плоскости, проходящей через точку и перпендикулярной прямой является

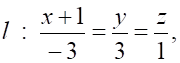
а.        б.       в.

2. Общее уравнение плоскости, содержащей точку и параллельной плоскости , имеет вид

а. 

б. 

в. 

г. 

3. Плоскость перпендикулярна плоскости

а. 

б. 

в. 

г. £

4. Прямая, проходящая через точки и , перпендикулярна плоскости

а. 

б. 

в. 

г. 

5. Даны три прямых на плоскости: , и Верным является утверждение

а.  и перпендикулярны

б.   и перпендикулярны

в.   и перпендикулярны

г.  перпендикулярных прямых нет

6. Уравнением плоскости, проходящей через точку и перпендикулярной прямой является

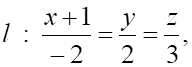
а. 

б. 

в. 

г. 

тест 7. Общее уравнение плоскости, содержащей точку и параллельной плоскости , имеет вид

а. 

б. 

в. 

г. 

8. Плоскость перпендикулярна плоскости

а. 

б. 

в. 

г. 

Прямые на плоскости

Правильный ответ выделен и подчёркнут.

1. Прямая, проходящая через точку и параллельная прямой имеет вид

а. 

б. 

в. 

г. 

2. Уравнением прямой, содержащей точку и параллельной прямой является

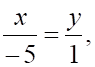
а. 

б. 

в. 

г.  

3. Общее уравнение прямой, содержащей точки и имеет вид

а. 

б. 

£

£

Треугольник на плоскости

Правильный ответ выделен и подчёркнут.

1. Длина стороны в треугольнике с вершинами , , равна

а.        б.          в.           г.  

2. Длина медианы в треугольнике с вершинами , , равна

а.          б.         в.           г.  

3. Угол в треугольнике с вершинами , и

а.  прямой     б. тупой        в. острый

4. В треугольнике , где , , , угол при вершине равен

а.          б.            в.            г. 

5. В треугольнике , где , , , угол

а. прямой         б. тупой         в. острый

Линейная алгебра. Алгебра матриц. Обратная матрица. Определители

Правильный ответ выделен и подчёркнут.

1тест. Обратной к матрице 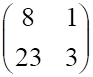является матрица

а.          б.             в.               г.  

2. Определитель матрицы 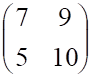равен

а.         б.          в.             г. 

3. Определитель матрицы 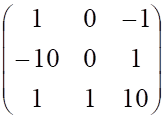равен

а.        б.          в.             г.  

4. Определитель матрицы 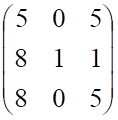равен

а.        б.          в.          г. 

5. Определитель матрицы 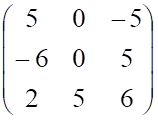равен

а.       б.       в.        г. 

6. Уравнение для нахождения собственных значений матрицы имеет вид

а. 

б. 

в. 

г. £

Сумма и произведение матриц

Правильный ответ выделен и подчёркнут.

1. Выражение эквивалентно

а.        б.        в.          г. 

2. Выражение эквивалентно

а.       б.        в.          г. 

3. Произведение матриц 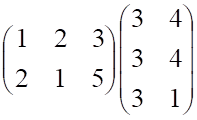равно

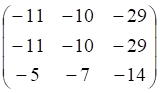
а.            б.                в.                 г. 

4. Заданы матрицы 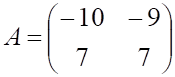и . Произведение равно

а.                б.                        в.                       г. 

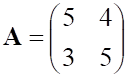
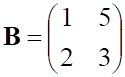
5. Заданы матрицы и . Произведение равно

а.             б.              в.                г. 

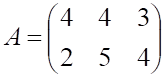
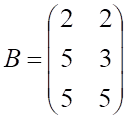
6. Заданы матрицы и . Сумма равна

а.            б.                 в.                    г. 

тест №7. Транспонированной к матрице 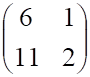является матрица

а.         б.          в.            г. 

Векторная алгебра

Правильный ответ выделен и подчёркнут.

1. Заданы векторы и . Выражение равно

а.       б.       в.        г. 

2. Заданы векторы и . Длина вектора равна

а.         б.          в.          г. 

3. Из векторов , и , ортогональными являются

а. и

б.  и

в.  и

г.  и , и

Комплексные числа

Правильный ответ выделен и подчёркнут.

1. Сумма если , , равна

а.         б.           в.           г. 

2. Произведение если , , равно

а.         б.        в.         г. 

Системы линейных уравнений

Правильный ответ выделен и подчёркнут.

1. Система линейных уравнений 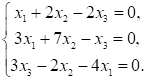имеет

а. одно нулевое решение

б. бесконечно много решений

в. одно ненулевое решение

г. нет решений

2. Частным решением системы линейных уравнений 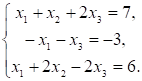является

а.         б.          в.            г. 

3. Система линейных уравнений 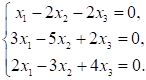имеет

а. одно решение£ два решения

б. бесконечно много решений

в. нет решений

4. Матричное уравнение с невырожденной квадратной матрицей А имеет решение

а.         б.           в.         г.

5. Матричное уравнение с невырожденной квадратной матрицей А имеет решение

а.            б.           в.            г. 

Математический анализ. Дифференциальное исчисление

Правильный ответ выделен и подчёркнут.

1 — тест. Производная функции равна

а. 

б. 

в.  

г. 

2. Производная функции равна

а. 

б. 

в. 

г. 

3. Производная функции 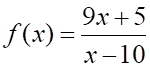равна

а.           б.            в.             г. 

4. Частной производной для функции является

а.           б.            в.           г. 

5. Производная функции равна

а.          б.         в.           г. 

6. Градиент функции равен

а. 

б. 

в. 

г. 

7. Смешанная производная для функции равна

а.            б.           в.           г. 

8. Достаточным условием выпуклости функции на интервале является

а.  на  

б.  на

в.  на

г.  на

9. Достаточным условием убывания функции на интервале является

а.  на

б.  на

в.  на

г.  на

10. Точкой локального экстремума функции является

а.       б.         в.         г.

11. Градиент функции равен

а. 

б. 

в. 

г. 

Дифференциальные уравнения

Правильный ответ выделен и подчёркнут.

тест — 1. Общим решением дифференциального уравнения является

а. 

б. 

в. 

г. 

Интегральное исчисление

Правильный ответ выделен и подчёркнут.

1. Определенный интеграл 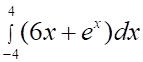равен

а.        б.        в.         г. 

2. Несобственный интеграл равен

а.       б.      в.        г. 

3. Несобственный интеграл 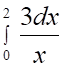равен

а.        б.      в.       г. 

4. Определенный интеграл 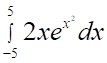равен

а.        б.       в.        г. 

5. Несобственный интеграл 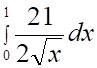равен

а.       б.         в. 

Последовательности

Правильный ответ выделен и подчёркнут.

1. Примером неограниченной последовательности является последовательность

а.      б.         в.      г. 

2. Примером сходящейся последовательности является последовательность

а.         б.          в.          г. 

3. Примером ограниченной последовательности является последовательность

а.       б.        в.         г. 

4. Примером бесконечно малой последовательности является последовательность

а.       б.        в.         г. 

5. Примером бесконечно большой последовательности является последовательность

а.        б.         в.        г. 

6. Примером ограниченной последовательности является последовательность

а.        б.        в.        г. 

7. Примером бесконечно малой последовательности является последовательность

а.        б.        в.          г. 

8. Примером бесконечно большой последовательности является последовательность

а.        б.         в.        г. 

9_тест. Примером ограниченной последовательности является последовательность

а.       б.       в.        г. 

Предел функции

Правильный ответ выделен и подчёркнут.

1. Предел 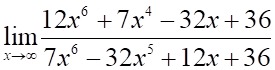равен

а.         б.           в.           г. 

2. Предел 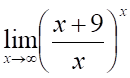равен

а.         б.        в.          г. 

3. Предел равен

а.        б.       в.          г. 

Ряды

Правильный ответ выделен и подчёркнут.

1. Радиус сходимости ряда 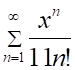равен

а.       б.        в.         г. 

2. Радиус сходимости ряда 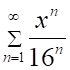равен

а.         б.         в.        г. 

3. Радиус сходимости ряда 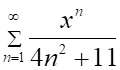равен

а.       б.        в.         г. 

Теория вероятностей

Правильный ответ выделен и подчёркнут.

1. Распределение дискретной случайной величины задано таблицей

Математическое ожидание равно

а.        б.       в.        г. 

2. Распределение дискретной случайной величины задано таблицей

Математическое ожидание равно

а.      б.      в.      г. 

3. Распределение дискретной случайной величины задано таблицей

Дисперсия равна

а.      б.       в.       г. 

тест_4. Распределение дискретной случайной величины задано таблицей

Дисперсия равна

а.        б.         в.        г. 

Классическая вероятность

Правильный ответ выделен и подчёркнут.

1. Вероятность, что кубик упадет на грань « «, при условии, что выпадет нечетная грань, равна

а.       б.       в.        г. 

2. В урне находится красных и черных шаров. Вероятность на удачу достать два красных шара равна

а.      б.      в.       г. 

3. Вероятность попадания в цель при одном выстреле равна Вероятность того, что из двух выстрелов попали оба раза, равна

а.       б.       в.         г. 

4. Урна содержит белых и черных шаров. Вероятность наудачу достать первым белый шар, а вторым черный, равна

а.        б.        в.         г. 

5. Количество способов, которыми можно выбрать экзаменационных билетa из , равно

а.      б.       в.        г.

Примеры решений задач по высшей математике

На этой странице мы собрали простые и сложные примеры из курса высшей математики — от векторов и матриц до дифференциальных уравнений. На каждую тему приведен один решенный пример и даны ссылки на разделы, где собраны другие решения. Фактически, это шпаргалка-каталог типовых задач и решений к ним.

Если вам нужна помощь, узнайте больше о заказе решений по высшей математике.

Далее решенные задачи по темам:

Высшая математика. Комплексные числа

Задача. Вычислить сумму $(z_1 + z_2)$ и разность $(z_1 — z_2)$ комплексных чисел, заданных в показательной форме, переведя их в алгебраическую форму. Построить операнды и результаты на комплексной плоскости.

$$ z_1 = 2 e^{-pi i}, z_2=4 e^{pi i}.$$

Все решения о комплексных числах

Высшая математика. Матрицы

Задача. Найти матрицу, обратную матрице $A$. Сделать проверку.

$$A=
begin{pmatrix}
1 & 2 & 1 & -1\
1 & 1 & 0 & 0\
0 & 2 & 0 & -1\
1 & 1 & 1 & 0\
end{pmatrix}
$$

Высшая математика. Определители

Задача. Вычислить определитель матрицы $A$

$$A=
begin{pmatrix}
4 & 5 & 6 & 5 & 11\
1 & 4 & 2 & 0 & 13\
1 & 1 & 0 & -1 & 5\
3 & 2 & 3 & 0 & 7\
4 & 1 & 2 & 3 & 8\
end{pmatrix}
$$

Высшая математика. Системы уравнений

Задача. Исследовать на совместность и решить систему уравнений:

Все решения по линейной алгебре

Высшая математика. Векторы

Задача. Написать разложение вектора $X$ по векторам $(a, b, c)$.

$$X=(-4;4;4), a=(3;1;0), b=(-1;0;6), c=(-1;2;0).$$

Все решения по векторной алгебре

Аналитическая геометрия на плоскости

Задача. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.

Все решения по АГ на плоскости

Аналитическая геометрия в пространстве

Задача. Для пирамиды с вершинами в точках $A_1, A_2, A_3, A_4$ найти:
А) длину ребра $A_1A_2$;
Б) угол между ребрами $A_1A_2$ и $A_1A_4$;
В) уравнение плоскости $A_1A_2A_3$;
Г) площадь грани $A_1A_2A_3$;
Д) угол между ребрами $A_1A_4$ и плоскостью $A_1A_2A_3$;
Е) уравнение высоты, опущенной из точки $A_4$ на грань $A_1A_2A_3$;
Ж) объем пирамиды $A_1A_2A_3A_4$.

$$A_1(2,3,1), A_2(4,1,-2), A_3(6,3,7), A_4(-5,-4,8).$$

Все решения по АГ в пространстве

Высшая математика. Пределы

Задача. Найти предел функции

$$
lim_{xto infty}left(frac{3x^2+1}{3x^2-x+1} right)^{3x+4}.
$$

Все решения по пределам

Высшая математика. Производные

Задача. Найти производную от следующей функции

$$
y=left[sqrt[3]{frac{1}{7+x^2}}+frac{sqrt{x}}{sqrt{x}+1} right]cdot 24; quad
y'(1).
$$

Все решения по производным

Высшая математика. Исследование функции

Задача. Провести полное исследование функции и построить график.

$$y=frac{x}{sqrt{x^2+x}}.$$

Все решения на исследование функции

Высшая математика. Интегралы

Задача. Найти неопределенный интеграл
$$intfrac{4x^2+7x-23}{(x^2-4x+8)(x+1)^2}dx.$$

Все решения по интегралам

Высшая математика. Применение интегралов

Задача. Найти длину дуги кривой, заданной параметрическими уравнениями:

$$
x=3(1-cos t)cos t, quad y=3(1-cos t)sin t, quad 0leq t leq pi.
$$

Все решения о применении интегралов

Высшая математика. Ряды

Задача. Исследовать сходимость числового ряда

$$sum_{n=1}^{infty} u_n=sum_{n=1}^{infty}frac{2n+1}{sqrt{n 2^n}}.$$

Все решения по рядам

Высшая математика. Дифференциальные уравнения

Задача. Найти общее решение линейного дифференциального уравнения первого порядка

$$ xy’+x^2+xy-y=0.$$

Все решения по дифф.уравнениям

Высшая математика. Теория вероятностей

Задача. Бросаются две игральные кости. Определить вероятность того, что: а) сумма числа очков не превосходит 8; б) произведение числа очков не превосходит 8; в) произведение числа очков делится на 8.

Все решения по теории вероятностей

Полезное на сайте

Учебники, лекции, видео Высшая математика для чайников Решенные контрольные Как решать задачи онлайн

Формулы и справочники Сдача тестов Решаем высшую математику на заказ Онлайн помощь

Вопрос №1: «Матрицы и алгебра матриц».

Матрицы  и многомерные векторы. Матрицей называется
прямоугольная таблица чисел, содержащая n строк и m столбцов.

Виды матриц.

Две матрицы называются равными, если их
соответствующие элементы равны.

Если в матрице число строк равно числу столбцов (n=m), то матрица называется квадратной.

Матрица, у которой все элементы, стоящие вне главной
диагонали равны 0, называется диагональной.

Диагональная матрица, у которой все диагональные элементы
равны 1, называется единичной.

Матрица, состоящая из одних нулей, называется нулевой.

Если в квадратной матрице все элементы стоящие ниже (выше)
главной диагонали равны 0, то она называется верхний (нижний)
треугольник.

Если в матрице А строки записать столбцами с теми же
номерами, то полученная матрица будет называться транспонированной
к матрице А.

Если матрица А равна транспонированной, то она называется симметричной.

Действия над матрицами:

1) Умножение матрицы на число. В результате умножения
матрицы на число получается матрица такой же размерности, что и исходная,
каждый элемент которой является результатом произведения соответствующего
элемента исходной матрицы на число. Мы получим одинаковый результат, умножая
число на матрицу, или матрицу на число. Из определения следует, что общий
множитель всех элементов матрицы можно выносить за знак матрицы.

2) Сложение и вычитание матриц. Складывать и вычитать можно
только матрицы одинаковой размерности. Суммой (разностью) двух матриц
называется матрица той же размерности, что и исходные, каждый элемент которой
определяется как сумма (разность) соответствующих элементов матриц. Очевидно,
результат сложения не изменится, если слагаемые матрицы поменять местами. Если
к матрице прибавить или от нее отнять нулевую матрицу той же размерности, то получим
исходную матрицу.

3) Умножение матрицы на матрицу. Умножать друг на друга
можно только те матрицы, для которых число столбцов первого сомножителя равно
числу строк второго сомножителя. Результатом умножения является матрица, у
которой число строк равно числу строк первого сомножителя, а число столбцов
совпадает с числом столбцов второго сомножителя. Иными словами, перемножать
можно те матрицы, у которых совпадают средние индексы. Крайние индексы
определяют размерность получаемого результата.

Свойства операций над матрицами.

1) В общем случае . Если  то матрицы А и В называются перестановочными по
отношению друг к другу.

2)  Ассоциативность;

3)  Дистрибутивность;

4) При умножении любой квадратной матрицы на единичную
первоначальная матрица не меняется .

Вопрос №2: «Определители. Вычисление
определителей».

Определители 2-го и 3-го порядка и их
свойства. Если
квадратная матрица имеет определитель, отличный от нуля (Δ ≠ 0), то говорят,
что матрица невырожденная, в противном случае — матрица вырожденная или особая.

Определителем квадратной матрицы 2-го порядка,
называется число равное разности произведений элементов главной и побочной
диагонали матрицы.

Определителем квадратной матрицы 3-го
порядка, называется число равное:

Таким образом, вычисление определителя третьего порядка
сводится к вычислению определителей второго порядка.

Вопрос №3: «Свойства определителей».

Свойства определителей:

1) Если строка (столбец) матрицы состоит из 0, то ее
определитель равен 0.

2) Если все элементы, какой либо строки (столбца) матрицы
умножить на одно и тоже число, то и ее определитель умножится на это же число.

3) При транспонировании матрицы ее определитель не
меняется.

4) При перестановки, каких либо двух строк (столбцов)
матрицы знак матрицы меняется на противоположный. Доказательство вытекает из
того, что при перестановке одной транспозиции четность инверсии меняется.

5) Если квадратная матрица содержит две одинаковые строки
(столбца), то её определитель равен 0.

6) Сумма произведений элементов, какой либо строки
(столбца) на алгебраические дополнения какой либо строки (столбца) равно 0.

7) Если элементы, какой либо строки (столбца) равны сумме
двух слагаемых, то определитель равен сумме двух определителей, у которых все
строки (столбцы) кроме указанных, те же что и в исходном определителе, а рассматриваемая
k-строка (столбец) в первом определителе
содержит первые слагаемые, во втором вторые.

Определитель матрицы не изменится если к элементам какой
либо строки (столбца) прибавить элемент какой либо строки (столбца)
предварительно умноженные на одно и то же число.

Вопрос №4: «Обратная матрица и её
вычисление».

Обратная матрица. Матрицей, обратной матрице А,
называется матрица A^-1 такая, что A^-1A = A A^-1
= E.

Обратная матрица может существовать только для квадратной
матрицы. Причем сама является той же размерности, что и исходная матрица.

Можно показать, что для того, чтобы квадратная матрица
имела обратную, она должна быть невырожденной (т.е. Δ ≠ 0 ). Это условие
является и достаточным для существования A^-1 матрице А. Итак, всякая
невырожденная матрица имеет обратную, и, притом, единственную.

Сформулируем правило нахождения обратной матрицы на примере
матрицы А.

1. Находим определитель матрицы. Если Δ ≠ 0, то матрица A^-1
существует.

2. Составим матрицу В алгебраических дополнений элементов
исходной матрицы А. Т.е. в матрице В элементом i — ой строки и j — го столбца
будет алгебраическое дополнение A_ij элемента a_ij исходной
матрицы.

3. Транспонируем матрицу В и получим B^T.

Теорема существования и единственности обратной матрицы. Для
квадратной матрицы А существует и при том единственная обратная матрица А^-1
тогда и только тогда, когда эта матрица не вырождена. 

Вопрос №5: «Системы линейных уравнений,
их решение матричная запись».

Системы линейных уравнений. Уравнение называется линейным,
если оно содержит неизвестные в первой степени и не содержит их произведений.

Запись в матричной форме.

— система линейных уравнений.

Обозначим, — матрица коэффициентов,   —
вектор неизвестных,

— вектор свободных членов. A_mn
X_n1 + B_m1 = 0 — матричная запись системы уравнений.

Если система уравнений имеет решение, она называется совместной,
не имеет – несовместной. Совместная система, имеющая одно
решение, называется определенной, если много – неопределенной.
Две системы уравнений называются равносильными или эквивалентными,
если каждое решение является решением уравнения системы или наоборот.

Вопрос №6: «Решение систем линейных
уравнений с помощью обратной матрицы». Матричным методом могут быть решены
только те системы, у которых число уравнений совпадает с числом неизвестных и
определитель матрицы коэффициентов отличен от нуля (матрица А невырожденная). Из
этих условий следует, что  и,
следовательно, система совместна и определена. Решение системы можно получить
так: . Используя
свойства произведения матриц и свойство обратной матрицы . Т.е., для получения столбца
неизвестных нужно обратную матрицу матрицы коэффициентов системы умножить на
столбец свободных членов.

Пример. Решить систему  матричным методом. Решение. Найдем
обратную матрицу для матрицы коэффициентов системы .

Вычислим определитель, раскладывая по первой строке: . Поскольку Δ ≠ 0, то A^-1
существует.

Обратная матрица найдена верно.

Найдем решение системы .

Следовательно, x₁ = 1, x₂ = 2, x₃
= 3.

Матричный метод годится для решения любых систем, у которых
матрица А квадратная и невырожденная.

Вопрос №7: «Теорема Крамера, формулы
Крамера».

Пусть Δ = |A| определитель матричной системы
n линейных уравнений с n
неизвестных, а Δ_j определитель матрицы,
полученный из матричной системы заменой j-того
столбца на столбец правых частей. Тогда если Δ ≠ 0, то система имеет
единственное решение, определенное по формулам.

Вопрос №8: «Решение систем линейных
уравнений методом Гаусса».

Решение и исследование систем линейных
уравнений методом Гаусса.
Этот метод решения систем линейных уравнений пригоден для решения систем с
любым числом уравнений и неизвестных.

Суть метода Гаусса заключается в преобразовании заданной
системы уравнений с помощью элементарных преобразований в эквивалентную систему
ступенчатого треугольного вида.

Полученная система содержит все неизвестные в первом
уравнении. Во втором уравнении отсутствует первое неизвестное, в третьем
уравнении отсутствуют первое и второе неизвестные и т. д.

Если система совместна и определена (единственное решение),
то последнее уравнение содержит одно неизвестное. Найдя последнее неизвестное,
из предыдущего уравнения находим еще одно — предпоследнее. Подставляя
полученные величины неизвестных, мы последовательно найдем решение системы.

Элементарными преобразованиями системы линейных уравнений,
используемыми для приведения системы к треугольному виду, являются следующие
преобразования:

— перестановка местами двух уравнений;

— умножение обеих частей одного из уравнений на любое
число, отличное от нуля;

— прибавление к обеим частям одного уравнения
соответствующих частей другого уравнения, умноженных на любое число.

Элементарные преобразования переводят данную систему
линейных алгебраических уравнений в эквивалентную систему.

Две системы называются эквивалентными, если
всякое решение первой системы является решением другой системы и наоборот.

Вопрос №9: «Понятие вектора. Сложение
векторов, умножение вектора на скаляр».

Векторы на плоскости и в пространстве. Вектором
называется направленный отрезок (упорядоченная пара точек). К векторам
относится также и нулевой вектор, начало и конец которого совпадают.

Векторы и линейные операции над ними. Линейными операциями над
векторами называется сложение и умножение на число.

Суммой двух векторов a и b называется вектор c, направленный из начала вектора a в конец вектора b при условии, что начало b совпадет с концом вектора a.
Если векторы заданы их разложениями по базисным ортам, то при сложении векторов
складываются их соответствующие координаты.

Сумма любого конечного числа векторов может быть найдена по
правилу многоугольника: чтобы построить сумму конечного числа
векторов, достаточно совместить начало каждого последующего вектора с концом
предыдущего и построить вектор, соединяющий начало первого вектора с концом
последнего.

Вопрос №10: «Декартова и полярная
система координат на плоскости».

Декартовы прямоугольные координаты на
плоскости и в пространстве.

Системы координат на плоскости.

Декартовы прямоугольные координаты (рис.
4.1). О — начало координат, Ох — ось абсцисс, Оy — ось ординат,  — базисные векторы,  — абсцисса точки M ( — проекция точки M на ось Ох
параллельно оси Оy),  —
ордината точки M ( —
проекция точки M на ось Oy параллельно оси Ox).

Системы координат в пространстве.

Декартовы прямоугольные координаты (рис.
4.4). О — начало координат, Ох — ось абсцисс, Оy — ось ординат, Оz — ось
аппликат , — базисные
векторы. Oxy, Oxz, Oyz — координатные плоскости,  — абсцисса точки M ( — проекция точки M на ось Ох параллельно
плоскости Оyz),  —
ордината точки M ( —
проекция точки M на ось Oy параллельно плоскости Oxz),  — ордината точки M ( — проекция точки M на ось Oz параллельно
плоскости Oxy).

Полярные координаты на плоскости.  О — полюс, Ox — полярная ось,  — полярный радиус,  — полярный угол. Главные
значения  и :  (иногда ).

Выражение декартовых прямоугольных координат через полярные:

  

Выражение полярных координат через декартовы прямоугольные:

                              

Вопрос 11: «Цилиндрическая и сферическая
системы координат в пространстве».

Сферические и цилиндрические координаты
в пространстве.

Цилиндрические координаты. Главные значения , , :

Связь между декартовыми прямоугольными и цилиндрическими
координатами:

Сферические координаты. Главные значения , , θ:

Иногда вместо θ  рассматривают :

Вопрос №12: «Скалярное произведение
векторов и его свойства».

Скалярное произведение и его свойства.

Скалярным произведением двух векторов называется число,
равное произведению длин этих векторов на косинус угла между ними, т.е.  Из определения следует  где φ — угол между векторами.

В зависимости от значения угла между векторами, проекция
может принимать отрицательные, положительные или нулевые значения.

Свойства скалярного произведения.

Вопрос №13: «Векторное произведение
векторов и его свойства».

Векторным произведением вектора  на вектор  называется третий вектор , определяемый следующим образом:

1) длина его равна площади параллелограмма, построенного на
векторах  и , т.е.  где φ — угол между векторами  и ;

2) вектор  перпендикулярен векторам  и ;

3) векторы  после приведения к общему началу образуют правую
тройку векторов.

Свойства векторного произведения

Вопрос №14: «Смешанное произведение
векторов и его свойства».

Смешанным произведением трех векторов  называется число

Модуль смешанного произведения трех векторов численно равен
объему параллелепипеда, построенного на этих векторах.

Свойства смешанного произведения:

Вопрос №15: Двойное векторное
произведение».

Вопрос №16: «Уравнение прямой с угловым
коэффициентом».

 

Вопрос №17: «Угол между прямыми. Условия
параллельности и перпендикулярности двух прямых.

Определение. Если заданы две прямые y = k₁x
+ b₁,  y = k₂x + b₂, то острый угол между
этими прямыми будет определяться как . Две прямые параллельны, если k₁ = k₂.
Две прямые перпендикулярны, если k₁ = -1/k₂.

Теорема. Прямые Ах + Ву + С = 0 и А₁х
+ В₁у + С₁ = 0 параллельны, когда пропорциональны
коэффициенты А₁ = lА,  В₁ = lВ. Если еще и С₁
= lС, то прямые совпадают.

Координаты точки пересечения двух прямых находятся как
решение системы  уравнений этих прямых.

Вопрос №18: «Общее уравнение прямой».

 

Вопрос №19: «Общее уравнение плоскости.
Нормальный вектор плоскости».

Вопрос №20: «Угол между двумя
плоскостями. Условия параллельности и перпендикулярности двух плоскостей».

Вопрос №21: «Канонические уравнения
прямой в пространстве».

Вопрос №22: «Угол между прямыми в
пространстве. Условия параллельности и перпендикулярности двух плоскостей.

Вопрос №23: «Условие параллельности
прямой и плоскости в пространстве».

Вопрос №24: « Условие перпендикулярности
прямой и плоскости в пространстве».

Вопрос №25: «Угол между прямой и
плоскостью».

Вопрос №26: «Каноническое уравнение
эллипса. Исследование формы эллипса».

  

                                                                                 
                   

Вопрос №27: «Каноническое
уравнение гиперболы. Исследование формы гиперболы».

Вопрос №28: «Каноническое
уравнение параболы. Исследование формы параболы».

Вопрос №29: «Общее уравнение
линии второго порядка. Понятие типа линии второго порядка».

 

Уравнение такого вида может определять: 1) эллипс (в
частности, окружность), 2) гиперболу, 3) параболу, 4) пару прямых
(параллельных, пересекающихся либо совпадающих), 5) точку или не определять
никакой линии.

В простейшем случае, при В = 0, тип кривой можно
определить, выделив полные квадраты переменных.

Вопрос №30:
«Числовые последовательности и операции над ними, ограниченные и неограниченные
последовательности».

Вопрос №31: «Бесконечно большие
и бесконечно малые последовательности, основные свойства бесконечно малых последовательностей».

Вопрос №32: «Сходящиеся
последовательности: предел последовательности, основные свойства сходящихся
последовательностей».

Вопрос №33: «Монотонные
последовательности, число е».

Вопрос №34: «Определение
функции. Способы задания функций».

Вопрос №35: «Предел функции.
Односторонние пределы. Свойства пределов. Два замечательных предела».

Предел функции (предельное
значение функции) в заданной точке, предельной для области определения функции, —
такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной
точке.

Односторонний предел числовой функции в точке — это специфический предел,
подразумевающий, что аргумент функции приближается к указанной точке с
определённой стороны (слева или справа). Числовая функция имеет предел в точке
тогда и только тогда, когда она имеет в этой точке совпадающие левый и правый
пределы.

      

 

Вопрос №36: «Непрерывность и
разрывы и функций».

Вопрос №37: «Обратные функции».

Пусть X и Y – некоторые
множества и пусть задана функция f, т.е. множество пар чисел (x;y) (x ϵ X; y ϵ Y), в котором каждое
число x входит в
одну и только одну пару, а каждое число y – по крайней мере в одну пару.
Если в каждой паре этого множества числа x и y поменять
местами, то получим множество пар чисел (y;x), которое называется обратной функцией φ к
функции f.

Вопрос №38: «Сложные функции».

Если на некотором множестве X определена
функция z = φ(x) со множеством
значений Z, а на
множестве Z – функций
y = f [φ(x)] называется сложной
функцией от x [или
суперпозицией (иногда композицией) функций φ(x) и f(z)], а переменная z – промежуточной переменной
сложной функции.

Вопрос №39: «Производная. Ее
физический и геометрический смысл».

                                

Вопрос №40: «Правила
дифференцирования».

Вопросы 41: «Производные от
элементарных функций. Таблица производных».

Вопрос №42: «Дифференциал.
Определение и геометрический смысл».

Вопрос №43: «Производные и
дифференциалы высших порядков».

Вопрос №44: «Раскрытие
неопределенностей. Правило Лопиталя».

Вопрос №45: «Формулы Тейлора и
Маклорена».

Вопрос №46: «Разложение в ряд
Маклорена элементарных функций, вычисление числа е».