Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
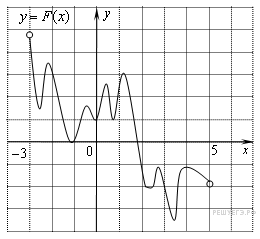
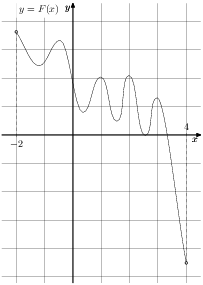
На рисунке изображён график функции y = F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (−3;5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [−2;4].
Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 2.
2
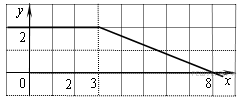
На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F(x) — одна из первообразных функции f(x).
Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 1.
4
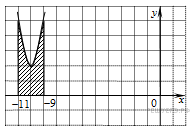
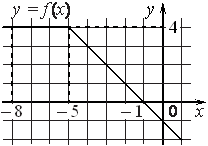
На рисунке изображён график некоторой функции y = f(x). Функция — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
5
На рисунке изображен график некоторой функции Пользуясь рисунком, вычислите определенный интеграл
Пройти тестирование по этим заданиям
Формулы для профильного ЕГЭ-2022 по математике
Первообразные
| Первообразная: | `F'(x)=f(x)` | |||
| Неопределённый интеграл: | `intf(x)dx=F(x)+C` | |||
| Определённый интеграл (формула Ньютона-Лейбница): | `int_a^bf(x)dx=F(b)-F(a)` |
Таблица первообразных
| `f(x)` | `F(x)` | `f(x)` | `F(x)` | |
|---|---|---|---|---|
| `a` | `ax` | |||
| `x^n` | `x^(n+1)/(n+1)` | `1/x` | `lnx` | |
| `e^x` | `e^x` | `a^x` | `a^x/lna` | |
| `sinx` | `-cosx` | `cosx` | `sinx` | |
| `1/cos^2x` | `text(tg)x` | `1/sin^2x` | `-text(ctg)x` | |
| `1/(x^2+a^2)` | `1/atext(arctg)x/a` | `1/(x^2-a^2)` | `1/(2a)ln|(x-a)/(x+a)|` | |
| `1/sqrt(a^2-x^2)` | `text(arcsin)x/a` | `1/sqrt(x^2+a)` | `ln|x+sqrt(x^2+a)|` |
Все формулы для профильного ЕГЭ-2022 по математике
Все формулы для базового ЕГЭ-2022 по математике
Файл к занятию 23
Нахождение наибольшего и наименьшего значения функции на отрезке
Задание 1. Найдите наибольшее значение функции y=x5+20x3−65x на отрезке [− 4; 0]. Ответ: 44
Задание 2. Найдите наибольшее значение функции y =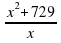
Задание 3. Найдите наименьшее значение функции y= 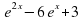
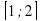
Ответ: -6
Дополнительно. Найдите наименьшее значение функции y=e2x−2ex+8 на отрезке [− 2; 1]. Ответ: 7
Задание 4. Найдите наибольшее значение функции y=15x−3sinx+5 на отрезке [− π/2; 0]. Ответ: 5
Дополнительно. Найдите наибольшее значение функции y=59x−56sinx+42 на отрезке [− π/2; 0]. Ответ: 42
Задание 5. Найдите наименьшее значение функции y=13cosx+17x+21 на отрезке [0; 3π/2]. Ответ: 34
Задание 6. Найдите наибольшее значение функции y=25x−25tgx+41 на отрезке [0; π/4]. Ответ: 41
Задание 7. Найдите наименьшее значение функции y= 3x—ln(x+3)3 на отрезке [−2,5; 0]. Ответ: -6
Дополнительно. Найдите точку минимума функции y= 2x—ln(x+8)2 . Ответ: -7
Задание 8. Найдите точку минимума функции y= (1-2x)cosx + 2sinx +7 на отрезке 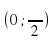
Дополнительно. Найдите точку максимума функции y=(x+5)2⋅e2 − x.
Первообразная.
Первообразной функцией F(x) для функции f(x) называется функция, производная которой равна исходной функции. F‘ (x)= f(x).
Любая непрерывная на некотором множестве функция имеет на этом множестве первообразную.
Пример. Функция F(x)=x3 является первообразной функции f(x)=3x2 так как (x3)’=3x2. Функции F1(x)=x3 +5 и F2(x)=x3 — 7 также являются первообразными функции f(x). Любая функция вида F(x)=x3 +с, где с – произвольное число, является первообразной функции f(x).
Каждая функция может иметь бесконечно много первообразных, которые отличаются на постоянное слагаемое.
Задание 9. На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x), определённой на интервале (− 7; 8). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [0; 5]. Ответ:1
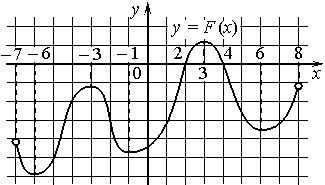
Задание 10. На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-2;4). Пользуясь рисунком, определите количество решений уравнения f (x) = 0 на отрезке [−1; 3]. Ответ: 6
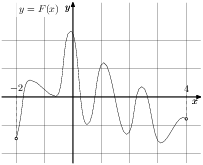
Дополнительно.
1. На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x), определённой на интервале (− 7; 5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [− 5; 2]. Ответ: 3
2. На рисунке изображён график функции y=F(x) и одной из первообразных некоторой функции f(x), определённой на интервале (-2;4). Пользуясь рисунком, определите количество решений уравнения f(x) = 0на отрезке [−1; 3]. Ответ: 7.
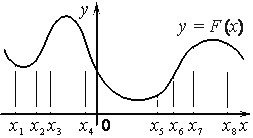
Задание 11. На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x) и отмечены восемь точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7, x8. В скольких из этих точек функция f(x) отрицательна?
Решение: Т.к f(x)= F`(x), то функция f(x) отрицательна, если F(x) убывает и функция f(x) положительна, если F(x) возрастает. По рисунку определим, сколько точек попали на промежуток убывания F(x). Это точки х1, х4, х8.
Значит, таких точек 3. Ответ: 3
Задание 12. На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x) и отмечены десять точек на оси абсцисс: x1,x2, x3, x4, x5, x6, x7, x8, x9, x10. В скольких из этих точек функция f(x) положительна? Ответ:6 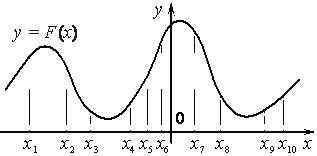
Криволинейная трапеция
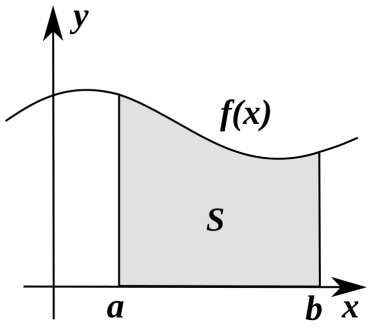
Пусть на отрезке [а; в] задана непрерывная функция, не меняющая на нем знака. Фигуру, ограниченную графиком этой функции, отрезком [а; в] и прямыми х=а и х=b называют криволинейной трапецией.
Если функция непрерывная и неотрицательная на отрезке [а; в], а F- ее первообразная на этом отрезке, то площадь S соответствующей криволинейной трапеции равна приращению первообразной на этом отрезке[а; в].
S= F(b)-F(a)
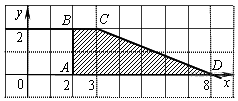
Задание 13. На рисунке изображён график некоторой функции y=f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F(x) — одна из первообразных функции f(x). Ответ:7
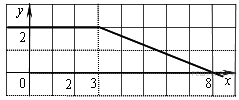
Решение: Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции ABCD. Поэтому
S= F(b) – F(a)= 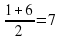
Задание 14. На рисунке изображён график некоторой функции y=f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(− 1)−F(− 8), где F(x) — одна из первообразных функции f(x). Ответ: 20
Каждая функция может иметь бесконечно много первообразных, которые отличаются на постоянное слагаемое. Совокупность всех первообразных данной непрерывной функции называется неопределенным интегралом от этой функции и обозначается 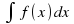
Если F(x) — некоторая первообразная данной функции, то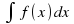
Процесс нахождения неопределенного интеграла называется интегрированием данной функции, или взятием интеграла от данной функции.
Площадь S криволинейной трапеции равна приращению первообразной на отрезке[а; в].
S= F(b)-F(a)=
Задание 15. На рисунке изображён график функции y = f(x). Функция F(x)= x3+30x2+302x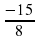
Задание 16. На рисунке изображён график некоторой функции y=f(x). Функция F(x)=12x3−3x2+152x−92 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры. Ответ: 592
Задание 17. На рисунке изображён график некоторой функции y=f(x). Функция F(x)=− x3−92x2−6x+2 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры. Ответ: 263
Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.
Все материалы доступны по лицензии Creative Commons — «Attribution-NonCommercial»
Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.
Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.
Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.
© 2014-2023 Все права на дизайн сайта принадлежат С.Є.А.
1. На рисунке изображён график функции 

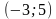
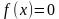
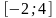
2. На рисунке изображён график некоторой функции 
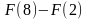
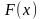

3. На рисунке изображён график функции 
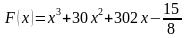

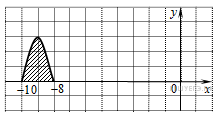
4. На рисунке изображён график некоторой функции 
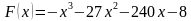


5. На рисунке изображён график функции 

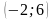

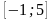



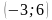

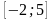
7. На рисунке изображён график функции 


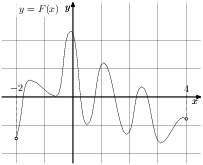



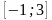

9. На рисунке изображён график функции 

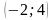

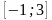

10. На рисунке изображён график функции 

Пользуясь рисунком, определите количество решений уравнения

11. На рисунке изображён график функции 

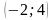

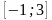
12. . На рисунке изображён график некоторой функции 
, где
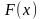

13. На рисунке изображён график некоторой функции 
, где
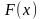

14. . На рисунке изображён график некоторой функции 
, где
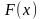

15. На рисунке изображён график функции 

16. На рисунке изображён график функции 
Функция — одна из первообразных функции 
17. На рисунке изображён график функции 

18. На рисунке изображён график функции 

19. На рисунке изображён график функции 

20. На рисунке изображён график функции 

21. На рисунке изображён график функции 

22. На рисунке изображен график некоторой функции 
23. На рисунке изображён график функции 

Найдите количество решений уравнения
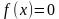
.
24. На рисунке изображён график функции 

. Найдите количество решений уравнения
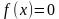
.
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Первообразная функции»
Открытый банк заданий по теме первообразная функции. Задания B7 из ЕГЭ по математике (профильный уровень)
Геометрические фигуры на плоскости: вычисление величин с использованием углов
Геометрические фигуры в пространстве: нахождение длины, площади, объема
Задание №1164
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображён график функции y=f(x) (являющийся ломаной линией, составленной из трёх прямолинейных отрезков). Пользуясь рисунком, вычислите F(9)-F(5), где F(x) — одна из первообразных функции f(x).
Показать решение
Решение
По формуле Ньютона-Лейбница разность F(9)-F(5), где F(x) — одна из первообразных функции f(x), равна площади криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми y=0, x=9 и x=5. По графику определяем, что указанная криволинейная трапеция является трапецией с основаниями, равными 4 и 3 и высотой 3.
Её площадь равна frac{4+3}{2}cdot 3=10,5.
Ответ
10,5
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1158
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-5; 5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-3; 4].
Показать решение
Решение
Согласно определению первообразной выполняется равенство: F'(x)=f(x). Поэтому уравнение f(x)=0 можно записать в виде F'(x)=0. Так как на рисунке изображён график функции y=F(x), то надо найти те точки промежутка [-3; 4], в которых производная функции F(x) равна нулю. Из рисунка видно, что это будут абсциссы экстремальных точек (максимума или минимума) графика F(x). Их на указанном промежутке ровно 7 (четыре точки минимума и три точки максимума).
Ответ
7
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1155
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображён график функции y=f(x) (являющийся ломаной линией, составленной из трёх прямолинейных отрезков). Пользуясь рисунком, вычислите F(5)-F(0), где F(x) — одна из первообразных функции f(x).
Показать решение
Решение
По формуле Ньютона-Лейбница разность F(5)-F(0), где F(x) — одна из первообразных функции f(x), равна площади криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми y=0, x=5 и x=0. По графику определяем, что указанная криволинейная трапеция является трапецией с основаниями, равными 5 и 3 и высотой 3.
Её площадь равна frac{5+3}{2}cdot 3=12.
Ответ
12
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1149
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-5; 4). Пользуясь рисунком, определите количество решений уравнения f (x)=0 на отрезке (-3; 3].
Показать решение
Решение
Согласно определению первообразной выполняется равенство: F'(x)=f(x). Поэтому уравнение f(x)=0 можно записать в виде F'(x)=0. Так как на рисунке изображён график функции y=F(x), то надо найти те точки промежутка [-3; 3], в которых производная функции F(x) равна нулю.
Из рисунка видно, что это будут абсциссы экстремальных точек (максимума или минимума) графика F(x). Их на указанном промежутке ровно 5 (две точки минимума и три точки максимума).
Ответ
5
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1146
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображен график некоторой функции y=f(x). Функция F(x)=-x^3+4,5x^2-7 — одна из первообразных функции f(x).
Найдите площадь заштрихованной фигуры.
Показать решение
Решение
Заштрихованная фигура является криволинейной трапецией, ограниченной сверху графиком функции y=f(x), прямыми y=0, x=1 и x=3. По формуле Ньютона-Лейбница её площадь S равна разности F(3)-F(1), где F(x) — указанная в условии первообразная функции f(x). Поэтому S= F(3)-F(1)= -3^3 +(4,5)cdot 3^2 -7-(-1^3 +(4,5)cdot 1^2 -7)= 6,5-(-3,5)= 10.
Ответ
10
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №907
Тип задания: 7
Тема:
Первообразная функции
Условие
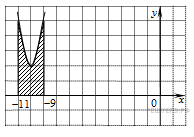
На рисунке изображён график некоторой функции y=f(x). Функция F(x)=x^3+6x^2+13x-5 — одна из первообразных функции f(x). Найдите площадь заштрихованной фигуры.
Показать решение
Решение
Заштрихованная фигура является криволинейной трапецией, ограниченной графиком функции y=f(x) и прямыми y=0, x=-4 и x=-1. По формуле Ньютона-Лейбница её площадь S равна разности F(-1)-F(-4), где F(x) — указанная в условии первообразная функции f(x).
Поэтому S= F(-1)-F(-4)= (-1)^3+6(-1)^2+13(-1)-5-((-4)^3+6(-4)^2+13(-4)-5)= -13-(-25)=12.
Ответ
12
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №307
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображен график некоторой функции y=f(x). Функция F(x)=x^3+18x^2+221x-frac12 — одна из первообразных функции f(x). Найдите площадь заштрихованной фигуры.
Показать решение
Решение
По формуле Ньютона-Лейбница S=F(-1)-F(-5).
F(-1)= (-1)^3+18cdot(-1)^2+221cdot(-1)-frac12= -204-frac12.
F(-5)= (-5)^3+18cdot(-5)^2+221cdot(-5)-frac12= -125+450-1105-frac12= -780-frac12.
F(-1)-F(-5)= -204-frac12-left (-780-frac12right)= 576.
Ответ
576
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №306
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображен график некоторой функции y=f(x).Пользуясь рисунком, вычислите F(9)-F(3), где F(x) — одна из первообразных функции f(x).
Показать решение
Решение
F(9)-F(3)=S, где S — площадь фигуры, ограниченной графиком функции y=f(x), прямыми y=0 и x=3,:x=9. Рассмотрим рисунок ниже.
Данная фигура — трапеция с основаниями 6 и 1 и высотой 2. Ее площадь равна frac{6+1}{2}cdot2=7.
Ответ
7
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №104
Тип задания: 7
Тема:
Первообразная функции
Условие
На координатной плоскости изображен график функции y=f(x). Одна из первообразных этой функции имеет вид: F(x)=-frac13x^3-frac52x^2-4x+2. Найдите площадь заштрихованной фигуры.
Показать решение
Решение
На рисунке видно, что заштрихованная фигура ограничена по оси абсцисс точками −4, −1, а по оси ординат графиком функции: f(x). Значит площадь фигуры мы можем найти с помощью разности значений первообразных в точках −4 и −1, по формуле определенного интеграла:
intlimits_{-4}^{-1}f(x)dx=F(-1)-F(-4)
Подставим значение первообразной из условия и получим площадь фигуры:
F(-1)-F(-4)=
=frac13-frac52+4+2-frac{64}{3}+frac{80}{2}-16-2=
=-frac{63}{3}+frac{75}{2}-12=-21+37,5-12=4,5
Ответ
4,5
Задание №103
Тип задания: 7
Тема:
Первообразная функции
Условие
Первообразная y=F(x) некоторой функции y=f(x) определена на интервале (−16; −2). Определите сколько решений имеет уравнение f(x) = 0 на отрезке [−10; −5].
Показать решение
Решение
Формула первообразной имеет следующий вид:
f(x) = F'(x)
По условию задачи нужно найти точки, в которых функция f(x) равна нулю. Принимая во внимание формулу первообразной, это значит, что, нужно найти точки, в которых F'(x) = 0, то есть те точки, в которых производная от первообразной равна нулю.
Мы знаем, что производная равна нулю в точках локального экстремума, т.е. функция имеет решения в тех точках, в которых возрастание F(x) сменяется убыванием и наоборот.
На отрезке [−10; −5] видно что это точки: −9; −7; −6. Значит уравнение f(x) = 0 имеет 3 решения.
Ответ
3
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928
Первообразная в ЕГЭ
Тело разгоняется на прямолинейном участке пути, при этом зависимость пройденного телом пути S от времени t имеет вид:

Чему равна скорость тела в момент времени t = 2 c при таком движении? (Ответ дайте в метрах в секунду.)
Материальная точка движется прямолинейно по
закону , где x — расстояние от точки отсчёта в метрах, t — время в секундах, измеренное с начала движения. Найдите её скорость (в метрах в секунду) в момент времени t = 10 с.
Материальная точка движется от начального до конечного положения. На рисунке изображён график её движения. На оси абсцисс откладывается время в секундах, на оси ординат — расстояние от начального положения точки (в метрах). Найдите среднюю скорость движения точки. Ответ дайте в метрах в секунду.
Решение :
Чтобы найти среднюю скорость движения точки, необходимо пройденное расстояние поделить на время прохождения:
8 : 5 = 1,6 (м/с)
Ответ :1,6
Материальная точка движется вдоль прямой от начального до конечного положения. На рисунке изображён график её движения. На оси абсцисс откладывается время в секундах, на оси ординат – расстояние от начального положения точки(в метрах). Найдите среднюю скорость движения точки. Ответ дайте в метрах в секунду.
Решение :
Чтобы найти среднюю скорость движения точки, нужно пройденное расстояние разделить на время: 18:10=1,8(м/с)
Ответ : 1,8
Материальная точка движется от начального до конечного положения. На рисунке изображён график её движения. На оси абсцисс откладывается время в секундах, на оси ординат — расстояние от начального положения точки (в метрах). Найдите среднюю скорость движения точки. Ответ дайте в метрах в секунду.
Решение :
- Для нахождения средней скорости нужно длину пройденного пути s разделить на время его прохождения t: v = s : t
- Здесь следует заметить, что при вычислении пути нужно учитывать расстояния, в которых точка возвращалась обратно. То есть, весь путь s будет складываться s=6+4+6=16 метров. Таким образом, средняя скорость равна v = 16: 4 = 4 (м/с)
Ответ :4
1)Функция F(x) является первообразной для функции f(x) = 2x , причем F(2) = 5.
1)Функция F(x) является первообразной для функции f(x) = 2x , причем F(2) = 5.
Найти F(-3).
2) Функция G(x) является первообразной для функции g(x) = 3 , причем G(-1) = 2.
Найти G(2).
3)
если F(4) = 5. Найти F(1).
F(9)
Ответ: 17
6 .
этой точки.
Ответ : -6
4)Наименьшее значение первообразной F(x) для функции
5) Найдите первообразную F(x) для функции
6) График первообразной F(x) для функции
значение F(0,5)
Решение:
1)
2)
3)
4) Так как
х = 0 , х = -1
Ответ : — 1
Первообразная её геометрический и физический смысл
1. Задачи на определение первообразной.
Функция F(x)называется первообразной для функции f(x)
на некотором промежутке, если для всех x из этого
промежутка выполняется равенство
На рисунке изображен график функции y = F (x) –
одной из первообразных некоторой функции y = f (x) опре —
деленной на интервале (- 3; 6). Пользуясь рисунком, определи-
те количество решений уравнения f (x) = 0 на отрезке [ — 1; 4]
— 1
4
8
Т.е производная положительна,
а значит функция
y = F (x)
возрастает.
•
•
•
3
На рисунке изображён график некоторой функции у = f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F(x) — одна из первообразных функции f(x).
На рисунке изображен график некоторой функции у =f(x) Пользуясь рисунком, вычислите
определенный интеграл
Основные правила и свойства определенного интеграла
Найти работу материальной точки, которая перемещается под действием силы F(x) = x — 2 на отрезке [2;4].
Функция у = f (х) определена на всей чистовой прямой и является периодической с периодом 6. На рисунке изображен график этой функции при  Найдите значение
выражения  .

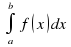
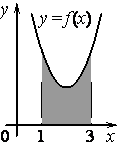
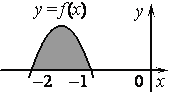









.png)

.png)