Пирамида, подготовка к ЕГЭ по математике
- 22.12.2017
Таблицы с теорией на тему: «Пирамида» для подготовки к ЕГЭ по математике. В кратком содержании изложена вся необходимая теория для этой темы.
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Сохранить ссылку:
Комментарии (0)
Добавить комментарий
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
Имя (обязательное)
E-Mail
Подписаться на уведомления о новых комментариях
Отправить
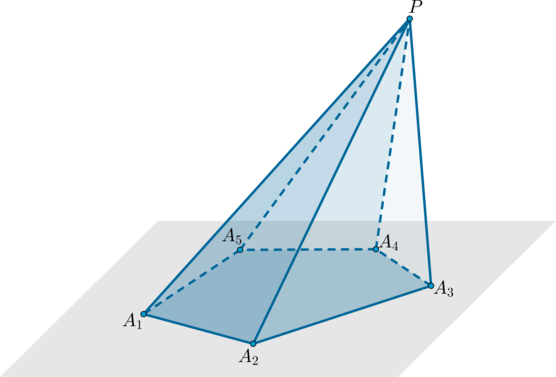
Определение
Пирамида – это многогранник, составленный из многоугольника (A_1A_2…A_n) и (n) треугольников с общей вершиной (P) (не лежащей в плоскости многоугольника) и противолежащими ей сторонами, совпадающими со сторонами многоугольника.
Обозначение: (PA_1A_2…A_n).
Пример: пятиугольная пирамида (PA_1A_2A_3A_4A_5).
Треугольники (PA_1A_2, PA_2A_3) и т.д. называются боковыми гранями пирамиды, отрезки (PA_1, PA_2) и т.д. – боковыми ребрами, многоугольник (A_1A_2A_3A_4A_5) – основанием, точка (P) – вершиной.
Высота пирамиды – это перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
Пирамида, в основании которой лежит треугольник, называется тетраэдром.
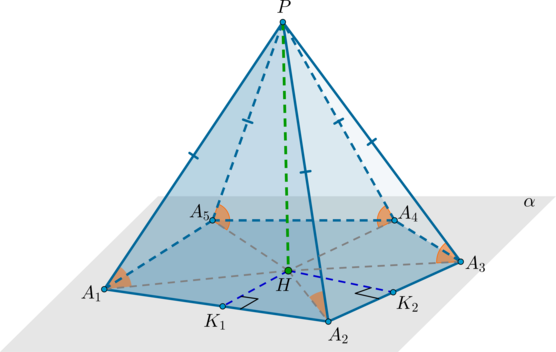
Пирамида называется правильной, если в ее основании лежит правильный многоугольник и выполнено одно из условий:
((a)) боковые ребра пирамиды равны;
((b)) высота пирамиды проходит через центр описанной около основания окружности;
((c)) боковые ребра наклонены к плоскости основания под одинаковым углом.
((d)) боковые грани наклонены к плоскости основания под одинаковым углом.
Правильный тетраэдр – это треугольная пирамида, все грани которой – равные равносторонние треугольники.
Теорема
Условия ((a), (b), (c), (d)) эквивалентны.
Доказательство
Проведем высоту пирамиды (PH). Пусть (alpha) – плоскость основания пирамиды.
1) Докажем, что из ((a)) следует ((b)). Пусть (PA_1=PA_2=PA_3=…=PA_n).
Т.к. (PHperp alpha), то (PH) перпендикулярна любой прямой, лежащей в этой плоскости, значит, треугольники (PA_1H, PA_2H, PA_3H,…,
PA_nH) – прямоугольные. Значит, эти треугольники равны по общему катету (PH) и гипотенузам (PA_1=PA_2=PA_3=…=PA_n). Значит, (A_1H=A_2H=…=A_nH). Значит, точки (A_1, A_2, …, A_n) находятся на одинаковом расстоянии от точки (H), следовательно, лежат на одной окружности с радиусом (A_1H). Эта окружность по определению и есть описанная около многоугольника (A_1A_2…A_n).
2) Докажем, что из ((b)) следует ((c)).
Аналогично первому пункту треугольники (PA_1H, PA_2H, PA_3H,…,
PA_nH) прямоугольные и равны по двум катетам. Значит, равны и их углы, следовательно, (angle PA_1H=angle PA_2H=…=angle PA_nH).
3) Докажем, что из ((c)) следует ((a)).
Аналогично первому пункту треугольники (PA_1H, PA_2H, PA_3H,…,
PA_nH) прямоугольные и по катету и острому углу. Значит, равны и их гипотенузы, то есть (PA_1=PA_2=PA_3=…=PA_n).
4) Докажем, что из ((b)) следует ((d)).
Т.к. в правильном многоугольнике совпадают центры описанной и вписанной окружности (вообще говоря, эта точка называется центром правильного многоугольника), то (H) – центр вписанной окружности. Проведем перпендикуляры из точки (H) на стороны основания: (HK_1,
HK_2) и т.д. Это – радиусы вписанной окружности (по определению). Тогда по ТТП ((PH) – перпендикуляр на плоскость, (HK_1, HK_2) и т.д. – проекции, перпендикулярные сторонам) наклонные (PK_1, PK_2) и т.д. перпендикулярны сторонам (A_1A_2, A_2A_3) и т.д. соответственно. Значит, по определению (angle PK_1H, angle PK_2H) равны углам между боковыми гранями и основанием. Т.к. треугольники (PK_1H, PK_2H, …) равны (как прямоугольные по двум катетам), то и углы (angle PK_1H, angle PK_2H, …) равны.
5) Докажем, что из ((d)) следует ((b)).
Аналогично четвертому пункту треугольники (PK_1H, PK_2H, …) равны (как прямоугольные по катету и острому углу), значит, равны отрезки (HK_1=HK_2=…=HK_n). Значит, по определению, (H) – центр вписанной в основание окружности. Но т.к. у правильных многоугольников центры вписанной и описанной окружности совпадают, то (H) – центр описанной окружности. Чтд.
Следствие
Боковые грани правильной пирамиды – равные равнобедренные треугольники.
Определение
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.
Апофемы всех боковых граней правильной пирамиды равны между собой и являются также медианами и биссектрисами.
Важные замечания
1. Высота правильной треугольной пирамиды падает в точку пересечения высот (или биссектрис, или медиан) основания (основание – правильный треугольник).
2. Высота правильной четырехугольной пирамиды падает в точку пересечения диагоналей основания (основание – квадрат).
3. Высота правильной шестиугольной пирамиды падает в точку пересечения диагоналей основания (основание – правильный шестиугольник).
4. Высота пирамиды перпендикулярна любой прямой, лежащей в основании.
Определение
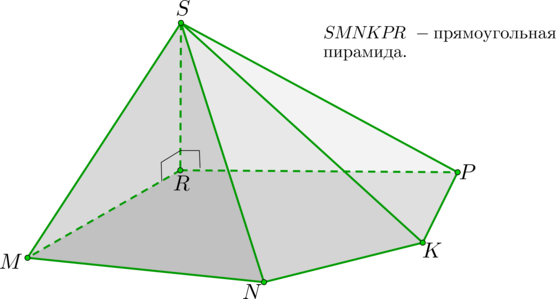
Пирамида называется прямоугольной, если одно ее боковое ребро перпендикулярно плоскости основания.
Важные замечания
1. У прямоугольной пирамиды ребро, перпендикулярное основанию, является высотой пирамиды. То есть (SR) – высота.
2. Т.к. (SR) перпендикулярно любой прямой из основания, то (triangle SRM, triangle SRP) – прямоугольные треугольники.
3. Треугольники (triangle SRN, triangle SRK) – тоже прямоугольные.
То есть любой треугольник, образованный этим ребром и диагональю, выходящей из вершины этого ребра, лежащей в основании, будет прямоугольным.
[{Large{text{Объем и площадь поверхности пирамиды}}}]
Теорема
Объем пирамиды равен трети произведения площади основания на высоту пирамиды: [V_{text{пирамиды}}=dfrac13 S_{text{осн}}cdot h]
Следствия
Пусть (a) – сторона основания, (h) – высота пирамиды.
1. Объем правильной треугольной пирамиды равен (V_{text{прав.треуг.пир.}}=dfrac{sqrt3}{12}a^2h),
2. Объем правильной четырехугольной пирамиды равен (V_{text{прав.четыр.пир.}}=dfrac13a^2h).
3. Объем правильной шестиугольной пирамиды равен (V_{text{прав.шест.пир.}}=dfrac{sqrt3}{2}a^2h).
4. Объем правильного тетраэдра равен (V_{text{прав.тетр.}}=dfrac{sqrt3}{12}a^3).
Теорема
Площадь боковой поверхности правильной пирамиды равна полупроизведению периметра основания на апофему.
[{Large{text{Усеченная пирамида}}}]
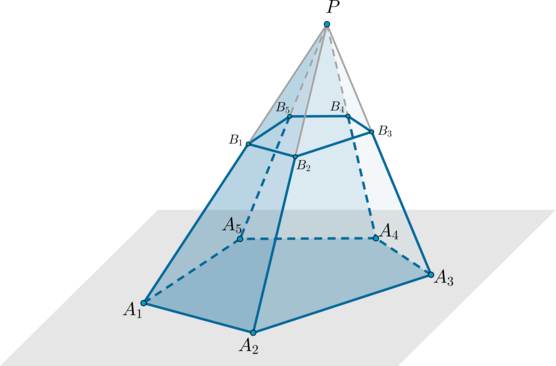
Определение
Рассмотрим произвольную пирамиду (PA_1A_2A_3…A_n). Проведем через некоторую точку, лежащую на боковом ребре пирамиды, плоскость параллельно основанию пирамиды. Данная плоскость разобьет пирамиду на два многогранника, один из которых – пирамида ((PB_1B_2…B_n)), а другой называется усеченная пирамида ((A_1A_2…A_nB_1B_2…B_n)).
Усеченная пирамида имеет два основания – многоугольники (A_1A_2…A_n) и (B_1B_2…B_n), которые подобны друг другу.
Высота усеченной пирамиды – это перпендикуляр, проведенный из какой-нибудь точки верхнего основания к плоскости нижнего основания.
Важные замечания
1. Все боковые грани усеченной пирамиды – трапеции.
2. Отрезок, соединяющий центры оснований правильной усеченной пирамиды (то есть пирамиды, полученной сечением правильной пирамиды), является высотой.
Пирамида – многогранник, основание которого — многоугольник , а остальные грани — треугольники, имеющие общую вершину.
По числу углов основания различают пирамиды треугольные, четырёхугольные и т. д.
Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.
Основание — многоугольник, которому не принадлежит вершина пирамиды.
Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.
Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).
Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.
Некоторые свойства пирамиды
1) Если все боковые ребра равны, то
– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр
– боковые ребра образуют с плоскостью основания равные углы
Верно и обратное.
Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.
Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.
2) Если все грани пирамиды наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр
Верно и обратное.
Виды пирамид
Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания.
Для правильной пирамиды справедливо:
– боковые ребра правильной пирамиды равны;
– в правильной пирамиде все боковые грани — равные равнобедренные треугольники;
– в любую правильную пирамиду можно вписать сферу;
– около любой правильной пирамиды можно описать сферу;
– площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Видео
Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. Тогда это ребро и есть высота пирамиды.
Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.
Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.
Смотрите также таблицу «Объемы пирамиды и призмы. Площадь поверхности пирамиды и призмы».
Определение
Правильная пирамида
Пирамида называется правильной, если её основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.
Пусть (displaystyle a=1) – сторона основания правильной пирамиды, (displaystyle h=sqrt{3}) – высота данной пирамиды.
Воспользуемся формулой для вычисления объема пирамиды.
Правило
Объём пирамиды
Объём пирамиды (displaystyle V) равен одной трети произведения площади основания на высоту.
(displaystyle V=frac{1}{3}S_{осн} cdot h { small ,} )
где (displaystyle S_{осн} ) – площадь основания,
(displaystyle h) – высота пирамиды.
(displaystyle S_{осн}=frac{sqrt{3}}{4} )
Подставим (displaystyle S_{осн}) и (displaystyle h) в формулу для объема пирамиды:
(displaystyle V=frac{1}{3}S_{осн} cdot h =frac{1}{3}cdot frac{sqrt{3}}{4} cdot sqrt{3} =frac{1}{3}cdot frac{3}{4}=frac{1}{4}=0{,}25{small .})
Ответ: (displaystyle 0{,}25{small .})
Объем правильной треугольной пирамиды
Пусть сторона основания равна ( displaystyle a), а боковое ребро равно ( displaystyle b). Нужно найти ( displaystyle {{S}_{осн}}) и ( displaystyle H).
( displaystyle {{S}_{осн}}) – это площадь правильного треугольника ( displaystyle ABC).
Вспомним, как искать эту площадь.
Используем формулу площади:
( displaystyle S=frac{1}{2}abcdot sin gamma )
У нас «( displaystyle a)» – это ( displaystyle a), а «( displaystyle b)» – это тоже ( displaystyle a), а ( displaystyle sin gamma =sin 60{}^circ =frac{sqrt{3}}{2})
Значит, ( displaystyle {{S}_{ABC}}=frac{1}{2}{{a}^{2}}frac{sqrt{3}}{2}=frac{{{a}^{2}}sqrt{3}}{4}).
Теперь найдем ( displaystyle H).
По теореме Пифагора для ( displaystyle Delta SOC)
( displaystyle {{H}^{2}}={{b}^{2}}-O{{C}^{2}})
Чему же равно ( displaystyle OC)?
Это радиус описанной окружности в ( displaystyle Delta ABC), потому что пирамида правильная и, значит, ( displaystyle O) – центр ( displaystyle Delta ABC)
Найдем ( displaystyle OC) (Подробнее смотри в теме «Правильный треугольник»).
( displaystyle OC=frac{2}{3}CK), так как ( displaystyle O) – точка пересечения и медиан тоже.
( displaystyle C{{K}^{2}}=A{{C}^{2}}-A{{K}^{2}}) (теорема Пифагора для ( displaystyle Delta ACK))
( displaystyle C{{K}^{2}}-{{a}^{2}}-frac{{{a}^{2}}}{4}=frac{3{{a}^{2}}}{4}); ( displaystyle CK=frac{asqrt{3}}{2})
Значит, ( displaystyle OC=frac{2}{3}cdot frac{asqrt{3}}{2}=frac{asqrt{3}}{3})
Подставим ( displaystyle OC) в формулу для ( displaystyle H).
( displaystyle {{H}^{2}}={{b}^{2}}-O{{C}^{2}}={{b}^{2}}-{{left( frac{asqrt{3}}{3} right)}^{2}}={{b}^{2}}-frac{{{a}^{2}}}{3})
И подставим все в формулу объема:
( displaystyle V=frac{1}{3}{{S}_{ABC}}cdot H=frac{1}{3}cdot frac{{{a}^{2}}sqrt{3}}{4}cdot sqrt{{{b}^{2}}-frac{{{a}^{2}}}{3}})
( displaystyle V=frac{{{a}^{2}}sqrt{3}}{12}sqrt{{{b}^{2}}-frac{{{a}^{2}}}{3}}).
Внимание: если у тебя правильный тетраэдр (т.е. ( displaystyle b=a)), то формула получается такой:
( displaystyle V=frac{{{a}^{3}}}{6sqrt{2}}).
Задание 974
Объем пирамиды SABC равен 54. На ребрах SA, АВ и АС взяты точки М, N и Р соответственно так, что SM:MA= BN:NA=CP:PA=1:2. Найдите объем пирамиды МАNP.
Ответ: 16
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Треугольники AHS и AKM подобны (SH и MK высоты в пирамидах) и коэффициент подобия равен 2/3 (так как AM:MS = 2:1, значит AS составляет 3 (2+1) части)
Аналогично треугольники APN и ACB подобны и коэффициент подобия равен 2/3. Пусть h — высота ABCS (SH), a h1 — высота ANPM (MK), S — площадь ABC, а S1 — площадь ANP.
Тогда, $$frac{1}{3}Sh=54$$.
$$h_1=frac{2}{3}h$$
$$S_1=frac{4}{9}S$$ (так как площади относятся, как квадрат коэффициента подобия)
$$frac{1}{3}S_1h_1=frac{1}{3}*frac{4}{9}Sfrac{2}{3}h=frac{8}{27}*frac{1}{3}Sh=frac{8}{27}*54=16$$
Задание 3198
Объем правильной четырехугольной пирамиды SABCD равен 60. Точка E – середина ребра SB. Найдите объем треугольной пирамиды EABC.
Ответ: 15
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$S_{ABC}=frac{1}{2}S_{ABCD}$$ $$h_{2}=frac{1}{2}h_{1}$$ $$V_{ABCDS}=frac{1}{3}S_{ABCD}cdot h_{1}$$ $$V_{ABCS}=frac{1}{3}S_{ABC}cdot h_{2}=frac{1}{3}cdotfrac{1}{2}S_{ABCD}=$$ $$=frac{1}{4}V_{ABCD}=frac{1}{4}cdot60=15$$
Задание 3284
В правильной четырехугольной пирамиде боковое ребро равняется 4 и образует с плоскостью основания угол 30 . Найдите объём пирамиды.
Ответ: 16
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Введем обозначения как показано на рисунке
∠SDH=30 (по условию), значит ∠HSD = 90 — 30 = 60. SH = 2 (катет, лежащий на против угла в 30 градусов равен половине гипотенузы)
$$HD = SD * sin HSD = 4 * frac{sqrt{3}}{2}=2sqrt{3}$$
$$BD = 2HD = 4sqrt{3}$$
Из треугольника BAD : пусть BA = AD = x, тогда $$x^{2}+x^{2}=(4sqrt{3})^{2}$$
Отсюда $$x^{2}=24$$ — площадь основания.
Тогда $$V = frac{1}{3}S*h=frac{1}{3}*24*2=16$$
Задание 3419
Найдите сторону основания правильной треугольной пирамиды, если её боковая поверхность равна 72, а высота равна 2.
Ответ: 12
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1) $$S_{b}=72$$ $$DH=2$$
$$S_{DCB}=frac{72}{3}=24$$
2) из $$bigtriangleup ABC$$: $$HM=frac{1}{3}AM$$
$$AM=frac{sqrt{3}AB}{2}$$
Пусть $$AB=x$$ $$Rightarrow$$ $$AM=frac{sqrt{3}x}{2}$$ $$Rightarrow$$ $$HM=frac{sqrt{3}x}{6}$$ $$Rightarrow$$ $$DM=sqrt{DH^{2}+HM^{2}}=sqrt{2^{2}+frac{3X^{2}}{36}}=sqrt{4+frac{x^{2}}{12}}$$
$$Rightarrow$$ $$S_{BDC}=frac{1}{2}cdot DMcdot BC$$ $$Rightarrow$$ $$24=frac{1}{2}xcdotsqrt{4+frac{x^{2}}{12}}$$
$$48=xcdotsqrt{4+frac{x^{2}}{12}}$$
$$2304=x^{2}cdot(4+frac{x^{2}}{12})$$ $$Leftrightarrow$$
$$frac{x^{4}}{12}+4x^{2}-2304=0$$
$$D=16+768=784$$
$$x^{2}=frac{-4+28}{frac{1}{6}}=24cdot6$$ $$Leftrightarrow x=12$$
Задание 3760
В правильной треугольной пирамиде SABC с вершиной S биссектрисы треугольника ABC пересекаются в точке O. Площадь треугольника ABC равна 2; объем пирамиды равен 6. Найдите длину отрезка OS.
Ответ: 9
Задание 3762
В правильной четырехугольной пирамиде $$SABCD$$ точка $$O$$ – центр основания, $$S$$ – вершина, $$SO=15,BD=16$$. Найдите боковое ребро $$SA$$.
Ответ: 17
Задание 3767
В правильной треугольной пирамиде SABC точка M – середина ребра AB, S – вершина. Известно, что BC = 3, а площадь боковой поверхности пирамиды равна 45. Найдите длину отрезка SM.
Ответ: 10
Задание 3768
В правильной треугольной пирамиде SABC точка L — середина ребра AC, S — вершина. Известно, что BC = 6, а SL = 5. Найдите площадь боковой поверхности пирамиды.
Ответ: 45
Задание 3769
В правильной треугольной пирамиде SABC точка K – середина ребра BC, S – вершина. Известно, что SK = 4, а площадь боковой поверхности пирамиды равна 54. Найдите длину ребра AC.
Ответ: 9
Задание 3771
В правильной треугольной пирамиде $$SABC$$ Q– середина ребра $$AB$$, $$S$$ – вершина. Известно, что $$BC=7$$, а площадь боковой поверхности пирамиды равна 42. Найдите длину отрезка $$SQ$$.
Ответ: 4
Задание 3772
Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
Ответ: 340
Задание 3773
Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
Ответ: 360
Задание 3774
Объем параллелепипеда $$ABCDA_{1}B_{1}C_{1}D_{1}$$ равен 9. Найдите объем треугольной пирамиды $$ABCA_{1}$$.
Ответ: 1,5
Задание 3775
Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?
Ответ: 8
Задание 3776
Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.
Ответ: 4
Площадь поверхности – это суммарная площадь всех поверхностей, которые составляют объемную фигуру.
Призма
1. Призма — это многогранник, у которого две грани (основания) — равные (n)-угольники, лежащие в параллельных плоскостях, остальные (n) граней (боковые) — параллелограммы. Призмы подразделяются на треугольные, четырехугольные, пятиугольные и т. д. в зависимости от количества сторон основания.
Высотой призмы называется перпендикуляр, опущенный из точки верхнего основания на плоскость нижнего.
2. Призма, у которой боковое ребро перпендикулярно основанию, называется прямой. Ее боковые грани — прямоугольники, и высота равна боковому ребру.
Прямая призма, в основании которой лежит правильный многоугольник, называется правильной. Ее боковые грани, равные прямоугольники.

3. Площадь боковой поверхности призмы равна сумме площадей ее боковых граней: (S_{бок}= S_1+ S_2+…+ S_n).
Площадь поверхности призмы равна сумме площади боковой поверхности и двух площадей оснований: (S_{полн} = S_{бок}+ 2S_{осн}).
4. Объем произвольной призмы равен произведению площади основания на высоту: (V_{призмы}=S_{осн}cdot h).
Параллелепипед
5. Параллелепипедом называется призма, в основании которой лежит параллелограмм. Противоположные боковые грани параллелепипеда равны.
Прямой параллелепипед — это параллелепипед, у которого боковое ребро перпендикулярно основанию.
Прямоугольный параллелепипед — это прямой параллелепипед, у которого в основании лежит прямоугольник.
Диагональ прямоугольного параллелепипеда выражается через его измерения (ширину, длину и высоту) формулой (d^2=a^2+b^2+c^2).
Куб — параллелепипед, у которого все грани квадраты. Диагональ куба с ребром (a): (d=asqrt{3}).


Пирамида
6. Пирамидой называется многогранник, у которого одна грань (основание) — (n)—угольник, а остальные (n) граней (боковые) — треугольники с общей вершиной. Пирамиды подразделяются на треугольные, четырехугольные, пятиугольные и т. д. в зависимости от количества сторон основания.
Тетраэдер – другое название треугольной пирамиды.
Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на основание.
7. Пирамида называется правильной, если ее боковые ребра равны, а в основании лежит правильный многоугольник.
Основание высоты правильной пирамиды совпадает с центром ее основания, углы наклона боковых ребер к основанию равны, двугранные углы при основании равны, все боковые грани — равные равнобедренные треугольники.
Апофема – высота боковой грани правильной пирамиды, проведенная из её вершины к ребру основания.
8. Площадь боковой поверхности пирамиды равна сумме площадей ее боковых граней: (S_{бок}= S_1+ S_2+…+ S_n).
Площадь полной поверхности пирамиды равна сумме площади боковой поверхности и площади основания: (S_{полн} = S_{бок}+ S_{осн}).

9. Объем произвольной пирамиды равен произведению одной трети площади основания на высоту: (V=frac{1}{3} S_{осн}cdot h).

Сфера и шар
10. Сфера — это множество всех точек пространства, равноудаленных от данной точки, называемой центром сферы.
Радиусом сферы называется отрезок, соединяющий центр сферы с точкой на сфере, или длина этого отрезка.
Хордой сферы называется отрезок, соединяющий две точки на сфере.
Диаметр сферы — это хорда, которая проходит через центр сферы. Диаметр сферы равен двум радиусам сферы.
11. Площадь сферы находится по формуле: (S_{сф}=4πR^2).
12. Шаром называется часть пространства, ограниченная сферой, вместе с самой сферой и ее центром. Данная сфера называется поверхностью шара.
Сечение шара с радиусом (R) плоскостью, проходящей через центр шара, называется большим кругом шара. Радиус, хорда, диаметр шара те же, что и его сферы.
13. Объем шара находится по формуле (V_{шара}=frac{4}{3} πR^2).

Цилиндр
14. Цилиндром называется тело, полученное при вращении прямоугольника вокруг прямой, проходящей через одну из его сторон.
Прямая вращения называется осью цилиндра.
Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.Осевое сечение цилиндра — прямоугольник со сторонами (2r) и (l), где (r) — радиус основания цилиндра, (l) — его образующая.
Образующая цилиндра — отрезок (обозначается (l) или (L)), перпендикулярный основаниям цилиндра и соединяющий точку окружности верхнего основания с точкой окружности нижнего основания.
Высотой цилиндра называется расстояние между плоскостями оснований (обозначается (h) или (H)).
15. Площадь боковой поверхности цилиндра: (S_{бок}=2πrh); (S_{полн} = S_{бок}+ 2S_{осн}=2πrh+2πr^2).
16. Объем цилиндра (V_{цил}=S_{осн} h=πr^2 h).

Конус
17. Конусом называется тело, полученное при вращении прямоугольного треугольника вокруг прямой, проходящей через один из его катетов.
Прямая вращения называется осью конуса.
Сечение конуса, проходящее через ось, называется осевым сечением. Осевое сечение конуса — равнобедренный треугольник со стороной основания (2r) боковой стороной (l), где (r) — радиус основания конуса, (l) — его образующая.
Вершина осевого сечения является вершиной конуса.
Образующая конуса (обозначается (l) или (L)) — отрезок, соединяющий вершину конуса и точку окружности основания.
Высотой конуса называется расстояние от вершины конуса до плоскости основания (обозначается (h) или (H)). Высота конуса равна высоте осевого сечения, опущенной на основание.
18. Площадь боковой поверхности конуса: (S_{бок кон}=πrl), (S_{кон}=S_{бок}+S_{осн}=πrl+2πr^2).
19. Объем конуса: (V_{кон}=frac{1}{3}S_{осн}h=frac{1}{3}πr^2 h).