Математика — обязательный предмет на ЕГЭ. При этом, если он не нужен для поступления, вы можете сдать упрощенный экзамен. Он позволит проверить, насколько хорошо усвоена школьная программа. У медали есть и обратная сторона: если не перейти порог по базовой математике, то аттестат не получаешь.
Структура экзамена
По демоверсии 2021 года, серьезных изменений в структуре экзамена не предвидится. Количество заданий, система их оценивания и предоставленные формулы остались прежними.
На решение КИМ дается 3 часа.
Взять с собой на экзамен предложено можно простую линейку. Однако подготовка к ЕГЭ по математике, базовый уровень которой предполагает отсутствие номеров с развернутым ответом, не требует специального оборудования.
Навыки, необходимые для решения экзамена:
- выполнять вычисления и преобразования,
- решать уравнения и неравенства,
- выполнять действия с функциями,
- выполнять действия с геометрическими фигурами,
- строить и исследовать математические модели,
- решать простые текстовые задачи, в том числе на комбинаторику.
Количество заданий — 20.
Вторая часть отсутствует.
Оценка заданий ЕГЭ по базовой математике
Точная шкала перевода первичных баллов в оценку будет известна только после проверки экзаменационных работ. Подготовка к ЕГЭ по математике (базовый уровень в том числе) необходима, чтобы после экзамена не возникло неприятного сюрприза.
На данный момент нет оснований предполагать, что шкала перевода изменится в сравнении с прошлым годом:
- 0-6 баллов — «2»,
- 7-11 баллов — «3»,
- 12-16 баллов — «4»,
- 17-20 баллов — «5».
Все задания имеют одинаковый вес — один балл.
План подготовки к ЕГЭ по математике базового уровня
Когда в школе начинается подготовка к ЕГЭ по математике, базовый уровень экзамена часто игнорируют. Это может привести к досадным ошибкам. Чтобы их избежать, нужно разработать план подготовки.
Во-первых, стоит повторить основы, то есть математику 5-6 класса. Для этого можно использовать учебники, рекомендованные ФГОС, которые легко получить в школьной библиотеке или найти в интернете. От основ зависит успешная подготовка к ЕГЭ по математике: базовый уровень знаний обрести просто необходимо.
Во-вторых, прорешивайте задания каждого типа, не пропуская. Экзамен — всегда лотерея, поэтому никогда не предугадаешь, что тебе попадется. При решении некоторых заданий может оказаться бесполезна вся подготовка к ЕГЭ по математике: базовый уровень, несмотря на название, не предполагает, что все номера составлены без подводных камней.
В-третьих, не игнорируйте программу одиннадцатого класса. Структура экзамена редко совпадает с тем, что изучается в школе, но есть и исключения из правила. Когда начинается специализированная подготовка к ЕГЭ по математике, базовый уровень стереометрии, комбинаторики и некоторых других разделов, заложенный именно в одиннадцатом классе, позволяет успешно решать часть заданий КИМ.
Разбор заданий ЕГЭ по базовой математике
Когда в школах начинается подготовка к ЕГЭ по математике, базовый уровень предмета просто нарешивают, не пытаясь разобрать задания. Чтобы разобраться в решении номеров, следует помнить основные типы встречающихся задач:
- Текстовые задачи — сюда входят задачи на проценты, округление и смелкалку. Задачи на проценты решаются через умножение (процент принимается за десятичную дробь — 15% = 0,15). Задачи на округление решаются через деление с помощью логики. Задача №20 решается методом подбора.
- Вычисления и преобразования — блок заданий, проверяющих умение обращаться с дробями и степенями, а также с тригонометрическими и иррациональными выражениями. Предполагается, что когда начинается подготовка к ЕГЭ по математике, базовый уровень знаний и умение обращаться с формулами, данными в начале КИМ, у вас уже имеется. В заданиях важно уметь подставлять необходимые значения в формулы и производить вычисления по этим формулам, а также записывать числа в разных видах.
- Размеры и единицы измерения — чтобы решить задания этого раздела, необходимо знать порядок возрастания величин времени, длины, массы, объема, площади и уметь сопоставлять их с реальными объектами.
- Фигуры — для решения заданий данного блока нужно знать основные понятия (единицы измерения и части фигур), а также уметь сопоставлять их с реальными фигурами и использовать эти данные при решении задач. Например, когда идет подготовка к ЕГЭ по математике, базовый уровень владения стереометрией должен позволять определить объем фигур, площадь их боковых граней и тому подобное.
- Анализ информации — на экзамене информация представлена в виде графиков, диаграмм и текста. Для решения заданий нужно пронаблюдать за изменениями величин, а также найти наибольшую из них. Проверяется умение анализировать информацию или выбирать оптимальный вариант, опираясь на логическое мышление.
- Уравнения и неравенства — проверяется умение использовать данные формулы, выводить из них другие, а также отмечать значения на числовой прямой. Все это обеспечит хорошая подготовка к ЕГЭ по математике: базовый уровень заданий раздела предполагает, что они с большей вероятностью будут типовыми и без подводных камней, к которым привыкают выпускники, сдающие профиль, и учителя.
- Теория вероятностей (1 задание) — задание, решающееся с помощью определения нужной формулы комбинаторики (их всего три) и подставления в нее значений из задачи.
Материалы для подготовки к базе по математике ЕГЭ
Решение актуальных заданий экзамена — это почти гарантированно хорошая подготовка к ЕГЭ по математике: базовый уровень предмета также имеет демоверсию, кодификатор и спецификатор, опубликованные на сайте ФИПИ.
Найти дополнительный практический материал можно в открытом банке заданий также на сайте ФИПИ.
Также можно использовать дополнительные пособия:
- комплекс материалов для подготовки учащихся от ФИПИ,
- «Математика в схемах и таблицах» (И.В. Третьяк),
- типовые варианты от разработчиков (И.В. Ященко) и др.
Одно из самых важных дел одиннадцатиклассника — подготовка к ЕГЭ по математике, базовый уровень или профильный, при этом, не важно. От экзамена любого уровня сложности зависит получение аттестата и возможность поступить в вуз, поэтому откладывать подготовку на потом не стоит.
Обычно базовую математику выбирают ребята, у которых есть план: надо как можно скорее разделаться с бесполезным для поступления предметом и сосредоточиться на своем наборе вступительных. Из этой статьи вы узнаете, как сдать базовую математику максимально быстро и просто.
В этом материале мы сделаем акцент на простых номерах, которые принесут вам балл почти задаром! Они обозначены пометкой «Обязательно делать» — таких заданий 10. Как раз с запасом на ошибки, ведь минимум для сдачи базовой математики — 7 баллов.
Для тех, кто хочет получить выше тройки — это 12 баллов и выше, — мы дали рекомендации по еще 3 задачам. В сумме получается 13 номеров. Решите их все, и твердая четверка у вас в кармане.
Какие задания решать, чтобы сдать базовую математику
Задание 1: обязательно делать
Проверяется ваше умение разделить случаи, когда требуется округлить величину в большую сторону, а когда — в меньшую.

Если вы ходите в магазин с наличными, то сталкиваетесь с подобными задачами каждый день. Разделим 100 рублей на стоимость одной упаковки йогурта. Не забывайте приводить все величины к одной размерности:
100 : 14,6 = 6, 849…
Так сколько баночек йогурта вам продадут? На 7 штук денег не хватает, значит, округлить полученную величину надо до целого в меньшую сторону. Математическое правило округление в этой задаче не поможет.
Ответ: 6.

Если одна пачка рассчитана на 6 рулонов, то на 63 рулона:
63 : 6 = 10,5.
Но полпачки вам не продаст. Включаем логику: возьмем меньше — не хватит еще половины пачки на три последних рулона. Значит, округлить надо в большую сторону, взять клей с небольшим запасом. Математическое правило округления снова игнорируем.
Ответ: 11.
Задание 2: обязательно делать
Это задача на здравый смысл. Нужно соотнести величины с их возможными значениями.

Вряд ли грузовой автомобиль может весить как 3 шоколадки (300 г), а взрослый человек — 8 т.
Давайте вместе подберем значения.
- Взрослый человек обычно весит от 50 до 100 кг — что из этого подходит? Конечно, 65 кг.
- Грузовой автомобиль достаточно большой и тяжелый, скорее всего, он весит несколько тонн. Нам подходит 8 т.
- Книга обычно не такая большая и весит до 1 кг. Из оставшегося подойдет 300 г.
- А пуговка совсем маленькая. Значит, берем самый легкий вес — 5 г.
Ответ:
Главное — внимательно перенести ответы в бланк: 3142.
Задание 3: обязательно делать
Задание на работу с графиком, диаграммой или таблицей. Вооружайтесь карандашом, читайте условие с предельной внимательностью и безжалостно отмечайте нужные по условию значения на изображении в КИМ. Вы и представить не можете, сколько выпускников теряет тут баллы по невнимательности.
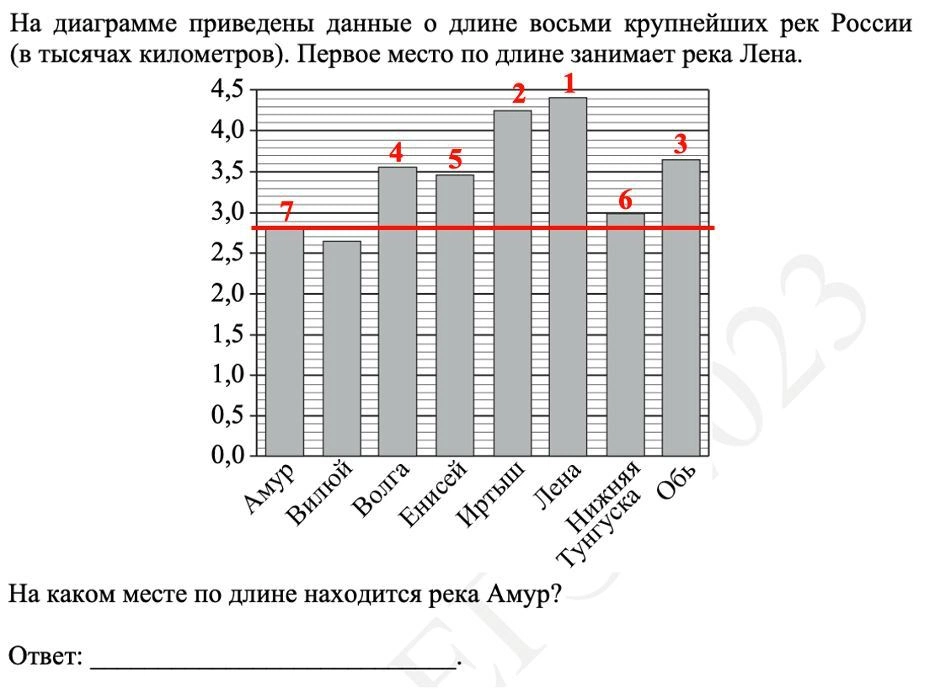
Мы ярко отметили уровень, соответствующий Амуру, в итоге посчитать все более длинные реки стало проще простого. У вас на экзамене будет так же наглядно!
Ответ: 7.
Задание 4: обязательно делать
Задание проверяет навык работы с формулами. Алгоритм решения напоминает решение задачек на уроке по физике:
- Выписываем формулу из условия.
- Определяем, что нужно найти: единственную букву, значение которой не дано.
- Выражаем искомую величину.
- Подставляем значения из условия в формулу.
- Ищем неизвестное.
Самое трудное тут — правильно выразить искомую величину. Для этого повторяем порядок выполнения арифметических операций, свойства умножения, тренируемся перекидывать через равно множители и слагаемые.
И да, в базе эта задача проста настолько, что даже перекидывать ничего не придется. Нужная величина уже будет слева от равно.
Задание 5: обязательно делать
Простая задача на определение вероятности, которая поможет вам точно сдать базовую математику.
Решаем с помощью формулы:
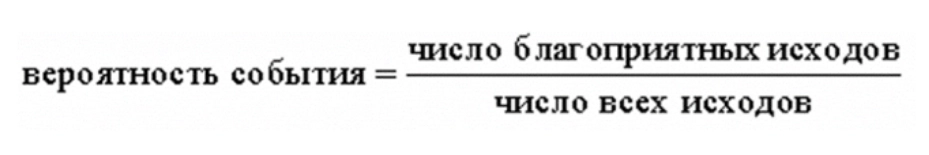

Внимательно читайте вопрос: спрашивают вероятность купить исправную лампочку. Если из ста 3 неисправны, значит, остальные в порядке и подойдет любая из оставшихся 97. Это и есть наши благоприятные исходы из формулы.
97 : 100 = 0,97.
Ответ: 0,97.
Будьте внимательны: иногда в задаче есть указание к округлению. Значит, ответ у вас выйдет некрасивый, в виде бесконечной десятичной дроби, которую вы округлите до нужного разряда.
Еще один подвох: формулировка с предлогом «на». К примеру, «На 100 лампочек 3 неисправны. Найдите вероятность купить неисправную». Подходящие исходы тут даны явно: 3 неисправные лампочки. А вот число всех исходов спрятано, и найти его будет нужно сложением исправных и неисправных лампочек: 100 + 3 = 103.
Задание 6: обязательно делать
Задание проверяет навык чтения информации из таблицы и подбора подходящего по условию варианта.
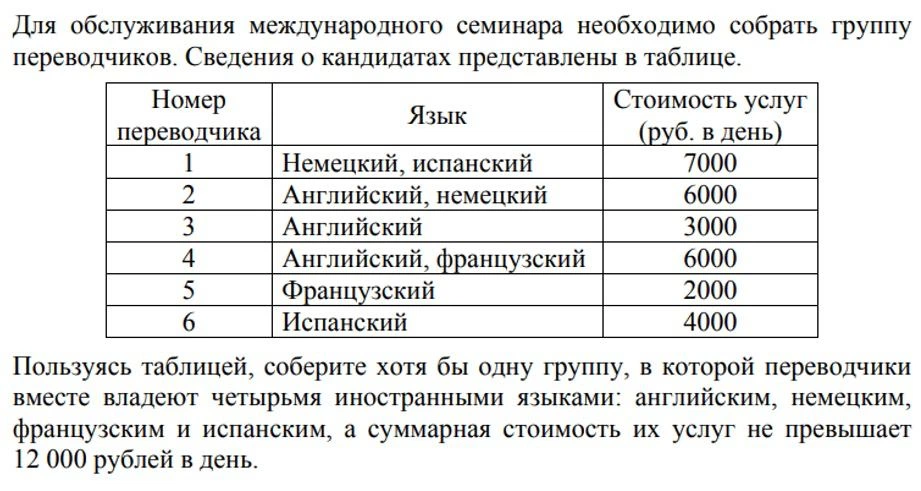
Например, вы нашли вариант позвать первого, третьего и пятого переводчиков. Получите весь набор языков как раз за 12 тысяч. Но обратите внимание, что это решение далеко не единственное.
Ответ: 135.
Задание 7
Мы не выделяем это задание в обязательные, так как для его выполнения понадобится навык анализа поведения функции по графику. Но, как его решать, сейчас коротко расскажем.
Запомним: точка максимума будет на «горке», точка минимума — в «ямке». Функция убывает, если идет вниз слева направо. Возрастает, если идет вверх слева направо.
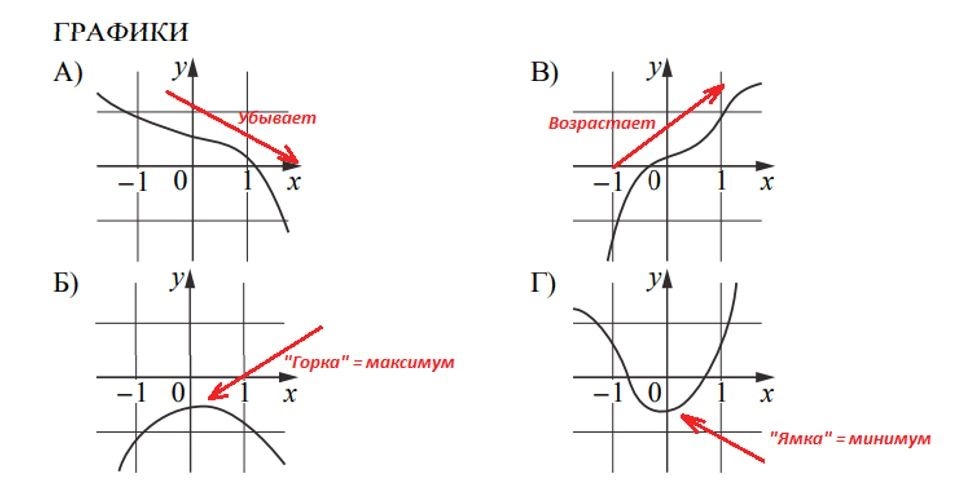
Если не повезет, то придется вспомнить азы теории по производной.
Здесь все дело в касательных. Нужно внимательно к ним присмотреться. Если касательная к графику возрастает, то значение производной будет положительное, если убывает — отрицательное. Производная будет тем больше по величине (модулю), чем быстрее возрастает или убывает касательная.
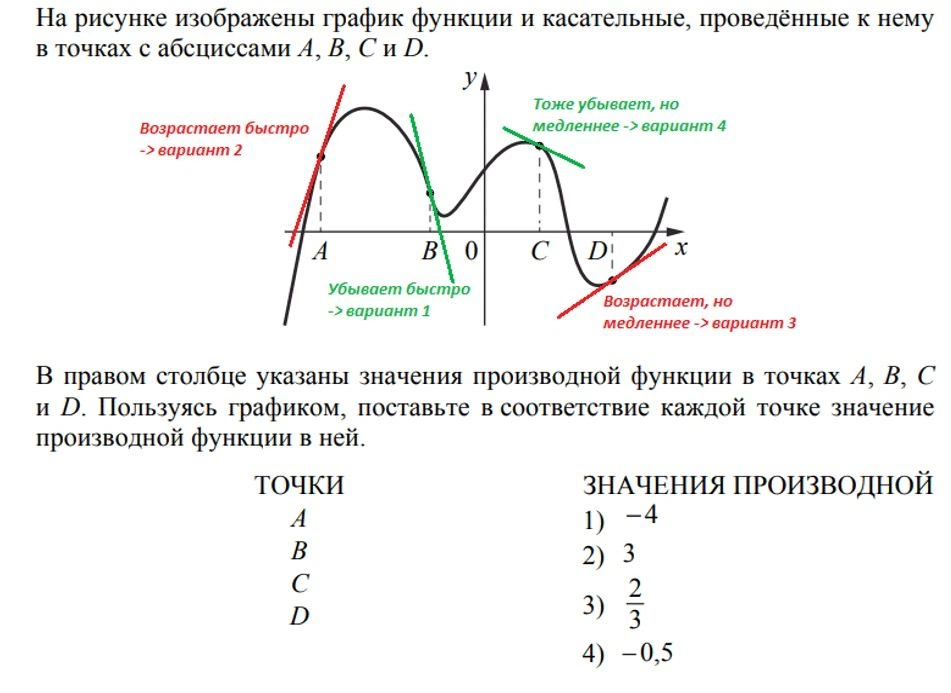
Ответ: 2143.
Задание 8: обязательно делать
Задача проверяет умение делать логичные выводы из утверждения. Иногда попадаются совсем простые задания, к таким даже дополнительно готовиться не надо.

Все, что от вас требуется, — схематично изобразить на черновике ясень, рябину и осину, указать известную разницу в высоте и внимательно сопоставить картинку с утверждениями.
Важно: не додумывайте дополнительные условия, не указанные в тексте задачи. Учитесь читать строго то, что написано.
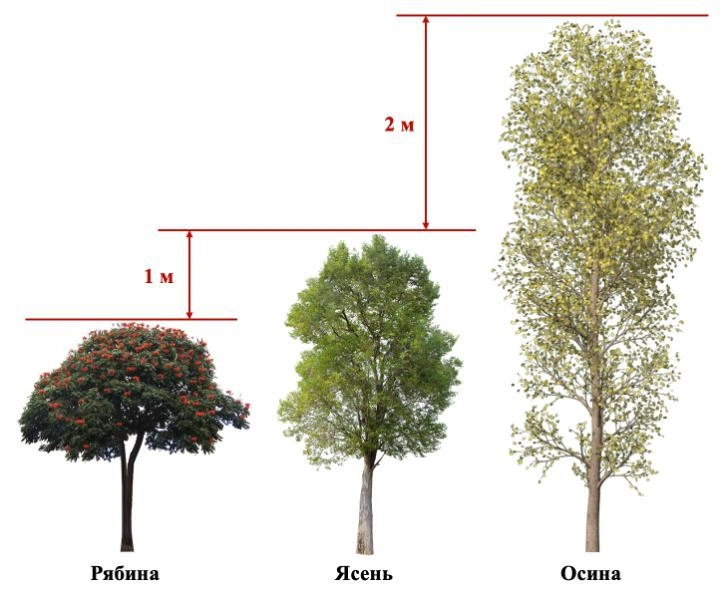
Исходя из рисунка выше получаем, что верны только утверждения 1 и 4.
Ответ: 14.
А бывают случаи, когда с визуализацией задачки придется постараться.

Тут иллюстрация не так очевидна, но нам помогут круги Эйлера. Этот инструмент позволяет наглядно изобразить множество объектов. В данном случае — школьников. Давайте прикинем, как ребята могут распределиться по кружкам.
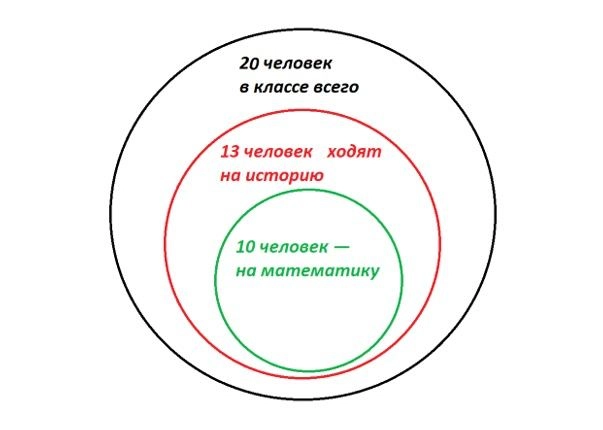
Например, так. Тут из 20 человек на кружки в итоге ходят 13. Причем 10 из них очень активны и выбрали сразу два предмета. Трое ограничились только историей.
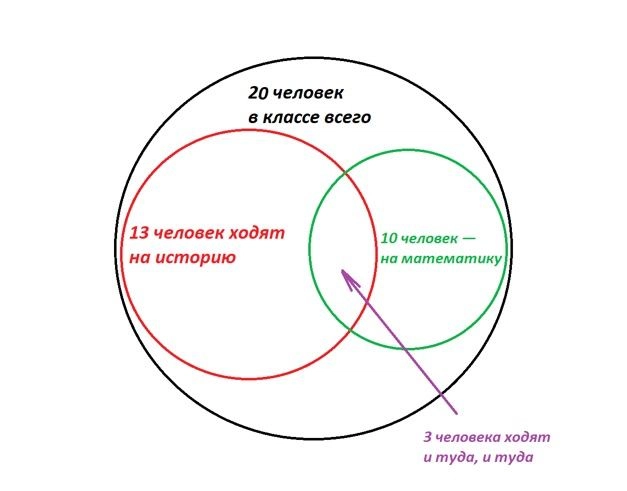
Или вот так. Если ребята задались целью по максимуму не пересекаться на дополнительных занятиях, то… У них не получится, и как минимум трое запишутся сразу на оба факультатива.
Конечно, возможны еще промежуточные варианты, но мы нарисовали два крайних. Теперь попробуем ответить на вопросы.
- Смотрим на первую картинку. Даже если все ребята будут очень стараться посетить оба кружка, они ограничены условиями задачи и максимум на оба попадут 10 человек из 20. Нет.
- Тут надо рассмотреть другую крайность, которую мы изобразили на второй картинке. Как бы ребята ни старались не встречаться на кружках, хотя бы трое попадут на оба сразу. Да.
- Уж точно неверно. На обеих наших картинках есть ребята, которые ходят на историю, но не ходят на математику. Нет.
- Смотрим на первую картинку. Оба кружка могут посещать максимум 10 человек.
Ответ: 24.
Так что для решения иногда мало логики — понадобится еще немного воображения. Потренируйтесь, и ваши шансы получить балл увеличатся.
Задание 14: обязательно делать
Задание проверяет базовые навыки счета, которым учат в 5–6-м классах. Чтобы получить балл и сдать базовую математику, надо:
- уметь выполнять арифметические действия с обыкновенными и десятичными дробями;
- правильно расставлять порядок действий;
- быть предельно внимательными.
Уделите пару вечеров отработке алгоритмов сложения, вычитания, умножения и деления обыкновенных и десятичных дробей, и это задание у вас в кармане.
Задание 15
Составители экзамена проверяют ваш навык работы с процентами и единицами отношения. Такие задачи бывают четырех типов.
Тип 1. Найти часть от числа
Часть может быть выражена в процентах или сразу в виде дроби. Например, придется искать треть от чего-то.
Рассмотрим на примере реальной задачи из экзамена:

Прочувствуйте специфику задачи: нам известно целое — вся зарплата до вычета налога. А работать мы будем с кусочком — 13 процентами. Сколько это в рублях, нам еще предстоит узнать.
Чтобы ответить на вопрос задачи, нужно сделать три шага:
1. Перевести процент в десятичную дробь.
Для этого всегда надо количество процентов поделить на 100.
13 : 100 = 0,13.
2. Найти, сколько это от зарплаты в рублях.
Запоминаем главное правило для этого типа задач: чтобы найти дробь от числа, надо число умножить на эту дробь.
12 500 ∙ 0,13 = 1 625 (руб.) — налог, который удержат с зарплаты Ивана Кузьмича.
3. Ответить на вопрос задачи.
У нас просили зарплату после вычета налога, а не сам налог.
12 500 – 1625 = 10 875 (руб.).
Ответ: 10 875.
Будьте внимательны: многие совершают ошибку именно на последнем шаге!
Тип 2. Найти число по его части

Прочувствуйте разницу с прошлой задачей: тут 124 — и есть 25%, то есть одна и та же величина выражена в процентах и в абсолютных величинах, в данном случае — в учениках. Просят узнать целое — 100%.
1. Переводим процент в десятичную дробь:
25 : 100 = 0,25.
2. Находим, сколько учеников всего.
Правило для этого типа задач: чтобы найти целое, надо часть разделить на дробь.
124 : 0,25 = 496 (уч.) — всего.
Ответ: 496.
Тип 3. Найти, сколько процентов часть составляет от целого

Особенность подобных заданий: не дано процентов, есть только абсолютные величины. В данном случае — стоимость футболки в рублях.
1. Находим, какую долю новая цена составляет от первоначальной.
Запоминаем правило: чтобы найти, какую долю часть составляет от целого, надо часть разделить на целое.
680 : 800 = 0,85.
2. Переводим долю в процент.
В прошлых задачах мы уже дважды выполнили обратное действие. В этот раз сделаем наоборот: умножим полученную дробь на 100.
0,85 ∙ 100 = 85% — столько процентов новая цена составляет от старой.
3. Отвечаем на вопрос задачи.
Нас спросили, на сколько процентов цена снизилась, что стала 85% от первоначальной. Конечно, изначально она была 100%. Итого:
100 – 85 = 15%.
Ответ: 15%.
Тип 4. Задачи на соотношение

Если перефразировать условие, то за первого кандидата проголосовали 3 части избирателей, а за второго — 2 части. Особенность этих частей в том, что они одинаковые по величине.
Если одна будет состоять из 10 человек, то за первого кандидата будет 30, а за второго — 20.
1. Считаем общее количество частей:
3 + 2 = 5.
2. Узнаем, сколько голосов составляет одна такая часть.
Тут речь о процентах проголосовавших. Сколько всего проголосовало? Конечно, 100%! Значит, каждая из пяти частей «весит»
100 : 5 = 20%.
3. Отвечаем на вопрос задачи.
За проигравшего проголосовало меньше частей избирателей. В нашем случае 2.
20 ∙ 2 = 40%.
Ответ: 40%.
Решение этих задач удобнее всего оформить табличкой:

1 часть = 100% : 5 = 20%.
Если рассчитываете решать текстовую задачу, включите здравый смысл. Ответ всегда можно проверить на адекватность благодаря обычной логике.
Задание 16: обязательно делать
Задание на решение выражения. На самом деле оно проверяет знание теории, так как в этом задании вам могут встретиться:
- выражения со степенями,
- иррациональные выражения,
- логарифмические выражения,
- тригонометрические выражения.
Ваша задача, соответственно, — знать:
- свойства степеней

- свойства корней

- свойства логарифмов
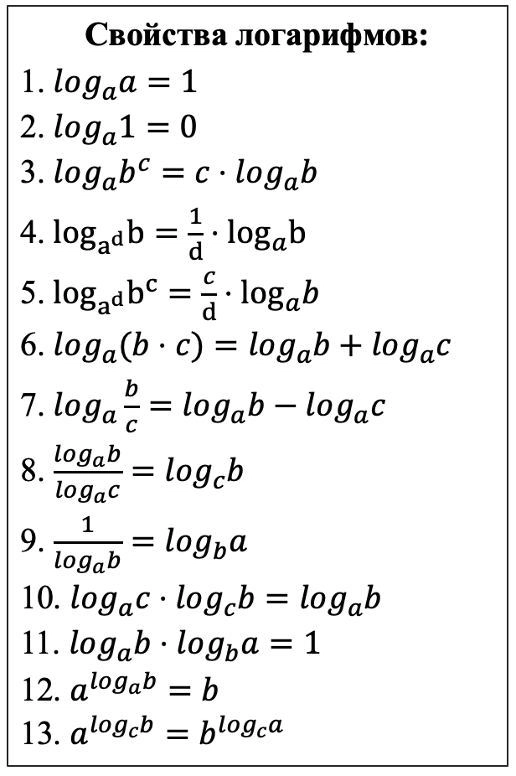
- формулы тригонометрии
Вы можете подробно ознакомиться с ними и научиться выводить в этой статье.
Обратите внимание: нужная теория будет в справочных материалах на экзамене, но это не поможет, если вы не научитесь применять ее для решения заданий. Практика обязательна!
Задание 17: обязательно делать
В номере с уравнениями вам не встретятся тригонометрические. Зато вы точно увидите там:
- линейные уравнения
Раскрываем скобки, если они есть, слагаемые с х переносим в одну сторону от равно, без х — в другую. Приводим подобные и решаем простейшее уравнение.
- квадратные уравнения
Бывают полные и неполные, всего надо повторить три алгоритма решения! А формула дискриминанта еще и в справочных материалах есть.
- иррациональные уравнения
Это те, что с корнем. Чтобы избавиться от корня, возводим обе части уравнения в квадрат и решаем получившееся уравнение. Есть нюансы с областью допустимых значений: подставьте полученные корни в исходное уравнение и проверьте, выполняется ли равенство. Если нет, то подставленное значение решением не будет.
- показательные уравнения
Ваша задача — с помощью формул свойств степеней привести уравнение к виду, когда слева и справа от равно в основании степени будет одно и то же число. После приравниваем показатели и решаем. Вот так:

Ответ: 7.
- логарифмические уравнения
С помощью формул свойств логарифмов приводим уравнение к виду, когда слева и справа от равно будет логарифм с одинаковым основанием. После приравниваем выражения под логарифмом и решаем.

Ответ: 67.
Прелесть уравнений в том, что ответ всегда можно проверить подстановкой вместо x в уравнение. Не забывайте проверять, ведь это возможность убедиться на 100%, что вы не упустите заветный балл.
Задание 19
Если хотите сдать базовую математику и решить номер 19, надо ознакомиться со свойствами целых чисел и признаками делимости. Иногда решение можно найти даже подбором! Попробуйте — времени на базовом ЕГЭ вам точно хватит.
Для начала нужно запомнить все признаки делимости.

А теперь посмотрим на типичное задание 19.

Тут помогут признаки делимости. Отдельного признака для 12 нет, потому нам надо разложить его на множители, признаки делимости для которых есть.
- На 3: сумма всех цифр делится на 3.
- На 4: число, образованное последними двумя цифрами, делится на 4.
Начнем с признака для 4. Пока что наше число заканчивается на 13 и на 4 не делится. Попробуем вычеркнуть последнюю цифру, и число будет заканчиваться на 61. Тоже не подходит. Вычеркнем еще одну: теперь на конце 76… Вот оно! От изначального числа осталось 751576, две цифры уже вычеркнули, осталось убрать одну.
Теперь проверим признак для 3: 7 + 5 + 1 + 5 + 7 + 6 = 31. Какое ближайшее число разделится на 3? Конечно, 30. Если мы вычеркнем единичку, все сойдется.
Ответ: 75576.
Другой вариант задания:

А задание такого типа можно попытаться подобрать, расположений не слишком много. Мы все же постараемся порассуждать, чтобы уменьшить количество возможных вариантов.
Чтобы число делилось на 10, оно должно заканчиваться на 0. Например, это получится, если сложить 7 + □7 + □□6. Уже немного легче. Остальное просто подберем. Под условие задачи подойдет 7 + 27 + 356 = 390.
Ответ: 390.
Какие задания мы не разобрали и почему
Теперь вы знаете, как сдать базовую математику, решив всего семь заданий. Но некоторые номера базового ЕГЭ включают слишком большое разнообразие прототипов, и методы их решения не ограничиваются парой простых алгоритмов.
Например, в эту группу относятся все задания по геометрии: с 9 по 13. Чтобы решать геометрию, мало знать основные фигуры и формулы. Необходим навык, который вырабатывается только практикой. Однако у нас есть статья про окружность — в ней вы найдете много полезной информации.
Задание 18 обычно, хотя и не всегда, содержит неравенство.

Это объемный блок теории, которую тоже необходимо подкреплять практикой. Но, может, вам повезет и попадется задачка на расположение значений на числовой прямой.

Тут достаточно примерно прикинуть значения и аккуратно внести ответы в бланк. Ясно, что 7/3 больше 2, но меньше 3. Корень из 26 равен 5 с копейками, а степень –1 из 3/5 сделает 5/3, или чуть больше 1,5. Подобные задания надо пытаться делать обязательно!
Задание 20. С этим заданием ученики знакомы еще с 9-го класса, так как оно было под номером 21 на ОГЭ. Это текстовая задача:
- на производительность,
- движение (по прямой, воде, окружности),
- сплавы и смеси,
- проценты (пиджаки, рубашки, брюки; бюджет семьи; акции, которые растут и падают),
- прогрессии.
В задании 21 на ОГЭ не было прогрессий, но они были в первой части на ОГЭ, так что ничего нового.
Задание 21. Здесь попадаются разные типы неочевидных задач на логику — чем-то они даже похожи на олимпиадные. Решение каждой нужно рассматривать отдельно и подробно. Если хотите прочитать о том, какие задачи бывают в 21-м номере, пишите в комментариях, и Maximum поделится своими методами решения!
Не знаете, какой вуз выбрать? Воспользуйтесь бесплатной консультацией в нашем центре. Что это такое? Все просто: вы расскажете о себе и о своих интересах. А специалист посоветует, на какие специальности обратить внимание, в какой вуз поступать, какие ЕГЭ сдавать. Так вы сэкономите время на подготовку и сможете выбрать образование, которое точно окажется для вас интересным и полезным!
Муниципальное общеобразовательное учреждение
«Смирновская средняя школа»
План подготовки к ЕГЭ
по математике
11 класс
(базовый уровень)
Учитель: Киселева Г.А.
2016 — 2017 учебный год.
План подготовки к ЕГЭ по математике в 2016-2017 уч.году
|
Тема занятия |
Дата проведения |
Примечания |
|
|
Планир. |
Фактич. |
||
|
Структура и содержание КИМ ЕГЭ по математике 2017 г |
07.09. |
||
|
ДЕМО версия уровень базовый уровень |
14.09. |
||
|
Практический расчет, оценка и прикидка. |
|||
|
Задачи с целочисленным ответом. |
21.09. |
||
|
Диагностическая работа №1. |
23.09. |
||
|
Задачи на проценты. |
28.09. |
||
|
Выбор наилучшего вариана. |
05.10. |
||
|
Вычисление значения выражения. |
|||
|
Действия с дробями. |
12.10 |
||
|
Действия с числами, записанными в стандартном виде. |
19.10. |
||
|
Вычисление степеней. |
26.10. |
||
|
Диагностическая работа 2. |
28.10. |
||
|
Иррациональные выражения. |
02.11. |
||
|
Логарифмические выражения. |
16.11. |
||
|
Тригонометрические выражения. |
23.11. |
||
|
Чтение графиков и диаграмм. |
|||
|
Чтение графиков и диаграмм. |
30.11. |
||
|
Площади фигур. |
|||
|
Вычисление площадей фигур. |
7.12. |
||
|
Решение уравнений. |
|||
|
Линейные и дробно- рациональные уравнения. |
14.12. |
||
|
Диагностическая работа №3. |
16.12. |
||
|
Иррациональные уравнения. |
21.12. |
||
|
Степенные уравнения. |
28.12 |
||
|
Логарифмические уравнения. |
18.01. |
||
|
Основные задачи планиметрии. |
|||
|
Длины. Углы. |
25.01. |
||
|
Диагностическая работа №4. |
27.01. |
||
|
Окружность. |
01.02. |
||
|
Свойства треугольника. |
08.02. |
||
|
Соответствие величин. |
|||
|
Задачи на соответствие величин. |
15.02. |
||
|
Координатная прямая. |
|||
|
Расположение на координатной прямой. |
22.02. |
||
|
Неравенства. |
|||
|
Линейные и дробно- рациональные неравенства. |
01.03. |
||
|
Прикладные задачи. |
|||
|
Задачи на движение. |
15.03. |
||
|
Диагностическая работа №5. |
17.03. |
||
|
Задачи на работу. |
22.03. |
||
|
Пробный экзамен по математике. |
По графику |
||
|
Применение производной для исследования функции. |
05.04. |
||
|
Чтение графика производной функции. |
12.04. |
||
|
Основные задачи стереометрии. |
|||
|
Параллелепипед. Призма. Пирамида. |
19.04. |
||
|
Цилиндр. Конус. Шар. |
26.04. |
||
|
Задачи повышенного уровня сложности. |
|||
|
Комбинации цифр. |
03.05 |
||
|
Перебор вариантов. |
10.05. |
||
|
Логические задачи. |
17.05. |
||
|
Итоговая контрольная работа. |
24.05. |
График проведения диагностических работ по математике
11 класс ( базовый уровень)
2016-2017 уч.год.
|
№1 |
№2 |
№3 |
№4 |
№5 |
Пробные экзамены |
Итоговая работа. |
|
23.09. |
28.10. |
16.12. |
27.01. |
17.03. |
Апрель |
Май |
Учитель: Киселева Г.А.
Муниципальное учреждение «___________________________________»
Муниципальное бюджетное
общеобразовательное учреждение
«___________________________________________________________»
(МБОУ
«_________________»)
Муниципальни учреждени «_________________________»
Муниципальни
бюджетни юкъарадешаран учреждени
«_____________________________________________________»
(МБЮУ «___________________»)
________________________________________________________________________________
|
ОБСУЖДЕНО педагогическим МБОУ «________________» Приказ № ___ от |
УТВЕРЖДЕНО: директор МБОУ «______________» (протокол № __ от |
Рабочая программа
консультаций по математике:
ПОДГОТОВКА К ЕГЭ ПО МАТЕМАТИКЕ
БАЗОВОГО УРОВНЯ 2022
Учитель: ФИО
Класс: 11
Всего часов в год: 34
Всего часов в неделю:
1
г. __________
2021 г.
Актуальность. Единый
государственный экзамен в настоящее время совмещает два экзамена — выпускной за среднюю школу и вступительный в высшие учебные заведения
и имеет два уровня: базовый и профильный. Поэтому в рамках ЕГЭ осуществляется проверка овладения материалом курса алгебры и начал анализа, геометрии, усвоение которых должно
проверяться на выпускном школьном экзамене,
а также материалом некоторых тем курса алгебры основной школы и
геометрии основной и средней школы, которые традиционно даются на вступительных экзаменах в вузы. Поэтому успешная сдача к
экзамену позволит ученику поступить в ВУЗ.
Цель и задачи программы:
Обучающая цель: создание условий для систематизации
полученных знаний, овладение приемами и методами решения задач, подготовка к
итоговой аттестации в форме ЕГЭ.
Задачи:
·
повторить и
закрепить знания, умения и навыки, полученные в 5- 9,10 классах;
·
развить
способность самоконтроля: времени, поиска ошибок в планируемых проблемных
заданиях;
·
сформировать
спокойное, уравновешенное отношение к экзамену;
·
вести
планомерную подготовку к экзамену;
·
знакомство с
новыми методами и приемами решения задач;
·
формирование
специальных умений и навыков обучающихся: алгоритмических умений и
вычислительных навыков;
·
освоение
нестандартных приемов и методов решения задач;
·
формирование умений применять полученные знания при решении «нетипичных», нестандартных
задач.
·
закрепить
математические знания, которые пригодятся в обычной жизни и при продолжении
образования.
Развивающая цель: развитие у обучающихся аналитического и
логического мышления при проектировании решения задачи.
Задачи:
·
развитие
мышление обучающихся через использование активных методов изучения;
·
создание
условий для творческого развития и самореализации обучающихся через решение
нестандартных задач;
·
развитие
самостоятельности мышления;
·
развитие
поисковых, исследовательских навыков, творческих способностей.
Воспитательная цель: воспитание качеств личности —
самостоятельность, целеустремленность, конкурентоспособность.
Задачи:
·
воспитание
нравственно-волевых качеств обучающихся:
·
воспитание
чувства товарищества, взаимопомощи, создание дружного коллектива;
·
создание
условий для формирования коммуникативной культуры обучающихся;
·
совершенствование
способностей к совместной деятельности со сверстниками, педагогом.
Отличительные особенности программы и
используемые в ней ключевые понятия:
·
Программа
консультаций по математике «Подготовка к ЕГЭ по математике» рассчитана на всех
обучающихся 11 класса.
·
Программа
консультаций «Подготовка к ЕГЭ по математике», построена на деятельности
обучающихся, а именно на совместной учебно-познавательной, деятельности,
имеющая общую цель, согласованные методы, способы деятельности.
Сроки и этапы реализации программы
Данная программа предполагает одногодичное обучение,
рассчитана на учащихся 11 класса. Занятия проводятся 1 раз в неделю, 34 часа в
год. Программа разработана с учетом возрастных и психологических особенностей
детей. В содержании программы предусмотрен дифференцированный подход к
обучающимся, поэтому могут заниматься дети с различным уровнем развития.
В предлагаемой программе предусмотрена
серия заданий для подготовки старшеклассников к ЕГЭ базового уровня. Данный курс
дает учащимся возможность познакомиться с нестандартными способами
решения математических задач, способствует формированию и развитию таких качеств,
как интеллектуальная восприимчивость и способность к усвоению новой информации,
гибкость и независимость логического мышления.
Раздел 1. Программа рассчитана
на достижение требований, с учетом изученного материала, математической
подготовки учащихся (Требования (умения), проверяемые заданиями экзаменационной
работы):
Личностных:
1. Готовность и способность
обучающихся к саморазвитию и самообразованию, выбору дальнейшего образования
на базе ориентировки в мире профессий и профессиональных предпочтений;
2. Готовность и способность к
самостоятельной информационно-познавательной деятельности, включая умение
ориентироваться в различных источниках информации, критически оценивать и
интерпретировать информацию, получаемую из различных источников;
3. Развитие логического мышления,
пространственного воображения, критичности мышления на уровне, необходимом для
будущей профессиональной деятельности, а также для последующего обучения в
высшей школе;
4. Сформированность коммуникативной
компетентности в общении и сотрудничестве со сверстниками, взрослыми и младшими
в образовательной, общественно – полезной, учебно-исследовательской, творческой
и других видах деятельности.
Метапредметных: освоение способов деятельности
познавательные:
1. Овладение навыками познавательной,
учебно – исследовательской и проектной деятельности, навыками разрешения
проблем; способность и готовность к самостоятельному поиску методов решения
практических задач, применению различных методов познания;
2. Самостоятельное создание алгоритмов
познавательной деятельности для решения задач творческого и поискового
характера;
3. Творческое решение учебных и
практических задач: умение мотивированно отказаться от образца, искать
оригинальное решение.
Коммуникативные:
1. Умение развёрнуто обосновывать
суждения, давать определения, приводить доказательства;
2. Адекватное восприятие языка
средств массовой информации;
3. Владение основными видами
публичных выступлений (высказывание, монолог, дискуссия, полемика), следование
этическим нормам и правилам ведения диалога (диспута);
4. Умение организовывать учебное
сотрудничество и совместную деятельность с учителем и сверстниками: определять
цели, распределять роли и функции участников, общие способы работы;
5. Использование мультимедийных
ресурсов и компьютерных технологий для обработки, передачи, систематизации
информации, создание базы данных, презентации результатов познавательной и
практической деятельности.
Регулятивные:
1. Умение самостоятельно планировать
альтернативные пути достижения целей, осознанно выбирать наиболее эффективные
способы решения учебных и познавательных задач;
2. Понимание ценности образования
как средства развития культуры личности;
3. Объективное оценивание своих
учебных достижений, поведения, черт своей личности;
4. Умение соотносить приложенные
усилия с полученными результатами своей деятельности;
5. Конструктивное восприятие иных
мнений и идей, учёт индивидуальности партнёров по деятельности;
6. Умение ориентироваться в
социально-политических и экономических событиях, оценивать их последствия;
7. Осуществление осознанного выбора
путей продолжения образования или будущей профессиональной деятельности.
Предметных:
1. Уметь выполнять вычисления и
преобразования
1.1. Выполнять арифметические действия, сочетая устные и письменные
приемы; находить значения корня натуральной степени, степени с рациональным
показателем, логарифма;
1.2. Вычислять значения числовых и буквенных выражений, осуществляя
необходимые подстановки и преобразования;
1.3. Проводить по известным формулам и правилам
преобразования буквенных выражений, включающих степени, радикалы, логарифмы и
тригонометрические функции;
2. Уметь решать уравнения и неравенства:
2.1. Решать рациональные, иррациональные, показательные, тригонометрические
и логарифмические уравнения, их системы;
2.2. Решать уравнения, простейшие системы уравнений,
используя свойства функций и их графиков; использовать для приближенного
решения уравнений и неравенств, графический метод;
2.3. Решать рациональные, показательные и логарифмические неравенства,
их системы.
3. Уметь выполнять действия с функциями
3.1. Определять значение функции по значению аргумента при различных
способах задания функции; описывать по графику поведение и свойства функции,
находить по графику функции наибольшее и наименьшее значения; строить графики изученных
функций;
3.2. Вычислять производные и первообразные элементарных функций;
3.3. Исследовать в простейших случаях функции на
монотонность, находить наибольшее и наименьшее значения функции;
4. Уметь выполнять действия с
геометрическими фигурами и координатами
4.1. Решать планиметрические задачи на нахождение геометрических
величин (длин, углов, площадей);
4.2. Решать простейшие стереометрические задачи на
нахождение геометрических величин (длин, углов, площадей, объёмов); использовать
при решении стереометрических задач планиметрические факты и методы;
5. Уметь строить и исследовать
простейшие математические модели:
5.1. Моделировать реальные ситуации на языке алгебры,
составлять уравнения и неравенства по условию задачи; исследовать построенные
модели с использованием аппарата алгебры;
5.2. Моделировать реальные ситуации на языке геометрии, исследовать
построенные модели с использованием геометрических понятий и теорем, аппарата
алгебры; решать практические задачи, связанные с нахождением геометрических величин;
5.3. Проводить доказательные рассуждения при решении задач,
оценивать логическую правильность рассуждений, распознавать логически
некорректные рассуждения;
5.4. Моделировать реальные ситуации на языке теории вероятностей
и статистики, вычислять в простейших случаях вероятности событий.
6. Уметь использовать приобретенные
знания и умения в практической деятельности и повседневной жизни:
6.1. Анализировать реальные числовые данные, информацию статистического
характера; осуществлять практические расчеты по формулам; пользоваться оценкой
и прикидкой при практических расчетах;
6.2. Описывать с помощью функций различные реальные зависимости
между величинами и интерпретировать их графики; извлекать информацию,
представленную в таблицах, на диаграммах, графиках;
6.3. Решать прикладные задачи, в том числе
социально-экономического и физического характера, на наибольшие и наименьшие
значения, на нахождение скорости и ускорения.
Раздел 2. Содержание учебного
курса.
Введение. Структура вариантов КИМ 2022.
Спецификация. Типы заданий.
Алгебра. Вычисления. Действия с дробями. (Задание №
1 БУ). Простейшие текстовые задачи (Задание № 2 БУ). Размеры и единицы измерения (Задание № 3 БУ). Простейшие текстовые задачи (Задание № 6 БУ). Вычисления и преобразования (Задание № 7 БУ). Преобразования выражений (Задание № 8 БУ). Задачи на смекалку (Задание № 21 БУ). Текстовые задачи (Задание № 20 БУ). Выбор оптимального варианта (Задание № 12 БУ). Числа и их свойства (Задание № 19 БУ)
Уравнения и неравенства. Простейшие уравнения (Задание № 9
БУ). Неравенства (Задание № 17 БУ). Анализ утверждений (Задание № 18 БУ).
Функции. Чтение графиков и диаграмм (Задание № 4
БУ).
Начала математического анализа. Анализ графиков и диаграмм
(Задание № 14 БУ).
Геометрия. Задачи на квадратной решетке (Задание № 5
БУ). Прикладная геометрия (Задание № 10 БУ). Стереометрия (Задание № 13 БУ). Планиметрия (Задание № 15 БУ). Задачи по стереометрии (Задание № 16 БУ).
Элементы комбинаторики, статистики и
теории вероятности. Начала теории вероятностей (Задание № 11 БУ).
Диагностики, повторение. Диагностика (1 и 2 задания КИМ ЕГЭ
МБУ). Пробный экзамен (ЕГЭ) по математике
базового уровня № 1. Диагностика (3-5 задания КИМ ЕГЭ МБУ). Диагностика (6-8 задания КИМ ЕГЭ МБУ). Диагностика (9-11 задания КИМ ЕГЭ МБУ). Пробный экзамен (ЕГЭ) по математике базового уровня № 2.
Диагностика (15-17 задания КИМ ЕГЭ МБУ). Диагностика
(12-14 задания КИМ ЕГЭ МБУ). Пробный экзамен (ЕГЭ) по
математике базового уровня № 3. Диагностика (18-21 задания КИМ ЕГЭ
МБУ). Пробный экзамен (ЕГЭ) по математике
базового уровня № 4. Анализ допущенных ошибок. Решение вариантов ЕГЭ.
Раздел 3. Тематическое
планирование.
|
№ |
Раздел |
Количество часов |
|
Введение |
1 |
|
|
1 |
Алгебра |
10 |
|
2 |
Уравнения и неравенства |
3 |
|
3 |
Функции |
1 |
|
4 |
Начала математического анализа |
1 |
|
5 |
Геометрия |
5 |
|
6 |
Элементы |
1 |
|
Диагностики, |
12 |
|
|
Всего |
34 |
Подготовка к ЕГЭ по математике
Из каких частей состоит ЕГЭ по математике в 2023 году
Математика — один из двух обязательных предметов на ЕГЭ. Но, в отличие от русского языка, эта дисциплина предлагает 2 уровня сложности: профильный и базовый. Какий именно вариант выбрать, зависит от вашей цели. Если вуз, в который вы хотите поступить, требует профильного уровня, нужно сдавать его. Обычно это касается технических специальностей.
Для получения аттестата выпускникам школ хватит и базового. Но финальное решение за вами. Если вы хотите сдать профильный вариант, просто чтобы проверить свои знания и уровень подготовки, — дерзайте!
Структура базового уровня ЕГЭ по математике
Базовый уровень проверяет основные знания школьника по математике. Такой экзамен не делится на части: в него входит только 21 задание с кратким ответом. Ответом может быть целое число, десятичная дробь или ряд цифр. По уровням сложности задания экзамена тоже не делятся — все задачи в нем базового уровня. Чтобы выполнить такую работу, ученику дают 180 минут.
Структура профильного уровня ЕГЭ по математике
Варианты профильного уровня проверяют основные и углубленные знания школьника. В 2023 году ЕГЭ состоит из 2 частей:
-
1-я часть: 11 задач с кратким ответом;
-
2-я часть: 7 задач с развернутым ответом.
В первой части ответом может быть целое число, десятичная дробь или ряд цифр. Во второй части — полное обоснованное решение и ответ. Чтобы выполнить задания экзамена, школьнику дают 235 минут.
Задачи ЕГЭ по математике профильного варианта делятся на категории по уровням сложности. В таблице ниже можно увидеть, как именно.
| Базовый | 6 |
| Повышенный | 10 |
| Высокий | 2 |
| Всего | 18 |
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Демоурок по подготовке к экзаменам
Составим ваш личный путь к высоким баллам — учтем сроки, уровень знаний и цель.
Как сдать ЕГЭ по математике: разбор сложных задач
Экзамен по математике не зря считают одним из самых трудных. Даже в заданиях базового варианта можно легко ошибиться по невнимательности. Что уж говорить о действительно сложных задачах с полным решением, где много «подводных камней»? Чтобы вы знали, как подготовиться к ЕГЭ по профильной математике, мы разобрали несколько из них.
Задание 16
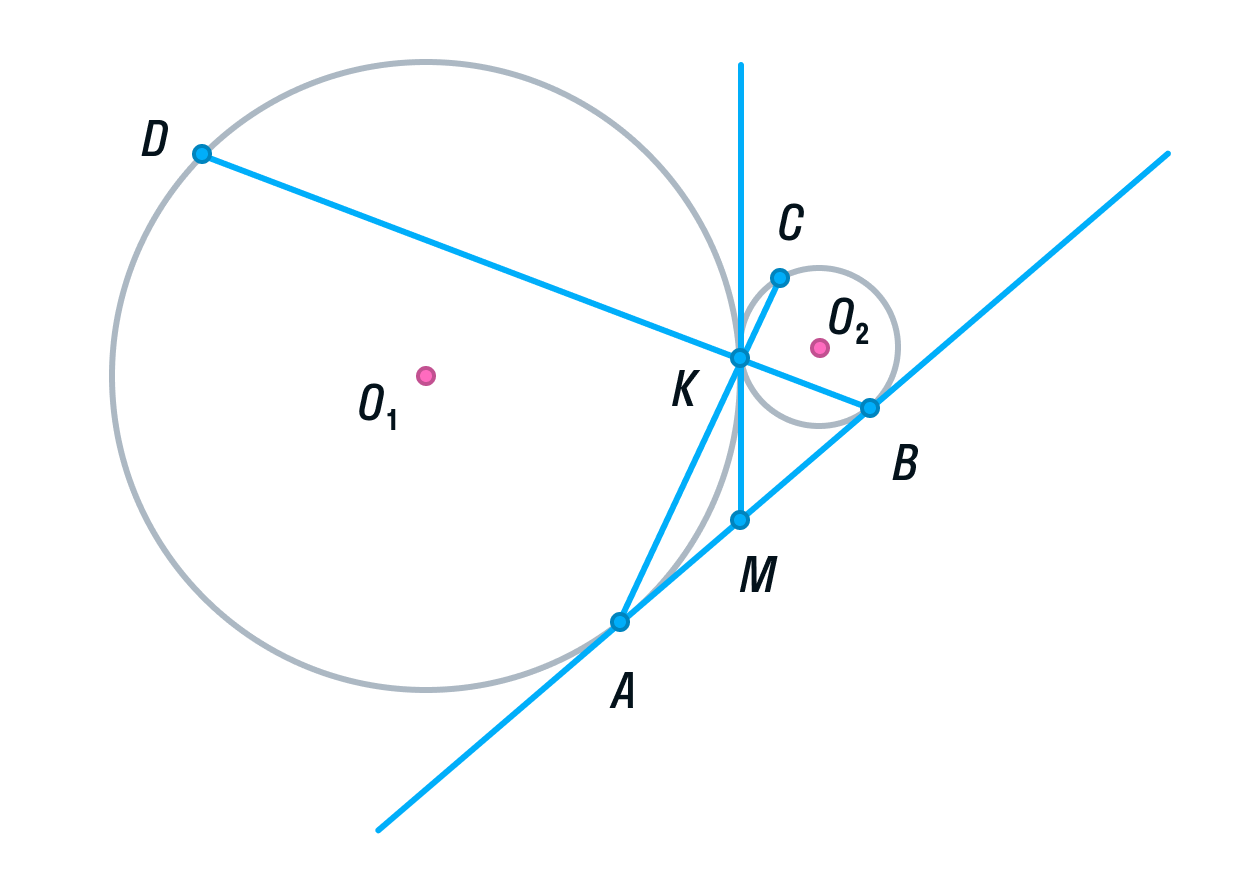
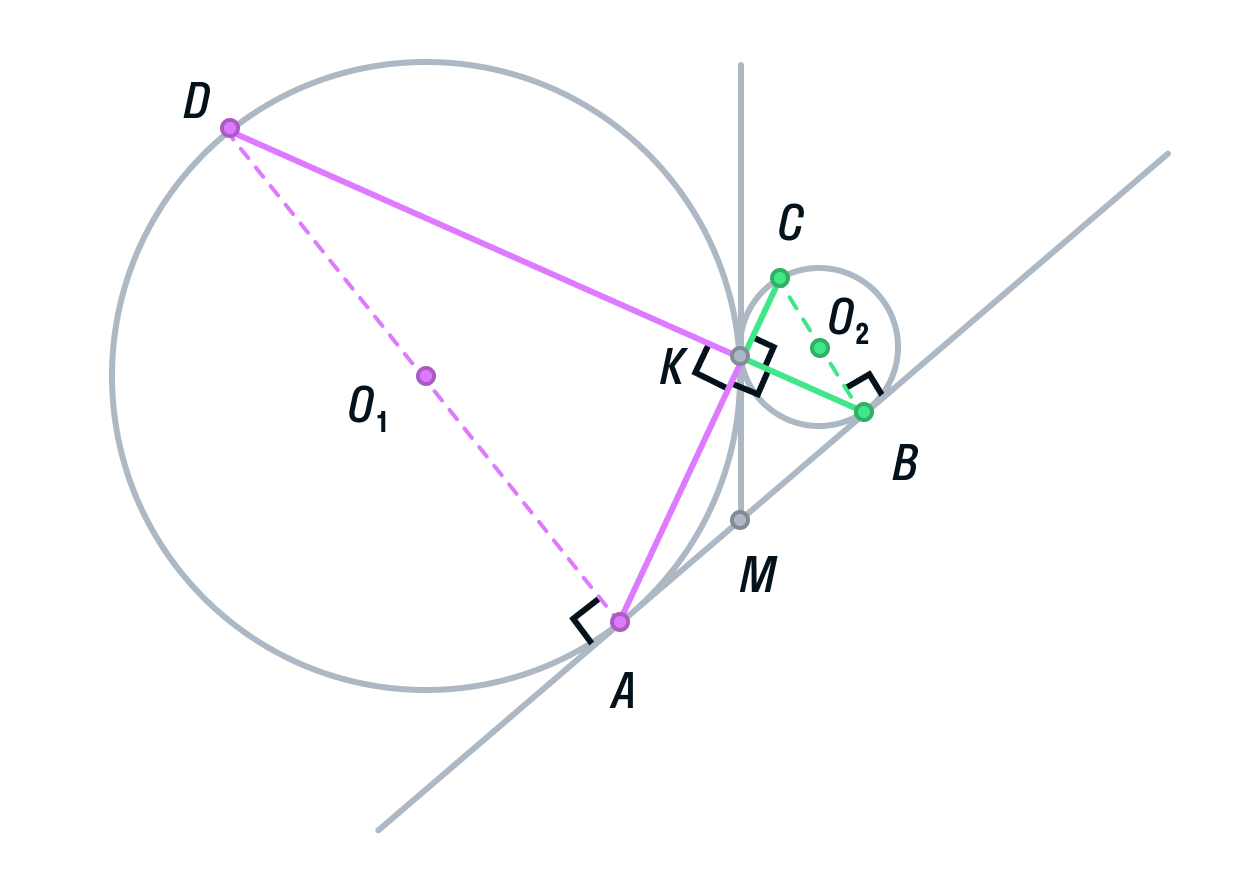
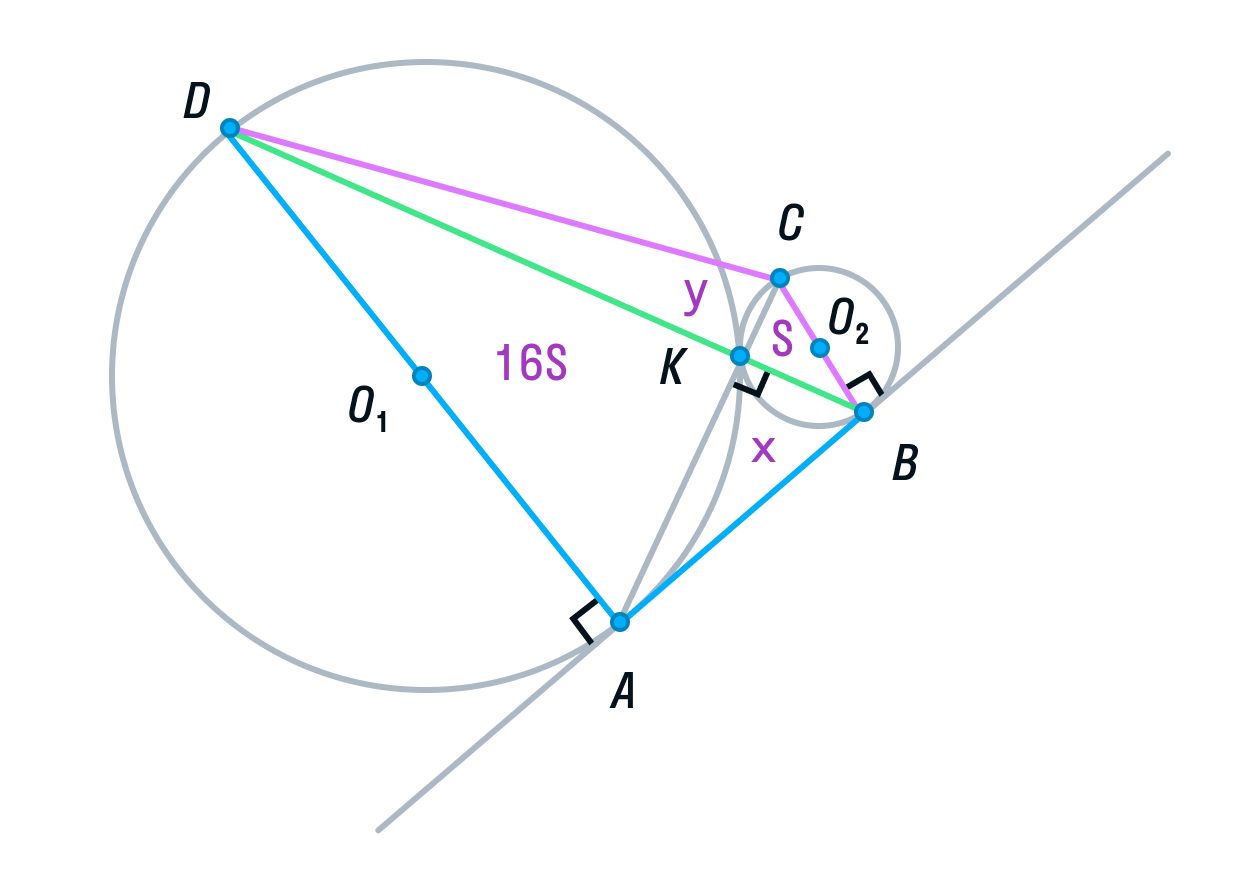
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Совет
Для этого задания советуем повторить темы:
-
Касательные к окружности и их свойства.
-
Свойства вписанных углов.
-
Взаимное расположение окружностей.
-
Свойства прямоугольного треугольника.
-
Признаки и свойства параллельных прямых.
-
Подобные треугольники, площади подобных фигур.
-
Свойство площадей (в частности: отношение площадей треугольников с одинаковой стороной).
-
Трапеция, её свойства. Площадь трапеции.
-
Теорема Пифагора.
Проследите, чтобы они были в вашем плане подготовки к профилю ЕГЭ по математике.
Решение
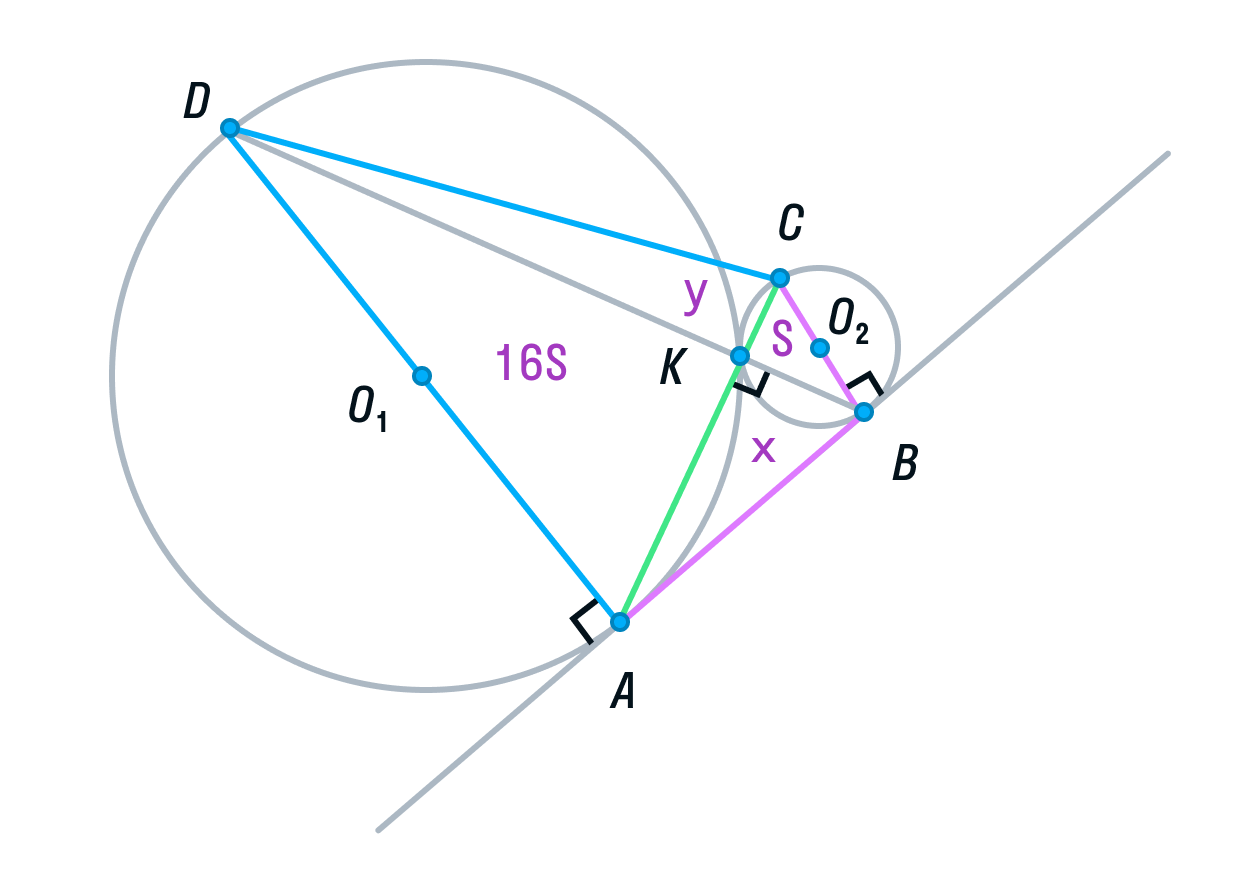
а) Выполним построение.
-
Окружности с центрами О1 и О2 соответственно касаются друг друга в одной точке К.
-
Прямая АВ касается обеих окружностей в точках А и В соответственно.
-
Прямые АК и ВК пересекают окружности в точках С и D соответственно
-
Пусть общая касательная окружностей в точке К, пересекает прямую АВ в точке М.
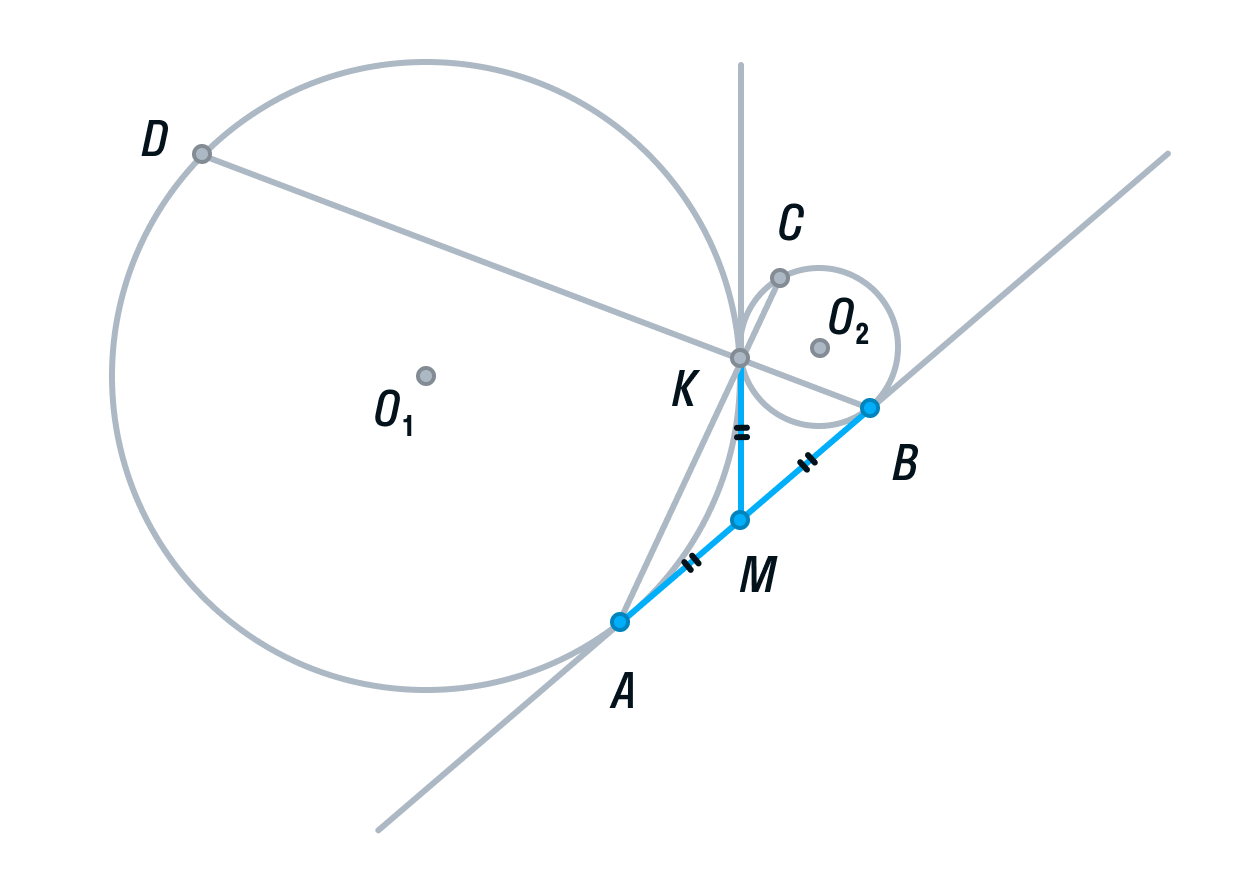
Тогда по свойству касательных, проведенных из одной точки, AM = KM и KM = BM.
-
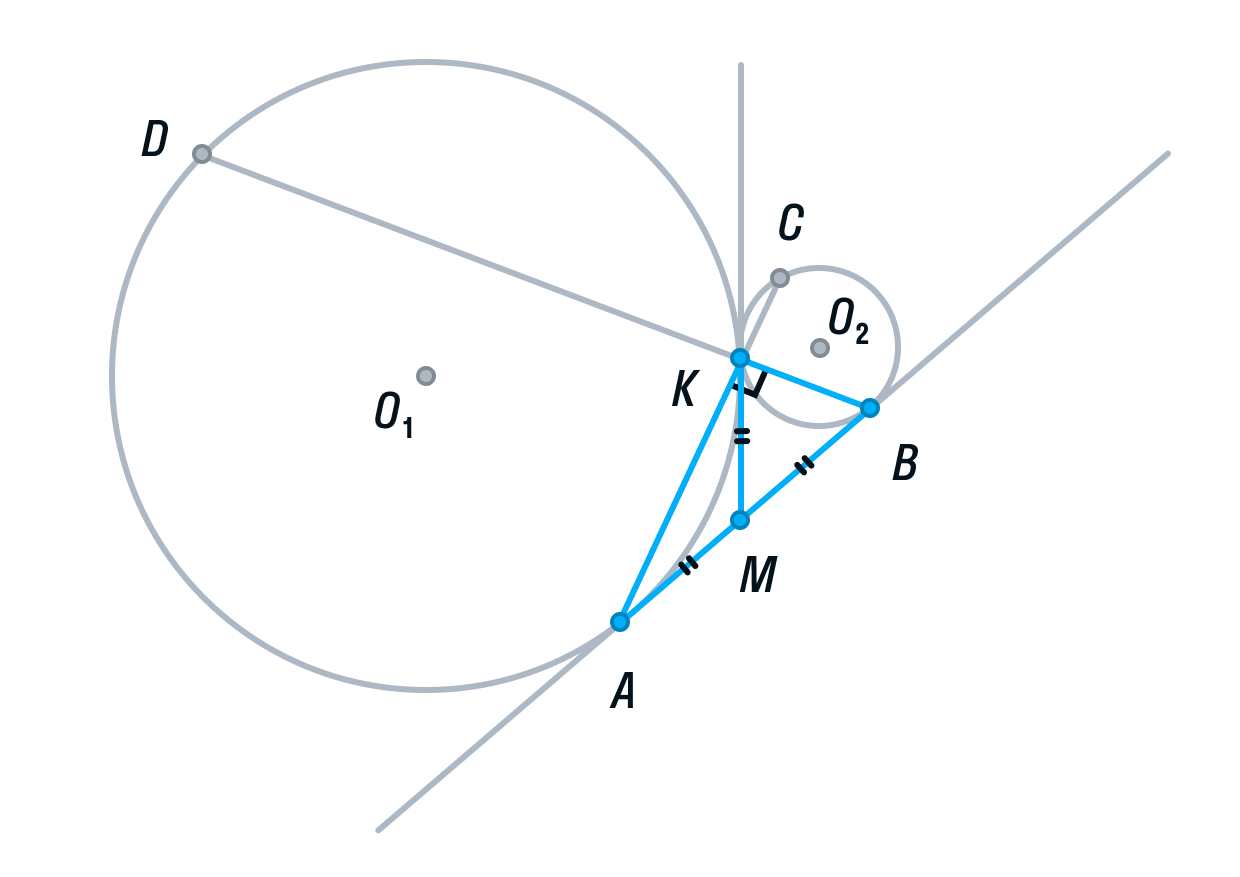
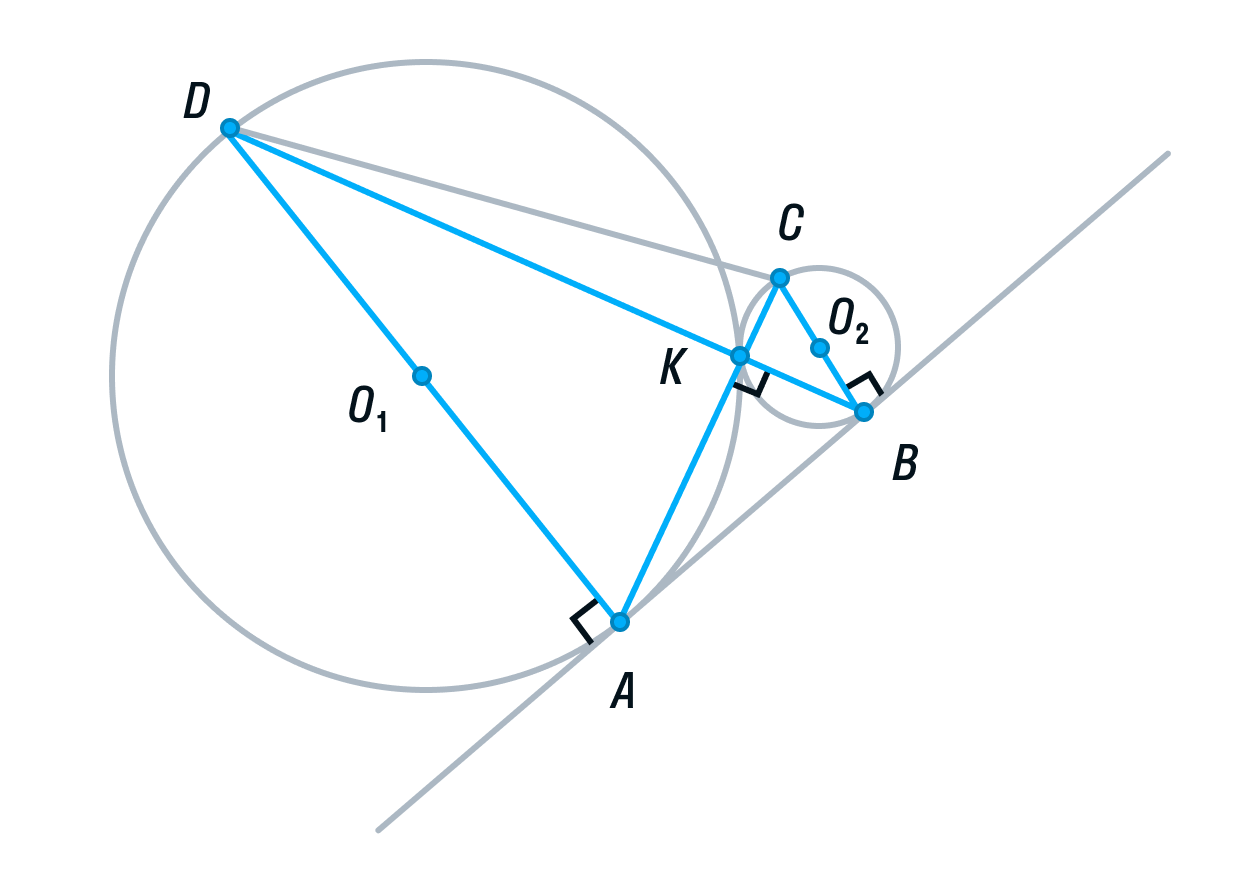
Рассмотрим треугольник АВК. Его медиана АМ равна половине стороны, которую она разбивает. Следовательно, делаем вывод, что треугольник АВК прямоугольный, а угол К = 90°.
-
Вписанный угол AKD является смежным углом АКВ, а значит, он тоже 90° как прямой. Следовательно, угол AKD опирается на диаметр AD. Значит, AD ⊥ AB, так как радиус, а в данном случае диаметр, перпендикулярен касательной в точке касания.
-
Аналогично рассмотрев угол ВКС, получим, что BC⊥ AB.
-
Прямые AD и ВС перпендикулярны третьей прямой АВ, следовательно, прямые AD и BC параллельны. Ч. т. д.
б) Пусть радиус первой окружности равен 4, а радиус второй окружности равен 1. Тогда АD = 8, ВС = 2.
-
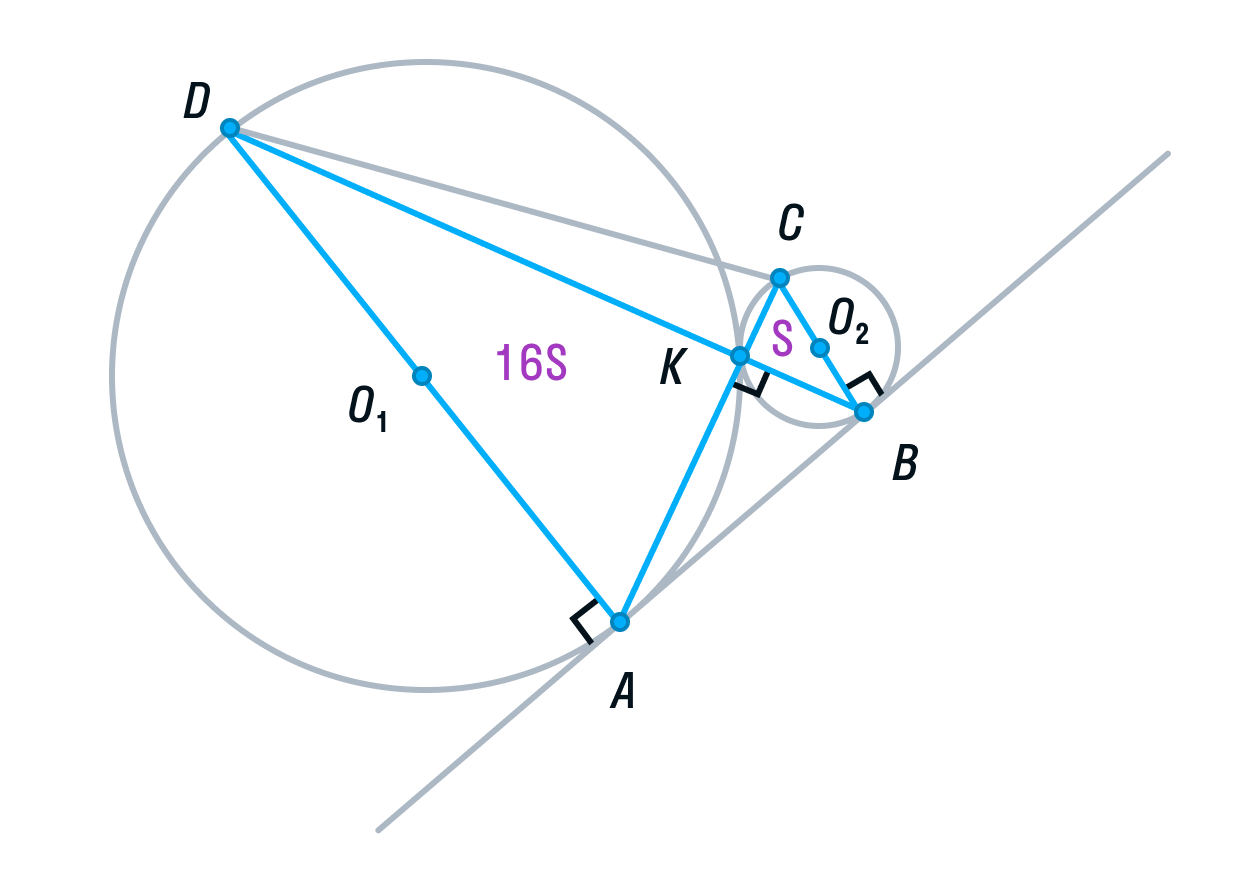
Рассмотрим треугольники ADK и СВК. Они подобны, т. к. имеют два равных угла (К – вертикальный, С и А — накрест лежащие). Из подобия треугольников следует, что их площади относятся как коэффициент подобия в квадрате:
-
Обозначим площадь треугольника СВК за S, тогда площадь треугольника ADK будет равна 16S.
-
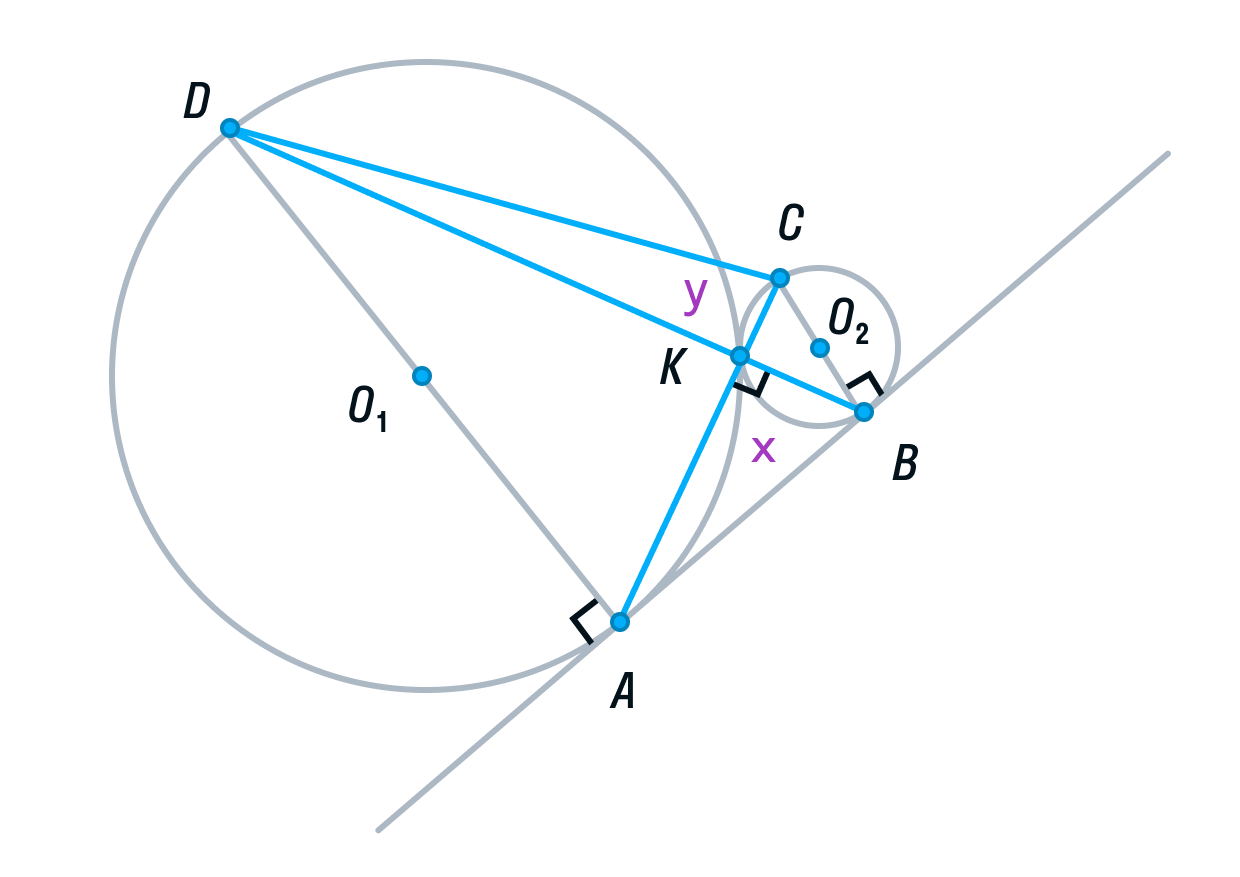
Пусть площади треугольников АВК и CDK будут равны х и у соответственно.
-
Вспомним свойство, связывающее высоты треугольников с общим основанием и получим следующие равенства: DB — общая сторона треугольников ADB и СDB, следовательно:
(равно 4 из подобия треугольников ADK и СВК, см. выше),
-
Аналогично, AC — общая сторона треугольников ADС и ABC, следовательно,
(равно 4 из подобия треугольников ADK и СВК, см. выше),
-
Решим полученную систему уравнений:
-
Из первого уравнения
подставим во второе и найдем y.
следовательно,
подставим во второе и найдем y.
-
Площадь ABCD равна 16S + 4S + 4S + S = 25S.
-
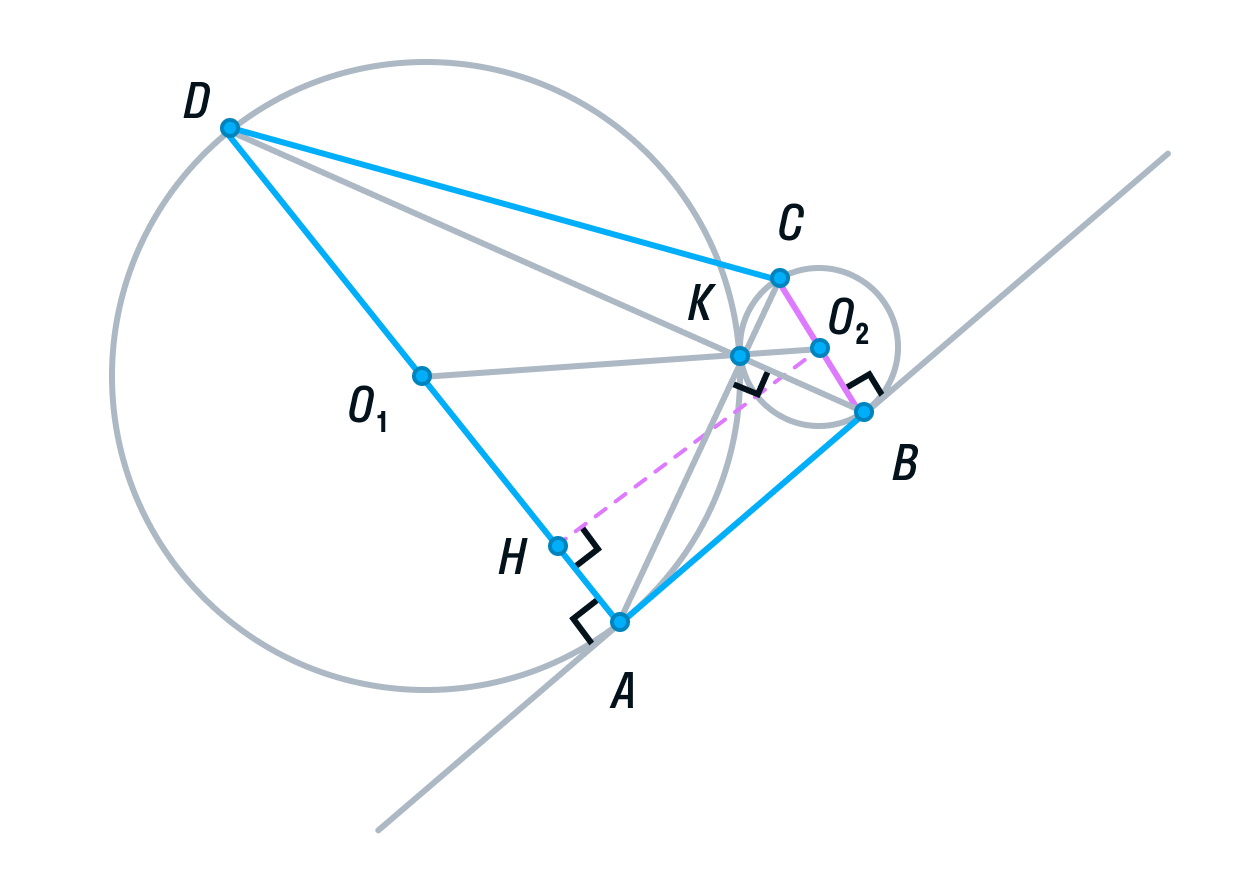
Заметим, что ABCD — прямоугольная трапеция (AD||BC, AB — перпендикулярна основаниям). Для вычисления ее площади нужно полусумму оснований умножить на высоту.
-
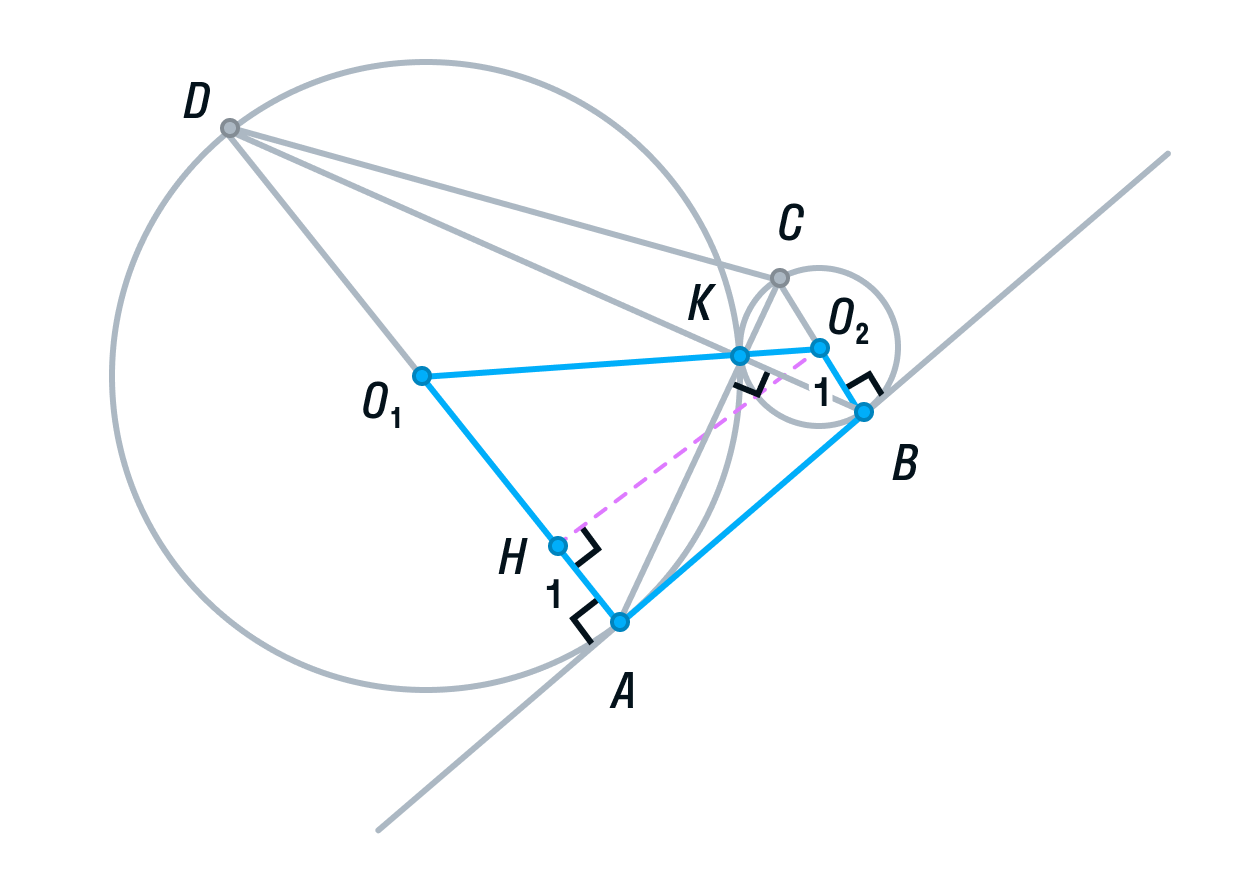
Для того, чтобы найти высоту, рассмотрим меньшую трапецию AO1O2B.
Ее основания равны 1 и 4, так как О2В и О1А — радиусы. O1O2 = 5, так как О2К и О1К — радиусы. О2H — высота трапеции AO1O2B.
-
По теореме Пифагора найдём О2H:
-
Вычислим площадь трапеции ABCD:
-
С другой стороны мы нашли
Отсюда S = 0,8.
-
Площадь треугольника АКВ = 4S, следовательно,
Ответ: 3,2.
Задание 18
В школах № 1 и № 2 учащиеся писали тест. В каждой школе тест писали по крайней мере 2 учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешел из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе № 1 уменьшиться в 10 раз?
б) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе № 2 равняться 7?
в) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.
Совет
Чтобы справиться с этой задачей, нужно повторить темы:
-
Понятие натурального и целого числа.
-
Среднее арифметическое.
-
Делимость чисел.
-
Процент. Нахождение процента от числа, уменьшение числа на заданный процент.
-
Составление и решение линейных уравнений.
Добавьте их в ваш план подготовки к ЕГЭ по математике, если собираетесь сдавать профиль.
Решение:
а)
-
Допустим, что в школе № 1 писали тест 2 учащихся, один из них набрал 1 балл, а второй набрал Х баллов и перешёл в другую школу. Тогда средний балл в школе был равен (1 + Х) : 2 = 10, а стал равен 1, т. е. уменьшился в 10 раз.
-
Решим уравнение и получим Х = 19 — натуральное число. Следовательно, наше предположение верно.
-
Или мы можем предположить другой вариант: что один учащийся набрал 2 балла. Тогда средний балл изначально равняется 20, а после ухода второго станет 2, т. е. изменится в 10 раз.
-
Решим уравнение (2 + Х) : 2 = 20, отсюда Х = 38 — натуральное число, что тоже удовлетворяет условию задачи.
Ответ: средний балл в школе № 1 мог уменьшиться в 10 раз.
б)
-
Пусть в школе № 2 писали тест m учащихся, n — сумма баллов m учащихся, средний балл равнялся B, а перешедший в неё учащийся набрал u баллов.
-
Умножим обе части полученного уравнения на 10, получим:
-
По условию B = 7, тогда получим, что 10u кратно 10, а
не делится на 10, так как ни один из множителей не делится на 10. Это противоречие.
Ответ: Первоначальный средний балл в школе № 2 не мог равняться 7.
в)
-
Пусть в школе № 1 средний балл равнялся A, общее количество баллов — p, количество писавших работу — (9 – m).
(из пункта б).
Следовательно,
-
Попробуем найти средний балл в школе № 2 методом подбора. Пусть:
В = 1, тогда:
кратно 10, а
не делится на 10.
В = 2, тогда:
пусть u = 1, тогда m = 4:
— не является целым числом.
u = 2 не может быть, т. к. m ≥ 1
В = 3, тогда:
кратно 10, а
не делится на 10.
В = 4, тогда:
Чтобы m было натуральным числом u должно быть четным, u = 2, тогда m = 4, что невозможно (доказали при В = 2).
u = 4, тогда m меньше 0, что невозможно т. к. m ≥ 1.
В = 5, тогда:
пусть u = 1, тогда m = 7, что невозможно (доказали в пункте б);
пусть u = 2, тогда m = 5:
— не является целым числом;
пусть u = 3, тогда m = 3:
-
Этот случай реализуется, например, в школе № 2 при m = 3, B = 5. Предположим, что каждый ученик набрал по 5 баллов. Тогда в школе № 1 писали 9 – m = 9 – 3 = 6 учащихся, 3 из них набрали по 1 баллу, а 3 – по 3 балла, тогда средний балл:
-
Переход из школы № 1 в школу № 2 совершил ученик с 3 баллами, тогда
средний балл в школе № 1 стал равен:что на 10% меньше от первоначального значения.
-
Тогда средний балл в школе № 2 стал равен:
что на 10% меньше от первоначального значения.
Ответ: наименьшее значение первоначального среднего балла в школе № 2 равно 5.
Ответ: а) да; б) нет; в) 5.
Как выставляют баллы за ЕГЭ по математике
С базовым уровнем сложности все просто: за каждый правильный ответ вашего варианта вы получаете по 1 первичному баллу. То же самое касается и первой части профиля: задания 1–11 тоже оценивают в 1 балл.
Как вы помните, во 2-й части профильного варианта нужны и решение, и ответ. Здесь задания оценивают по нескольким критериям. Они сложнее, но и баллов за них можно получить больше. Давайте же разберемся, как выставляют баллы во второй части профиля. Это поможет вам подготовиться к заданиям ЕГЭ по математике как самостоятельно, так и с учителем.
| Задание № 12 | Баллы |
|---|---|
| В обоих пунктах есть обоснованные ответы | 2 |
| Есть обоснованный ответ только в пункте а или есть неверный ответ из-за ошибки в вычислениях, но шаги в решениях обоих пунктов верные |
1 |
| Все остальные случаи | 0 |
| Максимальный балл | 2 |
| Задание № 13 | Баллы |
|---|---|
| Верно доказан пункт а, в пункте б есть обоснованный ответ | 3 |
| Есть только обоснованный ответ в пункте б или верно доказан пункт а, в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ |
2 |
| Есть только верное доказательство пункта а, или в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ, или есть обоснованный ответ в пункте в, который получен с помощью пункта а, но сам пункт а не выполнен |
1 |
| Все остальные случаи. | 0 |
| Максимальный балл | 3 |
| Задание № 14 | Баллы |
|---|---|
| Есть обоснованный ответ | 2 |
| Ответ обоснован, но он отличается от верного исключением точек –12 и/или 0 или шаги решения верные, но из-за ошибки в вычислениях получен неверный ответ |
1 |
| Все остальные случаи | 0 |
| Максимальный балл | 2 |
| Задание № 15 | Баллы |
|---|---|
| Есть обоснованный ответ | 2 |
| Ученик верно построил математическую модель | 1 |
| Все остальные случаи | 0 |
| Максимальный балл | 2 |
| Задание № 16 | Баллы |
|---|---|
| Верно доказан пункт а, в пункте б есть обоснованный ответ | 3 |
| Есть только обоснованный ответ в пункте б иЛИ Верно доказан пункт а, в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ |
2 |
| Есть только верное доказательство пункта а, или в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ, или есть обоснованный ответ в пункте в, который получен с помощью пункта а, но сам пункт а не выполнен |
1 |
| Все остальные случаи | 0 |
| Максимальный балл | 3 |
| Задание № 17 | Баллы |
|---|---|
| Есть обоснованный ответ | 4 |
| Рассуждения и значения параметра верные, но в ответе есть 1–2 неверных значения или решение недостаточно обосновано | 3 |
| Есть верное рассуждение и хотя бы одно правильное значение | 2 |
| Задача сведена к исследованию взаимного расположения 3 окружностей или двух квадратных уравнений с параметром | 1 |
| Все остальные случаи | 0 |
| Максимальный балл | 4 |
| Задание № 18 | Баллы |
|---|---|
| Есть обоснованный ответ в пунктах а, б, в | 4 |
| Есть обоснованный ответ в пункте в и есть обоснованный ответ в пунктах а или б | 3 |
| Есть обоснованный ответ в пунктах а и б или есть обоснованный ответ в пункте в. |
2 |
| Есть обоснованный ответ в пунктах а или б | 1 |
| Все остальные случаи | 0 |
| Максимальный балл | 4 |
Узнать больше о структуре экзамена, вариантах и критериях, по которым оценивают работы, можно на официальном сайте ФИПИ, в разделе «Демоверсии, спецификации, кодификаторы». Там же вы найдете методические указания для подготовки.
Сколько баллов нужно набрать, чтобы получить 3, 4 и 5
Теперь, когда мы разобрали критерии, можно посчитать, сколько баллов нужно набрать на конкретную оценку. В этом нам помогут таблицы ниже. Заодно разберемся, как первичные баллы переводятся в тестовые — финальные.
| Шкала перевода баллов в базовой математике | |
|---|---|
| Первичные баллы | Оценка |
| <7 | 2 |
| 7–11 | 3 |
| 12–16 | 4 |
| 17–21 | 5 |
| Максимальный балл | 4 |
Обратите внимание: с 2008 года официально баллы ЕГЭ не переводят в привычные нам оценки по пятибальной системе. Но если вам хочется это сделать, можно примерно оценить работу по таблице ниже.
| Шкала перевода баллов в профильной математике (неофициальная) | ||
|---|---|---|
| Первичные баллы | Тестовые баллы | Оценка |
| <5 | <27 | 2 |
| 5–8 | 27–49 | 3 |
| 8–20 | 50–67 | 4 |
| 21–31 | 68–100 | 5 |
6 советов от эксперта, как готовиться к ЕГЭ по математике
Мы занимаемся подготовкой учеников к экзамену каждый год и понимаем, насколько это важно и волнительно. Вам предстоит ответственная работа, от которой многое зависит. Чтобы облегчить ее, мы собрали несколько советов, которые помогут вам как можно лучше подготовиться к ЕГЭ по математике:
-
Осознанно выберите уровень сложности и поставьте цель в баллах.
-
Составьте план подготовки к ЕГЭ по математике: больше времени уделяйте темам, которые у вас «западают». Чтобы выявить их, ученики Skysmart проходят тест на бесплатном уроке.
-
Узнайте все о ЕГЭ: сколько времени длится экзамен, из каких частей состоит, по каким темам будут задания, сколько вариантов, какие дадут справочные материалы и т. д.
-
Составьте сбалансированное расписание для подготовки и следите, чтобы в нем было достаточно времени для отдыха.
-
Много практикуйтесь: решайте варианты из Открытого банка заданий ЕГЭ и сдавайте тестовые экзамены.
-
Систематически консультируйтесь и занимайтесь с наставником, который часто имеет дело с подготовкой к ЕГЭ — преподавателем в школе или репетитором.
Все пункты в этом списке важны для тех, кто хочет набрать 80–100 баллов, но последний — особенно. Преподаватель расскажет о том, что представляет из себя ЕГЭ, и тогда на реальном экзамене не будет неприятных сюрпризов.
На курсах подготовки к ЕГЭ по математике в Skysmart учителя помогают школьникам разобраться в КИМах и прорешать каждый тип задач. Ученики заранее знакомятся с частыми ошибками, что помогает избегать их в работе и сохранять баллы. А еще мы учим готовиться морально, чтобы не допустить ошибок из-за паники и невнимательности. Начните подготовку к ЕГЭ по математике с нуля вместе со Skysmart: первый урок — бесплатно!
Выбирают сдавать базовый уровень обычно выпускники, собирающиеся поступать на гуманитарные направления. Для них не так и важны супер глубокие знания по предмету, к тому же таким способом гораздо легче получить в аттестате хорошую оценку по матеше. Но все-таки готовиться к экзамену придется, даже если ты считаешь, что у тебя очень хорошие знания и навыки. Да, времени и сил это займет не очень много, но все равно добавь в свое расписание несколько часов на проработку КИМа. Если действительно уверен в силах — просто раз в неделю прорешивай вариант, чтобы не потерять навык: все равно это займет не более часа, если твои навыки действительно хороши. Но если с математикой у тебя вечные проблемы, тебе тем более нужно уделять время на подготовку.
Структура
Перед тем как начать готовиться, изучи КИМ. Лучшим вариантом будет сайт ФИПИ — на нем есть три важных для тебя документа — кодификатор, спецификация и демоверсия. Если коротко:
- Спецификация отвечает за организационные вопросы и изменения в структуре.
- В кодификаторе будут все темы, которые стоит знать, чтобы точно сдать ЕГЭ. Если у тебя мало знаний по предмету — сделай себе чек-лист на основе этого файла: таким образом ты точно не упустишь важные разделы.
- Демоверсия — прототип КИМа. Как и все остальные файлы его обновляют к началу учебного года. Здесь можно узнать количество заданий, баллы и примерный вид варианта на текущий учебный год.
Сам тест состоит из двадцати одного номера — проверяются знания как по алгебре, так и по геометрии. В самом начале КИМа даются справочные материалы —
- Таблица квадратов,
- Свойства квадратного корня,
- Корни квадратного уравнения,
- Формулы сокращенного умножения,
- Свойства степени и логарифмов,
-
Геометрическая теория:
- Средняя линия треугольника и трапеции,
- Теорема Пифагора,
- Длина окружности,
- Площадь круга, параллелограмма, трапеции, ромба,
- Площади поверхности и объемы тел, а именно, призмы, пирамиды, конуса, параллелограмма, цилиндра, шара;
- Св-ва правильного треугольника,
-
Тригонометрия:
- Основное тождество,
- Определение синуса, косинуса, тангенса,
- Некоторые значения тригонометрических функций,
- Линейная функция,
- Геометрический смысл производной.
Эта информация очень помогает, особенно если у тебя не получается понять и запомнить геометрию. Именно благодаря справочным материалам, главное, что потребуется на экзамене — умение вычислять. Вспомни, как работать с обыкновенными и смешанными дробями, отрицательными числами, степенями. Если у тебя очень хорошо развит этот навык, то сильно волноваться за результат тебе не придется. В целом, если ты хорошо учился в школе и не было проблем с предметом, то тебе не нужно будет ничего заново учить — просто практиковаться немного, но структурировано — не пропускать запланированные тобой пробники.
План подготовки к ЕГЭ по математике 2023
Вернемся к структуре: как говорилось ранее, все задания только тестового типа — развернутых решений, как в остальных экзаменах, не будет. То есть изучать дополнительные критерии, правильное оформление тебе не нужно. Немало номеров имеют прикладной характер — то есть, например, рассчитать, какие чемоданы можно сдать в багаж по определенным критериям кампании или кого из работников, которые предлагают свои цены за услугу, будет выгоднее взять. Также будут вопросы по графикам на поиск производной, задачки с расчетами, уравнения, стереометрические и планиметрические задачи, теория вероятностей, неравенства и задачи на смекалку. За каждый верный ответ дается по одному баллу. Ответ может быть как в форме числа, получившего после вычисления, так и последовательности цифр — например, задание на сопоставление величины и значения.
Разбалловка
Самая плохая оценка — двойка, если получишь ее, то ты официально не перейдешь порог, и тебе не смогут выдать аттестат об окончании школы. Наивысшая — пятерка.
| Оценка | Баллы |
|---|---|
| 2 | 0-6 |
| 3 | 7-11 |
| 4 | 12-16 |
| 6 | 17-21 |
Как можно заметить — чтобы получить пять, нужно написать на семнадцать-плюс баллов из двадцати одного. То есть, если допустишь три-четыре ошибки, то все еще получишь наивысший результат. Но не стоит этим злоупотреблять — готовиться только к 17 или 18 номерам, чтобы пройти точно по грани. Для успешной сдачи тестирования понадобится достаточно базовая теория, поэтому проще выучить ее и наработать все навыки, чтобы не зависеть от стресса в аудитории. Без хорошей концентрации у тебя есть шанс неправильно прочитать условие, что за собой поведет неверный ответ. Лучше дать себе гораздо более прочную подушку безопасности из четырех номеров, чем чересчур надеяться на свои силы.