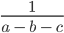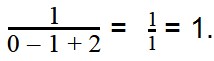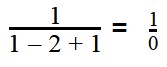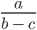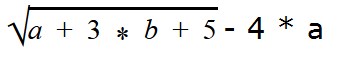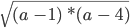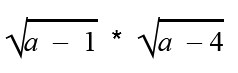Почему нельзя писать одз в егэ по математике

Раньше и трава была зеленее

Всю жизнь все при решении неравенств и уравнений в ЕГЭ по профильной математике писали ОДЗ (Область Допустимых Значений), понимая под этим ограничения, накладываемые на аргумент “непростыми” функциями типа квадратного корня или логарифма. И не было проблем. Пока в сеть не попали разъяснения методиста из Кемеровской области.

За ТАКОЕ точно снизят

Семинар Трушкиной Т.П., методиста из Кемеровской области, наделал много шума. Оказалось, что на ЕГЭ по математике можно получит 0 баллов за задачу, даже имея верный ответ и верную последовательность рассуждений. Все из-за неправильного использования понятия “ОДЗ”. Первое, что ясно совершенно точно: если вы выписали “ОДЗ” “не полностью” – прощайтесь с баллами за задачу. Если вы решили выписать лишь ограничения, вносимые логарифмической функцией, а условие отличия знаменателя от нуля оставить на потом (“ну они ведь и далее сохранятся, “переход равносилен””), и назвали эти “неполные” ограничения словом ОДЗ – то это 0 баллов. И можно было даже не браться за задачу =(

Если хотите пользоваться равносильными переходами – пользуйтесь, никто это не запрещает. Но тогда ОДЗ вам вообще ни к чему – работайте спокойно через систему условий, и будет вам счастье.

Скажите детям – пусть они ОДЗ выбросят!

Но даже при правильной, полностью выписанной ОДЗ, есть риск нарваться на неприятности. Эксперт заявляет: в школьных учебниках по математике понятие области допустимых значений (ОДЗ) определен лишь для функций. Поэтому использовать это понятие при решении уравнений и неравенств не рекомендуется. Однако использование ОДЗ в неравенствах и уравнениях активно использовалось преподавателями ВУЗов, в том числе при работе со школьниками, постепенно “мигрировало” в методички и сборники по подготовке к ЕГЭ, и теперь уже прочно укоренилось в умах репетиторов, учителей и абитуриентов. Как показывает практика, полностью выписанные ограничения на переменную под заголовком “ОДЗ” не ведут к снижению баллов на ЕГЭ по профильной математике. Тем не менее, эксперт не рекомендует использовать эту конструкцию.

“Коллеги, лучше вообще ничего не писать; Скажите детям – пусть они ОДЗ выбросят!” – столько эмоций на пустом, казалось бы, месте.

Эксперт рекомендует накладывать ограничения на переменную, при этом никак это не “озаглавливать”. При это заголовки типа “ограничения”, “условия”, “важные замечания” и т.п. возбраняться не должны.

---

Наша бесплатная Игра-тренажер “ударения на ЕГЭ”

---

А что говорят интернет-гуру?

Специалисты в области подготовки к ЕГЭ по профильной математике разделились во взглядах. Многие известные Ютуб-блогеры (Борис Трушин, Wild Mathing) придерживаются того мнения, что полностью выписанная ОДЗ ни в коем случае к снижению баллов не приведет. Однако выписаны ограничения, действительно, должны быть полностью. То есть если у вас, например, имеется неравенство с логарифмом, да который ещё и стоит в знаменателе дроби – будьте любезны, потребуйте, чтобы аргумент логарифма был положителен, основание положительно и отлично от единицы, а также чтобы знаменатель вашей дроби был отличен от нуля.

То, что за верно выписанную ОДЗ вам не снизят баллы, подтверждают и официальные методические рекомендации по оцениванию выполнения заданий с развернутым ответом ЕГЭ по профильной математике от РосОбрНадзора. Ниже приведен пример работы с верно выписанной ОДЗ. Работа оценена на максимальный балл. К ОДЗ никто не придирался.

---

Если Вам нужна методичка для экспертов по оцениванию работ ЕГЭ по профильной математике – можете написать нам в сообщения сообщества ВК. Подскажем, где скачать.

---

И как же быть?

1. Если Вы привыкли использовать ОДЗ – используйте, но пишите его полностью. Если снизят – идите на апелляцию. Методичка по оцениванию – вам в помощь.
2. Если Вы умеете работать с равносильными переходами – вы красавчик =) Это самый безопасный вариант. Но писанины будет… Запасайтесь бланками заранее.
3. Если не устраивают предыдущие два пункта – озаглавьте ОДЗ словом “ограничения” или вообще никак не называйте. Это безопасно, даже если забудете какое-то важное условие.

О наших курсах ЕГЭ

А где пруфы?

Ну, если вам мало всего выше написанного – смотрите полную запись вебинара

Страшная история и ответ ФИПИ!

Друзья и коллеги, пора поставить точку в одной очень стрррашной и запутанной истории. Можно ли писать: «ОДЗ»? Узнаем ответ специалистов ФИПИ.

История началась весной 2018 года, когда старшеклассники и учителя оказались очень сильно напуганы. Они говорили нам: «Нам учительница запретила писать ОДЗ! Нам сказали: Забудьте про эти страшные три буквы! Лучше ничего не пишите! Или пишите: Ограничения»!

Но что такое «ограничения»? Дал ли кто-нибудь определение этому слову как математическому термину? И можно ли взять и отменить математический термин? Нет, конечно! Ни теорему синусов, ни область допустимых значений уравнения (или неравенства) отменить нельзя.

Страсти не утихают уже почти 2 года.

Можно ли писать: «ОДЗ»? Ответы специалистов ФИПИ.

И меня постоянно спрашивают: «Можно ли писать: «ОДЗ» ? Не снимут ли мне все баллы за мою работу?

Меня также спрашивают, правда ли, что теперь при записи ответа в неравенстве нельзя использовать знак объединения и вместо него надо ставить точку с запятой.

Я задала эти вопросы специалистам ФИПИ – Федерального института педагогических измерений.

Вот что мне ответили:

Уважаемая Анна,

при выполнении заданий с развернутым ответом ЕГЭ по математике профильного уровня участник экзамена должен привести полное обоснованное решение задачи. При этом он может выбирать любой математически корректный способ решения, а также формы записи решения и ответа.

Ни в одном документе ФГБНУ «ФИПИ» нет запрета на использование тех или иных понятий, фактов, способов записи.

В частности, полное, обоснованное решение, корректно использующее понятие «Область допустимых значений», а также запись ответа с использованием знака объединения при проверке работ, согласно критериям, оценивается максимальным баллом.

С уважением, специалисты ФГБНУ «ФИПИ»

Вот и всё. Писать «ОДЗ» можно, только делать это надо правильно. Ведь, по определению, область допустимых значений уравнения или неравенства – это множество значений переменной, при которых обе части данного уравнения имеют смысл.

Например, ОДЗ неравенства

задается системой условий:

Если вы напишете просто «ОДЗ: х>0» — это ошибка. И не потому, что вы написали буквы О, Д и З, а потому, что не полностью указали область допустимых значений.

Вот такие (и многие другие) интересные тонкости оформления мы разбираем на нашем Онлайн-курсе.

Этот курс особенно полезен для учителей и репетиторов. Он дает то самое профессиональное общение, которого учителям так часто не хватает. Дает возможность выяснить все непонятные моменты. И конечно, намного лучше, если мы не пугаем детей иррациональными запретами, не ставим лишних «ограничений», а спокойно и профессионально объясняем то, что непонятно.

В курсе есть все, чтобы подготовить на 100 баллов +.мастер-классы по методике подготовки. Ближайший в эти выходные. И пусть вас не пугает срок доступа. Летом будут специальные акции на продление преподавательского тарифа.

Готовьтесь к ЕГЭ с профессионалами!

Курс «10 класс»

— Теория: текст + 72 ч видеоразборов.
— 35 ч. онлайн занятий с Анной Малковой в месяц.
— ДЗ с проверкой, чат, 2 репетиционных ЕГЭ.

Курс «11 класс, 80 баллов»

— Теория: текст + 72 ч видеоразборов.
— 54 ч. онлайн занятий с Анной Малковой, 3 в месяц.
— ДЗ с проверкой, чат, 9 репетиционных ЕГЭ.

Курс «11 класс, 100 баллов»

— Теория: текст + 72 ч видеоразборов.
— 120 ч. онлайн занятий с Анной Малковой, 8 в месяц.
— ДЗ с проверкой, чат, 9 репетиционных ЕГЭ.

Курс для преподавателей

— Вся теория профильного ЕГЭ, все задачи.
— 4 онлайн занятия в месяц (70 ч.).
— Мастер-классы по методике преподавания раз в месяц (18 ч.).

Повышение цен через 2 дня!

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «ОДЗ писать нельзя? Ответ ФИПИ. Учителя, расскажите ученикам!» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.03.2023

Мы используем файлы cookie, чтобы персонализировать контент, адаптировать и оценивать результативность рекламы, а также обеспечить безопасность. Перейдя на сайт, вы соглашаетесь с использованием файлов cookie.

30 мая 2018

В закладки

Обсудить

Жалоба

Изменение требований к оформлению заданий с развернутым ответом на ЕГЭ по математике

Важные моменты при оформлении второй части профильного ЕГЭ по математике.

1) ОДЗ. Писать ОДЗ можно, но если написали это слово, то писать его нужно целиком. Например, если в знаменателе есть логарифм, то нужно написать не только, что его аргумент >0, но и, что сам знаменатель не равен 0. И так со всеми имеющимися ограничениями. Иначе, это будет неправильное ОДЗ и оценка 0 баллов. Если пишите только часть ограничений, то не пишите слово «ОДЗ». Просто что-нибудь вроде фразы «Должны выполняться условия».

3) ОТБОР КОРНЕЙ ПО ОКРУЖНОСТИ. Обязательно нарисовать на окружности дугу, соответствующую нужному промежутку, обязательно подписать границы этой дуги, поставить точки (решения уравнения) и пояснить, как были отобраны корни, попадающие на дугу.

2) МЕТОД РАЦИОНАЛИЗАЦИИ. Использовать можно, доказывать не обязательно, но надо пояснять. Например, фразой «По методу рационализации в силу строго монотонного возрастания функции y=log_a(x) при a>1 и строго монотонного убывания функции y=log_a(x) при 0 < a < 1 »

4) ИСПОЛЬЗОВАНИЕ ГОТОВЫХ ФОРМУЛ в задаче 17. Без вывода нельзя. Этих формул нет в учебниках, а всё, чего в учебниках нет надо выводить.

5) ОТВЕТЫ НА ПУНКТЫ а) и б) в задаче 19. Просто слова «да/нет» недостаточно. Нужен пример или обоснование.

Подробнее в вебинаре

Каждый выпускник знает, что не так сложно решить задачу с развернутым решением, как ее оформить. Из-за стресса и обидных огрехов на экзамене теряются драгоценные баллы.

Главными правилами оформления заданий в карточках поделилась автор экзаменационных курсов для преподавателей Skysmart Ирина Чегринская.

Первое правило

Три самые опасные буквы на экзамене? ОДЗ. Писать ОДЗ можно, если выписывать все ситуации, в которых выражение не имеет смысла. Если выписать не все, балл будет снижен.

Что делать:

• писать слово «ограничения»,
• пользоваться равносильными переходами,
• или писать ОДЗ и выписывать все ограничения.

Второе правило

Отбор корней в 12 задании. Ученик решил уравнение — один балл. Чтобы заработать второй балл, нужно соблюсти несколько рекомендаций:

1. Корни отбираем любым способом: с помощью графика, числовой окружности, решения двойных неравенств и тому подобное.

2. Серии корней записываем с разными переменными. При выборке корней эта хитрость поможет не запутаться.

3. Перебор корней не останавливаем на корне, принадлежащему отрезку. Такой способ будет недостаточно обоснованным, пункт «б» не засчитают.

4.  При отборе корней с помощью числовой (тригонометрической) окружности отмечаем концы числового отрезка, выделяем дугу, обозначаем корни.

Третье правило

При доказательстве в заданиях 13 и 15 либо указываем теорему, которую использовали, либо ее формулировку.

Четвертое правило

Не так страшен 18 номер, как его малюют. В последнем номере при решении пункта «а» можно пользоваться методом подбора. Если ответ положительный, то достаточно привести пример. Если ответ отрицательный, что бывает реже, то нужно написать доказательство.

Обязательно разбирайте со школьниками 18 номер: с некоторыми пунктами справится даже ученик со средним уровнем подготовки.

Пятое правило

Важно научить ребенка не только решать, оформлять, но и проверять свои ответы, чтобы не было вычислительных ошибок.

Что делать ученику на уроках:

• проверять ход решения,
• самостоятельно искать свои ошибки,
• подставлять ответы в исходные уравнения, неравенства,
• проверять, насколько логичный ответ получился. 

Например, катет не может быть больше гипотенузы, ежемесячный платеж по кредиту должен быть действительно возможным.

Другие статьи автора:

ОДЗ (Область допустимых значений) – подробнее

Давай разберем пример, наглядно показывающий, что такое ОДЗ:

Решим уравнение ( displaystyle sqrt{2x+3}=x).

Все очень просто, если ты уже освоил тему «Иррациональные уравнения».

Возводим левую и правую части уравнения в квадрат:

( displaystyle 2x+3={{x}^{2}}text{ }Leftrightarrow text{ }{{x}^{2}}-2{x}-3=0).

Теперь решаем квадратное уравнение. Я воспользуюсь теоремой Виета (если забыл, что это такое, – посмотри тему «Квадратные уравнения»).

Получаем корни:

( displaystyle x=3:text{ }sqrt{2cdot 3+3}=3text{ }Leftrightarrow text{ }sqrt{9}=3) – все верно.

( displaystyle x=-1:text{ }sqrt{2cdot left( -1 right)+3}=-1text{ }Leftrightarrow text{ }sqrt{1}=-1) – неверно! А все почему?

Да потому, что мы не учли ОДЗ! 

По определению квадратный корень из любого числа не может быть отрицательным. 

Значит, глядя на уравнение ( displaystyle sqrt{2x+3}=x) мы должны сразу же написать:

Итак, с помощью этих рассуждений приходим к такой области допустимых значений:

( displaystyle xge 0).

Тогда сразу становится ясно, что корень ( displaystyle x=-1) не подходит. И остается единственный ответ ( displaystyle x=3).

Всего мы изучаем несколько разных функций, для которых важна ОДЗ. Вот они со своими ОДЗ в удобной табличке.

Изменение требований к оформлению заданий с развернутым ответом

в ЕГЭ по математике.

Оформление номеров второй (письменной) части ЕГЭ по профильной математике – одна из наиважнейших тем, нюансы которой так важно освоить всем ученикам, претендующим на высокие баллы. На этом, казалось бы, не главнейшем моменте возможно как сильно «погореть», так и закрепить результат, получив максимально возможные баллы – разница может доходить до 10 первичных баллов за вторую часть – при более внимательном подходе. Рассмотрим основные пункты надлежащего оформления номеров 13, 15 и 17 – тех, которые входят в так называемую стратегию подготовки к ЕГЭ — «Ударим по нечетным».

Задание №13. Тригонометрические, показательные, логарифмические и иррациональные (последний вид был на досрочном тестировании в прошлом году) уравнения.

Под буквой (а) — решение, под буквой (б) — отбор корней на отрезке/интервале (по 1 баллу за каждый пункт, макс. — 2 балла).

Основные «подводные камни» — в оформлении пункта (б), а именно:

— Отбор корней нельзя назвать обоснованным, если перебор остановлен на корне, принадлежащем отрезку. В таком случае — 0 баллов за букву (б) номера 13 ДАЖЕ ПРИ ВЕРНОМ ОТВЕТЕ!

— Также очень придирчивы эксперты к методу отбора корней с помощью тригонометрической окружности. Особенно, если не обозначены границы «дуги», а в итоге также при правильном ответе его «нельзя считать достаточно обоснованным», а значит — 0 баллов за второй пункт. Обидно. Действительно, метод отбора по окружности не очень нагляден, поэтому мы и выбираем самый оптимальный — отбор с помощью двойного неравенства, что позволяет избежать вышеозначенных коллизий.

2. Задание №15. Дробно-рациональные, показательные, логарифмические и другие неравенства (макс. — 2 балла)

Первоочередной вопрос — ОДЗ:

— Аббревиатуры ОДЗ нет ни в одном учебнике федерального комплекта (Мордкович был из перечня исключен). Есть область допустимых значений ФУНКЦИИ, а вот ПЕРЕМЕННОЙ в федеральных программах мы не встретим.

— Есть большой риск указать не все допустимые значения, а значит сразу свести все усилия на нет, ведь написание слова ОДЗ обязывает нас учесть все ограничения, а значит — 0 баллов при идеальном решении основного неравенства, «четко и жестко», как нам объясняют на видео.
НО! Мне не хочется раньше времени «расхолаживать» своих учеников — мол, да не пишите вы слово ОДЗ, а значит — зачем вам знать, какие необходимые условия должны в нем содержаться.
Нет. Знать все ограничения можно и нужно, и на каждом занятии мы будем системно их оттачивать, но на самом экзамене, чтобы минимизировать риски ввиду нервов, ввиду появления номера, прототипов к которому не было и вы можете запутаться и учесть не всё, — вот на самом ЕГЭ слово ОДЗ мы писать НЕ БУДЕМ. Ограничения — приведем, это необходимо. Но связывать себе руки самим термином не станем.

Второй момент — использование рационализации и соответствующее оформление решения логарифмического неравенства данным методом.
Комиссия решила следующее: метод имеет место быть, даже если не всегда рассматривается в обычной школьной программе.
НО! Тогда эксперты предлагают упоминать в решении о монотонном возрастании логарифмической функции. На мой взгляд, наше оформление с приведением совокупности двух систем — двух случаев, на которые распадается исходное неравенство в зависимости от расположения основания относительно единицы и последующая фраза «данная совокупность равносильна неравенству» — представляется мне наиболее системным и понятным способом. По крайней мере, не встретилось еще ни одного случая, чтобы за это «отбирали» балл, напротив — всё проходит гладко. Вот и не будем менять курс. Методу рационализации официально дан «зеленый свет».

​​​​​​​ 3. Задание №17. Текстовая задача с экономическим содержанием (макс. — 3 балла):

— Если применять готовую формулу без ее выведения, решение считается недостаточно обоснованным даже если получен верный ответ. Лучшее — это построение т.н. математической модели (таблица, цепочка логических шагов в строчку в зависимости от вида задачи). В таком случае, даже если в конце допущена арифметическая ошибка, будет поставлено 2 балла из 3-х возможных, что имеет вес. И в конце. Не пренебрегайте оформлением. Не думайте, что проверяющий автоматически склониться в вашу сторону и будет искать логику в разрозненных кусках решений, в хаотическом нагромождении вычислений. Эксперты обязаны накладывать данные критерии оценки, принятые комиссией на федеральном уровне (!) для каждого абитуриента, какими бы строгими и абсурдными они вам не казались. Обидно получать 0 баллов за номер, на который вы потратили столько времени и сил, получили верный ответ, но не сочли важным оформить его должным образом. Будьте внимательнее и аккуратнее. Все полученные знания должны работать на вас, ведь другого случая уже не предоставится. Впереди финишная прямая.

Когда нужно искать одз в уравнениях

Главная
• Список секций
• Математика
• ОДЗ. Зачем, когда и как?

ОДЗ. Зачем, когда и как?

Автор работы награжден дипломом победителя III степени

Введение

Я начал работу с того, что в Интернете пересмотрел множество тем по математике и выбрал эту тему, потому что уверен, что важность нахождения ОДЗ играет огромную роль в решении уравнений и задач. В своей исследовательской работе я рассмотрел уравнения, в которых достаточно только нахождения ОДЗ, опасность, необязательность, ограниченность ОДЗ, некоторые запреты в математике. Самое главное для меня хорошо сдать ЕГЭ по математике, а для этого надо знать: когда, зачем и как находить ОДЗ. Это и подтолкнуло меня к исследованию темы, целью которой, стало показать, что овладение данной темой поможет учащимся правильно выполнить задания на ЕГЭ. Чтобы достичь этой цели, я исследовал дополнительную литературу и другие источники. Мне стало интересно, а знают учащиеся нашей школы: когда, зачем и как находить ОДЗ. Поэтому я провёл тест по теме «Когда, зачем и как находить ОДЗ?» (было дано 10 уравнений). Количество учащихся – 28. Справились – 14 %, опасность ОДЗ (учли) – 68 %, необязательность (учли) – 36 %.

Цель: выявление: когда, зачем и как находить ОДЗ.

Проблема: уравнения и неравенства, в которых нужно находить ОДЗ, не нашли места в курсе алгебры систематического изложения, возможно поэтому я и мои сверстники часто делаем ошибки при решении таких примеров, уделив много времени их решению, забыв при этом об ОДЗ.

Задачи:

1. Показать значимость ОДЗ при решении уравнений и неравенств.
2. Провести практическую работу по данной теме и подвести её итоги.

Я думаю полученные мною, знания и навыки помогут мне решить вопрос: искать ОДЗ или не надо? Я перестану делать ошибки, научившись правильно делать ОДЗ. Получится ли у меня это, покажет время, точнее ЕГЭ[4].

Глава 1

Что такое ОДЗ?

ОДЗ — это область допустимых значений, то есть это все значения переменной, при которых выражение имеет смысл.

Важно. Для нахождения ОДЗ мы не решаем пример! Мы решаем кусочки примера для нахождения запретных мест.

Некоторые запреты в математике. Таких запретных действий в математике очень мало. Но их не все помнят…

• Выражения, состоящие под знаком чётной кратности или должно быть>0 или равно нулю , ОДЗ:f(x)
• Выражение, стоящее в знаменателе дроби не может быть равно нулю , ОДЗ:f(x)
• |f(x)|=g(x), ОДЗ: g(x) 0

Как записать ОДЗ? Очень просто. Всегда рядом с примером пишите ОДЗ. Под этими известными буквами, глядя на исходное уравнение, записываем значения х, которые разрешены для исходного примера. Преобразование примера может изменить ОДЗ и, соответственно ответ.

Алгоритм нахождения ОДЗ:

1. Определите вид запрета.
2. Найти значения, при которых выражение не имеет смысла.
3. Исключить эти значения из множества действительных чисел R[6].

Область допустимых значений (ОДЗ): теория, примеры, решения

Любое выражение с переменной имеет свою область допустимых значений, где оно существует. ОДЗ необходимо всегда учитывать при решении. При его отсутствии можно получить неверный результат.

В данной статье будет показано, как правильно находить ОДЗ, использовать на примерах. Также будет рассмотрена важность указания ОДЗ при решении.

Допустимые и недопустимые значения переменных

Данное определение связано с допустимыми значениями переменной. При введении определения посмотрим, к какому результату приведет.

Начиная с 7 класса, мы начинаем работать с числами и числовыми выражениями. Начальные определения с переменными переходят к значению выражений с выбранными переменными.

Когда имеются выражения с выбранными переменными, то некоторые из них могут не удовлетворять. Например, выражение вида 1 : а , если а = 0 , тогда оно не имеет смысла, так как делить на ноль нельзя. То есть выражение должно иметь такие значения, которые подойдут в любом случае и дадут ответ. Иначе говоря, имеют смысл с имеющимися переменными.

Если имеется выражение с переменными, то оно имеет смысл только тогда, когда при их подстановке значение может быть вычислено.

Если имеется выражение с переменными, то оно не имеет смысл, когда при их подстановке значение не может быть вычислено.

То есть отсюда следует полное определение

Существующими допустимыми переменными называют такие значения, при которых выражение имеет смысл. А если смысла не имеет, значит они считаются недопустимыми.

Для уточнения вышесказанного: если переменных более одной, тогда может быть и пара подходящих значений.

Для примера рассмотрим выражение вида 1 x — y + z , где имеются три переменные. Иначе можно записать, как x = 0 , y = 1 , z = 2 , другая же запись имеет вид ( 0 , 1 , 2 ) . Данные значения называют допустимыми, значит, можно найти значение выражения. Получим, что 1 0 — 1 + 2 = 1 1 = 1 . Отсюда видим, что ( 1 , 1 , 2 ) недопустимы. Подстановка дает в результате деление на ноль, то есть 1 1 — 2 + 1 = 1 0 .

Что такое ОДЗ?

Область допустимых значений – важный элемент при вычислении алгебраических выражений. Поэтому стоит обратить на это внимание при расчетах.

Область ОДЗ – это множество значений, допустимых для данного выражения.

Рассмотрим на примере выражения.

Если имеем выражение вида 5 z — 3 , тогда ОДЗ имеет вид ( − ∞ , 3 ) ∪ ( 3 , + ∞ ) . Эта область допустимых значений, удовлетворяющая переменной z для заданного выражения.

Если имеется выражения вида z x — y , тогда видно, что x ≠ y , z принимает любое значение. Это и называют ОДЗ выражения. Его необходимо учитывать, чтобы не получить при подстановке деление на ноль.

Область допустимых значений и область определения имеет один и тот же смысл. Только второй из них используется для выражений, а первый – для уравнений или неравенств. При помощи ОДЗ выражение или неравенство имеет смысл. Область определения функции совпадает с областью допустимых значений переменной х к выражению f ( x ) .

Как найти ОДЗ? Примеры, решения

Найти ОДЗ означает найти все допустимые значения, подходящие для заданной функции или неравенства. При невыполнении этих условий можно получить неверный результат. Для нахождения ОДЗ зачастую необходимо пройти через преобразования в заданном выражении.

Существуют выражения, где их вычисление невозможно:

• если имеется деление на ноль;
• извлечение корня из отрицательного числа;
• наличие отрицательного целого показателя – только для положительных чисел;
• вычисление логарифма отрицательного числа;
• область определения тангенса π 2 + π · k , k ∈ Z и котангенса π · k , k ∈ Z ;
• нахождение значения арксинуса и арккосинуса числа при значении, не принадлежащем [ — 1 ; 1 ] .

Все это говорит о том, как важно наличие ОДЗ.

Найти ОДЗ выражения x 3 + 2 · x · y − 4 .

Решение

В куб можно возводить любое число. Данное выражение не имеет дроби, поэтому значения x и у могут быть любыми. То есть ОДЗ – это любое число.

Ответ: x и y – любые значения.

Найти ОДЗ выражения 1 3 — x + 1 0 .

Решение

Видно, что имеется одна дробь, где в знаменателе ноль. Это говорит о том, что при любом значении х мы получим деление на ноль. Значит, можно сделать вывод о том, что это выражение считается неопределенным, то есть не имеет ОДЗ.

Ответ: ∅ .

Найти ОДЗ заданного выражения x + 2 · y + 3 — 5 · x .

Решение

Наличие квадратного корня говорит о том, что это выражение обязательно должно быть больше или равно нулю. При отрицательном значении оно не имеет смысла. Значит, необходимо записать неравенство вида x + 2 · y + 3 ≥ 0 . То есть это и есть искомая область допустимых значений.

Ответ: множество x и y , где x + 2 · y + 3 ≥ 0 .

Определить ОДЗ выражения вида 1 x + 1 — 1 + log x + 8 ( x 2 + 3 ) .

Решение

По условию имеем дробь, поэтому ее знаменатель не должен равняться нулю. Получаем, что x + 1 — 1 ≠ 0 . Подкоренное выражение всегда имеет смысл, когда больше или равно нулю, то есть x + 1 ≥ 0 . Так как имеет логарифм, то его выражение должно быть строго положительным, то есть x 2 + 3 > 0 . Основание логарифма также должно иметь положительное значение и отличное от 1 , тогда добавляем еще условия x + 8 > 0 и x + 8 ≠ 1 . Отсюда следует, что искомое ОДЗ примет вид:

x + 1 — 1 ≠ 0 , x + 1 ≥ 0 , x 2 + 3 > 0 , x + 8 > 0 , x + 8 ≠ 1

Иначе говоря, называют системой неравенств с одной переменной. Решение приведет к такой записи ОДЗ [ − 1 , 0 ) ∪ ( 0 , + ∞ ) .

Ответ: [ − 1 , 0 ) ∪ ( 0 , + ∞ )

Почему важно учитывать ОДЗ при проведении преобразований?

При тождественных преобразованиях важно находить ОДЗ. Бывают случаи, когда существование ОДЗ не имеет место. Чтобы понять, имеет ли решение заданное выражение, нужно сравнить ОДЗ переменных исходного выражения и ОДЗ полученного.

• могут не влиять на ОДЗ;
• могут привести в расширению или дополнению ОДЗ;
• могут сузить ОДЗ.

Рассмотрим на примере.

Если имеем выражение вида x 2 + x + 3 · x , тогда его ОДЗ определено на всей области определения. Даже при приведении подобных слагаемых и упрощении выражения ОДЗ не меняется.

Если взять пример выражения x + 3 x − 3 x , то дела обстоят иначе. У нас имеется дробное выражение. А мы знаем, что деление на ноль недопустимо. Тогда ОДЗ имеет вид ( − ∞ , 0 ) ∪ ( 0 , + ∞ ) . Видно, что ноль не является решением, поэтому добавляем его с круглой скобкой.

Рассмотрим пример с наличием подкоренного выражения.

Если имеется x — 1 · x — 3 , тогда следует обратить внимание на ОДЗ, так как его необходимо записать в виде неравенства ( x − 1 ) · ( x − 3 ) ≥ 0 . Возможно решение методом интервалов, тогда получаем, что ОДЗ примет вид ( − ∞ , 1 ] ∪ [ 3 , + ∞ ) . После преобразования x — 1 · x — 3 и применения свойства корней имеем, что ОДЗ можно дополнить и записать все в виде системы неравенства вида x — 1 ≥ 0 , x — 3 ≥ 0 . При ее решении получаем, что [ 3 , + ∞ ) . Значит, ОДЗ полностью записывается так: ( − ∞ , 1 ] ∪ [ 3 , + ∞ ) .

Нужно избегать преобразований, которые сужают ОДЗ.

Рассмотрим пример выражения x — 1 · x — 3 , когда х = — 1 . При подстановке получим, что — 1 — 1 · — 1 — 3 = 8 = 2 2 . Если это выражение преобразовать и привести к виду x — 1 · x — 3 , тогда при вычислении получим, что 2 — 1 · 2 — 3 выражение смысла не имеет, так как подкоренное выражение не должно быть отрицательным.

Следует придерживаться тождественных преобразований, которые ОДЗ не изменят.

Если имеются примеры, которые его расширяют, тогда его нужно добавлять в ОДЗ.

Рассмотрим на примере дроби вида x x 3 + x . Если сократить на x , тогда получаем, что 1 x 2 + 1 . Тогда ОДЗ расширяется и становится ( − ∞ 0 ) ∪ ( 0 , + ∞ ) . Причем при вычислении уже работаем со второй упрощенной дробью.

При наличии логарифмов дело обстоит немного иначе.

Если имеется выражение вида ln x + ln ( x + 3 ) , его заменяют на ln ( x · ( x + 3 ) ) , опираясь на свойство логарифма. Отсюда видно, что ОДЗ с ( 0 , + ∞ ) до ( − ∞ , − 3 ) ∪ ( 0 , + ∞ ) . Поэтому для определения ОДЗ ln ( x · ( x + 3 ) ) необходимо производить вычисления на ОДЗ, то есть ( 0 , + ∞ ) множества.

При решении всегда необходимо обращать внимание на структуру и вид данного по условию выражения. При правильном нахождении области определения результат будет положительным.

Область допустимых значений функции

О чем эта статья:

Допустимые и недопустимые значения переменных

В 7 классе заканчивается математика и начинается ее-величество-алгебра. Первым делом школьники изучают выражения с переменными.

Мы уже знаем, что математика состоит из выражений — буквенных и числовых. Каждому выражению, в котором есть переменная, соответствует область допустимых значений (ОДЗ). Если игнорировать ОДЗ, то в результате решения можно получить неверный ответ. Получается, чтобы быстро получить верный ответ, нужно всегда учитывать область допустимых значений.

Чтобы дать верное определение области допустимых значений, разберемся, что такое допустимые и недопустимые значения переменной.

Рассмотрим все необходимые определения, связанные с допустимыми и недопустимыми значениями переменной.

Выражение с переменными — это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.

Значение числового выражения — это число, которое получается после выполнения всех действий в числовом выражении.

Выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение.

Выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.

Теперь, опираясь на данные определения, мы можем сформулировать, что такое допустимые и недопустимые значения переменной.

Допустимые значения переменных — это значения переменных, при которых выражение имеет смысл.

Если при переменных выражение не имеет смысла, то значения таких переменных называют недопустимыми.

В выражении может быть больше одной переменной, поэтому допустимых и недопустимых значений может быть больше одного.

Пример 1

Рассмотрим выражение

В выражении три переменные (a, b, c).

Запишем значения переменных в виде: a = 0, b = 1, c = 2.

Такие значения переменных являются допустимыми, поскольку при подстановке этих значений в выражение, мы легко можем найти ответ:

Таким же образом можем выяснить, какие значения переменных — недопустимые.

Подставим значения переменных в выражение

На ноль делить нельзя.

Что такое ОДЗ

ОДЗ — это невидимый инструмент при решении любого выражении с переменной. Чаще всего, ОДЗ не отображают графически, но всегда «держат в уме».

Область допустимых значений (ОДЗ) — это множество всех допустимых значений переменных для данного выражения.

Пример 2

Рассмотрим выражение

ОДЗ такого выражения выглядит следующим образом: ( — ∞; 3) ∪ (3; +∞).

Читать запись нужно вот так:
Область допустимых значений переменной x для выражения 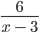— это числовое множество ( — ∞; 3) ∪ (3; +∞).

Пример 3
Рассмотрим выражение

ОДЗ такого выражения будет выглядеть вот так: b ≠ c; a — любое число.

Такая запись означает, что область допустимых значений переменных b, c и a = это все значения переменных, при которых соблюдаются условия b ≠ c; a — любое число.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Как найти ОДЗ: примеры решения

Найти ОДЗ — это значит, что нужно указать все допустимые значения переменных для выражения. Часто, чтобы найти ОДЗ, нужно выполнить преобразование выражения.

Чтобы быстро и верно определять ОДЗ, запомните условия, при которых значение выражения не может быть найдено.

Мы не можем вычислить значение выражения, если:

• требуется извлечение квадратного корня из отрицательного числа;
• присутствует деление на ноль (математическое правило номер раз: никогда не делите на ноль).

Теперь, приступая к поиску ОДЗ, вы можете сверять выражение по всем этим пунктам.

Давайте потренируемся находить ОДЗ.

Пример 4

Найдем область допустимых значений переменной выражения a 3 + 4 * a * b − 6.

В куб возводится любое число. Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a 3 + 4 * a * b − 6 при любых значениях переменной.

ОДЗ переменных a и b — это множество таких пар допустимых значений (a, b), где a — любое число и b — любое число.

Ответ: (a и b), где a — любое число и b — любое число.

Пример 5

Найдем область допустимых значений (ОДЗ) переменной выражения

Здесь нужно обратить внимание на наличие нуля в знаменатели дроби. Одним из условий, при котором вычисление значения выражения невозможно явлется наличие деления на ноль.

Это значит, что мы может сказать, что ОДЗ переменной a в выражении 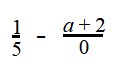— пустое множество.

Пустое множество изображается в виде вот такого символа Ø.

Пример 6

Найдем область допустимых значений (ОДЗ) переменных в выражении

Если есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа. Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.

Ответ: ОДЗ переменных a и b — это множество всех пар, при которых a + 3 * b + 5 ≥ 0.

Запомните

• Если число входит в ОДЗ, то около числа ставим квадратные скобки.
• Если число не входит в ОДЗ, то около него ставятся круглые скобки.

Например, если х > 6, но х

Зачем учитывать ОДЗ при преобразовании выражения

Иногда выражение просто невозможно решить, если не выполнить ряд тождественных преобразований. К ним относятся: перестановки, раскрытие скобок, группировка, вынесение общего множителя за скобки, приведение подобных слагаемых.

Кроме того, что видов таких преобразований довольно много: нужно понимать, в каких случаях какое преобразование возможно. В этом может помочь определение ОДЗ.

Тождественное преобразование может:

• расширить ОДЗ
• никак не повлиять на ОДЗ
• сузить ОДЗ

Рассмотрим каждый случай в отдельности.

Пример 7

Рассмотрим выражение a + 4/a — 4/a

Поскольку мы должны следить за тем, чтобы в выражении не возникало деление на ноль, определяем условие a ≠ 0.

Это условие отвечает множеству (−∞ ; 0) ∪ (0 ; +∞).

В выражении есть подобные слагаемые, если привести подобные слагаемые, то мы получаем выражение вида a.

ОДЗ для a — это R — множество всех вещественных чисел.

Преобразование расширило ОДЗ — добавился ноль.

Пример 8

Рассмотрим выражение a 2 + a + 4 * a

ОДЗ a для этого выражения — множество R.

В выражении есть подобные слагаемые, выполним тождественное преобразование.

После приведения подобных слагаемых выражение приняло вид a 2 + 5 * a

ОДЗ переменной a для этого выражения — множество R.

Это значит, что тождественное преобразование никак не повлияло на ОДЗ.

Пример 9

Рассмотрим выражение

ОДЗ a определяется неравенством (a — 1) * (a — 4) ≥ 0.

Решить такое неравенство можно методом интервалов, что дает нам ОДЗ (−∞; 1] ∪ [4 ; +∞).

Затем выполним преобразование исходного выражения по свойству корней: корень произведения = произведению корней.

Приведем выражение к виду

ОДЗ переменной a для этого выражения определяется неравенствами:
a — 1 ≥ 0
a — 4 ≥ 0

Решив систему линейных неравенств, получаем множество [4; + ∞).

Отсюда видно, что тождественные преобразования сузили ОДЗ.
От (−∞; 1] ∪ [4 ; +∞) до [4; + ∞).

Решив преобразовать выражение, внимательно следите за тем, чтобы не допустить сужение ОДЗ.

Запомните, что выполняя преобразование, следует выбирать такие, которые не изменят ОДЗ.