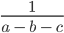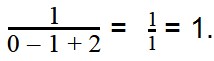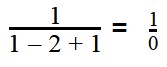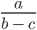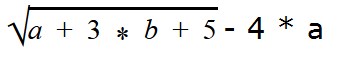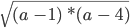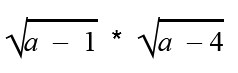Почему одз запретили в егэ

Страшная история и ответ ФИПИ!

Друзья и коллеги, пора поставить точку в одной очень стрррашной и запутанной истории. Можно ли писать: «ОДЗ»? Узнаем ответ специалистов ФИПИ.

История началась весной 2018 года, когда старшеклассники и учителя оказались очень сильно напуганы. Они говорили нам: «Нам учительница запретила писать ОДЗ! Нам сказали: Забудьте про эти страшные три буквы! Лучше ничего не пишите! Или пишите: Ограничения»!

Но что такое «ограничения»? Дал ли кто-нибудь определение этому слову как математическому термину? И можно ли взять и отменить математический термин? Нет, конечно! Ни теорему синусов, ни область допустимых значений уравнения (или неравенства) отменить нельзя.

Страсти не утихают уже почти 2 года.

Можно ли писать: «ОДЗ»? Ответы специалистов ФИПИ.

И меня постоянно спрашивают: «Можно ли писать: «ОДЗ» ? Не снимут ли мне все баллы за мою работу?

Меня также спрашивают, правда ли, что теперь при записи ответа в неравенстве нельзя использовать знак объединения и вместо него надо ставить точку с запятой.

Я задала эти вопросы специалистам ФИПИ – Федерального института педагогических измерений.

Вот что мне ответили:

Уважаемая Анна,

при выполнении заданий с развернутым ответом ЕГЭ по математике профильного уровня участник экзамена должен привести полное обоснованное решение задачи. При этом он может выбирать любой математически корректный способ решения, а также формы записи решения и ответа.

Ни в одном документе ФГБНУ «ФИПИ» нет запрета на использование тех или иных понятий, фактов, способов записи.

В частности, полное, обоснованное решение, корректно использующее понятие «Область допустимых значений», а также запись ответа с использованием знака объединения при проверке работ, согласно критериям, оценивается максимальным баллом.

С уважением, специалисты ФГБНУ «ФИПИ»

Вот и всё. Писать «ОДЗ» можно, только делать это надо правильно. Ведь, по определению, область допустимых значений уравнения или неравенства – это множество значений переменной, при которых обе части данного уравнения имеют смысл.

Например, ОДЗ неравенства

задается системой условий:

Если вы напишете просто «ОДЗ: х>0» — это ошибка. И не потому, что вы написали буквы О, Д и З, а потому, что не полностью указали область допустимых значений.

Вот такие (и многие другие) интересные тонкости оформления мы разбираем на нашем Онлайн-курсе.

Этот курс особенно полезен для учителей и репетиторов. Он дает то самое профессиональное общение, которого учителям так часто не хватает. Дает возможность выяснить все непонятные моменты. И конечно, намного лучше, если мы не пугаем детей иррациональными запретами, не ставим лишних «ограничений», а спокойно и профессионально объясняем то, что непонятно.

В курсе есть все, чтобы подготовить на 100 баллов +.мастер-классы по методике подготовки. Ближайший в эти выходные. И пусть вас не пугает срок доступа. Летом будут специальные акции на продление преподавательского тарифа.

Готовьтесь к ЕГЭ с профессионалами!

Курс «10 класс»

— Теория: текст + 72 ч видеоразборов.
— 35 ч. онлайн занятий с Анной Малковой в месяц.
— ДЗ с проверкой, чат, 2 репетиционных ЕГЭ.

Курс «11 класс, 80 баллов»

— Теория: текст + 72 ч видеоразборов.
— 54 ч. онлайн занятий с Анной Малковой, 3 в месяц.
— ДЗ с проверкой, чат, 9 репетиционных ЕГЭ.

Курс «11 класс, 100 баллов»

— Теория: текст + 72 ч видеоразборов.
— 120 ч. онлайн занятий с Анной Малковой, 8 в месяц.
— ДЗ с проверкой, чат, 9 репетиционных ЕГЭ.

Курс для преподавателей

— Вся теория профильного ЕГЭ, все задачи.
— 4 онлайн занятия в месяц (70 ч.).
— Мастер-классы по методике преподавания раз в месяц (18 ч.).

Повышение цен через 2 дня!

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «ОДЗ писать нельзя? Ответ ФИПИ. Учителя, расскажите ученикам!» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.03.2023

Мы используем файлы cookie, чтобы персонализировать контент, адаптировать и оценивать результативность рекламы, а также обеспечить безопасность. Перейдя на сайт, вы соглашаетесь с использованием файлов cookie.

30 мая 2018

В закладки

Обсудить

Жалоба

Изменение требований к оформлению заданий с развернутым ответом на ЕГЭ по математике

Важные моменты при оформлении второй части профильного ЕГЭ по математике.

1) ОДЗ. Писать ОДЗ можно, но если написали это слово, то писать его нужно целиком. Например, если в знаменателе есть логарифм, то нужно написать не только, что его аргумент >0, но и, что сам знаменатель не равен 0. И так со всеми имеющимися ограничениями. Иначе, это будет неправильное ОДЗ и оценка 0 баллов. Если пишите только часть ограничений, то не пишите слово «ОДЗ». Просто что-нибудь вроде фразы «Должны выполняться условия».

3) ОТБОР КОРНЕЙ ПО ОКРУЖНОСТИ. Обязательно нарисовать на окружности дугу, соответствующую нужному промежутку, обязательно подписать границы этой дуги, поставить точки (решения уравнения) и пояснить, как были отобраны корни, попадающие на дугу.

2) МЕТОД РАЦИОНАЛИЗАЦИИ. Использовать можно, доказывать не обязательно, но надо пояснять. Например, фразой «По методу рационализации в силу строго монотонного возрастания функции y=log_a(x) при a>1 и строго монотонного убывания функции y=log_a(x) при 0 < a < 1 »

4) ИСПОЛЬЗОВАНИЕ ГОТОВЫХ ФОРМУЛ в задаче 17. Без вывода нельзя. Этих формул нет в учебниках, а всё, чего в учебниках нет надо выводить.

5) ОТВЕТЫ НА ПУНКТЫ а) и б) в задаче 19. Просто слова «да/нет» недостаточно. Нужен пример или обоснование.

Подробнее в вебинаре

Каждый выпускник знает, что не так сложно решить задачу с развернутым решением, как ее оформить. Из-за стресса и обидных огрехов на экзамене теряются драгоценные баллы.

Главными правилами оформления заданий в карточках поделилась автор экзаменационных курсов для преподавателей Skysmart Ирина Чегринская.

Первое правило

Три самые опасные буквы на экзамене? ОДЗ. Писать ОДЗ можно, если выписывать все ситуации, в которых выражение не имеет смысла. Если выписать не все, балл будет снижен.

Что делать:

• писать слово «ограничения»,
• пользоваться равносильными переходами,
• или писать ОДЗ и выписывать все ограничения.

Второе правило

Отбор корней в 12 задании. Ученик решил уравнение — один балл. Чтобы заработать второй балл, нужно соблюсти несколько рекомендаций:

1. Корни отбираем любым способом: с помощью графика, числовой окружности, решения двойных неравенств и тому подобное.

2. Серии корней записываем с разными переменными. При выборке корней эта хитрость поможет не запутаться.

3. Перебор корней не останавливаем на корне, принадлежащему отрезку. Такой способ будет недостаточно обоснованным, пункт «б» не засчитают.

4.  При отборе корней с помощью числовой (тригонометрической) окружности отмечаем концы числового отрезка, выделяем дугу, обозначаем корни.

Третье правило

При доказательстве в заданиях 13 и 15 либо указываем теорему, которую использовали, либо ее формулировку.

Четвертое правило

Не так страшен 18 номер, как его малюют. В последнем номере при решении пункта «а» можно пользоваться методом подбора. Если ответ положительный, то достаточно привести пример. Если ответ отрицательный, что бывает реже, то нужно написать доказательство.

Обязательно разбирайте со школьниками 18 номер: с некоторыми пунктами справится даже ученик со средним уровнем подготовки.

Пятое правило

Важно научить ребенка не только решать, оформлять, но и проверять свои ответы, чтобы не было вычислительных ошибок.

Что делать ученику на уроках:

• проверять ход решения,
• самостоятельно искать свои ошибки,
• подставлять ответы в исходные уравнения, неравенства,
• проверять, насколько логичный ответ получился. 

Например, катет не может быть больше гипотенузы, ежемесячный платеж по кредиту должен быть действительно возможным.

Другие статьи автора:

ОДЗ. Зачем, когда и как?

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Я начал работу с того, что в Интернете пересмотрел множество тем по математике и выбрал эту тему, потому что уверен, что важность нахождения ОДЗ играет огромную роль в решении уравнений и задач. В своей исследовательской работе я рассмотрел уравнения, в которых достаточно только нахождения ОДЗ, опасность, необязательность, ограниченность ОДЗ, некоторые запреты в математике. Самое главное для меня хорошо сдать ЕГЭ по математике, а для этого надо знать: когда, зачем и как находить ОДЗ. Это и подтолкнуло меня к исследованию темы, целью которой, стало показать, что овладение данной темой поможет учащимся правильно выполнить задания на ЕГЭ. Чтобы достичь этой цели, я исследовал дополнительную литературу и другие источники. Мне стало интересно, а знают учащиеся нашей школы: когда, зачем и как находить ОДЗ. Поэтому я провёл тест по теме «Когда, зачем и как находить ОДЗ?» (было дано 10 уравнений). Количество учащихся – 28. Справились – 14 %, опасность ОДЗ (учли) – 68 %, необязательность (учли) – 36 %.

Цель: выявление: когда, зачем и как находить ОДЗ.

Проблема: уравнения и неравенства, в которых нужно находить ОДЗ, не нашли места в курсе алгебры систематического изложения, возможно поэтому я и мои сверстники часто делаем ошибки при решении таких примеров, уделив много времени их решению, забыв при этом об ОДЗ.

Задачи:

1. Показать значимость ОДЗ при решении уравнений и неравенств.
2. Провести практическую работу по данной теме и подвести её итоги.

Я думаю полученные мною, знания и навыки помогут мне решить вопрос: искать ОДЗ или не надо?  Я перестану делать ошибки, научившись правильно делать ОДЗ. Получится ли у меня это, покажет время, точнее ЕГЭ[4].

Глава 1

Что такое ОДЗ?

 ОДЗ — это область допустимых значений, то есть это все значения переменной, при которых выражение имеет смысл.

Важно. Для нахождения ОДЗ мы не решаем пример! Мы решаем кусочки примера для нахождения запретных мест.

Некоторые запреты в математике. Таких запретных действий в математике очень мало. Но их не все помнят…

• Выражения, состоящие под знаком чётной кратности или должно быть>0 или равно нулю , ОДЗ:f(x)
• Выражение, стоящее в знаменателе дроби не может быть равно нулю , ОДЗ:f(x)
• |f(x)|=g(x), ОДЗ: g(x) 0

 Как записать ОДЗ? Очень просто. Всегда рядом с примером пишите ОДЗ. Под этими известными буквами, глядя на исходное уравнение, записываем значения х, которые разрешены для исходного примера. Преобразование примера может изменить ОДЗ и, соответственно ответ.

 Алгоритм нахождения ОДЗ:

1. Определите вид запрета.
2. Найти значения, при которых выражение не имеет смысла.
3. Исключить эти значения из множества действительных чисел R[6].

Решить уравнение: =

Без ОДЗ	С ОДЗ
= = х-9=1-х х+х=9+1 2х=10 х=5 Ответ: х=5 Оценка  2	= ОДЗ: => => Ответ: корней нет Оценка 5

Область допустимых значений оберегает нас от таких серьёзных ошибок. Честно говоря, именно из-за ОДЗ многие «ударники» превращаются в «троечников». Считая, что поиск и учёт ОДЗ малозначимым шагом в решении, они пропускают его, а потом удивляются: «почему учитель поставил 2?». Да потому и поставил, что ответ неверен! Это не «придирки» учителя, а вполне конкретная ошибка, такая же как неверное вычисление или потерянный знак[7].

Дополнительные уравнения:

а) = ;      б) -42=14х+ ;      в) =0;       г) |x-5|=2x-2 [5]

Глава 2

 ОДЗ. Зачем? Когда? Как?

 Область допустимых значений – есть решение

1. ОДЗ представляет собой пустое множество, а значит, исходный пример не имеет решений

• = ОДЗ:    

Ответ: корней нет.

• = ОДЗ:

Ответ: корней нет.

• + =2

ОДЗ:   х 0

0, уравнение не имеет корней

Ответ: корней нет.

Дополнительные примеры:

а) + =5;   б) + =23х-18;   в) =0[6].

1. В ОДЗ находится одно или несколько чисел, и несложная подстановка быстро определяет корни.

• +    

ОДЗ: х=2, х=3

Проверка: х=2, + ,  0<1,   верно

Проверка: х=3, + , 0<1, верно.

Ответ: х=2, х=3[8].

• >   ОДЗ: х=1,х=0

Проверка: х=0, > , 0>0, неверно

Проверка: х=1, > , 1>0, верно

Ответ: х=1.

• + =х ОДЗ: х=3

Проверка:  + =3, 0=3, неверно.

Ответ: корней нет.

Дополнительные примеры:

а) = ;   б) + =0;   в) + =х -1[5]

 Опасность ОДЗ

Заметим, тождественные преобразования могут:

• не влиять на ОДЗ;
• приводить к расширенному ОДЗ;
• приводить к сужению ОДЗ.

Известно также, что в результате некоторых преобразований, изменяющих исходное ОДЗ, может привести к неверным решениям.

Давайте поясним каждый случай примером.

1)   Рассмотрим выражение х +4х+7х, ОДЗ переменной х для этого есть множество R. Приведём подобные слагаемые. В результате оно примет вид x²+11x. Очевидно, ОДЗ переменной x этого выражения тоже является множество R. Таким образом, проведенное преобразование не изменило ОДЗ.

2)   Возьмем уравнение x+ — =0. В этом случае ОДЗ: x≠0.  Это выражение тоже содержит подобные слагаемые, после приведения которых, приходим к выражению x, для которого ОДЗ есть R. Что мы видим: в результате проведенного преобразования произошло расширение ОДЗ (к ОДЗ переменной x для исходного выражения добавилось число нуль).

3)   Возьмем выражение .    ОДЗ переменной x определяется неравенством (x−5)·(x−2)≥0, ОДЗ: (−∞, 2]∪[5, +∞).   А теперь преобразуем исходное выражение к виду .    ОДЗ переменной x для этого выражения определяет система линейных неравенств , решение которой дает множество [5, +∞). Таким образом, в результате проведенного преобразования произошло сужение ОДЗ с множества (−∞, 2]∪[5, +∞) до множества [5, +∞)[9].

Решим уравнение:

а)   3х+ = +15.  Перенесём дробь

ОДЗ: х-5 0,  х 5

3х+ — =15

х=5,    5 ОДЗ.       Ответ: корней нет.

б)   =0        х-х=0        =0.      Снова ловушка!

ОДЗ: х-3 0, х 3.     Ответ: х-любое число, кроме х=3.

в)   ,   ОДЗ: х .

Сокращение дробей даёт =0,  х=0. Ловушка!   Ответ: корней нет[6].

Дополнительные примеры: а) =0,   б) =0;

в) 214х+ = +642,   г) + =92[5].

Вывод. Итак, на каждом шаге преобразования выражения постоянно спрашивайте себя: «Не изменяет ли это преобразование ОДЗ»? Если не изменяет, то выполняйте его. Если сужает, то откажитесь от него. А если расширяет, то выполняйте его, но оставайтесь в рамках ОДЗ переменных для исходного выражения. Самый верный шаг – найдите сразу ОДЗ[2].

 Необязательность ОДЗ

Решим уравнение:

а) — =2

=2+ ,   f(x)=  — убывает, g(x)=2+ — возрастает

Значит, уравнение имеет не более одного корня. Решаем методом подбора: х=-1.  Ответ: х=-1.

б) =13-х,   f(x)=  —  возрастает,    g(x)= 13-х – убывает, значит, уравнение имеет не более одного корня. Решаем методом подбора: х=11.

ОДЗ:  х-7≥0 х≥7   

Квадратный корень всегда неотрицателен, значит 13-х>0.

Ответ: х=11.

в) + =0

Так как система, достаточно решить одно из уравнений и проверить, подставив во второе.

х +3х-4=0       а+в+с=0 х =1,  х = , значит х =-4

х=1:    1 +12 1 -11 1-2=0

х=-4:  (-4)  +12 (-4) -11 (-4)-2 0.    Ответ: х=1.

Вывод: нахождение ОДЗ не всегда является обязательным, часто не нужно, а иногда и невозможно — и всё это без какого бы то ни было ущерба для решения примера. Но я согласен с тем, что на уроках математики от нас требуют нахождения ОДЗ в каждом примере[3].

 Нестандартные уравнения

1)|х+4|=2х-10   ОДЗ: 2х-10 0, х 5

х+4=2х-10	-х-4=2х-10
х-2х=-10-4 -х=-14 х=14	-х-2х=4-10 -3х=-6 х=2, 2 ОДЗ

Ответ: х=14.

2) — =23х-18    ОДЗ:  

Так как полученная система решений не имеет, то область решений не имеет, таким образом, область определения уравнения не содержит ни одного корня, значит, данное уравнение не имеет корней[8].

3) + = —           ОДЗ: х

— = =

+ =

f(x)= +  — возрастает ,    g(x)=  — убывает

(так как если h(x) возрастает, то — убывает).

Уравнение имеет не более одного корня. Метод подбора. Ответ: х=2[4].

4) + + + =2

ОДЗ: х=2,х=0. Подставляем числа 2 и 0 в уравнение.

+ + + =2,  2=2

+ + + .

Ответ: х=2[4].

Глава 3

Практическая работа «ОДЗ: когда, зачем и как?»

 Было дано 10 уравнений, 2 неравенства. Количество учащихся – 28. Справились — 14 %, опасность ОДЗ(учли) – 68 %, необязательность (учли)-36%.

	ОДЗ -решение	Опасность ОДЗ	Необязательность ОДЗ	Нестандартные уравнения и неравенства
Иррациональные уравнения	61%	68%	82%	43%
Дробные уравнения	69%	89%	86%	50%
Неравенства	50%	89%	82%	64%
Уравнения, содержащие модуль	86%	96%	43%	61%

Заключение

 Тема работы раскрыта. Цель: выявление: когда, зачем и как находить ОДЗ – раскрыта. В исследовательской работе рассмотрены уравнения, в которых достаточно только нахождения ОДЗ, опасность, необязательность, ограниченность ОДЗ, некоторые запреты в математике. Самое главное для выпускников хорошо сдать ЕГЭ по математике, а для этого надо знать: когда, зачем и как находить ОДЗ.

Задачи, поставленные в работе, решены. Разобраны стандартные и нестандартные уравнения и неравенства. Проведена практическая работа по теме «ОДЗ. Когда? Зачем и как?» И подведены итоги. Полученные читателями, знания и навыки помогут им решить вопрос- искать ОДЗ или не надо?[10]

Каждому выражению с переменными соответствует область допустимых значений (ОДЗ) переменных, которую ОБЯЗАТЕЛЬНО нужно учитывать при работе с этим выражением. Акцент на слове «обязательно» сделан не случайно: при решении примеров и задач халатное отношение к ОДЗ может привести к получению неверных результатов.

Овладение данной темой поможет учащимся правильно выполнить задания на ЕГЭ[4].

Литература

 М.Я. Выгодский «Справочник по элементарной математике». М.: «Наука», 1966.

1. Газета «Математика» №17. 2002.
2. Г.И. Глейзер «История математики в школе VII-VIII классы». М.: «Просвещение», 1982.
3. Л.О. Денищева и др. «ЕГЭ. Математика. Универсальные материалы для подготовки учащихся/ФИПИ» — М.: «Интеллект-центр», 2009.
4. [Электронный ресурс]/Режим доступа: Материалы сайтов www.fipi.ru, www.eg
5. Область допустимых значений – есть решение [Электронный ресурс]/Режим доступа: rudocs.exdat.com›docs/index-16853.html
6. ОДЗ – область допустимых значений, как найти ОДЗ [Электронный ресурс]/Режим доступа: cleverstudents.ru›expressions/odz.html
7. Область допустимых значений: теория и практика [Электронный ресурс]/Режим доступа: pandia.ru›text/78/083/13650.php
8. Что такое ОДЗ [Электронный ресурс]/ Режим доступа: www.cleverstudents.ru›odz.html
9. Что такое ОДЗ и как его искать — объяснение и пример. Электронный ресурс]/ Режим доступа: cos-cos.ru›math/82/

Приложение 1

Практическая работа «ОДЗ: когда, зачем и как?»

Вариант 1	Вариант 2
	= 0
9х+  =  + 27	≤ +
+  = –1
│х+14│= 2 – 2х	=
	8х +  =  – 32
≥  +	+  = 1
= 0	│3-х│=1 – 3х

Приложение 2

Ответы к заданиям практической работы «ОДЗ: когда, зачем и как?»

Вариант 1	Вариант 2
Ответ: корней нет	ОДЗ: х 5 Ответ: х-любое число, кроме х=5
9х+ = +27  ОДЗ: х≠3 Ответ: корней нет	≤+ ОДЗ:→ ОДЗ: х=-3, х=5. Ответ:-3;5.
+=-1 у=  –убывает, у=  –возрастает Значит, уравнение имеет не более одного корня.    Ответ: х=6.	ОДЗ: → →х≥5 → Ответ:х≥5, х≤-6.
│х+14│=2-2х  ОДЗ:2-2х≥0, х≤1 х=-4, х=16, 16 не принадлежит ОДЗ Ответ:-4	=  – убывает,  –возрастает Уравнение имеет не более одного корня.  Ответ: корней нет.
0,  ОДЗ: х≥3,х≤2 Ответ: х≥3,х≤2	8х+ = -32, ОДЗ: х≠-4. Ответ:  корней нет.
≥+ ОДЗ:→ х=7, х=1. Ответ: решений нет	+=1 — возрастает, — убывает Ответ: х=2.
=0     ОДЗ: х≠15 Ответ: х- любое число, кроме х=15.	│3-х│=1-3х, ОДЗ: 1-3х≥0, х≤ х=-1, х=1 не принадлежит ОДЗ.  Ответ:  х=-1.

Просмотров работы: 7658

Весть о марафоне «ЕГЭ — это про100!» вызвала шквал обращений в «МК». Особую активность проявили ребята, сдающие математику и сплошь и рядом опасающиеся, что экзамен будет трудным.

— Больше всего в ЕГЭ по математике меня пугает моя забывчивость. Бывает, что из-за волнения из головы напрочь вылетает какая-то очевидная формула, что может привести к провалу задачи, — опасается одиннадцатиклассница Аня из Москвы. — Еще боюсь, что дадут какие-нибудь задачи нового формата, к которым не будешь готов.

— Самое сложное написать идеально. Во второй части очень многое надо уточнять: расписывать все, даже очевидные вычисления, пояснять формулы и т. д. Иногда за отсутствие какой-нибудь малозначительной детали снимают баллы, — волнуется ученик 11-го класса Павел (г. Балашиха, Московская область).

Подобные опасения, благодаря интерактиву, прилетали на круглый стол чуть ли не ежеминутно. Но так ли уж сложен ЕГЭ по профильной математике?

— Все знания, необходимые для решения задач, ребята получили в школе, и ничего нового на экзамене не будет! — заверил Дмитрий Щербаков. (Вот он, ответ Ане! — «МК».) — Не изменилась и структура экзамена: 19 задач, включая 12 с кратким ответом и 7 с подробным решением. Максимальная оценка 32 первичных балла.

— Все тренировочные материалы с осени размещены на сайте ФИПИ, причем задачи 1-го блока можно найти не только в открытом банке, но и в учебниках. Но прорешивать все демоверсии подряд и уж тем более заучивать их наизусть не надо, — предупредил Ященко. Лучший результат ЕГЭ — тот, что соответствует твоим знаниям. Поэтому не ставь себе заоблачных планок! Исходя из этого, выбирай и вуз.

Как спрогнозировать свой будущий балл ЕГЭ. Лайфхак от экспертов «МК».

Прорешай пару вариантов демоверсий и прикинь, что выходит по баллам. Если для поступления их хватает, готовясь к ЕГЭ, сосредоточься на задачах, которые умеешь решать. Можно глянуть и те, что пока не получаются — это шанс на дополнительный балл (например, за задачу 19А, подсказал Дмитрий Щербаков). — Можно рассчитать, и сколько времени на ЕГЭ тебе потребуется на выполнение ч.I, — разъяснил Иван Ященко Веронике Болотенковой, — порешай эти задания дома, засеки потраченное время и прибавь 15–20 минут, так как на экзамене все будет медленнее.

Задание №19 явно заинтересовало выпускников — о нем в ходе включения Рязани спросил ученик гимназии №5 Николай Бородин.

Это задача на сообразительность, уточнил Дмитрий Щербаков: «Решение требует минимума знаний школьной программы, но ее считают трудной. Поэтому надо очень внимательно прочесть задание и ясно представить, что там происходит. Пункт «А» простой, и заработать не нем балл очень легко. Пункт «Б» труднее, тут надо глубже вникнуть в происходящее: почему те или иные конструкции реализуются или нет. Пункт «В» самый сложный: там надо не только найти решение (например, максимум учащихся в классе), но и доказать, почему их число не может быть больше».

Хит вопросов с ленты — типичные ошибки ЕГЭ по математике.

Лидер — арифметические ошибки: ежегодно более половины не состоявшихся стобалльников выполняют сложные задания ч.II, но глупо ошибаются в простенькой задачке ч.I с кратким ответом. На втором месте ошибки от невнимательности.

К счастью, на эту беду имеется другой лайфхак от Дмитрия Щербакова, им лично опробованный:

— При вычислениях не делай в уме несколько действий сразу: раскрыть скобки, сократить дроби и т. п. Это резко повышает вероятность сделать ошибку, которая потом «не ловится» по черновику. (Помните, Павел из Балашихи спрашивал, зачем нужна подробная запись решения? Вот за этим! — «МК».). Получив ответ, проверь его разумность, а то был случай, когда, решая задачу на расчет стоимости электроэнергии по показаниям счетчика, написали ответ: 300 тыс. руб. И еще, если в задаче надо найти время, ответ не может быть в метрах! Кстати, в 1980-х годах у канадского самолета прямо в полете внезапно закончилось топливо. Его удалось посадить и никто не погиб. А когда стали разбираться в причинах, выяснилось: заправщики спутали килограммы с фунтами, а литры с галлонами, и в результате залили вчетверо меньше топлива, чем нужно для полета.

Другой хит: как готовиться к ЕГЭ?

Ответ прост, как все гениальное: больше решать каждый день задач, включая самые простые — из ч.I, а то и вовсе из базовой математики или даже таблицы умножения. Плюс, делая домашние задания по математике, не поддаваться соблазну и не пользоваться калькулятором. Это отличная зарядка для мозгов!

Но больше всего вопросов было о том, как вести себя на экзамене.

Страх снимает мысленное повторение фразы: «Все нужное для успешной сдачи экзамена мы прошли в школе!» На случай, когда не берется конкретная задача, другие волшебные слова: «Все знания у меня есть, я просто пока не вижу решения!» Начинать надо с задач, которые получаются — если закапываться в трудное задание, на легкие может не остаться времени. Не получается легкая, тоже брось и решай следующую. Потом к ней вернешься, и решение может найтись. Сделал все, что смог — минутный перерыв и проверка. Следующий шаг — задачи, которые понятно, как решать, но это требует больше времени. Сделал — проверил. Затем проверил всю работу. Осталось время — попробуй решить еще что-то, хоть ту же 19А. И не стремись досрочно сдать работу: будешь выходить из класса и поймешь, что сделал ошибку. Но исправить ее будет уже нельзя.

Избежать ошибок позволят и советы экспертов по решению конкретных заданий. Можно ли при решении задания №15 записывать ограничения не в рамках ОДЗ (области допустимых значений)? — спросил при включении г. Грозного Магомед Гуноев из гимназии №1 им. А.-Х. Кадырова.

Единого канонического способа нет. Эксперты принимают любое математически верное решение, так что выбирай на свой вкус. Важно лишь не смешивать разные способы решения: это может привести к ошибкам.

Можно ли использовать метод координат в задании №14?

Да, но проще пользоваться геометрическим методом решения — тогда вероятность ошибки в 6 (!) раз ниже, предупредил Ященко.

Экономические задания №17 (на вклады, проценты и т. п.) не требуют знания вузовских учебников по экономике и финансам: нужен лишь перевод задачи на математический язык и его решение. А задачи №18 с параметрами, хоть и очень яркие, но требуют для решения много времени. Учитывай это, приступая к ним.

Задач на иррациональные неравенства на ЕГЭ не будет, что подтверждает перечень тем на сайте ФИПИ. Так что «левые» источники подготовки к ЕГЭ пугают ими зря! С ними вообще надо бы поосторожнее, предупредили эксперты, отвечая на вопрос, прилетевший из Костромы: «Можно ли решать задания ЕГЭ с помощью теорем и положений, которые не проходят в школе?» Лучше не надо. Для выполнения работы достаточно школьной программы и никаких «тайных» приемов не требуется. Правда, прямых запретов на их использование нет. Но это чревато ошибками и требует в ответе подробной росписи, откуда что взялось — иначе эксперты могут счесть ответ недостаточно обоснованным и снизят балл. Короче, не ведись на посулы обучить экзотическим «универсальным методикам»!

Нужно ли в ответе указывать единицу измерения?

Если ответ записан в тех единицах, что даны в условиях, не нужно.

— Стоит ли перед экзаменом пить успокоительное, — спросил Чинь Хоанг Чунг.

Точно нет, ведь эти снадобья плохо сказываются на сообразительности. Да это и не нужно, подытожил Иван Ященко: «Мы составляли задачи ЕГЭ с любовью, и я надеюсь, вы получить радость от их решения, а потом и от результатов ЕГЭ!»

Третий эфир марафона «МК» «ЕГЭ — это про100!» посвящен обществознанию. Свои вопросы можно прислать на сайт «МК», нашу страницу в соцсети «ВКонтакте» или официальную страницу Рособрнадзора. Ждем вас на наших онлайн-консультациях! И помните: «ЕГЭ — это про100!»

МЕЖДУ ТЕМ. Советы методиста отделения математики Олимпиадных школ МФТИ Татьяны Бабичевой. Чтобы увеличить шансы на сто баллов, надо изучить критерии прошлого года; постоянно повторять теорию и на нее опираться; ощущать, как в голове выстраивается каркас школьной математики — это успокаивает; в каждой задачке, даже самой простой, стараться увидеть ее красоту и логичность; для сложной задачи всегда проверять, все ли данные условия использованы; пользоваться качественными материалами для подготовки. И главное — знать, что мозг может все. Надо лишь ему доверять!

0+

Следите за прямыми эфирами в наших соцсетях VK, YouTube.

Vlad Bel

3 года назад

1) «Проблема» ОДЗ появилась не сегодня и не 2 года назад. Проблема появилась лет 50 назад с хвостиком. Школа только-только становилась обязательной десятилеткой.
В те времена выпускной состоял из 5-6 заданий по алгебре старшей школы (геометрия сдавалась устно и отдельно), все решения которых надо было дать в развернутом виде. И педагоги искали МЕТОДИЧЕСКИЙ приём запоминания алгоритма решения уравнений и неравенств с выражениями, область определения которых была ограничена.
Прием был найден: слабый ученик был обязан вести решение по определенному сценарию, выписывая отдельно области определения каждого выражения, входящего в задание. В уравнениях это позволяло отсечь посторонние корни.
Ошибок у троечников стало меньше. После чего, как это часто бывало в СССР, «передовой опыт» стали внедрять повсеместно, а кое-где при оценивании выпускных экзаменов (а то и вузовских вступительных) стали требовать указание системы ограничений на области определения (пресловутую ОДЗ) в обязательном порядке, снижая оценку даже тогда, когда решение было безукоризненным. Нематематическую ОДЗ стали требовать, как элемент математического знания. Мало того, стали требовать предварительное нахождение ОДЗ в уравнениях, где корни достаточно было проверить простой подстановкой.
После этого в журнале «Математика в школе» появилось несколько разъясняющих статей, в которых было указано, что ОДЗ не просто выдумка методистов, пекущихся о проблемах троечников, но выдумка достаточно вредная, т.к. решающий формально выписывает ОДЗ, а не приучается следить за равносильностью всех преобразований на каждом этапе решения.
Упирающимся рогом методистам (безграмотных методистов хватало во все времена) были продемонстрированы задания, в которых указание ОДЗ не приводило к отсечению, например, всех посторонних корней уравнения, т.к. ОДЗ не могла учесть всех ограничений, появившихся в ходе решения.
«Панацея» не работала. А потому методический термин ОДЗ и алгоритм, с ней связанный, были признаны ВРЕДНЫМИ, свидетельствующими о слабой подготовке ученика, формальном решении им заданий.
Для правильного грамотного решения вполне хватает чисто математических понятий: равносильность, равносильный переход, область определения выражения и т.п.
ОДЗ запретили считать обязательным элементом решения. Методисты стали разрабатывать прием «равносильных преобразований».
2) Нет дыма без огня. Видимо, сегодня нашелся идиот, готовый считать упоминание об ОДЗ рассуждениями ошибочными. Маятник просто качнулся в другую сторону.
3) Можно ли указывать ОДЗ на ЕГЭ? Разумеется, можно. Хотя это и вызывает вопрос «А не троечник ли ты?».
Стоит ли использовать методику решения с помощью ОДЗ? Для очень слабых учеников, с трудом понимающих смысл, но хорошо запоминающих непонятный алгоритм, видимо, стоит.
Я при работе в матклассе НИКОГДА термином ОДЗ не пользовался, считая его дурным тоном.

Когда нужно искать одз в уравнениях

Главная
• Список секций
• Математика
• ОДЗ. Зачем, когда и как?

ОДЗ. Зачем, когда и как?

Автор работы награжден дипломом победителя III степени

Введение

Я начал работу с того, что в Интернете пересмотрел множество тем по математике и выбрал эту тему, потому что уверен, что важность нахождения ОДЗ играет огромную роль в решении уравнений и задач. В своей исследовательской работе я рассмотрел уравнения, в которых достаточно только нахождения ОДЗ, опасность, необязательность, ограниченность ОДЗ, некоторые запреты в математике. Самое главное для меня хорошо сдать ЕГЭ по математике, а для этого надо знать: когда, зачем и как находить ОДЗ. Это и подтолкнуло меня к исследованию темы, целью которой, стало показать, что овладение данной темой поможет учащимся правильно выполнить задания на ЕГЭ. Чтобы достичь этой цели, я исследовал дополнительную литературу и другие источники. Мне стало интересно, а знают учащиеся нашей школы: когда, зачем и как находить ОДЗ. Поэтому я провёл тест по теме «Когда, зачем и как находить ОДЗ?» (было дано 10 уравнений). Количество учащихся – 28. Справились – 14 %, опасность ОДЗ (учли) – 68 %, необязательность (учли) – 36 %.

Цель: выявление: когда, зачем и как находить ОДЗ.

Проблема: уравнения и неравенства, в которых нужно находить ОДЗ, не нашли места в курсе алгебры систематического изложения, возможно поэтому я и мои сверстники часто делаем ошибки при решении таких примеров, уделив много времени их решению, забыв при этом об ОДЗ.

Задачи:

1. Показать значимость ОДЗ при решении уравнений и неравенств.
2. Провести практическую работу по данной теме и подвести её итоги.

Я думаю полученные мною, знания и навыки помогут мне решить вопрос: искать ОДЗ или не надо? Я перестану делать ошибки, научившись правильно делать ОДЗ. Получится ли у меня это, покажет время, точнее ЕГЭ[4].

Глава 1

Что такое ОДЗ?

ОДЗ — это область допустимых значений, то есть это все значения переменной, при которых выражение имеет смысл.

Важно. Для нахождения ОДЗ мы не решаем пример! Мы решаем кусочки примера для нахождения запретных мест.

Некоторые запреты в математике. Таких запретных действий в математике очень мало. Но их не все помнят…

• Выражения, состоящие под знаком чётной кратности или должно быть>0 или равно нулю , ОДЗ:f(x)
• Выражение, стоящее в знаменателе дроби не может быть равно нулю , ОДЗ:f(x)
• |f(x)|=g(x), ОДЗ: g(x) 0

Как записать ОДЗ? Очень просто. Всегда рядом с примером пишите ОДЗ. Под этими известными буквами, глядя на исходное уравнение, записываем значения х, которые разрешены для исходного примера. Преобразование примера может изменить ОДЗ и, соответственно ответ.

Алгоритм нахождения ОДЗ:

1. Определите вид запрета.
2. Найти значения, при которых выражение не имеет смысла.
3. Исключить эти значения из множества действительных чисел R[6].

Область допустимых значений (ОДЗ): теория, примеры, решения

Любое выражение с переменной имеет свою область допустимых значений, где оно существует. ОДЗ необходимо всегда учитывать при решении. При его отсутствии можно получить неверный результат.

В данной статье будет показано, как правильно находить ОДЗ, использовать на примерах. Также будет рассмотрена важность указания ОДЗ при решении.

Допустимые и недопустимые значения переменных

Данное определение связано с допустимыми значениями переменной. При введении определения посмотрим, к какому результату приведет.

Начиная с 7 класса, мы начинаем работать с числами и числовыми выражениями. Начальные определения с переменными переходят к значению выражений с выбранными переменными.

Когда имеются выражения с выбранными переменными, то некоторые из них могут не удовлетворять. Например, выражение вида 1 : а , если а = 0 , тогда оно не имеет смысла, так как делить на ноль нельзя. То есть выражение должно иметь такие значения, которые подойдут в любом случае и дадут ответ. Иначе говоря, имеют смысл с имеющимися переменными.

Если имеется выражение с переменными, то оно имеет смысл только тогда, когда при их подстановке значение может быть вычислено.

Если имеется выражение с переменными, то оно не имеет смысл, когда при их подстановке значение не может быть вычислено.

То есть отсюда следует полное определение

Существующими допустимыми переменными называют такие значения, при которых выражение имеет смысл. А если смысла не имеет, значит они считаются недопустимыми.

Для уточнения вышесказанного: если переменных более одной, тогда может быть и пара подходящих значений.

Для примера рассмотрим выражение вида 1 x — y + z , где имеются три переменные. Иначе можно записать, как x = 0 , y = 1 , z = 2 , другая же запись имеет вид ( 0 , 1 , 2 ) . Данные значения называют допустимыми, значит, можно найти значение выражения. Получим, что 1 0 — 1 + 2 = 1 1 = 1 . Отсюда видим, что ( 1 , 1 , 2 ) недопустимы. Подстановка дает в результате деление на ноль, то есть 1 1 — 2 + 1 = 1 0 .

Что такое ОДЗ?

Область допустимых значений – важный элемент при вычислении алгебраических выражений. Поэтому стоит обратить на это внимание при расчетах.

Область ОДЗ – это множество значений, допустимых для данного выражения.

Рассмотрим на примере выражения.

Если имеем выражение вида 5 z — 3 , тогда ОДЗ имеет вид ( − ∞ , 3 ) ∪ ( 3 , + ∞ ) . Эта область допустимых значений, удовлетворяющая переменной z для заданного выражения.

Если имеется выражения вида z x — y , тогда видно, что x ≠ y , z принимает любое значение. Это и называют ОДЗ выражения. Его необходимо учитывать, чтобы не получить при подстановке деление на ноль.

Область допустимых значений и область определения имеет один и тот же смысл. Только второй из них используется для выражений, а первый – для уравнений или неравенств. При помощи ОДЗ выражение или неравенство имеет смысл. Область определения функции совпадает с областью допустимых значений переменной х к выражению f ( x ) .

Как найти ОДЗ? Примеры, решения

Найти ОДЗ означает найти все допустимые значения, подходящие для заданной функции или неравенства. При невыполнении этих условий можно получить неверный результат. Для нахождения ОДЗ зачастую необходимо пройти через преобразования в заданном выражении.

Существуют выражения, где их вычисление невозможно:

• если имеется деление на ноль;
• извлечение корня из отрицательного числа;
• наличие отрицательного целого показателя – только для положительных чисел;
• вычисление логарифма отрицательного числа;
• область определения тангенса π 2 + π · k , k ∈ Z и котангенса π · k , k ∈ Z ;
• нахождение значения арксинуса и арккосинуса числа при значении, не принадлежащем [ — 1 ; 1 ] .

Все это говорит о том, как важно наличие ОДЗ.

Найти ОДЗ выражения x 3 + 2 · x · y − 4 .

Решение

В куб можно возводить любое число. Данное выражение не имеет дроби, поэтому значения x и у могут быть любыми. То есть ОДЗ – это любое число.

Ответ: x и y – любые значения.

Найти ОДЗ выражения 1 3 — x + 1 0 .

Решение

Видно, что имеется одна дробь, где в знаменателе ноль. Это говорит о том, что при любом значении х мы получим деление на ноль. Значит, можно сделать вывод о том, что это выражение считается неопределенным, то есть не имеет ОДЗ.

Ответ: ∅ .

Найти ОДЗ заданного выражения x + 2 · y + 3 — 5 · x .

Решение

Наличие квадратного корня говорит о том, что это выражение обязательно должно быть больше или равно нулю. При отрицательном значении оно не имеет смысла. Значит, необходимо записать неравенство вида x + 2 · y + 3 ≥ 0 . То есть это и есть искомая область допустимых значений.

Ответ: множество x и y , где x + 2 · y + 3 ≥ 0 .

Определить ОДЗ выражения вида 1 x + 1 — 1 + log x + 8 ( x 2 + 3 ) .

Решение

По условию имеем дробь, поэтому ее знаменатель не должен равняться нулю. Получаем, что x + 1 — 1 ≠ 0 . Подкоренное выражение всегда имеет смысл, когда больше или равно нулю, то есть x + 1 ≥ 0 . Так как имеет логарифм, то его выражение должно быть строго положительным, то есть x 2 + 3 > 0 . Основание логарифма также должно иметь положительное значение и отличное от 1 , тогда добавляем еще условия x + 8 > 0 и x + 8 ≠ 1 . Отсюда следует, что искомое ОДЗ примет вид:

x + 1 — 1 ≠ 0 , x + 1 ≥ 0 , x 2 + 3 > 0 , x + 8 > 0 , x + 8 ≠ 1

Иначе говоря, называют системой неравенств с одной переменной. Решение приведет к такой записи ОДЗ [ − 1 , 0 ) ∪ ( 0 , + ∞ ) .

Ответ: [ − 1 , 0 ) ∪ ( 0 , + ∞ )

Почему важно учитывать ОДЗ при проведении преобразований?

При тождественных преобразованиях важно находить ОДЗ. Бывают случаи, когда существование ОДЗ не имеет место. Чтобы понять, имеет ли решение заданное выражение, нужно сравнить ОДЗ переменных исходного выражения и ОДЗ полученного.

• могут не влиять на ОДЗ;
• могут привести в расширению или дополнению ОДЗ;
• могут сузить ОДЗ.

Рассмотрим на примере.

Если имеем выражение вида x 2 + x + 3 · x , тогда его ОДЗ определено на всей области определения. Даже при приведении подобных слагаемых и упрощении выражения ОДЗ не меняется.

Если взять пример выражения x + 3 x − 3 x , то дела обстоят иначе. У нас имеется дробное выражение. А мы знаем, что деление на ноль недопустимо. Тогда ОДЗ имеет вид ( − ∞ , 0 ) ∪ ( 0 , + ∞ ) . Видно, что ноль не является решением, поэтому добавляем его с круглой скобкой.

Рассмотрим пример с наличием подкоренного выражения.

Если имеется x — 1 · x — 3 , тогда следует обратить внимание на ОДЗ, так как его необходимо записать в виде неравенства ( x − 1 ) · ( x − 3 ) ≥ 0 . Возможно решение методом интервалов, тогда получаем, что ОДЗ примет вид ( − ∞ , 1 ] ∪ [ 3 , + ∞ ) . После преобразования x — 1 · x — 3 и применения свойства корней имеем, что ОДЗ можно дополнить и записать все в виде системы неравенства вида x — 1 ≥ 0 , x — 3 ≥ 0 . При ее решении получаем, что [ 3 , + ∞ ) . Значит, ОДЗ полностью записывается так: ( − ∞ , 1 ] ∪ [ 3 , + ∞ ) .

Нужно избегать преобразований, которые сужают ОДЗ.

Рассмотрим пример выражения x — 1 · x — 3 , когда х = — 1 . При подстановке получим, что — 1 — 1 · — 1 — 3 = 8 = 2 2 . Если это выражение преобразовать и привести к виду x — 1 · x — 3 , тогда при вычислении получим, что 2 — 1 · 2 — 3 выражение смысла не имеет, так как подкоренное выражение не должно быть отрицательным.

Следует придерживаться тождественных преобразований, которые ОДЗ не изменят.

Если имеются примеры, которые его расширяют, тогда его нужно добавлять в ОДЗ.

Рассмотрим на примере дроби вида x x 3 + x . Если сократить на x , тогда получаем, что 1 x 2 + 1 . Тогда ОДЗ расширяется и становится ( − ∞ 0 ) ∪ ( 0 , + ∞ ) . Причем при вычислении уже работаем со второй упрощенной дробью.

При наличии логарифмов дело обстоит немного иначе.

Если имеется выражение вида ln x + ln ( x + 3 ) , его заменяют на ln ( x · ( x + 3 ) ) , опираясь на свойство логарифма. Отсюда видно, что ОДЗ с ( 0 , + ∞ ) до ( − ∞ , − 3 ) ∪ ( 0 , + ∞ ) . Поэтому для определения ОДЗ ln ( x · ( x + 3 ) ) необходимо производить вычисления на ОДЗ, то есть ( 0 , + ∞ ) множества.

При решении всегда необходимо обращать внимание на структуру и вид данного по условию выражения. При правильном нахождении области определения результат будет положительным.

Область допустимых значений функции

О чем эта статья:

Допустимые и недопустимые значения переменных

В 7 классе заканчивается математика и начинается ее-величество-алгебра. Первым делом школьники изучают выражения с переменными.

Мы уже знаем, что математика состоит из выражений — буквенных и числовых. Каждому выражению, в котором есть переменная, соответствует область допустимых значений (ОДЗ). Если игнорировать ОДЗ, то в результате решения можно получить неверный ответ. Получается, чтобы быстро получить верный ответ, нужно всегда учитывать область допустимых значений.

Чтобы дать верное определение области допустимых значений, разберемся, что такое допустимые и недопустимые значения переменной.

Рассмотрим все необходимые определения, связанные с допустимыми и недопустимыми значениями переменной.

Выражение с переменными — это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.

Значение числового выражения — это число, которое получается после выполнения всех действий в числовом выражении.

Выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение.

Выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.

Теперь, опираясь на данные определения, мы можем сформулировать, что такое допустимые и недопустимые значения переменной.

Допустимые значения переменных — это значения переменных, при которых выражение имеет смысл.

Если при переменных выражение не имеет смысла, то значения таких переменных называют недопустимыми.

В выражении может быть больше одной переменной, поэтому допустимых и недопустимых значений может быть больше одного.

Пример 1

Рассмотрим выражение

В выражении три переменные (a, b, c).

Запишем значения переменных в виде: a = 0, b = 1, c = 2.

Такие значения переменных являются допустимыми, поскольку при подстановке этих значений в выражение, мы легко можем найти ответ:

Таким же образом можем выяснить, какие значения переменных — недопустимые.

Подставим значения переменных в выражение

На ноль делить нельзя.

Что такое ОДЗ

ОДЗ — это невидимый инструмент при решении любого выражении с переменной. Чаще всего, ОДЗ не отображают графически, но всегда «держат в уме».

Область допустимых значений (ОДЗ) — это множество всех допустимых значений переменных для данного выражения.

Пример 2

Рассмотрим выражение

ОДЗ такого выражения выглядит следующим образом: ( — ∞; 3) ∪ (3; +∞).

Читать запись нужно вот так:
Область допустимых значений переменной x для выражения 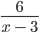— это числовое множество ( — ∞; 3) ∪ (3; +∞).

Пример 3
Рассмотрим выражение

ОДЗ такого выражения будет выглядеть вот так: b ≠ c; a — любое число.

Такая запись означает, что область допустимых значений переменных b, c и a = это все значения переменных, при которых соблюдаются условия b ≠ c; a — любое число.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Как найти ОДЗ: примеры решения

Найти ОДЗ — это значит, что нужно указать все допустимые значения переменных для выражения. Часто, чтобы найти ОДЗ, нужно выполнить преобразование выражения.

Чтобы быстро и верно определять ОДЗ, запомните условия, при которых значение выражения не может быть найдено.

Мы не можем вычислить значение выражения, если:

• требуется извлечение квадратного корня из отрицательного числа;
• присутствует деление на ноль (математическое правило номер раз: никогда не делите на ноль).

Теперь, приступая к поиску ОДЗ, вы можете сверять выражение по всем этим пунктам.

Давайте потренируемся находить ОДЗ.

Пример 4

Найдем область допустимых значений переменной выражения a 3 + 4 * a * b − 6.

В куб возводится любое число. Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a 3 + 4 * a * b − 6 при любых значениях переменной.

ОДЗ переменных a и b — это множество таких пар допустимых значений (a, b), где a — любое число и b — любое число.

Ответ: (a и b), где a — любое число и b — любое число.

Пример 5

Найдем область допустимых значений (ОДЗ) переменной выражения

Здесь нужно обратить внимание на наличие нуля в знаменатели дроби. Одним из условий, при котором вычисление значения выражения невозможно явлется наличие деления на ноль.

Это значит, что мы может сказать, что ОДЗ переменной a в выражении 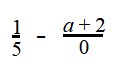— пустое множество.

Пустое множество изображается в виде вот такого символа Ø.

Пример 6

Найдем область допустимых значений (ОДЗ) переменных в выражении

Если есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа. Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.

Ответ: ОДЗ переменных a и b — это множество всех пар, при которых a + 3 * b + 5 ≥ 0.

Запомните

• Если число входит в ОДЗ, то около числа ставим квадратные скобки.
• Если число не входит в ОДЗ, то около него ставятся круглые скобки.

Например, если х > 6, но х

Зачем учитывать ОДЗ при преобразовании выражения

Иногда выражение просто невозможно решить, если не выполнить ряд тождественных преобразований. К ним относятся: перестановки, раскрытие скобок, группировка, вынесение общего множителя за скобки, приведение подобных слагаемых.

Кроме того, что видов таких преобразований довольно много: нужно понимать, в каких случаях какое преобразование возможно. В этом может помочь определение ОДЗ.

Тождественное преобразование может:

• расширить ОДЗ
• никак не повлиять на ОДЗ
• сузить ОДЗ

Рассмотрим каждый случай в отдельности.

Пример 7

Рассмотрим выражение a + 4/a — 4/a

Поскольку мы должны следить за тем, чтобы в выражении не возникало деление на ноль, определяем условие a ≠ 0.

Это условие отвечает множеству (−∞ ; 0) ∪ (0 ; +∞).

В выражении есть подобные слагаемые, если привести подобные слагаемые, то мы получаем выражение вида a.

ОДЗ для a — это R — множество всех вещественных чисел.

Преобразование расширило ОДЗ — добавился ноль.

Пример 8

Рассмотрим выражение a 2 + a + 4 * a

ОДЗ a для этого выражения — множество R.

В выражении есть подобные слагаемые, выполним тождественное преобразование.

После приведения подобных слагаемых выражение приняло вид a 2 + 5 * a

ОДЗ переменной a для этого выражения — множество R.

Это значит, что тождественное преобразование никак не повлияло на ОДЗ.

Пример 9

Рассмотрим выражение

ОДЗ a определяется неравенством (a — 1) * (a — 4) ≥ 0.

Решить такое неравенство можно методом интервалов, что дает нам ОДЗ (−∞; 1] ∪ [4 ; +∞).

Затем выполним преобразование исходного выражения по свойству корней: корень произведения = произведению корней.

Приведем выражение к виду

ОДЗ переменной a для этого выражения определяется неравенствами:
a — 1 ≥ 0
a — 4 ≥ 0

Решив систему линейных неравенств, получаем множество [4; + ∞).

Отсюда видно, что тождественные преобразования сузили ОДЗ.
От (−∞; 1] ∪ [4 ; +∞) до [4; + ∞).

Решив преобразовать выражение, внимательно следите за тем, чтобы не допустить сужение ОДЗ.

Запомните, что выполняя преобразование, следует выбирать такие, которые не изменят ОДЗ.