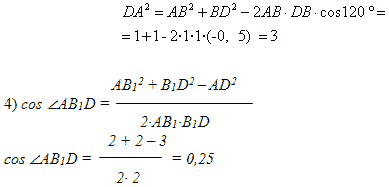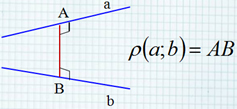Подготовка к егэ 14 задание математика профиль презентация - Помощь в подготовке к экзаменам и поступлению

Слайд 1

Решение заданий №14 ЕГЭ профильного уровня (нахождение углов, расстояний, построение сечений)

Слайд 2

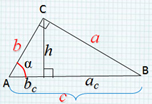
Соотношения между сторонами и углами прямоугольного треугольника Повторение. C A В a 2 + b 2 = c 2 c b a b c a c h α

Слайд 3

a 2 = B a A C c b Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними . b 2 + c 2 – 2bc cosA Теорема косинусов

Слайд 4

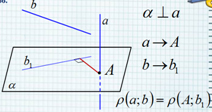
Угол между пересекающимися и скрещивающимися прямыми α 180 0 — α 0 0 < α 90 0 1. 2. Угол между скрещивающимися прямыми АВ и С D определяется как угол между пересекающимися прямыми А 1 В 1 и С 1 D 1 , при этом А 1 В 1 || АВ и С 1 D 1 || CD. А В D С А 1 В 1 С 1 D 1 α М 1

Слайд 5

A D C H ∠ ( (АСН); (СН D )) – это двугранный ∠ АСН D , где СН-общее ребро. Точки А и D лежат на гранях этого угла. AF⊥CH, FD⊥CH. F ∠ AFD – линейный угол двугранного ∠ А CHD Угол между плоскостями

Слайд 6

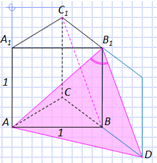
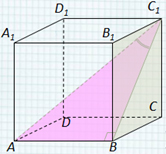
В правильной треугольной призме ABCA 1 B 1 C 1 , все рёбра которой равны 1, найдите косинус угла между прямыми АВ 1 и ВС 1 . Задача № 1 1 А С В D А 1 С 1 В 1 1 3) из ∆ABD по теореме косинусов Продлим плоскость ВСС 1 , тогда ∠(AB 1 , ВС 1 ) = ∠(AB 1 , DВ 1 ) = ∠ AВ 1 D, т. к. C 1 В || B 1 D. Решение:

Слайд 7

В правильной треугольной призме ABCA 1 B 1 C 1 , все рёбра которой равны 1, найдите косинус угла между прямыми АВ 1 и ВС 1 . Задача № 1 (продолжение) 1 А С В D А 1 С 1 В 1 1 Решение: 4) cos ∠ AB 1 D = AB 1 2 + B 1 D 2 – AD 2 2·AB 1 · B 1 D cos ∠ AB 1 D = = 2 + 2 – 3 1 2· 2 4 Ответ: 0,25 .

Слайд 8

В кубе ABCDA 1 B 1 C 1 D 1 найдите угол между прямой AC 1 и плоскостью ВС C 1 . Задача № 2 С В D А 1 С 1 В 1 D 1 А Решение: ВС 1 — проекция прямой АС 1 на плоскость(В C С 1 ), так как AB ⊥ (В C С 1 ) AB ⊥ ВС 1 ; ∠( AC 1 , ( В C С 1 ) ) = ∠( A С 1 ,С 1 В) = ∠ AC 1 B , т.е. ∆ АВC 1 – прямоугольный 3) tg ∠ AC 1 B = = = AB a 1 BC 1

Слайд 9

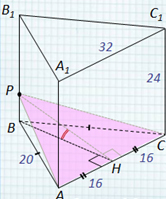
Основанием прямой треугольной призмы ABCA 1 B 1 C 1 , является равнобедренный треугольник АВС , в котором АВ = ВС = 20, АС = 32. Боковое ребро призмы равно 24. Точка Р принадлежит ребру ВВ 1 , причем ВР : РВ 1 = 1 : 3. Найдите тангенс угла между плоскостями А 1 В 1 С 1 и АСР . 20 А С В А 1 С 1 В 1 24 Ответ: 0,5 . Задача № 3 Р Н 16 16 Решение: 1) Так как (АВС) ∥ (А 1 В 1 С 1 ), то ∠(( А 1 В 1 С 1 ) , (АСР)) = ∠( (АВС),(АСР)). 2) Т.к. ВН  АС (высота р / б ∆ ), то по теореме о трех перпендикулярах РН  АС. 3) Тогда ∠ РНВ – линейный угол двугранного ∠ РАСВ. Найдем его из прямоугольного ∆ РНВ. 4) РВ = ¼ ВВ 1 = ¼ · 24 = 6, 5) ВН 2 = АВ 2 – АН 2 (из ∆ A НВ) ВН 2 = 20 2 – 16 2 = 144, ВН = 12; 6) tg ∠ РНВ = PB / HB = 6 / 12 = 0,5. 32

Слайд 10

Решение: Так как ABCD – квадрат, то АВ ⊥ AD . Поэтому проекция AB на плоскость (SAD) будет ⊥ AD. Значит, искомый угол – двугранный угол при ребре основания AD. В правильной четырехугольной пирамиде S ABCD, все ребра которой равны 1, найдите косинус угла между прямой AB и плоскостью SAD . Задача № 4 С В D А S O M N 3) ∠ SMO – искомый угол, косинус которого найдем из прямоугольного ∆ SMO cos ∠ SMO = = = MO 0,5 1 SM

Слайд 11

Расстояние от точки до прямой Определение. Расстоянием от точки до прямой в пространстве называется длина перпендикуляра, проведённого из данной точки к данной прямой. перпендикуляр Повторение.

Слайд 12

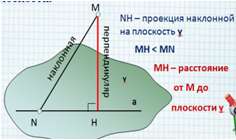
Расстояние от точки до плоскости Определение. Расстоянием от точки до плоскости является длина перпендикуляра, проведённого из данной точки к данной плоскости. перпендикуляр a ɣ M H N наклонная NH – проекция наклонной на плоскость ɣ MH < MN М H – расстояние от М до плоскости ɣ

Слайд 13

Общим перпендикуляром двух скрещивающихся прямых называют отрезок с концами на этих прямых, являющийся перпендикуляром к каждой из них. a b A B Определение. Расстоянием между скрещивающимися прямыми называют длину их общего перпендикуляра. Расстояние между скрещивающимися прямыми

Слайд 14

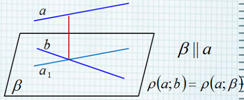
Способы вычисления расстояния между скрещивающимися прямыми Расстояние между скрещивающимися прямыми равно расстоянию от любой точки одной из этих прямых до плоскости, проходящей через вторую прямую параллельно первой прямой. 1 способ.

Слайд 15

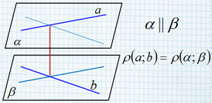
Способы вычисления расстояния между скрещивающимися прямыми Расстояние между скрещивающимися прямыми равно расстоянию между двумя параллельными плоскостями, содержащими эти прямые. 2 способ.

Слайд 16

Способы вычисления расстояния между скрещивающимися прямыми Расстояние между скрещивающимися прямыми равно расстоянию между их проекциями на плоскость, перпендикулярную одной из них. 3 способ.

Слайд 17

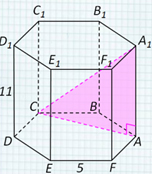
В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , стороны основания которой равны 5, а боковые рёбра равны 11, найдите расстояние от точки С до прямой A 1 F 1 . Задача № 5 Решение: 1)Так как ABCDEF – правильный шестиугольник, то C A ⊥ AF . C A ⊥ A 1 А по определению правильной призмы. C A ⊥(А A 1 F 1 ) по признаку перпендикулярности прямой и плоскости, т.е. СА –перпендикуляр к плоскости, C A 1 — наклонная , A 1 А – проекция наклонной, A 1 А ⊥ A 1 F 1 ; A 1 F 1 – прямая в плоскости. 5 А С В D F E А 1 С 1 В 1 D 1 F 1 E 1 11 Тогда по теореме о трёх перпендикулярах CA 1 ⊥ A 1 F 1 , значит длина отрезка C A 1 равна искомому расстоянию .

Слайд 18

В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , стороны основания которой равны 5, а боковые рёбра равны 11, найдите расстояние от точки С до прямой A 1 F 1 . Задача № 5 (продолжение) Решение: 2) Из ∆ АВС (АВ=ВС=5, ) по теореме косинусов найдём СА: , , C A = . 3) Из ∆ CAA 1, по теореме Пифагора найдём CA 1 : CA 1 2 = 75 + 121 = 196 . CA 1 = 14 Ответ: 14 . 5 А С В D F E А 1 С 1 В 1 D 1 F 1 E 1 11 Доказано, что C A 1 — искомое расстояние .

Слайд 19

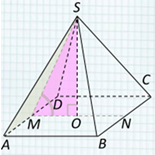
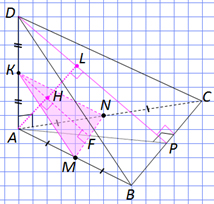
Ребро AD пирамиды DABC перпендикулярно плоскости основания АВС . Найдите расстояние от А до плоскости, проходящей через середины ребер АВ , АС и А D , если А D = , АВ = АС = 10, ВС = . D C B A N F М К Р Искомое расстояние AH равно половине расстояния от вершины А до плоскости BCD , т.к. (KMN) ∥ (BCD) и KF – средняя линия ∆ ADP . L Н Задача № 6 Решение: Построим плоскость КМ N. Т. к. КМ – средняя линия ∆А D В, КМ∥ D В, MN — средняя линия ∆АВ C , М N ∥ C В, то (KMN) ∥ (BCD) по признаку ∥ плоскостей. АР–медиана и высота р/б , KF –медиана и высота р/б DP ⊥ BC по теореме о трёх перпендикулярах. ∆АВ C ∆ KMN . KF ∥ DP .

Слайд 20

Ребро AD пирамиды DABC перпендикулярно плоскости основания АВС . Найдите расстояние от А до плоскости, проходящей через середины ребер АВ , АС и А D , если А D = , АВ = АС = 10, ВС = . D C B A N F М К Р Решение: Доказано, что AH — искомое расстояние. Найдём АР из ∆АВР по теореме Пифагора ( АВ= 10, ВР = ): AP 2 = AB 2 – BP 2 = 100 – 20 = = 80 ; АР= Найдём D Р из ∆А D Р по теореме Пифагора: DP 2 = AD 2 + AP 2 = = 20 + 80 = 100 ; DP = 10 . Тогда AL =( · ) : 10=4 Итак, АН = ½ AL = 2 . L Н Ответ: 2. Задача № 6 (продолжение). 2) ∆ LDA и ∆ ADP подобны по двум углам, LA:AP=AD:DP , тогда AL=(AP*AD):DP.

Слайд 21

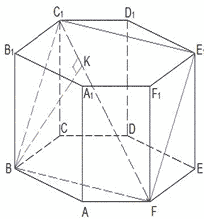
Задача № 7 В правильной шестиугольной призме АВCDEFA 1 B 1 C 1 D 1 E 1 F 1 все рёбра равны 1. а) Постройте сечение призмы плоскостью, проходящей через точки B, С 1 и F. б) Найдите расстояние от точки В до прямой C 1 F. Решение: а) 1) ВС 1 , BF, F Е 1 // С 1 B , Е 1 C 1 => Сечение – четырёхугольник BC 1 E 1 F с диагональю C 1 F. 4) Так как ∠ CBF=90°, то по теореме о трёх перпендикулярах, BF ⟘ BC 1 . Значит, сечение BC 1 E 1 F – прямоугольник. Диагональ прямоугольника C 1 F 2 =BF 2 +BC 1 2 ; C 1 F 2 =3+2=5.

Слайд 22

Задача № 7 (продолжение) Решение. б) Сечение – прямоугольник BC 1 E 1 F. ВК ⊥C 1 F, ВК – искомое расстояние от точки В до прямой C 1 F. Найдем ВК как высоту из ∆FBС 1 , Используя 2 формулы площади треугольника. В правильной шестиугольной призме АВCDEFA 1 B 1 C 1 D 1 E 1 F 1 все рёбра равны 1. а) Постройте сечение призмы плоскостью, проходящей через точки B, С 1 и F. б) Найдите расстояние от точки В до прямой C 1 F.

Слайд 23

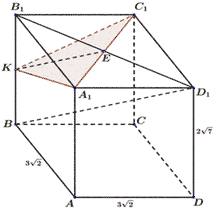
Задача №8 Основанием прямой четырехугольной призмы является квадрат ABCD со стороной , высота призмы равна . Точка K − середина ребра ВВ1. Через точки K и С1 проведена плоскость α, параллельная прямой BD1. а) Докажите, что сечение призмы плоскостью α является равнобедренным треугольником. б) Найдите периметр треугольника, являющегося сечением призмы плоскостью α. Решение. а) Для построения сечения призмы плоскостью α, проведём КЕ|| BD 1 , E € B 1 D 1 . Плоскость α проходит через точки К, С 1 и Е. Так как К – середина ВВ 1 и КЕ|| BD 1 , то Е – середина диагонали А 1 С 1 квадрата А 1 В 1 С 1 D 1 . Значит, плоскость α пересекает грань А 1 В 1 С 1 D 1 по диагонали А 1 С 1 . Соединив точки К, С 1 и А 1 , получаем ∆А 1 КС 1 — сечение призмы плоскостью α. ∆А 1 КВ 1 = ∆С 1 КВ 1 по двум сторонам и углу между ними (А 1 В 1 =С 1 В 1 ), В 1 К – общая сторона, . Из равенства треугольников следует, что А 1 К=С 1 К, значит ∆А 1 КС 1 — равнобедренный.

Слайд 24

Задача №8 (продолжение) Основанием прямой четырехугольной призмы ABCDA 1 B 1 C 1 D 1 является квадрат ABCD со стороной , высота призмы равна . Точка K − середина ребра ВВ 1 . Через точки K и С 1 проведена плоскость α, параллельная прямой BD 1 . а) Докажите, что сечение призмы плоскостью α является равнобедренным треугольником. б) Найдите периметр треугольника, являющегося сечением призмы плоскостью α. Решение. б)

Источник

Свидетельство о регистрации
СМИ: ЭЛ № ФС 77-58841
от 28.07.2014

Зачем размещать разработки
у нас?

Свидетельство бесплатно
Нам доверяют
Нужно использовать при аттестации

Свидетельство о публикации
в СМИ

Дождитесь публикации материала
и скачайте свидетельство
о публикации в СМИ бесплатно.

Диплом за инновационную
профессиональную
деятельность

Опубликует не менее 15
материалов в методической
библиотеке портала и скачайте
документ бесплатно.

16.08.2022

Презентация для подготовки к ЕГЭ по математике профильного уровня Общие методы решения неравенств (14 задание ЕГЭ)
Данную презентацию можно сохранить в формате ПДФ, для использования на интерактивной доске или при проведении онлайн-уроков или репетиторства по подготовке к ЕГЭ

Оценить

133

«Свидетельство участника экспертной комиссии»

Оставляйте комментарии к работам коллег и получите документ
БЕСПЛАТНО!

Источник

1. Повторение.

1.1.Соотношения между сторонами и углами
прямоугольного треугольника

Формулы: a² + b²= c²

1.2.Теорема косинусов

Квадрат стороны треугольника равен сумме
квадратов двух других сторон минус удвоенное
произведение этих сторон на косинус угла между
ними.

a² = b² + c²– 2bc·cosA

1.3. Угол между пересекающимися и
скрещивающимися прямыми.

За
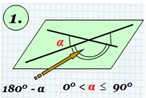
угол между пересекающимися прямыми принимают
острый угол, образованный этими прямыми.

Угол между скрещивающимися прямыми АВ и СD
определяется как угол между пересекающимися
прямыми А₁В₁ и С₁D₁, при
этом А₁В₁|| АВ и С₁D₁|| CD.

1.4. Угол между плоскостями (АСН) и (СНD) – это
двугранный угол АСНD, где СН ребро.

Точки
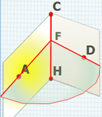
А и D лежат на гранях этого угла. AF CH, FD CH.

Угол AFD – линейный угол двугранного угла АCHD

2. Решение задач.

Задача №1.В правильной треугольной
призме ABCA₁B₁C₁, все рёбра которой
равны 1, найдите косинус угла между прямыми АВ₁
и ВС₁.

Решение:

1) Продлим плоскость ВСС₁, тогда (AB₁, ВС₁) = (AB₁, DВ₁) =
AВ₁D, т. к. C₁В || B₁D.

2) AB_{1 =}B₁D =из ABB_1.

3) из ABD по теореме
косинусов:

Ответ: 0,25.

Задача №2. В кубе ABCDA₁B₁C₁D₁
найдите угол между прямой AC₁ и плоскостью
ВСC₁.

Решение:

1) ВС₁ — проекция прямой АС₁ на
плоскость (ВCС₁), так как AB (ВCС₁), то AB ВС₁;

(AC₁, (ВCС₁))
= (AС₁,С₁В) = AC₁B, т.е. АВC₁ – прямоугольный.

2) Пусть АВ = а, тогда ВС₁ = а из C₁CB.

3) .

4) AC₁B = arctg .

Ответ: arctg .

Задача №3. Основанием прямой
треугольной призмы ABCA₁B₁C₁,
является равнобедренный треугольник АВС, в
котором АВ = ВС = 20, АС = 32. Боковое ребро
призмы равно 24. Точка Р принадлежит ребру ВВ₁,
причем ВР : РВ₁= 1 : 3. Найдите тангенс
угла между плоскостями А₁В₁С₁
и АСР.

Решение:

1) Так как (АВС) || (А₁В₁С₁), то (( А₁В₁С₁) ,
(АСР)) = ((АВС),(АСР)).

2) Т.к. ВН АС (высота
р/б ),то по теореме о
трех перпендикулярах РН АС.

3) Тогда РНВ –
линейный угол двугранного РАСВ. Найдем его из прямоугольного РНВ.

4) РВ = 1/4 ВВ₁ = 1/4 · 24 = 6,

5) ВН² = АВ² – АН²(из AНВ)

ВН² = 20² – 16² = 144, ВН = 12;

6) tg РНВ = PB/HB = 6/12 = 0,5.

Ответ: 0,5.

Задача №4. В правильной
четырехугольной пирамиде SABCD, все ребра которой
равны 1, найдите косинус угла между прямой AB и
плоскостью SAD.

Решение:

1) Так как ABCD – квадрат, то АВ AD. Поэтому проекция AB на плоскость (SAD)
будет AD. Значит,
искомый угол – двугранный угол при ребре
основания AD.

2) SM – высота грани SAD, SM =/2,
МО || АВ, МО = 0,5АВ = 0,5.

3) ?SMO – искомый угол, косинус которого найдем из
прямоугольного SMO.

сos ?SMO =
= =

Ответ :.

3. Повторение.

3.1. Расстояние от точки до прямой.

Определение. Расстоянием от
точки до прямой в пространстве называется длина
перпендикуляра, проведённого из данной точки к
данной прямой.

3.2. Расстояние от точки до плоскости.

Определение. Расстоянием от
точки до плоскости является длина
перпендикуляра, проведённого из данной точки к
данной плоскости.

3.3. Расстояние между скрещивающимися
прямыми.

Общим перпендикуляром двух скрещивающихся
прямых называют отрезок с концами на этих прямых,
являющийся перпендикуляром к каждой из них.

Определение. Расстоянием между
скрещивающимися прямыми называют длину их
общего перпендикуляра.

1 способ. Расстояние между скрещивающимися
прямыми равно расстоянию от любой точки одной из
этих прямых до плоскости, проходящей через
вторую прямую параллельно первой прямой.

2 способ. Расстояние между скрещивающимися
прямыми равно расстоянию между двумя
параллельными плоскостями, содержащими эти
прямые.

3 способ. Расстояние между скрещивающимися
прямыми равно расстоянию между их проекциями на
плоскость, перпендикулярную одной из них.

4. Решение задач.

Задача №5. В правильной шестиугольной
призме ABCDEFA₁B₁C₁D₁E₁F₁,
стороны основания которой равны 5, а боковые
рёбра равны 11, найдите расстояние от точки С
до прямой A₁F₁.

Решение:

1) Так как ABCDEF – правильный шестиугольник, то
прямые AC и AF перпендикулярны.

CA AFпо доказанному,

CA A₁А по
определению правильной призмы

CA (АA₁F₁)
по признаку перпендикулярности прямой и
плоскости, т.е.

СА – перпендикуляр к плоскости, CA₁—
наклонная, A₁А – проекция наклонной,

A₁А A₁F₁;
A₁F₁– прямая в плоскости.

Тогда по теореме о трёх перпендикулярах CA₁ A₁F₁, значит,
длина отрезка CA₁ равна искомому расстоянию.

2) Из АВС (АВ=ВС=5, B = 120^o)

по теореме косинусов найдём СА: , ,

3) Из CAA_1,по теореме
Пифагора найдём CA₁:

CA₁²= 75 + 121 = 196

CA₁ = 14

Ответ: 14.

Задача №6.

Ребро AD пирамиды DABC перпендикулярно
плоскости основания АВС. Найдите расстояние
от А до плоскости, проходящей через середины
ребер АВ, АС и АD, если АD = 2, АВ = АС = 10, ВС
= 4.

Решение:

1) Построим плоскость КМN.

Т. к. КМ – средняя линия АDВ,
КМ?DВ,

MN — средняя линия АВC, МN
||| CВ, то (KMN) || (BCD) по признаку

параллельности плоскостей. АР – медиана и
высота р/б АВC.

KF – медиана и высота р/б KMN.

DP BC по теореме о трёх
перпендикулярах, KF || DP.

Искомое расстояние AH равно половине расстояния
от вершины А до плоскости BCD, т.к. (KMN) || (BCD) и KF –
средняя линия ADP.

2) LDA и ADP подобны по двум углам, тогда LA:AP=AD:DP,
тогда AL = (AP*AD):DP.

Найдём АР из АВР по
теореме Пифагора (АВ=10, ВР = 2 ):

AP² = AB² – BP² = 100 – 20 = 80, АР= 4

Найдём DР из АDР по
теореме Пифагора: DP² = AD² + AP² = 20 +
80 = 100, DP = 10.

Тогда AL =( 4 · 2):10=4. Итак, АН = 1/2 AL =
2.

Ответ: 2.

Задача №7.

В правильной шестиугольной призме АВCDEFA₁B₁C₁D₁E₁F₁ все
рёбра равны 1.

а) Постройте сечение призмы плоскостью,
проходящей через точки B, С₁ и F.

б) Найдите расстояние от точки В до прямой C₁F.

Решение.

а) Сечение – четырёхугольник BC₁E₁F с
диагональю C₁F.

Сторона ВC₁= — диагональ квадрата ВВ1С1С со
стороной 1.

Сторону BF найдём из ABF по
теореме косинусов:

BF²=AB²+AF²-2 * AB * AF * cosBAF;

BF²=AB²+AF²-2 * AB * AF * cos120⁰= 3.

Тогда

Так как CBF=90°, то по
теореме о трёх перпендикулярах, BF BC₁.

Значит,
сечение BC₁E₁F – прямоугольник.
Диагональ прямоугольника C₁F²=BF²+BC₁²;
C₁F²=3+2=5.

Отсюда

б) Сечение – прямоугольник BC₁E₁F.

ВК C₁F, ВК –
искомое расстояние от точки В до прямой C₁F.

Найдем ВК как высоту из FBС₁,

Используя 2 формулы площади треугольника.

Задача №8.

Основанием прямой четырехугольной призмы
является квадрат ABCD со стороной , высота призмы равна . Точка K — середина ребра ВВ1.
Через точки K и С₁ проведена плоскость a,
параллельная прямой BD₁.

а) Докажите, что сечение призмы плоскостью a
является равнобедренным треугольником.

б) Найдите периметр треугольника, являющегося
сечением призмы плоскостью a.

Решение.

а) Для построения сечения призмы плоскостью a,
проведём КЕ || BD₁, E € B₁ D₁.

Плоскость a проходит через точки К, С₁и
Е.

Так как К – середина ВВ₁ и КЕ || BD₁, то
Е – середина диагонали А₁ С₁квадрата
А₁ В₁ С₁ Д₁. Значит,
плоскость a пересекает

грань А₁ В₁ С₁ Д₁по
диагонали А₁ С₁.

Соединив точки К, С₁ и А₁, получаем А₁ КС₁ — сечение
призмы плоскостью a.

А₁КВ₁ = С₁ КВ₁ по двум
сторонам и углу между ними (А₁ В₁ = С ₁В₁
, , В₁ К –
общая сторона).

Из равенства треугольников следует, что А₁К
= С₁К, значит А₁
КС₁ — равнобедренный.

5. Задачи для самостоятельного решения.

На ребре AA₁ прямоугольного
параллелепипеда ABCDA₁B₁C₁D₁
взята точка E так, что A₁E : EA = 2:5, на ребре BB₁
— точка F так, что B₁F : FB =1: 6, а точка Т —
середина ребра B₁ C₁. Известно, что AB = 5,
AD = 6 , AA₁ =14.

а) Докажите, что плоскость EFT проходит через
вершину D₁ .

б) Найдите угол между плоскостью EFT и плоскостью
AA₁B₁ .

Ответ. б) arctg .

2) Дана правильная треугольная призма ABCA₁B₁C₁,
все рёбра которой равны 4.

Через точки A, С₁ и середину T ребра
А₁В₁ проведена плоскость.

а) Докажите, что сечение призмы указанной
плоскостью является прямоугольным
треугольником.

б) Найдите угол между плоскостью сечения и
плоскостью ABC .

Ответ. б) arctg 2.

3) В правильной шестиугольной призме А…F₁
все рёбра равны 2.

а) Докажите, что плоскость ВВ₁F
перпендикулярна прямой В₁С_1.

б) Найдите расстояние от точки В до плоскости F В₁С_1.

Ответ. б) .

4) В пирамиде DАВС известны длины ребер
АВ=АС=DВ=DС=13, DА =6, ВС=24.

а) Постройте прямую, перпендикулярную прямым DА
и ВС.

б) Найдите расстояние между прямыми DА и ВС.

Ответ. б) 4.

5) Высота правильной треугольной пирамиды равна
20, а медиана её основания равна 6.

а) Постройте сечение пирамиды плоскостью,
проходящей через её вершину и перпендикулярной
ребру основания.

б) Найдите тангенс угла, который образует
боковое ребро с плоскостью основания.

Ответ. б) 5.

6) В правильной четырёхугольной пирамиде МАВСD с
вершиной М сторона основания равна 3, а боковое
ребро равно 6.

а) Постройте сечение пирамиды плоскостью,
проходящей через точку С и середину ребра МА
параллельно прямой ВD.

б) Найдите площадь этого сечения.

Ответ. б) 6.

Презентация.

Используемая литература.

1) И.В. Ященко, С.А. Шестаков, А.С. Трепалин
“Подготовка к ЕГЭ по математике 2016, профильный
уровень”, Москва, издательство МЦНМО, 2016.

2) Интернет-ресурсы:

http://www.fipi.ru/
http://mathege.ru/or/ege/Main
https://math-ege.sdamgia.ru/
http://alexlarin.net/
https://ege-ok.ru/

Источник

Цель урока:

научиться находить полное решение задачи, применяя эффективный способ.
Задачи
1) Систематизировать, расширить и углубить теоретические знания по курсу планиметрии и стереометрии.
2) Рассмотреть различные методы решения геометрических задач.
3) Применить рассматриваемые приемы, методы, подходы при решении конкретных задач.

Раздел: Презентации по математике для 11 класса

Скачивая материал, я соглашаюсь с условиями публичной оферты.

Скачать презентацию

Другие полезные презентации:

Логарифмдік теңдеулерді шешу
Метод координат
Устный счет 11 класс
Логарифмический мир
Тела вращения
Прототипы заданий 1, 3, 7, 10 (алгебра)
Особенности аудита бухгалтерской (финансовой) отчётности субъектов малого предпринимательства
Система подготовки обучающихся к ЕГЭ по математике
Лабиринты. Решение задач
Сфера и Шар

Для вывода других вариантов — обновите страницу.

Скачать QR-код

Автор: Пирожик Галина Кирилловна
учитель МКОУ СШ№2 г. Котельниково

Размер файлов: 3.15 MB

Дата публикации:

29.06.2020

Внести правки в свой материал

Выходные данные (библиографическая ссылка):

Пирожик Г. К. Три способа решения задачи №14 // Международный каталог для учителей, учеников и преподавателей «Презентации» // URL: https://edupres.ru/prezentatsii-po-matematike/11-klass/file/35004-urok-podgotovki-k-ege-na-temu-tri-sposoba-resheniya-zadachi-14-ege-profil-naya-matematika (дата обращения: 11.03.2023)

Скачать сертификат о публикации— как получить такой сертификат

Источник

Слайд 1Решение задач 14 ЕГЭ
Попов Сергей 10 МБОУ «Ергачинская СОШ»

Руководитель: Кучукбаева Т.А.
20.12.2017

Слайд 2Цель проекта
Научится решать задачи 14 части ЕГЭ различными способами

Слайд 3Задачи
Рассмотреть различные типы задач 14 ЕГЭ
Рассмотреть различные способы решения

задач 14 ЕГЭ

Слайд 4Типы задач
Расстояние между скрещивающимися прямыми
Расстояние от точки до прямой

и до плоскости
Расстояние между плоскостями
Угол между прямой и плоскостью
Угол

между плоскостями
Угол между скрещивающимися прямыми
Сечения многогранников
Объёмы многогранников

Первое полугодие

Второе полугодие

Слайд 5Нахождение расстояния от точки до прямой

Слайд 6S
A
B
C
D
P
T
M
h
О
Источник: Задания С2 ЕГЭ 2014
Аналитический

метод
Дано: SABСD-правильная четырехугольная пирамида. AB=

, высота h= ,т. Р-середина AD, т.Т-середина BC, т.М-середина SC.
Найти: расстояние от т.Р до МТ.

Решение:
Доп. построение PT
PT=AB=√6
ΔABD: ∠DAB=90°, тогда по т.Пифагора DB=
OB=DB/2=√3
ΔSOB: ∠SOB=90°, тогда по т.Пифагора SB=

Слайд 7 KM||PT
PT||DC
PT||(SDC)
PT⊂(PTM)
(PTM)∩(SDC)=MK

Построим сечение (PTM):
PT||DC
DC⊂(SDC)

S
A
B
D
P
T
M
С
=> PT||(SDC) по признаку параллельности прямой

и плоскости
=>MK||PT по теореме
K
=>KM||DC, SM=MC, тогда по теореме Фалеса K-середина

PK-средняя линия, тогда PK=AS/2=SB/2=MT=3

P,K,M,T∈(MTP), KM||PT=>□KMTP-равнобокая трапеция c основаниями KM и PT

KM= по свойству средней линии

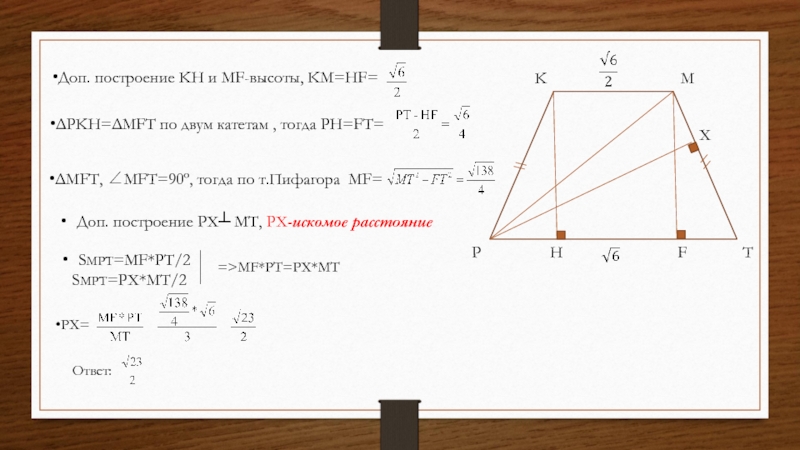
Слайд 8K
M
P
T
H
F
X
=>MFPT=PXMT
Доп. построение KH и MF-высоты, KM=HF=
ΔPKH=ΔMFT по двум катетам

, тогда PH=FT=
ΔMFT, ∠MFT=90º, тогда по т.Пифагора MF=
Доп. построение PX┴

MT, PX-искомое расстояние

SMPT=MF*PT/2
SMPT=PX*MT/2

PX=

Ответ:

Слайд 9H
M
S
A
B
C
D
P
T
x
z
y
(0;0;0)
Векторный метод
Дано: SABСD-правильная четырехугольная пирамида. AB=√6 , высота h=

√33 ,т. Р-середина AD, т.Т-середина BC, т.М-середина SC.
Найти: расстояние от

т.Р до МТ.

(0;√6;0)

(x;y;z)

Решение:
Поместим фигуру в систему координат
Пусть PH-искомое расстояние, тогда

Слайд 10

, тогда x=√6-y

, тогда z=2√33- √22y

(0;0;0)

(0;√6;0)

(x;y;z)

Слайд 11Нахождение расстояния от точки до плоскости

Слайд 12Дано: куб ABCDA1B1C1D1 со стороной 12. т.P ∈ DC,

DP=4, т.Q ∈ AB, B1Q=3.
Найти: расстояние h от т. С

до (APQ).

Решение:
Построим сечение (APQ):
K,P,X ∈(APQ)=> искомое расстояние будет равно расстоянию от т. С до (XKP), тогда h-высота тетраэдра KXPC, проведенная из вершины С.
Рассмотрим ΔXCP и ΔXBA:
∠ABC=∠XCP=90º
∠AXB-общий

=> ΔXCP ~ ΔXBA по Ι признаку подобия треугольников

Источник: Задания 14 ЕГЭ 2016

VXPKC=SXKP*h/3=SXPC*KC/3

Метод объемов

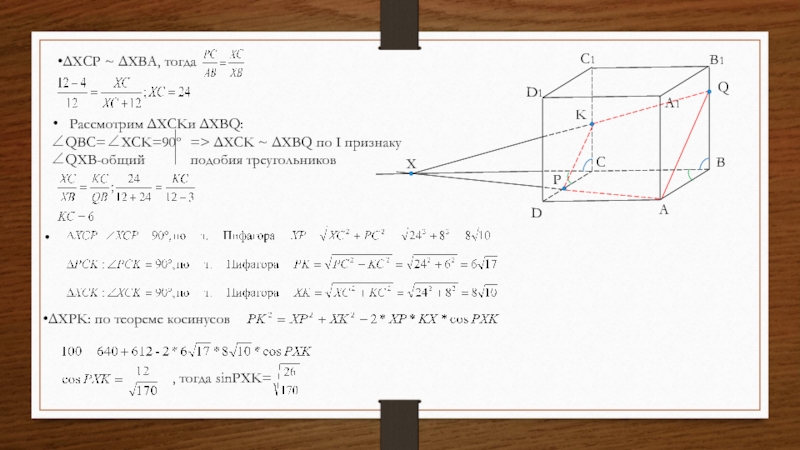
Слайд 13Рассмотрим ΔXCKи ΔXBQ:
∠QBC=∠XCK=90º
∠QXB-общий

A
B
C
D
A1
B1
C1
D1
Q
P
X
K
=> ΔXCK ~ ΔXBQ по Ι признаку

подобия треугольников
ΔXCP ~ ΔXBA, тогда

ΔXPK: по теореме косинусов

, тогда sinPXK=

Слайд 14C
P
X
K
SXKP=sinPXKXKXP/2
SXKP=
SXPC=XCPC/2=248/2=96
VXPKC=SXKPh/3=SXPCKC/3

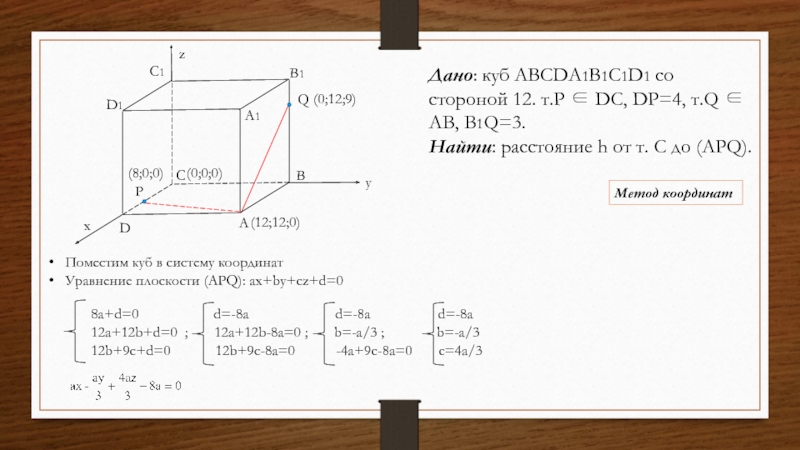
Слайд 15Дано: куб ABCDA1B1C1D1 со стороной 12. т.P ∈ DC,

DP=4, т.Q ∈ AB, B1Q=3.
Найти: расстояние h от т. С

до (APQ).

(12;12;0)

(8;0;0)

(0;12;9)

Метод координат

Поместим куб в систему координат
Уравнение плоскости (APQ): ax+by+cz+d=0

8а+d=0 d=-8a d=-8a d=-8a
12a+12b+d=0 ; 12a+12b-8a=0 ; b=-a/3 ; b=-a/3
12b+9c+d=0 12b+9c-8a=0 -4a+9c-8a=0 c=4a/3

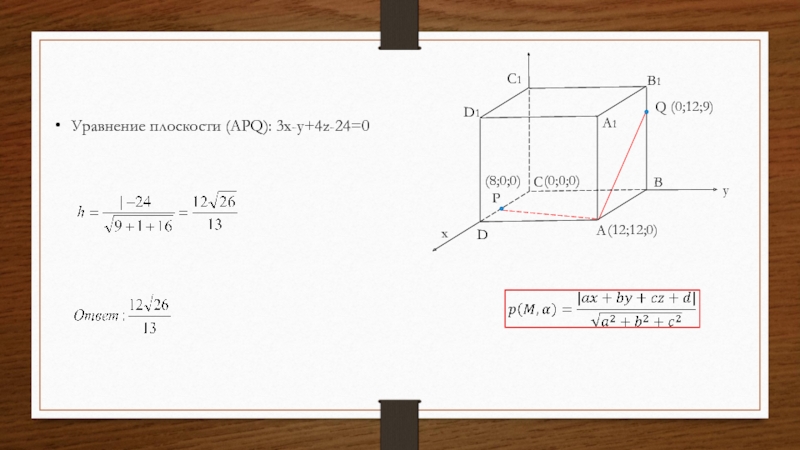
Слайд 16A
B
C
A1
B1
C1
D1
Q
D
P
x
y
(0;0;0)

(12;12;0)
(8;0;0)
(0;12;9)
Уравнение плоскости (APQ): 3x-y+4z-24=0

Слайд 17Дано: куб ABCDA1B1C1D1 со стороной 12. т.P ∈ DC,

DP=4, т.Q ∈ AB, B1Q=3.
Найти: расстояние h от т. С

до (APQ).

Доп. построение CH-высота ΔXCP
KH-наклонная к плоскости (XCP)
CH-проекция KH на (XCP)
CH┴XP
CH┴XP
KH ┴XP
KH∩CH=H

=> KH ┴XP по теореме о трех перпендикулярах

=>XP ┴(KHC) по признаку перпендикулярности прямой и плоскости

Аналитический метод

Слайд 18XP ┴(KHC)
XP⊂(XPK)

Доп. построение СN-высота ΔCHK
(XPK)┴(KHC)
(XPK)∩(KHC) =HK
CN┴HK
CN⊂(KHС)
Значит CN-искомое расстояние
KH=2SKXP/XP=

СH=2SXCP/XP=
C
P
X
K
H
=>(XPK)┴(KHC)

по признаку перпендикулярности плоскостей
N
=>CN ┴(XKP) по свойству перпендикулярных плоскостей

Слайд 19Нахождение расстояния между плоскостями

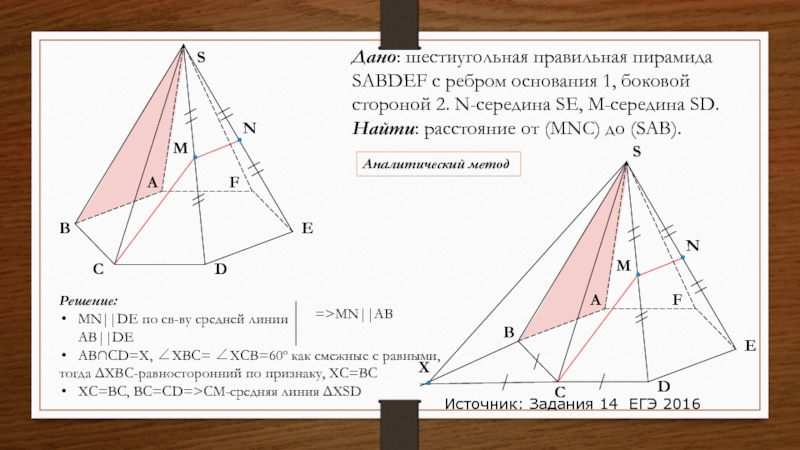
Слайд 20Дано: шестиугольная правильная пирамида SABDEF с ребром основания 1,

боковой стороной 2. N-середина SE, M-середина SD.
Найти: расстояние от (MNC)

до (SAB).

Решение:
MN||DE по св-ву средней линии
AB||DE
AB∩CD=X, ∠XBC= ∠XCB=60º как смежные с равными,
тогда ΔXBC-равносторонний по признаку, XC=BC
XC=BC, BC=CD=>CM-средняя линия ΔXSD

=>MN||AB

Источник: Задания 14 ЕГЭ 2016

Аналитический метод

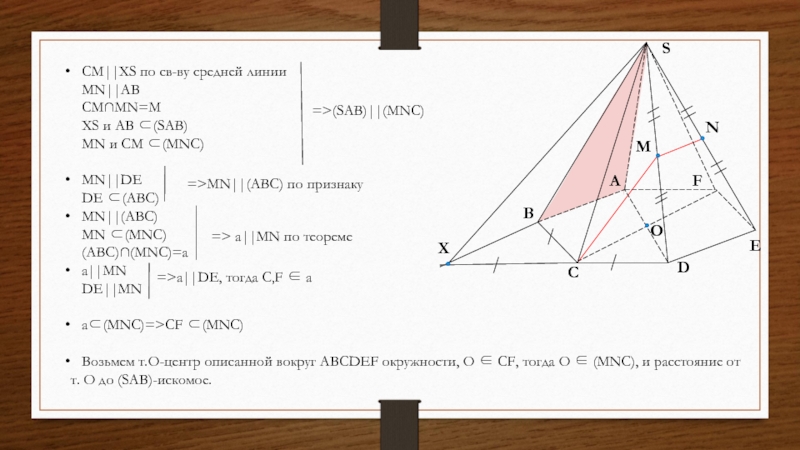
Слайд 21O
CM||XS по св-ву средней линии
MN||AB

CM∩MN=M
XS и AB ⊂(SAB)

MN и CM ⊂(MNC)

MN||DE
DE ⊂(ABC)
MN||(ABC)
MN ⊂(MNC)
(ABC)∩(MNC)=a
a||MN
DE||MN

a⊂(MNC)=>CF ⊂(MNC)

Возьмем т.O-центр описанной вокруг ABCDEF окружности, O ∈ CF, тогда O ∈ (MNC), и расстояние от
т. O до (SAB)-искомое.

=> a||MN по теореме

=>MN||(ABC) по признаку

=>a||DE, тогда C,F ∈ a

Слайд 22H
K
S
A
B
C
D
F
E
O
Пусть т. K-середина AB, OH┴SK
OK┴AB, SK┴AB по св-ву равнобедренного

треугольника
SK∩KO=K
SK ⊂(SKO)
KO ⊂(SKO)

SK┴AB
OK┴AB

OH┴SK
OH┴ AB
SK∩AB=K
SK⊂(ABS)
AB⊂(ABS)

=>AB┴(SOK) по признаку перпендикулярности прямой
и плоскости, тогда OH┴ AB

OH┴(ABS) по признаку
перпендикулярности прямой и плоскости, тогда OH-искомое расстояние

Слайд 23S
A
B
C
D
F
E
O
K
H
ΔABO-равносторонний, тогда OK=
ΔAKS: ∠SKA=90º, по т.Пифагора SK=
SO-высота пирамиды, тогда

ΔOKS: ∠SOK=90º, по т.Пифагора SO=
ΔSOK: ∠SOK=90º, тогда OH=

Слайд 24Дано: шестиугольная правильная пирамида SABDEF с ребром основания 1,

боковой стороной 2. N-середина SE, M-середина SD.
Найти: расстояние h от

(MNC) до (SAB).

Метод объемов

Слайд 25O
S
A
B
1
2
Дано: шестиугольная правильная пирамида SABDEF с ребром основания 1,

боковой стороной 2. N-середина SE, M-середина SD.
Найти: расстояние h от

(MNC) до (SAB).

(0;0;0)

(1;0;0)

Метод координат

Решение:
Поместим SABOв систему координат

Доп. построение AY ┴OY, AX┴OX

ΔAXO: ∠AXO=90º, cos60º=OX/AO
OX=1/2

Слайд 26z
O
S
A
B
x
y
(1;0;0)
(0;0;0)
Уравнение плоскости (ABS): ax+by+cx+d=0

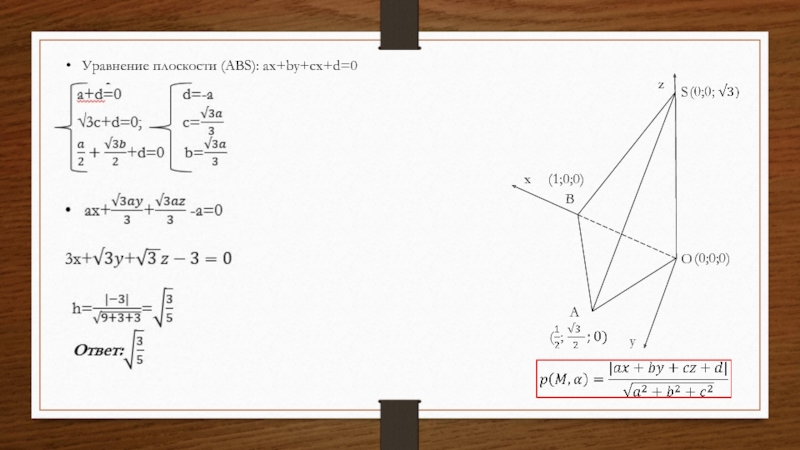
Слайд 27Нахождение расстояния между скрещивающимися прямыми

Слайд 28Дано: четырехугольная правильная пирамида SABD, длина каждого ребра равна

4, т. К-середина AS.
Найти: расстояние между AD и BK.
S
A
B
C
D
K
Решение:
Построим сечение

(KBC):
BC||AD
AD ⊂(ASD)
BC||(ASD)
BC ⊂(KBC)
(ASD)∩(KBC)=KL
KL||BC, AD||BC, тогда AD||KL

=> BC||(ASD) по признаку параллельности прямой и плоскости

=> KL||BC по теореме

Источник: Задания 14 ЕГЭ 2015

Аналитический метод

Слайд 29S
A
B
C
D
K
L
AD||KL
KL ⊂(KBC)
тогда расстояние между AD и

KB равно расстоянию от любой точки AD до (KBC)
Доп. построение

KN┴AD, MN┴AD, MK┴NH
KN┴AD
KL||AD
KN┴AD
MN┴AD
MN ⊂(KMN)
KN ⊂(KMN)
AD||KL
AD ┴NH
NH ┴KL
NH ┴MK
KL∩KM=K
KL ⊂(KBC)
KM ⊂(KBC)

=>AD||(KBC) по признаку параллельности прямой и плоскости,

=>KN ┴KL

AD ┴(KMN) по признаку ,
NH ⊂(KMN), тогда AD ┴NH по определению прямой, перпендикулярной к плоскости

=>NH ┴KL по лемме

=>NH ┴(KBC) по признаку, тогда NH-искомое расстояние

Слайд 30S
A
B
C
D
K
L
N
M
H
B
K
L
C
M
M1
=>BC ┴(NKM) по теореме, тогда KM ┴BC по определению

и KM-высота □BKLC
KL||AD, AK=KS,тогда по т. Фалеса SL=LD, KL-средняя

линияΔASD, KL=AD/2=2
KB=CL как медианы в равных равносторонних треугольниках ASB и DCS
KL||BC, KB=LC, тогда □BKLC –равнобокая трапеция с основаниями KL и BC

KB=LC-высоты, тогда KB=LC=2√3

AD┴(NKM)
AD||BC

KL=MM1=2

ΔBKM=ΔLCM1по гипотенузе и катету,
BM=CM1=(BC-MM1)/2=1

ΔBKM: ∠BMK=90º, по т. Пифагора KM=

Слайд 31S
A
B
C
D
K
N
M
H
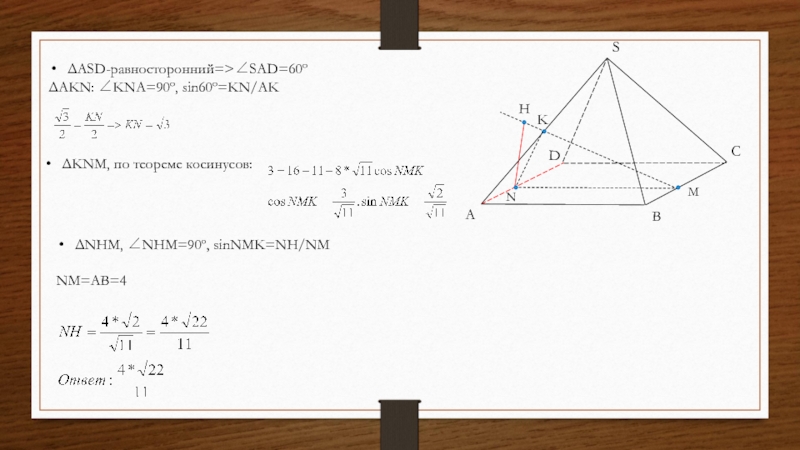
ΔASD-равносторонний=>∠SAD=60º
ΔAKN: ∠KNA=90º, sin60º=KN/AK
ΔKNM, по теореме косинусов:
ΔNHM,

∠NHM=90º, sinNMK=NH/NM

NM=AB=4

Слайд 32Дано: четырехугольная правильная пирамида SABD, длина каждого ребра равна

4, т. К-середина AS.
Найти: расстояние h между AD и BK.
A
B
C
D
K
O
Решение:
Поместим

пирамиду в систему координат

т.O-проекция т.S на (ABC), т.O-точка пересечения диагоналей □ABCD

(0;0;0)

(4;0;0)

(4;4;0)

Метод координат

Слайд 33A
B
C
D
K
O
x
y
(0;0;0)
(4;0;0)
z
S
(4;4;0)
Уравнение плоскости (BKC): ax+by+cz+d=0

4a+d=0

d=-4a

d=-4a
4a+4b+d=0; b=0; b=0;

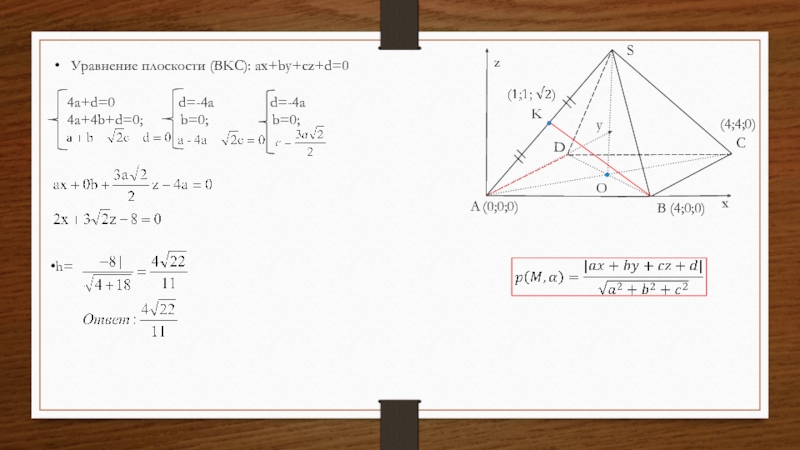
Слайд 34Дано: четырехугольная правильная пирамида SABD, длина каждого ребра равна

4, т. К-середина AS.
Найти: расстояние h между AD и BK.
A
B
C
D
K
S
A
B
C
K
Метод

объемов

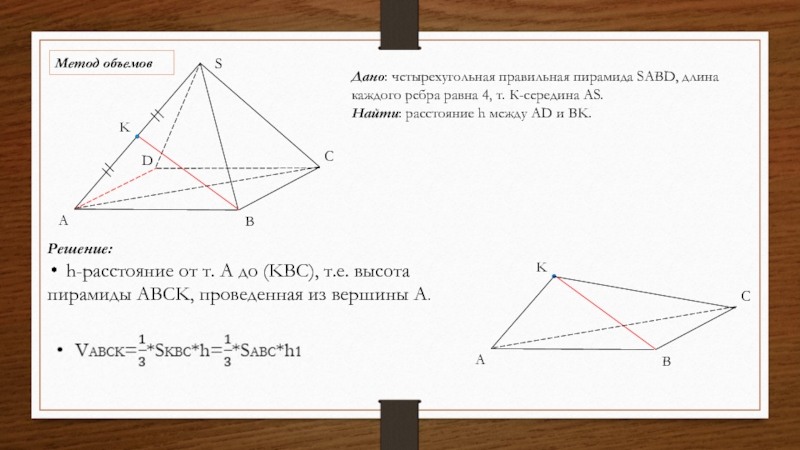
Решение:
h-расстояние от т. A до (KBC), т.е. высота
пирамиды ABCK, проведенная из вершины A.

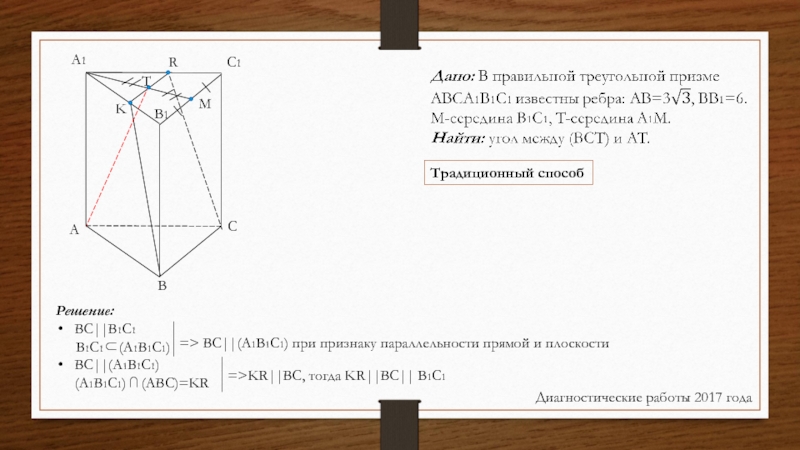
Слайд 37Традиционный способ
Диагностические работы 2017 года
A1
B1
C1
A
B
C
M
T
K
R
Решение:
BC||B1C1

B1C1⊂(A1B1C1)
BC||(A1B1C1)
(A1B1C1) ⋂ (ABC)=KR

=> BC||(A1B1C1) при признаку параллельности

прямой и плоскости

=>KR||BC, тогда KR||BC|| B1C1

Слайд 38A1
B1
C1
A
B
C
M
T
K
R
N
Доп. построение AN⊥BC, AH⊥TN

KR||B1C1
A1T=TM

KB1=RC1, BB1=CC1, ∠BB1K=∠RC1C=90º=>

ΔKB1B=ΔRC1C по двум катетам, тогда BK=RC

A1M⊥B1C1=>A1T⊥KR, тогда ΔA1TK= ΔA1RT по

катету и гипотенузе=>
KT=TR

=> A1K=KB1=A1R=RC1 т.к. A1B1=A1C1 по теореме Фалеса.

=>BC ⊥(ANT) по признаку, тогда BC ⊥AH по определению

=> AH ⊥(BCT) по признаку, тогда ∠ATH-искомый

A1M=AN=3*√3* √3/2=4,5
AA1 ⊥ (A1B1C1)=>AA1⊥A1T по определению, по т. Пифагора AT= √657/4,
аналогично TN=AT= √657/4

Слайд 40z
Векторный способ
A1
B1
C1
A
B
C
M
T
x
y
(0;0;0)
Решение:
Поместим призму в систему координат

Слайд 41A1
B1
C1
A
B
C
M
T
z
x
y
(0;0;0)
Составим уравнение плоскости (BTC)
Уравнение плоскости (BTC):

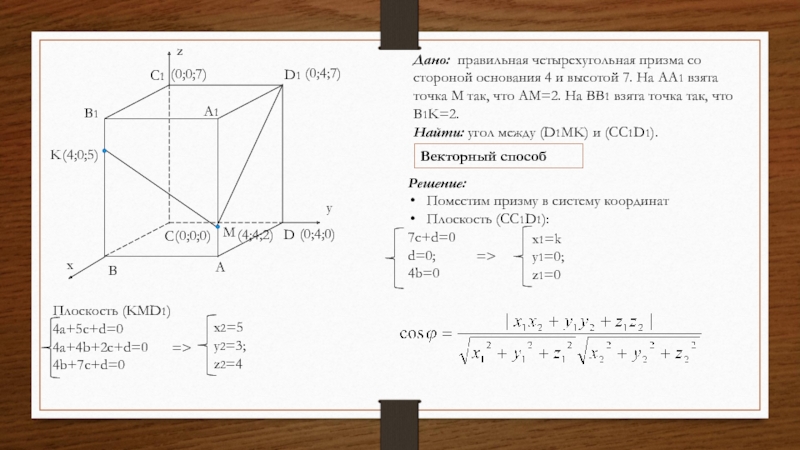
Слайд 43Дано: правильная четырехугольная призма со стороной основания 4 и

высотой 7. На АА1 взята точка М так, что АМ=2.

На BB1 взята точка так, что B1K=2.
Найти: угол между (D1MK) и (CC1D1).

Диагностические работы 2017 года

Традиционный способ

Решение:
(АBB1)∩ (D1MK)=KM
(D1MK) ∩ (CC1D1)=XD1
(АBB1)|| (CC1D1)
Аналогично KX||MD1, тогда □XKMD1-параллелограмм по определению, KM=XD1, KX=MD1
Доп. построение KH ⊥XD1, KN||B1C1, B1C1 ⊥ (CC1D1), тогда KN ⊥ (CC1D1)=>NH-проекция KH на (CC1D1),
По теореме о трех перпендикулярах NH ⊥XD1, тогда ∠KHN-искомый

=>KM||XD1 по св-ву параллельных плоскостей

Слайд 44A
B
C
D
A1
B1
C1
D1
M
K
X
H
N
N
X
D1
H
=> ∠KNH=90º по определению
ΔKNH, ∠KNH=90º, NK=NH=4, тогда ∠KHN=45 º
Ответ:

∠KHN=45 º

KN=B1C1=4
KX=MD1=√41 (находится через т. Пифагора)
ΔXNK, ∠XNK=90º, по т.Пифагора XN=5,

тогда XC1=3
ΔXC1D1, ∠ XC1D1=90º, по т.ПифагораXD1=5
ΔNС1D1, ∠NC1D1=90º, по т.ПифагораND1=2√5

ΔXND1, по т. косинусов cosND1X

тогда sinND1X

ΔHND1,∠NHD1=90º,NH=2√5* =4

KN⊥(CC1D1)
NH⊂(CC1D1)

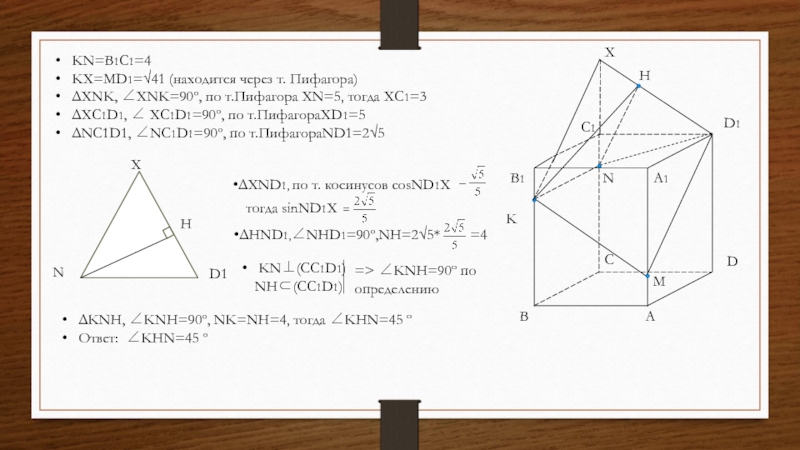
Слайд 45Плоскость (KMD1)
4a+5c+d=0
4a+4b+2c+d=0
4b+7c+d=0
Дано: правильная четырехугольная призма со стороной основания 4

и высотой 7. На АА1 взята точка М так, что

АМ=2. На BB1 взята точка так, что B1K=2.
Найти: угол между (D1MK) и (CC1D1).

Векторный способ

Решение:
Поместим призму в систему координат
Плоскость (СС1D1):
7c+d=0
d=0;
4b=0

(0;0;0)

(0;0;7)

(0;4;7)

(4;0;5)

(0;4;0)

x1=k
y1=0;
z1=0

(4;4;2)

x2=5
y2=3;
z2=4

Слайд 47Угол между скрещивающимися прямыми

Слайд 48Задания для школы экспертов. Математика. 2016 год
A
S
B
C
D
=>SA ⊥(ABC) по

признаку
E
Традиционный способ
ΔSAD,

тогда SA⊥ AD

ΔSAB, тогда SA⊥ AB

Доп. Построение CE|| BD, тогда ∠SCE-искомый
SA ⊥(ABC), тогда SA⊥AC, SA⊥AE
□BDCE-параллелограмм по определению, тогда BE=CD=8, BD=CE=10
ΔSAC, SA ⊥AC, по т.Пифагора SC=11
ΔSAE,SA⊥AE, по т.Пифагора SE=√277
ΔSCE, по т. косинусов cosSCE=

Слайд 49Поместим пирамиду в систему координат
x1=-6
y1=-8;
A
S
B
C
D
Векторный способ
z
x
y
x2=6
y2=-8;
z2=0
z1=√21

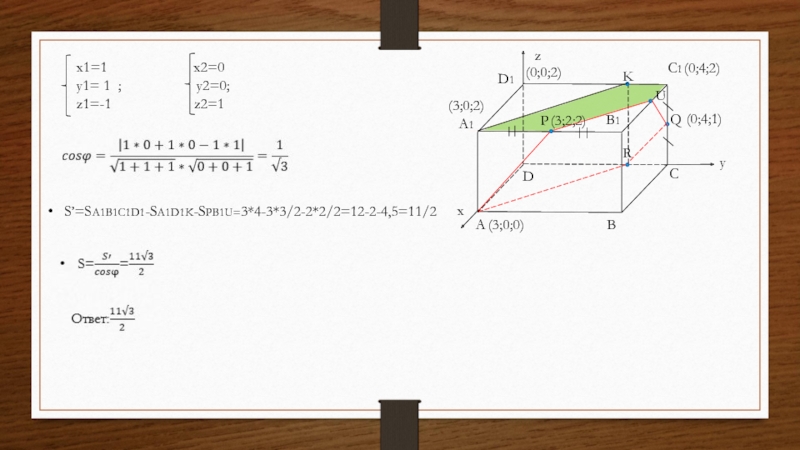
Слайд 51Дано: в прямоугольном параллелепипеде ABCDA1B1C1D1 AB=4, BC=3,AA1=2. Точки P

и Q- середины A1B1 и CC1 соответственно. Плоскость (APQ) пересекает

B1C1 в точке U.
Найти: площадь сечения параллелепипеда ABCDA1B1C1D1 плоскостью (APQ).

Задания 14 ЕГЭ 2016

Традиционный способ

Решение:
Построим сечение плоскостью (APQ)
ΔXAB~ΔXPB1(по первому признаку подобия)=>
Аналогично

ΔUC1Q=ΔQYC( по стороне и двум прилежащим к ней углам)=>CY=UC1, тогда 3+CY=6-2CY
CY=1

ΔYCR~ΔYBA (по первому признаку подобия)=>

Слайд 52A
B
C
D
A1
C1
B1
D1
P
Q
X
U
Y
R
A
P
U
Y
h
ΔCQY,∠QCY=90º, по т.ПифагораYQ=√2

Аналогично RQ=RY =√2

SRQY=
ΔXPU~ΔXAY (по второму признаку

подобия), тогда PU||AY,
□APUY-трапеция

ΔABY,∠ABY=90º, по т.ПифагораAY=4√2

ΔPB1U, ∠ PB1U =90º, по т.ПифагораPU=2√2

QY=UQ=

√2 =>UY=AP=2√2

SAPUY=√6*3 √2=6 √3

SAPUQR=SAPUY-SRQY= Ответ:

Слайд 53Дано: в прямоугольном параллелепипеде ABCDA1B1C1D1 AB=4, BC=3,AA1=2. Точки P

и Q- середины A1B1 и CC1 соответственно. Плоскость (APQ) пересекает

B1C1 в точке U.
Найти: площадь сечения параллелепипеда ABCDA1B1C1D1 плоскостью (APQ).

Способ ортогональной проекции

Решение:
A1KC1UP-проекция ARQUP на (A1B1C1);
Поместим параллелепипед в систему координат
Плоскость (APQ):
3a+d=0
3a+2b+2c+d=0;
4b+c+d=0

(3;0;0)

(3;2;2)

(0;0;2)

(0;4;1)

(0;4;2)

(3;0;2)

Уравнение плоскости: x+y-z-3=0;

Плоскость (A1B1C1):
2с+d=0
3a+2c+d=0;
4b+2c+d=0

Уравнение плоскости: z-2=0;

Слайд 54×1=1

x2=0
y1= 1 ;

y2=0;
z1=-1 z2=1

(3;0;0)

(3;2;2)

(0;0;2)

(0;4;1)

(0;4;2)

(3;0;2)

S’=SA1B1C1D1-SA1D1K-SPB1U=3*4-3*3/2-2*2/2=12-2-4,5=11/2

Слайд 56H
Дано: В четырехугольной пирамиде SABCD (четырехугольник в основании выпуклый)

боковые ребра SA, SB и SC попарно перпендикулярны и имеют

длину 3. Длина SD равна 9.
Найти: наибольшее возможное при этих условиях значение объема пирамиды SABCD.

Тренировочный вариант 2017

Решение:
Разобьем пирамиду на два тетраэдра
По т. Пифагора AB=BC=AC= , тогда ΔABC-правильный
т. S равноудалена от вершин основания, значит высота пирамиды SH проходит через центр описанной окружности около ΔABC
Значение объема SABCD максимально при наибольших SH, SABC, SACD, но SH и SABC -постоянные величины=> нам надо найти наибольшую SACD
BH=

Слайд 57H
S
A
B
C
D
P
ΔSHB, по т. Пифагора SH=
SD=9, тогда в ΔSHD по

т. Пифагора HD=√78
SACD наибольшая, когда его высота –DH
DH┴AC, BH┴AC, через точку,

не лежащую на данной прямой, можно провести только одну прямую, перпендикулярную данной, тогда B,H,P,D лежат на одной прямой
SABCD=

VSABCD=

Источник

Данная презентация 1Подготовка к ЕГЭ Задание 14 подготовлена для проведения занятий с учащимися к экзамену. В презентации наглядно и подрбно показывается решение некоторых задач стереометрии. Рассмотрены различные способы решения задач. Чертежи очень подробные, разбиваются на мини подзадач. Материал объясняется доступно.Презентация для подготовки к ЕГЭ Задание 14

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

Источник

1.

МБОУ «Ергачинская СОШ»
Решение заданий 14 (С2)
по материалам ЕГЭ
профильного уровня
(нахождение углов,
расстояний, построение сечений)

2.

Соотношения между сторонами и
углами прямоугольного треугольника
Повторение.
C
b
A
α
bc
a
h
c
h bc ac
a2 + b2 = c2
ac
a ac c
a
sin
c
В
b
cos
c
a
tg
b
b bc c

3.

Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других
сторон минус удвоенное произведение этих сторон на косинус угла
сумме квадратов двух других сторон
между ними.
минус удвоенное произведение этих сторон
на косинус угла между ними.
2
a
=
2
b
+
2
c
– 2bc cosA
C
b
A
a
c
B

4.

Угол между пересекающимися и
скрещивающимися прямымиА
1.
С
α
D
1800 — α
00 < α
900
В
2.
Угол между скрещивающимися
прямыми АВ и СD определяется
как угол между пересекающимися
М1
прямыми А1В1 и С1D1, при
D1
этом А1В1|| АВ и С1D1|| CD.
В1
А1
α
С1

5.

Угол между плоскостями
C
F
D
A
H
∠ ((АСН); (СНD))
– это двугранный
∠ АСНD, где СНобщее ребро.
Точки А и D лежат
на гранях этого
угла.
AF⊥CH, FD⊥CH.
∠ AFD – линейный угол двугранного ∠ АCHD

6.

Задача № 1
В правильной треугольной призме ABCA1B1C1,
все рёбра которой равны 1, найдите косинус угла
между прямыми АВ1 и ВС1.
С1
Решение:
1) Продлим плоскость ВСС1,
В1
тогда ∠(AB1, ВС1) =
∠(AB1, DВ1) = ∠ AВ1D,
т. к. C1В || B1D.
А1
1
А
С
1
В
3) из ∆ABD по теореме
косинусов
DА2 AВ 2 ВD 2 2 AВ DВ cos120
1 1 — 2·1·1·(-0, 5) 3
D

7.

Задача № 1 (продолжение)
В правильной треугольной призме ABCA1B1C1, все
рёбра которой равны 1, найдите косинус угла
между прямыми АВ1 и ВС1.
С1
Решение:
А1
В1
4) cos∠AB1D =
1
А
2·AB1·B1D
2+2–3
cos∠AB1D =
2· 2
С
1
AB12 + B1D2 – AD2
В
Ответ: 0,25 .
D
1
=
4

8.

Задача № 2
В кубе ABCDA1B1C1D1 найдите угол между
прямой AC1 и плоскостью ВСC1.
Решение:
1) ВС1- проекция
С1
D1
прямой АС1 на
плоскость(ВCС1),
А1
В1
так как AB⊥(ВCС1)
AB⊥ВС1;
∠(AC1, (ВCС1)) =
∠(AС1,С1В) = ∠ AC1B,
С т.е. ∆АВC1 –
прямоугольный
D
А
В
3) tg∠AC1B =
AB
=
BC1
a
=
1

9.

Задача № 3
Основанием прямой треугольной призмы ABCA1B1C1,
является равнобедренный треугольник АВС, в котором
АВ = ВС = 20, АС = 32. Боковое ребро призмы равно 24.
Точка Р принадлежит ребру ВВ1, причем ВР : РВ1 = 1 : 3.
Найдите тангенс угла между плоскостями А1В1С1 и АСР.
Решение:
В1
С1 1) Так как (АВС)∥(А1В1С1), то
∠(( А1В1С1) , (АСР)) =
∠((АВС),(АСР)).
32
2) Т.к. ВН АС (высота р/б ∆),
А1
24 то по теореме о трех
Р
перпендикулярах РН АС.
3) Тогда ∠РНВ – линейный угол
двугранного ∠ РАСВ. Найдем его
В
С из прямоугольного ∆РНВ.
16 4) РВ = ¼ ВВ1 = ¼ · 24 = 6,
20
Н
5) ВН2 = АВ2 – АН2 (из ∆AНВ)
16
ВН2 = 202 – 162 = 144, ВН = 12;
А
6) tg∠РНВ = PB/HB = 6/12 = 0,5.
Ответ: 0,5 .

10.

Задача № 4
В правильной четырехугольной пирамиде
SABCD, все ребра которой равны 1, найдите
косинус угла между прямой AB и плоскостью
SAD.
Решение:
1) Так как ABCD – квадрат,
S
то АВ ⊥ AD. Поэтому
проекция AB на плоскость
(SAD) будет ⊥ AD.
Значит, искомый угол –
С двугранный угол при ребре
основания AD.
D
M
O
N
В
А 3) ∠SMO – искомый
угол, косинус которого
найдем из прямоугольного ∆SMO
MO
0,5
1
cos∠SMO =
=
=
SM

11.

Повторение.
Расстояние от точки до прямой
Определение. Расстоянием от точки до
прямой в пространстве называется
длина перпендикуляра, проведённого из
данной точки к данной прямой.

12.

Расстояние от точки до плоскости
Определение. Расстоянием от точки до
плоскости является длина перпендикуляра,
проведённого из данной точки к данной
плоскости.
M
перпендикуляр
N
H
NH – проекция наклонной
на плоскость ɣ
MH < MN
МH – расстояние
ɣ
от М до
a
плоскости ɣ

13.

Расстояние между
скрещивающимися прямыми
Общим перпендикуляром двух скрещивающихся
прямых называют отрезок с концами на этих прямых,
являющийся перпендикуляром к каждой из них.
A
a
а; b AB
B
b
Определение.
Расстоянием
между
скрещивающимися прямыми называют
длину их общего перпендикуляра.

14.

Способы вычисления расстояния между
скрещивающимися прямыми
1 способ.
а
b
|| a
а1
a; b a;
Расстояние между скрещивающимися прямыми
равно расстоянию от любой точки одной из этих
прямых до плоскости, проходящей через вторую
прямую параллельно первой прямой.

15.

Способы вычисления расстояния между
скрещивающимися прямыми
2 способ.
а
||
a; b ;
b
Расстояние между скрещивающимися прямыми
равно расстоянию между двумя параллельными
плоскостями, содержащими эти прямые.

16.

Способы вычисления расстояния между
скрещивающимися прямыми
3 способ.
b
b1
а
а
А
а А
b b1
a; b A; b1
Расстояние между скрещивающимися прямыми
равно расстоянию между их проекциями на
плоскость, перпендикулярную одной из них.

17.

Задача № 5
В
правильной
шестиугольной
призме
ABCDEFA1B1C1D1E1F1, стороны основания которой равны
5, а боковые рёбра равны 11, найдите расстояние от точки С
Решение:
до прямой A1F1.
1)Так как ABCDEF – правильный
С1
В1
шестиугольник, то
CA⊥AF.
А1 CA⊥A1А по определению
D1
правильной призмы.
E1
F1
CA⊥(АA1F1) по признаку
перпендикулярности прямой
и плоскости, т.е.
11
СА –перпендикуляр к плоскости,
С
В
CA1 — наклонная ,
A1А – проекция наклонной,
1F1 ;
D
А AA1АF ⊥A
1 1 – прямая в плоскости.
E
5
F
Тогда по теореме о трёх перпендикулярах CA1⊥A1F1, значит
длина отрезка CA1 равна искомому расстоянию.

18.

Задача № 5
(продолжение)
В
правильной
шестиугольной
призме
ABCDEFA1B1C1D1E1F1, стороны основания которой равны
5, а боковые рёбра равны 11, найдите расстояние от точки С
до прямой A1F1.
Решение:
С1
В1
1) Доказано, что
CA1 — искомое расстояние.
А1
D1
E1
2) Из ∆ АВС (АВ=ВС=5, В 120 0 )
по теореме косинусов найдём СА:
F1
СА2 СВ 2 ВА 2 2СВ АВ соs В ,
11
С
cos1200 cos 600 0,5 ,
В
D
А
CA =5 3 .
0
3) Из ∆CAA1, А 90 по
теореме Пифагора найдём CA1:
СА1 СА2 АА1
2
E
5
Ответ: 14.
F
2
CA1 2 = 75 + 121 = 196.
CA1 = 14

19.

Задача № 6
Ребро AD пирамиды DABC
перпендикулярно
плоскости основания АВС. Найдите расстояние от А
до плоскости, проходящей через середины ребер АВ,
АС и АD, если АD = 2 5 , АВ = АС = 10, ВС = 4 5 .
D
L
К
Н
A
N
F
М
Решение:
1) Построим плоскость КМN.
Т. к. КМ – средняя линия ∆АDВ, КМ∥DВ,
MN — средняя линия ∆АВC, МN∥CВ, то
(KMN)∥(BCD) по признаку ∥
плоскостей. АР–медиана и
C высота р/б ∆АВC ,
KF–медиана и высота
р/б ∆KMN.
DP⊥BC по теореме о трёх
Р перпендикулярах. KF ∥ DP.
Искомое расстояние AH
равно половине расстояния
от вершины А до плоскости
B
BCD, т.к. (KMN)∥(BCD) и
KF – средняя линия ∆ ADP.

20.

Задача № 6 (продолжение).
Ребро AD пирамиды DABC
перпендикулярно
плоскости основания АВС. Найдите расстояние от А
до плоскости, проходящей через середины ребер АВ,
АС и АD, если АD = 2 5 , АВ = АС = 10, ВС = 4 5 .
Решение:
D
К
A
1) Доказано, что
AH — искомое расстояние.
2) ∆LDA и ∆ADP подобны по двум углам,
L
LA:AP=AD:DP, тогда AL=(AP*AD):DP.
C Найдём АР из ∆АВР по теореме
Н
Пифагора (АВ=10, ВР = 2 5 ):
N
AP2 = AB2 – BP2 = 100 – 20 =
= 80; АР= 4 5
Найдём DР из ∆АDР
F
Р по теореме Пифагора:
М
DP2 = AD2 + AP2 =
= 20 + 80 = 100; DP = 10.
B
Тогда AL =(4 5 ·2 5 ):10=4
Итак, АН = ½ AL = 2.
Ответ: 2.

21.

Задача № 7
В правильной шестиугольной призме АВCDEFA1B1C1D1E1F1
все рёбра равны 1.
а) Постройте сечение призмы плоскостью, проходящей через
точки B, С1 и F.
б) Найдите расстояние от точки В до прямой C1F.
Решение:
а) 1) ВС1, BF, FЕ1 // С1B , Е1C1 =>
Сечение – четырёхугольник
BC1E1F с диагональю C1F.
4) Так как ∠CBF=90°, то по теореме о трёх перпендикулярах,
BF⟘BC1. Значит, сечение BC1E1F – прямоугольник. Диагональ
прямоугольника C1F2=BF2+BC12; C1F2=3+2=5.

22.

Задача № 7 (продолжение)
В правильной шестиугольной призме
АВCDEFA1B1C1D1E1F1 все рёбра равны 1.
а) Постройте сечение призмы плоскостью, проходящей через
точки B, С1 и F.
б) Найдите расстояние от точки В до прямой C1F.
Решение.
б) Сечение – прямоугольник BC1E1F.
ВК ⊥C1F, ВК – искомое расстояние
от точки В до прямой C1F.
Найдем ВК как высоту из ∆FBС1,
Используя 2 формулы площади
треугольника.

23.

Задача №8
Основанием прямой четырехугольной призмы АВСDА1В1С1D1
является квадрат ABCD со стороной 3 2 , высота призмы равна
2 7 . Точка K − середина ребра ВВ1. Через точки K и С1
проведена плоскость α, параллельная прямой BD1.
а) Докажите, что сечение призмы плоскостью α является
равнобедренным треугольником.
б) Найдите периметр треугольника, являющегося сечением
призмы плоскостью α. Решение.
а) Для построения сечения призмы
плоскостью α, проведём КЕ||BD1, E € B1D1.
Плоскость α проходит через точки К, С1 и Е.
Так как К – середина ВВ1 и КЕ||BD1, то
Е – середина диагонали А1С1 квадрата
А1В1С1D1. Значит, плоскость α пересекает
грань А1В1С1D1 по диагонали А1С1.
Соединив точки К, С1 и А1, получаем
∆А1КС1- сечение призмы плоскостью α.
∆А1КВ1= ∆С1КВ1 по двум сторонам
и углу между ними (А1В1=С1В1),
0
В1К – общая сторона, А1В1К С1В1К 90 .
Из равенства треугольников следует, что А1К=С1К, значит
∆А1КС1 — равнобедренный.

24.

Задача №8
(продолжение)
Основанием прямой четырехугольной призмы ABCDA1B1C1D1
является квадрат ABCD со стороной 3 2 , высота призмы равна
2 7 . Точка K − середина ребра ВВ1. Через точки K и С1
проведена плоскость α, параллельная прямой BD1.
а) Докажите, что сечение призмы плоскостью α является
равнобедренным треугольником.
б) Найдите периметр треугольника, являющегося сечением
призмы плоскостью α. Решение.
б)

25.

Задачи для самостоятельного решения
1) На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1
взята точка E так, что A1E : EA = 2:5, на ребре BB1 — точка F
так, что B1F : FB =1: 6, а точка Т — середина ребра B1 C1 .
Известно, что AB = 5, AD = 6 , AA1 =14 .
а) Докажите, что плоскость EFT проходит через вершину D1 .
б) Найдите угол между плоскостью EFT и плоскостью AA1B1 .
2) Дана правильная треугольная призма ABCA1B1C1, все рёбра
которой равны 4.
Через точки A, С1 и середину T ребра А1В1 проведена плоскость.
а) Докажите, что сечение призмы указанной плоскостью является
прямоугольным треугольником.
б) Найдите угол между плоскостью сечения и плоскостью ABC .
Ответ: б) arctg 2.

26.

Задачи для самостоятельного решения
3) В правильной шестиугольной призме А…F1 все рёбра равны 2.
а) Докажите, что плоскость ВВ1F перпендикулярна прямой В1С1.
б) Найдите расстояние от точки В до плоскости F В1С1.
4) В пирамиде DАВС известны длины ребер АВ=АС=DВ=DС=13,
DА =6, ВС=24.
а) Постройте прямую, перпендикулярную прямым DА и ВС.
б) Найдите расстояние между прямыми DА и ВС.
Ответ: б) 4.

27.

Задачи для самостоятельного решения
5) Высота правильной треугольной пирамиды равна 20, а медиана
её основания равна 6.
а) Постройте сечение пирамиды плоскостью, проходящей через её
вершину и перпендикулярной ребру основания.
б) Найдите тангенс угла, который образует боковое ребро с
плоскостью основания.
Ответ: б) 5.
6) В правильной четырёхугольной пирамиде МАВСD с вершиной
М сторона основания равна 3, а боковое ребро равно 6.
а) Постройте сечение пирамиды плоскостью, проходящей через
точку С и середину ребра МА параллельно прямой ВD.
б) Найдите площадь этого сечения.
Ответ: б) 6.

28.

Используемая литература:
1) И. В. Ященко, С.А. Шестаков, А. С.
Трепалин «Подготовка к ЕГЭ по математике
2016,
профильный
уровень»,
Москва,
издательство МЦНМО, 2016.
2) Интернет-ресурсы:
http://www.fipi.ru/
http://mathege.ru/or/ege/Main
https://math-ege.sdamgia.ru/
http://alexlarin.net/
https://ege-ok.ru/
3) Шаблон презентации сайт http://pedsovet.su/ ,
автор Фокина Л. П.

Источник

Свидетельство о регистрации СМИ: ЭЛ № ФС 77-58841 от 28.07.2014

Слайд 1Решение задач 14 ЕГЭПопов Сергей 10 МБОУ «Ергачинская СОШ»

Руководитель: Кучукбаева Т.А.20.12.2017

Слайд 2Цель проектаНаучится решать задачи 14 части ЕГЭ различными способами

Слайд 3ЗадачиРассмотреть различные типы задач 14 ЕГЭРассмотреть различные способы решения

задач 14 ЕГЭ

Слайд 4Типы задачРасстояние между скрещивающимися прямымиРасстояние от точки до прямой

и до плоскости Расстояние между плоскостямиУгол между прямой и плоскостьюУгол

Слайд 5Нахождение расстояния от точки до прямой

Слайд 6SABCDPTMhОИсточник: Задания С2 ЕГЭ 2014Аналитический

метод Дано: SABСD-правильная четырехугольная пирамида. AB=

Слайд 7 KM||PTPT||DCPT||(SDC)PT⊂(PTM)(PTM)∩(SDC)=MK Построим сечение (PTM):PT||DCDC⊂(SDC) SABDPTMС=> PT||(SDC) по признаку параллельности прямой

и плоскости=>MK||PT по теоремеK=>KM||DC, SM=MC, тогда по теореме Фалеса K-середина

Слайд 8KMPTHFX=>MF*PT=PX*MTДоп. построение KH и MF-высоты, KM=HF=ΔPKH=ΔMFT по двум катетам

, тогда PH=FT=ΔMFT, ∠MFT=90º, тогда по т.Пифагора MF=Доп. построение PX┴

Слайд 9HMSABCDPTxzy(0;0;0)Векторный методДано: SABСD-правильная четырехугольная пирамида. AB=√6 , высота h=

√33 ,т. Р-середина AD, т.Т-середина BC, т.М-середина SC.Найти: расстояние от

Слайд 10

, тогда x=√6-y

Слайд 11Нахождение расстояния от точки до плоскости

Слайд 12Дано: куб ABCDA1B1C1D1 со стороной 12. т.P ∈ DC,

DP=4, т.Q ∈ AB, B1Q=3.Найти: расстояние h от т. С

Слайд 13Рассмотрим ΔXCKи ΔXBQ:∠QBC=∠XCK=90º∠QXB-общий ABCDA1B1C1D1QPXK=> ΔXCK ~ ΔXBQ по Ι признаку

подобия треугольниковΔXCP ~ ΔXBA, тогда ΔXPK: по теореме косинусов

Слайд 14CPXKSXKP=sinPXK*XK*XP/2SXKP=SXPC=XC*PC/2=24*8/2=96VXPKC=SXKP*h/3=SXPC*KC/3

Слайд 15Дано: куб ABCDA1B1C1D1 со стороной 12. т.P ∈ DC,

DP=4, т.Q ∈ AB, B1Q=3.Найти: расстояние h от т. С

Слайд 16ABCA1B1C1D1QDPxy(0;0;0) (12;12;0)(8;0;0) (0;12;9)Уравнение плоскости (APQ): 3x-y+4z-24=0

Слайд 17Дано: куб ABCDA1B1C1D1 со стороной 12. т.P ∈ DC,

DP=4, т.Q ∈ AB, B1Q=3.Найти: расстояние h от т. С

Слайд 18XP ┴(KHC)XP⊂(XPK) Доп. построение СN-высота ΔCHK(XPK)┴(KHC) (XPK)∩(KHC) =HKCN┴HKCN⊂(KHС)Значит CN-искомое расстояниеKH=2*SKXP/XP= СH=2*SXCP/XP=CPXKH=>(XPK)┴(KHC)

по признаку перпендикулярности плоскостейN=>CN ┴(XKP) по свойству перпендикулярных плоскостей

Слайд 19Нахождение расстояния между плоскостями

Слайд 20Дано: шестиугольная правильная пирамида SABDEF с ребром основания 1,

боковой стороной 2. N-середина SE, M-середина SD.Найти: расстояние от (MNC)

Слайд 21OCM||XS по св-ву средней линии MN||AB

CM∩MN=M XS и AB ⊂(SAB)

Слайд 22HKSABCDFEOПусть т. K-середина AB, OH┴SKOK┴AB, SK┴AB по св-ву равнобедренного

треугольникаSK∩KO=K SK ⊂(SKO) KO ⊂(SKO)

Слайд 23SABCDFEOKHΔABO-равносторонний, тогда OK=ΔAKS: ∠SKA=90º, по т.Пифагора SK=SO-высота пирамиды, тогда

ΔOKS: ∠SOK=90º, по т.Пифагора SO=ΔSOK: ∠SOK=90º, тогда OH=

Слайд 24Дано: шестиугольная правильная пирамида SABDEF с ребром основания 1,

боковой стороной 2. N-середина SE, M-середина SD.Найти: расстояние h от

Слайд 25OSAB12Дано: шестиугольная правильная пирамида SABDEF с ребром основания 1,

боковой стороной 2. N-середина SE, M-середина SD.Найти: расстояние h от

Слайд 26zOSABxy(1;0;0)(0;0;0)Уравнение плоскости (ABS): ax+by+cx+d=0

Слайд 27Нахождение расстояния между скрещивающимися прямыми

Слайд 28Дано: четырехугольная правильная пирамида SABD, длина каждого ребра равна

4, т. К-середина AS.Найти: расстояние между AD и BK.SABCDKРешение:Построим сечение

Слайд 29SABCDKLAD||KL KL ⊂(KBC)тогда расстояние между AD и

KB равно расстоянию от любой точки AD до (KBC)Доп. построение

Слайд 30SABCDKLNMHBKLCMM1=>BC ┴(NKM) по теореме, тогда KM ┴BC по определению

и KM-высота □BKLC KL||AD, AK=KS,тогда по т. Фалеса SL=LD, KL-средняя

Слайд 31SABCDKNMHΔASD-равносторонний=>∠SAD=60ºΔAKN: ∠KNA=90º, sin60º=KN/AK ΔKNM, по теореме косинусов:ΔNHM,

∠NHM=90º, sinNMK=NH/NM NM=AB=4

Слайд 32Дано: четырехугольная правильная пирамида SABD, длина каждого ребра равна

4, т. К-середина AS.Найти: расстояние h между AD и BK.ABCDKOРешение:Поместим

Слайд 33ABCDKOxy(0;0;0)(4;0;0)zS(4;4;0)Уравнение плоскости (BKC): ax+by+cz+d=0 4a+d=0

d=-4a

Слайд 34Дано: четырехугольная правильная пирамида SABD, длина каждого ребра равна

4, т. К-середина AS.Найти: расстояние h между AD и BK.ABCDKSABCKМетод

Слайд 37Традиционный способДиагностические работы 2017 годаA1B1C1ABCMTKRРешение:BC||B1C1

B1C1⊂(A1B1C1)BC||(A1B1C1) (A1B1C1) ⋂ (ABC)=KR => BC||(A1B1C1) при признаку параллельности

Слайд 38A1B1C1ABCMTKRNДоп. построение AN⊥BC, AH⊥TN KR||B1C1 A1T=TM KB1=RC1, BB1=CC1, ∠BB1K=∠RC1C=90º=>

ΔKB1B=ΔRC1C по двум катетам, тогда BK=RC A1M⊥B1C1=>A1T⊥KR, тогда ΔA1TK= ΔA1RT по

Слайд 40zВекторный способA1B1C1ABCMTxy(0;0;0)Решение:Поместим призму в систему координат

Слайд 41A1B1C1ABCMTzxy(0;0;0)Составим уравнение плоскости (BTC)Уравнение плоскости (BTC):

Слайд 43Дано: правильная четырехугольная призма со стороной основания 4 и

высотой 7. На АА1 взята точка М так, что АМ=2.

Слайд 44ABCDA1B1C1D1MKXHNNXD1H=> ∠KNH=90º по определениюΔKNH, ∠KNH=90º, NK=NH=4, тогда ∠KHN=45 ºОтвет:

∠KHN=45 º KN=B1C1=4KX=MD1=√41 (находится через т. Пифагора)ΔXNK, ∠XNK=90º, по т.Пифагора XN=5,

Слайд 45Плоскость (KMD1)4a+5c+d=04a+4b+2c+d=04b+7c+d=0Дано: правильная четырехугольная призма со стороной основания 4

и высотой 7. На АА1 взята точка М так, что

Слайд 47Угол между скрещивающимися прямыми

Слайд 48Задания для школы экспертов. Математика. 2016 годASBCD=>SA ⊥(ABC) по

признаку EТрадиционный способΔSAD,

Слайд 49Поместим пирамиду в систему координатx1=-6 y1=-8;ASBCDВекторный способzxyx2=6y2=-8; z2=0z1=√21

Слайд 51Дано: в прямоугольном параллелепипеде ABCDA1B1C1D1 AB=4, BC=3,AA1=2. Точки P

и Q- середины A1B1 и CC1 соответственно. Плоскость (APQ) пересекает

Слайд 52ABCDA1C1B1D1PQXUYRAPUYhΔCQY,∠QCY=90º, по т.ПифагораYQ=√2 Аналогично RQ=RY =√2 SRQY=ΔXPU~ΔXAY (по второму признаку

Свидетельство о регистрации
СМИ: ЭЛ № ФС 77-58841
от 28.07.2014

Слайд 1Решение задач 14 ЕГЭ
Попов Сергей 10 МБОУ «Ергачинская СОШ»

Руководитель: Кучукбаева Т.А.
20.12.2017

Слайд 2Цель проекта
Научится решать задачи 14 части ЕГЭ различными способами

Слайд 3Задачи
Рассмотреть различные типы задач 14 ЕГЭ
Рассмотреть различные способы решения

Слайд 4Типы задач
Расстояние между скрещивающимися прямыми
Расстояние от точки до прямой

и до плоскости
Расстояние между плоскостями
Угол между прямой и плоскостью
Угол

Слайд 6S
A
B
C
D
P
T
M
h
О
Источник: Задания С2 ЕГЭ 2014
Аналитический

метод
Дано: SABСD-правильная четырехугольная пирамида. AB=

Слайд 7 KM||PT
PT||DC
PT||(SDC)
PT⊂(PTM)
(PTM)∩(SDC)=MK

Построим сечение (PTM):
PT||DC
DC⊂(SDC)

S
A
B
D
P
T
M
С
=> PT||(SDC) по признаку параллельности прямой

и плоскости
=>MK||PT по теореме
K
=>KM||DC, SM=MC, тогда по теореме Фалеса K-середина

Слайд 8K
M
P
T
H
F
X
=>MFPT=PXMT
Доп. построение KH и MF-высоты, KM=HF=
ΔPKH=ΔMFT по двум катетам

, тогда PH=FT=
ΔMFT, ∠MFT=90º, тогда по т.Пифагора MF=
Доп. построение PX┴

Слайд 9H
M
S
A
B
C
D
P
T
x
z
y
(0;0;0)
Векторный метод
Дано: SABСD-правильная четырехугольная пирамида. AB=√6 , высота h=

√33 ,т. Р-середина AD, т.Т-середина BC, т.М-середина SC.
Найти: расстояние от

DP=4, т.Q ∈ AB, B1Q=3.
Найти: расстояние h от т. С

Слайд 13Рассмотрим ΔXCKи ΔXBQ:
∠QBC=∠XCK=90º
∠QXB-общий

A
B
C
D
A1
B1
C1
D1
Q
P
X
K
=> ΔXCK ~ ΔXBQ по Ι признаку

подобия треугольников
ΔXCP ~ ΔXBA, тогда

ΔXPK: по теореме косинусов

Слайд 14C
P
X
K
SXKP=sinPXKXKXP/2
SXKP=
SXPC=XCPC/2=248/2=96
VXPKC=SXKPh/3=SXPCKC/3

DP=4, т.Q ∈ AB, B1Q=3.
Найти: расстояние h от т. С

Слайд 16A
B
C
A1
B1
C1
D1
Q
D
P
x
y
(0;0;0)

(12;12;0)
(8;0;0)
(0;12;9)
Уравнение плоскости (APQ): 3x-y+4z-24=0

DP=4, т.Q ∈ AB, B1Q=3.
Найти: расстояние h от т. С

Слайд 18XP ┴(KHC)
XP⊂(XPK)

Доп. построение СN-высота ΔCHK
(XPK)┴(KHC)
(XPK)∩(KHC) =HK
CN┴HK
CN⊂(KHС)
Значит CN-искомое расстояние
KH=2SKXP/XP=

СH=2SXCP/XP=
C
P
X
K
H
=>(XPK)┴(KHC)

по признаку перпендикулярности плоскостей
N
=>CN ┴(XKP) по свойству перпендикулярных плоскостей

боковой стороной 2. N-середина SE, M-середина SD.
Найти: расстояние от (MNC)

Слайд 21O
CM||XS по св-ву средней линии
MN||AB

CM∩MN=M
XS и AB ⊂(SAB)

Слайд 22H
K
S
A
B
C
D
F
E
O
Пусть т. K-середина AB, OH┴SK
OK┴AB, SK┴AB по св-ву равнобедренного

треугольника
SK∩KO=K
SK ⊂(SKO)
KO ⊂(SKO)

Слайд 23S
A
B
C
D
F
E
O
K
H
ΔABO-равносторонний, тогда OK=
ΔAKS: ∠SKA=90º, по т.Пифагора SK=
SO-высота пирамиды, тогда

ΔOKS: ∠SOK=90º, по т.Пифагора SO=
ΔSOK: ∠SOK=90º, тогда OH=

боковой стороной 2. N-середина SE, M-середина SD.
Найти: расстояние h от

Слайд 25O
S
A
B
1
2
Дано: шестиугольная правильная пирамида SABDEF с ребром основания 1,

боковой стороной 2. N-середина SE, M-середина SD.
Найти: расстояние h от

Слайд 26z
O
S
A
B
x
y
(1;0;0)
(0;0;0)
Уравнение плоскости (ABS): ax+by+cx+d=0

4, т. К-середина AS.
Найти: расстояние между AD и BK.
S
A
B
C
D
K
Решение:
Построим сечение

Слайд 29S
A
B
C
D
K
L
AD||KL
KL ⊂(KBC)
тогда расстояние между AD и

KB равно расстоянию от любой точки AD до (KBC)
Доп. построение

Слайд 30S
A
B
C
D
K
L
N
M
H
B
K
L
C
M
M1
=>BC ┴(NKM) по теореме, тогда KM ┴BC по определению

и KM-высота □BKLC
KL||AD, AK=KS,тогда по т. Фалеса SL=LD, KL-средняя

Слайд 31S
A
B
C
D
K
N
M
H
ΔASD-равносторонний=>∠SAD=60º
ΔAKN: ∠KNA=90º, sin60º=KN/AK
ΔKNM, по теореме косинусов:
ΔNHM,

∠NHM=90º, sinNMK=NH/NM

NM=AB=4

4, т. К-середина AS.
Найти: расстояние h между AD и BK.
A
B
C
D
K
O
Решение:
Поместим

Слайд 33A
B
C
D
K
O
x
y
(0;0;0)
(4;0;0)
z
S
(4;4;0)
Уравнение плоскости (BKC): ax+by+cz+d=0

4a+d=0

4, т. К-середина AS.
Найти: расстояние h между AD и BK.
A
B
C
D
K
S
A
B
C
K
Метод

Слайд 37Традиционный способ
Диагностические работы 2017 года
A1
B1
C1
A
B
C
M
T
K
R
Решение:
BC||B1C1

B1C1⊂(A1B1C1)
BC||(A1B1C1)
(A1B1C1) ⋂ (ABC)=KR

=> BC||(A1B1C1) при признаку параллельности

Слайд 38A1
B1
C1
A
B
C
M
T
K
R
N
Доп. построение AN⊥BC, AH⊥TN

KR||B1C1
A1T=TM

KB1=RC1, BB1=CC1, ∠BB1K=∠RC1C=90º=>

ΔKB1B=ΔRC1C по двум катетам, тогда BK=RC

A1M⊥B1C1=>A1T⊥KR, тогда ΔA1TK= ΔA1RT по

Слайд 40z
Векторный способ
A1
B1
C1
A
B
C
M
T
x
y
(0;0;0)
Решение:
Поместим призму в систему координат

Слайд 41A1
B1
C1
A
B
C
M
T
z
x
y
(0;0;0)
Составим уравнение плоскости (BTC)
Уравнение плоскости (BTC):

Слайд 44A
B
C
D
A1
B1
C1
D1
M
K
X
H
N
N
X
D1
H
=> ∠KNH=90º по определению
ΔKNH, ∠KNH=90º, NK=NH=4, тогда ∠KHN=45 º
Ответ:

∠KHN=45 º

KN=B1C1=4
KX=MD1=√41 (находится через т. Пифагора)
ΔXNK, ∠XNK=90º, по т.Пифагора XN=5,

Слайд 45Плоскость (KMD1)
4a+5c+d=0
4a+4b+2c+d=0
4b+7c+d=0
Дано: правильная четырехугольная призма со стороной основания 4

Слайд 48Задания для школы экспертов. Математика. 2016 год
A
S
B
C
D
=>SA ⊥(ABC) по

признаку
E
Традиционный способ
ΔSAD,

Слайд 49Поместим пирамиду в систему координат
x1=-6
y1=-8;
A
S
B
C
D
Векторный способ
z
x
y
x2=6
y2=-8;
z2=0
z1=√21

Слайд 52A
B
C
D
A1
C1
B1
D1
P
Q
X
U
Y
R
A
P
U
Y
h
ΔCQY,∠QCY=90º, по т.ПифагораYQ=√2

Аналогично RQ=RY =√2

SRQY=
ΔXPU~ΔXAY (по второму признаку

подобия), тогда PU||AY,
□APUY-трапеция

ΔABY,∠ABY=90º, по т.ПифагораAY=4√2

ΔPB1U, ∠ PB1U =90º, по т.ПифагораPU=2√2

QY=UQ=

x2=0
y1= 1 ;

Слайд 56H
Дано: В четырехугольной пирамиде SABCD (четырехугольник в основании выпуклый)

Слайд 57H
S
A
B
C
D
P
ΔSHB, по т. Пифагора SH=
SD=9, тогда в ΔSHD по

т. Пифагора HD=√78
SACD наибольшая, когда его высота –DH
DH┴AC, BH┴AC, через точку,