1. Найдите площадь квадрата, изображённого
на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ
дайте в квадратных сантиметрах.
2. Найдите вписанный угол, опирающийся на дугу, равную 15 окружности.
Ответ дайте в градусах.

пирамиде О центр основания, SO=35, Найдите длину отрезка ВД
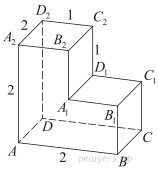
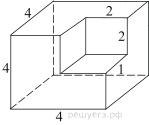
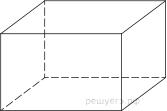
4. Найдите объём многогранника, изображённого на рисунке (все
двугранные углы прямые).

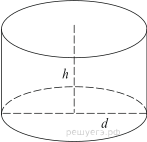
Найдите высоту цилиндра.
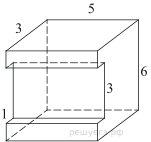
6. Найдите площадь поверхности многогранника, изображённого на
рисунке
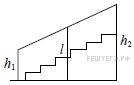
7. Найдите площадь трапеции, изображённой на рисунке.
8.В треугольнике АВС
угол С=58,биссектрисы АD и ВЕ пересекаются в точке О.Найти угол АОВ.
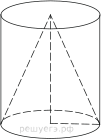
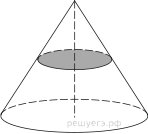
9. Диаметр основания конуса равен
40, а длина образующей — 25. Найдите высоту конуса.
10. В цилиндрическом сосуде уровень
жидкости достигает 98 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр
которого в 7 раз больше диаметра первого? Ответ выразите в сантиметрах.
11. В треугольнике
АВС высоты СЕ и ВД пересекаются в точке О.Угол А равен 56 градусов.Найдите угол
ДОЕ .Ответ дайте в градусах.
12. В прямоугольном параллелепипеде ВВ1=16,А1В1=2,А1Д1=8,Найти АС1.
13. В цилиндрическом сосуде уровень
жидкости достигает 64 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого
в 4 раза больше диаметра первого? Ответ выразите в сантиметрах.
14. В треугольнике АВС АС=ВС, АВ=20,
высота АН=8. Найти синус ВАС.
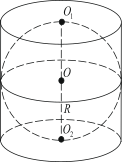
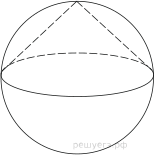
15. Около конуса описана сфера (сфера
содержит окружность основания конуса и его вершину). Центр сферы совпадает с
центром основания конуса.
Радиус сферы равен Найдите
образующую конуса.
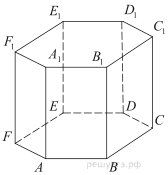
16. Найдите объём многогранника, вершинами
которого являются точки D ,A1,B1,C1,D1,E1,F1, правильной шестиугольной призмы
площадь основания которой равна 12, 
17. Найдите
площадь параллелограмма, изображённого на рисунке.
18.В треугольнике
АВС АD биссектриса ,угол С 104 градуса, угол САD равен 6 градусов.Нацйти угол В
19. Найдите объём многогранника,
вершинами которого являются точки С, А1,В1,С1 правильной треугольной
призмы АВСА1В1С1 площадь основания которой равна 4, а боковое ребро равно 9.
20. Два угла вписанного в окружность
четырёхугольника равны 56 и 77 градусов.
Найдите меньший из оставшихся
углов. Ответ дайте в градусах.
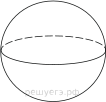
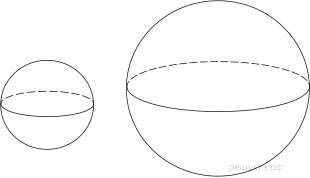
21. Дано два шара. Радиус первого шара в 2
раза больше радиуса второго. Во сколько раз площадь поверхности первого шара
больше площади поверхности второго?
22. Диагональ куба равна .Найдите его объём.
23.
В
прямоугольном параллелепипеде АВ-7, АД=3, ААВ1=4.Найти площадь сечения,
проходящего через точки А,В,С1
24. Угол между биссектрисой и
медианой прямоугольного треугольника, проведёнными из вершины прямого угла,
равен 14°.
Найдите меньший угол прямоугольного треугольника. Ответ дайте в градусах.
25. Площадь основания конуса равна 36π, высота =10 см . Найдите площадь осевого сечения
этого конуса.
26. Через
среднюю линию основания треугольной призмы, объём которой равен 52, проведена
плоскость, параллельная боковому ребру. Найдите объём отсечённой треугольной
призмы.
27. Площадь основания конуса равна
48. Плоскость, параллельная плоскости основания конуса, делит его высоту на
отрезки длиной 4 и 12, считая от вершины. Найдите площадь сечения конуса этой
плоскостью.
28. Объём треугольной призмы, отсекаемой
от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной
вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен
1,5. Найдите объём куба
29. Куб описан около сферы радиуса 2.
Найдите объём куба.
30. В правильной четырёхугольной
пирамиде все рёбра равны 2. Найдите площадь сечения пирамиды плоскостью,
проходящей через середины боковых рёбер.
По теме: методические разработки, презентации и конспекты
Решение стереометрической задачи тремя различными способами
Здесь представлено на трех файлах моё решение решение задачи С2 (вариант 13) из пособия «МАТЕМАТИКА. Подготовка к ЕГЭ-2011» под редакцией Ф.Ф. Лысенко, С.Ю. Калабухова. Эта-же задача встречается в пос…
Методическая разработка по теме: «Применение аналитической геометрии к решению стереометрических задач».
ВЫЧИСЛЕНИЕ РАССТОЯНИЙ И УГЛОВ Рассмотрим несколько геометрических задач, для решения которых необходимо вычислить те или иные расстояния или углы в пространст…
Тема 36. ГЕОМЕТРИЯ.ОСНОВНЫЕ СВЕДЕНИЯ ДЛЯ РЕШЕНИЯ СТЕРЕОМЕТРИЧЕСКИХ ЗАДАЧ.
Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к единому государственному экзамену (ЕГЭ) по математике, а также абитуриентов к вступительным э…
Тема 37.ИТОГОВЫЙ КОНТРОЛЬ ПО ТЕМАМ 34-36: «РЕШЕНИЕ ПЛАНИМЕТРИЧЕСКИХ И СТЕРЕОМЕТРИЧЕСКИХ ЗАДАЧ»
Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к государственной итоговой аттестации (ГИА) и единому государственному экзамену (ЕГЭ) по математике, …
Методическая разработка по теме: «Применение векторно-координатного метода в решении стереометрических задач»
Учёные всегда стремились упростить себе жизнь – придумывали новые, простые методы решения, универсальные для множества задач, позволяющие быстро решить даже самую трудную задачу. …
Методическая разработка по теме: «Применение векторно-координатного метода в решении стереометрических задач»
Учёные всегда стремились упростить себе жизнь – придумывали новые, простые методы решения, универсальные для множества задач, позволяющие быстро решить даже самую трудную задачу. …
Программа внеурочной деятельности «Практикум решения стереометрических задач». Пропедевтика стереометрических знаний на примере качественных стереометрических задач.
Всем известная трудность в изучении стереометрии, возникающая у учащихся 10 классов, в значительной степени объясняется низким уровнем развитием их пространственных представлений. Ученики теряю…
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В перпендикулярно АМ, пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9.
а) докажите, что биссектриса угла С делит отрезок МN пополам
б) пусть Р — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.
Источник: ЕГЭ по математике 19.06.2014. Основная волна, резервная волна. Запад. Вариант 1
2
Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка E лежит вне прямоугольника, причём ∠BEC = 120°.
а) Докажите, что ∠CBE = ∠COE.
б) Прямая OE пересекает сторону AD прямоугольника в точке K. Найдите EK, если известно, что BE = 40 и CE = 24.
3
Медианы AA1, BB1 и CC1 треугольника ABC пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 12.
4
На сторонах AC и BC треугольника ABC вне треугольника построены квадраты ACDE и BFKC. Точка M — середина стороны AB.
а) Докажите, что
б) Найдите расстояние от точки M до центров квадратов, если AC = 10, BC = 32 и ∠ACB = 30°.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016
5
На гипотенузу AB прямоугольного треугольника ABC опустили высоту CH. Из точки H на катеты опустили перпендикуляры HK и HE.
а) Докажите, что точки A, B, K и E лежат на одной окружности.
б) Найдите радиус этой окружности, если AB = 12, CH = 5.
Пройти тестирование по этим заданиям
Геометрия 10-11 класс, задания по темам. Математика для школьников. Подготовка к ЕГЭ и ОГЭ

Подготовка к ЕГЭ по геометрии 11 класс и другие
полезные материалы для учителя геометрии, которые вы можете выбрать и скачать бесплатно в этом разделе.
Показывать
Подготовка к ЕГЭ

- Все разработки
- Уроки
- Тесты
- Презентации
- Планирование
- Мероприятия
- Видеоуроки
- Кабинет
- Подготовка к ЕГЭ
- Проверочные работы
- Практикумы
- Подготовка к ОГЭ
- Факультативы
- Классные часы
- Разное
Геометрия

- Все предметы
- Дошкольное образование
- Начальные классы
- Информатика
- Математика
- Алгебра
- Геометрия
- Химия
- Физика
- Русский язык
- Английский язык
- Немецкий язык
- Французский язык
- История
- Всемирная история
- Всеобщая история
- История России
- Право
- Биология
- Обществознание
- Литература
- География
- Музыка
- Технология девочки
- Технология мальчики
- Технология
- Физкультура
- ИЗО
- Окружающий мир
- Искуcство
- ОБЖ
- Внеурочка
- Астрономия
- Директору
- Завучу
- Классному руководителю
- Коррекционная школа
- Логопедия
- ОРК
- Психологу
- МХК
- Всем учителям
- Прочее
- Естествознание
- Экономика
- Экология
- Финансовая грамотность
- ОРКиСЭ
- Школьному библиотекарю
- Родной язык и литература
- Истоки
11 класс

- Все классы
- Дошкольникам
- 1 класс
- 2 класс
- 3 класс
- 4 класс
- 5 класс
- 6 класс
- 7 класс
- 8 класс
- 9 класс
- 10 класс
- 11 класс
- Прочее
Все учебники

- Все учебники
- Геометрия (базовый и углубленный уровень), 10-11 классы, Александров А.Д., Вернер А.Л. и др., Москва : Просвещение, 2019. — 159 с.
- Геометрия (базовый и углублённый уровни), 11 класс, Козлов В.В., Никитин А.А. и др./ Под ред. Козлова В.В. и Никитина А.А., Изд. «Русское слово” 2016
- Геометрия. 10-11 классы. (профильный уровень) Калинин А.Ю., Терёшин Д.А. (2011, 640с.)
- Геометрия. 10-11 классы. Александров А.Д., Вернер А.Л., Рыжик В.И. (2014, 255с.)
- Геометрия. 10-11 классы. Базовый уровень. Шарыгин И.Ф. М.: 2013. — 240 с.
- Геометрия. 10-11 классы. Учебник (базовый и профильный уровни). Смирнова И.М., Смирнов В.А. (2008, 288с.)
- Геометрия. 11 класс. (углубленное и профильное обучение). Потоскуев Е.В., Звавич Л.И. (2004, 368с.)
- Геометрия. Учебник для 10-11 классов. Погорелов А.В. 13-е изд. — М.: 2014 — 175 с.
Вариант 1 8. Стереометрия
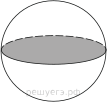
1.Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
2. Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.
3. Найдите угол CAD2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
4. Площадь боковой поверхности цилиндра равна , а диаметр основания — 8. Найдите высоту цилиндра.
5. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 112. Найдите объём конуса.
6. Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.
7. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
8. Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
9. Радиусы двух шаров равны 32 и 60. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров.
10. Объем конуса равен 10. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Вариант 2 8. Стереометрия
1. Диаметр основания конуса равен 42, а длина образующей равна 75. Найдите высоту конуса.
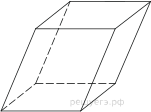
2. Гранью параллелепипеда является ромб со стороной 4 и острым углом 30°. Одно из ребер параллелепипеда составляет с этой гранью угол в 30° и равно 6. Найдите объем параллелепипеда.
3. Найдите объем многогранника, вершинами которого являются точки A, B, C, D, A1, B1, C1, D1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 9, а боковое ребро равно 10.
4. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 4 и 16. Найдите ребро равновеликого ему куба.
5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
6. В правильной четырехугольной пирамиде точка
— центр основания,
вершина,
,
Найдите длину отрезка
7. Гранью параллелепипеда является ромб со стороной 1 и острым углом 45°. Одно из ребер параллелепипеда составляет с этой гранью угол в 45° и равно 5. Найдите объем параллелепипеда.
8. Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 1:1, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.
9. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 112. Найдите объём конуса.
10.Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.
Вариант 3 8. Стереометрия
1. На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите тангенс угла C2C3B2.
2. Найдите угол CAD2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
3. Найдите угол многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
4. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
6. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 0,5 и 16. Найдите ребро равновеликого ему куба.
7. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 24. Найдите объем пирамиды.
8. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60°. Высота пирамиды равна 6. Найдите объем пирамиды.
9. Объем правильной четырехугольной пирамиды SABCD равен 116. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC.
10. В прямоугольном параллелепипеде известно, что Найдите длину ребра
Вариант 4 8. Стереометрия
1. Найдите квадрат расстояния между вершинами и
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
2. В прямоугольном параллелепипеде известно, что Найдите длину ребра
3. Площадь боковой поверхности цилиндра равна 18, а диаметр основания равен 9. Найдите высоту цилиндра.
4. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в три раза?
5. Найдите объём многогранника, вершинами которого являются точки правильной треугольной призмы площадь основания которой равна 9, а боковое ребро равно 8.
6. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 2 и 3. Объем призмы равен 18. Найдите ее боковое ребро.
7. Найдите объем многогранника, вершинами которого являются точки ,
,
,
,
,
,
правильной шестиугольной призмы , площадь основания которой равна 4, а боковое ребро равно 3.
8. Конус описан около правильной четырехугольной пирамиды со стороной основания 3 и высотой 13. Найдите его объем, деленный на π.
9. Диагональ куба равна 13. Найдите площадь его поверхности.
10. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 48 и высота равна 7.
Вариант 5 8. Стереометрия
1. Диагональ куба равна 1. Найдите площадь его поверхности.
2. Найдите объем пирамиды, высота которой равна 6, а основание – прямоугольник со сторонами 3 и 4.
3. В правильной треугольной призме ABCA1B1C1 стороны оснований равны 2, боковые рёбра равны 5. Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер AB, AC, A1B1 и A1C1.
4. Найдите квадрат расстояния между вершинами и
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
5. В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в раза больше первого? Ответ выразите в см.
6. В сосуд, имеющий форму правильной треугольной призмы, налили 2300 воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 27 см. Найдите объем детали. Ответ выразите в см3.
7. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.
8. В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.
9. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы
.
10.Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.
Вариант 6 8. Стереометрия
1. В правильной треугольной пирамиде SABC точка K – середина ребра BC, S – вершина. Известно, что SK = 4, а площадь боковой поверхности пирамиды равна 54. Найдите длину ребра AC.
2. Найдите угол ABD многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
3. Во сколько раз увеличится объем куба, если его ребра увеличить в пятнадцать раз?
4. Найдите объем многогранника, вершинами которого являются точки ,
,
,
,
,
,
,
правильной шестиугольной призмы , площадь основания которой равна 6, а боковое ребро равно 2.
5. Найдите объем многогранника, вершинами которого являются точки A, B, C, D, A1, B1, C1, D1 правильной шестиугольной призмыABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 2.
6. Гранью параллелепипеда является ромб со стороной 1 и острым углом 60°. Одно из ребер параллелепипеда составляет с этой гранью угол в 60° и равно 2. Найдите объем параллелепипеда.
7. Цилиндр описан около шара. Объем цилиндра равен 33. Найдите объем шара.
8. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
9. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
10. Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра.
Вариант 7 8. Стереометрия
1. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
2. Найдите объем части конуса, изображенной на рисунке. В ответе укажите
3. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.
4. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
5. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
6. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
7. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
8. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
9. Найдите объем части конуса, изображенной на рисунке. В ответе укажите
10. Найдите объем части конуса, изображенной на рисунке. В ответе укажите
Вариант 8 8. Стереометрия
1. Объем одного куба в 729 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
2. В правильной четырехугольной пирамиде точка
— центр основания,
вершина, , Найдите длину отрезка
3. В правильной треугольной пирамиде SABC точка R — середина ребра BC, S — вершина. Известно, что AB = 1, а SR = 2. Найдите площадь боковой поверхности.
4. В правильной треугольной пирамиде SABC точка N — середина ребра BC, S — вершина. Известно, что AB = 1, а площадь боковой поверхности равна 3. Найдите длину отрезка SN.
5. В правильной треугольной пирамиде SABC точка L — середина ребра BC, S — вершина. Известно, что SL = 2, а площадь боковой поверхности равна 3. Найдите длину отрезка AB.
6. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, объем пирамиды равен 1. Найдите длину отрезка MS.
7. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, MS = 1. Найдите объем пирамиды.
8. В правильной треугольной пирамиде медианы основания пересекаются в точке Объем пирамиды равен
,
Найдите площадь треугольника
9. В прямоугольном параллелепипеде известно, что , , Найдите длину ребра
10. Высота конуса равна 4, а диаметр основания — 6. Найдите образующую конуса.
Вариант 9 8. Стереометрия
1. Найдите расстояние между вершинами и
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
2. Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.
3. Высота конуса равна 6, образующая равна 10. Найдите площадь его полной поверхности, деленную на
4. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
5. Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 1:1, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.
6. Объем одного шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
7. Радиусы двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров.
8. Объём куба равен 12. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.
9. Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
10. В правильной четырёхугольной пирамиде высота равна 2, боковое ребро равно 5. Найдите её объём.
Вариант 10 8. Стереометрия
1. Найдите объем многогранника, вершинами которого являются точки A, B, C, D, A1, B1, C1, D1 правильной шестиугольной призмыABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 2.
2.Высота конуса равна 12, образующая равна 15. Найдите его объем, деленный на
3. В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SO = 4, AC = 6. Найдите боковое ребро SC.
4. В правильной четырехугольной пирамиде точка О — центр основания,
вершина, , Найдите длину отрезка
5. В правильной четырехугольной пирамиде точка
— центр основания,
вершина, , Найдите длину отрезка
6. ЗВ правильной треугольной пирамиде SABC точка R — середина ребра BC, S — вершина. Известно, что AB = 1, а SR = 2. Найдите площадь боковой поверхности.
7. В правильной треугольной пирамиде SABC точка N — середина ребра BC, S — вершина. Известно, что AB = 1, а площадь боковой поверхности равна 3. Найдите длину отрезка SN.
8. В правильной треугольной пирамиде SABC точка L — середина ребра BC, S — вершина. Известно, что SL = 2, а площадь боковой поверхности равна 3. Найдите длину отрезка AB.
9. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, объем пирамиды равен 1. Найдите длину отрезка MS.
10. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, MS = 1. Найдите объем пирамиды.
|
8. Стереометрия |
||||
|
Вариант 1
|
Вариант 2
|
Вариант 3
|
Вариант 4
|
Вариант 5
|
|
Вариант 6
|
Вариант 7
|
Вариант 8
|
Вариант 9
|
Вариант 10
|
Варианты для подготовки к ЕГЭ (задания по геометрии)
Вариант № 1
1. 
2. Электрику ростом 1,8 метра нужно поменять лампочку, закреплённую на стене дома на высоте 4,2 м. Для этого у него есть лестница длиной 3 метра. На каком наибольшем расстоянии от стены должен быть установлен нижний конец лестницы, чтобы с последней ступеньки электрик дотянулся до лампочки? Ответ запишите в метрах.
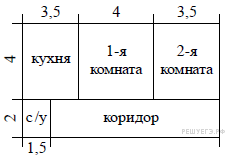
3. 
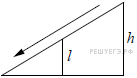
4. 
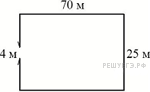
5. 
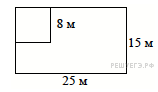
6.
Дачный участок имеет форму прямоугольника со сторонами 25 метров и 15 метров. Хозяин отгородил на участке квадратный вольер со стороной 8 метров (см. рисунок). Найдите площадь оставшейся части участка. Ответ дайте в квадратных метрах.
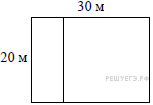
7. 
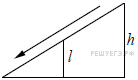
8. 
9. Пол в комнате, имеющей форму прямоугольника со сторонами 4 м и 6 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 30 см. Сколько потребуется таких дощечек?
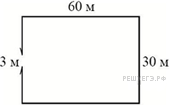
10. 
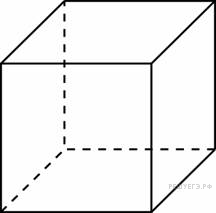
11. 
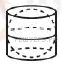
12. 
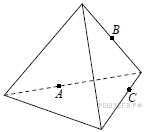
13. 
14. В прямоугольном параллелепипеде известно, что
,
,
. Найдите длину диагонали
.
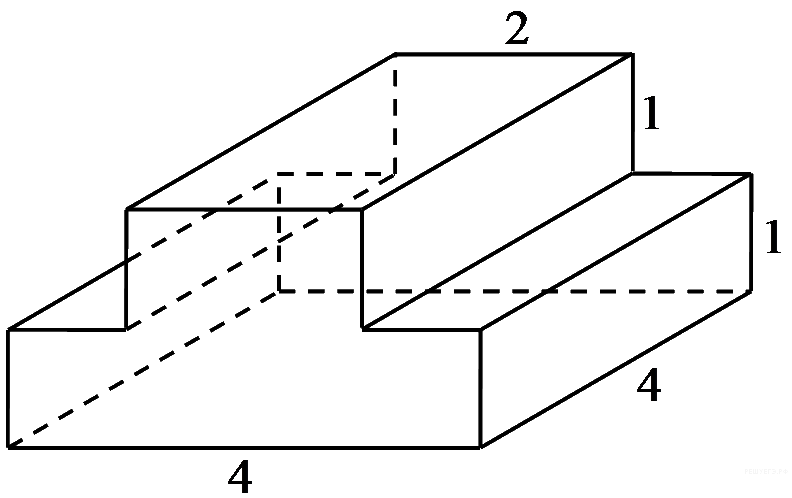
15. 
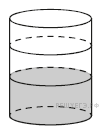
16.
17. 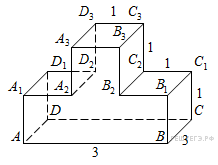
и
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
18. 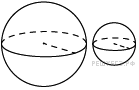
19. Площадь боковой поверхности цилиндра равна , а высота — 1. Найдите диаметр основания.
20. 
Ключ Вариант № 1
|
№ п/п |
Ответ |
|
1 |
1400 |
|
2 |
1,8 |
|
3 |
66 |
|
4 |
1 |
|
5 |
186 |
|
6 |
311 |
|
7 |
120 |
|
8 |
1 |
|
9 |
800 |
|
10 |
177 |
|
11 |
24 |
|
12 |
72 |
|
13 |
6 |
|
14 |
27 |
|
15 |
60 |
|
16 |
1200 |
|
17 |
11 |
|
18 |
9 |
|
19 |
2 |
|
20 |
93 |
Вариант № 2
1. 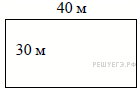
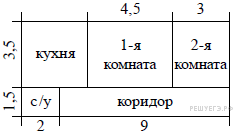
2. 
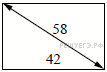
3. 
4. Рыболовное хозяйство строит бассейн для разведения рыбы. Бассейн имеет форму прямоугольника со сторонами 4 м и 12 м. В центре бассейна находится техническая постройка, которая имеет форму прямоугольника со сторонами 2 м и 3 м. Найдите площадь оставшейся части бассейна.
5. 
6.
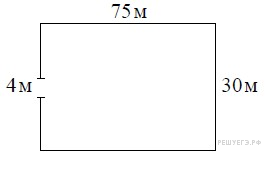
Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 30 м и 75 м. Найдите длину забора (в метрах), которым нужно огородить участок, если в заборе предусмотрен проезд шириной 4 м.
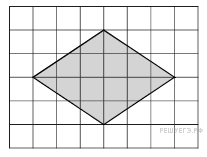
7. 
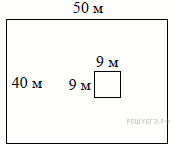
8. 
9. Какой угол (в градусах) образуют минутная и часовая стрелки в 16:00?
10. 
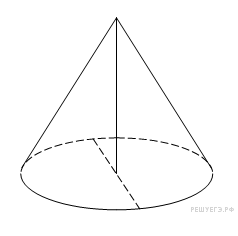
11. 
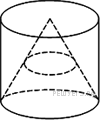
12. 
13.
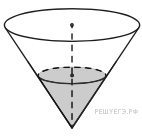
В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объём сосуда 960 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.
14. 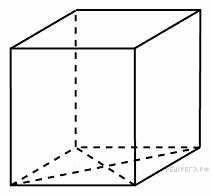
15. 
и
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
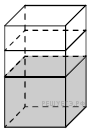
16. 
17. 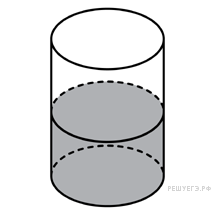
.
18. 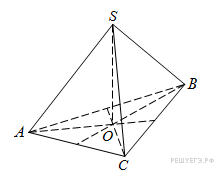
медианы основания
пересекаются в точке
. Площадь треугольника
равна 4; объем пирамиды равен 6. Найдите длину отрезка
.
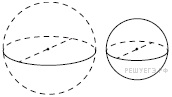
19. 
20.
К правильной шестиугольной призме с ребром основания 1 приклеили правильную шестиугольную пирамиду с ребром основания 1 так, что основания совпали. Сколько граней у получившегося многогранника (невидимые рёбра на рисунке не изображены)?
Ключ
|
№ п/п |
Вариант № 1 |
Вариант № 2 |
|
1 |
1400 |
100 |
|
2 |
1,8 |
55 |
|
3 |
66 |
40 |
|
4 |
1 |
42 |
|
5 |
186 |
186 |
|
6 |
311 |
206 |
|
7 |
120 |
12 |
|
8 |
1 |
1919 |
|
9 |
800 |
120 |
|
10 |
177 |
1,1 |
|
11 |
24 |
17 |
|
12 |
72 |
63 |
|
13 |
6 |
120 |
|
14 |
27 |
42 |
|
15 |
60 |
11 |
|
16 |
1200 |
3200 |
|
17 |
11 |
2500 |
|
18 |
9 |
4,5 |
|
19 |
2 |
48 |
|
20 |
93 |
13 |