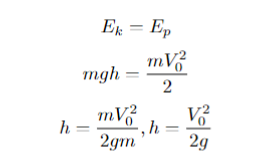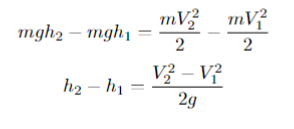в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 36 1–20 | 21–36
Добавить в вариант
На гладком горизонтальном столе покоится брусок с прикреплённой к нему гладкой изогнутой в вертикальной плоскости тонкой жёсткой трубкой (см. рис.). Общая масса бруска с трубкой равна M = 0,8 кг. В верхний конец вертикальной части трубки, находящийся на высоте H = 70 см над бруском, опускают без начальной скорости маленький шарик массой m = 50 г. Другой конец трубки наклонён к горизонту под углом α = 30° и находится на высоте h = 20 см над бруском. Найдите модуль скорости, с которой будет двигаться брусок после того, как шарик вылетит из трубки.
Какие законы Вы используете для описания движения и взаимодействия трубки и шарика? Обоснуйте их применение к данному случаю.
Источник: Тренировочная работа по физике 28.04.2017, вариант ФИ10503
Задания Д1 B1 № 131
Лодка должна попасть на противоположный берег реки по кратчайшему пути в системе отсчета, связанной с берегом. Скорость течения реки u, а скорость лодки относительно воды Чему должен быть равен модуль скорости лодки относительно берега?
1)
2)
3)
4)
Автобус везёт пассажиров по прямой дороге со скоростью 10 м/с. Пассажир равномерно идёт по салону автобуса со скоростью 1 м/с относительно автобуса, двигаясь от задней двери к кабине водителя. Чему равен модуль скорости пассажира относительно дороги? (Ответ дайте в метрах в секунду.)
Задания Д29 C2 № 9072
На гладком горизонтальном столе покоится брусок с прикреплённой к нему гладкой изогнутой в вертикальной плоскости тонкой жёсткой трубкой (см. рис.). Общая масса бруска с трубкой равна M = 0,8 кг. В верхний конец вертикальной части трубки, находящийся на высоте H = 70 см над бруском, опускают без начальной скорости маленький шарик массой m = 50 г. Другой конец трубки наклонён к горизонту под углом α = 30° и находится на высоте h = 20 см над бруском. Найдите модуль скорости, с которой будет двигаться брусок после того, как шарик вылетит из трубки.
Задания Д1 B1 № 5952
Два камня одновременно бросили из одной точки: первый — вертикально вверх, второй — под углом 45° к горизонту. Сопротивление воздуха пренебрежимо мало. Как движется первый камень в системе отсчёта, связанной со вторым камнем?
1) покоится
2) движется по параболе
3) движется равномерно и прямолинейно
4) движется по дуге окружности
Задания Д1 B1 № 5987
Два камня одновременно бросили из одной точки: первый — вертикально вверх, второй — под углом 30° к горизонту. Сопротивление воздуха пренебрежимо мало. Как движется второй камень в системе отсчёта, связанной с первым камнем?
1) покоится
2) движется по параболе
3) движется равномерно и прямолинейно
4) движется по дуге окружности
Мотоцикл едет по прямой дороге с постоянной скоростью 50 км/ч. По той же дороге навстречу ему едет автомобиль с постоянной скоростью 70 км/ч. Чему равен модуль скорости движения мотоцикла относительно автомобиля? (Ответ дайте в километрах в час.)
Мотоцикл едет по прямой дороге с постоянной скоростью 50 км/ч. По той же дороге в том же направлении едет автомобиль с постоянной скоростью 70 км/ч. Чему равен модуль скорости движения мотоцикла относительно автомобиля? (Ответ дайте в километрах в час.)
Задания Д2 B2 № 6637
Маша взяла в руку монету и, стоя в комнате своей квартиры, выпустила её из пальцев без начальной скорости. Монета полетела вдоль вертикали и упала на пол комнаты. Затем Маша вышла из дома, села в подъехавший автобус и, дождавшись, пока он начнёт двигаться равномерно и прямолинейно по горизонтальной дороге, повторила опыт с бросанием монеты. Оказалось, что монета в равномерно движущемся автобусе падает точно так же, как и в квартире. Иллюстрацией какого закона или принципа может служить этот опыт?
1) первого закона Ньютона
2) второго закона Ньютона
3) третьего закона Ньютона
4) принципа относительности Галилея
Задания Д2 B2 № 6676
Саша взял в руку монету и, стоя в равномерно движущемся вниз лифте, выпустил её из пальцев без начальной скорости. Монета полетела вдоль вертикали и упала на пол лифта. Затем Саша вышел из дома, сел в подъехавший автобус и, дождавшись, пока он начнёт двигаться равномерно и прямолинейно по горизонтальной дороге, повторил опыт с бросанием монеты. Оказалось, что монета в равномерно движущемся автобусе падает точно так же, как и в равномерно опускающемся лифте. Иллюстрацией какого закона или принципа может служить этот опыт?
1) Первого закона Ньютона
2) Второго закона Ньютона
3) Третьего закона Ньютона
4) принципа относительности Галилея
Задания Д1 B1 № 125
Вертолет поднимается вертикально вверх. Какова траектория движения точки на конце лопасти винта вертолета в системе отсчета, связанной с винтом?
1) точка
2) прямая
3) окружность
4) винтовая линия
Задания Д3 B3 № 4412
Два бруска массой m и
равномерно движутся вдоль прямой OX (см. рис.). В системе отсчёта, связанной с бруском
модуль импульса второго бруска равен
1)
2)
3)
4)
Задания Д3 B3 № 4447
Два бруска массой m и
равномерно движутся вдоль прямой OX (см. рис.). В системе отсчёта, связанной с бруском
модуль импульса первого бруска равен
1) mV
2)
3)
4)
Из двух городов навстречу друг другу с постоянной скоростью движутся два автомобиля. На графике показано изменение расстояния между автомобилями с течением времени. Каков модуль скорости первого автомобиля в системе отсчёта, связанной со вторым автомобилем? Ответ приведите в метрах в секунду.
Источник: Демонстрационная версия ЕГЭ—2020 по физике.
Задания Д1 B1 № 3357
Вертолет равномерно поднимается вертикально вверх. Какова траектория крайней точки лопасти вертолета в системе отсчета, связанной с корпусом вертолета?
1) прямая линия
2) винтовая линия
3) окружность
4) эллипс
Пловец плывет по течению реки. Определите скорость пловца относительно берега, если скорость пловца относительно воды 0,4 м/с, а скорость течения реки 0,3 м/с. (Ответ дайте в метрах в секунду.)
Из незакреплённой пушки стреляют снарядом массой 20 кг, который вылетает из ствола в горизонтальном направлении со скоростью 102 м/с относительно пушки. Пушка при этом откатывается, приобретая относительно земли скорость 2 м/с. Чему равна масса пушки, если массой сгоревшего порохового заряда можно пренебречь? Ответ дайте в килограммах.
Из незакреплённой пушки массой 800 кг стреляют снарядом, который вылетает из ствола в горизонтальном направлении со скоростью 102 м/с относительно пушки. Пушка при этом откатывается, приобретая относительно земли скорость 2 м/с. Чему равна масса снаряда, если массой сгоревшего порохового заряда можно пренебречь? Ответ дайте в килограммах.
Пароход движется по реке против течения со скоростью 5 м/с относительно берега. Определите скорость течения реки, если скорость парохода относительно берега при движении в обратном направлении равна 8 м/с. (Ответ дайте в метрах в секунду.)
Всего: 36 1–20 | 21–36
- ЕГЭ по физике
Задачи по механике для подготовки к ЕГЭ по физике.
Большинство заданий с ответами.
→ скачать сборник
→ презентация: «Задачи по механике»
Пример заданий:
1. Начальная скорость снаряда, выпущенного из пушки вертикально вверх, равна v0 = 10 м/с. В точке максимального подъема снаряд разорвался на два осколка, массы которых относятся как 2 : 1. Осколок большей массы упал на землю первым со скоростью v1 = 2v0. До какой максимальной высоты поднялся осколок меньшей массы?
2. Начальная скорость снаряда, выпущенного из пушки вертикально вверх, равна v0 = 10 м/с. В точке максимального подъема снаряд разорвался на два осколка, массы которых относятся как 1 : 2. Осколок меньшей массы упал на землю со скоростью v1 = 2v0. Какова скорость большего осколка при падении на землю? Считать поверхность земли плоской и горизонтальной.
17. Звезда и массивная планета обращаются вокруг общего неподвижного центра масс по круговым орбитам. Найдите радиус орбиты планеты r, если известно, что масса планеты равна m, а период обращения звезды и радиус ее орбиты равны Т и R соответственно.
27. Пуля летит горизонтально со скоростью v0 = 160 м/с, пробивает стоящую на горизонтальной шероховатой поверхности коробку и продолжает движение в прежнем направлении со скоростью v0/4. Масса коробки в 12 раз больше массы пули. Коэффициент трения скольжения между коробкой и поверхностью μ = 0,3. На какое расстояние S переместится коробка к моменту, когда его скорость уменьшится на 20 % ?
Связанные страницы:
ЕГЭ Решение задач по физике. Глава 1. МЕХАНИКА (кинематика, динамика, статика, колебания и волны).
Задачи ЕГЭ по физике М11 — М20 с указаниями, подсказками, ответами и решениями (ГДЗ по ЕГЭ). Материал для подготовки к ЕГЭ по физике может быть использован репетиторами, учителями и самими учащимися.
Вернуться к Списку заданий тренинга по физике.
Задачи по физике.
Механика 11-20
Задача 1.11. Тело массой m = 400 г брошено с некоторой высоты по направлению к земле под углом α = 30° к горизонту. Начальная скорость тела ʋ0 = 20 м/с. Определите, через сколько времени скорость тела будет направлена под углом β = 60° к горизонту. Определите изменение потенциальной энергии тела за это время. Ускорение свободного падения g ≈ 10 м/с2.
Указания (подсказка)
Покажите на рисунке направление горизонтальной, вертикальной и полной скоростей тела в начальный момент времени и в искомый момент времени. Учтите, что горизонтальная составляющая скорости не изменяется, а вертикальная увеличивается с течением времени. Вспомните определение тангенса угла и из треугольника скоростей получите уравнение для времени. Изменение потенциальной энергии определите из закона сохранения энергии или как работу силы тяжести за указанный промежуток времени.
Решение и ответ
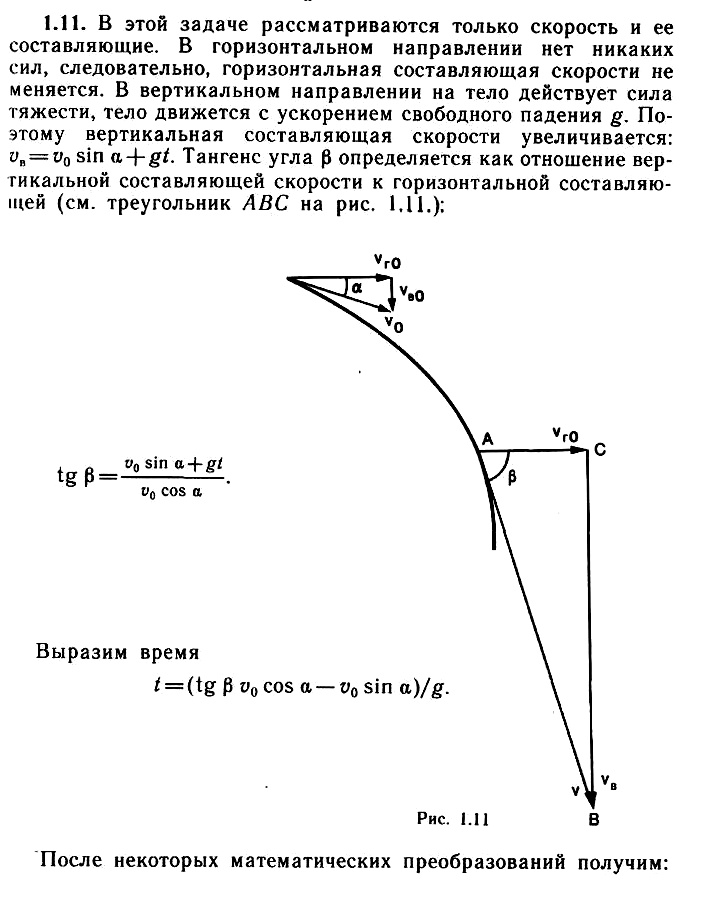

Задача 1.12. Тело массой m = 0,5 кг брошено со скоростью ʋ0 = 20 м/с под углом α = 30° к горизонту. Определите наибольшую высоту полета н изменение импульса за время полета. Сопротивлением воздуха можно пренебречь. Примите g ≈ 10 м/с2.
Указания (подсказка)
Наибольшую высоту подъема определите или из уравнения движения, или из закона сохранения энергии (см. задачу 1.10). Изменение импульса определите как разность векторов конечного и начального импульсов. Внимание! Не забывайте о векторном характере импульса. Можно воспользоваться вторым законом Ньютона. Изменение импульса системы равно импульсу внешней силы. Этой силой является сила тяжести.
Решение и ответ

Задача 1.13. Катер пересекает реку шириной l = 360 м. Скорость течения ʋ = 2 м/с. Рулевой держит курс перпендикулярно течению. Двигатель обеспечивает постоянное ускорение а = 0,1 м/с2. Начальная скорость катера равна нулю. Определите, через сколько времени катер пересечет реку. На какое расстояние он будет снесен течением?
Указания (подсказка)
Катер участвует в двух движениях: по течению реки он движется равномерно, а перпендикулярно течению относительно воды его движение равноускоренное.
Решение и ответ

Задача 1.14. Из окна вагона поезда, движущегося по горизонтальной дороге со скоростью ʋ = 54 км/ч, бросают в горизонтальном направлении предмет. Предмет падает на землю на расстоянии s = 12,1 м от места, над которым он находился в момент бросания. Определите скорость ʋ0 предмета относительно вагона сразу после бросания, если она была направлена перпендикулярно скорости движения поезда. Высота окна над поверхностью земли H = 2,5 м. Сопротивлением воздуха можно пренебречь.
Указания (подсказка)
Необходимо воспользоваться принципом относительности движения, рассматривая движение одного тела относительно другого или относительно Земли. Вспомните правило сложения скоростей: скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости этой подвижной системы относительно неподвижной. Помните о векторном характере скоростей. Если вам трудно запомнить такие «сложные» закономерности, вспомните простое правило сложения скоростей для лодки, переплывающей реку: течение ее сносит вдоль берега, а рулевой стремится переправиться на противоположный берег. И тогда любая задача, связанная с относительностью движения, будет вами решена.
Решение и ответ

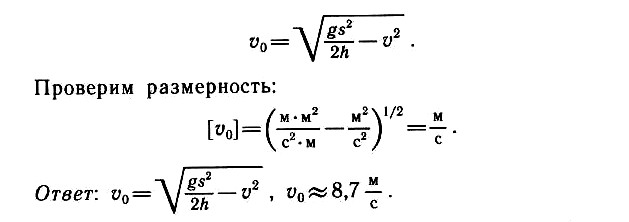
Задача 1.15. Тело 1 бросают вертикально вверх с начальной скоростью ʋ0 = 30 м/с. Тело 2, находящееся на высоте Н = 40 м по вертикали и на расстоянии l = 20 м по горизонтали от точки бросания тела 1, бросают горизонтально со скоростью ʋ1 =20 м/с. Определите, с каким запаздыванием или опережением т надо бросить тело 2, чтобы тела столкнулись в полете. Ускорение свободного падения g ≈ 10 м/с2.
Указания (подсказка)
Необходимо воспользоваться принципом относительности движения, рассматривая движение одного тела относительно другого или относительно Земли. Вспомните правило сложения скоростей: скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости этой подвижной системы относительно неподвижной. Помните о векторном характере скоростей. Если вам трудно запомнить такие «сложные» закономерности, вспомните простое правило сложения скоростей для лодки, переплывающей реку: течение ее сносит вдоль берега, а рулевой стремится переправиться на противоположный берег.
Решение и ответ
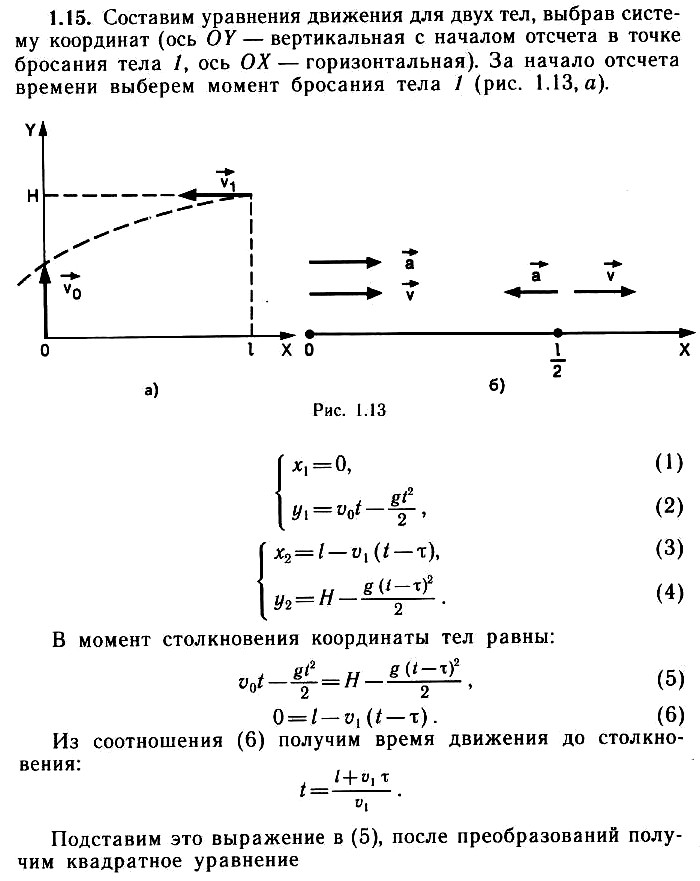
Задача 1.16. Человек начинает подниматься по движущемуся вверх эскалатору метро с ускорением а = 0,21 м/с2. Добежав до середины эскалатора, он останавливается, поворачивает и начинает спускаться вниз с тем же ускорением. Определите, сколько времени человек находится на эскалаторе. Длина эскалатора l = 100 м, а скорость его движения ʋ = 2 м/с.
Указания (подсказка)
Смотрите указание к задаче 1.14
Решение и ответ

Задача 1.17. Самолет, пролетая над зенитной батареей на высоте H = 1 км, начинает пикировать с выключенным двигателем на цель со скоростью ʋ1 = 540 км/ч, направленной под углом а = 60° к горизонту. Самолет сбивают выстрелом из орудия, произведенным в тот момент времени, когда он находился над батареей. Определите, на каком расстоянии от батареи, считая по горизонтальному направлению, снаряд попал в сaмолет. Скорость снаряда при вылете из ствола орудия ʋ2 = 600 м/с. Сопротивлением воздуха можно пренебречь.
Указания (подсказка)
Смотрите указание к задаче 1.14. Выберите систему отсчета, связанную с Землей, и составьте уравнения движения для снаряда и самолета. Равенство соответствующих координат и означает момент столкновения.
Решение и ответ
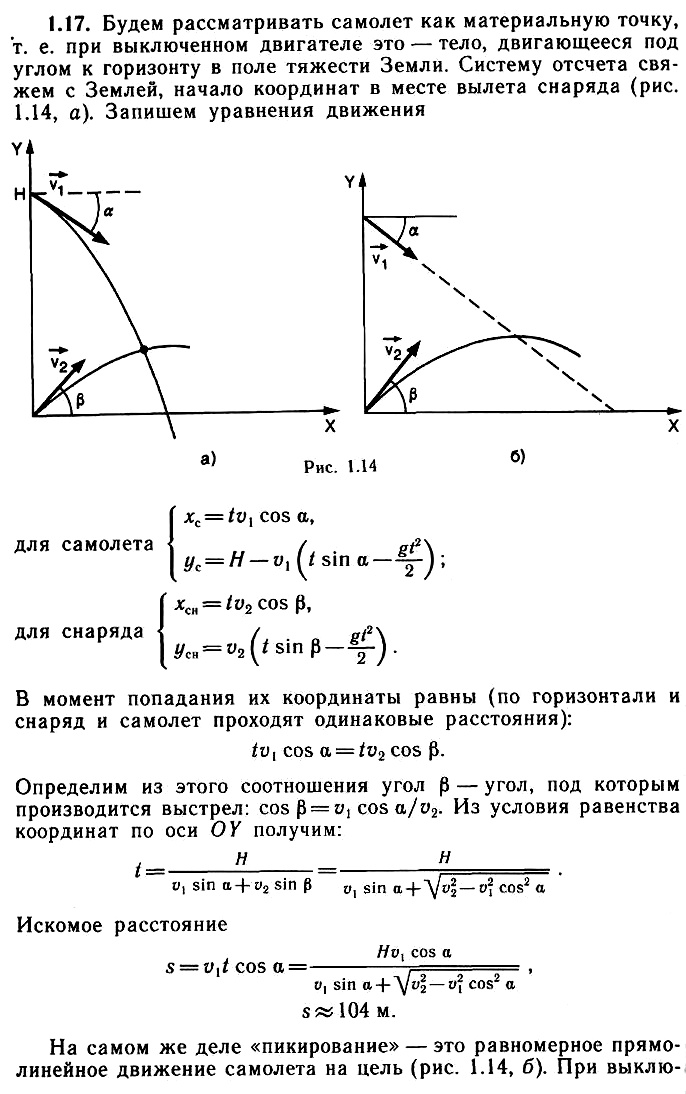

Задача 1.18. Две лодки переплывают реку, отправляясь одновременно из пунктов A и В, расположенных на противоположных берегах реки против друг друга. Скорость течения реки ʋp = 20 м/мин, ширина реки l = 200 м. Скорости лодок относительно воды равны ʋ1 = 15 м/мин, ʋ2 = 20 м/мин. Первая лодка начала движение перпендикулярно течению, а вторая держит курс под углом α = 150° к скорости течения реки. Определите, на каком расстоянии от пункта А будет находиться первая лодка, когда расстояние между лодками будет наименьшим.
Указания (подсказка)
После построения векторов скоростей учтите, что наименьшее расстояние между лодками будет определяться перпендикуляром из точки А на направление относительной скорости для лодки, выходящей из пункта В. Для того чтобы это понять, мысленно остановите лодку в пункте А, тогда вторая лодка должна двигаться в направлении относительной скорости, это ее перемещение, а наименьшее расстояние есть перпендикуляр, опущенный из точки на выбранное направление!
Решение и ответ
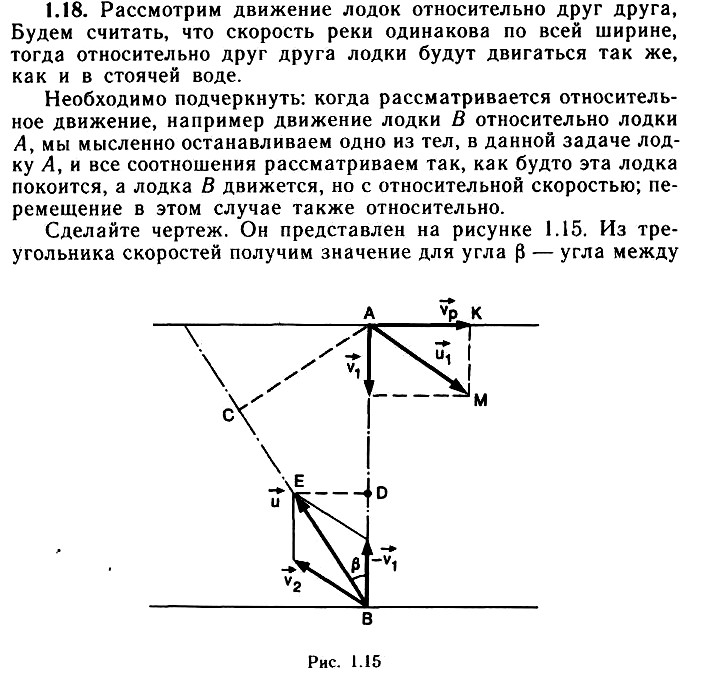

Задача 1.19. Лодочник отплывает из пункта А, держа курс перпендикулярно берегу. Скорость течения реки ʋp = 2 м/с, ее ширина h = 144 м. Лодка в течение времени t1 движется равноускоренно с ускорением а = 1 м/с2, а затем в течение промежутка времени t2 движется равномерно и, наконец, в течение промежутка времени t3 – равнозамедленно с тем же ускорением а. Определите промежутки времени t1 и t2, если известно, что лодка пришла в пункт В, расположенный на противоположном берегу реки на расстоянии l = 80 м вниз по течению. Постройте траекторию движения лодки в системе координат (XOY), связанной с берегом.
Указания (подсказка)
Выберите оси координат по течению реки и в перпендикулярном направлении. Запишите уравнения движения по обеим осям. Решите полученную систему.
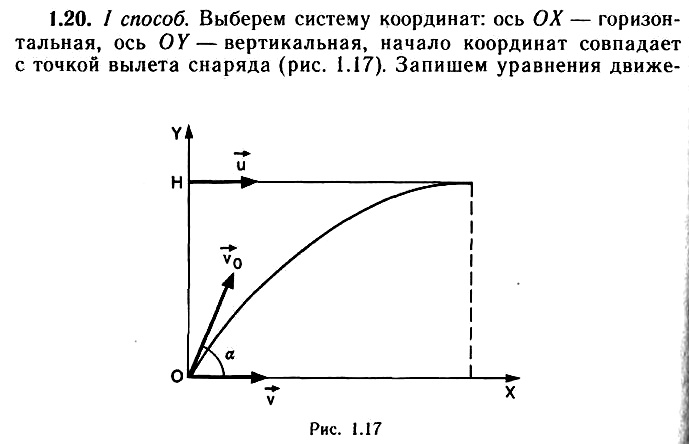
Задача 1.20. Из танка, движущегося со скоростью ʋ = 70 км/ч, стреляют по горизонтально летящему на высоте Н = 6 км самолету. Скорость самолета ʋ = 790 км/ч, а ее направление совпадает с направлением движения танка. Определите угол вылета α снаряда относительно горизонта. Известно, что в момент выстрела самолет находился над танком, а снаряд попал в самолет в высшей точке траектории.
Указания (подсказка)
Выберите систему отсчета, связанную с Землей, и составьте уравнения движения для снаряда и самолета. Равенство соответствующих координат и означает момент столкновения.
Решение и ответ

Вы смотрели «ЕГЭ Решение задач по физике. Механика 11-20». Задачи ЕГЭ по физике с указаниями, подсказками, ответами и решениями (ГДЗ по ЕГЭ). Материал для подготовки к ЕГЭ по физике.
Вернуться к Списку заданий тренинга по физике.
Просмотров:
15 751
В ЕГЭ по физике примерно 11 задач по механике, включая три сложные задачи из второй части. Так получилось потому, что этот раздел науки в школьной программе изучают дольше всего.
Хорошо разбираясь в механике, можно набрать достаточно большое количество баллов! Мы разберем один из часто встречающихся типов задач.
С чего начать
Все задачи по механике можно условно разделить на четыре раздела (плюс один дополнительный). Это задачи типа 3-8 в бланке ЕГЭ:
- описание движения (кинематика),
- сила и импульс (динамика),
- работа и энергия (механическое действие),
- условия равновесия и рычаги (статика, механизмы),
- дополнительный раздел “Механические колебания” (маятники).
В сложных задачах механика может встретиться в заданиях типа 25, 26: одна из них качественного характера, другая расчётная.
Последняя задача строго механическая и считается самой сложной — за нее дают аж 4 первичных балла. Также механика часто встречается там, где комбинируют два раздела физики, например: механика и термодинамика, или механика и электричество.
Поэтому учителю при подготовке ученика к ЕГЭ стоит много времени уделить именно механике – уж очень много баллов можно собрать именно с этого раздела.
В этой статье мы обратим внимание на те задачи, которые могут попасться в типе задач 3, 5-8 в первой части и 25, 30 во второй части.
Задачи на броски
Часто встречающийся формат задач – это броски. Они делятся на два основных вида:
- броски ровно вертикально,
- броски под углом к горизонту.
При этом сразу отметим, что можно применять в решении два основных подхода: систему уравнений движения и закон сохранения энергии.
Задачи на броски вертикально вверх
Здесь четыре типа движения:
- падение объекта,
- бросок объекта вниз,
- бросок объекта вверх,
- бросок объекта с определенной высоты.
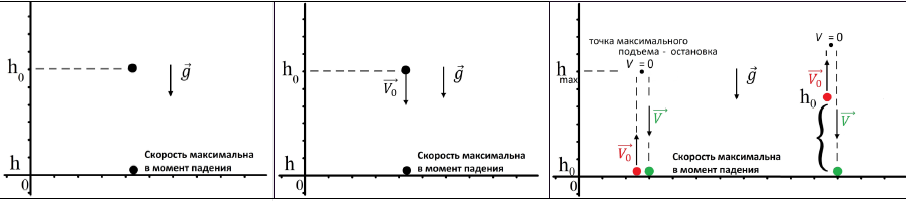
При любом из типов вертикального движения мы можем использовать систему уравнения движения. Давайте выведем, например, для случая «бросок вверх» максимальную высоту подъема через скорость и ускорение, ведь ускорение нам известно (g примерно 10):
А теперь найдем выражение для той же самой высоты, но уже через закон сохранения энергии, зная, что вся кинетическая энергия перейдет в потенциальную:
Как мы видим, формулы идентичные. Следовательно, при решении задач можно использовать либо один подход, либо другой.
Но главное, что нужно понимать: скорость будет соответствовать высоте. Необязательно брать начальную скорость и максимальную высоту, можно взять изменение высоты и изменения скорости:
Это вывод нужно обязательно показать ученику, ведь гораздо проще понять смысл и запомнить, как решаются задачи или какие принципы используются, если есть доказательства и пояснения.
Стоит отметить, что применять уравнения движения мы можем абсолютно всегда. Но когда речь идет о законах сохранения, мы можем применять их только тогда, когда система замкнутая, то есть нет воздействия внешних сил.
Лайфхак: можно посоветовать ученику при чтении условия обратить внимание на то, что в задаче дано.
— Если в задаче не дано время, то, скорее всего, данную задачу можно решить двумя способами, и быстрее вывести уравнение через закон сохранения энергии.
— Если же есть время, то лучше воспользоваться уравнением движения, а потом проверить с помощью закона сохранения.
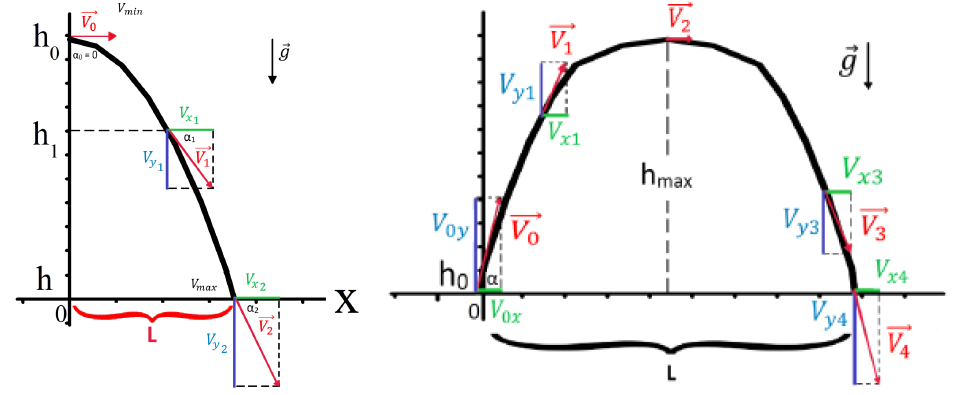
Задачи на броски под углом к горизонту
Броски к горизонту бывают всего двух типов. Либо бросают с какой-то высоты (чаще всего горизонтально), либо бросают с поверхности земли под углом (бывают еще броски из ям, но такие задачи в ЕГЭ крайне редки).
Важно пояснить ученику, что в таких типах задач ничего принципиально другого нет. Единственное — мы должны рассматривать в таких задачах два типа движения.
Стандартное равномерное движение по оси Х и с ускорением вертикальное по оси У. А также скорость, которая была в формулах ранее, изменится на две составляющие — по оси Х и по оси У:
Все остальное останется таким же, и в итоге мы получаем следующую формулу для максимальной высоты:
Примеры задачи
Рассмотрим, как применить эти два метода, чтобы решить задачи из ЕГЭ.
Тело брошено вертикально вверх. Через 0,5 с после броска его скорость 20 м/с. На какой высоте окажется тело? Сопротивлением воздуха пренебречь. (Ответ дайте в метрах.)
Сначала решим методом уравнения движения:
А теперь решим с помощь закона сохранения энергии:
Единственное, что нужно учесть — при уменьшении кинетической энергии увеличивается потенциальная, поэтому в конце минус пропадает.
Таким образом, мы получили одинаковые ответы двумя способами.
Краткий вывод
Такого рода задания достаточно часто встречаются в ЕГЭ как в первой, так и во второй части, поэтому важно знать два метода решения, чтобы у ученика были запасные варианты проверки правильного ответа.
И помните: «Fortis fortuna adiuvat» — удача на стороне сильных. Старайтесь, и все будет хорошо!
Задание №1. Первое задание ЕГЭ по физике проверяет знания по разделу «Кинематика». Это задание относится к заданию базового уровня. В нём отсутствует возможность выбора ответа. Для его решения необходимо проанализировать условие задачи, внимательно рассмотреть график зависимости кинематической величины от времени (при наличии такого графика), правильно подобрать формулу, провести расчет и записать ответ в предлагаемых единицах измерения.
Определение кинематических величин по графику
1. На рисунке приведён график зависимости проекции скорости тела vx от времени t.
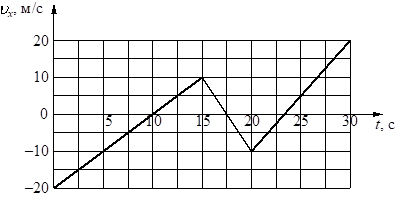
Определите проекцию ускорения тела ax в промежутке времени от 15 до 20 с.
Ответ: ___________ м/с2.
На графике представлена зависимость проекции скорости от времени. На участке от 15 до 20 с скорость тела изменяется от 10 м/с до -10 м/с. Это говорит о равноускоренном движении, при котором проекция ускорения тела должна быть отрицательной. Для решения задачи необходимо воспользоваться формулой для определения проекции ускорения:
. Проведем расчет:
(м/с2). Полученный результат подтверждает, что движение равноускоренное, причем проекция ускорения отрицательная.
Ответ: -4 м/с2.
Пояснение. Долгое время движение с переменной скоростью делилось на равноускоренное (ax > 0) и равнозамедленное (ax < 0) Но в последнее время говорят, в основном, только о равноускоренном движении, подразумевая постоянство ускорения. И только лишь знак проекции ускорения определяет возрастание или убывание скорости движения тела.
2. На рисунке приведён график зависимости координаты тела x от времени t при его прямолинейном движении по оси x.
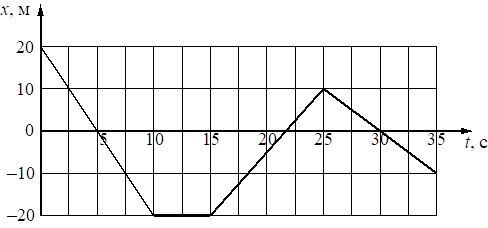
Определите проекцию скорости тела vx в промежутке времени от 25 до 30 с.
Ответ: _____________ м/с.
Согласно представленному графику зависимость координаты тела от времени является линейной. Это указывает на равномерный характер движения тела. Для решения задачи необходимо воспользоваться формулой для определения скорости при равномерном движении:
. Проведем расчет:
Ответ: -2 м/с.
Пояснение. Проекция скорости получилась отрицательной, это означает, что в указанный временной интервал тело двигалось в направлении, противоположном выбранной оси Ох.
3. Автомобиль движется по прямой улице вдоль оси Ox. На графике представлена зависимость проекции его скорости от времени.
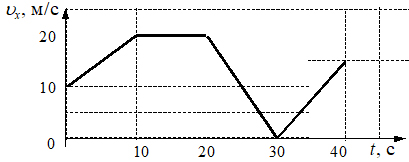
Определите путь, пройденный автомобилем за 30 с от момента начала наблюдения.
Ответ: ___________ м.
Так как по условию задачи нам дается график зависимости проекции скорости от времени, то пройденный путь будет определяться площадью геометрической фигуры под графиком. Для вычисления площади получившегося пятиугольника его можно разбить на несколько фигур, например, на две трапеции (см. рис.)
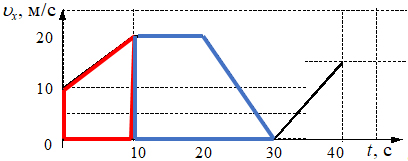
Используя известные формулы для нахождения площади трапеции, можно рассчитать путь за первые 10 с и последующие 20 с (от 10 с до 30 с).
;
S = 150 + 300 = 450 (м)
Ответ: 450 м.
Пояснение. Полученный пятиугольник можно разбить не только на две трапеции, здесь можно выделить трапецию, прямоугольник, треугольник. Тогда необходимо рассчитывать площади трех фигур и также их суммировать.
4. На рисунке приведен график зависимости проекции скорости тела, движущегося вдоль оси Ох от времени.
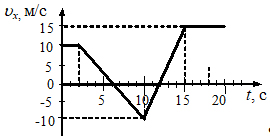
Определите проекцию перемещения пройденного телом, за 10 с от начала наблюдения.
Ответ: _________ м.
Так же как в задаче №3 модуль перемещения будет определяться площадью геометрической фигуры под графиком. Но проекция перемещения за время от 0 до 6 с будет положительной, а от 6 до 10 с отрицательной. Общая проекция перемещения будет определяться их суммой.
;
S = 40 + (-20) = 20 (м)
Ответ: 20 м.
Пояснение. При расчете S2x можно получить положительное число, но надо помнить, что в интервале от 6 до 10 с, тело движется в направлении противоположном оси Ох. Это означает, что проекция перемещения будет отрицательной. Пройденный путь за указанное время от 0 до 10 с определяется суммой модулей проекций перемещений и будет равным 60 м.
Относительность движения
5. Из двух городов навстречу друг другу с постоянной скоростью движутся два автомобиля. На графике показана зависимость расстояния между автомобилями от времени. Скорость второго автомобиля 25 м/с. С какой скоростью движется первый автомобиль?
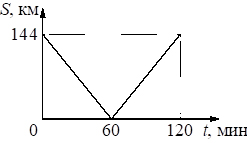
Формула для нахождения относительной скорости в векторной форме имеет вид:
Если два тела движутся навстречу друг другу, то в проекциях на ось OХ это уравнение преобразуется в следующий вид:

С учетом данных графика можно рассчитать относительную скорость этих автомобилей при движении навстречу друг другу. Это происходит на интервале от 0 до 60 мин.
, отсюда скорость первого автомобиля v1 = 40 — 25 = 15 (м/c)
Ответ: 15 м/с.
Пояснение. В курсе математики при изучении движения двух тел вводятся понятия скорость сближения и скорость удаления. В первом случае скорости тел суммируются, во втором вычитаются. Эти действия основаны на знаках проекций скоростей движущихся тел. Действия с векторами и их проекциями на оси координат используются как в физике, так и в математике.
6. Два точечных тела начинают двигаться из одной точки вдоль оси OX в противоположных направлениях. На рисунке показаны графики зависимостей проекций их скоростей Vx на ось OX от времени t. Чему будет равно расстояние между этими телами через 8 секунд после начала движения?
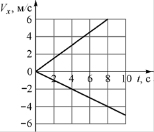
Ответ: _________ м.
Эта задача является комбинированной. Для её решения необходимо воспользоваться материалом двух тем: «Определение кинематических величин по графику» и «Относительность движения». Для определения проекций перемещений тел за 8 с необходимо рассчитать площади фигур под графиком.
Знак «минус» для S2x показывает, что тела движутся в противоположных направлениях. Поэтому расстояние между ними через 8 с равно сумме модулей перемещений.
Ответ: 40 м.
Пояснение. Самое главное в этой задаче — выяснить в каких направлениях двигаются тела. Для этого надо уметь извлекать информацию из графических зависимостей, другими словами, надо уметь «читать» графики. Это умения необходимы почти во всех разделах физики.
7. Катер плывёт по прямой реке, двигаясь относительно берега перпендикулярно береговой линии. Модуль скорости катера относительно берега равен 6 км/ч. Река течёт со скоростью 4,5 км/ч. Чему равен модуль скорости катера относительно воды?
Ответ: ________ км/ч
Решение задачи удобно сопроводить чертежом или рисунком. Выберем направление скорости реки вправо, тогда для движения перпендикулярно береговой линии, катеру необходимо держать курс немного левее.
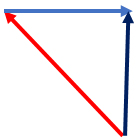
Скорость катера, скорость реки и скорость катера относительно береговой линии можно связать по теореме Пифагора:
; отсюда
;
(км/ч).
Ответ: 7,5 км/ч.
Пояснение. Подобные задачи необходимо для себя представлять в виде чертежа или рисунка. Тогда указанные в условии параметры будут наглядно изображены и это поможет геометрически решить задачу.
Равномерное движение тел по окружности
8. Установленная на станке фреза равномерно вращается с частотой 600 оборотов в минуту. Чему равен модуль ускорения точек, находящихся на расстоянии 3 см от оси фрезы? Ответ округлите до целого числа.
Ответ: ___________ м/с2
Так как тело движется равномерно по окружности, то в этой задаче требуется найти центростремительное ускорение. Его можно рассчитать по формуле: Линейная скорость v связана с угловой w соотношением Подставляя это выражение в первое уравнение и проводя сокращения, получим . При частоте вращения 600 оборотов в минуту тело будет совершать 10 оборотов за секунду.
Проведем расчет: .
Ответ:
Пояснение. В теме «Равномерное движение тел по окружности» достаточно много формул, которые трудно запоминаются. Из них надо знать базовые, которые относятся к периоду, частоте, линейной скорости, угловой скорости и центростремительному ускорению. Все остальные можно получить через достаточно простые рассуждения и выводы.
9. Две шестерни, сцепленные друг с другом, вращаются вокруг неподвижных осей. Большая шестерня радиусом 20 см делает 20 оборотов за 10 секунд. Сколько оборотов в секунду делает меньшая шестерня радиусом 10 см?
Ответ: _________ Гц.
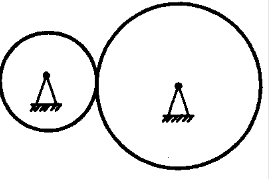
Так шетерни касаются друг друга, то это условие говорит о равенстве линейных скоростей этих тел. Выразим скорости вращения через радиусы и периоды обращения.
Приравняем скорости и проведем сокращения.
;
;
с учетом того, что период и частота величины обратные, запишем следующее равенство:
Проведем расчет:
Ответ: 4 Гц.
Пояснение. В задачах подобного типа всегда надо искать физическую величину, которая является общей для нескольких тел. В этой задаче — это скорость вращения обеих шестерней. Но надо иметь ввиду, что частоты их вращения и угловые скорости различны.
10. Волчок, вращаясь с частотой 20 с-1, свободно падает с высоты 5 м. Сколько оборотов сделает волчок за время падения?
Ответ: _________ оборотов
Определим вначале время падения волчка с высоты 5 м. Так как он падает свободно, то начальную скорость надо принять равной 0. Тогда высота и время падения будут связаны формулой отсюда
Проведем расчет времени падения
=1 (с). Так как волчок вращается с частотой 20 с-1, то это означает, что за 1 секунду он делает 20 оборотов. Так как время падения составляет 1 с, то количество оборотов также равно 20.
Ответ: 20.
Пояснение. Эта задача является комбинированной. В ней связаны два раздела кинематики: «Равноускоренное движение» и «Равномерное движение тел по окружности». Надо знать, что суть формул при движении тел с ускорением по горизонтали или по вертикали под действием силы тяжести не меняется. Главное — не ошибиться со знаками проекций для скорости и ускорения.
См. продолжение статьи