В БЛОГАХ…
еще…
еще…
Очень благодарна Вам, Зоя Андреевна, что находите время посмотреть и оценить рес…
Татьяна Владимировна, большое спасибо за очередной ресурс по функциональной грам…
Ирина Александровна, Вы подготовили очень интересный материал, посвящённый творч…
Наталья Александровна, спасибо за замечательный ресурс! Ну, ОЧЕНЬ эмоциональный!
Зоя Андреевна, спасибо за очередной тренажёр по теме «Основное свойство дро…
ЕГЭ по математике
Фильтры отменить
Категория ЕГЭ по математике содержит материалов: 415
Страницы: 1 2 3 … 20 21 »
Скачать материал

Скачать материал


- Сейчас обучается 1081 человек из 83 регионов


- Сейчас обучается 38 человек из 28 регионов


- Сейчас обучается 96 человек из 32 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Подготовка к ЕГЭ
Решение текстовых задач задач
Профиль №11
составила Шапиева Л.С.
Решение задач является наиболее
характерной и специфической
разновидностью свободного мышления
У.Джеймс -
2 слайд
Текстовые задачи условно можно разбить на следующие основные группы:
Задачи на производительность
задачи на работу
задачи на бассейны и трубы
Задачи на проценты, концентрацию, части и доли
Задачи на проценты и доли
Задачи на концентрацию, смеси и сплавы -
3 слайд
Задачи на движение
по прямой (навстречу и вдогонку)
по замкнутой трассе
по воде
на среднюю скорость
протяженных тел
Задачи на арифметическую и геометрическую прогрессии -
4 слайд
Алгоритм решения текстовых задач
Ввод переменных, т.е. обозначение буквами x, y, z,… величины, которые требуется найти по условию задачи.
Перевод условий задачи на язык математических соотношений, т.е. составление уравнений, неравенств, введение ограничения.
Решение уравнений или неравенств.
Проверка полученных решений на выполнение условий задачи. -
5 слайд
Указания к решению текстовых задач
Набор неизвестных должен быть достаточным для перевода условий задачи на язык математических соотношений. Как правило, за неизвестные следует принимать искомые величины.
Выбрав неизвестные, в процессе перевода условий задачи в уравнения или неравенства необходимо использовать все данные и условия задачи.
При составлении уравнений или неравенств необходимо исходить из требования о решении задачи в общем виде.
В составленных уравнениях надо проверить размерность членов уравнений
В процессе решения задачи, надо избегать результатов, противоречащих физическому смыслу. -
6 слайд
Задачи на проценты, концентрацию, части и доли
-
7 слайд
Задачи на проценты и доли
-
8 слайд
Задача №1: Влажность свежескошенной травы 60%, сена – 20%.
Сколько сена получится из 1 т свежескошенной травы?
Решение: 1000 0,4 = 400 кг сухого вещества в траве
80 % — 400 кг
100 % — х кг
х = (100 400):80 = 500 кг
Ответ: 500 кг.
Вода
20 %
Вода
60 %
Сухое
вещество
80 %
Сухое
вещество
40 %
1 т
? кг -
9 слайд
Задача № 2: Яблоки подешевели на 20 %. Сколько яблок можно
теперь купить на те же деньги, на которые раньше покупали
2,8 кг яблок?
Решение:
100 % 2,8 кг
80 % х кг
х = 3,5 кгОтвет: 3,5 кг
-
10 слайд
Задача № 3: Арбуз весил 20 кг и содержал 99 % воды, когда он немного усох, то стал содержать 98 % воды. Сколько теперь весит арбуз?
Решение:
20 0,99 = 19,8 кг воды в арбузе
20 – 19,8 = 0,2 кг сухого вещества
После усыхания 100 98 = 2% — это 0,2 кг
0,2 : 0,02 = 10 кг
Ответ: 10 кг. -
11 слайд
Задача №4: В школьной столовой обед из двух блюд стоит на 40 % дешевле, чем в кафе, расположенном вблизи школы, причем «первое» стоит на 60%, а «второе» – на 30 % дешевле, чем в кафе. Во сколько раз в школьной столовой «второе» стоит дороже, чем «первое»?
Решение: пусть х цена «первого» в кафе, y цена «второго» в кафе, тогда
х+ y 0,4 (х +y) — стоимость в школьной столовой
0,4 х и 0,7 y – стоимость в школьной столовой отдельно каждого блюда
х+ y 0,4 (х +y) = 0,4 х + 0,7 y
0,6х +0,6 y = 0,4 x + 0,7 y
0,2х = 0,1 y
2x = y
х= 0,5y стоимость «первого» в кафе; 0,4 0,5 y = 0,2y стоимость «первого»
в столовой
0,7y : 0,2y = 3,5
то есть второе блюдо в столовой в 3,5 раза дороже
Ответ: 3,5 -
12 слайд
Задача №5: В начале 2009 года мистер Джонс приобрёл по 100 акций компаний А и В. Через год он продал эти акции за сумму на 10 % большую той, что была заплачена им при покупке . При этом акции компании А были проданы на 5 % дороже, а акции компании В – на 20 % дороже, чем были им куплены. Во сколько раз акции компании В стоила дешевле акции компании А при их покупке мистером Джонсом?
Решение: пусть х цена одной акции А, y цена одной акции В
100 х+ 100 y цена купленных акций
100 х + 100 y +0,1 (100x + 100y) – цена акций через год
х + 0,05 х =1,05 х – цена одной акции А через год
y + 0,2y = 1, 2y – цена одной акции В через год
100 х + 100 y +0,1 (100x + 100y) = 100 1,05х + 100 1,2 y
110х + 110 y= 105 x +120 y
5x = 10y
x=2y
то есть акции компании А в 2 раза дороже акций компании В
Ответ: 2 -
13 слайд
Задача №6: Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 6 килограммов изюма, если виноград содержит 90 % воды, а изюм содержит 5 % воды.
Вода
90 %
Вода
5 %
Сухое
вещество
10 %
Сухое
вещество
95 %
6 кг
? кг
Решение: 6 0,95 = 5,7 кг сухого вещества в изюме, его количество не изменилось
5,7 кг – 10 %
х кг – 100 %
х = (5,7 100) : 10 = 57 кг изюма
Ответ : 57 -
14 слайд
Задача №7: На аукционе одна картина была продана с прибылью 20%, а другая – с прибылью 50%. Общая прибыль от продажи двух картин составила 30%. У какой картины первоначальная стоимость была выше и во сколько раз?
Ответ: 2
Решение: пусть x стоимость первой картины, y – второй картины.
Прибыль от продажи первой 0,20х , второй – 0,50y.
Общая прибыль 0,30 (x + y)
0,20 х + 0,50y = 0,30 (x + y)
0,20x 0,30x = 0,30 y 0,50y
0,10x = 0,20y -
15 слайд
Задача №8: В четверг акции компании подорожали на некоторое количество процентов, а пятницу подешевели на то же самое количество процентов. В результате они стали стоить на 36 % дешевле, чем при открытии торгов в четверг. На сколько процентов подорожали акции компании в четверг?
1 + 0,01х – (1+0,01х)0,01х = 1 – 0,36
1 + 0,01х – 0,01х+0,0001х2 = 0,64
0,0001х2 = 0,36
х2 = 3600
х1 = 60
х2 = 60 не удов. условию задачи
Ответ: 60 %.Решение:
Четверг – подорожали на х % 1 + 0,01х
Пятница – на столько же подешевели 1 + 0,01х – (1+0,01х)0,01х -
16 слайд
Задача №9: В кувшин налили 3 литра молока 8 % жирности, некоторое количество молока 2 % жирности и тщательно перемешали. Определите сколько литров молока 2 % жирности было налито в кувшин, если известно, что жирность молока, полученного после перемешивания, составила 6 %?
Решение: Пусть х л молока – 2 % жирности
3 0,08 = 0,24 жира в 3 литрах 8 % молока
х 0,02 – жира в х литрах 2 % молока
0,24 + 0,02х = 0,06(3+ х)
0,24 + 0,02х = 0,18 + 0,06х
х = 1,5 лОтвет: 1,5
-
17 слайд
Задача №10: В апреле мобильный телефон стоил на 10 % больше, чем в июле, а в июле он стоил на 15 % больше, чем в декабре. На сколько процентов стоимость телефона в апреле была выше, чем стоимость телефона в декабре?
Решение: пусть х цена в декабре
Апрель – 1,15 х+ 0,11,15х = 1,265х
Июль – 0,15 х + х = 1,15х
Декабрь – х
1,265х х = 0,265х разница в цене между апрелем и декабрем
х – 100 %
0,265 х – y %
y = (0,265х 100) : х = 26,5 %
Ответ: 26,5 -
18 слайд
Задачи на концентрацию, смеси и сплавы
-
19 слайд
Задача №1: В сосуд , содержащий 10 литров 15-процентного водного раствора некоторого вещества добавили 15 литров 10-процентного водного раствора этого же вещества. Сколько процентов составит концентрация получившегося раствора?
+
=
Решение:
10 0,15 = 1,5 л вещества в
первом растворе
15 0,1 = 1,5 л вещества во 2 растворе
1,5 +1,5 = 3 л масса вещества в новом растворе10 + 15 = 25 л масса нового раствора
25 л – 100 %
3 л – х %
х = 12 %
Ответ: 12 -
20 слайд
Задача №2: В емкость содержащую 600 граммов 2 % раствора соли, добавили 1050 граммов воды, некоторое количество соли и тщательно перемешали полученную смесь. Определите, сколько граммов соли было добавлено, если известно, что после перемешивания получился раствор, содержащий 2,5 % соли.
+
=
Решение: пусть х гр. соли добавили
600 0,02 = 12 гр. соли было в емкости
600 +1050 = 1650 гр. масса после добавления воды
1650 + х масса раствора после добавления соли
х +12 масса соли в новом растворе
(1650 + х) 0,025 = х + 12
41,25+ 0,025х = х + 12
х= 30 грОтвет: 30
+ -
21 слайд
Задача №3: В двух бочках содержится сахарный сироп различной концентрации. В первой бочке содержится 150 кг сиропа, а во второй – 250 кг. Если перемешать весь сироп, находящийся в этих бочках, то получится сироп в котором 30 % сахара. А, если смешать равные массы сиропа из каждой бочки, то полученный сироп будет содержать 28 % сахара. Какова масса сахара в (кг), содержащегося в сиропе из второй бочки.
Решение: пусть х% сахара в первом сиропе, y % сахара во втором сиропе
150 + 250 = 400 кг масса нового сиропа
400 0,3 = 120 кг сахара в новом растворе
150 0,01 х + 250 0,01 y = 120
1 кг +1 кг = 2 кг – равные массы
0,01х + 0,01y = 0,28 2
x=20 % , y = 36 %
250 0,36 = 90 кг сахара во втором сиропе
Ответ: 90
+
= -
22 слайд
Задача №4: (ЕГЭ 05.06.14) Имеется два раствора .Первый раствор содержит 10 % соли, второй – 30 % соли. Из этих двух растворов получили третий раствор массой 200 кг, содержащий 25 % соли. На сколько килограммов масса первого раствора меньше массы второго раствора.
+
=
Решение: пусть х кг масса первого раствора,
y кг масса второго раствора
х + y = 200 кг масса нового раствора
200 0,25 = 50 кг соли в новом растворе
0,1х масса соли в первом растворе
0,3y масса соли во втором растворе
0,1х + 0,3y соли после смешивания в новом растворе т.е. 50 кг -
23 слайд
Задача №5:
Сколько граммов 30 %-го раствора надо добавить к 80 г 12 %-го раствора этой же соли, чтобы получить 20 %-й раствор соли?Решение.
Пусть надо добавить х г 30 % раствора соли.
Получится (80 + х) г 20 % раствора.
В 80 г 12 % раствора содержится 800,12 г соли
0,3х г соли — в х г 30 % раствора,
0,2(80 + х) г соли — в (80 + х) г 20 % раствора.
Получаем уравнение:
0,3х + 0,1280 = 0,2(80 + х)
0,3 х + 9,6 =16 + 0,2х,
0,3 х 0,2 х = 16 – 9,6,
0,1 х = 6,4,
х = 64.
О т в е т: 64 -
24 слайд
Задача №6: При смешивании первого раствора соли , концентрация которого 40 % ,и второго раствора этой же соли, концентрация которого 48 %, получился раствор с концентрацией 42 %. В каком отношении взяты первый и второй растворы?
40 %
48 %
+
=
42 %
I – 40 % , х масса I , 0,40 х соли в I растворе
II 48 %, y масса II, 0,48y соли во II растворе
0,40х + 0,48 y = 0,42 (x + y)
0,40х + 0,42х = 0,42y + 0,48y
0,02х = 0,06y
х/y = 3/1
Ответ: 3 : 1. -
25 слайд
Задача №7: Сколько граммов воды надо добавить к 50 г раствора, содержащего 8 % соли, чтобы получить 5 % раствор?
Решение:
Пусть х — количество воды, которое надо добавить.
Новое количество раствора (50 + х) г.
Количество соли в исходном растворе 50 0,08 г.
Количество соли в новом растворе составляет 5 % от (50+ х) г,
т. е. 0,05(50+ х) г.
Так как количество соли от добавления воды не изменилось, то оно одинаково в исходном и новом растворах. Получаем уравнение. Иногда в химии это уравнение называют кратко «баланс по соли».
50 0,08 = 0,05(50+х),
508 = 5(50+х),
80 = 50 + х,
х = 30.
Ответ: 30 -
26 слайд
Задача№ 8: Два слитка, один из которых содержит 35% серебра, а другой 65% , сплавляют и получают слиток массой 30 г, содержащий 47 % серебра. Какова масса каждого из этих слитков.
Решение: Пусть х г масса первого слитка, а y г – второго слитка.
35 %
65 %
x г.
y г.
47 %
Ответ: 18 и 12. -
27 слайд
Задача №9: Если смешать 8 кг и 2 кг растворов серной кислоты разной концентрации , то получим 12 % раствор кислоты. При смешивании двух одинаковых масс тех же растворов получим 15 % раствор. Определите первоначальную концентрацию каждого раствора.
Решение: x % – концентрация в первом растворе,
y % концентрация во втором растворе
Ответ: 10 и 20. -
28 слайд
Задача №10: Имеются смеси апельсинового и ананасового соков. Первая смесь содержит 40 % апельсинового сока, а вторая – 80 %. Сливаются вместе p л первой смеси и q л второй смеси, а в результате получается 20 л смеси, содержащей 70 % апельсинового сока. Определите p и q.
p
q
40 %
80 %
20 л
70 %
Ответ: 5 и 15. -
29 слайд
Задачи на производительность
-
30 слайд
Задачи на работу обычно содержат следующие величины:
– время, в течение которого производится работа,
– производительность труда, работа, произведенная в единицу времени (возможны и другие обозначения N, W);
– работа, произведенная за время t
Уравнения, связывающее эти три величины:
vt
A
=
v
A
t
=
t
A
v
=
v
A
t -
31 слайд
В другой столбик
внесем
Урожай, собранный каждым звеномПервый столбик – урожайность.
Это условие поможет нам
составить уравнение.
х
х + 5
S, га
1
2
А, ц
урожайность, ц/га
<
на 2 га
875
920
875
х
920
х + 5
1. Одно звено собрало со своего участка 875 ц пшеницы,
а другое звено с участка, меньшего на 2 га, — 920 ц пшеницы. Сколько центнеров пшеницы собрало каждое звено с 1 га, если известно, что
с 1 га во втором звене собрали на 5 ц пшеницы больше, чем в первом?
875
х
–
920
х+5
= 2
920
х + 5
=
875
х
+ 2
920
х + 5
– 2
875
х
=
1 способ
2 способ
3 способ
Из большей величины вычтем 2, уравняем с меньшей величиной
В новом столбике можно
выразить площадь участков,
для этого
весь урожай : урожайность
Из большей величины вычтем меньшую, разность равна 2
К меньшей величине прибавим 2, уравняем с большей величиной
Это условие поможет ввести х …
Решив, любое из уравнений, мы сразу получим ответ на вопрос задачи, без дополнительных действий. -
32 слайд
Первый столбик – время, необходимое на выполнение работы каждым насосом отдельно.
В другой столбик внесем выполненную работу – это 1 часть
В новом столбике можно
выразить производительность (скорость) работы,
для этого
работу : время
х-2
х
1
2
1
1
1
х-2
2. При одновременной работе двух насосов пруд был очищен за
2 ч 55 мин. За сколько времени мог бы очистить пруд каждый насос, работая отдельно, если
один из них может эту работу выполнить на 2 ч быстрее другого?
справка
справка
справка
Формула A = vt поможет
нам составить уравнение
Скорость совместной работы находим сложением скоростей
Работа выполнена полностью, т.е. выполнена 1 часть
Это условие поможет ввести х …
, часть/ч
v
, часть
A
, ч
t
1
х
t
A
v
=
1
х-2
1
х
+
vсовм=
A = 1
t =
1
х-2
1
х
+
= 1
35
12
Реши уравнение самостоятельно -
33 слайд
1
х-4
1
х
+
В новом столбике можно
выразить производительность (скорость) работы,
для этого
работу : время
= 5
Первый столбик – время, необходимое на выполнение работы каждой бригадой отдельно.
В другой столбик внесем выполненную работу – это 1 часть
х
х- 4
1
2
1
1
1
х
3. Одна из дорожных бригад может заасфальтировать некоторый участок дороги на 4 ч быстрее, чем другая. За сколько часов может заасфальтировать участок каждая бригада, если известно, что за 24 ч совместной работы они заасфальтировали 5 таких участков?
справка
справка
справка
Формула A = vt поможет
нам составить уравнение
Скорость совместной работы находим сложением скоростей
За 24ч заасфальтировали 5 участков, т.е. работа составляет 5 частей
Это условие поможет ввести х …
, часть/ч
v
, часть
A
, ч
t
х- 4
1
t
A
v
=
1
х-4
1
х
+
vсовм=
A = 5
t =
24
24
Реши уравнение самостоятельно -
34 слайд
В новом столбике можно
выразить производительность (скорость) работы,
для этого
работу : время
Первый столбик – время, необходимое на заполнение бассейна каждой трубе отдельно.
В другой столбик внесем выполненную работу –
это 1 часть
х
х- 5
1
2
1
1
1
х
4. Бассейн наполняется через первую трубу на 5 ч быстрее, чем через вторую. Бассейн можно наполнить, если открыть сначала первую трубу на 5 ч, а затем вторую на 7,5 ч. За сколько часов наполнится бассейн при совместной работе обеих труб?
справка
справка
Найдем работу, которую выполнит
I труба за 5 ч по формуле A = vt
Найдем работу, которую выполнит
II труба за 7,5 ч по формуле A = vt
Это условие поможет ввести х …
, часть/ч
v
, часть
A
, ч
t
х- 5
1
t
A
v
=
7,5
х
A1=
A2 =
1
х-5
5
1
= 1
= 1
х-5
5
х
7,5
+
Реши уравнение самостоятельно -
35 слайд
В новом столбике можно
выразить производительность (скорость) работы,
для этого
работу : время
Первый столбик – время, необходимое на выполнение всей работы каждой бригаде отдельно.
В другой столбик внесем выполненную работу –
это 1 часть
х
х- 12
1
2
1
1
1
х
5. На строительстве работали две бригады. После 5 дней совместной работы вторую бригаду перевели на другой объект. Оставшуюся часть работы первая бригада закончила через 9 дней. За сколько дней могла бы выполнить всю работу каждая бригада, работая отдельно, если известно, что второй бригаде на выполнение всей работы потребовалось бы на 12 дней меньше, чем одной первой бригаде?
Это условие
поможет
ввести х …
, часть/дн.
v
, часть
A
, дн.
t
х-12
1
t
A
v
=
= 1
= 1
5
справка
справка
справка
По формуле A = vt найдем работу, выполненную за 9дн. I бригадой
Скорость совместной работы находим сложением скоростей
По формуле A = vt найдем работу, выполненную за 5дн. совместно
1
х-12
1
х
+
vсовм=
A =
A =
9
1
х-12
1
х
+
1
х
+
1
х-12
1
х
+
5
1
х
9
Реши уравнение самостоятельно -
36 слайд
Задача №6 : При одновременно работающих принтерах расход бумаги составляет 1 пачку за 12 минут. Определите, за сколько минут израсходует пачку первый принтер, если известно, что он сделает это на 10 минут быстрее, чем второй.
-
37 слайд
Задача №7: Бассейн наполняется двумя трубами, действующими одновременно, за 2 часа. За сколько часов может наполнить бассейн первая труба, если она, действуя одна, наполняет бассейн на 3 часа быстрее, чем вторая?
-
-
39 слайд
Задача №8: В городе имеются три завода по выпуску рыбных консервов. Первый завод может переработать 50 тонн рыбы за трое суток, второй – 45 тонн за двое суток, а третий – 95 тонн за шесть суток. Определите минимальное время, за которое на этих заводах можно переработать 110 тонн рыбы.
-
40 слайд
Решение:
110 : 55 = 2 сут
Ответ: 2 суток. -
41 слайд
Задача №9: Первый наборщик текста набирает за час 5 страниц текста, второй – 6 страниц, а третий – 7 страниц. Определите, по сколько страниц текста нужно отдать для набора каждому из них, если требуется, чтобы весь текст, объем которого 216 страниц, был набран как можно быстрее.
Решение:
5 + 6 + 7 = 18 частей всего
216 : 18 = 12 страниц 1 часть
12 5 = 60 стр.
12 6 = 72 стр.
12 7 = 84 стр.
Ответ: 60, 72, 84 страницы. -
42 слайд
Задачи на движение
-
43 слайд
Задачи на движение
по прямой (навстречу и вдогонку)
по замкнутой трассе
по воде
на среднюю скорость
протяженных тел -
44 слайд
При решении задач на движение принимают такие допущения:
движение считается равномерным, если нет специальных оговорок;
изменение направления движения и переходы на новый режим движения считаются происходящими мгновенно;
если два тела начинают движение одновременно (если одно тело догоняет другое), то в случае, если или встречаются, каждое тело с момента выхода и до встречи затрачивает одинаковое время; -
45 слайд
всякие переходы на новый режим движения, на новое направление движения считают происходящим мгновенно;
если тела выходят в разное время, то до момента встречи из них затрачивает время больше то, которое выходит раньше;
все величины, как правило, положительные (в природе скорость расстояние и время положительны), поэтому можно смело умножать, делить и возводить в квадрат получающиеся уравнения и неравенства, не делая необходимых в таких случаях оговорок. -
46 слайд
В задачах на движение используются обычно формулы, выражающие законы равномерного движения: S=V·t , где S- пройденное расстояние, V- скорость равномерного движения, t — время движения.
При составлении уравнений в таких задачах часто бывает удобно прибегнуть к геометрической иллюстрации процесса движения: путь изображается в виде отрезка прямой, место встречи движущихся с разных сторон объектов точкой на отрезке и т.д.
Часто для усложнения задачи её условие формулируется в различных единицах измерения(метры, километры, часы, минуты и т.д.). В этом случае при выписывании уравнений необходимо пересчитывать все данные задачи в одинаковых единицах измерения: -
47 слайд
Движение навстречу:
Движение вдогонку:
Движение по окружности
(замкнутой трассе):
Средняя скорость:
-
48 слайд
Задачи на движение
Встречное движение
v1 v2
t1 t2s1 tвстр s2
s
t1=t2=tвстр. Vсбл=v1+v2 s=vсбл*tсближ
Обьекты, начавшие двигаться навстречу друг другу одновременно, движутся до момента встречи одинаковое время . -
49 слайд
Задача№ 1.Из городов A и B навстречу друг другу выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 3 часа раньше, чем велосипедист приехал в A, а встретились они через 48 минут после выезда. Сколько часов затратил на путь из B в A велосипедист?
1
1
у
х
S,
часть
Велосипедист
Мотоциклист
v,
часть/ч
t,
ч
1
у
1
х
на весь путь
Если в задаче не дано расстояние, очень удобно считать весь путь, как 1 целая часть.
На 3 часа
>
x – у = 3
1
у
1
х
+
навстречу
v
48
60
встречи
t
S
1
1
у
1
х
+
= 1
4
5
1 часть
часть/ч
1
у
1
х
часть/ч
4
5
ч
Ответ: 4 ч -
50 слайд
Движение в одном направлении
v1 v2
t1 t2s s2
s1 vсближ =v1-v2,.s=s1-s2 , s=vсбл*tвстр
-
51 слайд
10 км/ч
Задача№ 2: Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.
2
x
3
15 км/ч
Удобно показать на схеме тот момент, когда 1-й вел. был в пути уже 2 ч, а 2-й вел. один час.
t
30 км
10 км
3
1
2
+
t
х – 10
3й и 2й
v,
вдогонку
S,
км
t,
ч
3й и 1й
х – 15
t
3
1
2
+
t
3
1
2
+
(t )
(х – 15)
(х – 10)
t
= 10
= 30
С системой придется потрудиться. При выборе ответа учтем, что скорость 3-го велосипедиста должна быть больше 15. Ответ: 25.
1
2
1
3
Отметим на схеме примерное место встречи 2го и 3го
И примерное место встречи 1го и 3го
t
3
1
2
+
t -
52 слайд
Движение в противоположных направлениях
В таких задачах два тела могут начинать движение в противоположных направлениях из одной точки:
а) одновременно;
б) в разное время.
А могут начинать свое движение из двух разных точек, находящихся на заданном расстоянии, и в разное время.
Общим теоретическим положением для них будет следующее:
v удал. = v1+ v2, где v1 и v2 соответственно скорости первого и второго тел.
(Схематический чертеж строится аналогично предыдущим). -
53 слайд
Задача№ 3. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 72 км. На следующий день он отправился обратно со скоростью на 6 км/ч больше прежней. По дороге он сделал остановку на 6 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
Путь В-А
х
Путь А-В
v,
км/ч
t,
ч
S,
км
72
х
72
х+6
72
=
х+6
Чтобы найти время надо расстояние разделить на скоростьt =
S
v
72
Остановка
6
72
х+6
+ 6 =
72
х
А
В
72 км
6ч
Это условие поможет ввести х …
6 км/ч -
54 слайд
Движение по воде
скорость перемещения лодки V по воде, при скорости течения реки Vр и собственной скорости движения Vс, выражается:
V по течению=Vс+Vр при движении лодки по течению реки.
V против течения=Vс−Vр при движении лодки против течения реки.
Движущийся плот всегда имеет скорость течения реки. -
55 слайд
Задача№ 4:Теплоход проходит по течению реки до пункта назначения 560
км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 8 часов, а в пункт отправления теплоход возвращается через 56 часов после отплытия из него. Ответ дайте в км/ч.
х–4
По. теч.
Пр. теч.
560
Пусть vсоб. = x
х+4
v,
км/ч
560
S,
км
справка
Это условие поможет ввести х …
Чтобы найти время надо расстояние разделить наскорость
t =
S
v
560
х+4
t,
ч
справка
560
х–4
56ч
Стоянка
8
+ + =
560
х+4
560
х–4
8
56
Чтобы найти скорость по течению надо к собственной скорости прибавить скорость течения
Стоянка длилась 8 ч – это время
также надо учесть
Чтобы найти скорость против течения надо из собственной скорости отнять скорость течения
Ответ: 24 -
56 слайд
движение по замкнутой трассе
-
57 слайд
Если два велосипедиста одновременно начинают движение по окружности в одну сторону со скоростями v1 и v2 соответственно
(v1 > v2 соответственно), то 1-й велосипедист
приближается ко 2 со скоростью v1 – v2.
В момент, когда 1-й велосипедист
в первый раз догоняет 2-го,
он проходит расстояние на
один круг больше.
Продолжить
Показать
В момент, когда 1-й
велосипедист во
второй раз догоняет
2-го, он проходит
расстояние на два
круга больше и т.д. -
58 слайд
1
2
Задача№ 5: Из одной точки круговой трассы, длина которой равна15 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 60 км/ч, скорость второго равна 80 км/ч. Сколько минут с момента старта пройдет, прежде чем первый автомобиль будет опережать второй ровно на 1 круг?
1 красный
2 зеленый
60
80
v,
км/ч
на 15 км меньше (1 круг)
Уравнение:
Ответ: 45
х получим в часах.
Не забудь перевести в минуты.
t,
ч
х
х
S,
км
60х
80х
Показать -
59 слайд
2
1
Задача№6: Из одной точки круговой трассы, длина которой равна 10 км, одновременно в одном направлении стартовали два автомобиля.
Скорость первого автомобиля равна 90 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
1 автомоб.
2 автомоб.
90
х
v,
км/ч
на 10 км больше (1 круг)
Ответ: 75
t,
ч
2
3
2
3
S,
км
2
3
90
2
3
х
Уравнение:
Показать -
60 слайд
Задача№ 7: Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного
из них на 21 км/ч больше скорости другого?
1 красный
2 синий
х
х+21
v,
км/ч
на 7 км меньше (половина круга)
Уравнение:
Ответ: 20
t получим в часах.
Не забудь перевести в минуты.
t,
ч
t
t
S,
км
tх
t(х+21)
Сколько кругов проехал
каждый мотоциклист
нам не важно. Важно, что синий проехал до точки встречи на половину круга больше, т.е. на 7 км.
Еще способ в комментариях.
Показать -
61 слайд
старт
финиш
2
1
2
1
1
2
2
1
1
2
Пусть полный круг – 1 часть.
Задача№ 8: Лыжные соревнования проходят на круговой лыжне. Первый лыжник проходит один круг на 2 минуты быстрее второго и через час опережает второго ровно на один круг. За сколько минут второй лыжник проходит один круг?
Показать -
62 слайд
Задача№ 9. Лыжные соревнования проходят на круговой лыжне. Первый лыжник проходит один круг на 2 минуты быстрее второго и через час опережает второго ровно на один круг. За сколько минут второй лыжник проходит один круг?
на 1 круг больше
Ответ: 10
1 лыжник
2 лыжник
v,
круг/мин
t,
мин
60
60
S,
км
х
х+2
1
1
t,
мин
1 лыжник
2 лыжник
S,
часть
v,
часть/мин
1
х+2
1
х
1
х+2
1
х
60
х
60
х+2
Сначала выразим скорость каждого лыжника. Пусть за х мин 1-й лыжник проходит полный круг. Второй на 2 минуты больше, т.е. х+2.
60
х
60
х+2
– = 1
Это условие поможет ввести х … -
63 слайд
Задача№ 10: Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
1 желтый
2 синий
S,
км
80
х
v,
км/ч
t,
ч
2
3
2
3
2
3
80
2
3
х
на 14 км больше (1 круг)
Уравнение:
Можно было сначала найти скорость вдогонку: 80 – х
Тогда уравнение будет выглядеть так:
v
S
=
t
Ответ: 59
Нажать на кнопку можно несколько раз. Сколько кругов проехал каждый автомобиль нам
не важно. Важно, что желтый автомобиль проехал на 1 круг больше, т.е. на 14 км.
Показать
1
2 -
64 слайд
Задача№ 11: Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз.
Найдите скорость мотоциклиста,
если длина трассы равна 30 км.
Ответ дайте в км/ч.
1 мотоцик.
2 велосип.
S,
км
х
у
v,
км/ч
t,
ч
1
6
2
3
2
3
у
1 уравнение:
1
6
х
=
Показать
1 встреча. Велосипедист был до 1 встречи 40 мин (2/3 ч), мотоциклист 10 мин (1/6ч). А расстояние за это время они проехали равное.
-
65 слайд
Задача №12. Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км.
Ответ дайте в км/ч.
1 мотоцик.
2 велосип.
S,
км
х
у
v,
км/ч
t,
ч
1
2
1
2
1
2
у
на 30 км больше (1 круг)
2 уравнение:
Ответ 80
1
2
х
Искомая величина – х
Показать (2)
2 встреча. Велосипедист и мотоциклист были в пути
до 2-й встречи 30 мин (1/2 ч).
А расстояние за это время мотоциклист проехал на 1 круг больше.
-
66 слайд
Задача №13. Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?
минутная
часовая
х
S,
круг
v,
круг/ч
t,
ч
1
1
12
х
1х
1
12
х
на круга больше
2
3
3
1х – =
1
12
х
2
3
3
Ответ: 240 мин
2
3
1
3
В первый раз минутной стрелке надопройти на круга больше, чтобы догнать минутную стрелку.
Во 2-й раз – еще на 1 круг больше.
В 3-й раз – еще на 1 круг больше.
В 4-й раз – еще на 1 круг больше.Всего
2
3
на круга больше
2
3
3 -
67 слайд
6
12
1
2
9
11
10
8
7
4
5
3
Показать (4)
В первый раз минутной стрелке надопройти на круга больше, чтобы догнать минутную стрелку.
Во 2-й раз – еще на 1 круг больше.
В 3-й раз – еще на 1 круг больше.
В 4-й раз – еще на 1 круг больше.Всего
2
3
на круга больше
2
3
3
Проверка
Другой способ – в комментариях. -
68 слайд
Задачи на движение протяженных тел
В задачах на движение протяжных тел требуется определить длину одного из них. Наиболее типичные ситуации: определение длины поезда проезжающего мимо
придорожного столба
идущего параллельно путям пешехода
лесополосы определенной длины
другого двигающегося поезда
Если поезд движется мимо столба, то он проходит расстояние равное его длине. Если поезд движется мимо протяженной лесополосы, то он проходит расстояние равное сумме длины самого поезда и лесополосы. -
69 слайд
Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо придорожного столба за 36 секунд. Найдите длину поезда в метрах.
Пройденное расстояние = длине поезда
Решение. Зная скорость движения v = 80 км/ч и время, за которое он проезжает мимо столба t = 36 с, можно найти длину поезда как пройденное расстояние по формуле:
vt
S
=
1 мин
1 с
1ч
: 60
: 60
* 60
* 60
: 60
: 60
Выразим время в часах
* 1000
Задача № 1 -
70 слайд
Задача № 2 Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 400 метрам, за 1 минуту. Найдите длину поезда в метрах.
400 м
Пройденное расстояние = длине поезда + длина лесополосы
Решение. Зная скорость движения v = 60 км/ч и время, за которое он проезжает мимо лесополосы t = 1 мин, можно найти расстояние, которое прошел поезд (длина лесополосы + длина поезда).
vt
S
=
1 мин
1 с
1ч
: 60
: 60
* 60
* 60
: 60
Выразим время в часах -
71 слайд
Задача № 3 Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 400 метрам, за 1 минуту. Найдите длину поезда в метрах.
400 м
Решим задачу с помощью уравнения
x
S
x+400
t
v
60000 м/ч
, м
, ч
, м/ч
v
S
=
t -
72 слайд
При решении задач на движение двух тел часто очень
удобно считать одно тело неподвижным, а другое — приближающимся к нему со скоростью, равной сумме скоростей
этих тел (при движении навстречу) или разности скоростей
(при движении вдогонку). Такая модель помогает разобраться
с условием задачи.
Задача № 4 По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй — длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?
Воспользуемся предложенной моделью -
73 слайд
2
По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй — длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?
Решение. Будем считать, что первый сухогруз неподвижен, а второй приближается к нему со скоростью v (м/мин) , равной разности скоростей второго и первого сухогрузов. Тогда за 12 минут второй сухогруз проходит расстояние
120 м
400 м
600 м
80 м
1200 м
t
S
v
=
* 60
: 1000
+
+
+
1 -
74 слайд
Задача № 6 По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах.
600 м
* 1000
: 60
Скорость вдогонку (на сколько скорость пассажирского поезда больше скорости товарного) -
75 слайд
Задача № 7 По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах.
600 м
Решим задачу с помощью уравнения
x
S
x+600
t
v
1000 м/мин
, м
, мин
, м/мин
v
S
=
t -
76 слайд
Задача № 8 По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.
700 м
* 1000
Скорость навстречу друг другу
(сумма скоростей при движении навстречу друг другу)
: 60
: 60 -
77 слайд
Задача № 9 По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.
700 м
Решим задачу с помощью уравнения
x
S
x+700
t
v
100000 м/ч
, м
, ч
, м/ч
v
S
=
t -
78 слайд
Задача № 10 Поезд, двигаясь равномерно со скоростью 54 км/ч, проезжает
мимо идущего параллельно путям со скоростью 6 км/ч
навстречу ему пешехода за 30 секунд. Найдите длину поезда
в метрах.
*1000
: 60
Выразим время в минутах
Решение. Будем считать, что пешеход неподвижен, а поезд двигается со скоростью v (м/мин), равной сумме скоростей пешехода и поезда (скорость навстречу друг другу). Сам пешеход не имеет «протяженной» длины (если бы это была колонна солдат, то мы бы учли это).
Скорость навстречу друг другу (сумма скоростей при движении навстречу друг другу) -
79 слайд
Задача № 11 Поезд, двигаясь равномерно со скоростью 65 км/ч, проезжает
мимо идущего в том же направлении параллельно
путям со скоростью 5 км/ч пешехода за 30 секунд. Найдите
длину поезда в метрах.
*1000
: 60
Выразим время в минутах
Решение. Будем считать, что пешеход неподвижен, а поезд двигается со скоростью v (м/мин), равной разности скоростей пешехода и поезда. Пешеход не имеет «протяженной» длины.
Скорость навстречу друг другу (сумма скоростей при движении навстречу друг другу) -
80 слайд
Чтобы определить среднюю скорость при неравномерном движении, надо весь пройденный путь разделить на все время движения:
Задачи на нахождение
средней скорости -
-
82 слайд
Задача №12: Автомобиль двигался 3,2ч по шоссе со скоростью 90км/ч, затем 1,5ч по грунтовой дороге со скоростью 45км/ч, наконец, 0,3ч по проселочной дороге со скоростью 30км/ч. Какова средняя скорость движения автомобиля на всем пути?
Средняя скорость движения определяется по формуле: -
83 слайд
3. Определим все время движения:
2. Определим весь путь:
.
90
3,2
=
288
(км)
(км)
67,5
45
1,5
=
.
288 + 67,5 + 9 =
(км)
9
30
=
0,3
.
3,2 + 1,5 + 0,3 =
1. Определим длину каждого участка пути:
364,5
(км)
5
(ч)
4. Найдем среднюю скорость движения:
364,5 : 5 =
72,9
(км/ч)
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 154 998 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 31.10.2019
- 153
- 0
- 31.10.2019
- 197
- 2
- 31.10.2019
- 118
- 0
- 31.10.2019
- 153
- 2




Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Управление персоналом и оформление трудовых отношений»
-
Курс профессиональной переподготовки «Логистика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Экономика: инструменты контроллинга»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Основы менеджмента в туризме»
-
Курс повышения квалификации «Использование активных методов обучения в вузе в условиях реализации ФГОС»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Управление информационной средой на основе инноваций»
-
Курс повышения квалификации «Международные валютно-кредитные отношения»
-
Курс повышения квалификации «Информационная этика и право»
ЕГЭ В 5.ppt.pps
Microsoft Power Point Presentation
309.0 KB
ЕГЭ В6 (вписанная окружность).ppt.pps
Microsoft Power Point Presentation
643.5 KB
ЕГЭ В6(вписанная окружность).ppt.pps
Microsoft Power Point Presentation
727.0 KB
ЕГЭ В6(окружность).ppt.pps
Microsoft Power Point Presentation
373.5 KB
ЕГЭ В6(тригонометрия в прямоугольном тре
Microsoft Power Point Presentation
1.1 MB
ЕГЭ В12.ppt.pps
Microsoft Power Point Presentation
1.6 MB
ЕГЭ В13 (движение по окружности).ppt.pps
Microsoft Power Point Presentation
1.5 MB
ЕГЭ В13 (проценты, сплавы).ppt.pps
Microsoft Power Point Presentation
1.1 MB
ЕГЭ В 2.ppt.pps
Microsoft Power Point Presentation
297.0 KB
ЕГЭ В 3.ppt.pps
Microsoft Power Point Presentation
1.8 MB
ЕГЭ В 5(логарифмы) .ppt.pps
Microsoft Power Point Presentation
2.7 MB
ЕГЭ В 6(трапеция).ppt.pps
Microsoft Power Point Presentation
1.3 MB
ЕГЭ В 7.ppt.pps
Microsoft Power Point Presentation
446.5 KB
ЕГЭ В 13 (задачи).ppt.pps
Microsoft Power Point Presentation
405.5 KB
ЕГЭ В 13 задача.ppt.pps
Microsoft Power Point Presentation
608.0 KB
Элементы статистики, комбинаторики и тео
Microsoft Power Point Presentation
2.9 MB
ЕГЭ В 14.ppt.pps
Microsoft Power Point Presentation
2.9 MB
ЕГЭ В 14 экстремумы.ppt.pps
Microsoft Power Point Presentation
743.5 KB
Слайд 1
Алгебра Часть 1 Задачи на сплавы Преподаватель высшей категории Анисимова Оксана Михайловна ВИФК Кадетский корпус (спортивная школа)
Слайд 2
?? всего концентрация Масса вещества Было 5 14 % Добавили 5 — — стало 5+5=10 ? 0,7 Решение задач «задание 11» №1 Ответ: 7 В сосуд, содержащий 5 литров 14-процентного водного раствора некоторого вещества, добавили 5 литров воды. Сколько процентов составляет концентрация получившегося раствора?
Слайд 3
?? всего концентрация Масса вещества I x 15% 0,15x II x 17% 0,17x I+II 2x ? 0,15x + 0,17x = 0,32x Решение задач «задание 11» № 2 Ответ: 16 Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 17-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Слайд 4
?? всего концентрация Масса вещества I 4 20% 0,2·4=0,8 II 6 35% 0,35·6=2,1 I+II 4+6=10 ? 0,8 + 2,1 = 2,9 Решение задач «задание 11» № 3 Ответ: 29 Смешали 4 литра 20-процентного водного раствора некоторого вещества с 6 литрами 35- процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Слайд 5
?? всего концентрация Масса вещества I II I+II Решение задач «задание 11» № 4 .1 Ответ: 90 Имеется два сплава. Первый содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава была меньше массы второго? ?? всего концентрация Масса вещества I x 10% 0,1x II y 35% 0,35y I+II 150 30% 0,3·150=45 0,1x+0,35y=45
Слайд 6
?? всего концентрация Масса вещества I II I+II Решение задач «задание 11» № 4 .2 Ответ: 18 Имеется два сплава. Первый содержит 20% никеля, второй — 45% никеля. Из этих двух сплавов получили третий сплав массой 90 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава была больше массы второго? ?? всего концентрация Масса вещества I x 2 0% 0, 2 x II y 4 5% 0, 4 5y I+II 90 30% 0,3· 90 = 27 0, 2 x+0, 4 5y=27
Слайд 7
Первый год Второй год I II I+II Решение задач «задание 11» № 5 Ответ: 110 Численность волков в двух заповедниках составляла 210 особей. Через год обнаружили, что в первом заповеднике численность волков возросла на 10%, а во втором — на 30%. В результате общая численность волков в двух заповедниках составила 251.Сколько волков было в первом из заповедников первоначально? ?? Первый год Второй год I x x+0,1x II y y+0,3y I+II 210 251
Слайд 8
?? всего Процентное содержание Масса вещества I II I+II Решение задач «задание 11» № 6 .1 Ответ: 27 Имеется два сплава. Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 9 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава. Ответ дайте в килограммах. ?? всего Процентное содержание Масса вещества I x 5% 0,05x II x+9 14% 0,14(x+9) I+II 2x+9 11% 0,11(2x+9)= 0,05x+0,14(x+9)
Слайд 9
?? всего Процентное содержание Масса вещества I II I+II Решение задач «задание 11» №6.2 Ответ: 9 Имеется два сплава. Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третье го сплава. Ответ дайте в килограммах. ?? всего Процентное содержание Масса вещества I x 10 % 0,1x II x+ 3 40 % 0,4(x+3) I+II 2x+3 30 % 0,3(2x+3)= 0,1x+0,4(x+3)
Слайд 10
Решение задач «задание 11» №7.1 Смешав 6-процентный и 74-процентный растворы кислоты и добавив 10 кг чистой воды, получили 19-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50- процентного раствора той же кислоты, то получили бы 24-процентный раствор кислоты. Сколько килограммов 6-процентного раствора использовали для получения смеси? ?? всего Процент Масса вещества I x 6% 0,06x II y 74% 0,74y Добавили 1 раз 10 — — Получили 1 раз x+y+10 19% 0.19(x+y+10)= =0,06x+0,74y Добавили 2раз 10 50% 0,5·10=5 Получили 2 раз x+y+10 24% 0. 24 (x+y+10)= =0,06x+0,74y +5
Слайд 11
Решение задач «задание 11» №7.1 ?? всего Процент Масса вещества I x 6% 0,06x II y 74% 0,74y Добавили 1 раз 10 — — Получили 1 раз x+y+10 19% 0.19(x+y+10)= =0,06x+0,74y Добавили 2раз 10 50% 0,5·10=5 Получили 2 раз x+y+10 24% 0. 24 (x+y+10)= =0,06x+0,74y +5
Слайд 12
Решение задач «задание 11» №7.1 Ответ: 70
Слайд 13
Самостоятельно Сборник «4000 задач» № 1586 , № 1590 № 1587 , № 11 вариант1 №11 вариант2
Слайд 14
Алгебра Урок №11 Часть 2 Задачи на совместную работу Преподаватель высшей категории Анисимова Оксана Михайловна ВИФК Кадетский корпус (спортивная школа)
Слайд 15
Объем работы Производительность (скорость) время I II Решение задач «задание 11» №1 .1 Ответ: 6 Объем работы Производительность (скорость) время I 20 x+4 II 60 x
Слайд 16
На изготовление 16 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 40 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает второй рабочий? Объем работы Производительность (скорость) время I II Решение задач «задание 11» №1 .2 Ответ: 5 Объем работы Производительность (скорость) время I 16 x+3 II 40 x
Слайд 17
Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на 1 минуту дольше, чем вторая труба? Объем работы Производительность (скорость) время I II Решение задач «задание 11» №1 .3 Ответ: 10 Объем работы Производительность (скорость) время I 110 x II 110 x+1
Слайд 18
Решение задач «задание 11» № 2.1 Ответ: 16 Объем работы Производительность (скорость) время I 12y·10 12y 10 24yx 12y+12y X II 21y·10 21y 10 9yx 21y-12y=9y X !!!
Слайд 19
Решение задач «задание 11» № 2.2 Ответ: 16 Объем работы Производительность (скорость) время I 16y·7=112y 16y 7 24yx 16y+8y=24y X II 25y·7=175y 25y 7 17yx 25y-8y=17y X !!! Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали выполнять два одинаковых заказа. В первой бригаде было 16 рабочих, а во второй — 25 рабочих. Через 7 дней после начала работы в первую бригаду перешли 8 рабочих из второй бригады. В итоге оба заказа были выполнены одновременно. Найдите, сколько дней потребовалось на выполнение заказов.
Слайд 20
Самостоятельно Сборник «4000 задач» № 1639 №1652 № 1622
Слайд 21
Интернет ссылки
1.
ПРАКТИКУМ. ПРОФИЛЬНАЯ МАТЕМАТИКА. ЕГЭ 2022.
ЗАДАЧА 9. ГРАФИКИ ФУНКЦИЙ
Лектор: Тыкынаева Оксана Павловна
учитель математики
МОБУ Якутский городской лицей
2.
3.
Ответ : -10
4.
5.
Ответ : -7
6.
7.
Ответ: 31
8.
9.
Ответ: 26
10.
11.
Ответ: 48
12.
13.
Ответ: 0,75
14.
15.
Ответ: -15
16.
17.
Ответ: 0,15
18.
19.
Ответ: 14
20.
21.
Ответ: 1
22.
23.
Ответ: 9
24.
25.
Ответ: 1,5
26.
27.
Ответ: -1
28.
29.
Ответ: 2,5
30.
31.
Ответ: -1,5
32.
33.
Ответ: -0,1
34.
35.
Ответ: -20
36.
37.
Ответ: 2
38.
39.
Ответ: 1,5
40.
41.
Ответ: 5
42.
43.
Ответ: -7
44.
45.
46.
47.
Ответ:15
48.
49.
Ответ:1
50.
51.
Ответ: х=2
52.
53.
Ответ: 5
Презентация на тему «Разбор типовых заданий ЕГЭ по математике базового уровня» 11 класс
-
Скачать презентацию (0.55 Мб)
-
117 загрузок -
0.0 оценка
Ваша оценка презентации
Оцените презентацию по шкале от 1 до 5 баллов
- 1
- 2
- 3
- 4
- 5
Комментарии
Добавить свой комментарий
Аннотация к презентации
Скачать презентацию (0.55 Мб). Тема: «Разбор типовых заданий ЕГЭ по математике базового уровня». Предмет: математика. 35 слайдов. Для учеников 11 класса. Добавлена в 2021 году.
-
Формат
pptx (powerpoint)
-
Количество слайдов
35
-
Аудитория
-
Слова
-
Конспект
Отсутствует
Содержание
-
Слайд 1
Разбор типовых заданий ЕГЭ по математике базового уровня
Геометрия
-
Слайд 2
Прикладная геометрия1. Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту l этого столба, если наименьшая высота h1 перил равна 1,25 м, а наибольшая высота h2 равна 2,25 м. Ответ дайте в метрах.
!Алгоритм выполнения
Определить, что за фигура на рисунке.
Вспомнить определение средней линии трапеции.
Записать формулу для нахождения средней линии трапеции.
Подставить данные.
Вычислить среднюю линию трапеции. -
Слайд 3
2. План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м х 1 м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
! Алгоритм выполнения
Определить что за фигура на рисунке.
Записать формулу нахождения площади данной фигуры.
Определить по чертежу все необходимые данные.
Вычислить площадь участка. -
Слайд 4
3. План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м х 1 м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
! Алгоритм выполнения
Определить что за фигура на рисунке.
Записать формулу нахождения площади данной фигуры.
Определить по чертежу все необходимые данные.
Вычислить площадь участка. -
Слайд 5
4. Дачный участок имеет форму прямоугольника со сторонами 25 метров и 30 метров. Хозяин планирует обнести его забором и разделить таким же забором на две части, одна из которых имеет форму квадрата. Найдите суммарную длину забора в метрах.
!Алгоритм выполнения
Вычислить периметр прямоугольника.
Прибавить длину разделяющей части.
P = 30 м + 30 м + 25 м + 25 м = 110 м.
110 м – длина забора без перегородки.
Прибавим длину разделяющей части.
По рисунку видно, что длина разделяющей части 25 м.
110 м + 25 м = 135 м. -
Слайд 6
5. Какой угол (в градусах) образуют минутная и часовая стрелки в 16:00?
! Алгоритм выполнения
Сначала мы найдем, сколько в градусах занимает один час.
Затем найдем угол, который образуют стрелки в 16:00
Так как вся окружность — 360°, а часов 12, то один час:
360° : 12 = 30°
Значит, в четыре часа угол будет равен:
30° • 4 = 120° -
Слайд 7
6. Пожарную лестницу длиной 10 м приставили к окну дома. Нижний конец лестницы отстоит от стены на 6 м. На какой высоте находится верхний конец лестницы? Ответ дайте в метрах.
! Алгоритм выполнения
Приставленная к стене лестница образует с этой стеной и горизонтальной площадкой возле дома прямоугольный треугольник. Высота, на которой находится верхний конец лестницы, является одним из катетов этого треугольника. Следовательно, для нахождения ее величины нужно использовать теореме Пифагора. -
Слайд 8
7. Дачный участок имеет форму прямоугольника, стороны которого равны 35 и 45 м. Дом, расположенный на участке, имеет на плане форму квадрата со стороной 7 м. Найдите площадь оставшейся части участка, не занятой домом. Ответ дайте в квадратных метрах.
! Алгоритм выполнения
Находим площадь прямоугольного участка.
Находим площадь квадратного дома.
Находим разность этих площадей, отняв от большего числа меньшее.
35 · 45 = 1575 (кв.м) – площадь всего участка
7 · 7 = 49 (кв.м) – площадь дома
1575 – 49 = 1526 (кв.м) – площадь оставшейся части участка -
Слайд 9
8. На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 5 м?
! Алгоритм выполнения
Рассматриваем 2 подобных треугольника. В первом стороны образуют линия фонаря и расстояние от его основания до верхней точки тени от человека. Во втором – линия роста человека и линия его тени.
Поскольку треугольники подобны, то можем соотнести соответствующие стороны и оставить из этих отношений пропорцию.
Из полученной пропорции выражаем искомую величину. Вычисляем ее.
Обозначим искомое расстояние через х.
Из рисунка имеем 2 треугольника. Один (больший) построен на сторонах 5 м и (х+9) м. Другой (меньший) – 1,8 м и 9 м. Составим пропорцию из отношений соответствующих сторон этих треугольников:
5 : 1,8 = (х + 9) : 9.
Из пропорции получим:
5 · 9 = 1,8 · (х + 9)
1,8х + 16,2 = 45
1,8х = 28,8
х = 16 (м) -
Слайд 10
Наглядная стереометрия9. Вода в сосуде цилиндрической формы находится на уровне h = 80 см. На каком уровне окажется вода, если ее перелить в другой цилиндрический сосуд, у которого радиус основания в 4 раза больше, чем у данного? Ответ дайте в сантиметрах.
! Алгоритм выполнения:
Записать формулу объема цилиндра.
Подставить значения для цилиндра с жидкостью в первом и во втором случае.
Объем жидкости не изменялся, следовательно, можно приравнять объемы.
Полученное уравнение решить относительно второй высоты h2.
Подставить данные и вычислить искомую величину.
V1 = π r1 2 h1
V2 = π r2 2 h2
Объем жидкости не изменялся, следовательно, можно приравнять объемы.
V1 = V2
π r1 2 h1 = π r2 2 h2
h2 =( π r1 2 h1)/ π r2 2
По условию площадь основания стала в 4 раза больше, то есть r2 = 4 r1 .
Подставим r2 = 4 r1 в выражение для h1.
Получим: h2 =( π r1 2 h1)/ π (4 r1) 2
Полученную дробь сократим на π, получим h2 =( r1 2 h1)/ 16 r1 2
Полученную дробь сократим на r1, получим h2 = h1/ 16.
Подставим известные данные: h2 = 80/ 16 = 5 см.
Ответ: 5. -
Слайд 11
10. Даны две коробки, имеющие форму правильной четырёхугольной призмы. Первая коробка в четыре с половиной раза выше второй, а вторая втрое шире первой. Во сколько раз объём первой коробки меньше объёма второй?
! Алгоритм выполнения:
Записать формулу, для вычисления объема правильной четырехугольной призмы.
Записать в общем виде формулу для нахождения объема в первом и втором случае.
Найти отношение объемов.
Преобразовать полученное выражение с учетом соотношения измерений первой и второй призмы.
Сократить получившуюся дробь.
V1 = a1 · b1 · c1
V2 = a2 · b2 · c2
Найдем отношение объемов.
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2)
По условию c1 = 4,5 c2 (первая коробка в четыре с половиной раза выше второй),
b2 = 3 b1 (вторая коробка втрое шире первой).
Так как это правильные четырехугольные призмы, то в основании лежит квадрат, а значит глубина второй коробки тоже втрое больше глубины первой, то есть a2 = 3 a1
Подставим эти выражения в формулу отношения объемов:
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2) = (a1 · b1 · 4,5c2)/ ( 3a1 · 3b1 · c2) = (a1 · b1 · 4,5c2)/ ( 9a1 · b1 · c2)
Сократим получившуюся дробь на a1 · b1 · c2. Получим:
V1 / V2 = (a1 · b1 · 4,5c2)/ ( 9a1 · b1 · c2) = 4,5/9 = ½.
Объем первой коробочки в 2 раза меньше объема второй.
Ответ: 2. -
Слайд 12
11. От деревянного кубика отпилили все его вершины (см. рис.). Сколько граней у получившегося многогранника (невидимые ребра на рисунке не изображены)?
! Сначала вспомним сколько всего граней и вершин у куба: шесть граней и восемь вершин. Теперь на месте каждой вершины образуется новая грань после отпила, значит у модифицированного в задании куба шесть родных граней и восемь новых (после отпила). Итого получаем: 6 + 8 = 14 граней.
Ответ: 14.
Если бы нас спросили, а сколько вершин у нового «куба». Очевидно, если вместо одной становится три, а их всего восемь, то получаем: 8 • 3 = 24 -
Слайд 13
12. Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 6, а второго – 6 и 4. Во сколько раз объем второго цилиндра больше объема первого?
! Алгоритм выполнения
Записываем ф-лу для вычисления объема цилиндра.
Вводим обозначения для радиуса основания и высоты 1-го цилиндра. Выражаем подобным образом аналогичные параметры 2-го цилиндра.
Формируем формулы для объема 1-го и 2-го цилиндров.
Вычисляем отношение объемов.
V1=πR12H1,V2=πR22H2.
-
Слайд 14
13. В бак, имеющий форму прямой призмы, налито 5 л воды. После полного погружения в воду детали уровень воды в баке поднялся в 1,4 раза. Найдите объем детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.
! Алгоритм выполнения
Вводим обозначения для объема до погружения детали и после. Пусть это будет соответственно V1 и V2.
Фиксируем значение для V1. Выражаем V2 через V1. Находим значение V2.
Переводим результат, полученный в литрах, в куб.см.
Объем бака до погружения V1=5 (л). Т.к. после погружения детали объем стал равным V2. Согласно условию, увеличение составило 1,4 раза, поэтому V2=1,4V1.
Отсюда получаем: V2=1,4·5=7 (л).
Т.о., разница объемов, которая и составляет объем детали, равна:
V2–V1=7–5=2 (л).
2 л=2·1000=2000 (куб.см). -
Слайд 15
14. В сосуде, имеющем форму конуса, уровень жидкости достигает ½ высоты. Объем сосуда 1600 мл. Чему равен объем налитой жидкости? Ответ дайте в миллилитрах.
! Алгоритм выполнения
Доказываем, что данные в условии конусы подобны.
Определяем коэффициент подобия.
Используя свойство для объемов подобных тел, находим объем жидкости.
Если рассматривать сечение конуса по двум его противоположно расположенным образующим (осевое сечение), то видим, что полученные таким способом треугольники большого конуса и малого (образованного жидкостью) подобны. Это следует из равенства их углов. Т.е. имеем: у конусов подобны высоты и радиусы основания. Отсюда делаем вывод: т.к. линейные параметры конусов подобны, то и конусы подобны.
По условию высота малого конуса (жидкости) составляет ½ высоты конуса. Значит, коэффициент подобия малого и большого конусов равен ½.
Применяем св-во подобия тел, которое заключается в том, их объемы относятся как коэффициет подобия в кубе. Обозначим объем большого конуса V1, малого – V2. Получим:
Поскольку по условию V1=1600 мл, то V2=1600/8=200 мл. -
Слайд 16
15. Даны два шара с радиусами 4 и 1. Во сколько раз объем большего шара больше объема меньшего?
! Алгоритм выполнения
Записываем формулу для вычисления объема шара.
Адаптируем формулу для каждого из шаров. Для этого используем индексы 1 и 2.
Записываем отношение объемов, вычисляем его, подставив числовые данные из условия.
Вывод: объем большего шара в 64 раза больше. -
Слайд 17
16. Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 4 и 18, а второго – 2 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?
! Алгоритм выполнения
Записываем формулу для определения площади бок.поверхности цилиндра.
Переписываем ее дважды с использованием соответствующих индексов – для 1-го (большего) и 2-го (меньшего) цилиндров.
Находим отношение площадей. Вычисляем отношения, используя числовые данные из условия.
Вывод: площадь боковой поверхности 1-го цилиндра больше в 12 раз. -
Слайд 18
17. Однородный шар диаметром 3 см весит 162 грамма. Сколько граммов весит шар диаметром 2 см, изготовленный из того же материала?
! Алгоритм выполнения
Записываем формулу для определения массы большего шаров через плотность и объем.
Объем в этой формуле расписываем через ф-лу объема шара (через его радиус).
Записываем ф-лу для массы меньшего шара, расписываем объем через радиус (по аналогии с пп.1 и 2).
Поскольку оба шара изготовлены из одного и того же материала, то найденное значение для плотности можем использовать в ф-ле для массы меньшего шара. Вычисляем искомую массу.
m1=ρV1.
V1=(4/3)πR13. Отсюда получаем: m1=(4/3)πρR13
.
m2=ρV2V2=(4/3)πR23
-
Слайд 19
Планиметрия. №1518. В треугольнике ABC угол ACB равен 90°, cos A = 0,8, AC = 4. Отрезок CH – высота треугольника ABC(см. рисунок). Найдите длину отрезка AH.
! Алгоритм выполнения:
Вспомнить определение косинуса угла.
Записать выражение для нахождения косинуса угла.
Выразить неизвестную величину.
Вычислить.
cos A = АН/АС.АН = АС · cos A
АН = АС · cos A = 4 · 0,8 = 3,2
Ответ: 3,2. -
Слайд 20
19. Найдите вписанный угол, опирающийся на дугу, длина которой равна 5/18 длины окружности. Ответ дайте в градусах.
! Алгоритм выполнения:
Вспомнить соотношение величины вписанного угла и градусной меры угла, на который он опирается.
Вычислить градусную меру угла, на который опирается дуга.
Вычислить вписанный угол.
Весь круг составляет 360°, а 5/18 от его длины этоТак как вписанный угол равен половине градусной меры дуги, на которую он опирается, вписанный угол равен
100°:2 = 50°.
Ответ: 50. -
Слайд 21
20.В треугольнике АВС известно, что АВ=ВС=15, АС=24. Найдите длину медианы ВМ
! Алгоритм выполнения
Определяем вид треугольника.
Доказываем, что медиана ВМ является и высотой.
Из прямоугольного треугольника АМВ по т. Пифагора находим медиану ВМ.
Если АВ=ВС, то ∆АВС – равнобедренный.
Т.к. АМ медиана, то AM=АС:2=24:2=12. -
Слайд 22
21. На стороне ВС прямоугольника АВСD, у которого АВ=12 и АD=17, отмечена точка Е так, что треугольник АВЕ равнобедренный. Найдите ЕD.
! Алгоритм выполнения
Находим ЕС.
Определяем значение СD.
Из прямоугольного треугольника АСD по т.Пифагора
находим ЕD.
Т.к. по условию ∆АВЕ равнобедренный, то ВЕ=АВ=12.
Т.к. АВСD прямоугольник, то ВС=АD=17, СD=АВ=12.
ЕС=ВС–ВЕ=17–12=5.
∆ЕСD прямоугольный.
Тогда по т.Пифагора ЕD2=ЕC2+СD2. -
Слайд 23
22. В треугольнике АВС угол С равен 900, АВ=25, АС=24. Найдите cos B.
! Алгоритм выполнения
По т.Пифагора находим величину катета ВС.
По формуле-определению для косинуса находим cos B как отношение прилежащего катета к гипотенузе.
Из прямоугольного ∆АВС по теореме Пифагора имеем: АВ2=АС2+ВС2. -
Слайд 24
23. В равнобедренном треугольнике АВС боковая сторона АВ=25, sin A=3/5. Найдите площадь треугольника АВС.
! Алгоритм выполнения
Из вершины В проводим высоту BD к основанию ∆АВС. Получаем прямоугольного ∆ADB.
Из ∆ADB находим катет ВD, используя sin A.
Находим АD из ∆ADB по т.Пифагора. Далее определяем АС как 2AD.
Находим площадь ∆АВС по формуле S=ah/2.
В ∆ADB sin A=BD/AB → BD = AB · sin A = 25 · 3 / 5 = 15.
Из ∆ADB по т.Пифагора имеем: AB2=AD2+BD2
АС=2АD=2·20=40. -
Слайд 25
24. В треугольнике АВС угол В равен 1200. Медиана ВМ делит угол В пополам и равна 27. Найдите длину стороны АВ.
! Алгоритм выполнения
Определяем величину угла АВМ.
Доказываем, что ∆АМВ прямоугольный.
Находим АВ, используя формулу-определение для косинуса.
По условию угол АВМ равен половине угла В. Значит, угол АВМ составляет
1200:2=600.
Т.к. ВМ – медиана, опущенная на основание равнобедренного ∆АВС, то ВМ является и высотой. Поэтому ∆АМВ прямоугольный с прямым углом АМВ. -
Слайд 26
25. В равнобедренном треугольнике АВС медиана ВК=10, боковая сторона ВС=26. Найдите длину отрезка МN, если известно, что он соединяет середины боковых сторон.
! Алгоритм выполнения
Доказываем, что ∆АКВ прямоугольный.
Из ∆АКВ по т.Пифагора находим АК.
Находим АС как 2АК.
Находим МN как среднюю линию.
Из прямоугольного ∆АКВ по т.Пифагора АВ2=АК2+ВК2.
Поскольку ВК медиана, то АС=2АК=2·24=48.
Значит, MN=AC:2=48:2=24. -
Слайд 27
26. В треугольнике АВС высота АС=56, ВМ – медиана, ВН – высота, ВС=ВМ. Найдите длину отрезка АН.
! Алгоритм выполнения
Находим длину отрезков АМ и МС как половину от АС.
Доказываем, что ВН является медианой в ∆МВС.
Отсюда определяем, что МН – половина от МС.
3. Находим АН как сумму АМ и МН.
Рассмотрим ∆АВС. Т.к. ВМ медиана, то АМ=МС=АС/2=56/2=28.
МН=НС=МС/2=28/2=14.
АН=АМ+МН=28+14=42. -
Слайд 28
Стереометрия (№16)27. Радиус основания цилиндра равен 13, а его образующая 18. Сечение, параллельное оси цилиндра, удалено от нее на расстояние, равное 12. Найдите площадь этого сечения.
! Алгоритм выполнения:
Определить тип фигуры, образующей сечение.
Записать формулу для нахождения площади фигуры, образующей сечение.
Вычислить недостающие данные.
Вычислить искомую площадь сечения.
Сечение является прямоугольником, одна из сторон которого образующая цилиндра.
Длина прямоугольника – 18, из условия. Осталось вычислить ширину. Сделаем дополнительный чертеж цилиндра сверху: -
Слайд 29
Ширина прямоугольника – CD.
По условию «Сечение, параллельное оси цилиндра, удалено от нее на расстояние, равное 12». Расстояние от точки до прямой – это длина перпендикуляра, проведенного из этой точки на прямую. То есть на чертеже АВ = 12.
СD = СВ + ВD. СВ = ВD
Рассмотрим треугольник ВСА. Треугольник ВСА – прямоугольный.
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
В данном случае СА2 = СВ2 + АВ2
СВ2 — неизвестное слагаемое. Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
СВ2 = СА2 — АВ2
СВ = √(СА2 — АВ2)
СВ = √(132 — 122) = √(169 — 144) = √25 = 5
Для решения задачи необходимо знать СD = СВ + ВD = 5 + 5 = 10
Вычислим искомую площадь сечения.
10 · 18 = 180
Ответ: 180. -
Слайд 30
29. Стороны основания правильной треугольной пирамиды равны 24, а боковые рёбра равны 37. Найдите площадь боковой поверхности этой пирамиды.
! Алгоритм выполнения:
Проанализировать какие данные необходимо вычислить для ответа на вопрос задачи.
Найти площади треугольников.
Найти площадь боковой поверхности пирамиды.
В основании правильной треугольной пирамиды лежит равносторонний треугольник. Боковые ребра пирамиды, равные 37, образуют три равнобедренных треугольника, которые составляют ее боковую поверхность.
Найдем площади треугольников.Так как треугольник равнобедренный, AH=AC:2=24:2=12.Р/м треугольник АВН.АВ2 = ВН2 + АН2.ВН2 = АВ2 — АН2
Боковая поверхность пирамиды состоит из трех треугольников -
Слайд 31
30. Найдите объем правильной четырехугольной пирамиды, сторона основания которой равна 4, а боковое ребро равно √17.
Вспомним формулу площади правильной пирамиды — одна треть от произведения площади основания и высоты.
После этого перейдем к нахождению высоты. Для этого нам необходимо рассмотреть прямоугольный (так как основание перпендикулярно высоте) треугольник AMH. AH — половина диагонали квадрата, которая равна √2 его стороны, то есть в нашем случае диагональ равна 4√2, ну а половина — AH = 2√2. Зная гипотенузу и один из катетов, найдем высоту:
V = 1/3 • 16 •3 = 16
-
Слайд 32
31. Сторона основания правильной треугольной призмы АВСА1В1С1 равна 2, а высота этой призмы равна 4√3. Найдите объем призмы АВСА1В1С1.
! Алгоритм выполнения
Находим площадь основы призмы через формулу для площади правильного треугольника.
Записываем формулу для объема призмы. Подставляем в нее числовые данные, вычисляем искомую величину.
Объем призмы: V=Sh -
Слайд 33
32. Объем конуса равен 25π, а его высота равна 3. Найдите радиус основания конуса.
! Алгоритм выполнения
Записываем формулу для объема конуса. Из нее выражаем площадь основания.
Площадь основания расписываем по формуле площади круга, поскольку именно круг лежит в основании конуса.
Из этих двух формул выражаем искомую величину. Вычисляем ее.
Sосн=3V/h.
S=πR2
Поскольку в данном случае Sосн=S, то πR2=3V/h -
Слайд 34
33. Два ребра прямоугольного параллелепипеда равны 8 и 5, а объем параллелепипеда равен 280. Найдите площадь поверхности этого параллелепипеда.
! Алгоритм выполнения
Записываем формулу для объема прямоугольного параллелепипеда. Из нее выражаем 3-е (неизвестное) ребро. Вычисляем величину этого ребра.
Записываем формулу для площади поверхности. Подставляем в него числовые данные, находим искомое значение.
Объем прямоугольного параллелепипеда равен:
V=abc, где a, b, c – ребра. Будем считать, что a и b нам известны, а с – неизвестно.
Тогда: с=V/(ab).
с=280/(8·5)=7.
Площадь поверхности прямоугольного параллелепипеда вычисляется так:
S=2(ab+bc+ac).
Отсюда имеем:
S=2(8·5+5·7+8·7)=2(40+35+56)=2·131=262. -
Слайд 35
34. Объем конуса равен 24π, а радиус его основания равен 2. Найдите высоту конуса.
! Алгоритм выполнения
Записываем формулу для объема конуса. Из нее выражаем высоту.
Записываем формулу для площади круга, лежащего в основе конуса. Вычисляем эту площадь.
Подставляем числовые данные в формулу для объема, вычисляем искомую величину.
Площадь основания (как площадь круга) равна:
Sосн=πR2.
Вычисляем площадь:
Sосн=π·22=4π.
Посмотреть все слайды
Сообщить об ошибке
Похожие презентации










Спасибо, что оценили презентацию.
Мы будем благодарны если вы поможете сделать сайт лучше и оставите отзыв или предложение по улучшению.
Добавить отзыв о сайте
В
данной
работе
предлагаются
решения
сложных
заданий
(№13
—
№19)
ЕГЭ-2021
по
математике.
Представленный
здесь
материал
предназначен
для
подготовки
к
ЕГЭ
учащихся,
имеющих
навыки
в
решении
заданий
подобного
уровня
сложности.
Задания
№13,
№15,
№17
могут
быть
предложены
сильным
учащимся
обычных
классов,
а
вот
задания
№14,
№16,
№18,
№19
целесообразно
решать
с
учащимися
физико-
математических
классов,
причем
задание
№19
под
буквой
«в»
под
силу
только
тем,
кто
имеет
определенную
подготовку
в
решении
олимпиадных
задач.
Для
оформления
всех
решений
использована
мультимедиа
презентация,
где
материал
представлен
наглядно
в
ярком,
интересном
и
доступном
виде,
что
для
учителя
и
учащихся
будет
ценно
и
полезно.
Эту
презентацию
можно
применять
как
на
уроке,
так
и
для
индивидуальной
работы.
Условия
заданий
и
методические
рекомендации
по
их
решению.
№13.
а)
Решите
уравнение
Решите
уравнение
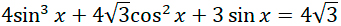
б)
Укажите
корни
этого
уравнения,
принадлежащие
отрезку
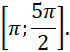
Это
задание
считается
одним
из
самых
решаемых
среди
заданий
второй
части
ЕГЭ.
Применяя
основное
тригонометрическое
тождество,
получаем
в
левой
части
данного
уравнения
тригонометрическое
выражение
относительно,
которое
можно
способом
группировки
разложить
на
множители.
Решить
получившиеся
простейшие
тригонометрические
уравнения
предлагается
с
помощью
числовой
окружности.
Важно,
чтобы
учащиеся
имели
хорошие
навыки
в
работе
с
этой
математической
моделью.
Тогда
и
отбор
корней
лучше
всего
сделать
на
числовой
окружности.
№14.
В
правильной
четырёхугольной
пирамиде
SABCD
сторона
основания
AD
равна
14,
высота
SН
равна
6.
Точка
К
—
середина
бокового
ребра
SD.
Плоскость
AKB
пересекает
боковое
ребро
SC
в
точке
P.
а)
Докажите,
что
площадь
четырёхугольника
CDKP
составляет
¾
площади
треугольника
SCD.
б)
Найдите
объем
пирамиды
ACDKP.
Стереометрическая
задача
является
для
учащихся
одной
из
сложных.
В
лучшем
случае
учащимися
выполняется
только
первая
часть
на
доказательство,
тогда,
как
вторая
часть
задачи
под
силу
лишь
не
многим.
Решение
второй
части
задачи
предлагается
тремя
способами:
-
применением
классического
определения
расстояния
от
точки
до
плоскости; -
методом
координат; -
методом
объёмов.
№15.
Решите
неравенство
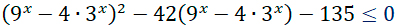
Данное
неравенство
достаточно
хорошего
уровня
сложности.
Его
решение
возможно:
-
методом
замены
переменной,
причем
эту
замену
приходится
выполнять
дважды,
что
в
целом
усложняет
решение; -
методом
замены
множителей,
которому
желательно
обучать
учащихся,
так
как
в
некоторых
случаях,
а
именно
в
этом
неравенстве
он
приводит
к
более
простому
решению.
№16.
Точки
A,
B,
C,
D
и
Е
лежат
на
окружности
в
указанном
порядке,
причем
AE
=
ED
=
CD,
а
прямые
AC
и
BE
перпендикулярны.
Отрезки
AC
и
BD
пересекаются
в
точке
T.
а)
Докажите,
что
прямая
EC
пересекает
отрезок
TD
в
его
середине.
б)
Найдите
площадь
треугольника
ABT,
если
BD
=
6,
AE
=
.
Данная
планиметрическая
задача
решается
здесь
двумя
разными
способами.
Здесь
важно
увидеть
свойства
различных
геометрических
фигур,
которые
позволяют
выбрать
то
или
иное
решение
задачи.
№17.
В
июле
2025
года
планируется
взять
кредит
в
банке
на
сумму
600
тысяч
рублей
на
6
лет.
Условия
его
возврата
таковы:
—
в
январе
2026,
2027,
2028
годов
долг
возрастает
на
20%
по
сравнению
с
концом
предыдущего
года;
—
в
январе
2029,
2030,
2031
годов
долг
возрастает
на
r%
по
сравнению
с
концом
предыдущего
года;
—
с
февраля
по
июнь
каждого
года
необходимо
выплатить
часть
долга;
—
в
июле
каждого
года
долг
должен
быть
на
одну
и
ту
же
величину
меньше
долга
на
июль
предыдущего
года;
Известно,
что
общая
сумма
выплат
после
полного
погашения
кредита
составит
984
тысячи
рублей.
Найдите
r.
Эта
задача
на
дифференцированный
платеж.
В
работе
предлагается
табличный
способ
решения
задачи.
Все
величины
и
данные,
и
искомые
обозначаются
переменными,
устанавливается
между
ними
связь,
а
числовые
значения
подставляются
в
самом
конце,
чтобы
получить
уравнение
с
одной
переменной
и
решить
его.
№18
Найдите
все
значения
а,
при
каждом
из
которых
имеет
ровно
два
различных
корня
уравнение
.
Это
самое
сложное
задание
данной
работы.
Его
решение
предлагается
двумя
способами:
-
аналитическим,
где
находятся
корни
данного
уравнения,
содержащие
параметр,
и
проверяются
условия
их
принадлежности
ОДЗ
и
совпадения; -
координатно-параметрическим
в
системе
xOa.
№19.
Отношение
трёхзначного
натурального
числа
к
сумме
его
цифр
—
целое
число.
а)
Может
ли
это
отношение
быть
равным
55?
б)
Может
ли
это
отношение
быть
равным
87?
в)
Какое
наименьшее
значение
может
принимать
это
отношение,
если
первая
цифра
трёхзначного
числа
равна
7?
В
этой
задаче
вполне
можно
решить
первые
два
пункта.
В
пункте
а)
достаточно
привести
пример,
то
есть
можно
просто
подобрать
числа,
удовлетворяющие
условию
задачи.
В
пункте
б)
необходимо
обоснованное
доказательство
того,
что
такого
отношения
не
может
быть.
Решение
в
пункте
в)
сложное,
здесь
применяется
метод:
оценка
плюс
пример.