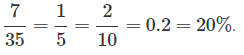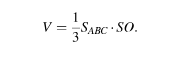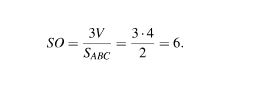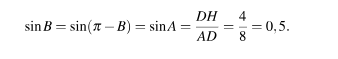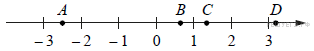Подготовка к егэ по математике разбор заданий

В данном разделе мы занимаемся подготовкой к ЕГЭ по математике как базового, профильного уровня — у нас представлены разборы задач, тесты, описание экзамена и полезные рекомендации. Пользуясь нашим ресурсом, вы как минимум разберетесь в решении задач и сможете успешно сдать ЕГЭ по математике в 2020 году. Начинаем!

ЕГЭ по математике является обязательным экзаменом любого школьника в 11 классе, поэтому информация, представленная в данном разделе актуальна для всех. Экзамен по математике делится на два вида — базовый и профильный. В данном разделе я приведен разбор каждого вида заданий с подробным объяснением для двух вариантов. Задания ЕГЭ строго тематические, поэтому для каждого номера можно дать точные рекомендации и привести теорию, необходимую именно для решения данного вида задания. Ниже вы найдете ссылки на задания, перейдя по которым можно изучить теорию и разобрать примеры. Примеры постоянно пополняются и актуализируются.

---

Структура базового уровня ЕГЭ по математике

---

Экзаменационная работа по математике базового уровня состоит из одной части, включающей 20 заданий с кратким ответом. Все задания направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях.

Ответом к каждому из заданий 1–20 является целое число, конечная десятичная дробь, или последовательность цифр.

Задание с кратким ответом считается выполненным, если верный ответ записан в бланке ответов №1 в той форме, которая предусмотрена инструкцией по выполнению задания.

---

Разбор заданий ЕГЭ по математике (база)

---

В данном разделе мы занимаемся подготовкой к ЕГЭ по математике как базового, профильного уровня — у нас представлены разборы задач, тесты, описание экзамена и полезные рекомендации. Пользуясь нашим ресурсом, вы как минимум разберетесь в решении задач и сможете успешно сдать ЕГЭ по математике в 2023 году. Начинаем!

ЕГЭ по математике является обязательным экзаменом любого школьника в 11 классе, поэтому информация, представленная в данном разделе актуальна для всех. Экзамен по математике делится на два вида — базовый и профильный. В данном разделе я приведен разбор каждого вида заданий с подробным объяснением для двух вариантов. Задания ЕГЭ строго тематические, поэтому для каждого номера можно дать точные рекомендации и привести теорию, необходимую именно для решения данного вида задания. Ниже вы найдете ссылки на задания, перейдя по которым можно изучить теорию и разобрать примеры. Примеры постоянно пополняются и актуализируются.

---

Структура базового уровня ЕГЭ по математике

---

Экзаменационная работа по математике базового уровня состоит из одной части, включающей 20 заданий с кратким ответом. Все задания направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях.

Ответом к каждому из заданий 1–20 является целое число, конечная десятичная дробь, или последовательность цифр.

Задание с кратким ответом считается выполненным, если верный ответ записан в бланке ответов №1 в той форме, которая предусмотрена инструкцией по выполнению задания.

---

Разбор заданий ЕГЭ по математике (база)

Обычно базовую математику выбирают ребята, у которых есть план: надо как можно скорее разделаться с бесполезным для поступления предметом и сосредоточиться на своем наборе вступительных. Из этой статьи вы узнаете, как сдать базовую математику максимально быстро и просто.

В этом материале мы сделаем акцент на простых номерах, которые принесут вам балл почти задаром! Они обозначены пометкой «Обязательно делать» — таких заданий 10. Как раз с запасом на ошибки, ведь минимум для сдачи базовой математики — 7 баллов.

Для тех, кто хочет получить выше тройки — это 12 баллов и выше, — мы дали рекомендации по еще 3 задачам. В сумме получается 13 номеров. Решите их все, и твердая четверка у вас в кармане.

Какие задания решать, чтобы сдать базовую математику

Задание 1: обязательно делать

Проверяется ваше умение разделить случаи, когда требуется округлить величину в большую сторону, а когда — в меньшую.

Если вы ходите в магазин с наличными, то сталкиваетесь с подобными задачами каждый день. Разделим 100 рублей на стоимость одной упаковки йогурта. Не забывайте приводить все величины к одной размерности:

100 : 14,6 = 6, 849…

Так сколько баночек йогурта вам продадут? На 7 штук денег не хватает, значит, округлить полученную величину надо до целого в меньшую сторону. Математическое правило округление в этой задаче не поможет.

Ответ: 6.

Если одна пачка рассчитана на 6 рулонов, то на 63 рулона:

63 : 6 = 10,5. 

Но полпачки вам не продаст. Включаем логику: возьмем меньше — не хватит еще половины пачки на три последних рулона. Значит, округлить надо в большую сторону, взять клей с небольшим запасом. Математическое правило округления снова игнорируем.

Ответ: 11.

Задание 2: обязательно делать

Это задача на здравый смысл. Нужно соотнести величины с их возможными значениями.

Вряд ли грузовой автомобиль может весить как 3 шоколадки (300 г), а взрослый человек — 8 т.

Давайте вместе подберем значения.

• Взрослый человек обычно весит от 50 до 100 кг — что из этого подходит? Конечно, 65 кг.
• Грузовой автомобиль достаточно большой и тяжелый, скорее всего, он весит несколько тонн. Нам подходит 8 т.
• Книга обычно не такая большая и весит до 1 кг. Из оставшегося подойдет 300 г.
• А пуговка совсем маленькая. Значит, берем самый легкий вес — 5 г.

Ответ:

Главное — внимательно перенести ответы в бланк: 3142.

Задание 3: обязательно делать

Задание на работу с графиком, диаграммой или таблицей. Вооружайтесь карандашом, читайте условие с предельной внимательностью и безжалостно отмечайте нужные по условию значения на изображении в КИМ. Вы и представить не можете, сколько выпускников теряет тут баллы по невнимательности.

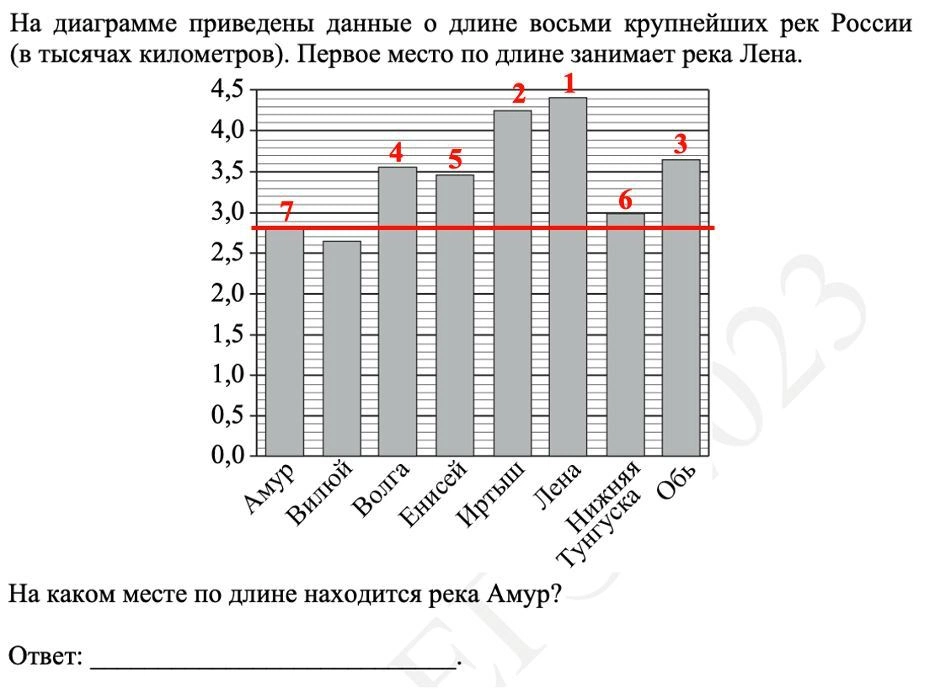
Мы ярко отметили уровень, соответствующий Амуру, в итоге посчитать все более длинные реки стало проще простого. У вас на экзамене будет так же наглядно!

Ответ: 7.

Задание 4: обязательно делать

Задание проверяет навык работы с формулами. Алгоритм решения напоминает решение задачек на уроке по физике:

• Выписываем формулу из условия.
• Определяем, что нужно найти: единственную букву, значение которой не дано.
• Выражаем искомую величину.
• Подставляем значения из условия в формулу.
• Ищем неизвестное.

Самое трудное тут — правильно выразить искомую величину. Для этого повторяем порядок выполнения арифметических операций, свойства умножения, тренируемся перекидывать через равно множители и слагаемые.

И да, в базе эта задача проста настолько, что даже перекидывать ничего не придется. Нужная величина уже будет слева от равно.

Задание 5: обязательно делать

Простая задача на определение вероятности, которая поможет вам точно сдать базовую математику.

Решаем с помощью формулы:

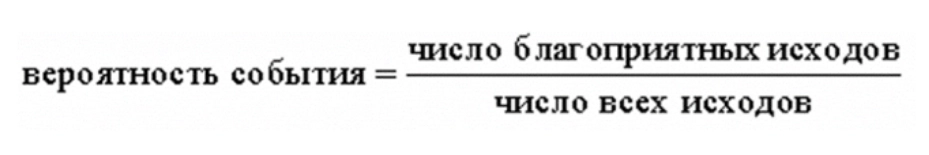
Внимательно читайте вопрос: спрашивают вероятность купить исправную лампочку. Если из ста 3 неисправны, значит, остальные в порядке и подойдет любая из оставшихся 97. Это и есть наши благоприятные исходы из формулы.

97 : 100 = 0,97.

Ответ: 0,97.

Будьте внимательны: иногда в задаче есть указание к округлению. Значит, ответ у вас выйдет некрасивый, в виде бесконечной десятичной дроби, которую вы округлите до нужного разряда.

Еще один подвох: формулировка с предлогом «на». К примеру, «На 100 лампочек 3 неисправны. Найдите вероятность купить неисправную». Подходящие исходы тут даны явно: 3 неисправные лампочки. А вот число всех исходов спрятано, и найти его будет нужно сложением исправных и неисправных лампочек: 100 + 3 = 103.

Задание 6: обязательно делать

Задание проверяет навык чтения информации из таблицы и подбора подходящего по условию варианта.

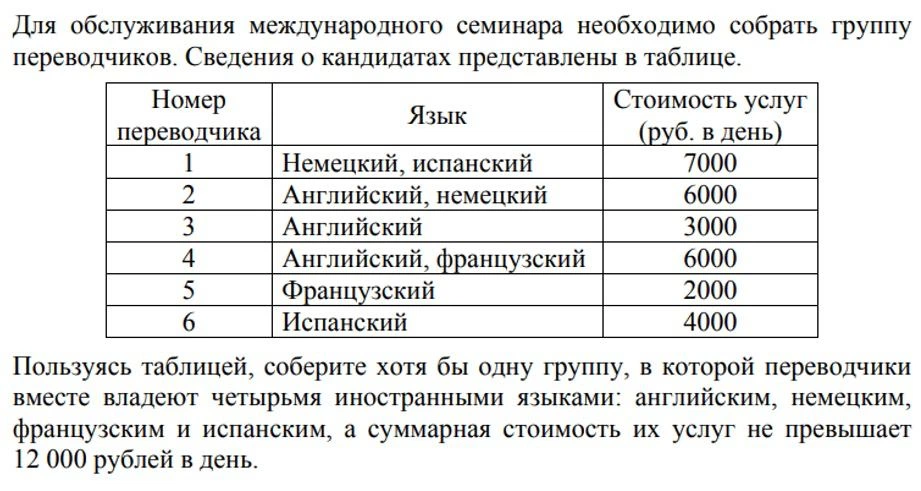
Например, вы нашли вариант позвать первого, третьего и пятого переводчиков. Получите весь набор языков как раз за 12 тысяч. Но обратите внимание, что это решение далеко не единственное.

Ответ: 135.

Задание 7

Мы не выделяем это задание в обязательные, так как для его выполнения понадобится навык анализа поведения функции по графику. Но, как его решать, сейчас коротко расскажем.

Запомним: точка максимума будет на «горке», точка минимума — в «ямке». Функция убывает, если идет вниз слева направо. Возрастает, если идет вверх слева направо.

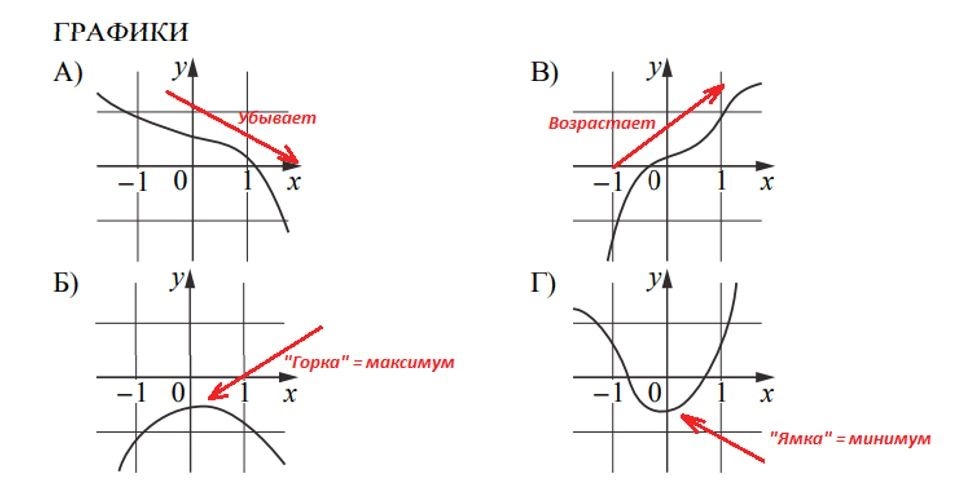
Если не повезет, то придется вспомнить азы теории по производной.

Здесь все дело в касательных. Нужно внимательно к ним присмотреться. Если касательная к графику возрастает, то значение производной будет положительное, если убывает — отрицательное. Производная будет тем больше по величине (модулю), чем быстрее возрастает или убывает касательная.

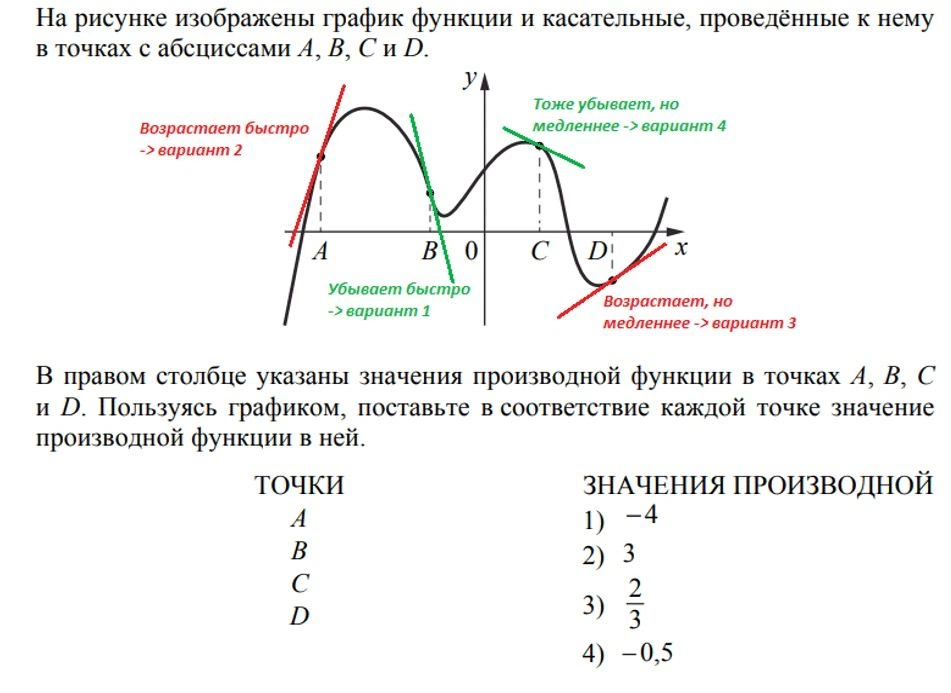
Ответ: 2143.

Задание 8: обязательно делать

Задача проверяет умение делать логичные выводы из утверждения. Иногда попадаются совсем простые задания, к таким даже дополнительно готовиться не надо.

Все, что от вас требуется, — схематично изобразить на черновике ясень, рябину и осину, указать известную разницу в высоте и внимательно сопоставить картинку с утверждениями.

Важно: не додумывайте дополнительные условия, не указанные в тексте задачи. Учитесь читать строго то, что написано.

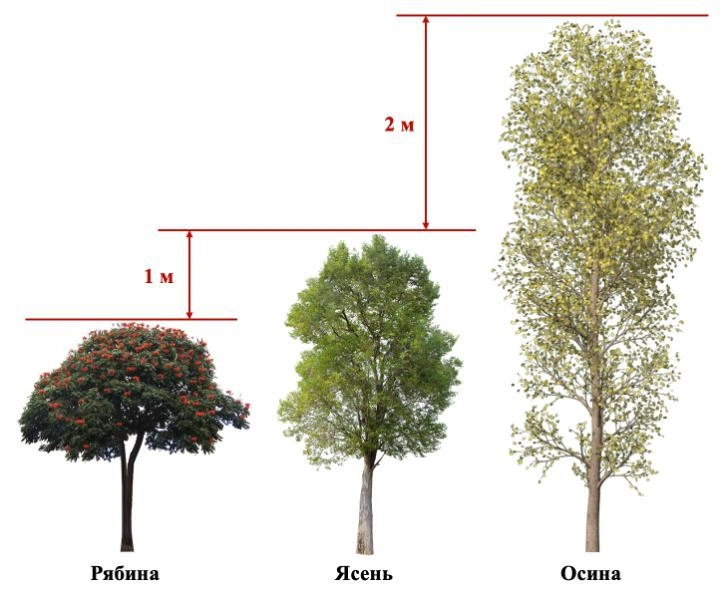
Исходя из рисунка выше получаем, что верны только утверждения 1 и 4.

Ответ: 14.

А бывают случаи, когда с визуализацией задачки придется постараться.

Тут иллюстрация не так очевидна, но нам помогут круги Эйлера. Этот инструмент позволяет наглядно изобразить множество объектов. В данном случае — школьников. Давайте прикинем, как ребята могут распределиться по кружкам.

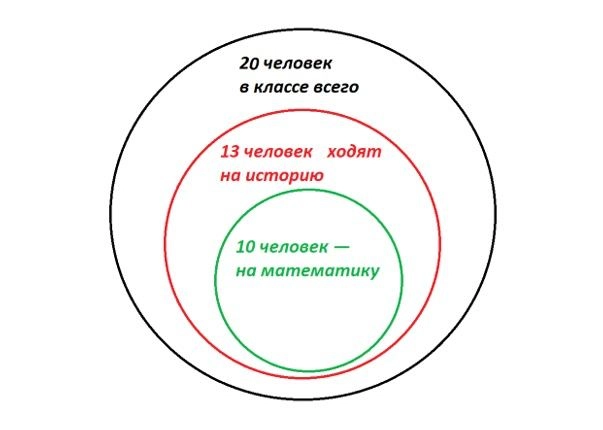
Например, так. Тут из 20 человек на кружки в итоге ходят 13. Причем 10 из них очень активны и выбрали сразу два предмета. Трое ограничились только историей.

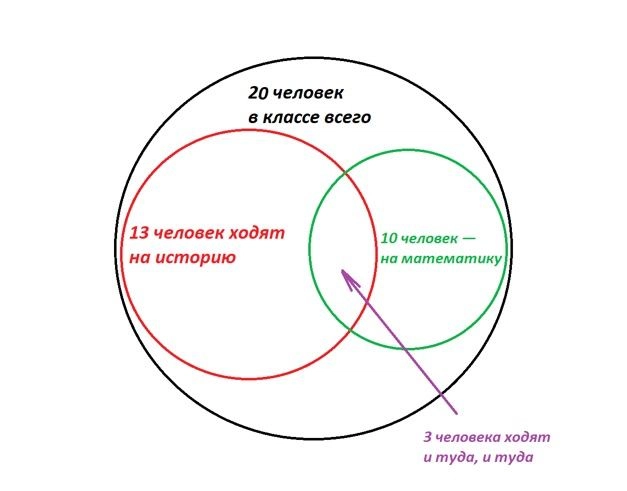
Или вот так. Если ребята задались целью по максимуму не пересекаться на дополнительных занятиях, то… У них не получится, и как минимум трое запишутся сразу на оба факультатива.

Конечно, возможны еще промежуточные варианты, но мы нарисовали два крайних. Теперь попробуем ответить на вопросы.

1. Смотрим на первую картинку. Даже если все ребята будут очень стараться посетить оба кружка, они ограничены условиями задачи и максимум на оба попадут 10 человек из 20. Нет.
2. Тут надо рассмотреть другую крайность, которую мы изобразили на второй картинке. Как бы ребята ни старались не встречаться на кружках, хотя бы трое попадут на оба сразу. Да.
3. Уж точно неверно. На обеих наших картинках есть ребята, которые ходят на историю, но не ходят на математику. Нет.
4. Смотрим на первую картинку. Оба кружка могут посещать максимум 10 человек. 

Ответ: 24.

Так что для решения иногда мало логики — понадобится еще немного воображения. Потренируйтесь, и ваши шансы получить балл увеличатся.

Задание 14: обязательно делать

Задание проверяет базовые навыки счета, которым учат в 5–6-м классах. Чтобы получить балл и сдать базовую математику, надо:

• уметь выполнять арифметические действия с обыкновенными и десятичными дробями;
• правильно расставлять порядок действий;
• быть предельно внимательными.

Уделите пару вечеров отработке алгоритмов сложения, вычитания, умножения и деления обыкновенных и десятичных дробей, и это задание у вас в кармане.

Задание 15

Составители экзамена проверяют ваш навык работы с процентами и единицами отношения. Такие задачи бывают четырех типов.

Тип 1. Найти часть от числа

Часть может быть выражена в процентах или сразу в виде дроби. Например, придется искать треть от чего-то.

Рассмотрим на примере реальной задачи из экзамена:

Прочувствуйте специфику задачи: нам известно целое — вся зарплата до вычета налога. А работать мы будем с кусочком — 13 процентами. Сколько это в рублях, нам еще предстоит узнать.

Чтобы ответить на вопрос задачи, нужно сделать три шага:

1. Перевести процент в десятичную дробь.

Для этого всегда надо количество процентов поделить на 100.

13 : 100 = 0,13.

2. Найти, сколько это от зарплаты в рублях.

Запоминаем главное правило для этого типа задач: чтобы найти дробь от числа, надо число умножить на эту дробь.

12 500 ∙ 0,13 = 1 625 (руб.) — налог, который удержат с зарплаты Ивана Кузьмича.

3. Ответить на вопрос задачи.

У нас просили зарплату после вычета налога, а не сам налог.

12 500 – 1625 = 10 875 (руб.).

Ответ: 10 875.

Будьте внимательны: многие совершают ошибку именно на последнем шаге!

Тип 2. Найти число по его части

Прочувствуйте разницу с прошлой задачей: тут 124 — и есть 25%, то есть одна и та же величина выражена в процентах и в абсолютных величинах, в данном случае — в учениках. Просят узнать целое — 100%.

1. Переводим процент в десятичную дробь:

25 : 100 = 0,25.

2. Находим, сколько учеников всего.

Правило для этого типа задач: чтобы найти целое, надо часть разделить на дробь.

124 : 0,25 = 496 (уч.) — всего.

Ответ: 496.

Тип 3. Найти, сколько процентов часть составляет от целого

Особенность подобных заданий: не дано процентов, есть только абсолютные величины. В данном случае — стоимость футболки в рублях.

1. Находим, какую долю новая цена составляет от первоначальной.

Запоминаем правило: чтобы найти, какую долю часть составляет от целого, надо часть разделить на целое.

680 : 800 = 0,85.

2. Переводим долю в процент.

В прошлых задачах мы уже дважды выполнили обратное действие. В этот раз сделаем наоборот: умножим полученную дробь на 100.

0,85 ∙ 100 = 85% — столько процентов новая цена составляет от старой.

3. Отвечаем на вопрос задачи.

Нас спросили, на сколько процентов цена снизилась, что стала 85% от первоначальной. Конечно, изначально она была 100%. Итого:

100 – 85 = 15%.

Ответ: 15%.

Тип 4. Задачи на соотношение

Если перефразировать условие, то за первого кандидата проголосовали 3 части избирателей, а за второго — 2 части. Особенность этих частей в том, что они одинаковые по величине.

Если одна будет состоять из 10 человек, то за первого кандидата будет 30, а за второго — 20.

1. Считаем общее количество частей:

3 + 2 = 5.

2. Узнаем, сколько голосов составляет одна такая часть.

Тут речь о процентах проголосовавших. Сколько всего проголосовало? Конечно, 100%! Значит, каждая из пяти частей «весит»

100 : 5 = 20%.

3. Отвечаем на вопрос задачи.

За проигравшего проголосовало меньше частей избирателей. В нашем случае 2.

20 ∙ 2 = 40%.

Ответ: 40%.

Решение этих задач удобнее всего оформить табличкой:

1 часть = 100% : 5 = 20%.

Если рассчитываете решать текстовую задачу, включите здравый смысл. Ответ всегда можно проверить на адекватность благодаря обычной логике. 

Задание 16: обязательно делать

Задание на решение выражения. На самом деле оно проверяет знание теории, так как в этом задании вам могут встретиться:

• выражения со степенями,
• иррациональные выражения,
• логарифмические выражения,
• тригонометрические выражения.

Ваша задача, соответственно, — знать:

• свойства степеней

• свойства корней

• свойства логарифмов

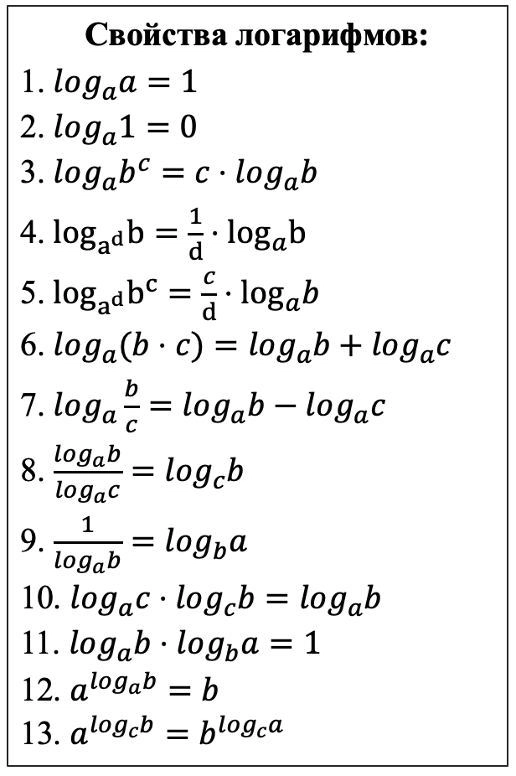
• формулы тригонометрии

Вы можете подробно ознакомиться с ними и научиться выводить в этой статье.

Обратите внимание: нужная теория будет в справочных материалах на экзамене, но это не поможет, если вы не научитесь применять ее для решения заданий. Практика обязательна!

Задание 17: обязательно делать

В номере с уравнениями вам не встретятся тригонометрические. Зато вы точно увидите там:

• линейные уравнения

Раскрываем скобки, если они есть, слагаемые с х переносим в одну сторону от равно, без х — в другую. Приводим подобные и решаем простейшее уравнение.

• квадратные уравнения

Бывают полные и неполные, всего надо повторить три алгоритма решения! А формула дискриминанта еще и в справочных материалах есть.

• иррациональные уравнения

Это те, что с корнем. Чтобы избавиться от корня, возводим обе части уравнения в квадрат и решаем получившееся уравнение. Есть нюансы с областью допустимых значений: подставьте полученные корни в исходное уравнение и проверьте, выполняется ли равенство. Если нет, то подставленное значение решением не будет.

• показательные уравнения

Ваша задача — с помощью формул свойств степеней привести уравнение к виду, когда слева и справа от равно в основании степени будет одно и то же число. После приравниваем показатели и решаем. Вот так:

Ответ: 7.

• логарифмические уравнения

С помощью формул свойств логарифмов приводим уравнение к виду, когда слева и справа от равно будет логарифм с одинаковым основанием. После приравниваем выражения под логарифмом и решаем.

Ответ: 67.

Прелесть уравнений в том, что ответ всегда можно проверить подстановкой вместо x в уравнение. Не забывайте проверять, ведь это возможность убедиться на 100%, что вы не упустите заветный балл.

Задание 19

Если хотите сдать базовую математику и решить номер 19, надо ознакомиться со свойствами целых чисел и признаками делимости. Иногда решение можно найти даже подбором! Попробуйте — времени на базовом ЕГЭ вам точно хватит.

Для начала нужно запомнить все признаки делимости.

А теперь посмотрим на типичное задание 19.

Тут помогут признаки делимости. Отдельного признака для 12 нет, потому нам надо разложить его на множители, признаки делимости для которых есть. 

• На 3: сумма всех цифр делится на 3.
• На 4: число, образованное последними двумя цифрами, делится на 4.

Начнем с признака для 4. Пока что наше число заканчивается на 13 и на 4 не делится. Попробуем вычеркнуть последнюю цифру, и число будет заканчиваться на 61. Тоже не подходит. Вычеркнем еще одну: теперь на конце 76… Вот оно! От изначального числа осталось 751576, две цифры уже вычеркнули, осталось убрать одну.

Теперь проверим признак для 3: 7 + 5 + 1 + 5 + 7 + 6 = 31. Какое ближайшее число разделится на 3? Конечно, 30. Если мы вычеркнем единичку, все сойдется.

Ответ: 75576.

Другой вариант задания:

А задание такого типа можно попытаться подобрать, расположений не слишком много. Мы все же постараемся порассуждать, чтобы уменьшить количество возможных вариантов.

Чтобы число делилось на 10, оно должно заканчиваться на 0. Например, это получится, если сложить 7 + □7 + □□6. Уже немного легче. Остальное просто подберем. Под условие задачи подойдет 7 + 27 + 356 = 390.

Ответ: 390.

Какие задания мы не разобрали и почему

Теперь вы знаете, как сдать базовую математику, решив всего семь заданий. Но некоторые номера базового ЕГЭ включают слишком большое разнообразие прототипов, и методы их решения не ограничиваются парой простых алгоритмов.

Например, в эту группу относятся все задания по геометрии: с 9 по 13. Чтобы решать геометрию, мало знать основные фигуры и формулы. Необходим навык, который вырабатывается только практикой. Однако у нас есть статья про окружность — в ней вы найдете много полезной информации.

Задание 18 обычно, хотя и не всегда, содержит неравенство.

Это объемный блок теории, которую тоже необходимо подкреплять практикой. Но, может, вам повезет и попадется задачка на расположение значений на числовой прямой.

Тут достаточно примерно прикинуть значения и аккуратно внести ответы в бланк. Ясно, что 7/3  больше 2, но меньше 3. Корень из 26 равен 5 с копейками, а степень –1 из 3/5 сделает 5/3, или чуть больше 1,5. Подобные задания надо пытаться делать обязательно!

Задание 20. С этим заданием ученики знакомы еще с 9-го класса, так как оно было под номером 21 на ОГЭ. Это текстовая задача:

• на производительность,
• движение (по прямой, воде, окружности),
• сплавы и смеси,
• проценты (пиджаки, рубашки, брюки; бюджет семьи; акции, которые растут и падают),
• прогрессии.

В задании 21 на ОГЭ не было прогрессий, но они были в первой части на ОГЭ, так что ничего нового.

Задание 21. Здесь попадаются разные типы неочевидных задач на логику — чем-то они даже похожи на олимпиадные. Решение каждой нужно рассматривать отдельно и подробно. Если хотите прочитать о том, какие задачи бывают в 21-м номере, пишите в комментариях, и Maximum поделится своими методами решения!

Не знаете, какой вуз выбрать? Воспользуйтесь бесплатной консультацией в нашем центре. Что это такое? Все просто: вы расскажете о себе и о своих интересах. А специалист посоветует, на какие специальности обратить внимание, в какой вуз поступать, какие ЕГЭ сдавать. Так вы сэкономите время на подготовку и сможете выбрать образование, которое точно окажется для вас интересным и полезным!

Подготовка к ЕГЭ по математике (профильный уровень): задания, решения и объяснения

Разбираем задания и решаем примеры с учителем

12 июля 2017

Экзаменационная работа профильного уровня длится 3 часа 55 минут (235 минут). 

Минимальный порог — 27 баллов.

Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и числу заданий. 

Определяющим признаком каждой части работы является форма заданий:

• часть 1 содержит 8 заданий (задания 1-8) с кратким ответом в виде целого числа или конечной десятичной дроби;
• часть 2 содержит 4 задания (задания 9-12) с кратким ответом в виде целого числа или конечной десятичной дроби и 7 заданий (задания 13–19) с развернутым ответом (полная запись решения с обоснованием выполненных действий).

---

Панова Светлана Анатольевна, учитель математики высшей категории школы, стаж работы 20 лет:  

«Для того чтобы получить школьный аттестат, выпускнику необходимо сдать два обязательных экзамена в форме ЕГЭ, один из которых математика. В соответствии с Концепцией развития математического образования в Российской Федерации ЕГЭ по математике разделен на два уровня: базовый и профильный. Сегодня мы рассмотрим варианты профильного уровня».

---

Задание № 1 — проверяет у участников ЕГЭ умение применять навыки, полученные в курсе 5 — 9 классов по элементарной математике, в практической деятельности. Участник должен владеть вычислительными навыками, уметь работать с рациональными числами, уметь округлять десятичные дроби, уметь переводить одни единицы измерения в другие.

Пример 1.

В квартире, где проживает Петр, установили прибор учета расхода холодной воды (счетчик). Первого мая счетчик показывал расход 172 куб. м воды, а первого июня — 177 куб. м. Какую сумму должен заплатить Петр за холодную воду за май, если цена 1 куб. м  холодной воды составляет 34 руб 17 коп? Ответ дайте в рублях.

Решение:

1)    Найдем количество потраченной воды за месяц:

177 — 172 = 5 (куб м)

2)    Найдем сколько денег заплатят за потраченную воду:

34,17 · 5 = 170,85 (руб)

Ответ: 170,85.

---

---

Задание № 2 —является одним из простейших заданий экзамена. С ней успешно справляется большинство выпускников, что свидетельствует о владении определением понятия функции. Тип задания № 2 по кодификатору требований — это задание на использования приобретённых знаний и умений в практической деятельности и повседневной жизни. Задание № 2 состоит из описания с помощью функций различных реальных зависимостей между величинами  и интерпретация их графиков. Задание № 2 проверяет умение извлекать информацию, представленную в таблицах, на диаграммах, графиках. Выпускникам нужно уметь определять значение функции по значению аргумента при различных способах задания функции и описывать поведение и свойства функции по её графику. Также необходимо уметь находить по графику функции наибольшее или наименьшее значение и строить графики изученных функций. Допускаемые ошибки носят случайный характер в чтении условия задачи, чтении диаграммы.

#ADVERTISING_INSERT#

Задание №  2 проверяет умение читать диаграммы.

Пример 2. На рисунке показано изменение биржевой стоимости одной акции добывающей компании в первой половине апреля 2017 года. 7 апреля бизнесмен приобрёл 1000 акций этой компании. 10 апреля он продал три четверти купленных акций, а 13 апреля продал все оставшиеся. Сколько потерял бизнесмен в результате этих операций?

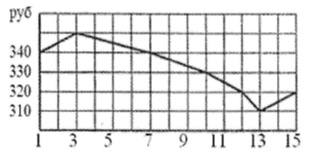
Решение: 

1)    340 · 1000 = 340000 (руб) — бизнесмен потратил 7 апреля при покупке 1000 акций.

2)    1000 · 3/4 = 750 (акций) — составляют  3/4 от всех купленных акций.

3)    330 · 750 = 247500 (руб) — бизнесмен получил 10 апреля после продажи 750 акций.

4)    1000 – 750 = 250 (акций) — остались после продажи 750 акций 10 апреля.

5)    310 · 250 = 77500 (руб) — бизнесмен получил 13 апреля после продажи 250 акций.

6)    247500 + 77500 = 325000 (руб) — бизнесмен получил после продажи 1000 акций.

7)    340000 – 325000 = 15000 (руб) — потерял бизнесмен в результате всех операций.

Ответ: 15000.

---

Здесь представлен бесплатный видеокурс по подготовке к ЕГЭ по математике профильного уровня.

Список заданий:

Задание 1. Прямоугольные, равнобедренные треугольники, треугольники общего вида, параллелограмм, трапеция, вписанные и центральные углы, вписанные и описанные окружности.

Задание 2. Стереометрия: куб, параллелепипед, призма, пирамида, цилиндр, конус,шар, комбинация тел, элементы, площади и объемы составных многогранников

Задание 3. Классическое определение вероятности.

Задание 4. Теоремы о вероятности событий.

Задание 5. Линейные, квадратичные, дробно-рациональные, степенные, иррациональные, тригонометрические, показательные и логарифмические уравнения

Задание 6. Рациональные, иррациональные, степенные, логарифмические, тригонометрические выражения.

Задание 7. Производная и первообразная: физический смысл производной, геометрический смысл производной и касательная, применение производной к исследованию функций, первообразная

Задание 8. Задачи с прикладным содержанием: линейные, квадратные, степенные, рациональные, иррациональные, показательные, логарифмические, тригонометрические и смешанные уравнения и неравенства.

Задание 9. Текстовые задачи на движение по прямой и окружности, на движение по воде, на проценты и сплавы, на совместную работу и прогрессии.

Разбор всех типов задания номер 1 из ЕГЭ (профильный уровень) по математике

Разбор всех типов задания номер 2 из ЕГЭ (профильный уровень) по математике

Разбор всех типов задания номер 3 из ЕГЭ (профильный уровень) по математике

Разбор всех типов задания номер 4 из ЕГЭ (профильный уровень) по математике

Разбор всех типов задания номер 5 из ЕГЭ (профильный уровень) по математике

Разбор всех типов задания номер 6 из ЕГЭ (профильный уровень) по математике

Разбор всех типов задания номер 7 из ЕГЭ (профильный уровень) по математике

Разбор всех типов задания номер 8 из ЕГЭ (профильный уровень) по математике

Разбор всех типов задания номер 9 из ЕГЭ (профильный уровень) по математике

Базовая математика — обязательный предмет ЕГЭ, который ежегодно сдают все российские школьники. Для того, чтобы получить школьный аттестат, вполне достаточно минимального балла по базовой математике, а вот для поступления в вуз может потребоваться экзамен по профильной математике. Минимальный балл, который необходимо набрать для получения аттестата — 23. Чтобы поступить в вуз, понадобится не менее 27 баллов. Рассмотрим демовариант ЕГЭ по математике 2019 и разберем некоторые из этих заданий.

Задание №1

Это задание основано на проверке простейших математических навыков: сложение, вычитание, деление, умножение, а также действия десятичными дробями и перевод одних единиц измерения в другие.

Пример задачи

В 23.50 минут по московскому времени из Санкт-Петербурга в Москву выехал поезд. В Москву он приехал на следующие сутки в 7 часов 50 минут. Необходимо вычислить, какое количество времени поезд был в пути.

Решение

Зная о том, что в сутках всего 24 часа, и их начало приходится на 00:00, а конец — на 24 часа, вычисляем: в первые сутки поезд находился в пути десять минут, во вторые — 7 часов и 50 минут.

7 ч. 50 мин. + 0 ч. 10 мин. = 7 ч. 60 мин. или 8 часов

Задание №2

Задание проверяет, насколько хорошо выпускники умеют интерпретировать различные таблицы, графики и диаграммы, а также совершать с их помощью простейшие вычисления. Как правило, речь идет об анализе графика функции и поиске наибольших и наименьших значений.

Пример задачи

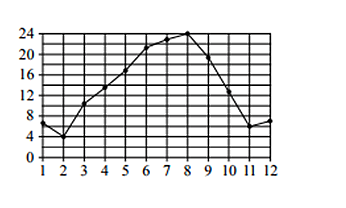
В задаче представлен график, отображающий среднюю температуру Сочи за каждый месяц 1920 года. Необходимо определить, сколько месяцев в году температура была выше 18 градусов Цельсия.

Решение

Для того, чтобы найти правильное решение, необходимо провести горизонтальную линию от точки с цифрой 18 (указана температура в градусах Цельсия). Таким образом станет очевидно, что такая температура держалась 4 месяца подряд: в июне, июле, августе и сентябре.

Задание №3

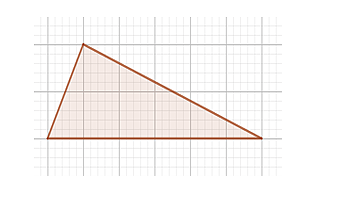
Школьники должны продемонстрировать знание основ планиметрии, а именно: уметь вычислять площадь фигур, рассчитывать градусные меры углов, диаметры и находить другие значения. Например, найти площадь треугольника, начерченного на бумаге с размером клеток 1х1. В этом задании важно продемонстрировать знание формул и умение пользоваться различными способами решения задачи.

Задание №4

Задача из курса “Теория вероятностей и статистика”. Выпускникам предлагается высчитать вероятность того или иного события, произошедшего в повседневной ситуации.

Пример задачи

Ученикам предложено выучить 25 билетов по биологии. Лишь два из них содержат вопрос о грибах. Каждому школьнику предстоит ответить лишь на один билет. Вычислите вероятность того, что вопрос о грибах будет содержаться именно в этом билете.

Решение

Вероятность события можно рассчитать по формуле Р(А) = m/n, где m — количество благоприятных исходов, а n — общее их количество. 25 билетов означают 25 исходов, 2 из которых — благоприятные. Значит, вероятность равна 2/25, то есть 0,08.

Задача №5

Здесь проверяется умение решать уравнения, находить неизвестные, извлекать корни и т. д.

Пример задачи

Найти корень уравнения 3x-5 = 81

Решение

3х-5 = 34
х-5 = 4
х = 9

Задание №6

Здесь необходимо продемонстрировать умение моделировать различные ситуации при помощи геометрических понятий. Важно знание теорем, умение определять длину, градус угла и другие величины.

Пример задачи

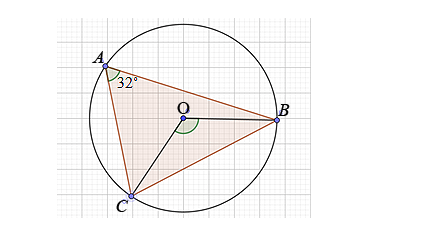
Треугольник с углами А, B и С вписан в окружность с центром О. Угол BAC — 32 градуса. необходимо найти угол BOC.

Решение

COB — центральный угол, равный дуге CB
САВ — вписанный угол, равный ½ дуги СВ
Значит, САВ = ½ СОВ. Так как ½ угла СОВ равна 32 градусам, то угол СОВ равен 64о

Ответ: 64о

Задача №7

Выпускник должен продемонстрировать знание понятия “функция” и умение выполнять с ним различные действия: руководствуясь графиком, описывать свойства и поведение функции; находить наибольшие и наименьшие значения; самостоятельно строить графики.

Пример задачи

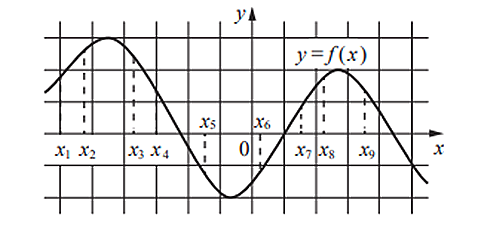
На графике дифференцируемой функции y = f(x) на оси абсцисс отмечены девять точек. Необходимо найти все точки, в которых производная функции f(х) отрицательна.

Решение

Необходимо проследить, в каких местах графика убывает функция: именно там ее производная будет отрицательна. Всего на этом графике 4 таких точки.

Задача №8

Задачи на знание основ стереометрии, простейших геометрических понятий и умение использовать при решении стереометрических задач планиметрические методы.

Пример задачи

В условии даны два цилиндрических сосуда. Уровень жидкости в первом достигает 16 сантиметров. Всю жидкость перелили во второй сосуд, диаметр которого дважды превышает диаметр основания первого. Необходимо определить уровень жидкости во втором сосуде.

Решение

Для вычисления объема цилиндра следует воспользоваться этой формулой: V = πR2H, где R — это радиус цилиндра, а Н — его высота. Так как уровень жидкости поднимается до 16 см, значит, высота также равна 16.

V = πR2H = πR216

Зная о том, что диаметр второго сосуда в два раза больше первого, мы можем сделать вывод, что радиус второго сосуда в два раза больше первого (2R). Вычисляем объем жидкости во втором сосуде: V = π(2R)2h или V = 4R2h

При переливании жидкости из одного сосуда в другой ее объем не изменился.

πR216 = π4R2h

4h = 16

Задача №9

В этом разборе задания очень важно уметь выполнять простейшие вычисления и преобразования, поэтому знание формул просто необходимо.

Пример задачи

Необходимо найти sin2α, если учесть, что cosα = 6, а π < α < 2π

Решение

sin2α = 2sinα х cosα
(sinα)2 + (cosα)2 = 1
(sinα)2 + (0,6)2 = 1
(sinα)2 = 1 — 0,36
(sinα)2 = ±0,8
sinα = –0,8
sin2α = 2 х (–0,8) х (0,6)
sin2α = –0,96

Задача №10

Здесь выпускники демонстрируют умение решать прикладные задачи социально-экономической и физической направленности. Необходимо знать и уметь пользоваться формулами, быть точным в расчетах и внимательным при записи ответа.

Пример задачи

В чемпионате по прыжкам в воду участвуют 35 спортсменов: 7 из России, 12 из Китая, 9 из Японии и 7 из США. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий̆ первым, окажется из России.

Решение

Вероятность определяется, как количество положительных вариантов к количеству всех вариантов. Например, у вас есть 10 монеток и только 2 из них — десятирублёвые, то если вы возьмёте одну монетку, вероятность того, что она будет десятирублёвой, составит

В нашей задаче 35 спортсменов, из которых 7 — из России.

Значит, вероятность того, что первый спортсмен будет из России, составляет:

Ответ: 0.2.

Задача №11

Текстовые задачи с чуть более сложными условиями нужны для того, чтобы экзаменуемый продемонстрировал не только свои знания, но также аналитические способности и умение мыслить логически.

Пример задачи

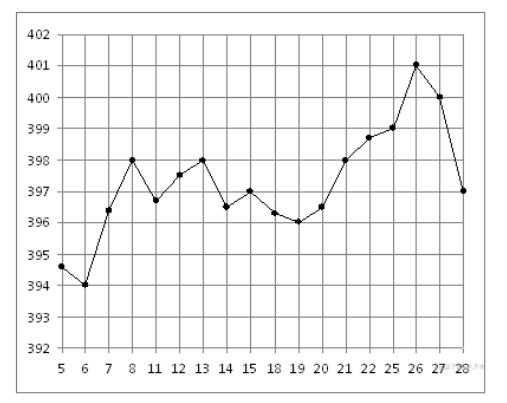
На рисунке жирными точками показана цена золота на момент закрытия биржевых торгов во все рабочие дни с 5 по 28 марта 1996 года. По горизонтали указываются числа месяца, по вертикали — цена унции золота в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа цена золота на момент закрытия торгов была наименьшей за данный период.

Решение

Из графика видно, что наименьшей цена была 6 марта.

Ответ: 6.

Задача №12

12 задача из демоверсии ЕГЭ по математике базового уровня посвящена теме “экстремум”. Здесь необходимо найти производную функции и ее критические точки.

Пример задачи

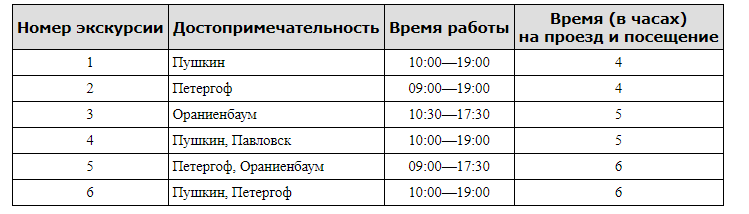
Турист подбирает себе экскурсионную программу. Сведения о некоторых музеях и парках, подготовленные туристическим бюро, представлены в таблице.

Пользуясь таблицей, подберите экскурсионную программу так, чтобы турист посетил не ме-нее трёх достопримечательностей за один день.

В ответе для подобранной программы укажите номера экскурсий без пробелов, запятых и других дополнительных символов.

Решение

У туриста всего 10 часов. Если он выберет шестую экскурсию, то на третью экскурсию времени уже не хватит, а вот если выберет пятую, то вполне успевает и на первую. Та-ким образом, 5 и 1.

При выборе четвертой успевает только на вторую. Таким образом, 4 и 2. При выборе третьей посмотреть три достопримечательности никак не успеет.

Ответ: 1 и 5 или 2 и 4.

Задача №13

Задания из этого раздела демо-варианта ЕГЭ проверяют знание стереометрии. Необходимо знать формулы нахождения площадей разных фигур: прямоугольного параллелепипеда, призмы, пирамиды, куба, цилиндра и т. д.

Пример задачи

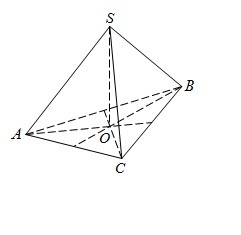
В правильной треугольной пирамиде SABC медианы основания ABC пересекаются в точке O. Площадь треугольника ABC равна 2; объем пирамиды равен 4. Найдите длину отрезка OS.

Решение

Отрезок OS высотой треугольной пирамиды SABC, ее объем выражается формулой

Значит,

Ответ: 6.

Задача №14

Для решения этого задания стоит повторить свойства функций. Необходимо знать, что такое область определения и область значений, экстремальные значения, убывание и возрастание.

Пример задачи

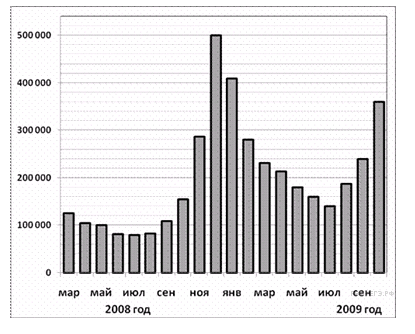
На диаграмме показано количество запросов со словом СНЕГ, сделанных на поисковом сайте Yandex.ru во все месяцы с марта 2008 по октябрь 2009 года. По горизонтали указываются месяцы, по вертикали — количество запросов за данный месяц.

Пользуясь диаграммой, установите связь между промежутками времени и характером изме-нения количества запросов.

ПРОМЕЖУТКИ ВРЕМЕНИ	ХАРАКТЕР ИЗМЕНЕНИЯ КОЛИЧЕСТВА ЗАПРОСОВ
А) Весна 2008 года	1) Количество запросов резко снижалось
Б) Лето 2008 года	2) Количество запросов заметно увеличивалось
В) Осень 2008 года	3) Количество запросов практически не менялось
Г) Зима 2008-2009 года	4) Количество запросов плавно снижалось

Решение

Весной 2008 года количество запросов падало примерно со 120 000 до 100 000.
Летом 2008 года количество запросов изменялось примерно с 82 000 до 80 000.
Осенью 2008 года количество запросов возрастало примерно со 115 000 до 283 000.
Зимой 2008 года количество запросов падало с 500 000 до 280 000.
Таким образом, получаем следующее: A — 4, Б — 3, В — 2, Г — 1.

Ответ: 4321.

Задача №15

Еще одна задача по планиметрии, для решения которой необходимо повторить формулы нахождения площади фигур на плоскости. и основные теоремы.

Пример задачи

В параллелограмме ABCD высота, опущенная на сторону AB, равна 4, AD=8. Найдите синус угла B.

Решение

Ответ: 0,5.

Задача №16

Задача на знание стереометрии. Для ее решения необходимо разбираться в типах пространственных фигур, знать их элементы, а также основные формулы: объем, площадь поверхности и т. д.

Пример задачи

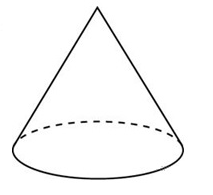
Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.

Решение

Площадь основания конуса равна Sосн = πr2, а площадь боковой поверхности Sбок = πrl. Из условия имеем:

Значит, в прямоугольном треугольнике, образованном высотой, образующей и ра-диусом основания конуса, катет, равный радиусу, вдвое меньше гипотенузы. Тогда он лежит напротив угла 30°. Значит, угол между образующей конуса и плоскостью осно-вания равен 60°.

Задача №17

Решение простейших неравенств. В этом задании необходимо составить математическую модель и прописать, что является здесь переменной x, p и переменной z. Даже если само уравнение решить не получится, за правильно составленную задачу вы сможете получить один балл.

Пример задачи

На координатной прямой отмечены точки A, B, C, и D.

Число m равно log54.

Каждой точке соответствует одно из чисел в правом столбце. Установите соответ-ствие между указанными точками и числами.

ТОЧКИ ЧИСЛА

А) A
Б) B
В) C
Г) D

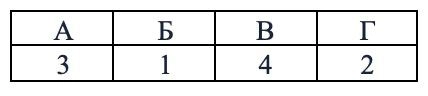
В таблице под каждой буквой укажите соответствующий номер.

Решение

Ответ: 2431.

Задача №18

Выпускникам предлагается решить задачу с параметром, в которой необходимо будет проявить аналитические способности и владение логикой.

Пример задачи

Когда какая-нибудь кошка идёт по забору, пёс Шарик, живущий в будке возле дома, обязательно лает. Выберите утверждения, которые верны при приведённом условии.

1) Если Шарик не лает, значит, по забору идёт кошка.
2) Если Шарик молчит, значит, кошка по забору не идёт.
3) Если по забору идёт чёрная кошка, Шарик не лает.
4) Если по забору пойдёт белая кошка, Шарик будет лаять.

В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Решение

Согласно условию, если кошка идёт по забору, то Шарик лает. Рассмотрим предложенные утверждения:

1. Если Шарик не лает, значит, по забору идёт кошка — неверно, так как, если кошка идёт, то Шарик обязательно лает.
2. Если Шарик молчит, значит, кошка по забору не идёт — верно, так как, если молчит — значит, никакая кошка не идет.
3. Если по забору идёт чёрная кошка, Шарик не лает — неверно, так как, если любая кошка идет по забору — Шарик лает.
4. Если по забору пойдет белая кошка, Шарик будет лаять — верно, согласно условию.

Задача №19

Чтобы решить задание под номером 19 по математике базового уровня, необходимо владеть следующими понятиями: числа и их свойства, числовые последовательности и прогрессии, признаки делимости чисел. В самом задании выпускникам для разбора будет предложена задача.

Пример задачи

Найдите трёхзначное число, сумма цифр которого равна 25, если известно, что его квадрат делится на 16.

Решение

Разложим число 25 на слагаемые: 25 = 9 + 9 + 7 = 9 + 8 + 8.

Квадрат числа делится на 16, значит, само число делится на 4. Это значит, что оно заканчивается на чётную цифру. То есть первый набор отпадает, так как в нём нет четных чисел. Из второго мы можем составить числа 988 и 898. Первое число походит по условия задачи.

Ответ: 988.

Задача №20

Одно из самых интересных заданий заставляет задействовать не только логику, но и смекалку: правильный ответ необходимо найти при помощи рассуждений и внимательного отношения к каждой детали.

Пример задачи

На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 15 кусков, если по жёлтым — 5 кусков, а если по зелёным — 7 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?

Решение

Если распилить палку по красным линиям, то получится 15 кусков, следовательно, линий — 14. Если распилить палку по желтым — 5 кусков, следовательно, линий — 4. Если распилить по зеленым — 7 кусков, линий — 6. Всего линий: 14 + 4 + 6 = 24 линии, следовательно, кусков будет 25.

Ответ: 25.

Таким образом видим, что разбор заданий для подготовки к ЕГЭ не представляет особых трудностей: при желании к экзамену можно как следует подготовиться и сдать его на максимально высокие баллы.