Подготовка к егэ по математике выступление

Методика
подготовки обучающихся к ЕГЭ по математике.

Колосовская Е.В.
учитель математики МОУ СОШ № 3

Хабаровский край
г.Комсомольск-на-Амуре

Единый
государственный экзамен (ЕГЭ) является единственной формой итоговой аттестации
выпускников средней школы. И как бы к нему не относились ЕГЭ приходиться
сдавать всем выпускникам. А с недавних пор получение аттестата о среднем
образовании не возможно без успешной сдачи ЕГЭ по математике. Математика
является не только важным учебным предметом, без которого немыслимо
всестороннее развитие личности, но и весьма сложным. Математическими
способностями обладают далеко не все школьники, а от успешной сдачи экзамена
зависит дальнейшая судьба и технарей и гуманитариев. Эта проблема в равной мере
волнует и учителей и учеников, а также родителей будущих выпускников.

Изменение формы
контроля соответственно ведет за собой необходимость изменения системы
подготовки к успешной сдаче экзамена. Учителя выпускных классов снова и снова
задают вопрос: «Как помочь школьнику при подготовке к ЕГЭ и успешно его
сдать?».

Основным
направлением работы учителя является методическая подготовка к ЕГЭ, которую я
провожу в двух направлениях: тематической и по содержательным линиям курса
математики. Тематическую подготовку начинаю в 10 классе. Перед началом изучения
каждой темы, я обязательно просматриваю задания, которые предлагают авторы
учебника и литературу по подготовке к ЕГЭ, с той целью, чтобы дополнить набор
упражнений учебника, заданиями, которые могут встретиться учащимся на экзамене
по изучаемой теме. Тематическую подготовку выстраиваю «по правилу спирали»,- от
простых к заданиям со звездочкой в учебнике, от комплексных типовых заданий
части 1 до заданий раздела 2 части. В конце изучения параграфа провожу уроки
решения задач ЕГЭ. Это и обычные по форме уроки, и уроки организации работы в
группах, когда каждый учит каждого, т.е. уроки, на которых применяется
технология сотрудничества. Наблюдая за работой на уроке, заметила, что вместе
учиться не только легче и интереснее, но и значительно эффективнее. При разборе
задач у учащихся часто возникают различные вопросы, и оказать каждому помощь на
уроке невозможно, но если ученики работают в группах, они быстрее находят пути
решения и могут оказать друг другу консультативную помощь.

В течении всего
учебного года я провожу с учащимися 10 и 11 классов тренировочные и
диагностические работы ЕГЭ и составляю диагностику по качеству усвоения заданий
в виде диаграммы. Эту диагностику, используя ИКТ, показываю детям в сравнении.
Провожу подробный анализ. По результатам этой диагностики определяю набор тем,
хорошо усвоенных и, так сказать, провальных для всего класса и для каждого
ученика в отдельности. Например, выясняется: учащиеся не выполнили задания из 2
части № 10 и №11. Выясняю причину: дети отвыкли читать большие тексты. Встает
вопрос: «Что делать?». Я даю в начале урока в течение нескольких дней каждому
по одной единственной текстовой задаче типа 11 и 10, на оценку. Тех учеников,
которые выполнили правильно менее половины задач, приглашаю во внеурочное время
на дополнительное занятие, после которого они работают над ошибками.

Для эффективной
подготовки к ЕГЭ использую методику разноуровневого обучения, основанного на
дифференцированном подходе к учащимся. Класс условно делится на три группы. 1
группа — группа «риска» — учащиеся, которые могут не набрать
минимальное количество баллов, подтверждающее освоение общеобразовательной
программы среднего (полного) общего образования.

2 группа —
учащиеся, которые при добросовестном отношении могут набрать балл, достаточный
для поступления в учебное заведение, не предъявляющего высокие требования к
уровню математической подготовки.

3 группа —
учащиеся, которые поставили перед собой цель получить высокий балл, необходимый
для поступления в ВУЗ.

Такое деление на
группы провожу на определенных этапах урока.

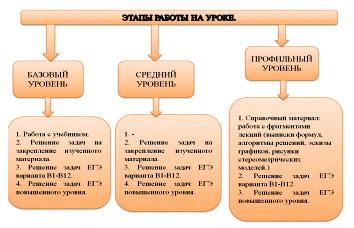
Набор заданий
формирую для каждой группы отдельный: группа 3- минимальное количество заданий
базового уровня, задачи повышенного и высокого уровня сложности, для учеников
группы 2 предлагаю задания базового и повышенного уровней, а для учащихся
группы 1 основную часть составляют задачи базового уровня. Ребята знают, что со
временем можно перейти из одной группы в другую в соответствии с результатами
обучения.

Для каждой группы
можно сформулировать несколько принципов организации подготовки к ЕГЭ.
Учащиеся первой группы должны уверенно выполнить 6-7 заданий 1
части. После проведения диагностических работ, выявляю у каждого сильные и
слабые стороны математической подготовки и закрепляю то, что уже получается. В работе
с учащимися первой группы отрабатываю в первую очередь практико-ориентированные
задачи на проценты, чтение графиков, геометрические понятия, т.к. именно эти
задачи являются для них наиболее понятными.

Выпускникам второй
группы, необходимо уверенно выполнять 8 заданий первой части, а также
стараться выполнить задания 2 части №9 — № 12. Учащиеся этой группы чаще
ошибаются в вычислениях при решении заданий практико-ориентированного
характера, чем в применении алгебраических алгоритмов. Поэтому в работе с
учащимися этой группы в основном ставлю задачу сформировать навыки самопроверки
при выполнении заданий 1 части, повторить темы, необходимые для решения
определенных заданий части 2.

С
выпускниками третьей группы отрабатываю умение уверенно
выполнять задания с 1 по 12 и ориентирую на выполнение заданий № 13,14,15.

Еженедельно в 11
классе провожу консультации по подготовке к ЕГЭ. Вначале занятия кратко
повторяется теоретический материал, остальное время уделяю решению ключевых
задач. Таким образом, базовый уровень получают все, затем использую
дифференцированный подход.

Результаты ЕГЭ по
математике прошлых лет показывают, что к решению заданий 2 части, начиная с
№13, приступает небольшая часть тестируемых. Поэтому, с этой категорией
выпускников провожу отдельные занятия углубленного характера.

Ещё мне хочется
остановиться на системе устных упражнений. Развитие скорости устных вычислений
и преобразований, а также развитие навыков решения простейших задач «в уме»
является важным моментом подготовки ученика к ЕГЭ. Для организации устной
работы на уроке мне помогают информационные технологии, которые способствуют
активизации учебного процесса, развивают познавательный интерес. Я использую
систему презентаций устных упражнений. Презентации незаменимы в тех случаях,
когда задания содержат рисунки и графики, то есть то, что практически
невозможно подготовить перед уроком на доске, а использование интерактивной
доски позволяет на слайде делать необходимые пометки, в случае, если возникают
какие-то вопросы. При этом следует обратить внимание и на упражнения
сопутствующего повторения. Почти все уроки я начинаю с небольшой устной работы,
на которой предлагаю задания по изучаемой теме и задачи на повторение.

Особую роль уделяю
самостоятельной учебной работе ученика в интерактивной среде обучения,
используя готовые электронные учебные курсы, обучающие, тренировочные и
проверочные работы в системе Интернет:

http://reshuege.ru/.
Все задачи открытого банка заданий ЕГЭ по математике с образцами решений.

http://alexlarin.net/.
Материалы прошлых лет. Диагностические и тренировочные работы.

http://ege.ru- это
сайт информационной поддержки ЕГЭ в компьютерной форме. Демонстрационные тесты
по предметам, тесты по психологической готовности к ЕГЭ, онлайн-тесты на выбор
профессии, профильного класса, вуза; демоверсии.

Здесь ученик может
пройти онлайн-тестирование, создать индивидуальный тест для тренировки,
ознакомится с планом экзаменационной работы ЕГЭ по математике .

Сайт содержит
раздел для централизованного контроля уровня подготовки учащихся учителем.
Учитель может сгенерировать неограниченное количество необходимых ему тестов.
Для каждого теста система выдаст индивидуальную ссылку, которую нужно сообщить
учащимся.

Учащиеся (дома или
в школе) вводят полученную ссылку на странице «Ученику» и проходят
тестирование. В зависимости от выбора учителя после окончания тестирования
система сообщит или не сообщит учащимся правильные ответы и решения задач.

Система
автоматически проверяет решения задач части В, а также выводит на экран учителю
загруженные учащимися решения задач части С. Учитель может просмотреть и
оценить их.

Система запоминает
результаты тестирования и выводит их по каждому учащемуся и каждому из тестов
на странице статистики.

http://mathege.ru
. Задания, тренировочные работы, документы.

http://www.fipi.ru/.
Документы, КИМы

http://ege.edu.ru/.
Документы, новости, мероприятия.

http://uztest.ru.
Пробное тестирование учащихся проводится в онлайн-режиме по заданиям,
аналогичным тем, которые будут у выпускников на ЕГЭ, с последующим оцениванием
их ответов.

Использовать для
подготовки учащихся к выполнению заданий С5 и С6 сайт www.problems.ru.

На указанных
сайтах выпускник может получить полную информацию о проведении ЕГЭ,
самостоятельно проверить уровень своей подготовки в режиме он-лайн и
протестировать себя, воспользовавшись интерактивным тестом.

Немаловажную роль
при подготовке к ЕГЭ играет психологическая подготовка учащихся. В первую
очередь работаю над повышением уровня мотивации как основы хороших результатов.

Продолжаю
развивать такие качества личности, как усидчивость, сосредоточенность,
внимательность, способность к самопроверке, самостоятельность.

Необходимо не
допускать нервозности, не нагнетать психоз, но требовать обязательности,
исполнительности, самостоятельности.

Каждый обучающийся
должен иметь адекватное представление об уровне собственной подготовки по
предмету независимо от своих способностей; знать свои пробелы в знаниях и
стремиться их устранить.

Готовлю учащихся к
длительному самостоятельному занятию предметом, требую объяснить каждый шаг
своего решения, выстраивать свои индивидуальные ассоциации по подходам к
решению.

Обязательно учу
стратегии выполнения работы, правильно распределять свое время при выполнении
работы, уметь конкретизоваться на выполнении работы, что достигается
настойчивыми тренировками.

Экзамен не должен
стать для выпускника испытанием на прочность нервной системы. Чем раньше
начнется подготовка к экзамену, тем легче пройдет сдача экзамена.

Основная цель
работы учителя — подготовить всех учащихся к успешной сдаче ЕГЭ с хорошим
качеством.

Подготовка — это
не только натаскивание и отработка заданий прошлых лет, а это готовность
учащихся работать с КИМами, изучение программного материала с включением
заданий текстов и в той форме, что и в ЕГЭ, работа над устранением пробелов в
знаниях, развитие умений рационально организовывать свою деятельность, уметь
ориентироваться во времени, в выборе посильных заданий.

Для этого
необходимо:

Учителю обладать
необходимыми компетенциями.

Совершенствовать
структуру и содержание учебного материала в ходе подготовки к ЕГЭ.

Включать в
изучение текущего учебного материала задания, соответствующие экзаменационным.

На каждом уроке
проводить обязательный устный счет.

Уделять должное
внимание геометрической подготовке

Систематизировать
повторение программного материала.

Организовать
самостоятельную работу по материалам в интернете.

Таким образом,
кропотливая совместная работа учителя и учеников способна повысить
математическую грамотность школьников и дать возможность успешно сдать ЕГЭ.

13.12.2019

Выступление на педсовете «Подготовка к ЕГЭ по математике (обмен опытом)» Дергачев А. Н.

Единый государственный экзамен (ЕГЭ) является единственной формой итоговой аттестации выпускников средней школы. И как бы к нему не относились ЕГЭ приходиться сдавать всем выпускникам. Получение аттестата о среднем образовании невозможно без успешной сдачи ЕГЭ по математике. Математика является не только важным учебным предметом, без которого немыслимо всестороннее развитие личности, но и весьма сложным. Математическими способностями обладают далеко не все школьники, а от успешной сдачи экзамена зависит дальнейшая судьба и технарей, и гуманитариев. Эта проблема в равной мере волнует и учителей, и учеников, а также родителей будущих выпускников.

Я готовлю учащихся к ЕГЭ по математике уже шестой год. Наработан определённый опыт в этой области. Хотелось бы поделиться этим опытом со своими коллегами.

В основу программы подготовки к ЕГЭ должны быть положены следующие концептуальные положения: личностный подход, педагогика успеха, педагогика сотрудничества. Необходимо индивидуализировать обучение «трудных» и «одаренных».      Обязательна органическая связь индивидуальной и коллективной деятельности.

Подготовленность к чему-либо понимается как комплекс приобретенных знаний, навыков, умений, качеств, позволяющих успешно выполнять определенную деятельность. В готовности учащихся к сдаче экзамена в форме ЕГЭ можно выделить следующие составляющие:

• информационная готовность (информированность о правилах поведения на экзамене, информированность о правилах заполнения бланков и т.д.);

• предметная готовность или содержательная (готовность по определенному предмету, умение решать тестовые задания);

• психологическая готовность (состояние готовности — «настрой», внутренняя настроенность на определенное поведение, ориентированность на целесообразные действия, актуализация и приспособление возможностей личности для успешных действий в ситуации сдачи экзамена).

Ориентируясь на данные компоненты, актуальными вопросами в подготовке к ЕГЭ по математике являются следующие:

• организация информационной работы по подготовки учащихся к ЕГЭ;

• содержательная подготовка;

• мониторинг качества.

Информационная работа

Подготавливаются материалы ЕГЭ по математике: демонстрационный вариант КИМ, инструкция по выполнению работы, инструкция по заполнению бланков, спецификация экзаменационной работы по математике единого государственного экзамена, методические особенности подготовки к сдаче ЕГЭ по математике (рекомендации для выпускников), график консультативных занятий по подготовке к ЕГЭ, список литературы и адреса сайтов.

Содержательная подготовка

Зачастую учителя, репетиторы и родители, помогающие своим детям подготовиться к ЕГЭ, пытаются прорешать как можно больше вариантов предыдущих лет. На мой взгляд, такой путь неперспективен. Во-первых, варианты не повторяются. Во-вторых, у школьника не формируется устойчивый общий способ деятельности с заданиями соответствующих видов. В-третьих, у детей появляется чувство растерянности и полной безнадежности: заданий так много и все они такие разные. И каждый раз нужно применять соответствующий подход. Естественно, запомнить решения всех заданий невозможно, поэтому намного разумнее учить школьников общим универсальным приемам и подходам к решению.

Сформулируем принципы построения методической подготовки к ЕГЭ.

• Первый принцип — тематический. Эффективнее выстраивать такую подготовку, соблюдая принцип от простых типовых заданий к сложным.

• Второй принцип — логический. На этапе освоения знаний необходимо подбирать материал в виде логически взаимосвязанной системы, где из одного следует другое. На следующих занятиях полученные знания способствуют пониманию нового материала.

• Третий принцип — тренировочный. Для эффективной подготовки к ЕГЭ нужна тренировка, тренировка и еще раз тренировка. Необходимо довести решение задач до автоматизма. На уроках и консультациях учащимся предлагаются тренировочные тесты, выполняя которые дети могут оценить степень подготовленности к экзаменам.

• Четвёртый принцип — индивидуальный. На моих уроках ученик может не только выполнить тест, но и получить ответы на вопросы, которые вызвали затруднение.

• Пятый принцип — временной. Все тренировочные тесты следует проводить с ограничением времени, чтобы учащиеся могли контролировать себя — за какое время сколько заданий они успевают решить.

• Шестой принцип — контролирующий. Максимализация нагрузки по содержанию и по времени для всех учащихся одинакова. Это необходимо, поскольку тест по своему назначению ставит всех в равные условия и предполагает объективный контроль результатов.

Следуя этим принципам, формирую у учеников навыки самообразования, критического мышления, самостоятельной работы, самоорганизации и самоконтроля.

Моя цель состоит в том, чтобы помочь каждому школьнику научиться быстро решать задачи, оформлять их чётко и компактно. Развиваю способность мыслить свободно, без страха, творчески. Стараюсь давать возможность каждому школьнику расти настолько, насколько он способен. Общеизвестно, что даже небольшие пробелы в знаниях ведут к существенным потерям в баллах. Но очень часто выпускники, хорошо успевающие по математике, но совершенно не подготовленные к ЕГЭ психологически, также не получают высоких баллов. Приступая к работе по подготовке к ЕГЭ, учителю, прежде всего, надо сломить сопротивление и неуверенность учащихся. Именно поэтому перед нами встает задача – определить возможные направления психолого-педагогической работы с учащимися по снятию напряжения и страха перед тестированием, рассказать о тех методах и приемах самоорганизации, которые помогут ученику актуализировать свои знания в процессе тестирования. А для этого, прежде всего, каждый должен определить степень обученности каждого ученика и класса в целом на данный момент. Здесь же мы не должны забывать и об обучаемости каждого ученика. Я получаю необходимую информацию с помощью системы тестов, фронтальной работы, устных опросов и т.д. Предварительную проверку сочетаю с так называемым компенсационным обучением, направленным на устранение пробелов в знаниях и умениях.

Я убежден, что преподавание математики в целом, и подготовка к ЕГЭ, в частности, выполнят свое предназначение только в том случае, когда дадут ученику необходимый объем информации и технических навыков, но и помогут ему овладеть культурой математических рассуждений, т.е. научат его самостоятельно пользоваться математическими методами и методами самоорганизации и самоконтроля. А учитель получит удовлетворение только в том случае, если он передаст ученику не просто знания, но и разовьет гибкость его мышления и обеспечит психологическую готовность к различным испытаниям, в том числе и к ЕГЭ.

Психологическая подготовка

• следует работать над повышением уровня мотивации в первую очередь;

• необходимо работать над такими качествами как усидчивость, сосредоточенность, внимательность, способность к самопроверке;

• следует приучать учащихся работать самостоятельно;

• необходимо не допускать нервозности, не нагнетать психоз, но требовать обязательности, исполнительности, самостоятельности;

• каждый ученик должен иметь адекватное представление об уровне собственной подготовки по предмету независимо от своих способностей; знать свои пробелы в знаниях и стремиться их устранить;

• быть готовым к длительному самостоятельному занятию предметом, уметь объяснить каждый шаг своего решения, выстраивать свои индивидуальные ассоциации по подходам к решению, вносить дополнения в свой индивидуальный справочник(блокнот);

• обязательно нужно учить стратегии выполнения работы, правильно распределять своё время при выполнении работы, уметь концентрироваться на выполнении работы, что достигается настойчивыми тренировками.

Экзамены представляют собой нелёгкую, но неизбежную часть нашей жизни. Одни воспринимают экзамены достаточно легко и идут на них, уверенные в успехе. У других экзамен и оценки за него тесно связаны с беспокойством и тревогой. Они не только накануне экзамена, но иногда лишь при мысли о нем испытывают состояние страха, неуверенности в себе, тревоги. Каждый ребенок по своей природе индивидуален и обладает целым рядом особенностей: спецификой мышления, памяти, внимания, темпом деятельности, личностными особенностями, учебной мотивацией и т.д.

Подготовка к ЕГЭ по математике требует индивидуального, личностно — ориентированного подхода. Для реализации такого подхода в рабочую программу включаю темы уроков по подготовки к ЕГЭ. Кроме того провожу консультации. Для организации разноуровневого обучения и обобщающего повторения разделяю класс на 2 группы.

1 группа — база.

2 группа — профиль.

Для каждой группы можно сформулировать несколько принципов организации подготовки к ЕГЭ.

Учащиеся первой группы должны уверенно выполнить 7-20 заданий. Выпускникам второй группы, необходимо уверенно выполнять №1-12 и ориентирую на выполнение заданий №13,14,15

Для реализации принципа дифференциации мною собран банк упражнений презентаций по определенным заданиям первой и второй частей контрольно-измерительных материалов с образцами решений, рекомендациями по их выполнению. Ежемесячно провожу проверку вычислительных навыков, начиная с простейших математических действий: сложения, вычитания, умножения и деления.

Уделяю внимание технике выполнения экзаменационной работы:

• обучение постоянному жесткому контролю времени;

• обучение оценке объективной и субъективной трудности заданий и, конечно, разумному выбору этих заданий;

• обучение прикидке границ результатов и минимальной подстановке как приёму проверки, проводимой сразу после решения задания.

Для того, чтобы наилучшим образом подготовиться к ЕГЭ по математике, надо иметь не только хорошие знания по предмету, но также хорошо представлять себе структуру экзаменационной работы, процедуру экзамена, знать какие и когда действия при этом происходят.

За время подготовки учащихся к ЕГЭ я пришёл к выводу, что необходимо начинать готовить детей к экзамену как можно раньше.

Проанализировав содержание вариантов по ЕГЭ, можно сделать вывод, что часть 1 содержит порядка 70% материала, который прямо или косвенно формируется в основной школе, а также параметрический и геометрический материал во 2 части. В связи с этим уже в основной школе необходимо начинать подготовку по таким разделам:

а) действительные числа и действия с ними;

б) степенные выражения и их преобразования;

в) свойства арифметического корня;

г) функции и их свойства;

д) уравнения, неравенства и их системы;

е) решение текстовых задач на проценты;

ж) арифметическая и геометрическая прогрессии;

з) решение комплексных задач по геометрии.

Необходимо с 5-го класса внедрять в учебный процесс разноуровневые тематические тесты.

А теперь расскажу, как я решаю поставленные задачи. С чего я начинаю эту работу.

Во-первых, с первых же дней учёбы убеждаю детей в том, что если очень постараться, то можно получить вполне приличный балл. Главное не упустить время.

Во-вторых, в течение всего учебного года знакомлю детей с материалами ЕГЭ. Устный счёт на каждом уроке строю только на основе упражнений ЕГЭ. Кроме этого, систематически на уроках каждому раздаю тест ЕГЭ. Прошу ребят найти в тесте те задания, с которыми они могут справиться уже сегодня и решить их. Стараюсь выслушать все подходы к решению каждой задачи и только потом раскрываю секрет, как можно было решить задачу рациональнее, чтобы сэкономить время.

В-третьих, когда уже удалось заинтересовать детей, знакомлю их с особенностями формы итоговой аттестации: со структурой теста, временными рамками, нормами оценивания экзаменационной работы, условиями проведения экзамена и начинаю обучать «технике сдачи теста»:

• обучаю строгому самоконтролю времени;

• учу определять трудность заданий;

• знакомлю с приёмом «прикидки» результата подстановкой;

• знакомлю с приёмом «спирального движения по тесту».

• самопроверке;

• разумного выбора ответа;

• сравнения, угадывания;

• различным «хитростям» быстрых вычислений

Говорю ученикам, чтобы успешно выполнить тест, на каждое задание первой части надо затрачивать не более двух, трёх минут.

Как учу определять трудность заданий? Сначала прошу учеников просмотреть тест от начала до конца и отметить карандашом те задания, которые кажутся им простыми и лёгкими и выполнить их в «режиме скорости». Затем, отметить 2-3 задания, которые им понятны по формулировке, но требуют большего времени и выполнить их; и только после этого, если останется время, можно поразмышлять над остальными.

Обязательно напоминаю о том, что полученный результат можно проверить подстановкой, т. е. «прикинуть» имеет ли он смысл. Двигаясь по тесту, дети знают, что сложность заданий нарастает, поэтому всегда советую настойчиво и добросовестно отрабатывать первую часть, только затем можно приступать ко второй части – это и есть принцип «спирального движения» по тесту. По результатам достижений сам определяю двух, трёх учеников, которых можно подготовить к выполнению более сложных заданий и работаю с ними индивидуально.

Практика показывает, что при выполнении заданий базового и повышенного уровня выпускники допускают много вычислительных ошибок. Для их устранения уже в 5, 6 классах отрабатываю навыки действий с десятичными и обыкновенными дробями, положительными и отрицательными числами, обязательно требую учить наизусть правила, отрабатываю их и повторяю при каждом возможном случае и при устном счёте, которому уделяю особое внимание.

Ещё одна составляющая – выполнение вариантов ЕГЭ, сгенерированных с помощью специальных программ (генератор вариантов на сайте «Решу ЕГЭ», «alekslarin.net»), демоверсий текущего года, варианта пробного экзамена, работа по сборникам «Варианты ЕГЭ» текущего года.

На уроках математики при подготовке к ЕГЭ очень важно применение ИКТ. Возможности компьютера могут быть использованы в предметном обучении в следующих вариантах:

• использование диагностических и контролирующих материалов;

• выполнение домашних самостоятельных и творческих заданий;

• использование компьютера для вычислений, построения графиков;

• создание уроков с помощью программы “PowerPoint”

Поскольку наглядно-образные компоненты мышления играют исключительно важную роль в жизни человека, то использование их в изучении материала с использованием ИКТ повышают эффективность обучения:

Памятка выпускнику.

В день экзамена

Успокойся!

В этом поможет простое дыхательное упражнение: закрой глаза и дыши медленно, глубоко. Выдох должен быть в 2-3 раза продолжительнее, чем вдох. При этом не забывай про себя думать: «Я спокоен и уверен в себе!», «Я всё помню!».

Поставь цель!

Пусть достижения не всегда совпадают с идеалом, зато они твои личные.

Сосредоточься!

Забудь об окружающих. Для тебя существуют только задания экзаменационной работы и время, отведенное на выполнение теста.

Распредели своё время!

Запланируй «два круга» для решения заданий и время для проверки. Две трети всего времени отведи легким заданиям. Далее сосредоточься на более сложных заданиях.

Торопись не спеша!

Задания необходимо читать внимательно и до конца.  Жесткие рамки времени не должны влиять на качество твоих ответов. Перед тем, как оформить ответ в бланке, перечитай вопрос и убедись – правильно ли ты понял задание, что поможет избежать обидных ошибок.

Начни с легкого!

Пробегись глазами по всем заданиям экзаменационной работы. Выбери наиболее легкие и начинай отвечать на них. Таким образом, ты освободишься от нервозности и быстрее вникнешь в более трудные вопросы.

Пропускай!

Специалисты рекомендуют пропускать трудные или непонятные задания. К ним можно вернуться позже. 

Думай только о текущем задании!

Создатели контрольных измерительных материалов стараются охватить весь объем школьной программы. Поэтому вопросы в тестах не связаны друг с другом. Принцип решения одной задачи не поможет в ответе на другой.

Исключай! Форма проведения ЕГЭ (тестирование) даёт определённые преимущества. Среди заданий Части А и В есть вопросы с четырьмя вариантами ответов. Среди них один правильный. Следует помнить, что некоторые задания быстрее решить методом исключения.

Угадывай!

Бывают вопросы, в ответах на которые абитуриент не до конца уверен. Отвечай интуитивно! При этом выбирай ответ, который, на твой взгляд, имеет большую вероятность.

Не бойся ошибок!

Известно, что не ошибается только тот, кто ничего не делает. Тестовые задания рассчитаны на максимальный уровень трудности. Задания решают разные выпускники, в том числе, учащиеся профильных классов. На практике трудно набрать максимальное количество баллов. Главное, набрать баллы выше минимального порога.

Приложение 2.

Семь заповедей педагога

1) Не пытаться тянуть ученика до уровня, выходящего за пределы его способностей.

Каждый человек имеет определенный резерв возможностей в силу особенностей своего мышления и памяти.

2) Не проводить занятие без подготовки.

Перед занятием я просматриваю учебники, дидактические материалы, изучаю динамику ошибок в тетрадях и составляю индивидуальный комплект упражнений именно для данной учебной ситуации.

3) Не нужно мешать ученику думать.

Если школьник сконцентрирован — это всегда видно. При неумелом владении искусством невмешательства в мыслительный процесс педагог по математике будет только отвлекать ребенка от размышлений над понятиями, формулами и преобразованиями. Помощь должна поступать именно в тот момент, когда ученик в ней нуждается, а не тогда, когда, когда он готов решить задачу самостоятельно.

4) Не «навредить» ученику.

Математика допускает разные пути решения задач, разную их подачу, разные обоснования этих решений и разные оформления. Дезориентировать и запутать ученика проще пареной репы.

5) Не пропускать ни один вопрос ученика

Если ребенок что-то задумал спросить — нужно обязательно дать ему эту возможность (не перебивать его) и помочь сформулировать мысль. Вопрос ученика — сигнал для учителя математики. И тревожный, и позитивный одновременно. Тревожный симптом в том, что ребенок чего-то не понимает.

6) Не повышать голос на ученика и не ругать его.

Криком никто никогда ничего не добивался. К месту будет отметить, что человеческое ухо больше чувствительно к частоте звука, чем к его амплитуде и уровню. Интонация преподавателя, с которой он ведет занятия, вибрации и динамика тона позволяют не только заострять внимание и концентрироваться ученику, но выделять из общего потока слов самые важные.

7) Не выполнять за ученика ту работу, которую он должен сделать самостоятельно.

Иначе ребенок не получит должную умственную нагрузку и не разовьет навыки.

ФКОУ СОШ УФСИН России по Томской области

Доклад на тему:

«Эффективные методы подготовки выпускников

к сдаче ГИА по математике»

Из опыта работы

Чунарёвой О.К.- учителя математики

высшей квалиф.категории

Томск, 2019г.

          Возрастание роли математики в современной жизни привело к тому, что для адаптации в современном обществе и активному участию в нем необходимо быть математически грамотным человеком. В связи со стратегическими направлениями социально-экономического развития России до 2020 года: «Приоритетной государственной задачей является обеспечение качественного базового уровня математических и естественнонаучных знаний у всех выпускников школы, не только будущих ученых, но и будущих квалифицированных рабочих…»

          Каждый школьник в процессе обучения должен иметь возможность получить полноценную подготовку к выпускным экзаменам.

          Формула успеха хорошо сдать экзамен по математике:

Высокая степень восприимчивости + мотивация + компетентный педагог.

          В любом случае натаскивание на варианты ГВЭ и ЕГЭ необходимо, но его нужно сочетать с фундаментальной подготовкой, формируя системные знания и навыки. В готовности учащихся к сдаче экзамена в форме ЕГЭ и ГВЭ можно выделить следующие составляющие:

—информационная готовность;

—предметная готовность;

—психологическая.

         Ориентируясь на данные компоненты, актуальными вопросами в подготовке к экзамену являются следующие:

1. Организация информационной работы:

— по подготовке учащихся к экзамену в форме инструктажа (содержание — правила поведения на экзамене; правила заполнения бланков);

— информирование родителей о процедуре ЕГЭ и ГВЭ, особенностях подготовки к тестовой форме сдачи экзаменов. Информирование о ресурсах Интернет;

— информирование о результатах пробного внутри школьного диагностического тестирования;

— индивидуальное консультирование родителей.

2. Психологическая подготовка к ГВЭ и ЕГЭ.

         Состояние готовности – «настрой», внутренняя настроенность на определенное поведение, ориентированность на целесообразные действия, актуализация и приспособление возможностей личности для успешных действий в ситуации сдачи экзамена.

         Являясь классным руководителем учащихся 9 класса, провожу внеклассные мероприятия, которые помогают преодолеть страхи учеников перед ГВЭ и правильно подготовиться к экзамену. Как можно заставить ребенка поверить в свои силы, в то, что всегда есть надежда на разрешимость любой ситуации? Да просто показать ему то, что данные задания он способен выполнить, если будет использовать определенный алгоритм или логические рассуждения. На занятиях стараюсь создать атмосферу комфортности, взаимопонимания. На своих уроках я делаю установку на то, чтобы любой ребенок должен быть понят и услышан учителем и соучеником: учение должно проходить в «атмосфере непринужденности, чтобы дети и учитель свободно дышали на уроках». От учителя требуется и мастерство, и большое терпение, и любовь к учащимся. Доброжелательное отношение к ученикам снимает у них страх перед трудностями обучения: ребенок не должен бояться ошибиться, спросить учителя, если он что-то прослушал или не понял. Психологическая подготовка учащихся, может заключается в следующем: отработка поведения в период подготовки к экзамену; обучение навыкам само регуляции, самоконтроля, повышение уверенности в себе, в своих силах. Методы проведения занятий по психологической подготовке учащихся разнообразны: групповая дискуссия, игровые методы, медитативные техники, анкетирование, мини-лекции. Содержание занятий должно ориентироваться на следующие вопросы: как подготовиться к экзаменам, поведение на экзамене, способы снятия нервно-психического напряжения, как противостоять стрессу. Работа с учащимися проводится по желанию учащихся – со всем классом или выборочно.

3. Организация работы по предмету:

 Организация правильной, ответственной самоорганизации у обучающегося:

— ведение отдельной тетради для прорешивания тестовых заданий ОГЭ или ЕГЭ;

— справочника, который мы начинаем вести с восьмого класса, записывая и повторяя основные формулы и правила по математике, алгебре и геометрии;

— наличие сборников разных авторов для самостоятельной подготовки к экзамену (например — 8 и 10 классы уже должнырешать задачи из сборников)

 Устный счет – один из важных приемов при подготовке учащихся к ЕГЭ и ОГЭ по математике. В связи с введением обязательного ЕГЭ и ОГЭ по математике возникает необходимость научить учащихся решать быстро и качественно задачи базового уровня. При этом необыкновенно возрастает роль устных вычислений, так как на экзамене не разрешается использовать калькулятор и таблицы. Можно научить учащихся выполнять простейшие (и не очень) преобразования устно. Конечно, для этого потребуется организовать отработку такого навыка до автоматизма, на каждом уроке необходимо отводить 5-7 минут для проведения упражнений устных вычислений, предусмотренных программой каждого класса.

Устные упражнения активизируют мыслительную деятельность учащихся, требуют осознанного усвоения учебного материала; при их выполнении развивается память, речь, внимание, быстрота реакции.        

Если в 5-6 классах устный счет – это выполнение действий с числами: натуральные числа, обыкновенные дроби, десятичные дроби, то в старших классах – это могут быть:

7 класс:

 Формулы сокращенного умножения. Решение простейших ЛУР. Действия со степенью. График линейной функции.

8 класс:

 Линейные неравенства и числовые промежутки. Решение простейших линейных неравенств. Решение КВУР с помощью теоремы Виета и частных случаев.  Решение КВУР рациональными способами. Арифметический квадратный корень и его свойства.

9 класс: Решение неравенств 2 степени. Преобразование графиков функций. Формулы приведения. Значения тригонометрических функций.

10-11 классах:

Вычисление производных. Простейшие тригонометрические неравенства.  Тригонометрические формулы. Простейшие тригонометрические уравнения.  Функции, обратные тригонометрическим. Преобразование графиков функций. Вычисление первообразных. Свойства логарифмов. Простейшие показательные уравнения и неравенства. Простейшие логарифмические уравнения и неравенства.

          Практика показала, что систематическая работа с устным счетом  способствует значительному повышению продуктивности вычислений и преобразований. Сокращается время на выполнение таких операций, что  переводит их из разряда самостоятельной задачи в разряд вспомогательной и становится инструментом (“таблицей умножения”) для решения более сложных задач.              

          Учитель по математике, знающий, с чем придется столкнуться школьнику на экзамене, кроме фундамента уделяет большую часть времени на занятии отработке вопросов специфики ЕГЭ и ОГЭ.

        Правильность оформления заданий, тактика и стратегия решения в условиях дефицита выделенного времени на экзамене, а также банальная невнимательность. Эти и масса других особенностей составляют суть специфики.

         Для эффективной подготовки к ЕГЭ и ОГЭ нужна тренировка, тренировка и еще раз тренировка. Довести решение задач до автоматизма.

Применение ИКТ на уроках математики при подготовке к ГИА.

          Поскольку наглядно-образные компоненты мышления играют исключительно важную роль в жизни человека, то использование их в изучении материала с использованием ИКТ повышают эффективность обучения:

— графика и мультипликация помогают ученикам понимать сложные логические математические построения;

– повышение мотивации учащихся;

– экономия времени при выполнении заданий;

– формированию навыков самоконтроля, взаимоконтроля и самообучения;

– включению у учащихся всех каналов восприятия информации.

          Использую  интернет-ресурсы, открытый банк математических задач, обеспечивающий цель поддержки работы учителя и самостоятельной работы учащихся по подготовке к сдаче экзамена.

        Мониторинг качества.

        Особое внимание в процессе деятельности по подготовке учащихся к ЕГЭ и ОГЭ занимает мониторинг качества обученности по предмету. Мониторинг – отслеживание, диагностика, прогнозирование результатов деятельности. Мониторинг качества должен быть системным и комплексным. Он должен включать следующие параметры: контроль текущих оценок по предмету, оценок по контрольным и самостоятельным работам, результаты пробного внутри школьного диагностического тестирования в форме ЕГЭ и ГВЭ. Учитель анализирует их, выносит на обсуждение, доводит до сведения родителей. Мониторинг обеспечивает возможность прогнозирования оценок на выпускном ЕГЭ и ГВЭ.

       Использование дифференцированного подхода при подготовке к ЕГЭ.

       На каждого ученика 11 класса есть мониторинг выполнения диагностических работ по каждому заданию. Для организации подготовки школьников к экзамену по результатам первой диагностической работы определены 3 группы учащихся:

первая группа – учащиеся, которые поставили перед собой цель – преодоление нижнего рубежа;

вторая группа – учащиеся, которые поставили перед собой цель – сдать экзамен на оценку «4».

третья группа – учащиеся, которые поставили перед собой цель – получить высокие баллы.

Для каждой группы были определены принципы организации подготовки к ЕГЭ.

Первая группа. Для этой группы необходимо преодолеть рубеж 6 баллов. Выявляем сильные и слабые позиции математической подготовки каждого и работаем с сильными позициями (закрепляем то, что уже получается), добавляя посильные задания из слабых позиций.

 Цель такой работы – отработать решение выбранных заданий и вселить уверенность в учащихся, что нижний рубеж им по силам.

Вторая группа. Для этой группы необходимо уверенно получить 12-16 баллов. Работаем со слабыми позициями, постоянно держа под контролем сильные позиции выполнением соответствующих задач (добиваемся выполнения того, что не получается). Цель работы – сформировать навыки самопроверки и добиться устойчивого результата (на уровне ожидаемого) по работе с задачами в которых ученик более успешен, повторить темы, дающие возможность решения наиболее сложных заданий.

Третья группа. Для этой группы вырабатываем умение уверенно выполнять задания части 2,чтобы набрать 17-20 баллов.  Регулярно решаем, задания, развивающие творческие способности учащихся к решению задач повышенного уровня сложности. Цель работы — сформировать умения и навыки, позволяющие получить наивысшие баллы.

При дифференцированной работе каждый ученик имеет возможность овладевать учебным материалом в зависимости от его способностей и индивидуальных особенностей

Принцип Парето: «20% усилий дают 80% результата, а остальные 80% усилий — лишь 20% результата». Как же не распыляться и направить 20% усилий в нужное русло и достигнуть 80% результата? Предлагаю инструкцию:

1. Поставь цель – какой балл ты хочешь получить по экзамену?
2. Пройди пробный экзамен и посмотри, сколько баллов ты набрал, и сколько тебе не хватило.
3. Определи, какие задания ты:
a)  всегда решаешь,
b)  решаешь, но иногда допускаешь ошибки,
c)  обычно не решаешь, но уверен, что сможешь быстро и легко в них разобраться.
4. Тренировка по типам заданий, которые ты отметил в пунктах b) и с), а так же не забывай повторять задачи из пункта a).

         Мы работаем в простой школе, наши ученики имеют средние учебные возможности и понятно, что без прочного усвоения базовых знаний детьми невозможно дальнейшее обучение. Уделяю внимание технике выполнения экзаменационной работы:

В своей работе применяю следующие принципы для эффективной подготовки к ГИА:

1. Эффективнее выстраивать такую подготовку, соблюдая принцип от простых типовых заданий к сложным.

2. На этапе освоения знаний необходимо подбирать материал в виде логически взаимосвязанной системы, где из одного следует другое.

3. На консультациях учащимся предлагаются тренировочные тесты, выполняя которые дети могут оценить степень подготовленности к экзаменам.

4. На консультациях ученик может не только выполнить тест, но и получить ответы на вопросы, которые вызвали затруднение.

5. Все тренировочные тесты следует проводить с ограничением времени, чтобы учащиеся могли контролировать себя — за какое время сколько заданий они успевают решить.

6. Максимализация нагрузки по содержанию и по времени для всех учащихся одинаково. Это необходимо, поскольку тест по своему назначению ставит всех в равные условия и предполагает объективный контроль результатов.

            Следуя этим принципам, формирую у учеников навыки самообразования, критического мышления, самостоятельной работы, самоорганизации и самоконтроля.

             Моя цель состоит в том, чтобы помочь каждому школьнику научиться быстро решать задачи, оформлять их чётко и компактно. Развиваю способность мыслить свободно, без страха, творчески. Стараюсь давать возможность каждому школьнику расти настолько, насколько он способен.

              Литература:

1. Бабанский Ю.К. Активность и самостоятельность учащихся в обучении / М.Ю. Бабанский — М., Педагогика, 1989.
2. Беспалько В.П. Слагаемые педагогической технологии / Беспалько В.П. – М., 1989.
3. Красновский Э.А. Активизация учебного познания / Красновский Э.А. // Советская педагогика. – 1989. — №5.
4. Эльконин Д. Б. Избранные педагогические труды. / Под ред. В.В. Давыдова, В.П. Зинченко.-М., 1989.
5. Щукина Г.И. Активизация познавательной деятельности в учебном процессе/ Щукина Г.И. — М., 1979.
6. http://nsportal.ru/shkola/algebra/library/2015/02/08/podgotovka-uchashchikhsya-k-ege-i-oge-po-matematike
7. http://youclever.org/matematika/effektivnaya-podgotovka-k-ege/
8. https://infourok.ru/sistema-raboti-uchitelya-matematiki-po-podgotovki-k-ege-i-oge-748992.html

Организационные формы работы при подготовке к ЕГЭ по математике

Выполняя заказ государства по подготовке и проведению ЕГЭ, мы вынуждены работать в предложенных обстоятельствах. Для этого необходимо грамотно спланировать работу на всех ступенях обучения, со всеми категориями учащихся. Одним словом, научить школьника математике и подготовить к успешному написанию ЕГЭ по математике – это две абсолютно разные вещи. Думаю, что это осознал каждый учитель, и каждый встал перед вопросом: «С чего начать?».

Ежегодно, на первом занятии я провожу анкетирование учащихся класса. В начале подводим итоги прошлого года, формулируем задачи на текущий: чему хочу научиться, что предстоит для этого сделать, прогнозируемые итоги, куда буду поступать (основной и запасные варианты), в каком настроении начинаю год? В этом году, в 11 классе планирую добавить вопрос: сколько денег своей семье я смогу сэкономить, если поступлю на бюджет?

Теперь предлагаю рассмотреть модель подготовки к ЕГЭ по математике (слайд 2), которая включает все возможные формы организации деятельности обучающихся: урок, дополнительные занятия, система консультаций, проектная деятельность, МАН, использование ИКТ и т.д.

В условиях обязательной для всех выпускников сдачи экзамена по математике в формате ЕГЭ приходится по-иному подходить к подготовке и проведению уроков, учитывая необходимость обеспечить овладение всеми школьниками учебным материалом не только на запланированном (базовом или профильном) уровне, но и дать возможность мотивированным учащимся заинтересованным в получении высоких баллов для поступления в вуз, динамично продвигаться в овладении материалом на повышенном и высоком уровне.

При проведении уроков приходится активнее включать в учебный процесс дифференцированное обучение, использовать практические разработки по индивидуализации обучения. Теперь уже недостаточно привычных обобщения и систематизации знаний и способов действий. Не менее важным является необходимость формирования у выпускников умений: быстро переключиться с одного типа задания на другой; выбирать оптимальную стратегию при решении как одной задачи, так и всей работы в целом; проверять полученный результат решения.

Основной характеристикой методики проведения занятий является активизирующее воздействие на обучаемых: систематическое убеждение их в том, что лишь при активной позиции по отношению к данному предмету — можно рассчитывать на успех.

Слайд 3 представляет

видение данного процесса.

На мой взгляд, целенаправленно готовить учащихся к ЕГЭ необходимо уже с пятого класса.

Так, анализируя кодификатор и спецификацию заданий ЕГЭ, я пришла к выводу о том, что задачи В1, В3 вполне можно предложить ученикам 5-го класса. (Слайды 4, 5).

В шестом к этим заданиям добавляются В2 и частично В5. (Слайд 6).

Серьезное внимание нужно уделить обучению в 7 классе, где необходимо до автоматизма отработать применение формул сокращенного умножения, решение линейных уравнений, содержащих модуль и параметры. (Слайд 7).

В 8 классе – отработать В4, В12 (слайд .

В 9 классе В10, В12, С4, расширять использование задач с модулями и параметрами (слайд 9).

В 10 классе – В7, В8, В11, В14, С1, С2 (слайд 10).

Тогда к 11 классу мы подходим с надежным багажом знаний и можем сосредоточиться на подготовке к решению задач В5, В7, В9, С2, С3, С5, С6, С7 (слайд 11).

Возвращусь к организации учебного процесса на старшей ступени. В начале учебного года провожу диагностику учащихся 10-11 классов для установления уровня остаточных знаний и степени усвоения программного материала через проведение административных тренировочных и диагностических работ. Параллельно составляются справочники по изученной ранее теории (слайд12).

После проведения административных, тренировочных и диагностических работ заполняю диагностическую карту подготовки к ЕГЭ, проанализировав результаты учащихся, вырабатываю стратегию организации разноуровневого обобщающего повторения параллельно с изучением нового материала.

Немаловажным считаю развитие у учащихся навыков самоанализа и самоконтроля. Считаю, что этому учащихся надо обучать, начиная с 5-го класса при проведении анализа самостоятельных и контрольных работ.

На третьей ступени обучения необходимо использовать и еще один ресурс подготовки к единому государственному экзамену – дополнительные занятия по подготовке к ЕГЭ. В выпускных классах обязательно еженедельно провожу такие двухчасовые занятия.

Сопутствующей, однако, не менее эффективной, считаю и организацию исследовательской и проектной деятельности учащихся при подготовке к ЕГЭ.

Учебные проекты сочетаются с традиционной системой предметного классно-урочного обучения, дополняют её, позволяют отрабатывать межпредметные связи и вместе с этим работают на повышение качества образования. Метод проектов способствует развитию основных компетенций: информационных, коммуникационных, учебно – познавательных. Проекты, имеющие наибольшую практическую значимость, использую для подготовки к ЕГЭ по определённым темам.

Стоит отметить так же, что использование компьютерных технологий в обучении расширяет не только технические, но и дидактические возможности урока, прежде всего, за счет управления учебной деятельностью школьников, а, именно (слайд 13):

создания положительных мотивов изучения материала, объяснения, показа и фиксации формируемой деятельности и входящих в неё знаний;

контроля деятельности учащихся;

передачи машине рутинной части учебной деятельности;

составления и предъявления учебных заданий, соответствующих разным этапам процесса усвоения, а также индивидуальным особенностям ученика и уровню развития его учебной деятельности в данный момент.

Работы с компьютером вызывает у учащихся повышенный интерес и усиливает мотивы учения. Очень часто именно при работе с цифровыми ресурсами удается создать проблемную ситуацию, сформулировать исследовательскую задачу перед конкретным учащимся.

Активно использую известные интернет ресурсы, особенно http://alexlarin.net и http://reshuege.ru (слайд 14).

Анализ результатов ЕГЭ показывает, что наиболее высокие баллы получают учащиеся, занимавшиеся в кружках по математике (МАНах), призеры и победители олимпиад различного уровня. Они же в основном досрочно по этим результатам поступают в вузы.

Также важной в успешной подготовке учащихся к ЕГЭ считаю систематическую разъяснительную и координационную работу с их родителями.

Таким образом, результативность сдачи ЕГЭ во многом определяется тем, насколько эффективно организован процесс подготовки на всех ступенях обучения, со всеми категориями учащихся. А если мы сумеем сформировать у учащихся самостоятельность, ответственность и готовность к продолжению обучения в течение всей последующей жизни, то мы не только выполним заказ государства и общества, но и повысим собственную самооценку.

В заключение хочу отметить, что кроме подготовки по предмету, важно обеспечить правильную мотивацию учащихся к участию в ЕГЭ.

Каждый ученик должен четко понимать, что для него важно при сдаче ЕГЭ. От выбранной цели зависит подготовка к ЕГЭ и стратегия его сдачи.

Итоги ЕГЭ предыдущих лет позволяют высказать некоторые общие рекомендации, направленные на совершенствование процесса преподавания и подготовки учащихся средней школы (слайд 15).

Шесть правил, которые позволяют развивать самостоятельность

1. Стараться не навязывать учебных целей «сверху». Совместная работа с учеником по выработке целей и задач может оказаться значительно эффективнее.

2. Следить за тем, чтобы учебные задания не только соответствовали возрастным ограничениям, но имели уровень оптимальной сложности, способствовали проявлению мастерства и компетентности учащегося.

3. Предоставлять ученику право выбора учебной задачи, не ограничивая при этом его свободы.

4. Желательно подбирать учебные задания с элементом новизны и непредсказуемости, что способствует формированию внутреннего интереса в процессе их выполнения.

5. Как можно реже использовать на уроке ситуации соревнования. Лучше приучать ребенка к анализу и сравнению своих собственных результатов и достижений. Ситуацию соревнования можно переключить на игровые виды деятельности.

6. Также необходимо помнить о том, что наказание за неправильное решение учебной задачи является крайней и наименее эффективной мерой, которая всегда вызывает негативные эмоции и отрицательно влияет на отношение ученика к учебной деятельности.

Закончить свое выступление хочется словами Марии Монтессори (Сайд 16) «Человек не может быть свободным, если он не самостоятельный», приглашая вас работать над формированием самостоятельности и ответственности у учащихся за результат.

ДОКЛАД

Эффективные приемы и методы подготовки учащихся к успешной сдаче ЕГЭ по математики.

В основу построения рекомендаций положены принципы развития математического образования, определение приоритетных и перспективных направлений, а также анализ наиболее типичных ошибок, допущенных в решении заданий базового и профильного экзамена.

Возрастание роли математики в современной жизни привело к тому, что для адаптации в современном обществе и активному участию в нем необходимо быть   математически   грамотным   человеком.   В   связи   со   стратегическими направлениями   социально — ­экономического   развития   России   до   2020   года: «Приоритетной   государственной   задачей   является   обеспечение   качественного базового уровня математических и  естественнонаучных знаний у всех выпускниковшколы, не только будущих ученых, но и будущих квалифицированных рабочих…»           Каждый школьник в процессе обучения должен иметь возможность получить полноценную подготовку к выпускным экзаменам.           Формула успеха хорошо сдать экзамен ЕГЭ и ОГЭ по математике: Высокая степень восприимчивости + мотивация + компетентный педагог.

Практика показывает, что прорешивание открытых вариантов ЕГЭ прошлых лет не даёт ожидаемого эффекта. Разобрав вариант в классе, учитель даёт аналогичный вариант для домашнего разбора. После удачного разбора в классе домашний вариант не представляет большого труда, и у обучающегося и учителя складывается ложное впечатление, что подготовка идет эффективно и цель достигнута. Многократное повторение этих манипуляций не улучшает ситуацию. Когда участник на ЕГЭ получает свой вариант, он обнаруживает, что этот вариант он с учителем не решал. Привычка повторять разобранные ранее варианты часто идет во вред обучению.

Правильным подходом является систематическое изучение материала, решение большого числа задач по каждой теме – от простых к сложным, изучение отдельных методов решения задач. Разумеется, варианты подготовительных сборников, открытые варианты можно и нужно использовать в качестве источника заданий, но их решение не должно становиться главной целью; они должны давать возможность иллюстрировать и отрабатывать те или иные методы. В любом случае, при проведении диагностических работ следует подбирать задачи, прямые аналоги которых в классе не разбирались. Только так учитель может составить верное представление об уровне знаний и умений своих учеников.

Компенсирующее обучение в старших классах.

Часто мы сталкиваемся с ситуацией, когда главенствующим методическим принципом оказывается принцип «прохождения программы», – то есть программа должна быть пройдена во что бы то ни стало, невзирая на то, что содержание этой программы может не отвечать реальным возможностям и подготовке обучающихся.

С введением нового ФГОС, реализацией Концепции развития математического образования, принятием федеральных примерных образовательных программ по математике принцип прохождения программы приобретает новый смысл – обучающийся должен участвовать в посильной интеллектуальной математической деятельности, дающей осязаемые плоды обучения.

Компенсирующая программа как вариант базовой программы для старших классов даёт возможность учителю сделать уроки математики для наименее подготовленных обучающихся осмысленными. При этом появляется реальная возможность  эффективно  подготовить   обучающихся  к решению 8 – 10 заданий профильного ЕГЭ.

Практико-ориентированная математика.

Важной частью ЕГЭ по математике и современных программ являются задачи на применение математических знаний в быту, в реальных жизненных ситуациях. Это задачи на проценты, оптимальный выбор из предложенных вариантов, чтение данных, представленных в виде диаграмм, графиков или таблиц, вычисление площадей или других геометрических величин по рисунку, задачи на вычисление по формулам и т.п.

Круг практико-ориентированных задач в ЕГЭ постоянно расширяется; дополнительно к ним следует отнести задачи вероятностно-статистического блока.

Сложилась практика, когда к практическим задачам учитель приступает только в последний год перед сдачей ЕГЭ. К этому времени обучающиеся успели прочно забыть, как вычислять проценты, как находить площади фигур с помощью палетки или на клетчатой бумаге – все эти задачи для них оказываются новыми.

На протяжении всего периода обучения математике не следует отрываться от простых практических задач; их следует включать в блоки повторения в начале и конце учебного года, в текущий, внутришкольный контроль. Задачи на вычисление сумм налогов, процентов по банковскому вкладу или кредиту, другие задачи финансового характера должны стать постоянным инструментом на уроках математики, поскольку эти задачи связывают наш предмет с окружающим миром и повседневной жизнью.

Практико-ориентированные задачи по финансовой грамотности, геометрического плана, чтение таблиц и графиков нужно включать в изучение математики в средней и старшей школе. При этом характер и трудность задач могут меняться со временем, более того, это необходимо для органического вплетения практических тем в изучение теоретических вопросов. Например, задачи на вклады и кредиты органично возникают при изучении прогрессий, показательной функции и производных. Вычисление площадей по клеточкам очень часто помогает при изучении совершенно абстрактной, казалось бы, темы «первообразная и интеграл». Чтение простых графиков помогает понять и грамотно на качественном уровне применять производную.

Отдельную важную роль в сближении школьной математики с задачами окружающего мира играют вопросы вероятностей и статистики.

Теория вероятности и статистика.

В Концепции развития математического образования ТВ и статистика названы в числе перспективных и важных направлений развития школьной математики. С 2012 года задачи по ТВ формально включаются в КИМ ОГЭ и ЕГЭ. При этом учителя понимают, что те задачи, которые сейчас есть в открытом банке заданий и те, что включены в экзамен, в большинстве случаев сводятся к перечислению равновозможных исходов.

Ясно, что роль ТВ и статистики в школьной математике будет расти. Одновременно будет расширяться круг тем, подлежащих контролю.

При обучении математике следует больше внимания уделять темам вероятности и статистики, постепенно нарабатывая опыт преподавания этих разделов, которые оказываются наиболее практически направленными. Изучение вероятности и статистики требуется вести в тесной привязке к темам алгебры и геометрии, поскольку систематический подход к вопросам ТВ требует от обучающихся знаний о свойствах геометрической прогрессии преобразованиях многочленов, корнях и степенях, площадях фигур.

Таким образом, правильно выстроенное преподавание вероятности не отнимает время, а, напротив, поддерживает изучение традиционных разделов школьной математики. В 2012 – 2014 году задачи по ТВ, появившись в экзамене, вызывали большие трудности, и выполнение этих заданий редко поднималось выше 50%. В настоящее время ситуация изменилась. На данный момент медиана выполнения задания 4 – около 90%.

Некоторые эффективные приёмы обучения математике.

Остановимся подробнее на некоторых приёмах обучения математике, доказавших свою эффективность.

1) При решении задач одним из эффективных приёмов является использование примеров и образцов. Скажем, ученик получает задачу и готовое решение, которое он должен разобрать самостоятельно. Решение может быть дополнено советами, комментариями трудных или «опасных» моментов, другими способами решения и т.п. Когнитивная нагрузка в данном случае получает управляющий импульс и осуществляется в заданном направлении. Важным условием является выход на стратегию, которую можно будет применить в дальнейшем при решении широкого круга задач. Следующим этапом может стать работа не с готовым решением, а с заданным алгоритмом решения, который ученик должен самостоятельно применить к данной ему задаче. После этого можно провести решение полностью самостоятельно. Покажем это (без потери общности) на простой задаче.

Условие. Каждый из двух друзей одновременно показывает на руке случайное количество пальцев от 1 до 5. С какой вероятностью в сумме получится число 8?

Решение. Общее число исходов равно: 25. Благоприятными событию «получится в сумме число 8» будут исходы: 3 + 5, 5 + 3, 4 + 4. Вероятность события равна: 3/25 = 0,12. Ответ: 0,12.

Комментарий. Следует различать две комбинации, когда один из друзей показывает 3 пальца, а другой – 5 пальцев. Ответ можно записать как обыкновенной дробью, так и десятичной.

Задание для самостоятельного решения. Каждый из двух друзей показывает на руке случайное количество пальцев от 1 до 5. С какой вероятностью в сумме получится число 7?

Описанный приём может использоваться применительно к отдельному заданию, однако из таких заданий – с решениями и комментариями – можно составить тематическую проверочную работу, которую можно использовать и в рамках подготовки к экзамену. Решения могут быть написаны учителем самостоятельно, могут быть взяты из публикуемых сборников для подготовки к ЕГЭ, а также из материалов журнала «Математика» или других источников.

2) Весьма эффективно использование при решении задач подсказок,  то есть некоторой дополнительной информации, которая дается ученику после (что важно!) того, как он начал работать над задачей. Чем определеннее подсказка,  тем больше  из нее можно  извлечь.  Фразы: «Хорошо подумай», «Внимательно прочти условие задачи», «Подумай о других способах решения» подсказками не являются, поскольку они никак не направляют ход мысли и не помогают найти решение.

Пример. Решите уравнение.

Подсказка. Можно применить формулу синуса суммы двух углов. Подсказкой может быть похожая задача, которая решалась недавно, указание на конкретный метод. Всегда полезно использовать результаты, методы уже решённых задач, а также опыт, приобретенный при решении. Это широко используется в школьном курсе геометрии, где многие важные геометрические факты, которыми целесообразно пользоваться при решении других задач, даны не в виде утверждений (теорем), а в виде задач. Кроме того, это возможность использования еще одного метода – аналогии.

При решении тригонометрических уравнений подсказкой может быть определённая формула, а при решении логарифмического уравнения – свойство логарифма. Полезно учить пользоваться подсказками, искать их самостоятельно, а также учить давать подсказки.

3) При обучении решению сложных или трудоёмких в плане вычислений и преобразований задач полезно использовать групповые формы работы, а в качестве приёма – мозговой штурм. Основные принципы мозгового штурма: на первом этапе – предложение как можно большего количества решений, без оценки их применимости, рациональности и проч., на втором – анализ и вывод о целесообразности предложенного, выбор наиболее удачных идей и предложений. Ценность приема – в стимулировании поисковой активности на первом этапе и критичности мышления на втором. Хорошо применим данный прием при поиске различных способов решения геометрических задач и тригонометрических уравнений.

4) При решении текстовых задач важным приёмом, необходимым для усвоения, является переформулирование условия, отношений, связывающих входящие в задачу величины. Ниже приводится пример такой задачи из варианта профильного экзамена.

«Задание 11. Заказ на изготовление 323 деталей первый рабочий выполняет на 2 ч быстрее, чем второй. Сколько деталей изготавливает первый рабочий, если известно, что он изготавливает на 2 детали больше второго?»

Данную задачу экзаменуемые решили существенно хуже, чем аналогичную задачу с более привычной и хорошо отработанной фабулой, связанной с движением двух велосипедистов.

Умение переформулировать условие важно и при решении нестандартных  задач,  то  есть  таких,  метод  решения  которых   ученику   не известен, не изучался и не отрабатывался на уроках.

Ещё более актуально это умение при решении практико- ориентированных задач, представляющих собой некоторую ситуацию из реальной жизни, которую необходимо преобразовать и описать на языке математики (то есть самостоятельно сформулировать задачу). В самом простом случае основа задачи будет следующая: за лестницей, которую прислонили к стене дома, надо распознать прямоугольный треугольник, гипотенузой которого и будет данная лестница.

5).В связи с введением обязательного ЕГЭ и ОГЭ по математике возникает необходимость научить учащихся решать быстро и качественно задачи базового уровня. При этом необыкновенно возрастает роль устных

 вычислений, так как   на   экзамене   не   разрешается   использовать   калькулятор   и   таблицы.   Можно научить   учащихся   выполнять простейшие (и   не   очень)   преобразования   устно. Конечно,  для   этого   потребуется   организовать   отработку   такого   навыка   до автоматизма,

 на каждом уроке необходимо отводить 5 — ­7 минут для проведения упражнений устных вычислений, предусмотренных программой каждого

класса. Устные упражнения активизируют мыслительную деятельность учащихся, требуют осознанного усвоения учебного материала; при их выполнении

 развивается память, речь, внимание, быстрота реакции.

Если в 5 — ­6 классах устный счет – это выполнение действий с числами:

 натуральные числа, обыкновенные дроби, десятичные дроби, то в старших

 классах – это могут быть:

7 класс:   Формулы   сокращенного   умножения.   Решение   простейших   ЛУР.   Действия со степенью. График линейной

 функции.

8 класс:   Линейные неравенства и числовые промежутки. 

Решение простейших линейных неравенств. Решение КВУР с помощью

 теоремы Виета и частных случаев.  Решение КВУР   рациональными   способами.   Арифметический   квадратный   корень   и   его свойства. 9 класс: Решение неравенств 2 степени. Преобразование графиков функций.  Формулы приведения. Значения тригонометрических функций.

10 — 11 классах: Вычисление   производных.   Простейшие   тригонометрические   неравенства. Тригонометрические   формулы.   Простейшие   тригонометрические   уравнения. Функции,   обратные  тригонометрическим.   Преобразование   графиков   функций. Вычисление   первообразных.   Свойства   логарифмов.   Простейшие   показательные уравнения

 и неравенства. Простейшие логарифмические уравнения и неравенства. Практика   показала,   что   систематическая   работа   с   устным   счетом способствует   значительному   повышению   продуктивности   вычислений   и преобразований.   Сокращается   время   на   выполнение   таких   операций,   что переводит   их   из   разряда   самостоятельной   задачи   в   разряд   вспомогательной   и становится инструментом (“таблицей

 умножения”) для решения более сложных задач.                         Учитель по математике, знающий, с чем придется столкнуться школьнику на экзамене,   кроме   фундамента   уделяет   большую   часть   времени   на   занятии отработке вопросов специфики ЕГЭ и ОГЭ.                Правильность оформления заданий,  тактика   и  стратегия   решения   в условиях  дефицита   выделенного   времени  на   экзамене,   а   также   банальная невнимательность. Эти и масса других особенностей составляют

 суть специфики.          Для эффективной подготовки к ЕГЭ и ОГЭ нужна тренировка, тренировка и еще раз тренировка. Довести решение задач до автоматизма.

Развитие геометрических представлений

Процент выполнения экзаменующимися геометрических заданий традиционно ниже, чем процент выполнения заданий алгебраических. Одна из основных причин – недостатки в формировании пространственного мышления учащихся. Массово эта проблема проявилась с уходом из общего образования такого учебного предмета, как черчение, и вряд ли стоит ожидать его возвращения – профессия конструктора перестала быть столь массово востребованной с приходом компьютерных технологий.

Эта проблема легла на плечи учителей математики, однако решение её известно: непрерывное развитие геометрических представлений и геометрического воображения обучающихся с 1 по 11 класс; наглядная геометрия в 1–6 классах; больше внимания геометрическому моделированию и конструированию (из плоских и пространственных фигур), геометрическим чертежам, построениям, изображениям от руки и с помощью различных чертёжных инструментов, на нелинованной и клетчатой бумаге.

Это отнюдь не означает, что всю геометрию надо свести к наглядности и к работе руками. Определения и доказательства, логика и аксиоматика важны для современного человека и для изучения геометрии не менее, но надо понимать, что в развитии человека всему отводится свое время, а несформированное наглядно-образное мышление, которое должно быть основой и этапом на пути формирования логического мышления, просто мешает его формированию.

Если вернуться к этапу обучения в старшей школе, то целесообразно использовать любые приёмы и средства, которые способствовали бы визуализации предлагаемых обучающимся задач. Это не только построение чертежей по условию задачи (что непросто сделать при проблемах с пространственным воображением), это прежде всего различные предметные модели (полезно для каждой решаемой задачи иметь соответствующую ей модель-подсказку, чтобы использовать её для визуализации условия, поиска и проверки решения), компьютерные программы, позволяющие выполнять стереометрические чертежи.

Полезно выделить эту работу в отдельный тематический практикум, на котором обучающиеся тренировались бы в изображении и моделировании пространственных тел, построении чертежей по условию задачи (в различных ракурсах, выбирая наиболее удобный для поиска решения), можно также организовать данную работу в рамках проекта.

Mногие старшеклассники считают, что могут обойтись без знания планиметрии. Что, занимаясь только алгеброй, смогут сдать ЕГЭ на высокие баллы и поступить в выбранный вуз.

Работает ли эта стратегия?

Oтвет преподавателей-экспертов: нет, не работает. На ЕГЭ вам может встретиться сложное неравенство (задание 15) и тем более — сложная «экономическая» задача. Так было в 2018 году. И всё, баллов фатально не хватает! Тех самых баллов, которые можно было легко получить за планиметрическую задачу, не хватает для поступления!

Cтоит учесть, что задачи вариантов ЕГЭ по планиметрии и стереометрии бывают намного проще, чем по алгебре.

1) Cамое важное — правильная методика подготовки. Не нужно начинать с реальных задач ЕГЭ. Cначала — теория. Cвойства геометрических фигур. Oпределения и теоремы. Учить наизусть.

Лучшая тренировка на этом этапе — задания №3 и №6 из первой части ЕГЭ по математике

2) Задача 16 Профильного ЕГЭ по математике оценивается в 3 первичных балла и состоит из двух пунктов. Первый пункт — доказательство. Здесь нам помогут наши «домашние заготовки» — полезные факты, которые мы учимся доказывать задолго до экзамена. A на ЕГЭ остается только вспомнить и записать решение.

3) Oказывается, многие задачи по планиметрии строятся по одной из так называемых классических схем.

4) Есть такие теоремы, которые вроде и входят в школьную программу — а попробуй их найди в учебнике. Например, теорема о секущей и касательной или свойство биссектрисы.

5.) Любая задача из варианта ЕГЭ решается без сложных формул. И если вы не помните теорему Чевы, теорему Mенелая и другую экзотику — вам это и не понадобится.

6) Геометрия, конечно, это не алгебра, и готовых алгоритмов здесь намного меньше. Зато, когда вы отлично знаете все теоремы, формулы, свойства геометрических фигур — у вас в голове выстраивается цепочка ассоциаций. Например, в условии задачи дан радиус вписанной окружности. B каких формулах он встречается? — Правильно, в теореме синусов и в одной из формул для площади треугольника.

7) Если вы вдруг не можете решить пункт (а), но решили пункт (б), вы получите за него один балл. A это лучше, чем ничего. Но вообще пункт (а), как правило, бывает простым. Иногда вопрос в пункте (а) очень простой. И это не только для того, чтобы вы получили «утешительный» балл. Помните, что пункт (а) часто содержит подсказку, идею для решения пункта (б).

 Саморегуляция и обратная связь «ученик-учитель».

Известно, что эффективность обучения возрастает в случае самооценивания, поскольку ученик самостоятельно получает информацию о своих результатах, сам её анализирует, делает выводы о своем прогрессе, корректирует цели в случае необходимости. Но для этого необходимы критерии оценивания работы, которые должны быть у ученика не просто до начала выполнения конкретной работы, но желательно и в самом начале изучения темы. К сожалению, на практике более распространена ситуация, когда работа выдаётся ученику без критериев ее выполнения.

К саморегуляции относятся также вопросы, связанные с осознанностью знания и незнания. Объяснение учителя сродни лекционной форме предъявления новых знаний. В связи с этим подчеркнём важность обратной связи. Учитель должен получать сигналы от обучающихся: «Я понимаю, могу объяснить», «Я не уверен, правильно ли я понимаю», «Я не понимаю». Учитель может прервать своё объяснение вопросом к тем, кто  ещё не понял, предложением высказать свои сомнения тем, кто не уверен в понимании, предоставлением слова тем, кто всё понял.

Доказано, что обратная связь эффективна, если ученик получает сообщение о верно выполненных заданиях, а не только об ошибках, если он получает не просто маркеры, свидетельствующие о положительном результате, не просто похвалу за решённую задачу, а и некоторый содержательный комментарий. Этот комментарий может включать в себя такую оценку, как «рациональное решение», «интересная идея», «грамотная запись». Может быть отмечена актуальность проверки результата, удачное прохождение «ловушек» и «опасных» мест и т.п.

Обратная связь эффективна в случае, если она конкретна, то есть связана с известными ученику результатами и действиями, подлежащими усвоению. Важное значение имеет информированность ученика относительно того, чему он должен научиться, какие задания должен научиться решать, а какие может научиться решать для того, чтобы получить желаемое количество баллов на экзамене. Если ученик фиксирует и отслеживает сам, умеет ли он выполнять требуемое задание или нет, то минимизируется время на выполнение заданий, при этом работа становится более эффективной и рациональной. Отсюда необходимость в открытости предъявляемых требований к результатам обучения, а на этапе подготовки к экзамену – в ориентации на конечный запланированный результат.

И еще об одном факторе следует упомянуть – это повторяющееся тестирование. Уже имеющийся опыт российской школы и более продолжительный зарубежный опыт не позволяют говорить о нём, как об эффективном факторе. Положительные эффекты возникают только в тех случаях, когда учитель учитывает результаты тестирования для корректировки процесса обучения и приспосабливает методы обучения к возможностям конкретного ученика, учитывая его сильные и слабые стороны, или при условии содержательной обратной связи, с которой ученик может работать самостоятельно, то есть имеет возможность учиться на тестах.

Завершающие рекомендации.

Необходимо отметить, что создание ЕГЭ по математике базового уровня и появление акцента на использование математических знаний в реальных ситуациях были неверно истолкованы некоторыми учителями в качестве генеральной идеи обучения, что привело к поверхностному освоению обучающимися программы старшей школы. В частности, это зафиксировано и результатами экзамена: результаты выполнения заданий по темам курса старшей школы ниже результатов выполнения заданий из «реальной математики».

Для того чтобы успешно сдать ЕГЭ по математике, важно пройти всю программу целиком, а не только «то, что пригодится на экзамене», повысить свою культуру вычислений, то есть минимизировать использование калькуляторов, развивать умение читать графики, правильно использовать терминологию и учить формулы.

Для учащихся, которые могут успешно освоить курс математики средней (полной) школы на базовом уровне, образовательный акцент должен быть сделан на полное изучение традиционных курсов алгебры и начал анализа и геометрии на базовом уровне. Помимо заданий базового уровня в образовательном процессе должны использоваться задания повышенного уровня. Количество часов математики должно быть не менее 5 часов в неделю.

Для учащихся, которые могут успешно освоить курс математики полной (средней) школы на профильном (повышенном) уровне, образовательный акцент должен быть сделан на полное изучение традиционных курсов алгебры и начал анализа и геометрии на профильном уровне. Количество часов математики должно быть не менее 6–7 часов в неделю.

В первую очередь нужно выработать у обучающихся быстрое и правильное выполнение заданий части 1, используя, в том числе и банк заданий экзамена базового уровня. Умения, необходимые для выполнения заданий базового уровня, должны быть под постоянным контролем.

Задания с кратким ответом (повышенного уровня) части 2 должны находить отражение в содержании математического образования, и аналогичные задания должны включаться в систему текущего и рубежного контроля.

В записи решений к заданиям с развернутым ответом нужно особое внимание обращать на построение чертежей и рисунков, лаконичность  пояснений, доказательность рассуждений.

И в завершение необходимо отметить, что еще одним важным фактором является психологический климат в учебном коллективе: дружеские отношения среди одноклассников, спокойная рабочая атмосфера на уроке, методичная, прозрачная и последовательная подготовка к экзамену, доверительные отношения учителя с учениками, вера в достижение более высоких результатов и эмоциональная поддержка.

 На занятиях стараюсь создать атмосферу комфортности, 

взаимопонимания. На своих уроках я делаю   установку   на   то,   чтобы   любой   ребенок   должен   быть   понят   и   услышан учителем   и   соучеником:   учение   должно   проходить   в   «атмосфере непринужденности,   чтобы   дети   и   учитель   свободно   дышали   на   уроках».   От учителя   требуется   и   мастерство,   и   большое   терпение,   и   любовь к   учащимся. Доброжелательное отношение к ученикам снимает у них страх перед трудностями обучения: ребенок не должен бояться 

ошибиться, спросить учителя, если он что­ то прослушал   или   не   понял.   Психологическая   подготовка   учащихся, может заключается в следующем:

 отработка поведения в период подготовки к экзамену; обучение навыкам 

саморегуляции, самоконтроля, повышение уверенности в себе, в   своих   силах.   Методы   проведения   занятий   по   психологической   подготовке учащихся   разнообразны:   групповая   дискуссия,   игровые   методы,   медитативные техники,   Содержание   занятий   должно ориентироваться   на следующие   вопросы:   как   подготовиться   к   экзаменам, поведение   на   экзамене,   способы   снятия   нервно­психического   напряжения,   как противостоять стрессу. 

Литература:

Методические рекомендации для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2019 года по математике, подготовленные ФГБНУ «ФИПИ».

Методические рекомендации для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2020 года по математике, подготовленные ФГБНУ «ФИПИ».

Бабанский Ю.К. Активность и самостоятельность учащихся в обучении / М.Ю. Бабанский ­ М., Педагогика, 1989.

Беспалько В.П. Слагаемые педагогической технологии / Беспалько В.П. – М., 1989.

Красновский Э.А. Активизация учебного познания / Красновский Э.А. // Советская педагогика. – 1989. ­ №5.

Эльконин Д. Б. Избранные педагогические труды. / Под ред. В.В. Давыдова, В.П. Зинченко.­М., 1989.

Щукина Г.И. Активизация познавательной деятельности в учебном процессе/ Щукина Г.И. ­ М., 1979.  

---

Представление практик, повышающих эффективность подготовки учащихся к ЕГЭ по математике

© 2007 — 2023 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.

---

Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.

---

Фотографии предоставлены

«Система подготовки учащихся к ЕГЭ по математике».

Повышение качества образования всегда было и остается

приоритетным направлением в работе любого

общеобразовательного учреждения.

Основными целями данной работы являются:

-грамотная организация действий каждого учителя в режиме

подготовки учащихся к итоговой аттестации;

— обеспечение методическим сопровождением процесса

подготовки с учетом учебных возможностей и способностей

учащихся;

— своевременное информирование учащихся и их родителей по

всем аспектам итоговой аттестации.

Мы, математики, пришли к выводу о том, что только комплексный

подход к деятельности по подготовке учащихся к ЕГЭ способствует

повышению эффективности и качества результатов экзамена в

тестовой форме. Под комплексным подходом мы понимаем

целенаправленное сотрудничество администрации, учителей-

предметников, учащихся и их родителей.

Вот уже много лет в нашей стране введен новый формат

оценки уровня качества образования выпускников – Единый

государственный экзамен (ЕГЭ). Практика показывает, что для

большинства учащихся 11-х классов и их родителей, многих

педагогов, а особенно молодых и малоопытных, «камнем

преткновения» является ЕГЭ по математике. С одной стороны, ЕГЭ

по математике является обязательным. С другой стороны,

математика, как учебный предмет, относится к первой степени

сложности.

В нашей школе сложилась определенная система подготовки к

экзамену в форме ЕГЭ, так и к ОГЭ. Система-это целое, состоящее

из частей, связанных между собой.

С годами совершенствуется экзамен, совершенствуется и

методика подготовки учащихся. Поэтому очень важным является то,

чтобы сам учитель был готов к экзамену:

-представлял его структуру,

— количество заданий по разделам математики и по типам заданий,

-знал перечень элементов содержания,

-понимал принципы оценивания.

Только в этом случае учитель эффективно может выстроить

подготовку к экзамену.

Учителя-математики нашей школы имеют достаточный опыт

подготовки учащихся к выпускным экзаменам.

Подготовка к сдаче

ОГЭ и ЕГЭ по математике идет через приобретение и освоение

конкретных математических знаний. Только это обеспечит

выпускнику успешную сдачу экзамена.

В своей работе применяем следующие принципы подготовки к

экзаменам

Первый принцип – тематический. Позволяет эффективнее

выстраивать подготовку, соблюдая принцип от простых типовых

заданий к более сложным.

Второй принцип – логический. На этапе освоения знаний

подбираем материал в виде логически взаимосвязанной системы,

где из одного следует другое. На следующих занятиях полученные

знания способствуют пониманию нового материала.

Третий принцип – тренировочный. На консультациях учащимся

предлагаются тренировочные тесты, выполняя которые дети могут

оценить степень подготовленности к экзаменам.

Четвёртый принцип – индивидуальный. На консультациях ученик

может не только выполнить тест, но и получить ответы на вопросы,

которые вызвали затруднение.

Пятый принцип – временной. Все тренировочные тесты проводим

с ограничением времени, чтобы учащиеся могли контролировать

себя — за какое время сколько заданий они успевают решить.

Шестой принцип – контролирующий. Максимализация нагрузки

по содержанию и по времени для всех учащихся одинакова. Это

необходимо, поскольку тест по своему назначению ставит всех в

равные условия и предполагает объективный контроль результатов.

И надо отметить, что систематическая планомерная работа по

данному направлению, которую из года в год мы совершенствуем с

учетом новых образовательных методик и технологий, сказывается

только положительным образом на конечный результат.

Я расскажу о тех главных, на мой взгляд, составляющих, которые

обеспечивают подготовку к выпускному экзамену по математике за

курс основной и средней школы. Подготовленность к чему-либо

понимается как комплекс приобретенных знаний, навыков, умений,

качеств, позволяющих успешно выполнять определенную

деятельность. В готовности учащихся к сдаче экзамена в форме ОГЭ

и ЕГЭ можно выделить следующие составляющие:

— информационная готовность (информированность о правилах

поведения на экзамене, информированность о правилах

заполнения бланков и т.д.);

— предметная готовность или содержательная (готовность по

определенному предмету, умение решать тестовые задания);

— психологическая готовность (состояние готовности – «настрой»,

внутренняя настроенность на определенное поведение,

ориентированность на целесообразные действия, актуализация и

приспособление возможностей личности для успешных действий в

ситуации сдачи экзамена).

Содержание информационной работы с учащимися.

1) Организация информационной работы в форме инструктажа

учащихся:

— правила поведения на экзамене;

— правила заполнения бланков;

— расписание работы кабинета информатики (часы свободного

доступа к ресурсам Интернет).

2) Информационный стенд для учащихся: нормативные документы,

бланки, правила заполнения бланков, ресурсы Интернет по

вопросам ОГЭ и ЕГЭ

3) Проведение занятий по тренировке заполнения бланков.

4) Пробные внутри школьные ОГЭ и ЕГЭ

Содержание информационной работы с родителями учащихся.

1) Родительские собрания:

— информирование родителей о процедуре проведения экзамена

об особенностях подготовки к тестовой форме сдачи экзаменов.

Информирование о ресурсах Интернет;

— информирование о результатах пробного внутри школьного ОГЭ и

ЕГЭ;

— пункт проведения экзамена.

2) Индивидуальное консультирование родителей.

Психологическая подготовка к ОГЭ.

Психологическая подготовка учащихся заключается в следующем:

отработка стратегии и тактики поведения в период подготовки к

экзамену; обучение навыкам саморегуляции, самоконтроля,

повышение уверенности в себе, в своих силах. Психологом нашей

школы рассматриваются следующие вопросы:

— как подготовиться к экзаменам,

— поведение на экзамене,

-способы снятия нервно-психического напряжения,

— как противостоять стрессу.

Работа с учащимися проводится со всем классом и выборочно,

кто пожелает, индивидуально.

Предметная готовность или содержательная

Именно на этом я остановлюсь подробнее.

Предметная готовность к сдаче экзамена складывается в

процессе всего периода обучения с 1 по 11 класс. И здесь трудно

переоценить роль учителей начальных классов. В результатах ОГЭ

есть и их вклад: либо положительный, либо со знаком минус.

Так же большую роль играет количество часов по предмету.

В общем, факторов, которые влияют на предметную подготовку

большое количество.

Я хочу рассказать о тех элементах системы подготовки к

экзаменам,

которые,

по

моему

мнению,

являются

наиболее

значимыми.

Устный счет – один из важных приемов при подготовке учащихся

к ОГЭ и ЕГЭ по математике.

В методике математики различают устные и письменные

приемы вычисления. Устная работа на уроках имеет большое

значение – это и беседы учителя с классом или отдельными

учениками, и рассуждения учащихся при выполнении тех или иных

заданий и т.п. Среди этих видов устной работы можно выделить так

называемые устные упражнения. В начальной школе они

сводились в основном к вычислениям, поэтому за ними

закрепилось название “устный счет”, хотя в современных

программах содержание устных упражнений весьма разнообразно

и велико за счет введения алгебраического и геометрического

материала, а также за счет большого внимания к свойствам

действий над числами и величинами.

Важность и необходимость устных упражнений велика в

формировании вычислительных навыков и в совершенствовании

знаний по нумерации, и в развитии личностных качеств ученика.

Создание определённой системы повторения ранее изученного

материала дает учащимся возможность усвоения знаний на уровне

автоматического навыка. В связи с введением обязательной ОГЭ по

математике возникает необходимость научить учащихся старших

классов решать быстро и качественно задачи базового уровня. При

этом необыкновенно возрастает роль устных вычислений и

вычислений вообще, так как на экзамене не разрешается

использовать калькулятор и таблицы. Для достижения

правильности и беглости устных вычислений, преобразований,

решения задач в течение всех лет обучения в среднем звене на

каждом уроке отводим 5-7 минут для проведения упражнений в

устных вычислениях, предусмотренных программой каждого

класса.

Устные упражнения активизируют мыслительную деятельность

учащихся, требуют осознанного усвоения учебного материала; при

их выполнении развивается память, речь, внимание, быстрота

реакции.

Устные упражнения как этап урока имеют свои задачи:

1) воспроизводство и корректировка знаний, умений и навыков

учащихся, необходимых для их самостоятельной деятельности на

уроке или осознанного восприятия объяснения учителя;

2) контроль состояния знаний учащихся;

3) автоматизация навыков простейших вычислений и

преобразований.

Если в 5-6 классах устный счет – это выполнение действий с

числами: натуральные числа, обыкновенные дроби, десятичные

дроби, то в старших классах – это могут быть совершенно

различные операции, навык выполнения которых стараемся

довести до автоматизма. Например, на уроках математики мы

используем УС по темам:

7 класс:

1) Запись чисел в стандартном виде и действия с ними.

2) Формулы сокращенного умножения.

3) Решение простейших ЛУР.

4) Действия со степенью.

5) График линейной функции.

8 класс:

1) Линейные неравенства и числовые промежутки.

2) Решение простейших линейных неравенств.

3) Решение КВУР с помощью теоремы Виета и частных случаев.

4) Решение КВУР рациональными способами.

5) Арифметический квадратный корень и его свойства.

9 -10 класс-:

1) Решение неравенств 2 степени.

2) Преобразование графиков функций.

3) Формулы приведения.

4) Тригонометрические формулы.

5) Значения тригонометрических функций.

Устный счёт на каждом уроке стараемся строить на основе

упражнений ЕГЭ и ОГЭ. Практика показала, что систематическая

работа с УС способствует значительному повышению

продуктивности вычислений и преобразований. Сокращается

время на выполнение таких операций, как решение КВУР, линейных

неравенств и неравенств 2-ой степени, разложение на множители,

построение графиков функций, преобразования иррациональных

выражений и другие. Эти операции переходят из разряда

самостоятельной задачи в разряд вспомогательной и становятся

инструментом (“таблицей умножения”) для решения более

сложных задач.

Виды устного счёта, которые мы используем:



Математический диктант



Презентация



Раздаточные таблицы

Основные задачи по подготовке детей к ЕГЭ:

1. Начинать подготовку к ЕГЭ с 5 класса;

2. Создавать учебный материал (по типу ЕГЭ) для обучающих

программ,

тренингов

и

использовать

готовые

печатные

и

электронные пособия;

3. Учить школьников «технике сдачи теста»;

4.Через систему дополнительных занятий (элективных курсов,

индивидуальных консультаций) повышать интерес к предмету и

личную ответственность школьника за результаты обучения.

Как мы решаем поставленные задачи? С чего начинаем эту

работу?

Во-первых, с первых же дней учёбы убеждаем детей в том, что

если

очень

постараться,

то

можно

получить

вполне

приличный

балл. Главное не упустить время.

Во-вторых, в течение всего учебного года знакомим детей с

материалами ОГЭ и ЕГЭ.

Кроме этого, систематически на уроках

каждому раздаем тест ЕГЭ: в 7- 9 классах – за основную школу, в

10-11 классах – за полную среднюю школу. Просим ребят найти в

тесте те задания, с которыми они могут справиться уже сегодня и

решить их. Стараемся выслушать все подходы к решению каждой

задачи и только потом раскрываем секрет, как можно было решить

задачу рациональнее, чтобы сэкономить время.

В-третьих, когда уже удалось заинтересовать детей, знакомим

их

с

особенностями

новой

формы

итоговой

аттестации:

со

структурой

теста,

временными

рамками,

нормами

оценивания

экзаменационной

работы,

условиями

проведения

экзамена

и

начинаем обучать «технике сдачи теста»:



обучаем строгому самоконтролю времени;



учим определять трудность заданий;



знакомим

с

приёмом

«прикидки»

р е зул ьт а т а

подстановкой;



знакомим с приёмом «спирального движения по тесту»



.

Начну

с

первого

пункта.

Говорим

ученикам,

чтобы

успешно

выполнить тест, на каждое задание первой части надо затрачивать

не более 5

минут. И из урока в урок отрабатываем

тесты на

скорость: например, за 12 минут школьникам необходимо решить 4

– 6 заданий теста. При этом даем настоящие тесты ОГЭ или ЕГЭ с

отмеченными в нём заданиями, посильными на данный момент

обучения.

Обязательно

отмечаем

количество

человек

уложившихся во времени, и сразу анализируем ситуацию и опять

даем совет,

какое задание

можно было решить рациональнее.

Постепенно

приучаем

ребят

к

методу

«пристального

взгляда»

—

внимательно посмотри: «Нет ли короткого пути решения? Так как

ты

ограничен

во

времени».

Поверьте,

если

разбирать

тест,

над

которым

ученик

уже

потрудился,

то

заинтересованность

и

внимание 100%. Все рекомендации учителя воспринимаются более

осознанно.

Как

учим

определять

трудность

заданий?

Сначала

просим

учеников

просмотреть

тест

от

начала

до

конца

и

отметить

карандашом те задания, которые кажутся им простыми и лёгкими и

выполнить их в «режиме скорости». Затем, отметить 2-3 задания,

которые

им

понятны

по

формулировке,

но

требуют

большего

времени и выполнить их; и только после этого, если останется

время, можно поразмышлять над остальными.

Двигаясь

по

тесту,

дети

знают,

что

сложность

заданий

нарастает, поэтому всегда советуем настойчиво и добросовестно

отрабатывать

первую

часть,

только

затем

можно

приступать

ко

второй части – это и есть принцип «спирального движения» по

тесту.

С введением новой формы аттестации у нас появилось ещё

несколько методических приёмов и хитростей. Чтобы

работу по

подготовке к экзамену проводить в течение всего учебного года в

кабинете

имеется

огромное

количество

тестового

материала,

кроме

этого

11классники

работают

с

сайтом

Ларина.

Решают

выложенные

варианты

с

понедельника,

в

четверг

сдают

на

проверку. Это очень трудоемко, но зато эффективно Отдельно хочу

сказать о консультациях.

Консультации индивидуальные. Ребята

знают, что с вопросами по первой, части, можно подойти в любое

время,

но

вопросы

второй

части

подают

заранее

и

приходят

в

назначенное

время.

Консультации

проводим

по

своей

инициативе, труд этот не оплачивается, я просто рассказываю о

нашей,

годами

сложившейся

традиции.

Ребята

знают,

что

проконсультироваться можно на любой большой перемене и после

уроков, если учитель свободен.

Коротко расскажу ещё о некоторых факторах успешности на

ЕГЭ.

Для

хорошей

подготовки

к

экзамену

необходимо

целенаправленное

повторение. Во втором полугодии начинаем

тематическое повторение. Готовясь к уроку, учителю приходится

искать задания по каждой теме в разных источниках, что занимает

много

времени.

Кроме

того,

повторять

материал

темы

удобно,

когда задания расположены в одном месте. Наиболее оптимальное

решение — это тематические и комплексные тесты, учим ребят

оценивать итоги работы над тестом в целом. Ребята проходят в

течении

года

предварительное

тестирование

в

системе

работы

Стат-Град. Это тестирование становится генеральной репетицией по

заполнению бланков, сдачи экзамена.

Преимущества тематического теста:

-в нём собраны разные задания по одной теме;

-на уроках можно рассматривать отдельные задания из теста;

-по такому тесту удобно проводить повторение;

-осуществлять контроль знаний и умений учащихся по данной теме.

Итоговое повторение строим исключительно на отработке

умений и навыков, требующихся для получения положительной

отметки на экзамене.

Примерные экзаменационные работы берем из различных

сборников для подготовки к ЕГЭ

Кроме этого ребята могут проверить свои знания, решая

примерные работы в режиме on-lain (См. сайт Савченко Е.М.), а так-

ж

е работы, размещённые на сайте Стат-Града.

Применение ИКТ на уроках математики при подготовке к ЕГЭ.

для повторения теоретического материала проводим

обобщающие уроки с применением компьютерных технологий.

Уроки с применением презентаций зрелищны и эффективны в

работе над информацией. Особенно, если это уроки повторения и

обобщения материала определённой темы.

Презентация обладает наглядностью и выразительностью, это

прекрасное дидактическое и мотивационное средство,

способствующее лучшему запоминанию учебного материала.

При её систематическом использовании увеличивается

продуктивность обучения. С помощью презентации можно

повысить объём повторяемого материала и выполняемой работы.

В работе используем свои презентации и презентации,

созданные коллегами и представленные на различных

образовательных сайтах в Интернете:

-Интернет-сообщество учителей

-Сеть творческих учителей

-Фестиваль педагогических идей «Открытый урок»

-Информационно-методический сайт

Хорошие презентации с сайта Каратановой Марии

Николаевны. Эти презентации помогли нам построить

систематическое повторение и отработку навыков. (показать

презентации).

Можно использовать презентации, сделанные другими

учителями. Но не всегда они содержат всю нужную информацию

для реализации задумок учителя, но почти всегда их можно

отредактировать. С этой целью полезно посещать сайты

-«Интернет – сообщество учителей»,

-«Сеть творческих учителей»,

-«Фестиваль педагогических идей

-«Открытый урок»,

-«Информационно методический сайт» и другие.

В работе мы часто используем презентации Савченко Елены

Михайловны, учителя математики МОУ гимназии №1, г. Полярные

Зори. Как сделала это она, я думаю, лучше никому не сделать. И

тогда .почему бы не использовать в работе этот образовательный

продукт?!

Использование компьютерных презентаций на уроках

математики и при подготовке к итоговой аттестации

открывает огромные возможности:

-компьютер может взять на себя функцию контроля знаний,

-поможет сэкономить время на уроке для решения

экзаменационных задач,

-богато иллюстрировать материал,

-трудные для понимания моменты показать в динамике,

-повторить то, что вызвало затруднения,

-дифференцировать урок в соответствии с индивидуальными

особенностями учащихся,

-быстро повторить теоретический материал.

Особенно эти презентации помогли при итоговом повторении

теоретического материала по геометрии.

Мы стали экономить время на теории, чтобы использовать его

на практику. Всегда стараемся выдать теорию по теме за 1-2 урока и

лекцию

построить

так,

чтобы

она

содержала

все

необходимые

сведения

для

решения

текущей

контрольной

работы

и

экзаменационного

материала.

Остальные

уроки

посвящаем

практике.

Уроки-практикумы

попутно

дополняем

недостающим

теоретическим материалом. И еще учителя математики знают, что

учебники

почти

не

готовят

детей

к

ЕГЭ,

в

них

по-прежнему

традиционные

формулировки

заданий.

Какой

мы

нашла

выход:

сразу

после

объяснения

нового

материала

и

его

первичного

закрепления показываем, как эта тема вышла на ЕГЭ. Стараемся

при

этом

продемонстрировать

всё

разнообразие

заданий

из

первой и второй части, используя сборники с материалами ЕГЭ

разных лет. Иногда прошу найти подобные задания в учебнике.

Убедившись,

что

таких

заданий

почти

нет,

ученики

осознают

значимость, приобретённых материалов для подготовки к экзамену

и

уже

практически

не

расстаются

с

ними.

Регулярно

проводим

диагностические

работы

для

определения

пробелов

в

знаниях.

Полученные

результаты

определяют

индивидуальную

и

дифференцированную

работу.

Мониторинг

и

диагностику

планируем на основе экзаменационных

материалов.

Работая с

КИМами

с

5

класса,

ребята

привыкают

к

структуре

теста,

к

необычности

формулировок

заданий,

разнообразию

методов

и

приёмов

при

решении

задач,

систематическому

пополнению

копилки по теории (набору шпаргалок те опорным конспектам). У

них

постепенно

исчезает

чувство

растерянности

и

полной

безнадёжности,

появляется

уверенность

и

психологическая

готовность к новой форме аттестации.

Конечно,

максимально

используем

урочное

время

для

подготовки

к

экзамену,

но

этого

недостаточно,

поэтому

в

8-11

классах

систематически

проводим

углублённую

факультативную

работу по предмету. Элективные курсы:

«Модуль»,

«Квадратный трёхчлен и его приложения»,

«Дробно-рациональные и линейные уравнения и неравенства с

параметрами»,

«Самый простой способ решения непростых неравенств».

-«Решение уравнений и неравенств с параметрами».

— «Нестандартные методы решения неравенств и их систем».

Программы

курсов

рассматривают

ключевые

и

сложные

темы

школьной

математики,

помогают

расширить

спектр

задач,

п о с и л ь н ы х

д л я

у ч а щ и х с я

и

р е а л и з о в а т ь

п р и н ц и п ы

дифференцированного обучения.

Ежегодно

пополняем

кабинет

математики

новыми

дидактическими

материалами

для

урочной

и

внеурочной

деятельности, способствующими развитию у школьников интереса

к

математике,

активизации

мыслительной

деятельности,

выявлению детей, проявляющих особый интерес к предмету и в

первую очередь повышению качества знаний по подготовке к ЕГЭ.

Разработали и систематизировали тестовый материал, создали

подборку

текстовых

задач

по

подготовке

к

промежуточным

аттестациям,

ОГЭ

и

ЕГЭ.

Приобрели

для

кабинета

большое

количество

методической

и

математической

литературы

по

ключевым

вопросам

ЕГЭ.

Конечно,

очень

важен

позитивный

настрой детей на серьёзный самостоятельный труд по подготовке к

экзамену,

поэтому

в

начале

каждого

учебного

года

с

большим

удовольствием

сообщаем

им

информацию

о

том,

что

снова,

практически все наши выпускники поступили в высшие и средние

учебные заведения и обучаются на бюджетной основе.

В заключении хочу сказать, что такая система подготовки детей

к итоговой аттестации помогла нам в течение четырёх лет получить

результаты

ЕГЭ

по

математике

значительно

выше

средних

по

району

и

области

и

выше

средних

по

России. Ну

и

следует

добавить,

что

работа

проводимая

учителем

в

ходе

подготовки

выпускников

к

итоговой

аттестации

достаточно

объемная

и

тяжелая.

Но

если

она

грамотно

спланирована,

то

многие

проблемные моменты можно избежать еще на начальной стадии и

в

результате

получить

достойную

оценку

качества

образования

собственных учеников.

P.

S.

После

сдачи

ЕГЭ

выпускники

перебивая

друг

друга,

с

огромным волнением рассказывают, что было на экзамене. И как

приятно слышать от детей, что все задания экзамена

им были

знакомы. А потом долгое ожидание результатов, переживание и,

наконец, радость со слезами на глазах – ЕГЭ успешно сдали все.

Это самая большая награда учителю!