Подготовка к ЕГЭ по геометрии 11 класс и другие
полезные материалы для учителя геометрии, которые вы можете выбрать и скачать бесплатно в этом разделе.
Показывать
Подготовка к ЕГЭ

- Все разработки
- Уроки
- Тесты
- Презентации
- Планирование
- Мероприятия
- Видеоуроки
- Кабинет
- Подготовка к ЕГЭ
- Проверочные работы
- Практикумы
- Подготовка к ОГЭ
- Факультативы
- Классные часы
- Разное
Геометрия

- Все предметы
- Дошкольное образование
- Начальные классы
- Информатика
- Математика
- Алгебра
- Геометрия
- Химия
- Физика
- Русский язык
- Английский язык
- Немецкий язык
- Французский язык
- История
- Всемирная история
- Всеобщая история
- История России
- Право
- Биология
- Обществознание
- Литература
- География
- Музыка
- Технология девочки
- Технология мальчики
- Технология
- Физкультура
- ИЗО
- Окружающий мир
- Искуcство
- ОБЖ
- Внеурочка
- Астрономия
- Директору
- Завучу
- Классному руководителю
- Коррекционная школа
- Логопедия
- ОРК
- Психологу
- МХК
- Всем учителям
- Прочее
- Естествознание
- Экономика
- Экология
- Финансовая грамотность
- ОРКиСЭ
- Школьному библиотекарю
- Родной язык и литература
- Истоки
11 класс

- Все классы
- Дошкольникам
- 1 класс
- 2 класс
- 3 класс
- 4 класс
- 5 класс
- 6 класс
- 7 класс
- 8 класс
- 9 класс
- 10 класс
- 11 класс
- Прочее
Все учебники

- Все учебники
- Геометрия (базовый и углубленный уровень), 10-11 классы, Александров А.Д., Вернер А.Л. и др., Москва : Просвещение, 2019. — 159 с.
- Геометрия (базовый и углублённый уровни), 11 класс, Козлов В.В., Никитин А.А. и др./ Под ред. Козлова В.В. и Никитина А.А., Изд. «Русское слово” 2016
- Геометрия. 10-11 классы. (профильный уровень) Калинин А.Ю., Терёшин Д.А. (2011, 640с.)
- Геометрия. 10-11 классы. Александров А.Д., Вернер А.Л., Рыжик В.И. (2014, 255с.)
- Геометрия. 10-11 классы. Базовый уровень. Шарыгин И.Ф. М.: 2013. — 240 с.
- Геометрия. 10-11 классы. Учебник (базовый и профильный уровни). Смирнова И.М., Смирнов В.А. (2008, 288с.)
- Геометрия. 11 класс. (углубленное и профильное обучение). Потоскуев Е.В., Звавич Л.И. (2004, 368с.)
- Геометрия. Учебник для 10-11 классов. Погорелов А.В. 13-е изд. — М.: 2014 — 175 с.
-
Итоговый тест по теме «Сфера, шар, площадь сферы» геометрия 11 класс
-
Данный тест является контрольной работой по геометрии 11 класса по теме «Объемы тел».
Время выполнения сорок пять минут.Только одна попытка. -
Решение заданий №6 (часть 1)по материалам открытого банка задач Единого Государственного Экзамена по математике
-
Данный тест будет полезным учителю для осуществления быстрого контроля на уроке, а также ребятам, которые желают проверить свои знания по данной теме.
-
Тест сотоит из 10 вопросов по теме «Площадь сферы. Объём шара». Шесть из них предполагают выбор одного правильного ответа. В других четырёх заданиях следует записать ответ в виде целого числа или десятичной дроби. Верный ответ-1 балл, неверный -0 баллов.
-
Тест содержит три задачи, необходимо в строке ответов внести только ответ получившийся при решении задачи
-
Данный тест предназначен для определения знания предмета «Геометрия» за курс 11 класса.
-
Раздел Геометрия. Тест для студентов СПО ,обучающихся на базе основного среднего образования.
-
Тест составлен для учащихся 11-ых классов для закрепления раннее пройденных тем «Сфера. Шар. Цилиндр. Конус. Площади и объёмы данных тел»
-
Тест предназначен для проверки усвоения учащимися 11 класса тем «Элементы тел вращения», «Объемы тел вращения».
-
Тест предназначен для определения сформированности у выпускников умения решать задачи по геометрии, являющиеся прототипами заданий ЕГЭ №3, №6, №8. Тест содержит 15 заданий с кратким ответом.
-
Тест предназначен для учащихся 9-11 классов для проверки уровня подготовки к ГИА по геометрии. Профильный уровень. Ответом для каждого задания служит целое число или десятичная дробь.
-
Данный тест предназначен для контроля знаний по теме «Векторы» учащихся 11 классов образовательной школы, а также учащихся 12 классов вечерней сменной школы. Содержание заданий данной тематики не превышает школьный курс изучения геометрии.
-
Тест предназначен для учащихся 11 классов для проверки уровня подготовки к государственной итоговой аттестации по геометрии, в нём содержатся задачи по разделу «Стереометрия». В тесте 9 задач из Открытого банка. Ответом для каждого задания служит целое число или десятичная дробь.
Варианты для подготовки к ЕГЭ (задания по геометрии)
Вариант № 1
1. 
2. Электрику ростом 1,8 метра нужно поменять лампочку, закреплённую на стене дома на высоте 4,2 м. Для этого у него есть лестница длиной 3 метра. На каком наибольшем расстоянии от стены должен быть установлен нижний конец лестницы, чтобы с последней ступеньки электрик дотянулся до лампочки? Ответ запишите в метрах.
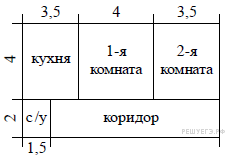
3. 
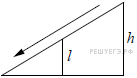
4. 
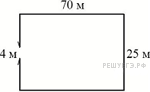
5. 
6.
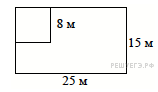
Дачный участок имеет форму прямоугольника со сторонами 25 метров и 15 метров. Хозяин отгородил на участке квадратный вольер со стороной 8 метров (см. рисунок). Найдите площадь оставшейся части участка. Ответ дайте в квадратных метрах.
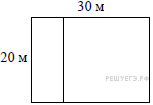
7. 
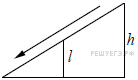
8. 
9. Пол в комнате, имеющей форму прямоугольника со сторонами 4 м и 6 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 30 см. Сколько потребуется таких дощечек?
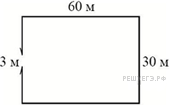
10. 
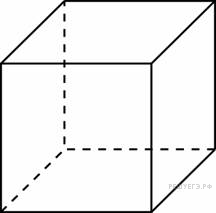
11. 
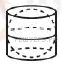
12. 
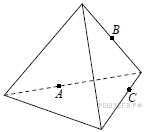
13. 
14. В прямоугольном параллелепипеде известно, что
,
,
. Найдите длину диагонали
.
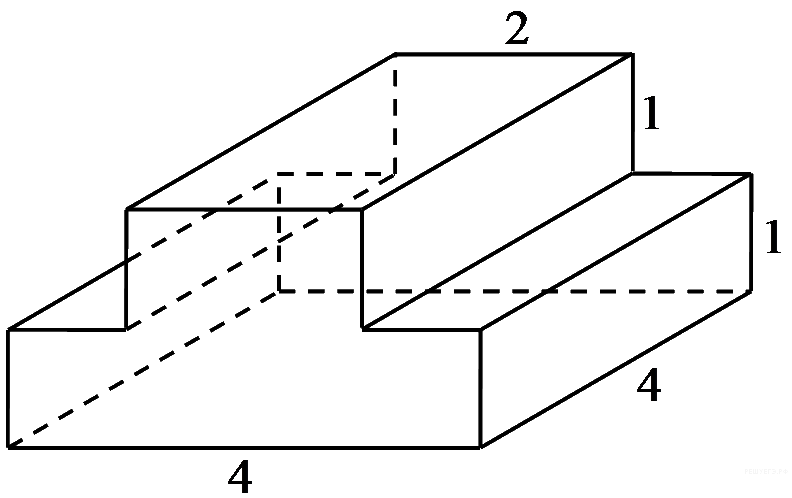
15. 
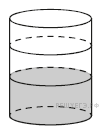
16.
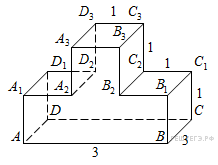
17. 
и
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
18. 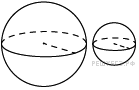
19. Площадь боковой поверхности цилиндра равна , а высота — 1. Найдите диаметр основания.
20. 
Ключ Вариант № 1
|
№ п/п |
Ответ |
|
1 |
1400 |
|
2 |
1,8 |
|
3 |
66 |
|
4 |
1 |
|
5 |
186 |
|
6 |
311 |
|
7 |
120 |
|
8 |
1 |
|
9 |
800 |
|
10 |
177 |
|
11 |
24 |
|
12 |
72 |
|
13 |
6 |
|
14 |
27 |
|
15 |
60 |
|
16 |
1200 |
|
17 |
11 |
|
18 |
9 |
|
19 |
2 |
|
20 |
93 |
Вариант № 2
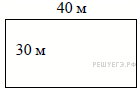
1. 
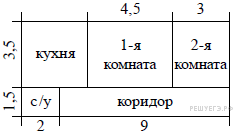
2. 
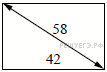
3. 
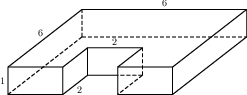
4. Рыболовное хозяйство строит бассейн для разведения рыбы. Бассейн имеет форму прямоугольника со сторонами 4 м и 12 м. В центре бассейна находится техническая постройка, которая имеет форму прямоугольника со сторонами 2 м и 3 м. Найдите площадь оставшейся части бассейна.
5. 
6.
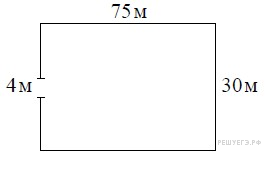
Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 30 м и 75 м. Найдите длину забора (в метрах), которым нужно огородить участок, если в заборе предусмотрен проезд шириной 4 м.
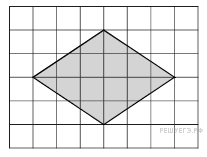
7. 
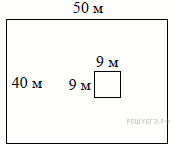
8. 
9. Какой угол (в градусах) образуют минутная и часовая стрелки в 16:00?
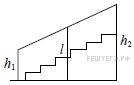
10. 
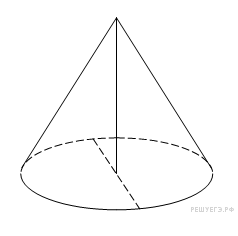
11. 
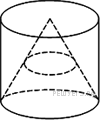
12. 
13.
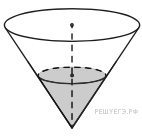
В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объём сосуда 960 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.
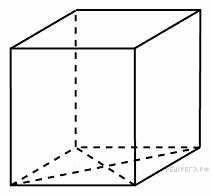
14. 
15. 
и
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
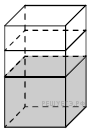
16. 
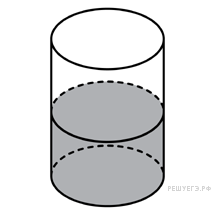
17. 
.
18. 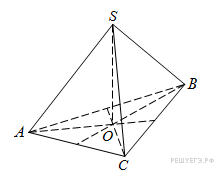
медианы основания
пересекаются в точке
. Площадь треугольника
равна 4; объем пирамиды равен 6. Найдите длину отрезка
.
19. 
20.
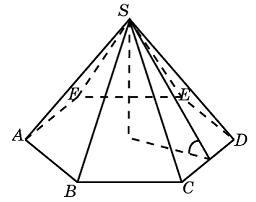
К правильной шестиугольной призме с ребром основания 1 приклеили правильную шестиугольную пирамиду с ребром основания 1 так, что основания совпали. Сколько граней у получившегося многогранника (невидимые рёбра на рисунке не изображены)?
Ключ
|
№ п/п |
Вариант № 1 |
Вариант № 2 |
|
1 |
1400 |
100 |
|
2 |
1,8 |
55 |
|
3 |
66 |
40 |
|
4 |
1 |
42 |
|
5 |
186 |
186 |
|
6 |
311 |
206 |
|
7 |
120 |
12 |
|
8 |
1 |
1919 |
|
9 |
800 |
120 |
|
10 |
177 |
1,1 |
|
11 |
24 |
17 |
|
12 |
72 |
63 |
|
13 |
6 |
120 |
|
14 |
27 |
42 |
|
15 |
60 |
11 |
|
16 |
1200 |
3200 |
|
17 |
11 |
2500 |
|
18 |
9 |
4,5 |
|
19 |
2 |
48 |
|
20 |
93 |
13 |
Геометрия 11 класс.
Пакет заданий по геометрии 11 класса.
Материал может быть использован для подготовки к итоговой аттестации по математике, как на базовом, так и на профильном уровне.
- Название темы: Площадь геометрических фигур
Геометрия 11 класс (подготовка к ЕГЭ-2018).
- Найдите площадь трапеции, изображённой на клетчатой бумаге с размером клетки
- Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 2. Найдите объём параллелепипеда.
- Найдите площадь трапеции, изображённой на клетчатой бумаге с размером клетки
- Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 3. Объём параллелепипеда равен 36. Найдите высоту цилиндра.
- Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см
- Найдите объём прямоугольного параллелепипеда,
у которого АВ=3, АD=4. AA1=5
.
- Найдите площадь квадрата, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
- Найдите вписанный угол, опирающийся на дугу, равную 1/5 окружности
9.
В правильной четырёхугольной пирамиде
с вершиной
точка
– центр основания,
,
. Найдите длину отрезка
.
- Найдите объём многогранника, изображённого на рисунке (все двугранные углы – прямые).
- Площадь круга, изображённого на клетчатой бумаге, равна 16. Найдите площадь заштрихованного кругового сектора.
- Площадь боковой поверхности цилиндра равна 12п, а диаметр основания равен 6. Найдите высоту цилиндра.
- Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы – прямые).
- Найдите площадь трапеции, изображённой на рисунке.
- Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах
- В прямоугольном параллелепипеде АВСД ВВ1=16, А1В1=2, А1Д1=8 Найти длину диагонали АС1.
- Найдите площадь трапеции, изображённой на рисунке.
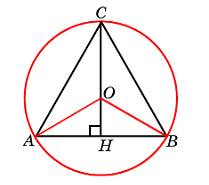
18.В треугольнике АВС АС=ВС. АВ=20, высота АH=8. Найдите синус угла ВАС
19. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен 10√2
Найдите образующую конуса.
20. Найдите объём многогранника, вершинами которого являются точки правильной шестиугольной призмы, площадь основания которой равна 12, а боковое ребро равно 2.
21. В треугольнике АВС, АС=ВС, АВ=15, AH-высота, ВH=6. Найти косинус угла ВАС.
22. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Образующая конуса равна 50√2. Найти радиус сферы
23. Найдите площадь трапеции, изображённой на рисунке.
24. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Образующая конуса равна
50√2. Найти радиус сферы.
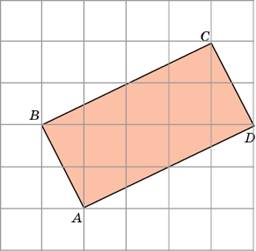
25. Найдите площадь параллелограмма, изображённого на рисунке.
26. Высота конуса равна 21, а длина образующей равна 29.
Найдите диаметр основания конуса.
27. Найдите площадь параллелограмма, изображённого на рисунке.
28. Высота конуса равна 9, а длина образующей равна 41.
Найдите диаметр основания конуса.
29. Найдите объём многогранника, вершинами которого являются точки АВСДА1В1С1Д1
правильной треугольной призмы АВСА1В1С1,
площадь основания которой равна 7, а боковое ребро равно 6.
30. Найдите площадь параллелограмма, изображённого на рисунке.
31. Диаметр основания конуса равен 18, а длина образующей равна 41. Найдите высоту конуса.
32. Найдите объём многогранника, вершинами которого являются точки АВСА1В1С1
правильной треугольной призмы АВСА1В1С1,
площадь основания которой равна 3, а боковое ребро равно 9.
33. Найдите площадь параллелограмма, изображённого на рисунке.
34. В треугольнике АВС AD — биссектриса, угол С равен 62°, угол СAD равен31°. Найти угол В. .
35. Диаметр основания конуса равен 32, а длина образующей равна 65. Найти высоту конуса
Геометрия 10-11 класс, задания по темам. Математика для школьников. Подготовка к ЕГЭ и ОГЭ

Карточка 4
-
Н
айдите площадь прямоугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
-
Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.
-
У
гол при вершине, противолежащей основанию равнобедренного треугольника, равен 30
. Боковая сторона треугольника равна 10. Найдите площадь этого треугольника.
-
Д
ва угла треугольника равны
и
. Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.
-
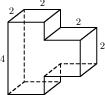
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
-
С
торона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды.
Карточка 5
-
Н
айдите площадь трапеции, вершины которой имеют координаты (1;1), (10;1), (8;6), (5;6).
-
Н
а клетчатой бумаге с размером клетки
изображён четырёхугольник
. Найдите его периметр.
-
В треугольнике ABC
,
. Найдите AB.
-
Т
очки A, B, C, расположенные на окружности, делят ее на три дуги, градусные меры которых относятся как
. Найдите больший угол треугольника ABC. Ответ дайте в градусах.
-
В
сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если её перелить в другой сосуд такой же формы, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в сантиметрах.
-
В прямоугольном параллелепипеде
ребро
, ребро
, ребро
. Точка
— середина ребра
. Найдите площадь сечения, проходящего через точки
,
и
Карточка 6
-
Н
айдите площадь S круга, считая стороны квадратных клеток равными 1. В ответе укажите
.
-
В треугольнике ABC угол C равен
, CH — высота,
,
. Найдите BH.
-
В треугольнике ABC угол C равен
, CH — высота,
,
. Найдите
.
-
В
прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен
. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.
-
С
тороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
-
Н
айдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны
и наклонены к плоскости основания под углом 30
.
-
Найдите угол
прямоугольного параллелепипеда, для которого
,
,
. Ответ дайте в градусах.
Карточка 7
-
Н
а клетчатой бумаге с размером клетки
изображён прямоугольный треугольник
. Найдите радиус окружности, описанной около этого треугольника.
-
В треугольнике ABC угол C равен
, высота CH равна 8,
. Найдите
-
О
стрые углы прямоугольного треугольника равны
и
. Найдите угол между биссектрисой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
-
Х
орда AB стягивает дугу окружности в
. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.
-
Д
ва ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда.
-
Найдите объем многогранника, вершинами которого являются точки
,
,
,
прямоугольного параллелепипеда
, у которого
,
,
.
-
В правильной четырехугольной пирамиде
точка
— центр основания,
вершина,
,
. Найдите длину отрезка
.
Карточка 8
-
Н
а клетчатой бумаге с размером клетки
изображён равносторонний треугольник. Найдите радиус описанной около него окружности.
-
В тупоугольном треугольнике ABC
, высота AH равна 20. Найдите
.
-
Н
айдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 30
.
-
У
гол
равен
. Градусная мера дуги
окружности, не содержащей точек
и
, равна
. Найдите угол
. Ответ дайте в градусах.
-
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
-
Н
айдите объем пирамиды, высота которой равна 6, а основание — прямоугольник со сторонами 3 и 4.
-
Найдите объем многогранника, вершинами которого являются точки
,
,
,
правильной треугольной призмы
, площадь основания которой равна 2, а боковое ребро равно 3.
-
В правильной шестиугольной призме
все ребра равны 1. Найдите тангенс угла
.
Карточка 9
-
Н
айдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
-
В
параллелограмме ABCD
,
,
. Найдите большую высоту параллелограмма.
-
Площадь прямоугольника равна 18. Найдите его большую сторону, если она на 3 больше меньшей стороны.
-
В
треугольнике
угол
равен
, угол
равен
,
— биссектриса,
— такая точка на
, что
. Найдите угол
. Ответ дайте в градусах.
-
В
правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.
-
О
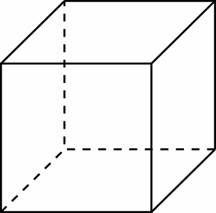
бъём куба равен 12. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.
Карточка 10
-
Н
айдите (в см2) площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см на 1 см (см. рис.). В ответе запишите
.
-
В
треугольнике ABC
, AH — высота,
. Найдите BH.
-
Площадь ромба равна 30. Одна из его диагоналей равна 6. Найдите другую диагональ.
-
В треугольнике
угол
равен ,
— биссектриса, угол равен
. Найдите угол
. Ответ дайте в градусах.
-
С
торона AB треугольника ABC равна 22. Противолежащий ей угол C равен
. Найдите радиус окружности, описанной около этого треугольника.
-
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Карточка 11
-
Н
айдите площадь трапеции, изображенной на рисунке.
-
В
треугольнике ABC угол C равен
, высота CH равна 7,
. Найдите
.
-
Найдите площадь ромба, если его высота равна 32, а острый угол
.
-
В
равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 30. Найдите ее среднюю линию.
-
Р
адиус окружности равен 1. Найдите величину острого вписанного угла, опирающегося на хорду, равную
. Ответ дайте в градусах.
-
Площадь поверхности куба равна 1568. Найдите его диагональ.
-
В кубе
точка
— середина ребра
, точка
— середина ребра
, точка
— середина ребра
. Найдите угол
. Ответ дайте в градусах.
-
Площадь треугольника
равна 10,
— средняя линия, параллельная стороне
. Найдите площадь трапеции
Карточка 12
-
Н
айдите площадь ромба, вершины которого имеют координаты (6;4), (9;5), (10;8), (7;7).
-
В тупоугольном треугольнике ABC
, AH — высота,
. Найдите
.
-
Площадь прямоугольника равна 65. Найдите его большую сторону, если она на 8 больше меньшей стороны.
-
П
ериметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника.
-
У
гол
равен 21°. Градусная мера дуги
окружности, не содержащей точек
и E, равна 114°. Найдите угол
. Ответ дайте в градусах.
-
Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 8, а высота — 3.
-
Н
а рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите тангенс угла
Карточка 13
-
Найдите площадь четырехугольника, вершины которого имеют координаты
,
,
,
.
-
В
тупоугольном треугольнике ABC
, высота AH равна 7,
. Найдите
.
-
Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1 : 2.
-
О
снования равнобедренной трапеции равны 14 и 24, а ее площадь равна 228. Найдите периметр трапеции.
-
Н
айдите вписанный угол, опирающийся на дугу, длина которой равна длины окружности. Ответ дайте в градусах.
-
Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 30, а площадь поверхности равна 2760.
-
От треугольной призмы, объем которой равен 102, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.
Карточка 14
-
Найдите площадь четырехугольника, вершины которого имеют координаты
,
,
,
.
-
Меньшее основание равнобедренной трапеции равно 23. Высота трапеции равна 36. Тангенс острого угла равен
. Найдите большее основание.
-
Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.
-
В
ысота правильного треугольника равна 99. Найдите радиус окружности, описанной около этого треугольника.
-
О
бъем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 41. Найдите объем шестиугольной пирамиды.
-
Площадь поверхности правильной треугольной призмы равна 6. Какой станет площадь поверхности призмы, если все её рёбра увеличатся в три раза, а форма останется прежней?
Карточка 15
-
В параллелограмме ABCD
,
,
. Найдите большую высоту параллелограмма.
-
П
лощадь треугольника
равна 176.
— средняя линия. Найдите площадь треугольника
.
-
О
снования трапеции равны 14 и 26, боковая сторона равна 13. Площадь трапеции равна 130. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ дайте в градусах.
-
О
коло окружности, радиус которой равен 2, описан многоугольник, периметр которого равен 29. Найдите его площадь.
-
Объем параллелепипеда
равен 81. Найдите объем треугольной пирамиды
.
-
На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите расстояние между вершинами
и
.
Карточка 16
-
О
снования равнобедренной трапеции равны 35 и 14. Высота трапеции равна 4,2. Найдите тангенс острого угла.
-
В треугольнике ABC угол A равен
, CH — высота, угол BCH равен
. Найдите угол ACB. Ответ дайте в градусах.
-
Т
очка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 9. Найдите его большую сторону.
-
Н
айдите угол ACB, если вписанные углы ADB и DAE опираются на дуги окружности, градусные меры которых равны соответственно
и
. Ответ дайте в градусах.
-
Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,8 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.
-
Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в тридцать один раз?
К
-
Найдите площадь ромба, если его диагонали равны 27 и 4.
-
В
треугольнике
угол равен
, угол
равен
,
— медиана. Найдите угол
. Ответ дайте в градусах.
-
В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 17. Найдите ее среднюю линию.
-
О
стрый угол ромба равен
. Радиус вписанной в этот ромб окружности равен 5,5. Найдите сторону ромба.
-
Ч
ерез среднюю линию основания треугольной призмы, объём которой равен 76, проведена плоскость, параллельная боковому ребру. Найдите объём отсеченной треугольной призмы.
-
В правильной треугольной призме
, все ребра которой равны 2, найдите угол между прямыми
и
. Ответ дайте в градусах.
Карточка 18
-
В
треугольнике ABC угол A равен
, внешний угол при вершине B равен
. Найдите угол C. Ответ дайте в градусах.
-
У
гол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен
. Найдите меньший угол этого треугольника. Ответ дайте в градусах.
-
Р
адиус окружности равен 1. Найдите величину тупого вписанного угла, опирающегося на хорду, равную
. Ответ дайте в градусах.
-
В
треугольнике ABC
,
, угол C равен
. Найдите радиус вписанной окружности.
-
В
правильной четырехугольной пирамиде высота равна 2, боковое ребро равно 5. Найдите ее объем.
-
В правильной треугольной призме
, все ребра которой равны 4, найдите угол между прямыми
и
. Ответ дайте в градусах.
Карточка 19
-
П
рямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 19, отсекает треугольник, периметр которого равен 39. Найдите периметр трапеции.
-
К
асательные CA и CB к окружности образуют угол ACB, равный
. Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
-
Площадь треугольника
равна 41,
— средняя линия, параллельная стороне
. Найдите площадь трапеции
.
-
Д
ва ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 8 и 6. Объем параллелепипеда равен 240. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
-
Сторона основания правильной шестиугольной пирамиды равна 7, а угол между боковой гранью и основанием равен 45
. Найдите объем пирамиды.
Карточка 20
-
П
ерпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 102 и 55. Найдите среднюю линию этой трапеции.
-
Н
айдите величину острого вписанного угла, опирающегося на хорду, равную радиусу окружности. Ответ дайте в градусах.
-
С
торона AB треугольника ABC равна 33. Противолежащий ей
-
угол C равен
. Найдите радиус окружности, описанной около этого треугольника.
-
Объем куба равен
. Найдите его диагональ.
-
О
бъём тетраэдра равен 55. Найдите объём многогранника, вершинами которого являются середины рёбер данного тетраэдра.
-
В прямоугольном параллелепипеде
известно, что
,
,
. Найдите угол
. Ответ дайте в градусах.
Карточка
-
О
снования трапеции равны 12 и 60. Найдите отрезок, соединяющий середины диагоналей трапеции.
-
У
гол A четырехугольника ABCD, вписанного в окружность, равен
. Найдите угол C этого четырехугольника. Ответ дайте в градусах.
-
К
атеты равнобедренного прямоугольного треугольника равны
. Найдите радиус окружности, вписанной в этот треугольник.
-
Если каждое ребро куба увеличить на 3, то его объем увеличится на 513. Найдите ребро куба.
-
О
бъем правильной четырехугольной пирамиды SABCD равен 40. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC.
-
О
бъем параллелепипеда
равен 42. Найдите объем треугольной пирамиды
.
Карточка 22
-
В
равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 36. Найдите ее среднюю линию.
-
Н
айдите хорду, на которую опирается угол
, вписанный в окружность радиуса
-
П
лощадь треугольника
равна 10,
— средняя линия, параллельная стороне
. Найдите площадь трапеции
.
-
Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 3 и 6, боковое ребро призмы равно 5. Найдите объём призмы.
-
П
лощадь поверхности тетраэдра равна 48. Найдите площадь поверхности многогранника, вершинами которого являются середины рёбер данного тетраэдра.
-
С
тороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
Карточка 23
-
Д
иагонали четырехугольника равны 57 и 8. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
-
Т
очки
,
,
, расположенные на окружности, делят ее на три дуги, градусные меры которых относятся как
. Найдите больший угол треугольника
. Ответ дайте в градусах.
-
В
о сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в одиннадцать раза?
-
На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите тангенс угла
.
-
О
бъем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.
Карточка 24
-
Д
уга окружности
, не содержащая точки
, имеет градусную меру
, а дуга окружности
, не содержащая точки
, имеет градусную меру
. Найдите вписанный угол
. Ответ дайте в градусах.
-
В
треугольнике ABC
,
, угол C равен
. Найдите радиус вписанной окружности.
-
О
т треугольной пирамиды, объем которой равен 92, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
-
В
сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 32 см. На какой высоте будет находиться уровень воды, если её перелить в другой сосуд такой же формы, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в сантиметрах.
-
Найдите объем многогранника, вершинами которого являются точки
,
,
,
,
,
параллелепипеда
, у которого
,
,
.
Карточка 25
-
О
трезки
и
— диаметры окружности с центром
. Угол
равен
. Найдите вписанный угол
. Ответ дайте в градусах.
-
О
дна сторона треугольника равна радиусу описанной окружности. Найдите угол треугольника, противолежащий этой стороне. Ответ дайте в градусах.
-
К
атеты равнобедренного прямоугольного треугольника равны
. Найдите радиус окружности, вписанной в этот треугольник.
-
О
снованием пирамиды является прямоугольник со сторонами 4 и 6. Ее объем равен 48. Найдите высоту этой пирамиды.
-
О
бъем куба равен 27. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
-
В кубе
точка
— середина ребра
, точка
— середина ребра
, точка
— середина ребра
. Найдите угол
. Ответ дайте в градусах.
Карточка 26
-
С
тороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно
,
,
,
. Найдите угол B этого четырехугольника. Ответ дайте в градусах.
-
С
торона ромба равна 58, острый угол равен
. Найдите радиус вписанной окружности этого ромба.
-
Во сколько раз увеличится площадь поверхности куба,
-
если все его рёбра увеличить в 24 раза?
-
О
бъём тетраэдра равен 47. Найдите объём многогранника, вершинами которого являются середины рёбер данного тетраэдра.
-
Н
а рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите квадрат расстояния между вершинами
и
.
Карточка 27
-
Т
очки A, B, C, D, расположенные на окружности, делят эту окружность на четыре дуги AB, BC, CD и AD, градусные величины которых относятся соответственно как
. Найдите угол A четырехугольника ABCD. Ответ дайте в градусах.
-
Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен
. Найдите число вершин многоугольника.
-
П
лощадь параллелограмма
равна 153. Найдите площадь параллелограмма
, вершинами которого являются середины сторон данного параллелограмма.
-
О
снованием прямой треугольной призмы служит прямоугольный треугольник с катетами 7 и 24, высота призмы равна 15. Найдите площадь ее поверхности.
-
Сторона основания правильной шестиугольной пирамиды равна 11, а угол между боковой гранью и основанием равен 45
. Найдите объем пирамиды.
-
В кубе
найдите угол между прямыми
и
. Ответ дайте в градусах.
Геометрия на ЕГЭ по математике
Геометрия на профильном ЕГЭ по математике — одна из сложных тем для абитуриентов. Дело в том, что когда-то экзамен по геометрии в школе был обязательным, а сейчас — нет. В результате у большинства абитуриентов знания по геометрии близки к нулю.
Геометрия на профильном ЕГЭ — это три задачи в части 1 (сюда входит и планиметрия, и стереометрия), а также задача 14 (стереометрия) и для многих недосягаемая задача 16 (геометрия) из второй части. Как же научиться их решать?
Начнем с планиметрии. Прежде всего, выучите основные формулы геометрии.
На нашем сайте вы найдете курс геометрии с нуля — основные определения, формулы и теоремы, а также разбор множества экзаменационных задач по геометрии из части 1.
Для решения задач по геометрии из части 2 нужна более серьезная подготовка.
Первый этап — теория. Необходимый материал есть в учебнике по геометрии за 7-9 класс (автор — А. В. Погорелов или Л. С. Атанасян). Выпишите в тетрадь определения и формулировки теорем. Сделайте чертежи. Доказывать теоремы старайтесь самостоятельно.
Программа по геометрии.
1. Треугольники. Элементы треугольника. Вершины и стороны. Высоты, медианы, биссектрисы (определения).
2. Построение треугольника: практические задания.
а) Три стороны треугольника равны
и
сантиметров соответственно. Постройте треугольник
с помощью циркуля и линейки.
б) В треугольнике угол
равен
градусов, сторона
равна
,
равна
. Постройте треугольник
.
в) В треугольнике сторона
равна
, угол
равен
, угол
равен
. Постройте треугольник
.
3. Три признака равенства треугольников. Неравенство треугольника.
4. Постройте с помощью циркуля и линейки:
а) серединный перпендикуляр к отрезку;
б) биссектрису угла.
5. Углы при параллельных прямых и секущей. Вертикальные, смежные, соответственные, односторонние и накрест лежащие углы. Их определение и свойства.
6. Теорема о сумме углов треугольника.
7. Внешний угол треугольника.
8. Постройте в одном и том же треугольнике
а) Три высоты. Рассмотрите также случаи тупоугольного и прямоугольного треугольника.
б) Три биссектрисы.
в) Три медианы.
9. Равнобедренный треугольник. Определение и свойства. Высота в равнобедренном треугольнике.
10. Средняя линия треугольника и ее свойства.
11. Прямоугольный треугольник. Теорема Пифагора.
12. Определения синуса, косинуса и тангенса:
— для острого угла прямоугольного треугольника;
— для произвольного угла.
13. Четырехугольники. Сумма углов четырехугольника.
14. Параллелограмм. Определение и свойства. Площадь параллелограмма.
15. Виды параллелограммов и их свойства (ромб, прямоугольник, квадрат).
16. Трапеция. Средняя линия трапеции. Площадь трапеции.
17. Подобные треугольники. Три признака подобия треугольников.
18. Площадь треугольника. Формулы и
.
19. Теоремы синусов и косинусов.
20. Чему равно отношение площадей подобных фигур.
21. Свойство медианы (в каком отношении делятся медианы в точке пересечения?)
22. Свойство биссектрисы (в каком отношении биссектриса делит противоположную сторону?)
23. Окружность и круг. Длина окружности. Площадь круга. Длина дуги и площадь сектора.
24. Теорема о радиусе, проведенном в точку касания.
25. Центральный и вписанный углы. Связь между ними.
26. Теоремы о вписанных углах.
27. Теорема о пересекающихся хордах.
28. Теорема об отрезках длин касательных, проведенных из одной точки.
29. Теорема о секущей и касательной.
30. Дан треугольник . Постройте:
а) окружность, вписанную в данный треугольник;
б) окружность, описанную вокруг данного треугольника.
Где находятся центры этих окружностей?
31. Еще три формулы площади треугольника (через радиус вписанной окружности, через радиус описанной окружности и формула Герона).
32. Когда можно вписать окружность в четырехугольник? Когда — описать вокруг четырехугольника?
Программа по стереометрии
Разбирая и решая задания ЕГЭ по геометрии, вы заметите очень интересную вещь. Простые задачи из части 1, разобранные на нашем сайте, часто оказываются базовыми схемами, на которых строятся сложные задачи из части 2 профильного ЕГЭ.
Решая на ЕГЭ задачи по геометрии, обращайте особое внимание на оформление. Помните совет, который дал абитуриентам автор бестселлера «Математика — абитуриенту» В. В. Ткачук. Вот он, этот ценнейший совет:
«Подробность решения должна быть такова, чтобы его мог понять человек в 10 (десять) раз глупее вас».
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Геометрия на ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
09.03.2023















 айдите площадь прямоугольника, изображенного на клетчатой бумаге с размером клетки 1 см
айдите площадь прямоугольника, изображенного на клетчатой бумаге с размером клетки 1 см 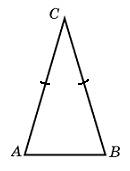 гол при вершине, противолежащей основанию равнобедренного треугольника, равен 30
гол при вершине, противолежащей основанию равнобедренного треугольника, равен 30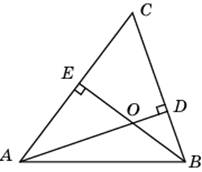
 ва угла треугольника равны
ва угла треугольника равны 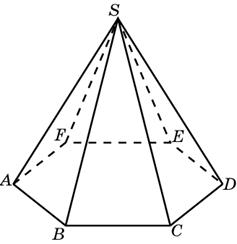 торона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды.
торона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды.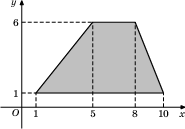 айдите площадь трапеции, вершины которой имеют координаты (1;1), (10;1), (8;6), (5;6).
айдите площадь трапеции, вершины которой имеют координаты (1;1), (10;1), (8;6), (5;6). 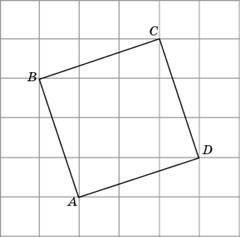 а клетчатой бумаге с размером клетки
а клетчатой бумаге с размером клетки 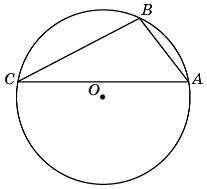 очки A, B, C, расположенные на окружности, делят ее на три дуги, градусные меры которых относятся как
очки A, B, C, расположенные на окружности, делят ее на три дуги, градусные меры которых относятся как 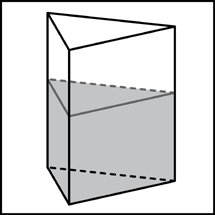 сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если её перелить в другой сосуд такой же формы, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в сантиметрах.
сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если её перелить в другой сосуд такой же формы, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в сантиметрах.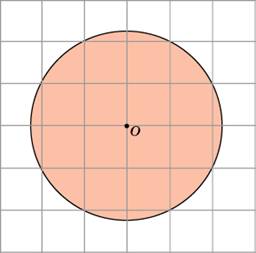 айдите площадь S круга, считая стороны квадратных клеток равными 1. В ответе укажите
айдите площадь S круга, считая стороны квадратных клеток равными 1. В ответе укажите 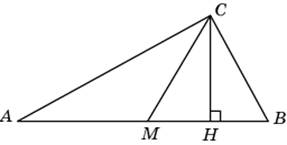 прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен
прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен 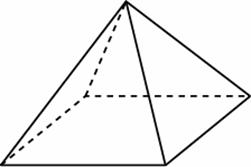 тороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
тороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.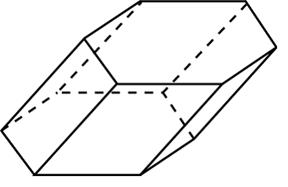 айдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны
айдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны 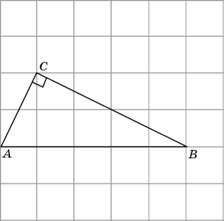 а клетчатой бумаге с размером клетки
а клетчатой бумаге с размером клетки 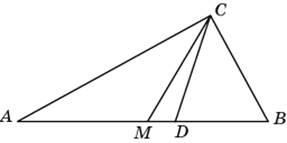 стрые углы прямоугольного треугольника равны
стрые углы прямоугольного треугольника равны 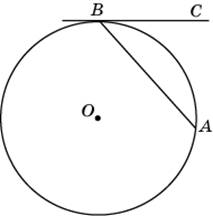 орда AB стягивает дугу окружности в
орда AB стягивает дугу окружности в 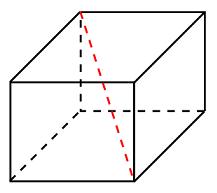 ва ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда.
ва ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда. 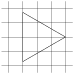 а клетчатой бумаге с размером клетки
а клетчатой бумаге с размером клетки 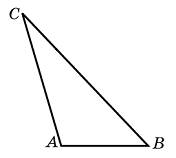 айдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 30
айдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 30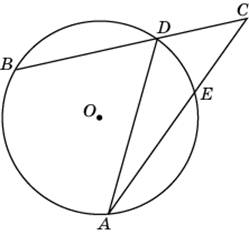
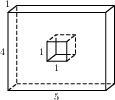 гол
гол 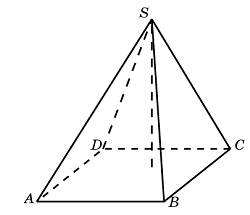 айдите объем пирамиды, высота которой равна 6, а основание — прямоугольник со сторонами 3 и 4.
айдите объем пирамиды, высота которой равна 6, а основание — прямоугольник со сторонами 3 и 4.  айдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
айдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см  параллелограмме ABCD
параллелограмме ABCD 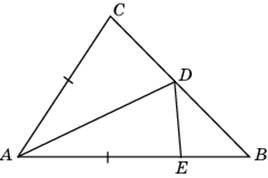 треугольнике
треугольнике 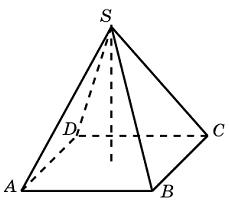 правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.
правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды. 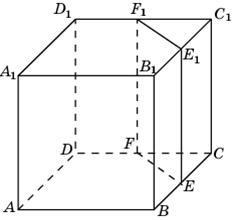 бъём куба равен 12. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.
бъём куба равен 12. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.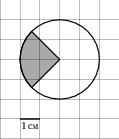 айдите (в см2) площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см на 1 см (см. рис.). В ответе запишите
айдите (в см2) площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см на 1 см (см. рис.). В ответе запишите 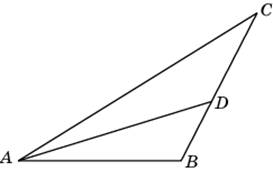
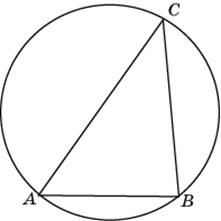
 торона AB треугольника ABC равна 22. Противолежащий ей угол C равен
торона AB треугольника ABC равна 22. Противолежащий ей угол C равен 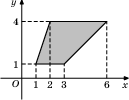 айдите площадь трапеции, изображенной на рисунке.
айдите площадь трапеции, изображенной на рисунке. 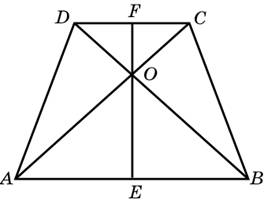 равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 30. Найдите ее среднюю линию.
равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 30. Найдите ее среднюю линию.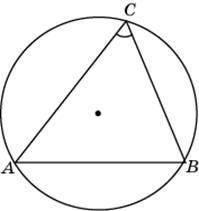
 адиус окружности равен 1. Найдите величину острого вписанного угла, опирающегося на хорду, равную
адиус окружности равен 1. Найдите величину острого вписанного угла, опирающегося на хорду, равную 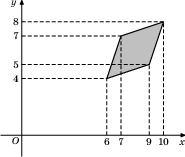 айдите площадь ромба, вершины которого имеют координаты (6;4), (9;5), (10;8), (7;7).
айдите площадь ромба, вершины которого имеют координаты (6;4), (9;5), (10;8), (7;7). 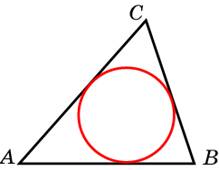 ериметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника.
ериметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника. 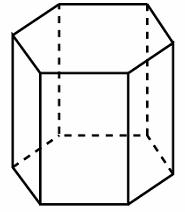
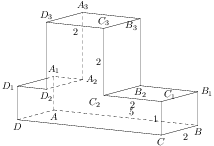 а рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите тангенс угла
а рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите тангенс угла  тупоугольном треугольнике ABC
тупоугольном треугольнике ABC  снования равнобедренной трапеции равны 14 и 24, а ее площадь равна 228. Найдите периметр трапеции.
снования равнобедренной трапеции равны 14 и 24, а ее площадь равна 228. Найдите периметр трапеции. 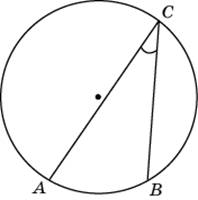
 ысота правильного треугольника равна 99. Найдите радиус окружности, описанной около этого треугольника.
ысота правильного треугольника равна 99. Найдите радиус окружности, описанной около этого треугольника.
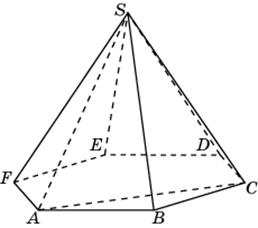 бъем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 41. Найдите объем шестиугольной пирамиды.
бъем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 41. Найдите объем шестиугольной пирамиды. 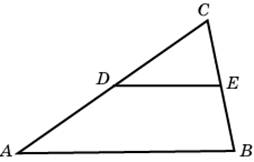 лощадь треугольника
лощадь треугольника 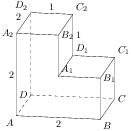 снования трапеции равны 14 и 26, боковая сторона равна 13. Площадь трапеции равна 130. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ дайте в градусах.
снования трапеции равны 14 и 26, боковая сторона равна 13. Площадь трапеции равна 130. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ дайте в градусах.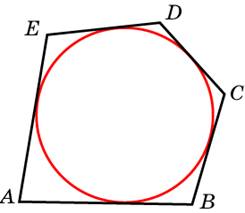
 коло окружности, радиус которой равен 2, описан многоугольник, периметр которого равен 29. Найдите его площадь.
коло окружности, радиус которой равен 2, описан многоугольник, периметр которого равен 29. Найдите его площадь. 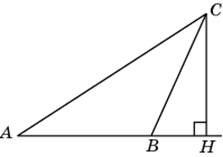 снования равнобедренной трапеции равны 35 и 14. Высота трапеции равна 4,2. Найдите тангенс острого угла.
снования равнобедренной трапеции равны 35 и 14. Высота трапеции равна 4,2. Найдите тангенс острого угла.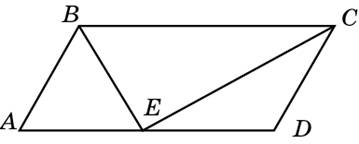 очка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 9. Найдите его большую сторону.
очка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 9. Найдите его большую сторону.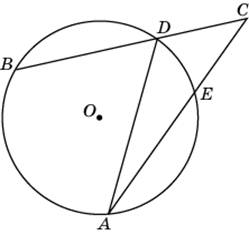
 айдите угол ACB, если вписанные углы ADB и DAE опираются на дуги окружности, градусные меры которых равны соответственно
айдите угол ACB, если вписанные углы ADB и DAE опираются на дуги окружности, градусные меры которых равны соответственно 
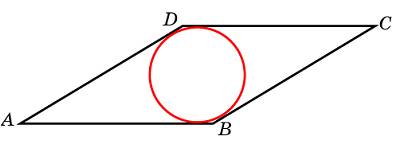 стрый угол ромба равен
стрый угол ромба равен 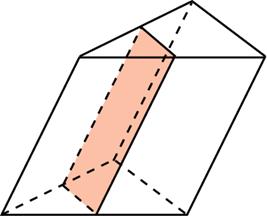 ерез среднюю линию основания треугольной призмы, объём которой равен 76, проведена плоскость, параллельная боковому ребру. Найдите объём отсеченной треугольной призмы.
ерез среднюю линию основания треугольной призмы, объём которой равен 76, проведена плоскость, параллельная боковому ребру. Найдите объём отсеченной треугольной призмы. 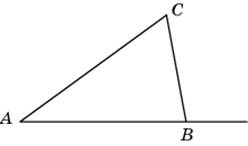 треугольнике ABC угол A равен
треугольнике ABC угол A равен 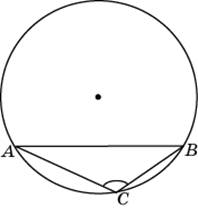 адиус окружности равен 1. Найдите величину тупого вписанного угла, опирающегося на хорду, равную
адиус окружности равен 1. Найдите величину тупого вписанного угла, опирающегося на хорду, равную 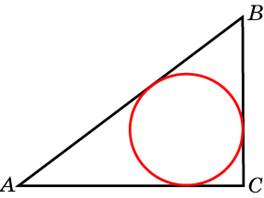 треугольнике ABC
треугольнике ABC 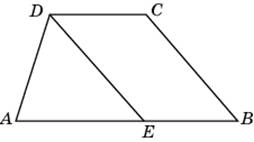 рямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 19, отсекает треугольник, периметр которого равен 39. Найдите периметр трапеции.
рямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 19, отсекает треугольник, периметр которого равен 39. Найдите периметр трапеции.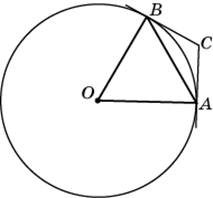 асательные CA и CB к окружности образуют угол ACB, равный
асательные CA и CB к окружности образуют угол ACB, равный 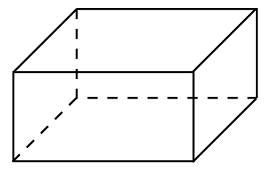
 ва ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 8 и 6. Объем параллелепипеда равен 240. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
ва ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 8 и 6. Объем параллелепипеда равен 240. Найдите третье ребро параллелепипеда, выходящее из той же вершины. 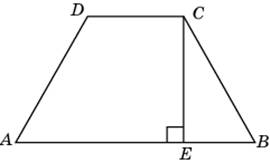 ерпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 102 и 55. Найдите среднюю линию этой трапеции.
ерпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 102 и 55. Найдите среднюю линию этой трапеции.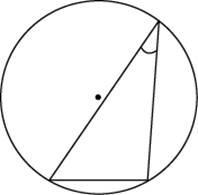 айдите величину острого вписанного угла, опирающегося на хорду, равную радиусу окружности. Ответ дайте в градусах.
айдите величину острого вписанного угла, опирающегося на хорду, равную радиусу окружности. Ответ дайте в градусах.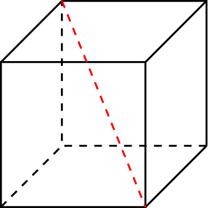 торона AB треугольника ABC равна 33. Противолежащий ей
торона AB треугольника ABC равна 33. Противолежащий ей 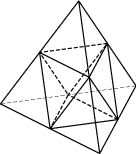 бъём тетраэдра равен 55. Найдите объём многогранника, вершинами которого являются середины рёбер данного тетраэдра.
бъём тетраэдра равен 55. Найдите объём многогранника, вершинами которого являются середины рёбер данного тетраэдра.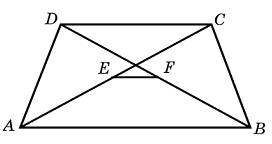 снования трапеции равны 12 и 60. Найдите отрезок, соединяющий середины диагоналей трапеции.
снования трапеции равны 12 и 60. Найдите отрезок, соединяющий середины диагоналей трапеции.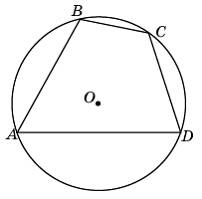 гол A четырехугольника ABCD, вписанного в окружность, равен
гол A четырехугольника ABCD, вписанного в окружность, равен 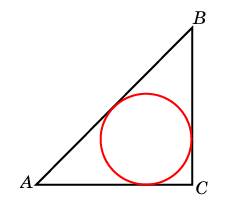 атеты равнобедренного прямоугольного треугольника равны
атеты равнобедренного прямоугольного треугольника равны 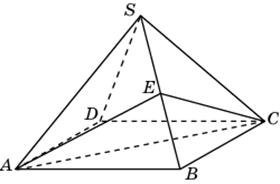 бъем правильной четырехугольной пирамиды SABCD равен 40. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC.
бъем правильной четырехугольной пирамиды SABCD равен 40. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC. 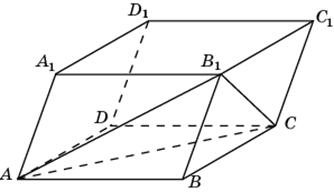 бъем параллелепипеда
бъем параллелепипеда 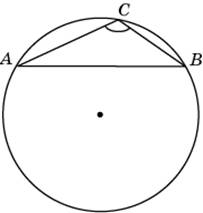 айдите хорду, на которую опирается угол
айдите хорду, на которую опирается угол 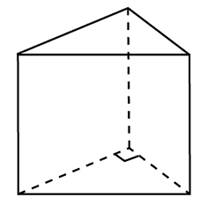 лощадь треугольника
лощадь треугольника 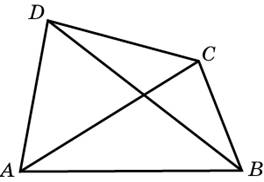 иагонали четырехугольника равны 57 и 8. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
иагонали четырехугольника равны 57 и 8. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.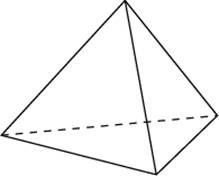
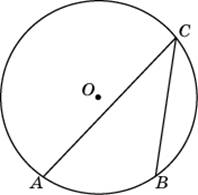 треугольнике ABC
треугольнике ABC 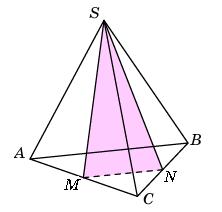 т треугольной пирамиды, объем которой равен 92, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
т треугольной пирамиды, объем которой равен 92, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды. 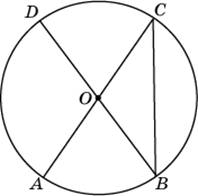 трезки
трезки 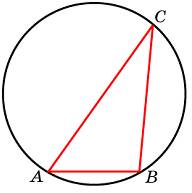 дна сторона треугольника равна радиусу описанной окружности. Найдите угол треугольника, противолежащий этой стороне. Ответ дайте в градусах.
дна сторона треугольника равна радиусу описанной окружности. Найдите угол треугольника, противолежащий этой стороне. Ответ дайте в градусах.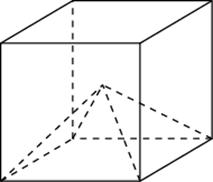 бъем куба равен 27. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
бъем куба равен 27. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.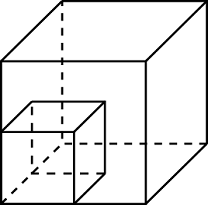 торона ромба равна 58, острый угол равен
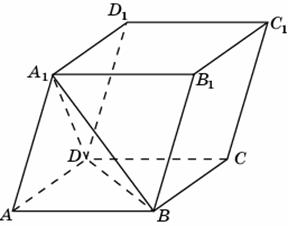
торона ромба равна 58, острый угол равен 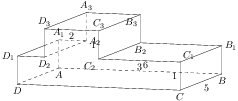 а рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите квадрат расстояния между вершинами
а рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите квадрат расстояния между вершинами 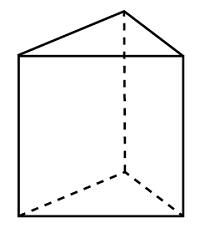 лощадь параллелограмма
лощадь параллелограмма