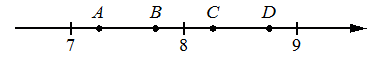Подготовка к устному экзамену по математике 9 класс

ЧАСТЬ 1

Билет
по математике ГВЭ-9 6 устноЙ форме

1.                                                   
из
двух заданий.

а) Найдите
значение выражения — + 0, 07 .

Ответ:

б) Значение какого
из выражений является рациональным числом?

² 4)
(Гб-з)

2.                                                   
Решите
одно из трёх заданий.

а) Решите
уравнение 7х — 9 = 40.

Ответ:

2

5a-9b

б) Найдите значение выражения 9b +               при
а         Ь=З6.

Ответ:

в) Решите систему
неравенств

На каком рисунке
изображено множество её решений?

3.
                          из трёх заданий.

а) В равнобедренном треугольнике АВС
с основанием АС внешний угол при вершине С равен 123 ⁰ . Найдите
величину угла ВАС. Ответ дайте в градусах.

Ответ:

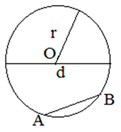
б) Найдите длину хорды окружности
радиусом 13 см, если расстояние от центра окружности до хорды равно 5 см. Ответ
дайте в см.

Ответ:

в) Укажите номера верных утверждений.

1)     
Через
точку, не лежащую на данной прямой, можно провести прямую, параллельную этой
прямой.

2)     
Треугольник
со сторонами 1, 2, 4 существует.

3)     
Если
в ромбе один из углов равен 90 ⁰ , то такой ромб —квадрат.

Ответ:

4. Решите одно из трёх заданий.

а) В таблице приведены
нормативы по бегу на 30 метров для учащихся 9-х классов.

	Мальчики	Девочки
Отметка	«отл.»	«хор.»	«удовл.»	«отл.»	«хор.»	«удовл.»
Время. секунды	4,6	4.9			5,5

Какую отметку получит девочка, пробежавшая
эту дистанцшо за 5,36 секунды?

1)
«отлично»                                                    2) «хорошо»

З)
«удовлетворительно»                               4) Норматив не выполнен.

б) Стоимость проезда в пригородном
электропоезде составляет 198 рублей. Школьникам предоставляется скидка 50%.
Сколько рублей стоит проезд группы из 4 взрослых и 12 школьников?

Ответ:

в) На тарелке лежат пирожки,
одинаковые на вид: 4 с мясом, 8 с капустой и З с яблоками. Петя наугад выбирает
один пирожок. Найдите вероятность того, что пирожок окажется с яблоками.

Ответ:

5.
                      из двух заданий.

а) Рыболов в 5 часов утра на моторной
лодке отправился от пристани против течения реки, через некоторое время бросил
якорь, 2 часа ловил рыбу и вернулся обратно в 10 часов утра того же дня. На
какое расстояние от пристани он отплыл, если скорость течения реки равна 2
км/ч, а собственная скорость лодки равна 6 км/ч?

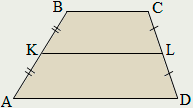
б) В параллелограмме ABCD точка Е середина
стороны АВ . Известно, что ЕС ED. Докажите, что данный параллелограмм
прямоугольник.

Сборник
тренировочных материалов то МАТЕМАТИКЕ

Ответы к заданиям
части 1

М задания	Ответ
	0,32
		125	2
	57	24	в, 31
4	2	1980

5. Решите одно из двух заданий.

а) й1болов в 5 часов утра на моторной
лодке отправился от пристани против течения реки, через некоторое время бросил
якорь, 2 часа ловил рыбу и вернулся обратно в 10 часов утра того же дня. На
какое расстояние от пристани он отплыл, если скорость течения реки равна 2
км,’ч, а собственная скорость лодки равна б км/ч?

Пример выполнения задания

Пусть искомое
расстояние равно х км. Скорость лодки при движении против течения равна 4 км’ч,
при движении по течению равна 8 юшч_ Время, за которое лодка доплывёт от места
отправления до места назначения и обратно, равно  часа
Из у:ловия задачи следует, что это время

равно З часам. Составим уравнение: —
+ — = З Решив уравнение, получим = 8.

Ответ: S юм.

б) В параллелограмме ABCD точка Е — середина стороны
АВ_ Известно, что EC=ED_ Докажите, что данный параллелограмм — прямоугольник.

Слайд 1

Устная работа «Графики функций» ОГЭ-2015

Слайд 2

1) k > 0, b < 0 2) k < 0, b < 0 3) k < 0, b > 0 4) k > 0, b > 0 А Б В 1. На рисунке изображены графики функций вида y = kx + b . Установите соответствие между знаками коэффициентов k и b и графиками функций. Коэффициенты Графики 1 3 2

Слайд 3

А) k < 0, b < 0 Б) k > 0, b > 0 В) k > 0, b < 0 А Б В 2. На рисунке изображены графики функций вида y = kx + b . Установите соответствие между знаками коэффициентов k и b и графиками функций. Графики 3 2 1 Коэффициенты

Слайд 4

А) Б) В) 4. Установите соответствие между графиками функций и формулами, которые их задают. Графики 1) 2) 3) 4) Формулы А Б В 3 1 4

Слайд 5

5. Установите соответствие между графиками функций и формулами, которые их задают. Графики 1) 2) 3) 4) Формулы А Б В 3 2 1

Слайд 6

6. На рисунке изображён график квадратичной функции y = f ( x ). Какие из следующих утверждений о данной функции неверны? Запишите их номера. 1) f (−1) = f (3). 2) Наибольшее значение функции равно 3. 3) f ( x )>0 при −1< x <3.

Слайд 7

А) Б) В) 7. Установите соответствие между графиками функций и формулами, которые их задают. Графики 1) 2) 3) 4) Формулы А Б В 4 2 1 1) 2) 3) 4)

Слайд 8

УТВЕРЖДЕНИЯ ПРОМЕЖУТКИ А) функция возрастает на промежутке Б) функция убывает на промежутке 1) [1;2 ] 2 ) [0;2] 3) [-1;0 ] 4 ) [-2;3] 8. На рисунке изображён график функции y = ax 2 + bx + c . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру. А Б 3 1

Слайд 9

А) Б) В) Г) 1) a > 0, c < 0 2) a < 0, c > 0 3) a > 0, c > 0 4) a < 0, c < 0 9. На рисунке изображены графики функций вида y = ax 2 + c . Установите соответствие между графиками и знаками коэффициентов a и c . А Б В Г 4 1 2 3

Слайд 10

1) k < 0, b < 0 2) k > 0, b > 0 3) k > 0, b < 0 4) k < 0, b > 0 А Б В 10. На рисунке изображены графики функций вида y = kx + b . Установите соответствие между знаками коэффициентов k и b и графиками функций. Коэффициенты Графики 2 1 4

Слайд 11

Устная работа «Геометрия» ОГЭ-2015

Слайд 12

19. Какие из следующих утверждений верны? 1) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8. 2) Любые два равнобедренных треугольника подобны. 3) Любые два прямоугольных треугольника подобны. 4) Треугольник ABC , у которого AB = 3, BC = 4, AC = 5, является тупоугольным.

Слайд 13

24. Какие из следующих утверждений верны? 1) Площадь многоугольника, описанного около окружности, равна произведению его периметра на радиус вписанной окружности. 2) Если диагонали ромба равна 3 и 4, то его площадь равна 6. 3) Площадь трапеции меньше произведения суммы оснований на высоту. 4) Площадь прямоугольного треугольника меньше произведения его катетов.

Слайд 14

23. Какие из следующих утверждений верны? 1) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на синус угла между ними. 2) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13. 3) Треугольник ABC , у которого AB = 5, BC = 6, AC = 7, является остроугольным. 4) В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.

Слайд 15

21. Какие из следующих утверждений верны? 1) Сумма углов выпуклого четырехугольника равна 180°. 2) Если один из углов параллелограмма равен 60°, то противоположный ему угол равен 120°. 3) Диагонали квадрата делят его углы пополам. 4) Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник — параллелограмм.

Слайд 16

22. Какие из следующих утверждений верны? 1) Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник. 2) Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб. 3) Если один из углов, прилежащих к стороне параллелограмма, равен 50°, то другой угол, прилежащий к той же стороне, равен 50°. 4) Если сумма трех углов выпуклого четырехугольника равна 200°, то его четвертый угол равен 160°.

Слайд 17

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания. 20. Какое из следующих утверждений верно? 1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2) Диагонали ромба равны. 3) Тангенс любого острого угла меньше единицы.

Слайд 18

13. Найдите площадь трапеции, изображённой на рисунке.

Слайд 19

15. Найдите тангенс угла В треугольника ABC , изображённого на рисунке.

Слайд 20

16. Найдите площадь трапеции, изображённой на рисунке.

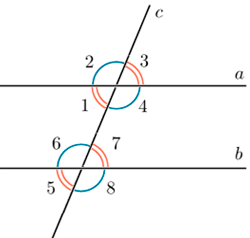
1. Углы

Вертикальные углы равны (на рис. 1 и 3; 6 и 8 и др.).

Внутренние накрест лежащие углы при параллельных прямых и секущей равны. (на рис. 4 и 6; 1 и 7).

Сумма внутренних односторонних углов при параллельных прямых и секущей равна 180˚ (на рис. 4 и 7; 1 и 6).

Соответственные углы при параллельных прямых и секущей равны. (на рис. 3 и 7; 1 и 5 и др.).

Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая перпендикулярна третьей прямой.

2. Медиана, биссектриса, высота

Биссектриса треугольника — отрезок, соединяющий вершину треугольника с точкой на противоположной стороне и делящий угол треугольника пополам.

Высота треугольника – перпендикуляр опущенный из вершины угла на противоположную сторону.

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

В любом треугольники все биссектрисы пересекаются в одной точке, все медианы пересекаются в одной точке, все медианы пересекаются в одной точке.

3. Треугольник

Сумма углов в любом треугольнике 180˚.

Средняя линия треугольника – прямая проходящая через середины двух сторон. Средняя линия параллельна одной из сторон и равна половине этой стороны.

Виды треугольников: тупоугольный (один угол тупой), прямоугольный (один угол прямой 90˚), остроугольный (все углы острые, меньше 90˚).

Равнобедренный треугольник — треугольник, у которого равны две стороны.

Свойства равнобедренного треугольника:

• в равнобедренном треугольнике углы при основании равны;
• в равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой;

Равносторонний треугольник — треугольник,
у которого все стороны равны. (все углы по 60 градусов)

Всякий равносторонний треугольник является равнобедренным,
но не всякий равнобедренный — равносторонним.

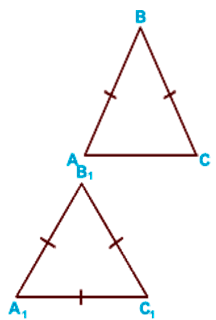
Три признака равенства треугольников

I признак по двум сторонам и углу между ними

II признак (по стороне и прилежащим углам)

III признак (по трем сторонам)

Признаки подобия треугольников

I признак по двум равным углам

II признак по двум пропорциональным сторонам и углу между ними

III признак по трем пропорциональным сторонам

Площади подобных фигур относятся как коэффициент подобия в квадрате.

Объемы подобных фигур относятся как коэффициент подобия в кубе.

Треугольник называется прямоугольным, если один из его углов прямой.

Стороны, прилежащие к прямому углу называются катетами, а сторона, лежащая против прямого угла, – гипотенузой. (самая большая сторона это гипотенуза, две др катеты).

Свойства прямоугольного треугольника

Сумма острых углов прямоугольного треугольника равна 90 градусов.

Катет, лежащий против угла в 30˚, равен половине гипотенузы.

Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы.

Медиана прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, является радиусом описанной около этого треугольника окружности.

Теорема Пифагора:

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: a² + b² = c².

Пифагоровы тройки:

• 3, 4, 5
• 6, 8, 10
• 5, 12, 13
• 9, 12, 15

Признаки равенства прямоугольных треугольников

• По двум катетам.
• По гипотенузе и катету.
• По катету и прилежащему острому углу.
• По катету и противолежащему острому углу.
• По гипотенузе и острому углу.

Признаки подобия прямоугольных треугольников:

• По острому углу.
• По пропорциональности двух катетов.
• По пропорциональности катета и гипотенузы.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

Высота, проведенная из вершины прямого угла, разбивает прямоугольный треугольник на два подобных треугольника. Каждый из этих треугольников подобен исходному.

Высота прямоугольного треугольника: h=ab/c или h = (где АВ гипотенуза, СЕ высота опущенная на гипотенузу).

В прямоугольном треугольнике медиана, проведённая из вершины прямого угла, равна половине гипотенузы: m=c/2 (R=​с/2=m​c).

3. Четырехугольники

Сумма углов в любом четырехугольнике 360˚.

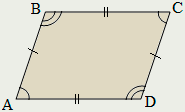
Параллелограмм

Параллелограммом называется четырёхугольник, противолежащие стороны которого попарно параллельны.

У параллелограмма противолежащие стороны равны и противолежащие углы равны.

Сумма любых двух соседних углов параллелограмма равна 180°.

Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

Каждая диагональ делит параллелограмм на два равных треугольника.

Две диагонали параллелограмма делят его на четыре равновеликих треугольника.

Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

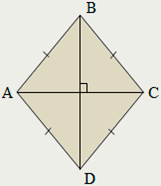
Ромб

Ромбом называется параллелограмм, у которого все стороны равны.

Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.

Прямоугольник

Прямоугольником называется параллелограмм, у которого все углы прямые.

Диагонали прямоугольника равны и точкой пересечения делятся на четыре равных отрезка.

Квадрат.

Квадрат – это прямоугольник, у которого все стороны равны.

Диагонали квадрата равны и перпендикулярны.

Сторона и диагональ квадрата связаны соотношениями: .

Трапеция

Трапецией называется четырёхугольник у которого только две противолежащие стороны параллельны.

Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.

Средняя линия трапеции параллельна её основаниям и равна их полусумме.

Равнобокой называется трапеция, у которой боковые стороны равны.

У равнобокой трапеции: диагонали равны; углы при основании равны; сумма противолежащих углов равна 180.

Стороны и диагональ равнобокой трапеции связаны соотношением: d² = ab+c².

Трапеция называется прямоугольной, если одна из её боковых сторон перпендикулярна основаниям.

4. Окружность

Отрезок, соединяющий центр окружности с любой точкой окружности называется радиусом (r) окружности.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром окружности.

Прямая, имеющая с окружностью одну общую точку, называется касательной. Касательная и радиус проведенный в точку касания пересекаются под прямым углом.

Прямая, имеющая с окружностью две общие точки, называется секущей.

Центральный угол окружности – это угол, вершина которого лежит в центре окружности. Центральный угол равен дуге на которую он опирается.

Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают ее. Вписанный угол равен половине дуги на которую опирается.

Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.

Вписанный угол, опирающийся на диаметр равен 90˚.

Все вписанные углы, опирающиеся на одну и туже дугу равны.

Теорема косинусов:

a² = b² + c² – 2bccosa

Теорема синусов:

5. Формулы площадей

См. продолжение статьи