Подготовка учителя математики к проведению огэ егэ

ООО Учебный центр

«ПРОФЕССИОНАЛ»

Реферат по дисциплине:

«Подготовка учителя математики к проведению ОГЭ (ЕГЭ)»

 По теме:

«Система
работы учителя математики по подготовке учащихся к ЕГЭ, ОГЭ на уроках и во
внеурочное время»

 Исполнитель:

Ершова Екатерина Алексеевна

Балхаш-3,
2018 год.

 «
Школа не должна научить на всю жизнь,
                                           
школа должна научить учиться всю жизнь».

Математика – одна из самых сложных школьных дисциплин,
которая и вызывает трудности у многих учащихся. Однако мы понимаем, что есть
дети, которые имеют явно выраженные способности к этому предмету, и дети, для
которых математика – вечная проблема. И от того, насколько мы грамотно построим
его, зависит наш результат.

При
написании данной работы, хотелось бы ответить на следующий вопрос: «Как сделать
так, чтобы каждый ребенок лучше, чем ранее, развил свой потенциал и был успешен
на итоговой аттестации по математике?»

Подготовка к ЕГЭ и ОГЭ требует как от
учителя, так и от ученика полной выкладки, это, конечно, огромный труд. Для
того, чтобы ученик успешно сдал экзамен, учитель должен всячески поддерживать,
вдохновлять ученика  своей неутомимостью применяя многочисленные формы и методы
работы по подготовке к итоговой аттестации.

Например
такие как:

ü  Полное
информирование учащихся о порядке и форме проведения ОГЭ (ЕГЭ), содержании
КИМов, правилах поведения и заполнения КИМов заполнении бланков и т. д.

ü  Организация
подготовки учащихся к ОГЭ (ЕГЭ) на уроках через включение тестовых заданий или
тех демонстрационных задач из литературы по подготовке к ОГЭ (ЕГЭ),  проведение
контрольных работ в формате данном формате;

ü  Помимо
урочной деятельности возможна подготовка учащихся к ОГЭ (ЕГЭ) на внеклассных
занятиях;

ü  Проведение
мероприятий по подготовке к ЕГЭ в рамках предметной недели естественно-научного
цикла в школе; участие в школьных, региональных, всероссийских, международных
олимпиадах, научно-практических;

ü  Организация
тестирования учащихся в формате ЕГЭ по материалам ФИПИ (пробные испытания на
основе демонстрационных вариантов за этот год или за прошлый) и др.;

ü  Организация
индивидуальной и групповой работы с учащимися разного уровня (т.е. с «сильными»
учащимися разбор более сложных заданий, требующих знания помимо школьного
курса, с более «слабыми» учащимися, разбор обязательной части ОГЭ(ЕГЭ)
включающей стандартный минимум)

ü  Помощь
в организации самоподготовки, в предоставлении книг, печатных изданий и книг в
электронном виде, других источников информации с целью организации
самостоятельной подготовки учащихся к ОГЭ (ЕГЭ);

ü  Обязательная
организация занятий по заполнению бланков регистрации и бланков ответов №1 и
№2;

ü  Проведение
бесед с учащимися с целью оказания психологической помощи в процессе подготовки
и проведения ОГЭ (ЕГЭ).

Предлагаю на ваше рассмотрение примерный план мероприятий по
повышению эффективности подготовки обучающихся к итоговой аттестации по
математике.

I.                  
РАБОТА С УЧАЩИМИСЯ ВО ВРЕМЯ ПОДГОТОВКИ К
ЭКЗАМЕНАМ

1. 
Обеспечение школьников достоверной и своевременной информацией  о нормативных
документах (с сентября, далее в течение года).

2. 
Консультативная поддержка учащихся (в течение года).

3. 
Индивидуальная и групповая работа по подготовке к ОГЭ (ЕГЭ)   на уроках,
внеклассных мероприятиях (в течение года).

4.Обеспечение
учащихся необходимым тестовым, диагностическим, дидактическим материалами,
КИМами (в течение года).

5.Проведение
тренингов с учащимися по заполнению бланков, по     решению КИМов (в течение
года).

6.Проведение
тренировочных и диагностических работ (в течение года).

7.Индивидуальная
работа со слабоуспевающими — выявление личных пробелов, их ликвидация (в
течение года).

8.Участие
школьников в интернет-олимпиадах, выездных олимпиадах ВУЗов, международном
конкурсе «Кенгуру выпускникам».

II.                  
РАБОТА С РОДИТЕЛЯМИ ВО ВРЕМЯ ПОДГОТОВКИ К
ЭКЗАМЕНАМ

1.        
Ознакомление с нормативными документами (в
течение года).

2.        
Проведение разъяснительной работы о целях
и технологии проведения ОГЭ (ЕГЭ)   на родительских собраниях, в индивидуальных
беседах (в течение года).

3.        
Ознакомление родителей с источниками
информации о ОГЭ (ЕГЭ) (перечень необходимых сайтов (сентябрь).

4.        
Систематическое информирование родителей
на родительских собраниях, в индивидуальных беседах, на консультациях о
подготовке к ОГЭ (ЕГЭ):

— 
ознакомление с результатами диагностических работ;

— 
ознакомление с результатами индивидуальной работы;

5. 
Индивидуальная работа, консультирование родителей (в течение года).

III.              
РАБОТА  С  ИНФОРМАЦИОННЫМИ  РЕСУРСАМИ

1.          
Ознакомление учащихся с возможностью использования
Интернет-ресурсов, сайтов  для подготовки
к экзамену (сентябрь)

2.          
Контроль за использованием доступа к
информационным ресурсам для подготовки к ОГЭ (ЕГЭ) (в течение года).

3.          
Индивидуальная работа с учащимися на
сайтах.

Теперь
разберем немного подробнее все то, о чем говорилось выше.  Начиная
с самого начала преподавания у детей предмета, ведется мониторинг уровня
обученности  учащихся по всем темам математики, начиная с 5 по 11 классы. А
затем и работа с детьми по ликвидации пробелов знаний для повышения успешности
изучения математики.

Одно
из направлений организационно-методической работы — создание банка
заданий, подбор учебно-методической литературы.

 За
последние годы работы приобретено множество различной литературы, существует
множество разработок за прошлые годы (которыми пользуемся как на уроках, так и
на внеурочной работе), широкое применение нашли онлайн – экзамены (с
определённой периодичностью, для мониторинга успеваемости при подготовки к ОГЭ
(ЕГЭ)).

Другое
направление организационно-методической работы – освоение тестовых
технологий. Использую тестовые технологии на этапах изучения нового
материала, закрепления, обобщения и проверки знаний. Помимо этого активно
использую тестовые технологии и во внеклассной работе. 

Мои обучающиеся —  активные
участники всероссийских, международных особенно заочных (дистанцинных)
конкурсов и олимпиад по математике.
При создании и компоновке обучающих блоков учитываю, что дети по-разному
воспринимают визуальную и звуковую информацию, по-разному анализируют задания,
использующие формулы, схемы, текст и т.д. В тренировочных блоках одно и то же
понятие закрепляю при выполнении заданий в виде словесных конструкций, заданий,
требующих анализа, в виде таблиц.

В
течение года провожу неоднократно тренировочные, репетиционные работы.

Также считаю, что наиболее
эффективной при подготовке в ЕГЭ и ОГЭ является методика разноуровневого урока,
основанная на дифференцированном подходе к учащимся. Важно определение
стартового уровня знаний для каждого ученика, поэтому в начале учебного года провожу
контрольные срезы.

Что я считаю самым важным при подготовке к ЕГЭ?

1.     
Вычислительные навыки.

2.     
Обязательное знание правил и формул

3.     
 Постоянное совершенствование учебных
навыков на практике.

4.     
Проверка знаний и умений учащихся

5.     
Система работы учителя математики с
родителями

Эффективность
обучения в большей степени зависит от согласованности усилий семьи и школы,
единства их требований к учащимся. От того, умеет ли школа грамотно побудить и
направить инициативы родителей в нужное русло, способна ли она выстроить такую
систему взаимодействия, которая перейдет в сотрудничество, зависит результат
воспитания и подготовки к экзамену выпускников школы.

Конечно, очень важен позитивный настрой детей на
серьёзный самостоятельный труд по подготовке к экзамену, поэтому в
начале каждого учебного года с большим удовольствием сообщаю им информацию о
том, что снова, практически все наши выпускники поступили в высшие и средние
учебные заведения, многие обучаются на бюджетной основе. Обязательно при этом
прошу подсчитать, сколько родительских денег ребята сэкономят за 4-5 лет
обучения. Думаю, что этот стимул для большинства семей  немаловажен.

Роль учителя в школе действительно
велика, но он не всемогущ, и обучить может лишь того, кто хочет учиться и кто
сам учится.

Контроль за качественным, регулярным
выполнением учащимися домашних заданий полностью лежит на родителях. Я
стараюсь, как можно чаще им об этом напоминать.

В заключение хочу остановиться на
пяти принципах, которые мне помогают в работе. Это немного, на то они и принципы.
Зато каждый из них реализуется с помощью гаммы конкретных приёмов.

Принцип свободы выбора.

В любом обучающем или управляющем
действии, где только возможно, предоставлять ученику право выбора. С одним
важным условием – право выбора всегда уравновешивается осознанной
ответственностью за свой выбор.

Принцип открытости.

«Я знаю, что я ничего не знаю», —
говорил мудрый грек. Печально то, что ученик не знает главного: ОН НЕ ЗНАЕТ,
ЧЕГО ОН НЕ ЗНАЕТ. Весьма смутно представляет сегодня школьник границы своей
информированности, границы познания наук. Поэтому необходимо показывать
границы, сталкивать ученика с проблемами, решения которых лежат за пределами
курса.

Принцип деятельности.

Бернард Шоу утверждал: «Единственный путь,
ведущий к знанию, — это деятельность».

Освоение учениками знаний, умений, навыков
преимущественно в форме деятельности.

Принцип обратной связи.

Регулярно контролировать процесс обучения
с помощью развитой системы приёмов обратной связи.

Принцип идеальности (высокого КПД).

Максимально использовать возможности,
знания, интересы самих учащихся с целью повышения результативности, уменьшения
затрат в процессе образования.

Я надеюсь, что предложенная система
подготовки к ОГЭ по математике позволит учащимся получить достойный результат.

Система работы учителя математики по подготовке учащихся к единому государственному экзамену и ОГЭ .

Подготовила учитель математики Поляковской средней школы Аксененко Анна Николаевна

Из всего накопленного опыта и имеющихся знаний хочу поделиться использованной мною технологией разноуровневого подхода в обучении математике. Считаю, что наиболее эффективной при подготовке в ЕГЭ и ГИА является методика разноуровневого урока, основанная на дифференцированном подходе к учащимся. Важно определение стартового уровня знаний для каждого ученика, поэтому в начале учебного года провожу контрольные срезы.

Итак, в классе формирую три уровня учащихся: уровень 1 – учащиеся, которые имеют низкие математические способности, уровень 2 – учащиеся, которые имеют средние математические способности, уровень 3 – учащиеся, которые имеют высокие математические способности. Ребята знают, что со временем можно перейти из одной группы в другую в соответствии с результатами обучения.

На уроках использую технологии уровневой дифференциации, что особенно помогает при подготовке к сдаче экзаменов в форме и по материалам ЕГЭ. После изучения индивидуальных особенностей учеников в классе, работаю в трех направлениях:

1)  провожу разноуровневые уроки, на которых использую ИКТ и разноуровневые задания (обучающие и контролирующие). Учащиеся должны уметь оценивать себя и своих товарищей, знать, что необходимо уметь на оценки «3», «4», «5».

2)  учу самостоятельной работе с учебником, с дополнительной литературой, ресурсами Интернет.

На разноуровневых уроках осуществляю дифференцированный подход на любом из этапов урока.

Огромное внимание уделяю устной работе. Главное условие здесь — систематичность, работа на каждом уроке. Во время устной работы половину повторяемого материала можно отработать в течение 5-7 минут. устный счет всегда провожу так, чтобы ребята начинали с легкого, затем выполняли более сложное. Имею подбор устных упражнений по всем темам, например, решение уравнений 3^х=1, 3^2х-1=27, 5^х=8^х, 3×9^х=81, log₇x=0, log₇(14x)=2, log₇x= log₇3+ log₇5 и так далее.

При изучении нового материала и закреплении: первый урок провожу одинаково для всех, на следующих уроках происходит разноуровневая работа. Уровень 1 – возвращается к основным моментам, повторяет снова теоретический материал и решает простейшие задания. Уровень 2 – сосредотачивается на упражнениях, которые требуют решения, старания и понимания основных положений тем и умений. Задания для уровня 3 – переходят от обязательных в творческие.

Закрепление пройденного материала проводится следующим образом: дети уровня 3 работают по карточкам индивидуально, уровня 2 — работают на месте, а учащиеся уровня 1 работают у доски с учителем.

Провожу самостоятельную работу так же трех уровней, например:

I II

III При каких k система не имеет решений

Домашняя работа так же разноуровневая: уровню1 – соответствующие обязательным результатам обучения, уровню2 – такие же задания плюс еще более сложные задачи и упражнения из учебника, для уровня3 – задания из учебника дополняются задачами из учебных пособий.

Часто перед многими учениками стоит проблема общения ученик-учитель. Им трудно бывает задать вопрос, попросить объяснить снова из-за индивидуальных особенностей личности. У одноклассников проще спросить непонятное, получить в нужный момент помощь. Этому способствует групповая форма работы. Класс разбивается на группы по 2 человека. Дети в парах организованы с разным уровнем развития: средний – низкий, высокий – средний. Все пары получают задания. Задания выполняют парой, при этом идёт обсуждение, опрос друг друга. Затем пара должна защитить перед классом свое решение. Выслушав все пары или часть пар, учащиеся приходят к общему выводу. Таким образом, абсолютно все ученики всё полезное время потратили на достижение главной цели урока. Я направляю работу, частично помогаю, корректирую.

Так же провожу уроки математики, которые мы с детьми называем «Блиц уроки». Решение задач проводится в форме блицтурниров: определённое количество задач нужно решить за отведённый норматив времени (3-5 задач за 1-2 минуты). На блиц – уроке учащимся предлагается весь урок решать задачи. На первый взгляд затея скучная и малоэффективная. Учитель подбирает задачи 3-х уровней сложностей, а право выбора сложности задач оставляет за учащимися. Оценивание за урок проводится рейтинговое, в зависимости от сложности и количества решённых задач. Для высокого рейтинга ученик должен решить, например, 3 сложные или 6 простых задач – выбор за ним. Сильные учащиеся, быстро набрав нужные баллы, выступают в роли консультантов для более слабых учащихся, учатся, обучая. Даже самые слабые ученики ощущают свою успешность, ведь задачи с низким уровнем трудности им по плечу, и, в случае затруднения, всегда можно взять другую задачу или воспользоваться помощью товарища. Эта форма урока наиболее эффективна при закреплении решения задач для подготовки к итоговой аттестации.

Практикую в своей работе зачёты и смотры знаний по темам, что положительно сказывается на подготовке к экзаменам. Зачеты провожу в конце темы в виде теста, который составлен из задач трех уровней. Всего заданий 14. Первые 8 более простые, остальные соответсвуют заданиям ЕГЭ, уровня В и С Задания для смотра знаний учащиеся получают заранее, я помещаю их на стенд «Сегодня на уроке».

Первый этап смотра знаний предусматривает повторение теоретического материала, ребята готовят презентации и отвечают на вопросы теории. Второй этап включает решение задач В1-В14, т.е. умение применять теоретический материал на практике. Третий этап предусматривает решение заданий С1, С2, С3. Приветствуется, если учащиеся применяют различные способы решения.

Одной из задач повседневного учительского труда является необходимость осуществлять контроль знаний учащихся. Тестирование как эффективный способ проверки знаний находит в школе всё большее применение. Одним из основных и несомненных его достоинств является минимум временных затрат на получение надёжных итогов контроля. При тестировании используют как бумажные, так и электронные варианты. Последние особенно привлекательны, так как позволяют получить результаты практически сразу по завершении теста.

Так же для подготовки к ЕГЭ важную роль играют индивидуальные консультации для слабых и сильных, которые провожу еженедельно. Вся эта система работы как на уроках, так и внеурочное время помогает моим учащимся получать хорошие результаты на экзаменах ГИА и ЕГЭ.

Учебная деятельность по подготовке к ЕГЭ реализуется через: урочную систему и внеурочную работу.
      Моя цель заключается в том, чтобы:
адаптировать содержания образования к современным требованиям ЕГЭ;
стремиться к приобретению учащимися универсальных учебных действий, которые пригодятся и в жизни и в приобретении новых знаний по всем предметам, показать способы действий, которые помогут им учить себя всю жизнь  — работа просто с  книгой, поиск информации в сети, получение информации при общении с людьми, практикумы с широкой организацией диалогического общения,  систематический контроль обученности учащихся; мониторинг выполнения типовых заданий.
   Что делаю, чтобы эту цель  увидели и прочувствовали мои ученики и родители. Основные три слона на которых строится успешное достижение цели- успешная сдача экзаменов и конечно формирование универсальных учебных действий при этом- это учитель, ученик и информационные технологии. Причём учитель, не как авторитарная личность(как я сказала так и будет),а учитель помощник, организатор учебного процесса. Ученик- не чан который просто надо наполнить знаниями, а активная личность, которая способна грамотно поставить себе цель и реализовать её различными способами. Информационные технологии как помощники в достижении цели.
      На первом родительском собрании в 5 классе- показываю демонстрационные версии экзаменов( в печатном виде ) и рассказываю о их содержании, откуда берутся задания(открытый банк ФИПИ, открытый банк заданий по математике http://mathege.ru), кто составляет, материал каких классов выносится на экзамен.  Детям демонстрационные версии ЕГЭ и ОГЭ вывешиваю на стенд вместе с бланком , который они будут заполнять на экзамене. И посильные задания ЕГЭ выполняем в спец тетради. За счёт этого у учащихся цель всегда перед глазами. То есть подготовка к экзамену начинается задолго до экзамена.
Хочется начать с того, что в математике нет царских путей. Математика — высокая винтовая лестница. Чтобы взобраться по ней к вершинам знаний, надо пройти каждую ступеньку, от первой до последней. Прежде чем достичь вершины, нам вместе с учениками нужно пройти долгий путь познания.

Задачи по подготовке детей к ЕГЭ:

1. Начинать подготовку к ЕГЭ с 7 класса;

2. Создавать учебный материал (по типу ЕГЭ) для обучающих программ и использовать готовые печатные пособия;

3. Учить школьников «технике сдачи теста»;

4. Психологическая подготовка к ЕГЭ;

5.Через систему дополнительных занятий (индивидуальных консультаций) повышать интерес к предмету и личную ответственность школьника за результаты обучения.

А теперь расскажу, как я решаю поставленные задачи. С чего я начинаю эту работу.

Во-первых, с первых же дней учёбы убеждаю детей в том, что если очень постараться, то можно получить вполне приличный балл. Главное не упустить время.

Во-вторых, в течение всего учебного года знакомлю детей с материалами ГИА и ЕГЭ. Устный счёт на каждом уроке строю только на основе упражнений ЕГЭ и ГИА. Кроме этого, систематически на уроках каждому раздаю тест ЕГЭ: в 7- 9 классах – за основную школу, в 10-11 классах – за полную среднюю школу. Прошу ребят найти в тесте те задания, с которыми они могут справиться уже сегодня и решить их. Стараюсь выслушать все подходы к решению каждой задачи и только потом раскрываю секрет, как можно было решить задачу рациональнее, чтобы сэкономить время.

​ В-третьих, когда уже удалось заинтересовать детей, знакомлю их с особенностями новой формы итоговой аттестации: со структурой теста, нормами оценивания экзаменационной работы, условиями проведения экзамена и начинаю обучать «технике сдачи теста»:

Моя цель заключается в том, чтобы:

• адаптировать содержания образования к современным требованиям ЕГЭ;

• развивать творческие способности и самостоятельную активность учащихся;

• сочетать лекции, самостоятельную работу, поиск информации в сети, практикумы с широкой организацией диалогического общения, консультации;

• систематический контроль обученности учащихся;

• мониторинг выполнения типовых заданий.

В современных условиях, в образовательной деятельности важна ориентация на развитие познавательной самостоятельности учащихся. Решить эту проблему старыми методами невозможно. Всё это побудило меня к разработке своей системы обучения, направленной на повышение качества знаний учащихся, развития их творческих способностей посредством новых информационных технологий. Более плотная подготовка к ЕГЭ начинается в 10 классе. В конце 10 класса ребята пишут контрольную работу по математике в форме ЕГЭ.

Конечно, идеальный вариант к которому стремится каждый учитель — самостоятельная учебная работа ребёнка в интерактивной среде обучения, используя готовые электронные учебные курсы, обучающие, тренировочные и проверочные работы в системе Интернет.

Опыт реализации ЕГЭ подсказал, что подготовка к нему не должна быть самоцелью (школа призвана учить, а не готовить к сдаче экзамена), но в то же время проходить постоянно, но не натаскиванием на тестирование, а в ходе планомерного использования тестов в течение нескольких лет школьного обучения

Чрезвычайно важным представляется отработка алгоритма выполнения тестовых заданий ЕГЭ. Связано это с тем, что учащиеся не умеют правильно распределить свое время. Получив КИМы и инструкции, ученик поставлен в жесткие рамки.

Инструктаж определяет рамки: за 240 минут нужно выполнить 32 задания, правильно оформить ответ, буквы и цифры ставить строго по образцу.. Выпускники, добравшиеся до части «С», сталкивались с заданиями подчас не только трудными, но и громоздкими, а времени на их выполнение оставалось уже немного. Выполнить эти задания нужно было так, чтобы они соответствовали критериям.

Что я считаю самым важным при подготовке к ЕГЭ?

Вычислительные навыки. Обязательное знание правил и формул, теорем. Постоянное совершенствование универсальных учебных действий  на практике. Проверка знаний и умений учащихся.
  Вычислительные навыки, формулы удобно проверять с помощью, так называемой матрицы- в начале урока 5 заданий даю, тут же проверяем или сами или товарищ по парте или учитель- быстро, так как в матрицу вписывают только ответы. Среднее арифметическое всех оценок за 5 работ – выставляю в журнал, удобно.
Пользоваться калькулятором не рекомендую, объясняя его вред. Показываю ребятам некоторые способы быстрого умножения чисел, возведения в степень, извлечения корней др.

Обязательное знание правил и формул. Прежде всего всю теорию собираем в теоретическую папку (существующие справочники часто перегружены информацией не нужной для ЕГЭ, уже давно на экзамене, например нет формул сложения, усечённые конусы и .т.д.) и пишем содержание, чтобы информацию можно было быстро найти. Проверяю теорию очень строго- на парте листок и ручка (в начале урока, когда ещё на парту ничего не положили).
Для этого после изучения теоретических вопросов темы, даю на 5 — 7 минут математический диктант, в котором часть вопросов касается теории и вторая часть — простейшие примеры не её применение.

Постоянное совершенствование учебных навыков на практике.

Проверка знаний и умений учащихся. Выполнение тренировочных и диагностических работ, представленных в сети Интернет.Подготовка к выпускному экзамену в форме ЕГЭ началась в 10 классе. В кабинете математики собраны образцы демоверсий экзаменационных работ, диагностические работы за предшествующие годы, литература для подготовки к ЕГЭ.

Система работы учителя математики с родителями при подготовке учащихся к итоговой аттестации в форме ЕГЭ.

Проблема взаимодействия семьи и школы не нова. Время идет, мир меняется, меняются и взаимоотношения родителей и школы. Но ответственными за воспитание и образование детей остаются родители и школа. Следовательно, учитель и родители должны быть партнерами в этом вопросе. Нередко трудно бывает привлечь родителей к процессу воспитания детей, и часто родителям самим требуется помощь учителя в решении многих вопросов.

Эффективность воспитания в большей степени зависит от согласованности усилий семьи и школы, единства их требований к учащимся. От того, умеет ли школа грамотно побудить и направить инициативы родителей в нужное русло, способна ли она выстроить такую систему взаимодействия, которая перейдет в сотрудничество, зависит результат воспитания и подготовки к экзамену выпускников школы.

Давайте посмотрим, как решается эта проблема в нашей школе. Хочу поделиться своим опытом работы.

В начале учебного года, я обычно посещаю первое родительское собрание. Я на этих собраниях:

знакомлю родителей с планом работы по математике на предстоящий учебный год;

разъясняю позицию Министерства РФ по проблеме ЕГЭ,

характеризую структуру контрольно измерительных материалов (КИМов) по математике;

рассказываю о формах заданий и поясняю подходы к оценке результатов выполнения заданий разной формы;

анализируя содержание проверяемых на экзамене разделов и тем школьного курса математики, обращаю внимание родителей какими знаниями, умениями и навыками должен обладать каждый ученик. Отдельно хочу сказать о консультациях. Провожу их каждое утро в 8,15 часов (занятия в нашей школе начинаются с девяти). Консультации индивидуальные. Ребята знают, что с вопросами по первой, второй части, можно подойти в любое время, но вопросы третьей части подают заранее и приходят в назначенное время. Консультации провожу по своей инициативе, труд этот не оплачивается, я просто рассказываю о своей, годами сложившейся традиции. Ребята знают, что проконсультироваться можно на любой большой перемене и после уроков, если учитель свободен. Коротко расскажу ещё о некоторых факторах успешности на ЕГЭ. Для хорошей подготовки к экзамену необходимо целенаправленное повторение. Однако, упражнения для повторения в учебниках очень объёмны и трудоёмки, требуют письменного выполнения. Поэтому на каждом уроке, организую повторение через систему упражнений составленных на основе материалов ЕГЭ. Я стала экономить время на теории, чтобы использовать его на практику. Всегда стараюсь выдать теорию по теме за 1-2 урока и лекцию построить так, чтобы она содержала все необходимые сведения для решения текущей контрольной работы и экзаменационного материала. Остальные уроки посвящаю практике. Уроки-практикумы попутно дополняю недостающим теоретическим материалом. И еще учителя математики знают, что учебники почти не готовят детей к ЕГЭ, в них по-прежнему традиционные формулировки заданий. Какой я нашла выход: сразу после объяснения нового материала и его первичного закрепления показываю, как эта тема вышла на ЕГЭ. Стараюсь при этом продемонстрировать всё разнообразие заданий из первой и второй части, используя сборники с материалами ЕГЭ разных лет. Иногда прошу найти подобные задания в учебнике. Убедившись, что таких заданий нет, ученики осознают значимость, приобретённых материалов для подготовки к экзамену и уже практически не расстаются с ними. Регулярно провожу диагностические работы для определения пробелов в знаниях. Полученные результаты определяют индивидуальную и дифференцированную работу. Мониторинг и диагностику планирую на основе экзаменационных материалов. Работая с КИМами с 7 класса, ребята привыкают к структуре теста, к необычности формулировок заданий, разнообразию методов и приёмов при решении задач, систематическому пополнению копилки по теории (набору шпаргалок в конверте для запоминания). У них постепенно исчезает чувство растерянности и полной безнадёжности, появляется уверенность и психологическая готовность к новой форме аттестации. Четвёртую четверть в 9, 11 классах посвящаю переходу к комплексным тестам, учу ребят оценивать итоги работы над тестом в целом. Ученики с удовольствием обмениваются печатными пособиями по подготовке к ЕГЭ. Ребят, успешно справляющихся с 1, 2 частью, привлекаю в качестве консультантов. Разработала и систематизировала тестовый материал, создала подборку текстовых задач по подготовке к промежуточным аттестациям, ГИА и ЕГЭ. Конечно, очень важен позитивный настрой детей на серьёзный самостоятельный труд по подготовке к экзамену, поэтому в начале каждого учебного года с большим удовольствием сообщаю им информацию о том, что снова, практически все наши выпускники поступили в высшие и средние учебные заведения и обучаются на бюджетной основе. Обязательно при этом прошу подсчитать, сколько родительских денег ребята сэкономят за 4-5 лет обучения. Думаю, что этот стимул для большинства семей села немаловажен.

Отношение к ЕГЭ школьников и их родителей неоднозначно. Во многом оно зависит от того, насколько они знакомы с содержанием экзамена и насколько высоко оценивают собственную готовность к нему.

Рекомендации ученику

1. ПОМНИТЕ! Фундамент математических знаний закладывается на обычных уроках математики и при систематической подготовке к ним.

2. Необходимо внимательно выслушивать теоретический материал, который учитель объясняет на уроках.

3. Старайтесь не пропускать без уважительной причины уроки математики, потому что качественно восполнить пропущенный теоретический или практический материал самостоятельно сложно.

4. Не допускайте формального усвоения программного материала.

5. Все математические понятия и утверждения нужно обязательно понимать и уметь самостоятельно воспроизводить.

6. Помните, что умение решать задачи является следствием глубоко понятого соответствующего теоретического материала.

7. Выполняйте все домашние задания самостоятельно, консультируйтесь с учителем.

8. Составьте свой, личный справочник теоретического материала и старайтесь постепенно все выучить наизусть, регулярно повторяя выученное.

9. Чем больше информации Вы запомните, тем лучше и быстрее будете выполнять как устные задания, так и задания, требующие значительных умственных усилий.

10. Составьте свой личный план подготовки к экзамену. Покажите его учителю или другому квалифицированному специалисту для подтверждения его правильности и соответствия вашим индивидуальным способностям.

11. Регулярно занимайтесь по личному плану, не реже 1 раза в неделю.

12. На каждом индивидуальном занятии считайте устно. Пытайтесь закрепить (или сформировать) навыки устных вычислений.

Помните: вся подготовка к экзамену зависит лично от каждого из вас. Как вы относитесь к учебе, какой интерес проявляете к учебе, самостоятельно ли выполняете все учебные задания, как используете при этом учебные пособия, какие мысли и чувства вызывает у вас изучение математики, используете ли вы полученные знания и умения по математике в своей жизненной практике, и если используете то как.

Роль учителя в школе действительно велика, но он не всемогущ, и обучить может лишь того, кто хочет учиться и кто сам учится.

Рекомендации родителям.

Уважаемые папы и мамы!

Неверно думать, что если у Вас нет математического образования, то Вы ничем не можете помочь своему ребенку при подготовке к ЕГЭ.

1. Это всегда можно сделать, организуя и контролируя его самоподготовку. Здесь Ваша помощь просто необходима.

2. Ознакомьтесь с “Рекомендациями ученику” и помогайте ребенку их выполнять.

3. Контролируйте его работу и посещаемость на уроках математики в школе (не реже 1 раза в месяц встречайтесь с учителем математики и старайтесь выполнять его рекомендации).

4. Организуйте качественное питание и отдых ребенка в течение всего учебного года (особенно в период сдачи экзаменов). Вечером накануне экзамена родители должны проследить, чтобы ребенок прогулялся и лег спать вовремя. Последние двенадцать часов должны уйти на подготовку организма, а не знаний. Не повышайте тревожность ребенка накануне экзаменов — это может отрицательно сказаться на результате тестирования. Ребенку всегда передается волнение родителей, и если взрослые в ответственный момент могут справиться со своими эмоциями, то ребенок в силу возрастных особенностей может эмоционально «сорваться».

По сравнению с другими учебными предметами математика, несомненно, выделяется своей трудоемкостью, необходимостью большой самостоятельной, повседневной работы. Надо вдумчиво, ежедневно, серьезно работать, чтобы овладеть математикой даже в минимальных размерах, не говоря, уже о более значительных успехах. Поэтому усилия учителя должны быть направлены на формирование у школьников потребности в учебной деятельности, неуемного желания учиться. Необходимо выработать положительное отношение учеников и родителей к математике, создавать ситуации успеха, ликвидировать боязнь решения математических задач, формировать у детей уверенность в своих способностях.

Некоторые рекомендации учителю.

1. Материал на уроках необходимо излагать в простой, доступной, понятной большинству учащихся, форме.

2. Формы работы на уроках необходимо разнообразить, повышая тем самым интерес к предмету.

3. Необходимо добиваться от учащихся не формального усвоения программного материала, а глубокого осознанного его понимания.

4. В процессе преподавания необходимо делать определенные акценты на те разделы, которые представлены в тестах ЕГЭ.

5. Объяснение нового материала необходимо строить как можно более наглядно, создавать яркие образы и конкретные представления об изучаемом материале, чтобы в наибольшей степени воздействовать на чувства ученика, вызвать у него наглядно– образное мышление.

6. Необходимо разработать систему контроля знаний учеников и возможность устранения пробелов в их знаниях.

7. Необходимо сформировать у всех учащихся достаточно высокий уровень учебной самодеятельности, которая явилась бы для них формой самоосуществления, формой свободной, творческой деятельности.

Особое, важное место в подготовке к экзамену, конечно, занимает система домашних заданий. Домашние занятия учащихся способствуют воспитанию у них внимательности и воли, точности и аккуратности, развитию трудолюбия и настойчивости в преодолении встречающихся трудностей, самоконтроля и самооценки. Но все эти качества развиваются у учащихся лишь при правильной организации домашних заданий.

Контроль за качественным, регулярным выполнением учащимися домашних заданий полностью лежит на родителях. Я стараюсь, как можно чаще им об этом напоминать.

С сильными учащимися проще: они контролируют свою работу сами; они более добросовестны; волнуются за свои оценки и хотят знать больше; сами задают вопросы и просят дополнительные, индивидуальные задания. Для “проблемных” детей этот контроль мной осуществляется с помощью системы индивидуальных заданий.

Обязательной составляющей процесса обучения, считаю умение учащихся анализировать свои возможности. Я стараюсь учить их самостоятельно определять для себя приоритетные вопросы при изучении нового материала или при ликвидации пробелов в знаниях; видеть динамику сформированности навыков своей учебной деятельности; учу их оценивать результаты своего труда.

Динамику роста или неудач учащихся регулярно показываю и обсуждаю с родителями, призывая их участвовать в процессе обучения и контролировать работу своих детей.

Советую детям во время экзамена обратить внимание на следующее:

пробежать глазами весь тест, чтобы увидеть, какого типа задания в нем содержатся, это поможет настроиться на работу;

-внимательно прочитать вопрос до конца и понять его смысл (характерная ошибка во время тестирования не дочитав до конца, по первым словам уже предполагают ответ и торопятся его вписать);

· если не знаешь ответа на вопрос или не уверен, пропусти его и отметь, чтобы потом к нему вернуться;

· если не смог в течение отведенного времени ответить на вопрос, есть смысл положиться на свою интуицию и указать наиболее вероятный вариант.

Таким образом, в своей работе я попыталась раскрыть основные направления психолого-педагогического сопровождения при подготовке к ЕГЭ.

После сдачи ЕГЭ выпускники все до единого бегут ко мне домой и очень долго, перебивая друг друга, с огромным волнением рассказывают, что было на экзамене. И как приятно слышать от детей, что все задания экзамена им были знакомы. А потом долгое ожидание результатов, переживание и, наконец, радость со слезами на глазах – ЕГЭ успешно сдали все. Это самая большая награда учителю.

Литература.

1.                Математика: Тематическое планирование уроков подготовки к экзамену. А.В. Белошистая. Москва. Издательство «Экзамен»2013.

2.                Готовимся к ЕГЭ по математике. Обобщающее повторение курса алгебры и начал анализа. Под редакцией Семенко Е.А. Краснодар: «Просвещение-Юг», 2012

3.                ГИА. Математика. 9 класс. Государственная итоговая аттестация (в новой форме). Тематические тренировочные задания. Повышенный уровень. Под редакцией Е.А Семенко

СИСТЕМА РАБОТЫ УЧИТЕЛЯ МАТЕМАТИКИ ПО ПОДГОТОВКЕ УЧАЩИХСЯ К СДАЧЕ ОГЭ И ЕГЭ

А.Ш. ИКСАНОВА, РОССИЯ, ЯНАО, г. Новый Уренгой, МБОУ «СШ№15»

SYSTEM WORK TEACHING MATHEMATICS ON PREPARATION SEPOE OGE AND EGE

A.SH. IXANOVA, RUSSIA, YANAO, New URENGOY, «SSN№15»

Матема́тика (др.-греч. μᾰθημᾰτικά[17] < μάθημα«изучение; наука») — наука об отношениях между объектами, о которых ничего не известно, кроме описывающих их некоторых свойств, — именно тех, которые в качестве аксиом положены в основание той или иной математической теории[18]. Исторически сложилась на основе операций подсчёта, измерения и описания формы объектов[19].  Математика — фундаментальная наука, предоставляющая (общие) языковые средства другим наукам; тем самым она выявляет их структурную взаимосвязь и способствует нахождению самых общих законов природы[20].

Математика — обязательный для всех выпускников основной школы экзамен, и альтернативы ОГЭ как формы проведения его сегодня нет. Подготовка к ОГЭ требует индивидуального, личностного ориентированного подхода. Одним из немаловажных факторов качественной подготовки к ОГЭ, на мой взгляд, является информация, связанная с ОГЭ, а так же материалы ОГЭ по математике. Подготовка учащихся к ОГЭ по алгебре будет более эффективна, если на уроках систематически повторять и обобщать материал, входящий в государственную итоговую аттестацию, составить алгоритмы и опорные схемы типовых задач и разработать факультативный курс по решению второй части ОГЭ.  Но каким образом, можно повысить  качество знаний на экзамене по алгебре в форме основного государственного экзамена (ОГЭ)? Для достижения этой цели необходимо:

Во-первых, проанализировать необходимую математическую литературу;

Во-вторых, проанализировать понятие ОГЭ по алгебре и геометрии, их цели, особенности организации и проведения:

В-третьих, выявить особенности выполнения заданий 2 части ОГЭ;

 В-четвертых, разработать методику подготовки к ОГЭ по алгебре и геометрии;

В-пятых, апробировать разработанную методику с учащимися  9-11  классов;

В-шестых, провести анализ эффективности методики подготовки учащихся к ОГЭ по математике в 9-х классах.

Как учитель математики с начало необходимо изучить педагогические опыты своих коллег, пронаблюдать их работу, сравнить их успехи и просчеты, обобщить их опыт работы. В соответствии с поставленными задачами перед собой, мне необходимо использовать следующие методы работы.

Полученные в ходе анализа литературы, позволят мне избрать основной способ реализации подготовки к ОГЭ по алгебре – решение задач на факультативных занятиях, а также выделить основу для их составления – систему понятий, умений и навыков, необходимых для изучения курса математики. Проведённый мною эксперимент позволит сделать выводы о доступности и эффективности методики подготовки к ОГЭ по алгебре и геометрии в 9-11 классах. Практическая значимость моей работы состоит в том, что разработанная методика подготовки к ОГЭ по алгебре и геометрии  9-11х классов может быть активно использована в школьном преподавании математики. Задачи доступны учащимся, органически связаны с материалом курса математики и в зависимости от их видов могут выполнять различные функции (мотивация, введение новых знаний, формирование понятий, умений и навыков, закрепление изучаемого материала, применение знаний).  

ОГЭ – это форма государственной итоговой аттестации по образовательным программам основного общего образования. При проведении ОГЭ используются контрольные измерительные материалы стандартизированной формы.  Назначение КИМ ОГЭ – оценить уровень общеобразовательной подготовки по математике выпускников IX классов общеобразовательных организаций в целях государственной итоговой аттестации выпускников. Результаты экзамена могут быть использованы при приёме обучающихся в профильные классы средней школы.  ОГЭ проводится в соответствии с Федеральным законом от 29.12.2012 № 273-ФЗ «Об образовании в Российской Федерации». С 2016 года выпускники девятых классов должны сдавать четыре экзамена формата ОГЭ, два из которых обязательные, а два по выбору. Одним из обязательных предметов является математика. Содержание экзаменационной работы ОГЭ определяется на основе Федерального компонента государственного стандарта основного общего образования по математике (приказ Минобразования России от 05.03.2004 № 1089 «Об утверждении федерального компонента государственных образовательных стандартов начального, общего, основного общего и среднего (полного) общего образования»). Кроме того, в экзаменационной работе нашли отражение концептуальные положения Федерального государственного образовательного стандарта основного общего образования (приказ Минобрнауки России от 17.12.2010 № 1897 «Об утверждении федерального государственного образовательного стандарта основного общего образования»). КИМ разработаны с учётом положения, что результатом освоения основной образовательной программы основного общего образования должна стать математическая компетентность выпускников, т.е. они должны: овладеть специфическими для математики знаниями и видами деятельности; научиться преобразованию знания и его применению в учебных и внеучебных ситуациях; сформировать качества, присущие математическому мышлению, а также овладеть математической терминологией, ключевыми понятиями, методами и приёмами.  Структура КИМ ОГЭ отвечает цели построения системы дифференцированного обучения математике в современной школе.

Ведущей целью школьного математического образования является интеллектуальное развитие и формирование качеств мышления учащихся, необходимых для полноценной жизни в обществе. Каждый школьник в процессе обучения должен иметь возможность получить полноценную подготовку к выпускным экзаменам, освоить тот объем знаний, умений и навыков, который необходим для успешной сдачи ОГЭ и дальнейшего обучения в школе. Развитие ОГЭ и ЕГЭ по математике определяется основными задачами, которые стоят перед образованием в связи со стратегическими направлениями социально-экономического развития России до 2020 года: «Приоритетной государственной задачей является обеспечение качественного базового уровня математических и естественнонаучных знаний у всех выпускников школы, не только будущих ученых, но и будущих квалифицированных рабочих. Сильное математическое и естественнонаучное образование, его фундаментальность являются конкурентным преимуществом России. В обучении математике и естественным наукам мы должны максимально использовать существующий потенциал и российские традиции, дополняя их последними научными достижениями, современными образовательными технологиями». Чтобы решить данную проблему необходимо улучшить качество подготовки учащихся средней школы по математике, добиться успешной сдачи ОГЭ и ЕГЭ по математике с высоким результатом. Высокий балл служит необходимым критерием отбора учащихся для поступления  в технический ВУЗ. Повышение качества математической подготовки учащихся педагоги математики видят в совершенствовании процесса обучения на разных ступенях образования.  Одним из направлений совершенствования процесса обучения педагоги выделяют профильное обучение в старших классах, а также предпрофильную подготовку 8-9 классов.  Факультативные курсы как  один из методов предпрофильной подготовки служит эффективной формой работы с учащимися при подготовке к ОГЭ по математике. В современной школе необходимо создавать факультативные курсы, для того, чтобы учащимся было интересно в дальнейшем изучать выбранный профильный предмет, и они делали это целенаправленно.  Необходимость  создания  факультативного курса «Решение второй части ОГЭ по математике»  легло в основу повышения качества математического образования в моей школе.

Факультативный курс направлен на подготовку учащихся к сдаче экзамена по математике в форме ОГЭ. Основной особенностью этого курса является отработка заданий по разделу модуля «Алгебра» повышенного уровня сложности.  Структура творческой разработки, факультативного курса обязательно должна включать следующие разделы: Пояснительная записка Тематическое планирование  Содержание курса Средства обучения Перечень рекомендуемой литературы  Приложения. Пояснительная записка Программа элективного курса ««Решение второй части ОГЭ по математике», ориентирована на приобретение определенного опыта решения задач различных типов 2 части ОГЭ (модуль алгебра), что позволит ученику получить дополнительную подготовку для сдачи экзамена по математике за курс основной школы. С переходом на стандарты второго поколения изменились требования к знаниям, умениям и навыкам учащихся по математике. Само содержание образования существенно не изменилось, но существенно сместился акцент к требованиям умений и навыкам. Изменилась формулировка вопросов: вопросы стали нестандартными, задаются в косвенной форме, задачи носят практический характер.  Факультативный курс, позволит повторить, расширить и углубить изучаемый материал по школьному курсу, развить мышление и исследовательские знания учащихся; сформирует базу общих универсальных приемов и подходов к решению заданий соответствующих типов. Специфика факультативных занятий выражается в том, что в нем основное время и значительное место отводятся задачам самого разнообразного плана, начиная с элементарных упражнений репродуктивного характера и кончая задачами, требующими нестандартных подходов к решению. В связи с этим важнейшая цель учителя состоит в том, чтобы учащиеся овладели технологией решения основных типов алгебраических задач, к которым относятся задания на вычисления, тождественные преобразования выражений, решение уравнений, неравенств, систем, решение текстовых задач с помощью уравнений и систем, построение и чтение графиков функций и т.п.

В процессе проведения факультативных занятий в 9 классе следует продолжить работу, направленную на формирование умений и навыков по данному предмету, которые отвечают таким требованиям, как правильность, осознанность, автоматизм, рациональность, обобщенность и прочность.

 Цель курса:

Подготовить учащихся к сдаче ОГЭ в соответствии с требованиями, предъявляемыми новыми образовательными стандартами. Задачи курса:

   Обобщение, систематизация, расширение и углубление математических знаний, необходимых для изучения смежных дисциплин и продолжения образования.

  Сформировать у учащихся навык решения более сложных задач и умение ориентироваться в теоретическом материале этого уровня.

 Интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности. В процессе обучения учащиеся приобретают умения и навыки:

 – преобразование целых и дробных выражений;

 – решения уравнений, неравенств и систем неравенств;

 – исследования функций;

– построения графиков;

 – выполнять вычисления;

 – проводить обобщение, классификацию, систематизацию объектов;

 – сопоставлять, проводить сравнения и аналогии;

 – переносить знания в новую ситуацию.

 Формы организации занятий – практикумы по решению задач, зачетные работы, лекции, беседы. Основной тип занятий  комбинированный урок. Каждая тема курса начинается с постановки задачи. Теоретический материал излагается в форме мини лекции. После изучения теоретического материала выполняются практические задания для его закрепления. В ходе обучения периодически проводятся непродолжительные, рассчитанные на 30-45 минут, контрольные работы и тестовые испытания для определения глубины знаний и скорости выполнения заданий. Контрольные замеры обеспечивают эффективную обратную связь, позволяющую учащимся корректировать свою деятельность. Систематическое повторение способствует более целостному осмыслению изученного материала, поскольку целенаправленное обращение к изученным ранее темам позволяет учащимся встраивать новые понятия в систему уже освоенных знаний. Занятия строятся с учётом индивидуальных особенностей учащихся, их темпа восприятия и уровня усвоения материала. Контроль и система оценивания Текущий контроль уровня усвоения материала осуществляется по результатам выполнения учащимися самостоятельных и практических работ. Количественная оценка предназначена для снабжения учащихся объективной информацией об овладении ими учебным материалом и производится по пятибалльной системе. Итоговый контроль реализуется в двух формах: традиционного зачёта и тестирования.

Виды деятельности учащихся:

 – поиск информации, заданий в ресурсах сети Интернет, в печатных изданиях,

 – рефлексия своей учебной деятельности при изучении курса,

 – выполнение домашних заданий / по выбору учащихся /, Форма проведения итоговой аттестации – итоговое тестирование в форме ОГЭ. Структура курса Курс рассчитан на 17 занятий. Включенный в программу материал предполагает повторение и углубление следующих разделов алгебры:

  21 (C1). Алгебраические выражения, уравнения, неравенства и их системы

 Алгебраические выражения

 Неравенства

 Системы неравенств

  Уравнения

  Системы уравнений  22 (C2).

Девятиклассникам необходима определённая система подготовки при решении второй части ОГЭ по математике, которая направлена на проверку овладения материалом на повышенных уровнях, основное её назначение – дифференцировать хорошо успевающих учеников по уровню подготовки. Задания второй части модуля «Алгебра» направлены на проверку владения таких качеств математической подготовки выпускников, как:

 формально-оперативным алгебраическим аппаратом;

 умения решить комплексную задачу, включающую в себя знания из разных тем курса алгебры;

1. умения математически грамотно и ясно записать решение, приводя при этом необходимые пояснения и обоснования;

  владения широким спектром приёмов и способов рассуждений. Вторая часть модуль «Алгебра» содержит три задания, предусматривающих развернутый ответ с записью хода решения. Все задачи представляют разные разделы математики.  Основные проверяемые требования к математической подготовке учащихся  Основные проверяемые требования к математической подготовке Разделы элементов содержания Разделы элементов требований Максимальный балл за выполнение задания

2.1 Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций

1.Алгебраические выражения;

2.Уравнения и неравенства;

3.Функции и графики

4.Уметь выполнять преобразования алгебраических выражений

2.2 Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций, строить и исследовать простейшие математические модели

1.Алгебраические выражения;

 2.Уравнения и неравенства;

3.Числовые последовательности;

 4.Функции и графики;

 5.Координаты на прямой и плоскости

Уметь решать уравнения, неравенства и их системы;  7.Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни,  уметь строить и исследовать простейшие математические модели.

2.3 Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций, строить и исследовать простейшие математические модели

1 Алгебраические выражения; 3.Уравнения и неравенства; 2.Числовые последовательности; 5. Функции и графики; 6. Координаты на прямой и плоскости

3. Уметь строить и читать графики функций; 2. Уметь выполнять преобразования алгебраических выражений

Требования к выполнению заданий с развернутым ответом заключаются в следующем: решение должно быть математически грамотным и полным, из него должен быть понятен ход рассуждений учащегося. Оформление решения должно обеспечивать выполнение указанных выше требований, а в остальном может быть произвольным.  При подготовке учащихся к ОГЭ учителю необходимо:

  формировать у учащихся навыки самоконтроля;

 формировать умения проверять ответ на правдоподобие;

 систематически отрабатывать вычислительные навыки;

 формировать умение переходить от словесной формулировки соотношений между величинами к математической.

Задания второй части считаются выполненными верно, если учащийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае ему выставляется полный балл, соответствующий данному заданию. Если в решении допущена ошибка, не носящая принципиального характера и не влияющая на общую правильность хода решения, то учащемуся засчитывается балл, на 1 меньше указанного. В факультативном курсе «Решение второй части ОГЭ по математике» необходимо  методически грамотно выстроить задания второй части ОГЭ. С этой целью задания в разделах выстраиваются по нарастанию сложности – от относительно простой задачи до задач достаточно сложных, требующих свободного владения материалом и высокого уровня математического развития. Последние задачи наиболее сложные, они рассчитаны на учащихся, изучавших математику более основательно, чем в рамках пятичасового курса. Задания второй части экзаменационной работы носят комплексный характер. Их выполнение требует уверенного владения формально оперативным алгебраическим аппаратом, способности к интеграции знаний из различных тем курса, владения широким  набором приемов и способов рассуждений. Кроме того, учащиеся должны продемонстрировать умение математически грамотно записать решение, приводя при этом необходимые пояснения. Расстановка заданий по уровням сложности позволит  создать условия для дифференцированного обучения. Их относительную сложность можно условно разделить на три уровня и обозначить количеством баллов: 2 балла, 4 балла, 6 баллов.

Такой способ расстановки заданий позволит структурировать содержание курса по спирали, что позволяет возвращаться к изученному ранее материалу на новом уровне, включать знания в новые связи, формировать их в системе.

 Рассмотрим задание 21 (C1). Алгебраические выражения, уравнения, неравенства и их системы

1. Выражения и их преобразования: Задания направлены на проверку умений:

 выполнять разложение многочленов на множители с использованием нескольких способов;

 выполнять многошаговые преобразования целых и дробных выражений, применяя широкий набор изученных алгоритмов;

 выполнять преобразования выражений, содержащих степени с целыми показателями, квадратные корни;

 применять преобразования для решения задач из различных разделов курса (например, нахождение наибольшего или наименьшего значения выражения). Задания, оцениваемые 2 баллами и т.д.

2. Уравнения. Задания направлены на проверку умений:

  решать целые и дробно-рациональные уравнения; применять при решении уравнений алгебраические преобразования, а так же такие приемы, как разложение на множители, замена переменной;

  отвечать на вопросы, связанные с исследованием уравнений, содержащих буквенные коэффициенты, используя при необходимости графические представления;

  решать уравнения графически. Алгоритм решения 1. Линейные уравнения         решаются следующим образом:

  перенос слагаемого из одной части уравнения в другую с противоположным знаком,

  а также умножение или деление обе частей уравнения на одно и то же отличное от нуля число. При этом линейное уравнение a·x+b=0 имеет

  единственный корень    

          не имеет корней при,  

          имеет бесконечно много корней при, в этом случае любое число является корнем линейного уравнения.

  2. Квадратные уравнения решаются по готовой формуле или используется теорема Виета для приведенных уравнений (а=1):        

При решении квадратных уравнений можно использовать опорную схему. см. Приложение 1 3. Дробно–рациональные уравнения решаются по следующей схеме: а) перенести все члены уравнения в левую часть; б) все члены уравнения в левой части привести к общему знаменателю, т.е. уравнение записать в виде                в) решить уравнение                        Так же при решении уравнений используют графический метод. 4. Иррациональные уравнения можно решить различными методами

 Метод возведения обеих частей уравнений в одну и ту же степень.

  Решение уравнений с использованием замены переменной.

  Метод разложения на множители выражений, входящих в уравнение и др. 2 балла

Разработана система работы по подготовке к ОГЭ по математике. Система работы по подготовке к ОГЭ в 9 классе на факультативном занятии включает следующие компоненты:

 1. При изучении учебного материала разбирать соответствующие экзаменационные задания.

 2. В текущий контроль включать экзаменационные задачи.

 3. Итоговое повторение построить на отработке умений и навыков, требующихся для получения положительной оценки на экзамене. Важным условием успешной подготовки к экзаменам является не только тщательное отслеживание результатов ученика по всем темам и своевременной коррекции уровня усвоения учебного материала, но и мотивация учеников и родителей. Ученики обычно сами знают, какие задания у них вызывают трудности. Сначала надо выполнять задания, в которых ученик хорошо ориентируется. Задача учителя в том, чтобы ученик самостоятельно мог набрать максимально возможное количество баллов. Необходимо учить технике выбора ответа методом «исключения» неверного ответа, приучать внимательно, перечитывать условие и вопрос. Обучать

приему «спирального движения» по тесту. Ученик, просматривая тест, отмечает для себя простые и понятные задания, которые выполняются без особых усилий. Затем найти задания, которые поняли сразу, затем перейти к тем, которые «не поддались» сразу. Так необходимо делать несколько раз «по спирали» и делать то, что стало понятным к данному моменту. Подготовка осуществляется во внеурочное время. Для подготовки использую различные сборники, рекомендованные ФИПИ, открытый банк заданий ФИПИ, интернет ресурсы. В течение 9 класса проводим неоднократно пробные экзамены. Знакомлю их с временными рамками, нормами оценивания экзаменационной работы, условиями проведения экзамена: обучаю строгому самоконтролю времени. Полученные результаты определяют индивидуальную и дифференцированную работу на занятиях факультативного курса. Работая с КИМами, ребята привыкают к структуре теста, разнообразию методов и приёмов при решении задач. Использование новых информационных технологий оказывают существенную помощь в моей работе. Мульдимедийные презентации позволяют представить учебный материал как систему ярких опорных образов наполненных исчерпывающей информацией в алгоритмическом порядке. Задействуются различные каналы восприятия, что позволяет заложить информацию не только в фактографическом, но и в ассоциативном виде в долговременную память учащихся. Наиболее успешных учеников я привлекаю к созданию презентаций из подборок заданий и способов их решений как базового, так и повышенного уровня сложности по различным темам программы. В процессе работы над этой презентацией ученик повторяет и систематизирует материал, подбирает типовые задания по данной теме определенного уровня сложности, самостоятельно их решает и защищает проект во время урока. В результате чего, усвоение материала повышается в несколько раз.

Понимание изучаемого материала или задачи достигается только в результате активных мыслительных действий, тогда и сама деятельность становится для учащегося интересной. Чтобы повысить интерес учащихся, совсем не обязательно подбирать какой–либо особо интересный материал – достаточно добиться активизации мыслительной деятельности над изучаемым материалом. Каждый этап деятельности учащегося должен быть оценен на своем уровне, но и поощрение оценкой допустимо. На каждом уроке учащийся должен знать, какие задания он должен уметь выполнять, какой этап деятельности будет следующим, какие основные вопросы по теории должен выучить. При дифференцированной работе каждый ученик имеет возможность овладевать учебным материалом в зависимости от его способностей и индивидуальных особенностей личности, когда за критерий оценки деятельности ученика принимаются его усилия по овладению этим материалом и творческому применению знаний. Разноуровневые задания облегчают организацию занятий в классе, создают условия для продвижения школьников в учебе в соответствии с их возможностями. Не менее важным является контроль выполнения заданий, своевременная помощь учащимся в случае возникновения у них затруднений. Время урока используется более эффективно. Введение учебного материала должно быть произведено с учетом закономерностей процесса познания при высокой мыслительной активности учащихся. Выделение уровня обязательной математической подготовки для всех учащихся и одновременное создание условий для достижения более высоких результатов теми учащимися, которые проявили склонность и интерес к предмету. Поскольку необходимые знания по математике, умения и навыки учащиеся приобретают только путем самостоятельных, интеллектуальных усилий, то работу учащихся следует направлять. Можно использовать следующие методы:

 – метод целесообразных задач,

 – эвристический метод,

 – вопросно–ответный метод, алгоритмический метод.

Сущность метода целесообразных задач сводится к тому, что для лучшего понимания изучаемого материала учащимся предлагаются подготовительные задачи.  Например,

  Решите в целых числах уравнение                                          

 Необходимо, чтобы знаменатель был равен 1 или числитель был равен нулю, иначе y не будет выражаться целым числом:                      // При изложении новой темы с использованием метода целесообразных задач желательно подбирать минимальное число подготовительных задач, причем одна и та же задача может быть рассмотрена несколько раз, помогая оттенить отдельные детали темы.

Чаще всего мною для объяснения нового материала используется вопросно–ответный метод (беседа). Пример. Проиллюстрируем эти разновидности вопросно-ответного метода при доказательстве одного из свойств неравенств: Дано: с — любое число, a > b. Доказать: a + c > b + c.  Проводя беседу аналитико-синтетическим способом, приходится изменять структуру рассуждения, приведенного в учебнике, что, конечно, требует более тщательной подготовки к уроку, например:

1. Вспомним, что для отыскания способа доказательства рекомендуется заменять понятия их определениями. Поэтому вспомним, при каком условии разность a – b положительна. По определению a > b если разность a – b положительна.

 2. Что достаточно знать для доказательства неравенства a + c > b + c?  Достаточно доказать, что разность (a + c) – (b + c) положительна. Попытайтесь это доказать.  (a + c) – (b+c) = a + c – b – c = a – b, но a – b – положительное число, так как a > b. Очень важно организовать работу таким образом, чтобы каждый ученик «проговаривал» в ходе подробных записей соответствующий фрагмент правила. Практически все правила, мы переформулируем в «рабочие». Многие из них начинаются со слов:

«Для того чтобы…» и «Если…, то…». Например: Для того чтобы перенести слагаемое из одной части неравенства в другую, необходимо изменить знак этого слагаемого на противоположный. Если коэффициент, а >0, то ветви параболы направлены вверх. Алгоритмический метод обеспечивает возможность выполнения упражнения с необходимыми объяснениями и в той же последовательности, как дается в алгоритме. Например:  Алгоритм решения квадратичного уравнения  ах2+bх+с=0:

1)Вычислить дискриминант D по формуле D = b2 – 4ас.

2) Если D < 0, то квадратное уравнение не имеет корней.

3) Если D = 0, то квадратное уравнение имеет один корень:

4) Если D > 0, то квадратное уравнение имеет два корня:

 Итак, умения применять алгоритмы развивают устную и письменную речь учащихся в такой мере, что они довольно быстро переходят к более сложным умениям — самостоятельному составлению новых алгоритмов. Алгоритм решения рационального уравнения

1. Перенести все члены уравнения в одну часть.

2. Преобразовать эту часть уравнения к виду алгебраической дроби  (х)

3. Решить уравнение  

4. Для каждого корня уравнения сделать проверку: удовлетворяет ли он условию        или нет.

   Если да, то это корень заданного уравнения;

   если нет, то это посторонний корень и в ответ его включать не следует.

Пример 2: Решить уравнение 22.    

Так как небезызвестно, что знаменатель дроби не может равняться нулю, то, для того, чтобы равенство было верным, необходимо, чтобы числитель равнялся 0. Не стоит забывать проверить знаменатель. Если при некоторых найденных корнях знаменатель будет обращаться в ноль, то следует исключить их из решения. Удовлетворяет условию только Ответ: 4 Естественно, необходимо сочетание с применением образца ответа. При решении квадратного неравенства методом неравенств после объяснения того, как оно решается, дается опорная схема «Решение квадратного неравенства». Но для полного понимания от учащихся требуется объяснение каждого шага. Решить неравенство

1)Умножить на (–1), чтобы старший член был положительным.

2) Решить квадратное уравнение

  Если D  — найти корни уравнения

  Если D=0 – найти один корень

  Если D    то определить направление ветвей параболы, выбрать ответ в соответствии со знаком неравенства.

2) Разложить на множители (х–4)(х+1)<0

3)Отметить на числовой прямой корни уравнения, которые разбивают прямую на интервалы.

4) Расставить, чередуя знаки на интервалах справа налево.

5)Выбрать ответ в соответствии со знаком неравенства.

Указания в алгоритме всегда даю в таком виде, чтобы они содержали в себе все необходимые объяснения, какие должны быть услышаны от учащихся по ходу решения задач. Слабые учащиеся охотно выполняют задания, содержащие инструктивный материал, особенно те упражнения, в которых приведены данные для самоконтроля (образцы решений). Просто выяснив, что получен неверный ответ, ученик не в состоянии проследить всю цепочку и найти ошибку. В таком случае он может проследить ход решения по образцу и самостоятельно выполнить подобное задание. Такая организация учебной работы учащихся дает возможность каждому ученику в силу своих возможностей, способностей и собранности постепенно углублять и закреплять полученные и получаемые знания, вырабатывать необходимые умения, навыки, формировать потребности в самообразовании. При диагностическом тестирование выявляются пробелы в знаниях учащихся по изученной теме, у учителя появляется возможность классифицировать типичные ошибки. Серьезное внимание уделяю проблеме устранения имеющихся пробелов в знаниях учащихся, развиваю мыслительную деятельность учеников через систему подобранных заданий.  Устанавливается уровень усвоения учащимися изученного материала. Ученику предоставляется возможность повторно проработать (самостоятельно или с помощью учителя) те элементы, которые им не усвоены. Каждый ученик работает в своем темпе, на своем уровне. Для выработки в чем–либо прочного навыка надо выполнить несколько однотипных действий. Поэтому на любое правило составляется заведомо большое количество однотипных самостоятельных работ. Ученик получает самостоятельную работу на то или иное правило. Ошибся, получил помощь и дальше делает следующую работу на это же правило. Снова ошибка – снова помощь. И так до тех пор, пока ученик правило не усвоит.

Трудность возникает в составлении вариантов такой работы, но здесь на помощь приходят ученики, они помогают составлять варианты работ на основные правила. В процессе обучения математике важное место отводится организации повторения изученного материала. На факультативных занятиях больше использую сопутствующее повторение, которое зависит от материала, привлекаемого для изучения очередного вопроса, от возможности установить связи между новым и старым, от состояния знаний учащихся в данный момент. Сопутствующим повторением учитель по ходу работы устраняет неточности в знаниях, напоминает вкратце давно пройденное, указывает их связь с новым. На одном из последних  занятий проводится заключительное повторение по темам курса. На итоговой самостоятельной работе подводится итог всей работы по теме, ученик выполняет задание своего уровня, выставляется итоговая оценка. При оценивании выполненных работ я основываюсь на «принципе сложения»: положительная оценка выставляется за достижение определенного минимально достаточного уровня подготовки. Более высокий уровень подготовки является личным делом ученика и соответственно оценивается более высоким баллом. Поэтому для большей объективности оценки результатов усвоения учащимися учебного материала необходим индивидуальный учет.  Технология с дифференцированными заданиями позволяет включить в работу каждого ученика, не принуждая его, убеждая принять то содержание, которое заложено наукой. Ученики не просто усваивают готовые образцы, а осознают, как они получены, в какой мере соответствуют не только научному знанию, но и личностно значимым ценностям. Построение технологии обучения математике на основе индивидуальных особенностей и учета целей развития каждого ребенка способствует не только повышению качества знаний учащихся, но и их саморазвитию, самореализации, что является одной из важнейших целей современного образования. Повторная проверка знаний проходит по тому же плану, что и  входной контроль. Использовались демонстрационные варианты заданий 21, 22, 23 с  банка заданий, таких как  ФИПИ, Решу  ОГЭ.

Подготовка учащихся к сдаче экзаменов всегда является очень важным и ответственным мероприятием. И от того, насколько учитель, ученик и его родители это осознают, зависит результат. В ходе работы мною была выдвинута гипотеза: Подготовка учащихся к ОГЭ по алгебре будет более эффективна, если на уроках систематически повторять и обобщать материал, входящий в государственную итоговую аттестацию, составить алгоритмы и опорные схемы типовых задач и разработать факультативный курс по решению второй части ОГЭ. Для решения данной гипотезы были выдвинуты следующие задачи:

 1. Провести анализ научно-методической, математической, психолого-педагогической литературы по теме исследования;

 2. Проанализировать понятие ОГЭ по алгебре, его цели, особенности организации и проведения.

При проведении ОГЭ используются контрольные измерительные материалы стандартизированной формы.  

И именно благодаря проведению факультативных курсов по математике можно достичь более высоких результатов сдачи ОГЭ. Мною был разработан факультативный курс «Решение второй части ОГЭ по алгебре»,  целью которого является подготовка учащихся к сдаче ОГЭ в соответствии с требованиями, предъявляемыми новыми образовательными стандартами. Раскрыта методика по выполнению 2 части ОГЭ по алгебре, которая предусматривает выстраивание заданий в разделах по нарастанию сложности – от относительно простой задачи до задач достаточно сложных, требующих свободного владения материалом и высокого уровня математического развития.  Расстановка заданий по уровням сложности позволила  создать условия для дифференцированного обучения. Такой способ расстановки заданий позволил структурировать содержание курса по спирали, что позволяет возвращаться к изученному ранее материалу на новом уровне, включать знания в новые связи, формировать их в системе. В параграфе «Методические аспекты решения заданий 2 части ОГЭ по математике (Модуль «Алгебра»)» приведен разбор  задач №21,22,23 ОГЭ по математике, которые структурированы по темам изучения и дифференцированы по уровню сложности. Эту  разработанную методику апробирую с учащимися  9  классов; Апробация проводится в МБОУ «СШ №15» г. Новый Уренгой. Занятия проводились во внеурочное время. Всего проведено 34 занятий.  Ежегодно необходимо проводить анализ эффективности методики подготовки учащихся к ОГЭ по математике в 9-х классах.  Факультативный курс эффективен при организации занятий, ориентированных на подготовку  к итоговой аттестации. Содержание факультативного курса систематизирует знания учащихся, что позволяет им более успешно сдать основной государственный экзамен по математике. Методы, применяемые на занятиях, соответствуют возрастным особенностям, темам занятия, содержанию, поставленным задачам, уровню обученности детей, что в свою очередь помогло решить проблему: Каким образом, можно повысить  качество знаний на экзамене по алгебре в форме основного государственного экзамена (ОГЭ).

ПРИМЕЧАНИЕ:

1. Алгебра: сб. заданий для подгот. к гос. итоговой аттестации в 9 кл. /[Л. В. Кузнецова,  С.  Б.  Суворова,  Е.  А.  Бунимович  и  др.]. — 5-е  изд. —М.  : Просвещение, 2010.
2. Алгебра: сб. заданий для подгот. к гос. итоговой аттестации в 9 кл. /[Л. В. Кузнецова, С. Б. Суворова, Е. А. Бунимович и др.]. —4-е изд., перераб. —М. : Просвещение, 2009.  
3. Кузнецова Л. В., Суворова С. Б., Бунимович Е. А., Колесникова Т. В.,  Рослова Л. О. Государственная итоговая аттестация выпускников 9 классов в новой форме. Алгебра. 2016/ ФИПИ.—М.: Интеллект-Центр, 2016.
4. ГИА-2017: Экзамен в новой форме: Алгебра 9-й кл.: Тренировочные варианты экзаменационных работ для проведения государственной итоговой аттестации в новой форме / авт.-сост. Л.В. Кузнецова, СБ. Суворова Е.А.Бунимович и др.—М.: ACT: Астрель, 2017.
5. Математика. Типовые задания. ОГЭ (создано разработчиками ФИПИ).
6.  Математика. ОГЭ. Типовые тестовые задания. 50 вариантов. Изд. «Экзамен» (по ред. Ященко И.В.) 2017
7. Математика  (универсальный  справочник).  Подготовка  к  ЕГЭ  и  ОГЭ –высший уровень качества).–Москва, Эксмо, 2012.
8. И. В. Ященко, А. В. Семенов, П. И. Захаров Подготовка к экзамену по математике ГИА 9 (новая форма). -Методические рекомендации.  -М., МЦНМО, 2009.
9. Математика. 9 класс. Подготовка к ГИА — 2012:  учебнометодическое пособие / Под ред. Ф.Ф. Лысенко, С.Ю. Кулабухова. – Ростов – на-Дону: Легион — М. 2011.
10. Алгебра. 9-й класс. Подготовка к государственной итоговой аттестации -2010: учебно-методическое пособие / Под ред. Ф. Ф. Лысенко. — Ростов-на-Дону: Легион М., 2009.
11. Колесникова Т.В., Минаева С.С. Типовые тестовые задания 9 класс. М.:«Экзамен», 2010.
12.  Мордкович А.Г.Алгебра. Часть 1. Учебник. 7-9 классы. М.: «Мнемозина», 2013.
13.  Алгебра.  Решебник.  9  класс.  Подготовка  к  государственной  итоговой аттестации -2011. Под ред. Лысенко Ф.Ф., Кулабухова С.Ю.  —Ростов-на-Дону: Легион — М., 2011.
14. Глазков, Ю.А. ГИА. Алгебра. 9 класс. Государственная итоговая аттестация (в  новой  форме).  Тематические  тестовые  задания  /  Ю.А.  Глазков,  М.Я. Гаиашвили. —М.: Издательство «Экзамен», 2010.
15.  Минаева,  С.С.,  Колесникова  Т.В.  ГИА  2010.  Математика. 9 класс. Государственная итоговая аттестация (в новой форме). Типовые тестовые задания / Минаева С.С., Колесникова Т.В. —М.: Издательство «Экзамен», 2010
16. Третьяк И.В. Математика в схемах и таблицах/И.В.Третьяк. – Москва: Эксмо 2017.
17. https://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0#cite_note-1
18. https://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0#cite_note-burbakiDef-2
19. https://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0#cite_note-3
20. https://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0#cite_note-4

Календарно-тематическое планирование факультативного курса

«Решение второй части ОГЭ по алгебре»

№ п/п        №        №	Тема
Тема 1. Алгебраические выражения. (5часов)
1	Алгебраические выражения	1
2	Уравнения	2
4	Системы уравнений	2
4	Неравенства	1
5	Системы неравенств	1
Тема 2. Текстовые задачи (4часа)
6	Задачи на проценты, сплавы и смеси	2
7	Движение по прямой	1
8	Задачи на движение по воде	1
9	Задачи на совместную работу	1
10	Задачи на логику	2
Тема 3. Функции и их свойства. Графики функций (3 часа)
11	Линейная и квадратичная функция	2
12	Функция обратной пропорциональности	1
13	Кусочно-непрерывные функции	1
14	Функции с модулем	2
Тема4. Геометрические задачи на вычисление  (10часов)
15	Углы	1
16	Треугольники	1
17	Четырехугольники	1
18	Окружности	1
Тема 5. Геометрическая задача на доказательство.(3часа)
19	Правильные многоугольники	1
20	Треугольники и их элементы	1
21	Четырёхугольники и их элементы	1
22	Окружности и их элементы	1
Тема 6.  Геометрическая задача повышенной сложности
23	Касательная к окружности.	2
24	Взаимное расположение двух окружностей.	1
25	Общая касательная к двум окружностям.	2
26	Комбинация многоугольников и окружностей	1



Система работы учителя математики по подготовке к ГИА (ОГЭ ЕГЭ)

---

С этим файлом связано 1 файл(ов). Среди них: 1118845 (1).ppt.
Показать все связанные файлы

---

Подборка по базе: Методические рекомендации по профилактике суицида среди детей и , Методические рекомендации.docx, _ 2 курс Методические рекомендации по подготовке и защите курсов, Методические рекомендации по выполнению практической работы _Изу, 7. Развитие риторики как научной дисциплины и отмежевание ее от , Экономическая безопасность. Методические указания по написанию к, Методические рекомендации практика 5 дн, 6 заоч 2022-2023.doc, (ДР) МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ДИПЛОМНЫХ РАБОТ.d, Методические рекомендации кр Теория организации 2022.pdf, Теоретические и методические основы физического воспитания и раз

---

ООО «Инфоурок»
МАТЕМАТИКА
МОДУЛЬ 3
«ПРЕДМЕТНАЯ ДЕЯТЕЛЬНОСТЬ»
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ИЗУЧЕНИЮ дисциплины
«Подготовка учителя математики к проведению ОГЭ (ЕГЭ)»

Оглавление

1. Введение.

Экзамен по ОГЭ (ЕГЭ) по математике при правильной подготовке хорошо может сдать каждый. Формула успеха проста – высокая степень восприимчивости, мотивация и компетентный педагог. В любом случае натаскивание на варианты ОГЭ (ЕГЭ) необходимо, но его нужно сочетать с фундаментальной подготовкой, формируя системные знания и навыки.

В ЕГЭ по математике встречаются специфические, каверзные вопросы и задачи. Их часто не может быстро решить даже опытный специалист. Эти задачи на первый взгляд незаметны и их немного, но обязательно включаются разработчиками в ЕГЭ. Однако даже в таких нетиповых заданиях можно выделить шаблоны, что позволяет подготовленному правильным образом ученику уметь распознавать ход мыслей составителя и часто обыгрываемые типы каверзных задач.

Каверзные и специфические задачи составляют только часть так называемой специфики ОГЭ (ЕГЭ) по математике. Подготовленность в плане специфики подразумевает знание нюансов и особенностей экзамена. К таким особенностям можно отнести правильность оформления заданий, тактика и стратегия решения в условиях дефицита выделенного времени на экзамене, а также банальная невнимательность. Эти и масса других особенностей и составляют суть специфики. Учитель по математике, хорошо знающий, с чем придется столкнуться школьнику на экзамене, кроме фундамента уделяет большую часть времени на занятии отработке вопросов специфики ОГЭ (ЕГЭ).

Для эффективной подготовки к ОГЭ (ЕГЭ) нужна тренировка, тренировка и еще раз тренировка. Довести решение задач до автоматизма. Видеть единственный возможный вариант ответа среди четырех предложенных.

Подготовленность к чему-либо понимается как комплекс приобретенных знаний, навыков, умений, качеств, позволяющих успешно выполнять определенную деятельность. В готовности учащихся к сдаче экзамена в форме ОГЭ (ЕГЭ) можно выделить следующие составляющие:

-информационная готовность (информированность о правилах поведения на экзамене, информированность о правилах заполнения бланков и т.д.);

-предметная готовность или содержательная (готовность по определенному предмету, умение решать тестовые задания);

-психологическая готовность (состояние готовности – «настрой», внутренняя настроенность на определенное поведение, ориентированность на целесообразные действия, актуализация и приспособление возможностей личности для успешных действий в ситуации сдачи экзамена).

Ориентируясь на данные компоненты, актуальными вопросами в подготовке к ОГЭ (ЕГЭ) являются следующие:

-организация информационной работы по подготовки учащихся к ЕГЭ;

-мониторинг качества;

-психологическая подготовка к ЕГЭ.

ЕГЭ – серьёзный шаг в жизни каждого выпускника, обдумывающего выбор своего будущего, стремящегося самореализоваться в новой социокультурной ситуации, продолжить образование и овладеть профессиональными навыками.

Подготовка к сдаче ЕГЭ по математике должна идти через приобретение и освоение конкретных математических знаний. Только это обеспечит выпускнику успешную сдачу экзамена.

В своей работе применяю следующие принципы подготовки к ЕГЭ.

Первый принцип – тематический. Эффективнее выстраивать такую подготовку, соблюдая принцип от простых типовых заданий к сложным.Второй принцип – логический. На этапе освоения знаний необходимо подбирать материал в виде логически взаимосвязанной системы, где из одного следует другое. На следующих занятиях полученные знания способствуют пониманию нового материала.Третий принцип – тренировочный. На консультациях учащимся предлагаются тренировочные тесты, выполняя которые дети могут оценить степень подготовленности к экзаменам.Четвёртый принцип – индивидуальный. На консультациях ученик может не только выполнить тест, но и получить ответы на вопросы, которые вызвали затруднение.Пятый принцип – временной. Все тренировочные тесты следует проводить с ограничением времени, чтобы учащиеся могли контролировать себя — за какое время сколько заданий они успевают решить.Шестой принцип – контролирующий. Максимализация нагрузки по содержанию и по времени для всех учащихся одинакова. Это необходимо, поскольку тест по своему назначению ставит всех в равные условия и предполагает объективный контроль результатов.

Следуя этим принципам, формирую у учеников навыки самообразования, критического мышления, самостоятельной работы, самоорганизации и самоконтроля.

Моя цель состоит в том, чтобы помочь каждому школьнику научиться быстро решать задачи, оформлять их чётко и компактно. Развиваю способность мыслить свободно, без страха, творчески. Стараюсь давать возможность каждому школьнику расти настолько, насколько он способен.

2. Комплексный подход к деятельности по подготовке учащихся к ОГЭ (ЕГЭ).

Только комплексный подход к деятельности по подготовке учащихся к ОГЭ (ЕГЭ) способствует повышению эффективности и качества результатов экзамена в тестовой форме. Под комплексным подходом понимается целенаправленное сотрудничество администрации, учителей-предметников, учащихся и их родителей.

В информационной деятельности образовательного учреждения по подготовке к ОГЭ (ЕГЭ) выделяем

три направления: информационная работа с педагогами, с учащимися, с родителями.

Содержание информационной работы с педагогами.

1) Информирование учителей на производственных совещаниях:

— нормативно-правовыми документами по ОГЭ (ЕГЭ);

— о ходе подготовки к ОГЭ (ЕГЭ) в школе, в городе и крае;

2) Включение в планы работы школьных методических объединений (ШМО) следующих вопросов:

— проведение пробных ОГЭ (ЕГЭ), обсуждение результатов пробных ОГЭ (ЕГЭ);

— творческая презентация опыта по подготовке учащихся к ОГЭ (ЕГЭ) (на методической или научной конференции в рамках школы);

— выработка совместных рекомендаций учителю-предметнику по стратегиям подготовки учащихся к ОГЭ (ЕГЭ) (с учетом психологических особенностей учащихся);

— психологические особенности 9,11-классников.

3) Педагогический совет «ОГЭ (ЕГЭ) – методические подходы к подготовке учащихся».

4) Направление учителей на городские семинары и курсы по вопросам ОГЭ (ЕГЭ).

Содержание информационной работы с учащимися.

1) Организация информационной работы в форме инструктажа учащихся:

— правила поведения на экзамене;

— правила заполнения бланков;

— расписание работы кабинета информатики (часы свободного доступа к ресурсам Интернет).

2) Информационный стенд для учащихся: нормативные документы, бланки, правила заполнения бланков, ресурсы Интернет по вопросам ОГЭ (ЕГЭ).

3) Проведение занятий по тренировке заполнения бланков.

4) Пробные внутришкольные ОГЭ (ЕГЭ) по различным предметам.

Содержание информационной работы с родителями учащихся.

1) Родительские собрания:

— информирование родителей о процедуре ОГЭ (ЕГЭ), особенностях подготовки к тестовой форме сдачи экзаменов. Информирование о ресурсах Интернет;

— информирование о результатах пробного внутришкольного ОГЭ (ЕГЭ);

— пункт проведения экзамена, вопросы проведения ОГЭ (ЕГЭ).

2) Индивидуальное консультирование родителей.

3. Мониторинг качества образования.

Одна из задач, которые решаем на уроках математики — подготовка учащихся 9-х, 11-х классов к итоговой аттестации в новой форме и в форме единого государственного экзамена, поэтому стараемся найти такие способы организации учебного процесса, которые будут ускорять, интенсифицировать развитие учащихся и при этом учитывать, возможности каждого.

Особое внимание в процессе деятельности ОУ по подготовке учащихся к ОГЭ (ЕГЭ) занимает мониторинг качества обученности по предметам, которые учащихся будут сдавать в форме и по материалам ОГЭ (ЕГЭ). Мониторинг – отслеживание, диагностика, прогнозирование результатов деятельности, предупреждающие неправомерную оценку события, факта по данным единичного измерения (оценивания). Мониторинг качества образования – «следящая» и в определенной степени контрольно-регулирующая система по отношению к качеству образования.

Мониторинг качества должен быть системным и комплексным. Он должен включать следующие параметры: контроль текущих оценок по предметам, выбираемыми учащимися в форме ОГЭ (ЕГЭ), оценок по контрольным работам, оценок по самостоятельным работам, результаты пробного внутришкольного ОГЭ (ЕГЭ). Учитель анализирует их, выносит на обсуждение на административные и производственные совещания, доводит до сведения родителей. Мониторинг обеспечивает возможность прогнозирования оценок на выпускном ОГЭ (ЕГЭ).

4. Психологическая подготовка к ОГЭ (ЕГЭ).

Психологическая подготовка учащихся может заключается в следующем: отработка стратегии и тактики поведения в период подготовки к экзамену; обучение навыкам саморегуляции, самоконтроля, повышение уверенности в себе, в своих силах.

Методы проведения занятий по психологической подготовке учащихся разнообразны: групповая дискуссия, игровые методы, медитативные техники, анкетирование, мини-лекции, творческая работа, устные или письменные размышления по предложенной тематике. Содержание занятий должно ориентироваться на следующие вопросы: как подготовиться к экзаменам, поведение на экзамене, способы снятия нервно-психического напряжения, как противостоять стрессу.

Работа с учащимися проводится по желанию учащихся – со всем классом или выборочно.

5. Устный счет – один из важных приемов при подготовке учащихся к ОГЭ (ЕГЭ) по математике.

В методике математики различают устные и письменные приемы вычисления. Устная работа на уроках имеет большое значение – это и беседы учителя с классом или отдельными учениками, и рассуждения учащихся при выполнении тех или иных заданий и т.п. Среди этих видов устной работы можно выделить так называемые устные упражнения. В начальной школе они сводились в основном к вычислениям, поэтому за ними закрепилось название “устный счет”, хотя в современных программах содержание устных упражнений весьма разнообразно и велико за счет введения алгебраического и геометрического материала, а также за счет большого внимания к свойствам действий над числами и величинами.

Важность и необходимость устных упражнений велика в формировании вычислительных навыков и в совершенствовании знаний по нумерации, и в развитии личностных качеств ученика. Создание определённой системы повторения ранее изученного материала дает учащимся возможность усвоения знаний на уровне автоматического навыка. Устные вычисления не могут быть случайным этапом урока, а должны находиться в методической связи с основной темой и носить проблемный характер.

Однако устный счет как этап урока до сих пор применяется в основном в начальной школе или в 5-6 классах, имея своей главной целью отработку вычислительных навыков. В связи с введением обязательного ОГЭ (ЕГЭ) по математике возникает необходимость научить учащихся старших классов решать быстро и качественно задачи базового уровня. При этом необыкновенно возрастает роль устных вычислений и вычислений вообще, так как на экзамене не разрешается использовать калькулятор и таблицы. Заметим, что многие вычислительные операции, которые имеем обыкновение записывать в ходе подробного решения задачи, в рамках теста совершенно не требуют этого. Можно научить учащихся выполнять простейшие (и не очень) преобразования устно. Конечно, для этого потребуется организовать отработку такого навыка до автоматизма.

Для достижения правильности и беглости устных вычислений, преобразований, решения задач в течение всех лет обучения в среднем и старшем звене на каждом уроке необходимо отводить 5-7 минут для проведения упражнений в устных вычислениях, предусмотренных программой каждого класса.

Устные упражнения активизируют мыслительную деятельность учащихся, требуют осознанного усвоения учебного материала; при их выполнении развивается память, речь, внимание, быстрота реакции.

Устные упражнения как этап урока имеют свои задачи:

1) воспроизводство и корректировка знаний, умений и навыков учащихся, необходимых для их самостоятельной деятельности на уроке или осознанного восприятия объяснения учителя;

2) контроль состояния знаний учащихся;

3) автоматизация навыков простейших вычислений и преобразований.

Устные упражнения должны соответствовать теме и цели урока и помогать усвоению изучаемого на данном уроке или ранее пройденного материала. Чтобы навыки устных вычислений постоянно совершенствовались, необходимо установить правильное соотношение в применении устных и письменных приёмов вычислений, а именно: вычислять письменно только тогда, когда устно вычислить трудно.

Если в 5-6 классах устный счет – это выполнение действий с числами: натуральные числа, обыкновенные дроби, десятичные дроби , то в старших классах – это могут быть совершенно различные операции, навык выполнения которых надо довести до автоматизма. Например, на уроках математики используем УС по темам:

7 класс:

1) Запись чисел в стандартном виде и действия с ними.

2) Формулы сокращенного умножения.

3) Решение простейших ЛУР.

4) Действия со степенью.

5) График линейной функции.

8 класс:

1) Линейные неравенства и числовые промежутки.

2) Решение простейших линейных неравенств.

3) Решение КВУР с помощью теоремы Виета и частных случаев.

4) Решение КВУР рациональными способами.

5) Арифметический квадратный корень и его свойства.

9 класс:

1) Решение неравенств 2 степени.

2) Преобразование графиков функций.

3) Формулы приведения.

4) Тригонометрические формулы.

5) Значения тригонометрических функций.

10 класс:

1) Вычисление производных.

2) Простейшие тригонометрические неравенства.

3) Тригонометрические формулы.

4) Простейшие тригонометрические уравнения.

5) Функции, обратные тригонометрическим.

6) Преобразование графиков функций.

11 класс:

1) Вычисление первообразных .

2) Свойства логарифмов.

3) Простейшие показательные уравнения и неравенства.

4) Простейшие логарифмические уравнения и неравенства.

Практика показала, что систематическая работа с УС способствует значительному повышению продуктивности вычислений и преобразований. Сокращается время на выполнение таких операций, как решение КВУР, линейных неравенств и неравенств 2-ой степени, разложение на множители, построение графиков функций, преобразования иррациональных выражений и другие. Эти операции переходят из разряда самостоятельной задачи в разряд вспомогательной и становятся инструментом (“таблицей умножения”) для решения более сложных задач.

6. Применение ИКТ на уроках математики при подготовке к ОГЭ (ЕГЭ).

По данным исследований, в памяти человека остается 1/4 часть услышанного материала, 1/3часть увиденного, 1/2часть увиденного и услышанного, ¾ части материала, если ученик привлечен в активные действия в процессе обучения.

Технология применения средств ИКТ в предметном обучении основывается на:

использовании участниками образовательного процесса некоторых формализованных моделей содержания;

деятельности учителя, управляющего этими средствами;

повышении мотивации и активности обучающихся, вызываемой интерактивными свойствами компьютера.

Возможности компьютера могут быть использованы в предметном обучении в следующих вариантах:

использование диагностических и контролирующих материалов;

выполнение домашних самостоятельных и творческих заданий;

использование компьютера для вычислений, построения графиков;

создание уроков с помощью программы “Notebook”, “PowerPoint”

Поскольку наглядно-образные компоненты мышления играют исключительно важную роль в жизни человека, то использование их в изучении материала с использованием ИКТ повышают эффективность обучения:

графика и мультипликация помогают ученикам понимать сложные логические математические построения;

возможности, предоставляемые ученикам, манипулировать (исследовать) различными объектами на экране дисплея, позволяют детям усваивать учебный материал с наиболее полным использованием органом чувств и коммуникативных связей головного мозга.

Компьютер может использоваться на всех этапах процесса обучения: при объяснении нового материала, закреплении, повторении, контроле, при этом для ученика он выполняет различные функции: учителя, рабочего инструмента, объекта обучения, сотрудничающего коллектива.

Компьютер позволяет усилить мотивацию учения путем активного диалога ученика с компьютером, разнообразием и красочностью информации. На практике реализуется принцип успешности

(компьютер позволяет довести решение любой задачи, опираясь на необходимую помощь).

При применении компьютера и внедрения ИКТ на уроках учитываются возрастные возможности и образовательные потребности учащихся, специфика развития мышления и других психических процессов в условиях информатизации учебной деятельности. Здесь решается задача – закладываются основы рационального и эффективного общения учащегося с компьютером, как главным инструментом нового информационного общества. Использование программы PowerPoint на уроках математики способствует:

– стимулированию процесса обучения, таких как восприятие и осознание информации;

– повышению мотивации учащихся;

– развитию навыков совместной работы и коллективного познания у обучаемых;

– развитию у учащихся более глубокого подхода к обучению, и, следовательно, влечет формирование более глубокого понимания изучаемого материала;

– осуществлению дифференцированного подхода;

– формированию коммуникативных и учебно-познавательных компетенций учащихся;

– развитию вычислительных навыков учащихся;

– формированию навыков самоконтроля, взаимоконтроля и самообучения;

– реализации межпредметных связей;

– включению у учащихся всех каналов восприятия информации.

Применение информационных технологий помогают:

создать у школьника положительную мотивацию в изучении нового материала;

развить познавательный интерес к предмету;

первично закрепить знания учащихся;

проверить прочность усвоения знаний.

Применение презентации, созданной в среде PowerPoint. Нестандартная подача материала в виде электронной презентации повышает качество любого урока. При изучении нового материала она позволяет иллюстрировать учебный материал разнообразными наглядными средствами. Это могут быть: слайды, в которых отсутствует текст; презентация, которая состоит только из текста, если это урок лекция; конспект урока. В этом случае презентация состоит из темы урока, цели, ключевых понятий и домашнего задания.

Очень часто у учителя нет времени на составление презентации. Тогда нам на помощь в этом случае приходят интернет-ресурсы:

А) Серверы образовательных центров, где учителя обмениваются своим опытом:

Б) энциклопедические ресурсы:

http: // www.rubricon.ru — группа энциклопедических ресурсов «Рубрикон»;

http: // www.mega.km.ru – виртуальная энциклопедия Кирилла и Мефодия;

http: // www.college.ru — «Открытый колледж» компании «Физикон».

На уроках закрепления знаний хорошо применять программы – тренажеры для отработки теоретических знаний и развития практических умений и навыков. Здесь на помощь учителю может прийти тренажер по математике издательства «Кирилл и Мефодий» для 11 классов, «Математика – семейный наставник» фирмы «1С» для 5-6 классов, а для 5-9 классов «Витаминный курс по математике». А также тренажеры можно найти у своих коллег на сайте «Первое сентября». Они более адаптированы к нашим учебникам.

7. Роль математических олимпиад при подготовке к ОГЭ (ЕГЭ).

Цель математической олимпиады:

дать возможность как можно большему количеству детей раскрыть свои творческие и интеллектуальные способности; развить интерес к учебе и уверенность в своих силах; привлечь внимание детей к математике; создать для одаренных детей атмосферу радости и праздника.

Основные принципы разработки заданий олимпиады.

Международная олимпиада по основам наук включает в себя 25 различных заданий, 5 заданий по 2 балла, 5 заданий по 3 балла, 15 заданий по 5 баллов.

Задания олимпиады подбираются таким образом, чтобы для их выполнения хватало базовых школьных знаний соответствующего уровня. В то же время большинство заданий для своего решения требуют определенной гибкости ума и сообразительности. В каждом варианте даются легкие задачи, с которыми могут справиться большинство участников. Также даются задачи, с которыми заведомо могут справиться единицы. В целом задания подбираются максимально разнообразно, так, чтобы охватить различные разделы математики. Общий объем варианта подбирается так, чтобы только наиболее подготовленные дети могли решить все задания.

Задания по математике, в основном, подбираются по следующим направлениям:

1. числовые ряды, закономерности, ребусы;

2. «текстовые» задачи (классические арифметические задачи);

3. логика (в том числе алгоритмизация);

4. геометрия (задачи на наглядно-образное мышление: «разрезалки», «складывалки», развертки и т.д.);

5. комбинаторика (задачи на перебор вариантов);

6. творческое задание.

План работы по подготовке учащихся к ОГЭ- 2016 по математике.

№ п/п	Мероприятия	Сроки проведения
1	Работа по изучению индивидуальных особенностей учащихся (с целью выработки оптимальной стратегии подготовки к ОГЭ- 2016 по математике).	В течение года
2	Психологическая подготовка к ОГЭ- 2016 Индивидуальное консультирование учащихся.	В течение года
3	Использование современных образовательных технологий, новых форм организации учебно- воспитательного процесса, способствующих повышению качества подготовки школьников к итоговой аттестации, формированию предметной компетенции.	В течение года
4	Беседа с учащимися: «Подготовка к ОГЭ- 2016 по математике: от устранения пробелов в знаниях до итоговой аттестации»	1 четверть
5	Пополнение методической и информационной литературой по подготовке к ОГЭ- 2016. Обеспечение участников государственной (итоговой) аттестации по новой форме в IX классе учебно-тренировочными материалами, обучающими программами, методическими пособиями, информационными и рекламными материалами.	В течение года
6	Проведение с учащимися цикла бесед: « Знакомство с Положением о формах и порядке проведения государственной (итоговой) аттестации». «Ознакомление с основными направлениями самостоятельной работы по подготовке к ОГЭ- 2016 в 9 классе».	2 четверть
7	Работа с учащимися: Использование тематических тестов по материалам ОГЭ на уроках математики Подготовка графика проведения консультаций для учащихся по разноуровневым группам. Анализ типичных ошибок учащихся при сдаче ОГЭ- по новой форме в IX классе в 2014 г. Семинар — практикум «Работа с бланками: типичные ошибки при заполнении бланков» -обучение работе с КИМами, -выбор оптимальной стратегии выполнеия заданий ОГЭ, — помощь в выработке индивидуального способа деятельности в процессе выполнения экзаменационных заданий, — систематическое решение текстовых задач: • задачи на части и проценты, · задачи на сплавы и смеси; · задачи на работу; · задачи на бассейны и трубы. Психологическая подготовка к ОГЭ по новой форме в IX классе. Индивидуальное консультирование учащихся. Работа с заданиями различной сложности. Практические занятия  по заполнению бланков ответов. Практикум по решению заданий повышенной сложности (ОГЭ- 2016)-разбор 2 части. Практикум по решению нестандартных заданий из контрольно-измерительных материалов.	В течение года
9	Разбор заданий демонстрационного варианта экзамена по математике (ОГЭ- 2016)-новый проект, состоящий из 3-х модулей: алгебра, геометрия, реальная математика.	1 четверть
10	Подготовка, оформление информационного стенда «Подготовка к ОГЭ- 2016» для учащихся и их родителей	4 четверть
11	Индивидуальные консультации родителей	В течение года
12	Работа с заданиями различной сложности. Практикум по решению заданий второй части экзаменационной работы	Индивидуальная работа по группам в течение года
13	Регулярное проведение классных родителских собраний: «Ознакомление с нормативными документами по подготовке к проведению новой формы аттестации 9-тиклассников», «Нормативные документы по ОГЭ- 2016 по новой форме в IX классе в 2014- 2016 учебном  году», «Построение режима дня во время подготовки к экзаменам с учётом индивидуальных особенностей ребенка», «Цели и технологии проведения ОГЭ- 2016 по новой форме в IX классе».	В течение года
14	Беседа с учащимися: «ГИА- новая форма оценки качества школьного образования»	2 четверть
15	Подготовка материалов для проведения пробной внутришкольной ОГЭ- 2016 по новой форме в IX классе (бланки, тесты).	3 четверть
16	Регулярное участие в диагностических работах, проводимых РЦМКО	В течение года
17	Мониторинг качества подготовки учащихся к ГИА	В течение года
18	Информирование по вопросам подготовки к ГИА: знакомство с инструкцией по подготовке к ГИА; правила поведения на ГИА; КИМы; инструктирование учащихся; проведения ГИА; официальные сайты ГИА. Индивидуальное информирование и консультирование по всем вопросам, связанных с ГИА.	В течение года
19	Индивидуальные консультации для учащихся и их родителей по вопросам подготовки и проведения ОГЭ- 2016 по новой форме в IX классе. Оформление протокола родительского собрания и листа ознакомления с информацией о проведении ОГЭ- 2016. Анализ работы учителя и учащихся. О порядке подготовки и проведения ГИА (нормативные документы, КИМы, сайты )	В течение года май

План работы по подготовке учащихся к ЕГЭ — 2016 по математике.

№ п/п	Мероприятия	Сроки проведения
1	Работа по изучению индивидуальных особенностей учащихся (с целью выработки оптимальной стратегии подготовки к ЕГЭ — 2016 по математике).	В течение года
2	Психологическая подготовка к ЕГЭ — 2016 Индивидуальное консультирование учащихся.	В течение года
3	Использование современных образовательных технологий, новых форм организации учебно- воспитательного процесса, способствующих повышению качества подготовки школьников к итоговой аттестации, формированию предметной компетенции.	В течение года
4	Беседа с учащимися: «Подготовка к ЕГЭ — 2016 по математике: от устранения пробелов в знаниях до итоговой аттестации»	1 четверть
5	Пополнение методической и информационной литературой по подготовке к ЕГЭ — 2016. Обеспечение участников государственной (итоговой) аттестации по новой форме в XI классе учебно-тренировочными материалами, обучающими программами, методическими пособиями, информационными и рекламными материалами.	В течение года
6	Проведение с учащимися цикла бесед: « Знакомство с Положением о формах и порядке проведения государственной (итоговой) аттестации». «Ознакомление с основными направлениями самостоятельной работы по подготовке к ЕГЭ — 2016 в 11 классе».	2 четверть
7	Работа с учащимися: Использование тематических тестов по материалам ЕГЭ на уроках математики Подготовка графика проведения консультаций для учащихся по разноуровневым группам. Анализ типичных ошибок учащихся при сдаче ЕГЭ — в XI классе в 2014 г. Семинар — практикум «Работа с бланками: типичные ошибки при заполнении бланков» -обучение работе с КИМами, -выбор оптимальной стратегии выполнеия заданий ОГЭ, — помощь в выработке индивидуального способа деятельности в процессе выполнения экзаменационных заданий, — систематическое решение текстовых задач: • задачи на части и проценты, · задачи на сплавы и смеси; · задачи на работу; · задачи на бассейны и трубы. Психологическая подготовка к ЕГЭ по новой форме в XI классе. Индивидуальное консультирование учащихся. Работа с заданиями различной сложности. Практические занятия  по заполнению бланков ответов. Практикум по решению заданий повышенной сложности (ОГЭ- 2016)-разбор 2 части. Практикум по решению нестандартных заданий из контрольно-измерительных материалов.	В течение года
9	Разбор заданий демонстрационного варианта экзамена по математике (ЕГЭ — 2016)-новый проект, состоящий из двух видов работ: базовый уровень, профильный уровень	1 четверть
10	Подготовка, оформление информационного стенда «Подготовка к ЕГЭ — 2016» для учащихся и их родителей	4 четверть
11	Индивидуальные консультации родителей	В течение года
12	Работа с заданиями различной сложности. Практикум по решению заданий второй части экзаменационной работы	Индивидуальная работа по группам в течение года
13	Регулярное проведение классных родителских собраний: «Ознакомление с нормативными документами по подготовке к проведению новой формы аттестации 11-тиклассников», «Нормативные документы по ЕГЭ — 2016 по новой форме в XI классе в 2014- 2016 учебном  году», «Построение режима дня во время подготовки к экзаменам с учётом индивидуальных особенностей ребенка», «Цели и технологии проведения ЕГЭ — 2016 по новой форме в XI классе».	В течение года
14	Беседа с учащимися: «ЕГЭ — новая форма оценки качества школьного образования»	1 четверть
15	Подготовка материалов для проведения пробной внутришкольной ЕГЭ — 2016 по новой форме в XI классе (бланки, тесты).	2 четверть
16	Регулярное участие в диагностических работах, проводимых МИОО системой СтатГрад	В течение года
17	Регулярное участие в тренировочных работах, проводимых МИОО системой СтатГрад	В течение года
18	Мониторинг качества подготовки учащихся к ЕГЭ	В течение года
19	Информирование по вопросам подготовки к ЕГЭ: знакомство с инструкцией по подготовке к ЕГЭ; правила поведения на ЕГЭ КИМы; инструктирование учащихся; проведения ЕГЭ; официальные сайты ЕГЭ. Индивидуальное информирование и консультирование по всем вопросам, связанных с ЕГЭ.	В течение года
20	Индивидуальные консультации для учащихся и их родителей по вопросам подготовки и проведения ЕГЭ — 2016 по новой форме в XI классе. Оформление протокола родительского собрания и листа ознакомления с информацией о проведении ЕГЭ- 2016. Анализ работы учителя и учащихся в системе СтатГрад. О порядке подготовки и проведения ГИА (нормативные документы, КИМы, сайты )	В течение года май

. Формы аттестации и оценочные материалы

Форма контроля	Виды оценочных материалов
Зачет	Контрольное задание (Требования к оформлению контрольного в Приложении 1).

Для перехода к обучению по следующей дисциплине программы пройдите тест. Для этого перейдите на сайт:

http://infourok.ru и авторизуйтесь. Перейдите в раздел «Мой сайт», далее «Мои курсы» выберите нужный Вам курс, модуль и дисциплину программы. Нажмите кнопку «Загрузить работу» и выберите файл с разработкой на своем компьютере.

Внимание! Разрабатываемые материалы не рецензируются. В названии документа указывайте вид работы и название.

Доступные форматы для загрузки: doc, docx.

Приложения

1. Справка о планируемых изменениях КИМ основного государственного экзамена (ОГЭ) в 2016 году

2. Демонстрационный вариант контрольных измерительных материалов для проведения в 2016 году основного государственного экзамена по МАТЕМАТИКЕ

3. Рекомендации по использованию и интерпретации результатов выполнения экзаменационных работ для проведения в 2016 году основного государственного экзамена (ОГЭ)

4. Типичные ошибки ЕГЭ 2015 по Математике

5. Пробный ЕГЭ 2016 по математике с ответами.

6. Пробный экзамен по математике (база) (05.04.2016)

«Система работы учителя математики по подготовке учащихся к итоговой аттестации»

Учителя математики МОУ «СОШ №22» Лопатиной Марины Владимировны

Математика – одна из самых сложных школьных дисциплин, и вызывает трудности у многих учащихся. В то же время есть дети, которые имеют явно выраженные способности к этому предмету, и дети, для которых математика – вечная проблема. Как сделать так, чтобы каждый ребенок развил свой потенциал и был успешен на итоговой аттестации по математике? Хотелось бы поделиться опытом своей работы при подготовке выпускников к ОГЭ и ЕГЭ по математике.

Для этого мной разработана информационно-образовательная среда, которая включает в себя:

• Диагностические карты, индивидуальные маршруты

• Домашняя работа по тестам ОГЭ и ЕГЭ

• Сайт и группа в ВК

• Пробные тесты ОГЭ и ЕГЭ

• Прототипы задания ОГЭ и ЕГЭ

• Консультации со слабыми и с сильными учащимися

• Элективные курсы

• Уроки ОГЭ по алгебре и геометрии

• Уроки ЕГЭ профильный, базовый уровни

Для разработки этой информационно-образовательной среды был использован педагогический дизайн.

Педагогический дизайн – это область науки и практической деятельности, которая за-нимается проблемами разработки информационно-образовательной среды, структуры обуче-ния и учебных материалов для обеспечения наиболее рационального, эффективного и ком-фортного образовательного процесса.

Сайт и группа в ВК

Создан сайт, на котором располагаются презентации и видеоуроки тем с 5 по 11 класс, домашняя работа по математике, алгебре и геометрии, материалы для подготовки к ОГЭ и ЕГЭ, материалы для подготовки к олимпиадам.

А также создана группа в ВК, для оповещения учеников о выложенных презентациях, домашних работах и др.

Домашняя работа по тестам ОГЭ и ЕГЭ

После проведения вводной беседы о структуре экзамена, времени проведения, задается домашняя работа в форме теста ОГЭ или ЕГЭ для ознакомления с заданиями КИМ.

Задается домашняя работа на одну-две недели. Домашних работ задается до 5.

Пробные тесты ОГЭ и ЕГЭ

Пробные тесты составляются мной лично, используются материалы сайта ФИПИ. Вариантов теста столько же, сколько учащихся в классе. По результатам этих тестов составляются диагностические карты и индивидуальные маршруты.

Диагностические карты.

Диагностическая карта ОГЭ

Диагностические карты ЕГЭ

В них входят содержания заданий вариантов КИМ по ОГЭ и ЕГЭ.

Например, диагностическая карта ЕГЭ базового уровня, 15 задание:

• Треугольник

• Прямоугольник: длины и площади

• Параллелограмм: длины и площади

• Ромб: длины и площади

• Трапеция: длины и площади

• Произвольный четырехугольник

• Многоугольник

• Задачи на квадратной решетке

• Круг и его элементы

• Вписанная и описанная окружности

• Векторы

• Координатная плоскость

• Прямоугольный треугольник: вычисление углов

• Прямоугольный треугольник: вычисление внешних углов

• Прямоугольный треугольник: вычисление элементов

• Равнобедренный треугольник: вычисление углов

• Равнобедренный треугольник: вычисление элементов

• Треугольники общего вида

• Параллелограмм углы

• Прямоугольник углы

• Ромб углы

• Трапеция углы

• Центральные и вписанные углы

• Касательная, хорда, секущая

• Окружность, вписанная в треугольник

• Окружность, вписанная в четырехугольник

• Окружность, вписанная в многоугольник

• Окружность, описанная вокруг треугольника

• Окружность, описанная вокруг четырехугольника

• Окружность, описанная вокруг многоугольника

В диагностических картах не только выставляется + или – за задание, например, №15, но и указывается тема, в которой была допущена ошибка или выполнено верно. Это позволяет ликвидировать пробелы в знаниях учащихся по конкретной теме.

В конце диагностических карт выставляется общее количество баллов, которое набрал ученик за проверочный тест. И сразу же видна динамика роста ученика по предмету.

Например,

Индивидуальные маршруты

Но среди учащихся есть очень слабые ученики, в силу лени или других причин. На них составляются индивидуальные маршруты, в которых указывается причина неуспеваемости, а также план работы с этими учащимися по дням до конца года.

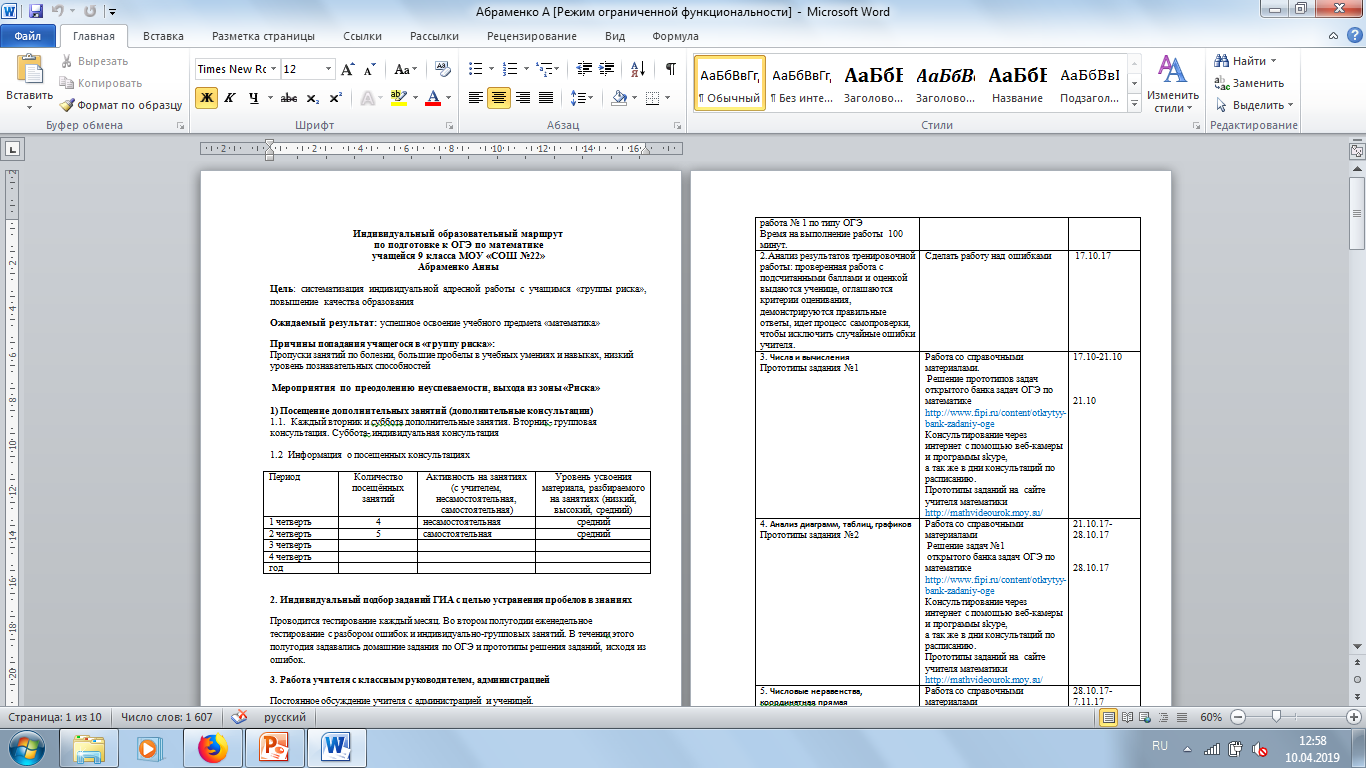
Индивидуальные маршруты ОГЭ

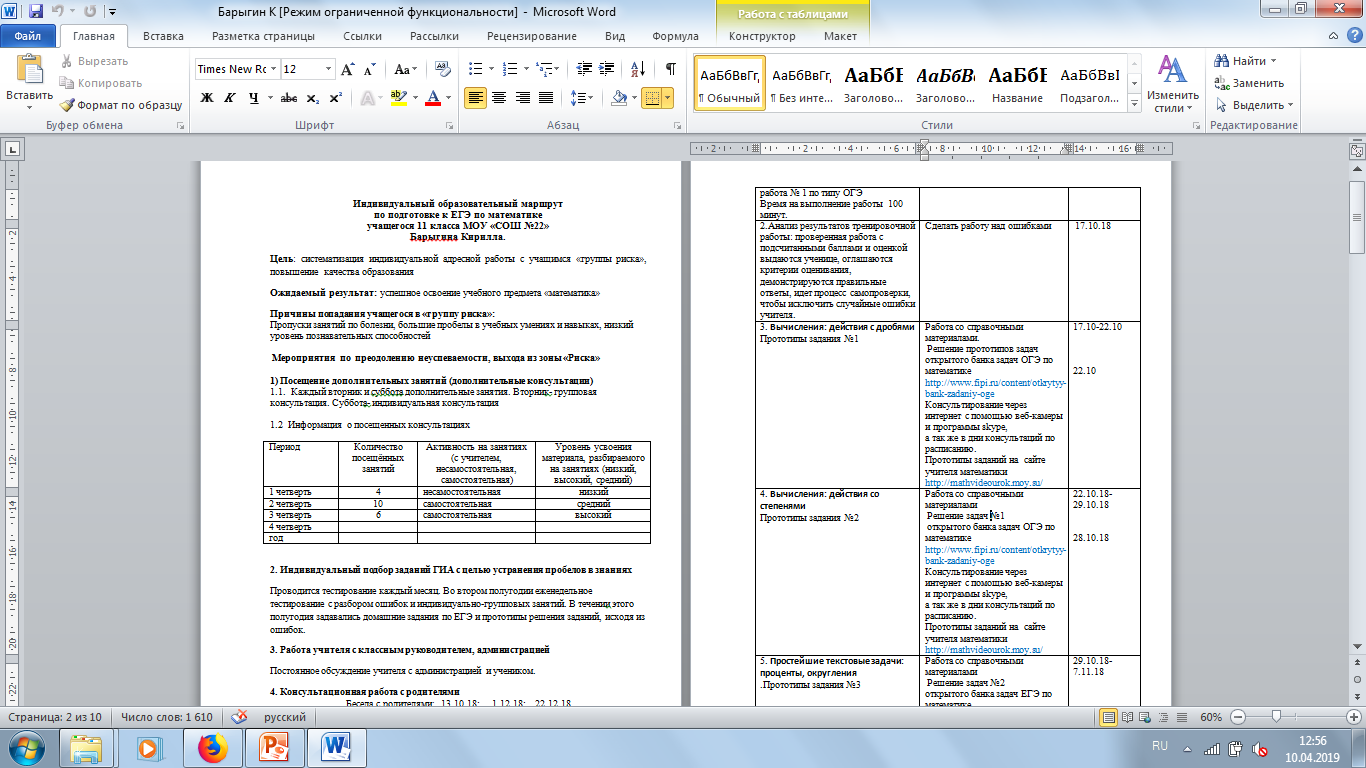
Индивидуальные маршруты ЕГЭ

Консультации со слабыми и с сильными учащимися

Просматривая диагностические карты, анализ пробных тестов провожу консультации по прототипам заданий ОГЭ или ЕГЭ для сильных и слабых учеников. Весь материал консультаций представлен мной в презентациях с подробным решением и объяснением. Но данный материал на сайт не выкладываются, поскольку это интеллектуальная собственность. Но ученики, которые отсутствовали на консультации по какой-либо причине получают материал индивидуально на электронный носитель.

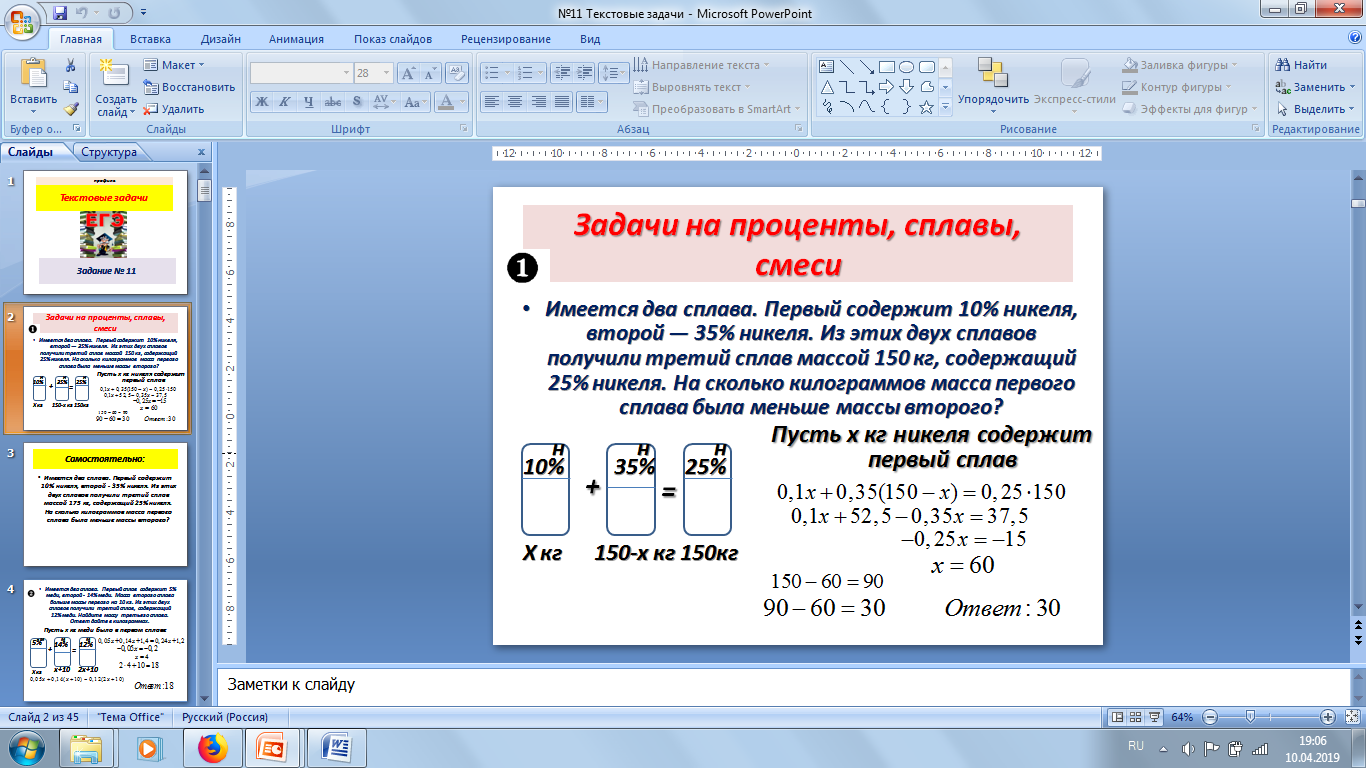
Пример презентации с консультации 11 класс ЕГЭ профильный уровень задание №11

Прототипы заданий ОГЭ и ЕГЭ

Прорешиваются прототипы заданий ОГЭ и ЕГЭ, составленные по материалам ФИПИ. Сами задания выкладываются на сайт без решений.

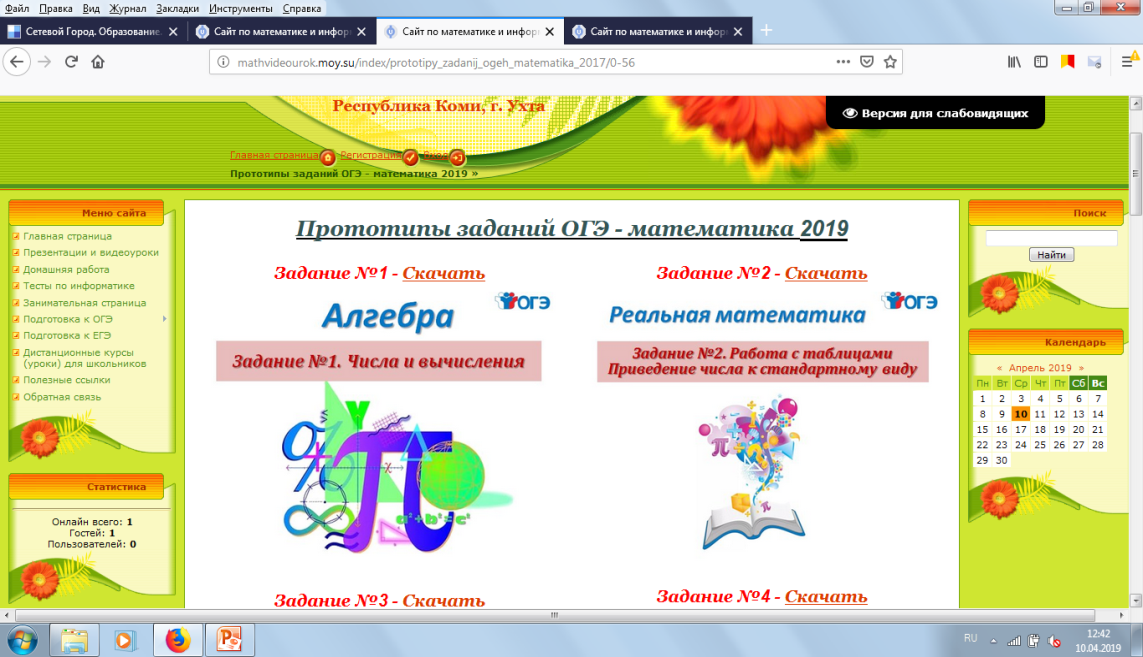
Прототипы ОГЭ

Прототипы ЕГЭ

Также по прототипам составляются пробные тесты, с использованием Google-тестов. Тесты составлены не на все прототипы. Находятся в стадии внедрения. В дальнейшем планируется сделать на все задания КИМ ОГЭ и ЕГЭ. Плюсы этих тестов в том, что система сама проверяет тест, и выставляет количество баллов, набранное за тест, а также выводит подробный отчет по прорешенному тесту, в котором указываются верные и неверные задания. И ученик может посмотреть, где он ошибся, и как нужно было правильно решить данное задание. Тест он может проходить несколько раз. А учителю в личный кабинет приходит диаграмма на каждое задание, где видна динамика выполнения заданий.

Пример теста

Элективные курсы

Параллельно провожу элективные курсы, на которых разбираю дополнительные темы. Решаем уравнения и неравенства с модулем и параметрами. У меня написана книга, где собран материал за все года работы. Ученики старших классов по ней занимаются.

Уроки ОГЭ по алгебре и геометрии

Уроки ЕГЭ профильный, базовый уровни

После того, как в основном пройдена программа по предмету, повторение идет по разработанным урокам ОГЭ и ЕГЭ. Периодически по этим урокам проводятся зачеты. Это ликвидирует пробелы в знаниях.

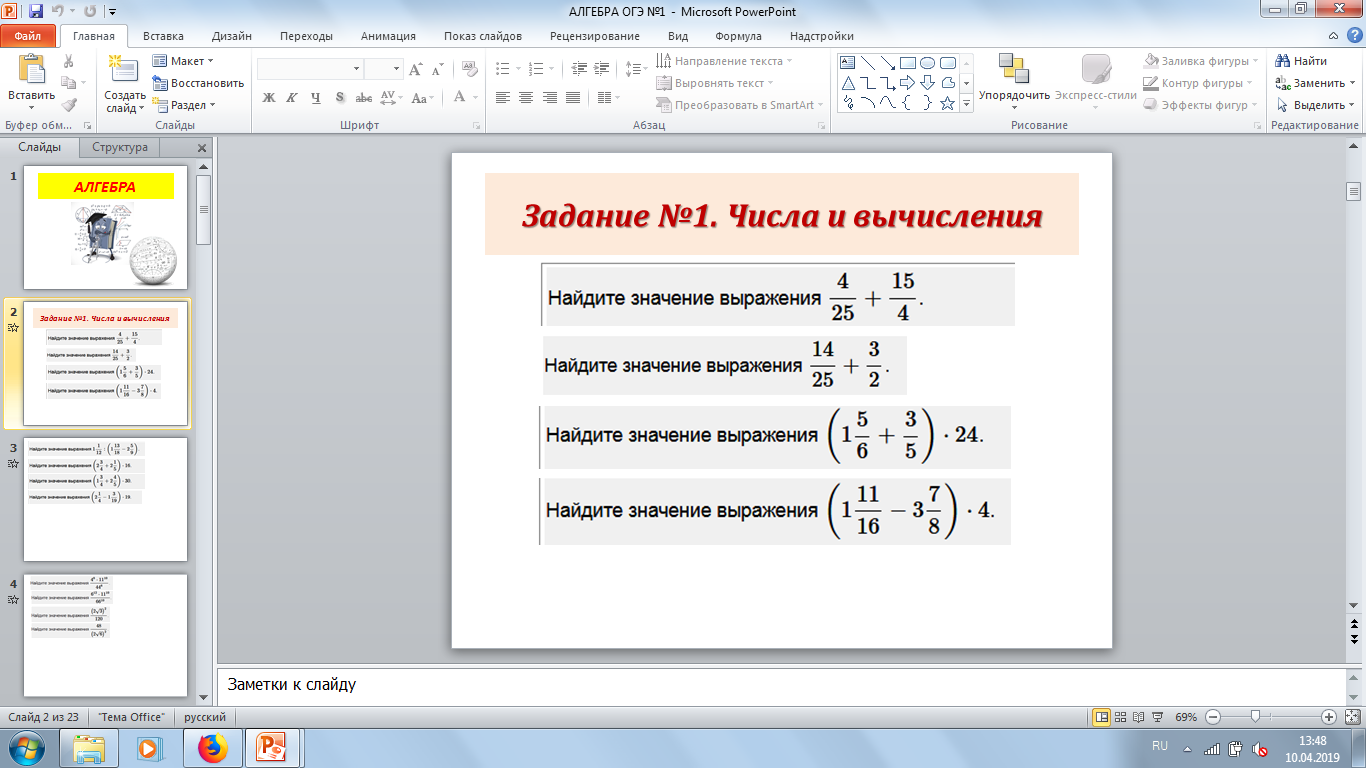
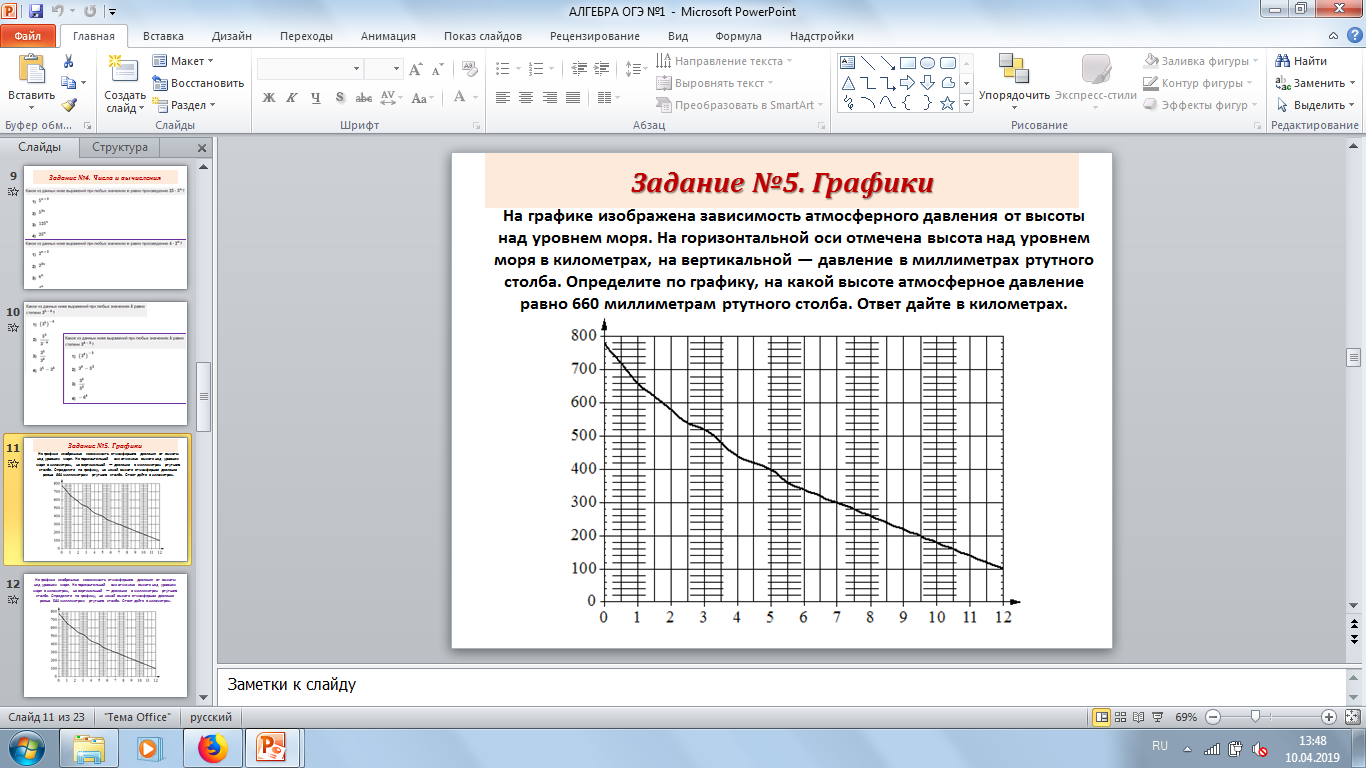
Пример урока по алгебре ОГЭ

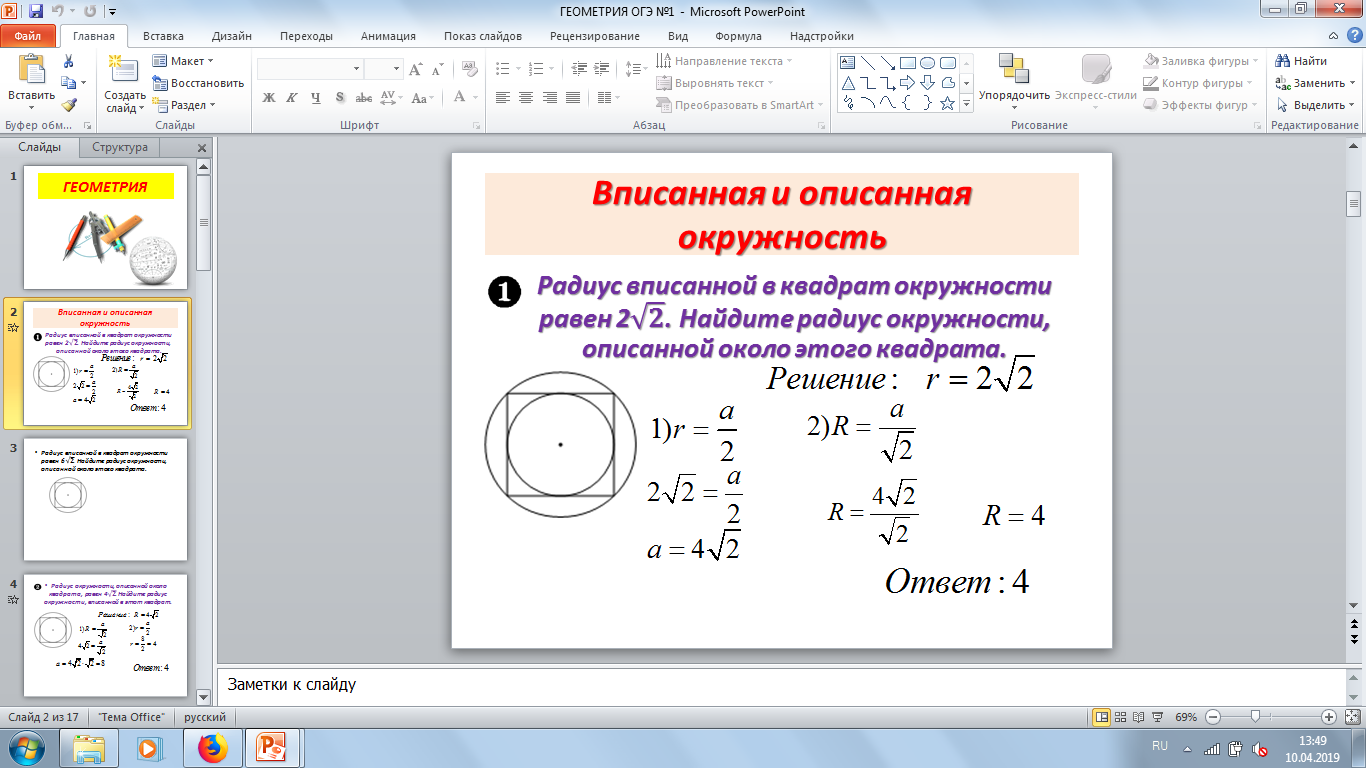
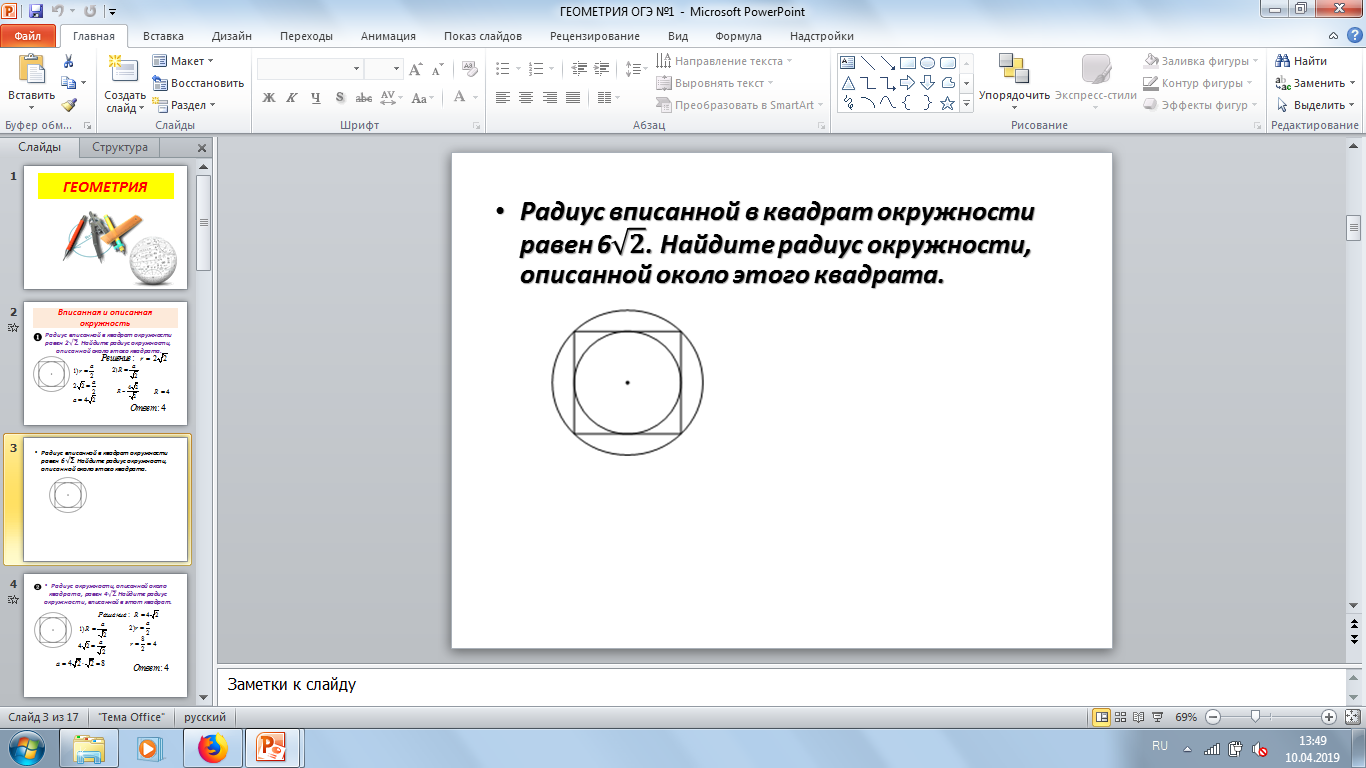
Пример урока геометрии ОГЭ

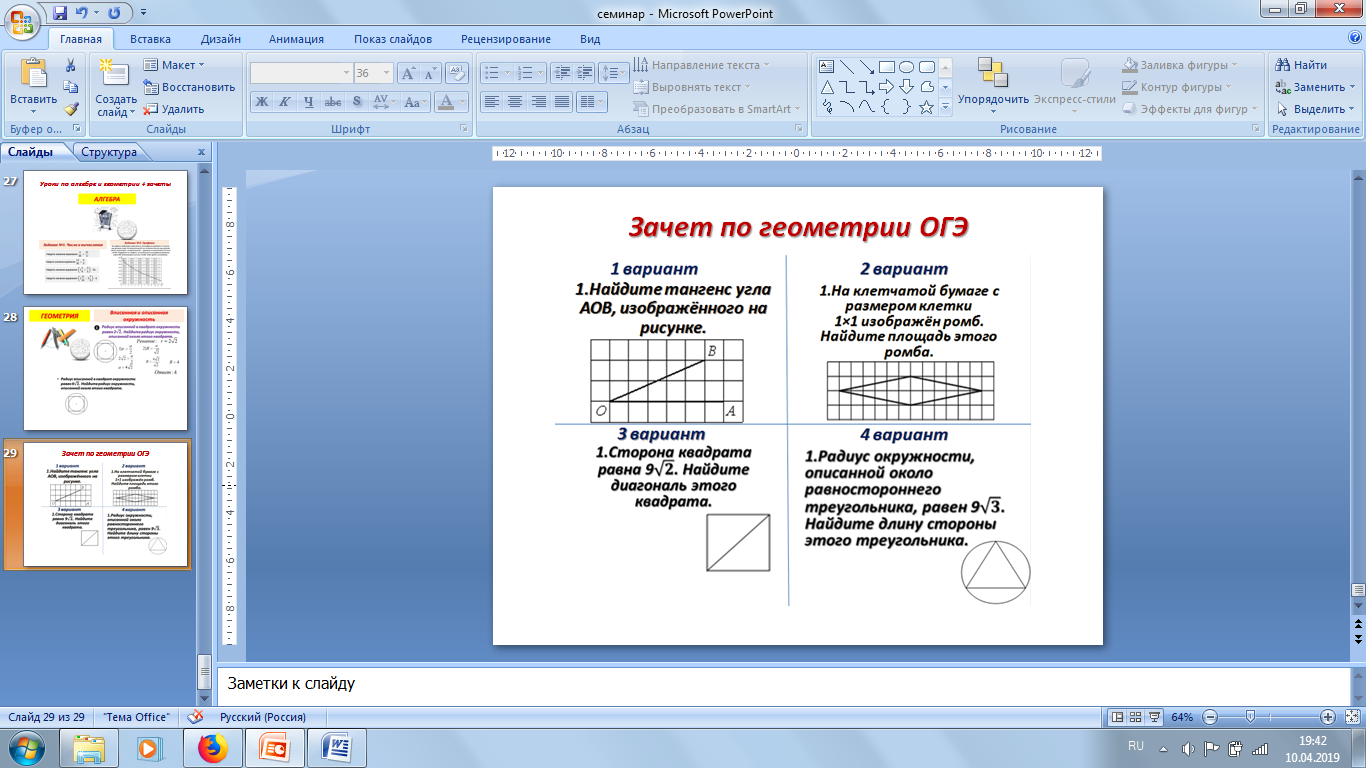
Пример зачета по геометрии ОГЭ

В конце учебного года итоговая контрольная работа проводится в форме ОГЭ и ЕГЭ.

Система работы

учителя математики по подготовке учащихся к ОГЭ

Я люблю математику не только потому,

что она находит применение в технике,

но и потому, что она красива.

(Р. Петер)

Математика – одна из самых сложных школьных дисциплин, и вызывает трудности у многих учащихся. Подготовка к выпускным экзаменам – это всегда ответственный процесс. И от того, насколько мы грамотно построим его, зависит наш результат.

ОГЭ по математике – первый независимый  рубеж проверки знаний, полученных за время обучения в школе. Это первые государственные экзамены,  то есть организованные не школой, а органами, призванными работу этой самой школы контролировать. Отсюда все организационные сложности. Работа пишется в другой школе, контролируют незнакомые педагоги, проверяют независимые эксперты… Все это добавляет нервозности к тому факту, что это большой экзамен, включающий задания  практически по всей школьной программе, пройденной за 9 лет.

Как учитель со стажем замечу, что нельзя забывать и про переходный возраст. У всех подростков он протекает по-разному, но мало никому из родителей не кажется. Поэтому, если вопросы успеваемости и подготовки к ОГЭ выходят на первый план, то это еще, возможно, и благополучный вариант.

         Однако оставим психологию и вернемся к математике. Как я уже сказал, экзамен тестирует знания, умения, навыки за весь 9-тилетний курс. Поэтому главная проблема, с которой приходится сталкиваться при подготовке – это пробелы в знаниях.

         Поэтому первую задачу, которую надо решить учителю – это выявить и ликвидировать все пробелы в базовых знания. А то сейчас девятиклассники плохо знают таблицу умножения, а уж уголком делить многих приходится учить практически с нуля.

Начиная с самого начала преподавания у детей предмета, веду мониторинг уровня обученности учащихся по всем темам, начиная с 5 по 9 классы.

В своей работе наряду с тренировочными вариантами, содержащими задания на все темы, как реальный экзаменационный вариант, я активно использую различные тематические подборки. Это особенно важно, когда какой-то раздел ученику дается с большим трудом. Например, задания на функции или геометрические задачи. В этом случае большой объем решенных задач по одной теме позволяет перевести количество в качество и твердо усвоить эту тему.

Для учащихся 9-х классов провожу групповые и индивидуальные консультации после уроков в строго определённое время. Эти консультации охватывают как сильных обучающихся, с которыми разбираем задания повышенной сложности, так и слабоуспевающих учащихся, с которыми отрабатываем базовые знания умения и навыки.

Также считаю, что наиболее эффективной при подготовке в ОГЭ является методика разноуровневого урока, основанная на дифференцированном подходе к учащимся. На уроках использую технологии уровневой дифференциации, что особенно помогает при подготовке к сдаче экзаменов в форме и по материалам ОГЭ.

Огромное внимание уделяю самостоятельной, групповой работе, практикую в своей работе зачёты и смотры знаний по темам, что положительно сказывается на подготовке к экзаменам. Зачеты провожу в конце темы в виде теста, который составлен из задач трех уровней. При тестировании используют как бумажные, так и электронные варианты. Последние особенно привлекательны, так как позволяют получить результаты практически сразу по завершении теста. Главное условие здесь — систематичность, работа на каждом уроке.

Конечно, идеальный вариант, к которому стремится каждый учитель — самостоятельная учебная работа ребёнка в интерактивной среде обучения, используя готовые электронные учебные курсы, обучающие, тренировочные и проверочные работы в сети Интернет.

Успешной реализации ИКТ на уроках математики для меня является применение Интернета с его практически неограниченными возможностями сбора и хранения информации. Благодаря использованию сети Интернет обучающиеся получают доступ к большому потоку новой информации по темам, проводимым в рамках изучения математики.

Обучать математике несомненно помогают электронные образовательные ресурсы. На уроках математики использую электронные средства обучения. Это тренажеры и программы тестирования по различным темам.

Огромную возможность для участия в различных конкурсах и форумах предоставляют различные сайты. Использование Интернет-ресурсов позволяет обучающимся участвовать в дистанционных конкурсах, олимпиадах в режиме online. Принимают участие в районной олимпиаде по математике среди 7-11 классов.

Проверка знаний и умений учащихся. Выполнение тренировочных и диагностических работ, представленных в сети Интернет.

Ну и, конечно, очень важна система работы учителя математики с родителями при подготовке учащихся к итоговой аттестации.

Проблема взаимодействия семьи и школы не нова. Время идет, мир меняется, меняются и взаимоотношения родителей и школы. Но ответственными за воспитание и образование детей остаются родители и школа. Следовательно, учитель и родители должны быть партнерами в этом вопросе. Нередко трудно бывает привлечь родителей к процессу воспитания детей, и часто родителям самим требуется помощь учителя в решении многих вопросов.

Конечно, очень важен позитивный настрой детей на серьёзный самостоятельный труд по подготовке к экзамену, поэтому в начале каждого учебного года с большим удовольствием сообщаю им информацию о том, что снова, практически все наши выпускники поступили в высшие и средние учебные заведения, многие обучаются на бюджетной основе. Обязательно при этом прошу подсчитать, сколько родительских денег ребята сэкономят за 4-5 лет обучения. Думаю, что этот стимул для большинства семей немаловажен.

Роль учителя в школе действительно велика, но он не всемогущ, и обучить может лишь того, кто хочет учиться и кто сам учится.

По сравнению с другими учебными предметами математика, несомненно, выделяется своей трудоемкостью, необходимостью большой самостоятельной, повседневной работы. Надо вдумчиво, ежедневно, серьезно работать, чтобы овладеть математикой даже в минимальных размерах, не говоря, уже о более значительных успехах.

Поэтому усилия всех участников обучения должны быть направлены на формирование у школьников потребности в учебной деятельности, неуемного желания учиться. Необходимо выработать положительное отношение учеников и родителей к математике, создавать ситуации успеха, ликвидировать боязнь решения математических задач, формировать у детей уверенность в своих способностях.

         В заключение хочу отметить. Успешная подготовка к ОГЭ требует усилий всех участников процесса: и ученика, и учителя, и родителей. Контроль и внимание со стороны родителей просто необходимы для большинства детей.

         Подготовка к ОГЭ – задача не простая, но совместными усилиями решаемая! Успешной вам подготовки и отличных результатов!

Д. Н. Муравлёв,

учитель математики ТОГБОУ «Жердевская школа-интернат»