Решение задач
*** КАНАЛ ЮТЬЮБ ***
Выберите номер задания ЕГЭ с разбором примеров:
Структура заданий ЕГЭ по информатике
С 2021 года структура заданий и начисления баллов:
- Длительность ЕГЭ по информатике составляет 3 часа 55 минут или 235 минут.
- Задания выполняются с помощью компьютера. На протяжении всего экзамена будут доступны текстовый редактор, редактор электронных таблиц и системы программирования.
- На ЕГЭ допустимо использование следующих языков программирования: С++, Java, C#, Pascal, Python, Школьный алгоритмический язык.
- На экзамене будет разрешено использование программы Microsoft Windows «Калькулятор», а также графического редактора Microsoft Paint.
- При проведении ЕГЭ по информатике выдача КИМ на бумажных носителях не планируется.
- Кроме того, учащемуся будет предоставлен бумажный черновик для решения заданий «на бумаге». Но ответ необходимо внести в систему на компьютере.
- Задания ЕГЭ по информатике делятся на два типа: с использованием заготовленных на компьютере файлов (для выполнения которых требуется использование специализированного программного обеспечения) и без использования таковых.
- По уровню сложности: Базовый – 10 заданий (с № 1 по № 10), Повышенный – 13 (с № 11 по № 23), Высокий – 4 (с № 24 по № 27).
- Максимальный первичный балл за работу – 30.
- Общее время выполнения работы – 235 мин
Инструкция для участника КЕГЭ по использованию ПО для сдачи экзамена по информатике и ИКТ в компьютерной форме
Дата проведения (ГИА) ЕГЭ по информатике в 2023 году (ФИПИ)
Досрочный период:
Основной период:
Резерв:
Дополнительный период:
Шкала перевода баллов ЕГЭ по информатике
Таблица перевода первичных баллов в тестовые баллы для проведения ЕГЭ:
(* таблица является ориентировочной (проект), данные уточняются, шкалы для 2023 года пока нет)
| Первич балл |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тестов балл |
7 | 14 | 20 | 28 | 35 | 40 | 44 | 46 | 49 | 51 | 54 | 56 | 59 | 61 | 64 | 66 | 69 | 71 |
| Первич балл |
19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Тестов балл |
74 | 77 | 80 | 82 | 85 | 87 | 90 | 92 | 95 | 97 | 100 |
Минимальное количество баллов в 2021 г. — 43 балла
1 балл начисляется за выполнение заданий 1-24
2 балла начисляется за выполнение заданий 25-27
Тренировочные варианты (КИМы)
Материалы для подготовки к ЕГЭ по информатике К. Ю. Полякова
Лицензионное соглашение
Все опубликованные ниже материалы для подготовки к ЕГЭ по информатике могут быть свободно использованы
в некоммерческих целях при условии сохранения авторства. Без письменного согласия автора
ЗАПРЕЩАЕТСЯ:
- публикация материалов в любой форме, в том числе размещение материалов на других Web-сайтах;
- распространение неполных или измененных материалов;
- включение материалов в сборники на любых носителях информации;
- получение коммерческой выгоды от продажи или другого использования материалов.
Скачивание материалов означает, что вы приняли условия этого лицензионного соглашения.
Информация (задания 4, 7, 8, 11)
Системы счисления (задание 14)
Логика (задания 2, 15)
Пользовательский курс (задания 1, 3, 9, 10, 13)
Алгоритмизация и основы программирования (задания 5, 6, 12, 16−27)
Ответы и решения
———-
Оригинал страницы: http://kpolyakov.spb.ru/school/ege.htm.
1. Кодирование
текста
2.
Анализ таблицы истинности
4. Бд и файловая система
6. Алгоритмы
Сколько 1, 0, целых A<X<B, вычислить, перевести (-а) в 2сс
Свойства чисел:
1.числа вида 2k записываются в двоичной системе как единица и k нулей, например:16 = 24 = 100002 (числа,
являющиеся степенями 2,3.. ( в любой СС!!)
2. числа вида 2k-1 записываются в двоичной системе k единиц, например: 15 = 24-1 = 11112 (числа
, предшествующие степеням «2»- состоят из «1» и на разряд меньше (в 3 из 2, 4
из 3 , т.е n-1))
3. Двоичное число (другая n CC), оканчивающееся — на 0 – четное(кратно n), — на 1- нечетное (и любое отличное от нуля число в той СС
говорит о том, что число не кратно n).
Отрицательное число =
1) а-1 2) (а-1)из10 перводим в 2сс 3) первая 1
сохраняется, все остальные цифры переворачиваем 1-0,0-1
|
10сс |
2сс |
8 сс |
триады |
16сс |
тетрады |
|
0 |
0 |
0 |
000 |
0 |
0000 |
|
1 |
1 |
1 |
001 |
1 |
0001 |
|
2 |
10 |
2 |
010 |
2 |
0010 |
|
3 |
11 |
3 |
011 |
3 |
0011 |
|
4 |
100 |
4 |
100 |
4 |
0100 |
|
5 |
101 |
5 |
101 |
5 |
0101 |
|
6 |
110 |
6 |
110 |
6 |
0110 |
|
7 |
111 |
7 |
111 |
7 |
0111 |
|
8 |
1000 |
10 |
8 |
1000 |
|
|
9 |
1001 |
11 |
9 |
1001 |
|
|
10 |
1010 |
12 |
A |
1010 |
|
|
11 |
1011 |
13 |
B |
1011 |
|
|
12 |
1100 |
14 |
C |
1100 |
|
|
13 |
1101 |
15 |
D |
1101 |
|
|
14 |
1110 |
16 |
E |
1110 |
|
|
15 |
1111 |
17 |
F |
1111 |
|
|
16 |
10000 |
20 |
10 |
10000 |
|
0+0=0 |
0-0=0 |
0*0=0 |
|
0+1=1 |
1-0=1 |
0*1=0 |
|
1+0=1 |
1-1=0 |
1*0=0 |
|
1+1=10 |
10-1=1 |
1*1=1 |

Сопоставлять
значений переменных с функциями (начинать с «одиночных»)
1. Отрицание
(НЕ,¬ , Ā) меняет знаки: < на >=,> на<=.<= на
>, >= на <
2.
Логическое умножение (И, •, ˄, &)
3.
Логическое сложение (ИЛИ, +, ˅, |)
Порядок
выполнения операций: ( ), не, и, или, →,º ….
|
А |
не(А) |
А |
В |
А ˄ В |
А |
В |
А ˅ В |
А |
В |
А→В |
А |
В |
АºВ |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
||
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1)внимательно читать задание
2)файловая система:?-точно 1 знак, *-произвольное количество или
их отсутствие
Автомат(10 СС):
1)определяем СС
2)записываем правило a+b, c+d или другое
3)определяем порядок записи , ¯
4) определяем максимально возможное числов этой СС и
максимальные суммы(!!!помнить о правилах сложения в разных СС)
5) помним о разрядах числа (десятки, сотни, единицы)
Автомат(2СС): четное оканчивается 0, нечетное на 1.
Обработка искаженных сообщений, Калькулятор и др.
5. Декодирование (условие Фано)
Условие Фано: ни одно кодовое слово
не является началом другого кодового слова (дерево 0-1): минимальный код,
короткое слово, сумма кодовых слов, только для конкретного слова и др.
Алгоритм Хаффмана
(оптимальный префиксный код): для самого частого- самый короткий код. Самое
частое повторение обычно 1 бит(0),самые малые повторения обычно 2-3 бита
(умножаем и складываем все ветви)
9.
Кодирование информации (+передача)
7. Анализ диаграмм и таблица Excel
8. Анализ программ (цикл while)
Звук: I=n*i*f*t (n-кол-во дорожек, i-бит на отсчет, f-частота дискретизации ,t-время)
1)
запись близка 2) секунды-минуты
3)
перезаписывают один и тот же файл — пропорция
1кГц=1000Гц, моно-1, стерео-2, квадро -4, …
Графика: I=k*i, N=2i(k –кол-во пикселей (200dpi= 200ppi=200*200)
i -инф. вес 1 пикселя, N-количество цветов)
1)определить кол-во цветов
2)не может превышать <
, >=, > , <=
3) перезаписывают один и тот же файл — пропорция
4) сохраняют каждые t сек(мин)
Передача информации: Iбит=Vбит/сек*tсек , V =I/t, t=I/V
I – размер файла, V – скорость , t – время передачи.
1)сравнение
способов передачи А и Б и на сколько
Наименьшая
единица информации 1 бит
1
байт = 8 бит = 23бит
1Кбайт(килобайт)
= 1024байт = 210байт
1Мбайт(мегабайт)
= 1024Кбайт = 210Кбайт
1Гбайт(гигабайт) = 1024Мбайт = 210Мбайт
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
|
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
210 |
211 |
|
N |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1024 |
2048 |
|
S передачи |
«Байт |
|
1 1 1 |
1 1 Кбайт/сек 1 Мбайт/сек |
!!!Важно в формулу подставлять значения в одинаковых единицах
измерения и переводить конечный результат в запрашиваемые в задаче единицы.
1)по формулам 2) по пропорции
1)геометрическая или арифметическая прогрессия
2)условие выполнения цикла (с предусловием)
1)вычисляем значения в ячейках по формулам какие можно
2) соотносим числовые величины и графические изображения
(подбираем число или формулу). Диапазон ячеек А1:D2 от первой ячейки до
последней. Весь круг соответствует сумме всех значений, по которым
строится диаграмма. Отдельные сектора пропорциональны доле одного значения в
общей сумм
В формулах * — умножение, / — деление, $ — абсолютная ссылка, при
копировании формулы значение не меняется
10. Перебор слов и СС
1)размещения(с повторениями, букву сколько угодно раз)Варианты =
2)перестановки (без повторов, букву 1 раз, буквы разные) Р=n!
2)перестановки (без повторов, букву 1 раз, есть одинаковые буквы
разные) Р=n!/n1! .n2!..
4) вероятности формула Шеннона.
5)Слова(определяем СС (= количество букв), переводим в ту СС, из
той в 10)
— На каком месте стоит слово +1
— Какое слово стоит под номером -1
3. Анализ информационной модели
15. Количество путей
Соотносим количество пересечений дорог и узлов вершин графа,
анализ начинаем с графа (вершин графа)
|
Город |
Откуда |
Кол-во путей |
|
А |
— |
1 |
|
Б |
А |
1 |
|
В |
АБ |
2 |
|
…… |
…. |
….. |
Потеря маршрутов, считая «вручную»
Траектория через А и
не через Б –внимательно!
22. Оператор ветвления
Строим дерево внимательно через те точки, которые указаны в
траектории
11.Рекурсия (функция возврата к самой себе)
14. Алгоритмы формальных исполнителей
1) Вызов функций F(n) или/и G(n) от предыдущих значений
2) Количество напечатанных
3) Сумма напечатанных
4) Какие выведет числа (!!!Важен порядок вызова (обращения к
рекурсии).
-если write
стоит в начале, то прямой последовательный обход.
— если write
стоит после какой-то первой функции, то выполняется вызов по этой ветке до
конца, по окончанию вызывается оставшаяся функция.
— если write
стоит после всех функций, аналогично предыдущему
Чертежник
Начал и вернулся туда же: (х,у)+…-…=(0,0)
Вернулся в другую точку: (х,у)+…-…=(х1,у1)
Повтори n
раз n*(3+2-4…)
Замена команды n*(а+2-4…)=0, n*(b+3-8….)=0
1)отдельно считаем смещение по x и по y;
2)внимательно читаем вопрос;
3)даём ответ на вопрос, поставленный в задаче.
Робот: клетка начала и конца
считается закрашенной, движение идет до упора и по условию.
Редактор: циклы считаем с НАЧАЛА!!!
17. Запросы интернета (Диаграммы Эйлера Венна)
23. Логические уравнения
19. Одномерные массивы
Знак
«&»-пересечение запросов (и) , а «|»-объединение запросов (или)
1) Обозначаем зоны запросов буквами a,b,c,d,e,f…..
2) !!! Два множества могут не пересекаться (просматриваем суммы
пересечений и объединений)
|
А ˄ В |
А ˅ В |
А→В |
АºВ |
А¹В |
|
1 и 1 |
1 и 1 |
1-1 |
1 и 1 |
0 и 1 |
|
0 и 1 |
0-0 |
0 и 0 |
1 и 0 |
|
|
1 и 0 |
0-1 |
1) замена переменных, если нужно
2) последовательное решение уравнений
Решение системы уравнений – это битовая цепочка (битовый вектор-
единичный объект)
3) уравнения–ограничения на битовый вектор (комбинации)
4) кол-во решений находиться по правилам комбинаторики (чаще
всего аn)
5) варианты комбинаций истинности и лжи для ˄,˅,→, º
Стратегия решения: трассировочная
таблица , узнать базовый алгоритм и проверить
а) алгоритм меняющий
элементы массива местами
б) массивы с индексами от 0
до 10 цикл for
в) цикл for или while в
нем ветвление (if)
г) двумерные
массивы(прямоугольная матрица A[i] , B[i]
Цикл for в цикле for
(выполняется первый внешний цикл, потом полностью выполняется внутренний цикл
for, далее 2 эл из 1, и все из
2го ) (прямоугольная матрица)
16. Уравнения в различных СС
26. Стратегия (теория игр)
13. Вычисление количества информации
21. Анализ программы с
подпрограммами
1)помнить,
что любое число в степени в соответвующей СС=
2)выражения
упрастить и определить СС, если сс 2,3,4,5,…..при вычитании 1 получается на
1 меньше чем СС.
3)
числа в конце переводим в нужную СС
4)
если произведение степени и числа, применяем правила арифменики в той СС
(арифметические операции выполняются в одной СС)
5) если
степень числа * на число, применяем арифметические правила той сс в которой
производиться *.
Важно!!!
Арифметика возможна только в одной и той же СС
Описывать стратегию для «выигравшего- выигрышную стратегию, для
проигравшего- все стратегии» (строим дерево игры)
1) камни (камни две кучи, 2 разных хода)
2) фишки (расстояние
3) карточки(таблички) с числами, убирать дубль, если нужно
укоротить, ставить дубль если нужно удлинить
4) слова (считаем количество букв в словах) Игрок 1- нечетные
ходы, Игрок 2- четные ходы
I=k*i, N=2i (N-алфавит, k–количество
символов в тексте, i–
инф. вес 1 символа:
КОИ-8(8 бит), ASCII(8 бит), Unicode (16
бит), др)
1) количество вариантов (кто прошел –это N из него находим i ( N=2i ), а I=k*i –это всего.
2) пароли и номера авто: доп. сведения + код+ пароль
!!!Внимательно читать условие (сведения могут быть в 2 коде или
другой СС)
1) Квадратичные
(биквадратные) уравнения:
Точки минимума =
,
=у(
или через F`(x)
Можно искать точки
(max, min), и
значения функций в точке (fmax, fmin). Оценивать
знаки , ¯ функции.
!!!Обязательно
проверять проверять значения на концах отрезков.
2) вызов функции k=10,64 и
т.п. min или max число
Если +1, то
интервал А £
х <В
Если ¯-1, то
интервал А < х £В
12. IP-адресация
20. Анализ алгоритма с циклами и ветвлениями
24. Поиск ошибки в программе
25. Обработка
массива
010=000000002 25510=111111112
маска-11111111.11111111.11111000.00000000 (1….потом 0)
1)мах количество 1 или 0 в маске
2)мах и min байт
маски
3) 2 байт маски, если 3 =0
4) сколько различных значений маски (сколько масок, варианты)
5)количество ПК в сети (2 в степени нулей маски )
6) номер ПК в сети (нули маски в проекции на ip-адрес)
7) два ip принадлежат
одной сети (однозначная маска для обоих)
Номер компьютера
Количество адресов в сети
1) Алгоритм Евклида (2 переменные и разность), НОД
прописан в условии, в условии смотреть какое х нужно вывести х>100, 150…
Выражаем L
через х, L кратно НОД, далее проверяем на числах.
Вычисление НОД(а,b)= НОД(а-b,b)= НОД(а,b—a)
Заменяем большее из двух чисел разностью большего и меньшего до
тех пор, пока они не станут равны. НОД(14,21)= НОД(14,7)= НОД(7,7)=7
Если разница велика и нужно определить количество шагов.
Заменяем большее остатком от деления на меньшее до тех пор, пока меньше не
станет равно нулю. НОД(21,28) (28mod21=7)= НОД(21,7) (21mod7=0)=НОД(0,7)=7
2) Обработка цифр в числе:
— на выводе отмечаем, какие числа выводит программа (указаны в
условии)
— ВАЖНО!!!определить СС в которой обрабатываются числа
x: = а div 10, x: = а div 2, x: = а div 3 , x: = а div 4 , x: = а div 5
ЗНАТЬ!!! числа входящие в конкретную СС (0- число четное!!!)
Перебор цифр в числе за счет цикла ( while x>0 ) пока оно не равно нулю.
— если определяют не просто число , а разрядное (трехзначное,
двузначное)- это дополнительное условие (первое двузначное-10n, трехзначное 100n и т.д конечная граница определяется переводом из 10 сс в нужную)
ЯЗЫК программирования Pascal не понимает другие СС, кроме 10!!
После решения задачи в какой-то СС , переводим полученное число
в 10СС
!!!Проверка на четность:
— в четных СС по последней цифре (0,2,4,6,8 СС)
— нечетных СС по сумме цифр в числе (1,3,5,7,9 СС)
Схема
решения задачи: прогнать задачу на требуемом числе или
на любом удобном Þ чаще всего можно сразу ответить на 1 и 3
вопрос задачи (найти ошибки) (прогнать и убедиться в правильности) Þ после
выполнить 2 задание задачи (найти число работающее правильно )
Решая
задачу делить ее на части:
1)
что выводит (writeln(…)) и
запрашивает readln(…))
2) проверять
инициализацию переменных s:=0, p:=1, k:=0
3)
проверяем условия циклов и условий (правила их работы) и сам алгоритм
Проверка
на степень: n=ak Þ , т.е if n=1.
Формулу для вычисления n-ого элемента арифметической прогрессии: аn=a1+d(n-1) формулу для вычисления суммы первых n членов арифметической прогрессии:,
где ai – i-ый
элемент последовательности,d – шаг (разность) последовательности
1) Организация ввода данных (уже есть)
2) Инициализация начальных значений некоторых переменных (требуется
задать!)
3)Обработка данных (требуется организовать!)
4) Вывод данных (требуется организовать!)
Обработка данных происходит в процессе циклической
обработки элементов ( может обрабатывается один, пара, тройка или
последовательность элементов, речь всегда идет о рядом стоящих элементах,
которые всегда можно обработать одним циклом) по некоторому комбинированному
условию, которое необходимо формализовать основе анализа условия задачи.
ВАЖНО!!! не писать программу полностью, а «дописать» её в рамках
уже организованного ввода, а также заданного количества переменных и их
типов: необходимо дописать инициализацию, организовать обработку и вывод.
Для проверки на кратность использовать —
a[i] mod
2 <> 0 (Кратность n)
18. Логические выражения
1) отрезки (преобразуем,
отделяем A (или Ā ) от отрезков, сумма должна
покрывать всю числовую прямую)
упростить А→В= Ā+В, А º В=А*В+Ā*, (см. табл задания№2)
2) неопределенный отрезок
(более чем 25 целых, т.е 26 чисел)преобразуем, пользуемся
распределительным законом)
Помнить два закона !А+В*С=(А+В)*(А+С)
и А*В+С=(А*В)+(А*С)
3) множества (отделяем
числа, отделяем А, делаем отрицание с числами и применяем закон де Моргана,
как с отрезками только на диаграммах Эйлера -Венна)
4) делители А=1,
остальное =0 (Ā=В, А= ) закон де Моргана
Если меду числами ˄-ищем
кратные, если ˅-делители
1. Если формула истинна (равна 1), и после упрощения A без
отрицания, то используется закон: Amin = ¬B
Если формула истинна (равна 1), и после
упрощения A с отрицанием, то используется закон:Amax =
B
2. Если формула ложна (равна 0), и после
упрощения A без отрицания, то используется закон: Amax =
¬B
Если формула ложна (равна 0), и 2. после
упрощения A с отрицанием, то используется закон: Amin =
B, где B — известная часть выражения
5)неравенства ( если А=1,
то остальное берется с отрицанием, если А=0 (отрицательно), то остальное не
меняем, оно положительно)
а)длина –это модуль от точки
до точки: (А..)→(….х ) ) ˄ ( (
….х) → (А..)) через
и
, если где-то парабола, то
модуль и отрезок значений параболы.
б) сколько существует
значений: кол-во чисел n+1
в) линейные неравенства
(графическим способом, как задача с параметром, определяем область и
пересечение графиков прямых линий, анализируем)
6) битовые операции
1) А→В= Ā+В
2) избавляемся от всех
отрицаний (закон де Моргана) и выстраиваем импликации
3) Упрощаем до выражений
следующего типа:
a) (Q•A) →P=1 , т.е Q+А=P
б) (Q•P) →А=1, т.е Q+ P = А
в) P→ (Q+A) =1, A→ (Q+P) =1,
г) (Q+Р) → (L+A) =1, т.е Q•А=A•L
(L•A) →(Q•Р) =1, т.е Q+А=A+L
д) побитовые операции равны числам
(переводим их в 2СС)
решаем как с делителями и отрезками А=1,
остальные =0, сначала находим маску х при =0 и варианты букв в маске х при ¹ 0) не решаем по общей схеме
4) применяем свойства 1)XP ˄XQ=XP or Q=P+Q
2) XP ˅ XQ=XP and Q=P•Q
В решение заданий демо-версии используется язык программирования Python.
|
Задание 1. Анализ информационных моделей На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова сумма протяжённостей дорог из пункта D в пункт В и из пункта F в пункт A. В ответе запишите целое число. |
На графе расставим веса вершин. Далее 2 и 7 вершины ведут нас к 5, значит А это 5, оставшаяся «тройка» это вершина Е под номером 6. Сумма дорог BD + AF = 53 + 5 = 58 Ответ: 58 |
||||||||||||||||||
|
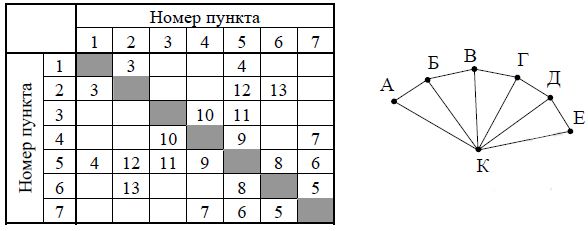
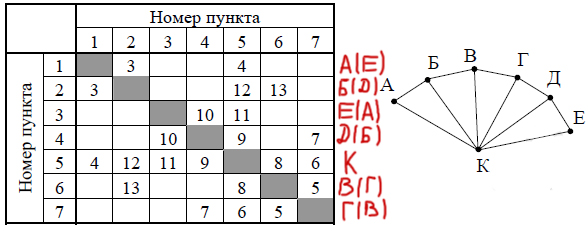
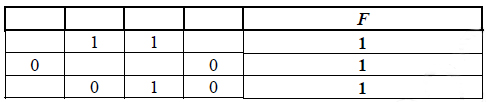
Задание 2. Построение таблиц истинности логических выражений Миша заполнял таблицу истинности логической функции F F= ¬(y → x) v (z→ w) v ¬z , но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z. Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z. В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. Пример. Функция задана выражением ¬x v y, зависящим от двух переменных, а фрагмент таблицы имеет следующий вид. В этом случае первому столбцу соответствует переменная y, а второму столбцу – переменная x. В ответе следует написать yx. |
¬(y → x) v (z→ w) v ¬z=0. Следовательно y → x =1, z→ w=0, z=1. Значит третий столбец z. z→ w=0, значит w=0, и это может быть только 4 столбец. y → x =1, следовательно из второй строки мы видим, что первый столбец может быть только у, а второй х.
Решение на Python Ответ: YXZW |
||||||||||||||||||
Задание 3. Базы данных. Файловая система В прикрепленном файле приведён фрагмент базы данных «Продукты» о поставках товаров в магазины районов города. База данных состоит из трёх таблиц. Таблица «Движение товаров» содержит записи о поставках товаров в На рисунке приведена схема указанной базы данных. Используя информацию из приведённой базы данных, определите общий вес |
На третьем листе книги применим фильтр по району и получим ID четырех магазинов. На втором листе применим фильтр по товару и получим ID товара. На первом листе применим фильтры по ID товара и ID магазинов и типу операции. Все даты попадают в интервал от 1 до 8 июня. Получим: Поступило в продажу 710 упаковок. В упаковке 0,5 кг. Получим 355 кг. Ответ: 355 |
||||||||||||||||||
|
Задание 4. Кодирование и декодирование информации По каналу связи передаются сообщения, содержащие только буквы из набора: А, З, К, Н, Ч. Для передачи используется двоичный код,удовлетворяющий прямому условию Фано, согласно которому никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: Н – 1111, З – 110. Для трёх оставшихся букв А, К и Ч кодовые слова неизвестны. Какое количество двоичных знаков потребуется для кодирования слова КАЗАЧКА, если известно, что оно закодировано минимально возможным количеством двоичных знаков? |
Ответ: 14 |
||||||||||||||||||
|
Задание 5. Анализ и построение алгоритмов для исполнителей На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему 1. Строится двоичная запись числа N. Полученная таким образом запись является двоичной записью искомого числа R.Например, для исходного числа 610 = 1102 результатом является число |
Минимальное R, большее 40, это 41. ИЛИ программное решение Ответ: 16
|
||||||||||||||||||
|
Задание 6. Определение результатов работы простейших алгоритмов Исполнитель Черепаха действует на плоскости с декартовой системой координат. Черепахе был дан для исполнения следующий алгоритм: Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 5 команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд n (где n– целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова; Назад n (где n– целое число), вызывающая передвижение в противоположном голове направлении; Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке, Налево m (где m– целое число), вызывающая изменение направления движения на m градусов против часовой стрелки. Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм: Определите, сколько точек с целочисленными координатами будут находиться внутри пересечения фигур, ограниченных заданными алгоритмом линиями, включая точки на границах этого пересечения. |
Сначала нужно построить фигуру. Далее мы находим уравнения прямых, которыми ограничена фигура и решаем ИЛИ Ответ: 1 задание — 38, 2 задание — 128 |
||||||||||||||||||
|
Задание 7. Кодирование и декодирование информации. Передача информации Музыкальный фрагмент был записан в формате моно, оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 28 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате стерео (двухканальная запись) и оцифрован с разрешением в 3,5 раза выше и частотой дискретизации в 2 раза меньше, чем в первый раз. Сжатие данных не производилось. Укажите размер полученного при повторной записи файла в Мбайт. В ответе запишите только целое число, единицу измерения писать не нужно. |
I = ν ⋅ i ⋅ t ⋅ k, где ν — частота дискретизации (Гц), i — разрешение (бит), t — время (с), k — количество дорожек (1 -моно, 2- стерео, 4 — квадро) I1 = ν ⋅ i ⋅ t I2 = 3,5 · 28 = 98 Ответ: 98 |
||||||||||||||||||
|
Задание 8. Перебор слов и системы счисления Определите количество пятизначных чисел, записанных в восьмеричной системе счисления, в записи которых только одна цифра 6, при этом никакая нечётная цифра не стоит рядом с цифрой 6. |
* * * * * — пятизначное число. 6 * * * * — вариантов 3 ⋅ 7 ⋅ 7 ⋅ 7 = 1029 Ответ: 2961 |
||||||||||||||||||
Задание 9. Работа с таблицами Файл с данными Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел. Определите количество строк таблицы, содержащих числа, для которых выполнены оба условия: |
Для решения этой задачи понадобится 10 вспомогательных столбцов. Сначала мы посчитаем количество повторяющихся чисел в каждой строке. Затем сумму каждой строки диапазона H:M. Если повторений нет, то эта сумма равна 6. Далее мы найдем среднее арифметическое неповторяющихся значений. Затем найдем сумму повторяющихся значений. Затем проверим соблюдение двух условий. И подсчитаем количество строк, в которых соблюдаются оба условия. Ответ: 2241 |
||||||||||||||||||
Задание 10. Поиск символов в текстовом редакторе Файл с данными Текст произведения Льва Николаевича Толстого «Севастопольские рассказы» представлен в виде файлов различных форматов. Откройте один из файлов и определите, сколько раз встречается в тексте отдельное слово «теперь» со строчной буквы. Другие формы этого слова учитывать не следует. |
В текстовом редакторе используем инструмент найти (по умолчанию он не учитывает регистр, в расширенном поиске есть кнопка больше, где можно проверить настройки). Ищем слово целиком. Ставим галочку учитывать регистр. Слово теперь со строчной буквы встречается 45 раз. Ответ: 45 |
||||||||||||||||||
|
Задание 11. Вычисление количества информации При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 250 символов и содержащий только десятичные цифры и символы из 1650-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит. Определите объём памяти (в Кбайт), необходимый для хранения 65 536 идентификаторов. В ответе запишите только целое число – количество Кбайт. |
I = K · i, N = 2 i ID : ****….**** – всего 250 различных символов в наборе N = 10 + 1650 = 1660, 1024<1660<2048, 2048 = 211, значит для кодирования одного символа нужно 11 бит. IID = 250 · 11 = 2750 бит = 343,75 байт ≈ 344 байт – отводится на идентификатор целое число байт I65536 = 65536 ⋅ 344 = 22544384 байта = 22016 Кбайт– всего Ответ: 22016 |
||||||||||||||||||
|
Задание 12. Выполнение алгоритмов для исполнителей Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр. А) заменить (v, w). Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Б) нашлось (v). Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется. Цикл выполняется, пока условие истинно. В конструкции ЕСЛИ условие выполняется команда 1 (если условие истинно). В конструкции ЕСЛИ условие выполняется команда 1 (если условие истинно) или команда 2 (если условие ложно). Дана программа для Редактора: |
def pr(n): #функция определяет простое ли число for n in range(100): #перебираем n if ‘>2’ in s: if ‘>0’ in s: sum_s = 0 Ответ: 5 |
||||||||||||||||||
|
Задание 13. Поиск путей в графе На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. |
Начнем подсчет из вершины Е налево через В и возвращаемся в Е через Л. Ответ: 21 |
||||||||||||||||||
|
Задание 14. Кодирование чисел. Системы счисления Операнды арифметического выражения записаны в системе счисления с основанием 15. |
for x in range(15): if n%14 == 0: Ответ: 8767 |
||||||||||||||||||
|
Задание 15. Преобразование логических выражений На числовой прямой даны два отрезка: D = [17; 58] и C = [29; 80]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение |
def deli(n,m): for A in range(1,1000): if Ok: Ответ: 94 |
||||||||||||||||||
|
Задание 16. Рекурсивные алгоритмы Алгоритм вычисления значения функции F(n), где n – натуральное число, |
F(2023) = 2023! = 2023 ⋅ 2022! F(2023)/F(2020) = (2023 ⋅ 2022 ⋅ 2021 ⋅ 2020!)/2020! = 2023 ⋅ 2022 ⋅ 2021 = = 8266912626 Ответ: 8266912626 |
||||||||||||||||||
Задание 17. Проверка на делимость Файл с данными В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от –10 000 до 10 000 включительно. Определите количество пар последовательности, в которых |
f= open(’17.txt’) k = 0 for i in p: for i in range(1,len(p)): #Осторожно, скобки! print(k,PP) Ответ: 180 190360573 |
||||||||||||||||||
Задание 18. Робот-сборщик монет Файл с данными Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота. Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную. Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.Пример входных данных:
Для указанных входных данных ответом должна быть пара чисел 41 и 22. |
Сначала скопируем таблицу рядом, начиная со столбца АА, можно уменьшить ширину столбца до 4-5. Ячейка АА1=А1. Ячейка АВ1 = АА1+В1, протягиваем ее до АТ1. Ячейка АА2 = АА1 + А2, протягиваем ее до АА20. Далее ячейка АВ2 = В2+МАКС(АА2;АВ1), протягиваем ее на весь оставшийся диапазон, копируем только значения, не трогая стен. Справа от стен формулы повторяют крайний левый рял, столбец АА, снизу от стен формулы копируют верхнюю строку 1. Далее делаем замену всех формул МАКС на МИН. Ответ: 1099 1026 |
||||||||||||||||||
|
Задание 19. Выигрышная стратегия. Задание 1 Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 129. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу из 129 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 128. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. |
При значениях S < 64 у Пети есть возможность сделать такой ход, что Ваня не сможет выиграть своим первым ходом. При значении S = 64 Петя своим первым ходом может получить 65 или 128 камней в куче. Во всех случаях Ваня увеличивает количество камней в куче в два раза и выигрывает своим первым ходом. Ответ: 64 |
||||||||||||||||||
|
Задание 20. Выигрышная стратегия. Задание 2 Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:
Найденные значения запишите в порядке возрастания. |
Значение S должно быть меньше 64, поскольку иначе Ваня сможет выиграть своим первым ходом. Ответ: 32 63 |
||||||||||||||||||
|
Задание 21. Выигрышная стратегия. Задание 3 Для игры, описанной в задании 19, найдите значение S, при котором одновременно выполняются два условия:
Если найдено несколько значений S, в ответе запишите минимальное из них. |
Ответ: 62 |
||||||||||||||||||
|
Задание 22. Многопроцессорные системы В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно. |
В независимых процессах время считается от 0, Ответ: 17 |
||||||||||||||||||
|
Задание 23. Анализ программы с циклами и условными операторами Исполнитель преобразует число на экране. |
def f(x, y): print (f(1,10) * f(10, 35)) Ответ: 98 |
||||||||||||||||||
Задание 24. Анализ программы с циклами и условными операторами Файл с данными Текстовый файл состоит из символов A, C, D, F и O. Определите максимальное количество идущих подряд пар символов вида согласная + гласная |
f=open(’24.txt’) PP = [‘CA’, ‘CO’, ‘DA’, ‘DO’, ‘FA’, ‘FO’] for i in range(1, len(p), 2): Ответ: 95 |
||||||||||||||||||
|
Задание 25. Анализ программы с циклами и условными операторами Назовём маской числа последовательность цифр, в которой также могут Например, маске 123*4?5 соответствуют числа 123405 и 12300405. Среди натуральных чисел, не превышающих 1010, найдите все числа, соответствующие маске 1?2139*4, делящиеся на 2023 без остатка. |
Самый простой способ использовать библиотеку fnmatch. или так полным перебором: y = {»,’0′,’00’,’000′} for x in range (1000): Ответ: 162139404 80148 |
||||||||||||||||||
Задание 26. Анализ программы с циклами и условными операторами В магазине для упаковки подарков есть N кубических коробок. Самой интересной считается упаковка подарка по принципу матрёшки – подарок упаковывается в одну из коробок, та в свою очередь в другую коробку и т.д. |
|||||||||||||||||||
Задание 27. Анализ программы с циклами и условными операторами У медицинской компании есть N пунктов приёма биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера, соответствующие расстоянию от нулевой отметки до конкретного пункта. Известно количество пробирок, которое ежедневно принимают в каждом из пунктов. Пробирки перевозят в специальных транспортировочных контейнерах вместимостью не более 36 штук. Каждый транспортировочный контейнер упаковывается в пункте приёма и вскрывается только в лаборатории. Файл А Дано два входных файла (файл A и файл B), каждый из которых в первой строке содержит число N (1 ≤ N ≤ 10 000 000) – количество пунктов приёма биоматериалов. В каждой из следующих N строк находится два числа: номер пункта и количество пробирок в этом пункте (все числа натуральные, количество пробирок в каждом пункте не превышает 1000). Пункты перечислены в порядке их расположения вдоль дороги, начиная от нулевой отметки. Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов. |
Ответ: 51063 5634689219329 |
1. Графы через матрицу смежности
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
ЕГЭ по информатике с решением
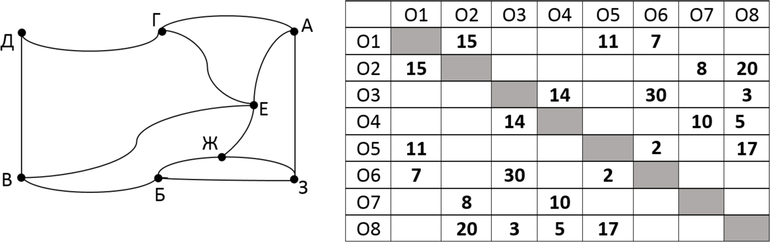
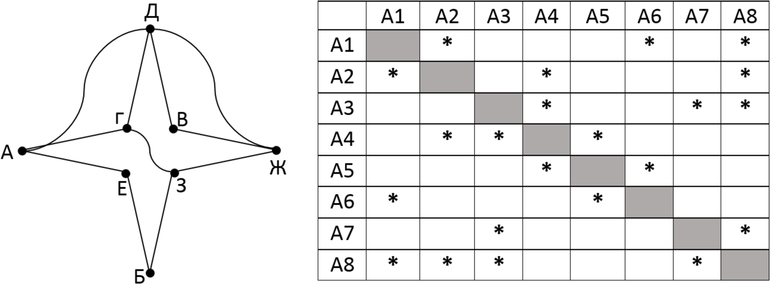
На рисунке представлена схема дорог около города Умь. В таблице звездочкой обозначено наличие дороги из одного населённого пункта в другой, отсутствие звездочки означает, что такой дороги нет. Каждому населенному пункту на схеме соответствует его номер в таблице, но неизвестно, какой именно.
Определите, какие номера населенных пунктов в таблице могут соответствовать населенным пунктам Б и Д на схеме. В ответе запишите эти два номера в порядке возрастания без пробелов и знаков препинания.
Рассмотрим наш граф. Заметим, что город С уникален в том смысле, что из него выходит уникальное число дорог, а именно 5. По таблице легко понять, что С = П4. Заметим, что город Б едиственный не связан дорогой с городом С. Так как нам известно, С = П4. По таблице строки П4 мы видим, что единственный пункт, не связанный с П4, – это П6. Таким образом, понимаем, что Б = П6. Теперь найдем номер города Д. Он связан с городом Б, также мы знаем, что из него выходят три дороги. По строке П6 из таблицы мы видим, что город Б связан с П1 и П7. Из П1 выходят три дороги, из П7 – две. Из графа видим, что от Д – три дороги, от Г – две. Следовательно, Д = П1. В ответ записываем два номера в порядке возрастания – 16.
Ответ: 16
Саша и Максим потерялись в лесу. На рисунке представлена схема тропинок в лесу между столетними дубами. В таблице содержатся сведения о длине тропинки от одного дуба к другому. Отсутствие значения означает, что такой тропинки нет. Каждому дубу на схеме соответствует его номер в таблице, но неизвестно, какой именно номер. Помогите Саше и Максиму определить длину тропинки между дубами Ж и З.
Рассмотрим наш граф. Заметим, что дубы Б и А уникальны в том смысле, что от них выходит уникальное число тропинок: из Б – одна, из А – пять. Следовательно, мы сразу можем определить, что Б = Д8 и А = Д3. Далее из таблицы мы видим, что Д8 связан с Д7, следовательно, Г = Д7. Нам нужно определить номер дуба З. Посмотрим на строчку Д7 таблицы: кроме того, что он связан с Д8 и Д3 (Б и А соответственно), также он связан с Д4 и Д5. Эти номера могут соответствовать дубам В и З. Заметим из таблицы, что Д4 связан с Д3 (то есть Д4 связан с А – видим из графа, что З не связан с А, то есть Д4 – это В), а значит, З = Д5. Далее по таблице определяем, что Д5 связан с Д6 и Д7 (т.е. З связан с Д6 и Г), а значит, Ж = Д6. По таблице определяем искомую длину тропинки между Д5 и Д6 – 4.
Ответ: 4
На рисунке представлена схема дорог около города Максимовка. В таблице звездочкой обозначено наличие дороги из одного населённого пункта в другой, отсутствие звездочки означает, что такой дороги нет. Каждому населенному пункту на схеме соответствует его номер в таблице, но неизвестно, какой именно.
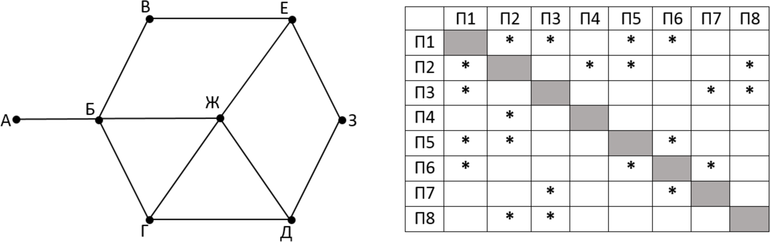
Определите, какие номера населенных пунктов в таблице могут соответствовать населенным пунктам Ж и З на схеме. В ответе запишите эти два номера в порядке возрастания без пробелов и знаков препинания.
Рассмотрим наш граф. Заметим, что пункт А уникален том смысле, что из него выходит уникальное число дорог, а именно одна. Следовательно, мы сразу можем определить его номер по таблице: А = П4. Также мы сможем определить номер города Б, так как он единственный связан дорогой с городом А: Б = П2. Заметим, что городов, от которых выходит по четыре дороги, всего два – Б и Ж. Следовательно, мы можем определить номер пункта Ж, так как Б нам уже известен: Ж = П1. Теперь поймем, какой номер соответствует городу З. Так как из него выходят две дороги так же, как из пункта В, то и З, и В могут соответствовать номера 7 и 8. Заметим из таблицы, что П8 связан с П2, следовательно, П8 – это город В. Тогда З = П7. В ответ запишем номера искомых пунктов в порядке возрастания – 17.
Ответ: 17
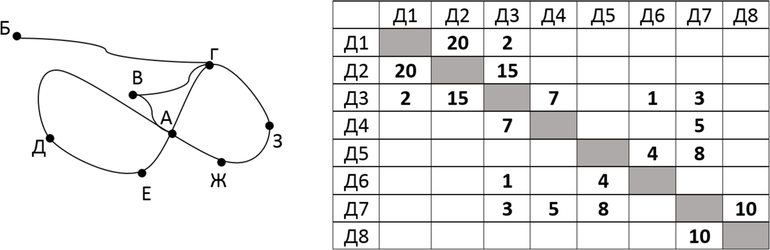
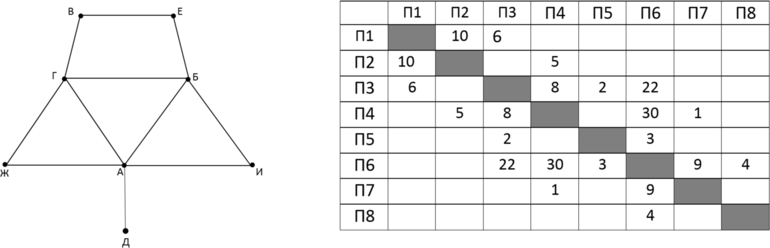
Аня и Таня нашли карту сокровищ. На рисунке представлена схема мостов между островами в океане Z. В таблице содержатся сведения о длине моста от одного острова к другому. Отсутствие значения означает, что такого моста нет. Каждому острову на схеме соответствует его номер в таблице, но неизвестно, какой именно. Чтобы спланировать путешествие, Ане и Тане нужно определить длину моста между островами Ж и Е.
Рассмотрим наш граф. Заметим, что острова Д и Е уникальны в том смысле, что от них построено уникальное число мостов: от Д – два, от Е – четыре. Следовательно, мы сразу можем определить по таблице, что Д = О7 и Е = О8. Заметим, что от остальных островов отходит по три моста. Но острова Б и З не связаны с островом Е, следовательно, им могут соответствовать номера 1 и 6 (определяем по строке О8: смотрим, с какими номерами отсутствует связь, – это номера 1, 6 и 7, но мы знаем, что О7 = Д). Далее по таблице определяем, с каким номером у О1 и О6 общая связь (смотрим на строки О1 и О6 и видим, что есть мост между О1 и О5 – и мост между О6 и О5). Следовательно, О5 = Ж. Далее находим длину моста между Ж и Е (то есть между О5 и О8). Искомая длина – 17.
Ответ: 17
Артём и Саша гуляют по парку аттракционов. На рисунке представлена схема проходов между аттракционами. В таблице звездочкой обозначено наличие прохода от одного аттракциона к другому, отсутствие звездочки означает, что такого прохода нет. Каждому аттракциону на схеме соответсвует его номер в таблице, но неизвестно, какой именно.
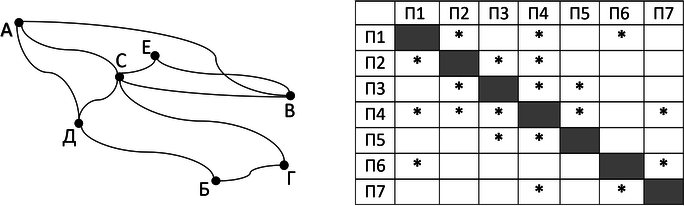
Определите, какие номера в таблице могут соответствовать аттракционам В и З на схеме. В ответе запишите эти два номера в порядке возрастания без пробелов и знаков препинания.
Рассмотрим наш граф. Заметим, что аттракционы Д и Б уникальны в том смысле, что из них выходит уникальное число проходов: из Д – четыре, от Б – два. Следовательно, мы сразу можем определить по таблице, что Д = А8 и Б = А5. Заметим, что Б связан с пунктами Е и З, причем из Е существует два прохода, а из З – три. Следовательно, по таблице мы можем определить, что З = А4 (находим строку А5 в таблице, определяем, что он связан с А4 и А6, из А4 – три прохода, из А6 – два). Далее заметим, что у нас два аттракциона, из которых выходят два прохода – Е и В. Так как мы знаем, что Е = А6, В = А7. В ответ запишем номера аттракционов в порядке возрастания: 47.
Ответ: 47
На рисунке представлена схема дорог около города Утьского района. В реестре учета дорог этого города содержатся сведения об их длине. Отсутствие значения означает, что такой дороги нет. Обозначения пунктов в реестре и на схеме не совпадают. Определите, какова длина пути из пункта Б в пункт Г. В ответе запишите только число.
Рассмотрим наш граф. Заметим, что из пунктов Б и Г выходит по четыре дороги. Из таблицы видим, что им могут соответствовать пункты под номерами 3 и 4. Так как нам нужна длина дороги между этими пунктами, необязательно точно определять их номера. Из таблицы находим искомую длину (длина пути из 3 пункта в 4 – или наоборот) – 8.
Ответ: 8

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Привет! Сегодня порешаем демонстрационный вариант ЕГЭ по информатике 2022.
В этой статье представлены задания с 1-ого по 5.
Источник задач: https://fipi.ru/ege/demoversii-specifikacii-kodifikatory#!/tab/151883967-5
Приятного прочтения!
Разбор демоверсии ЕГЭ по информатике 2022 (6-10 Задание)
Разбор демоверсии ЕГЭ по информатике 2022 (11-15 Задание)
Разбор демоверсии ЕГЭ по информатике 2022 (16-21 Задание)
Разбор демоверсии ЕГЭ по информатике 2022 (22-27 Задание)
Задание 1
На рисунке схема дорог Н-ского района изображена в виде графа, в таблице
содержатся сведения о протяжённости каждой из этих дорог (в километрах).
Так как таблицу и схему рисовали независимо друг от друга, то нумерация
населённых пунктов в таблице никак не связана с буквенными
обозначениями на графе. Определите, какова сумма протяжённостей дорог
из пункта Б в пункт В и из пункта Г в пункт Д.
В ответе запишите целое число.
Решение:
В начале нужно понять, какой город под какой буквой находится в таблице.
Точка К — особая точка, т.е. она отличается от остальных, т.к. только она имеет 6 дорог. Поэтому её легко найти в таблице, она под номером 5.
Рисунок имеет симметричную структуру. Поэтому например точки A и E мы не сможем отличить друг от друга. Но найдём примерное их расположение.
Города A и E имеют по две дороги. Значит, им соответствуют номера 1 и 3.
Городам Б и Д соответствуют номера 2 и 4. Т.к. эти номера по таблице связаны с 1 и 3. Опять, какому номеру соответствует конкретная буква, мы не сможем узнать.
С номерами 2 и 4, должны быть связаны уже В и Г. Значит, городам В и Г соответствуют номера 6 и 7.
Получается, чтобы ответить на вопрос задачи, нужно суммировать расстояния между 2 и 6 И 4 и 7.
13+7=20
Ответ: 20
Смотреть 1 Задание на YouTube
Задание 2
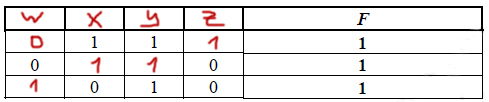
Миша заполнял таблицу истинности логической функции F
¬(y → (x ≡ w)) ∧ (z → x),
но успел заполнить лишь фрагмент из трёх различных её строк, даже
не указав, какому столбцу таблицы соответствует каждая из переменных
w, x, y, z.
Определите, какому столбцу таблицы соответствует каждая из переменных
w, x, y, z.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут
соответствующие им столбцы (сначала буква, соответствующая первому
столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы
в ответе пишите подряд, никаких разделителей между буквами ставить
не нужно.
Пример. Функция F задана выражением ¬x / y, зависящим от двух
переменных, а фрагмент таблицы имеет следующий вид.
В этом случае первому столбцу соответствует переменная y, а второму
столбцу – переменная x. В ответе следует написать: yx.
Решение:
Напишем шаблон для решения 2 задания на языке программирования Python.
print('x', 'y', 'z', 'w') for x in range(0, 2): for y in range(0, 2): for w in range(0, 2): for z in range(0, 2): if not(not(y) or (x==w)) and (not(z) or x): print(x, y, z, w)
Здесь мы перебираем все варианты с помощью вложенных циклов. И если наша функция превращается в истину, то печатаем значения переменных.
Отрицание меняется на not, следование представляем по формуле A->B = ¬A or B.
Получается
x y z w
0 1 0 1
1 1 0 0
1 1 1 0
Видно, что третий столбец — это y.
Т.к. у нас нет столбца, который состоит только из одних нулей, то в четвёртом столбце в пустой ячейке будет 1.
Получилась строчка из трёх 1. Значит, в первом столбце в пустой ячейке вверху будет 0. Следовательно, первый столбец — w.
Последний столбец достаётся z, т.к. из оставшихся переменных только у неё два 0 и одна 1. Второй столбец, по принципу исключения, — это x.
Ответ: wxyz
Смотреть 2 Задание на YouTube
Задание 3
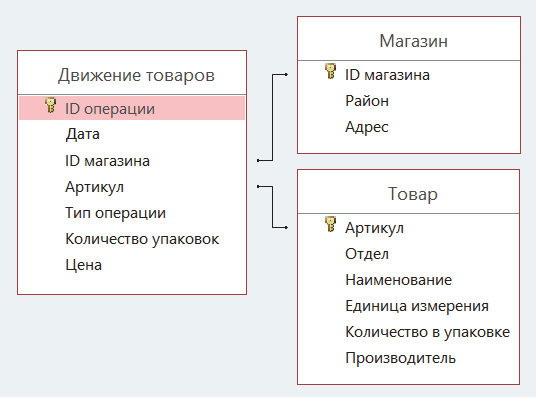
В файле приведён фрагмент базы данных «Продукты» о поставках товаров
в магазины районов города. База данных состоит из трёх таблиц.
Таблица «Движение товаров» содержит записи о поставках товаров в
магазины в течение первой декады июня 2021 г., а также информацию
о проданных товарах. Поле Тип операции содержит значение Поступление
или Продажа, а в соответствующее поле Количество упаковок, шт.
занесена информация о том, сколько упаковок товара поступило в магазин
или было продано в течение дня. Заголовок таблицы имеет следующий вид.
| ID операции |
Дата | ID магазина |
Артикул | Тип операции |
Количество упаковок, шт. |
Цена, руб./шт. |
Таблица «Товар» содержит информацию об основных характеристиках
каждого товара. Заголовок таблицы имеет следующий вид.
| Артикул | Отдел | Наименование | Ед. изм. |
Количество в упаковке |
Поставщик |
Таблица «Магазин» содержит информацию о местонахождении магазинов.
Заголовок таблицы имеет следующий вид.
На рисунке приведена схема указанной базы данных.
Используя информацию из приведённой базы данных, определите на
сколько увеличилось количество упаковок яиц диетических, имеющихся в
наличии в магазинах Заречного района, за период с 1 по 10 июня
включительно.
В ответе запишите только число.
Решение (через формулу):
Откроем файл Excel. Внизу у нас три вкладки (три таблицы).
Есть магазины, есть товары, есть операции, какие товары, куда перемещаются.
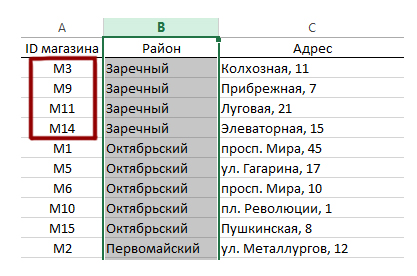
Прочитаем ещё раз внимательно вопрос задачи. Переходим на вкладку Магазин. Выделим столбец «Район» и отсортируем по данному столбцу таблицу (кнопка сортировки находится обычно в правом верхнем углу). Если появится вопрос об автоматическом расширении выделенного диапазона, отвечаем утвердительно.
Теперь удобно посмотреть ID магазинов Заречного Района. Всего получается 4 ID: M3, M9, M11, M14.
Переходим на вкладку Товар. Нас интересует яйцо диетическое. Ищем по поиску (Ctrl + F) и получаем Артикул данного товара. Это номер 15.
Данные мы собрали, теперь переходим на вкладку Движение товаров.
Сначала подсчитаем сколько поступило указанного товара в указанные торговые точки за период 1-10 июня. Убедимся, что первая строчка не подходит нам по условию и в ячейке H2 ставим значение 0. Это число олицетворяет количество поступивших товаров.
В ячейке H3 пропишем формулу:
=ЕСЛИ(И(ИЛИ(C3=«M3»;C3=«M9»;C3=«M11»; C3=«M14»); D3=15; F3=«Поступление»);H2+E3;H2)
Эту формулу мы распространяем на весь столбец H. Тогда она будет анализировать каждую строчку и подсчитывать количество поступившего товара, учитывая все обстоятельства задачи. В самой последней ячейке столбца H получается число 1420. Это и есть то количество нашего товара, которое поступило в указанные торговые точки. Про дату в этой задаче думать не нужно, т.к. вся таблица по операциям происходит в пределах 1-10 июня.
Аналогично, подсчитаем в столбце I, какое количество убыло. Тогда формула получается:
=ЕСЛИ(И(ИЛИ(C3=«M3»;C3=«M9»;C3=«M11»; C3=«M14»); D3=15; F3=«Продажа»);I2+E3;I2)
Получаем количество проданных товаров 454.
Подсчитаем на сколько же увеличилось товаров:
1420-454=966
Это и будет ответ.
Ответ: 966
Смотреть 3 Задание (решение через формулу) на YouTube
Решение (через фильтры)
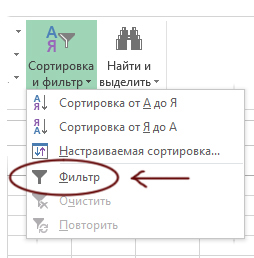
В подобных задачах удобно воспользоваться фильтрами!
Выбираем вкладку Магазин и нажимаем кнопку Фильтр.
При этом должна быть выделена не пустая ячейка.
Кнопка Фильтр может находится и на главной панеле.
Теперь можно отфильтровать магазины Заречного района.
Нажмём «ОК», и у нас останутся только магазины Заречного района. Фиксируем их ID.
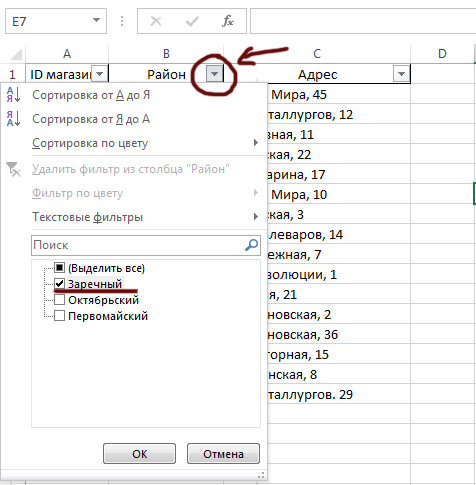
Переходим на вкладку Товар. Включаем фильтры. С помощью фильтров оставляем только яйцо диетическое и узнаём его Артикл.
Переходим на главную вкладку Движение товаров. Включаем фильтры. Фильтруем операции, которые подходят для наших магазинов и для нашего товара.
В начале найдём количество упаковок, которые поступили в магазины, поэтому в столбце Тип операции выбираем «Поступление«.
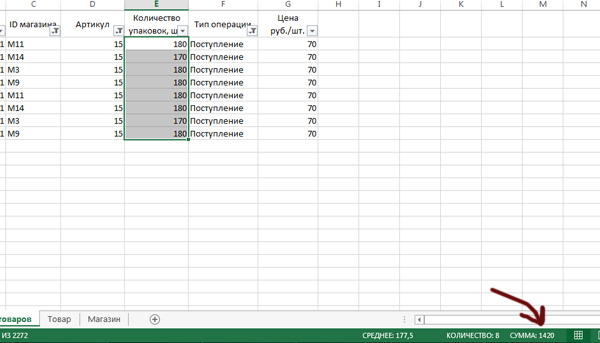
Выделяем ячейки столбца Количество упаковок для получившихся операций, и внизу смотрим сумму этих ячеек.
Здесь нельзя пользоваться стандартной функцией СУММ, потому что она суммируем ещё и скрытые ячейки. А так мы получаем сумму выделенных ячеек.
Получается количество поступивших упаковок равно 1420. Аналогично количество убывших получается 454.
1420-454=966
Ответ: 966
Смотреть 3 Задание (решение через фильтры) на YouTube
Задание 4
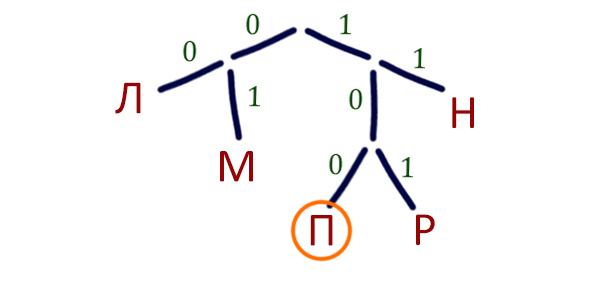
Для кодирования некоторой последовательности, состоящей из букв Л, М,
Н, П, Р, решили использовать неравномерный двоичный код,
удовлетворяющий условию, что никакое кодовое слово не является началом
другого кодового слова. Это условие обеспечивает возможность
однозначной расшифровки закодированных сообщений. Для букв Л, М, Н
использовали соответственно кодовые слова 00, 01, 11. Для двух оставшихся
букв П и Р кодовые слова неизвестны.
Укажите кратчайшее возможное кодовое слово для буквы П, при котором
код будет удовлетворять указанному условию. Если таких кодов несколько,
укажите код с наименьшим числовым значением.
Решение:
Т.к. никакое кодовое слово не является началом другого кодового слова, то, значит, выполняется условие Фано.
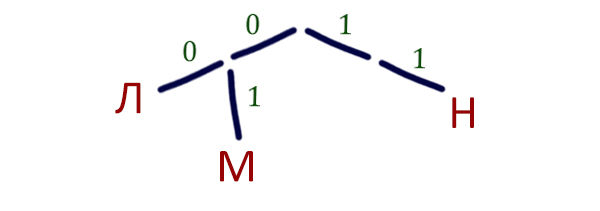
Следовательно, можно воспользоваться приёмом дерево Фано.
Разместим буквы для которых известны коды на дереве Фано.
При построении дерева Фано мы проращивает от корня две ветки 0 и 1. От каждой ветки тоже можно прорастить две ветки 0 и 1 и т.д. Если буква «села» на ветку, то она блокирует эту ветку, и больше нельзя проращивать новые ответвления от неё.
У нас остались две буквы П и Р, а прорастить можем только одну ветку (из 1 — прорастить 0). Мы проращиваем эту ветку и от неё проращиваем два ответвления, и теперь мы уже можем разместить оставшиеся буквы на дереве.
Для П выбираем код с меньшим числовым значением — 100, как написано в условии. Букве Р достаётся код — 101.
Ответ: 100
Смотреть 4 Задание на YouTube
Задание 5
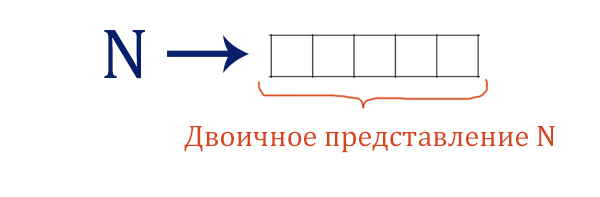
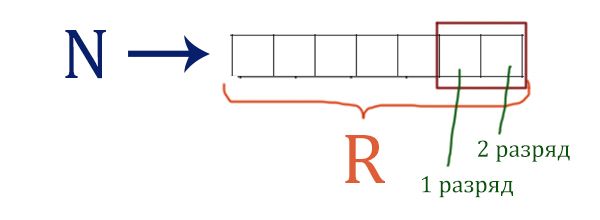
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему
новое число R следующим образом.
1. Строится двоичная запись числа N.
2. К этой записи дописываются справа ещё два разряда по следующему
правилу:
а) складываются все цифры двоичной записи числа N, и остаток от деления
суммы на 2 дописывается в конец числа (справа).
Например, запись 11100 преобразуется в запись 111001;
б) над этой записью производятся те же действия – справа дописывается
остаток от деления суммы её цифр на 2.
Полученная таким образом запись (в ней на два разряда больше, чем
в записи исходного числа N) является двоичной записью результирующего
числа R.
Укажите такое наименьшее число N, для которого результат работы
данного алгоритма больше числа 77. В ответе это число запишите
в десятичной системе счисления.
Решение:
На вход поступает натуральное (обычное, не дробное, положительное) число N.
Это число алгоритм переводит в двоичную систему.
Сказано, что дописываются два разряда справа к тому двоичному числу, которое получили в первом пункте.
Про первый дополнительный разряд написано в пункте a второго правила: «складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001».
Если сказать более просто, то автомат подсчитывает количество единиц у первоначального двоичного числа N, полученного в первом пункте. Если количество чётное, то автомат в первый дополнительный разряд должен поставить 0. Если количество нечётное, то автомат в первый дополнительный разряд должен поставить 1.
Про второй дополнительный разряд сказано в пункте б второго правила. Автомат сделает тоже самое, что и в предыдущем пункте, только теперь подсчёт единиц будет происходить не только в двоичной записи числа N, но и в первом дополнительном разряде.
В вопросе просят указать входящее наименьшее число N, чтобы автомат выдал число R больше 77.
Т.к. число R должно быть больше 77, то переведём число 78 (77 + 1) в двоичный вид, чтобы можно было оценить входящее число N.
Это можно сделать стандартным калькулятором windows, переключив его в режим «Программиста» (Вид->»Программист»).
Получилось число 1001110. Будем рассматривать (начиная с 1001110) числа на выполнение правил, которые заданы для алгоритма. Если все правила будут выполнены, значит, мы получили то число, по которому вычислим изначальное N. Нам нужно получить именно минимальное число, поэтому мы и начали с минимального возможного претендента для числа R (78).
Здесь нам сразу повезло, сразу число 78 удовлетворяет всем условиям. Нас просили написать именно число N, поэтому от числа 1001110 отбрасываем два разряда и переводим в десятичную систему.
Переводим в десятичную систему 10011 -> 19.
Ответ: 19
Смотреть 5 Задание на YouTube
Разбор демоверсии ЕГЭ по информатике 2022 (6-10 Задание)
Разбор демоверсии ЕГЭ по информатике 2022 (11-15 Задание)
Разбор демоверсии ЕГЭ по информатике 2022 (16-21 Задание)
Разбор демоверсии ЕГЭ по информатике 2022 (22-27 Задание)
Очень доступное объяснение. Жду разбор следующих заданий
Следующие задания уже разобраны из Демоверсии 2022. Можете посмотреть в разделе ЕГЭ.