Подсказки огэ математика 9 класс на экзамене

1. Углы

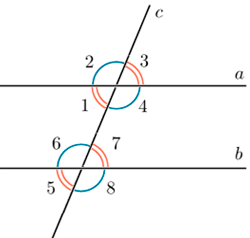
Вертикальные углы равны (на рис. 1 и 3; 6 и 8 и др.).

Внутренние накрест лежащие углы при параллельных прямых и секущей равны. (на рис. 4 и 6; 1 и 7).

Сумма внутренних односторонних углов при параллельных прямых и секущей равна 180˚ (на рис. 4 и 7; 1 и 6).

Соответственные углы при параллельных прямых и секущей равны. (на рис. 3 и 7; 1 и 5 и др.).

Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая перпендикулярна третьей прямой.

2. Медиана, биссектриса, высота

Биссектриса треугольника — отрезок, соединяющий вершину треугольника с точкой на противоположной стороне и делящий угол треугольника пополам.

Высота треугольника – перпендикуляр опущенный из вершины угла на противоположную сторону.

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

В любом треугольники все биссектрисы пересекаются в одной точке, все медианы пересекаются в одной точке, все медианы пересекаются в одной точке.

3. Треугольник

Сумма углов в любом треугольнике 180˚.

Средняя линия треугольника – прямая проходящая через середины двух сторон. Средняя линия параллельна одной из сторон и равна половине этой стороны.

Виды треугольников: тупоугольный (один угол тупой), прямоугольный (один угол прямой 90˚), остроугольный (все углы острые, меньше 90˚).

Равнобедренный треугольник — треугольник, у которого равны две стороны.

Свойства равнобедренного треугольника:

• в равнобедренном треугольнике углы при основании равны;
• в равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой;

Равносторонний треугольник — треугольник,
у которого все стороны равны. (все углы по 60 градусов)

Всякий равносторонний треугольник является равнобедренным,
но не всякий равнобедренный — равносторонним.

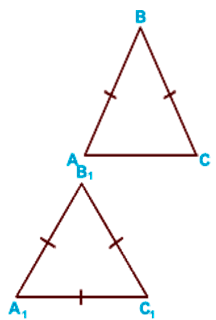
Три признака равенства треугольников

I признак по двум сторонам и углу между ними

II признак (по стороне и прилежащим углам)

III признак (по трем сторонам)

Признаки подобия треугольников

I признак по двум равным углам

II признак по двум пропорциональным сторонам и углу между ними

III признак по трем пропорциональным сторонам

Площади подобных фигур относятся как коэффициент подобия в квадрате.

Объемы подобных фигур относятся как коэффициент подобия в кубе.

Треугольник называется прямоугольным, если один из его углов прямой.

Стороны, прилежащие к прямому углу называются катетами, а сторона, лежащая против прямого угла, – гипотенузой. (самая большая сторона это гипотенуза, две др катеты).

Свойства прямоугольного треугольника

Сумма острых углов прямоугольного треугольника равна 90 градусов.

Катет, лежащий против угла в 30˚, равен половине гипотенузы.

Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы.

Медиана прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, является радиусом описанной около этого треугольника окружности.

Теорема Пифагора:

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: a² + b² = c².

Пифагоровы тройки:

• 3, 4, 5
• 6, 8, 10
• 5, 12, 13
• 9, 12, 15

Признаки равенства прямоугольных треугольников

• По двум катетам.
• По гипотенузе и катету.
• По катету и прилежащему острому углу.
• По катету и противолежащему острому углу.
• По гипотенузе и острому углу.

Признаки подобия прямоугольных треугольников:

• По острому углу.
• По пропорциональности двух катетов.
• По пропорциональности катета и гипотенузы.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

Высота, проведенная из вершины прямого угла, разбивает прямоугольный треугольник на два подобных треугольника. Каждый из этих треугольников подобен исходному.

Высота прямоугольного треугольника: h=ab/c или h = (где АВ гипотенуза, СЕ высота опущенная на гипотенузу).

В прямоугольном треугольнике медиана, проведённая из вершины прямого угла, равна половине гипотенузы: m=c/2 (R=​с/2=m​c).

3. Четырехугольники

Сумма углов в любом четырехугольнике 360˚.

Параллелограмм

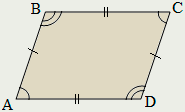
Параллелограммом называется четырёхугольник, противолежащие стороны которого попарно параллельны.

У параллелограмма противолежащие стороны равны и противолежащие углы равны.

Сумма любых двух соседних углов параллелограмма равна 180°.

Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

Каждая диагональ делит параллелограмм на два равных треугольника.

Две диагонали параллелограмма делят его на четыре равновеликих треугольника.

Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

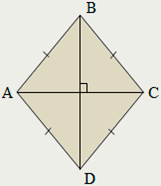
Ромб

Ромбом называется параллелограмм, у которого все стороны равны.

Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.

Прямоугольник

Прямоугольником называется параллелограмм, у которого все углы прямые.

Диагонали прямоугольника равны и точкой пересечения делятся на четыре равных отрезка.

Квадрат.

Квадрат – это прямоугольник, у которого все стороны равны.

Диагонали квадрата равны и перпендикулярны.

Сторона и диагональ квадрата связаны соотношениями: .

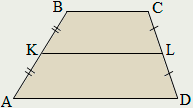
Трапеция

Трапецией называется четырёхугольник у которого только две противолежащие стороны параллельны.

Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.

Средняя линия трапеции параллельна её основаниям и равна их полусумме.

Равнобокой называется трапеция, у которой боковые стороны равны.

У равнобокой трапеции: диагонали равны; углы при основании равны; сумма противолежащих углов равна 180.

Стороны и диагональ равнобокой трапеции связаны соотношением: d² = ab+c².

Трапеция называется прямоугольной, если одна из её боковых сторон перпендикулярна основаниям.

4. Окружность

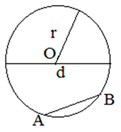
Отрезок, соединяющий центр окружности с любой точкой окружности называется радиусом (r) окружности.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром окружности.

Прямая, имеющая с окружностью одну общую точку, называется касательной. Касательная и радиус проведенный в точку касания пересекаются под прямым углом.

Прямая, имеющая с окружностью две общие точки, называется секущей.

Центральный угол окружности – это угол, вершина которого лежит в центре окружности. Центральный угол равен дуге на которую он опирается.

Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают ее. Вписанный угол равен половине дуги на которую опирается.

Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.

Вписанный угол, опирающийся на диаметр равен 90˚.

Все вписанные углы, опирающиеся на одну и туже дугу равны.

Теорема косинусов:

a² = b² + c² – 2bccosa

Теорема синусов:

5. Формулы площадей

См. продолжение статьи

ОГЭ по математике сдают все ученики 9-х классов. Без положительного результата не выдадут аттестат и не примут в 10-й класс. Разбираемся в структуре экзамена и вариантах подготовки к нему.

Структура ОГЭ по математике

ОГЭ по математике состоит из двух частей:

• первая часть — задания, требующие кратких ответов;
• вторая часть — задания с развёрнутыми ответами.

Всего в работе 25 заданий, а на их решение даётся 3 часа 55 минут.

Часть 1 — задания с кратким ответом

Первая часть экзамена содержит 19 заданий, каждое из которых может принести один балл. Во всех заданиях нужно дать краткий ответ. Задания охватывают основные темы школьного курса математики.

Для решения задач первой части нужны знания основных алгоритмов и математических понятий. Заданиями проверяют, умеют ли ученики 9-х классов применять базовые математические знания для решения разных задач.

В первой части ОГЭ по математике в основном встречаются задачи, в которых нужно выполнить простые вычисления, такие как вычисление процентов, решение уравнений и построение графиков. Но могут попасться и задачи, для решения которых необходимо использовать несколько формул для получения ответа.

Часть 2 — задания с развёрнутым ответом

Во второй части ОГЭ по математике 6 заданий. Каждое задание оценивается максимум в два балла. Ответы должны быть развёрнутыми. То есть нужно записать решение задачи, а не только ответ. Если ход решения верный, но в расчётах ошибка — выполнение задания оценят в один балл.

Вторая часть ОГЭ направлена на то, чтобы выявить школьников с уровнем знаний и навыков, достаточном для обучения в профильном классе. Поэтому задания сложнее, чем в первой части.

Задания идут от более простых к сложным. Для решения нужен тщательный анализ и глубокое понимание математических понятий, формул и методов. Важно уметь строить логические цепочки, которые приведут к правильному ответу. В ответ нужно записать всю последовательность решения задачи.

О втором обязательном экзамене рассказали в статье о том, как подготовиться к ОГЭ по русскому языку.

Сколько баллов нужно набрать на ОГЭ по математике

Чтобы сдать экзамен, нужно получить не меньше «тройки». Если перевести в баллы — это от 8 до 14 баллов.

Шкала перевода выглядит так:

• «2» = 0—7 баллов,
• «3» = 8–14 балла,
• «4» = 15–21 баллов,
• «5» = 22–31 балла.

Что нужно знать для сдачи ОГЭ по математике

Для успешной сдачи ОГЭ по математике нужно знать:

1. Базовые математические понятия и формулы.

Это включает знание основных математических операций, таких как сложение, вычитание, умножение и деление, а также понимание основных математических понятий из геометрии, алгебры и тригонометрии.

2. Теорию и методы решения разных типов задач.

То есть понимание математических формул, методов и правил, которые нужны для решения задач. Ученикам нужно уметь анализировать задачу, определять соответствующую формулу или метод и применять их для правильного решения.

3. Принципы построения графиков, таблиц и диаграмм.

Школьники должны уметь анализировать и интерпретировать предоставленные данные, а также использовать их для решения задач.

4. Методы решения сложных задач.

То есть задач, для решения которых нужно применить несколько формул или правил. Ученикам нужно уметь анализировать предоставленную информацию, определять важные факты и использовать их для решения задач.

Как готовиться к ОГЭ по математике

Для успешной сдачи ОГЭ по математике необходимо иметь чёткую стратегию подготовки к экзамену. Ученикам необходимо распределить своё время и ресурсы, чтобы иметь достаточно времени для изучения материала. Также стоит уделить внимание практическим заданиям и постоянно проходить тесты, чтобы отслеживать уровень готовности к экзамену.

Подготовиться к ОГЭ по математике можно с помощью следующих рекомендаций:

1. Изучи кодификатор и спецификацию.

Эти документы можно найти на сайте ФИПИ — составителей ОГЭ и ЕГЭ.

Если коротко, кодификатор — это список того, что проверяют на экзамене. Это перечень и теоретических знаний, и практических навыков.

Спецификация — это описание заданий в экзаменационной работе и того, как будут оценивать их выполнение. Это важная информация, без которой сложно успешно сдать ОГЭ. Например, можно верно решить задание, но неправильно записать ответ и потерять баллы.

Изучение кодификатора и спецификации поможет понять, что ждёт на ОГЭ.

2. Проверь текущий уровень подготовки.

Для этого можно решить демоверсию с того же ФИПИ или пройти одно из онлайн-тестирований. Это нужно, чтобы объективно оценить свои знания и найти, в чём есть пробелы.

3. Повтори теорию.

Повтори все формулы и правила из школьной программы по математике, которые перечислены в кодификаторе. Даже если кажется, что хорошо их помнишь, — повторяй до самого экзамена. Память может сыграть злую шутку, а нужная формула вылететь из головы во время ОГЭ. В другой статье подробнее рассказали, почему так происходит.

4. Тренируйся в решении задач.

Успешная сдача ОГЭ по математике зависит не только от количества знаний, которые ученик усвоил, но и от его способности применять эти знания в практических задачах.

Начинай с простых задач и постепенно переходи к более сложным. Для сдачи ОГЭ нужно уметь работать с числами, графиками, таблицами и диаграммами. Важно научиться разбираться в условиях задач и выбирать правильный подход к их решению.

5. Обратись за помощью.

Если готовиться самостоятельно трудно, попробуй подготовку в «СОТКЕ». Мы готовим школьников с нуля и на нужную оценку. Кроме видеоуроков и вебинаров у нас есть домашние задания с проверкой и пробники каждый месяц. Всю теорию закрепляем на практике — вместе с наставниками решаем много задач. Подробности здесь.

Подписаться

В данном разделе представлены все необходимые материалы для подготовки к ОГЭ по математике 2022. Мы предоставляем как разобранные варианты с теорией по заданиям, так и тестовые варианты для самоподготовки. Пройдя курс подготовки к ОГЭ на нашем сайте, вы уверенно напишете экзамен в 9 классе в 2022 году!

Справочные материалы ОГЭ 2022-2023 по математикеadmin2023-01-27T15:51:36+03:00

Используйте LaTeX для набора формулы