Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Чтобы оценить, с какой скоростью упадет на землю мяч с балкона 6-го этажа, используем для вычислений на калькуляторе формулу По оценке «на глазок» балкон находится на высоте
над землей. Калькулятор показывает на экране число 17,320508. Чему равна, с учетом погрешности оценки высоты балкона, скорость мяча при падении на землю? (Ответ дайте в метрах в секунду, значение и погрешность запишите слитно без пробела.)
2
Из куска тонкого медного провода длиной 2 м собираются согнуть окружность. Предварительно вычисляют диаметр окружности с помощью калькулятора и получают на экране число 0,6369426. Чему будет равен диаметр окружности, если точность измерения длины провода равна 1 см? (Ответ дайте в метрах, значение и погрешность запишите слитно без пробела.)
3
Чтобы определить массу гвоздя, на рычажные весы несколько раз кладут по таких гвоздей. Взвешивание показывает, что их общая масса
Чему равна масса одного гвоздя? (Ответ дайте в граммах, значение и погрешность запишите слитно без пробела.)
4
Толщина пачки из 200 листов бумаги равна Чему равна толщина одного листа бумаги? (Ответ дайте в мм, значение и погрешность запишите слитно без пробела.)
5
Тонкий провод намотали на круглый карандаш в один слой так, чтобы соседние витки соприкасались. Оказалось, что витков такой намотки занимают на карандаше отрезок длиной
Чему равен диаметр провода? (Ответ дайте в мм, значение и погрешность запишите слитно без пробела.)
Пройти тестирование по этим заданиям
22. Механика – квантовая физика (Измерение, погрешность)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Погрешность косвенных измерений
Тонкий провод намотали на круглый карандаш в один слой так, чтобы соседние витки соприкасались. Оказалось, что (N=25) витков такой намотки занимают на карандаше отрезок длиной (L=(25pm1)) мм. Чему равен диаметр провода? (Ответ дайте в мм, значение и погрешность запишите слитно без пробела.)
Погрешность измерения длины намотки провода на карандаше делится поровну между погрешностями диаметров провода на каждом отдельном витке, поскольку относительная погрешность для всей намотки и для одного витка совпадают. Таким образом, диаметр провода равен [dfrac{25}{25}pm dfrac{1}{25}=1pm 0,4 text{ мм}]
Ответ: 10,4
Тонкий провод намотали на круглый карандаш в один слой так, чтобы соседние витки соприкасались. Оказалось, что (N=40) витков такой намотки занимают на карандаше отрезок длиной (L=(22pm 0,5)) мм. Чему равен диаметр провода? (Ответ дайте в мм, значение и погрешность запишите слитно без пробела.)
Погрешность измерения длины намотки провода на карандаше делится поровну между погрешностями диаметров провода на каждом отдельном витке, поскольку относительная погрешность для всей намотки и для одного витка совпадают. Таким образом, диаметр провода равен [dfrac{22}{40}pm dfrac{0,5}{40}=0,55pm 0,0125 text{ мм}]
Ответ: 0,550,0125
При определении массы масла плотностью 0,75 г/см (^{3}) ученик измерил объём масла с использованием мерного цилиндра: (V = (19,0 pm 0,7)) см (^{3}). Запишите в ответ массу масла в граммах с учётом погрешности измерений. В ответе запишите значение и погрешность слитно без пробела.
Масса масла равна [m=rho V=0,75cdot 19,0=14,25text{ г}] Погрешность измерения: [0,75cdot0,7=0,525]
Ответ: 14,250,525

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
За это задание ты можешь получить 1 балл. Уровень сложности: базовый.
Средний процент выполнения: 42.8%
Ответом к заданию 22 по физике может быть последовательность цифр, чисел или слов. Порядок записи имеет значение.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
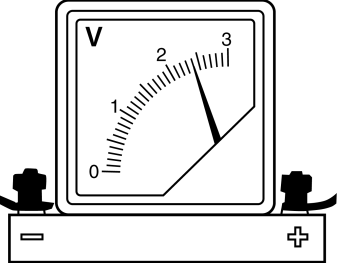
Что показывает вольтметр с учётом абсолютной погрешности? Принять абсолютную погрешность равной половине цены деления шкалы прибора.
В ответе запишите результат измерения с погрешностью без пробелов и других разделителей .
Решение
Цена деления$={3-2}/{10}={1}/{10}=0.1B; {ц.д.}/{2}={0.1}/{2}=0.05B$. Тогда имеем: $(2.40±0.05)B$. Согласно правилу записи ответа с погрешностью, результат измерения и погрешность должны иметь одинаковое количество знаков после запятой.
Ответ: 2.400.05
Задача 2
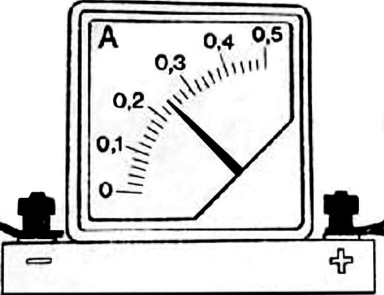
Что показывает амперметр с учётом абсолютной погрешности? Абсолютную погрешность принять равной половине цены деления прибора. Формат ответа: результат измерения и погрешность без пробелов и других разделительных знаков.
Решение
Цена деления$={0.3-0.2}/{5}={0.1}/{5}=0.02A; {ц.д.}/{2}={0.02}/{2}=0.01A$. Тогда имеем: $(0.24±0.01)A$
Ответ: 0.240.01
Задача 3

С помощью амперметра проводились измерения силы тока на участке электрической цепи. Чему равна сила тока с учётом погрешностей измерений, если погрешность прямого измерения составляет половину цены деления прибора, а его класс точности равен 0,5 (т.е. инструментальная погрешность составляет 0,5% от верхнего предела измерений данной шкалы амперметра)? Ответ: (_ ± _) А.
Решение
Определим погрешность прибора: если верхняя граница равна 10А, то инструментальная равна: $∆x_{пр}={10·0,5}/100=0,05$.
Погрешность измерения равна половина цены деления $∆x_{изм}=0,25$.
$∆x=∆x_{изм}+∆x_{пр}=0,05+0,25=0,3$.
$x=7.5±0.3$
Ответ: 7.50.3
Задача 4
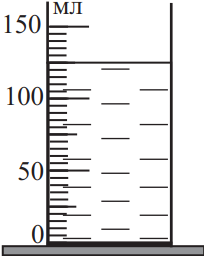
При определении массы воды, налитой в мензурку, ученик при помощи мензурки измерил объём воды. Запишите в ответ массу воды в граммах с учётом погрешности измерений (без пробелов). Погрешность измерения объёма равна половине цены деления мензурки. Ответ: (_ ± _) г.
Решение
Определим значение погрешности прямого измерения $∆V={V’}/{2}={5}/{2}=2.5г$. Тогда: $125±2.5г$. Количество знаков после запятой в измеренной величине должно совпадать с количеством знаков после запятой в значении погрешности. Поэтому $125.0±2.5г$
Ответ: 125.02.5
Задача 5
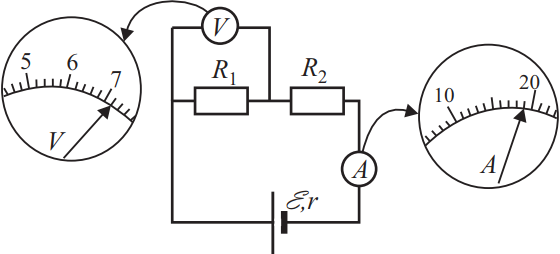
Ученик собрал электрическую цепь, состоящую из батарейки, двух резисторов, амперметра и вольтметра. После этого он провёл измерения напряжения на одном из резисторов и силы тока в цепи. Погрешности измерения силы тока в цепи и напряжения на источнике равны половине цены деления шкал приборов. Чему равно по результатам этих измерений значение напряжения на резисторе R1? Ответ: (_ ± _) В.
Решение
$U=U’+∆U; ∆U={0.2}/{2}=0.1$(половина угла деления). Запишем ответ $U’=7.2B$ как сумму, действующего измерения и погрешности: $7.2±0.1$.
Ответ: 7.20.1
Задача 6

Найдите длину проволоки, если погрешность прямого измерения составляет половину цены деления линейки, изображённой на рисунке. Ответ: (_ ± _) см.
Решение
Погрешность измерения равна половине цены деления ${0.5}/{2}-0.25$, тогда длина проволоки $23.00±0.25$см.
Ответ: 23.000.25
Задача 7
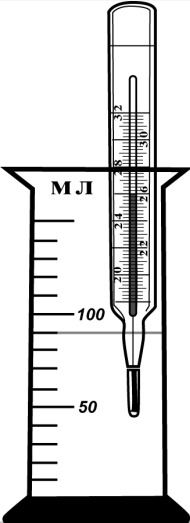
Запишите величину объёма с учётом погрешности, если погрешность равна половине цены деления. Ответ: (_ ± _) мл.
Решение
$∆V={V_1}/{2}={10}/{2}=5$мл (погрешность измерения половина цены деления). Запишем ответ исходя из рисунка $V=90$мл.
Ответ: 905
Задача 8
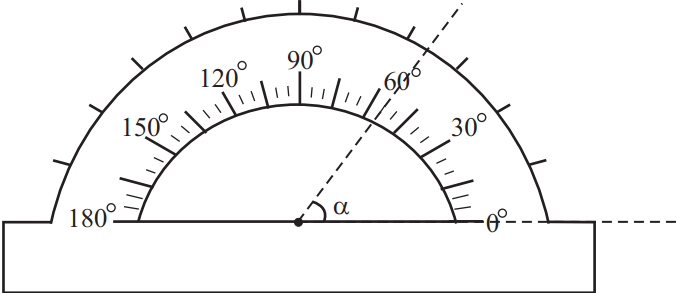
Запишите величину угла с учётом погрешности. С точностью до десятых. Ответ: (_ ± _)◦ .
Решение
Найдем погрешность, как половину цены деления ${5}/{2}=2.5°$. Тогда, исходя из графика получим: $55±2.5$.
Ответ: 55.02.5
Задача 9
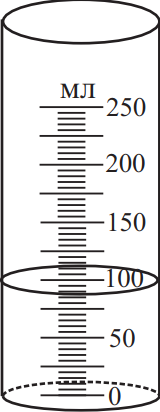
По рисунку определите объём жидкости с учётом погрешности измерения. Ответ: (_ ± _) мл.
Решение
По измерению проведенному измерим погрешность половины угла деления 2.5: $87.5±2.5$мл.
Ответ: 87.52.5
Задача 10
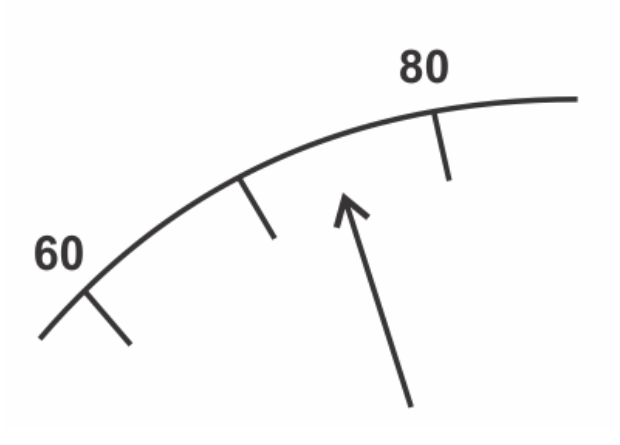
Запишите показания спидометра с учётом его погрешности, равной половине цены деления. Ответ: (_ ± _) км/ч. Значение величины и погрешность запишите слитно (без ±)
Решение
По рисунку видно, что стрелка ближе к 70, чем к 80 км/ч.
Погрешность измерения принимается за половину цены деления, а так как цена деления 10 км/ч, то показания спидометра (70 ± 5) км/ч.
Ответ: 705
Задача 11
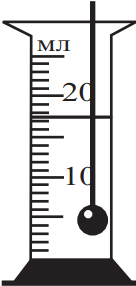
Запишите величину объёма, которая измеряется в данном эксперименте. Ответ: (_ ± _) мл.
Решение
Как известно, погрешность — это половина цены деления, где $V={V’}/{2}={1}/{2}=0.5$. Исходя из рисунка, определим объем и запишем ответ: $17.5±0.5$мл.
Ответ: 17.50.5
Задача 12
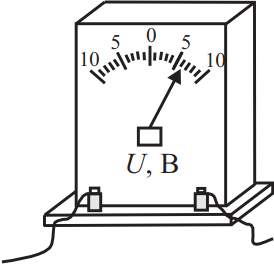
Запишите результат измерения электрического напряжения, учитывая, что погрешность равна половине цены деления. Укажите показание и погрешность. Ответ: (_ ± _) В.
Решение
Учитывая, что погрешность половины цены деления, определим ее: $∆U={1}/{2}=0.5B$. Запишем ответ, исходя из того, что прибор регестрирует $6В$: $6±0.5$.
Ответ: 6.00.5
Задача 13
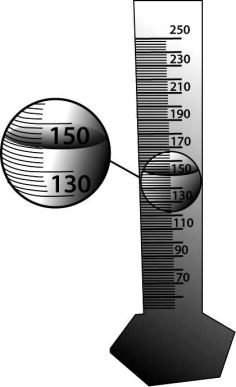
Для проведения опыта ученик налил воду в мензурку. Шкала мензурки проградуирована в миллилитрах (мл). Погрешность измерений объёма равна цене деления шкалы мензурки. Чему равен объём налитой учеником воды? Ответ: (__ ± __) мл.
Решение
Цена деления мензурки$={150-130}/{10}={20}/{10}=2мл$
Значит, объем налитой учеником воды равен: $V=(150±2)мл$
Ответ: 1502
Задача 14

На рисунке показана шкала универсального прибора, измеряющего величину атмосферного давления, температуру и влажность. Какова относительная погрешность показания шкалы барометра, проградуированной в гПа, если абсолютная погрешность равна цене деления шкалы. Ответ выразите в (%) и округлите до десятых.
Решение
Относительная погрешность $ε={∆p}/{p_{пр}}·100%$, где $∆p={ц.д.}={{(1000-950)}/{10}}={5}гПа$.
Показания прибора барометра равны: $p_{пр}=1050гПа$, тогда $ε={5·100%}/{1050}≈0.5%$
Ответ: 0.5
Задача 15

На фотографии представлена электрическая схема для определения сопротивления резистора. По показаниям приборов определите показания вольтметра с учётом погрешности, равной цене деления прибора. Ответ: (__ ± __) В.
Решение
Цена деления$={4-3}/{5}={1}/{5}=0.2B$
Тогда показания вольтметра равны: $(3.2±0.2)В$
Ответ: 3.20.2
Задача 16

Какую температуру показывает термометр, если погрешность прямого измерения равна половине цены деления прибора? Ответ: ( ± ) ◦ C, использовать точку, но не запятую как знак-разделитель, например 9.90.1 .
Решение
Цена деления$={40°С-30°С}/{10}={10°С}/{10}=1°С; {ц.д.}/{2}={1°С}/{2}=0.5°С$
Тогда показания термометра равны: $(26±0.5)°С$
Ответ: 26.00.5
Задача 17
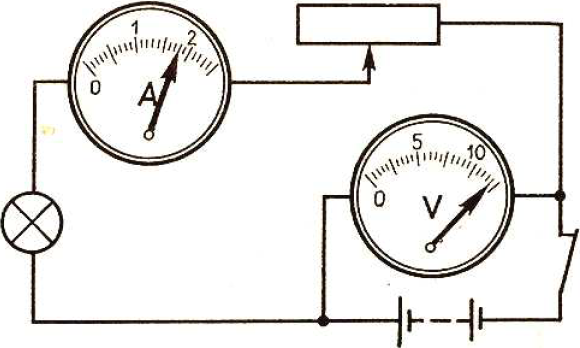
Каковы показания амперметра, если погрешность прямого измерения равна половине цены деления прибора? Ответ выразите в(___ ± ___) А.
Решение
Цена деления$={2A-1A}/{10}=0.1A; {ц.д.}/{2}={0.1A}/{2}=0.05A$
Тогда показания алтерметра равны: $(1.80±0.05)А$
Ответ: 1,800,05
Задача 18
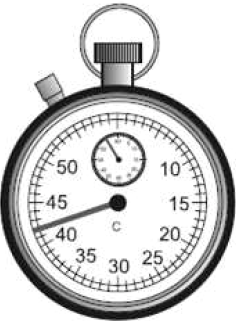
Каковы показания секундомера, если погрешность прямого измерения равна половине цены деления прибора? Ответ выразите в (___ ± ___) с.
Решение
Цена деления$={50-45}/{5}=1; {ц.д.}/{2}={1}/{2}=0.5c$
Тогда показания прибора: $t=(42±0.5)c$
Ответ: 42.00.5
Задача 19
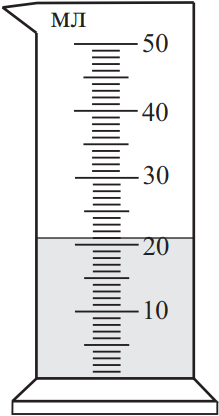
Каков объём воды в измерительном цилиндре, если погрешность прямого измерения равна половине цены деления прибора? Ответ выразите в (___ ± ____) мл.
Решение
Находим погрешность как половину цены деления и получаем 0.5. Соответственно записываем показание прибора с одной цифрой после запятой, чтобы это совпадало с записью погрешности.
Ответ: 21.00.5
Рекомендуемые курсы подготовки
Механика — квантовая физика, методы научного познания
В. З. Шапиро
В задании 22 ЕГЭ по физике проверяется, как вы применяете знание физики в практической деятельности и повседневной жизни. В задании дается изображение какого-либо школьного физического прибора, по которому надо определить показания с учетом погрешности измерения.
Что необходимо знать и уметь?
- Вычислять цену деления измерительного прибора. Для этого надо найти два ближайших штриха, обозначенных числами, из большего вычесть меньшее и поделить на число делений.
- Определить границы измерения для приборов, имеющих две шкалы измерения, например, вольтметра, амперметра, барометра. Соответственно, надо выбрать необходимую шкалу для определения показаний прибора.
- Определить погрешность измерения в соответствии с ее описанием в условии. Погрешность измерения может быть равна цене деления или половине цены деления измерительного прибора. Расчет в соответствии с условием задачи.
- В некоторых задачах погрешности измерений могут быть приведены в условии для разных шкал. При выборе определенной шкалы измерений выбирается соответствующая ей погрешность.
- Запись ответа в бланк с учетом требований: каждая цифра и запятая в отдельной клеточке. Если погрешность указана до десятых (или сотых), то показания прибора точно также должны быть указаны до десятых (или сотых).
- Чему равна сила тока в лампочке (см. рисунок), если погрешность прямого измерения силы тока амперметром на пределе измерения 3 А равна 0,15 А, а на пределе измерения 0,6 А равна 0,03 А?
Ответ: ( ± ) А.
Согласно рисунку, амперметр подключен к зажимам 0 и 0,6 А. Поэтому определять показания необходимо по нижней шкале. Цена деления этой шкалы равна (0,4 — 0,2):5 = 0,02 (А). Показания амперметра равны 0,28 А. Для выбранной шкалы погрешность измерений указана в условии задачи. Она равна 0,03 А.
Ответ: (0,28 ± 0,03) А.
В бланк надо записать ответ в следующем виде:
| 0 | , | 2 | 8 | 0 | , | 0 | 3 |
Секрет решения. Задание является достаточно простым, но требует внимательного чтения условия. Если в задаче приводится в качестве измерительного прибора термометр со шкалой, проградуированной в градусах Цельсия, а ответ требуется дать по шкале Кельвина, то надо учесть, что погрешности по этим двум шкалам одинаковые. Добавление к погрешности +273 является грубой ошибкой.
+273 требуется только для перевода температуры из шкалы Цельсия в шкалу Кельвина.
2. Погрешность прямого измерения силы динамометром, на котором висит груз, равна цене деления. Каков вес груза?
Ответ: ( ± ) Н.
Цена деления динамометра определяется следующим расчетом:
(1,5 – 1) : 5 = 0,1 (Н).
Показания динамометра равны 1,1 Н.
Погрешность измерения, согласно условию задачи, равна цене деления, т.е. 0,1 Н.
Ответ: (1,1 ± 0,1) Н.
В бланк надо записать ответ в следующем виде:
| 1 | , | 1 | 0 | , | 1 |
Секрет решения. Задание достаточно простое, но требует внимательного проведения простых расчетов. Главное – правильная запись в бланк ответов №1 показаний динамометра с учетом погрешности измерений.
- Определите показания вольтметра (см. рисунок), если погрешность прямого измерения напряжения составляет половину цены деления вольтметра.
Ответ: ( ___________ ± ___________) В.
Цена деления вольтметра определяется следующим расчетом:
(2 – 1) : 5 = 0,2 (Н).
Показания вольтметра равны 2 В.
Погрешность измерения, согласно условию задачи, составляет половину цены деления, т.е. 0,1 В.
Ответ: (2,0 ± 0,1) В.
| 2 | , | 0 | 0 | , | 1 |
Секрет решения. В этой задаче надо обратить внимание на то, что погрешность измерений равна половине цены деления. При заполнении бланка ответов №1 показания вольтметра необходимо указать с учетом десятичной записи числа (2,0).
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 22 ЕГЭ по физике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.03.2023
Чтобы найти погрешность косвенных измерений, надо воспользоваться формулами, приведенными в таблице. Эти формулы могут быть выведены «методом границ».
Сначала надо вспомнить основные понятия теории погрешности.
Абсолютная погрешность физической величины ΔА — это
разница между точным значением физической величины и ее приближенным значением и измеряется в тех же единицах, что и сама величина:
ΔА = А — Апр .
Так как мы никогда не знаем точного значения величины А, а лишь определяем из опыта ее приближенное значение, то и величину абсолютной
погрешности мы можем определить лишь приблизительно. Наиболее просто находится максимальная величина абсолютной погрешности, которая и используется нами в лабораторных работах.
Относительная погрешность измерения
εА равна:

При косвенных измерениях величину погрешности искомой величины вычисляют по формулам:

В случае, когда искомая величина находится по формуле, в которой в основном присутствуют произведение и частное, удобней находить сначала относительную погрешность. Если при этом один из
множителей представляет собой сумму или разность, нужно предварительно найти его абсолютную погрешность (сложением абсолютных погрешностей слагаемых), а затем относительную.
Зная относительную погрешность, найти абсолютную погрешность измерений можно так:
ΔА = εA· А.
«Правило ничтожных погрешностей»
при суммировании погрешностей любым из слагаемых можно пренебречь, если оно не превосходит ⅓ – ⅟4 от другого.
Запись результата с указанием погрешности.
Абсолютная погрешность измерений обычно округляется до 1 значащей цифры, а, если эта цифра 1, то до двух.
Пример:

Результат записывается в виде:
А = Аизм ± ΔА, например: ℓ = (13 ± 2) мм.
При этом в измеренном значении следует оставлять столько десятичных знаков, сколько их в значении
погрешности (последняя цифра погрешности «поправляет» последнюю цифру измеренного значения). Значение величины и погрешность следует
выражать в одних и тех же единицах!
Пример:

Пример оценки погрешностей косвенных измерений № 1

Пример оценки погрешностей косвенных измерений № 2

Задания для самостоятельного решения
Задание 1. Найдите плотность вещества, из которого сделан куб со стороной 7,00 ± 0,15 см, если его масса 847 ± 2 г. Что это за вещество?
Задание 2. Найдите удельную теплоту сгорания топлива, 2,10 ± 0,15 г которого хватило, чтобы нагреть 400 ± 10 мл воды на 35°С ± 2°С. Что это за
топливо?
Как определять погрешности измерений
Измерение – нахождение значения физической величины
опытным путем с помощью средств измерений.
Прямое
измерение
– определение значения физической
величины непосредственно средствами измерения.
Косвенное
измерение
– определение значения физической
величины по формуле, связывающей ее с другими физическими величинами, определяемыми
прямыми измерениями.
А, В, С, … — физические величины.
Апр. – приближенное значение физической величины.
А – абсолютная погрешность измерения физической
величины.
— относительная погрешность измерения
физической величины.
иА
– абсолютная
инструментальная погрешность, определяемая конструкцией прибора.
оА – абсолютная погрешность отсчета, она равна в
большинстве случаев
половине цены деления; при
измерении времени – цене деления секундомера или часов.
Абсолютную погрешность измерения
обычно округляют до одной значащей цифры:
Численное значение результата
измерений округляют так, чтобы его последняя цифра оказалась в том же разряде,
что и цифра погрешности:
Результат
измерения записывается так:
%
Определение погрешности методом среднего арифметического
При многократных
измерениях величины погрешность можно оценить следующим образом:
1.
Определить среднее
значение величины А:

измерениях).
2.Определить отклонение каждого значения от среднего:
3.Определить среднее значение отклонения,
его и принимают за абсолютную погрешность:
4.Определить
относительную погрешность и выразить ее в процентах:
|
|
|
|
|
|
|
1 |
|
|
||
|
2 |
|
|
||
|
3 |
|
|
Многократные измерения
предпочтительнее, так как при их проведении возможна компенсация случайных
факторов, влияющих на результат. Обычно многократные измерения проводят, слегка
изменяя условия опыта, но предполагая, что значение величины А не изменяются
Определение
погрешности косвенных измерений
При косвенных измерениях значение
физической величины находится путем расчетов по формуле.
Относительную погрешность
определяют так, как показано в таблице:
|
Формула величины |
Формула |
|
1. |
|
|
2. 3. |
|
|
4. |
|
Абсолютную погрешность определяют
по формуле:
( выражается десятичной дробью)
Пример: пусть измеряется сопротивление проводника. 
Результаты прямых измерений:
Тогда 


,
;
,
,
.
Графическое
представление результатов эксперимента
Правила построения
графиков
выберите соответствующую бумагу;
выберите масштаб по осям координат;
напишите обозначения измеряемых физических величин;
нанесите на график данные;
нанесите на график доверительные интервалы;
проведите кривую через нанесенные точки;
составьте заголовок графика.
Для построения графиков выпускают
специальную бумагу-миллиметровку.
При выборе масштабов по осям
координат следует руководствоваться следующими правилами:
— значение независимой переменной
откладывают вдоль оси абсцисс, функции – вдоль оси ординат;
— цена наименьшего деления масштабной
сетки должна быть сравнимой с величиной погрешности измерения;
— точка пересечения оси абсцисс и оси
ординат не обязательно должна иметь координаты (0,0).
При построении графиков следует
иметь в виду, что по результатам опытов мы получаем не точку, а прямоугольник
со сторонами и
.

В
|
|
|||||
|
|
|||||
0
А
При выполнении простых лабораторных
работ достаточно обвести экспериментальную точку кружком или пометить
крестиком, не указывая доверительных интервалов.
Этот кружок или крестик будут
обозначать, что данная точка получена с каким-то приближением и истинное
значение измеряемой величины лежит где-то в ее окрестности.
Правила
приближенных вычислений
1. Основное
правило округления.
Если первая
отброшенная цифра равна 5 или больше, то последнюю из сохраняемых цифр
увеличивают на единицу; если первая отброшенная цифра меньше 5, то последнюю из
сохраняемых цифр оставляют без изменения, например:
2. При сложении и
вычитании приближенных чисел
в полученном результате сохраняют столько десятичных знаков, сколько их в числе
с наименьшим количеством десятичных знаков, например:
3. При умножении
и делении приближенных чисел
в полученном результате нужно сохранить столько значащих цифр, сколько их имеет
приближенное число с наименьшим количеством значащих цифр, например:
4. При возведении
в квадрат приближенного числа
нужно в результате сохранять столько значащих цифр, сколько их имеет возводимое
в степень число, например:
5. При извлечении
квадратного корня в результате
нужно сохранять столько значащих цифр, сколько их имеет подкоренное число,
например:
6. При вычислении
промежуточных результатов в
них следует сохранять на одну цифру больше, чем требуют правила 2-5. Причем при
подсчете значащих цифр запасные цифры не учитываются. В окончательном
результате запасная цифра отбрасывается по основному правилу округления.
7. При нахождении
углов или тригонометрических функций значение соответствующего угла записывают с точностью до градуса, если
значение тригонометрической функции имеет две значащие цифры; если угол задан с
точностью до градусов, то в значении тригонометрической функции сохраняют две
значащие цифры, например:
Погрешность прямых и косвенных измерений | Физика ЕГЭ | Pi-Fi
Канал видеоролика: Математика ОГЭ и ЕГЭ с Пифагором
Смотреть видео:
Свежая информация для ЕГЭ и ОГЭ по Математике (листай):
С этим видео ученики смотрят следующие ролики:

ФИЗИКА ЕГЭ 22 ЗАДАНИЕ РАЗБОР точность и погрешность измерений
Владимир Романов

Погрешность измерений | Физика ЕГЭ | Pi-Fi
Математика ОГЭ и ЕГЭ с Пифагором

Приближённые вычисления: абсолютная и относительная погрешность
Павел Бердов

Погрешность
Математика без проблем
Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):
04.07.2020
- Комментарии
RSS
Написать комментарий
Нет комментариев. Ваш будет первым!
Ваше имя:
Загрузка…













