Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент:
| Ключевое слово | Найдено страниц |
|---|---|
| сканер | 200 |
| принтер | 250 |
| монитор | 450 |
Сколько сайтов будет найдено по запросу «(принтер | сканер) & монитор», если по запросу «принтер | сканер» было найдено 450 сайтов, по запросу «принтер & монитор» — 40, а по запросу «сканер & монитор» — 50.
2
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество страниц (тыс.) |
|---|---|
| торты | пироги | 12000 |
| торты & пироги | 6500 |
| пироги | 7700 |
Сколько страниц (в тысячах) будет найдено по запросу торты
3
Некоторый сегмент сети Интернет состоит из 5000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент:
| Ключевое слово | Количество сайтов,для которых данное слово является ключевым |
|---|---|
| принтеры | 400 |
| сканеры | 300 |
| мониторы | 500 |
Сколько сайтов будет найдено по запросу (принтеры | мониторы) & сканеры
если по запросу принтеры | сканеры было найдено 600 сайтов,
по запросу принтеры | мониторы – 900,
а по запросу сканеры | мониторы – 750.
4
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Лебедь & (Рак | Щука) | 320 |
| Лебедь & Рак | 200 |
| Лебедь & Рак & Щука | 50 |
Какое количество страниц (в тысячах) будет найдено по запросу
Лебедь & Щука
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
5
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Пекин & (Москва | Токио) | 338 |
| Пекин & Москва | 204 |
| Пекин & Москва & Токио | 50 |
Какое количество страниц (в тысячах) будет найдено по запросу Пекин & Токио?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Пройти тестирование по этим заданиям
Автор — Лада Борисовна Есакова.
Для быстрого поиска информации в Интернете используют поисковые запросы. Поисковый запрос – это набор ключевых слов, соединенных знаками логических операций И, ИЛИ, НЕ.
Приоритет выполнения операций, если нет специально поставленных скобок, следующий: сначала НЕ, затем И, затем ИЛИ.
Нужно понимать, что операция И (одновременное выполнение условий) сокращает объем получаемого результата, а операция ИЛИ (выполнение хотя бы одного из условий) наоборот увеличивает объем.
Если в запросе стоит фраза в кавычках, система будет искать точно такую фразу целиком.
1. Расположение запросов по возрастанию (убыванию)
Операция «И» (&) обозначает одновременное присутствие ключевых слов в искомых документах, а потому уменьшает количество найденной информации. Чем больше ключевых слов соединены операцией «И», тем меньше количество найденной информации. И наоборот, операция «ИЛИ» (|) обозначает присутствие хотя бы одного ключевого слова в искомых документах, а потому увеличивает количество найденной информации.
Пример 1.
В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
А) реферат | математика | Гаусс
Б) реферат | математика | Гаусс | метод
В) реферат | математика
Г) реферат & математика & Гаусс
Решение:
Самое маленькое количество страниц будет отобрано по запросу с наибольшим количеством операций «И» (запрос Г), Самое большое количество страниц будет отобрано по запросу с наибольшим количеством операций «ИЛИ» (запрос Б). По запросу А будет отобрано больше страниц, чем по запросу В, т.к. запрос А содержит больше ключевых слов, связанных операцией «ИЛИ».
Ответ: ГВАБ
2. Подсчет найденных по запросу страниц
Такой тип задач обычно решают системой уравнений. Предложу более наглядный и простой способ.
Принцип отбора информации по поисковым запросам хорошо иллюстрирует диаграмма Эйлера-Венна (круги Эйлера). На диаграмме множества изображаются пересекающимися кругами. Операция «И» (&) — это пересечение кругов, а операция «ИЛИ» (|) – это объединение кругов.
Например, обозначим кругами множества Яблоки, Груши, Бананы. По запросу Яблоки & Груши & Бананы будет отобрано пересечение (общая часть) всех трех кругов:
По запросу Яблоки | Груши будет отобрано объединение двух кругов:
Пример 2.
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
Сколько страниц (в тысячах) будет найдено по запросу шахматы?
Решение:
Нарисуем диаграмму Эйлера-Венна. Прием решения задачи состоит в подсчете количества страниц, соответствующего каждой области, ограниченной линиями:
Запросу шахматы & теннис соответствует средняя область (1000 тыс. страниц), а запросу теннис – весь правый круг (5500 тыс. страниц).
Тогда правый «обрезанный круг» — это 5500-1000=4500:
Запросу шахматы | теннис соответствуют оба круга (7770), тогда левый «обрезанный круг» — это 7770-5500=2270

Итак, мы посчитали количества страниц для каждой ограниченной линиями области:
Несложно увидеть, что по запросу шахматы будет найдено 2270+1000=3270 тыс. страниц.
Ответ: 3270
Пример 3.
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
Сколько страниц (в тысячах) будет найдено по запросу
Москва & (Париж | Лондон)
Решение:
Как и в предыдущей задаче, нарисуем диаграмму Эйлера-Венна и посчитаем количество страниц, соответствующее каждой известной области, ограниченной линиями:
Несложно увидеть, что запросу Москва & (Париж | Лондон) соответствует область:
Ответ: 427
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задача №17. Построение запросов для поисковых систем. Расположение запросов по возрастанию (убыванию). Подсчет количества страниц.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
|
Запросы для поисковых систем |
|
с использованием логических |
Разбор заданий № 17 ЕГЭ (11 кл)
Проверяемые элементы содержания: Умение осуществлять поиск информации в сети Интернет.
(повышенный уровень, время – 2 мин)
Что
нужно знать:
|
Поисковая |
|
компьютерных программ, предоставляющая пользователю |
|
доступа к необходимой ему информации при помощи поиска в |
|
доступных данных[1]. |
|
Для поиска информации с помощью поисковой системы |
|
поисковый запрос. Работа поисковой системы заключается в |
|
пользователя найти документы, содержащие либо указанные |
|
слова, как-либо связанные с ключевыми словами. При этом |
|
генерирует страницу результатов поиска. |
|
Поисковый |
|
вводит в поисковую строку, чтобы найти интересующую его |
|
Поисковый запрос задаётся в виде набора слов или фразы, |
|
расширенные возможности языка запросов поисковой системы. |
|
Язык |
|
данных и другим |
|
системам. |
|
В языке запросов поискового сервера для обозначения |
|
используется символ «|», а для обозначения логической |
Рекомендации:
|
1. проанализировать исходную таблицу и установить |
|
пересекаются; |
|
2. построить диаграмму Эйлера-Венна; |
|
3. определить искомые сегменты; |
|
4. составить тождества; |
|
5. найти решение. |
Информационные
ресурсы:
1.
Теория: Диаграмма Эйлера, Отношения между понятиями
2.
Задания для тренировки: https://inf-ege.sdamgia.ru/?redir=1
3.
Круги Эйлера: тренажер для задачи 17 с тремя областями
(А. Жуков)
4.
Онлайн-тест Константина Полякова для подготовки к ЕГЭ:
B17
— Запросы в поисковых системах
Задание
№ 17 (ДЕМО ЕГЭ-2020 ФИПИ)
|
В языке запросов поискового сервера для обозначения |
||||
|
используется символ «|», а для обозначения логической |
||||
|
В таблице приведены запросы и количество найденных по ним |
||||
|
сегмента сети Интернет. |
||||
|
Запрос |
Найдено страниц (в |
№ |
||
|
Поле |
54 |
N2 |
||
|
Пшеница |
40 |
N1 |
||
|
Напряжённость |
44 |
N3 |
||
|
Поле & Пшеница |
30 |
N4 |
||
|
Напряжённость & Поле |
14 |
N5 |
||
|
Напряжённость & Пшеница |
0 |
|||
|
Какое количество страниц (в сотнях тысяч) будет найдено по |
||||
|
Напряжённость | Поле | Пшеница? |

N1 + N2 + N3 — N4 — N5 – ?
54 + 40 + 44 — 30 — 14 = 94
Ответ: 94
Задание
№ 17 (ДЕМО ЕГЭ-2019 ФИПИ)
|
В таблице приведены запросы и количество найденных по ним |
||||
|
сегмента сети Интернет. |
||||
|
Запрос |
Найдено страниц (в сотнях тысяч) |
№ области на рисунке |
||
|
Горло |
35 |
N1 |
||
|
Корабль |
35 |
N2 |
||
|
Нос |
40 |
N3 |
||
|
Корабль & Нос |
20 |
N4 |
||
|
Горло & Нос |
13 |
N5 |
||
|
Горло & Корабль |
0 |
|||
|
Какое количество страниц (в сотнях тысяч) будет найдено по |
||||
|
Горло | Корабль | Нос? |
||||
|
Считается, что все запросы выполнялись практически |
||||
|
содержащих |
Решение:

N1 + N2 + N3 — N4 — N5 = ?
N1 + N2 + N3 — N4 — N5 = 35 + 35 + 40 — 20 — 13 =
= 110 — 33 = 77
Ответ: 77
Задание
№ 17 (ДЕМО ЕГЭ-2018 ФИПИ)
|
В таблице приведены запросы и количество найденных по ним |
||
|
сегмента сети Интернет. |
||
|
Запрос |
Найдено страниц (в |
№ области на рисунке |
|
Бабочка |
22 |
N1 |
|
Гусеница |
40 |
N2 |
|
Трактор |
24 |
N3 |
|
Трактор | Бабочка | |
66 |
N1+N2+N3-N4-N5 |
|
Трактор & Гусеница |
12 |
N5 |
|
Трактор & Бабочка |
0 |
— |
|
Какое количество страниц (в сотнях тысяч) будет найдено по |
||
|
Бабочка & Гусеница? |
||
|
Считается, что все запросы |
||
|
содержащих |

Найти: N4
N1 + N2 + N3 — N4 — N5 = 66
22 + 40 + 24 — 12 — N4 = 66
74 — N4 = 66
N4 = 74 — 66
N4 = 8
Ответ: 8
Разбор заданий № 17: СтатГрад.
Подготовка к ЕГЭ 2019[4]
Вариант № 1
|
В таблице приведены запросы и количество найденных по |
|||||
|
сегмента сети Интернет. |
|||||
|
Запрос |
Найдено страниц (в |
№ области на рисунке |
|||
|
Линкор | Корвет |
3400 |
N1+N2-N3 |
|||
|
Линкор & Корвет |
1300 |
N3 |
|||
|
Линкор |
2100 |
N1 |
|||
|
Какое количество страниц (в тысячах) будет найдено по |
|||||
|
Считается, что все запросы выполнялись |
|||||
|
одновременно, так что набор страниц, содержащих все |
|||||
|
не |
|||||

Найти: N2
N2 = 3400 — 2100 + 1300 = 2600
Ответ: 2600
Вариант № 3
|
В таблице приведены запросы и количество найденных по ним страниц |
||||
|
сегмента сети Интернет. |
||||
|
Запрос |
Найдено страниц (в |
№ области на рисунке |
||
|
Жираф |
75 |
N1 |
||
|
Слон |
109 |
N2 |
||
|
Моська |
14 |
N3 |
||
|
Слон & Жираф |
33 |
N4 |
||
|
Жираф & Моська |
0 |
|||
|
Жираф | Слон | Моська |
153 |
|||
|
Какое количество страниц (в тысячах) будет найдено по |
||||
|
Считается, |
||||
|
содержащих |
Решение:

Для Жираф
| Слон | Моська: N1+N2+N3 —
N4 — N5 =153
75+109 +14 — 33 — N5 = 153
N5 = 75+109 +14 — 33 — 153 =198 — 186 = 12
Ответ: 12
Вариант № 5
|
В таблице приведены запросы и количество найденных по ним |
||||
|
сегмента сети Интернет. |
||||
|
Запрос |
Найдено страниц (в |
№ области на рисунке |
||
|
Масло |
164 |
N1 |
||
|
Сыр |
44 |
N2 |
||
|
Холст |
150 |
N3 |
||
|
Холст & Масло |
108 |
N5 |
||
|
Сыр | Холст |
194 |
N2+N3 |
||
|
Холст | Сыр | Масло |
238 |
N |
||
|
Какое количество страниц (в тысячах) будет найдено по |
||||
|
Считается, |
||||
|
содержащих |

Найти: N4
Для Холст | Сыр | Масло:
N = N1 + N2 + N3 — N4 — N5 = 238
164 + 44 + 150 — N4 — 108 = 238
N4 = 358-108-238 = 12
Ответ: 12
Разбор заданий № 17: ЕГЭ
2020. Информатика. Ушаков Д.М. 10 тренировочных вариантов[5]
Вариант № 1
|
В таблице приведено количество страниц, которое находит |
|||
|
каждому запросу. |
|||
|
Запрос |
Количество найденных страниц |
||
|
Яблоки |
7300 |
||
|
Яблоки | Сливы |
14800 |
||
|
Яблоки & Сливы |
1400 |
||
|
Какое количество страниц будет найдено по запросу Сливы? |
|||
|
Считается, |
|||
|
содержащих |
Решение:
“Яблоки | Сливы” = “Яблоки” + “Сливы” — “Яблоки &
Сливы”
“Сливы” = “Яблоки | Сливы” — “Яблоки” + “Яблоки &
Сливы”
“Сливы” = 14800 — 7300 + 1400 =8900
Ответ: 8900
Вариант № 2
|
В таблице приведено количество страниц, которое находит |
||
|
каждому запросу. |
||
|
Запрос |
Количество найденных страниц |
номер области |
|
(Клавиатура | Мышь) & |
11700 |
N6+N5-N7 |
|
Клавиатура & Джойстик |
7300 |
N6 |
|
Мышь & Джойстик |
5900 |
N5 |
|
Какое количество страниц будет найдено по запросу |
||
|
Клавиатура & Мышь & Джойстик? |
||
|
Считается, |
||
|
содержащих |

Найти: N7
N6 + N5 — N7 = 11700
N7 = N6 + N5 — 11700
N7 = (7300 + 5900) — 11700
N7 = 1500
Ответ: 1500
Вариант № 3
|
В таблице приведено количество страниц, которое находит |
||
|
каждому запросу. |
||
|
Запрос |
Количество найденных (в |
номер области |
|
Колбаса | Сыр | Паштет |
26 |
N |
|
Паштет |
13 |
N2 |
|
Сыр |
8 |
N3 |
|
Колбаса & Паштет |
3 |
N4 |
|
Сыр & Паштет |
2 |
N5 |
|
Колбаса & Сыр |
2 |
N6 |
|
Колбаса & Сыр & Паштет |
1 |
N7 |
|
Какое количество страниц будет найдено по запросу Колбаса? |
Решение:

1. “Сыр
| Паштет” = N2 + N3 — N5 = 13+8-2 = 19;
2. N1
= N — “Сыр | Паштет” + N4 + N6 — N7;
N1 = 26 — 19 + 3 + 2 — 1 = 6 + 5 = 11
Ответ: 11
Вариант № 4
|
В таблице приведено количество страниц, которое находит |
||
|
каждому запросу. |
||
|
Запрос |
Количество найденных (в |
номер области |
|
Ангара |
24 |
N1 |
|
Лена |
31 |
N2 |
|
Енисей |
19 |
N3 |
|
Ангара |
21 |
N4 |
|
Ангара |
14 |
N5 |
|
Лена & |
17 |
N6 |
|
Ангара | |
35 |
N |
|
Какое количество страниц будет найдено по запросу Ангара & Лена & Енисей? |
Решение:

N7 =
N — N1 — N2 — N3 + N4 + N5 + N6; N7 = 35 — (24 + 31 +19) + (21 + 14 + 17); N7 =
35 — 74 + 52 = 13.
Ответ: 13
Вариант № 5
|
В таблице приведено количество страниц, которое находит |
||
|
каждому запросу. |
||
|
Запрос |
Количество найденных страниц (в |
номер области |
|
Авторучка | |
45 |
N |
|
Линейка |
23 |
N3 |
|
Карандаш |
18 |
N2 |
|
Авторучка |
15 |
N1 |
|
Карандаш |
0 |
|
|
Авторучка |
8 |
N4 |
|
Какое количество страниц будет найдено по запросу Авторучка & Линейка? |
Решение:

N = N1 + N2 + N3 — N4 — N5;
N5 = (N1 + N2 + N3) — N — N4;
N5 = (23+18+15) — 45 — 8 = 56 — 53 = 3
Ответ: 3
Вариант № 6
|
В таблице приведено количество страниц, которое находит |
||
|
каждому запросу. |
||
|
Запрос |
Количество найденных страниц |
номер области |
|
Арбузы |
9400 |
N1 |
|
Дыни |
4700 |
N2 |
|
Арбузы | |
11900 |
N |
|
Какое количество страниц будет найдено по запросу Арбузы & Дыни? |
Решение:
Найти: N3
N3 = N1 + N2 — N;
N3 = 9400 + 4700 — 11900 = 14100 — 11900 =
2200.
Ответ: 2200
Расположение запросов в порядке
убывания/возрастания
задания для
тренировки
№ 1. (№ 2705)
Ниже приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания
количества страниц,
которые найдет
поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» в запросе используется
символ |, а для логической операции «И» – &.
1) принтеры
& сканеры & продажа
2) принтеры
& продажа
3) принтеры
| продажа
4) принтеры
| сканеры | продажа
Ответ: 1234
№ 2. (№ 3151)
В
таблице приведены
запросы к поисковому серверу. Расположите номера запросов в порядке возрастания
количества страниц,
которые найдет
поисковый сервер по каждому запросу.
№ Запрос
1) канарейки | щеглы | содержание
2) канарейки & содержание
3) канарейки & щеглы & содержание
4) разведение & содержание & канарейки & щеглы Ответ: 4321
№ 4. (№ 3159)
Ниже
приведены запросы
к поисковому серверу. Расположите номера запросов в порядке убывания
количества страниц,
которые найдет поисковый сервер
по каждому запросу.
1) спорт & футбол & чемпионат
2) спорт | футбол & чемпионат
3) cпорт | футбол | чемпионат
& 2006
4) спорт | футбол | чемпионат
Ответ: 4321
№ 14. (№ 3183)
Приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания
количества страниц,
которые найдёт поисковый
сервер по каждому
запросу. В ответе запишите
четырехзначное число, соответствующее
порядку запросов, например, 2314.
1) История
& Россия & Мономах
2) История
& (Россия | Мономах)
3) История
& Россия & Владимир
& Мономах
4) История
| Россия | Мономах
Ответ: 3124
Что
нужно знать:
|
Релевантность |
|
общем смысле это соответствие документа ожиданиям пользователя. |
|
Релевантность |
|
ответ на его запрос поисковыми |
|
Релевантность |
|
заданному при поиске нужной |
|
словосочетанием. |
|
запроса. |
|
Релевантная информация — та |
|
данной задачи (например, задачи |
|
информация ненужная, |
|
относительно: например, в ходе |
|
момент, может стать в |
№ 30. (№ 3156)
Ниже приведены
части документов, найденных
по поисковому запросу.
Расположите эти документы
в порядке возрастания релевантности к запросу
«Порядок проведения ЕГЭ»
1) …Утверждение
порядка проведения
каждого ЕГЭ…
2) …Порядок
проведения ЕГЭ…
3) …Отсутствие
единого порядка проведения
ЕГЭ… 4) …Недостаток
документов о проведении ЕГЭ… . Ответ: 4132
№ 31. (№ 3157)
В
языке запросов поисковой
системы кавычки вокруг
части запроса означают, что эта часть должна встречаться точно в указанной форме
(т. е. это цитата). Ниже приведены поисковые
запросы, одновременно выданные к одной поисковой системе. Расположите их в
порядке возрастания количества
найденных документов:
1) Откуда берется мокрый
снег
2) «Откуда
берется мокрый
снег»
3) Мокрый&снег&(откуда
берется)
4) Мокрый&снег
Ответ: 2341
Сложные запросы
задания для
тренировки
№1. (№ 3452)
Некоторый
сегмент сети Интернет
состоит из 5000 сайтов.
Поисковый сервер в автоматическом
режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент:
|
Ключевое слово |
Количество |
|
принтеры |
400 |
|
сканеры |
300 |
|
мониторы |
500 |
Сколько сайтов
будет найдено по запросу (принтеры
| мониторы)
& сканеры если по запросу
принтеры
| сканеры
было найдено 600 сайтов,
по запросу принтеры
| мониторы – 900, а по запросу сканеры
| мониторы – 750.
Решение:
Вариант 1
Распределительный закон для логического умножения:
(П или М) и С = (П и С) или (М и С) = 100 + 50 =150
Вариант 2

N1=
400, N2 = 300, N3 = 500
N1+N2-N5
= 600 → N5 = 100 (N5 ≡ N1 ∩ N2)
N1+N3-N4
= 900 → N4 = 0 (N4 ≡ N1 ∩ N3) N2+N3-N6 = 750 → N6 = 50 (N6 ≡ N2 ∩ N3)
т.к.
N4 = 0, то и N7 = 0 (N7 ≡ N4 ∩ N5 ∩ N6)
N5+N6 = 150
Вариант 3
по
условию имеем: принтеры = 400, мониторы = 500, объединение множеств: принтеры | мониторы = 900 ⇒
эти множества не пересекаются.
Найти: N2 + N4
(обозначим отдельные сегменты)
1) (N1 + N2)
+ (N4 + N5) = 400 + 500 = 900 (принтеры
или мониторы)
2) (N1 + N2)
+ (N3 + N4) = 600 (принтеры
или сканеры)
3) N2 + N3 +
N4 + N5 = 750 (сканеры или мониторы)
4) N1 + N2 =
400 – (по условию – принтеры), тогда
a) из
(2) имеем N3 + N4 = 200
5) 
N2 = 100
6) N4 + N5 = 500 – (по условию), тогда
a) из
(3) имеем N2 + N3 = 250
b) из (5)
имеем N3 = 150
7) из (5)
имеем N4 = 300 – (100 +150) = 50, N4 = 50

=150 Ответ: 150
№21. Задание 17 № 6010
(Источник:
Демонстрационная версия ЕГЭ—2014 по информатике).
В языке запросов
поискового сервера для обозначения логической
операции «ИЛИ» используется символ
«|», а для логической
операции «И» – символ
«&».
В таблице приведены
запросы и количество
найденных по ним страниц
некоторого сегмента сети Интернет:
|
Запрос |
Найдено (в тысячах) |
|
хоккей & футбол & волейбол |
80 |
|
футбол |
260 |
|
хокей & волейбол |
230 |
Компьютер печатает
количество страниц (в тысячах), которое будет найдено по следующему
запросу:
 (хоккей
(хоккей
| футбол) & волейбол = (x•v+f•v)-x*v*f =
230+260-80=410

число, которое напечатает компьютер.
Считается, что
все запросы выполнялись
практически одновременно,
так что набор страниц, содержащих все искомые слова,
не изменялся за
время выполнения
запросов. Найти:
N2 + N4 + N7 Решение:
1) N7 = 80
2) N7 + N4 =
260, тогда из (1) имеем N4 = 180
3) N7 + N2 =
230, тогда из (1) имеем N2 = 150
4) N2 + N4 +
N7 = 150
+ 180 + 80 = 410
Ответ: 410
№31. Задание 17 № 6785
Источник:
МИОО: Тренировочная
работа по информатике
20.02.2014 вариант
ИН10601.
В таблице
приведены запросы
и количество найденных
по ним страниц некоторого
сегмента сети Интернет:
|
Запрос |
Найдено страниц (в тысячах) |
|
Львов & (Ужгород | Мукачево) |
275 |
|
Львов & Ужгород |
123 |
|
Львов & Ужгород & Мукачево |
41 |
Какое количество
страниц (в тыс.) будет найдено
по запросу Львов & Мукачево?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

1) N7 = 41
2) N7 + N4 =
123, тогда из (1) имеем N4 = 82
3) N7 + N4 +
N2 = 275, тогда из (1) и (2) имеем N2 = 152
4) N2 + N7 =
152 + 41 =193 Ответ: 193
№42. Задание 17 № 8105
Источник:
ЕГЭ 05.05.2015. Досрочная
волна.
В таблице
приведены запросы
и количество найденных
по ним страниц некоторого
сегмента сети Интернет.
|
Запрос |
Найдено страниц, тыс. |
|
Математика & Информатика |
330 |
|
Математика & Физика |
270 |
|
Математика |
520 |
Какое количество
страниц (в тысячах)
будет найдено по запросу Математика
& Информатика
& Физика?
Считается, что все запросы выполнялись практически
одновременно, так что набор страниц, содержащих
все искомые слова, не изменялся
за время выполнения
запросов.
Найти: N7

1) N7 + N4 =
330
2) N7 + N2 =
270
3) N7 + N4 +
N2 = 520, тогда
a) из
(3) – (1) имеем N2 = 190
b) из (3) –
(2) имеем N4 = 250
4) N7 = 520
– (190 + 250) = 80 Ответ: 80
Формула включений и исключений
задания для
тренировки
№1. Задание 17 № 2706
Некоторый
сегмент сети Интернет
состоит из 1000 сайтов.
Поисковый сервер в автоматическом
режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент:
|
Ключевое слово |
Найдено страниц |
|
|
сканер |
200 |
N3 |
|
принтер |
250 |
N1 |
|
монитор |
450 |
N2 |
Сколько
сайтов будет найдено
по запросу «(принтер | сканер) & монитор», если по запросу «принтер
| сканер» было найдено
450 сайтов, по запросу
«принтер & монитор»
— 40, а по запросу «сканер
& монитор» — 50.

1)
N1 + N3 — N6 = 450; N6 = 450 — (N1 + N3)
2)
N6 = 450 — 250 — 200; N6 = 0 ⇒
«принтер & сканер» = 0, т.е. N7 = 0;
3)
N4 = 40 – «принтер
& монитор»
4)
N5 = 50 – «сканер
& монитор»
5)
N4 + N5 = 40 +50 = 90
Ответ: 90
(Старый формат ЕГЭ) 17. Запросы в поисковых системах
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{ноутбук}&100\
hline
text{монитор}&200\
hline
text{стол}&350\
hline
text{ноутбук | стол}&450\
hline
text{ноутбук} & text{монитор}&50\
hline
text{стол} & text{монитор}&40\
hline
end{array}]
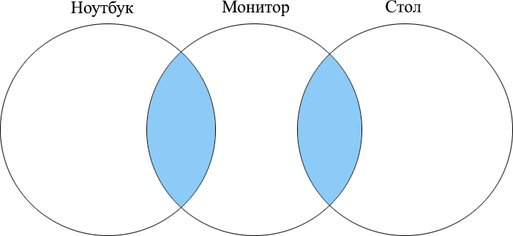
Сколько страниц будет найдено по запросу (ноутбук | стол) & монитор?
Если сложить количество страниц, найденных отдельно по запросам ”ноутбук” и ”монитор”, получим 450. Можно заметить, что (ноутбук | стол) так же равно 450. Это значит, что эти два множества не пересекаются, то есть (text{(ноутбук} & text{монитор)}=0).
Отметим на кругах Эйлера то, что нам необходимо найти по условию задачи:
Исходя из рисунка, нам нужно найти сумму (text{(ноутбук} & text{монитор)}+text{(стол} & text{монитор)}). Все данные приведены в таблице, значит, наш ответ (50+40=90).
Ответ: 90
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{чайка}&200\
hline
text{утка}&150\
hline
text{курица}&120\
hline
text{чайка} & text{утка}&80\
hline
text{утка} & text{курица}&70\
hline
text{чайка} & text{курица}&60\
hline
text{чайка} & text{курица} & text{утка}&10\
hline
end{array}]
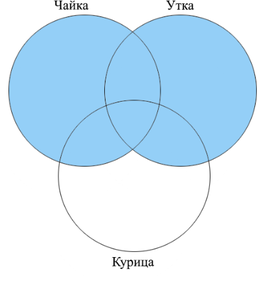
Сколько страниц будет найдено по запросу (чайка | утка)?
Первый способ решения
Отметим на кругах Эйлера то, что нам необходимо найти по условию задачи:
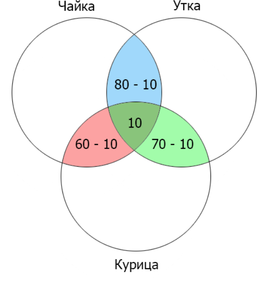
Посчитаем количество найденных страниц для каждого пересечения:
Посчитаем оставшиеся данные:
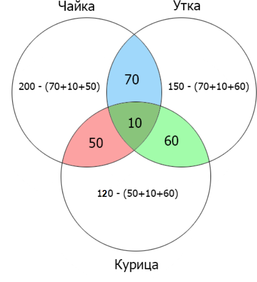
Затем складываем все данные, входящие в круги ”чайка” и ”утка”: (70+70+50+10+60+10=270)
Второй способ решения
Чтобы найти объединение (операция «ИЛИ») множеств, необходимо сложить отдельно количество страниц, найденных по каждому запросу, а затем вычесть их пересечение (операция «И»): (200+150-80=270)
Ответ: 270
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{карандаш}&300\
hline
text{линейка}&200\
hline
text{ручка}&280\
hline
text{ручка} & text{линейка}&80\
hline
text{ручка} & text{карандаш}&70\
hline
text{линейка} & text{карандаш}&0\
hline
end{array}]
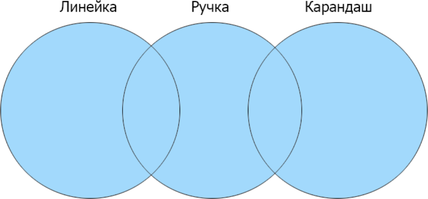
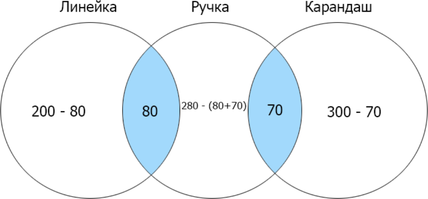
Сколько страниц будет найдено по запросу (линейка | ручка | карандаш)?
Первый способ решения
Отметим на кругах Эйлера то, что нам необходимо найти по условию задачи:
Отметим известные данные и посчитаем недостающее:
Затем складываем все данные, входящие в искомую область: (120+130+230+80+70=630).
Второй способ решения
Заметим, что по условию нам необходимо найти сумму всех найденных страниц по введенным запросам. Если мы сложим все отдельные значения найденных страниц, мы учтем по 2 раза каждое из двух пересечений. Таким образом, можем посчитать искомое по формуле: (линейка) + (ручка) + (карандаш) — (ручка & линейка) — (ручка & карандаш) (=300+200+280-80-70=630).
Ответ: 630
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{конверт}&100\
hline
text{книга}&200\
hline
text{журнал}&400\
hline
text{конверт | книга}&300\
hline
text{конверт} & text{журнал}&50\
hline
text{журнал} & text{книга}&60\
hline
end{array}]
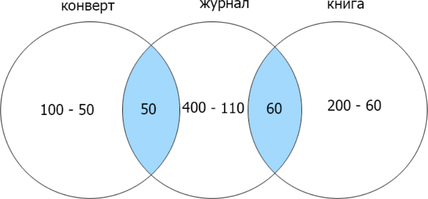
Сколько страниц будет найдено по запросу (конверт | книга | журнал)?
Заметим, что если сумма найденных страниц по каждому отдельному запросу равна их объедиению (операция «ИЛИ»), то их пересечение (операция «И») равно нулю. Т.к. сумма количества страниц, найденных по запросам конверт и книга = 300, а (конверт | книга) = 300, (конверт & книга) = 0. Теперь отобразим известные данные:
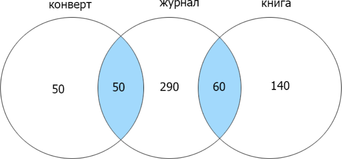
Отметим найденные данные и сложим каждую отдельную область для нахождения объедиения трех множеств:
(50+50+290+60+140=590).
Ответ: 590
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{шкаф} & text{стул}&50\
hline
text{стул} & text{стол}&60\
hline
text{стол} & text{шкаф}&70\
hline
text{(шкаф} & text{стул) | (стул} & text{стол) | (стол} & text{шкаф)}&120\
hline
end{array}]
Сколько страниц будет найдено по запросу (шкаф & стул & стол)?
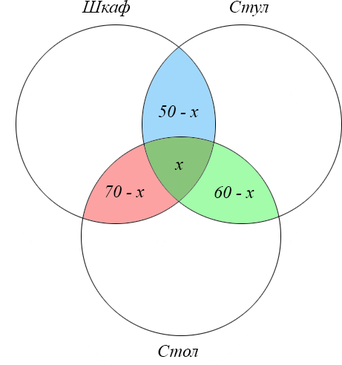
Обозначим искомую область за (x) и выразим данные через (x):
Из последней строки таблицы нам известно, что сумма всех отмеченных элементов равна 120. Значит, можем найти (x) через следующее уравнение:
((50-x)+(70-x)+(60-x)+x=120)
(180-2x=120)
(2x=60)
(x=30)
Ответ: 30
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{злодеи}&150\
hline
text{мягкие пушистики}&210\
hline
text{злодеи | мягкие пушистики}&300\
hline
end{array}]
Сколько страниц будет найдено по запросу кот, если известно, что коты находятся на пересечении множеств злодеев и мягких пушистиков?
Отметим искомую область:
Заметим, что кот = (злодеи & мягкие пушистики) = злодеи + пушистики — (злодеи | мягкие пушистики) = (150+210-300=60).
Ответ: 60
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
textbf{Запрос} & textbf{Найдено страниц (в тысячах)}\
hline
text{сок}&100\
hline
text{фрукты}&100\
hline
text{сахар | фрукты | сок}&300\
hline
text{сок | фрукты}&200\
hline
text{сок} ; & ; text{сахар}&20\
hline
text{сахар} ; & ; text{фрукты}&30\
hline
end{array}]
Сколько страниц будет найдено по запросу сахар?
Заметим, что если сумма найденных страниц по каждому отдельному запросу равна их объедиению (операция «ИЛИ»), то их пересечение (операция «И») равно нулю. Т.к.сумма количества страниц, найденных по запросам сок и фрукты = 200, а (сок | фрукты) = 200, (сок & фрукты) = 0. Теперь отобразим известные данные: 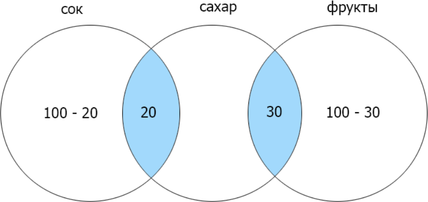
Ответ: 150

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
СОСТАВЛЕНИЕ ЗАПРОСОВ ДЛЯ ПОИСКОВЫХ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ
Задача 1: В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. Для обозначения логической операции «ИЛИ» в запросе используется символ |, а для логической операции «И» – &.
1) цветы & розы & ромашки
2) цветы & ромашки
3) ромашки | розы
4) цветы | ромашки | розы
Решение (вариант 1, рассуждение с использованием свойств операций «И» и «ИЛИ»):
- меньше всего результатов выдаст запрос с наибольшими ограничениями – первый (нужны одновременно цветы & розы & ромашки)
- на втором месте – второй запрос (одновременно цветы & ромашки)
- далее – третий запрос (ромашки | розы)
- четвертый запрос дает наибольшее количество результатов (цветы | ромашки | розы)
- таким образом, верный ответ – 1234 .
Решение (вариант 2, через диаграммы Эйлера-Венна):
- покажем области, определяемые этими выражениями, на диаграмме с тремя областями
- сравнивая диаграммы, находим последовательность областей в порядке увеличения: (1,2,3,4), причем каждая следующая область в этом ряду охватывает целиком предыдущую
- таким образом, верный ответ – 1234 .
|
1) цветы & розы & ромашки |
2) цветы & ромашки |
3) ромашки | розы |
4) цветы | ромашки | розы |
Задача 2:В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
|
Запрос |
Количество страниц (тыс.) |
||
|
пирожное & конфеты |
2500 |
||
|
пирожное |
7500 |
||
|
конфеты |
6100 |
Сколько страниц (в тысячах) будет найдено по запросу пирожное | выпечка.
Для обозначения логической операции «ИЛИ» в запросе используется символ | , а для логической операции «И» – &.
Решение (вариант 1, решение системы уравнений):
- количество сайтов, удовлетворяющих запросу, будем обозначать через Ni
- составляем уравнения, которые определяют запросы, заданные в условии:
- пирожное & конфеты N2 = 2500
- пирожное N1 + N2 = 7500
- конфеты N2 + N3 = 6100
- подставляя значение N2 из первого уравнения в остальные, получаем
- N1 = 7500 — N2 = 7500 – 2500 = 5000
- N3 = 6100 — N2 = 6100 – 2500 = 3600
- количество сайтов по запросу пирожное | выпечка равно
- N1 + N2 + N3 = 5000 + 2500 + 3600 = 11100
- таким образом, ответ – 11100.
Решение (вариант 2, рассуждения по диаграмме):
- построим диаграмму Эйлера-Венна:
- число сайтов в интересующей нас области равно N1 + N2 + N3 = (N1 + N2) + (N3 + N2) – N2
- поскольку нам известно, что по условию
пирожное N1 + N2 = 7500
пирожное & конфеты N2 = 2500
конфеты N2 + N3 = 6100
- Получаем N1 + N2 + N3 = 7500 + 6100 — 2500 = 11100
- таким образом, ответ – 11100.
Задачи для самостоятельного решения:
- В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. Ответ запишите в виде последовательности соответствующих букв.
a) Америка | путешественники | Колумб
b) Америка | путешественники | Колумб | открытие
c) Америка | Колумб
d) Америка & путешественники & Колумб
- В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу. Ответ запишите в виде последовательности соответствующих букв.
а ) Информатика & уроки & Excel
b ) Информатика | уроки | Excel | диаграмма
с) Информатика | уроки | Excel
d) Информатика | Excel
- В таблице приведены запросы к поисковому серверу, условно обозначенные буквами от А до Г. Расположите запросы в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. Ответ запишите в виде последовательности соответствующих букв.
А) Тенерифе & Климат & Флора & Фауна
Б) Тенерифе & Флора
В) (Тенерифе & Флора) | Фауна
Г) Тенерифе | Флора | Фауна
- В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.
а) Зенит & футбол
b) спорт | футбол | Петербург | Зенит
с) Зенит | футбол | Петербург
d) спорт & футбол & Петербург & Зенит
- В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
|
Запрос |
Количество страниц |
|
корабль | лодка |
3500 |
|
корабль |
2000 |
|
лодка |
2500 |
Сколько страниц (в тысячах) будет найдено по запросу корабль& лодка
- В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
|
Запрос |
Количество страниц |
|
яблоки & груши |
1500 |
|
яблоки |
2000 |
|
груши |
3000 |
Сколько страниц (в тысячах) будет найдено по запросу яблоки | груши
- В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
|
Запрос |
Количество страниц |
|
мальчики & девочки |
2500 |
|
мальчики | девочки |
6500 |
|
девочки |
4500 |
Сколько страниц (в тысячах) будет найдено по запросу мальчики
- В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
|
Запрос |
Количество страниц (тыс.) |
|
яхта | паром |
8000 |
|
яхта |
6800 |
|
паром |
4500 |
Сколько страниц (в тысячах) будет найдено по запросу яхта & паром
* — Использованные источники:
1. Материалы сайта http://kpolyakov.narod.ru/
2. О.Ю.Заславская, И.В.Левченко Информатика. Весь курс для подготовки к ЕГЭ – М.: Эксмо, 2009
3. Зорина Е.М. ЕГЭ 2010: Информатика. Сборник заданий – М.: Эксмо, 2009
4. Н.Д.Угринович Информатика и ИКТ. Учебник для 10-11 классов (профильный).- М.: БИНОМ. Лаборатория знаний, 2010
На уроке рассмотрен материал для подготовки к ОГЭ (ГИА) по информатике, разбор 8 задания. Объясняется тема об осуществлении поиска информации в Интернете, логических выражениях и запросах.
Содержание:
- ОГЭ по информатике 8 задания объяснение
- 8 задание как решать
- Актуальное
- Тренировочные
8-е задание: «Поиск информации в Интернете»
Уровень сложности — повышенный,
Максимальный балл — 1,
Примерное время выполнения — 5 минут.
* до 2020 г — это было задание № 18 ОГЭ
- Поисковые запросы:
-
- операция «И» (
&) в поисковом запросе всегда ограничивает поиск (уменьшает количество страниц в выдаче), т. е., в ответ на запрос яблоко И груша поисковый сервер выдаст меньше страниц, чем на запрос яблоко, потому что будет искать страницы, на которых присутствуют оба этих слова;
- операция «И» (
чем больше в запросе операций «И», тем меньше результатов
-
- операция «ИЛИ» (
|) в поисковом запросе всегда расширяет поиск (увеличивает количество страниц в выдаче), т. е., в ответ на запрос яблоко ИЛИ груша поисковик выдаст больше страниц, чем на запрос яблоко, потому что будет искать страницы, на которых присутствует хотя бы одно из этих слов (или сразу оба слова).
- операция «ИЛИ» (
чем больше в запросе «ИЛИ», тем больше результатов
- Круги Эйлера-Вена:
Решать 8 задание также можно, представляя запрос в виде кругов Эйлера-Вена:
- Операция «И» представляется как умножение (пересечение).
- Операция «ИЛИ» представляется как сложение (объединение).
- Заштрихованная область при объединении больше, чем при пересечении.
Пример использования кругов Эйлера:
Пример:
Известно количество сайтов, которых находит поисковый сервер по следующим запросам :
| Ключевое слово | Количество сайтов, для которых данное слово является ключевым |
|---|---|
| Глинка & Лист | 320 |
| Бах & Лист | 280 |
| (Глинка | Бах) & Лист | 430 |
Сколько сайтов будет найдено по запросу
Глинка & Бах & Лист
- Упрощение логических выражений:
(A & B) | C = (A | C) & (B | C)
(A | B) & C = (A & C) | (B & C)
8 задание как решать
Актуальное
Разбор задания 8.1: Демонстрационный вариант ОГЭ 2022 г.:
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
Какое количество страниц (в тысячах) будет найдено по запросу Рыбка?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Рыбак | Рыбка | 780 |
| Рыбак | 260 |
| Рыбак & Рыбка | 50 |
✍ Решение:
-
✎ Решим задание с помощью кругов Эйлера-Вена.
- Сначала отобразим первую строку таблицы — т.е. операцию
ИЛИ(|), которая обозначает объединение одновременно двух кругов: - Для второй строки таблицы отобразим отдельный круг, соответствующий количеству страниц для слова
Рыбак: - В третьей строке наблюдаем операцию И (
&), что соответствует области пересечения кругов: - Поскольку в задании требуется найти запрос
Рыбка, то для начала нам необходимо из общего объединения, т.е. из первого изображения, «вычесть» результат второго изображения, т.е.Рыбак; получим: - Теперь, чтобы получить полностью число страниц для запроса
Рыбка, необходимо добавить область пересечения кругов, которая равна 50 (вычисление для третьей строки); т.е. получим:
520 + 50 = 570
Ответ: 570
Тренировочные
Разбор задания 8.2:
В таблице приведены запросы к поисковому серверу. Для каждого запроса указан его код — соответствующая буква от А до Г. Расположите коды запросов слева направо в порядке убывания количества страниц, которые нашёл поисковый сервер по каждому запросу. По всем запросам было найдено разное количество страниц.
Для обозначения логической операции «ИЛИ» в запросе используется символ «|», а для логической операции «И» — «&»:
| Код | Запрос |
|---|---|
| А | (Муха & Денежка) | Самовар |
| Б | Муха & Денежка & Базар & Самовар |
| В | Муха | Денежка | Самовар |
| Г | Муха & Денежка & Самовар |
✍ Решение:
✎
Способ 1:
(Муха & Денежка) | Самовар = (Муха | Самовар) & (Денежка | Самовар)
Ответ: ВАГБ
✎ Способ 2:
- Для начала отобразим все 4 объекта задания в виде пересеченных кругов одинакового размера:
- Рассмотрим строку с кодом А. Сначала необходимо выполнить действие в скобках: (Муха & Денежка). Логическое «И» представляется, как область пересечения двух кругов:
- Теперь выполним операцию «ИЛИ» — результат пересечения | Самовар. Для этого нам необходимо к полученной области «добавить» круг для объекта Самовар:
- Таким образом, мы получили область для кода А.
- Рассмотрим строку для кода Б: операция «И» — Муха & Денежка & Базар & Самовар — обозначает область пересечения одновременно всех кругов:
- Рассмотрим строку для кода Б:
- Рассмотрим строку для кода В: операция «ИЛИ» — Муха | Денежка | Самовар — обозначает объединение одновременно всех трех кругов:
- Рассмотрим строку для кода Г: операция «И» — Муха & Денежка & Самовар — обозначает область пересечения одновременно всех трех кругов:
- То есть выделенная область одновременно принадлежит и кругу Муха, и кругу Денежка, и кругу Самовар.
- Сравним все четыре полученных области и расположим их в порядке убывания, то есть с самой большой области до самой маленькой: ВАГБ
Решим задание с помощью кругов Эйлера-Вена.
Ответ: ВАГБ
Разбор задания 8.3:
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Пьер & Наука | 180 |
| Пьер & (Наука | Кюри) | 410 |
| Пьер & Кюри | 320 |
Какое количество страниц (в тысячах) будет найдено по запросу:
Пьер & Наука & Кюри
✍ Решение:
- Везде присутствует сомножитель «Пьер &» (и в искомом запросе!), сократим его:
- Используем круги Эйлера для решения, обозначив цифрами каждую составляющую:
- Из схемы и исходных данных получим:
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Наука | 180 |
| Наука | Кюри | 410 |
| Кюри | 320 |
Искомый запрос: Наука & Кюри
1. №1 + №2 = 180 (Наука) 2. №2 + №3 = 320 (Кюри) 3. №1 + №2 + №3 = 410 (Наука | Кюри)
№1 + №2 + №3 = 180 + №3 = 410 №3 = 410 - 180 = 230
№2 + №3 = №2 + 230 = 320 №2 = 320 - 230 = 90
Результат: 90
Запросы для поисковых систем с использованием логических выражений
Расположение запросов в порядке убывания/возрастания
№1. В таблице приведены запросы к поисковому
серверу. Расположите номера запросов в порядке возрастания количества
страниц, которые найдет поисковый сервер по каждому запросу. Для
обозначения логической операции «ИЛИ» в запросе используется символ
|, а для логической операции «И» – &.
1) принтеры & сканеры & продажа
2) принтеры & продажа
3) принтеры | продажа
4) принтеры | сканеры | продажа
Пояснение.
(вариант 1, рассуждение с использованием свойств
операций «И» и «ИЛИ»):
1) меньше всего результатов выдаст запрос с наибольшими
ограничениями — первый (нужны одновременно принтеры, сканеры и
продажа)
2) на втором месте – второй запрос (одновременно принтеры
и продажа)
3) далее – третий запрос (принтеры или продажа)
4) четвертый запрос дает наибольшее количество результатов
(принтеры или сканеры или продажа)
№2. В таблице приведены запросы к поисковому
серверу. Расположите номера запросов в порядке возрастания количества
страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции “ИЛИ” в запросе
используется символ |, а для логической операции “И” – &.
№ Запрос
1 канарейки | щеглы | содержание
2 канарейки & содержание
3 канарейки & щеглы & содержание
4 разведение & содержание & канарейки &
щеглы
Пояснение.
Логическая операция “И” истинна только тогда, когда
истинны оба аргумента. Например, чтобы было истинно «канарейки
& содержание» необходимо, чтобы в тексте содержалось и слово «канарейки»
и слово «содержание».
Для истинности логической операции “ИЛИ” достаточно
истинности лишь одного из ее аргументов. Например, чтобы было истинно
«канарейки ∨ содержание» необходимо, чтобы в тексте содержалось
или слово
«канарейки» или слово «содержание».
Вывод: чем больше «&», тем меньшее количество страниц
найдет поисковик, чем больше «|», тем большее.
Следовательно ответ 4321
№3. Используя данные таблицы, расположите
номера запросов в порядке возрастания количества страниц, которые
найдет поисковый сервер по каждому запросу.
1) Модемы & факсы & продажа
2) Модемы & продажа
3) Модемы | продажа
4) Модемы | факсы | продажа
Пояснение.
Ответ: 1234
Логическая операция “И” истинна только тогда, когда
истинны оба аргумента. Например, чтобы было истинно «канарейки
& содержание» необходимо, чтобы в тексте содержалось и слово «канарейки»
и слово «содержание».
Для истинности логической операции “ИЛИ” достаточно
истинности лишь одного из ее аргументов. Например, чтобы было истинно
«канарейки ∨ содержание» необходимо, чтобы в тексте содержалось
или слово
«канарейки» или слово «содержание».
Вывод: чем больше «&», тем меньшее количество страниц
найдет поисковик, чем больше «|», тем большее.
№4. Ниже приведены запросы к поисковому
серверу. Расположите номера запросов в порядке убывания количества
страниц, которые найдет поисковый сервер по каждому запросу.
1) спорт & футбол & чемпионат
2) спорт | футбол & чемпионат
3) cпорт | футбол | чемпионат & 2006
4) спорт | футбол | чемпионат
Пояснение.
Логическая операция «И» истинна только тогда, когда
истинны оба аргумента. Например, чтобы было истинно «канарейки
& содержание» необходимо, чтобы в тексте содержалось и слово «канарейки»
и слово «содержание».
Для истинности логической операции «ИЛИ» достаточно
истинности лишь одного из ее аргументов. Например, чтобы было истинно
«канарейки ∨ содержание» необходимо, чтобы в тексте содержалось
или слово
«канарейки» или слово «содержание».
Вывод: чем больше «&», тем меньшее количество страниц
найдет поисковик, чем больше «|», тем большее.
Следовательно, на этом примере можно понять, как располагать
по убыванию количества страниц варианты в данной задаче.
Правильный ответ: 4321.
№5. В таблице приведены запросы к поисковому
серверу. Расположите номера запросов в порядке возрастания количества
страниц, которые найдет -поисковый сервер по каждому запросу. Для
обозначения логической операции «ИЛИ» в запросе используется символ
|, а для логической операции «И» — &.
1) живопись & литература
2) живопись | литература
3) живопись | литература | графика
4) живопись & литература & графика
Пояснение.
Логическая операция “И” истинна только тогда, когда
истинны оба аргумента. Например, чтобы было истинно «канарейки
& содержание» необходимо, чтобы в тексте содержалось и слово «канарейки»
и слово «содержание».
Для истинности логической операции “ИЛИ” достаточно
истинности лишь одного из ее аргументов. Например, чтобы было истинно
«канарейки ∨ содержание» необходимо, чтобы в тексте содержалось
или слово
«канарейки» или слово «содержание».
Вывод: чем больше «&», тем меньшее количество страниц
найдет поисковик, чем больше «|», тем большее.
Ответ:4123.
№6. Расположите номера запросов в порядке
убывания количества страниц, которые найдет поисковый сервер по
каждому запросу.Для обозначения логической операции «ИЛИ» в запросе
используется символ а для логической операции «И» — &.
1) барокко | классицизм
2) барокко | (классицизм & модерн)
3) (барокко & ампир) | (классицизм & модерн)
4) барокко | ампир | классицизм | модерн
Пояснение.
Логическая операция “И” истинна только тогда, когда
истинны оба аргумента. Например, чтобы было истинно «канарейки
& содержание» необходимо, чтобы в тексте содержалось и слово «канарейки»
и слово «содержание».
Для истинности логической операции “ИЛИ” достаточно
истинности лишь одного из ее аргументов. Например, чтобы было истинно
«канарейки ∨ содержание» необходимо, чтобы в тексте содержалось
или слово
«канарейки» или слово «содержание».
Вывод: чем больше «&», тем меньшее количество страниц
найдет поисковик, чем больше «|», тем большее.
Ответ: 4123.
№7. В таблице приведены запросы к поисковому
серверу. Расположите номера запросов в порядке возрастания количества
страниц, которые найдет поисковый сервер по каждому запросу. Для обозначения
логической операции «ИЛИ» в запросе используется символ |, а для логической
операции «И» — &.
1) живопись & литература & графика
2) живопись | литература | графика
3) живопись | литература
4) живопись & литература
Пояснение.
Логическая операция “И” истинна только тогда, когда
истинны оба аргумента. Например, чтобы было истинно «канарейки
& содержание» необходимо, чтобы в тексте содержалось и слово «канарейки»
и слово «содержание».
Для истинности логической операции “ИЛИ” достаточно
истинности лишь одного из ее аргументов. Например, чтобы было истинно
«канарейки ∨ содержание» необходимо, чтобы в тексте содержалось
или слово
«канарейки» или слово «содержание».
Вывод: чем больше «&», тем меньшее количество страниц
найдет поисковик, чем больше «|», тем большее.
Ответ: 1432.
№8 в порядке возрастания количества страниц,
которые найдет поисковый сервер по каждому запросу. Для обозначения
логической операции «ИЛИ» в запросе используется символ |, а для логической
операции «И» — &.
1) графика | литература
2) живопись | литература | графика
3) живопись & литература & графика
4) живопись & графика
Пояснение.
Логическая операция “И” истинна только тогда, когда
истинны оба аргумента. Например, чтобы было истинно «канарейки
& содержание» необходимо, чтобы в тексте содержалось и слово «канарейки»
и слово «содержание».
Для истинности логической операции “ИЛИ” достаточно
истинности лишь одного из ее аргументов. Например, чтобы было истинно
«канарейки ∨ содержание» необходимо, чтобы в тексте содержалось
или слово
«канарейки» или слово «содержание».
Вывод: чем больше «&», тем меньшее количество страниц
найдет поисковик, чем больше «|», тем большее.
№9. В таблице приведены запросы к поисковому
серверу. Расположите номера запросов в порядке убывания количества
страниц, которые найдёт поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» в запросе
используется символ а для логической операции «И» — &.
1) зайцы & кролики
2) зайцы & (кролики | лисицы)
3) зайцы & кролики & лисицы
4) кролики | лисицы
Пояснение.
Логическая операция “И” истинна только тогда, когда
истинны оба аргумента. Например, чтобы было истинно «канарейки
& содержание» необходимо, чтобы в тексте содержалось и слово «канарейки»
и слово «содержание».
Для истинности логической операции “ИЛИ” достаточно
истинности лишь одного из ее аргументов. Например, чтобы было истинно
«канарейки ∨ содержание» необходимо, чтобы в тексте содержалось
или слово
«канарейки» или слово «содержание».
Вывод: чем больше «&», тем меньшее количество страниц
найдет поисковик, чем больше «|», тем большее.
№10. Приведены запросы к поисковому серверу.
Расположите номера запросов в порядке возрастания количества
страниц, которые найдёт поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» в запросе
используется символ а для логической операции «И» — &.
1) яблоки & груши
2) яблоки | сливы
3) яблоки
4) яблоки & сливы & груши
Пояснение.
Логическая операция “И” истинна только тогда, когда
истинны оба аргумента. Например, чтобы было истинно «яблоки &
груши» необходимо, чтобы в тексте содержалось и слово «груши» и слово
«яблоки».
Для истинности логической операции “ИЛИ” достаточно
истинности лишь одного из ее аргументов. Например, чтобы было истинно
« яблоки ∨ груши» необходимо, чтобы в тексте содержалось
или слово
«груши» или слово «яблоки».
Вывод: чем больше «&», тем меньшее количество страниц
найдет поисковик, чем больше «|», тем большее.
Сложные запросы
№1. Некоторый сегмент сети Интернет состоит
из 5000 сайтов. Поисковый сервер в автоматическом режиме составил
таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент:
|
Ключевое слово |
Количество сайтов,для которых |
|
принтеры |
400 |
|
сканеры |
300 |
|
мониторы |
500 |
Сколько сайтов будет найдено по запросу (принтеры
| мониторы) & сканеры
если по запросу принтеры | сканеры было
найдено 600 сайтов,
по запросу принтеры | мониторы –
900,
а по запросу сканеры | мониторы –
750.
Пояснение.
Для сокращения записи обозначим через C, П, М высказывания
«ключевое слово на сайте – сканер» (соответственно принтер, монитор)
и нарисуем эти области виде диаграммы (кругов Эйлера). Заметим, что
поскольку по запросу принтеры | мониторы было найдено 900 страниц,
по запросам принтеры — 400, мониторы — 500, а
900 = 500 + 400, области П и М не пересекаются. Интересующему
нас запросу (П | M) & C соответствует объединение областей 4 и 2
(«зеленая зона» на рисунке). Количество сайтов, удовлетворяющих запросу
в области i, будем обозначать через Ni.
Из условия:
N1 + N4 + N7
+ N2= 750,
N1 +
N4 + N2 + N3= 600,
N2 +
N3 = 400,
N1 +
N2 + N4 = 300,
N4 +
N7 = 500.
Тогда из первого и пятого уравнений получаем, что N1 +
N2 = 250, а из четвёртого:
N4 = 300 − 250 = 50.
Из второго и четвёртого уравнений получаем, что N3 =
300, а из третьего:
N2 = 400 − 300 = 100.
Следовательно ответ N2 + N4 =
150.
№2. В языке запросов поискового сервера
для обозначения логической операции «ИЛИ» используется символ «|»,
а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных
по ним страниц некоторого сегмента сети Интернет.
|
Запрос |
Найдено страниц |
|
Спартак |
45000 |
|
Красс |
2000 |
|
Динамо |
49000 |
|
Спартак & Красс |
1700 |
|
Спартак & Динамо |
36000 |
По запросу Динамо & Красс ни одной
страницы найдено не было.
Какое количество страниц (в тысячах) будет найдено
по запросу Спартак | Динамо | Красс ?
Считается, что все запросы выполнялись практически
одновременно, так что набор страниц, содержащих все искомые слова, не
изменялся за время выполнения запросов.
Пояснение.
Наша цель — N1 + N4 + N2 +
N5 + N3.
Количество запросов в данной области будем обозначать
Ni.
Тогда из таблицы находим, что:
N1 + N4 = 49 000
N5 + N3 = 2 000
N2 + N4 + N5 =
45 000
N5 = 1 700
N4 = 36 000
Из первого и последнего уравнения: N1 =
13 000.
Из второго и предпоследнего уравнения: N3 =
300
Таким образом:
N1 + N4 + N2 +
N5 + N3 = 45 000 + 13 000 + 300 = 58300.
№3. В языке запросов поискового сервера
для обозначения логической операции «ИЛИ» используется символ «|»,
а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных
по ним страниц некоторого сегмента сети Интернет.
|
Запрос |
Найдено страниц |
|
Гоголь |
6000 |
|
Башмачкин |
40 |
|
Кряква |
600 |
|
Гоголь & Кряква |
200 |
|
Гоголь & Башмачкин |
30 |
По запросу Башмачкин & Кряква ни
одной страницы найдено не было.
Какое количество страниц (в тысячах) будет найдено
по запросу Гоголь | Башмачкин | Кряква? Считается, что все
запросы выполнялись практически одновременно, так что набор страниц,
содержащих все искомые слова, не изменялся за время выполнения запросов.
Пояснение.
Наша цель — N1 + N4 + N2 +
N5 + N3.
Количество запросов в данной области будем обозначать
Ni.
Тогда из таблицы находим, что:
N1 + N4 = 40
N5 + N3 = 600
N2 + N4 + N5 =
6 000
N5 = 200
N4 = 30
Из первого и последнего уравнения: N1 =
10.
Из второго и предпоследнего уравнения: N3 =
400
Таким образом:
N1 + N4 + N2 +
N5 + N3 = 6000 + 400 + 10 = 6410.
№4. В языке запросов поискового сервера
для обозначения логической операции «ИЛИ» используется символ «|»,
а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных
по ним страниц некоторого сегмента сети Интернет.
|
Запрос |
Найдено страниц |
|
(Суворов & Альпы) | (Суворов & Варшава) |
1100 |
|
Суворов & Варшава |
600 |
|
Суворов & Варшава & Альпы |
50 |
Какое количество страниц (в тыс.) будет найдено по запросу Суворов
& Альпы?
Считается, что все запросы выполнялись практически
одновременно, так что набор страниц, содержащих все искомые слова, не
изменялся за время выполнения запросов.
Пояснение.
Количество запросов в данной области будем обозначать
Ni.
Наша цель — N5 + N6.
Тогда из таблицы находим, что:
N4 + N5 = 600,
N5 = 50,
N4 + N5 + N6 =
1100.
Из первого и второго уравнения: N4 =
550.
Из последнего уравнения: N5 + N6 =
550.
№5. В языке запросов поискового сервера
для обозначения логической операции «ИЛИ» используется символ «|»,
а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных
по ним страниц некоторого сегмента сети Интернет.
|
Запрос |
Найдено страниц |
|
(Испания & Америка) | (Испания & Индия) |
800 |
|
Испания & Америка |
600 |
|
Испания & Индия & Америка |
50 |
Какое количество страниц (в тыс.) будет найдено по запросу Испания
& Индия?
Считается, что все запросы выполнялись практически
одновременно, так что набор страниц, содержащих все искомые слова, не
изменялся за время выполнения запросов.
Пояснение.
Количество запросов в данной области будем обозначать
Ni.
Наша цель — N5 + N6.
Тогда из таблицы находим, что:
N2 + N5 = 600,
N5 = 50,
N2 + N5 + N6 =
800.
Из первого и второго уравнения: N2 =
550.
Из последнего уравнения: N5 + N6 =
250.
№6. В языке запросов поискового сервера
для обозначения логической операции «ИЛИ» используется символ «|»,
а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных
по ним страниц некоторого сегмента сети Интернет:
|
Запрос |
Найдено страниц |
|
Леннон & Маккартни & Старр |
1100 |
|
Леннон & Маккартни & Харрисон |
1300 |
|
Леннон & Маккартни & Старр & Харрисон |
1000 |
Какое количество страниц (в тыс.) будет найдено по запросу
(Леннон & Маккартни & Старр) | (Леннон &
Маккартни & Харрисон)?
Считается, что все запросы выполнялись практически
одновременно, так что набор страниц, содержащих все искомые слова, не
изменялся за время выполнения запросов.
Пояснение.
Количество запросов в данной области будем обозначать
Ni. Наша цель — найти
N9 + N13 + N10.
Тогда из таблицы находим, что:
N9 + N13 = 1100,
N13 + N10 = 1300,
N13 = 1000.
Сложим первое и второе уравнение: N9 +
2N13 + N10 = 2400. Для того, чтобы найти количество
страниц по запросу «(Леннон & Маккартни & Старр) | (Леннон
& Маккартни & Харрисон)», вычтем из правой и левой частей
уравнения N13. Получим: N9 + N13 +
N10 = 1400.
№7. В языке запросов поискового сервера
для обозначения логической операции «ИЛИ» используется символ «|»,
а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных
по ним страниц некоторого сегмента сети Интернет:
|
Запрос |
Найдено страниц |
|
Ильф & Петров & Остап |
800 |
|
Ильф & Петров & Бендер |
600 |
|
Ильф & Петров & Бендер & Остап |
500 |
Какое количество страниц (в тыс.) будет найдено по запросу
(Ильф & Петров & Остап)|(Ильф & Петров
& Бендер)?
Считается, что все запросы выполнялись практически
одновременно, так что набор страниц, содержащих все искомые слова, не
изменялся за время выполнения запросов.
Пояснение.
Количество запросов в данной области будем обозначать
Ni. Наша цель — найти
N9 + N13 + N10.
Тогда из таблицы находим, что:
N9 + N13 = 600,
N13 + N10 = 800,
N13 = 500.
Сложим первое и второе уравнение: N9 +
2N13 + N10 = 1400. Для того, чтобы найти количество
страниц по запросу «(Ильф & Петров & Остап)|(Ильф & Петров
& Бендер)», вычтем из правой и левой частей уравнения N13.
Получим: N9 + N13 + N10 =
900.
Ответ: 900.
№8. В языке запросов поискового сервера
для обозначения логической операции «ИЛИ» используется символ «|»,
а для логической операции «И» – символ «&». В таблице приведены
запросы и количество найденных по ним страниц некоторого сегмента
сети Интернет:
|
Запрос |
Найдено страниц |
|
Толстой & Гоголь & Чехов |
110 |
|
Гоголь & Чехов |
275 |
|
Толстой & Чехов |
215 |
Компьютер печатает количество страниц (в тысячах),
которое будет найдено по следующему запросу: (Толстой|Гоголь)
& Чехов Укажите целое число, которое напечатает компьютер.
Считается, что все запросы выполнялись практически одновременно,
так что набор страниц, содержащих все искомые слова, не изменялся за
время выполнения запросов.
Пояснение.
Количество запросов в данной области будем обозначать
Ni. Наша цель — N2 + N5 + N4.
Тогда из таблицы находим, что:
N4 + N5 = 275,
N2 + N5 = 215,
N5 = 110.
Из первого и второго уравнения: N4 +
2N5 + N2 = 490.
Из последнего уравнения: N4 + N5 +
N2 = 380
Ответ: 380.
№9. В языке запросов поискового сервера
для обозначения логической операции «ИЛИ» используется символ «|»,
а для логической операции «И» – символ «&». В таблице приведены
запросы и количество найденных по ним страниц некоторого сегмента
сети Интернет:
|
Запрос |
Найдено страниц |
|
протон & бозон |
165 |
|
фотон & протон & бозон |
80 |
|
фотон & бозон |
125 |
Компьютер печатает количество страниц (в тысячах),
которое будет найдено по следующему запросу: (протон|фотон)
& бозон Укажите целое число, которое напечатает компьютер.
Считается, что все запросы выполнялись практически одновременно,
так что набор страниц, содержащих все искомые слова, не изменялся за
время выполнения запросов.
Пояснение.
Количество запросов в данной области будем обозначать
Ni. Наша цель — N4 + N5 + N6.
Тогда из таблицы находим, что:
N5 + N6 = 165,
N4 + N5 = 125,
N5 = 80.
Из первого и второго уравнения: N4 +
2N5 + N6 = 290.
Из последнего уравнения: N4 + N5 +
N2 = 210.
Ответ: 210.
№10. В языке запросов поискового сервера
для обозначения логической операции «ИЛИ» используется символ «|»,
а для логической операции «И» – символ «&». В таблице приведены
запросы и количество найденных по ним страниц некоторого сегмента
сети Интернет:
|
Запрос |
Найдено страниц |
|
Чацкий & Молчалин & Фамусов |
150 |
|
Чацкий & Фамусов |
350 |
|
Чацкий & Молчалин |
270 |
Компьютер печатает количество страниц (в тысячах),
которое будет найдено по следующему запросу: Чацкий &
(Молчалин|Фамусов) Укажите целое число, которое напечатает
компьютер. Считается, что все запросы выполнялись практически одновременно,
так что набор страниц, содержащих все искомые слова, не изменялся за
время выполнения запросов.
Пояснение.
Количество запросов в данной области будем обозначать
Ni. Наша цель — N2 + N5 + N4.
Тогда из таблицы находим, что:
N5 = 150,
N2 + N5 = 350,
N4 + N5 = 270.
Из второго и третьего уравнения: N2 +
2N5 + N4 = 620.
Из последнего уравнения: N2 + N5 + N4 =
470.
Ответ: 470.
Формула включений и исключений
№1. Некоторый сегмент сети Интернет состоит
из 1000 сайтов. Поисковый сервер в автоматическом режиме составил
таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент:
|
Ключевое слово |
Найдено страниц |
|
сканер |
200 |
|
принтер |
250 |
|
монитор |
450 |
Сколько сайтов будет найдено по запросу «(принтер |
сканер) & монитор», если по запросу «принтер | сканер» было найдено
450 сайтов, по запросу «принтер & монитор» — 40, а по запросу
«сканер & монитор» — 50.
Пояснение.
сканер 200
принтер 250
принтер | сканер 450
поскольку последнее число равно сумме двух предыдущих,
можно сразу же придти к выводу, что в этом сегменте сети нет сайтов, для
которых ключевыми словами являются одновременно принтер и сканер:
принтер & сканер 0
Следовательно, для того, чтобы определить, сколько
сайтов удовлетворяют заданному условию
достаточно просто сложить числа, соответствующие
запросам «принтер & монитор» и
«сканер & монитор»
40 + 50 = 90
№2. В таблице приведены запросы и количество
страниц, которые нашел поисковый сервер по этим запросам в некотором
сегменте Интернета:
|
Запрос |
Количество страниц |
|
крейсер | линкор |
7000 |
|
крейсер |
4800 |
|
линкор |
4500 |
Сколько страниц (в тыс.) будет найдено по запросу крейсер
& линкор
Пояснение.
По формуле включений и исключений имеем:
m(крейсер | линкор) = m(крейсер) + m(линкор) — m(крейсер
& линкор) = 4800 + 4500 — m(крейсер & линкор) = 7000.
=> m(крейсер & линкор) = 2300.
№3. В таблице приведены запросы и количество
страниц, которые нашел поисковый сервер по этим запросам в некотором
сегменте Интернета:
|
Запрос |
Количество страниц |
|
шахматы | теннис |
7770 |
|
теннис |
5500 |
|
шахматы & теннис |
1000 |
Сколько страниц (в тысячах) будет найдено
по запросу шахматы
Пояснение.
По формуле включений и исключений имеем:
m(шахматы | теннис) = m(теннис) + m(шахматы) — m(шахматы
& теннис) = 5500 + m(шахматы) — 1000 = 7770. => m(шахматы) = 3270.
№4. В таблице приведены запросы и количество
страниц, которые нашел поисковый сервер по этим запросам в некотором
сегменте Интернета:
|
Запрос |
Количество страниц |
|
фрегат | эсминец |
3000 |
|
фрегат |
2000 |
|
эсминец |
2500 |
Сколько страниц будет найдено по запросу фрегат
& эсминец
Пояснение.
По формуле включений и исключений имеем:
m(фрегат | эсминец) = m(фрегат) + m(эсминец) — m(фрегат
& эсминец) = 2000 + 2500 — m(фрегат & эсминец) = 3000. => m(фрегат
& эсминец) = 1500.
№5. В таблице приведены запросы и количество
страниц, которые нашел поисковый сервер по этим запросам в некотором
сегменте Интернета:
|
Запрос |
Количество страниц |
|
пирожное | выпечка |
14200 |
|
пирожное |
9700 |
|
пирожное & выпечка |
5100 |
Сколько страниц (в тысячах) будет найдено
по запросу
выпечка
Пояснение.
По формуле включений и исключений имеем:
m(пирожное | выпечка) = m(пирожное) + m(выпечка) —
m(пирожное & выпечка) = 9700 + m(выпечка) — 5100 = 14200. => m(выпечка)
= 9600.
№6. В таблице приведены запросы и количество
страниц, которые нашел поисковый сервер по этим запросам в некотором
сегменте Интернета:
|
Запрос |
Количество страниц |
|
фрегат & эсминец |
500 |
|
фрегат | эсминец |
4500 |
|
эсминец |
2500 |
Сколько страниц (в тысячах) будет найдено
по запросу фрегат
Пояснение.
По формуле включений и исключений имеем:
m(фрегат | эсминец) = m(фрегат) + m(эсминец) − m(фрегат
& эсминец) = m(фрегат) + 2500 − 500 = 4500.
Откуда получаем, что m(фрегат) = 4500 − 2500 + 500 =
2500.
Ответ: 2500.
№7. В таблице приведены запросы и количество
страниц, которые нашел поисковый сервер по этим запросам в некотором
сегменте Интернета:
|
Запрос |
Количество страниц |
|
торты | пироги |
12000 |
|
торты & пироги |
6500 |
|
пироги |
7700 |
Сколько страниц (в тысячах) будет найдено
по запросу торты
Пояснение.
По формуле включений и исключений имеем:
m(торты | пироги) = m(торты) + m(пироги) — m(торты &
пироги) = m(торты) + 7700 — 6500 = 12000. => m(торты) = 10800.
№8. В таблице приведены запросы и количество
страниц, которые нашел поисковый сервер по этим запросам в некотором
сегменте Интернета:
|
Запрос |
Количество страниц |
|
фрегат & эсминец |
500 |
|
фрегат |
2000 |
|
эсминец |
2500 |
Сколько страниц (в тысячах) будет найдено
по запросу фрегат | эсминец
Пояснение.
По формуле включений и исключений имеем:
m(фрегат | эсминец) = m(фрегат) + m(эсминец) − m(фрегат
& эсминец) = 2000 + 2500 − 500 = 4000.
№9. В языке запросов поискового сервера
для обозначения логической операции «ИЛИ» используется символ «|»,
а для логической операции «И» — символ «&». В таблице приведены
запросы и количество найденных по ним страниц некоторого сегмента
сети Интернет.
|
Запрос |
Найдено страниц |
|
Пушкин |
3500 |
|
Лермонтов |
2000 |
|
Пушкин |Лермонтов |
4500 |
Какое количество страниц (в тысячах) будет найдено
по запросу Пушкин & Лермонтов? Считается, что все запросы
выполнялись практически одновременно, так что набор страниц, содержащих
все искомые слова, не изменялся за время выполнения запросов.
Пояснение.
По формуле включений и исключений имеем:
m(Пушкин | Лермонтов) = m(Пушкин) + m(Лермонтов) —
m(Пушкин & Лермонтов) = 3500 + 2000 — m(Пушкин & Лермонтов) =
4500. => m(Пушкин & Лермонтов) = 1000.
№10. В языке запросов поискового сервера
для обозначения логической операции «ИЛИ» используется символ «|»,
а для логической операции «И» — символ
|
Запрос |
Количество страниц |
|
Сербия & Хорватия |
500 |
|
Сербия|Хорватия |
3000 |
|
Сербия |
2000 |
Какое количество страниц (в тысячах) будет найдено
по запросу Хорватия? Считается, что все запросы выполнялись
практически одновременно, так что набор страниц, содержащих все искомые
слова, не изменялся за время выполнения запросов.
Пояснение.
По формуле включений и исключений имеем:
m(Сербия|Хорватия) = m(Сербия) + m(Хорватия) — m(Сербия&Хорватия).
Тогда 3000 = 2000 + m(Хорватия) — 500, откуда m(Хорватия)
= 1500.