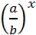Показательная функция
Показательная функция — это функция y = ax, где a > 0 и a ≠ 1.
Это одна из интереснейших функций в математике, и рассказ о ней мы начнём с древней индийской легенды.
Однажды царь узнал, что в его стране один мудрец изобрел замечательную игру — шахматы. Царь приказал доставить мудреца к себе во дворец, сыграл с ним несколько партий, и шахматы очень понравились ему. В восторге царь сказал мудрецу: «Выбирай себе любую награду. Всё получишь, чего ни пожелаешь!»
А мудрец ответил: «Пусть на первую клетку шахматной доски положат одно пшеничное зерно. На вторую — два, на третью — четыре, и на каждую следующую в два раза больше, чем на предыдущую. Всё это зерно и будет моей наградой».
Царь рассмеялся, решив, что мудрец, должно быть, спятил, раз просит о такой ничтожной вещи, как кучка зерна, но приказал слугам всё исполнить. И на первую клетку шахматной доски положили одно зерно (20 = 1), на вторую два (21 = 2), на третью 22 = 4. На десятой клетке уже не помещались 29 = 512 зёрен…
Несколько дней царский казначей вычислял требуемое количество зёрен. Оказалось, что выполнить просьбу мудреца невозможно — даже если все поля нашей планеты засеять пшеницей!
Зависимость, о которой говорится в легенде, описывается функцией y = 2x. Построим её график. Для этого посчитаем значения функции при целых x, нанесём точки на координатную плоскость и соединим их плавной линией.
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y |  |
 |
 |
 |
1 | 2 | 4 | 8 | 16 |
Мы видим, что эта функция является возрастающей, и растёт она очень быстро. Более того — чем больше значение x, тем больше в этой точке крутизна графика. То есть растёт не только функция, но и её производная.
Теперь построим график функции 
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 16 | 8 | 4 | 2 | 1 |  |
 |
 |
 |
Эта функция — убывающая. Её график зеркально симметричен графику функции y = 2x относительно оси Y.
Заметим, что при построении этих графиков мы сделали одно допущение.
Мы уже знаем, что такое степень с рациональным показателем — об этом рассказывается в статье «Степени и корни». Но понятия степени с иррациональным показателем мы не вводили (например, 
Тем не менее, свойства показательной функции y = ax активно используются при решении задач. Перечислим наиболее важные из них.
1. Область определения функции — все действительные числа: D(y) = R.
2. Область значений функции: E(y) = (0; ).
3. Поскольку a0 = 1, график проходит через точку (0, 1).
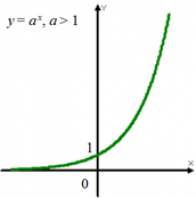
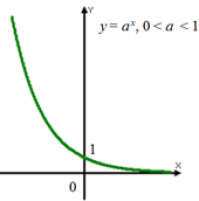
4. При a > 1 функция возрастает. При 0 < a < 1 функция убывает:
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Показательная функция» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
a > 0 , b > 0;
a0 = 1, 1x = 1;
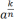
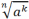
a−x = 
ax · ay = ax+y;
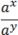
(ax)y = axy;
ax · bx = (ab)x;
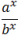
Функцию вида f (x) = aˣ, где a > 0 и a ≠ 1, называют показательной функцией.
Основные свойства показательной функции f (x) = aˣ:
|
при a > 1 |
0 < a < 1 |
|
|
Область определения |
D (f) = (−∞; +∞) |
D (f) = (−∞; +∞) |
|
Область значений |
E (f) = (0; +∞) |
E (f) = (0; +∞) |
|
Монотонность |
Возрастает |
Убывает |
|
Непрерывность |
Непрерывная |
Непрерывная |
График показательной функции
Графиком показательной функции является экспонента:
Простейшие показательные уравнения
Показательными называются уравнения, содержащие переменную в показателях каких-либо степеней.
Для решения показательных уравнений требуется знать и уметь использовать следующую несложную теорему:
Теорема 1.
Показательное уравнение af(ˣ) = ag(ˣ) (где a > 0, a ≠ 1) равносильно уравнению
f (x) = g (x).
Простейшее показательное уравнение — это уравнение вида:
ax = b, где а > 0, а ≠ 1. Такое уравнение не имеет корней при b ≤ 0, а при b > 0 имеет единственный корень: x = loga b.
Более сложные показательные уравнения решаются по следующей схеме:
- Перевести все степени к одинаковому основанию. Желательно, чтобы оно было целым и минимальным. Например, вместо 4x лучше писать 2²ˣ, а вместо 0,01x — вообще 10−²ˣ;
- В уравнениях, где есть умножение или деление, надо выполнить эти действия. Помните: при умножении степеней с одинаковым основанием показатели складываются, при делении — вычитаются;
- Если все сделано правильно, получим уравнение вида a f (x) = a g(x), где a — просто число. Его можно отбросить, поскольку показательная функция монотонна. Получим уравнение f (x) = g (x), которое легко решается.
- Помните, что корни — тоже степени, но с дробным основанием:
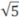
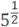
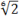
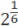
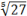
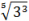
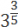
Задача. Решите уравнение: 4x = 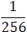
Решение:
Итак, приведем все степени к основанию 2:
4x = (22)x = 22x; 1 = 20; 256 = 28.
Теперь перепишем исходное уравнение и выполним деление:
4x = 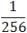

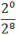


Получили простейшее показательное уравнение. Отбрасываем основание — получаем:
2x = −8 ⇒ x = −4.
Ответ: −4.
Задача: Решите уравнение: 92x = 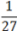
Решение
Снова приводим все степени к наименьшему целому основанию:
92x = (32)2x = 34x; 1 = 30; 27 = 33.
Обратите внимание: число 27 не является целой степенью девятки. Именно поэтому надо приводить все степени к основанию 3, а не 9. Возвращаемся к исходному уравнению:
92x = 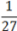

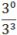


Осталось избавиться от основания степени:
4x = −3 ⇒ x = −3/4 = −0,75.
Ответ: −0,75.
Показательная функция: подготовка к ЕГЭ по математике
Разделы:
Математика
Классы:
10, 11
Ключевые слова:
математика,
ЕГЭ,
показательная функция
После полного изучения курсов алгебры, начал математического анализа и геометрии логично приступать к итоговому повторению и подготовке к единому государственному экзамену по математике. Один из традиционных подходов – повторение ранее изученного материала по блокам, при котором обращается внимание на важные детали и особенности, необходимые для успешной сдачи экзамена по математике в формате ЕГЭ. Очевидно, что одним из основных блоков материала, изучаемого в курсе алгебры X–XI классов, является показательная функция.
Безусловно, повторение курса необходимо начинать с графика и свойств показательной функции, методов решения показательных уравнений и неравенств. После тщательного повторения теоретического материала необходимо приступить к решению различных по уровню сложности заданий. Предлагаем один из возможных вариантов КИМов, содержащий набор заданий по данной теме различного уровня сложности. Главным достоинством предлагаемого КИМа является глубинная проработка всего материала, отработка решений начального уровня заданий (часть 1), повышенного уровня (часть 2 и высокого (часть 3). Данный вариант возможно предлагать как полностью (в качестве контрольной работы в формате, приближенном к ЕГЭ), так и по частям (часть 1, часть 2, часть 3). Возможен и другой подход – дифференцированный – для разных групп обучающихся в зависимости от их подготовленности.
Решение задач
Список использованной литературы
- Балаян Э.Н. Математика: 200 вариантов разноуровневых задач для подготовки к ЕГЭ, ГИА, олимпиадам и вступительным экзаменам в ВУЗ. – Ростов на Дону: Феникс, 2014.
- Башмаков М.И. Алгебра и начала анализа, 10-11 класс. – М.: Просвещение, 1992.
- Власова А.П., Латанова Н.И., Евсеева Н.В. Показательная и логарифмическая функция в задачах и примерах. – М., 2010
- Денищева Л.О. и др. Сдам ЕГЭ. Математика. – М.: Дрофа, 2007.
- Дуваева В.С., Шраер М.Г. Таблицы по алгебре и началам анализа для 10 класса и методические указания к ним. – М.: Просвещение, 1991.
- Карп А.П. Сборник задач по алгебре и началам анализа, 10-11 класс. – М.: Просвещение, 1995.
- Клово А.Г. Единственные реальные варианты заданий для подготовки к ЕГЭ. Математика. – М.: Астрель, 2007.
- Мальцев Д.А. и др. Математика. ЕГЭ 2018. Профильный уровень. – М., Народное образование, 2018.
- Мордкович А.Г., Семенов П.В. Алгебра 10 класс. – М.: Мнемозина, 2009.
- Нелин Е.П. Алгебра и начала анализа. Учебник для 10 класса. – М.: Илекса, 2012.
- Сугоняев И.М. Проверка готовности к ЕГЭ по математике. — Саратов, Лицей, 2012.
- http://alexlarin.net/
- https://ege.sdamgia.ru/
7.11.2019
Примеры на свойства степени
Подготовка к ЕГЭ по математике
Эксперимент
Урок 1. Повторение. Показательная функция. Показательные уравнения
Практика
Конспект урока
Давайте рассмотрим несколько примеров на использование свойств степени.
Пример № 1. Вычислить .
Правило: попытаться привести все степени к одинаковому основанию: .
Получаем:
Воспользуемся свойством степени :
Воспользуемся свойством степени :
.
Воспользуемся свойством степени :
.
Ответ: 0,125
Пример № 2. Найдите значение выражения 
Правило: попытаться привести степени к одинаковым основаниям (в данном случае — к нескольким): .

Воспользуемся свойством степени :
Ответ:.
Пример №3. Упростить выражение .
Воспользуемся свойствами степени для решения данного примера:
Ответ:.
Простейшие показательные уравнения
Пример №1. Решить уравнение .
Правило: привести обе части к одинаковому основанию, а затем приравнять показатели степени:
Ответ: 2.
Пример №2. Решить уравнение .
Рассмотрим решение данного уравнения двумя способами.
1 способ: ;
2 способ: (
, так как
)
Ответ: 0,5.
Пример №3. Решить уравнение .
Рассмотрим решение данного уравнения двумя способами.
1 способ:
2 способ: Возведем в куб обе части уравнения:
. Еще раз возведем в куб:
Ответ:.
Пример №4. Решить уравнение .
Вспомним, что Значит,
Ответ: 0
Пример №5. Решить уравнение .
Стандартная ошибка: Эти рассуждения принципиально неправильные.
Показательная функция принимает строго положительные значения. Поэтому данное уравнение решений не имеет.
Показательные уравнения, сводящиеся к простейшим
Пример №1. Решить уравнение
Ответ: 2,5.
Пример №2 (типовое задание В5). Найти корень уравнения .
Ответ: 0.
Пример № 3. Решить уравнение
Вспомним свойство степени . Тогда:
Стандартная ошибка: .
Ответ: 2.
С вынесением общего множителя за скобки
Пример № 1. Решить уравнение .
Правило: вынести наименьшую общую степень за скобки.
Ответ: 1.
Пример №2. Решить уравнение .
Рассмотрим решение этого уравнения двумя способами.
1 способ:
Тогда: . Выполним замену:
. Получим:
.
Обратная замена:
2 способ:
Ответ: 1.
Пример №3. Решить уравнение .
;
Ответ: 1.
Показательные уравнения, сводящиеся к квадратным
Пример №1. Решить уравнение .
Выполним замену: . Получим:
Обратная замена:
Ответ: 1.
Пример №2. Решить уравнение .
Замена: , получим:
Обратная замена:
Ответ: 0; 1.
Пример №3. Решить уравнение .
Замена: , получаем:
Обратная замена:
Ответ: -1; 1.
Однородные показательные уравнения
Пример №1. Решить уравнение .
Замена: , получаем:
Обратная замена:
Ответ: 0; 1.
Степени, корни и показательная функция в заданиях ЕГЭ
Просмотров: 1062

СКАЧАТЬ
Категория: Методическая копилка учителя математики