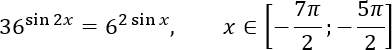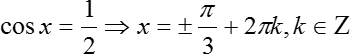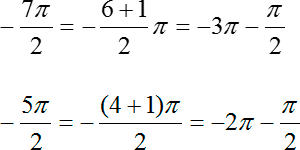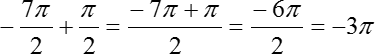Показательное тригонометрическое уравнение егэ - Помощь в подготовке к экзаменам и поступлению

Слайд 1

Задача 13. Уравнения смешанных типов с ограничениями Показательное с тригонометрией подготовка к ЕГЭ по математике (профильный уровень) Турышева Людмила Викторовна учитель математики МАОУ гимназия №18 г. Нижний Тагил 2020 г.

Слайд 2

Условие задания: а) Реши уравнение: ; б) Укажи корни уравнения, принадлежащие отрезку:

Слайд 3

Решение: а) Воспользуемся свойством степени Введем замену, не забывая про ограничения Умножим обе части уравнения на общий знаменатель t, t≠0. Решим квадратное уравнение

Слайд 4

Решение: Вернемся к замене Воспользуемся свойством показательной функции 2 Решим тригонометрическое уравнение

Слайд 5

Решение: б) Выберем решения уравнения с отрезка из неравенств: Корни уравнения ; Составим неравенство Разделим неравенство на Выберем целые значения , удовлетворяющие условию Найдем корни, принадлежащие данному отрезку

Слайд 6

Решение : б) Выберем решения уравнения с отрезка из неравенств: Корни уравнения Аналогично Ответ: а) .

Слайд 7

Примеры 1. a) ; б) а) Реши уравнение б) Укажи корни уравнения, принадлежащие отрезку 2. a) ; б) 3 . a) ; б) 4 . a) ; б) 5 . a) ; б)

Слайд 8

Ответы 1. а) 2. а) 3. а) 4 . а) 5 . а)

Источник

17 февраля 2014

Сегодня мы разберем еще одну комбинированную задачу из части С ЕГЭ по математике, где требуется решить уравнение, содержащее в себе и показательную, и тригонометрическую функцию.

Задача C1. Решите уравнение. Найдите все корни этого уравнения, принадлежащие промежутку:

Шаг 1: решение тригонометрического уравнения

Итак, нужно решить уравнение:

36^{sin 2x} = 6^{2sin x}

Очевидно, перед нами комбинированная конструкция, содержащая в себе и показательное, и тригонометрическое уравнение.

Синус двойного угла

Как решать такое уравнение? Давайте для начала выпишем все тригонометрические функции, которые присутствуют в этом уравнении, а именно:

sin 2x; 2sin x.

Что мы можем сказать о полученных выражениях? В первом (sin 2x) аргумент синуса — это 2х; а во втором (2sin x) аргумент — просто x. Итак, аргументы наших тригонометрических функций не совпадают. Это первое, на что нужно обратить внимание при решении любого тригонометрического уравнения. Следовательно, каким-то образом нужно сделать так, чтобы аргументы стали одинаковыми. В данном случае все очень просто, ведь мы знаем формулу двойного угла:

sin 2x = 2sin x · cos x;
36^{2sin x cos x} = 6^{2sin x}.

Решение показательного уравнения

Теперь у нас другая проблема: перед нами [показательное уравнение], в котором присутствуют функции с разными основаниями. Слева основание показательной степени 36, а справа — 6. И это еще один принципиальный момент: нам нужно сделать так, чтобы и слева, и справа основание показательной функции было одним и тем же. Для этого заметим, что 36 можно записать так:

36 = 6²

Следовательно, мы можем переписать наше уравнение в следующем виде:

(6²)^{2sin x cos x} = 6^{2sin x}

Теперь воспользуемся правилом возведения степени в степень: при возведении степень в степень, показатели этих степеней перемножаются. В нашем случае получаем:

(a²)^{f (x)} = a^{2f (x)};
6^{4sin x cos x} = 6^{2sin x}.

Итак, мы получили классическое показательное уравнение, в котором основания степеней являются константами и равны друг другу. Следовательно, мы можем просто убрать их и записать:

4sin x cos x = 2sin x

Решение тригонометрического уравнения

Тригонометрическое уравнение, которое мы получили, содержит несколько элементов с тригонометрической функцией. Для решения такого уравнения предлагаю перенести все слагаемые в левую часть, в результате чего получим:

4sin x cos x − 2sin x = 0

В полученном уравнении присутствуют два алгебраических слагаемых, причем и в первом, и во втором имеется множитель 2sin x. Выносим 2sin x за скобку:

2sin x (2cos x − 1) = 0

Вынесение за скобку общего множителя

Обратите внимание: на этом шаге многие ученики допускают ошибку! Давайте я еще раз напомню, как выносить общий множитель за скобку. Для этого выпишем наше выражение еще раз:

4sin x cos x − 2sin x

Перепишем эту конструкцию следующим образом:

2 · 2sin x cos x − 2sin x

Отсюда нам нужно вынеси [общий множитель]. Как вообще определяется, что можно вынести множитель за скобку? Простым перебором: мы берем самое первое слагаемое в нашем выражении и рассматриваем самый первый множитель, входящий в это слагаемое. Таким множителем является число 2.

А теперь — вопрос: встречается ли множитель 2 во втором нашем слагаемом? Конечно, встречается! Значит, ее мы выносим и идем далее. Следующий множитель тоже 2, но второй двойки во втором слагаемом не имеется, поэтому еще одну двойку вынести за скобку мы не можем.

Идем дальше: множитель sin x. Присутствует ли sin x во втором слагаемом? Да, безусловно. И последний множитель из первого слагаемого — cos x. Есть ли он во втором слагаемом? Нет, такого множителя во втором слагаемом нет. Поэтому вынести за скобку множитель cos x мы не можем. Вот и все. Получается, что из нашей конструкции можно вынести за скобку лишь множители 2 и sin x.

2 · 2sin x cos x − 2sin x = 2sin x (2cos x − 1)

Но на этом проблемы не заканчиваются. Когда ученики записывают элементы в скобках, здесь часто допускаются совершенно нелепые ошибки. Поэтому всем своим ученикам я рассказываю одно и то же правило, которое [гарантировано] избавит вас от всех подобных проблем. Правило звучит следующим образом:

При вынесении за скобку общего множителя обязательно ставьте единицу на месте каждого вынесенного элемента!

Такая запись является гарантом того, что вы не допустите ошибку при вынесении множителя за скобку. Давайте посмотрим, как это правило сработает для нашего выражения. Записываем готовое разложение — и мы получили именно то выражение, которое у нас получилось в самом начале:

2 · 2sin x cos x − 2sin x = 2sin x (1 · 2 · 1cos x − 1 · 1) = 2sin x (2cos x − 1)

Решение простейших тригонометрических уравнений

С вынесением общего множителя за скобку разобрались, возвращаемся к нашему уравнению. Произведение равно нулю тогда, когда хотя бы один из множителей равен нулю. Получаем несколько вариантов:

2 = 0; sin x = 0 (х = πn, n ∈ Z); 2cos x − 1 = 0.

Очевидно, что уравнение 2 = 0 корней не имеет (Что за бред вообще?). Второе уравнение мы разобрали сразу, т.к. это был частный случай. Рассмотрим теперь последнее уравнение:

2cos x − 1 = 0

Уравнение решено. Мы разобрали каждый вариант, поэтому других корней не будет.

Отбор корней на отрезке

Переходим ко второй части задачи C1 — отбору корней в отрезке:

И снова предлагаю вашему вниманию небольшое усовершенствование.

Хитрость: отмечаем корни на тригонометрическом круге

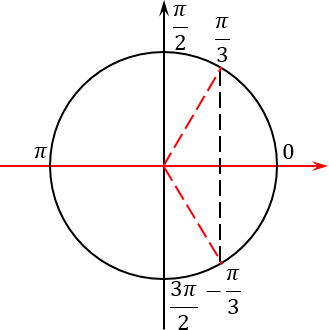
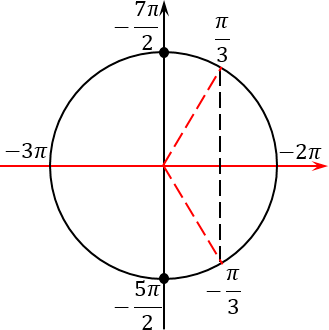
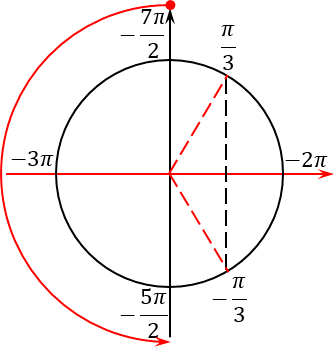
Этот прием я разработал совсем недавно вместе со своими учениками. Суть приема проста: чертим тригонометрический круг (в простонародье — радар) и отмечаем на нем наши корни. Сначала — первую группу:

x = πn

Это одна точка в самом начале круга и еще одна точка, которая диаметрально противоположна исходной.

Теперь отмечаем вторую группу корней:

Поскольку период 2πk — это полный оборот окружности, никаких других точек на тригонометрическом круге точно не появится. Итого получим следующую картинку:

Все, корни мы отметили. Теперь разбираемся с концами отрезка. Давайте перепишем их в таком виде:

По существу, мы просто выделили целую часть — по аналогии с неправильными дробями в арифметике. Отметим эти точки на том же тригонометрическом круге:

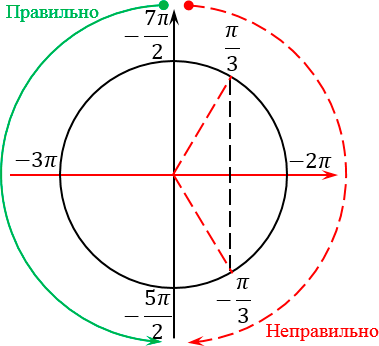
Отлично, концы искомого отрезка отмечены. Осталось грамотно отметить сам отрезок. Для этого нужно понять, как он расположен на нашем тригонометрическом круге. И вот тут многие ученики опять допускают ошибку: они путаются, в какую сторону «наматывать» этот отрезок. Ведь существует два варианта — против часовой стрелки (это правильный вариант) и по часовой (соответственно, неправильный):

На самом деле, чтобы никогда больше не путаться, нужно вспомнить основное правило: мы всегда накручиваем углы в сторону, противоположную движению часовой стрелки. Например, если бы мы хотели попасть из точки 0 в точку 2π, мы бы двигались именно против часовой стрелки:

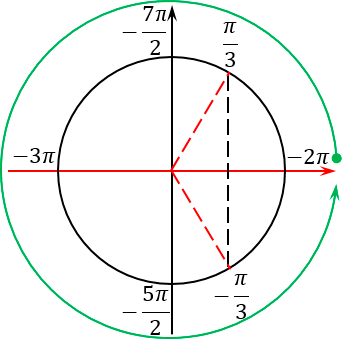
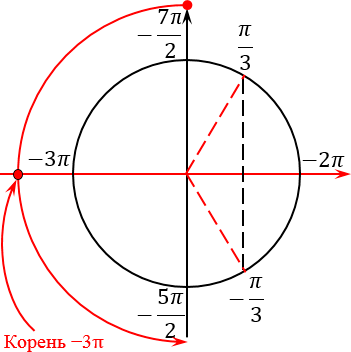
Это правило все прекрасно помнят, когда считают значение тригонометрических функций. Но почему-то забывают, что это правило работает для любых отрезков, а не только в пределах от 0 до 2π. Поэтому еще раз смотрим на наш исходный отрезок, берем его левый конец, т. е. самое маленькое число −7π/2, и идем от него в наш второй конец против часовой стрелки:

Прекрасно, отрезок отмечен. Для того, чтобы выявить интересующие нас корни, давайте продолжим лучи, проходящие через все корни, отмеченные красным, за пределы тригонометрического круга (по сути — до бесконечности). Таких лучей будет 4 штуки.

А теперь берем ручку, ставим ее в самый левый конец отрезка (точку −7π/2) и начинаем двигаться ко второму концу отрезка. Разумеется, мы тут же наткнемся на пересечение нашего отрезка и одного из лучей, отвечающих за корни. Так вот: любое такое пересечение означает, что мы нашли конкретный корень, который лежит на нашем рассматриваемом отрезке.

Возникает вопрос: как найти числовое значение этого корня? Но и тут все очень просто. Давайте подумаем: на какое расстояние нужно шагнуть из точки −7π/2, т. е. из начала нашего отрезка, чтобы попасть на горизонтальный диаметр? Очевидно, что это расстояние равно π/2. Прибавляем к концу нашего отрезка этот самый шаг:

В данном случае получилось, что этот корень уже изначально был отмечен, когда мы отмечали концы нашего отрезка: −7π/2 и −5π/2.

Если мы пойдем дальше, двигаясь из точки -3π к правому концу нашего отрезка, никаких других корней уже не встретим. Получается, что во время обхода мы столкнулись лишь с одним корнем — −3π. В принципе, это и неудивительно: в данной задаче нам попался довольно короткий отрезок, который на тригонометрическом круге занимает лишь половину полного оборота. И так уж получилось, что большинство корней, которые мы получили при решении уравнения, сосредоточены на второй половине нашего круга — в той самой, которую мы вообще не рассматривали.

В общем, не стоить удивляться, когда в процессе отбора корней у нас получился всего лишь один ответ. Это правильный ответ, и приведенный выше рисунок является полноценным тому обоснованием. Следовательно, задача решена полностью:

Мы решили само уравнение, последовательно разобравшись с показательным и тригонометрическим уравнением;
Затем отобрали те корни, которые лежат на требуемом отрезке, и обосновали этот выбор графически.

Замечание по поводу разложения на множители

Еще один тонкий момент в решении данной задачи состоит в том, что многие ученики неправильно выносят за скобку общие множители. Но это — тема отдельного урока, который вообще не относится к ЕГЭ по математике, поэтому сегодня я коснулся данного вопроса лишь вкратце. Ровно настолько, насколько это необходимо для решения конкретной задачи.

Однако если в сегодняшнем уроке вам все равно что-то непонятно, если вы хотите решать тригонометрию еще лучше, не нужно расстраиваться, просто заходите на мой сайт berdov.com. Там вас ждет еще больше уроков, а также тесты для самостоятельного решения.

Но и это еще не все: на любой странице моего сайта справа вверху есть форма для записи на занятие. Смело заполняйте ее, указывайте свое имя, телефон и хоть немного расскажите о своей математической проблеме. И как только вы нажмете на кнопку «Записаться», буквально через несколько секунд я получу ваше сообщение, и в течение нескольких минут (максимум — нескольких часов) я вам позвоню, и мы обсудим все интересующие проблемы и составим индивидуальную программу обучения, рассчитанную именно на вас.

И вот тогда вы точно убедитесь, что математика — это, на самом деле, легко, что никаких сложных формул и теорем в ней нет. Тем более, в школьном курсе. Пишите, звоните, приходите — и будем заниматься. А у меня на сегодня все. С Вами был Павел Бердов. До новых встреч!

Смотрите также:

Задача C1: тригонометрия и показательная функция — 1 вариант
Задача C1: показательные уравнения с ограничением
Умножение и деление дробей
Сводный тест по задачам B15 (2 вариант)
Однородные тригонометрические уравнения: общая схема решения
Задача B4: вклад в банке и проценты

Источник

Тригонометрические уравнения

Замена переменной и сведение к квадратному уравнению
Разложение на множители
Однородные уравнения
Введение дополнительного угла
Универсальная подстановка
Учет ОДЗ уравнения
Метод оценки
Тригонометрические уравнения повышенной сложности.
Приемы решения

В данной статье мы расскажем об основных типах тригонометрических уравнений и методах их решения. Тригонометрические уравнения чаще всего встречаются в задаче 12 ЕГЭ.

В вариантах ЕГЭ задача, где нужно решить уравнение, состоит из двух пунктов. Первый пункт – решение самого уравнения. Второй – нахождение его корней на некотором отрезке.

Некоторые из методов (например, замена переменной или разложение на множители) являются универсальными, то есть применяются и в других разделах математики. Другие являются специфическими именно для тригонометрии.

Необходимых формул по тригонометрии не так уж и много. Учите наизусть!
Тригонометрические формулы.

Любой метод решения тригонометрических уравнений состоит в том, чтобы привести их к простейшим, то есть к уравнениям вида sin x = a, cos x = a, tg x = a, ctg x = a.

Если вы не помните, как решать простейшие тригонометрические уравнения, — читайте материал на нашем сайте: Простейшие тригонометрические уравнения, часть 1.

О том, что такое арксинус, арккосинус, арктангенс и арккотангенс, — еще одна статья на нашем сайте: Простейшие тригонометрические уравнения,часть 2.

Теперь — сами методы. Теория и примеры решения задач.

к оглавлению ▴

Замена переменной и сведение к квадратному уравнению

Это универсальный способ. Применяется в любых уравнениях — степенных, показательных, тригонометрических, логарифмических, каких угодно. Замена не всегда видна сразу, и уравнение нужно сначала преобразовать.

1. а) Решите уравнение: $2cos^{2}x+5sinx=5.$
б) Найдите корни уравнения, принадлежащие отрезку $displaystyle left [ -frac{pi }{2}; 2pi right ].$

Решение:

а) Рассмотрим уравнение $2cos^{2}x+5sinx=5.$

Преобразуем его, применив основное тригонометрическое тождество:

$2left ( 1-sin^{2} xright )+5sinx=5;$

$2sin^{2}x-5sinx+3=0.$

Заменяя sin x на t, приходим к квадратному уравнению:

$2t^{2}-5t+3=0.$

Решая его, получим:

$displaystyle t_{1}=frac{3}{2}, t_{2}=1.$

Теперь вспоминаем, что мы обозначили за t. Первый корень приводит нас к уравнению $displaystyle sinx=frac{3}{2}.$
Оно не имеет решений, поскольку

Второй корень даёт простейшее уравнение sinx=1.

Решаем его: $displaystyle x=frac{pi }{2}+2pi n, nin Z.$

б) Найдем корни уравнения на отрезке $displaystyle left [ -frac{pi }{2}; 2pi right ]$ с помощью двойного неравенства.

$displaystyle -frac{pi }{2}leq frac{pi }{2}+2pi nleq 2pi .$

Разделим обе части неравенства на pi :

$displaystyle -frac{1}{2}leq frac{1}{2}+2nleq 2.$

Вычтем $displaystyle frac{1}{2}$ из обеих частей неравенства:

Разделим на 2 обе части неравенства:

Единственное целое решение – это n=0. Тогда $displaystyle x=frac{pi }{2}$ — это единственный корень, который принадлежит отрезку $displaystyle left [ -frac{pi }{2}; 2pi right ].$

Ответ: $displaystyle frac{pi }{2}.$

2. а) Решите уравнение:
б) Укажите корни этого уравнения, принадлежащие отрезку $displaystyle left [ -3pi ; -frac{3pi }{2} right ].$

Решение:

а)

Выразим косинус двойного угла по формуле $cos2x=2cos^{2}x-1.$

Получим:

$2cos^{2}x-1-5sqrt{2}cosx-5=0;$

$2cos^{2}x-5sqrt{2}cosx-6 =0.$

Заменяя cos⁡x на t, приходим к квадратному уравнению:

$2t^{2}-5sqrt{2}t-6=0;$

$displaystyle t_{1}=-frac{sqrt{2}}{2}; t_{2}=3sqrt{2}.$

1) $displaystyle cosx=-frac{sqrt{2}}{2}; x=pm frac{3pi }{4}+2pi n, nin Z;$

2) нет решений, т. к.

Получим: $displaystyle x=pm frac{3pi }{4}+2pi n, nin Z.$

б) Отметим отрезок $displaystyle left [ -3pi ; -frac{3pi }{2} right ]$ и найденные серии решений на единичной окружности.

Видим, что данному отрезку принадлежит только точка $displaystyle x=-2pi -frac{3pi }{4}=-frac{11pi }{4}.$

Ответ: а) $displaystyle x=pm frac{3pi }{4}+2pi n, nin Z.$
б) $displaystyle -frac{11pi }{4}.$

3. а) Решите уравнение: $displaystyle 8sin^{2}x-2sqrt{3}cosleft ( frac{pi }{2}-x right )-9=0.$
б) Найдите все корни этого уравнения, принадлежащие отрезку $displaystyle left [ -frac{5pi }{2}; -pi right ].$

Решение:

а) Чтобы упростить уравнение $displaystyle 8sin^{2}x-2sqrt{3}cosleft ( frac{pi }{2}-x right )-9=0,$ применяем формулу приведения.

Так как $displaystyle cosleft ( frac{pi }{2}-x right )=sinx,$ получим:

$displaystyle 8sin^{2}x-2sqrt{3}sinx-9=0.$

Сделаем замену: sinx=t. Получим квадратное уравнение:

$8t^{2}-2sqrt{3}t-9=0;$

$displaystyle frac{D}{4}=3+72=75.$

$displaystyle t_1={frac{3sqrt{3}}{4}}; t_{2}=-frac{sqrt{3}}{2}.$

Сделаем обратную замену.

1) $displaystyle sinx={frac{3sqrt{3}}{4}}$ — нет решений, т. к. $displaystyle {frac{3sqrt{3}}{4}}textgreater 1.$

2) $displaystyle sinx=-frac{sqrt{3}}{2}Leftrightarrow left[begin{array}{c}displaystyle x=-frac{pi }{3}+2pi k, kin Z\displaystyle x=-frac{2pi }{3}+2pi k\end{array}right. .$

б) Найдем корни уравнения, принадлежащие отрезку $displaystyle left [ -frac{5pi }{2}; -pi right ]$ , с помощью двойного неравенства.

Для серии решений $displaystyle x=-frac{pi }{3}+2pi k, kin Z$ получим:

$displaystyle -frac{5pi }{2}leq -frac{pi }{3}+2pi kleq -pi;$

$displaystyle -frac{13}{12}leq kleq -frac{2}{6}.$

Так как kin Z, то $displaystyle k=-1; x=-frac{7pi }{3}.$

Для серии решений $displaystyle x=-frac{2pi }{3}+2pi k$ получим:

$displaystyle -frac{5pi }{2}leq -frac{2pi }{3}+2pi kleq -pi;$ отсюда

$displaystyle -frac{11}{12}leq kleq -frac{1}{6}.$

У этого неравенства нет целых решенией, и значит, из второй серии ни одна точка в указанный отрезок не входит.

Ответ: а) $displaystyle -frac{pi }{3}+2pi k; -frac{2pi }{3}+2pi k, kin Z.$
б) $displaystyle -frac{7pi }{3}.$

к оглавлению ▴

Разложение на множители

Во многих случаях уравнение удаётся представить в таком виде, что в левой части стоит произведение двух или нескольких множителей, а в правой части — ноль. Произведение двух или нескольких множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю. Сложное уравнение, таким образом, распадается в совокупность более простых.

4. а) Решите уравнение:
б) Найдите все корни уравнения на отрезке

Решение:

а) Применяем формулу синуса двойного угла:

Ни в коем случае не сокращайте на косинус! Ведь может случиться, что cos x обратится в нуль, и мы потеряем целую серию решений. Переносим всё в одну часть, и общий множитель выносим за скобки:

Полученное уравнение равносильно совокупности двух уравнений: cosx = 0 и 2sinx — 1 = 0.

Получим:

$left[begin{array}{c}cosx=0\displaystyle sinx=frac{1}{2}\end{array}right. Leftrightarrow left[begin{array}{c}displaystyle x=frac{pi }{2}+2pi n, nin Z\\displaystyle x=frac{pi }{6}+2pi n\\displaystyle x=frac{5pi }{6}+2pi n\end{array}right. .$

Все эти три серии решений являются ответом в части (а).

б) Отметим отрезок и найденные серии решений на единичной окружности.

Видим, что данному отрезку принадлежат точки $displaystyle x_{1}=frac{pi }{6}; x_{2}=frac{5pi }{6}.$

Ответ: а) $displaystyle frac{pi }{6}+2pi n; frac{pi }{2}+2pi n; frac{5pi }{6}+2pi n, nin Z.$
б) $displaystyle frac{pi }{6}; frac{5pi }{6}.$

5. а) Решите уравнение:
б) Найдите все корни уравнения на отрезке $displaystyle left [ -frac{pi }{2}; pi right ].$

Решение:

Применим формулу суммы синусов:

Дальше действуем так же, как и в предыдущей задаче:

Решаем уравнение sin5x=0 :

$displaystyle x=frac{pi n}{5}, nin Z.$

(1)

Решаем уравнение :

(2)

Ну что, перечисляем обе серии (1) и (2) в ответе через запятую? Нет! Серия (2) является в данном случае частью серии (1). Действительно, если в формуле (1) число n кратно 5, то мы получаем все решения серии (2).

Поэтому ответ в пункте (а): $displaystyle x=frac{pi n}{5}, nin Z.$

б) Найдем корни уравнения, принадлежащие отрезку $displaystyle left [ -frac{pi }{2}; pi right ],$ с помощью двойного неравенства:

$displaystyle -frac{pi }{2}leq frac{pi n}{5}leq pi;$

$displaystyle -frac{5}{2}leq {n}leq 5.$

Этот промежуток содержит 8 целых чисел: -2; -1; 0; 1; 2; 3; 4; 5.

Для каждого из этих n найдем x. Получим 8 решений на данном промежутке:

$displaystyle -frac{2pi }{5}; -frac{pi }{5}; 0; frac{pi }{5}; frac{2pi }{5}; frac{3pi }{5}; frac{4pi }{5}; pi .$

Ответ: а) $displaystyle frac{pi n}{5}, nin Z.$
б) $displaystyle -frac{2pi }{5}; -frac{pi }{5}; 0; frac{pi }{5}; frac{2pi }{5}; frac{3pi }{5}; frac{4pi }{5}; pi .$

6. В следующей задаче также применяется метод разложения на множители. Но это заметно не сразу.

а) Решите уравнение: $sin^{2}2x+sin^{2}3x=1.$
б) Найдите все корни уравнения на отрезке $displaystyle left [ 0; frac{pi }{2} right ].$

Решение:

Используем формулу понижения степени: $displaystyle sin^{2}alpha =frac{1-cos2alpha }{2}.$

Получаем:

$displaystyle frac{1-cos4x}{2}+frac{1-cos6x}{2}=1;$

Применяем формулу суммы косинусов: $displaystyle cosalpha +cosbeta =2cosfrac{alpha +beta }{2}cdot cosfrac{alpha -beta }{2}.$

Получаем:

Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом имеет смысл. Уравнение равносильно совокупности:

$left[begin{array}{c}cos5x=0\cosx=0\end{array}right.Leftrightarrow left[begin{array}{c}displaystyle 5x=frac{pi }{2}+pi n, nin Z\\displaystyle x=frac{pi }{2}+pi k, kin Z\end{array}right. Leftrightarrow left[begin{array}{c}displaystyle x=frac{pi }{10}+frac{pi n}{5}, nin Z\\displaystyle x=frac{pi }{2}+pi k, kin Z\end{array}right. .$

б) Найдем корни уравнения, принадлежащие отрезку $displaystyle left [ 0; frac{pi }{2} right ],$ с помощью двойного неравенства:

1) $displaystyle 0leq frac{pi }{10}+frac{pi n}{5}leq frac{pi }{2}.$

Решив неравенство, получим:

Так как n ∈ Z, получим для n целые значения: 0, 1, 2.

Им соответствуют решения: $displaystyle frac{pi }{10}; frac{3pi }{10}; frac{pi }{2}.$

2) Из серии решений $displaystyle frac{pi }{2}+pi k, kin Z$ на указанном отрезке лежит только корень $displaystyle x=frac{pi }{2}.$ Но он уже входит в первую серию решений.

Можно также заметить, что вся вторая серия решений является подмножеством первой.

Ответ: а) $displaystyle frac{pi }{10}+frac{pi n}{5}, nin Z.$
б) $displaystyle frac{pi }{10}; frac{3pi }{10}; frac{pi }{2}.$

к оглавлению ▴

Однородные уравнения

7. а) Решите уравнение: $sin^{2}x+2sinxcosx-3cos^{2}x=0.$
б) Найдите все корни уравнения на отрезке $displaystyle left [ -frac{3pi }{2}; frac{pi }{2} right ].$

Решение:

Такое уравнение называется однородным.

Степень каждого слагаемого в левой части равна двум. Точно так же, как в обычном многочлене $a^{2}+2ab-3b^{2},$ степень каждого слагаемого равна двум. Мы помним, что степень одночлена — это сумма степеней входящих в него сомножителей.

Для однородных уравнений существует стандартный приём решения — деление обеих его частей на $cos^{2}x$ .

Возможность этого деления, однако, должна быть обоснована: а что, если косинус равен нулю?

Следующий абзац предлагаем выучить наизусть и всегда прописывать его при решении однородных уравнений.

Предположим, что cosx = 0. Тогда в силу уравнения и sinx = 0, что противоречит основному тригонометрическому тождеству. Следовательно, любое решение данного уравнения удовлетворяет условию cosx 0, и мы можем поделить обе его части на $cos^{2}x$ .

В результате деления приходим к равносильному квадратному уравнению относительно тангенса: $tg^{2}x+2tgx-3=0.$

Сделаем замену: tgx=t, получим:

$left[begin{array}{c}tgx=-3 \tgx=1\end{array}right. Leftrightarrow left[begin{array}{c}x=-arctg3+pi k, kin Z \displaystyle x=frac{pi }{4}+pi k, kin Z\end{array}right..$

б) Отметим отрезок $displaystyle left [ -frac{3pi }{2}; frac{pi }{2} right ]$ и найденные серии решений на единичной окружности.

О том, как отметить на единичной окружности точки из первой серии решений, то есть арктангенс минус трех, читайте здесь: Простейшие тригонометрические уравнения, часть 2.

Видим, что данному отрезку принадлежат точки:

$x_{1}=-pi -arctg3;$

$displaystyle x_{2}=-pi +frac{pi }{4}=-frac{3pi }{4};$

$x_{3}= -arctg3;$

$displaystyle x_{4}=frac{pi }{4}.$

Ответ: а) $displaystyle -arctg3+pi k; frac{pi }{4}+pi k, kin Z.$
б) $-pi -arctg3; displaystyle -frac{3pi }{4}; -arctg3; frac{pi }{4}.$

8. а) Решите уравнение: $10sin^{2}x+5sinxcosx+cos^{2}x=3.$
б) Найдите все корни уравнения на отрезке $displaystyle left [ 0; frac{pi }{2} right ].$

Если бы в правой части стоял нуль, уравнение было бы однородным. Мы поправим ситуацию изящным приёмом: заменим число 3 на выражение $3(sin^{2}x+cos^{2}x):$

$10sin^{2}x+5sinxcosx+cos^{2}x=3(sin^{2}x+cos^{2}x);$

$7sin^{2}x+5sinxcosx-2cos^{2}x=0.$

Получили однородное уравнение второй степени.

Так как не существует такой точки на единичной окружности, в которой одновременно синус и косинус равнялись бы нулю, мы разделим обе части уравнения на $cos^{2}xneq 0$ .

Получим: $7tg^{2}x+5tgx-2=0.$

Выполним замену: tgx = y, получим:

$7y^{2}x+5y-2=0.$

$displaystyle y_{1,2}=frac{-5pm 9}{14};left[begin{array}{c}y=-1\displaystyle y=frac{2}{7}\end{array}right. .$

Обратная замена: $left[begin{array}{c}tgx=-1\displaystyle tgx=frac{2}{7}\end{array}right. Leftrightarrow left[begin{array}{c}displaystyle x=-frac{pi }{4}+pi k, kin Z\displaystyle x=arctgfrac{2}{7}+pi k, kin Z\end{array}right. .$

Ответом в пункте (а) являются две серии решений.

б) Найдем корни уравнения, принадлежащие отрезку $displaystyle left [ 0; frac{pi }{2} right ],$ с помощью единичной окружности. Для этого отметим на ней данный отрезок и найденные серии решений.

Видим, что данному отрезку принадлежит только точка $displaystyle x_1=arctgfrac{2}{7}.$

Ответ: а) $displaystyle -frac{pi }{4}+pi k; arctgfrac{2}{7}+pi k, kin Z.$
б) $displaystyle arctgfrac{2}{7}.$

к оглавлению ▴

Введение дополнительного угла

Этот метод применяется для уравнений вида acosx + bsinx=c. Он присутствует в школьных учебниках. Правда, в них рассматриваются только частные случаи — когда числа a и b являются значениями синуса и косинуса углов в 30°, 45° или 60°.

9. а) Решим уравнение:
б) Найдите все корни уравнения на отрезке

Решение:

Делим обе части на 2:

$displaystyle frac{sqrt{3}}{2}sinx+frac{1}{2}cosx=1.$

Замечаем, что $displaystyle frac{sqrt{3}}{2}=cosfrac{pi }{6}; frac{1}{2}=sinfrac{pi }{6}:$

$displaystyle cosfrac{pi }{6}sinx+sinfrac{pi }{6}cosx=1.$

В левой части получили синус суммы:

$displaystyle sinleft ( x+frac{pi }{6} right )=1,$ отсюда $displaystyle x+frac{pi }{6}=frac{pi }{2}; x=frac{pi }{3}+2pi n, nin Z.$

б) Отметим на единичной окружности отрезок и найденные серии решений.

Обратите внимание, что в этой задаче отрезок больше, чем полный круг. Как нам поступить? Один из способов – нарисовать рядом две окружности.

Видим, что данному отрезку принадлежат точки: $displaystyle x_{1}=frac{pi }{3}; x_{2}=2pi +frac{pi }{3}=frac{7pi }{3}.$

Ответ: а) $displaystyle frac{pi }{3}+2pi n, nin Z.$
б) $displaystyle frac{pi }{3}; frac{7pi }{3}.$

Другой пример.

10. а) Решите уравнение:
б) Найдите все корни уравнения на отрезке

Решение:

Делим обе части на

$displaystyle frac{1}{sqrt{2}}cosx+frac{1}{sqrt{2}}sinx=frac{1}{sqrt{2}}.$

Сделаем теперь для разнообразия в левой части косинус разности:

$displaystyle cosfrac{pi }{4}cosx+sinfrac{pi }{4}sinx=frac{1}{sqrt{2}};$

$displaystyle cosleft ( x-frac{pi }{4} right )=frac{1}{sqrt{2}};$

$displaystyle x-frac{pi }{4}=pm frac{pi }{4}+2pi n;$

$displaystyle x_{1}=frac{pi }{2}+2pi n; x_{2}=2pi n, nin Z.$

б) Найдем корни уравнения, принадлежащие отрезку с помощью единичной окружности. Отметим на ней данный отрезок и найденные серии решений.

Видим, что данному отрезку принадлежат точки 0 и $displaystyle frac{pi }{2}.$

Ответ: а) $displaystyle frac{pi }{2}+2pi n; 2pi n, nin Z.$
б) $displaystyle frac{pi }{2}.$

Покажем, как применяется метод введения дополнительного угла в общем случае.

Рассмотрим уравнение

Делим обе части на $sqrt{a^{2}+b^{2}}:$

$displaystyle frac{a}{sqrt{a^{2}+b^{2}}}cosx+frac{b}{sqrt{a^{2}+b^{2}}}sinx=frac{c}{sqrt{a^{2}+b^{2}}}.$

(4)

Для чего мы выполнили это деление? Всё дело в получившихся коэффициентах при косинусе и синусе. Легко видеть, что сумма их квадратов равна единице:

$displaystyle left ( frac{a}{sqrt{a^{2}+b^{2}}} right )^{2}+left ( frac{b}{sqrt{a^{2}+b^{2}}} right )^{2}=1.$

Это означает, что данные коэффициенты сами являются косинусом и синусом некоторого угла varphi :

$displaystyle frac{a}{sqrt{a^{2}+b^{2}}}=cosalpha , frac{b}{sqrt{a^{2}+b^{2}}}=sinalpha.$

Соотношение (4) тогда приобретает вид:

$displaystyle cosalpha cosx+sinalpha sinx=frac{c}{sqrt{a^{2}+b^{2}}}$

или

$displaystyle cos(x-alpha )=frac{c}{sqrt{a^{2}+b^{2}}}.$

Исходное уравнение сведено к простейшему. Теперь понятно, почему рассматриваемый метод называется введением дополнительного угла. Этим дополнительным углом как раз и является угол alpha .

к оглавлению ▴

Универсальная подстановка

Запомним две важные формулы:

Их ценность в том, что они позволяют выразить синус и косинус через одну и ту же функцию — тангенс половинного угла. Именно поэтому они получили название универсальной тригонометрической подстановки.

Единственная неприятность, о которой не надо забывать: правые части этих формул не определены при . Поэтому если применение универсальной подстановки приводит к сужению ОДЗ, то данную серию нужно проверить непосредственно.

11. а) Решите уравнение:
б) Найдите все корни уравнения на отрезке

Решение:

Выражаем , используя универсальную тригонометрическую подстановку:

Делаем замену :

Получаем кубическое уравнение:

Оно имеет единственный корень .

Стало быть, , откуда .

Сужения ОДЗ в данном случае не было, так как уравнение с самого начала содержало .

б) Найдем корни уравнения, принадлежащие отрезку с помощью двойного неравенства:

$displaystyle 0leq frac{pi }{4}+pi nleq pi , nin Z;$

$displaystyle -frac{1}{4}leq nleq frac{3}{4}.$

Получим, что $displaystyle n=0; x=frac{pi }{4}.$

Ответ: а) $displaystyle frac{pi }{4}+pi n, nin Z.$
б) $displaystyle frac{pi }{4}.$

Универсальная тригонометрическая подстановка может также пригодиться при решении задач по планиметрии из второй части ЕГЭ. Поэтому формулы лучше выучить.

к оглавлению ▴

Учет ОДЗ уравнения

12. а) Рассмотрим уравнение:
б) Найдите все корни уравнения на отрезке $displaystyle left [ -frac{pi }{2}; frac{3pi }{2} right ].$

Решение:

Перепишем уравнение в виде, пригодном для возведения в квадрат:

Тогда наше уравнение равносильно системе:

Решаем уравнение системы:

Второе уравнение данной совокупности не имеет решений, а первое даёт две серии:

Теперь нужно произвести отбор решений в соответствии с неравенством . Серия не удовлетворяет этому неравенству, а серия удовлетворяет ему. Следовательно, решением исходного уравнения служит только серия .

Ответ в пункте (а): .

б) Найдем корни уравнения, принадлежащие отрезку $displaystyle left [ -frac{pi }{2}; frac{3pi }{2} right ],$ с помощью двойного неравенства:

$displaystyle frac{-pi }{2}leq -frac{pi }{3}+2pi nleq frac{3pi }{2};$

$displaystyle -frac{1}{12}leq nleq frac{11}{12}.$

Неравенство имеет единственное целое решение n=0.

Тогда $displaystyle x=-frac{pi }{3}.$

Ответ: а) $displaystyle -frac{pi }{3}+2pi n, nin Z.$
б) $displaystyle -frac{pi }{3}.$

Мы рассмотрели основные методы решения тригонометрических уравнений, которые применяются в задаче 12 ЕГЭ.

Где же еще нам могут встретиться тригонометрические уравнения? Конечно, в задачах с параметрами. Или на олимпиадах по математике. Сейчас мы увидим еще несколько полезных приемов решения.

к оглавлению ▴

Метод оценки

В некоторых уравнениях на помощь приходят оценки .

13. Рассмотрим уравнение:

Так как оба синуса не превосходят единицы, данное равенство может быть выполнено лишь в том случае, когда они равны единице одновременно:

Таким образом, должны одновременно выполняться следующие равенства:

Обратите внимание, что сейчас речь идёт о пересечении множества решений (а не об их объединении, как это было в случае разложения на множители). Нам ещё предстоит понять, какие значения x удовлетворяют обоим равенствам. Имеем:

Умножаем обе части на 90 и сокращаем на π:

;

Правая часть, как видим, должна делиться на 5. Число n при делении на 5 может давать остатки от 0 до 4; иначе говоря, число n может иметь один из следующих пяти видов: 5n, 5m + 1, 5m + 2, 5m + 3 и 5m + 4, где. Для того, чтобы 9n+ 1 делилось на 5, годится лишь n = 5m + 1.

Искать k, в принципе, уже не нужно. Сразу находим x:

Ответ:

14. Рассмотрим уравнение:

Ясно, что данное равенство может выполняться лишь в двух случаях: когда оба синуса одновременно равны 1 или −1. Действуя так, мы должны были бы поочерёдно рассмотреть две системы уравнений.

Лучше поступить по-другому: умножим обе части на 2 и преобразуем левую часть в разность косинусов:

;

Тем самым мы сокращаем работу вдвое, получая лишь одну систему:

Имеем:

Ищем пересечение:

Умножаем на 21 и сокращаем на π:

Данное равенство невозможно, так как в левой части стоит чётное число, а в правой — нечётное.

Ответ: решений нет.

Это был тренировочный пример. А в задачах ЕГЭ решения есть всегда.

Посмотрите, как применяется метод оценки в задачах с параметрами.

15. Страшное с виду уравнение также решается методом оценок.

В самом деле, из неравенства следует, что .

Следовательно, , причём равенство возможно в том и только в том случае, когда

$left{begin{matrix}sin^{5}x=sin^{2}x\cos^{8}x=cos^{2}x\end{matrix}right. .$

Остаётся решить полученную систему. Это не сложно.

Перенесем в левую часть и вынесем общий множитель за скобки , получим:

$left{begin{matrix}sin^{2}x(sin^{3}x-1)=0 \cos^{2}x(cos^{6}x-1)=0 \end{matrix}right. .$

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом имеет смысл.

Каждое уравнение равносильно совокупности:

$left{begin{matrix}left[begin{array}{c}sinx=0\sinx=1\end{array}right. \left[begin{array}{c}cosx=0\cosx=1\cosx=-1\end{array}right. \end{matrix}right. .$

Это значит, что синус угла х равен нулю, а его косинус равен 0, 1 или -1.

Или синус угла х равен 1, а косинус этого угла равен 0, 1 или -1.

Такие углы легко найти на тригонометрическом круге. Найденные серии решений запишем в ответ.

Ответ: $displaystyle 2pi n; frac{pi }{2}+2pi n; pi +2pi n, nin Z.$

к оглавлению ▴

Тригонометрические уравнения повышенной сложности.
Приемы решения

16. Рассмотрим такое уравнение:

Сделаем замену .

Как выразить через t? Имеем:

откуда . Получаем:

$t^{2}-1=t+1;$

$t^{2}-t-2=0;$

$t_{1}=-1; t_{2}=2.$

$left[begin{array}{c}cosx+sinx=-1\cosx+sinx=2\end{array}right. .$

Начнем со второго уравнения.

Так как и то их сумма может быть равна 2, только оба слагаемых равны 1. Но на единичной окружности не существует точки, в которой одновременно синус и косинус равен единице. Значит, второе уравнение корней не имеет.

Решим первое уравнение методом введения дополнительного угла.

Для этого разделим обе части уравнения на sqrt{2} и получим:

$displaystyle cosx+sinx=-1Leftrightarrow frac{1}{sqrt{2}}cosx+frac{1}{sqrt{2}}sinx=-frac{1}{sqrt{2}}Leftrightarrow$

$displaystyle Leftrightarrow cosxcdot cosfrac{pi }{4}+sinxcdot sinfrac{pi }{4}=-frac{1}{sqrt{2}}Leftrightarrow cosleft ( x+frac{pi }{4} right )=-frac{1}{sqrt{2}}Leftrightarrow$

$displaystyle Leftrightarrow x+frac{pi }{4}=pm frac{3pi }{4}+2pi k, kin Z;$

$left[begin{array}{c}displaystyle x=frac{pi }{2}+2pi k, kin Z\x=-pi +2pi k, kin Z\end{array}right. .$

Ответ: $displaystyle frac{pi }{2}+2pi k; -pi +2pi k, kin Z.$

17. Помним формулы косинуса и синуса тройного угла:

Вот, например, уравнение:

Оно сводится к уравнению относительно :

$left[begin{array}{c}sinx=0\4sin^{2}x+4sinx-3=0\end{array}right. .$

Решим второе уравнение с помощью замены sinx = t.

Получим: $displaystyle 4t^{2}+4t-3=0; D=16+48=64; t=-frac{3}{2}$ или $displaystyle t=frac{1}{2}.$

Обратная замена:

$left[begin{array}{c}displaystyle sinx=-frac{3}{2}\\displaystyle sinx=frac{1}{2}\end{array}right. Leftrightarrow left[begin{array}{c}xin O \\displaystyle x=frac{pi }{6}+2pi n, nin Z\\displaystyle x=frac{5pi }{6}+2pi n, nin Z\end{array}right. .$

А решением первого уравнения sinx = 0 являются числа вида

Ответ: $displaystyle pi k, kin Z; frac{pi }{6}+2pi n; frac{5pi }{6}+2pi n, nin Z.$

Интересно, что формулы синуса и косинуса тройного угла также могут пригодиться вам в решении задач по планиметрии из второй части ЕГЭ.

18. Как бороться с суммой четвёртых степеней синуса и косинуса?

Рассмотрим уравнение:

Выделяем полный квадрат!

;

19. А как быть с суммой шестых степеней?

Рассмотрим такое уравнение:

Раскладываем левую часть на множители как сумму кубов: .

Получим:

;

С суммой четвёртых степеней вы уже умеете обращаться.

Мы рассмотрели основные методы решения тригонометрических уравнений. Знать их нужно обязательно, это — необходимая база.

В более сложных и нестандартных задачах нужно ещё догадаться, как использовать те или иные методы. Это приходит только с опытом. Именно этому мы и учим на наших занятиях.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Тригонометрические уравнения» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Показательные, логарифмические, тригонометрические уравнения

(blacktriangleright) На ОДЗ верны следующие формулы:

[large{begin{array}{|ll|}
hline a^0=1 &a^1=a\
a^{nm}=(a^n)^m &a^ncdot a^m=a^{n+m}\
dfrac{a^n}{a^m}=a^{n-m}&a^{-n}=dfrac{1}{a^n}\
a^ncdot b^n=(acdot b)^n &\
a^{frac{k}{r}}=sqrt[r]{a^k} qquad qquad qquad qquad&
dfrac{a^n}{b^n}=left(dfrac{a}{b}right)^n\&\
a,b>0, a,bne 1, kin mathbb{Z},& rinmathbb{N}, m,ninmathbb{R}\
hline
end{array}}]

[large{begin{array}{|lcl|}
hline log_a1=0& qquad & log_aa=1\
&&\
log_{a^n}{b^m}=frac mnlog_{|a|}{|b|}&& a^{log_bc}=c^{log_ba}\
&&\
log_a{bc}=log_a{|b|}+log_a{|c|}&& log_a{dfrac bc}=log_a{|b|}-log_a{|c|}\
&&\
log_abcdot log_bc=log_ac & Longleftrightarrow & log_bc=dfrac{log_ac}{log_ab}\
&&\
log_abcdot log_ba=1 & Longleftrightarrow & log_ab=dfrac1{log_ba}\
&&\
hline
end{array}}]

Задание
1

#3823

Уровень задания: Равен ЕГЭ

а) Решите уравнение [(2cos^2x+11cos x+5)cdot log_{18}(sin
x)=0]

б) Найдите все корни этого уравнения, принадлежащие промежутку ([0;pi].)

а) Произведение равно нулю тогда и только тогда, когда один из множителей равен нулю, а другие при этом не теряют смысла: [left[begin{gathered}begin{aligned}
&2cos^2x+11cos x+5=0\[1ex]
&log_{18}(sin
x)=0end{aligned}end{gathered}right.quadLeftrightarrowquad
begin{cases}
left[begin{gathered}begin{aligned}
&2cos^2x+11cos x+5=0\[1ex]
&sin x=18^0end{aligned}end{gathered}right.\
sin x>0end{cases}] Назовем (sin x>0) ОДЗ.

1) Рассмотрим первое уравнение. Заменой (cos x=t), (-1leqslant
tleqslant 1), данное уравнение сводится к квадратному: (2t^2+11t+5=0). Корнями будут (t_1=-frac12) и (t_2=-5). Видим, что корень (t_2) не подходит. Таким образом: [cos x=-dfrac12quadLeftrightarrowquad x=pm dfrac{2pi}3+2pi n,
ninmathbb{Z}] Заметим, что углы (x=dfrac{2pi}3+2pi n) находятся во второй четверти, где (sin x>0), следовательно, подходят по ОДЗ. Углы (x=-dfrac{2pi}3+2pi n) находятся в третьей четверти, где (sin x
<0), следовательно, не подходят по ОДЗ. Итог: [x=dfrac{2pi}3+2pi n,
ninmathbb{Z}]

2) Рассмотрим второе уравнение: (sin x=1) (подходит под ОДЗ). Решением будут [x=dfrac{pi}2+2pi k, kinmathbb{Z}]

б) Отберем корни.

1) (0leqslant dfrac{2pi}3+2pi nleqslant pi
quadRightarrowquad n=0 quadRightarrowquad
x=dfrac{2pi}3)

2) (0leqslant dfrac{pi}2+2pi kleqslant pi
quadRightarrowquad k=0quadRightarrowquad x=dfrac{pi}2)

Ответ:

а) (dfrac{2pi}3+2pi n, dfrac{pi}2+2pi k; k, ninmathbb{Z})

б) (dfrac{pi}2; dfrac{2pi}3)

Задание
2

#3821

Уровень задания: Равен ЕГЭ

а) Решите уравнение [{large{dfrac{4^{sin 2x}-2^{2sqrt3sin
x}}{sqrt{7sin x}}=0}}]

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[-dfrac{13pi}2; -5pi right].)

а) Дробь равна нулю тогда и только тогда, когда числитель равен нулю, а знаменатель при этом не равен нулю: [begin{cases}
4^{sin 2x}-2^{2sqrt3sin x}=0\[1ex]
sqrt{7sin x}ne 0end{cases}] Так как ОДЗ выражения (sqrt{7sin
x}) — это (sin xgeqslant 0), но (sqrt{7sin x}ne 0), то есть (sin xne 0), то данная система равносильна: [begin{cases}
4^{sin 2x}-2^{2sqrt3sin x}=0\[1ex]
sin x>0end{cases}] Назовем неравенство ОДЗ.
Рассмотрим уравнение системы: [2^{2sin 2x}=2^{2sqrt3sin x}quadLeftrightarrowquad
2cdot 2sin xcos x=2sqrt3sin xquadLeftrightarrowquad sin
x(2cos x-sqrt3)=0] Следовательно:

1) (sin x=0). Данное уравнение не удовлетворяет ОДЗ (sin x>0).

или

2) (cos x=dfrac{sqrt3}2), что равносильно (x=dfrac{pi}6+2pi n) или (x=-dfrac{pi}6+2pi m), (n,minmathbb{Z}).
Так как по ОДЗ (sin x>0), то серия корней (x=-dfrac{pi}6+2pi m) нам не подходит, так как эти углы находятся в четвертой четверти, где (sin x<0).

Следовательно, ответом будут: (x=dfrac{pi}6+2pi n), (ninmathbb{Z}).

б) Отберем корни.

(-dfrac{13pi}2leqslant dfrac{pi}6+2pi nleqslant
-5piquadLeftrightarrowquad -dfrac{10}3leqslant nleqslant
-dfrac{31}{12}quadRightarrowquad n=-3quadRightarrowquad
x=-dfrac{35pi}6)

Ответ:

а) (dfrac{pi}6+2pi n), (ninmathbb{Z})

б) (-dfrac{35pi}6)

Задание
3

#3822

Уровень задания: Равен ЕГЭ

а) Решите уравнение [{large{dfrac{log^2_2(sin x)+log_2(sin
x)}{2cos x-sqrt3}=0}}]

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[dfrac{pi}2; 2piright].)

а) Дробь равна нулю тогда и только тогда, когда числитель равен нулю, а знаменатель при этом не равен нулю: [begin{cases}
log^2_2(sin x)+log_2(sin
x)=0\[1ex]
2cos x-sqrt3ne 0end{cases}] Неравенство (cos xne
dfrac{sqrt3}2) назовем ОДЗ.
Рассмотрим уравнение системы: (log^2_2(sin x)+log_2(sin x)=0).
Сделаем замену (log_2(sin x)=t). Тогда уравнение примет вид [t^2+t=0quadLeftrightarrowquad t(t+1)=0quadLeftrightarrowquad
left[begin{gathered}begin{aligned} &t=0\
&t=-1end{aligned}end{gathered}right.] Следовательно, [left[begin{gathered}begin{aligned}
&log_2(sin x)=0\
&log_2(sin x)=-1
end{aligned}end{gathered}right.quadLeftrightarrowquad
left[begin{gathered}begin{aligned}
&sin x=2^0=1\[1ex]
&sin x=2^{-1}=dfrac12
end{aligned}end{gathered}right.quadLeftrightarrowquad
left[begin{gathered}begin{aligned}
&x_1=dfrac{pi}2+2pi n\[2ex]
&x_2=dfrac{pi}6+2pi m\[2ex]
&x_3=dfrac{5pi}6+2pi k
end{aligned}end{gathered}right.] (n,m,kinmathbb{Z}).
Вернемся к ОДЗ. По ОДЗ (xne dfrac{pi}6+2pi l) и (xne
-dfrac{pi}6+2pi p), (l,pinmathbb{Z}).
Таким образом мы видим, что серия корней (x_2) не подходит под ОДЗ, значит, не будет входить в ответ.
Ответом будут являться серии (x_1) и (x_3).

б) Отберем корни.

1) (dfrac{pi}2leqslant dfrac{pi}2+2pi nleqslant 2pi
quadLeftrightarrowquad 0leqslant nleqslant
dfrac34quadRightarrowquad n=0quadRightarrowquad
x=dfrac{pi}2)

2) (dfrac{pi}2leqslant dfrac{5pi}6+2pi kleqslant 2pi
quadLeftrightarrowquad -dfrac16leqslant kleqslant
dfrac7{12}quadRightarrowquad k=0quadRightarrowquad
x=dfrac{5pi}6)

Ответ:

а) (dfrac{pi}2+2pi n, dfrac{5pi}6+2pi k), (n,kinmathbb{Z})

б) (dfrac{pi}2; dfrac{5pi}6)

Задание
4

#3971

Уровень задания: Равен ЕГЭ

а) Решите уравнение [(10cos^2x-7cos x-6)cdot log_{8}(-sin
x)=0]

б) Найдите все корни этого уравнения, принадлежащие отрезку (left[2pi;dfrac{7pi}2right]).

а) Произведение равно нулю тогда и только тогда, когда один из множителей равен нулю, а другие при этом не теряют смысла: [begin{cases}
left[begin{gathered}begin{aligned}
&10cos^2x-7cos x-6=0\
&log_{8}(-sin x)=0
end{aligned}end{gathered}right. \
-sin x>0end{cases} quadLeftrightarrowquad
begin{cases}
left[begin{gathered}begin{aligned}
&10cos^2x-7cos x-6=0\
&sin x=-1
end{aligned}end{gathered}right. \
sin x<0end{cases}] Назовем (sin x<0) – ОДЗ.

1) Рассмотрим первое уравнение. Заменой (cos x=t), (-1leqslant
tleqslant 1), данное уравнение сводится к квадратному (10t^2-7t-6=0). Корнями будут (t=-frac12) и (t=frac65). Видим, что второй корень не подходит. Таким образом: [cos x=-dfrac12quadLeftrightarrowquad
x=pm dfrac{2pi}3+2pi n, ninmathbb{Z}] Заметим, что углы (x=dfrac{2pi}3+2pi n), (ninmathbb{Z}) находятся во второй четверти, где (sin x>0), следовательно, не подходят по ОДЗ. Углы (x=-dfrac{2pi}3+2pi n), (ninmathbb{Z}) находятся в третьей четверти, где (sin x<0), следовательно, подходят по ОДЗ. Итог: [x=-dfrac{2pi}3+2pi n, ninmathbb{Z}]

2) Рассмотрим второе уравнение: (sin x=-1) (подходит по ОДЗ). Решением будут [x=-dfrac{pi}2+2pi k, kinmathbb{Z}]

б) Отберем корни.

(2pileqslant -dfrac{2pi}3+2pi nleqslant
dfrac{7pi}2quadLeftrightarrowquad dfrac43leqslant nleqslant
dfrac{25}{12}quadRightarrowquad
n=2quadRightarrowquad x=dfrac{10pi}3)

(2pi leqslant -dfrac{pi}2+2pi kleqslant
dfrac{7pi}2quadLeftrightarrowquad dfrac54leqslant kleqslant
2quadRightarrowquad k=2quadRightarrowquad x=dfrac{7pi}2)

Ответ:

а) (-dfrac{2pi}3+2pi n, -dfrac{pi}2+2pi k, n,kinmathbb{Z})

б) (dfrac{10pi}3; dfrac{7pi}2)

Задание
5

#3972

Уровень задания: Равен ЕГЭ

а) Решите уравнение [dfrac{log^2_2(sin x)+log_2(sin x)}{2cos
x+sqrt3}=0]

б) Найдите все корни этого уравнения, принадлежащие отрезку (left[0;dfrac{3pi}2right]).

а) ОДЗ уравнения: (sin x>0) и (cos xne -frac{sqrt3}2).
Решим уравнение на ОДЗ: [dfrac{log_2(sin x)cdot left(log_2(sin x)+1right)}{2cos x+sqrt3}=0
quadRightarrowquad left[begin{gathered}begin{aligned}
&log_2(sin x)=0\ &log_2(sin x)=-1
end{aligned}end{gathered}right.
quadRightarrowquad left[begin{gathered}begin{aligned} &sin
x=1\[2ex]
&sin x=dfrac12
end{aligned}end{gathered}right.] Видим, что оба уравнения подходят под условие (sin x>0) из ОДЗ.
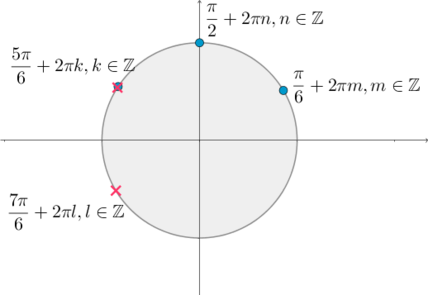
Таким образом, нам нужно отобрать корни, которые подходят под условие (cos xne -dfrac{sqrt3}2). Сделаем это по окружности:

Таким образом, видим, что отбрасывается только одна серия корней: (dfrac{5pi}6+2pi k). Итоговый ответ: [x= dfrac{pi}2+2pi n; dfrac{pi}6+2pi m; n,minmathbb{Z}]

б) Отберем корни.

(0leqslant dfrac{pi}2+2pi nleqslant
dfrac{3pi}2quadLeftrightarrowquad -dfrac14leqslant nleqslant
dfrac12quadRightarrowquad n=0quadRightarrowquad
x=dfrac{pi}2)

(0leqslant dfrac{pi}6+2pi mleqslant
dfrac{3pi}2quadLeftrightarrowquad -dfrac1{12}leqslant
mleqslant dfrac23quadRightarrowquad m=0quadRightarrowquad
x=dfrac{pi}6)

Ответ:

а) (dfrac{pi}2+2pi n, dfrac{pi}6+2pi m, n,minmathbb{Z})

б) (dfrac{pi}6; dfrac{pi}2)

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Шаг 1: решение тригонометрического уравнения

Синус двойного угла

Решение показательного уравнения

Решение тригонометрического уравнения

Вынесение за скобку общего множителя

Решение простейших тригонометрических уравнений

Отбор корней на отрезке

Хитрость: отмечаем корни на тригонометрическом круге

Замечание по поводу разложения на множители

Тригонометрические уравнения

Замена переменной и сведение к квадратному уравнению

Разложение на множители

Однородные уравнения

Введение дополнительного угла

Универсальная подстановка

Учет ОДЗ уравнения

Метод оценки

Тригонометрические уравнения повышенной сложности. Приемы решения

Показательные, логарифмические, тригонометрические уравнения

Тригонометрические уравнения повышенной сложности.
Приемы решения