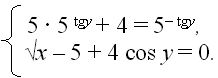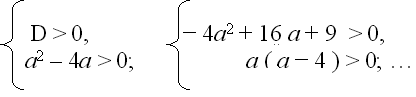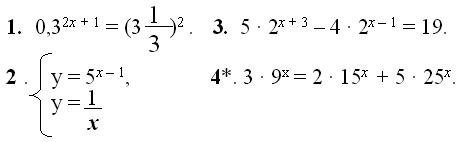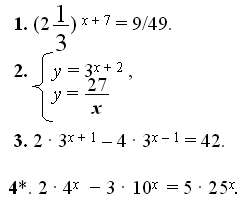УМК ПО ДИСЦИПЛИНЕ МАТЕМАТИКА для 1 курсаРешение показательных уравнений
ГБОУ СПО КК«АРМАВИРСКИЙ ЗООВЕТЕРИНАРНЫЙ ТЕХНИКУМ» комиссия естественно-математических наук
Решить уравнения
Решить уравнение
Дробь равна 0, если числитель равен 0, а знаменатель нет.
Получив корни, проверить входят ли они в ОДЗ. Исключим лишний корень
Решить уравнение
Простейшее тригонометрическое уравнение вида sinx=a
Решить уравнение
Решить уравнение
Ограничений на область допустимых значений у уравнения нет, так как подкоренное выражение имеет смысл при любом значении x (показательная функция y = 94-x положительна и не равна нулю)
Решить уравнение
Найдём ОДЗ уравнения, подкоренное выражение неотрицательно
Решений нет
Возведём обе части уравнения в квадрат
Данный корень удовлетворяет ОДЗ
Решить уравнение
Разделим каждое слагаемое на
x=1, x=2
Решить уравнение
Рассмотрим выражение
Решить уравнение
Так как t > 0, то -15 посторонний корень
Решить уравнение
Так как t>0, то -8 посторонний корень
ИсточникиАлгебра и начала анализа 3600 задач для школьников и поступающих в вузы Звавич Л.И., Шляпочкин Л.Я., Чинкина М.В.Соболь Б. В., Виноградова И. Ю., Рашидова Е. В. Пособие для подготовки к ЕГЭ и централизованному тестированию по математике. Изд. 3-е. – Р н/Д: «Феникс», 2003. – 352 с. http://www.math.md/school/praktikum/expr/exper.html http://webmath.exponenta.ru/s/c/algebra/content/chapter3/section1/paragraph9/theory.html
Показательные уравнения
11 класс
Деревянкина С. Е.
МКОУ Лисянская СОШ
«Без знания математики нельзя понять ни основ современной техники, ни того, как
ученые изучают природные и социальные явления»
Колмогоров. А.Н
Цели урока:
- Образовательные: обобщить методы решения показательных уравнений, отрабатывать умения решать показательные уравнения различными методами, применять полученные знания для решения заданий ЕГЭ различной сложности.
- Воспитательные: воспитывать трудолюбие, самостоятельность, умение принимать решение в нестандартной ситуации, способности к взаимосотрудничеству, самокритичности.
- Развивающие : развитие навыков анализа, систематизации информации, творческого мышления, самоконтроля и самооценки.
Проверка знаний:
- Какие уравнения называют показательными?
- Ответ: Уравнения вида аf(x)=ag(x), где a>0, a≠1.)
- Какому уравнению равносильно уравнение аf(x)=ag(x),
- Ответ: (f(x)=g(x)).
- Назовите основные методы решения показательных уравнений.
- Ответ:
- функционально-графический,
- уравнивания показателей,
- метод введения новой переменной,
- метод разложения на множители)
Решите уравнения
Решаем уравнения
Распределите уравнения по способам решения:
- 1) 3-1-х=( )2х+3;
- 2) 24х-1+24х-2-24х-3=160;
- 3) 22х+1-5·2х-88=0;
- 4) 32х-6·3х-27=0;
- 5) 7х+1-5·7х=98;
- 6) 2х·( )х = ;
- 7) 3х= 4-х;
-
9х+6х=22х+1;
- 9)( )х=х+3;
Методы решения уравнений
1.Уравнивание показателей:
3.Функционально- графический
2. Введение новой переменной
4.Разложение на множители.
9х+6х=22х+1;
Однородное уравнение
Проверка:
- 1) 3-1-х=( )2х+3;
- 2)24х-1+24х-2-24х-3=160;
- 3) 22х+1-5·2х-88=0;
- 4) 32х-6·3х-27=0;
- 5) 7х+1-5·7х=98;
- 6) 2х·( )х = ;
- 7) 3х= 4-х;
-
9х+6х=22х+1;
- 9)( )х=х+3;
- х=-2
- Х=2
- Х=3
- Х=2
- Х=2
- Х=-2
- Х=1
- Х=0
- Х=-1
Показательная функция, подобно линейной и квадратичной, очень часто реализуется в физических, биологических и иных законах.
И это, конечно, не является случайностью.
В жизни нередко приходится встречаться с такими фактами, когда скорость изменения какой-либо величины пропорциональна самой величине (размножение бактерий, ход химической реакции и т.д.). В этом случае рассматриваемая величина будет изменяться по закону, имеющему вид: y = y0aх
Применение показательной функции в науке и жизни.
- Если бы все маковые зерна давали всходы, то через 5 лет число “потомков” одного растения равнялось бы 243• 1015 или приблизительно 2000 растений на 1 м2 суши
- Потомство комнатных мух за лето только от одной самки может составить 8 • 1014. Эти мухи весили бы несколько миллионов тонн, а выстроенные в одну цепочку, они составили бы расстояние, большее, чем расстояние от Земли до Солнца. Потомство пары мух за 2 года имело бы массу, превышающую массу земного шара. И только благодаря сообществу животных и растений, когда увеличение одного вида влечет за собой рост количества его врагов, устанавливается динамическое равновесие в природе.
- По закону показательной функции размножалось бы все живое на Земле, если бы для этого имелись благоприятные условия, т. е. не было естественных врагов и было вдоволь пищи. Доказательство тому –распространение Австралии кроликов, которых там раньше не было. Достаточно было выпустить пару особей, как через некоторое время их потомство стало национальным бедствием.
- Радий распадается в зависимости от времени по закону
- М = М0 e-kt , где: М0 –начальное количество радия, k –некоторый коэффициент. Пользуясь этой формулой, ученые смогли подсчитать возраст Земли, то есть время, в течение которого радий смог распадаться нормально.
Показательная функция в ЕГЭ
- Задания В5
- Задания В12
Задание С1 9х+6х=22х+1;
Реши самостоятельно:
Масса радиоактивного вещества уменьшается по закону
m(t)=m02
В лаборатории получили вещество, содержащее
в начальный момент времени m0=12 мг изотопа натрия -24,
период полураспада которого равен Т=15ч. В течение
скольких часов содержание натрия -24 в веществе будет
превосходить 3 мг?
Подведем итоги!
Домашнее задание:
Индивидуальная самостоятельная работа 2-х уровней сложности.
Спасибо за урок!
Презентация по предмету «Математика» на тему: «Готовимся к ЕГЭ по математике Повторяем показательные уравнения и неравенства.». Скачать бесплатно и без регистрации. — Транскрипт:
1
Готовимся к ЕГЭ по математике Повторяем показательные уравнения и неравенства
2
У Х У Х График показательной функции Е(f) = (0; ) D (f) = R
3
Какие из перечисленных ниже функций являются возрастающими, а какие убывающими? возрастающая возрастающая возрастающая убывающая убывающая
4
Между числами m и n поставить знак > или или <, если известно,что:
5
Показательные уравнения 1)Общий вид уравнения: a x =a b x=b a x = b, b 0 x=log a b 2) Методы решения уравнений: a x-2 + a x+1 =b a 2x + a x+1 =b Метод разложения на множители; метод введения новой переменной; метод логарифмирования обеих частей уравнения; смешанные методы решения. (X-20)e X-19 =0
6
Найти корень уравнения X = 2,5 X = -1 X = 8 X = 0
7
Показательные неравенства 1)Общий вид неравенства: a x a b x b, если a 1 x b, если 0 a 1 2) Методы решения неравенств: a x-2 + a x+1 b a 2x + a x+1 b Метод разложения на множители; метод введения новой переменной; метод логарифмирования обеих частей неравенства; смешанные методы решения.
8
9
Какой учебный материал необходимо повторить, чтобы справиться с показательными уравнениями и неравенствами на ЕГЭ? Решение простейших уравнений Решение простейших неравенств Решение показательных уравнений различными способами Решение показательных неравенств различными способами Свойства График
10
Показательная функция,
показательные уравнения
и неравенства.
ЦЕЛИ:
1) Повторение и обобщение понятия показательной функции.
2) Закрепление и углубление знания учащихся по решению показательных уравнений и неравенств.
3) Расширение математического кругозора.
4) Развитие познавательной и исследовательской деятельности учащихся.
5) Формирование умения осуществлять взаимосотрудничество.
Введение
Функция – это одно из математических и общенаучных понятий. Она выражает зависимость между переменными величинами. Каждая область знаний – физика, химия, биология, социология, лингвистика и др. – имеют свои объекты изучения, устанавливает свойства и взаимосвязи между этими объектами.
Задание 1. «Из истории математики»
Как известно, начиная с 18 века, одним из основных понятий в математике является понятие функции.
1 вопрос.
Назовите имя одного из крупнейших математиков своего времени, который в 13 лет поступил на факультет искусств Базельского университета, где преподавалась и математика, и астрономия, ставшего впоследствии академиком Петербургской Академии Наук и внесшего огромный вклад в развитие функции, учителя М.В. Ломоносова.
Леонард Эйлер 1707 , Базель, Швейцария – 1783 , Санкт-Петербург Научная сфера: математика, механика, физика, астрономия
Задание 1. «Из истории математики»
2 вопрос.
Он был философом и лингвистом, историком и биологом, дипломатом и политическим деятелем, математиком и изобретателем.
Готфрид Вильгельм фон Лейбниц 1646, Лейпциг, Германия – 1716, Ганновер, Германия Значительные идеи: математический анализ, врождённые идеи, оптимизм, монада
Задание 1. «Из истории математики»
3 вопрос.
Назовите имя учёного, с чьим именем связывают развитие понятия «функция» в 20 веке.
Георг Кантор 1845, Санкт-Петербург – 1918, Галле, Германия
Научная сфера: математика
Задание 2. «Отгадайте слово»
Дайте определение показательной функции.
Определение показательной функции.
Показательной функцией называется функция , где заданное число,
, .
Перечислите основные свойства показательной функции.
Задание 2. «Отгадайте слово»
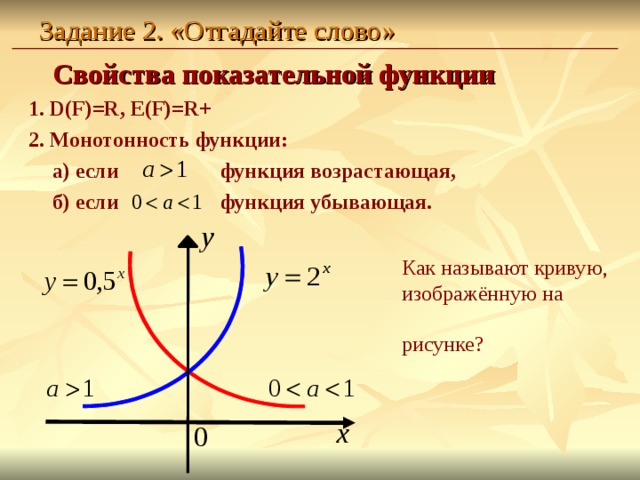
Свойства показательной функции
1. D(F)=R, E(F)=R+
2. Монотонность функции:
а) если функция возрастающая,
б) если функция убывающая.
Как называют кривую,
изображённую на
рисунке?
0
Задание 3. «Применение показательной функции»
Показательная функция применяется
- в физике – радиоактивный распад, изменение атмосферного давления, охлаждение тела;
- в химии – цепные реакции;
- в биологии – расчет роста колоний живых организмов;
- в медицине – расчет выброса адреналина в кровь;
- в банковской структуре.
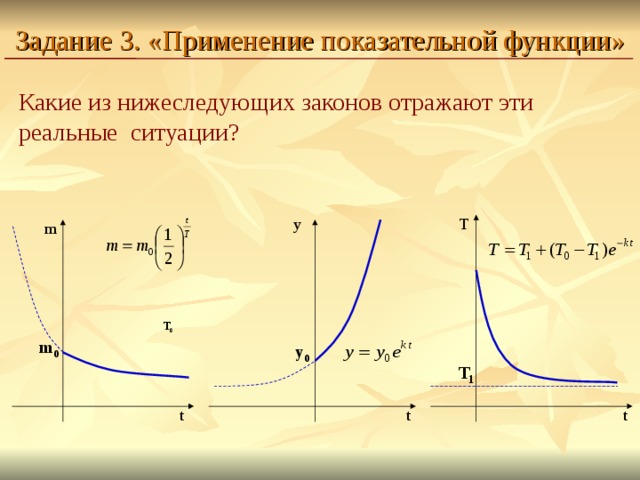
Задание 3. «Применение показательной функции»
Какие из нижеследующих законов отражают эти реальные ситуации?
T
y
m
t
t
t
Задание 4. «Устная работа»
Задание 5. «Задачи ЕГЭ»
Дайте определение показательного уравнения.
Показательным называется уравнение, содержащее переменную в показателе степени.
Пример:
, .
равносильно уравнению
при любом , .
Задание 5. «Задачи ЕГЭ»
Существует несколько методов решения показательных уравнений.
- Функционально-графический метод.
- Метод уравнивания показателей.
- Метод введения новой переменной.
Задание 5. «Задачи ЕГЭ»
Решите уравнения:
1)
2)
3)
4)
5)
6)
Найдите произведение целочисленных решений уравнений.
Задание 6. «Чтение графиков» ЕГЭ
В практической деятельности встречаются задачи на
«чтение» графиков и диаграмм, когда необходимо
перечислить свойства, определить зависимость.
Задание 7. Аукцион «Периодичность»
Периодичностью в обыденной жизни называют
всякую повторяемость. Но повторяемость может
быть более или менее строгой. Безупречные
примеры может дать только математика.
Приведите примеры периодических функций,
встречающихся вокруг нас.
Задание 8. «Как построить график?»
При построении графиков сложных функций необходимо выяснить, каким преобразованиям подвергался график более простой аналогичной функции.
1) Какой из графиков получается в результате следующего преобразования?
- сжатие по оси О x ;
- параллельный перенос вверх на 1;
- параллельный перенос вправо на 2.
а) б) в)
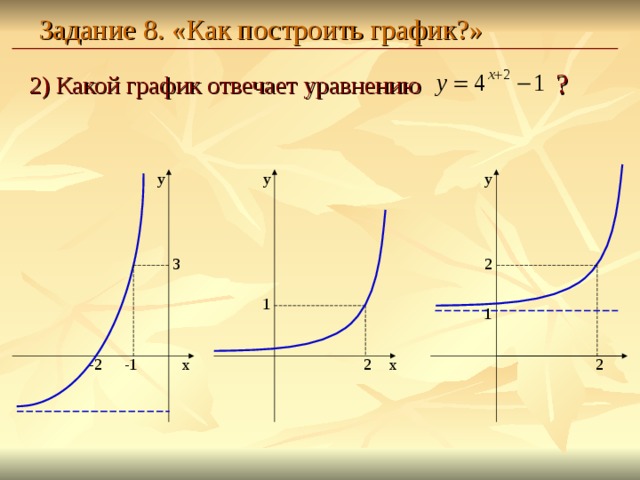
Задание 8. «Как построить график?»
2) Какой график отвечает уравнению ?
y
y
y
3
2
1
1
x
x
-2
-1
2
2
Из истории
Число одна из важнейших постоянных в математике. Обозначение ввёл Леонард Эйлер в 1736 г. Он вычислил первые 23 знака в десятичной записи, а само число назвали в честь Непера «неперовым числом».
Число играет особую роль в математическом анализе. Показательная функция с основанием e, называется экспонентой и обозначается .
Первые знаки числа запомнить несложно: два, запятая, семь, год рождения Льва Толстого два раза, сорок пять, девяносто, сорок пять.
Л. Эйлер в 13 лет поступил на факультет искусств Базельского университета, где преподавалась и математика, и астрономия.
Презентация на тему «Показательные уравнения. Подготовка к ЕГЭ»
-
Скачать презентацию (0.6 Мб)
-
67 загрузок -
1.0 оценка
Ваша оценка презентации
Оцените презентацию по шкале от 1 до 5 баллов
- 1
- 2
- 3
- 4
- 5
Комментарии
Добавить свой комментарий
Аннотация к презентации
Скачать презентацию (0.6 Мб). Тема: «Показательные уравнения. Подготовка к ЕГЭ». Предмет: математика. 11 слайдов. Добавлена в 2017 году. Средняя оценка: 1.0 балла из 5.
-
Формат
pptx (powerpoint)
-
Количество слайдов
11
-
Слова
-
Конспект
Отсутствует
Содержание
-
Слайд 1
Муниципальное общеобразовательное учреждение«Тарко-Салинская средняя общеобразовательная школа № 2»Обобщающий урокпо теме «Показательные уравнения» Подготовка к ЕГЭ
Учитель математики
Балахнина Т. Д.
г. Тарко-Сале
2010 г.
1 -
Слайд 2
Обобщающий урокпо теме «Показательные уравнения»Подготовка к ЕГЭ
Всякое умение
трудом даётся
Цель:
Повторить и обобщить материал по теме «Показательные уравнения»;
Решение показательных уравнений различных видов;
Подготовка к ЕГЭ.
2 -
Слайд 3
Задания ЕГЭ
ЕГЭ — 2007
В4 Найдите наибольшее значение х∙у, где (х;∙у) – решение системы:5х (у – 0,2) = − 1,
5х – у = 5.
ЕГЭ – 2008
В1 Решить уравнения:
а) х∙63х − 36∙63х = 0
б) 4 х +1 + 8∙4х = 3
ЕГЭ — 2009
В4Найдите
х + у, где:
х – у = 1,
64х – 56∙8у = 8.
ЕГЭ — 2010
В3 7х – 2 = 49.С1 Решите уравнение:
4 х2+3х–2 − 0,5 2х2+2х–1= 0
ЕГЭ – 2010
Решите систему ур-ий:С35∙5 tgy + 4 = 5 -tgy,
√х – 5 + 4сosy = 0.
3
-
Слайд 4
Основные способы их решения
Метод уравнивания показателей
(основан на теореме о показательных ур-ий
аf(x) = ag(x)f(x) = g(x))
Метод введения новой переменной
Примеры
1) 3х = 4х + 15
2) 2 2х – 4 = 64
3) 22х+2х − 2 = 0
Функционально — графичекий(основан на графике или на свойствах функции)Показательные уравнения
4
Ответы:3; 5; 0. -
Слайд 5
Показательные уравнения
Разложение на множители(Основан на свойствах степеней с одинаковыми основаниями. Приём: вынос за скобку степень с наименьшим показателем)
Приём деления или умножения
на показательное выражение, отличное
от нуля(в однородных уравнениях)
Совет:при решении показательных уравнений полезно сначала произвести преобразования, получив в обеих частях уравнения
степени с одинаковыми основаниями
Методы решения
5 -
Слайд 6
Примеры
4 х + 1 − 2 ∙ 4 х – 2 = 124,
4 х – 2 ∙ (43 − 2) = 124, 4 х – 2 ∙ 62 = 124,
4 х – 2 = 2, 4 х — 2 = 40,5,…
2 ∙ 22х − 3 ∙ 2х ∙ 5х − 5 ∙ 52х = 0│
: 52х ≠ 0,
2 ∙ (2/5)2х − 3 ∙ (2/5) х − 5 = 0,
t= (2/5) х(t > 0), 2t2 − 3t− 5 = 0,
t= − 1,t= 5/2 (?…).
5/2 = (2/5)х,6
х= 2,5
х = −1
МОЛОДЦЫ! -
Слайд 7
Решение заданий ЕГЭ – 2010 года
В3: а) 7 х – 2 = 49, б) (1/6) 12 – 7х = 36.
Ответ:а) х= 4, б) х = 2.
С1: 4 х2 + 3х – 2 − 0,5 2х2 + 2х – 1= 0.(Можно0,5 = 4– 0,5)
Решение.4 х2 + 3х – 2 = 4 −х2 − х + 0,5
х2 + 3х – 2 = −х2 − х + 0,5, …
Ответ:х= −5/2,х = ½.
С3: 5 ∙ 5 tgy+ 4 = 5 −tgy, при сosy -
Слайд 8
Задание повышенной сложности
С5:При каком параметреауравнение
22х – 3 ∙ 2х+ а2 – 4а = 0 имеет два корня?
Решение.
Пустьt = 2х, t > 0,t2 – 3t + (а2 – 4а) = 0 .
1) Т. к. уравнение имеет два корня, тоD =…
2)Т. к.t1, 2 > 0,тоt1 ∙ t2 > 0,т. е.а2 – 4а> 0 (?…).
Значит,
D > 0,−4а2 + 16а + 9 > 0,
а2 – 4а > 0;а (а − 4) > 0; …
Ответ:а(-0,5; 0)или(4; 4,5).8
D > 0. -
Слайд 9
Проверочная работа
1. 0,32х + 1 = (3 )2
2.у = 5х – 1
у =3. 5∙2х + 3 − 4∙2х – 1 = 19
4*. 3∙9х = 2∙15х+ 5∙25х
9
-
Слайд 10
Задание на дом
Из материалов ЕГЭ 2008 – 2010 годов
выбрать задания по теме и решить их.
Решить уравнения и систему уравнений:
1. (2 )х + 7 = 9/492.у = 3х + 2
у =3. 2 ∙ 3х + 1 − 4 ∙ 3х – 1 = 42
4* 2 ∙ 4х − 3 ∙ 10х = 5 ∙ 25х10
-
Слайд 11
Показательные уравнения
11
Посмотреть все слайды
Сообщить об ошибке
Похожие презентации









Спасибо, что оценили презентацию.
Мы будем благодарны если вы поможете сделать сайт лучше и оставите отзыв или предложение по улучшению.
Добавить отзыв о сайте
Тип урока: урок обобщения и комплексных
применений знаний, умений и навыков по теме
“Показательные уравнения и способы их решения”.
Цели урока.
- Обучающие: повторить и систематизировать
основной материал темы “Показательные
уравнения, их решения”; закрепить способность к
использованию соответствующих алгоритмов при
решении показательных уравнений различных
видов; подготовка к ЕГЭ. - Развивающие: развивать логическое и
ассоциативное мышление учащихся; способствовать
развитию навыка самостоятельного применения
знаний. - Воспитательные: воспитывать
целеустремленность, внимание и аккуратность при
решении уравнений.
Оборудование: компьютер и
мультимедийный проектор.
На уроке используются информационные
технологии: методическое обеспечение к
уроку – презентация в программе
Microsoft Power Point.
Ход урока
Всякое умение трудом даётся
I. Постановка цели урока (Слайд
№ 2)
На этом уроке подведём итог и обобщим тему
“Показательные уравнения, их решения”.
Познакомимся с типовыми заданиями ЕГЭ разных лет
по данной теме.
Задачи на решение показательных уравнений
могут встречаться в любой части заданий ЕГЭ. В
части “В” обычно
предлагают решить простейшие показательные
уравнения. В части “С”
можно встретить более сложные показательные
уравнения, решение которых обычно является одним
из этапов выполнения задания.
Например (Слайд № 3).
- ЕГЭ – 2007
В4 – Найдите наибольшее значение
выражения х • у, где (х; у) – решение
системы:
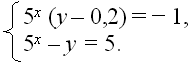
- ЕГЭ – 2008
В1– Решить уравнения:
а) х • 63х – 36 • 63х = 0;
б) 4х +1 + 8 • 4х = 3.
- ЕГЭ – 2009
В4 – Найдите значение выражения х
+ у, где (х; у) – решение системы:
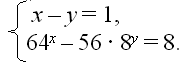
- ЕГЭ – 2010
В3 – Решите уравнение: 7х –
2 = 49.
С1 – Найдите корни уравнения: 4х2
+ 3х – 2 — 0,52х2 + 2х – 1 = 0.
С3 – Решите систему уравнений:
II. Актуализация опорных знаний. Повторение (Слайды № 4 – 6 презентации к
уроку)
На экран демонстрируется опорный
конспект теоретического материала по
теме.
Обсуждаются следующие вопросы:
- Какие уравнения называются показательными?
- Назвать основные способы их решения. Привести
примеры их видов (Слайд № 4) - Какую теорему используют при решении
простейших показательных уравнений вида: а f(x)
= a g(x)? - Какие ещё методы решения показательных
уравнений существуют? (Слайд № 5)
(Самостоятельно решить предлагаемые уравнения
к каждому способу и выполнить самопроверку с
помощью слайда)
- Метод разложения на множители (основан на
свойствах степеней с одинаковыми
основаниями, приём: выносится за скобку степень с
наименьшим показателем). - Приём деления (умножения) на показательное
выражение, отличное от нуля, при решении
однородных показательных уравнений.
- Совет: при решении показательных
уравнений полезно сначала произвести
преобразования, получив в обеих частях уравнения
степени с одинаковыми основаниями.
- Решение уравнений двумя последними методами
с последующими комментариями
(Слайд № 6).
Пример. 4х + 1 – 2 • 4х – 2
= 124, 4х – 2 • (43 — 2) = 124, 4х – 2 •
62 = 124,
4 х – 2 = 2, 4 х – 2 = 4 0,5, х
– 2 = 0,5, х = 2,5.
Пример. 2 • 22х – 3 • 2х • 5х
– 5 • 52х = 0¦: 52х 0,
2 • (2/5)2х – 3 • (2/5) х — 5 = 0,
t = (2/5)х, t > 0, 2t2 — 3 t —
5 = 0, t = -1(?…), t = 5/2; 5/2 = (2/5)х , х =
?…
III. Решение заданий ЕГЭ 2010
Учащиеся самостоятельно решают предлагаемые в
начале урока на слайде № 3 задания, используя
указания к решению, проверяют свой ход решения и
ответы к ним с помощью презентации (Слайд
№ 7). В процессе работы обсуждаются
варианты и способы решения, обращается внимание
на возможные ошибки при решении.
В3: а) 7х – 2 = 49, б) (1/6)12
– 7 х = 36. Ответ: а) х = 4, б) х = 2.
С1: 4х2 + 3х – 2 — 0,52х2
+ 2х – 1 = 0. (Можно заменить 0,5 = 4– 0,5)
Решение. ,
х2 + 3х – 2 = —х2 — 4х + 0,5
…
Ответ: х = -5/2, х = 1/2.
С3: 5 • 5tgy + 4 = 5-tgy,
при сos y < 0.
Указание к решению. 5 • 5tgy + 4 = 5
-tgy ¦•5tgy 0,
5 • 52gy + 4 • 5 tgy – 1 = 0. Пусть х
= 5 tgy , …
5tgy = -1 (?…), 5tgy =1/5.
Так как tgy = -1 и сos y < 0, то у II координатной
четверти
Ответ: у = 3/4 + 2
k, k
N.
IV. Совместная работа у доски
Рассматривается задание высокого уровня
обученности – Слайд № 8. С
помощью данного слайда происходит диалог
учителя и учащихся, способствующий развитию
решения.
С5 – При каком параметре а уравнение
22х – 3 • 2х + а2 – 4а
= 0 имеет два корня?
Решение.
Пусть t = 2х, где t > 0.
Получаем t 2 – 3t + (а2
– 4а) = 0 .
1). Так как уравнение имеет два корня, то D > 0;
2). Так как t1,2 > 0, то t1 • t2
> 0, то есть а2 – 4а > 0 (?…).
Значит,
Ответ: а (–
0,5; 0) или (4; 4,5).
V. Проверочная работа (Слайд
№ 9)
Учащиеся выполняют проверочную
работу на листочках, осуществляя
самоконтроль и самооценку выполненной работы с
помощью презентации, утверждаясь в теме.
Самостоятельно определяют для себя программу
регулирования и коррекции знаний по допущенным
ошибкам в рабочих тетрадях. Листы с выполненной
самостоятельной работой сдаются учителю на
проверку.
Подчёркнутые номера – базового уровня, со
звёздочкой – повышенной сложности.
Решение и ответы.
- 0,32х + 1 = 0,3– 2, 2х + 1 = -2, х = -1,5.
- (1; 1).
3. 2х – 1(5 • 2 4 — 4) = 19, 2х –
1 • 76 = 19, 2х – 1 = 1/4, 2х – 1 = 2
– 2, х – 1 = -2,
х = -1.
4*. 3 • 9х = 2 • 3х • 5х +
5 • 25х | : 25х,
3 • (9/25)х = 2 • (3/5)х + 5,
3 • (9/27)х = 2 • (3/5)х + 5 = 0,
3 • (3/5)2х – 2 • (3/5)х — 5 = 0,…, (3/5)
х = -1 (не подходит),
(3/5)х = 5, х = -1.
VI. Задание на дом (Слайд № 10)
- Повторить § 11, 12.
- Из материалов ЕГЭ 2008 – 2010 г. выбрать задания по
теме и решить их. - Домашняя проверочная работа:
Слайды и текст этой презентации
Слайд 1Дорогу осилит идущий,
а математику –
мыслящий.

Слайд 2Показательная функция,
показательные уравнения
и неравенства.

Слайд 31) Повторение и обобщение понятия показательной функции.
2) Закрепление и
углубление знания учащихся по решению показательных уравнений и неравенств.
3) Расширение
математического кругозора.
4) Развитие познавательной и исследовательской деятельности учащихся.
5) Формирование умения осуществлять взаимосотрудничество.
ЦЕЛИ:

Слайд 4Введение
Функция – это одно из математических и общенаучных понятий.
Она выражает зависимость между переменными величинами. Каждая область знаний –
физика, химия, биология, социология, лингвистика и др. – имеют свои объекты изучения, устанавливает свойства и взаимосвязи между этими объектами.

Слайд 5Как известно, начиная с 18 века, одним из основных
понятий в математике является понятие функции.
Назовите имя одного из
крупнейших математиков своего времени, который в 13 лет поступил на факультет искусств Базельского университета, где преподавалась и математика, и астрономия, ставшего впоследствии академиком Петербургской Академии Наук и внесшего огромный вклад в развитие функции, учителя М.В. Ломоносова.
Задание 1. «Из истории математики»
1 вопрос.
Леонард Эйлер
1707, Базель, Швейцария –
1783, Санкт-Петербург
Научная сфера: математика, механика, физика, астрономия

Слайд 6Задание 1. «Из истории математики»
Он был философом и лингвистом,
историком и биологом, дипломатом и политическим деятелем, математиком и изобретателем.
2 вопрос.
Готфрид Вильгельм фон Лейбниц
1646, Лейпциг, Германия –
1716, Ганновер, Германия
Значительные идеи:
математический анализ, врождённые идеи, оптимизм, монада

Слайд 7Назовите имя учёного, с чьим именем связывают развитие понятия
«функция» в 20 веке.
Задание 1. «Из истории математики»
3 вопрос.
Георг
Кантор
1845, Санкт-Петербург –
1918, Галле, Германия
Научная сфера: математика

Слайд 8Дайте определение показательной функции.
Задание 2. «Отгадайте слово»
Определение показательной функции.
Показательной
функцией называется функция , где
заданное число,
, .
Перечислите основные свойства показательной функции.

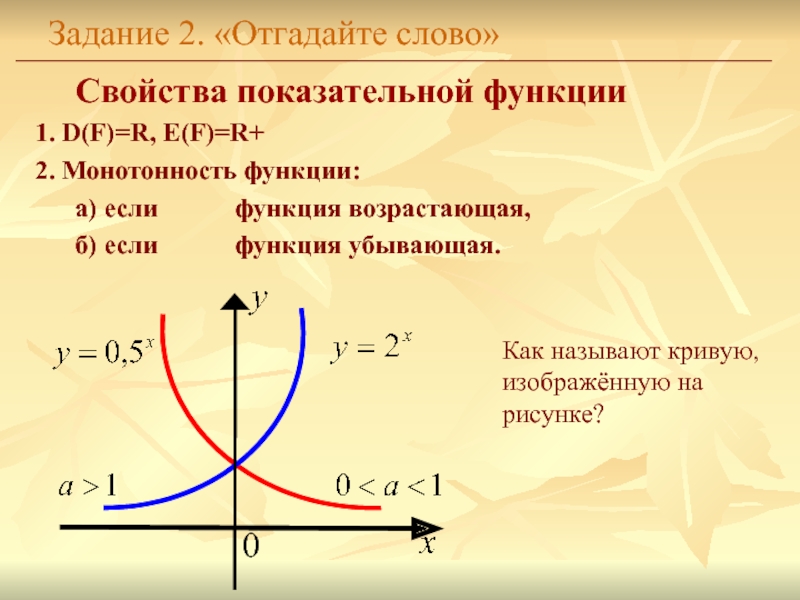
Слайд 9Задание 2. «Отгадайте слово»
Свойства показательной функции
1. D(F)=R, E(F)=R+
2. Монотонность
функции:
а) если функция возрастающая,
б) если функция убывающая.
0
Как называют кривую,
изображённую на
рисунке?
Слайд 10Задание 3. «Применение показательной функции»
в физике – радиоактивный распад,
изменение атмосферного давления, охлаждение тела;
в химии – цепные
реакции;
в биологии – расчет роста колоний живых организмов;
в медицине – расчет выброса адреналина в кровь;
в банковской структуре.
Показательная функция применяется

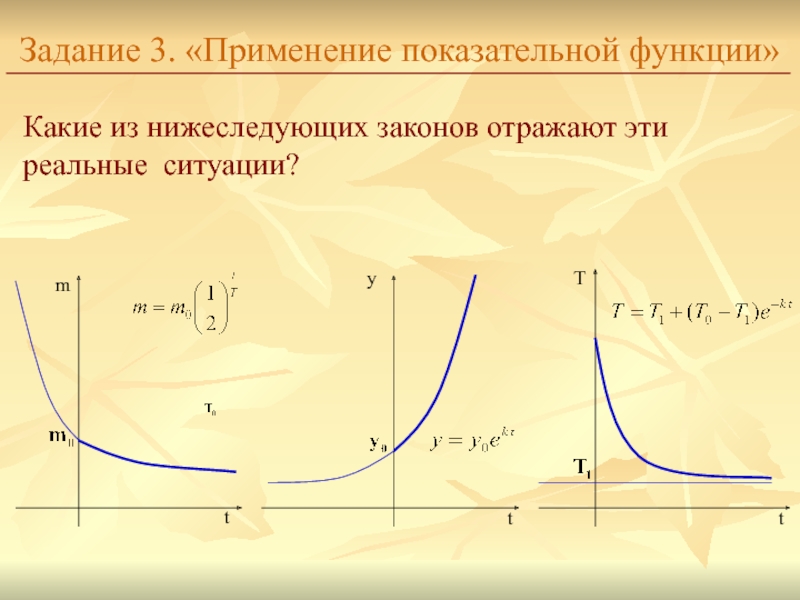
Слайд 11Задание 3. «Применение показательной функции»
Какие из нижеследующих законов отражают
эти реальные ситуации?
m
t
t
t
y
T
Слайд 14Показательным называется уравнение,
содержащее переменную в показателе степени.
Задание 5. «Задачи
ЕГЭ»
Дайте определение показательного уравнения.
Пример:
, .
равносильно
уравнению
при любом , .

Слайд 15Функционально-графический метод.
Метод уравнивания показателей.
Метод введения новой переменной.
Задание 5. «Задачи
ЕГЭ»
Существует несколько методов решения
показательных уравнений.

Слайд 16Задание 5. «Задачи ЕГЭ»
Решите уравнения:
1)
2)
3)
4)
5)
6)
Найдите произведение целочисленных решений
уравнений.

Слайд 17Задание 6. «Чтение графиков» ЕГЭ
В практической деятельности встречаются задачи
на
«чтение» графиков и диаграмм, когда необходимо
перечислить свойства, определить зависимость.

Слайд 18Задание 7. Аукцион «Периодичность»
Периодичностью в обыденной жизни называют
всякую
повторяемость. Но повторяемость может
быть более или менее строгой. Безупречные
примеры может дать только математика.
Приведите примеры периодических функций,
встречающихся вокруг нас.

Слайд 19Задание 8. «Как построить график?»
1) Какой из графиков получается
в результате следующего преобразования?
сжатие по оси Оx;
параллельный перенос вверх на
1;
параллельный перенос вправо на 2.
а) б) в)
При построении графиков сложных функций необходимо выяснить, каким преобразованиям подвергался график более простой аналогичной функции.

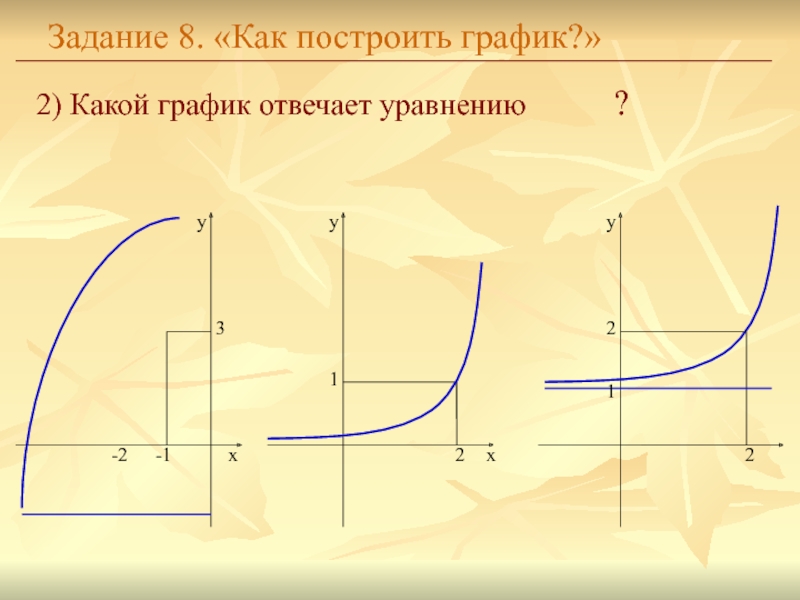
Слайд 20Задание 8. «Как построить график?»
2) Какой график отвечает уравнению
?
y
y
y
x
x
-2
3
-1
1
2
2
2
1
Слайд 21Из истории
Число
одна из важнейших постоянных в математике. Обозначение ввёл Леонард Эйлер в 1736 г. Он вычислил первые 23 знака в десятичной записи, а само число назвали в честь Непера «неперовым числом».
Число играет особую роль в математическом анализе. Показательная функция с основанием e, называется экспонентой и обозначается .
Первые знаки числа запомнить несложно: два, запятая, семь, год рождения Льва Толстого два раза, сорок пять, девяносто, сорок пять.
Л. Эйлер в 13 лет поступил на факультет искусств Базельского университета, где преподавалась и математика, и астрономия.

Слайд 22Мир освещается солнцем,
а человек знанием.


 9х+6х=22х+1;
9х+6х=22х+1;