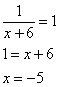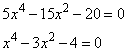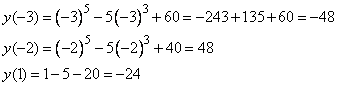Полный разбор 12 задания егэ математика профиль - Помощь в подготовке к экзаменам и поступлению

Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.

Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.

Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.

Задачи из сборников Ященко, 2021 год

Квадратные уравнения

Показательные уравнения

Логарифмические уравнения

Модуль числа

Уравнения с модулем

Тригонометрический круг

Формулы тригонометрии

Формулы приведения

Простейшие тригонометрические уравнения 1

Простейшие тригонометрические уравнения 2

Тригонометрические уравнения

Что необходимо помнить при решении уравнений?

1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть tg x — помним, что он существует, только если

2) Стараемся записывать решение в виде цепочки равносильных переходов.

3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.

4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.

5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений $x=frac{pi}{3}+2pi n$ , где — целое, а найти надо корни на отрезке $left [frac{5 pi}{2};frac{9 pi}{2} right ].$ На указанном промежутке лежит точка 4 pi . От нее и будем отсчитывать. Получим: $x=4 pi +frac{pi}{3}=frac{13 pi}{3}.$

6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!

Давайте потренируемся.

а) Решите уравнение $2{{sin}^2 left(frac{pi }{2}+xright)}=-sqrt{3}{cos x}$

б) Найдите все корни этого уравнения, принадлежащие промежутку $left[-3pi right.;left.-frac{3pi }{2}right]$

$2{{sin}^2 left(frac{pi }{2}+xright)}=-sqrt{3}{cos x}$

Упростим левую часть по формуле приведения.

$2{{cos}^2 x+sqrt{3}{cos x}=0}$

Вынесем {cos x} за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

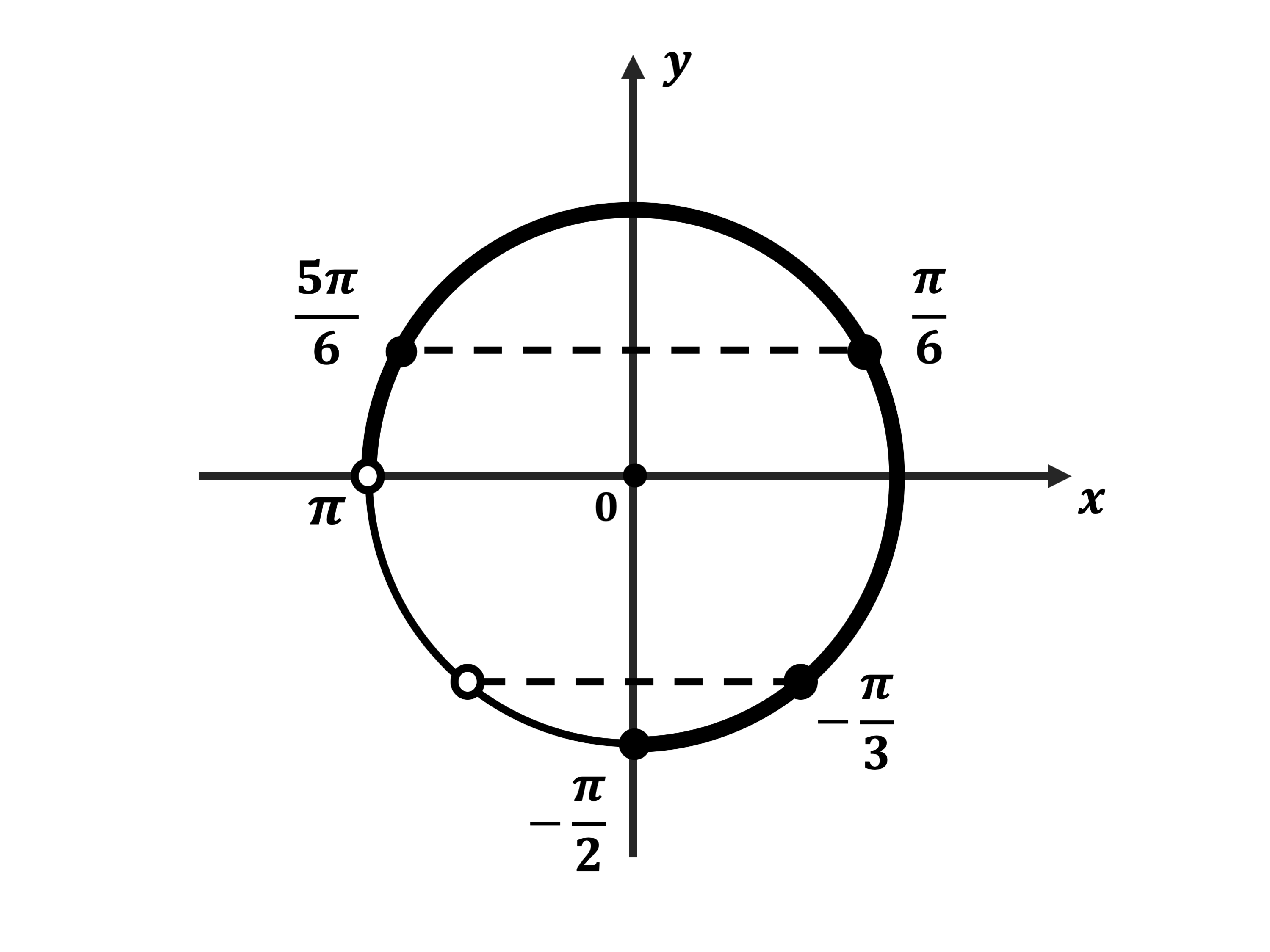
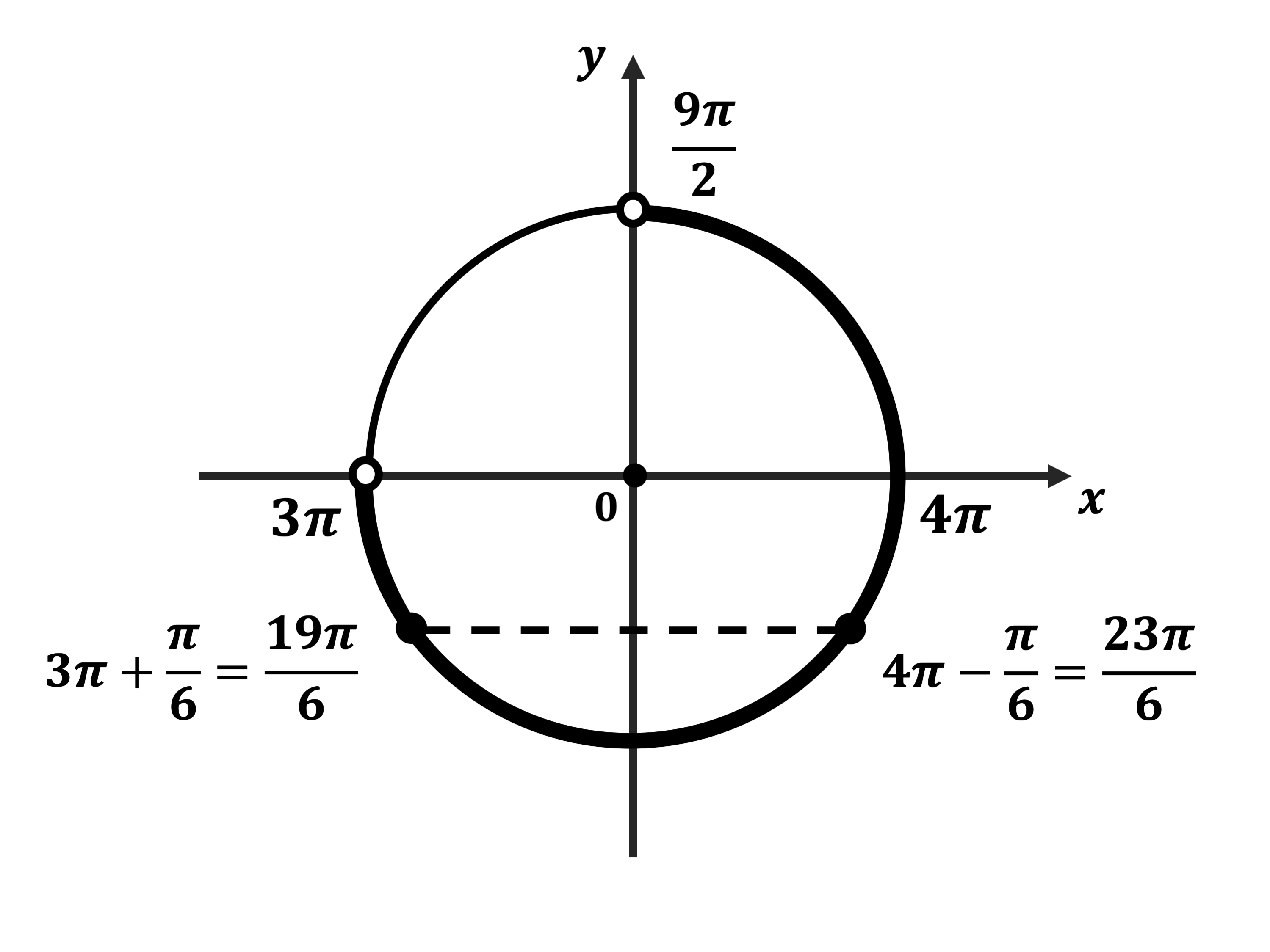
б) Отметим на тригонометрическом круге найденные серии решений и отрезок $left[-3pi right.;left.-frac{3pi }{2}right].$

Видим, что указанному отрезку принадлежат решения $-frac{17pi }{6};-frac{5pi }{2};-frac{3pi }{2}.$

Ответ: $-frac{17pi }{6};-frac{5pi }{2};-frac{3pi }{2}.$

Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.

Например, вы нашли серию решений $x=frac{pi }{3}+2pi n$ , где — целое, а найти надо корни на отрезке $[frac{5pi }{2};frac{9pi }{2}].$ На указанном промежутке лежит точка 4 pi. От нее и отсчитываем.

Получим: $x=4pi +frac{pi }{3}=frac{13pi }{3}.$

2. а) Решите уравнение ${({27}^{{cos x}})}^{{sin x}}=3^{frac{3{cos x}}{2}}$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-pi ;frac{pi }{2}right].$

Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.

а) $3^{3{cos x{sin x}}}=3^{frac{3{cos x}}{2}}$

Степени равны, их основания равны. Значит, равны и показатели.

$3{cos x{sin x}}=frac{3{cos x}}{2}$

${cos x({sin x-frac{1}{2})=0}}$

Это ответ в пункте (а).

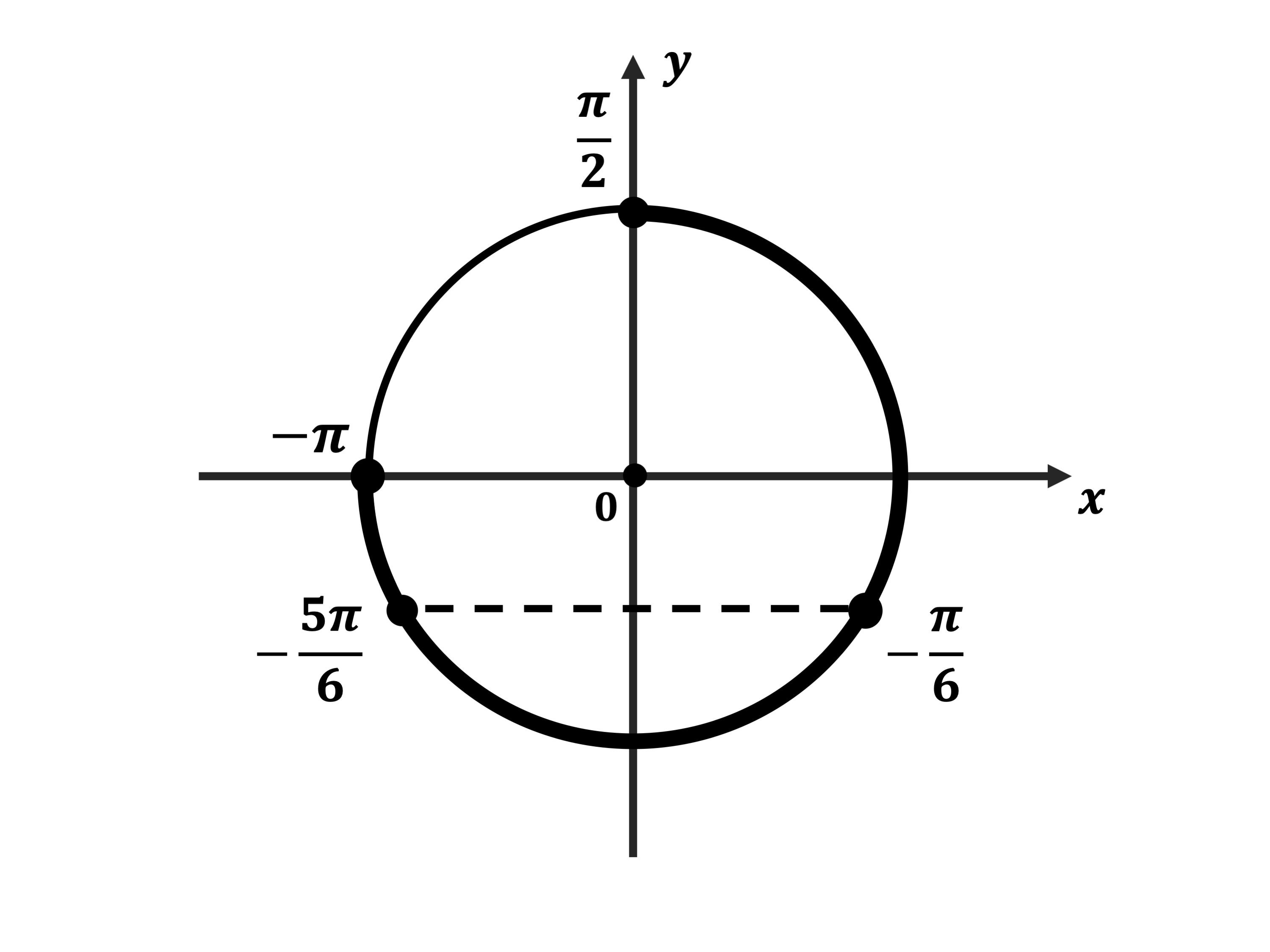
б) Отберем корни, принадлежащие отрезку $left[-pi ;frac{pi }{2}right].$

Отметим на тригонометрическом круге отрезок $left[-pi ;frac{pi }{2}right]$ и найденные серии решений.

Видим, что указанному отрезку принадлежат точки $x=-frac{pi }{2}$ и $x=frac{pi }{2}$ из серии $x=frac{pi }{2}+pi n,nin z.$

Точки серии $x=frac{5pi }{6}+2pi n,nin z$ не входят в указанный отрезок.

А из серии $x=frac{pi }{6}+2pi n,nin z$ в указанный отрезок входит точка $x=frac{pi }{6}.$

Ответ в пункте (б): $-frac{pi }{2},frac{pi }{6} , frac{pi }{2}.$

3. а) Решите уравнение ${cos 2x}+{{sin}^2 x=0,5}$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-frac{7pi }{2}right.;left.-2pi right].$

а)
${cos 2x}+{{sin}^2 x=0,5}$

Применим формулу косинуса двойного угла: $boldsymbol{cos2alpha =1-{2sin}^2alpha }$

$1-2{{sin}^2 x}+{{sin}^2 x}=0,5$

${{-sin}^2 x=-0,5}$

${{sin}^2 x=0,5}$

Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.

Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.

б) Для разнообразия отберем корни на отрезке $left[-frac{7pi }{2}right.;left.-2pi right]$ с помощью двойного неравенства.

Сначала серия $x=frac{pi }{4}+pi n,nin Z.$

$-frac{7pi }{2}le frac{pi }{4}+pi nle -2pi$

$-frac{7}{2}le frac{1}{4}+nle -2$

$n=-3, x_1=frac{pi }{4}-3pi =-frac{11pi }{4}$

Теперь серия $x=-frac{pi }{4}+pi n,nin Z$

$-frac{7pi }{2}le -frac{pi }{4}+pi nle -2pi$

$-frac{7}{2}le -frac{1}{4}+nle -2$

$n=-3, x_2=-frac{pi }{4}-3pi =-frac{13pi }{4}$

$n=-2, x_3=-frac{pi }{4}-2pi =-frac{9pi }{4}$

Ответ: $-frac{13pi }{4};-frac{11pi }{4};-frac{9pi }{4}$ .

Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».

Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.

Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии $x=-frac{pi }{4}+2pi n,nin Z$ на отрезке $left[-frac{pi }{2}right.;left.20pi right].$ Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.

4. а) Решите уравнение $left({tg}^2x-3right)sqrt{11{cos x}}=0.$

б) Найдите все корни этого уравнения, принадлежащие отрезку $left[-frac{5pi }{2};-pi right].$

Самое сложное здесь — область допустимых значений (ОДЗ). Условие заметно сразу. А условие появляется, поскольку в уравнении есть ${tg x=frac{{sin x}}{{cos x}}}.$

ОДЗ:

Уравнение равносильно системе:

Отберем решения с помощью тригонометрического круга. Нам нужны те серии решений, для которых , то есть те, что соответствуют точкам справа от оси .

Ответ в пункте а) $x=pm frac{pi }{3}+2pi n, nin z$

б) Отметим на тригонометрическом круге найденные серии решений и отрезок $left[-frac{5pi }{2};-pi right].$

Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки

$x=frac{pi }{3}-2pi =-frac{5pi }{3}$ и $x=-frac{pi }{3}-2pi =-frac{7pi }{3}.$

5. а) Решите уравнение $sqrt{{cos x+{sin x}}}({{cos}^2 x-frac{1}{2})=0}$

б) Найдите корни, принадлежащие отрезку

Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

Это значит, что уравнение равносильно системе:

Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых ${cos x}=frac{sqrt{2}}{2}$ или ${cos x}=-frac{sqrt{2}}{2}$ . Заметим, что среди них находятся и углы, для которых tgx=-1.

Числа серии $x=-frac{3pi }{4}+2pi n$ не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие . Остальные серии решений нас устраивают.

Тогда в ответ в пункте (а) войдут серии решений:

б) Отберем корни, принадлежащие отрезку любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.

На отрезке нам подходит корень $x =-frac{pi }{4}$ .

На отрезке нам подходят корни $x=frac{pi }{4};frac{3pi }{4};frac{7pi }{4}$ .

На отрезке — корни $x= frac{9pi }{4} ; frac{11pi }{4};frac{15pi }{4}.$

Ответ в пункте б): $-frac{pi }{4};frac{3pi }{4};frac{7pi }{4};frac{pi }{4};frac{9pi }{4} ; frac{11pi }{4};frac{15pi }{4}.$

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание №12. Уравнения u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Значения функции: наибольшее и наименьшее

В задании №12 ЕГЭ по математике профильного уровня нам необходимо найти наибольшее или наименьшее значение функции. Для этого необходимо воспользоваться, очевидно, производной. Посмотрим на типовом примере.

Разбор типовых вариантов заданий №12 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

[su_note note_color=”#defae6″]

Найти точку максимума функции y = ln(x+4)²+2x+7.

[/su_note]

Алгоритм решения:

Определяем область определения функции.
Находим производную.
Определяем, в каких точках производная равна 0.
Исключаем точки, не принадлежащие области определения.
Среди оставшихся точек ищем значения х, в которых функция имеет максимум.
Записываем ответ.

Решение:

1. Ищем значения х, при которых логарифм имеет смысл. Для этого решаем неравенство:

(x+4)² > 0

Поскольку квадрат любого числа неотрицателен. Решением неравенства будет лишь то значение х, при котором х+4≠ 0, т.е. при х≠-4.

2. Находим производную:

у’=(ln(x+4)² + 2x + 7)’

По свойству логарифма получаем:

у’=(ln(x+4)² )’+(2x)’+(7)’.

По формуле производной сложной функции:

(lnf)’=(1/f)∙f’. У нас f=(x+4)²

у^, = (ln(x+4)² )’+ 2 + 0 = (1/(x+4)² )∙((x+4)²)’ + 2=(1/(x+4)² 2)∙(х² + 8х + 16)’ +2=2(х + 4) /((х + 4)²) + 2

у’= 2/(х + 4) + 2

3. Приравниваем производную к нулю:

у^, = 0 → (2+2∙(х + 4))/(х + 4)=0,

2 +2х +8 =0, 2х + 10 = 0,

2х = -10,

х = -5

Ответ: -5.

Второй вариант задания (из Ященко, №1)

[su_note note_color=”#defae6″]

Найдите точку минимума функции y = x – ln(x+6) + 3.

[/su_note]

Алгоритм решения:

Определяем область определения функции.
Находим производную.
Определяем, в каких точках производная равна 0.
Исключаем точки, не принадлежащие области определения.
Среди оставшихся точек ищем значения х, в которых функция имеет минимум.
Записываем ответ.

Решение:

1. ОДЗ: .

2. Найдем производную функции:

3. Приравниваем полученное выражение к нулю:

4. Получили одну точку x=-5, принадлежащую области определения функции.

5. В этой точке функция имеет экстремум. Проверим, минимум ли это. При х=-4

При х=-5,5 производная функции отрицательна, так как

Значит, точка х=-5 является точкой минимума.

Ответ: -5.

Третий вариант задания (из Ященко, №12)

[su_note note_color=”#defae6″]

Найдите наибольшее значение функции на отрезке [-3; 1].

[/su_note]

Алгоритм решения:.

Находим производную.
Определяем, в каких точках производная равна 0.
Исключаем точки, не принадлежащие заданному отрезку.
Среди оставшихся точек ищем значения х, в которых функция имеет максимум.
Находим значения функции на концах отрезка.
Ищем среди полученных значений наибольшее.
Записываем ответ.

Решение:

1. Вычисляем производную от функции, получим

2. Приравниваем производную к нулю:

Решение уравнения дает два корня

– не принадлежит множеству действительных чисел

3. Значение и остается одна точка .

4. Вычисляем значения функции в точке -2 и на концах отрезка -3 и 1, получим:

Наибольшее значение функции на заданном отрезке равно 48 в точке х=-2.

Ответ: 48.

Даниил Романович | Просмотров: 11.8k

Источник

Задание №12. Уравнения — профильный ЕГЭ по математике

Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.

Что необходимо помнить при решении уравнений?

1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть — помним, что он существует, только если

2) Стараемся записывать решение в виде цепочки равносильных переходов.

Например, вы нашли серию решений , где — целое, а найти надо корни на отрезке На указанном промежутке лежит точка . От нее и будем отсчитывать. Получим:

6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!

а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие промежутку

Упростим левую часть по формуле приведения.

Вынесем за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

б) Отметим на тригонометрическом круге найденные серии решений и отрезок

Видим, что указанному отрезку принадлежат решения

Например, вы нашли серию решений , где — целое, а найти надо корни на отрезке На указанном промежутке лежит точка От нее и отсчитываем.

2. а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку

Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.

Степени равны, их основания равны. Значит, равны и показатели.

Это ответ в пункте (а).

б) Отберем корни, принадлежащие отрезку

Отметим на тригонометрическом круге отрезок и найденные серии решений.

Видим, что указанному отрезку принадлежат точки и из серии

Точки серии не входят в указанный отрезок.

А из серии в указанный отрезок входит точка

Ответ в пункте (б):

3. а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку

Применим формулу косинуса двойного угла:

Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.

б) Для разнообразия отберем корни на отрезке с помощью двойного неравенства.

Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии на отрезке Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.

4. а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку

Самое сложное здесь — область допустимых значений (ОДЗ). Условие заметно сразу. А условие появляется, поскольку в уравнении есть

Уравнение равносильно системе:

Ответ в пункте а)

б) Отметим на тригонометрическом круге найденные серии решений и отрезок

Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки

5. а) Решите уравнение

б) Найдите корни, принадлежащие отрезку

Это значит, что уравнение равносильно системе:

Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых или . Заметим, что среди них находятся и углы, для которых

Числа серии не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие . Остальные серии решений нас устраивают.

Тогда в ответ в пункте (а) войдут серии решений:

Материал для подготовки к заданию номер 12 из ЕГЭ по профильной математике

Все уравнения можно разделить на несколько групп:

— Целые рациональные уравнения

Каждая группа уравнений имеет свои особенности. На первый взгляд может показаться, что это очень большой материал и на его изучение понадобится много времени, однако на самом деле для подготовки в экзамену и выполнению задания номер 12 можно подготовиться достаточно быстро, используя верно подобранные материалы и разбирая примеры заданий

Комбинируя все представленные в данных материалах способы и обладая базовыми знаниями математики, можно успешно решить большинство уравнений, которые могут встретиться учащимся во время обучения в средней и старшей школе а так же успешно решить задания на данную тему в контрольно-измерительных материалах

СОВЕТ: после прохождения какой-либо темы в моём пособии, необходимо прорешать похожие уравнения (этой же группы) на одном из подобранных мной сайтов (смотрите ниже)

Часть I. Способы решения уравнений. Метод “Замена переменной”

Уравнение вида af²(x)+bf (x)+c=0 Такие уравнения (их иногда называют трехчленными) являются одними из наиболее распространенных. Скорее всего, самый известный и яркий пример этого типа уравнений — биквадратное уравнение ax⁴ + bx2 + c = 0 (здесь f (x) = x 2 ). Заменой переменной t = f (x) трехчленное уравнение сводится к квадратному относительно переменной t уравнению at² + bt + c = 0

Решить уравнение (2x² – 3x + 1) = 22x² – 33x + 1.

Задание 12. Тригонометрическое уравнение

Типичная задача №12 из ЕГЭ по математике 2022 содержит два пункта:

Решить несложное тригонометрическое уравнение (хотя иногда попадаются довольно сложные).
Среди полученных корней отобрать те, которые принадлежат заданному отрезку. Вот здесь большинство учеников «пасует».

Все видеоуроки по задачам 12, опубликованные на моем сайте, содержат оба пункта: и решение уравнения (со всеми тонкостями), и различные подходы к отбору корней.

Глава 1. Тригонометрические уравнения § 1. Задача C1: тригонометрические уравнения с ограничением § 2. Задача C1: тригонометрические уравнения и формула двойного угла § 3. Задача C1: тригонометрия и показательная функция — 1 вариант § 4. Задача C1: тригонометрия и показательная функция — 2 вариант Глава 2. Показательные и логарифмические уравнения § 1. Задача C1: показательные уравнения с ограничением § 2. Задача C1: еще одно показательное уравнение § 3. Логарифмические уравнения в задаче C1 § 4. Задача C1: логарифмы и тригонометрия в одном уравнении § 5. Вебинар по заданию 13: тригонометрия § 6. Формулы двойного угла в тригонометрических уравнениях из ЕГЭ § 7. Отбор корней из некрасивых арктангенсов, арксинусов и т.д. § 8. Нестандартные периоды и отбор корней в тригонометрическом уравнении § 11. Задача из пробного ЕГЭ 2016 от 3 марта § 12. Вебинар по заданию 13: предварительное задание

источники:

http://vc.ru/u/1019775-egor-borodin/330865-material-dlya-podgotovki-k-zadaniyu-nomer-12-iz-ege-po-profilnoy-matematike

http://www.berdov.com/ege/equation-root/

Источник

По статистике, лишь 5% школьников сдают госэкзамен по математике на 80+ баллов с первой попытки. Неспроста этот предмет считается одним из сложнейших в школьной программе. Вы готовы начать с простейших тригонометрических уравнений? Давайте проверим! Наша серия видеоуроков посвящена подробному разбору 12 задания ЕГЭ по математике 2023 года, то есть разделу тригонометрии. Посмотрите все 8 видео по порядку – и вы станете экспертом в этом вопросе.

Радианы – инструкция по применению. Разбор 12 задания ЕГЭ математика профиль. Теория.

Начинаем с простого: угол в 1 радиан. Старший эксперт ЕГЭ по математике и член проверочной комиссии ЕГЭ Михаил Попов напомнит, что же это такое. Вы узнаете, чему соответствует угол 30^о, 60^о, 90^ои так далее, а также что делать с непонятными углами, которые нередко встречаются в госэкзамене по математике.

Не забывайте, что в задачах на радианы важно записывать все ответы не в градусах, а в радианах!

Тригонометрический круг, уравнения – быстрый старт. 12 задание ЕГЭ профильная математика. Теория

Тригонометрия – не самая простая наука. Особенно когда дело касается вычислений нестандартных углов. Что же с этим делать? Ответит на данный вопрос наш эксперт. В видеоразборе задания вы узнаете, как находить синусы и косинусы углов окружности единичного радиуса и почему нужно идти по окружности по часовой стрелке, а не наоборот. Посмотрите видео – педагог все объяснит простыми словами.

12 задания ЕГЭ по математике профильный уровень. Простейшие тригонометрические уравнения (часть 1,2)

Простейшие тригонометрические уравнения – фундамент, который позволяет решать остальные уравнения в математике. Несколько подробных разборов примеров дадут каждому школьнику базу для понимания задачи 12. Михаил Попов покажет два варианта, как расписать ответ. Подробнее смотрите в видео о способах решения 12 задания ЕГЭ по математике.

Вторая часть рассматривает общий случай поиска косинуса и арккосинуса угла. На графике становится видно, как и что использовать для решения задачи. Подробный разбор 12 задания ЕГЭ по математике смотрите по ссылке ниже.

Как запомнить табличные значения синуса, косинуса и т.д.?

Если вы еще не знаете основных табличных значений, пора приступить к их заучиванию. Сделать этот процесс более простым и увлекательным поможет наш эксперт ЕГЭ по математике. Разбираемся в вопросе максимально быстро – потребуется всего 5 минут!

ЕГЭ по математике 2023. Задание 12. Теория. Синус, косинус и все, все, все

В этом видео речь пойдет о том, как разложить по полочкам все основные понятия тригонометрии: синус, косинус, тангенс, котангенс. Наш преподаватель знает в этом толк и способен объяснить теорию просто и понятно даже последнему двоечнику.

Хотите заниматься с этим преподавателем? Записывайтесь на бесплатное пробное занятие в учебный центр Годограф.

ЕГЭ по математике – задание 12 2023 года. Практика. Решение задач. Задача 1

Пора перейти к практическим занятиям. Перед нами довольно простая задача по тригонометрии, которая идеально подойдет для разгона. Что нужно сделать, чтобы найти ответ:

С помощью формул заменить тригонометрическое уравнение на обычное уравнение.
Решить обычное уравнение.
Вернуться и решить простейшее тригонометрическое уравнение.

Кажется, что все легко! Однако не обойтись без каверзных моментов, которые важно учитывать при решении задания 12 ЕГЭ по математике. Наш педагог по полочкам все разложит.

Вторая часть практических видео – про отбор корней. Небольшое теоретическое вступление, и можно приступать к решению задачи. Обязательно делаем полное обоснование, иначе можно вообще не получить ни одного балла! Как это сделать – смотрите в нашем видеоролике.

В целом, решение 12 задания ЕГЭ профильной математики не назвать одним из самых сложных. Важно только разобраться в основах и запомнить основные алгоритмы решения. Остальные учебные материалы смотрите на нашем канале.

Рассылка с лучшими статьями. Раз в неделю для самых занятных

Для тех, кто ценит свое время. Выбирайте интересную вам тему и подписывайтесь, чтобы ничего не пропустить. Это бесплатно!

Источник


3661	а) Решите уравнение 2cos^3(x)=-sin((3pi)/2+x) б) Найдите все корни этого уравнения, принадлежащие отрезку [3pi; 4pi]. Решение График	а) Решите уравнение 2cos3 x = -sin(3/2pi+x) ! Статград 28-02-2023 11 класс Вариант МА2210309 Задание 12

3626	а) Решите уравнение (x^2+4x-2)*(4^(3x+1)+8^(2x-1)-11)=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [-0,5; 0,5] Решение График	а) Решите уравнение (x2+4x-2)(4^3x+1+8^2x-1-11) = 0 ! 36 вариантов ФИПИ Ященко 2023 Вариант 24 Задание 12

3619	а) Решите уравнение 5sin(2x)-5cos(x)+14sin(x)-7=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [(3pi)/2; 3pi]. Решение График	а) Решите уравнение 5sin2x — 5cosx + 14sinx — 7 = 0 ! Тренировочная работа №1 по математике 10 класс Статград 08-02-2023 Вариант МА2200109 Задание 12

3598	а) Решите уравнение 2sin^2(pi/2-x)+sin(2x)=0 б) Укажите корни этого уравнения, принадлежащие отрезку [3pi; (9pi)/2]. Решение График	а) Решите уравнение 2sin^2(pi/2-x) +sin2x =0 ! 36 вариантов ФИПИ Ященко 2023 Вариант 21 Задание 12

3595	а) Решите уравнение 36(log_{1/8}(x))^2+4log_{1/4}(x)-5=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [0,5; 5] Решение График	а) Решите уравнение 36log2 1/8 x-+ 4log1/4 x — 5 = 0 ! 36 вариантов ФИПИ Ященко 2023 Вариант 20 Задание 12 # Ошибка в ответе пособия у Ященко : color{red}{sqrt2/2; 4sqrt2}

3570	а) Решите уравнение 15^(sin(x))=3^(sin(x))*5^(-cos(x)) б) Найдите все корни этого уравнения, принадлежащие отрезку [(3pi)/2; 3pi]. Решение График	а) Решите уравнение 15 sinx =3 sinx 5 -cosx ! Тренировочная работа по математике №2 СтатГрад 11 класс 13.12.2022 Задание 12 Вариант МА2210209

3561	а) Решите уравнение cos(2x)+sin(2x)+1=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [3pi; (9pi)/2]. Решение График	а) Решите уравнение cos2x + sin2x +1 = 0 ! 36 вариантов ФИПИ Ященко 2023 Вариант 16 Задание 12

3551	а) Решите уравнение 25^(x-0.5)-13*10^(x-1)+4^(x+0.5)=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [-pi/2; pi]. Решение График	а) Решите уравнение 25^ x-0,5 — 13 10^ x-1 +4^ x+0,5 =0! 36 вариантов ФИПИ Ященко 2023 Вариант 14 Задание 12

3536	а) Решите уравнение 2cos(x)*sin(2x)=2sin(x)+cos(2x) б) Найдите все корни этого уравнения, принадлежащие отрезку [3pi; (9pi)/2]. Решение График	а) Решите уравнение 2cos x sin 2x =2sinx +cos2x ! 36 вариантов ФИПИ Ященко 2023 Вариант 9 Задание 12

3528	а) Решите уравнение (log_{2}(8x^2))^2-log_{4}(2x)-1=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [0,4; 0,8] Решение График	а) Решите уравнение log2 2(8×2) -log4 (2x) -1 =0 ! 36 вариантов ФИПИ Ященко 2023 Вариант 8 Задание 12

Показана страница 1 из 36

Источник

За это задание ты можешь получить 2 балла. На решение дается около 10 минут. Уровень сложности: повышенный.
Средний процент выполнения: 45.3%
Ответом к заданию 12 по математике (профильной) может быть развернутый ответ (полная запись решения с обоснованием выполненных действий).

Разбор сложных заданий в тг-канале

Задачи для практики

Задача 1

а) Решите уравнение $11cos 2x=7sin (x-{π} / {2})-9$.

б) Укажите корни этого уравнения, принадлежащие отрезку $[-π;0]$.

Решение

а) $11cos 2x=7sin (x-{π} / {2})-9$,

$11(2cos^2 x-1)=-7cos x-9$,

$22cos^2 x -11+7cos x +9=0$,

$22cos^2 x+7cos x -2=0$.

Обозначим $cos x=t$, $|t|⩽1$.

Тогда уравнение примет вид: $22t^2+7t-2=0$.

Решим его. $22t^2+7t-2=0$,

$D=49+2⋅ 4⋅ 22=225$. $t_{1,2}={-7±15} / {44}$,

$t_1=-{1} / {2}$, $t_2={8} / {44}={2} / {11}$.

$1$. $cos x=-{1} / {2}$, $x=±(π-{π} / {3})+2π n$;

$x=± {2π} / {3}+2π n$, $n∈ Z$.

$2$. $cos x={2} / {11}$, $x=± arccos {2} / {11}+2π k$, $k∈ Z$.

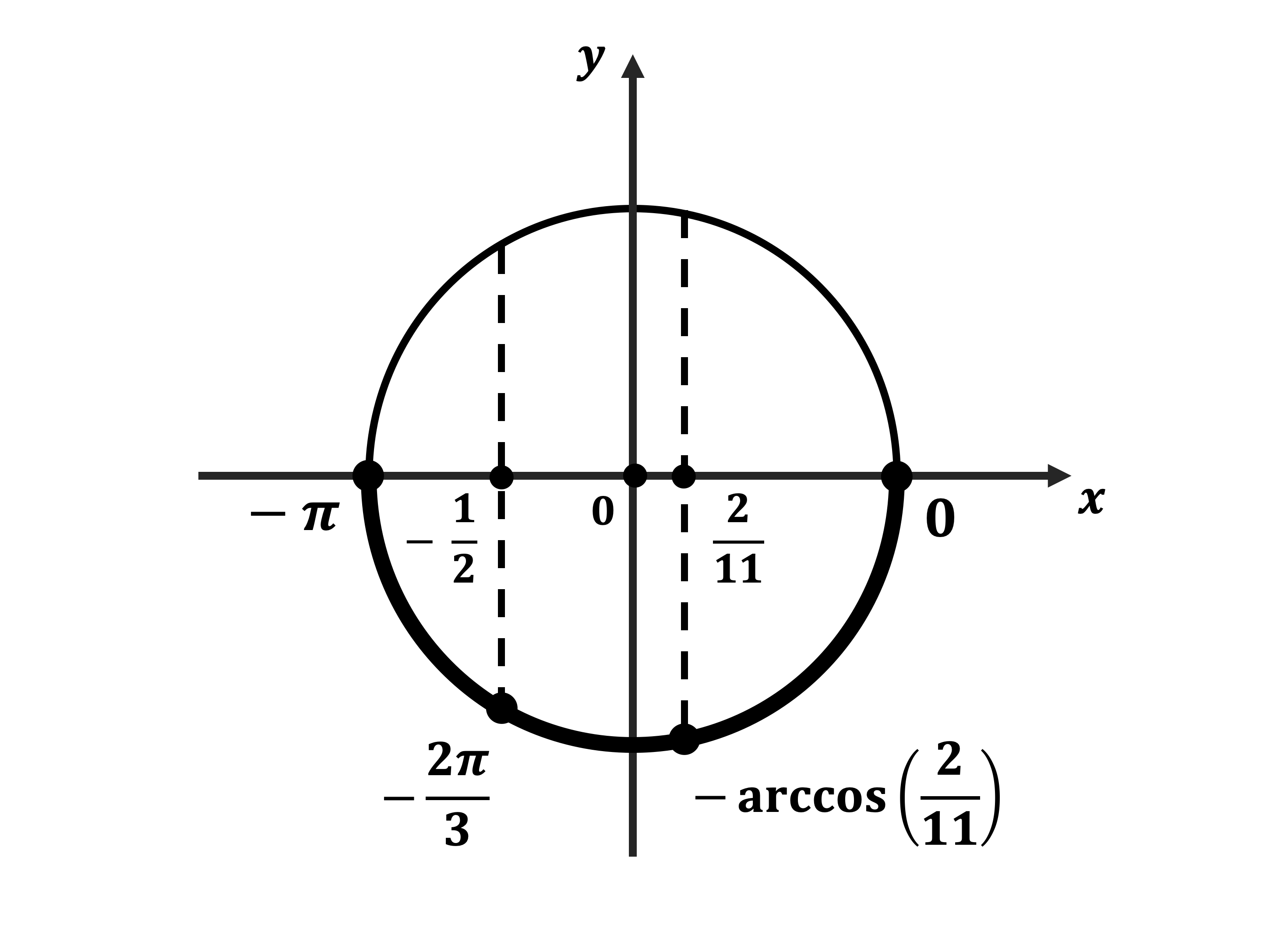
б) Найдём корни этого уравнения, принадлежащие промежутку $[-π;0]$.

$x_1=-π+{π} / {3}=-{2π} / {3}$

$x_2=-arccos {2} / {11}$.

Ответ: а)$± {2π} / {3}+2πn, n∈ Z; ± arccos {2} / {11}+2π k, k∈ Z;б)-{2π}/{3}, -arccos{2}/{11}$

Задача 2

а) Решите уравнение $2 sin^2 x — 7 cos(x + {π}/{2})- 4 = 0$.

б) Найдите все корни этого уравнения, принадлежащие промежутку $[-2π;-{π}/{2}]$.

Решение

а) Преобразуем уравнение, согласно формуле приведения:

$cos(x+{π}/{2})=-sinx,$

$2sin^2x + 7sinx -4 = 0$

Обозначим $sin x = t, −1 ≤ t ≤ 1$, получим

$2t^2 + 7t -4 = 0.$

$t_1 = {−7 − 9}/{2·2} = −4$ — не удовлетворяет условию $−1 ≤ t ≤ 1. $

$t_2 = {−7 + 9}/{2·2} = {1}/{2}$.

Вернёмся к исходной переменной:

$sinx ={1}/{2}$,

$x = {π}/{6} + 2πn, n ∈ Z$

$x = {5π}/{6} + 2πk, k ∈ Z$

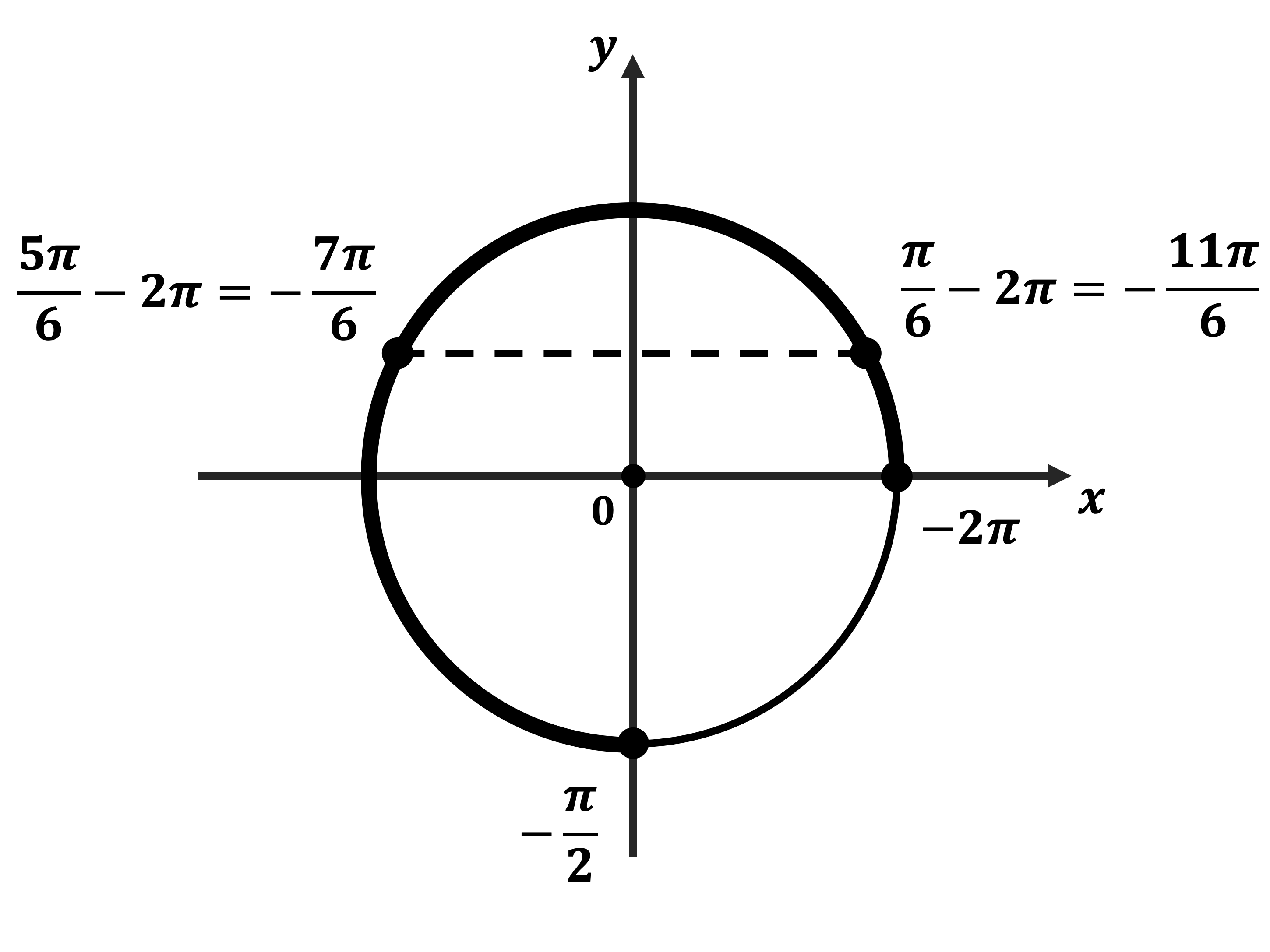
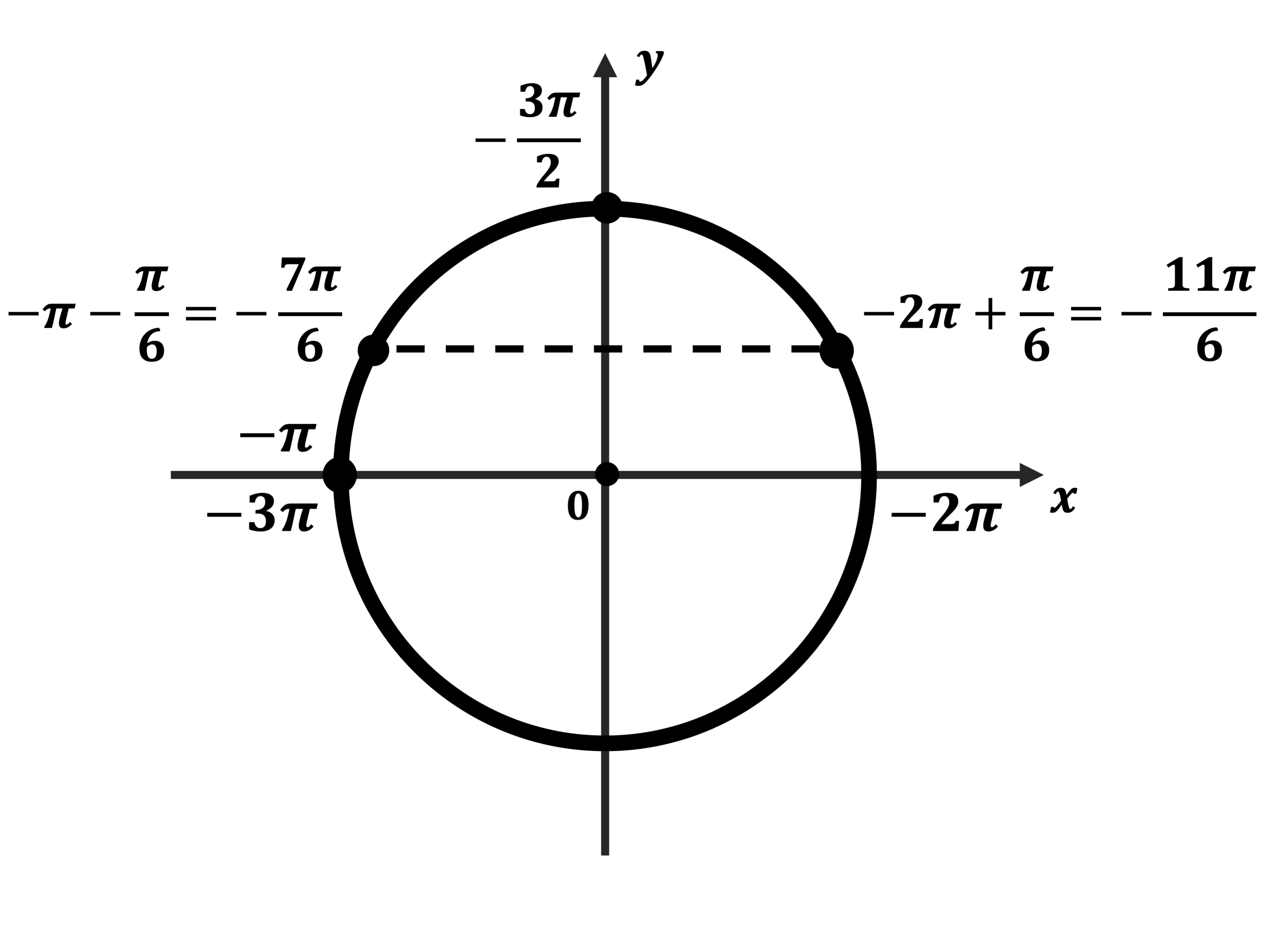
б) Корни, принадлежащие отрезку $[-2π; -{π}/{2}]$, найдём с помощью единичной окружности. Получим: ${π}/{6}-2π=-{11π}/{6}; {5π}/{6}-2π=-{7π}/{6}$.

Ответ: а) $ {π}/{6} + 2πn, n ∈ Z$; $ {5π}/{6} + 2πk, k ∈ Z$ б) $-{11π}/{6};-{7π}/{6}$

Задача 3

а) Решите уравнение $2 cos^2 x — 5 sin(x + {3π}/{2})+ 2 = 0$.

б) Найдите все корни этого уравнения, принадлежащие промежутку $[{π}/{2};{3π}/{2}]$.

Решение

а) Преобразуем уравнение, согласно формуле приведения:

$sin(x+{3π}/{2})=-cosx,$

$2cos^2x + 5 cos x + 2 = 0$

Обозначим $cos x = t, −1 ≤ t ≤ 1$, получим $2t^2 + 5t + 2 = 0. t_1 = {−5 − 3}/{2·2} = −2$ — не удовлетворяет условию $−1 ≤ t ≤ 1. t_2 = {−5 + 3}/{2· 2} = −{1}/{2}$.

Вернёмся к исходной переменной: $cos x = − {1}/{2}$,

$x = ±(π − {π}/{3}) + 2πn, n ∈ Z , x = ±{2π}/{3} + 2πn, n ∈ Z.$

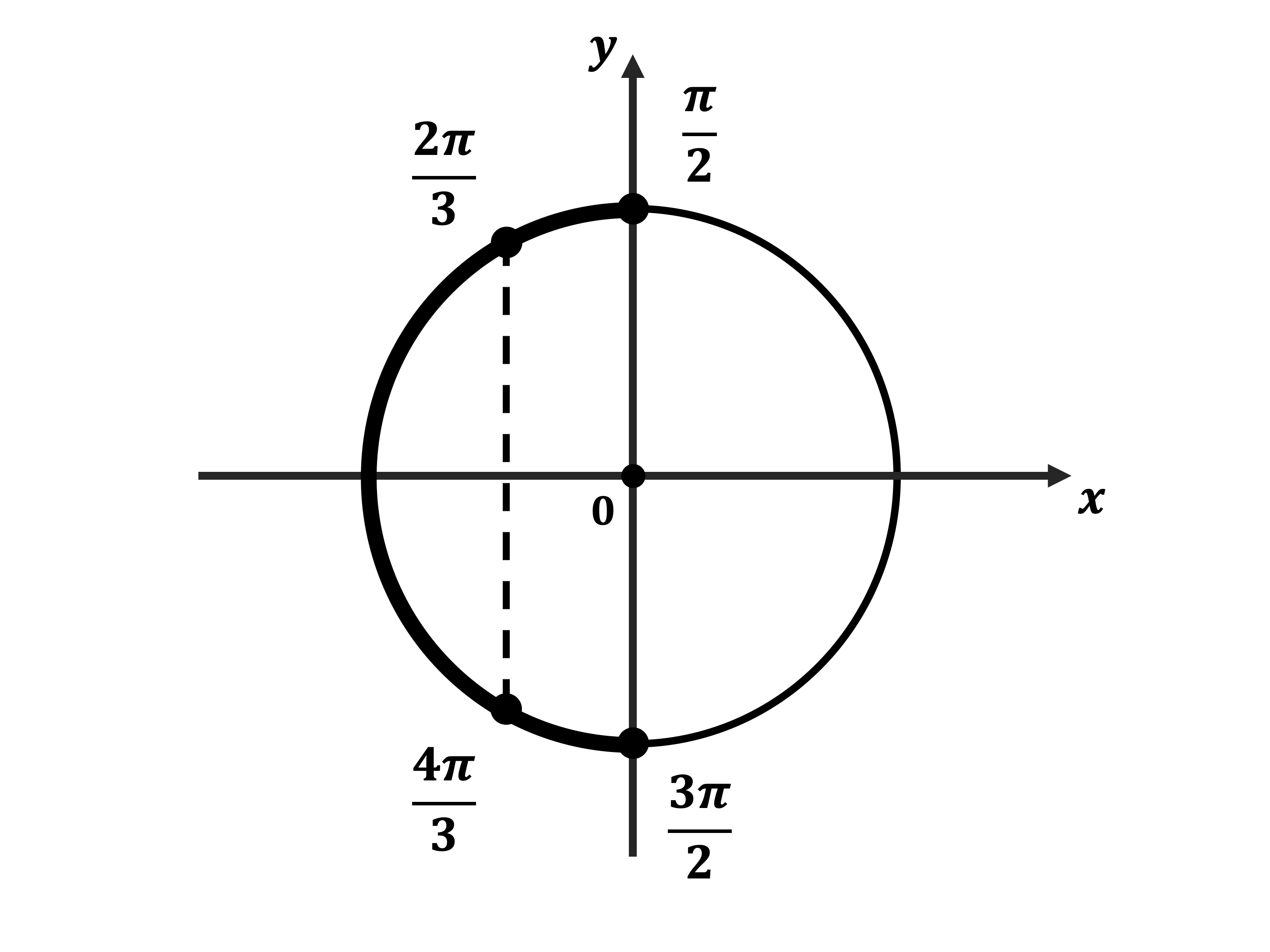
б) Корни, принадлежащие отрезку $[{π}/{2}; {3π}/{2}]$, найдём с помощью единичной окружности. Получим числа ${2π}/{3}; {4π}/{3}$.

Ответ: а)$±{2π}/{3}+2πn,n∈Z;$ б) ${2π}/{3};{4π}/{3}$

Задача 4

а) Решите уравнение $cos(x — {3π}/{2})= sin 2x$.

б) Найдите все корни этого уравнения, принадлежащие промежутку $[-{3π}/{2};0]$.

Решение

а) Преобразуем уравнение:

$−sin x = sin 2x,$

$sinx + 2 sin x cos x = 0,$

$sinx(1 + 2 cos x) = 0,$

$sin x = 0;x = πn, n ∈ Z,$

$cosx = -{1}/{2}; x = ±{2π}/{3} + 2πk, k ∈ Z .,$

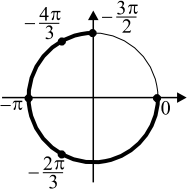
б) Корни, принадлежащие отрезку $[-{3π}/{2};0]$, найдём с помощью единичной окружности. Получим числа $−{4π}/{3}; −π; −{2π}/{3}; 0$.

Ответ: а) $x=±{2π}/{3}+2πk;x=πn,k,n∈Z$ б) $-{4π}/{3};-π;-{2π}/{3};0$.

Задача 5

а) Решите уравнение $sin({π}/{2}+ x)= sin (-2x)$.

б) Найдите все корни этого уравнения, принадлежащие промежутку $[0; π]$.

Решение

а) Преобразуем уравнение:

$cos x = − sin 2x,$

$cos x + 2 sin x cos x = 0,$

$cos x(1 + 2 sin x) = 0,$

$cos x = 0;$

$x = {π}/{2} + πn, n ∈ Z$

$sin x = −{1}/{2},$

$x = (−1)^{k+1}·{π}/{6} + πk, k ∈ Z$

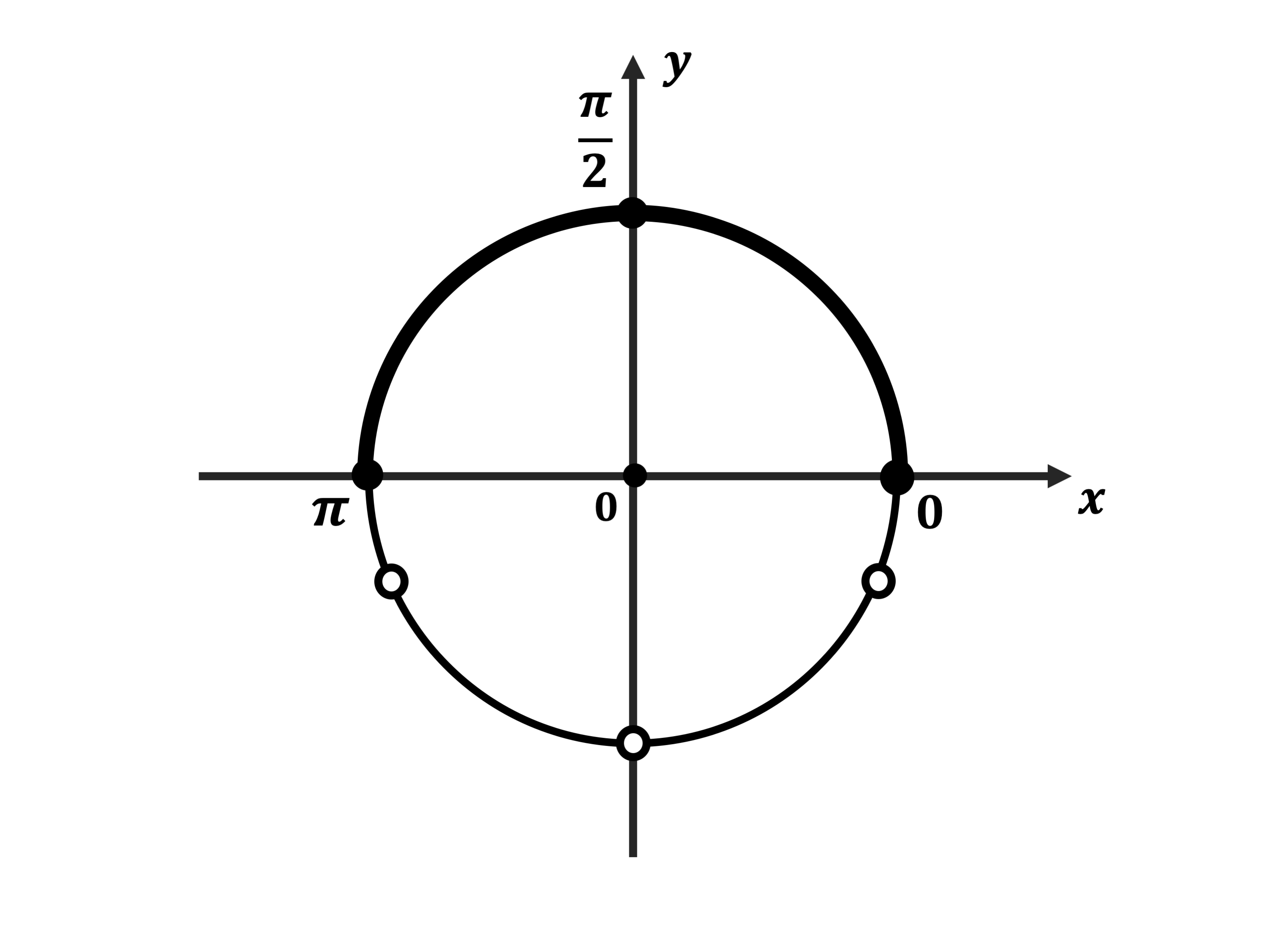
б) Корни, принадлежащие отрезку $[0; π]$, найдём с помощью единичной окружности.

Указанному промежутку принадлежит единственное число ${π}/{2}$.

Ответ: а) ${π}/{2}+πn,n∈Z;(-1)^{k+1}{π}/{6}+πk,k∈Z$; б) ${π}/{2}$

Задача 6

а) Решите уравнение $sin x(2 sin x — 1) + √3 sin x + sin {4π}/{3}= 0$.

б) Найдите все корни этого уравнения, принадлежащие промежутку $[-{π}/{2};π]$.

Решение

а) Решим уравнение $sinx(2sinx-1) +√3sinx + sin{4π}/{3} = 0$.

Так как $sin{4π}/{3} = sin(π +{π}/{3}) = − sin{π}/{3} = −{√3}/{2}$, то уравнение примет вид $sin x(2 sin x-1) +√3 sin x-{√3}/{2} = 0$. Отсюда $2 sin x(sin x-{1}/{2})+ √3(sin x-{1}/{2}) = 0; (2sinx+√3)(sin x-{1}/{2}) = 0$.

Тогда $sin x = {1}/{2}; x = (−1)^n{π}/{6} + πn$ или $sin x = −{√3}/{2}; x = (−1)^{n+1}{π}/{3} + πn$, где $n ∈ Z.$

б) Корни, принадлежащие промежутку $[−{π}/{2}; π]$, найдём с помощью числовой окружности: $−{π}/{3}; {π}/{6}; {5π}/{6}$.

Ответ: а)$(-1)^{n}{π}/{6}+πn;(-1)^{n+1}{π}/{3}+πn,n∈Z$; б) $-{π}/{3};{π}/{6};{5π}/{6}$

Задача 7

а) Решите уравнение $4cos^{2}x = 3cos2x + 1$.

б) Найдите корни уравнения, принадлежащие отрезку $[-4π;-{5π}/{4})$.

Решение

a) $4cos^{2}x = 3cos2x+1$,

$4cos^{2}x = 3(2cos^{2}x-1)+1$,

$4cos^{2}x=6cos^{2}x-3+1$,

$cos^{2}x=1, [tablecosx=1; cosx=-1;$ $[tablex=2πn, n ∈ Z; x=π+2πk, k ∈ Z;$ $x=πk, k ∈ Z$

б) Корни, принадлежащие промежутку $[-4π;-{5π}/{4})$, найдем из неравенства $-4π ≤ πk < -{5π}/{4}; k=-4, -3, -2$

$x_1=-4π, x_2=-3π, x_3=-2π$.

Ответ: а)$πn,n∈Z$;б)$-4π;-3π;-π$

Задача 8

а) Решите уравнение $cos (2x) + 3 sin x — 2 = 0$.

б) Найдите корни уравнения, принадлежащие отрезку $[-3π;-π]$.

Решение

a) $cos(2x) + 3sinx-2=0$,

$1 — 2sin^{2}x + 3 sin x -2 = 0$,

$2 sin^{2}x — 3sin x +1 = 0$,

Пусть $sin x = y, |sinx| ≤ 1$, уравнение примет вид

$2y^2 — 3y + 1 = 0$,

$y_{1,2} = {3±√{9-8}}/{4} = {3±1}/{4};$

$ y_1=1, y_2={1}/{2}$.

$sin x = 1, x = {π}/{2}+2πn, n ∈ Z; sinx={1}/{2}, x=(-1)^{k}{π}/{6} + πk, k ∈ Z$.

б) Найдём корни уравнения на отрезке $[-3π;-π]$.

С помощью числовой окружности отберём корни уравнения, принадлежащие $[-3π;-π]$.

Это числа $-{11π}/{6}, -{3π}/{2}, -{7π}/{6}$.

Ответ: а)${π}/{2}+2πn,n∈Z;(-1)^{k}{π}/{6}+πk,k∈Z$;б)$-{11π}/{6};-{3π}/{2};-{7π}/{6}$

Задача 9

а) Решите уравнение $2 cos^2 x + 19 sin x + 8 = 0$.

б) Найдите корни уравнения, принадлежащие отрезку $[-π;{π}/{2}]$.

Решение

a) $2 cos^{2}x + 19sinx+8=0$,

$2(1 — sin^{2}x) + 19 sin x +8 = 0$,

$-2 sin^{2}x + 19 sin x +10 = 0$,

$2 sin^{2}x — 19 sin x -10 = 0$.

Пусть $sin x = y, |y| ≤ 1$, уравнение примет вид $2y^2 — 19y -10 = 0$, решим его: $y_{1,2} = {19±√{361 + 80}}/{4} = {19±21}/{4}$.

$y_1 = 10$ или $y_2 = -{1}/{2}$. $y_1=10$ не удовлетворяет условию $|y| ≤ 1$. $sin x = -{1}/{2}, x = (-1)^{n+1}{π}/{6} + πn, n ∈ Z$.

б) Найдём корни уравнения на отрезке $[-π;{π}/{2}]$.

Это числа $-{5π}/{6}$ и $-{π}/{6}$.

Ответ: а)$(-1)^{n+1}{π}/{6}+πn,n∈Z$; б) $-{5π}/{6},-{π}/{6}$

Задача 10

а) Решите уравнение $8sin x + 4 cos^2 x = 7$.

б) Найдите корни уравнения, принадлежащие отрезку $[-{3π}/{2};-{π}/{2}]$.

Решение

a) $8 sin x + 4 cos^{2} x = 7$,

$4(1 — sin^{2}x) + 8 sin x — 7 = 0$,

$-4 sin^{2}x + 8 sin x — 3 = 0$,

$4 sin^{2}x — 8 sin x + 3 = 0$.

Пусть $sin x = t, |t| ≤ 1$, уравнение примет вид $4t^2 — 8t + 3 = 0$, решим его: $t_{1,2} = {8±√{64 — 48}}/{8} = {8±√{16}}/{8} = {8±4}/{8} = 1±{1}/{2}$.

$t_1 = {1}/{2}$ или $t_2 = {3}/{2}$. $t_2$ не удовлетворяет условию $|t| ≤ 1$. $sin x = {1}/{2}, x = (-1)^{n}{π}/{6} + πn, n ∈ Z$.

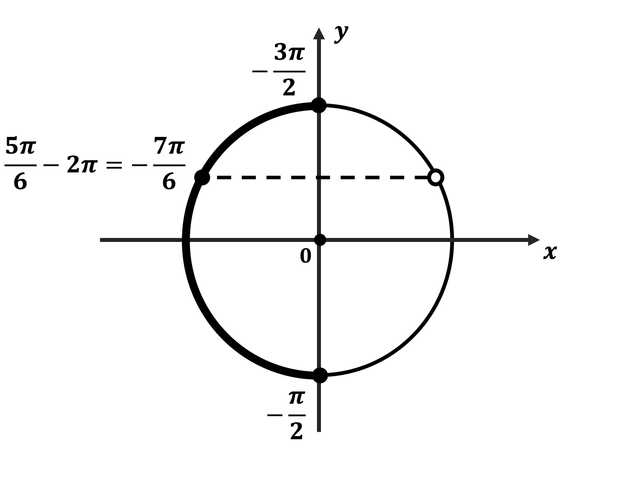
б) Найдём корни уравнения на отрезке $[-{3π}/{2};-{π}/{2}]$.

Это число ${5π}/{6} — 2π = -{7π}/{6}$.

Ответ: а)$(-1)^{n}{π}/{6}+πn,n∈Z$;б)$-{7π}/{6}$

Задача 11

а) Решите уравнение ${sin 2x}/{sin({3π}/{2}+ x)}= 1$.

б) Укажите корни этого уравнения, принадлежащие промежутку $(3π;{9π}/{2})$.

Решение

а) ${{sin2x}/{sin({3π}/{2} + x)} = 1$.

Зная, что $sin2x = 2sinxcosx$ и $sin({3π}/{2}+ x)= −cosx$, получим: ${2sinxcosx}/{−cosx}= 1$, где $cosx≠0, x≠{π}/{2}+ πm, m ∈ Z$.

$−2sinx = 1, sinx =−{1}/{2}$.

$x=−{π}/{6}+2πn, n ∈ Z;$

$x=-{5π}/{6}+ 2πk, k ∈ Z$.

б) Отберём корни уравнения, принадлежащие промежутку $(3π; {9π}/{2})$,с помощью числовой окружности.

$x_1=3π+{π}/{6}={19π}/{6}$,

$x_2=4π−{π}/{6}={23π}/{6}$.

Ответ: а)$-{π}/{6}+2πn,-{5π}/{6}+2πk,n,k∈Z$;б)${19π}/{6};{23π}/{6}$

Задача 12

а) Решите уравнение ${sin 2x}/{sin(π — x)}= √2$.

б) Укажите корни этого уравнения, принадлежащие промежутку $[-{5π}/{2};-π)$.

Решение

а)${sin2x}/{sin(π — x)}=√2$.

а) Применим формулу синуса двойного аргумента $sin2x = 2sinxcosx$ и формулу приведения $sin(π — x) = sin x$.

Уравнение примет вид: ${2sinxcosx}/{sinx} = √2$.

Учитывая, что $sinx≠0, x≠πn, n∈Z$, получим:

$2cosx=√2$,

$cosx = {√2}/{2}$,

$x = ±{π}/{4} + 2πk, k∈Z$;

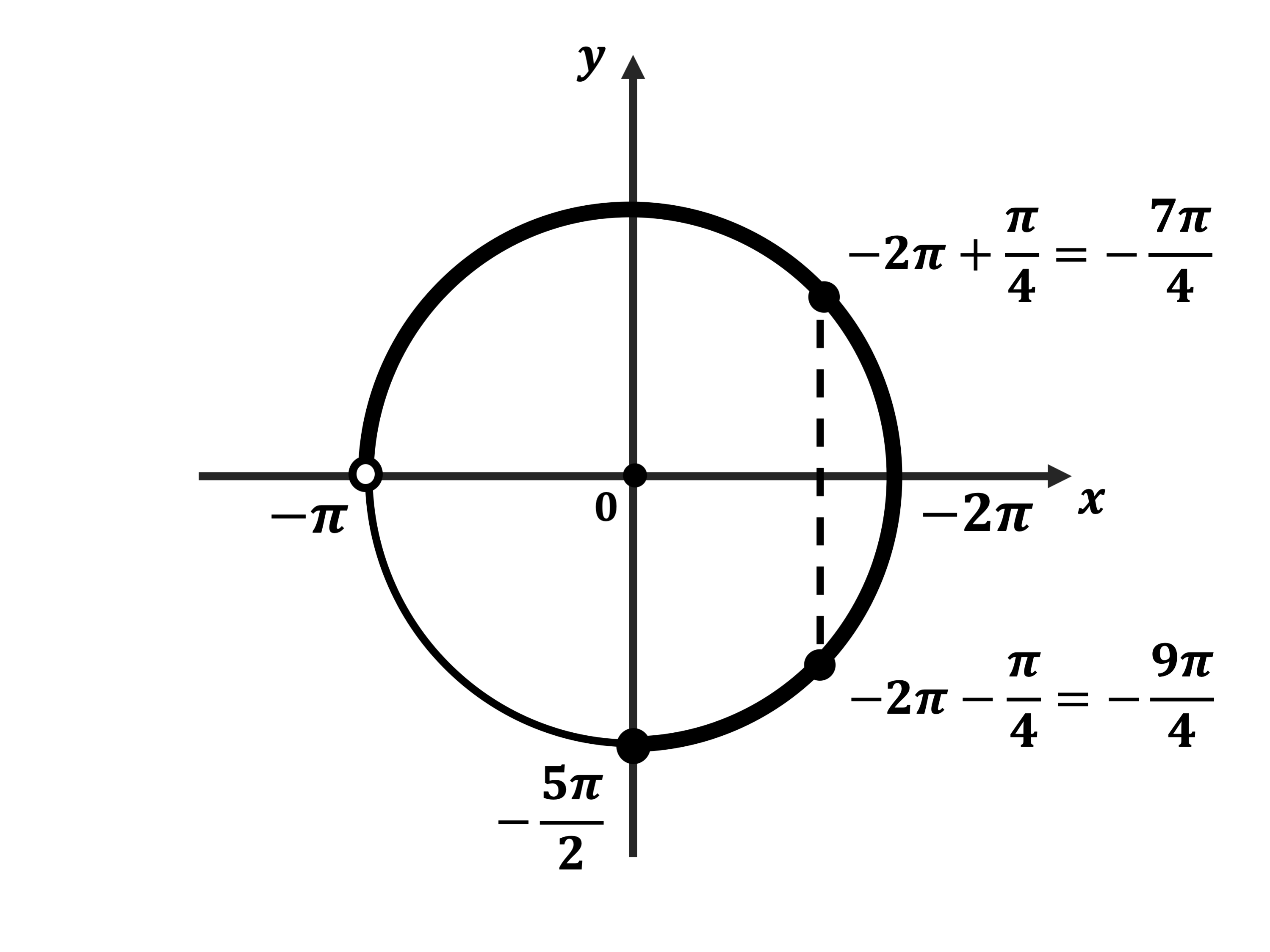
б) Отберём корни уравнения, принадлежащие промежутку $[-{5π}/{2};-π)$, с помощью окружности.

$x_1=-2π+{π}/{4}=-{7π}/{4}$

$x_2=-2π-{π}/{4}=-{9π}/{4}$

Ответ: а)$±{π}/{4}+2πk,k∈Z$;б)$-{9π}/{4};-{7π}/{4}$

Задача 13

а) Решите уравнение ${sin 2x}/{cos(π + x)}= -√2$.

б) Укажите корни этого уравнения, принадлежащие промежутку $(-2π;-{π}/{2})$.

Решение

а)${sin2x}/{cos(π + x)}=-√2$.

Зная, что $sin2x = 2sinxcosx, cos(π + x)=-cosx$, получим: ${2sinxcosx}/{-cosx}=-√2$.

Учитывая, что $cosx≠0, x≠{π}/{2} + πm, m∈Z$, имеем:

$2sinx=√2$,

$sinx = {√2}/{2}$,

$x = {π}/{4} + 2πn, n∈Z$;

$x = {3π}/{4} + 2πk, k∈Z$.

б) Отберём корни уравнения, принадлежащие промежутку $(-2π;-{π}/{2})$.

1. $x = {π}/{4} + 2πn, n∈Z$.

$-2π < {π}/{4} + 2πn < -{π}/{2},$

$-2 < {1}/{4} + 2n < -{1}/{2},$

$-2-{1}/{4} < 2n < -{1}/{2}-{1}/{4},$

$-{9}/{4} < 2n < -{3}/{4},$

$-{9}/{8} < n < -{3}/{8},$

$n = -1$.

При $n =-1$

$x = {π}/{4}-2π=-{7π}/{4}$.

2. $x = {3π}/{4} + 2πk, k∈Z$.

$-2π < {3π}/{4} + 2πk < -{π}/{2}$,

$-2 < {3}/{4} + 2k < -{1}/{2}$,

$-2-{3}/{4} < 2k < -{1}/{2}-{3}/{4}$,

$-{11}/{4} < 2k < -{5}/{4}$,

$-{11}/{8} < k < -{5}/{8}$,

$k = -1$.

При $k = -1$

$x = {3π}/{4}-2π = -{5π}/{4}$.

Ответ: а)${π}/{4}+2πn,{3π}/{4}+2πk,n,k∈Z$;б)$-{7π}/{4};-{5π}/{4}$

Задача 14

а) Решите уравнение $9·3^{2 cos x} — 10√3·3^{cos x} + 3 = 0$.

б) Укажите корни этого уравнения, принадлежащие отрезку $[{3π}/{2};4π]$.

Решение

а) После замены $t = 3^{cosx}$ исходное уравнение примет вид $9t^2 — 10√3t + 3 = 0$. Корни этого уравнения $t = √3; t = {√3}/{9}$. Возвращаясь к переменной $x$, получим

$[table3^{cosx}=√3; 3^{cosx}={√3}/{9};$ $[table3^{cosx}=3^{{1}/{2}}; 3^{cosx}=3^{-{3}/{2}};$ $[tablecosx={1}/{2}; cosx=-{3}/{2};$

Второе уравнение совокупности не имеет корней. Решая первое уравнение, получим $x =±{π}/{3} + 2πn; n ∈ Z$.

б) Запишем решение уравнения в виде $x =-{π}/{3} + 2πn; n ∈ Z$ или $x ={π}/{3} + 2πk; k ∈ Z$ и выясним, для каких целых значений $n$ и $k$ справедливы неравенства ${3π}/{2}≤-{π}/{3}+2πn≤4π$ и ${3π}/{2}≤{π}/{3}+2πk≤4π$.

Получим ${11}/{12} ≤ n ≤ {26}/{12}$ и ${7}/{12} ≤ k ≤{22}/{12}$.

Откуда следует, что два целых значения $n = 1$ и $n = 2$ удовлетворяют неравенству ${11}/{12} ≤ n ≤ {26}/{12}; k = 1$ — единственное целое $k$, удовлетворяющее неравенству ${7}/{12} ≤ k ≤{22}/{12}$.

При $n = 1$ $x = -{π}/{3} + 2π·1 = {5π}/{3}$.

При $n = 2$ $x = -{π}/{3} + 2π·2 = {11π}/{3}$.

При $k = 1$ $x = {π}/{3} + 2π·1 = {7π}/{3}$. Итак, ${5π}/{3}; {7π}/{3}; {11π}/{3}$ — корни уравнения, принадлежащие промежутку $[{3π}/{2};4π]$.

Ответ: а)$x=±{π}/{3}+2πn,n∈Z$;б)${5π}/{3};{7π}/{3};{11π}/{3}$

Задача 15

а) Решите уравнение $log_2^2(2 sin x + 1) — 17 log_2(2 sin x + 1) + 16 = 0$.

б) Укажите корни этого уравнения, принадлежащие отрезку $[{π}/{4};2π]$.

Решение

а) После замены $t = log_2(2 sin x+1)$ исходное уравнение примет вид $t^2-17t+16 = 0$. Корни этого уравнения $t = 1, t = 16$. Возвращаясь к переменной $x$, получим:

$[tablelog_2(2 sin x + 1) = 1; log_2(2 sin x + 1) = 16;$ $[table2 sin x + 1 = 2;; 2sin x + 1 = 2^{16};$

Второе уравнение совокупности не имеет корней. Решая первое уравнение, получим: $sin x = {1}/{2}; x = (-1)^n{π}/{6} + πn; n ∈ Z$.

б) Запишем решение уравнения в виде $x = {π}/{6} + 2πn; n ∈ Z$ или $x = {5π}/{6} + 2πk; k ∈ Z$ и выясним, для каких целых значений $n$ и $k$ справедливы неравенства ${π}/{4}≤{π}/{6}+2πn≤2π$ и ${π}/{4}≤{5π}/{6}+2πk≤2π$.

Получим: ${1}/{24}≤n≤{11}/{12}$ и $-{7}/{24}≤k≤{7}/{12}$, откуда следует, что нет целых значений $n$, удовлетворяющих неравенству ${1}/{24}≤n≤{11}/{12}; k = 0$ — единственное целое $k$, удовлетворяющее неравенству $-{7}/{24}≤k≤{7}/{12}$.

При $k = 0$ $x = {5π}/{6} + 2π·0 = {5π}/{6}$. Итак, ${5π}/{6}$ — корень уравнения, принадлежащий отрезку $[{π}/{4};2π]$.

Ответ: а)$(-1)^{n}{π}/{6}+πn,n∈Z$;б)${5π}/{6}$

Задача 16

а) Решите уравнение $6 log_2^2(2 cos x) — 9 log_2(2 cos x) + 3 = 0$.

б) Найдите все корни этого уравнения, принадлежащие отрезку $[-{π}/{2};π]$.

Решение

а) Решим уравнение $6log_2^2(2 cos x)-9 log_2(2 cos x)+3 = 0$. Обозначим $log_2(2 cos x) = t$ и решим получившееся квадратное уравнение.

$6t^2 — 9t + 3 = 0, t = {9±3}/{12}; t_1 = {1}/{2}; t_2 = 1$.

$[tablelog_2(2 cos x) ={1}/{2}; log_2(2 cos x) = 1;$ $[table2 cos x = √2; 2 cos x = 2;$

$[tablecos x = {√2}/{2}; cos x= 1;$ $[tablex = ±{π}/{4}+ 2π n; n ∊ Z; x = 2πk; k ∊ Z;$

б) Корни, принадлежащие отрезку $[-{π}/{2};π]$, найдём с помощью числовой окружности:

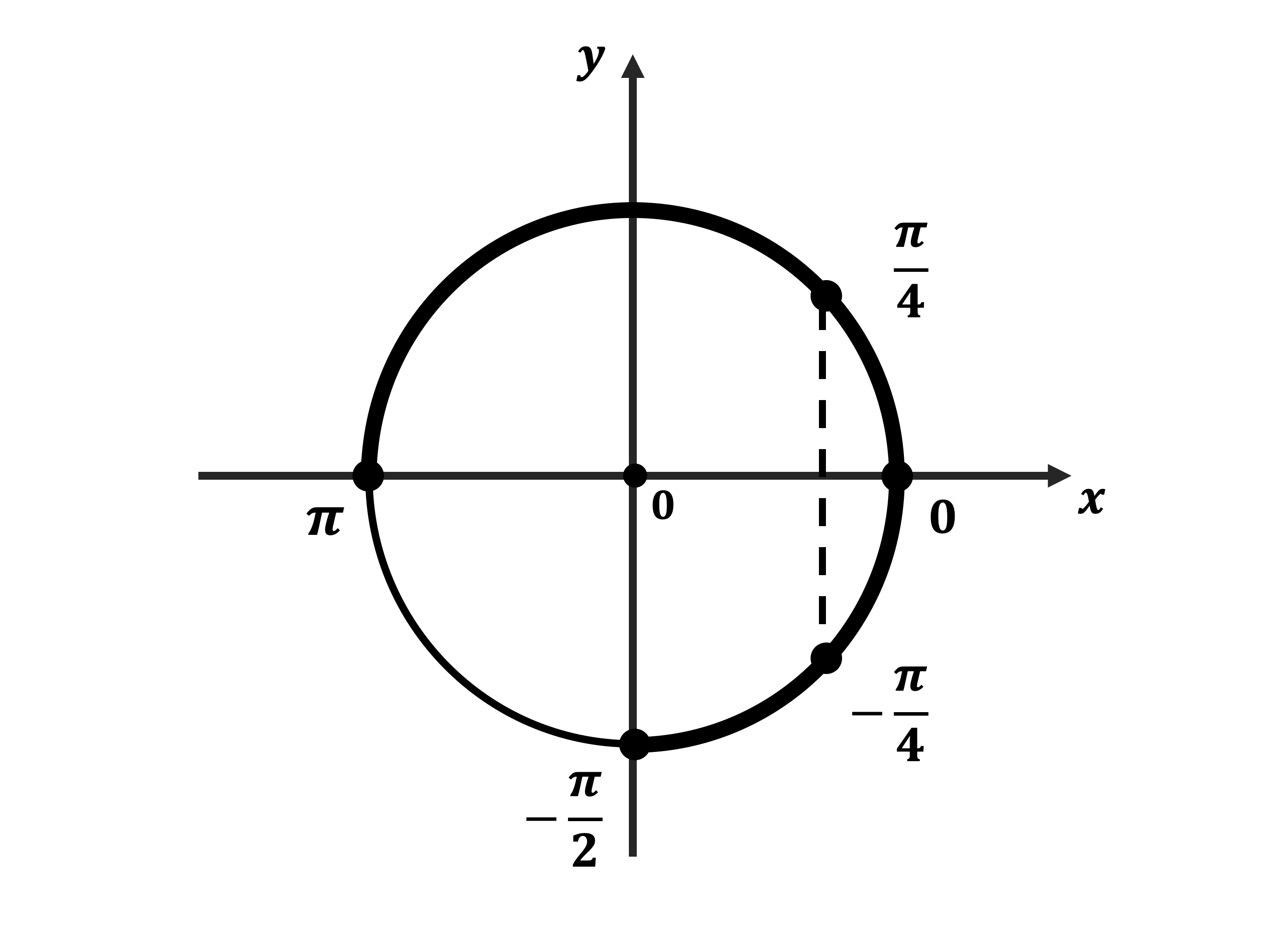
$x_1 = -{π}/{4}; x_2 = 0; x_3 ={π}/{4}$.

Ответ: а)$±{π}/{4}+2πn,n∈Z;2πk,k∈Z$;б)$-{π}/{4};0;{π}/{4}$

Задача 17

а) Решите уравнение $2log_2^2(2 sin x) — 3 log_2(2 sin x) + 1 = 0$.

б) Найдите все корни этого уравнения, принадлежащие отрезку $[{3π}/{2}; 3π]$.

Решение

а) Решим уравнение $2log_2^2(2 sin x) — 3 log_2(2 sin x) + 1 = 0$. Обозначим $log_2(2 sin x) = t$ и решим получившееся уравнение. $2t^2 — 3t + 1 = 0, t = {3±1}/{4}; t_1 = 1; t_2 ={1}/{2}$

$[tablelog_2(2 sin x) = 1; log_2(2 sin x) ={1}/{2};$ $[table2 sin x = 2; 2 sin x=√2;$

$[tablesin x = 1; sin x = {√2}/{2};$ $[tablex={π}/{2}+2πn; x=(-1)^k{π}/{4}+πk;$ $n,k∈Z$

б) Корни, принадлежащие отрезку $[{3π}/{2}; 3π]$, найдём с помощью числовой окружности:

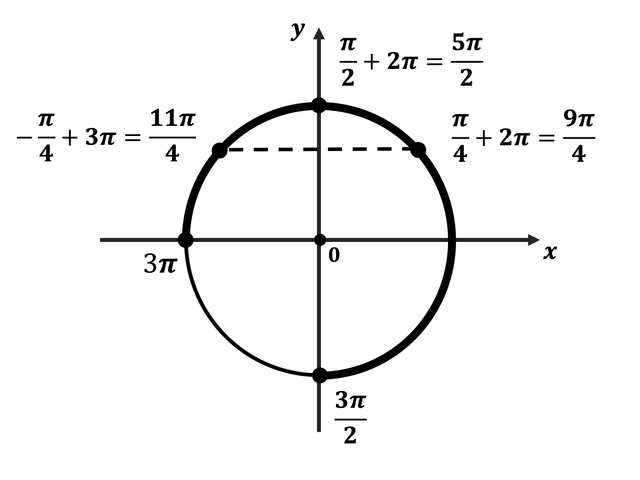
$x_1 = 2π + {π}/{4} = {9π}/{4}; x_2 = 2π + {π}/{2} ={5π}/{2}; x_3 = 3π -{π}/{4} = {11π}/{4}$.

Ответ: а)${π}/{2}+2πn,n∈Z;(-1)^k{π}/{4}+πk,k∈Z$;б)${9π}/{4};{5π}/{2};{11π}/{4}$

Задача 18

а) Решите уравнение $27^{x} — 5·9^{x} — 3^{x+4} + 405 = 0$.

б) Укажите все корни этого уравнения, принадлежащие отрезку $[log_{3}6; log_{3}10]$.

Решение

а) Преобразуем исходное уравнение и разложим на множители его левую часть.

$3^{3x} — 5·3^{2x} — 81·3^x + 405 = 0$,

$3^{2x}(3^x — 5) — 81(3^x — 5) = 0$,

$(3^{2x} — 81)(3^x — 5) = 0$.

Получаем: $3^{2x} -81 = 0$ или $3^x -5 = 0$. Значит, $3^{2x} = 81$, откуда $x = 2$ или $3^x = 5$, откуда $x = log_{3}5$.

б) Нам нужно выбрать те корни уравнения, которые принадлежат отрезку $[log_{3}6; log_{3}10]$. Заметим, что $2 = log_{3}9$. Тогда $log_{3}5 < log_{3}6 < 2 < log_{3}10$. Значит, указанному отрезку принадлежит корень $x = 2$.

Ответ: а)$2;log_{3}5$; б)$2$

Задача 19

а) Решите уравнение $3√{2}sin({π}/{2}+x)-2=2cos^{2}x$.

б) Укажите корни этого уравнения, принадлежащие отрезку $[{3π}/{2};{5π}/{2}]$.

Решение

а) Запишем исходное уравнение в виде $2 cos^2 x — 3√2 cos x + 2 = 0$.

Решая это уравнение как квадратное относительно $cos x$, получим $(cos x)_{1,2} ={3√2±√{18 — 16}}/{4}={3√2± √2}/{4}$.

Значит, $(cos x)_1 = {√2}/{2}$, откуда $x =π/4 + 2πn, n ∈ Z$ или $x =-π/4 + 2πn, n ∈ Z$.

Уравнение $(cosx)_2 = √2$ корней не имеет.

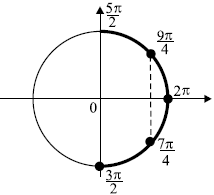
б) Отберём корни, принадлежащие отрезку $[{3π}/{2};{5π}/{2}]$ с помощью числовой окружности.

Получим числа

$2π -{π}/{4} ={7π}/{4}$;

$2π + {π}/{4} = {9π}/{4}$.

Ответ: а)$±{π}/{4}+2πn,n∈Z$;б)${7π}/{4},{9π}/{4}$

Задача 20

а) Решите уравнение $3√{3}cos({3π}/{2}+x)-3=2sin^{2}x$.

б) Укажите корни этого уравнения, принадлежащие отрезку $[2π; 3π]$.

Решение

а) Запишем исходное уравнение в виде $2sin^2 x — 3√3 sin x + 3 = 0$.

Решая это уравнение как квадратное относительно $sin x$, получим $(sin x)_{1,2} = {3√3±√{27-24}}/{4}= {3√3±√3}/{4}$.

Значит,$(sin x)_1 ={√3}/{2}$, откуда $x ={π}/{3} +2πn, n ∈ Z$ или $x ={2π}/{3}+2πm, m ∈ Z$.

Уравнение $(sin x)_2 = √3$ корней не имеет.

б) С помощью числовой окружности отберём корни, принадлежащие отрезку: $[2π; 3π]$

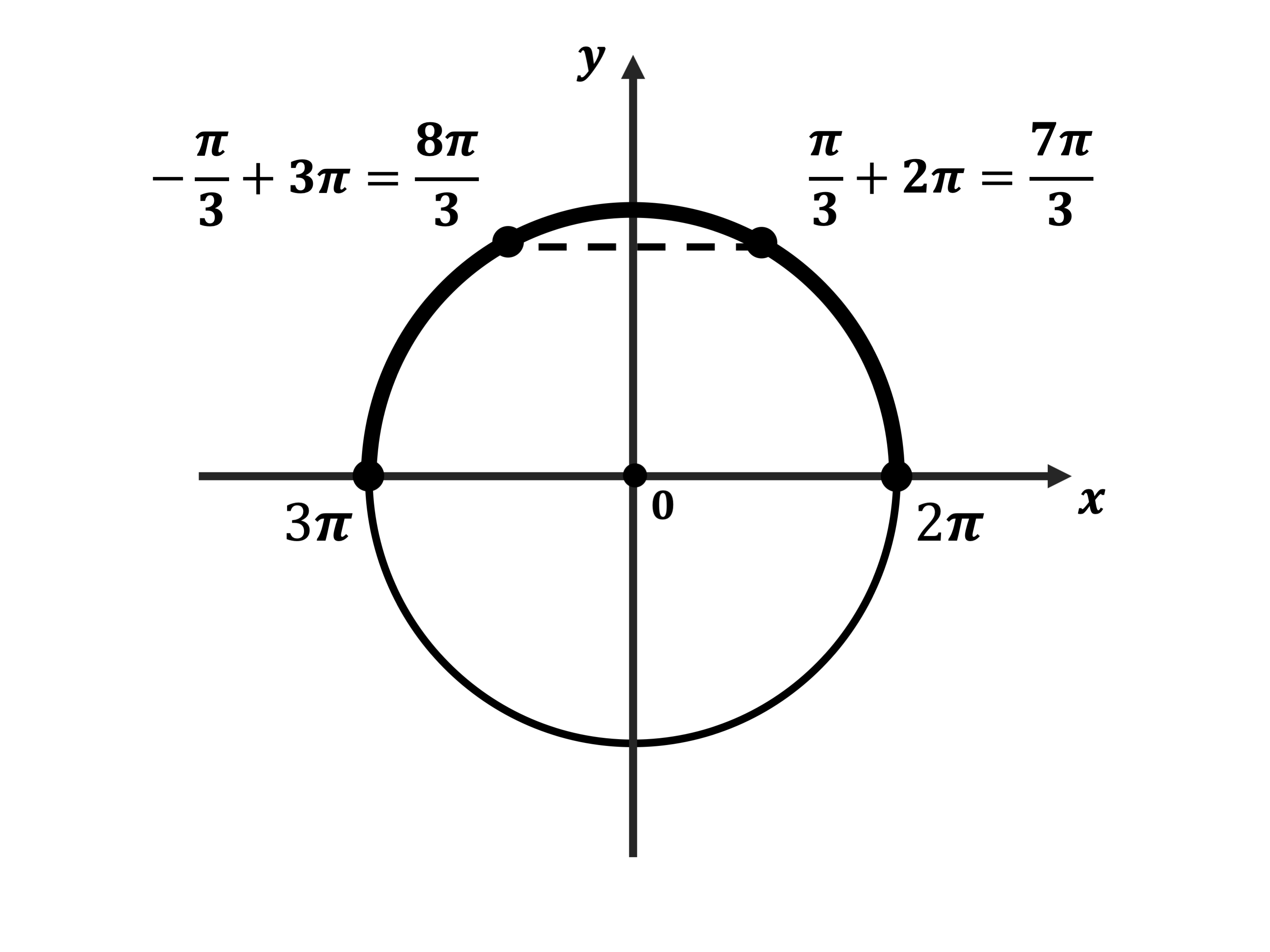
Получим числа:

$2π +{π}/{3}={7π}/{3}$;

$3π -{π}/{3}={8π}/{3}$.

Ответ: а)${π}/{3}+2πn,n∈Z;{2π}/{3}+2πm,m∈Z$;б)${7π}/{3},{8π}/{3}$

Значения функции: наибольшее и наименьшее

Разбор типовых вариантов заданий №12 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

Алгоритм решения:

Решение:

Второй вариант задания (из Ященко, №1)

Алгоритм решения:

Решение:

Третий вариант задания (из Ященко, №12)

Алгоритм решения:.

Решение:

Задание №12. Уравнения — профильный ЕГЭ по математике

Материал для подготовки к заданию номер 12 из ЕГЭ по профильной математике

Задание 12. Тригонометрическое уравнение

Радианы – инструкция по применению. Разбор 12 задания ЕГЭ математика профиль. Теория.

Тригонометрический круг, уравнения – быстрый старт. 12 задание ЕГЭ профильная математика. Теория

12 задания ЕГЭ по математике профильный уровень. Простейшие тригонометрические уравнения (часть 1,2)

Как запомнить табличные значения синуса, косинуса и т.д.?

ЕГЭ по математике 2023. Задание 12. Теория. Синус, косинус и все, все, все

ЕГЭ по математике – задание 12 2023 года. Практика. Решение задач. Задача 1

Задачи для практики

Задача 1

Решение

Задача 2

Решение

Задача 3

Решение

Задача 4

Решение

Задача 5

Решение

Задача 6

Решение

Задача 7

Решение

Задача 8

Решение

Задача 9

Решение

Задача 10

Решение

Задача 11

Решение

Задача 12

Решение

Задача 13

Решение

Задача 14

Решение

Задача 15

Решение

Задача 16

Решение

Задача 17

Решение

Задача 18

Решение

Задача 19

Решение

Задача 20

Решение

Рекомендуемые курсы подготовки