Посимвольное двоичное преобразование информатика егэ - Помощь в подготовке к экзаменам и поступлению

Привет! В этой статье будут различные примеры решения задач из 5-ого задания ЕГЭ по информатике 2022.

Задание 5 решается не сложно, но, как всегда, нужно потренироваться решать подобные задачи, чтобы уверенно себя чувствовать на ЕГЭ по информатике 2022.

Рассмотрим классический пример.

Задача (Классическая)

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R по следующему принципу.

1) Строится двоичная запись числа N.
2) К этой записи дописываются справа ещё два разряда по следующему правилу:
а) Складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописываются в конец числа (справа). Например, запись 11100 преобразуется в запись 111001.
б) Над этой записью производятся те же действия — справа дописывается остаток от деления суммы цифр на 2.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.

Укажите минимальное число R, которое превышает 42 и может являться результатом работы алгоритма. В ответе это число запишите в десятичной системе.

Решение:

Алгоритму на вход приходит обычное натуральное число N.

Это число преобразуется в двоичную запись (пункт 1).

Во втором пункте правил формирования нового числа сказано, что к числу, полученному в первом пункте, дописываются справа ещё два дополнительных разряда.

Про 1 дополнительный разряд указано в подпункте а): «Складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописываются в конец числа (справа). Например, запись 11100 преобразуется в запись 111001.»

Если по простому сказать, то мы подсчитываем количество единиц в двоичном представлении числа N. Если количество единиц чётное, то пишем в 1 дополнительный разряд ноль, если нечётное, то пишем в 1 дополнительный разряд единицу.

Со вторым дополнительным разрядом происходит всё тоже самое, что и с первым разрядом, только когда подсчитываем количество единиц, мы так же подсчитываем и в 1-ом дополнительном разряде.

В вопросе просят указать входящее наименьшее число N, чтобы автомат выдал число R больше 42.

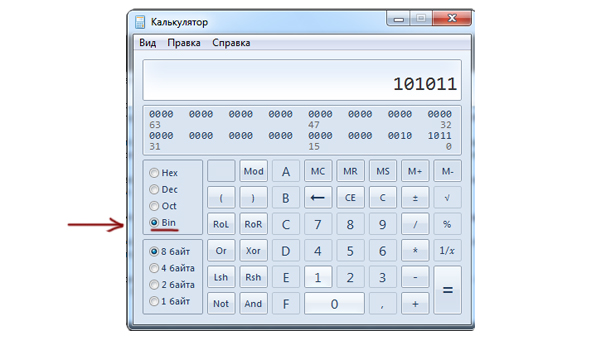
Возьмём наименьшее число, которое больше 42 (т.е. 43) и переведём его в двоичную систему. Это можно сделать с помощью стандартного windows калькулятора.

Вызываем калькулятор, выбираем Вид->Программист. Кликаем на отметку Dec (это означает, что мы находимся в десятичной системе) и набираем число 43. Затем кликаем на отметку Bin

Проверим число 101011₂. Может ли оно быть результатом работы нашего алгоритма?

Отделяем два дополнительных разряда справа. У нас, не считая двух дополнительных разрядов, количество единиц равно двум. Количество чётное, значит, в первом дополнительном разряде должен стоять 0. А у нас стоит 1.

Следовательно, число 101011₂ не может являться результатом работы алгоритма. И это число не подходит.

Проверим последующие числа. На калькуляторе можно прибавлять по 1 и получать следующее число в двоичной системе. Мы проверяем последовательно числа, чтобы не пропустить самое маленькое число.

Подходит число 101110₂. Количество единиц без двух дополнительных разрядов равно трём. Число нечётное. Значит, в первом дополнительном разряде должна стоять 1. В этом числе как раз стоит 1.

Количество единиц вместе с дополнительным разрядом равно 4. Число чётное, значит, во втором дополнительном разряде должен стоять 0. У нас и стоит во втором дополнительном разряде 0. Следовательно, число 101110₂ подходит по всем правилам и является наименьшим.

В десятичной системе это число 46.

Ответ: 46

Рассмотрим ещё одну интересную задачу для подготовки к ЕГЭ по информатике 2022.

Задача(Классическая, закрепление)

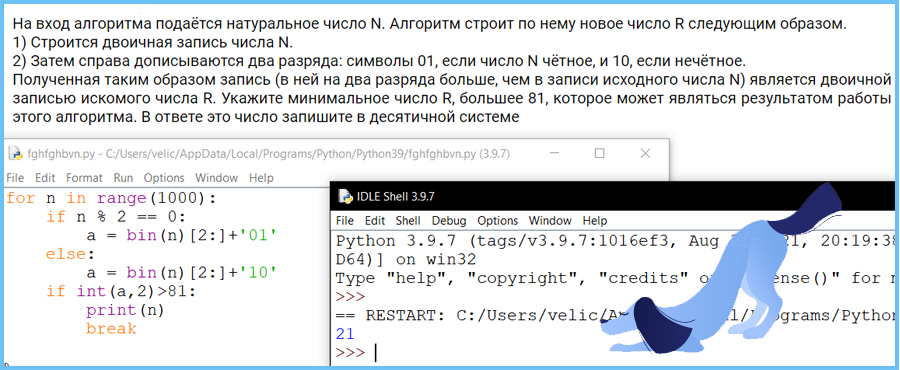
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.

1) Строится двоичная запись числа N.
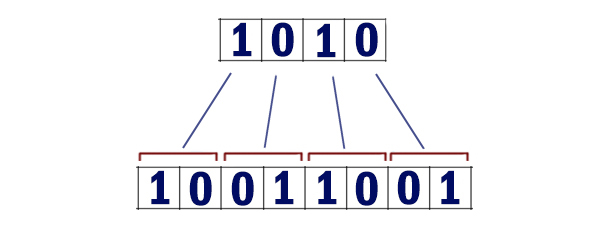
2) Каждый разряд этой записи заменяется двумя разрядами по следующему правилу: если в разряде стоит 0, то вместо него пишется 01; если в разряде стоит 1, то 1 заменяется на 10.
Например, двоичная запись 1010 числа 10 будет преобразована в 10011001.

Полученная таким образом запись (в ней в два раза больше разрядов, чем в записи исходного числа N) является двоичной записью искомого числа R.

Укажите максимальное нечётное число R, меньшее 256, которое может являться результатом работы данного алгоритма. В ответе это число запишите в десятичной системе.

Решение:

В этой задаче в начале строится двоичная запись числа N.

Каждый разряд превращается в два разряда! Единица превращается в 10. Ноль превращается в 01. На рисунке показан пример, как будет преобразовано число 10 = 1010₂.

Оценим первое число, которое меньше, чем 256. Это число 255.

255 = 11111111₂

Здесь количество разрядов равно 8. Это чётное число, значит, такое количество разрядов может быть в результате работы алгоритма. Только чётное количество разрядов может получится в результате работы алгоритма.

В старших двух разрядах должны быть цифры 10, т.к. исходное число N не может начинаться с нуля.

В остальных парах попробуем написать 10, чтобы число было как можно больше.

Получается, что число 10101010₂ удовлетворяет всем правилам алгоритма, является наибольшим, и оно меньше 256.

Но важный момент, нас просили в ответ записать нечётное число.

В двоичной системе число, которое оканчивается на ноль, является чётным.

В двоичной системе число, которое оканчивается на единицу, является нечётным.

Чтобы число было нечётным, изменим последние разряды на 01.

10101001₂ = 169

Ответ: 169

Набираем обороты в решении 5 задания из ЕГЭ по информатике 2022.

Задача(Классическая, закрепление)

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число следующим образом.

1) Строится двоичная запись числа N.

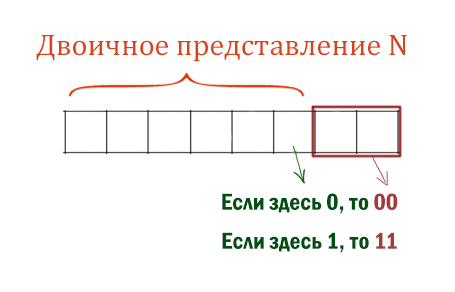
2) К этой записи дописываются справа ещё два разряда по следующему правилу: если N чётное, в конце числа справа дописываются два нуля, в противном случае справа дописываются две единицы. Например, двоичная запись 1101 будет преобразована в 110111.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа — результата работы данного алгоритма.

Укажите минимальное число N, для которого результат работы алгоритма будет больше 130. В ответе это число запишите в десятичной системе счисления.

Решение:

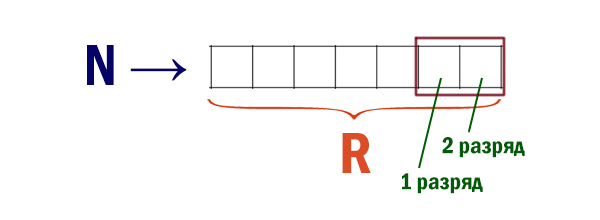
После перевода в двоичную систему исходного числа N, алгоритм строит новое число по следующему правилу:

Бордовым прямоугольником показаны дополнительные разряды.

Нужно найти минимальное число больше 130. Будем проверять последовательно числа, начиная с 131.

Подходит число 135. В ответе нужно указать число N. Отбросим от числа 10000111₂ дополнительные разряды и переведём в десятичную систему.

100001₂ = 33

Ответ: 33

Похожие задачи встречались в сборнике С. С. Крылова для подготовке к ЕГЭ по информатике.

Задача (Усложнённая)

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.

1. Из числа N вычитается остаток от деления N на 4.

2. Строится двоичная запись полученного результата.

3. К это записи справа дописываются ещё два дополнительных разряда по следующему правилу:

а) Складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописываются в конец числа (справа). Например, запись 11100 преобразуется в запись 111001.

б) Над этой записью производятся те же действия — справа дописывается остаток от деления суммы цифр на 2.

Полученная таким образом запись является двоичной записью числа R.

Укажите наибольшее число N, для которого результат работы данного алгоритма меньше 47. В ответе число N укажите в десятичной системе.

Решение:

Первый способ. Число R должно быть меньше 47. Переведём число 46 в двоичную систему.

46 = 101110₂

Результат от второго пункта не должен превышать 1011₂. Если результат от второго пункта будет превышать это число, то после добавления дополнительных разрядов получится число R, которое не меньше 47.

Проверим число 1011₂ = 11. Видим, что это число не может являться результатом пункта 2.

11 + 0 = 11 (остаток при делении 11 на 4 равен 3) —
11 + 1 = 12 (остаток при делении 12 на 4 равен 0) —
11 + 2 = 13 (остаток при делении 13 на 4 равен 1) —
11 + 3 = 14 (остаток при делении 13 на 4 равен 2) —

Здесь мы перебираем все остатки при делении на 4. Чтобы число 11 могло являться результатом пункта 2, число, помеченное зелёным цветом, должно совпадать с числом, помеченное оранжевым цветом. Стоит заметить, что если в первой строчке не совпадают числа, то и в остальных они тоже не совпадут. Верно и обратное. Если в первой строчке совпадут числа, то и для остальных остатков тоже числа будут совпадать.

Найдём, число, для которого будут совпадать эти числа, отмеченные зелёным и оранжевым цветом.

10 + 0 = 10 (остаток при делении 10 на 4 равен 2) Не подходит

9 + 0 = 9 (остаток при делении 9 на 4 равен 1) Не подходит

8 + 0 = 8 (остаток при делении 8 на 4 равен 0) Подходит!

Значит, число 8 нам подходит. Число 8 — это результат работы алгоритма в первом пункте. Нас просят найти максимальное число. Следовательно, возьмём остаток 3, чтобы исходное число N было как можно больше. Тогда N будет:

N = 8 + 3 = 11

Ответ получается 11.

Второй способ. Решим задачу с помощью Python’а.

Перебираем числа от 100 до 1 с помощью цикла for. Третий параметр «-1» в цикле for говорит о том, что мы перебираем числа в обратном порядке.

for i in range(100, 0, -1):
    n = i
    n = n - n % 4 # Выполняем первый пункт
    n = format(n, 'b') # Переводим в двоичную систему
    n = n + str(n.count('1') % 2) # Подпункт a) третьего пункта
    n = n + str(n.count('1') % 2) # Подпункт б) третьего пункта
    r = int(n, 2) # Переводим из двоичной системы в десятичную
    if r print(i)

В этой программе запрограммировали алгоритм, который указан в задаче. Если значение переменной r (результат работы алгоритма) меньше 47, то печатаем это значение на экран. Первое распечатанное число и есть ответ к задаче.

В переменную n по очереди подставляются числа из нашего диапазона (100-1). Команда % находит остаток от деления.

Функция count, в данном случае, подсчитывает количество единиц в строке, которая находится в переменной n.

Ответ: 11

Боковой вариант 5-ого задания из ЕГЭ по информатике.

Задача (Лучше знать)

Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам:

1. Перемножаются первая и вторая, а также третья и четвёртая цифры исходного числа.

2. Полученные два числа записываются друг за другом в порядке убывания (без разделителей).

Пример. Исходное число: 2465. Суммы: 2 * 4 = 8; 6 * 5 = 30. Результат: 308. Укажите наибольшее число, в результате обработки которого автомат выдаст число 124.

Решение:

В подобных задачах из ЕГЭ по информатике нумерация происходит начиная со старшего разряда.

Первое правило можно представить следующим образом:

Второе правило заключается в том, что мы «соединяем» два числа, полученных в первом пункте, причём, сначала идёт большее число, а затем меньшее.

Проанализируем число 124.

Чтобы четырёхзначное число было наибольшим, выгодно, чтобы в старшем разряде стояла 9. Но, не у числа 12, не у числа 4, нет такого делителя. Какой наибольший делитель мы можем получить? Это число 6. Число 6 является делителем 12-ти. Значит, первая цифра будет 6, а вторая цифра будет 2 (6*2=12).

Рассмотрим второе число 4. Третий разряд тоже желательно сделать побольше. Значит, в четвёртый разряд поставим 4, а в младший разряд 1 (4*1=4).

Ответ получается 6241.

Ответ: 6241

Счастливых экзаменов! Видеоролик можете посмотреть ниже!

За это задание ты можешь получить 1 балл. На решение дается около 2 минут. Уровень сложности: базовый.
Средний процент выполнения: 81%
Ответом к заданию 5 по информатике может быть цифра (число) или слово.

Урок посвящен тому, как решать 5 задание ЕГЭ по информатике

Объяснение 5 задания

5-е задание: «Анализ алгоритмов и исполнители»

Уровень сложности

— базовый,

Требуется использование специализированного программного обеспечения

— нет,

Максимальный балл

— 1,

Примерное время выполнения

— 4 минуты.

Проверяемые элементы содержания: Формальное исполнение алгоритма, записанного на естественном языке, или умение создавать линейный алгоритм для формального исполнителя с ограниченным набором команд

До ЕГЭ 2021 года — это было задание № 6 ЕГЭ

Типичные ошибки и рекомендации по их предотвращению:

«Как и в других заданиях базового уровня сложности, источником ошибок служит недостаточная внимательность и отсутствие или поверхностность самостоятельной проверки полученного ответа»

ФГБНУ «Федеральный институт педагогических измерений»

Проверка числовой последовательности на соответствие алгоритму

для выполнения некоторых заданий необходимо повторить тему системы счисления;
максимальное значение суммы цифр десятичного числа — это 18, так как 9 + 9 = 18;
для проверки правильности переданного сообщения иногда вводится бит четности — дополнительный бит, которым дополняется двоичный код таким образом, чтобы в результате количество единиц стало четным: т.е. если в исходном сообщении количество единиц было четным, то добавляется 0, если нечетным — добавляется 1:

например: 
 3₁₀ = 11₂ 
после добавления бита четности: 110
----
 4₁₀ = 100₂ 
после добавления бита четности: 1001

добавление к двоичной записи числа нуль справа увеличивает число в 2 раза:

например:
111₂ - это 7₁₀
добавим 0 справа:
1110₂ - это 14₁₀

Теперь будем рассматривать конкретные типовые экзаменационные варианты по информатике с объяснением их решения.

Разбор 5 задания

Задание демонстрационного варианта 2022 года ФИПИ
Плейлист видеоразборов задания на YouTube:

Решение задания про алгоритм, который строит число R

5_11: Задание 5 (6) ЕГЭ по информатике 2017 ФИПИ вариант 2 (Крылов С.С., Чуркина Т.Е.):

На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом:

Строится двоичная запись числа 4N.
К этой записи дописываются справа еще два разряда по следующему правилу:

складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 10000 преобразуется в запись 100001;
над этой записью производятся те же действия — справа дописывается остаток от деления суммы цифр на 2.

Полученная таким образом запись является двоичной записью искомого числа R.

Укажите такое наименьшее число N, для которого результат работы алгоритма больше 129. В ответе это число запишите в десятичной системе счисления.

Типовые задания для тренировки

✍ Решение:

✎ Решение аналитическим способом:

Заметим, что после выполнения второго пункта задания, будут получаться только четные числа! Наименьшим возможным четным числом, превышающим 129, является число 130. С ним и будем работать.
Переведем 130 в двоичную систему счисления. Используя компьютер это можно сделать с помощью программистского режима калькулятора. Либо в консоли интерпретатора Python набрать bin(130). Получим:

130₁₀ = 10000010₂

Это двоичное число получилось из исходного двоичного, после того как дважды был добавлен остаток от деления суммы цифр на 2. Т.е.:

в обратном порядке:
было 1000001 -> стало 10000010 
еще раз то же самое: 
было 100000 -> стало 1000001

Значит, необходимое нам двоичное число — это 100000.

Переведем 100000 в 10-ю систему. Для этого можно воспользоваться калькулятором, либо использовать интерпретатор Питона: int('100000',2).

100000₂ = 32₁₀

Так как по условию у нас 4*N, то 32 делим на 4 — > 8.

✎ Решение с использованием программирования:

PascalAbc.Net:

uses school;
 
begin
  var n_ := 1;
  while True do
  begin
    var n := 4*n_;
    var ost := bin(n).CountOf('1') mod 2; // остаток при делении на 2
    n := 2 * n + ost; //в двоичной с.с. добавляем разряд (*2) и остаток к этому разряру (+ost)
    ost := bin(n).CountOf('1') mod 2; // остаток при делении на 2
    n := 2 * n + ost;
    if n > 129 then
    begin
      println(n_);
      break
    end;
    n_ += 1;
  end;
end.

Python:

n_ = 1
while True:
    n = 4*n_
    r = str(bin(n))
    r = r[2:]
    for i in range(2):
        if r.count('1') % 2 == 0:
            r+='0'
        else:
            r+='1'
 
    n = int(r, base=2)
    if n > 129:
        print(n_)
        break
    n_+=1

Результат: 8

Для более детального разбора предлагаем посмотреть видео теоретического решения данного 5 задания ЕГЭ по информатике:

📹 Видеорешение на RuTube здесь (теоретическое решение)

5_12: Демоверсия ЕГЭ 2018 информатика:

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.

Строится двоичная запись числа N.
К этой записи дописываются справа ещё два разряда по следующему правилу:
складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;
над этой записью производятся те же действия – справа дописывается остаток от деления суммы её цифр на 2.

Укажите минимальное число R, которое превышает число 83 и может являться результатом работы данного алгоритма. В ответе это число запишите в десятичной системе счисления.

✍ Решение:

Заметим, что после второго пункта условия задачи получаются только четные числа (т.к. если число в двоичной системе заканчивается на 0, то оно четное). Таким образом, нас будут интересовать только четные числа.
Наименьшим возможным числом, превышающим 83, является число 84. С ним и будем работать.
Переведем 84 в двоичную систему счисления. На компьютерном ЕГЭ это можно сделать с помощью программистского режима калькулятора. Либо в консоли интерпретатора Python набрать bin(84). Получим:

84 = 1010100

В данном числе выделенная часть — это N. Значит, необходимое нам двоичное число — это 10101. После первого пункта задачи к данному числу должна была добавиться справа единица, так как оно нечетное. А мы имеем 0. Соответственно, это оно не подходит.

Возьмем следующее четное число — 86. Переведем его в двоичную систему счисления:

86 = 1010110

В данном числе выделенная часть — это N. Значит, необходимое нам двоичное число — это 10101. После первого пункта задачи к данному числу должна была добавиться справа единица, так и есть: 101011. А затем добавляется 0: 1010110. Соответственно, оно подходит.

Результат: 86

Подробное решение данного 5 (раньше №6) задания из демоверсии ЕГЭ 2018 года смотрите на видео:
Видеорешение с программированием (PascalAnc.Net):

📹 Видеорешение на RuTube здесь
Аналитическое видеорешение:

📹 Видеорешение на RuTube здесь -> аналитическое решение

5_18: Разбор 5 задания ЕГЭ с сайта К. Полякова (№ 242):

Алгоритм получает на вход натуральное число N > 1 и строит по нему новое число R следующим образом:
1. Строится двоичная запись числа N.
2. Подсчитывается количество нулей и единиц в полученной записи. Если их количество одинаково, в конец записи добавляется её последняя цифра. В противном случае в конец записи добавляется цифра, которая встречается реже.
3. Шаг 2 повторяется ещё два раза.
4. Результат переводится в десятичную систему счисления.

При каком наименьшем исходном числе N > 65 в результате работы алгоритма получится число, кратное 4?

Типовые задания для тренировки

✍ Решение:

✎ Решение с использованием программирования:

PascalAbc.Net:

uses school;
 
begin
  var n_ := 1;
  while True do
  begin
    var n := n_;
    for var i := 1 to 3 do 
    begin
      if bin(n).CountOf('1') = bin(n).CountOf('0') then // сравниваем
        if n mod 2 = 0 then // если четное, то в конце 0
          n := 2 * n  // добавляем разряд = 0
        else 
        n := 2 * n + 1 // иначе добавляем разряд = 1
      else if bin(n).CountOf('1') > bin(n).CountOf('0') then
        n := 2 * n
      else
        n := 2 * n + 1
    end;
    if (n_ > 65) and (n mod 4 = 0) then
    begin
      println(n_);
      break
    end;
    n_ += 1;
  end;
end.

Python:

n_ = 1
while True:
    n = n_
    r = str(bin(n))
    r = r[2:]
    for i in range(3):
        if r.count('1') == r.count('0'):
            r+=r[-1] 
        elif r.count('1')>r.count('0'):
            r+='0'
        else:
            r+='1'
    n = int(r, base=2)
    if n_ > 65 and n % 4 == 0 :
        print(n_,n)
        break
    n_+=1

Ответ: 79

5_19: Разбор 5 задания ЕГЭ с сайта К. Полякова (№ 267):

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Число N переводим в двоичную запись.
2) Инвертируем все биты числа кроме первого.
3) Переводим в десятичную запись.
4) Складываем результат с исходным числом N.
Полученное число является искомым числом R.

Укажите наименьшее нечетное число N, для которого результат работы данного алгоритма больше 99. В ответе это число запишите в десятичной системе счисления.

✍ Решение:

✎ Решение с использованием программирования:

PascalAbc.Net:

Python:

n_ = 1
while True:
    n = n_
    r = str(bin(n))
    r = r[2:]
    for i in range(1,len(r)):
        if r[i]== '0':
            r=r[:i]+'1'+r[i+1:] 
        else:
            r=r[:i]+'0'+r[i+1:] 
    n = int(r, base=2)
    n+=n_
    if n > 99 and n_ % 2 != 0 :
        print(n_,n)
        break
    n_+=1

Ответ: 65

5_13: Разбор 5 задания ЕГЭ вариант № 1, 2019 Информатика и ИКТ Типовые экзаменационные варианты (10 вариантов), С.С. Крылов, Т.Е. Чуркина:

На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом:

1. Строится двоичная запись числа N.
2. К этой записи дописываются справа еще два разряда по следующему правилу:
— если N делится нацело на 4, в конец числа (справа) дописывается сначала ноль, а затем еще один ноль;
— если N при делении на 4 дает в остатке 1, то в конец числа (справа) дописывается сначала ноль, а затем единица;
— если N при делении на 4 дает в остатке 2, то в конец числа (справа) дописывается сначала один, а затем ноль;
— если N при делении на 4 дает в остатке 3, в конец числа (справа) дописывается сначала один, а затем еще одна единица.

Например, двоичная запись 1001 числа 9 будет преобразована в 100101, а двоичная запись 1100 числа 12 будет преобразована в 110000.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа R — результата работы данного алгоритма.

Укажите максимальное число R, которое меньше 100 и может являться результатом работы данного алгоритма. В ответе это число запишите

в десятичной системе счисления

Типовые задания для тренировки

✍ Решение:

Поскольку требуется найти наибольшее число, то возьмем наибольшее из возможных чисел, которые — это число 99. Переведем его в двоичную систему. На компьютерном ЕГЭ это можно сделать с помощью программистского режима калькулятора. Либо в консоли интерпретатора Python набрать bin(99). Получим:

99 = 1100011₂

По алгоритму это число получилось путем добавления справа двух разрядов, значение которых зависит от исходного N:

1100011
  N

Т.е. в конце были добавлены две единицы — по алгоритму это значит, что исходное N должно в остатке при делении на 4 давать 3. Переведем найденное N в десятичную систему. Можно использовать калькулятор либо консоль пайтон: int('11000',2)

11000 = 24₁₀

24 делится на 4 нацело, т.е. в конце по алгоритму должны были добавиться два разряда — 00. У нас же в конце 11. Т.е. число 99 не подходит. Проверим следующее — 98.

98 = 1100010₂  : 10 в конце добавлено алгоритмом
N = 11000₂ = 24₁₀
24 делится нацело на 4. 
По алгоритму в конце должно быть 00, а мы имеем 10 
98 - не подходит

97 = 1100001₂ : 01 в конце добавлено алгоритмом
N = 11000₂ = 24₁₀
24 делится нацело на 4. 
По алгоритму в конце должно быть 00, а мы имеем 01 
97 - не подходит

96 = 1100000₂ : 00 в конце добавлено алгоритмом
N = 11000₂ = 24₁₀
24 делится нацело на 4. 
По алгоритму в конце должно быть 00, у нас 00 - верно!
96 - подходит!

Результат: 96

Предлагаем посмотреть видео теоретического решения:

📹 Видеорешение на RuTube здесь (теоретическое решение)

5_14: Разбор 5 задания ЕГЭ с сайта К. Полякова (№ 138):

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом:

1. Строится двоичная запись числа N.
2. К этой записи дописывается (дублируется) последняя цифра.
3. Затем справа дописывается бит чётности: 0, если в двоичном коде полученного числа чётное число единиц, и 1, если нечётное.
4. К полученному результату дописывается ещё один бит чётности.

Полученная таким образом запись (в ней на три разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.

Укажите минимальное число R, большее 114, которое может быть получено в результате работы этого алгоритма. В ответе это число запишите в десятичной системе.

Типовые задания для тренировки

✍ Решение:

✎ Решение аналитическим способом:

В постановке задания задано R > 114. R — это результат работы алгоритма. Для того, чтобы определить наименьшее возможно N, переведем сначала 114 в двоичную систему счисления и выделим в нем три добавленные по алгоритму цифры (перевод можно выполнить в консоли Питона: bin(114))

114 = 1110010₂

Проанализируем, как могло бы получиться двоичное число 114 (R) по алгоритму:

2. В полученное числе N = 1110 дублируется последняя цифра и получается 11100.
3. Поскольку число единиц (3) — нечетное, то справа добавляется 1: 111001.
4. Т.к. в полученном наборе цифр четное число единиц, то добавляем 0: 1110010

Поскольку из числа N = 1110 по алгоритму могла получиться только такая последовательность цифр (1110010), то для получения минимального R, но большего чем R = 114, увеличим в N = 1110 самый младший разряд на единицу и рассмотрим работу алгоритма с полученным числом:

1. N = 1110 + 1 = 1111

Работа по алгоритму:
2. 11111 - дублирование последней цифры.
3. 111111 - справа дописываем единицу, т.к. в полученном числе 5 единиц (нечетное)
4. 1111110 - дописываем ноль, т.к. в полученном числе четное число единиц.

Ответ нужно получить в десятичной системе счисления (для перевода можно воспользоваться интерпретатором Питона: int('1111110',2)):

min R = 1111110₂ = 126₁₀

✎ Решение с использованием программирования:

PascalAbc.Net:

uses school;
 
begin
  var n_ := 1;
  while True do
  begin
    var n := n_;
          // дублирвание последней цифры
    if n mod 2 = 0 then // если четное, то в конце 0
      n := 2 * n  // добавляем разряд = 0
    else 
      n := 2 * n + 1; // иначе добавляем разряд = 1
    for var i := 1 to 2 do
    begin
      if bin(n).CountOf('1') mod 2 = 0 then
        n := 2 * n  // добавляем разряд = 0
     else 
        n := 2 * n + 1 // иначе добавляем разряд = 1
    end;
    if n > 114 then
    begin
      println(n);
      break
    end;
    n_ += 1;
  end;
end.

Python:

n_ = 1
while True:
    n = n_
    r  = str(bin(n)) # строковое значение
    r = r[2:] # убираем 0b
    r=r+r[-1]
    for i in range (2):
        if r.count('1') % 2 == 0:
            r = r+'0'
        else:
            r = r+'1'
    r = int(r,base = 2) # в 10-ю с.с.
    if r > 114:
        print(r)
        break
    n_+= 1

Результат: 126

5_17: Досрочный вариант 1 ЕГЭ по информатике 2020, ФИПИ:
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописываются справа ещё два разряда по следующему правилу:
— если N чётное, в конец числа (справа) дописываются два нуля, в противном случае справа дописываются две единицы.

Например, двоичная запись 1001 числа 9 будет преобразована в 100111.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа – результата работы данного алгоритма.

Укажите минимальное число N, для которого результат работы алгоритма будет больше 134. В ответе это число запишите в десятичной системе счисления.

Ответ: 33

Видео -> теоретическое решение
📹 Видеорешение на RuTube здесь -> теоретическое решение

5_16: Разбор 5 задания ЕГЭ с сайта К. Полякова (№ 159):

Автомат обрабатывает целое число N (0 ≤ N ≤ 255) по следующему алгоритму:

1. Строится восьмибитная двоичная запись числа N.
2. Все цифры двоичной записи заменяются на противоположные (0 на 1, 1 на 0).
3. Полученное число переводится в десятичную запись.
4. Из нового числа вычитается исходное, полученная разность выводится на экран.

Какое число нужно ввести в автомат, чтобы в результате получилось 45?

✍ Решение:

Результатом выполнения алгоритма является число 45. Алгоритм работает в двоичной системе счисления, поэтому переведем число:

45 = 00101101₂

Пронумеруем биты слева направо, начиная с единицы. Рассмотрим каждый бит отдельно, начиная с левого бита под номером 1.

1. Так как биты в уменьшаемом и вычитаемом должны быть различны, то единица в результате может получится только 1 - 0, с учетом, что у разряда с единицей заняли. То есть бит:

   .
_{_}  1 _ _ _ _ _ _ _    N инвертируемое
₌  0 _ _ _ _ _ _ _    N исходное
   0 0 1 0 1 1 0 1  = 45   результат

2. 1 - 0 не может в результате дать 0, так как у следующей слева единицы мы заняли. Значит, 0 - 1. Чтобы не получить единицу в ответе, необходимо у нуля тоже занять:

   . .
_{_}  1 0 _ _ _ _ _ _ 
₌  0 1 _ _ _ _ _ _ 
   0 0 1 0 1 1 0 1  = 45   результат

3. 1 - 0 не может быть, так как у следующего слева нуля мы заняли.
Значит 0 - 1. То есть как раз чтобы получить единицу (10 - 1 = 1), занимаем у следующих слева разрядов:

   . .
_{_}  1 0 0 _ _ _ _ _ 
₌  0 1 1 _ _ _ _ _ 
   0 0 1 0 1 1 0 1  = 45   результат

4. 0 - 1 не может быть. Значит, чтобы получить в результате ноль, берем 1 - 0, у единицы должно быть занято.

   . .   .
_{_}  1 0 0 1 _ _ _ _ 
₌  0 1 1 0 _ _ _ _ 
   0 0 1 0 1 1 0 1  = 45   результат

5. 1 - 0 не может быть. Так как слева у единицы занято. Значит, чтобы получить в результате 1, берем 0 - 1:

   . .   .
_{_}  1 0 0 1 0 _ _ _ 
₌  0 1 1 0 1 _ _ _ 
   0 0 1 0 1 1 0 1  = 45   результат

6. 0 - 1 не даст в ответе единицу, значит, имеем 1 - 0:

   . .   .
_{_}  1 0 0 1 0 1 _ _ 
₌  0 1 1 0 1 0 _ _ 
   0 0 1 0 1 1 0 1  = 45   результат

7. 0 - 1 не может быть, значит, 1 - 0. Чтобы получить в результате 0, необходимо, чтобы у 1 было занято:

   . .   .     .
_{_}  1 0 0 1 0 1 1 _ 
₌  0 1 1 0 1 0 0 _ 
   0 0 1 0 1 1 0 1  = 45   результат

8. Чтобы получить 1, имеем 0 - 1:

   . .   .     .
_{_}  1 0 0 1 0 1 1 0 
₌  0 1 1 0 1 0 0 1
   0 0 1 0 1 1 0 1  = 45   результат

Полученное число (вычитаемое) и есть искомое N. Переведем его в 10-ю с.с.:

01101001 = 105₁₀

Ответ: 105

Смотрите теоретический разбор задания на видео и подписывайтесь на наш канал:

📹 Видеорешение на RuTube здесь -> теоретическое решение

Решение заданий для темы Проверка числовой последовательности (Автомат)

5_7: ЕГЭ по информатике задание 5 с сайта К. Полякова (задание под номером Р-06):

Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам.

Складываются первая и вторая, а также третья и четвёртая цифры исходного числа.
Полученные два числа записываются друг за другом в порядке убывания (без разделителей).

Пример. Исходное число: 3165. Суммы: 3 + 1 = 4; 6 + 5 = 11. Результат: 114.

Укажите наименьшее число, в результате обработки которого, автомат выдаст число 1311.

✍ Решение:

Результат: 2949

Процесс теоретического решения данного 5 задания представлен в видеоуроке:

📹 Видеорешение на RuTube здесь -> теоретическое решение

5_8: Задание 5 (раньше №6) ЕГЭ по информатике 2017 ФИПИ (Крылов С.С., Чуркина Т.Е.) вариант 13:

Автомат получает на вход четырехзначное число. По нему строится новое число по следующим правилам:

Складываются первая и вторая, затем вторая и третья, а далее третья и четвёртая цифры исходного числа.
Полученные три числа записываются друг за другом в порядке возрастания (без разделителей).

Пример: Исходное число: 7531. Суммы: 7+5=12; 5+3=8; 3+1=4. Результат: 4812.

Укажите наибольшее число в результате обработки которого автомат выдаст 2512.

Типовые задания для тренировки

✍ Решение:

Число 2512 можно разбить на 2, 5, 12

Начнем с 12. Необходимо получить наибольшее число, поэтому разобьем на слагаемые с наибольшей цифрой — 9:

12=9+3

То есть первые две цифры:

 93**

В число 2 тройка не входит, значит забираем тройку из 5. Остается 2. А, значит, из состава 2 остается 0.

Получим число: 9320.

Результат: 9320

Подробное теоретическое решение данного 5 задания можно просмотреть на видео:

📹 Видеорешение на RuTube здесь -> теоретическое решение

5_9: Задание 5 (раньше №6) ЕГЭ по информатике 2017 ФИПИ (Ушаков Д.М.) вариант 2:

Автомат получает на вход два двузначных шестнадцатеричных числа. В этих числах все цифры не превосходят цифру 6 (если в числе есть цифра больше 6, автомат отказывается работать). По этим числам строится новое шестнадцатеричное число по следующим правилам:

Вычисляются два шестнадцатеричных числа — сумма старших разрядов полученных чисел и сумма младших разрядов этих чисел.
Полученные два шестнадцатеричных числа записываются друг за другом в порядке убывания (без разделителей).

Пример: Исходные числа: 25, 66. Поразрядные суммы: 8, B. Результат: B8.

Какие из предложенных чисел могут быть результатом работы автомата?
Перечислите в алфавитном порядке буквы, соответствующие этим числам, без пробелов и знаков препинания.

Варианты:
A) 127
B) C6
C) BA
D) E3
E) D1

✍ Решение:

Проанализируем все варианты:

Вариант А. 127 не подходит, так как число 12 в шестнадцатеричной системе записывается как С.

Вариант В. С6 разбиваем на 12 и 6. Число может быть результатом работы автомата. Исходные числа, например, 35 и 37

Вариант С. BA разбиваем на 11 и 10. Число может быть результатом работы автомата. Исходные числа, например, 55 и 56

Вариант D. E3 разбиваем на 14 и 3. 14=6+8, но цифры большие 6 не принимает автомат. Не подходит.

Вариант E. D1 разбиваем на 13 и 1. 13=6+7, но цифры большие 6 не принимает автомат. Не подходит.

Результат: BC

Подробное теоретическое решение данного 5 задания можно просмотреть на видео:

📹 Видеорешение на RuTube здесь -> теоретическое решение

5_10: 5 задание ЕГЭ. Задание 4 ГВЭ 11 класс 2018 год ФИПИ

Автомат получает на вход два двузначных шестнадцатеричных числа. В этих числах все цифры не превосходят цифру 7 (если в числе есть цифра больше 7, автомат отказывается работать). По этим числам строится новое шестнадцатеричное число по следующим правилам.

1. Вычисляются два шестнадцатеричных числа: сумма старших разрядов полученных чисел и сумма младших разрядов этих чисел.
2. Полученные два шестнадцатеричных числа записываются друг за другом в порядке возрастания (без разделителей).

Пример. Исходные числа: 66, 43. Поразрядные суммы: A, 9. Результат: 9A.

Определите, какое из предложенных чисел может быть результатом работы автомата.

Варианты:
1) AD
2) 64
3) CF
4) 811

✍ Решение:

Теоретическое решение 4 задания ГВЭ 11 класса смотрите на видео:

📹 Видеорешение на RuTube здесь -> теоретическое решение

5_15: Задание 5 с сайта К. Полякова (задание под номером 109):

Автомат получает на вход натуральное число X. По этому числу строится трёхзначное число Y по следующим правилам:
1. Первая цифра числа Y (разряд сотен) – остаток от деления X на 7.
2. Вторая цифра числа Y (разряд десятков) – остаток от деления X на 2.
3. Третья цифра числа Y (разряд единиц) – остаток от деления X на 5.

Пример. Исходное число: 55. Остаток от деления на 7 равен 6; остаток от деления на 2 равен 1; остаток от деления на 5 равен 0. Результат работы автомата: 610.

Сколько существует двузначных чисел, при обработке которого автомат выдаёт результат 312?

Типовые задания для тренировки

✍ Решение:

Обозначим каждую цифру числа Y согласно заданию:

Y =    3       1       2
^{x mod 7    x mod 2    x mod 5}

Сделаем выводы:

1. x mod 2 = 1 => значит, X — нечетное число
2. x mod 5 = 2 => значит, X — либо ?2, либо ?7.
3. раз x — нечетное, то из пред. пункта получаем x = ?7
4. x mod 7 = 3 => переберем все варианты:

97 - не подходит, 
87 - подходит (87 / 7 = 12, остаток = 3)
77 - не подходит,
67 - не подходит,
57 - не подходит,
47 - не подходит,
37 - не подходит,
27 - не подходит,
17 - подходит (17 / 7 = 2, остаток = 3)

Результат: 2

Источник

1. Автомат получает на вход два двузначных шестнадцатеричных числа. В этих числах все цифры не превосходят цифру 6 (если в числе есть цифра больше 6, автомат отказывается работать). По этим числам строится новое шестнадцатеричное число по следующим правилам.

1) Вычисляются два шестнадцатеричных числа – сумма старших разрядов полученных чисел и сумма младших разрядов этих чисел.

2) Полученные два шестнадцатеричных числа записываются друг за другом в порядке возрастания (без разделителей).

Пример. Исходные числа: 66, 43. Поразрядные суммы: A, 9. Результат: 9A.

Определите, какое из предложенных чисел может быть результатом работы автомата.

1) 9F 2) 911 3) 42 4) 7A

2. Автомат получает на вход четырехзначное десятичное число. По этому числу строится новое число по следующим правилам.

1. Складываются первая и вторая, а также третья и четвёртая цифры.

2. Полученные два числа записываются друг за другом в порядке возрастания (без разделителей).

Пример. Исходное число: 8754. Суммы: 8 + 7 = 15; 5 + 4 = 9. Результат: 915. Определите, какое из следующих чисел может быть результатом работы автомата.

1) 219 2) 118 3) 1411 4) 151

3. Автомат получает на вход пятизначное число. По этому числу строится новое число по следующим правилам.

1. Складываются отдельно первая, третья и пятая цифры, а также вторая и четвёртая цифры.

2. Полученные два числа записываются друг за другом в порядке неубывания без разделителей.

Пример. Исходное число: 63 179. Суммы: 6 + 1 + 9 = 16; 3 + 7 = 10. Результат: 1016.

Укажите наименьшее число, при обработке которого автомат выдаёт результат 621.

4. Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам.

1. Складываются отдельно первая и вторая цифры, вторая и третья цифры, а также третья и четвёртая цифры.

2. Из полученных трёх чисел выбираются два наибольших и записываются друг за другом в порядке неубывания без разделителей.

Пример. Исходное число: 9575. Суммы: 9+5 = 14; 5+7 = 12; 7+5=12. Наибольшие суммы: 14, 12. Результат: 1214.

Укажите наибольшее число, при обработке которого автомат выдаёт результат 1515.

Источник

Смотрите также

Отказ от ответственности
Правообладателям
Постеры игр: © MobyGames.com
Полезное

Источник

Public user contributions licensed under
cc-wiki license with attribution required

Источник

Урок посвящен тому, как решать 5 задание ЕГЭ по информатике

Содержание:

Объяснение 5 задания
- Исполнитель для возведения в квадрат, деления, умножения и сложения
- Проверка числовой последовательности на соответствие алгоритму
Разбор 5 задания
- Решение задания про алгоритм, который строит число R
- Решение заданий для темы Проверка числовой последовательности (Автомат)

5-е задание: «Анализ алгоритмов и исполнители»

Уровень сложности

— базовый,

Требуется использование специализированного программного обеспечения

— нет,

Максимальный балл

— 1,

Примерное время выполнения

— 4 минуты.

До ЕГЭ 2021 года — это было задание № 6 ЕГЭ

Типичные ошибки и рекомендации по их предотвращению:

ФГБНУ «Федеральный институт педагогических измерений»

Проверка числовой последовательности на соответствие алгоритму

для выполнения некоторых заданий необходимо повторить тему системы счисления;
максимальное значение суммы цифр десятичного числа — это 18, так как 9 + 9 = 18;
для проверки правильности переданного сообщения иногда вводится бит четности — дополнительный бит, которым дополняется двоичный код таким образом, чтобы в результате количество единиц стало четным: т.е. если в исходном сообщении количество единиц было четным, то добавляется 0, если нечетным — добавляется 1:

например: 
 3₁₀ = 11₂ 
после добавления бита четности: 110
----
 4₁₀ = 100₂ 
после добавления бита четности: 1001

добавление к двоичной записи числа нуль справа увеличивает число в 2 раза:

например:
111₂ - это 7₁₀
добавим 0 справа:
1110₂ - это 14₁₀

Разбор 5 задания

Задание демонстрационного варианта 2022 года ФИПИ
Плейлист видеоразборов задания на YouTube:

Решение задания про алгоритм, который строит число R

5_11:

На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом:

Строится двоичная запись числа 4N.
К этой записи дописываются справа еще два разряда по следующему правилу:

складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 10000 преобразуется в запись 100001;
над этой записью производятся те же действия — справа дописывается остаток от деления суммы цифр на 2.

Полученная таким образом запись является двоичной записью искомого числа R.

Типовые задания для тренировки

✍ Решение:

✎ Решение аналитическим способом:

Заметим, что после выполнения второго пункта задания, будут получаться только четные числа! Наименьшим возможным четным числом, превышающим 129, является число 130. С ним и будем работать.
Переведем 130 в двоичную систему счисления. Используя компьютер это можно сделать с помощью программистского режима калькулятора. Либо в консоли интерпретатора Python набрать bin(130). Получим:

130₁₀ = 10000010₂

Это двоичное число получилось из исходного двоичного, после того как дважды был добавлен остаток от деления суммы цифр на 2. Т.е.:

в обратном порядке:
было 1000001 -> стало 10000010 
еще раз то же самое: 
было 100000 -> стало 1000001

Значит, необходимое нам двоичное число — это 100000.
Переведем 100000 в 10-ю систему. Для этого можно воспользоваться калькулятором, либо использовать интерпретатор Питона: int('100000',2).

100000₂ = 32₁₀

Так как по условию у нас 4*N, то 32 делим на 4 — > 8.

✎ Решение с использованием программирования:

PascalAbc.Net:

uses school;
 
begin
  var n_ := 1;
  while True do
  begin
    var n := 4*n_;
    var ost := bin(n).CountOf('1') mod 2; // остаток при делении на 2
    n := 2 * n + ost; //в двоичной с.с. добавляем разряд (*2) и остаток к этому разряру (+ost)
    ost := bin(n).CountOf('1') mod 2; // остаток при делении на 2
    n := 2 * n + ost;
    if n > 129 then
    begin
      println(n_);
      break
    end;
    n_ += 1;
  end;
end.

Python:

n_ = 1
while True:
    n = 4*n_
    r = str(bin(n))
    r = r[2:]
    for i in range(2):
        if r.count('1') % 2 == 0:
            r+='0'
        else:
            r+='1'
 
    n = int(r, base=2)
    if n > 129:
        print(n_)
        break
    n_+=1

Результат: 8

📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)

5_12: Демоверсия ЕГЭ 2018 информатика:

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.

Строится двоичная запись числа N.
К этой записи дописываются справа ещё два разряда по следующему правилу:
складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;
над этой записью производятся те же действия – справа дописывается остаток от деления суммы её цифр на 2.

✍ Решение:

Заметим, что после второго пункта условия задачи получаются только четные числа (т.к. если число в двоичной системе заканчивается на 0, то оно четное). Таким образом, нас будут интересовать только четные числа.
Наименьшим возможным числом, превышающим 83, является число 84. С ним и будем работать.
Переведем 84 в двоичную систему счисления. На компьютерном ЕГЭ это можно сделать с помощью программистского режима калькулятора. Либо в консоли интерпретатора Python набрать bin(84). Получим:

84 = 1010100

В данном числе выделенная часть — это N. Значит, необходимое нам двоичное число — это 10101. После первого пункта задачи к данному числу должна была добавиться справа единица, так как оно нечетное. А мы имеем 0. Соответственно, это оно не подходит.
Возьмем следующее четное число — 86. Переведем его в двоичную систему счисления:

86 = 1010110

В данном числе выделенная часть — это N. Значит, необходимое нам двоичное число — это 10101. После первого пункта задачи к данному числу должна была добавиться справа единица, так и есть: 101011. А затем добавляется 0: 1010110. Соответственно, оно подходит.

Результат: 86

Подробное решение данного 5 (раньше №6) задания из демоверсии ЕГЭ 2018 года смотрите на видео:
Видеорешение с программированием (PascalAnc.Net):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Аналитическое видеорешение:

📹 Видеорешение на RuTube здесь -> аналитическое решение

5_18:

При каком наименьшем исходном числе N > 65 в результате работы алгоритма получится число, кратное 4?

Типовые задания для тренировки

✍ Решение:

✎ Решение с использованием программирования:

PascalAbc.Net:

uses school;
 
begin
  var n_ := 1;
  while True do
  begin
    var n := n_;
    for var i := 1 to 3 do 
    begin
      if bin(n).CountOf('1') = bin(n).CountOf('0') then // сравниваем
        if n mod 2 = 0 then // если четное, то в конце 0
          n := 2 * n  // добавляем разряд = 0
        else 
        n := 2 * n + 1 // иначе добавляем разряд = 1
      else if bin(n).CountOf('1') > bin(n).CountOf('0') then
        n := 2 * n
      else
        n := 2 * n + 1
    end;
    if (n_ > 65) and (n mod 4 = 0) then
    begin
      println(n_);
      break
    end;
    n_ += 1;
  end;
end.

Python:

n_ = 1
while True:
    n = n_
    r = str(bin(n))
    r = r[2:]
    for i in range(3):
        if r.count('1') == r.count('0'):
            r+=r[-1] 
        elif r.count('1')>r.count('0'):
            r+='0'
        else:
            r+='1'
    n = int(r, base=2)
    if n_ > 65 and n % 4 == 0 :
        print(n_,n)
        break
    n_+=1

Ответ: 79

5_19:

✍ Решение:

✎ Решение с использованием программирования:

PascalAbc.Net:

Python:

n_ = 1
while True:
    n = n_
    r = str(bin(n))
    r = r[2:]
    for i in range(1,len(r)):
        if r[i]== '0':
            r=r[:i]+'1'+r[i+1:] 
        else:
            r=r[:i]+'0'+r[i+1:] 
    n = int(r, base=2)
    n+=n_
    if n > 99 and n_ % 2 != 0 :
        print(n_,n)
        break
    n_+=1

Ответ: 65

5_13:

На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом:

в десятичной системе счисления

Типовые задания для тренировки

✍ Решение:

Поскольку требуется найти наибольшее число, то возьмем наибольшее из возможных чисел, которые < 100 — это число 99. Переведем его в двоичную систему. На компьютерном ЕГЭ это можно сделать с помощью программистского режима калькулятора. Либо в консоли интерпретатора Python набрать bin(99). Получим:

99 = 1100011₂

По алгоритму это число получилось путем добавления справа двух разрядов, значение которых зависит от исходного N:

1100011
  N

Т.е. в конце были добавлены две единицы — по алгоритму это значит, что исходное N должно в остатке при делении на 4 давать 3. Переведем найденное N в десятичную систему. Можно использовать калькулятор либо консоль пайтон: int('11000',2)

11000 = 24₁₀

24 делится на 4 нацело, т.е. в конце по алгоритму должны были добавиться два разряда — 00. У нас же в конце 11. Т.е. число 99 не подходит. Проверим следующее — 98.

98 = 1100010₂  : 10 в конце добавлено алгоритмом
N = 11000₂ = 24₁₀
24 делится нацело на 4. 
По алгоритму в конце должно быть 00, а мы имеем 10 
98 - не подходит

97 = 1100001₂ : 01 в конце добавлено алгоритмом
N = 11000₂ = 24₁₀
24 делится нацело на 4. 
По алгоритму в конце должно быть 00, а мы имеем 01 
97 - не подходит

96 = 1100000₂ : 00 в конце добавлено алгоритмом
N = 11000₂ = 24₁₀
24 делится нацело на 4. 
По алгоритму в конце должно быть 00, у нас 00 - верно!
96 - подходит!

Результат: 96

Предлагаем посмотреть видео теоретического решения:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)

5_14:

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом:

Типовые задания для тренировки

✍ Решение:

✎ Решение аналитическим способом:

В постановке задания задано R > 114. R — это результат работы алгоритма. Для того, чтобы определить наименьшее возможно N, переведем сначала 114 в двоичную систему счисления и выделим в нем три добавленные по алгоритму цифры (перевод можно выполнить в консоли Питона: bin(114))

114 = 1110010₂

Проанализируем, как могло бы получиться двоичное число 114 (R) по алгоритму:

Поскольку из числа N = 1110 по алгоритму могла получиться только такая последовательность цифр (1110010), то для получения минимального R, но большего чем R = 114, увеличим в N = 1110 самый младший разряд на единицу и рассмотрим работу алгоритма с полученным числом:

1. N = 1110 + 1 = 1111

Работа по алгоритму:
2. 11111 - дублирование последней цифры.
3. 111111 - справа дописываем единицу, т.к. в полученном числе 5 единиц (нечетное)
4. 1111110 - дописываем ноль, т.к. в полученном числе четное число единиц.

Ответ нужно получить в десятичной системе счисления (для перевода можно воспользоваться интерпретатором Питона: int('1111110',2)):

min R = 1111110₂ = 126₁₀

✎ Решение с использованием программирования:

PascalAbc.Net:

uses school;
 
begin
  var n_ := 1;
  while True do
  begin
    var n := n_;
          // дублирвание последней цифры
    if n mod 2 = 0 then // если четное, то в конце 0
      n := 2 * n  // добавляем разряд = 0
    else 
      n := 2 * n + 1; // иначе добавляем разряд = 1
    for var i := 1 to 2 do
    begin
      if bin(n).CountOf('1') mod 2 = 0 then
        n := 2 * n  // добавляем разряд = 0
     else 
        n := 2 * n + 1 // иначе добавляем разряд = 1
    end;
    if n > 114 then
    begin
      println(n);
      break
    end;
    n_ += 1;
  end;
end.

Python:

n_ = 1
while True:
    n = n_
    r  = str(bin(n)) # строковое значение
    r = r[2:] # убираем 0b
    r=r+r[-1]
    for i in range (2):
        if r.count('1') % 2 == 0:
            r = r+'0'
        else:
            r = r+'1'
    r = int(r,base = 2) # в 10-ю с.с.
    if r > 114:
        print(r)
        break
    n_+= 1

Результат: 126

Например, двоичная запись 1001 числа 9 будет преобразована в 100111.

Ответ: 33

Видео -> теоретическое решение
📹 Видеорешение на RuTube здесь -> теоретическое решение

5_16:

Автомат обрабатывает целое число N (0 ≤ N ≤ 255) по следующему алгоритму:

Какое число нужно ввести в автомат, чтобы в результате получилось 45?

✍ Решение:

Результатом выполнения алгоритма является число 45. Алгоритм работает в двоичной системе счисления, поэтому переведем число:

45 = 00101101₂

Пронумеруем биты слева направо, начиная с единицы. Рассмотрим каждый бит отдельно, начиная с левого бита под номером 1.
1. Так как биты в уменьшаемом и вычитаемом должны быть различны, то единица в результате может получится только 1 - 0, с учетом, что у разряда с единицей заняли. То есть бит:

   .
_{_}  1 _ _ _ _ _ _ _    N инвертируемое
₌  0 _ _ _ _ _ _ _    N исходное
   0 0 1 0 1 1 0 1  = 45   результат

2. 1 - 0 не может в результате дать 0, так как у следующей слева единицы мы заняли. Значит, 0 - 1. Чтобы не получить единицу в ответе, необходимо у нуля тоже занять:

   . .
_{_}  1 0 _ _ _ _ _ _ 
₌  0 1 _ _ _ _ _ _ 
   0 0 1 0 1 1 0 1  = 45   результат

3. 1 - 0 не может быть, так как у следующего слева нуля мы заняли.
Значит 0 - 1. То есть как раз чтобы получить единицу (10 - 1 = 1), занимаем у следующих слева разрядов:

   . .
_{_}  1 0 0 _ _ _ _ _ 
₌  0 1 1 _ _ _ _ _ 
   0 0 1 0 1 1 0 1  = 45   результат

4. 0 - 1 не может быть. Значит, чтобы получить в результате ноль, берем 1 - 0, у единицы должно быть занято.

   . .   .
_{_}  1 0 0 1 _ _ _ _ 
₌  0 1 1 0 _ _ _ _ 
   0 0 1 0 1 1 0 1  = 45   результат

5. 1 - 0 не может быть. Так как слева у единицы занято. Значит, чтобы получить в результате 1, берем 0 - 1:

   . .   .
_{_}  1 0 0 1 0 _ _ _ 
₌  0 1 1 0 1 _ _ _ 
   0 0 1 0 1 1 0 1  = 45   результат

6. 0 - 1 не даст в ответе единицу, значит, имеем 1 - 0:

   . .   .
_{_}  1 0 0 1 0 1 _ _ 
₌  0 1 1 0 1 0 _ _ 
   0 0 1 0 1 1 0 1  = 45   результат

7. 0 - 1 не может быть, значит, 1 - 0. Чтобы получить в результате 0, необходимо, чтобы у 1 было занято:

   . .   .     .
_{_}  1 0 0 1 0 1 1 _ 
₌  0 1 1 0 1 0 0 _ 
   0 0 1 0 1 1 0 1  = 45   результат

8. Чтобы получить 1, имеем 0 - 1:

   . .   .     .
_{_}  1 0 0 1 0 1 1 0 
₌  0 1 1 0 1 0 0 1
   0 0 1 0 1 1 0 1  = 45   результат

Полученное число (вычитаемое) и есть искомое N. Переведем его в 10-ю с.с.:

01101001 = 105₁₀

Ответ: 105

Смотрите теоретический разбор задания на видео и подписывайтесь на наш канал:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение

Решение заданий для темы Проверка числовой последовательности (Автомат)

5_7:

Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам.

Складываются первая и вторая, а также третья и четвёртая цифры исходного числа.
Полученные два числа записываются друг за другом в порядке убывания (без разделителей).

Пример. Исходное число: 3165. Суммы: 3 + 1 = 4; 6 + 5 = 11. Результат: 114.

Укажите наименьшее число, в результате обработки которого, автомат выдаст число 1311.

✍ Решение:

Результат: 2949

Процесс теоретического решения данного 5 задания представлен в видеоуроке:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение

5_8:

Автомат получает на вход четырехзначное число. По нему строится новое число по следующим правилам:

Складываются первая и вторая, затем вторая и третья, а далее третья и четвёртая цифры исходного числа.
Полученные три числа записываются друг за другом в порядке возрастания (без разделителей).

Пример: Исходное число: 7531. Суммы: 7+5=12; 5+3=8; 3+1=4. Результат: 4812.

✍ Решение:

Число 2512 можно разбить на 2, 5, 12

Начнем с 12. Необходимо получить наибольшее число, поэтому разобьем на слагаемые с наибольшей цифрой — 9:

12=9+3

То есть первые две цифры:

 93**

В число 2 тройка не входит, значит забираем тройку из 5. Остается 2. А, значит, из состава 2 остается 0.

Получим число: 9320.

Результат: 9320

Подробное теоретическое решение данного 5 задания можно просмотреть на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение

5_9:

Вычисляются два шестнадцатеричных числа — сумма старших разрядов полученных чисел и сумма младших разрядов этих чисел.
Полученные два шестнадцатеричных числа записываются друг за другом в порядке убывания (без разделителей).

Пример: Исходные числа: 25, 66. Поразрядные суммы: 8, B. Результат: B8.

Варианты:
A) 127
B) C6
C) BA
D) E3
E) D1

✍ Решение:

Проанализируем все варианты:

Вариант А. 127 не подходит, так как число 12 в шестнадцатеричной системе записывается как С.

Вариант D. E3 разбиваем на 14 и 3. 14=6+8, но цифры большие 6 не принимает автомат. Не подходит.

Вариант E. D1 разбиваем на 13 и 1. 13=6+7, но цифры большие 6 не принимает автомат. Не подходит.

Результат: BC

Подробное теоретическое решение данного 5 задания можно просмотреть на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение

5_10: Задание 5 ГВЭ 11 класс 2018 год ФИПИ

Пример. Исходные числа: 66, 43. Поразрядные суммы: A, 9. Результат: 9A.

Определите, какое из предложенных чисел может быть результатом работы автомата.

Варианты:
1) AD
2) 64
3) CF
4) 811

✍ Решение:

Теоретическое решение 4 задания ГВЭ 11 класса смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь -> теоретическое решение

5_15:

Сколько существует двузначных чисел, при обработке которого автомат выдаёт результат 312?

Типовые задания для тренировки

✍ Решение:

Обозначим каждую цифру числа Y согласно заданию:

Y =    3       1       2
^{x mod 7    x mod 2    x mod 5}

Сделаем выводы:

97 - не подходит, 
87 - подходит (87 / 7 = 12, остаток = 3)
77 - не подходит,
67 - не подходит,
57 - не подходит,
47 - не подходит,
37 - не подходит,
27 - не подходит,
17 - подходит (17 / 7 = 2, остаток = 3)

Результат: 2

Источник

Канал видеоролика: Алекс ЕГЭ Информатика

Смотреть видео:

Свежая информация для ЕГЭ и ОГЭ по Информатике (листай):

С этим видео ученики смотрят следующие ролики:

Задание 6 ЕГЭ по Информатике посимвольное преобразование десятичных чисел

Алекс ЕГЭ Информатика

Информатика ЕГЭ 2021 | Задание 5 | Автомат и двоичное преобразование

GTai

ЕГЭ Информатика 2017. Задание 1

Готовые задания

ЕГЭ Информатика 2017. Задание 3.

Готовые задания

Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):

29.01.2020

Комментарии

RSS

Написать комментарий

Нет комментариев. Ваш будет первым!

Ваше имя:

Загрузка…

Источник

Задание 5_1

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.

Строится двоичная запись числа N.
К этой записи дописывается справа ещё три разряда по следующему правилу:

а) если число четное, то в конце числа (справа) дописывается 00, в противном случае дописывается 10.
б) если в полученном числе количество единиц чётное, то справа дописывается 0, в противном случае дописывается 1.

Укажите количество чисел R, которые принадлежат диапазону [130;350] и могут являться результатом работы алгоритма.

Решение:

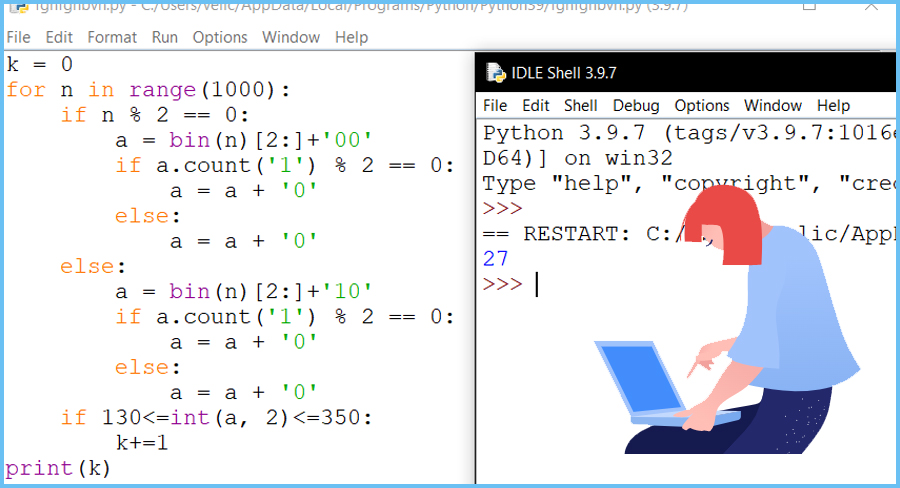
Ответ: 27

Задание 5_2

Источник