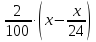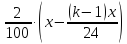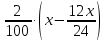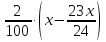Пособия по экономическим задачам егэ

Экономические задачи ЕГЭ, Колесникова С.И., 2019.

Это краткое методическое пособие содержит решения новых текстовых задач, так называемых «экономических». Это задачи на сложные проценты: кредиты, вклады; на исследование максимума прибыли и т.д. Большинство задач, по мнению автора, требует от учащегося умения сначала вывести необходимые формулы, а затем правильно провести арифметические операции. Часто оказывается, что гораздо проще работать с простыми дробями, а не с десятичными. Для лучшего усвоения темы приводим в тексте полные решения, а в ответах — более короткие. Условия задач взяты из Интернета.

Одинаковые выплаты.
В задачах этого пункта клиент ежегодно выплачивает одну и ту же сумму, которую мы обозначим буквой Ъ.
Пример 2. В июле планируется взять кредит на сумму 8 052 000 рублей. Условия его возврата таковы:
1) каждый январь долг возрастает на 20% по сравнению с концом предыдущего года,
2) с февраля по июнь каждого года необходимо выплатить некоторую часть долга.
Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен четырьмя равными платежами (т.е. за 4 года)?

Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:

Скачать книгу Экономические задачи ЕГЭ, Колесникова С.И., 2019 — fileskachat.com, быстрое и бесплатное скачивание.

Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу

Скачать
— pdf — Яндекс.Диск.

Дата публикации: 27.03.2020 13:38 UTC

Теги:

Колесникова :: тренировочный вариант ЕГЭ :: ЕГЭ по математике :: 11 класс :: математика :: подготовка к ЕГЭ :: ответы :: решения :: экономические задачи

Министерства спорта РС(Я)

ГБОУ РС(Я) «Чурапчинская республиканская спортивная средняя

школа- интернат олимпийского резерва им.Д.П.Коркина»

Экономические задачи в заданиях ЕГЭ по математике

Сборник

экономических задач и задач на оптимизацию

по математике

Учитель математики: Слепцова А.Н.

Чурапча

2017

«Особенную важность имеют те методы   науки, которые позволяют решать задачу, общую для всей практической деятельности человека: как располагать своими средствами для достижения наибольшей выгоды».

П. Л. Чебышев

Вступление

Начиная с 2015 года,  в заданиях ЕГЭ по математике профильного уровня  появилась  новая экономическая задача №17. В данных  задачах предлагается ознакомиться с разными  схемами выплаты кредита банку со стороны заемщика.

Кредит – это ссуда, предоставленная банком заемщику под определенные проценты за пользование деньгами.  Существует два вида платежей по кредиту: дифференцированный и аннуитетный.

Кроме задач о кредитах есть задачи на выбор оптимального решения. Эти задачи тесно связаны с практической деятельностью человека. Как добиваться наиболее высокого жизненного уровня, наивысшей производительности труда, наименьших потерь, максимальной прибыли, минимальной затраты времени.

Решение задач о кредитах в настоящее время очень актуально, так как жизнь современного человека тесно связана с экономическими отношениями, в частности, с операциями в банке.

Задачи на нахождение ежегодной платы (транша).

Задача 1 (Тренировочная работа 1). 31 декабря 2016 года Василий взял в банке 5460000 рублей в кредит под 20% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%), затем Василий переводит в банк х рублей. Какой должна быть сумма х, чтобы Василий выплатил долг тремя равными платежами (то есть за три года)?

Решение: S=5460000 — сумма кредита, х — ежегодная плата, r=20%

При начислении процентов оставшаяся сумма долга умножается на коэффициент 1+0,2=1,2.

Год	Долг банку	Остаток после ежегодной выплаты
0	S	—
1	1,2S	1,2S — x
2	1,2(1,2S — x) = 1,44S — 1,2x	1,44S — 1,2x — x= 1,44S — 2,2x
3	1,2(1,44S — 2,2x)=1,728S — 2,64x	1,728S — 2,64x — x= 1,728S — 3,64x

После третьего взноса кредит погашен полностью, значит, остаток равен нулю. Решаем полученное уравнение.

1,728S — 3,64x=0

3,64x=1,728∙5460000

x=2592000          Ответ: 2592000 рублей

Задача 2. (Тренировочная работа 42). 31 декабря 2014 года Дмитрий взял в банке 4290000 рублей в кредит под 14,5% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 14,5%), затем Дмитрий переводит в банк х рублей. Какой должна быть сумма х, чтобы Дмитрий выплатил долг двумя равными платежами (то есть за два года)?

Решение : S = 4290000  — сумма кредита, r = 14,5%,  х — ежегодная выплата

При начислении процентов оставшаяся сумма долга умножается на коэффициент 1+0,145=1,145.

Год	Долг банку	Остаток после ежегодной выплаты
0	S	—
1	1,145S	1,145S — x
2	1,145(1,145S — x) = 1,14522S — 1,145x	1,14522S — 1,145x — х = 1,14522S — 2,145x

После второго взноса кредит погашен полностью, значит, остаток равен нулю. Решаем полученное уравнение: 1,14522S — 2,145x = 0

2

.

Ответ: 2622050 рублей

При решении этих задач можно увидеть закономерность и, оформив  решение в общем виде, получаем формулу.

S-сумма кредита,

р=, где a — процентная ставка,

х – сумма ежегодных выплат;

I год: S·p-х

II год:

III год:

IV год:

и т.д.

Задача 3.  (Тренировочная работа 11) 31 декабря 2014 года Алексей взял в банке 6902000 рублей в кредит под 12,5% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Алексей переводит в банк х рублей. Какой должна быть сумма х, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за четыре месяца)?

Решение. S = 6902000 —  сумма кредита, r=12,5%,  х — ежегодная выплата

Применяем формулу:    , где

S-сумма кредита,

р=, где a— процентная ставка,

х – сумма ежемесячных выплат;

Ответ: 2 296 350 рублей.

Задачи на нахождение суммы кредита.

Задача 1. (Тренировочный вариант 6) 15 января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15 числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Известно, что за первые 12 месяцев нужно выплатить банку 1370тыс. рублей. Какую сумму планируется взять в кредит?

Решение: Пусть начальная сумма кредита равна S. По условию, ежемесячный долг перед банком должен уменьшаться равномерно. Этот долг состоит из двух частей: постоянной ежемесячной выплаты и ежемесячной равномерно уменьшающейся выплаты процентов.

;  ;  ; …;  .   — размеры долгов (остаток по кредиту на конец месяца), тогда ежемесячная выплата процентов выглядит следующим образом:

 ;   ;    ;   ; …;      —  ежемесячный %

Находим размеры выплат:

1-й месяц:  +  =

2-й месяц:  + ∙ =    

3-й месяц:  + ∙ =    и.т.д . Замечаем, что выходит последовательность, которая уменьшается на 2. Тогда используя формулу n-го члена арифметической прогрессии аn = а1 + d(n — 1) при а1=148, d= -2

находим 12-й месяц:  а12 = 148 — 2(11 — 1) = 126, т.е. .

Так как нам известна сумма первых двенадцати месяцев составляем уравнение:

  +    = 1370000

Вынесем за скобки общий множитель и воспользуемся формулой суммы членов арифметической прогрессии Sn =

                                  S = = 2000000             Ответ: 2000000

Задача 2. (Тренировочная работа 18). 31 декабря 2014 года Василий взял в банке некоторую сумму кредит под 11% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 11%), затем переводит в банк 3696300 рублей. Какую сумму взял Василий в банке, если он выплатил долг двумя равными платежами (то есть за два года)?

Решение: Воспользуемся формулой:     = 0, которую вывели при решении задач на нахождение ежегодной (ежемесячной) выплаты,

где  p= 1+0,11=1,11, х = 3696300

0  → S =  =  = 6330000.

Ответ: 6330000рублей

Задача 3. (Тренировочная работа 15)15 января планируется взять кредит в банке на 15 месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Известно, что восьмая выплата составила 99,2 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования.

Решение: S — сумма кредита, r = 3%

Сперва нужно вычислить сумму кредита. Известно, что восьмая выплата = 99,2тыс. Находим размеры выплат:

1-й месяц:  +  =

2-й месяц:  + ∙ =    

3-й месяц:  + ∙ =

….

8-й месяц:  →   = 99200 → S = 99200∙ = 1200000, то есть планируется взять в кредит 1200000рублей.

Теперь, чтобы найти сумму которую нужно вернуть банку в течение всего срока кредитования воспользуемся формулой суммы членов арифметической прогрессии Sn = . Для этого сперва найдем пятнадцатую выплату:

а15 = 145 — 3∙14 = 103, т.е.

Общая сумма равна:  ++…S

S15 =  = 1860,       т.е.  =  = 1488000

Ответ: 1488000

Задачи на вычисление процентной ставки.

Задача 1. (Тренировочная работа 19) 15 января планируется взять кредит в банке на 9 месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.

Известно, что общая сумма денег, которую нужно выплатить банку за весь срок кредитования, на 15% больше, чем сумма, взятая в кредит. Найдите r?

Решение. Пусть S сумма кредита равна. Долг перед банком должен уменьшаться до нуля равномерно. Тогда последовательность размеров долга будет иметь вид:

; ;….  — остаток по кредиту на конец месяца

Найдем выплаты:

1 месяц:  +  S=

2 месяц: +  

……………………………………………

9 месяц: 

Найдем сумму всех выплат. По условию общая сумма выплат после полного погашения кредита на 15% больше суммы, взятой в кредит, значит:     →   900 + 45r = 1035  →  r = 3.     Ответ: 3%

Задача 2. (Тренировочная работа 49). 31 декабря 2014 года Евгений взял в банке 1млн рублей в кредит. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на а%), затем Евгений переводит очередной транш. Евгений выплатил кредит за два транша, переведя в первый раз 540тыс. рублей, во второй 649,6 тыс. рублей. Найдите а?

Решение: S = 1000000, а — процентная ставка по кредиту.

В конце 1-го года долг составит:

 ∙ 1000000 — 540000 = 460000 + 10000а

В конце 2-го года:

 ∙(460000 + 10000а) — 649600 = 100а2 + 14600а — 189600

По условию, кредит будет погашен за два года, составляем уравнение:

100а2 + 14600а — 189600 = 0, сокращая на 100 получим

а2 + 146а — 1896 = 0. Решаем квадратное уравнение, находим дискриминант

Д = 1462 + 4∙1896 = 21316 + 7584 = 28900= 1702

а1 = ,        а2 = .

Ответ: 12%

Задача 3. (Тренировочная работа 26). 15 января планируется взять кредит в банке на 5 месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 5% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

Сколько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь срок кредитования?

Решение: S — сумма кредита r =5%

выплата за 1-й месяц:  +

2-й:   +

3-й:   ;   4-й: ;   5-й: .

Таким образом, за все 5 месяцев сумма выплат составит:

Из выражения видно, что первоначальная сумма кредита увеличилась на 1,15 раз, т.е. на 115%.

Ответ: 115%

Задача 4. (Демонстрационный вариант ЕГЭ 2018 ). 15 января планируется взять кредит в банке на шесть месяцев в размере 1млн. рублей. Условия его возврата таковы:

— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число.

-со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг (в млн рублей)	1	0,6	0,4	0,3	0,2	0,1	0

Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2млн рублей.

Решение: Составим ежемесячные выплаты

01.02. — (1 + )∙1 — 0,6

01.03. — (1 + )∙0,6 — 0,4

01.04 — (1 + )∙0,4 — 0,3

01.05 — (1 + )∙0,3 — 0,2

01.06 — (1 + )∙0,2 — 0,1

01.07 — (1 + )∙0,1 — 0.

Найдем общую сумму выплат:

(1 + )∙(1 + 0,6 + 0,4 + 0,3 + 0,2 + 0,1) — (0,6 + 0,4 + 0,3 + 0,2 + 0,1) =

= (1 + )∙2,6 — 1,6 =  + 1

 По условию:   + 1 < 1,2

 < 0,2,     r <       r <  , т.е. ежемесячно долг возрастал на 7%

Ответ: 7%

Задача 5. (досрочное ЕГЭ, 16.04.16) В июле 2016 года планируется взять кредит в размере 4,2 млн рублей. Условия его возврата таковы:

— каждый январь долг возрастает на r% по сравнению с концом предыдущего года;

— с февраля по июнь необходимо выплатить часть долга;

— в июле 2017,2018,2019 годов долг остается равным 4,2 млн рубле

— суммы выплат 2020 и 2021 годов равны.

Найдите r, если долг выплачен полностью и общие выплаты равны 6,1 млн рублей.

Решение. Сумма выплат за первые три года равна:

4,2∙0,01∙r∙3 =0,126∙r

Сумма выплат за последние два года равна 2∙Х.

Так как общие выплаты равны 6,1 млн рублей, то составляем уравнение:

0,126∙r + 2Х= 6,1 (1).

В январе 2020 года долг составит: 4,2 +4,2∙0,01r= 4,2 (1+0,01r). После выплаты суммы Х долг станет равным:

4,2 (1+0,01r) – Х= 4,2t –Х, где t=1+ 0,01r.

В январе 2021 года долг составит (4,2t –Х)∙t. После выплаты суммы Х долг станет равным нулю:

(4,2t –Х)∙t – Х= 0 (2).

Из уравнения (2)  выразим Х:

Х= и подставим в равенство (1):

12,6∙(t -1) + 2 = 6,1;

t =1, 1. Значит, r = 10%

Ответ: 10%

Задача 6. (Вариант 6. Лаппо Л.Д. ЕГЭ 2018) Лев взял кредит в банке на срок 40 месяцев. По договору Лев должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется р% этой суммы, затем следует платеж Льва.

а) Ежемесячные выплаты подбираются, таким образом, чтобы долг уменьшался равномерно.

б) Известно, что наибольший платеж Льва был в 25 раз меньше первоначальной суммы долга. Найдите р.

Решение: S — сумма кредита, р — процентная ставка.

Ежемесячный долг перед банком должен уменьшаться равномерно. Этот долг состоит из двух частей: постоянной ежемесячной выплаты и ежемесячной равномерно уменьшающейся выплаты процентов.

Выплата в 1-й месяц:  + ∙S и так как он будет наибольшим составим уравнение:  (  + ∙S)∙25 = S    →   + p = 1,   p = 1,5

Ответ: 1,5%

Задачи на нахождение количества лет выплаты кредита.

Задача 1. (Тренировочная работа 21) В июле Федор планирует взять в кредит 1,1 млн. рублей. Условия его возврата таковы:

— каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года Федор должен выплатить некоторую часть долга.

На какое минимальное минимальное количество лет Федор может взять кредит, чтобы ежегодные выплаты были не более 300тысяч рублей?

Решение:

1) В конце первого года долг составит:

        1100000∙1,1 — 300000 = 910000

2) В конце второго года долг составит:

        910000∙1,1 — 300000 = 701000

3) В конце третьего года долг составит:

        701000∙1,1 — 300000 = 471000

4) В конце четвертого года долг составит:

        471000∙1,1 — 300000 = 218210

5) В конце пятого года долг составит:

        218210∙1,1 — 300000  0 , т.е. кредит будет погашен за 5 лет.

Ответ: 5 лет

Задачи на оптимизацию.

Задача 1. (Тренировочная работа 16). У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свеклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 400ц/га, а на втором — 300ц/га. Урожайность свеклы на первом поле составляет 300ц/га, а на втором — 400ц/га.

Фермер может продавать картофель по цене 5000руб. за центнер, а свеклу — по цене 6000руб. за центнер. Какой наибольший доход может получить фермер?

Решение: Посчитаем доход фермера с 1-го поля:

1) если засеет на нем картофель, урожайность — 400ц/га, 1ц = 5000рублей

с 10 га он соберет 400ц/га∙10га = 4000ц  тогда доход:

4000∙5000= 20000000рб = 20млн.

2) если засеет свеклу, урожайность — 300ц/га, 1ц = 6000 рублей

с 10 га он соберет 300∙10=3000ц, тогда доход:

3000∙6000 = 18000000рублей = 18млн.

        Теперь посчитаем доход фермера со 2-го поля:

1) если засеет картофель, урожайность — 300ц/га

с 10 га он соберет 300∙10 = 3000 ц, тогда доход

3000∙5000 = 15000000 рублей = 15млн

2) если засеет свеклу, урожайность свеклы — 400ц/га

с 10 га он соберет 400∙10 = 4000ц, доход будет равен:

4000∙6000 = 24000000рублей = 24млн

Отсюда видно, что максимально возможный доход:

20млн + 24млн = 44млн.                  Ответ: 44млн.

Задача 2 (Тренировочная работа 34). Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 27 квадратных метров и номера «люкс» площадью 45 квадратных метров. Общая площадь, которую можно отвести под номера 981 квадратный метр. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 2000 рублей в сутки, а номер «люкс» — 4000 рублей в сутки. Какую наибольшую сумму денег может заработать в сутки на своем отеле предприниматель?

Решение:

Найдем стоимость 1м² стандартного номера = 2000:27=74руб.

Найдем стоимость 1м² номера «люкс» =4000:45=88=88руб.

Так как стоимость 1м2 номера «люкс» дороже, то выгоднее разместить на этой площади больше номеров «люкс», и как можно меньше номеров стандартных. Начнем перебор количества номеров стандартных с наименьшей цифры.

Пусть стандартных номеров будет:

 — 0, тогда 981:45≠ (нацело не делится), далее

 — 1, тогда  981 — 27 = 954, 954:45≠ также нацело не делится, далее

 — 2,тогда 981 — 54 = 927, 927:45≠ также не делится, идем далее

 — 3,тогда 981 — 81 = 900,  900:45=20 — номеров «люкс»

Тогда в сутки отель может заработать:

20∙4000+3∙2000=80000+6000=86000   Ответ:86000

Задача 3. (Тренировочная работа 14) В двух областях есть по 250 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает  0.2 кг. алюминия или 0.1 кг. никеля. Во второй области для добычи х кг. алюминия в день требуется у²  человеко-часов труда. Для нужд промышленности можно использовать или алюминий или никель, причем 1 кг. алюминия можно заменить 1 кг. никеля. Какую наибольшую массу металлов можно добыть в двух областях суммарно для нужд промышленности?

Решение: 1). В 1 области работают 250 рабочих, каждый работает по 5ч в сутки. За один час один рабочий добывает 0,2кг алюминия, или 0,1кг никеля, т.е в сутки могут добыть:

250∙5∙0.2= 250 кг. алюминия или

250∙5∙0,1=125 кг. никеля. Отсюда видно, что выгоднее будет, если все будут добывать алюминий.

2) Во второй области также работают 250 человек, также работают по 5ч в сутки. Для добычи х кг алюминия требуется х2 человеко-часов, а для добычи у кг никеля требуется у2 человеко-часов, т.е 250 рабочих нужно разделить таким способом, чтобы извлекался корень

==25 кг.(никель)          ==25 кг.(алюминий)

250+25+25=300 кг.

              Ответ: 300кг              

Задача 4. (Тренировочная работа 20) В двух областях есть по 100 рабочих, каждый из которых готов трудиться по 10 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,3кг алюминия или 0,1кг никеля. Во второй области для добычи х кг алюминия в день требуется х2 человеко-часов труда, а для добычи у кг никеля в день требуется у2 человеко-часов труда. Обе области поставляют добытый метал на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2кг алюминия приходится 1 кг никеля. При этом области договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?

Решение: Решение начнем со второй области

100 рабочих нужно разбить так, чтобы извлекался корень, т.е

= = 10кг алюминия

= = 30кг никеля

Теперь 1 область: пусть х — число рабочих добывающих алюминий,

тогда 100-х   число рабочих добывающих никель.

х∙10∙0,3 = 3х — кг алюминия

(100 — х)∙10∙0,1 = 100 — х   -кг никеля.

Составим уравнение учитывая, что на 2 кг алюминия приходится 1 кг никеля:     10 + 3х = 2(30+100 — х),

              10 + 3х = 260 — 2х

                5х = 250,            х = 50 — рабочих на добычу алюминия, следовательно 50 рабочих на добычу никеля

50∙10∙0,3 = 150 кг алюминия

50∙10∙0,1 = 50 кг никеля.

Тогда 150 + 50 + 10 + 30 = 240кг

Ответ: 240кг.

Задача 5. (Тренировочная работа 47). В двух шахтах добывают алюминий и никель. В первой шахте имеется 100 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 1кг алюминия или 3 кг никеля. Во второй шахте имеется 300 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 3кг алюминия или 1 кг никеля.

        Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?

Решение: Так как в 1-й шахте добывают больше никеля, то для наибольшей выгоды нужно, чтобы все рабочие добывали никель. Тогда

100∙5∙3 = 1500кг никеля будет добыто в 1-й шахте.

Пусть все 300 рабочих второй вахты добывают алюминий, тогда

300∙5∙3 = 4500кг алюминия будет добыто.

Так как для сплава нужно 2 раза больше алюминия, то рабочих второй шахты нужно распределить на добычу алюминия и никеля с учетом пропорции сплава.

Пусть х — число рабочих добывающих алюминий,

        300 — х   — число рабочих добывающих никель.

х∙5∙3 = 15х (кг) — алюминий

(300 — х)∙5∙1 = 1500 — 5х (кг) — никель

Составляем уравнение: 15х = 2(1500 — 5х + 1500)

                                            15х = 6000 — 10х

                                             25х = 6000,   х = 240 — количество рабочих добывающих алюминий, следовательно 60 рабочих добывают никель.

240∙5∙3 = 3600кг — алюминий

60∙5∙1 = 300кг — никель

Тогда  3600 + 300 + 1500 = 5400 кг.                    Ответ: 5400кг.

Задача 6. (ЕГЭ — 2017. Резервный день 28.06.2017г). Борис является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара.

        За каждый час работы на заводе, расположенном в первом городе, Борис платит рабочему 500 рублей, а на заводе, расположенном во втором городе, — 200 рублей.

        Борису нужно каждую неделю производить 70 единиц товара. Какую наименьшую сумму придется тратить еженедельно на оплату труда рабочих?

Решение: Пусть х — единиц товара 1-го завода,

                            у — единиц товара 2-го завода.

Тогда,   х + у = 70,   → х = 70 — у

               500х2 + 200у2 = S

500(700 — у)2 + 200у2 = S

700у2 — 70000у + 2450000 = S

700у2 — 70000у + 2450000 — квадратный трехчлен примет наименьшее значение при у =  = 50

Тогда S = 700∙502 — 70000∙50 + 2450000 = 700000

Ответ: 700000

Задача 7. (ЕГЭ — 2017. Резервный день). Антон является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара.

        За каждый час работы на заводе, расположенном в первом городе, Антон платит рабочему 250 рублей, а на заводе, расположенном во втором городе, — 200 рублей.

        Антон готов выделять 900000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?

Решение: пусть х — на оплату труда рабочих 1-го завода, следовательно,

                       900000 — х   — на оплату труда рабочих 2-го завода.

  — часов работы 1-го завода

  — часов работы 2-го завода

Количество произведенного товара за неделю  =  +  и нужно найти наибольшее значение этого выражения, для этого найдем производную и найдем нули.

 +  ∙(-) =

Решаем уравнение  = 0

 = 0,    , возводив в квадрат с двух сторон получим: 40(900000-х) = 50х,  х = 400000.

 =  = 40 — единиц товара 1 завод

 =  = 50 — единиц товара 2 завод

40+50=90 единиц.                      Ответ: 90.

Разные задачи

Задача 1. (Тренировочная работа 13) 15 января планируется взять в кредит в банке на сумму 2,4млн рублей на 24 месяца. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Какую сумму нужно выплатить банку за последние 12 месяцев?

Решение: S = 2400000. По условию, ежемесячный долг перед банком должен уменьшаться равномерно. Этот долг состоит из двух частей: постоянной ежемесячной выплаты и ежемесячной равномерно уменьшающейся выплаты процентов.

;  ;  ; …;  .   — размеры долгов (остаток по кредиту на конец месяца), тогда ежемесячная выплата процентов выглядит следующим образом:

 ;   ;    ;   ; …;      —  ежемесячный %

Находим размеры выплат:

1-й месяц:  +  =

2-й месяц:  + ∙ =    

3-й месяц:  + ∙ =    и.т.д . Замечаем, что выходит последовательность, которая уменьшается на 2. Тогда используя формулу n-го члена арифметической прогрессии аn = а1 + d(n — 1) при а1=148, d= -2

находим 13-й месяц:  а13 = 148 — 2(13 — 1) = 126, т.е.  и

 24-й месяц: а24 = 148 — 2(24 — 1) = 102S, т.е.

Выплата за последние 12 месяцев: + …+  

Вынесем за скобки общий множитель и воспользуемся формулой суммы членов арифметической прогрессии Sn =  ∙n

S12=  = 1356.

=  = 1356000

Ответ: 1356000рублей

Задача 2. (Тренировочная работа 12). В начале 2001 года Алексей приобрел ценную бумагу за 19000руб. В конце каждого года цена бумаги возрастает на 3000 руб. В начале любого года Алексей может продать бумагу и положить вырученные деньги на банковский счет. Каждый год сумма на счете будет увеличиваться на 10%. В начале какого года Алексей должен продать ценную бумагу, чтобы через пятнадцать лет после покупки этой бумаги сумма на банковском счете была наибольшей?

Решение: Продать ценную бумагу нужно в тот момент, когда 10% от стоимости станут составлять не меньше 3000 рублей, что возможно при стоимости бумаги не менее 30000 рублей. это произойдет через (19+3+3+3+3=31) четыре года. И в этот момент 10% от стоимости этой бумаги будут равны 3100 рублей, т.е. больше чем, 3000 рублей. Т.е. надо продать бумагу и положить счет в банке. 2001 + 4 = 2005.

Ответ: 2005 году

2 способ решения:  аn  =а1+(n-1)d,   а=19000

                                            d=3000

Ему будет выгодно отдать деньги в банк в том случае, если 10% от аn превышает d , т.е :

0,1 аn›3000

0,1(19000+3000(n-1))›3000  :0,1

19000+3000n-3000›30000

3000n›14000

n›=4

n=5 т.е бумагу можно продать в течении пятого года(сразу после 4-х лет)

 Ответ:2005

Задача 3. Вклад планируется открыть на четыре года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего и четвёртого годов вклад ежегодно пополняется на 3 млн. рублей. Найдите наименьший размер первоначального вклада, при котором через четыре года вклад будет больше 20 млн. рублей.

Решение:

Пусть первоначальный вклад составляет S млн. руб., тогда:

В конце первого года на вкладе будет 1,1 S млн. руб.,

В конце второго года на вкладе будет 1,1 S∙1,1=1,21 S млн .руб.,

В конце третьего года на вкладе будет (1,21 S+3)∙1,1=1,331 S+3,3 млн. руб.,

В конце четвертого года на вкладе будет (1,331 S+3,3+3)∙1,1=1,4641S+6,93 млн. руб.,

Далее необходимо решить неравенство:

1,4641S+6,93 > 20

1,4641S > 20-6,93

1,4641S > 13,07

S > 13,07:1,4641

S > 8,93

S = 9 млн.руб. так как по условию S — целое число.

Сделаем проверку:

В конце первого года на вкладе будет 1,1∙9 = 9,9млн. руб.,

В конце второго года на вкладе будет 9,9∙1,1 = 10,89 млн. руб.,

В конце третьего года на вкладе будет (10,89+3)∙1,1 = 15,279 млн. руб.,

В конце четвертого года на вкладе будет (15,279+3)∙1,1 = 20,1069 млн. руб.

Задача 4. (Вариант 19. Лаппо Л.Д. ЕГЭ 2018) В мае 2017 года планируется взять кредит в банке на 6 лет в размере S млн. рублей. Условия его возврата таковы:

— каждый декабрь каждого года долг возрастает на 10%;

— с января по апрель каждого года необходимо выплатить часть долга;

— в мае 2018, 2019 и 2020 годов долг остается равным S млн. рублей;

— выплаты в 2021, 2022 и 2023 годах равны между собой;

— к маю 2023 года долг будет выплачен полностью.

        Найдите наибольшее целое S, при котором общая сумма выплат не превысит 13млн. рублей.

Решение: Сумма выплат за первые три года: 0,1S∙3 = 0,3S

Сумма выплат за последние три года: 3∙х = 3х

По условию сумма выплат не превысит 13 млн:  0,3S + 3х ≤ 13       (1)

За последние три года долг станет равным нулю, т.е.

Sp3 — p2x — px — x = 0,      p=1,1

S∙1,13 — 1,12x — 1,1x — x = 0

1,331S — 1,21x — 1,1x — x = 0

x =   Полученное выражение  подставим в (1)

0,3S + 3∙ ≤ 13

S(0,3 +  ) ≤ 13,     S ≤ 8,63    Ответ: 8 млн.

Методичка по решению экономических задач

(задание 17 ЕГЭ)

Составитель: Мокина В.С.,

учитель математики

МАОУ гимназия №83

Тюмень 2021 год

Содержание

l. Задачи на оптимальный выбор.

2. Задачи на кредит с аннуитетным платежом

3. Задачи на дифференцированный платеж 

4. Задачи на нахождение суммы кредита

5. Задачи на нахождение суммы вклада

Все представленные в банке ЕГЭ задачи (задание 17), можно условно разделить на группы и подгруппы:

Задачи, не связанные с банковскими операциями (задачи на оптимизацию)

Банковские задачи на вклады

1) нахождение срока вклада;

2) вычисление процентной ставки по вкладу;

3) нахождение суммы вклада;

4) нахождение ежегодной суммы пополнения вклада

Банковские задачи на кредиты:

1) нахождение количества лет выплаты кредита;

2) вычисление процентной ставки по кредиту;

3) нахождение суммы кредита;

4) нахождение ежегодного транша.

В методичке показаны методы решения задач экономического содержания, связанные с банковскими кредитами, оптимизацией производства товаров и услуг.

Рассмотрим решение задач (задание 17), в которых требуется оптимальным образом распределить производство продукции для получения максимальной прибыли.

Задачи на оптимальный выбор. Например, нужно найти максимальную прибыль (при соблюдении каких-либо дополнительных условий), или минимальные затраты. Сначала в такой задаче нужно понять, как одна из величин зависит от другой (или других). Другими словами, нужна та функция, наибольшее или наименьшее значение которой мы ищем. А затем — найти это наибольшее или наименьшее значение. Иногда — с помощью производной. А если функция получится линейная или квадратичная — можно просто воспользоваться свойствами этих функций.

У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 500 ц/га, а на втором – 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а на втором – 500 ц/га. Фермер может продать картофель по цене 5000 руб. за центнер, а свёклу – по цене 8000 руб. за центнер. Какой наибольший доход может получить фермер?

Решение:

Величина дохода фермера будет зависеть от того как будет распределена площадь поля между картофелем и свёклой. Пусть х га, засажено картофелем на первом поле, тогда (10 – х) га, засаженных свеклой на первом поле. Полученная прибыль с первого поля, равна:

S(х) = х·500·5000 + (10 – х)·300·8000 = 24000000 + 100000х (руб.)

Функция возрастающая, т.к. к>0, значит, наибольшая доходность будет достигнута при наибольшем значении х = 10 га и прибыль с первого поля составит: S(10) = 24000000 + 100000·10 = 25000000 рублей.

Обозначим через у — количество гектар, засаженных картофелем на втором поле, а (10- у) — количество гектар, засаженных свеклой на втором поле. Прибыль со второго поля составит:

S(у) = 300·5000·у + (10 – у)·500·8000 = 40000000 – 2500000у ( руб.)

Функция убывающая, т.к. к<0, значит, наибольшая доходность будет достигнута при наименьшем значении х = 0 га и прибыль с первого поля составит: S(10) = 40000000 рублей.

Таким образом, максимальная прибыль с обоих полей, равна: S = 25000000 + 40000 = 65000000 рублей, что составляет 65 млн. рублей.

Ответ: 65млн. рублей.

Реши самостоятельно:

У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 400 ц/га, а на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а на втором — 400 ц/га.

Фермер может продавать картофель по цене 10 000 руб. за центнер, а свёклу — по цене 11 000 руб. за центнер. Какой наибольший доход может получить фермер?

У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 300 ц/га, а на втором — 200 ц/га. Урожайность свёклы на первом поле составляет 200 ц/га, а на втором — 300 ц/га.

Фермер может продавать картофель по цене 10 000 руб. за центнер, а свёклу — по цене 13 000 руб. за центнер. Какой наибольший доход может получить фермер?

У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 200 ц/га, а на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 250 ц/га, а на втором — 200 ц/га.

Фермер может продавать картофель по цене 15 000 руб. за центнер, а свёклу — по цене 18 000 руб. за центнер. Какой наибольший доход может получить фермер?

Кон­серв­ный завод вы­пус­ка­ет фрук­то­вые ком­по­ты в двух видах тары — стек­лян­ной и же­стя­ной. Про­из­вод­ствен­ные мощ­но­сти за­во­да поз­во­ля­ют вы­пус­кать в день 90 цент­не­ров ком­по­тов в стек­лян­ной таре или 80 цент­не­ров в же­стя­ной таре. Для вы­пол­не­ния усло­вий ас­сор­ти­мент­но­сти, ко­то­рые предъ­яв­ля­ют­ся тор­го­вы­ми се­тя­ми, про­дук­ции в каж­дом из видов тары долж­но быть вы­пу­ще­но не менее 20 цент­не­ров. В таб­ли­це при­ве­де­ны се­бе­сто­и­мость и от­пуск­ная цена за­во­да за 1 цент­нер про­дук­ции для обоих видов тары.

Пред­по­ла­гая, что вся про­дук­ция за­во­да на­хо­дит спрос (ре­а­ли­зу­ет­ся без остат­ка), най­ди­те мак­си­маль­но воз­мож­ную при­быль за­во­да за один день (при­бы­лью на­зы­ва­ет­ся раз­ни­ца между от­пуск­ной сто­и­мо­стью всей про­дук­ции и её се­бе­сто­и­мо­стью).

5) Фаб­ри­ка, про­из­во­дя­щая пи­ще­вые по­лу­фаб­ри­ка­ты, вы­пус­ка­ет блин­чи­ки со сле­ду­ю­щи­ми ви­да­ми на­чин­ки: ягод­ная и тво­рож­ная. В дан­ной ниже таб­ли­це при­ве­де­ны се­бе­сто­и­мость и от­пуск­ная цена, а также про­из­вод­ствен­ные воз­мож­но­сти фаб­ри­ки по каж­до­му виду про­дук­та при пол­ной за­груз­ке всех мощ­но­стей толь­ко дан­ным видом про­дук­та.

Для вы­пол­не­ния усло­вий ас­сор­ти­мент­но­сти, ко­то­рые предъ­яв­ля­ют­ся тор­го­вы­ми се­тя­ми, про­дук­ции каж­до­го вида долж­но быть вы­пу­ще­но не менее 15 тонн. Пред­по­ла­гая, что вся про­дук­ция фаб­ри­ки на­хо­дит спрос (ре­а­ли­зу­ет­ся без остат­ка), най­ди­те мак­си­маль­но воз­мож­ную при­быль, ко­то­рую может по­лу­чить фаб­ри­ка от про­из­вод­ства блин­чи­ков за 1 месяц.

Предприниматель купил здание и собирается открыть в нём отель. В отеле могут быть стандартные номера площадью 27 квадратных метров и номера «люкс» площадью 45 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 981 квадратный метр. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 2000 рублей в сутки, а номер «люкс» — 4000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своём отеле предприниматель?

Решение:

Пусть у — число номеров «люкс», а  х — число стандартных номеров и S = 981м2. Тогда должно соблюдаться неравенство: 27х + 45у = 981

Выразим число обычных номеров т.е.

х = 981 – 45у, х = = 36 + = 36 +

Найдем решение этого уравнения подбором, где х, у N

Если у = 2, то х = 33 у = 14, то х = 15

у = 5, то х = 28 у = 17, то х = 8

у = 11, то х =18 у = 20, то х = 3

f(х,у) = 2000х + 4000у.

Очевидно, что максимальная прибыль будет при максимальном числе номеров «люкс», поэтому выбираем у = 20, х = 3.

Тогда в сутки предприниматель получит:

4000·20 + 2000·3 = 80000 + 6000 = 86000 рублей.

Проверим оставшиеся варианты

2·4000 + 33·2000 = 74000 рублей

5·4000 + 28·2000 = 76000 рублей

11·4000 + 18·2000 = 74000 рублей

2·4000 + 33·2000 = 80000 рублей

14·4000 + 15·2000 = 86000 рублей

17·4000 + 8·2000 = 84000 рублей

Ответ: 86000 рублей

Реши самостоятельно:

Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 30 квадратных метров и номера «люкс» площадью 40 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 940 квадратных метров. Предприниматель может определить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 4000 рублей в сутки, а номер «люкс» — 5000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель?

Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 21 квадратный метр и номера «люкс» площадью 49 м2. Общая площадь, которую можно отвести под номера, составляет 1099 м2. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 2000 рублей в сутки, а номер «люкс» — 4500 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель?

Предприниматель купил здание и собирается открыть в нём отель. В отеле могут быть стандартные номера площадью 27 квадратных метров и номера «люкс» площадью 45 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 981 квадратный метр. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 2200 рублей в сутки, а номер «люкс» — 4000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своём отеле предприниматель?

Производство некоторого товара облагалось налогом в размере t0 руб. за ед. товара. Государство увеличило налог в 2.5 раза (t1= 2.5t0), но сумма налоговых поступлений не изменилась. На сколько процентов государству следует изменить налог, чтобы добиться максимальных налоговых сборов. если известно, что при налоге равном t руб. за ед. товара, объем производства товара составляет 9000 – 2t ед., если это число положительно, и 0 единиц?

Решение:

Обозначим Q(t) = 9000- 2t единиц товара, Q(t)- объем производства. Тогда налоговые сборы составляют S(t) = Q ·t, S(t) = (9000 — 2t)·t = 9000t – 2t2 руб. Рассмотрим функцию S(t) = 9000t – 2t2. Это квадратичная функция, графиком является парабола, ветви которой направлены вниз. Максимального значения эта функция достигает в вершине параболы. t = t = = 2250, 2250 руб. за единицу товара. При t= t0 налоговые сборы составляют 9000t0 – 2t02 руб. При t= 2,5t0 налоговые сборы составляют 9000·2,5t0 – 2·(2,5t0)2 = 22505t0 – 12,5t02 руб. Так как сумма налоговых поступлений не изменилась, то 9000t0 – 2t02 = 22505t0 – 12,5t02 / : t0 0 получим 9000 – 2t0 = 22505 – 12,5t0 , 10,5 t0 = 13500, t0 = 13500: 10,5 = , значит за единицу товара был налог руб., а стал руб. Теперь этот налог надо уменьшить на r%, чтобы налог стал равным 22500 руб. за единицу товара.

Значит государству необходимо на 30% уменьшить налог, чтобы добиться максимальных налоговых сборов.

Ответ: уменьшить на 30%

Решить самостоятельно

Производство некоторого товара облагалось налогом в размере t0 руб. за ед. товара. Государство увеличило налог в 2.5 раза (t1= 2.5t0),но сумма налоговых поступлений не изменилась. На сколько процентов государству следует изменить налог, чтобы добиться максимальных налоговых сборов. если известно, что при налоге равном t руб. за ед. товара, объем производства товара составляет 7000–2t ед., если это число положительно, и 0 единиц?

Производство некоторого товара облагалось налогом в размере t0 рублей за единицу товара. После того как государство, стремясь нарастить сумму налоговых поступлений, увеличило налог вдвое (до 2t0 рублей за единицу товара), сумма налоговых поступлений не изменилась. На сколько процентов государству следует изменить налог после такого увеличения, чтобы добиться максимальных налоговых поступлений, если известно, что при налоге, равном t рублей за единицу товара, объём производства составляет 10 000 – 2t единиц и это число положительно?

lll. 1. В начале 2001 года Алексей приобрел ценную бумагу за 11 000 рублей. В конце каждого года цена бумаги возрастает на 4 000 рублей. В начале любого года Алексей может продать бумагу и положить вырученные деньги на банковский счет. Каждый год сумма на счете будет увеличиваться на 10%. В начале каждого года Алексей должен продать ценную бумагу, чтобы через 15 лет после покупки этой бумаги сумма на счете была наибольшей?

Решение:

Используем арифметическую прогрессию, в которой а1=11000 — цена за бумагу в первый год покупки году, d=4000 — увеличение стоимости бумаги, аn — пока еще неизвестный нам год продажи бумаги (по счету от года покупки), n — номер года.

Формула n-ого члена арифметической прогрессии: an=a1+d(n-1).

Используя ее находим числа, отвечающие за стоимость бумаги на начало n-го года (по счету от года покупки).

Каждый год сумма на счете будет увеличиваться на 10% = 0,1 от данной суммы, и эти 10% должны быть больше или равны 4000.

Составим неравенство: 0,1·(a1+d(n-1)) ≥ 4000.

Подставим а1=11000, d=4000 и решим неравенство:

0,1·(11000+4000(n-1)) ≥ 4000 обе части неравенства умножим на 10, чтобы избавится от десятичной дроби, получим

11000+4000(n — 1) ≥ 40000;

11000+4000n — 4000 ≥ 40000;

4000n ≥ 33000;

n ≥ 8,25, n ∈Ν ⇒ n=8

через 8 лет надо продать бумагу, т.е. в 2001+8=2009 году

Или рассуждаем так: на восьмом году (т.е. в 2008) 10% от стоимости будет больше 4000, значит бумагу надо продать в следующем (т.е. 2009)).

Ответ: 2009 год.

Другое решение этой задачи.

Чтобы извлечь наибольшую прибыль, Алексей должен воспользоваться банковским депозитом, когда 10% от суммы, вырученной за ценную бумагу, превысит 4000 руб. Найдем значение суммы, от которой 10% будут равны 4000, получим: х·0,1 = 4000

х = 4000: 0,1 = 40000

То есть ценную бумагу в 11000 рублей нужно довести до суммы большей или равной 40000 рублей и полученную сумму положить в банк. Ценная бумага дойдет до этого уровня через 40000 – 11000 = 4000·n

n = 29000: 4000 = 7,25 n ∈Ν ⇒ n=8

то есть через 8 лет, и в начале 2009-го года полученную сумму нужно положить на банковский депозит.

Ответ: 2009.

Реши самостоятельно:

В начале 2001 года Алексей приобрел ценную бумагу за 7000 рублей. В конце каждого года цена бумаги возрастает на 2000 рублей. В начале любого года Алексей может продать бумагу и положить вырученные деньги на банковский счет. Каждый год сумма на счет будет увеличиваться на 10%. В начале какого года Алексей должен продать ценную бумагу, чтобы через пятнадцать лет после покупки этой бумаги сумма на банковском счете была наибольшей?

В начале 2001 года Алексей приобрел ценную бумагу за 19000руб. В конце каждого года цена бумаги возрастает на 3000 руб. В начале любого года Алексей может продать бумагу и положить вырученные деньги на банковский счет. Каждый год сумма на счете будет увеличиваться на 10%. В начале какого года Алексей должен продать ценную бумагу, чтобы через пятнадцать лет после покупки этой бумаги сумма на банковском счете была наибольшей?

Решение экономических задач: банки, проценты, кредиты.

1. Аннуитетный платеж – представляет собой равные ежемесячные платежи, растянутые на весь срок кредитования. В сумму платежа включены: часть ссудной задолженности и начисленный процент. При этом, в первые месяцы (или годы) кредита большую часть транша составляют проценты, а меньшую – погашаемая часть основного долга. Ближе к концу кредитования пропорция меняется: большая часть транша идет на погашение «тела» кредита, меньшая – на проценты. При этом общий размер платежа всегда остается одинаковым.

Задачи на кредит с аннуитетным платежом

1 января 2015 года Александр Сергеевич взял в банке 1,1 млн. рублей в кредит. Схема выплаты кредита следующая – 1-го числа каждого следующего месяца банк начисляет 1% на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Александр Сергеевич переводит в банк платёж. На какое минимальное количество месяцев Александр Сергеевич может взять кредит, чтобы ежемесячные выплаты были не более 275 тыс. рублей?
Решение:

Ответ: 5 месяцев

Реши самостоятельно:

1 января 2015 года Иван Сергеевич взял в банке 1 млн. рублей в кредит. Схема выплаты кредита следующая: 1-го числа каждого следующего месяца банк начисляет 2% на оставшуюся сумму долга (то есть увеличивает долг на 2%), затем Иван Сергеевич переводит в банк платёж. На какое минимальное количество месяцев Иван Сергеевич может взять кредит, чтобы ежемесячные выплаты были не более 200 тыс. рублей.

1 января 2015 года Андрей Владимирович взял в банке 1,1 млн. рублей в кредит. Схема выплаты кредита следующая: 1 числа каждого следующего месяца банк начисляет 3 процента на оставшуюся сумму долга (то есть увеличивает долг на 3%), затем Андрей Владимирович переводит в банк платёж. На какое минимальное количество месяцев Андрей Владимирович может взять кредит, чтобы ежемесячные выплаты были не более 220 тыс. рублей?

1 ян­ва­ря 2019 года Павел Васильевич взял в банке 1 млн. руб­лей в кре­дит. Схема вы­пла­ты кре­ди­та сле­ду­ю­щая: 1 числа каж­до­го сле­ду­ю­ще­го ме­ся­ца банк на­чис­ля­ет 1 про­цент на остав­шу­ю­ся сумму долга (то есть уве­ли­чи­ва­ет долг на 1%), затем Павел Васильевич пе­ре­во­дит в банк платёж. На какое ми­ни­маль­ное ко­ли­че­ство ме­ся­цев Павел Васильевич может взять кре­дит, чтобы еже­ме­сяч­ные вы­пла­ты были не более 125 тыс. руб­лей?

1 ян­ва­ря 2018 года Тимофей Ильич взял в банке 1,1 млн. руб­лей в кре­дит. Схема вы­пла­ты кре­ди­та сле­ду­ю­щая — 1 числа каж­до­го сле­ду­ю­ще­го ме­ся­ца банк на­чис­ля­ет 2 про­цен­та на остав­шу­ю­ся сумму долга (то есть уве­ли­чи­ва­ет долг на 2%), затем Тимофей Ильич пе­ре­во­дит в банк платёж. На какое ми­ни­маль­ное ко­ли­че­ство ме­ся­цев Тимофей Ильич может взять кре­дит, чтобы еже­ме­сяч­ные вы­пла­ты были не более 220 тыс. руб­лей?

IV.1. 31 декабря 2014 года Алексей взял в банке 9282000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%) затем Алексей переводит в банк X рублей. Какой должна быть сумма X, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за 4 года)?

Решение:

Пусть S = 9282000 рублей  размер взятого в банке кредита. 31 декабря каждого года размер кредита увеличился на 10%, а затем, Алексей переводит в банк X рублей, т.е. остаток через четыре года будет равен нулю.

Решим уравнение: ((1,12 S – 1,1х –х)1,1 – х)1,1 – х = 0

1,14 S – 1,13 х — 1,12 х — 1,1х –х = 0

Х =

Х =

Х = 2928200

Ответ: 2928200.

31 декабря 2018 года Роман взял в банке 8599000 рублей в кредит под 14% годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга(то есть увеличивает долг на 14%), затем Роман переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Роман выплатил долг тремя равными платежами (то есть за 3 года)?

31 декабря 2019 года Виктор взял в банке 3276000 рублей в кредит под 20 % годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20 %), затем Виктор переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Виктор выплатил долг тремя равными платежами (то есть за 3 года)?

31 декабря 2020 года Георгий взял в банке 2648000 рублей в кредит под 10 % годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10 %), затем Георгий переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Георгий выплатил долг тремя равными платежами (то есть за 3 года)?

IV.2. В августе 2020 года взяли кредит. Условия возврата таковы:

— каждый январь долг увеличивается на r %;

— с февраля по июль необходимо выплатить часть долга. Кредит можно выплатить за три года равными платежами по 56 595 рублей, или за два года равными платежами по 81 095 рублей. Найдите r.

Решение:

Пусть S рублей сумма кредита, ежегодные выплаты x руб., r % годовых,

к = 1 + r/100. Выплаты: b = 81095 руб., х = 56595 руб. По условию долг на июль меняется так:

Если долг выплачен двумя равными платежами b руб., то (кS – b)к – b = 0

к2 S – кb — b = 0; к2 S = (к + 1)b; S = ((к+1) b)/к2

Если долг выплачен тремя равными платежами х руб., то

((кS – х)к – х)к – х = 0

к3 S – к2 х – кх — х = 0

S = ((к2 + к+1) х)/к3

Решим систему уравнений

=

(к+1)к b = х(к2 + к+1)

(к2 + к) b = х(к2 + к) + х

(к2 + к) b — х(к2 + к) – х = 0

(к2 + к)( b – х) –х = 0

(81095 – 56595) (к2 + к) – 56595 = 0

24500к2 + 24500к — 56595 = 0

100к2 + 100к – 231 = 0

D = 102400, к = 1,1 к = -21 не удовлетворяет условию

к = 1 + r/100, r = 10%

Ответ: 10

Реши самостоятельно:

31 декабря 2017 года Пётр взял в банке некоторую сумму в кредит под некоторый процент годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на а %), затем Пётр переводит очередной транш. Если он будет платить каждый год по 2 592 000 рублей, то выплатит долг за 4 года. Если по 4 392 000 рублей, то за 2 года. Под какой процент Пётр взял деньги в банке?

В августе 2017 года взяли кредит. Условия возврата таковы:

— каждый январь долг увеличивается на r %;

— с февраля по июль необходимо выплатить часть долга.

Кредит можно выплатить за три года равными платежами по 38 016 рублей, или за два года равными платежами по 52 416 рублей.

Найдите r.

В августе 2020 года взяли кредит. Условия возврата таковы: — каждый год долг увеличивается на r — процентов с февраля по июнь необходимо выплатить часть долга Кредит можно выплатить за 4 года равными платежами по 777600 руб. или за 2 года равными платежами по 1317600 руб. Найдите r.

В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:

— каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.

Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите r.

2. Дифференцированный платеж – представляет собой неравные ежемесячные транши, пропорционально уменьшающиеся в течение срока кредитования. Наибольшие платежи – в первой четверти срока, наименьшие – в четвертой четверти. «Срединные» платежи обычно сравнимы с аннуитетом. Ежемесячно тело кредита уменьшается на равную долю, процент же насчитывается на остаток задолженности. Поэтому сумма транша меняется от выплаты к выплате. Если в задаче присутствуют слова «равными платежами» или «долг уменьшается на одну и ту же величину», то речь идет о дифференцированном платеже.

V. Планируется выдать льготный кредит на целое число миллионов рублей на четыре года. В середине каждого года действия кредита долг заёмщика возрастает на 25 % по сравнению с началом года. В конце 1-го и 2-го годов заёмщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 3-го и 4-го годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наименьший размер кредита, при котором общая сумма выплат заёмщика превысит 9 млн. рублей.

Решение:

Пусть S млн. рублей сумма первоначального кредита. В середине каждого года действия кредита долг возрастает на 25 %, x млн.рублей заёмщик выплачивает в конце 3-го и 4-го годов. В конце 1-го и 2-го годов заёмщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному.

В сумме за 2 года он погашает сумму 0,25S + 0,25S = 0,5S.

В последние два года (3-й и 4-й) сумма долга сначала возрастает в 1,25 раза, а затем, погашается равными долями в x млн.рублей.

На конец 4-го года, сумма долга составляет 0 рублей. Отсюда получаем

1,252 S — 1,25 х –х = 0,

1,252 S — 2,25 х = 0, х = =

За 4 года сумма выплат составила 0,5S + 2х. По условию общая сумма выплат превышает 9 млн. рублей, то есть, 0,5S + 2>9, 4,5S + 12,5S > 81,

17S > 81, S > 4 . При минимальном целом значении S = 5 это неравенство выполняется, следовательно, размер кредита составил 5 млн. рублей.

Ответ: 5 000 000

Реши самостоятельно:

Планируется выдать льготный кредит на целое число миллионов рублей на четыре года. В середине каждого года действия кредита долг заемщика возрастает на 20% по сравнению с началом года. В конце 1-го и 2-го годов заемщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 3-го и 4-го годов заемщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наименьший размер кредита, при котором общая сумма выплат заемщика превысит 10 млн. рублей.

Планируется выдать льготный кредит на целое число миллионов рублей на четыре года. В середине каждого года действия кредита долг заемщика возрастает на 25% по сравнению с началом года. В конце 1-го и 2-го годов заемщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 3-го и 4-го годов заемщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наименьший размер кредита, при котором общая сумма выплат заемщика превысит 5 млн. рублей.

Планируется выдать льготный кредит на целое число миллионов рублей на четыре года. В середине каждого года действия кредита долг заемщика возрастает на 15% по сравнению с началом года. В конце 1-го и 2-го годов заемщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 3-го и 4-го годов заемщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наименьший размер кредита, при котором общая сумма выплат заемщика превысит 7 млн. рублей.

Планируется  выдать  льготный  кредит  на  целое  число  миллионов  рублей  на  четыре года. В середине каждого года действия кредита долг заёмщика возрастает на 10 %  по сравнению  с  началом  года. По договоренности с  банком в конце 1-го и 3 – го года заемщик выплачивает только проценты  по  кредиту, начисленные  за  соответствующий  текущий  год.  В  конце  2‐го  и  4‐го  годов  заёмщик  выплачивает  одинаковые  суммы,  погашая  к  концу  4‐го  года  весь  долг  полностью. Найдите наименьший размер кредита, при котором общая сумма выплат заёмщика превысит 100 млн. рублей. 

Планируется выдать льготный кредит на целое число миллионов рублей на пять лет. В середине каждого года действия кредита долг заемщика возрастает на 10% по сравнению с началом года. В конце 1-го и 2-го и 3-го годов заемщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 4-го и 5-го годов заемщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наибольший размер кредита, при котором общая сумма выплат будет меньше 8 млн. рублей.

Решение банковских задач на нахождение суммы кредита

VI. В июле 2026 года планируется взять кредит в банке на три года в размере S млн. руб., где S — целое число. Условия его возврата таковы:

— каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;

-в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.

Найдите наибольшее значение S, при котором каждая из выплат будет меньше 4 млн. рублей.

Решение:

Долг перед банком (в млн. рублей) на июль каждого года должен уменьшаться до нуля следующим образом: S; 0,8S; 0,5S; 0

По условию, в январе каждого года долг увеличивается на 25%, значит, долг в январе каждого года равен: 1,25S; 1,25∙0,8S; 1,25∙0,5S

Следовательно, выплаты с февраля по июнь каждого года составляют:

1,25S — 0,8S = 0,45S 1,25∙0,8S — 0,5S = 0,5S 1,25∙0,5S – 0 = 0,725S

По условию, каждая из выплат должна быть меньше 4 млн. рублей. Это будет верно, если максимальная из выплат меньше 4 млн.рублей, т. е.

0,725S< 4; S< 6,4 S = 6

Наибольшее целое решение этого неравенства – число 6. Значит, искомый размер кредита 6 млн. рублей.

Ответ: 6 млн. рублей.

Реши самостоятельно:

В июле 2026 года планируется взять кредит в банке на три года в размере S млн. руб., где S — целое число. Условия его возврата таковы:

— каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;

-в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.

Найдите наименьшее значение S, при котором каждая из выплат будет больше 5 млн. рублей.

В июле 2020 года планируется взять кредит в банке на три года в размере S млн. руб., где S — целое число. Условия его возврата таковы:

— каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;

-в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.

Найдите наименьшее значение S, при котором каждая из выплат будет составлять целое число тысяч рублей.

В июле планируется взять кредит в банке в размере S тыс. рублей (S – натуральное число) сроком на 3 года. Условия возврата кредита таковы: ‐ каждый январь долг увеличивается на 22,5% по сравнению с концом предыдущего года; ‐ в июне каждого года необходимо выплатить одним платежом часть долга; ‐ в июле каждого года величина долга задается таблицей

Найдите наименьшее значение S, при котором каждая из выплат будет составлять целое число тысяч рублей.

В июле 2016 года планируется взять кредит в банке на четыре года в размере S млн. рублей, где S — целое число. Условия его возврата таковы:

— каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга;

— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.

Найдите наибольшее значение S, при котором общая сумма выплат будет меньше 50 млн. рублей.

В июле 2016 года планируется взять кредит в банке на четыре года в размере S млн. рублей, где S — натуральное число. Условия его возврата таковы:

— каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга;

— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.

Найдите наименьшее значение S, при котором общая сумма выплат будет составлять целое число миллионов рублей.

Решение банковских задач на нахождение суммы вклада

VII. 15-го января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

Известно, что в течении первого года кредитования нужно вернуть банку 466,5 тыс. руб. Какую сумму планируется взять в кредит?

Решение:

Обозначим через Х размер кредита, взятого в банке. Во втором месяце долг увеличивается на 3% и, затем, осуществляется выплата так, чтобы долг уменьшался на одну и ту же величину, т.е. в первый раз выплата будет составлять , и сумма долга во втором месяце составит:

1,03х – () = х — = . Аналогично для следующего месяца, только долг теперь будет составлять получаем остаток долга в размере

1,03· – () = — = .

Вторая выплата будет равна:

Аналогично третья выплата:

Аналогично четвертая выплата: и т.п.

………………………………………………………..

12- тая выплата:

Сумма выплат за первые 12 месяцев составит:

… + 13) =

В скобках получилась арифметическая прогрессия сумму, которой находим по формуле =

= + = = .

По условию в течении первого года нужно выплатить 466,5 тыс. руб.

= 466,5 Х= Х= 600 тыс. руб. или это 600000 руб.

Ответ: 600000 руб.

Реши самостоятельно:

15-го января планируется взять кредит в банке на 20 месяца. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

Известно, что за первые 10 месяцев нужно вернуть банку 1179 тыс. руб. Какую сумму планируется взять в кредит?

15-го января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

Известно, что за последние 12 месяцев нужно вернуть банку 1597,5 тыс. руб. Какую сумму планируется взять в кредит?

15-го января планируется взять кредит в банке на 16 месяца. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 4% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

Известно, что за первые 8 месяцев нужно вернуть банку 900 тыс. руб. Какую сумму планируется взять в кредит?

5-го января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

Какую сумму следует взять в кредит, чтобы общая сумма выплат после полного его погашения равнялась 1 млн рублей?

5)15 января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.

Известно, что в течение второго года кредитования нужно вернуть банку 339 тыс. рублей. Какую сумму нужно вернуть банку в течение первого года кредитования?

VIII. 15-го января планируется взять кредит в банке на 26 месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца с 1- го по 25 – й месяц долг должен быть на 40 тыс. руб. меньше долга на 15-е число предыдущего месяца.

— к 15 – му числу 26 – го месяца кредит должен быть полностью погашен.

Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1924 тыс. руб.

Решение:

Обозначим через S исходную сумму кредита. В течение первого месяца эта сумма возрастает на 3%, становится равной S+0,03S = 1,03 S. Выплату нужно сделать так, чтобы исходная сумма S уменьшилась на 40 тыс. рублей, то есть, нужно выплатить

0,03S+40 тыс. рублей.

Оставшаяся сумма S-40 в следующем месяце снова увеличивается на 3%, становится равной 1,03(S-40), и следует выплатить0,03(S-40) + 40 тыс. руб., Таким образом, в течении 25-ти месяцев, сумма выплат составит:

0,03S+40 + (0,03(S-40) + 40) + (0,03(S-2·40) + 40) + (0,03(S-2·40) + 40) +… + (0,03(S-24·40) + 40) = 0,03S·25 + 40·25 – 0,03·40·( 1 + 2 + 3 +… + 24) =

S24 = 1 + 2 + 3 +… + 24 =   24 = 25·12 = 300

= 0,75 S + 1000 – 360 =0,75 S + 640

В последний 26-й месяц выплачивается остаток  1,03(S -25·40) = 1,03(S – 1000)

В сумме за 26 месяцев имеем: 0,75 S + 640 +1,03(S – 1000). По условию общая сумма выплат после полного его погашения составит 1924 тыс. руб. Составим и решим уравнение: 0,75 S + 640 +1,03(S – 1000) = 1924

1,78 S = 1924 + 390

S = 2314/ 1,78

S = 1300 тыс.руб.

Ответ: 1300000 руб.

Реши самостоятельно:

15-го де­каб­ря пла­ни­ру­ет­ся взять кре­дит в банке на 11 ме­ся­цев. Усло­вия воз­вра­та та­ко­вы:

— 1-го числа каж­до­го ме­ся­ца долг воз­рас­та­ет на 3% по срав­не­нию с кон­цом преды­ду­ще­го ме­ся­ца;

— со 2-го по 14-е число каж­до­го ме­ся­ца не­об­хо­ди­мо вы­пла­тить часть долга;

— 15-го числа каж­до­го ме­ся­ца с 1-го по 10-й долг дол­жен быть на 80 тысяч руб­лей мень­ше долга на 15-е число преды­ду­ще­го ме­ся­ца;

— к 15-му числу 11-го ме­ся­ца кре­дит дол­жен быть пол­но­стью по­га­шен.

Какой долг будет 15-го числа 10-го ме­ся­ца, если общая сумма вы­плат после пол­но­го по­га­ше­ния кре­ди­та со­ста­вит 1198 тысяч руб­лей?

15-го де­каб­ря пла­ни­ру­ет­ся взять кре­дит в банке на сумму 300 тысяч руб­лей на 21 месяц. Усло­вия воз­вра­та та­ко­вы:

— 1-го числа каж­до­го ме­ся­ца долг воз­рас­та­ет на 2% по срав­не­нию с кон­цом преды­ду­ще­го ме­ся­ца;

— со 2-го по 14-е число каж­до­го ме­ся­ца не­об­хо­ди­мо вы­пла­тить часть долга;

— 15-го числа каж­до­го ме­ся­ца с 1-го по 20-й долг дол­жен быть на одну и ту же сумму мень­ше долга на 15-е число преды­ду­ще­го ме­ся­ца;

— 15-го числа 20-го ме­ся­ца долг со­ста­вит 100 тысяч руб­лей;

— к 15-му числу 21-го ме­ся­ца кре­дит дол­жен быть пол­но­стью по­га­шен.

Най­ди­те общую сумму вы­плат после пол­но­го по­га­ше­ния кре­ди­та.

15-го декабря планируется взять кредит в банке на 21 месяц. Условия возврата таковы:

— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца с 1-го по 20-й долг должен быть на 30 тысяч рублей меньше долга на 15-е число предыдущего месяца;

— к 15-му числу 21-го месяца кредит должен быть полностью погашен.

Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1604 тысяч рублей?

Ответы:

1) 84 млн. руб., 2) 69 млн. руб., 3) 90 млн. руб., 4)53500 руб., 5) 2685000 руб.

1) 125000 руб., 2)104500 руб. 3)86600 рублей.

1) 2 2) 25

III. l. 1) 2008 2) 2005

1) 6 месяцев 2) 6 месяцев 3) 9 месяцев 4) 6 месяцев

IV.1. 1) 3703860 рублей 2) 155520 рублей 3) 1064800 рублей

IV.2. 1) 20% 2) 20% 3) 20% 4) 10%

1) 6 млн. руб., 2) 3 млн. руб., 3) 5 млн. руб., 4) 77 млн. руб.,

5 млн. руб.

VI. 1) 11млн.руб. 2) 200 тыс. руб. 3) 400 тыс. руб. 4) 36 млн.руб.

5) 8 млн.руб.

VII. 1) 1200000руб. 2) 3000000 руб. 3) 1200000руб. 4) 0,8 млн. руб.

5) 411000 руб.

VIII. 1) 200000 руб. 2) 384000 руб. 3) 1100000 руб.

Используемая литература:

Шестаков С.А. ЕГЭ 2017. Математика. Задачи с экономическим содержанием. Задачи 17(профильный уровень)/Под ред.И.В.Ященко.-М.:МЦНМЩ, 2017

30 тренировочных вариантов ЕГЭ под редакцией И. В. Ященко» – 2021.

25 декабря 2016

В закладки

Обсудить

Жалоба

Сборник экономических задач и задач на оптимизацию по математике

В данном учебном пособии представлен материал по решению практико-ориентированных задач, экономических задач которые были включены на ЕГЭ по математике профильного уровня с 2015 года.

→ Задачи о кредитах.
→ Экономические задачи на оптимизацию.

→ econim-z.doc
→ Другое пособие к этому номеру

Мы используем куки-файлы, чтобы вы могли быстрее и удобнее пользоваться сайтом. Подробнее

Содержание

1. Введение…………………………………………………………….4

2. Решение задач …………..……………….…………………………5

2.1. Задачи на определение суммы выплат. ………………………..6

2.2. Задачи на определение процентной ставки банка……………10

2.3. Задачи на определение срока кредитования………………….12

2.4. Задачи на определение суммы ежегодного платежа…………14

2.5. Задачи на определение оптимального выбора варианта…….13

3. Приложения

4. Список литературы

.

Введение

Начиная с 2015 года, в контрольные измерительные материалы профильного ЕГЭ по математике во вторую часть была включена задача 19 с экономическим содержанием (в структуре ЕГЭ 2016 теперь это задание 17, далее по тексту «задание 17»).

Новое задание сразу привлекло внимание и учащихся, и учителей практико-ориентированной направленностью. Введение текстовых задач с экономическим содержанием в ЕГЭ 2015 есть наиболее заметное изменение во всём комплексе заданий контрольных измерительных материалов с развёрнутым ответом. Во всех заданиях второй части предыдущих лет условие с самого начала формулировалось в математических терминах и отдельно не предполагало построения какой-либо математической модели.

Существенно усилена сюжетная, практико-ориентированная, составляющая условия в заданиях 17. Сами сюжеты не есть прямые цитаты «из жизни», они уже являются некоторыми текстовыми упрощениями, моделями, реально возникающих ситуаций. Эти сюжеты условно можно разделить на два типа, использующих соответственно дискретные модели (проценты, погашение кредитов, …) и непрерывные модели (различные производства, протяжённые во времени, объёмы продукции, …). Критерии оценивания задания, спецификация КИМ ЕГЭ 2015 профильного уровня по математике, кодификатор требований к уровню подготовки выпускников и элементов содержания КИМ приведены в Приложении 1.

Работа с учащимися профильной школы, нацеленных на продолжение образования в высших учебных заведениях с повышенными требованиями к математической подготовке абитуриентов; работа с коллегами в городской проблемной группе «Системная подготовка обучающихся 9-11 классов к государственной итоговой аттестации по математике» вскрыла проблему, вставшую как перед учащимися, так и учителями. Для овладения прочными навыками решения задач с экономическим содержанием недостаточно учебных материалов, сборников задач. Материалы по данной теме приходится собирать из разных источников.

Работа экспертом предметной комиссии по проверке экзаменационных работ ЕГЭ и ГВЭ по математике, показала, что в экзаменационных работах ЕГЭ 2015 года самой распространённой ошибкой учащихся при решении задания 19 (ныне 17) было неверное понимание условия, поэтому текстовая задача с экономическим содержанием вызвала затруднения в составлении правильной математической модели. Процент учащихся Кемеровской области, получивших положительный балл (1, 2 или 3) за решение составил всего 2,3%. Процент выполнения учащимися нашей гимназии 3%. Количество учащихся, приступивших к выполнению задачи с экономическим содержанием, составил …% в Кемеровской области и …..% гимназии.

Статистика показывает, что решение текстовых задач в целом, и в частности, задач на проценты, вызывает у учащихся трудности. Многие ученики не приступают к их решению. Большой объём текста, экономические термины, используемые в условии, сбивают с толку учащихся, отталкивают от решения данных заданий.

Итоговая аттестация выпускников по математике в форме ЕГЭ является обязательной, поэтому проблема подготовки учащихся к этой процедуре сегодня актуальна.

С целью оказания помощи учителю математики при подготовке учащихся профильной школы к единому государственному экзамену, помощи учащимся в овладении знаний по решению задач с экономическим содержанием, решено собрать и систематизировать материал по данной теме. Это облегчит труд учителя, позволит не обращаясь к дополнительной литературе, получить желаемый результат: учителю научить, а учащимся научиться решению задач с экономическим содержанием.

Предлагаемый учебно – методический комплект «Математика. Подготовка к ЕГЭ. Задачи с экономическим содержанием. Задание 17», призван оказать помощь учителю математики и старшеклассникам при подготовке к ЕГЭ. Учебно – методический комплект включает в себя:

1. Методическое пособие для учителя.

2. Сборник задач экономического содержания. Часть 1(Сборник задач для проверки знаний, необходимых для решения задания 17.)

3. Сборник задач экономического содержания. Часть 2 (Задачник)

4. Буклет «Экономический словарь», объясняющий значение экономических терминов, встречающихся в условии текстовых задач.

Предлагаемый комплект может быть использован на дополнительных занятиях для подготовки к итоговой аттестации учащихся профильных классов.

Представленные материалы являются результатом работы с учащимися профильных классов учебного заведения, в котором работаю, и могут быть использованы на дополнительных занятиях для подготовки к итоговой аттестации учащихся профильных классов.

Методическое пособие для учителя является частью учебно–методического комплекта «Математика. Подготовка к ЕГЭ. Задачи с экономическим содержанием. Задание 17». Цель данного пособия: оказать методическую помощь учителям, работающим по указанному комплекту.

Пособие знакомит с алгоритмом решения задач различного типа задач с экономическим содержанием, предлагает методические рекомендации по составлению математической модели и отработки алгоритма решения задач. Если при решении задачи встретится незнакомое понятие, связанное с экономикой, следует обратиться к буклету «Экономический словарь».

Следует отметить не статичность экономического словаря. Так как задачи с экономическим содержанием включены в контрольные измерительные материалы профильного ЕГЭ по математике недавно, начиная с 2015 года, следует ожидать появления новых сюжетных практико-ориентированных составляющих условия задач. Это приведёт к использованию в тексте новых экономических терминов, значениями которых можно дополнить содержание буклета — четвёртой составляющей учебно-методического комплекта.

Сборник задач экономического содержания. Часть 1. Это сборник задач для проверки знаний учащихся, необходимых для решения задания 17. В нём приведены краткие теоретические сведения, представлены проверочные работы и задачи для корректировки знаний учащихся, позволяющие вспомнить соответствующий материал. Ко всем задачам и проверочным работам даны ответы.

Если при решении задачи встретится незнакомое понятие, связанное с экономикой, следует обратиться к буклету «Экономический словарь».

Сборник задач экономического содержания. Часть 2. Это задачник, в который вошли задачи из различных сборников и из разрешённых для публикации (открытых) вариантов ЕГЭ. Приводятся примеры решения задач, позволяющие лучше понять и запомнить, рассмотренные способы решения задач. Предложены задачи для самостоятельного решения. Ко всем задачам даны ответы.

Решение задач

Для успешного выполнения задач с экономическим содержанием необходимо познакомить учащихся с экономическими терминами, обратившись к буклету, научить выделять необходимую информацию из большого объёма, выработать устойчивые навыки работы с процентами.

Эффективным способом решения задач считаю использование таблиц. Он упрощает решение текстовых задач, просто потому, что это удобно. Данные таблицы позволяют в наглядном и понятном виде записать условие задачи и провести его анализ для составления уравнения.

Самой распространённой ошибкой при решении задачи 19 на итоговой аттестации 2015 года было неверное понимание условия задачи. Большая часть учащихся, приступивших к выполнению, трактовала условие « в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года» как « в июле каждого года долг должен быть на одну и ту же сумму меньше», то есть как «платёж был одинаковым». Изменив условие задачи, учащиеся решали другую задачу, что оценивалось 0 баллов. Этой ошибки можно было избежать, используя для решения таблицу:

Таблица 1

	1 месяц	2 месяц	3 месяц	4 месяц	k месяц
Кредит (долг)
Выплаты (тела кредита)
Выплаты (по процентам)

Работу с текстовыми задачами рекомендую организовывать по следующему алгоритму, сложившемуся в процессе работы:

Алгоритм решения задач

1. Внимательно прочитайте условие задачи, обращая внимание на единицы измерения.

2. Составьте таблицу, заполняя её ячейки данными из условия.

3. В незаполненные ячейки таблицы введите переменные x, y. Заполните оставшиеся ячейки через выражения, содержащие переменные.

4. Составьте математическую модель.

5. Решите уравнение (систему уравнений).

6. Выберите ответ. Прежде, чем его записать, следует прочитать задачу ещё раз для того, чтобы правильно выписать ответ.

Решить уравнение – это не значит решить задачу. Это правило работает для всех текстовых задач. Многие учащиеся сосредотачиваются на решении уравнения, но совершенно забывают о том, что требовалось найти.

Рассмотрим решение экономических задач 17 из третьей книги предлагаемого комплекта. Задания каждого типа следует подробно разобрать с учащимися.

Задачи на определение суммы выплат

Пример 1 (задача, решение которой полностью показывает учитель).

Решение: В задаче используется аннуитетная схема выплаты кредита, когда само тело кредита выплачивается равными частями, но платежи все разные по той причине, что каждый раз, внося платёж, кроме части тела кредита необходимо выплатить и все проценты по нему. Тогда вначале проценты могут даже превышать ту долю кредита, которую должны выплатить, но потом в платеже проценты уже не превалируют, а в конце срока становятся совсем небольшими, потому что начисляются на всё меньшую и меньшую часть долга.

Внимательно прочитав условие задачи, обратившись при необходимости к экономическому словарю, выпишем величины, с которыми предстоит работать при решении задачи:

кредит 2,4 млн. руб. = 2400000руб.; срок кредитования 24 месяца; процентная ставка 2%; сумма выплат за последние 12 месяцев — ? Обозначим для удобства заполнения таблицы и составления математической модели задачи кредит .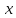

Запишем, что происходило с кредитом поэтапно:

— в январе взяли кредит 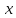млн. рублей;

— 1-го февраля сумма кредита возросла, по сравнению с концом предыдущего месяца, потому что банк начислил проценты: ;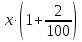

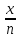
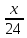
-15-го февраля долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца, то есть , в данном случае срок кредитования 24 месяца, значит на ;

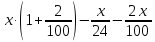
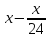
— после февральских выплат (выплаты по процентам и выплаты части тела кредита) долг перед банком составит , и так каждый месяц. Рассуждая аналогично, заполним таблицу. Для составления математической модели задачи важно выразить выплаты первых двух месяцев, чтобы показать, как образуются эти суммы ежемесячно, увидев в их образовании закономерность и выразив её в k месяц. Для нахождения суммы, которую нужно выплатить банку за последние 12 месяцев в таблице следует отразить выплаты в 13 и 24 месяцы кредитования (это первый и последний месяцы периода, о котором стоит вопрос задачи).

Таблица 2

	1 месяц	2 месяц	k месяц	13 месяц	24 месяц
Кредит (долг)
Выплаты (тела кредита)
Выплаты (по процентам)

Из таблицы видно, что ежемесячные выплаты состоят из суммы выплаты части тела кредита и выплаты по процентам, начисляемым на остаток тела кредита на данный период. Обозначим искомую величину S:

;

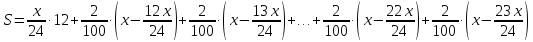
Заметим, слагаемые в квадратной скобке образуют арифметическую прогрессию: (13мес.)+(24мес.)=(14)+(23)=(15)+(22)=(16)+(21)=(17)+(20)=(18)+(19). Всего 6 пар.

Подставим в S:

Подставим в полученную формулу сумму кредита:

Найденное значение – сумма, которую нужно выплатить банку за последние 12 месяцев, то есть ответ задачи.

Ответ: рублей нужно выплатить банку за последние 12 месяцев.

Пример 2 (задача, которую учащиеся решают пошагово с комментариями под руководством учителя)

Решение: После знакомства учащихся с условием задачи можно задать вопросы:

— Что известно в условии и что требуется найти?

— Похожа эта задача на предыдущую?

— В чём отличие от разобранной ранее?

— Предложите этапы решения.

После этого обсуждения следует подвести итог: Зная величину суммы, которую нужно вернуть банку в течение первого года кредитования, найдём сумму кредита; затем определим какую сумму нужно выплатить банку за последние 12 месяцев.

Так как сумму выплат придётся составлять для двух периодов (для первого года кредитования и последних 12 месяцев), удобно для каждого случая составить таблицы отдельно. При составлении и заполнении таблицы рассуждения проводим как в первом примере.

Сумма выплат банку за первые 12 месяцев 2466 тыс. руб.=2466000руб.

24 месяца ; 2%; Сумма выплат за последние 12 месяцев -? Обозначим кредит .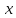

Таблица 3

	1 месяц	2 месяц	k месяц	12 месяц
Кредит (долг)
Выплаты тела кредита
Выплаты (по процентам)

Обозначим сумму выплат банку за первые 12 месяцев — :

;

Заметим, (1мес.)+(12мес.)=(2)+(11)=(3)+(10)=(4)+(9)=(5)+(8)=(6)+(7).

.

Подставим в : .

Найдём сумму кредита: ;

3600000 рублей — сумма кредита.

Таблица 4

	13 месяц	14 месяц	k месяц	24 месяц
Кредит (долг)
Выплаты (тела кредита)
Выплаты (по процентам)

Обозначим сумму выплат банку за последние 12 месяцев — :

;
.

Заметим, (13мес.)+(24мес.)=(14)+(23)=(15)+(22)=(16)+(21)=(17)+(20)=(18)+(19). Всего 6 пар.

.

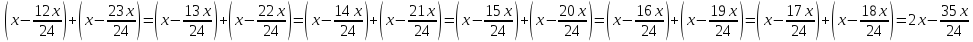
Подставим в :

Подставим в полученную формулу сумму кредита:

Ответ: 2034рублей нужно выплатить банку за последние 12 месяцев.

После выполнения примеров 1 и 2 для закрепления материала можно предложить учащимся рассмотреть решение примеров 3 и 4, (разобранных в третьей книге) и решить самостоятельно задачи № ………..из третьей книги комплекта.

Замечание: Необходимо обратить внимание учащихся на то, что количество месяцев кредитования по условию задачи не всегда бывает чётным. Если оно нечётное, выражая сумму выплат банку, следует не забывать выплаты месяца, для которого не досталось пары (Пример 3 третьей книги комплекта).

Задачи на определение процентной ставки банка

В задачах, в условии которых используется аннуитетная схема выплаты кредита, для определения процентной ставки банка можно составлять математическую модель по условию таким же образом, как и при решении разобранных выше заданий (Пример 5 третьей книги комплекта).

Задачи, в которых погашение кредита происходит траншами, удобно решать, выписывая построчно, что происходило с кредитом ежегодно.

Пример 7. (задача, решение которой полностью показывает учитель).

Решение: Внимательно прочитав условие задачи, обратившись при необходимости к экономическому словарю, выпишем величины, с которыми предстоит работать при решении задачи:

Обозначим кредит ; ; ; платёж , ; платёж .

Для решения воспользуемся формулой погашения кредита равными платежами: , где . Для понимания математической модели задачи, вывод формулы для учащихся необходимо осуществить (Приложение 2).

Выразим величину кредита в обоих случаях, а затем для нахождения процентной ставки кредитования приравняем полученные выражения.

1 случай: Олег выплатит долг за четыре года.

; ;

; (1);

2 случай: Олег выплатит долг за два года.

; ;

; (2).

(1) = (2); ; ;

; ; ; — не удовлетворяет условию задачи; .

Прочитаем условие задачи ещё раз для того, чтобы правильно выписать ответ. Нами получен промежуточный результат. Осталось найти величину процента, который начисляет банк.

; ; ; .

Ответ: банк начисляет на оставшуюся сумму долга .

Примечание: При вычислении (при возможности) можно использовать формулы сокращённого умножения, применять признаки делимости чисел при сокращении дроби. Значения величин в задачах указываются таким образом, что при правильном решении после сокращения знаменатель становится равным единице и дело остаётся за малым: не ошибиться при умножении чисел, оставшихся в числителе.

После выполнения примера 7, рассмотреть решение примера 6,затем можно предложить учащимся решить самостоятельно задачи № ………..из третьей книги комплекта.

После выполнения примеров 1 и 2 для закрепления материала можно предложить учащимся рассмотреть решение примеров 3 и 4, (разобранных в третьей книге) и решить самостоятельно задачи № ………..из третьей книги комплекта.

Задачи на определение срока кредитования

Для решения задач этого типа воспользуемся формулой погашения кредита равными платежами, с которой учащиеся уже познакомились.

Пример 8 (Вариант 36)

Решение: Чем больше срок, тем меньше платежи. По условию задачи необходимо, чтобы платежи не превышали 275 тыс. рублей, то есть срок должен быть не менее указанного. Подставив в формулу данные задачи, получим равенство Натурального значения подобрать нельзя, значит выбираем минимальное такое, чтобы выполнялось неравенство: . Приложение 3.

; .

Ответ: Александр Сергеевич может взять кредит на 5 месяцев.

После выполнения примеров 8, 9 можно предложить учащимся решить самостоятельно задачи № ………..из третьей книги комплекта.

Задачи на определение суммы ежегодного платежа

При решении задач данного типа удобно использовать формулу погашения кредита равными платежами.

Пример 10 (Вариант 33)

Решение: Для более глубокого понимания применяемой формулы можно расписать ещё раз, как формируется сумма равного платежа.

Кредит ; ; . Обозначим ежегодный платёж рублей; .

.

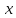
Ответ: ежегодный платёж 2296350 рублей.

После выполнения примеров 10, 12 можно предложить учащимся решить самостоятельно задачи № 11………..из третьей книги комплекта.

Задачи на определение оптимального выбора варианта

При решении задач оптимизации условие в наглядном и понятном виде лучше представить в таблице, которая позволит провести его анализ для составления математической модели задания. Так как эти сюжетные задачи разнообразны, шаблона таблиц для них нет, и в каждом случае она будет индивидуальна. Учащимся следует показать составление таблиц и математической модели задачи на различных сюжетах.

Пример 13 (задача, решение которой полностью показывает учитель).

При знакомстве с условием задачи следует обратить внимание учащихся на тот факт, что «часов в неделю» не означает, что рабочие заводов трудились в течение одинакового времени. Эта величина дана для того, чтобы выразить производительность труда на каждом из заводов.

Решение: Пусть 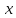единиц продукции выпускает первый завод, тогда единиц продукции выпускает второй завод. Следует обратить внимание учащихся на ограничения: .

Таблица 5

Завод	Время	Единицы продукции
1 завод
2 завод
итого

Оплата рабочим в неделю составит: ;

; ; ;

Введём функцию количества единиц продукции .

Переформулируем задачу: найти наибольшее значение функции . ;

=0; ; ;

; ; ; .

Определим знаки производной: S`(x) x

. 110

При определении знака производной следует обратить внимание учащихся на ограничение по 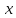, значение которого принадлежит только натуральным числам, при которых подкоренное выражение составленной функции имеет смысл, поэтому было взято только значение .

В найденной точке производная меняет знак с плюса на минус, поэтому в ней функция достигает максимума, совпадающего с наибольшим значением функции на исследуемой области.

. Это означает, что 110 единиц продукции будет выпущено первым заводом.

Прочитаем условие задачи ещё раз для того, чтобы правильно выписать ответ. Нами получен промежуточный результат. Осталось найти количество единиц продукции, выпущенное двумя заводами.

Ответ: 550 единиц продукции.

Пример 18 ( Вариант 8, 24)

Предприниматель купил здание и собирается открыть в нём отель. В отеле он могут быть стандартные номера площадью и номера «люкс» площадью . Общая площадь, которую можно отвести под номера, составляет 981. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 2000рублей в сутки, а номер «люкс» 4000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своём отеле предприниматель?

Решение: Пусть 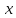количество стандартных номеров, а количество номеров «люкс».

Таблица 6

	один номер	коли- чество	площадь,	стоимость, руб.
площадь,	стоимость, руб.
стандарт	27	2000
«люкс»	45	4000
всего

Введём функцию заработанных за сутки средств .

Переформулируем задачу: найти наибольшее значение функции .

; ; .

;

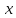
Учитывая, что , найдём решения уравнения, просто подбирая целое число и отыскивая целое число . Получим пары чисел : (3;20); (13;14); (23;8); (33;2).

Функция убывающая. Наибольшее значение функция будет принимать при:

Ответ: рублей – наибольшая сумма денег, которую сможет заработать в сутки на своём отеле предприниматель.

Замечание. При решении уравнения, полученного в ходе решения задачи, в целых числах, нахождение всех целочисленных пар можно не осуществлять. Достаточно определить пару с минимально возможным значением , так как в формуле перед ним стоит минус.

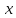
После выполнения примеров 13, 14, 15, 17, 18 можно предложить учащимся решить самостоятельно задачи № 16………..из третьей книги комплекта.

Приложение 1

При знакомстве с задачей с экономическим содержанием, содержащейся в демонстрационном варианте, следует обратить внимание учащихся на критерии проверки и оценивания решений. Такие же критерии будут использовать эксперты при проверке экзаменационной работы. Важно понять, какие этапы решения и какие обоснования относятся к ключевым, отслеживаемым в процессе проверки.

Каждый раз после решения задачи полезно сопоставить свои способы записи решений с критериями оценивания.

Критерии оценивания выполнения заданий на ЕГЭ

Таблица 7

Содержание критерия задания	Баллы
Обоснованно получен верный ответ	3
Верно построена математическая модель, решение сведено к исследованию этой модели, получен неверный ответ из-за вычислительной ошибки ИЛИ Получен верный ответ, но решение недостаточно обосновано	2
Верно построена математическая модель и решение сведено к исследованию этой модели. при этом решение не завершено1	1
Решение не соответствует ни одному из критериев, перечисленных выше	0
Максимальный балл	3

Следует отметить, что один и тот же сюжет может быть успешно сведён к различным математическим моделям и доведён до верного решения. По этой причине в критериях проверки нигде нет жёсткого упоминания о какой-либо конкретной модели.

Спецификация КИМ ЕГЭ 2015 профильного уровня по математике (фрагмент)

Таблица 8

19	Проверяемые требования (умения)	Проверяемые требования к уровню подготовки (по кодификатору)	Коды проверяемых элементов содержания (по кодификатору)	Уровень сложности задания	Максимальный балл за выполнение задание	Примерное время выполнения задания учащимися, изучающими математику, в минутах
на базовом уровне	на профильном уровне
Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни	6.1, 6.3	1.1.1, 1.1.3, 2.1.12	П	3	—	35

«Спецификация экзаменационной работы по математике единого государственного экзамена» содержит разделы, знакомство с которыми позволит иметь более полное представление о содержании будущей экзаменационной работы, в частности, задачи с экономическим содержанием.

Кодификатор требований к уровню подготовки выпускников, КИМ ЕГЭ 2015 по математике (фрагмент)

Таблица 9

6.1	Анализировать реальные числовые данные, информацию статистического характера; осуществлять практические расчёты по формулам; пользоваться оценкой и прикидкой при практических расчётах
6.3	Решать прикладные задачи, в том числе социально-экономического и физического характера, на наибольшие и наименьшие значения, на нахождение скорости и ускорения

Кодификатор элементов содержания КИМ ЕГЭ 2015 профильного уровня по математике (фрагмент)

Таблица 10

1.1.1	Целые числа
1.1.3	Дроби, проценты, рациональные числа
2.1.12	Применение математических методов для решения содержательных задач из различных областей науки и практики, интерпретация результата, учёт реальных ограничений

Знакомя с «Кодификатором элементов содержания по математике для составления контрольных измерительных материалов (КИМ) единого государственного экзамена», обратить внимание на список элементов содержания курса математики (понятий, свойств, формул, теорем, алгоритмов и прочее), знания которых может проверяться задачей экономического содержания на ЕГЭ текущего учебного года.

Приложение 2

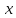
Пусть — сумма кредита, взятая в банке, – платёж (ежегодный или ежемесячный, но всегда один и тот же – равные платежи), — срок кредитования (лет или месяцев), — процент, начисляемый банком за пользование его деньгами.

При решении задач, когда выплаты банку (ежегодные или ежемесячные) являются равными платежами, удобно использовать формулу:

, где .

Рассмотрим вывод данной формулы, запишем, что происходило с кредитом поэтапно.

1 год: ;

2 год: ;

3 год: ;

4 год: ;

; ;

; ;

.

— формула выплат банку равными платежами.

Приложение 3.

Таблица 11

№ месяца
1	1,01
2	1,0201
3	1,030301
4	1,04060401
5	1,0510100501

Примечание: При вычислении (при возможности) можно использовать формулу сокращённого умножения, применять признаки делимости чисел при сокращении дроби. Значения величин в задачах указываются таким образом, что при правильном решении после сокращения знаменатель становится равным единице и дело остаётся за малым: не ошибиться при умножении чисел, оставшихся в числителе.

Список литературы

1. Единый государственный экзамен по математике. Демонстрационный вариант 2015г. Демонстрационный вариант экзаменационной работы подготовлен Федеральным государственным научным учреждением» Федеральный институт педагогических измерений». [Электронный ресурс].-Электрон. текст.дан.-Москва:ФИПИ.-2015.-Режим доступа: http://www.fipi.ru, свободный.

2. Единый государственный экзамен по математике. Демонстрационный вариант 2016 г. Демонстрационный вариант экзаменационной работы подготовлен Федеральным государственным научным учреждением» Федеральный институт педагогических измерений» . [Электронный ресурс].-Электрон. текст.дан.-Москва:ФИПИ.-2015.-Режим доступа: http://www.fipi.ru, свободный.

3. Единый государственный экзамен по математике. Кодификатор элементов содержания по математике для составления контрольных измерительных материалов (КИМ) единого государственного экзамена 2016г. [Электронный ресурс].-Электрон. текст.дан.-Москва:ФИПИ.-2015.-Режим доступа: http://www.fipi.ru, свободный.

4. Единый государственный экзамен по математике. Спецификация экзаменационной работы по математике единого государственного экзамена 2016г. [Электронный ресурс].-Электрон. текст.дан.-Москва:ФИПИ.-2015.-Режим доступа: http://www.fipi.ru, свободный.

5. ЕГЭ-2015 Открытый банк заданий по математике [Электронный ресурс]. Режим доступа: http:// mathege.ru/or/ege/Main, свободный.

6. ЕГЭ-2016 Открытый банк заданий по математике [Электронный ресурс].Режим доступа: http:// mathege.ru/or/ege/Main, свободный.

7. Решу ЕГЭ РФ Образовательный портал для подготовки к ЕГЭ по математике. [Электронный ресурс].-Электрон. текст.дан. Режим доступа: http:// reshuege.ru/

8. Рязановский А.Р., Мирошин В.В. Математика. Решение задач повышенной сложности.[Текст] — М.: Интеллект-Центр, 2012.-480с.

9. Словарь финансовых терминов и экономических понятий. [Электронный ресурс].-Электрон. текст.дан. Режим доступа: http://fingramota.org/servisy/slovar, свободный

10. Экономический словарь. [Электронный ресурс].-Электрон. текст.дан. Режим доступа: http://www.klerk.ru/slovar/econ/letter/193, свободный

8. Ященко И.В. ЕГЭ. Математика: типовые экзаменационные варианты: 36 вариантов. [Текст]. Ященко И.В./ М.: Национальное образование, 2015.-272с.

9. Ященко И.В. ЕГЭ 2016. Математика: типовые экзаменационные варианты: 50 вариантов. [Текст]; под ред. Ященко И.В./ М.: издательство «Экзамен», 2016 – 247с.

9

Баланов А.Б.

_______________________________________________________________________________________

Методическая разработка для учащихся 10-11
классов и учителей математики общеобразовательных школ

_______________________________________________________________________________________

Решение
«экономических» задач при подготовке к ЕГЭ

2018

Введение

В экзаменационных заданиях по математике (профильный уровень) задача с экономическим
содержанием присутствует во 2 части работы и, как правило, содержится под №17.
Она относится к повышенному уровню сложности и оценивается максимально в 3
балла.

Для успешного решения подобных задач требуется не только владеть
определенным математическим инструментарием, но и уметь строить простейшие
математические модели по заданным условиям.

В отличие от других экзаменационных заданий, «экономические» задачи не
отличаются большим разнообразием и встречаются лишь нескольких типов. В данной
методической разработке разобраны все типы задач №17, которые предлагаются
разработчиками ЕГЭ для подготовки к выпускным экзаменам в 2018 году.

Кроме того, для понимания учащимися требований оформления
экзаменационных работ в разработке размещено решение 17-ой задачи,
предоставленное автором на независимой диагностике учителей математики в 2018
году.

Оглавление

Введение

Отзывы

Языком цифр

1.    Типы задач с
экономическим содержанием

2. Кредиты

2.1 Погашение кредита
равными долями

2.2 Равномерное
уменьшение долга по сравнению с предыдущим периодом

2.3 Остаток долга по
заданной таблице

3. Вклады

3.1 Сравнение выгоды

3.2 Изменяющиеся
проценты

4. Задачи на
оптимальный выбор

4.1 Производительность

4.2 Окупаемость

5. Пример оформления 17
задачи на экзаменационном бланке

6.    Ответы

7.    Список используемой
литературы

Отзывы

Задачи о вкладах и кредитовании, а также задачи оптимизации
производства товаров и услуг сравнительно недавно включены во вторую часть ЕГЭ
по математике профильного уровня и вызывают значительные затруднения у
абсолютного большинства выпускников. В действующих в 10-11 классах учебниках
нет материала по решению задач с экономическим содержанием. Автор делает весьма
удачную попытку классифицировать и систематизировать типы «экономических» задач
и методы их решения. Хорошо, что в разработке по каждой теме представлены
задания для самостоятельного решения. Данная методическая разработка очень
своевременна и полезна и для учащихся, и для учителей, занимающихся подготовкой
к ЕГЭ.

Бугаенко Елена
Анатольевна, учитель математики высшей категории

Мы, инженеры,
сегодня не просто что-то разрабатываем, налаживаем, ремонтируем, но и постоянно
просчитываем экономическую составляющую. Что выгоднее – починить или заменить,
предложить новую модель или модернизировать старую, научить клиента обслуживать
оборудование или взять на себя. Я считаю, что задачи на оптимальный выбор нужно
начинать решать уже в школе. В конце концов, и в профессии, и в жизни сделать
правильный выбор – очень важно!

Белов Александр Ефимович,

Ведущий инженер компании «Данфосс» (Дания)

В своей работе я
часто сталкиваюсь с графиками, диаграммами, процентами. И мне кажется странным,
что выпускники школ не владеют элементарными навыками для вычисления, например,
полной суммы выплат кредита или налогов с зарплаты. На мой взгляд,
представленная работа вносит свой вклад в разрешение проблемы, и автор
правильно заострил внимание именно на экономической стороне стоящих задач.

Зацепин Валентин Сергеевич,

Менеджер по маркетингу и рекламе ИТ-компании «Терн»

В современной жизни важны не только знания математических
формул, но и умения сотрудников применять эти знания в конкретной ситуации.
Даже скажу больше: на первом месте именно умения, а не теоретические познания.
Поэтому я считаю правильным делом разработку именно тех материалов, которые
помогают выпускникам успешно влиться во взрослую жизнь. 

Коротков Александр Андреевич,

Директор строительной компании
«Афина» 

ПАО «Сбербанк»,
где я работаю, раздает в качестве кредита около 2 триллионов рублей в год. Я
вижу этот процесс изнутри, общаясь каждый день с десятком клиентов. Уверяю,
что, понимая механику работы кредитной системы, никто из вас не примет
невыгодного решения. Естественно, Ваша кредитная история будет привлекательной
для любого банка. Но начинать думать над этим нужно уже в школе – такова
современная жизнь!

Орлов Георгий Валерьевич,

Менеджер отдела кредитования ПАО
«Сбербанк»

Языком цифр

Задание 17, в основном, в 2017 году представляло задачу на
кредиты. Процент решаемости оказался в пределах статистики для решения подобных
заданий (1 балл получило 5,35% от общего числа участников экзамена, 2 балла –
5,35%, 3 балла – 17,16%).

Основные ошибки,
допущенные участниками экзамена:

– неверное
составление модели;

– вычислительные
(арифметические);

– прекращение решения
на промежуточном шаге, то есть без доведения ответа до числового значения;

– решение методом
перебора без обоснования единственности;

– решение без вывода
формул (решение имеет вид «формула – ответ»), что можно трактовать ка неумение
строить математическую модель.

Распределение
удовлетворенных апелляций по задачам с развернутым ответом:

Как видно из
диаграммы, каждая четвертая задача № 17 после апелляции засчитывалась. И хотя,
я считаю, что до апелляции доводить не стоит, хочется верить, что так или иначе
вы свои баллы с помощью этой книжки наберете!

1.  Типы задач с экономическим содержанием

2. Кредиты

2.1 Погашение кредита равными долями

Задача 1

31 декабря 2017 года Сергей взял в банке 2648000 рублей в кредит под 10%
годовых. Схема выплат кредита следующая — 31 декабря каждого следующего года
банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на
10%), затем Сергей переводит в банк x рублей.
Какой должна быть сумма x, чтобы Сергей выплатил долг тремя равными
платежами (то есть за три года)?

Решение

1 января 2018
года Сергей будет должен банку не только 2648000 руб., но и 10% от этой суммы,
т.е. 2648000 + 0,1*2648000 = 1,1*2648000 руб. Затем Сергей выплачивает х руб. и
остается должен (1,1*2648000 – х) руб.

1 января 2019
года Сергей будет должен банку оставшуюся сумму плюс проценты на нее, то есть
(1,1*2648000 – х) + 0,1*(1,1*2648000 – х) = 1,1*(1,1*2648000 – х). Затем
выплачивается снова сумма в х руб., и остаток долга будет составлять
(1,1*(1,1*2648000 – х) – х) руб.

Наконец, 1 января
2020 года банк еще раз начисляет проценты на остаток долга, в результате чего
Сергей должен (1,1*(1,1*2648000–х)–х)+0,1*(1,1*(1,1*2648000–х)–х)=1,1*(1,1*(1,1*2648000
– х)-х) руб. В течение года Сергей в последний раз выплачивает х руб., после
чего кредит считается погашенным (то есть остаток долга равен 0).

Приведенные
рассуждения удобно представить в виде таблицы ДОЛГ-ВЫПЛАТА-ОСТАТОК

	1 год (2018)	2 год (2019)	3 год (2020)
ДОЛГ	1,1*2648000	1,1*(1,1*2648000 – х)	1,1*(1,1*(1,1*2648000 –х) – х)
ВЫПЛАТА	х	х	х
ОСТАТОК долга	1,1*2648000 – х	1,1*(1,1*2648000 –х) — х	0

В приведенной
таблице ОСТАТОК = ДОЛГ ­­- ВЫПЛАТА. Из данных правого столбца составим
уравнение: 1,1*(1,1*(1,1*2648000 –х) – х) – х = 0

1,1* (1,1*1,1*2648000
– 1,1х – х) – х = 0

1,1*1,1*1,1*2648000
– 1,21х – 1,1х – х = 0

1,331*2648000
= 3,31х

Х=1064800

Ответ: 1064800 руб.

Задача 2

В сентябре Федор взял
кредит в 1,5 млн. руб. По условиям договора:

— каждый январь долг
возрастает на 10% по сравнению с концом предыдущего года;

— с февраля по август
каждого года Федор выплачивает часть долга.

На какое минимальное
количество лет может взять кредит Федор, чтобы не выплачивать более 450 тыс.
руб. в год?

Решение

В явном виде нам не указано, что гасить кредит
нужно равными долями, однако, это тот же тип задачи. Во-первых, логично, что
чем больше мы выплачиваем, тем быстрее погасим кредит, а, во-вторых, у нас есть
верхнее ограничение по сумме выплат – 450 тыс. руб. Значит, будем выплачивать
по максимуму в 0,45 млн., чтобы расплатиться как можно быстрее.

Составим таблицу, как в предыдущей задаче (для
удобства все суммы будем считать в млн. руб.):

	1 год	2 год	3 год
ДОЛГ на январь	1,1*1,5	1,1*(1,1*1,5 – 0,45)=1,12 — 0,45*1,1	1,1*(1,1*(1,1*1,5 – 0,45) – 0,45)=1,13*1,5 ­­- 0,45*1,12 — 0,45*1,1
ВЫПЛАТА с февраля по август	0,45	0,45	0,45
ОСТАТОК долга	1,1*1,5– 0,45	1,1*(1,1*1,5 – 0,45) – 0,45 = 1,12 — 0,45*1,1 – 0,45	1,1*(1,1*(1,1*1,5 – 0,45) – 0,45)=1,13*1,5 ­­- 0,45*1,12 — 0,45*1,1 – 0,45
	4 год	(n-1) год	n год
ДОЛГ на январь	1,1*(1,1*(1,1*(1,1*1,5 –0,45) – 0,45) – 0,45) = 1,14*1,5 – 0,45*1,13 — 0,45*1,12 – 0,45*1,1	1,1n-1*1,5 – 0,45*1,1n-2 — 0,45*1,12 – 0,45*1,1	1,1n*1,5 – 0,45*1,1n-1 — 0,45*1,12 – 0,45*1,1
ВЫПЛАТА с февраля по август	0,45	0,45	0,45
ОСТАТОК долга	1,1*(1,1*(1,1*(1,1*1,5 –0,45) – 0,45) – о,45) -0,45 = 1,14*1,5 – 0,45*1,13 — 0,45*1,12 – 0,45*1,1 – 0,45	1,1n-1*1,5 – 0,45*1,1n-2 — 0,45*1,12 – 0,45*1,1 – 0,45	0

После n лет
Федор расплатится по кредиту, то есть его остаток долга будет равен 0 (при решении может получиться и
отрицательное число, это означает, что в последний год Федору необязательно
выплачивать 450 тыс. руб., а достаточно меньшей суммы). Из данных правого столбца для n-го года составим
уравнение:

1,1ⁿ*1,5 – 0,45*1,1^n-1 — 0,45*1,1² –
0,45*1,1 – 0,45 = 0

1,1ⁿ*1,5 – 0,45*(1+1,1+1,1²+….+1,1^n-1)=0

Выражение в скобках – это сумма n членов геометрической
прогрессии с первым членом b₁=1 и последним членом b_n=b₁*q^n-1. Применяя
формулу для вычисления суммы n членов геометрической прогрессии, получим:

1,1ⁿ*1,5 – 0,45*(1,1ⁿ-1)/(1,1-1)=0

1,1ⁿ*1,5 – 4,5*1,1ⁿ +4,5=0

1,1ⁿ = 1,5

4<n<5

Значит, Федор погасит
кредит за 5 лет.

Ответ: 5.

Иногда
подобные задачи можно решить, не выводя формулу для n лет.
Достаточно последовательно посчитать остаток долга в цифрах – после 1 года, 2
года и т.д. Как только остаток долга станет 0 или отрицательным, значит,
искомый год найден.

В нашей задачe
получим:

·        
после 1 года: 1,1*1,5 –
0,45 = 1,2

·        
после 2 года 1,1*1,2 –
0,45 = 0,87

·        
после 3 года 1,1*0,87 –
0,45 = 0,507

·        
после 4 года 1,1*0,507 –
0,45= 0,1077

·        
после 5 года 1,1*0,1077 –
0,45 = -0,33153

Получив отрицательное
число, делаем вывод, что на 5 году кредит будет полностью выплачен.

Ознакомьтесь с
оформлением подобной задачи в разделе 5.

Задачи для
самостоятельной работы

2.1.1	31 декабря 2017 года Пал Палыч взял в банке некоторую сумму денег в кредит под 10% годовых. По условиям договора: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга, затем Пал Палыч переводит в банк 2928200 рублей. Сколько взял Пал Палыч в банке, если смог выплатить долг четырьмя равными платежами?
2.1.2	Федора не смутила история с первым кредитом, и он берет в банке 2 млн. руб. под 5% годовых.  Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. На какое минимальное количество лет должен взять кредит Федор, чтобы не выплачивать более 350 тыс.руб. ежегодно?

2.2 Равномерное уменьшение долга по
сравнению с предыдущим периодом

Для данного типа задач существует характерная
особенность – при заполнении таблицы мы отталкиваемся от графы «Остаток долга».
Поскольку остатки долга за каждый период отличаются друг от друга на равную величину,
чтобы найти эту величину достаточно поделить сумму долга на количество таких
периодов. Например, если сумма кредита составляет 10 млн руб., а количество лет
равно 4, то остатки будут отличаться на 10млн/4 = 2,5 млн. руб., а графа
«Остаток долга примет» вид:

В конце 1 года	В конце 2 года	В конце 3 года	В конце 4 года
7,5 млн.	5 млн.	2,5 млн.	0 млн.

Замечу, что при неизвестной сумме кредита и
неизвестном количестве периодов графу «Остаток» можно заполнить
последовательностью чисел:

S*(n-1)/n, S*(n-2)/n,…..,S*2/n, S/n, 0.

Задача 1

В январе планируется
взять кредит на 5 месяцев. Условия по договору следующие:

— 1-го числа каждого
месяца долг возрастает на 15% по сравнению с
концом предыдущего месяца;

— со 2–го по 14-е
число нужно выплатить часть долга;

— 15-го числа каждого
месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего
месяца. Сколько процентов от суммы кредита составит общая сумма выплат за весь
срок?

Решение

Пусть S – сумма
кредита. Тогда остатки долга будут отличаться на S/5 руб. Заполним таблицу
(сначала графу «Остаток», затем графу «Долг» и только потом «Выплату» как их
разность):

	1 месяц	2 месяц	3 месяц	4 месяц	5 месяц
ДОЛГ	1,15*S	1,15*4S/5	1,15*3S/5	1,15*2S/5	1,15*S/5
ВЫПЛАТА	1,15*S — 4S/5	1,15*4S/5 — 3S/5	1,15*3S/5 — 2S/5	1,15*2S/5 — S/5	1,15*S/5
ОСТАТОК	4S/5	3S/5	2S/5	S/5	0

Общая сумма выплат (суммируем выплаты 1-5 месяцев): 1,15*S — 4S/5 + 1,15*4S/5 — 3S/5 + 1,15*3S/5 — 2S/5 + 1,15*2S/5 — S/5 + 1,15*S/5 = 1,15*S(1+4/5+3/5+2/5+1/5) – S/5*(4+3+2+1) = 3,45S – 2S = 1,45S. Это означает, что
сумма выплат составляет 145% от суммы кредита.

Ответ: 145

Задача 2

Взят кредит на 18
месяцев. Условия его возврата таковы:

— 1-го числа каждого
месяца долг возрастает на 2% по сравнению с
концом предыдущего месяца;

— со 2–го по 14-е
число нужно выплатить часть долга;

— 15-го числа каждого
месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число
предыдущего месяца. Какую сумму планируется взять в кредит, если известно, что
за первые 9 месяцев нужно выплатить 2048 тыс. руб.?

Решение

Пусть S – сумма
кредита. Тогда остатки долга будут отличаться на S/18 руб. Заполним
таблицу на первые 9 месяцев:

	1 месяц	2 месяц	3 месяц	…	8 месяц	9 месяц
ДОЛГ	1,02*S	1,02*17S/18	1,02*16S/18	1,02*11S/18	1,02*10S/18
ВЫПЛАТА	1,02*S — 17S/18	1,02*17S/18 — 16S/18	1,02*16S/18 — 15S/18	1,02*11S/18 — 10S/18	1,02*10S/18 — 9S/18
ОСТАТОК	17S/18	16S/18	15S/18	10S/18	9S/18

В общем виде, для
каждого месяца ДОЛГ = 1,02*S*(19-n)/18,
ОСТАТОК = (18-n)*S/18, а ВЫПЛАТА = 1,02*S*(19-n)/18
— (18-n)*S/18, где n – номер месяца.

Просуммируем выплаты
за 9 месяцев и приравняем к данной в условии величине:

(1,02*S
— 17S/18) + (1,02*17S/18 — 16S/18) + (1,02*16S/18 — 15S/18) +…+ (1,02*11S/18 — 10S/18) + (1,02*10S/18 — 9S/18) = 2048

Сгруппируем отдельно
подчеркнутые и неподчеркнутые слагаемые:

(1,02*18S/18  + 1,02*17S/18 + 1,02*16S/18 +…
+ 1,02*11S/18 + 1,02*10S/18) – (17S/18 + 16S/18
+ 15S/18 + … +10S/18 + 9S/18) = 2048

1,02*S/18*(18
+17 + … + 10) – S/18*(17 + 16 + … + 9)=1024

Первая скобка – сумма
первых 9 членов арифметической прогрессии при a1=10, a9=18.

Вторая скобка – тоже
сумма первых 9 членов арифметической прогрессии при a1=9, a9=17.

Применяя формулу
для суммы n членов арифметической прогрессии, получим:

(1,02*S*14*9 –
S*13*9)/18 = 2048

S=3200 (тыс. руб.)

В ответе, если
условие задачи не требует иного, значения лучше указывать в единицах СИ.

Ответ: 3 200 000
руб.

Задача 3

В июле планируется взять кредит в банке на сумму 7 млн.
рублей на некоторый срок (целое число лет). Условия его возврата таковы: 1)
каждый январь долг возрастает на 20% по сравнению с концом предыдущего года; 2)
с февраля по июнь каждого года необходимо выплатить часть долга; 3) в июле
каждого года долг должен быть на одну и ту же сумму меньше долга на июль
предыдущего года. На сколько лет планируется взять кредит, если известно, что
общая сумма выплат после его полного погашения составит 17,5 млн. рублей?

Решение

Эту задачу можно
решить, как ранее, с помощью таблицы ДОЛГ-ВЫПЛАТА-ОСТАТОК, но есть и
альтернативный вариант. По моему мнению, он проще для тех, кто хорошо понимает
арифметические прогрессии.

Обозначим сумму
кредита за а₀ (это наши 7 млн. руб.) и а₁, а₂…
а_n – остатки после 1-го, 2-го, …n-го
года. Выплаты же обозначим через х₁, х₂, … x_n.

Тогда:

а₁ = 1,2* а₀
— х₁

а₂ = 1,2* а₁
– х₂

а₃ = 1,2* а₂
– х₃

…

a_n = 1,2* а_n-1 – х_n

Просуммируем
уравнения в системе:

а₁ + …. + a_n = 1,2*а₀ + 1,2*(а₁ +… + а_n-1) – (х₁ +…+
х_n)

Сумма х₁ +…+
х_n =
17,5 по условию задачи, a_n = 0, так как это — остаток долга в последний
год. Числа а₁, а₂… а_n – члены арифметической прогрессии (по условию
разность между соседними остатками одинакова).

В левой части
уравнения получим S_n= (а₁+ a_n)*n/2

В правой части в
скобку (а₁ +… + а_n-1) добавим a_n. От этого ничего не изменится, так a_n = 0, но скобка превратится в S_n.

S_n = 1,2*7 + 1,2* S_n – 17,5

S_n = 45,5

Значит, 45,5 = (а₁+
a_n)*n/2 => а₁=91/n

a_n = 0 = а₀ + n*d => d=-7/n

С другой стороны, а₁
= a₀
+ d = 7 + d = 7 + (-7/n)

Следовательно,
справедливо равенство: 91/n = 7 — 7/n

n=14 (лет)

Ответ: 14

Задачи для
самостоятельной работы:

2.2.1	Жанна взяла в банке в кредит 1,2 млн рублей на срок 24 месяца. По договору Жанна должна возвращать банку часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 2 %, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна вернёт банку в течение первого года кредитования?
2.2.2	Александр взял кредит в банке на срок 9 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на 12%, а затем уменьшается на сумму, уплаченную Александром. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Сколько процентов от суммы кредита составила общая сумма, уплаченная Александром банку (сверх кредита)?
2.2.3	15-го января планируется взять кредит в банке на некоторый срок (целое число месяцев). Условие его выплаты таковы: — 1-го числа каждого месяца долго возрастёт на 3% по сравнению с концом предыдущего месяца; — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. На сколько месяцев планируется взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит?

2.3 Остаток долга
по заданной таблице

Задача 1

В июле 2018 года
планируется взять кредит в банке на 4 года в размере S млн
рублей, где S — целое число. Условия его возврата
таковы:

— каждый январь долг
увеличивается на 15% по сравнению с концом предыдущего года;

— с февраля по июнь
каждого года необходимо выплатить часть долга;

— в июле каждого года
долг должен составлять часть кредита в соответствии со следующей таблицей: 

Месяц и год	Июль 2019	Июль 2020	Июль 2021	Июль 2022
Долг (в млн рублей)	0,8S	0,5S	0,1S	0

При каком наибольшем S
общая сумма выплат будет меньше 50 млн рублей?

Решение

	1 год	2 год	3 год	год
ДОЛГ	1,15*S	1,15*0,8S	1,15*0,5S	1,15*0,1S
ВЫПЛАТА	1,15*S — 0,8S	1,15*0,8S — 0,5S	1,15*0,5S — 0,1S	1,15*0,1S
ОСТАТОК	0,8S	0,5S	0,1S	0

Найдем общую сумму
выплат и сравним ее с 50 млн. руб.

(1,15*S — 0,8S) + (1,15*0,8S — 0,5S)
+ (1,15*0,5S — 0,1S) + (1,15*0,1S) < 50

1,36S <
50

S < 36,76

Так как по условию
задачи S – целое число, то выбираем ближайшее.

Ответ: 36

Задача 2

15 января
планируется взять кредит в банке на 6 месяцев в размере 1 млн руб. Условия его
возврата таковы:

− 1-го числа
месяца долг увеличивается на r % по
сравнению с концом предыдущего месяца, где r — целое число.

− Со 2-го
по 14-е число необходимо выплатить часть долга.

− 15-го
числа каждого месяца долг должен составлять некоторую сумму в соответствии с
таблицей: 

Месяц	Январь	Февраль	Март	Апрель	Май	Июнь	Июль
Долг	1	0,6	0,4	0,3	0,2	0,1	0

Найдите
наибольшее r, при котором сумма выплат будет
меньше 1,2 млн руб.

Решение

Переведем r из
процентов в десятичную дробь: r/100. Тогда долг на начало февраля будет
считаться как (1 +r/100)*1млн. = (1 +r/100), долг на начало марта (1 +r/100)*0,6
млн = 0,6*(1+r/100) и т.д.

После чего, как обычно,
заполним графу ВЫПЛАТА = ДОЛГ — ОСТАТОК

	Февраль	Март	Апрель	Май	Июнь	Июль
ДОЛГ	(1 +r/100)	0,6*(1+r/100)	0,4*(1+r/100)	0,3*(1+r/100)	0,2*(1+r/100)	01*(1+r/100)
ВЫПЛАТА	(1 +r/100) — 0,6	0,6*(1+r/100) — 0,4	0,4*(1+r/100) — 0,3	0,3*(1+r/100) — 0,2	0,2*(1+r/100) — 0,1	01*(1+r/100)
ОСТАТОК	0,6	0,4	0,3	0,2	0,1	0

Осталось сложить все
суммы выплат и сравнить с 1,2 млн.

(1 +r/100) — 0,6
+ 0,6*(1+r/100) — 0,4
+ 0,4*(1+r/100)
— 0,3 + 0,3*(1+r/100) — 0,2
+ 0,2*(1+r/100) — 0,1
+ 01*(1+r/100) < 1,2

Сгруппируем отдельно
подчеркнутые и неподчеркнутые слагаемые.

(1+r/100)*(1
+ 0,6 + 0,4 + 0,3 + 0,2 +0,1) — (0,6+0,4+0,3+0,2+0,1) < 1,2

(1+r/100) <
(1,2 + 1,6)/2,6

r/100 < 0, 077

r < 7,7

По условию задачи r –
целое число. Следовательно, r=7.

Ответ: 7

Задачи для
самостоятельной работы

2.3.1

16 января планируется взять кредит в банке на 6 месяцев в размере 1 млн. руб. По условиям договора: − 1-го числа месяца долг увеличивается на r % по сравнению с концом предыдущего месяца, где r — целое число. − Со 2-го по 15-е число необходимо выплатить часть долга. − 16-го числа каждого месяца долг должен составлять сумму в соответствии с таблицей:  Месяц Февраль Март Апрель Май Июнь Июль Долг 0,6 0,4 0,3 0,2 0,1 0  Найдите наибольшее r, при котором сумма выплат будет меньше 1,25 млн. руб.

3. Вклады

3.1 Сравнение выгоды

В задачах этого типа
нужно представить себе весь процесс, «вжиться» в ситуацию и понять на каком
этапе один вариант начинает перевешивать другой.

Задача 1

В начале 2018 года Юрий приобрел ценную
бумагу стоимостью 25000 рублей. В конце каждого года цена
бумаги увеличивается на 3000 рублей. В начале любого года Юрий может
продать бумагу и сразу положить вырученные деньги на банковский счет. В этом
случае каждый год сумма на счете будет расти на 10 %. Через сколько лет Юрий
должен продать ценную бумагу, чтобы через 5 лет после ее покупки сумма на его
банковском счете была наибольшей?

Решение

У Юрия альтернатива:
либо получать ежегодно по 3000 руб., либо попытаться превысить это доход за
счет процентов, начисляемых банком. Может оказаться, что в определенный момент
проценты на вклад будут больше дохода в 3000 руб., но возможен и вариант, что
стабильный доход в 3000 руб. будет выгоднее в течение указанного в условии
промежутка времени.

Пусть через N лет
после покупки ценной бумаги Юрий решается ее продать. К тому времени стоимость
бумаги будет составлять 19000 + N*3000 руб.

Сколько Юрий
заработает на процентах на следующий год? 0,1*(19000 +N*3000).

Вот эту величину и
нужно сравнить с 3000 руб., которые Юрий рискнул потерять.

0,1*(19000 + N*3000)
> 3000

N > (30000 – 19000)/3000

N > 3,3

Так как N – целое
число, то Юрию будет достаточно 4 года.

Ответ: 4

Задача 2

Компания «Омега»
работает с двумя банками под разные проценты годовых. В начале года она положила
60% прибыли в банк «Альфа», а оставшуюся часть —  в банк «Бета». К концу 1 года
сумма этих вкладов достигла 590 тыс. руб., а к концу 2-го года — 701 тыс. руб.
Если бы компания первоначально положила 60% своей прибыли в банк «Бета», а
оставшуюся часть в банк «Альфа», то по окончании 1-го года сумма вкладов стала
бы равной 610 тыс.  руб. Какова была бы сумма вкладов в этом случае к концу
2-го года?

Решение

Пусть S – сумма
прибыли, которой распоряжается компания. Тогда в банк «Альфа» она положила 0,6S, а в
банк «Бета» — 0,4S. Во втором случае деньги бы распределились 0,4S и
0,6S соответственно. Пусть x – проценты банка
«Альфа», а y – проценты банка «Бета».

Тогда получим
систему уравнений:

(1)  0,6*Sx +
0,4*Sy = 590

(2)  0,6*Sx² + 0,4*Sy² = 701

(3)  0,4*Sx +
0,6*Sy = 610

Получили систему из
трех уравнений с тремя неизвестными. Следовательно, система решаема. Как именно
решать – дело вкуса, приведу вариант, который мне кажется менее трудозатратным.

Алгоритм:

1.   
Складываем (1) и (3): Sx + Sy = 1200

2.   
Выражаем Sx через Sy: Sx = 1200 – Sy и подставляем в (1): 0,6*(1200 — Sy) +
0,4Sy = 590

3.   
Находим Sy = 650. Соответственно, Sx = 1200 –
650 =550

4.   
(2) представляем в виде 0,6*x*Sx +
0,4*y*Sy = 701 и подставляем найденные Sx и Sy. В итоге получим y
= 13x/11

5.   
Теперь y, Sx и Sy ставим в (1). Получаем 0,6*550*x
+0,4*650*y = 701. Находим x=1,1, y=1,3

Интересующая нас
сумма вкладов к концу 2 года при альтернативном выборе 0,4Sx²
+ 0,6Sy². Подставив все найденные значения, получим
749 (тыс. руб.).

Ответ: 749000

Задачи для самостоятельной
работы

3.1.1

Алексей приобрёл ценную бумагу за 7 тыс. рублей. Цена бумаги каждый год возрастает на 2 тыс. рублей. В любой момент Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 10%. В течение какого года после покупки Алексей должен продать ценную бумагу, чтобы через тридцать лет после покупки этой бумаги сумма на банковском счёте была наибольшей?

3.1.2

В начале года Алексей 5/6 всех своих денег положил в банк А, а 1/6 — в банк Б. К концу 1-го года сумма вкладов стала равна 670 тыс. руб., к концу 2-го – 749 тыс. руб. Если бы Алексей 5/6 суммы положил в банк Б, а 1/6 — банк А, то по окончании 1-го года сумма составила бы 710 тыс. руб. Какова была бы в этом случае сумма вкладов по окончании 2-го года?

3.2 Изменяющиеся
проценты

Задача 1

В январе 2016 года предприниматель положил в банк некоторую
сумму под х% годовых. Через год, в январе 2017 года, он снял 1/5 положенных денег,
а оставшиеся деньги оставил в банке под у%. Известно, что (х+у)=30%. Каков
должен быть х, чтобы в январе 2018 года сумма на счету предпринимателя была
максимальной?

Решение

Рассмотрим, что
происходит с суммой вклада S:

·        
1 января 2017 года банк
начислил х% за год хранения и сумма на вкладе стала S*(1 + x/100)

·        
Предприниматель снял 1/5
первоначальных денег, то есть осталось: S*(1 + x/100) – 1/5S

·        
1 января 2018 года банк
начислил у% за год хранения: (S*(1 + x/100) -1/5S)*( 1 + у/100)

Подставим у=30-х и после
упрощения получим: S*(4/5 + х/100)*(130-х)/100 = S*(80+х)(130-х)/50000

Данное выражение
является квадратной функцией от переменной х. Возьмем производную, приравняем
ее к нулю и найдем точку максимума: -2х+50=0 => X=25

Ответ: 25%

Задачи для
самостоятельной работы

3.2.1

Каждый год процент на вклад «Эффективный» увеличивается на 1%. При этом начальный процент составляет 5%, а максимальный процент — 12% и выше подняться не может. Максим положил в банк 1 млн. руб. с целью увеличить сумму до 1,5 млн. руб. Сколько лет потребуется Максиму?

4. Задачи на оптимальный выбор

4.1 Производительность

Задача 1

У фермера есть два
одинаковых поля по 10 га каждое. На каждом можно выращивать картофель и
кукурузу, причем какую площадь занять под каждую культуру, фермер решает сам.
Урожайность картофеля на 1 поле составляет 400 ц/га, а на 2 поле – 300 ц./га.
Урожайность кукурузы на 1 поле составляет 300 ц/га, а на 2 поле – 400 ц/га. Картофель
фермер продает по 5000 руб./ц, а кукурузу – по 6000 руб./ц. Какой максимальный
доход может получить фермер?

Решение

Доход находится в
прямой пропорциональной зависимости от площади, урожайности и цены, то есть Д =
П*У*Ц. Обозначим х и у – площади, отведенные под картофель на 1 и 2 поле
соответственно. Тогда под кукурузу будет отведено (10-х) и (10-у) гектаров
соответственно. Занесем все данные в таблицы для 1-го и 2-го поля:

1 поле

	Площадь	Урожайность	Цена
Картофель	х	400	5000
Кукуруза	10-х	300	6000

Доход с
первого поля будет равен сумме доходов от продажи картофеля и кукурузы, то есть
Д1=400*х*5000 + (10-х)*300*6000

2 поле

	Площадь	Урожайность	Цена
Картофель	у	300	5000
Кукуруза	10-у	400	6000

Доход со
второго поля тоже будет равен сумме доходов
от продажи картофеля и кукурузы, то есть Д2=300*у*5000 + (10-у)*400*6000

Общий доход с двух
полей, таким образом, Д=Д1+Д2=400*х*5000 + (10-х)*300*6000 + 300*у*5000 +
(10-у)*400*6000 = 2*10⁵*х – 9*10⁵*у + 42*10⁶

Очевидно, данное
выражение максимально при наибольшем х и наименьшем у. Следовательно, х=10, у=0
(то есть все 1 поле засеваем картофелем, а 2 поле – кукурузой). Осталось
посчитать доход: Д=2*10⁵*10 + 42*10⁶ =44*10⁶  руб.

Ответ: 44000000 руб.

Задача 2

В Шахтерске и Кузнецке
имеется по 250 рабочих. Они готовы трудиться по 5 часов в сутки на добыче
алюминия или никеля. В Шахтерске один рабочий добывает за 1 час 0,2 кг алюминия
или 0,1 кг никеля. В Кузнецке для добычи х кг алюминия требуется х²
человеко-часов, а для добычи у кг никеля требуется у²
человеко-часов. Какую наибольшую массу металлов можно добыть в двух городах за
сутки, если для промышленности неважно, что использовать – никель или алюминий?

Решение

В Шахтерске с выбором
все просто: поскольку успешнее добывается алюминий, то всех рабочих и
направляем на его добычу. За 5 часов работы 250 рабочих добудут 250*5*0,2=250
кг.

В Кузнецке
зависимость иная: для добычи 1 кг нужен 1 рабочий/час, для 2 кг – 4
рабочих/час, для 3 кг – 9 и т.д. Пусть на добыче алюминия будет работать t человек.
Тогда на добычу никеля выйдут (250-t) человек. За 5 часов работы будет добыто √(5t) + √(5*(250-t).

Введем функцию Z(t)= √(5t) + √(5*(250-t).
Найдем ее производную и приравняем к 0.

Z^’(t)= 5/(2√(5t)) —
5/(2√(5(250-t))) = 0

t=125

Таким образом, в
Кузнецке на никель и алюминий выйдут по 125 человек. Общая добыча в 2 городах
составит: 250 + √(5*125) + √(5*(250-125) = 250+25+25 = 300 кг.

Ответ: 300

Задачи для
самостоятельной работы

4.1.1

У фермера есть два одинаковых поля по 10 га каждое. На каждом можно выращивать картофель и кукурузу, причем какую площадь занять под каждую культуру, фермер решает сам. Урожайность картофеля на 1 поле составляет 200 ц/га, а на 2 поле – 300 ц./га. Урожайность кукурузы на 1 поле составляет 250 ц/га, а на 2 поле – 200 ц/га. Картофель фермер продает по 1500 руб./ц, а кукурузу – по 1800 руб./ц. Какой максимальный доход может получить фермер?

4.1.2

В двух шахтах добывают алюминий и никель. В первой шахте трудятся 100 рабочих по 7 часов в сутки. При этом один рабочий добывает в час 1 кг алюминия или 3 кг никеля. Во второй шахте трудятся 300 рабочих по 7 часов в день. При этом один рабочий добывает в час 3 кг алюминия или 1 кг никеля. Весь добытый металл отправляется на переплавку, где производится сплав из соотношения алюминий : никель =2:1. Какое наибольшую массу сплава можно изготовить в сутки?

4.2 Окупаемость

Задача 1

Строительство нового
завода стоит 115 млн рублей. Затраты на производство x тыс. единиц
продукции
на таком заводе равны (0,5х²+х+9) млн рублей в год.
Если
продукцию завода продать по цене р тыс. рублей
за единицу, то прибыль фирмы (в млн рублей) за один год составит рх – 0,5(х²+х+9).
Когда завод будет построен, фирма будет выпускать продукцию в
таком количестве, чтобы прибыль была наибольшей. При каком наименьшем
значении p строительство
завода окупится не более чем за 5 лет?

Решение

Прибыль за 1 год рх – 0,5(х²+х+9) = -0,5х² +х*(р-1) – 9. Получили
функцию F(х), которая показывает зависимость годовой прибыли от количества
продукции. Чтобы найти наибольшее значение прибыли, возьмем производную: F^’(x)=-x + p – 1, то есть при х=p-1 прибыль
максимальна и равна (p-1)²/2 – 9.

За пять лет прибыль составит
5*((p-1)²/2
– 9). Эта цифра должна быть не менее 115 тыс.руб.

Получим: 5*((p-1)²/2 –
9)≥115

(p-1)²)≥64

Решая квадратное уравнение,
получим 2 корня: р=-7 и р=9. Неравенству удовлетворяют интервалы р≥9 и р≤-7.
Цена может быть только положительной величиной, поэтому оставляем только
интервал р≥9. Очевидно, что минимальная цена р=9.

Ответ: 9

Задачи для
самостоятельной работы

4.2.1

Строительство нового завода стоит 122 млн рублей. Затраты на производство x тыс. единиц продукции на таком заводе равны (0,5х2 -2х+10) млн рублей в год. Если продукцию завода продать по цене р тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит рх – 0,5(х2-2х+10). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении p строительство завода окупится не более чем за 4 года?

5. Пример оформления 17 задачи на
экзаменационном бланке

В феврале 2018 года
на Независимой диагностике (ЕГЭ математика, профильный уровень) это оформление
задачи не вызвало нареканий у проверяющих. Соответственно, рекомендую и вам,
уважаемые читатели, придерживаться стиля оформления с таблицей и кратким
пояснением.

Задача

Дмитрий думает, на
сколько лет взять кредит в банке под 20% годовых: на 2 или на 4 года.  Условия
кредита: выплачивать ежегодно равными платежами. Сумма кредита 2013000
руб. Какова будет переплата Дмитрия, если он возьмет кредит на 4 года?

6.  Ответы

Ответы к задачам для самостоятельной работы

2.1.1	9282000
2.1.2	7
2.2.1	822000
2.2.2	60
2.2.3	19
2.3.1	9
3.1.1	8
3.1.2	841
3.2.1	6
4.1.1	9
4.1.2	5400
4.2.1	7

7.  Список используемой литературы

1.   
Под ред. Ященко И.В. «ЕГЭ 2018. Математика. 50 вариантов.
Профильный уровень. Типовые тестовые задания от разработчиков ЕГЭ».

2.   
Материалы
образовательного портала ege.sdamgia.ru

3.    Материалы образовательного портала infourok.ru

4.   
Прокофьев А.А. «Рекомендации по подготовке к
выполнению задания №17 (финансово-экономические задачи) ЕГЭ профильного уровня».