Десятичные приставки
| Наименование | Обозначение | Множитель |
| гига | Г | 109 |
| мега | М | 106 |
| кило | к | 103 |
| деци | д | 10–1 |
| санти | с | 10–2 |
| милли | м | 10–3 |
| микро | мк | 10–6 |
| нано | н | 10–9 |
| пико | п | 10–12 |
Физические постоянные (константы)
| число π | π = 3,14 |
| ускорение свободного падения | g = 10 м/с2 |
| гравитационная постоянная | G = 6,7·10–11 Н·м2/кг2 |
| газовая постоянная | R = 8,31 Дж/(моль·К) |
| постоянная Больцмана | k = 1,38·10–23 Дж/К |
| постоянная Авогадро | NA = 6,02·1023 1/моль |
| скорость света в вакууме | с = 3·108 м/с |
| коэффициент пропорциональности в законе Кулона | k = 1/(4πε0) = 9·109 Н·м2/Кл2 |
| модуль заряд электрона | e = 1,6·10-19 Кл |
| масса электрона | me = 9,1·10–31 кг |
| масса протона | mp = 1,67·10–27 кг |
| постоянная Планка | h = 6,62·10-34 Дж·с |
| радиус Солнца | 6,96·108 м |
| температура поверхности Солнца | T = 6000 K |
| радиус Земли | 6370 км |
Соотношение между различными единицами измерения
| температура | 0 К = –273 0С |
| атомная единица массы | 1 а.е.м. = 1,66·10–27 кг |
| 1 атомная единица массы эквивалентна | 931,5 МэВ |
| 1 электронвольт | 1 эВ = 1,6·10-19 Дж |
| 1 астрономическая единица | 1 а.е. ≈ 150 000 000 км |
| 1 световой год | 1 св. год ≈ 9,46·1015 м |
| 1 парсек | 1 пк ≈ 3,26 св. года |
Масса частиц
| электрона | 9,1·10–31кг ≈ 5,5·10–4 а.е.м. |
| протона | 1,673·10–27 кг ≈ 1,007 а.е.м. |
| нейтрона | 1,675·10–27 кг ≈ 1,008 а.е.м. |
Плотность
| воды | 1000 кг/м3 |
| древесины (сосна) | 400 кг/м3 |
| керосина | 800 кг/м3 |
| подсолнечного масла | 900 кг/м3 |
| алюминия | 2700 кг/м3 |
| железа | 7800 кг/м3 |
| ртути | 13 600 кг/м3 |
Удельная теплоёмкость
| воды | 4,2·10 3 Дж/(кг·К) |
| льда | 2,1·10 3 Дж/(кг·К) |
| железа | 460 Дж/(кг·К) |
| свинца | 130 Дж/(кг·К) |
| алюминия | 900 Дж/(кг·К) |
| меди | 380 Дж/(кг·К) |
| чугуна | 500 Дж/(кг·К) |
Удельная теплота
| парообразования воды | 2,3·10 6 Дж/кг |
| плавления свинца | 2,5·10 4 Дж/кг |
| плавления льда | 3,3·10 5 Дж/кг |
Нормальные условия:
| давление | 105 Па |
| температура | 00 C |
Молярная маcса молекул
| азота | 28·10–3 кг/моль |
| аргона | 40·10–3 кг/моль |
| водорода | 2·10–3 кг/моль |
| воздуха | 29·10–3 кг/моль |
| воды | 18·10–3 кг/моль |
| гелия | 4·10–3 кг/моль |
| кислорода | 32·10–3 кг/моль |
| лития | 6·10–3 кг/моль |
| неона | 20·10–3 кг/моль |
| углекислого газа | 44·10–3 кг/моль |
Перейти к контенту
Десятичные приставки
| Наименование | Обозначение | Множитель |
| гига | Г | 109 |
| мега | М | 106 |
| кило | к | 103 |
| деци | д | 10–1 |
| санти | с | 10–2 |
| милли | м | 10–3 |
| микро | мк | 10–6 |
| нано | н | 10–9 |
| пико | п | 10–12 |
Физические постоянные (константы)
| число π | π = 3,14 |
| ускорение свободного падения | g = 10 м/с2 |
| гравитационная постоянная | G = 6,7·10–11 Н·м2/кг2 |
| газовая постоянная | R = 8,31 Дж/(моль·К) |
| постоянная Больцмана | k = 1,38·10–23 Дж/К |
| постоянная Авогадро | NA = 6,02·1023 1/моль |
| скорость света в вакууме | с = 3·108 м/с |
| коэффициент пропорциональности в законе Кулона | k = 1/(4πε0) = 9·109 Н·м2/Кл2 |
| модуль заряд электрона | e = 1,6·10-19 Кл |
| масса электрона | me = 9,1·10–31 кг |
| масса протона | mp = 1,67·10–27 кг |
| постоянная Планка | h = 6,62·10-34 Дж·с |
| радиус Солнца | 6,96·108 м |
| температура поверхности Солнца | T = 6000 K |
| радиус Земли | 6370 км |
Соотношение между различными единицами измерения
| температура | 0 К = –273 0С |
| атомная единица массы | 1 а.е.м. = 1,66·10–27 кг |
| 1 атомная единица массы эквивалентна | 931,5 МэВ |
| 1 электронвольт | 1 эВ = 1,6·10-19 Дж |
| 1 астрономическая единица | 1 а.е. ≈ 150 000 000 км |
| 1 световой год | 1 св. год ≈ 9,46·1015 м |
| 1 парсек | 1 пк ≈ 3,26 св. года |
Масса частиц
| электрона | 9,1·10–31кг ≈ 5,5·10–4 а.е.м. |
| протона | 1,673·10–27 кг ≈ 1,007 а.е.м. |
| нейтрона | 1,675·10–27 кг ≈ 1,008 а.е.м. |
Плотность
| воды | 1000 кг/м3 |
| древесины (сосна) | 400 кг/м3 |
| керосина | 800 кг/м3 |
| подсолнечного масла | 900 кг/м3 |
| алюминия | 2700 кг/м3 |
| железа | 7800 кг/м3 |
| ртути | 13 600 кг/м3 |
Удельная теплоёмкость
| воды | 4,2·10 3 Дж/(кг·К) |
| льда | 2,1·10 3 Дж/(кг·К) |
| железа | 460 Дж/(кг·К) |
| свинца | 130 Дж/(кг·К) |
| алюминия | 900 Дж/(кг·К) |
| меди | 380 Дж/(кг·К) |
| чугуна | 500 Дж/(кг·К) |
Удельная теплота
| парообразования воды | 2,3·10 6 Дж/кг |
| плавления свинца | 2,5·10 4 Дж/кг |
| плавления льда | 3,3·10 5 Дж/кг |
Нормальные условия:
| давление | 105 Па |
| температура | 00 C |
Молярная маcса молекул
| азота | 28·10–3 кг/моль |
| аргона | 40·10–3 кг/моль |
| водорода | 2·10–3 кг/моль |
| воздуха | 29·10–3 кг/моль |
| воды | 18·10–3 кг/моль |
| гелия | 4·10–3 кг/моль |
| кислорода | 32·10–3 кг/моль |
| лития | 6·10–3 кг/моль |
| неона | 20·10–3 кг/моль |
| углекислого газа | 44·10–3 кг/моль |
Справочные данные из демоверсии, которые могут понадобиться вам при выполнении работы.
Десятичные приставки
Константы
Соотношения между различными единицами
Масса частиц
Астрономические величины
Плотность
Удельная теплоёмкость
Удельная теплота
Нормальные условия
Молярная маcса
→ sp-fizika.pdf
→ Другой справочник с формулами.
→ Основные формулы по физике.
→ 180 формул по физике на одном листе.
- Взрослым: Skillbox, Хекслет, Eduson, XYZ, GB, Яндекс, Otus, SkillFactory.
- 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
- До 7 класса: Алгоритмика, Кодланд, Реботика.
- Английский: Инглекс, Puzzle, Novakid.
Справочные материалы ЕГЭ по физике 2022-2023
Десятичные приставки
Наименование — Обозначение — Множитель
- гига — Г — 109
- мега — М — 106
- кило — к — 103
- гекто — г — 102
- деци — д — 10–1
- санти — с — 10–2
- милли — м — 10–3
- микро — мк — 10–6
- нано — н — 10–9
- пико — п — 10–12
Физические постоянные (константы)
- число π: π = 3,14
- ускорение свободного падения: g = 10 м/с2
- гравитационная постоянная: G = 6,7·10–11 Н·м2/кг2
- универсальная газовая постоянная: R = 8,31 Дж/(моль·К)
- постоянная Больцмана: k = 1,38·10–23 Дж/К
- постоянная Авогадро: NA = 6·1023 1/моль
- скорость света в вакууме: с = 3·108 м/с
- коэффициент пропорциональности в законе Кулона: k = 1/(4πε0) = 9·109 Н·м2/Кл2
- модуль заряд электрона (элементарный электрический заряд): e = 1,6·10−19 Кл
- постоянная Планка: h = 6,6·10-34 Дж·с
Соотношение между различными единицами измерения
- температура: 0 К = –273 0С
- атомная единица массы: 1 а.е.м. = 1,66·10–27 кг
- 1 атомная единица массы эквивалентна: 931,5 МэВ
- 1 электронвольт: 1 эВ = 1,6·10−19 Дж
Масса частиц
- электрона — 9,1·10–31 кг ≈ 5,5·10–4 а.е.м.
- протона — 1,673·10–27 кг ≈ 1,007 а.е.м.
- нейтрона — 1,675·10–27 кг ≈ 1,008 а.е.м.
Плотность
- воды — 1000 кг/м3
- древесины (сосна) — 400 кг/м3
- керосина — 800 кг/м3
- подсолнечного масла — 900 кг/м3
- алюминия — 2700 кг/м3
- железа — 7800 кг/м3
- ртути — 13 600 кг/м3
Удельная теплоёмкость
- воды — 4,2·103 Дж/(кг·К)
- льда — 2,1·103 Дж/(кг·К)
- железа — 460 Дж/(кг·К)
- свинца — 130 Дж/(кг·К)
- алюминия — 900 Дж/(кг·К)
- меди — 380 Дж/(кг·К)
- чугуна — 500 Дж/(кг·К)
Удельная теплота
- парообразования воды — 2,3·106 Дж/кг
- плавления свинца — 2,5·104 Дж/кг
- плавления льда — 3,3·105 Дж/кг
Нормальные условия
- давление: 105 Па
- температура: 0 °С
Молярная масса молекул
- азота: 28·10–3 кг/моль
- аргона: 40·10–3 кг/моль
- водорода: 2·10–3 кг/моль
- воздуха: 29·10–3 кг/моль
- воды: 18·10–3 кг/моль
- гелия: 4·10–3 кг/моль
- кислорода: 32·10–3 кг/моль
- лития: 6·10–3 кг/моль
- неона: 20·10–3 кг/моль
- углекислого газа: 44·10–3 кг/моль
- Взрослым: Skillbox, Хекслет, Eduson, XYZ, GB, Яндекс, Otus, SkillFactory.
- 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
- До 7 класса: Алгоритмика, Кодланд, Реботика.
- Английский: Инглекс, Puzzle, Novakid.
- Взрослым: Skillbox, Хекслет, Eduson, XYZ, GB, Яндекс, Otus, SkillFactory.
- 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
- До 7 класса: Алгоритмика, Кодланд, Реботика.
- Английский: Инглекс, Puzzle, Novakid.
Справочные материалы ЕГЭ по физике 2022-2023
Десятичные приставки
Наименование — Обозначение — Множитель
- гига — Г — 109
- мега — М — 106
- кило — к — 103
- гекто — г — 102
- деци — д — 10–1
- санти — с — 10–2
- милли — м — 10–3
- микро — мк — 10–6
- нано — н — 10–9
- пико — п — 10–12
Физические постоянные (константы)
- число π: π = 3,14
- ускорение свободного падения: g = 10 м/с2
- гравитационная постоянная: G = 6,7·10–11 Н·м2/кг2
- универсальная газовая постоянная: R = 8,31 Дж/(моль·К)
- постоянная Больцмана: k = 1,38·10–23 Дж/К
- постоянная Авогадро: NA = 6·1023 1/моль
- скорость света в вакууме: с = 3·108 м/с
- коэффициент пропорциональности в законе Кулона: k = 1/(4πε0) = 9·109 Н·м2/Кл2
- модуль заряд электрона (элементарный электрический заряд): e = 1,6·10−19 Кл
- постоянная Планка: h = 6,6·10-34 Дж·с
Соотношение между различными единицами измерения
- температура: 0 К = –273 0С
- атомная единица массы: 1 а.е.м. = 1,66·10–27 кг
- 1 атомная единица массы эквивалентна: 931,5 МэВ
- 1 электронвольт: 1 эВ = 1,6·10−19 Дж
Масса частиц
- электрона — 9,1·10–31 кг ≈ 5,5·10–4 а.е.м.
- протона — 1,673·10–27 кг ≈ 1,007 а.е.м.
- нейтрона — 1,675·10–27 кг ≈ 1,008 а.е.м.
Плотность
- воды — 1000 кг/м3
- древесины (сосна) — 400 кг/м3
- керосина — 800 кг/м3
- подсолнечного масла — 900 кг/м3
- алюминия — 2700 кг/м3
- железа — 7800 кг/м3
- ртути — 13 600 кг/м3
Удельная теплоёмкость
- воды — 4,2·103 Дж/(кг·К)
- льда — 2,1·103 Дж/(кг·К)
- железа — 460 Дж/(кг·К)
- свинца — 130 Дж/(кг·К)
- алюминия — 900 Дж/(кг·К)
- меди — 380 Дж/(кг·К)
- чугуна — 500 Дж/(кг·К)
Удельная теплота
- парообразования воды — 2,3·106 Дж/кг
- плавления свинца — 2,5·104 Дж/кг
- плавления льда — 3,3·105 Дж/кг
Нормальные условия
- давление: 105 Па
- температура: 0 °С
Молярная масса молекул
- азота: 28·10–3 кг/моль
- аргона: 40·10–3 кг/моль
- водорода: 2·10–3 кг/моль
- воздуха: 29·10–3 кг/моль
- воды: 18·10–3 кг/моль
- гелия: 4·10–3 кг/моль
- кислорода: 32·10–3 кг/моль
- лития: 6·10–3 кг/моль
- неона: 20·10–3 кг/моль
- углекислого газа: 44·10–3 кг/моль
- Взрослым: Skillbox, Хекслет, Eduson, XYZ, GB, Яндекс, Otus, SkillFactory.
- 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
- До 7 класса: Алгоритмика, Кодланд, Реботика.
- Английский: Инглекс, Puzzle, Novakid.
Модель идеального газа в МКТ
Идеальный газ — это теоретическая модель газа, в которой пренебрегают размерами и взаимодействиями частиц газа и учитывают лишь их упругие столкновения.
Другими словами, предполагается, что внутренняя энергия идеального газа определяется лишь кинетической энергией его частиц (т. е. потенциальной энергией взаимодействия молекул пренебрегают).
Модель идеального газа была предложена в 1847 г. Дж. Герапатом. На основе этой модели были теоретически выведены газовые законы (закон Бойля—Мариотта, закон Гей-Люссака, закон Шарля, закон Авогадро), которые ранее были установлены экспериментально. Модель идеального газа была положена в основу молекулярно-кинетической теории газа.
Основными законами идеального газа являются уравнение состояния и закон Авогадро, в которых впервые были связаны макрохарактеристики газа (давление, температура, масса) с массой молекулы (уравнение Менделеева-Клапейрона, или уравнение состояния идеального газа).
В современной физике ее используют также для описания ансамблей любых слабовзаимодействующих частиц. Модель идеального газа справедлива для реальных классических газов при достаточно высоких температурах и разрежениях, когда среднее расстояние между молекулами много больше размеров самих молекул. В этом случае силами притяжения можно пренебречь. Силы же отталкивания проявляются лишь при столкновении друг с другом в течение ничтожно малых интервалов времени.
В простейшей модели газа молекулы рассматриваются как очень маленькие твердые шарики, обладающие массой. Движение отдельных молекул подчиняется законам механики Ньютона. Конечно, не все процессы в разреженных газах можно объяснить с помощью такой модели, однако давление газа вычислить с ее помощью можно.
Основное уравнение МКТ (давление газа)
Основное уравнение молекулярно-кинетической теории устанавливает связь между давлением идеального газа и средней кинетической энергией его молекул.
Вывод основного уравнения МКТ основывается на допущениях модели идеального газа и утверждении: давление газа является результатом ударов молекул о стенку сосуда.
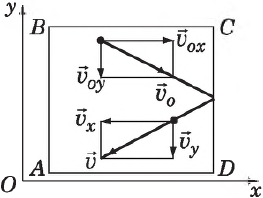
Определим давление газа на стенку площадью $S$ сосуда $ABCD$.
Каждая молекула массой $m_0$, отскакивая от стенки после упругого соударения со стенкой, передает ей импульс $2m_{0}υ_x$, где $υ_x$ — проекция скорости молекулы $υ↖{→}$ на ось $О_х$, перпендикулярную стенке. Всего за одну секунду суммарный импульс, получаемый стенкой от всех молекул, равен $2m_{0}υ_{x}Z$, где $Z$ — число таких столкновений (за $1$ с) всех молекул. Очевидно, что $Z=n={N}/{V}$, где $n$ — концентрация молекул в единице объема; $N$ — число всех молекул. Число $Z$ пропорционально также скорости молекул $υ_x$ и площади стенки $S:Z∼nυ_{x}S$. Поскольку все направления при хаотичном движении молекул газа равновероятны, то из всех молекул, имеющих составляющую скорости $υ_x$, только половина движется в сторону стенки $CD$ вторая половина — в сторону $АВ$ (т. е. в обратную). Поэтому $Z={1}/{2}nυ_{x}S$, а полный импульс, переданный стенке за $1$ с, равен $2m_{0}nυ_x^{2}S$. Поскольку изменение импульса точки (тела) за единицу времени равно действующей на него силе $F={∆(mυ)}/{∆t}$, то $F=m_{0}nυ_x^{2}S$. В действительности, поскольку речь идет о большом количестве молекул, движущихся с разными скоростями, силу следует усреднить: $F↖{-}={m_{0}nυ_x^{2}S}↖{-}$.
Сила эта зависит, таким образом, от среднего квадрата скорости ${υ_x^{2}}↖{-}$.
Поскольку вследствие хаотичности движения все направления равноправны, то
${υ_x^{2}}↖{-}={υ_y^{2}}↖{-}={υ_z^{2}}↖{-}$
С другой стороны, известно, что квадрат модуля любого вектора равен сумме квадратов его проекций на оси координат, поэтому:
$υ^2=υ_x^{2}+υ_y^{2}+υ_z^{2}$
Усредняя это выражение по всем молекулам и учитывая $υ^2=υ_x^{2}+υ_y^{2}+υ_z^{2}$, получим:
${υ^2}↖{-}={υ_x^{2}}↖{-}+{υ_y^{2}}↖{-}+{υ_z^{2}}↖{-}=3{υ_x^{2}}↖{-}$
Отсюда:
${υ_x^{2}}↖{-}={1}/{3}{υ_^2}↖{-}$
С учетом последней формулы $F↖{-}={1}/{3}m_{0}n{υ^2}↖{-}$
Следовательно, давление на стенку сосуда равно:
$p={F}/{S}={1}/{3}m_{0}n{υ^2}↖{-}$
Это основное уравнение молекулярно-кинетической теории. Это уравнение — первое количественное соотношение, полученное в МКТ.
Уравнение $p={F}/{S}={1}/{3}m_{0}n{υ^2}↖{-}$ позволяет получить связь между давлением и средней кинетической энергией молекул ${E_k}↖{-}={m_{0}{υ^2}↖{-}}/{2}:$
$p={2}/{3}n{E_k}↖{-}$
Давление идеального газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.
Важно подчеркнуть, что здесь речь идет о средней кинетической энергии молекул газа. Это означает, что давление газа — величина, органически связанная с тем, что газ состоит из большого числа молекул. Нет смысла говорить о давлении, создаваемом несколькими молекулами. Давление газа — понятие, имеющее статистический характер (так называют понятия, имеющие смысл только для систем с очень большим числом частиц).
Абсолютная температура
Согласно основному уравнению МКТ, давление $р$ прямо пропорционально средней кинетической энергии $E↖{-}$ поступательного движения молекул:
$p={2}/{3}n{E}↖{-}$
где $n$ — объемная концентрация молекул. Заменив в $p={2}/{3}n{E}↖{-}$ $n$ отношением числа молекул $N$ к объему газа $V(n={N}/{V})$, получим:
${pV}/{N}={2}/{3}{E}↖{-}$
В состоянии теплового равновесия при постоянном объеме средняя кинетическая энергия данной массы газа должна иметь вполне определенное значение, как и температура. Согласно формуле ${pV}/{N}={2}/{3}{E}↖{-}$, это означает, что отношение ${pV}/{N}$ для данной температуры должно быть одним и тем же для любых идеальных газов. То, что это действительно так, было подтверждено экспериментально для разных газов, находящихся в условиях теплового равновесия при постоянном объеме (измерялось давление).
Таким образом, величина $Θ={pV}/{N}$, которую, в отличие от микропараметра ${E}↖{-}$, легко измерить, является вполне однозначной характеристикой теплового состояния газа, как и температура. Измеряется $Θ$ (как и энергия) в джоулях. Зависит она только от температуры и может рассматриваться как естественная мера температуры. Однако в силу укоренившейся привычки измерять температуру в градусах был введен коэффициент пропорциональности $k$ между температурой $Θ$, выраженной в энергетических единицах, и температурой $Т$, выраженной в градусах:
$Θ=kT$
или
${pV}/{N}=kT$
Температура $Т$, определяемая равенством $Θ=kT$, называется абсолютной температурой.
Значения температуры, определенной по формуле ${pV}/{N}={2}/{3}{E}↖{-}$, всегда положительны в силу положительности $Θ={pV}/{N}$ (ни давление, ни объем, ни число частиц отрицательными быть не могут). Поэтому минимальным значением температуры является нуль. Температура может равняться нулю, если давление либо объем равны нулю. Из принятого определения температуры следует, что нулем температуры является температура, при которой прекращается хаотическое движение молекул. Она называется абсолютным нулем температуры.
Температура, как и давление, определяется средней кинетической энергией молекул идеального газа. Поэтому температура, как и давление, является статистической величиной (статистической называется величина, имеющая смысл только для систем, содержащих очень большое число частиц). Нельзя говорить о температуре одной или нескольких молекул.
Абсолютную шкалу температур ввел английский ученый У. Кельвин в 1850 г. Нулевая температура по абсолютной шкале (ее называют также шкалой Кельвина) соответствует абсолютному нулю, а каждая единица температуры по этой шкале равна градусу по шкале Цельсия.
Единица абсолютной температуры является одной из семи основных единиц СИ и измеряется в кельвинах (обозначается буквой $К$).
Связь между температурами, измеренными по шкалам Цельсия $t$ и Кельвина $Т$, описывается формулой:
$T(K)=t(°C)+273.15K$
Абсолютный нуль равен $-273.15°$С. Как правило, при расчетах пользуются округленным значением абсолютного нуля ($-273°$С).
Коэффициент пропорциональности к в формуле $Θ=kT$ называется постоянной Больцмана в честь Л. Больцмана — одного из основателей молекулярно-кинетической теории газа. Этот коэффициент составляет $k=1.38^{-23}$ Дж/К.
Постоянная Больцмана связывает температуру $Θ$ в энергетических единицах с температурой $Т$ в кельвинах. Это одна из наиболее важных постоянных в молекулярно-кинетической теории.
Температура как мера кинетической энергии
Из основного уравнения молекулярно-кинетической теории, записанного в форме $p={2}/{3}{E}↖{-}$
${pv}/{N}={2}/{3}{E}↖{-}$
и определения абсолютной температуры согласно ${pV}/{N}=kt$
${pv}/{N}=kT$
получим:
$E↖{-}={3}/{2}kT$
Средняя кинетическая энергия хаотического поступательного движения молекул газа пропорциональна абсолютной температуре.
Из полученного результата однозначно следует, что абсолютная температура есть мера средней кинетической энергии движения молекул.
Соотношение между температурой и кинетической энергией справедливо не только для разреженных газов (идеальных газов), но также для любых тел, подчиняющихся законам механики Ньютона. Оно справедливо и для жидкостей, и для твердых тел, атомы которых колеблются около положения равновесия.
Уравнение $р = nkТ$
Из формулы $p={2}/{3}n{E_k}↖{-}$ может быть получена зависимость давления газа от абсолютной температуры $Т$ и концентрации его молекул, если воспользоваться выражением для средней кинетической энергии:
$p=nkT$
где $k$ — постоянная Больцмана.
Из формулы $p=nkT$ очевидно, что при одинаковых давлениях и температурах концентрация молекул у всех газов одинакова.
Отсюда следует известный закон Авогадро: в равных объемах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.
Средняя скорость теплового движения молекул может быть также выражена через абсолютную температуру, если в формуле $E↖{-}={3}/{2}kT$ заменить $E↖{-}$ на ${m_{0}{υ^2}↖{-}}/{2}$:
${m_{0}{υ^2}↖{-}}/{2}={3}/{2}kT→{υ^2}↖{-}=3{kT}/{m_0}$
Квадратный корень из этой величины называется средней квадратичной скоростью:
$υ↖{-}=√{{3kT}/{m_0}}$
Уравнение Менделеева-Клапейрона (уравнение состояния идеального газа)
Уравнение состояния идеального газа — это зависимость между параметрами идеального газа — давлением $р$, объемом $V$ и абсолютной температурой $Т$, определяющими его состояние:
$pV=BT$
где $В$ зависит от массы газа $m$ и его молекулярной массы $М$. В таком виде уравнения впервые получено в 1834 г. французским ученым Б. П. Э. Клапейроном и называется уравнением Клапейрона.
В 1874 г. Д. И. Менделеев вывел уравнение состояния для одного моля идеального газа: $pV=RT$, где $R$ — универсальная газовая постоянная. Если молярная масса газа $М$, то
$pV={m}/{M}RT$
Уравнение состояния в форме $pV={m}/{M}RT$ называется уравнением Клапейрона-Менделеева. Оно объединяет газовые законы Гей-Люссака, Бойля—Мариотта, Авогадро, Шарля.
Уравнение состояния $pV={m}/{M}RT$ может быть получено из зависимости давления от температуры $p=nkT$, если в нее подставить концентрацию молекул $n$ из выражения
$n={N}/{V}={1}/{V}·{m}/{M}N_A$
где $N_А$ — постоянная Авогадро, $N$ — число молекул в теле.
В результате получим:
$pV={m}/{M}kN_{A}T$
где $kN_A=R$ — универсальная газовая постоянная, равная $8.31$ Дж/моль$·$К; $k$ — постоянная Больцмана, равная $1.38·10^{-23}$ Дж/К. Заменив в $pV={m}/{M}kN_{A}T$ $kN_A$ на $R$, получаем уравнение состояния в виде $pV={m}/{M}RT$. Отношение уравнений $pV={m}/{M}RT$ или $pV=BT$ при двух наборах параметров $p_1,V_1,T_1$ и $p_2,V_2,T_2$ дает:
${p_1V_1}/{T_1}={p_2V_2}/{T_2}=const$
Внутренняя энергия идеального одноатомного газа
Поскольку молекулы идеального газа не взаимодействуют друг с другом, их потенциальная энергия считается равной нулю. Внутренняя энергия идеального газа определяется только кинетической энергией беспорядочного поступательного движения его молекул. Для ее вычисления нужно умножить среднюю кинетическую энергию одного атома $E↖{-}={3}/{2}kT$ на число атомов $N={m}/{M}N_A$.
Учитывая, что $kN_A=R$, получим значение внутренней энергии идеального газа:
$U={3}/{2}·{m}/{M}RT$
Внутренняя энергия идеального одноатомного газа прямо пропорциональна его температуре.
Если воспользоваться уравнением Клапейрона-Менделеева, то выражение для внутренней энергии идеального газа можно представить в виде:
$U={3}/{2}pV$
Следует отметить, что, согласно выражению для средней кинетической энергии одного атома $(E↖{-}={3}/{2}kT)$ и в силу хаотичности движения, на каждое из трех возможных направлении движения или каждую степень свободы по оси $X,Y$ и $Z$ приходится одинаковая энергия ${kT}/{2}$.
Число степеней свободы — это число возможных независимых направлений движения молекулы.
Газ, каждая молекула которого состоит из двух атомов, называется двухатомным. Каждый атом может двигаться по трем направлениям, поэтому общее число возможных направлений движения — $6$. За счет связи между молекулами число степеней свободы уменьшается на одну, поэтому число степеней свободы для двухатомной молекулы равно пяти.
Средняя кинетическая энергия двухатомной молекулы равна ${5}/{2}kT$. Соответственно внутренняя энергия идеального двухатомного газа равна:
$U={5}/{2}·{m}/{M}RT={5}/{2}pV$
Формулы для внутренней энергии идеального газа можно обобщить:
$U={i}/{2}·{m}/{M}RT={i}/{2}pV$
где $i$ — число степеней свободы молекул газа ($i = 3$ для одноатомного и $i=5$ для двухатомного газа).
Для идеальных газов внутренняя энергия зависит только от одного макроскопического параметра — температуры и не зависит от объема, т. к. потенциальная энергия равна нулю (объем определяет среднее расстояние между молекулами).
Для реальных газов потенциальная энергия не равна нулю. Поэтому внутренняя энергия в термодинамике в общем случае однозначно определяется параметрами, характеризующими состояние этих тел: объемом ($V$) и температурой ($Т$).
Закон Дальтона
Закон Дальтона для смеси идеальных газов гласит: давление смеси газов равно сумме парциальных давлений ее компонент.
Парциальным давлением какого-либо газа — компонента газовой смеси называется давление, которое оказывал бы этот газ, если бы он один занимал весь объем, занимаемый смесью.
Для доказательства закона Дальтона перепишем уравнение $p=nkT$ в виде:
$pV=NkT$
Рассмотрим сосуд объемом $V$, в котором имеется смесь нереагирующих химически газов, находящихся в состоянии теплового равновесия. Уравнение состояния для такой смеси имеет вид:
$pV=(N_{1}+N_{2}+N_{3}+…)kT$
где $N_{1},N_{2},N_{3}…$ — числа компонент смеси.
Очевидно, что
$N_{1},N_{2},N_{3}+…=N$
где $N$ — общее число молекул в сосуде.
Давление смеси газа получим, поделив обе части $pV=(N_{1}+N_{2}+N_{3}+…)kT$ на объем $V$:
$p={N_1}/{V}kT+{N_2}/{V}kT+{N_3}/{V}kT+…$
Слагаемые этой суммы представляют собой давления каждой из компонент смеси, занимающей объем $V$, т. е. являются парциальными давлениями компонент смеси $р_1 р_2, р_3, …$ что и утверждает закон Дальтона:
$p=р_1+р_2+р_3+…$
То, что каждая группа молекул оказывает давление, не зависящее от давления, оказываемого другими группами, обусловлено отсутствием взаимодействия между молекулами. Последнее реально выполняется только для газов при невысоких давлениях, которые приближаются к идеальному газу.
Исторические данные
Как точная наука, физика не считается абсолютной без набора довольно весомых констант, которые интегрируются как универсальные коэффициенты в уравнения, устанавливающие связь между какими-либо величинами. Это фундаментальные элементы, благодаря которым многие вещи приобретают неизменность.
Между этими характеристиками, присущими материи Вселенной, существует постоянная Больцмана, значение которой входит в ряд весомых уравнений. Стоить сказать об определённом количестве решений с помощью неизменной.
Законы Ньютона управляют силами, массами и движениями объектов или систем и считаются детерминированными: то есть тот, кто полностью знает начальные условия в системе, может точно предсказать будущее. Именно так космические миссии размещают посадочные модули роботов в определённых желаемых местах в сотнях миллионов километров от Земли.
Для огромного комплекса объектов, таких как миллиарды триллионов горячих молекул, движущихся в паровом двигателе, доминирующей единицей расчёта является постоянная Больцмана, но невозможно определить состояние каждой независимой частицы: они движутся с разными скоростями и энергетическими диапазонами.
Например, молекулы воздуха при комнатной температуре 25 градусов по Цельсию (300 Кельвинов, или 77 гр. по Фаренгейту) движутся со средней скоростью около 500 метров в секунду (1100 миль в час). Но некоторые движутся 223 м/с и 717 м/с и так далее, и все они идут в разных направлениях. Каждое их свойство не может быть известно.
Однако понимание физики тепловых явлений требует некоторого способа сделать математически полезные утверждения о коллекциях огромного числа объектов. Больцман и другие учёные показали, что это можно вычислить с точки зрения статистики и вероятностей механики. Коллективные термодинамические свойства комбинаций вытекают из суммы энергий каждого отдельного объекта. Интересно, что разные значения энергии имеют иные вероятности возникновения. Для вычислений нужно знать, чему равно значение постоянной Больцмана. Вот уравнение: E=32kT
Молекулы и тепловые вещества
Физический смысл постоянной Больцмана и температуры применяется к свойству степени нагрева тела. В физике используется безусловная шкала, основанная на выводе молекулярно-кинетической доктрины в качестве меры, показывающей количество энергии теплового движения частиц.
Данные для вычислений, используемые в системе СГС, считаются очень большими единицами, чтобы выразить энергию молекул, и, таким образом, довольно сложно измерить температуру этим способом. Удобной единицей снятия данных считается градус, и данные фиксируются косвенно, путём регистрации изменяющихся макроскопических показаний вещества.
В однородном безупречном газе при определённой температуре энергия на любом поступательном уровне свободы равна, как следует из определения Максвелла. При комнатной температуре эта энергия равна j или 0,013 эВ. В одноатомном безупречном газе любой атом содержит 3 степени свободы, это соответствует 3 пространственным осям, что фактически означает, что любой атом содержит энергию B. С учётом тепловой энергии можно определить среднее значение квадрата скорости атомов, которое обратно пропорционально корню массы.
Особенности энергии
Для расчёта веществ при температурах и давлениях, ближайших к обычным, применяется совершенная газовая модель, то есть та, величина молекулы которой гораздо меньше занята конкретной численностью веществ, а расстояние между частичками гораздо больше радиуса их взаимодействия. Основываясь на уравнениях кинетической доктрины, средняя энергия этих частиц нацелена как ECP = 3/2 ∙ kT, где E-кинетическая энергия, T-температура, а 3/2 — коэффициент пропорциональности K, введённый Больцманом.
Численность здесь характеризует:
- количество степеней свободы поступательного движения молекулы;
- пространственные измерения.
Смысл k, который позднее был назван в честь Больцмана, демонстрирует, сколько Джоулей на уровне 1. В иных доктринах его смысл определяет, как статистически, в среднем, энергия термического неселективного перемещения 1-го моноатомного безупречного газа возрастает с температурой на 1 градус.
Статистическое рассредотачивание
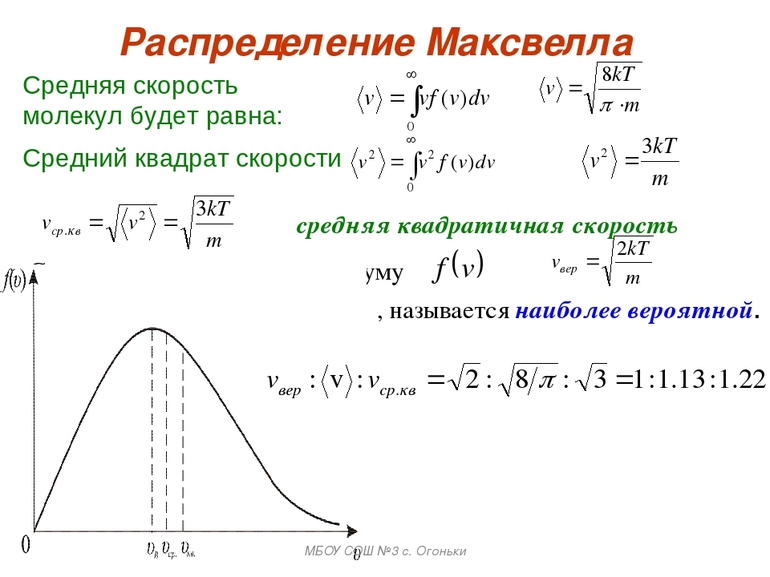
Так как макроскопические состояния материи считаются итогом поведения большого числа частиц, они описываются статистическими способами. Последнее подразумевает выяснение того, как распределяются энергосвойства молекул газа.
Рассредотачивание кинетических скоростей по Максвеллу происходит по-разному. Практически он показывает, что в равновесном газе главное множество молекул содержит части, более близкие к вероятным v = √ (2kT / m0), где m0-масса молекулы.
Определение Больцманом возможных энергий для газов будет пребывать на фоне всякой силы, к примеру, гравитации. Это зависит от пропорции 2-х вещей:
- притяжения к Земле;
- хаотического термического перемещения частиц газа.
В итоге чем меньше возможность энергии молекул (ближе к плоскости планеты), тем выше их сосредоточение.
Оба статистических способа связаны с рассредотачиванием Максвелла-Больцмана, содержащим экспоненциальный коэффициент eE / kT, где E — сумма кинетической и возможной энергий, а kT — средняя сила термического смещения, обусловленная ПБ. Формула постоянной Больцмана — коэффициент, равный k=1,38·10−23 ДжК.
Константа пропорциональности неизменна по Больцману. Это выражение, которое определяет связь между микроскопическим и макроскопическим состояниями, выражает центральную идею статистической механики. Планковское число измерений температуры составляет 1 416 785 (71) • 1032 К, что фактически соответствует энергии массового спокойствия.
Безграничная материя
С точки зрения теории неограниченного погружения материи, ПБ является величиной только 1-го атомного смысла. Как показывает идеальный тест физических единиц измерения значений, при использовании шкалы температуры и тепловой энергии, содержащиеся в единице количества вещества, они считаются неизменными. Отсюда выделяют данные, практически используя температуру как физическое определение на одном уровне. Вещества могут быть пересчитаны по значению неизменной со вступлением надлежащих коэффициентов схожести. Теоретическим критерием этой процедуры считается SPF-симметрия.
Можно получить определение звёздного неба и по теории Планка оно будет простым минусом импульса объектов. Его данные также равны понятию Kps = K ∙ f = 9,187 ∙ 1032 Дж / К, где f — коэффициент однородности массы.
ПБ определяет ассоциация между действенной температурой большого количества обычных звёздных объектов как меру термической энергии и средней кинетической при смещении. Не считая того, что она связывает внутреннюю температуру объектов с имеющейся энергией. Такие константы могут быть рассчитанными для любого значения материи.
В результате ПБ:
- позволяет оценивать кинетическую температуру частиц;
- подчёркивает вероятность нахождения и распределения температуры изнутри самих частиц.
Измерение постоянной Больцмана является одной из ведущих констант. Это не только разрешает установить ассоциацию между линиями микроскопичных явлений молекулярного значения с параметрами процессов, наблюдаемых в макромире. И дело не только в том, что эта величина включена в ряд значимых уравнений.
В настоящем времени непонятно, есть ли какой-нибудь вещественный принцип произведения, на базе которого он имел бы возможность получить вывод на теоретическом уровне. В иных доктринах ничего не рассказывается об этом. На самом деле смысл этой константы может быть практически схожим с другими величинами.
Изменения в фиксации постоянной
В 2017 году мировое сообщество измерений выполнило требования, чтобы дать точное толкование ПБ и переопределить Кельвин. Акустическая термометрия измерялась различными исследовательскими группами, и она использовалась в окончательном определении ПБ для системы СИ, которая была утверждена в ноябре 2018 года. На основании этих данных значение концентрации зависимости KB составляет 1,380649 x 10 -23 Дж к-1.
Хотя Кельвин не был основан на физическом артефакте, его изменение также важно. Более раннее определение размерности было основано на специфических свойствах универсальной постоянной природы. Основываясь на постоянной Стефана Больцмана, Кельвин также используют учёные, применя букву K в вычислениях. Это позволяет измерениям температуры быть действительно универсальными.
Десятичные приставки
|
Наименование |
Обозначение |
Множитель |
Наименование |
Обозначение |
Множитель |
|
мега- |
М |
106 |
санти- |
с |
10-2 |
|
кило- |
к |
103 |
милли- |
м |
10—3 |
|
гекто- |
г |
102 |
микро- |
мк |
10-6 |
Основные физические константы
|
Число π |
π = 3,14 |
|
Ускорение свободного падения на Земле |
g = 10 м/с2 |
|
Гравитационная постоянная |
G = 6,7 ∙ 10-11 Н ∙ м2/кг2 |
|
Универсальная газовая постоянная |
R = 8,31 Дж/(моль ∙ К) |
|
Постоянная Больцмана |
k = 1,38 ∙ 10—23 Дж/К |
|
Постоянная Авогадро |
NА = 6 ∙ 1023 1/моль |
|
Скорость света в вакууме |
с = 3 ∙ 108 м/с |
|
Коэффициент пропорциональности в законе Кулона |
k = 9 ∙ 109 Н ∙ м2/Кл2 |
|
Модуль заряда электрона (элементарный электрический заряд) |
е = 1,6 ∙ 10—19 Кл |
|
Постоянная Планка |
h = 6,6 ∙ 10-34 Дж ∙ с |
Соотношение между различными единицами
|
Температура |
0 К = -273,15° С |
|
Атомная единица массы |
1 а.е.м. = 1,66 ∙ 10—27 кг |
|
1 атомная единица массы эквивалентна |
931,5 МэВ |
|
1 электронвольт |
1 эВ = 1,6 ∙ 10—19 Дж |
Масса частиц
|
Электрона |
9,1 ∙ 10—31 кг ≈ 5,5 ∙ 10—4 а.е.м. |
|
Протона |
1,637 ∙ 10—27 кг ≈ 1,007 а.е.м. |
|
Нейтрона |
1,675 ∙ 10—27 кг ≈ 1,008 а.е.м. |
Нормальные условия
|
Давление |
105 Па |
Температура |
0° С |
Плотность тел
|
Бензин |
710 кг/м3 |
Древесина |
600 кг/м3 |
|
Спирт |
800 кг/ м3 |
Алюминий |
2700 кг/м3 |
|
Масло машинное |
900 кг/м3 |
Сталь |
7800 кг/м3 |
|
Вода морская |
1030 кг/м3 |
Медь |
8900 кг/м3 |
|
Вода |
1000 кг/м3 |
Мрамор |
2700 кг/м3 |
|
Ртуть |
13600 кг/м3 |
Лёд |
900 кг/м3 |
Удельное электрическое сопротивление (Ом ∙ мм2/м)
|
Алюминий 0,028 |
Ртуть 0,96 |
|
Железо 0,10 |
Медь 0,017 |
|
Удельная теплоёмкость |
|
|
Воды 4200 Дж/(кг ∙ град) Льда 2100 Дж/(кг ∙ град) Железа 444 Дж/(кг ∙ град) Меди 380 Дж/(кг ∙ град) |
Олова 230 Дж/(кг ∙ град) Свинца 130 Дж/(кг ∙ град) Стали 460 Дж/(кг ∙ град) |
|
Удельная теплота плавления |
|
|
Свинца 2,5 ∙ 104 Дж/кг Льда 3,3 ∙ 105 Дж/кг |
Стали 82 ∙ 103 Дж/ кг |
|
Удельная теплота парообразования |
|
|
Воды 2,3 ∙ 106 Дж/кг |
Термодинамика и молекулярно-кинетическая теория. Объяснение явлений; интерпретация результатов опытов, представленных в виде таблицы или графиков.
В. З. Шапиро
Одиннадцатое задание ЕГЭ по физике проверяет знания по различным разделам «Термодинамики». Они могут быть ориентированы на качественное понимание темы «Насыщенный пар, влажность воздуха», на умение работать с графиками зависимости термодинамических величин друг от друга (или от времени). Из представленных пяти утверждений нужно выбрать два правильных. Некоторые утверждения требуют расчетов, для других необходимы теоретические рассуждения.
1. В среду и четверг температура воздуха была одинаковой. Парциальное давление водяного пара в атмосфере в четверг было меньше, чем в среду. Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
1) Масса водяных паров, содержащихся в 1 м3 воздуха, в четверг была больше, чем в среду.
2) Относительная влажность воздуха в четверг была меньше, чем в среду.
3) Концентрация молекул водяного пара в воздухе в среду и четверг была одинаковой.
4) Давление насыщенных водяных паров в среду было больше, чем в четверг.
5) Плотность водяных паров, содержащихся в воздухе, в четверг была меньше, чем в среду.
Ответ:
Необходимая теория: Насыщенный пар
Относительная влажность воздуха определяется формулой где
– это парциальное давление водяного пара при определенной температуре, а
– давление насыщенного водяного пара при той же самой температуре. Эта формула также справедлива через отношение плотностей водяного пара и насыщенного пара
Заметим, что согласно этим формулам парциальное давление прямо пропорционально плотности водяного пара. Так как по условию парциальное давление водяного пара в атмосфере в четверг было меньше, чем в среду, то эта закономерность относится и к плотностям. То есть плотность водяного пара в четверг также меньше, чем в среду. В первом утверждении ответ дается через формальное определение плотности и, кроме того, оно сформулировано наоборот, поэтому оно неверное.
2. Достаточно «громоздкие» рассуждения по первому утверждению, помогают выбрать правильные ответы в дальнейшем. Если внимательно еще раз вчитаться в объяснение по первому пункту, то правильность второго утверждения станет очевидной.
3. Все предлагаемые утверждения взаимосвязаны. Если мы выбрали разные относительные влажности в среду и четверг, то концентрация молекул водяного пара не может быть одинаковой. Поэтому это утверждение неверное.
4. Давление насыщенного водяного пара является постоянным для данной температуры. Так как по условию температура постоянна, то и давление насыщенного водяного пара будет постоянным. Это утверждение неверное.
5. Так как относительная влажность зависит от плотности водяных паров, содержащихся в воздухе, то правильность второго утверждения приводит к тому, что и пятое утверждение принимается как верное.
Ответ: 2, 5
Секрет решения. В этой теме важно знать не только формулы для относительной влажности, но и понимать их взаимосвязь с точки зрения физических процессов. Иногда математическая запись этих формул помогает дополнить зависимость одной физической величины от другой, например, парциального давления от плотности водяного пара. Сочетание таких приемов позволит не растеряться и ничего не забыть в ответственный момент. Кроме того, надо быть внимательным к «посторонним» понятиям, например, относительная влажность в среду и четверг, что в какой день больше или меньше. В этом случае необходимо многократное прочтение предложенных утверждений.
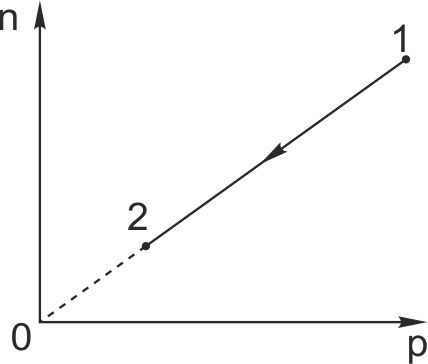
2. При переводе идеального газа из состояния 1 в состояние 2 концентрация молекул n пропорциональна давлению р (см. рисунок). Масса газа в процессе остаётся постоянной.
Из приведённого ниже списка выберите два правильных утверждения, характеризующие процесс 1–2.
1) Абсолютная температура газа уменьшается.
2) Плотность газа остаётся неизменной.
3) Происходит изотермическое расширение газа.
4) Среднеквадратичная скорость теплового движения молекул газа остаётся неизменной.
5) Средняя кинетическая энергия теплового движения молекул газа увеличивается.
Ответ:
- На графике представлена линейная зависимость концентрации от давления. Согласно формуле
это возможно только при постоянстве температуры (постоянная Больцмана также является постоянной величиной). Поэтому данное утверждение неверное.
- Плотность прямо пропорциональна концентрации газа. Изменение концентрации приведет к изменению плотности газа, что противоречит этому утверждению. Поэтому оно неверное.
- Рассуждения, проведенные в первом пункте, применимы и для третьего. Это утверждение верное.
- Так как среднеквадратичная скорость молекул связана с температурой, то постоянство температуры приведет к постоянству этой скорости. Утверждение верное.
- Средняя кинетическая энергия молекул зависит от среднеквадратичной скорости. Правильность четвертого утверждения исключает верность пятого. Утверждение неверное.
Ответ: 3, 4.
Секрет решения. Кроме формулы необходимо знать зависимость среднеквадратичной скорости от температуры
К сожалению, эта формула трудна для запоминания, но ее всегда легко вывести из равенства энергий
Кроме того, с изучения основ физики многократно повторяется следующее утверждение: «чем выше температура, тем больше скорость движения молекул». Сочетание таких подходов приведет к выбору верных утверждений.
3. На pV-диаграмме показаны два процесса, проведённые с одним и тем же количеством газообразного неона. Из приведённого ниже списка выберите два правильных утверждения, характеризующие процессы на графике.
1) В процессе 2 абсолютная температура неона изобарно увеличилась
в 2 раза.
2) В процессе 1 плотность неона увеличилась в 5 раз.
3) В процессе 1 неон изобарно увеличил свой объём в 5 раз.
4) В процессе 2 концентрация молекул неона увеличилась в 2 раза.
5) Работа, совершённая неоном в процессе 1, больше, чем в процессе 2.
Ответ:
Необходимая теория: Изопроцессы
- Согласно графику, в процессе 2 давление не изменяется, следовательно, это изобарный процесс. Рост объема в два раза возможен только при увеличении температуры так же в два раза. На основании закона Гей-Люссака
это утверждение верное.
- В процессе 1 происходит увеличение объема в 5 раз, но это приведет к уменьшению плотности в 5 раз. Поэтому это утверждение неверное.
- Рассуждения по предыдущему пункту приводят к правильности данного утверждения. Единственное добавление – процессы на графике изобарные.
- Так как концентрация молекул обратно пропорциональна объему газа, то это утверждение неверное. Рост объема приведет к уменьшению концентрации молекул газа.
- На графике зависимости давления от объема работа газа выражается через площадь фигуры под графиком. В данной задаче — это площади двух прямоугольников. Площади одинаковые (можно даже посчитать по клеточкам), поэтому работы газа также одинаковые. Утверждение неверное.
Ответ: 1, 3.
Секрет решения. Графики изопроцессов достаточно легки для понимания. Формулы, выражающие изопроцессы, также весьма доступны. Эти подходы взаимно дополняют друг друга. Графические зависимости помогают в проведении правильных рассуждений с позиции теории. Надо обратить внимание, что в подобных задачах не указаны единицы измерения физических величин на графике. В этом нет необходимости, так как идет сравнение изменений в условных единицах, в данной задаче, по числу клеточек. Этот прием часто используется в различных разделах физики.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 11 ЕГЭ по физике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
09.03.2023